Graph-Theoretic Detection of Anomalies in Supply Chains: A PoR-Based Approach Using Laplacian Flow and Sheaf Theory

Abstract

Based on Graph Balancing Theory, this study proposes an anomaly detection algorithm, the Supply Chain Proof of Relation (PoR), applied to enterprise procurement networks formalized as weighted directed graphs. A mathematical framework is constructed by integrating Laplacian flow conservation and the Sheaf topological coherence principle to identify anomalous nodes whose local characteristics deviate significantly from the global features of the supply network. PoR was empirically implemented on a dataset comprising 856 Taiwanese enterprises, successfully detecting 56 entities exhibiting abnormal behavior. Anomaly intensity was visualized through trend plots, revealing nodes with rapidly increasing deviations. To validate the effectiveness of this detection, the study further analyzed the correlation between internal and external performance metrics. The results demonstrate that anomalous nodes exhibit near-zero correlations, in contrast to the significant correlations observed in normal nodes—indicating a disruption of information consistency. This research establishes a graph-theoretic framework for anomaly detection, presents a mathematical model independent of training data, and highlights the linkage between structural deviations and informational distortions. By incorporating Sheaf Theory, the study enhances the analytical depth of topological consistency. Moreover, this work demonstrates the observability of flow conservation violations within a highly complex, non-physical system such as the supply chain. It completes a logical integration of Sheaf Coherence, Graph Balancing, and High-Dimensional Anomaly Projection, and achieves a cross-mapping between Graph Structural Deviations and Statistical Inconsistencies in weighted directed graphs. This contribution advances the field of graph topology-based statistical anomaly detection, opening new avenues for the methodological integration between physical systems and economic networks.

1. Introduction

Graph theory has long provided a solid mathematical foundation for modeling distributed systems and network structures. In systems characterized by multi-node interactions, limited information transmission, and strong structural evolution, graph-theoretic models not only offer structural representations but also serve as the logical core for algorithm design and behavioral analysis [1,2,3,4]. With the increasing demand for the integration of blockchain, supply chains, and enterprise data systems, issues of information transparency and consistency have become critical challenges to supply chain resilience and trust. Most existing approaches struggle to effectively detect information anomalies under conditions where data are unlabeled or abnormal patterns are not clearly defined, making it difficult to respond to potential risks in a timely manner. This necessitates a shift in graph-theoretic applications—from traditional static topology analysis toward integrated frameworks for anomaly detection and transparency evaluation in supply chain networks [5,6,7].

In distributed consensus systems, the Byzantine Generals Problem proposed by Lamport is regarded as a fundamental model for fault-tolerant computation, and its graph-theoretic structure has laid the mathematical foundation for subsequent consensus mechanisms such as Practical Byzantine Fault Tolerance (PBFT) and Proof of Work (PoW) [1]. Building on this foundation, the Supply Chain PoR proposed in this study treats inter-enterprise relationships as a prerequisite for achieving consensus. Unlike traditional models that rely solely on the proportion of node votes, PoR emphasizes whether a node’s behavior remains consistent with its historical actions and the structures of its neighboring nodes. Any significant deviation is treated as a potential anomaly, excluding the node from the consensus process and serving as a basis for anomaly detection.

The supply chain inherently constitutes a complex graph structure characterized by asymmetry, directionality, and weighted relationships. Procurement interactions among enterprises can be abstracted as a dynamic directed acyclic graph (DAG), where nodes represent enterprises, edges represent procurement directions, and edge weights characterize transaction-related features such as margin rates [8,9,10,11,12]. This type of model has been further extended to temporal graphs and stochastic graphs, enabling applications in behavioral prediction and supply chain evolution analysis [13,14]. Graph-theoretic methods have also been widely applied to anomaly detection within supply chains, including graph clustering [15], graph embedding learning [16], and deviation analysis based on structural conservation and topological feature consistency [17].

To address the challenges of information asymmetry and data consistency within the complex network structures of supply chains, Sheaf theory provides a formally rigorous topological framework. Sheaf theory allows the data of local nodes to be modeled as presheaves and establishes global consistency through gluing axioms [18,19,20]. This framework is particularly well-suited for representing systems like supply chains, where nodes cannot modify each other’s data but can interconnect and merge information, thereby serving as a structural reference for anomaly detection [21]. Furthermore, Sheaf theory has been integrated with spectral methods in graph theory to develop the eigenvalue theory of cellular sheaves, offering mathematical tools to trace local deviations and global inconsistencies [22]. This consistency logic can be traced back to the foundational work on fault-tolerant consensus in distributed systems proposed by Lamport [1], and it was preliminarily implemented in our earlier development of the PoR framework [23]. This study selects the supply chain as the application domain due to its inherently asymmetric and structurally complex nature. The hierarchical relationships formed by upstream and downstream supply-demand dependencies among enterprises align well with the modeling requirements of sheaf theory and graph-theoretic consistency analysis. Moreover, anomalies (information distortions) in supply chain often exhibit latent and propagative characteristics, making them difficult to detect using simple rules or static indicators. These properties make the supply chain a particularly suitable context for evaluating graph-based anomaly detection models. Accordingly, this research extends PoR to the supply chain domain to identify potential information distortions among nodes and validate its effectiveness in anomaly detection.

However, existing methods still exhibit significant limitations. First, most anomaly detection approaches are designed based on node attributes or local structural properties, and fail to address the issue of structural deviation across the entire network [16,17]. Second, many models heavily rely on training data or manually labeled anomalies, which is problematic in supply chain environments where abnormal events are inherently rare and heterogeneous, making it difficult for models to generalize or converge [14]. Third, although deep learning methods such as Graph Neural Networks (GNNs) have demonstrated strong performance in recent years, they often suffer from a lack of interpretability, creating barriers to trust and practical adoption [24,25,26]. In light of these limitations, this study proposes PoR as a novel anomaly detection framework that combines interpretability with structural consistency validation. To the best of our knowledge, this study presents the first integration of graph theory and sheaf theory specifically designed to detect information anomalies in the supply chain.

To address the aforementioned challenges, this study aims to establish a mathematically verifiable and interpretable anomaly detection mechanism that can identify potential information distortion and structural inconsistencies within the supply chain, thereby enhancing transparency and systemic coherence. To this end this study proposes a novel mathematical model, the Supply Chain PoR, designed to identify anomalous deviations in inter-enterprise relationships. The framework integrates Laplacian flow theory, Sheaf-theoretic topological consistency analysis, and structural deviation principles within graph theory, establishing an anomaly detection system with mathematically provable foundations. A deviation index, denoted as Δ_N, is introduced to quantify the consistency of each node relative to the overall network structure, enabling the ranking, visualization, and identification of potential anomalous enterprises.

To validate the effectiveness of the Supply Chain PoR, procurement data spanning 27 years (1995–2022) from 856 companies in Taiwan, obtained from the TEJ database, were used to construct a weighted directed graph based on the model assumptions. Through this framework, 56 enterprises exhibiting significantly elevated deviation levels were successfully identified. Cross-validation using internal and external performance data further demonstrated that PoR can consistently detect potential information anomalies, offering high interpretability and reproducibility. Moreover, PoR can be further integrated with neural network models to enhance Artificial Intelligence (AI) detection performance and computational efficiency, making it well-suited for practical deployment in supply chain risk early-warning systems.

The reminder of this paper is organized as follows: Section 2 covers the related works. Section 3 describes the methodologies. Section 4 presents the experimental evaluation and results. Section 5 is the conclusion.

2. Related Work

Graph theory has laid the mathematical foundation for the integration of distributed computation and anomaly detection, enabling the intelligentization of algorithms in practical systems. This chapter synthesizes the academic research most relevant to this study across five interconnected areas: graph-based modeling in distributed systems, anomaly detection methods based on Laplacian theory, topological consistency and Sheaf theory, applications of supply chain graph structures in anomaly identification, and graph-theoretic frameworks underlying PoR mechanism.

2.1. Graph Theory as the Theoretical Foundation for Distributed Algorithms

Graph theory has long served as a core language for modeling and designing algorithms within distributed systems. The Byzantine Generals Problem proposed by Lamport [1] is considered a classic in fault-tolerant computing, where directed graphs are used to represent the transmission of information and the consistency of decision-making among untrustworthy nodes. This foundational model later inspired the development of consensus mechanisms such as PBFT and PoW in blockchain systems, igniting a surge of graph-theoretic applications in distributed and decentralized technologies.

In recent years, research on distributed graph algorithms [4,5] has increasingly emphasized how network topology and communication constraints impact algorithmic convergence and fault tolerance boundaries. As a result, graph theory has evolved from a mere modeling tool to the very logical framework underpinning distributed computation itself. Foundational theories such as Algebraic Graph Theory [11,27], Spectral Graph Theory [12], and Network Science [7] have further enriched the mathematical analysis of graph structures, providing essential tools for the study of distributed systems.

2.2. Applications of Laplacian Flow and Graph Balancing in Anomaly Detection

The Laplacian matrix and graph flow models have been widely applied in recent years for anomaly detection in directed and weighted graphs [6,7]. In stable systems, any imbalance between incoming and outgoing flows indicates potential localized anomalies. In particular, Laplacian flow models for dynamic systems have been developed to trace the sources of deviations from global conservation laws [8,28]. Eigenvalue analysis of the graph Laplacian is widely utilized in community detection and clustering [29], and in structural investigations of networks for the identification of anomalous behavior [30].

Moreover, advances in Discrete Graph Signal Processing [6] and Spectral Network Analysis [17,24] have proposed methods for identifying anomalous nodes based on eigenvalue perturbations, complementing the structural deviation logic employed in PoR. These conservation-based detection methods emphasize violations of structural balance as key indicators of anomalies, providing mathematically provable and training-data-independent models for robust anomaly detection.

2.3. Sheaf Theory and Topological Consistency Models

Topological consistency has been formally and comprehensively modeled through Sheaf theory, which is particularly suited for applications involving the integration of local data into a coherent global structure [20,21,22]. The core of Sheaf theory lies in constructing presheaves and enforcing gluing axioms to ensure that information within local regions remains consistent and can be seamlessly assembled into global functions across a topological space [25,26].

In recent years, Sheaf-based data models [24,25] have been widely applied to sensor networks, knowledge graphs, and data correction fields, and have further extended into applications such as anomaly detection and calibration in power grids [30]. In the context of this study, Sheaf theory provides the mathematical foundation for modeling the functional consistency between local procurement information features (W_N) and the global supply chain performance features (W_SC). Specifically, its non-mutability principle—wherein W_N data cannot be arbitrarily altered by neighboring nodes but can be consistently merged—forms the theoretical basis for PoR, enabling the identification of abnormal behavior through the analysis of historical relational structures.

2.4. Supply Chains as Complex Directed Graph Models

The many-to-many procurement relationships within supply chains naturally form dynamic, weighted, directed graphs. Recent studies have formalized these structures as hierarchical DAG models [13,14], where nodes represent enterprises, edges represent the direction and edge weights characterize transaction-related features such as margin rates, highlighting the hierarchical and asymmetric nature of supply chain networks. These structures have been further modeled as temporal graphs [13], stochastic graphs [14], and DAG-optimized networks [3], enabling dynamic tracking of transaction patterns and behavioral deviations.

Moreover, the application of graph-theoretic methods such as graph clustering [15], graph embedding learning [16], and topological feature extraction combined with balance-conservation models [17,28] has rapidly expanded in the domain of supply chain anomaly detection. Brandes and Erlebach [17] emphasized that supply chain networks often exhibit structural biases and community-level anomalies, and that graph theory provides effective tools for identifying such irregularities.

2.5. PoR and Proof Algorithms in Graph Structures

PoR extends the spirit of Byzantine-style consensus frameworks [1,23], emphasizing the identification of anomalous nodes through deviations observed in graph structures before proceeding with consensus operations. Unlike anomaly detection methods that primarily rely on machine learning, PoR is founded on mathematically provable structural deviation conditions, ensuring both the transparency and rigor of its decision-making process.

The authors of [23] pointed out that in certain specific graph topologies, even when the theoretical condition n > 3m (where n is the total number of nodes and m is the maximum number of tolerated faulty nodes) is satisfied, the system may still fail to reach consensus due to asymmetric decision information and asynchronous communication. The study further proposed PoR consensus mechanism, which uses relationship deviations as a prerequisite for decision-making, thereby overcoming the limitations of traditional PoW or PBFT models that rely solely on the majority behavior of nodes.

The logical structure of PoR can be divided into three core steps:

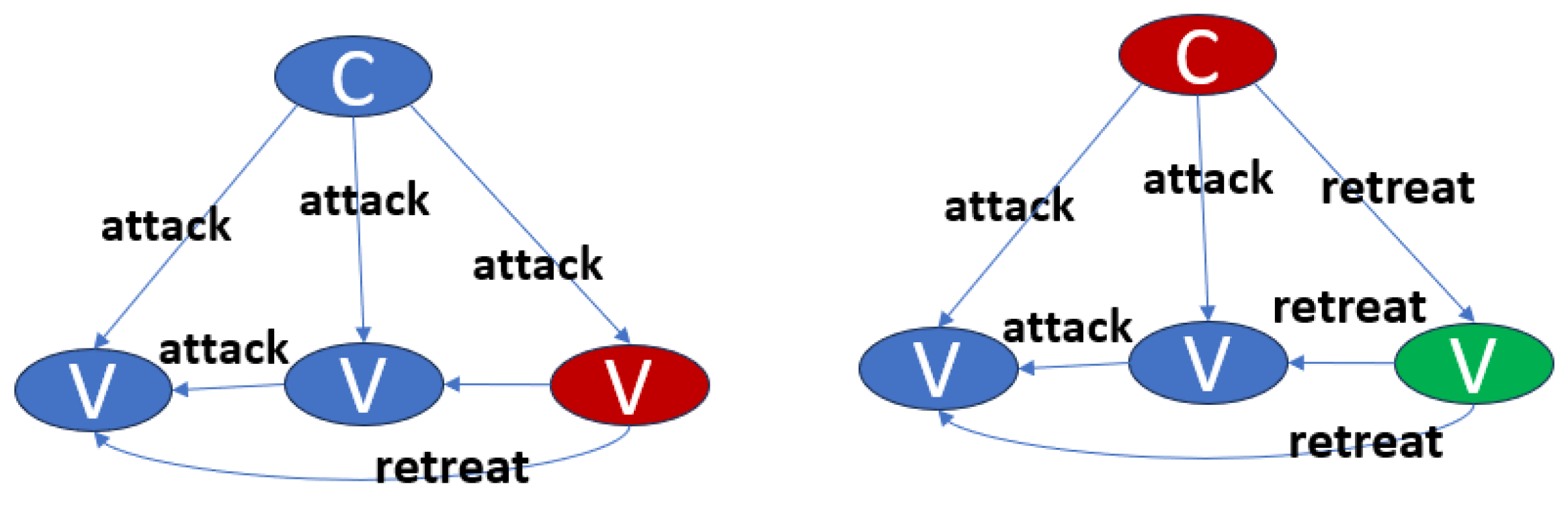
• Extract stable decision-making patterns from the historical records of nodes;
• Perform deviation analysis on current observed behaviors to determine whether they significantly violate past patterns;
• Use only non-deviating nodes to conduct subsequent consensus voting and state synchronization operations.

This design enables PoR to maintain robust decision-making consistency even when facing selective error propagation. In graph-theoretic terms, the model essentially constructs a virtual “consensus closure” subset within a partially disconnected topology by enforcing behavioral consistency, thereby forming a convergent evolutionary rule [25,30].

Building upon the framework proposed by [23], this study establishes the Supply Chain PoR, using structural deviation (Deviation from Balanced Graph) as the basis for anomaly detection and integrating it with Laplacian flow and Sheaf theory [24,25,30] to develop a mathematically provable anomaly identification system. Recent studies have also focused on flow-constrained anomaly detection [31] and topological consistency labeling in economic networks [32], which are closely related to the direction of this research.

2.6. Issues of Supply Chain Transparency and Trust

The supply chain plays a central role in economic activity and comprises countless enterprises. To meet customer demands, enterprises frequently engage in mutual procurement, and in the delivery of goods and services, forming highly complex and dynamic networks in which errors and conflicts are virtually unavoidable [33] and supply chain efficiency will be impaired. For instance, a firm may accept a customer order with deferred payment terms. However, the customer fails to fulfill the payment obligation and causes the supplier suffering financial losses and terminates future dealings with that customer. Nevertheless, the same customer may repeat the behavior with other suppliers. Affected firms may become more cautious in processing subsequent orders, leading to prolonged procurement cycles and reduced overall supply chain performance.

The authors of [23] proposed PoR to detect and isolate malicious behavior by analyzing historical records in distributed networks. Therefore, this study argues that malicious behaviors—such as receiving goods without fulfilling payment obligations— exhibits identifiable patterns. Based on PoR, this study argues that by analyzing historical transactional records, it is possible to detect information distortion and isolate these malicious entities to enhance overall supply chain transparency, trust, and operational stability.

3. Methodology: Graph-Based Modeling and PoR

3.1. Detection-Oriented Topological Modeling

The authoritative algorithm of the current blockchain consensus mechanism in cryptocurrencies, known as PoW, can be traced back to the Byzantine Generals Problem proposed by Lamport [1]. The core of this problem lies in exploring how a distributed system can achieve consistent decision-making under the premise that some nodes are untrustworthy. Lamport’s model employs a directed map from graph theory to describe decision-making nodes and communication edges (as illustrated in Figure 1), and mathematically proves that when the condition n > 3m is satisfied—where n denotes the total number of nodes and m the number of malicious nodes—fault-tolerant consensus can be achieved through a “Commander-Lieutenant” model (In Figure 1, nodes representing commanders are labeled as C, while nodes representing lieutenants are labeled as V. Red-circled nodes indicate traitors, which can be either C or V. Green-circled nodes represent loyal lieutenants (V) who have received incorrect messages sent by a traitorous commander (C)).

Building upon this model, ref. [23] further demonstrated, using graph-theoretic approaches, that in certain topological structures, consensus may still fail even if the condition n > 3m is satisfied (As illustrated in Figure 2, nodes representing commanders are labeled as C, while nodes representing lieutenants are labeled as L. Reference [23] replaces V with L to emphasize that the content is not identical to that of [1]. The commander node marked with a red circle represents a traitor. The lieutenant nodes marked with green circles are loyal, but have received incorrect messages sent by the traitorous commander C). To address this issue, a new consensus model called PoR was proposed. The core logic of the PoR consensus mechanism is as follows:

• Extract stable decision-making patterns from the historical records of nodes;
• Perform deviation analysis on current observed behaviors to determine whether they significantly violate past patterns;
• Use only non-deviating nodes to conduct subsequent consensus voting and state synchronization operations.

PoR emphasizes “identifying anomalies through relational patterns” as a prerequisite for the majority-voting process, thereby providing greater flexibility and enhanced resilience against potential protocol-level attacks.

This study extends the concept of PoR to supply chain systems, aiming to identify and exclude potential “malicious distortion behaviors” embedded within procurement transaction records, thereby maintaining the overall credibility and stability of supply chain information. To achieve this, the Supply Chain PoR algorithm is designed with the following steps:

• Construct the graph-theoretic structure of the overall supply chain procurement relationships along with the corresponding global feature functions;
• Estimate the degree to which individual enterprises deviate from the global features based on Graph Balancing and Laplacian Flow principles;
• Transform the degree of deviation into an “anomaly metric”, which is then used to determine whether a node exhibits potential data manipulation behavior.

The theoretical foundation of PoR can be traced back to the principles of Conservation Laws in physics and applied mathematics, as well as the concept of Graph Flow Balancing. It posits that in a stable supply chain structure, the profit margin characteristics resulting from transaction flows should exhibit global consistency; any significant deviation at the individual level may indicate potential anomalies.

The supply chain, by nature, constitutes a dynamic and highly decentralized many-to-many network system, characterized by complex connectivity and asymmetric information interactions, making it an ideal high-level structure to challenge and extend existing graph-theoretic models.

This study adopts a directed weighted graph as the mathematical modeling basis, where enterprises are represented as nodes, procurement directions as edges, and margin rates of transactions as edge weights. Furthermore, it introduces the global-local consistency framework from topological theory (Sheaf Consistency), enabling a verifiable structural relationship between the procurement information W_N recorded by individual enterprises and the overall supply chain performance W_SC. This establishes a mathematically provable foundation for anomaly detection.

To illustrate the graph-theoretic modeling structure adopted in this study, Figure 3 depicts a supply chain network composed of 12 enterprises (A~L), which is formalized as a directed weighted graph G = (V, E, W), where:

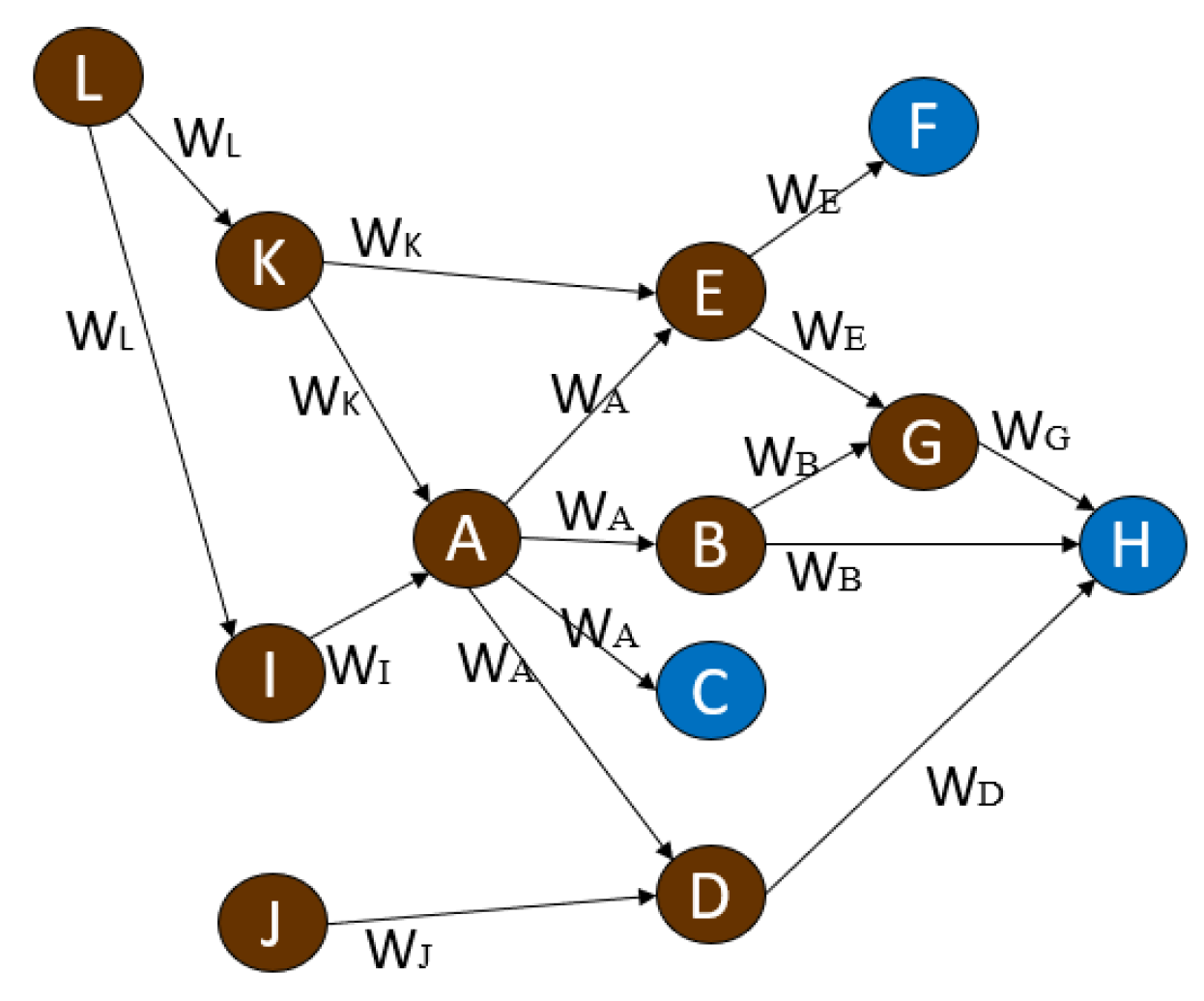
• V = {A, B, …, L} denotes the set of enterprise nodes;
  E⊆ V × V represents the set of directed edges, indicating the direction of procurements;
• The weight function W: E→R⁺ assigns to each edge the corresponding profit margin applicable to the transaction amount;
• Specific nodes C, F, H ∈ V represent terminal retailers, which are highlighted as blue nodes in the graph.

In Figure 3, each node is represented by a circle labeled with an English letter, denoting an enterprise. Each directed edge corresponds to a procurement transaction, with the direction pointing from the supplier to the buyer. Blue circles indicate terminal retailers. The symbol W_N represents the profit margin feature generated by the transaction flow. This structure reflects the practical flow of transactions wherein upstream enterprises supply products or services to downstream enterprises. Through this graph-theoretic formalization, the supply chain structure is concretized as a mathematical object, thereby enabling the establishment of subsequent conservation conditions and anomaly detection models.

Additionally, the directed graph G depicted in Figure 3 exhibits both a well-defined topological structure and hierarchical characteristics. From a topological perspective, it can be regarded as a type of layered DAG, representing the unidirectional flow of information and goods from upstream suppliers to downstream retailers. This structure possesses the following mathematical properties:

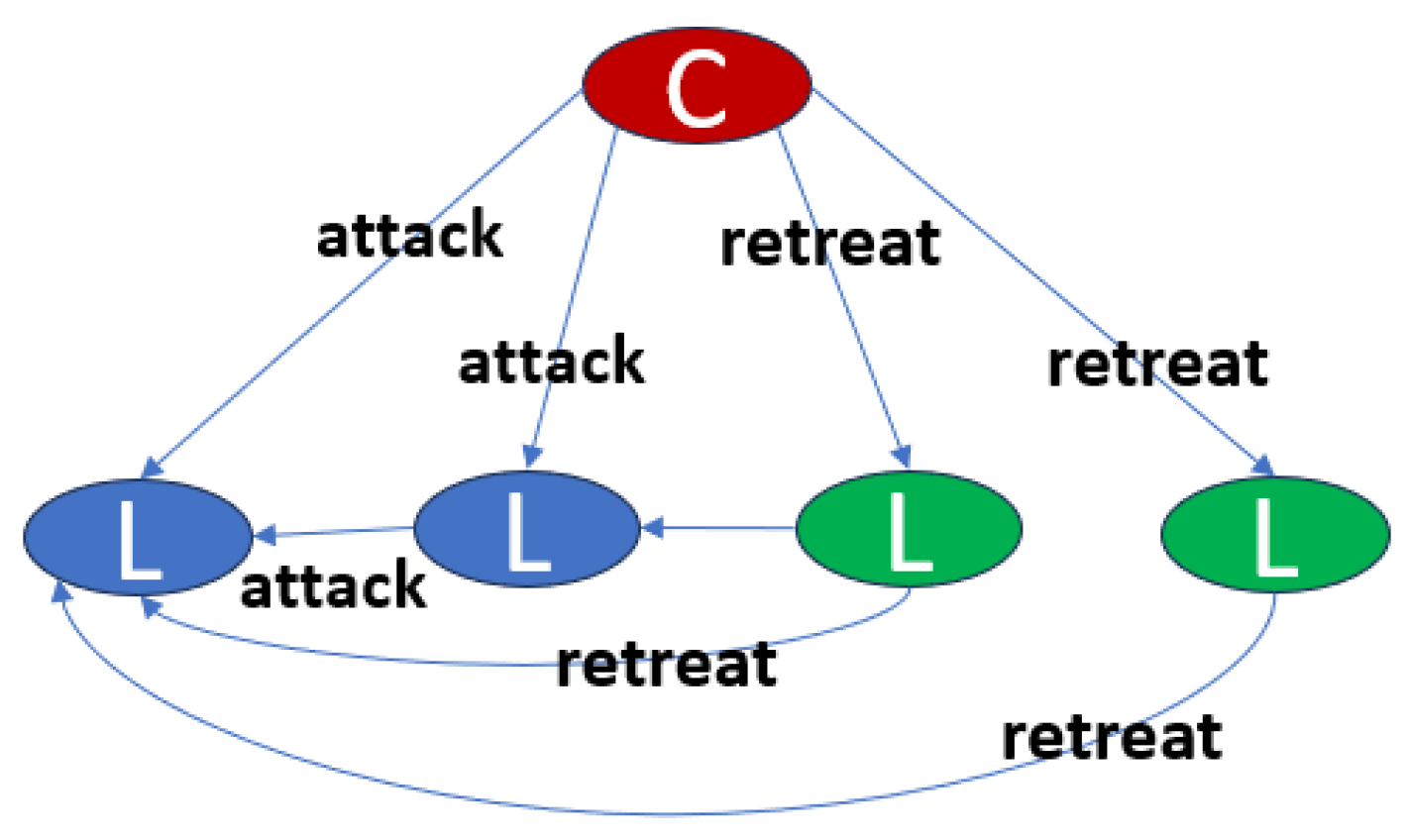
• Local Closedness: Each node v_N ∈ V can only receive information from its upstream adjacent nodes (in-degree), and its outgoing edges (out-degree) represent its supply to downstream nodes. This complies with the Sheaf-theoretic principle that local data functions cannot be arbitrarily modified across nodes;
• Global Consistency and Traceability: Through the combination of directed edges, any retail node v_N ∈ {C, F, H} has at least one directed path that can be traced back to its upstream suppliers, ensuring the weak connectivity of the overall graph. This property guarantees that the global profit function W_SC can be coherently assembled from local functions W_N;
• Topological Conservation Mapping: In this study, the local feature W_N at each node and the edge weight w(e_Nj) are constrained by a form of conservation condition (e.g., margin rate conservation), which can be mathematically characterized as a weighted Laplacian structure over the flow network. Violations of this balance form the basis for anomaly detection.

3.2. Mathematical Formulation Based on Laplacian Flow and Conservation Laws

This section formalizes the development of a graph-theoretic model based on Laplacian Flow and Conservation Laws, grounded in the topology of the weighted directed graph illustrated in Figure 3. By integrating local deviation measurements with global structural consistency, we establish the mathematical framework for the Supply Chain PoR algorithm. The model aims to provide a rigorous theoretical foundation for identifying anomalous behaviors arising from distorted procurement information within supply chains and to extend the application potential of graph theory in the domains of information integrity and anomaly detection. To formally define the procurement information structure analyzed in this study, consider a supply chain system composed of N nodes (enterprises), denoted as the set:

S = {(A, P_A), (B, P_B), (C, P_C), (D, P_D), (E, P_E), (F, P_F), (G, P_G), (H, P_H), (I, P_I), (J, P_J), (K, P_K), (L, P_L)}

(1)

In Equation (1), each pair (N, P_N) represents the enterprise N and its recorded and published set of procurement information P_N, where:

P_N ⊆ {(N→Y, w_NY) ∣ Y ∈ S, w_NY ∈ R⁺ ≥ 0}

(2)

Equation (2) represents the procurement actions performed by enterprise N toward other nodes Y, where w_NY denotes the profit margin implied in the corresponding procurement transaction. This margin serves as the core analytical variable of this study and is indicated as the edge weight in Figure 3. For the procurement information set P_N defined in Equation (2), since the performance of enterprise N derives from fulfilling the procurement demands issued by its downstream customers, each supply relationship (N→Y, w_NY) can be interpreted as carrying a dual meaning of both “procurement demand” and “performance contribution,” that is:

Performance_N^UpStream = Procurement_Y^DownStream

(3)

Equation (3) illustrates that the upstream supply performance of an enterprise can be equivalently interpreted as the procurement demand from its downstream customers. When a downstream customer further acts as a supplier to other enterprises, this causal chain propagates throughout the entire supply chain, layer by layer, forming a performance propagation chain across the network of nodes. Building upon this foundation, the present study proposes the following hypothesis: if every node within the supply chain system truthfully records the margin rates w_NY associated with their transactions with upstream and downstream partners, then the edge weights across the graph should satisfy a set of invertible and conserved structural conditions, thereby forming a stable Laplacian flow field.

However, if a particular enterprise deliberately distorts its recorded information, even though the transaction directions and node structures remain unchanged, the corresponding edge weights w_NY will deviate from the global flow field, resulting in the violation of local conservation properties. Such deviations are defined as “anomaly measures” within the PoR framework and serve as critical indicators for detecting anomalous behavior. In other words, the graph-theoretic model constructed under the Supply Chain PoR approach possesses the following characteristics:

• Each node has a local function P_N representing its recorded procurement margin rates;
• The global supply chain margin profile can be represented as a Laplacian structure integrated from the collection of P_N functions;
• When certain P_N significantly deviate from the structure, they can be identified as potential anomaly sources through PoR;
• This structure satisfies topological consistency and allows for the derivation of formal anomaly deviation indices and mathematical proofs (to be elaborated in the next subsection).

First, to formally characterize the local margin features of individual nodes (enterprises) within the supply chain, this study defines the following recursive weighted function model for a given node A:

P_A = w₅*P_E(w₆*P_F + w₇*P_G(w₈*P_H)) + w₂*P_B(w₇*P_G(w₈*P_H) + w₈*P_H) + w₃*P_C + w₄*P_D(w₈*P_H)

(4)

Here, P_A denotes the performance information disclosed by node (enterprise) A; it is derived from the transformation of the profit margins and performance metrics of its downstream nodes, including information from nodes such as P_E, P_B, P_C, and P_D, and further propagated weighted information from downstream nodes such as P_F, P_G, and P_H. Each coefficient w_N ∈ R⁺ represents the “profit transmission coefficient” between enterprises, corresponding to the edge weights in the graph-theoretic model. By way of a concrete example: if enterprise E purchases from A with a transaction amount of NT$500, and subsequently resells it to F after processing for NT$1000, then:

• The performance of enterprise E is P_E = 1000;
• The performance of enterprise A is P_A = 500;
• Therefore, the profit transmission ratio between A and E is w₅ = 500 / 1000 = 0.5.

In other words, the performance of A can be expressed by the following equation:

P_A = w₅*P_E = 0.5*1000 = 500

(5)

This result embodies the concept of information flow propagating along the edges of a weighted directed graph within the supply chain. Accordingly, each procurement relationship (N→Y, w_NY) in this study carries dual significance: first, as a record of the transactional behavior; and second, as the transmission and propagation of supply chain performance information between nodes. This result highlights the structural logic whereby information flows are derived and aggregated along the edges of the weighted directed graph, thus establishing the mathematical foundation for subsequent anomaly detection modeling. Furthermore, when enterprise E truthfully discloses its performance information as P_E = 1000 and enterprise A’s actual attributable performance is P_A = 500, the corresponding edge weight w₅ should be:

w₅ = 500/1000 = 0.5

(6)

However, if enterprise A inflates its reported performance to P_A = 700 in order to exaggerate its results, then the edge weight derived from that link in the system would become:

w₅′ = 700/1000 = 0.7

(7)

This deviation value (Δw₅ = w₅′ − w₅ = 0.2) constitutes one of the “deviation indicators” as defined in PoR framework, and serves as a basis for identifying anomalies in information disclosure and violations of corporate integrity. Through systematic measurement and analysis of such deviations, a graph-theoretic model for detecting anomalous behavior can be constructed, forming the core logic of the Supply Chain PoR developed in this study.

Before deriving the overall supply chain feature vector W_SC, this study first establishes the gross margin functions for each enterprise node by following the node directions along the topological structure of the graph and basing the modeling on actual procurement relationships, thereby concretely formalizing the edge weight structure of the entire system. According to the preceding definitions, each procurement action’s performance value can be regarded as the corresponding procurement amount—namely, the supplier’s performance is represented by the procurement made by its downstream customer. For instance, the procurement amount that enterprise F spends on E constitutes E’s performance; likewise, E’s procurement from upstream enterprise A forms A’s performance. This causal chain propagates backward along the supply chain nodes, forming a set of interdependent recursive relationships.

As an example, in Equation (4), P_E(w₆*P_F + w₇*P_G(w₈*P_H)) indicates that enterprise E simultaneously supplies products to F and G, where G further supplies to H. Thus, E’s performance is a weighted combination of multi-tier transaction relationships. The subsequent Equations (8)–(18) are derived following the same principle, systematically developing recursive expressions for the local performance at each node within the supply chain network, thereby laying the foundation for the subsequent global graph-theoretic feature analysis.

P_B = w₇*P_G(w₈*P_H) + w₈*P_H

(8)

P_C = P_C

(9)

P_D = w₈*P_H

(10)

P_E = w₆*P_F + w₇*P_G(w₈*P_H)

(11)

P_F = P_F

(12)

P_G = w₈*P_H

(13)

P_H = P_H

(14)

P_I = w₁*P_A(w₅*P_E(w₆*P_F + w₇*P_G(w₈*P_H))) + w₂*P_B(w₇*P_G(w₈*P_H) + w₈*P_H) + w₃*P_C + w₄*P_D(w₈*P_H)),

(15)

P_J = w₄*P_D(w₈*P_H)

(16)

P_K = w₁*P_A(w₅*P_E(w₆*P_F + w₇*P_G(w₈*P_H))) + w₂*P_B(w₇*P_G(w₈*P_H) + w₈*P_H) + w₃*P_C + w₄*P_D(w₈*P_H)) + w₅*P_E(w₆*P_F + w₇*P_G(w₈*P_H))

(17)

P_L = w₁₁*P_K(w₁*P_A(w₅*P_E(w₆*P_F + w₇*P_G(w₈*P_H))) + w₂*P_B(w₇*P_G(w₈*P_H) + w₈*P_H) + w₃*P_C + w₄*P_D(w₈*P_H)) + w₅*P_E(w₆*P_F + w₇*P_G(w₈*P_H))) + w₉*P_I(w₄*P_D(w₈*P_H))

(18)

Based on the node-level recursive relationships established in Equations (8)–(18), this study further formalizes the definition of the “Supply Chain Global Feature Vector” (W_SC) as the following mathematical model, representing the global distribution of gross margin information across the entire supply network. This vector integrates the local performance functions of all nodes and, through the weighted directed edge relationships in the graph structure, reflects the topological characteristics of information flow, transaction patterns, and performance contribution throughout the entire system.

W_SC = {w^A, w^B, w^C, w^D, w^E, w^F, w^G, w^H, w^I, w^J, w^K, w^L}

(19)

w^A = {w₁^A, w₂^A, w₃^A, w₄^A, w₅^A}

(20)

As previously described, in Equation (20), enterprise E is a downstream customer procuring materials from A, such that the disclosed performance information P_A of A directly depends on the performance information P_E of E, with their relationship weighted by w₅. Similarly, enterprises B, C, and D are also downstream customers of A, corresponding to weights w₂, w₃, and w₄, respectively. Therefore, the disclosed performance features of A can be regarded as the function defined by Equation (20): w^A = {w₁^A, w₂^A, w₃^A, w₄^A, w₅^A}.

Here, w₁ represents the relationship between the total amount of purchases made by downstream companies from A and the total amount of A’s procurement from its upstream suppliers (i.e., the average gross margin rate). w₁ thus serves as A’s equilibrium point under the “gross margin conservation” condition within the overall supply chain. The components w₁, w₂, w₃, w₄, and w₅ in Equation (20) constitute the performance feature vector disclosed by A. If A exaggerates or distorts its performance information, these w_i^A values would exhibit inconsistencies compared to the performance feature vectors disclosed by other enterprises. Accordingly, this study explicitly annotates the superscript ^A to indicate that the performance feature vector pertains to information disclosed by enterprise A. In subsequent Equations (21)–(31), the mathematical representations are similarly annotated to ensure traceability of information sources and to maintain consistency in the logic for anomaly detection and analysis.

w^B = {w₂^B, w₇^B, w₈^B}

(21)

w^C = {w₃^C}

(22)

w^D = {w₄^D, w₈^D}

(23)

w^E = {w₅^E, w₆^E, w₇^E}

(24)

w^F = {w₆^F}

(25)

w^G = {w₇^G, w₈^G}

(26)

w^H = {w₈^H}

(27)

w^I = {w₉^I, w₁^I}

(28)

w^J = {w₁₀^J, w₄^J}

(29)

w^K = {w₁₁^K, w₁^K, w₅^K}

(30)

w^L = {w₁₂^L, w₁₁^L, w₉^L}

(31)

3.3. Mathematical Proof of Anomaly Detection via PoR

Building upon the structure of the preceding model, this section mathematically demonstrates how the Supply Chain PoR algorithm can effectively identify anomalous disclosures when malicious nodes (e.g., enterprise A) exist within the supply chain. Given that the Supply Chain PoR developed in this study exhibits Sheaf-like properties of non-overlapping local data assignments, each enterprise is only able to disclose its own transaction information and cannot modify transaction data disclosed by other nodes. In other words, the performance feature vector w_i^N defined by each node is solely controlled by the node itself and cannot be altered by others. Therefore, if enterprise A deliberately exaggerates its disclosed performance information, w_i^A will deviate from the performance feature vectors w_i^N disclosed by its trading counterparts (such as B, C, D, E, etc.). Under these conditions, and based on the previously defined global supply chain feature vector W_SC, PoR treats the global feature as a “stable reference for supply chain performance” to measure the degree of deviation between enterprise A’s local feature w_i^A and the information disclosed by its neighboring nodes {w_i^N}_N≠A.

When the information disclosed by enterprise A fails to establish a consistent edge weight function relationship with other nodes within its supply chain network, the deviation indicators calculated by PoR will exhibit abnormal increases, thereby enabling the identification of malicious information distortion. This forms the core discrimination logic of the Supply Chain PoR proposed in this study. Based on the mathematical models and variable definitions presented above, the execution results of the Supply Chain PoR are outlined as follows:

PoR_SC(A) = {{w₁^K = w₁^I ≠ w₁^A}, {w₂^B ≠ w₂^A}, {w₃^C ≠ w₃^A}, {w₄^J = w₄^D ≠ w₄^A}, {w₅^K = w₅^E ≠ w₅^A}}

(32)

In the relational expression shown in Equation (32), if enterprise A has not manipulated its procurement transaction information, the disclosed performance feature vector w₁^A should be consistent with the corresponding features w₁^K and w₁^I observed or computed by other nodes (such as K and I), thereby satisfying the consistency condition: w₁^K = w₁^I = w₁^A. However, if enterprise A engages in information exaggeration or distortion, its disclosed w₁^A will deviate from the values computed by neighboring nodes, resulting in inconsistency, namely: w₁^K = w₁^I ≠ w₁^A. This inequality forms the basis of the PoR deviation indicator, revealing a structural inconsistency between node A and its adjacent nodes. The expansion of Equation (32) to further quantify the degree of deviation is presented as follows:

w₁^A ≠ {w₁^K, w₁^I},

(33)

w₂^A ≠ {w₂^B},

(34)

w₃^A ≠ {w₃^C},

(35)

w₄^A ≠ {w₄^J, w₄^D},

(36)

w₅^A ≠ {w₅^K, w₅^E},

(37)

In the weighted directed graph model constructed in this study, the overall supply chain is formalized as a graph G = (V, E, W), where enterprises are represented as nodes V, procurement activities as directed edges E, and the margin rates implied by transaction amounts as edge weights W.

According to the principle of conservation in graph balancing, the inflow and outflow at each node should theoretically be equal. Applying this concept to procurement activities between upstream and downstream enterprises in the supply chain, each enterprise should satisfy a consistent and balanced mathematical structure in its performance feature vector, such that the supply performance to downstream customers and the procurement from upstream suppliers are coherent when aggregated. Accordingly, the performance feature vector w_i^A of enterprise A (i.e., the margin rates implied by its supply performance) should be jointly determined by the procurement transactions from all its downstream enterprises (such as B, C, D, and E). Mathematically, this means that the relations defined in Equations (33)–(37) should hold as equalities. However, if enterprise A maliciously alters its disclosed performance information—thus changing the implied margin rates—these equalities will no longer hold, and inequalities will arise, as illustrated in Equations (5)–(7). Thus, a deviation function Δ_A is defined to measure the discrepancy between the information disclosed by enterprise A and the theoretical values derived from the graph structure. When Δ_A significantly deviates from the group (i.e., the distance from the group is too large), enterprise A can be regarded as deviating from the overall supply chain performance feature vector, suggesting potential anomalous behavior. It is worth noting that the Laplacian flow properties in graph theory further reinforce the mathematical validity of the proposed model: if the overall graph is balanced, any significant deviation by a node will disrupt the topological equilibrium and can thus be identified as a source of anomaly.

In summary, based on the above theories, this study establishes the Supply Chain PoR algorithm, whose core lies in using a graph-theoretic deviation detection model to quantify whether a node (enterprise) deviates from its expected role within the overall network. The following sections will detail the specific computational processes and algorithmic structure of PoR.

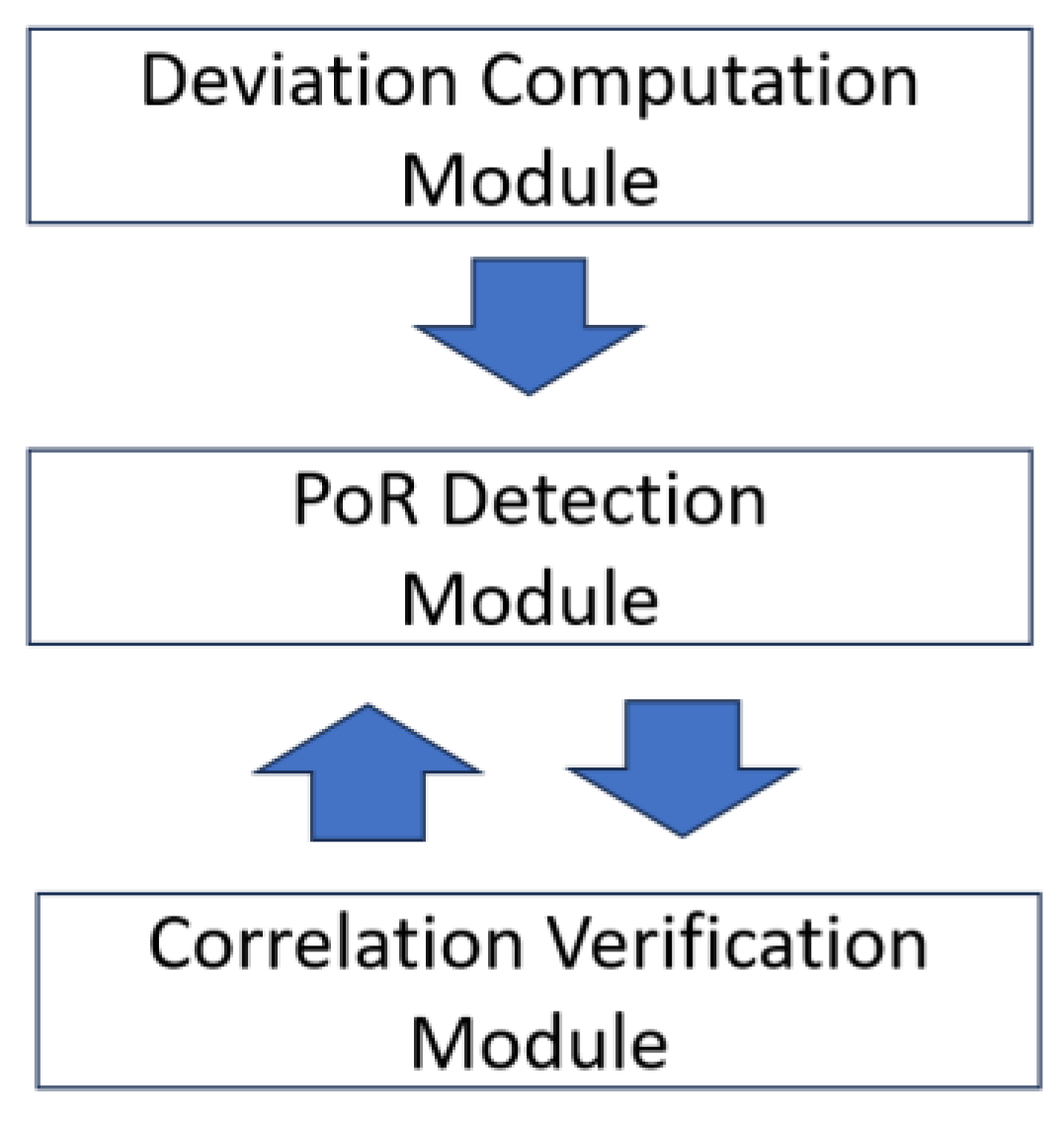
3.4. System Architecture

The system architecture of the proposed Supply Chain PoR algorithm is illustrated in Figure 4. The overall framework consists of three major modules:

• Deviation Computation Module;
• PoR Detection Module;
• Correlation Verification Module.

The system architecture is constructed in a bottom-up manner: it uses the Deviation Computation Module as the foundation for data processing, relies on graph-theoretic deviation as the basis for anomaly detection, presents detection results through ranking and visualization, and incorporates an independent verification mechanism to ensure the model’s usability and interpretability. This design achieves a balance of mathematical rigor, model transparency, and application scalability, making it broadly applicable to high-dimensional anomaly monitoring scenarios such as supply chain and information security.

3.4.1. Deviation Computation Module

This module is responsible for constructing deviation indicators for each supply chain node relative to the overall performance features. The specific process is as follows:

• Normalization: Each node v_N’s procurement data (u_i^N) is normalized by its total assets, i.e., u_i^N = u_i^N / Total Assets^N, to eliminate the influence of firm size differences;
• Percentile Mapping: For each procurement variable (u_i), the data across companies and years are ranked and transformed into percentile values;
• Cross-Year Variability Estimation: For each enterprise, the variability (standard deviation) of each procurement variable across years is calculated, and the average deviation across all variables is computed to derive a preliminary anomaly indicator Δ_N;
• Output of the Deviation Feature Set I = {Δ_N}: Finally, a multidimensional feature space is generated as the input for the subsequent PoR Detection Module.

3.4.2. PoR Detection Module

• The deviation indicators I = {Δ_N} produced by the previous module are derived based on the following concepts:
  • Graph-Level Aggregate Benchmark: All enterprises’ deviation indicators are statistically aggregated to construct a “global supply chain performance feature vector” W_SC, serving as the theoretical benchmark;
  • Deviation Magnitude Evaluation: The distance between each enterprise’s feature vector w^N and W_SC is computed, resulting in a new deviation measure δ^N=∥w^N − W_SC∥, which serves as the anomaly intensity indicator used for PoR detection.
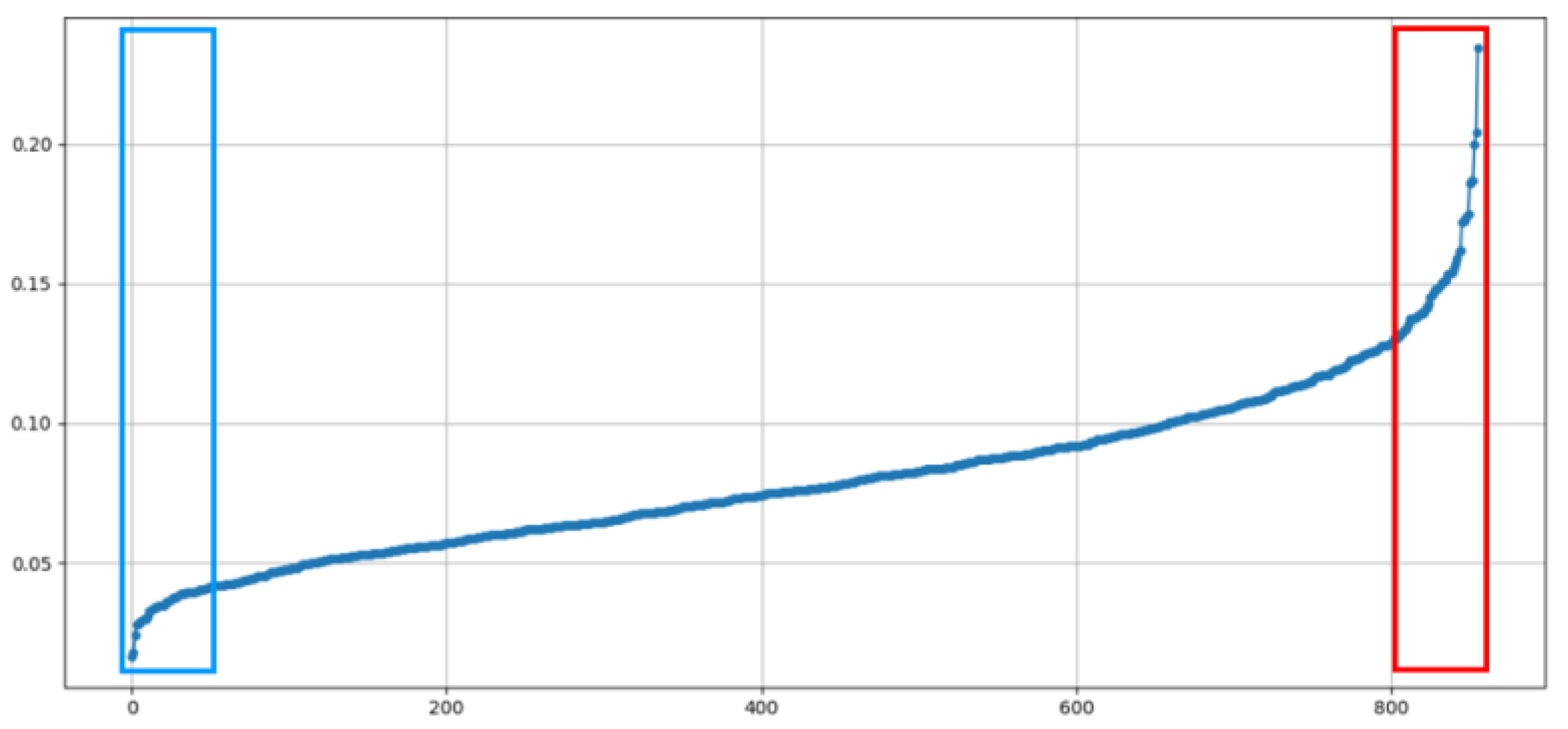
• Anomaly Ranking and Visualization: This module utilizes the deviation indicators I (δ^N) to rank the nodes based on graph-theoretic logic and presents the results through trend charts, assisting in the identification of enterprise nodes exhibiting significant deviation characteristics.

3.4.3. Correlation Verification Module

The pseudo-code for the deviation computation module is given in Algorithm 1.

Algorithm 1: The algorithm of deviation

1. Import S: A multidimensional array containing all procurement data from all sample companies across all years. 2. For each procurement metric u in S: 3.  Normalize u by total assets:    u ← u/total_assets 4. For each year y in S: 5.  For each procurement metric u in year y: 6.    Sort all values of u across sample companies in ascending order; 7.    For each value m in u: 8.     Compute the percentile rank of m within the sorted array;       m ← percentile_rank(m) 9. For each sample company c in S: 10.  For each procurement metric u: 11.    Append a new column std_u ← standard deviation of u across all years; 12. Define I as the multidimensional array composed of all procurement metrics and their standard deviations for all sample companies; 13. For each sample company c in I: 14.  Append a new column indicator ← mean of all std_u values for company c; 15. Export I.

The above algorithm of deviation can be subdivided into three logical processing stages:

• Enterprise Size Normalization (Steps 2–3): In this stage, all procurement figures for each sample company and each year are normalized by dividing by the company’s total assets, thereby converting the data into dimensionless relative proportions. This step eliminates statistical biases caused by differences in enterprise size and constitutes normalization for the original feature matrix;
• Global Performance Feature Shaping (Steps 4–8): After normalization, the ratio values of the same variable across companies for each year are ranked, and the original values are converted into percentile scores. The purpose of this operation is to establish a “global supply chain performance feature space” with consistent scales across companies, enabling each firm’s transaction features to correspond to a unified reference framework;
• Deviation Magnitude Calculation and Indexing (Steps 9–14): First, for each procurement variable of each sample company, the standard deviation σ_Nj of the variable’s percentile values across different years is computed, representing the deviation intensity of variable j for company N. Then, the average deviation intensity across all variables for each company is calculated to generate a single indicator value Δ_N, quantifying the company’s degree of deviation relative to the overall performance features.

This deviation indicator Δ_N serves as the basis for subsequent ranking and trend analysis in the PoR Detection Module, and provides the initial metric for determining whether a node in the overall graph G = (V, E, W) deviates from its expected role.

4. Experimental Evaluation and Results

Based on the consensus framework proposed in [23], this study constructs the mathematical model of the Supply Chain PoR algorithm and embeds it into a weighted directed graph G = (V, E, W). The model uses the degree of structural deviation from a balanced graph as the basis for anomaly detection and establishes provable discrimination conditions. The Supply Chain PoR further integrates Laplacian Flow and Sheaf theory [24,25,30], thereby endowing the framework with theoretical properties such as structural conservation, topological consistency, and non-mutability, and establishing a logically closed framework for anomaly identification.

Although the primary focus of this study lies in the mathematical construction and theoretical derivation of the graph-based structure and deviation algorithm, to further demonstrate its operability and classification capability in realistic graph structures, we also collected graph datasets satisfying the proposed premises to conduct numerical experiments. These experiments specifically focus on validating whether the proposed deviation index Δ_N ≫ 0 effectively corresponds to the emergence of anomalous edges and nodes, thereby verifying the theoretical proposition that “local deviation magnitude reflects anomaly intensity.” Experimental results show that the deviation features derived from PoR can effectively identify malicious nodes that distort procurement transaction information, thereby enhancing the model’s practical applicability and robustness in complex real-world structures such as supply chain networks. The overall verification process follows the system architecture developed in this study and consists of the following key components:

• Using the Deviation Computation Module to normalize the procurement information of sample enterprises and compute the cross-year variability (standard deviation) as a measure of deviation, further calculating the average deviation for each enterprise to obtain the initial anomaly indicator Δ_N;
• Employing the PoR Detection Module to rank enterprise nodes based on their degree of deviation and utilizing trend visualization to identify anomalous enterprises;
• Finally, applying the Correlation Verification Module to cross-validate the anomalous enterprise group by analyzing the statistical differences between internal and external performance evaluation indicators.

The following sections detail the experimental data, implementation procedures, and empirical result analysis.

4.1. Simulation and Implementation Setup

All simulation experiments in this study were implemented using Python 3.9 and executed on a standard desktop computing environment (All simulation programs could be completed within 30 s on a standalone machine and can be reproduced on standard laptop environments). The primary objective of the simulations was to validate the anomaly detection capability of the proposed PoR model under theoretical settings. The simulations did not rely on high-performance computing resources or parallel processing architectures, thereby demonstrating the model’s operational feasibility and reproducibility. The implementation environment was configured as follows:

• Processor: Intel Core i7 (12th Gen, 2.3GHz);
• Memory: 32GB DDR5;
• Graphics Card: NVIDIA GeForce RTX 3060 (6GB VRAM);
• Operating System: Windows 11.

4.2. Data Collection and Preprocessing

To validate the feasibility and anomaly detection capability of the proposed PoR model within real-world supply chain network structures, this study utilized procurement data from 856 companies in Taiwan, spanning the years 1995 to 2022, sourced from the TEJ database under the general industrial classification. Based on common supply chain transaction items—including current assets, accounts receivable/payable, and operating performance metrics—and aligned with the theoretical premises established in this study, thirteen variables highly relevant to procurement were extracted to construct the node feature vectors W_N. The selected variables are as follows:

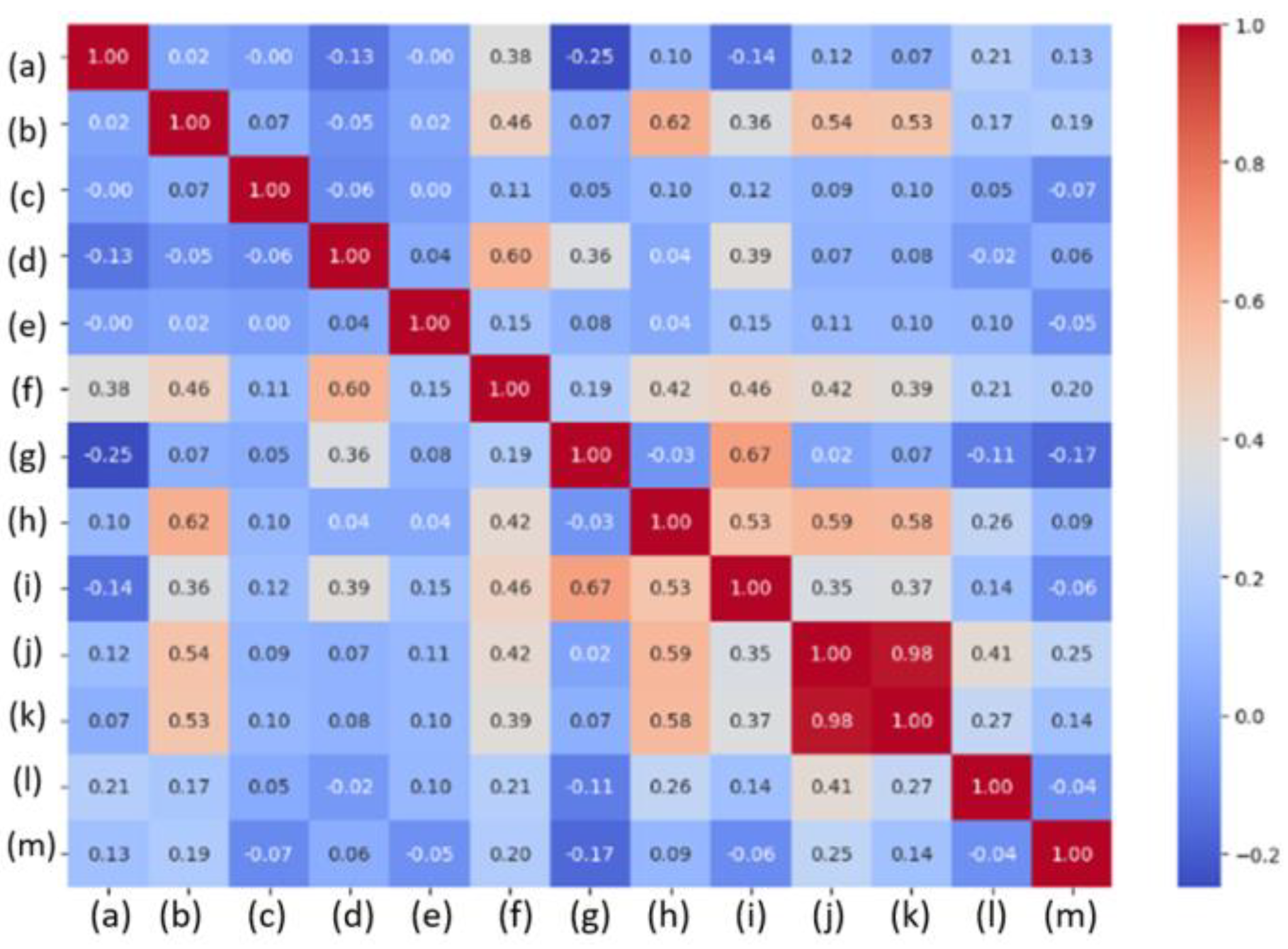
(a)

Cash and Cash Equivalents

(b)

Accounts and Notes Receivable

(c)

Other Receivables

(d)

Inventories

(e)

Prepaid Expenses and Advances

(f)

Total Current Assets

(g)

Short-term Borrowings

(h)

Accounts and Notes Payable

(i)

Total Current Liabilities

(j)

Net Operating Revenue

(k)

Cost of Goods Sold

(l)

Operating Expenses

(m)

Operating Profit

All variables were normalized into proportional values and converted into dimensionless percentile representations, forming the multi-dimensional vector matrix S, which served as the input for subsequent feature computation and graph model construction through the deviation algorithm.

To mitigate potential biases caused by high linear correlations among variables, this study first conducted a Pearson correlation analysis (See Equation (38) for an example) on the selected 13 variables to assess the degree of informational redundancy. The analysis results were visualized using a heatmap to illustrate the strength and direction of the correlations between variables (see Figure 5 below).

$$r={\displaystyle \frac{{\sum }_{i=1}^n\left(X_i-\frac{{\sum }_{i=1}^n{X}_i}{n}\right)\left(Y_i-\frac{{\sum }_{i=1}^n{Y}_i}{n}\right)}{\sqrt{{\sum }_{i=1}^n{\left(X_i-\frac{{\sum }_{i=1}^n{X}_i}{n}\right)}^2}\sqrt{{\sum }_{i=1}^n{\left(Y_i-\frac{{\sum }_{i=1}^n{Y}_i}{n}\right)}^2}}},$$

(38)

The analysis revealed that the following three pairs of variables exhibited relatively high correlations:

• Net Operating Revenue and Cost of Goods Sold (correlation coefficient: 0.9787);
• Short-term Borrowings and Total Current Liabilities (correlation coefficient: 0.6653);
• Accounts and Notes Receivable and Accounts and Notes Payable (correlation coefficient: 0.6165).

Among these, the correlation between Net Operating Revenue and Cost of Goods Sold was the most significant. According to statistical theory, pronounced multicollinearity among variables may adversely affect the stability and predictive power of analytical models. Nevertheless, this study opted to retain these variables in the model, because revenues and costs are typically structurally linked for most enterprises, often determined through cost-plus pricing strategies, resulting in relatively stable gross margins over time. If procurement information is authentic, a near-linear relationship (correlation close to 1) between revenue and cost is expected. However, in practice, some firms may engage in earnings management under performance pressures, such as inflating revenues mid-year and later adjusting figures through returns, allowances, or discounts at year-end. Thus, a high correlation may itself serve as an indicator of potential anomalous behavior. The Supply Chain PoR focuses not on the predictive power of individual variables but rather on the overall deviation of a node’s feature vector from the expected graph structure. In light of this objective, this study retained both Net Operating Revenue and Cost of Goods Sold in the subsequent modeling process, leveraging their structural relationship to enhance the identification of latent anomalies in corporate performance data.

4.3. Results of Anomalous Enterprise Detection

This study applied the proposed Supply Chain PoR algorithm to procurement data of 856 companies. First, using the Deviation Computation Module, 13 procurement variables for each company were normalized and distribution-standardized to construct the global feature vector of the supply chain performance. Subsequently, the deviation between each company’s feature vector and the global feature was computed, defined as the Deviation Index (Δ_N), to quantify the degree of divergence between individual company information and the overall supply chain. Next, the 856 companies were ranked based on their Deviation Index values, and the ranking results were visualized in a trend chart (see Figure 6 below).

Figure 6 presents the ranking of nodes along the horizontal axis (ordered from the lowest to the highest Deviation Index), with the corresponding Deviation Index values plotted along the vertical axis. To facilitate group-based comparison, the 56 nodes with the lowest deviation indices are enclosed within a blue box (designated as the control group), whereas the 56 nodes with the highest deviation indices are enclosed within a red box (designated as the suspected anomaly group). From the trend line in Figure 6, it is evident that a sharp rise in the Deviation Index begins around the 801st node, indicating that these firms exhibit significant structural deviations from the supply chain global feature and thus pose high possibility of anomalous behavior. In this study, these 56 nodes, representing 6.5% of the total sample, are preliminarily identified as anomalous nodes. To further validate the effectiveness of the anomaly identification, the 56 nodes with the lowest deviation indices were selected as a control group for subsequent performance correlation analysis and external evaluation comparison, ensuring PoR’s practical interpretability and discriminatory power in anomaly detection.

4.4. Validation of Algorithmic Effectiveness

Although the proposed Supply Chain PoR algorithm successfully identified 56 nodes exhibiting significant deviation characteristics as initial anomalies; to enhance the credibility and theoretical soundness of the identification results, it remains necessary to perform independent cross-validation using external metrics. This section introduces a verification framework based on the “consistency of internal performance information and external evaluation metrics” to assess the rationality of the PoR identification.

The theoretical basis is that internal operational metrics (e.g., earnings per share, EPS) are generated for management purposes, while external observers independently evaluate corporate performance based on news reports, industry data, and market dynamics (e.g., stock prices). If internal performance metrics authentically reflect the enterprise’s operational status, there should exist a statistically significant positive correlation between internal performance and external evaluations. Conversely, if information distortion exists, this structural correlation is likely to be disrupted. Therefore, this study conducts a correlation analysis between two groups: the 56 enterprises previously identified by the PoR model as suspected of procurement information distortion (“anomalous group”); and the 56 enterprises with the lowest deviation indices (“normal group”).

Two performance indicators were retrieved from the TEJ database:

• Internal performance indicator: Earnings Per Share (EPS);
• External performance indicator: Stock Price.

For each enterprise, the annual rates of change for EPS and stock price from 1995 to 2022 were calculated, and the Pearson correlation coefficient was used to measure the relationship between these two indicators. The results are summarized in

Table 1. Correlation of internal and external performance metrics.

Groups	Correlation Coefficient
normal group (56 nodes)	0.1476
anomalous group (56 nodes)	−0.0001

.

From the results presented in Table 1, it can be observed that the control group exhibits a positive correlation between the internal and external performance indicators, suggesting a consistent informational structure. In contrast, the anomaly group shows correlations approaching zero, indicating a disruption in the logical linkage between internal and external information. The theoretical foundation of this independent validation is built upon the relationship between corporate earnings and stock prices, a topic that has been extensively studied in the field of economics. Representative models include the Efficient Market Hypothesis formulated by Eugene Fama, recipient of the 2013 Nobel Prize in Economic Sciences [34], and the empirical research conducted by Robert Shiller, particularly his development of the Cyclically Adjusted P/E ratio (CAPE ratio) [35]. In addition, several classical studies have employed mathematical modeling and statistical methods to capture the association between earnings information and market valuation [36,37]. These works generally rest on the assumption that earnings accurately reflect a firm’s performance. However, when financial disclosures are biased or distorted, this relationship is expected to be undermined. Accordingly, this study interprets the near-zero correlation between EPS and stock prices observed among the anomalous group as an indicator of potential information distortion, thereby supporting its use as a signal for detecting anomalous corporate behavior.

This outcome further supports the validity of the Supply Chain PoR algorithm in identifying nodes with potential information distortion. This empirical evidence—showing that nodes with high deviation indices correspond to greater topological inconsistency—reinforces the structural validity and detection effectiveness of PoR.

4.5. Summary of Results

In the previous section, this study constructed the procurement feature relationships of supply chain nodes through a weighted directed graph framework, formulating a Graph Balancing structure. Building on the operational principles of Sheaf-theoretic Topological Consistency, the Supply Chain PoR algorithm was proposed, and mathematical modeling was employed to demonstrate that violations of Laplacian Flow Conservation at individual nodes can serve as provable indicators for detecting informational distortions and anomalous behaviors.

This section further validated the feasibility and consistency of the Supply Chain PoR framework within real-world supply chain graph structures through empirical evidence. By analyzing procurement behaviors of 856 Taiwanese enterprises, aligned with the weighted directed graph structure, the Supply Chain PoR successfully identified 56 highly anomalous nodes based on their deviation from the supply chain performance global features. The deviation patterns were visualized through trend analysis, concretely reflecting the structural disruptions caused by violations of Laplacian Flow Conservation.

Moreover, by extending the application of Sheaf Coherence, this study conducted an independent cross-validation through Pearson Correlation Coefficient analysis between internal performance (EPS) and external performance (stock prices). It was found that anomalous nodes exhibited near-zero correlations between internal and external performance fluctuations, in contrast to the strong positive correlations observed among normal nodes, thus validating the presence of informational distortions. These results not only corroborate the effectiveness of PoR anomaly identification but also realize a coherent topological validation logic and a cross-validation mechanism linking node deviation patterns in weighted directed graphs with external statistical behaviors.

The empirical findings of this section further substantiate the mathematical foundations of the Supply Chain PoR model. Through the identification of node-level deviations from global performance structures, corresponding to disruptions in local Laplacian Flow Conservation within the graph, and reinforced by Sheaf-theoretic consistency applied to informational coherence testing, this study successfully established a logically closed, deviation-quantifiable, and cross-domain verifiable framework for anomaly detection. The empirical results align with theoretical expectations, affirming that Graph Balancing, Flow Conservation, and Topological Consistency theories together form a robust foundation for detecting anomalies in complex supply chain networks.

These findings reinforce the assumption that structural deviation in procurement behavior is associated with underlying information distortion. The near-zero correlation in the anomalous group may reflect deliberate manipulation, inconsistent reporting practices, or asymmetric disclosure strategies. The ability of the PoR model to detect such patterns suggests its potential application in supplier vetting or credit assessment. Moreover, because the deviation index is derived from normalized financial variables, the method can be adapted to different industries or extended to time-series anomaly detection. Future research may further examine the behavioral drivers behind such distortions or combine PoR with explainable AI techniques to enhance interpretability and decision support.

5. Conclusions

5.1. Conclusions and Contributions

This study proposes a mathematically rigorous and structurally consistent anomaly detection framework tailored to supply chain networks, introducing the Supply Chain PoR model. From a graph-theoretic perspective, the transactional behaviors of enterprises are reinterpreted in terms of structural characteristics. In this model, enterprises are modeled as vertices in a weighted directed graph G = (V, E, W), with procurement activities represented by directed edges and edge weights corresponding to implicit gross margin features derived from procurement data.

The core concept of Supply Chain PoR lies in adopting the global performance characteristic vector as a reference, and quantifying the structural deviation of each individual node relative to this global feature using a deviation function Δ_N. The Supply Chian PoR is applied to procurement data from 856 companies in Taiwan (sourced from the TEJ database) spanning the years 1995–2022. Empirical analysis identified 56 companies with sharply increasing deviation indices Δ_N, indicating significant topological deviations between node local feature and the global characteristic vector derived from the supply chain graph. To further validate effectiveness of this detection result, this study compared the correlation between internal and external performance indicators and found that anomalous nodes exhibited near-zero correlation, in stark contrast to the significant correlations observed in normal nodes. These results provide statistical evidence for both graph-structured deviations and topological inconsistencies, aligning with the predictions of PoR based on flow imbalance and Sheaf-theoretic coherence violations.

This research presents a novel anomaly detection framework founded on Graph Balancing Theory, Laplacian Flow Conservation, and Sheaf-Theoretic Topological Consistency. The proposed system is theoretically provable, model-transparent, and computationally robust, without requiring large-scale labeled training data. It effectively identifies potential information anomalies within highly complex weighted directed graphs in supply chain networks, thereby laying a solid foundation for cross-disciplinary applications of graph theory in economic network analysis and risk early-warning systems.

5.2. Special Theoretical Contribution

From the perspective of theoretical advancement, this study builds upon the principle of Sheaf-theoretic Topological Consistency to establish a node-level anomaly detection method for weighted directed graphs by integrating mathematically regularized structural deviation analysis. Specifically, it identifies abnormal behaviors through deviations between local features and global characteristics of the supply chain network. This deviation effectively captures violations of Laplacian Flow Conservation and renders such violations observable by transforming them into visualized trend graphs, which highlight explicit anomaly projections in high-dimensional feature space associated with a small subset of nodes. To the best of our knowledge, this is the first time that such flow conservation violations have been empirically observed in a highly complex, non-physical system such as the supply chain. The study thereby constructs a complete logical chain that links Sheaf Coherence, Graph Balancing, and High-dimensional Anomaly Projection.

Furthermore, the study conducts cross-validation of the identified anomalies by examining the correlation between internal and external performance indicators beyond the graph structure. This enables a cross-mapping between Graph Structural Deviation and Statistical Inconsistency within the weighted directed graph. The proposed method not only extends the theory of graph-based anomaly detection into the domains of economic, but also incorporates topological coherence (Sheaf Coherence) as part of its validation logic. In doing so, it advances the field of graph topology–based statistical anomaly detection, and opens new methodological possibilities for integrating approaches across physical systems and economic network analysis.

5.3. Limitations

This research has several limitations:

• The global characteristic is constructed based on the empirical distribution of the sample data. Consequently, if the underlying data quality is poor or biased, the deviation index may be adversely affected or distorted;
• The deviation index Δ_N is constructed based on the statistical dispersion of node-level features. In scenarios where procurement data is sparse or unevenly distributed across nodes, additional calibration may be required to ensure the stability and sensitivity of the model.

5.4. Future Research Directions

Several potential directions can be pursued to extend the present study:

• Extension of PoR to Dynamic Graph Modeling: Future work may incorporate temporal variability into the PoR framework, enabling the construction of a dynamic PoR model capable of tracking structural changes over time;
• Application of Sheaf Cohomology: Building upon the current use of Sheaf-theoretic coherence, future research may further introduce Sheaf cohomology invariants as a mathematical foundation for analyzing structural consistency in graph-based systems;
• Integration with AI Models: PoR can be integrated with artificial intelligence algorithms to enhance anomaly detection accuracy. Moreover, by applying model compression techniques and parameter reduction strategies, it may be possible to lower data requirements and computational overhead, thereby improving AI model’s efficiency and sustainability in large-scale, real-time network environments.