Graph-Regularized Orthogonal Non-Negative Matrix Factorization with Itakura–Saito (IS) Divergence for Fault Detection
Abstract
1. Introduction
2. Preliminaries
3. Related Works
3.1. Non-Negative Matrix Factorization
3.2. Variants of Non-Negative Matrix Factorization
3.3. Model Construction
4. Optimization Process
4.1. Update , Fixed
4.2. Update , Fixed
4.3. Update , Fixed
4.4. Complexity Analysis
5. Simulation Experiments
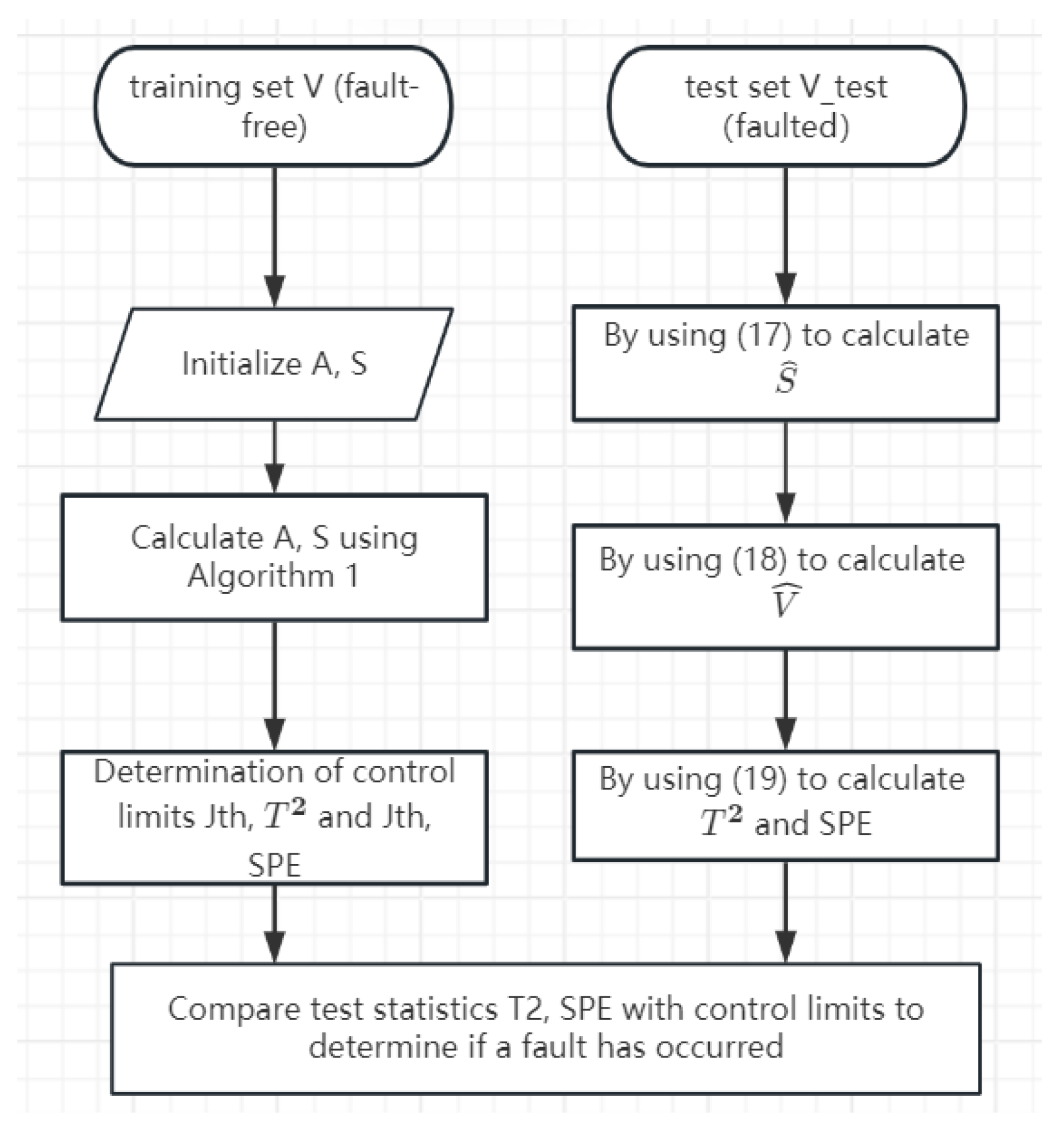
5.1. Fault Detection Process
| Algorithm 1. Algorithm for solving ISGONMF |
| Input: Sample matrix , parameter , , the rank of the decomposition k, iterations. |
| Initialize: , . |
| 1. Calculated Diagonal matrix . |
| 2. Calculated Laplace matrix . |
| 3. For i = 1 to k |
| calculated gradient matrix by Equation (10); |
| calculated gradient matrix by Equation (12); |
| calculated gradient matrix by Equation (14); |
| 4. end for |
| Output . |
5.2. Application on the TEP
5.2.1. Data Preparation
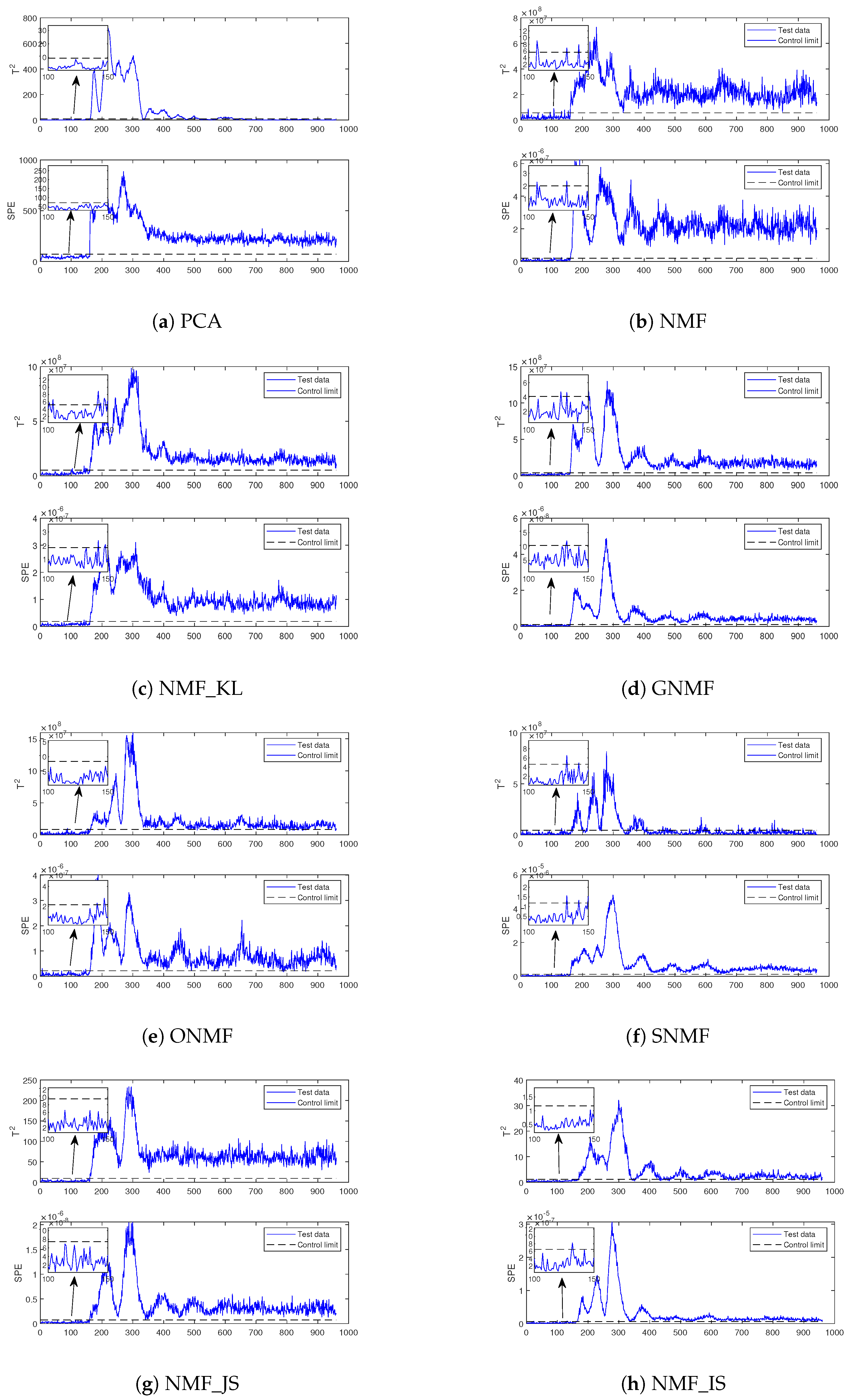
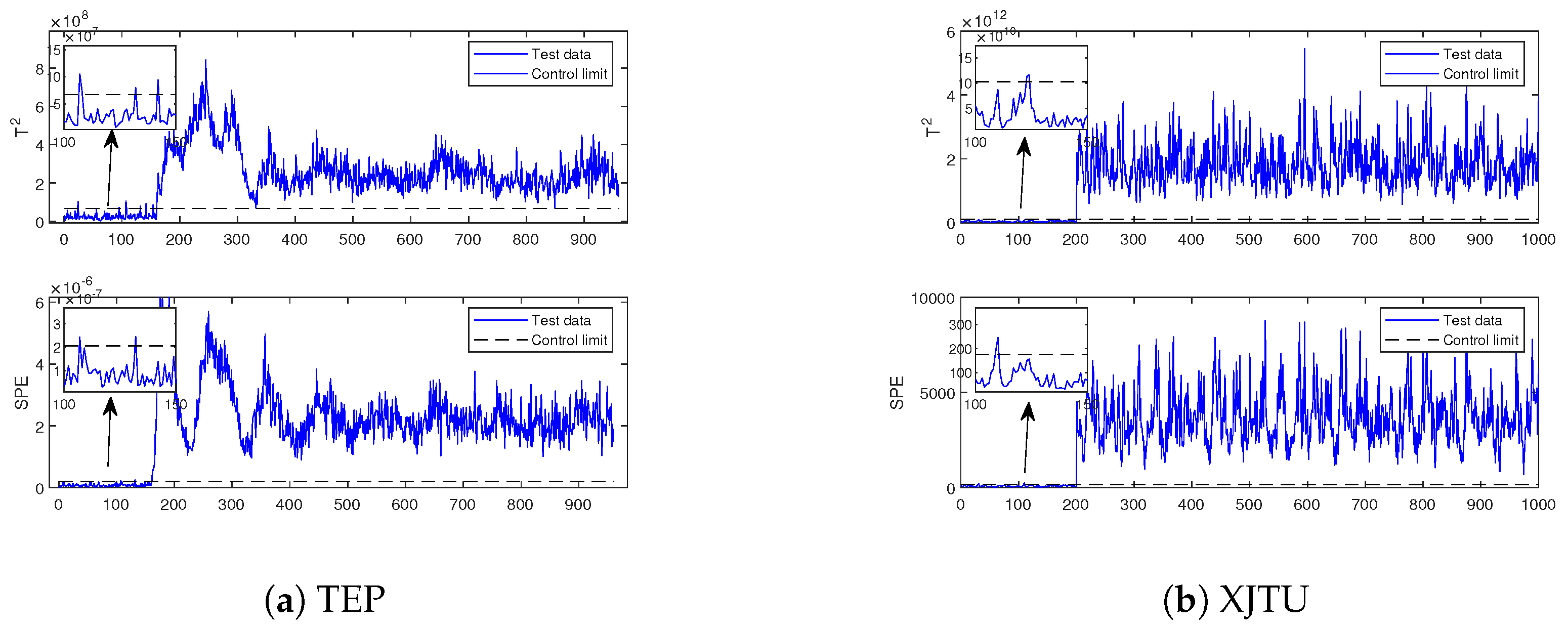
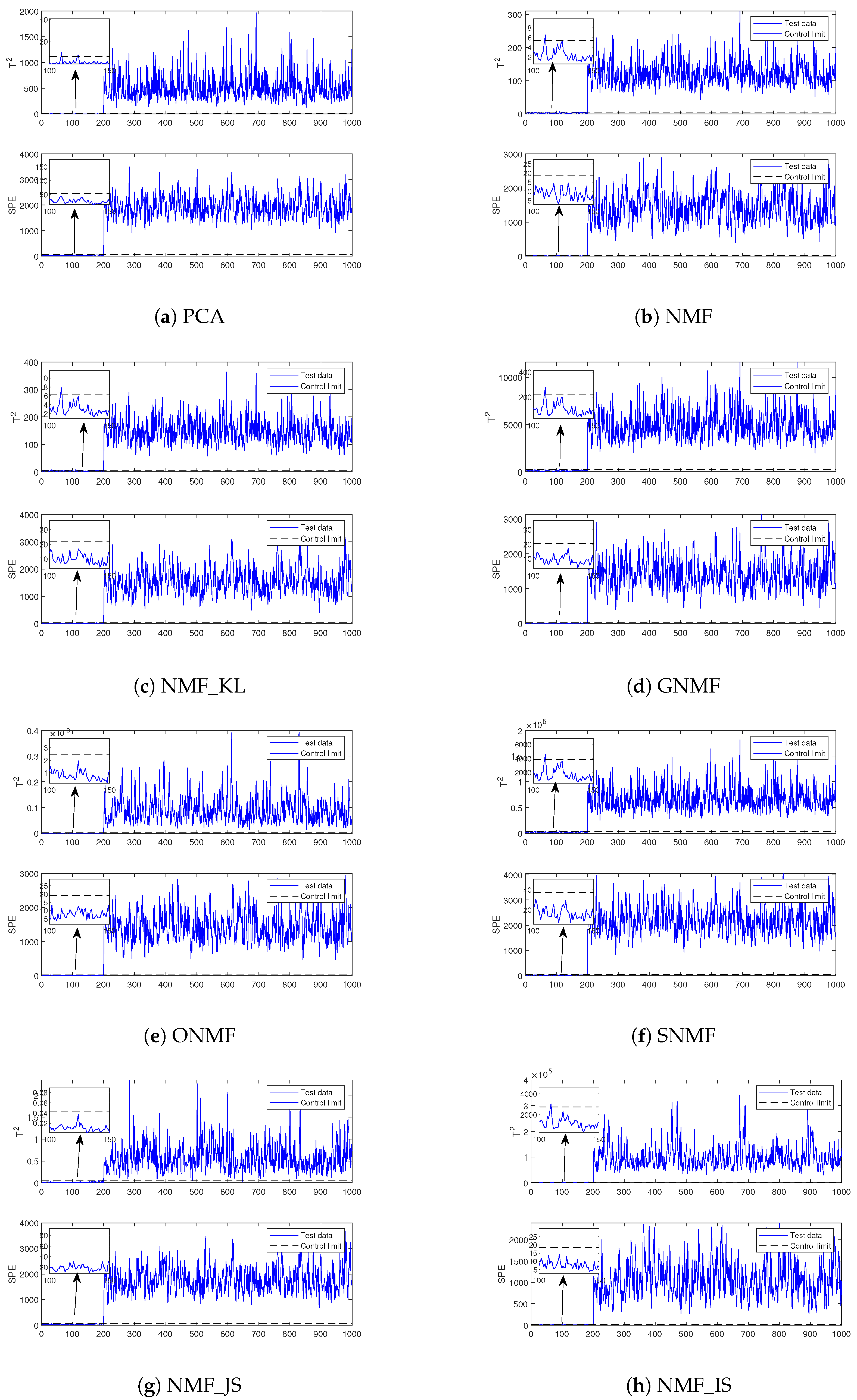
5.2.2. Results of the Experiment
5.3. XJTU
5.3.1. Data Preparation
5.3.2. Results of the Experiment
5.4. Ablation Study
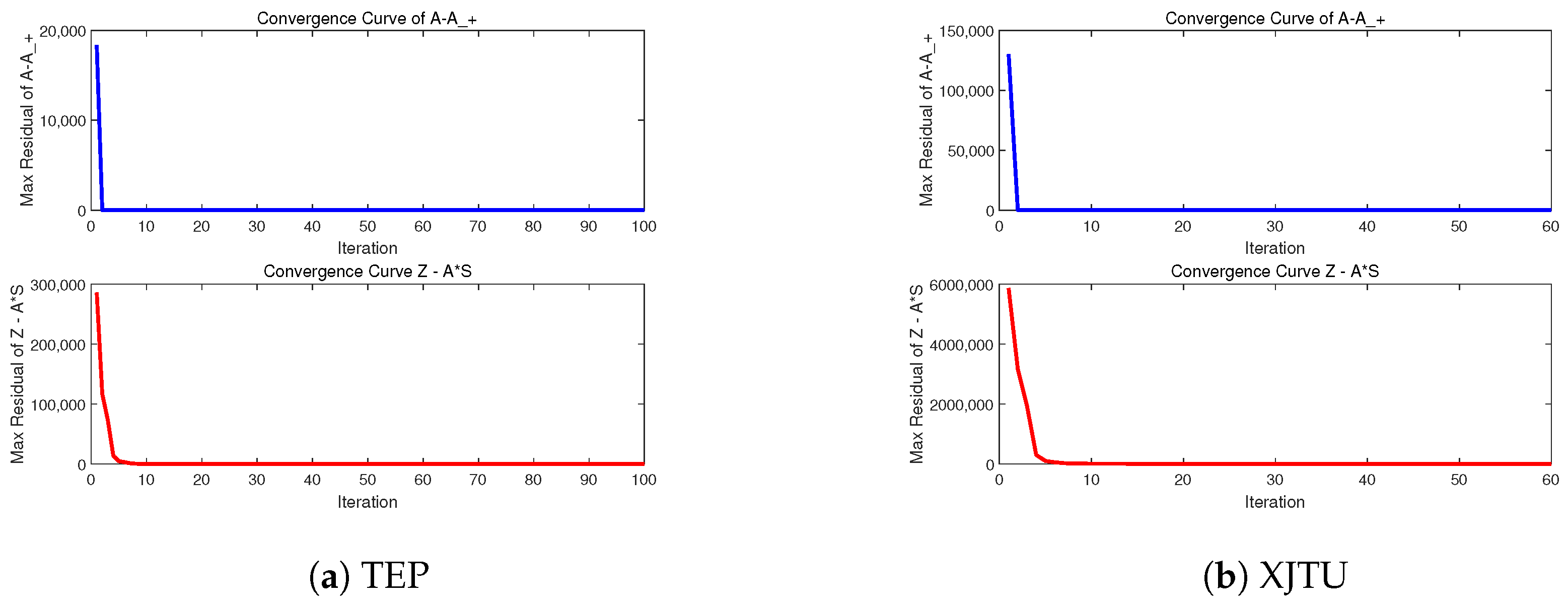
5.5. Experimental Convergence Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, Y.X.; Zhang, Y.J. Nonnegative matrix factorization: A comprehensive review. IEEE Trans. Knowl. Data Eng. 2012, 25, 1336–1353. [Google Scholar] [CrossRef]
- Kim, H.; Park, H. Sparse non-negative matrix factorizations via alternating non-negativity-constrained least squares for microarray data analysis. Bioinformatics 2007, 23, 1495–1502. [Google Scholar] [CrossRef] [PubMed]
- Lee, D.D.; Seung, H.S. Learning the parts of objects by non-negative matrix factorization. Nature 1999, 401, 788–791. [Google Scholar] [CrossRef]
- Belachew, M.T. Efficient algorithm for sparse symmetric nonnegative matrix factorization. Pattern Recognit. Lett. 2019, 125, 735–741. [Google Scholar] [CrossRef]
- Huang, S.; Wang, H.; Li, T.; Li, T.; Xu, Z. Robust graph regularized nonnegative matrix factorization for clustering. Data Min. Knowl. Discov. 2018, 32, 483–503. [Google Scholar] [CrossRef]
- Yoo, J.; Choi, S. Orthogonal nonnegative matrix factorization: Multiplicative updates on Stiefel manifolds. In Proceedings of the International Conference on Intelligent Data Engineering and Automated Learning, Daejeon, Republic of Korea, 2–5 November 2008; Springer: Berlin/Heidelberg, Germany, 2008; pp. 140–147. [Google Scholar]
- Cai, D.; He, X.; Han, J.; Huang, T.S. Graph regularized nonnegative matrix factorization for data representation. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 33, 1548–1560. [Google Scholar] [CrossRef]
- Berahmand, K.; Saberi-Movahed, F.; Sheikhpour, R.; Li, Y.; Jalili, M. A Comprehensive Survey on Spectral Clustering with Graph Structure Learning. arXiv 2025, arXiv:2501.13597. [Google Scholar]
- Choi, S. Algorithms for orthogonal nonnegative matrix factorization. In Proceedings of the 2008 IEEE International Joint Conference on Neural Networks (IEEE World Congress on Computational Intelligence), Hong Kong, China, 1–8 June 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 1828–1832. [Google Scholar]
- Ding, C.; Li, T.; Peng, W.; Park, H. Orthogonal nonnegative matrix t-factorizations for clustering. In Proceedings of the 12th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Philadelphia, PA, USA, 20–23 August 2006; pp. 126–135. [Google Scholar]
- Saberi-Movahed, F.; Berahman, K.; Sheikhpour, R.; Li, Y.; Pan, S. Nonnegative matrix factorization in dimensionality reduction: A survey. arXiv 2024, arXiv:2405.03615. [Google Scholar] [CrossRef]
- Chen, W.S.; Zeng, Q.; Pan, B. A survey of deep nonnegative matrix factorization. Neurocomputing 2022, 491, 305–320. [Google Scholar] [CrossRef]
- Li, C.; Che, H.; Leung, M.F.; Liu, C.; Yan, Z. Robust multi-view non-negative matrix factorization with adaptive graph and diversity constraints. Inf. Sci. 2023, 634, 587–607. [Google Scholar] [CrossRef]
- Zhang, W.; Yu, S.; Wang, L.; Guo, W.; Leung, M.F. Constrained symmetric non-negative matrix factorization with deep autoencoders for community detection. Mathematics 2024, 12, 1554. [Google Scholar] [CrossRef]
- Dong, Y.; Che, H.; Leung, M.F.; Liu, C.; Yan, Z. Centric graph regularized log-norm sparse non-negative matrix factorization for multi-view clustering. Signal Process. 2024, 217, 109341. [Google Scholar] [CrossRef]
- Yang, X.; Che, H.; Leung, M.F.; Liu, C. Adaptive graph nonnegative matrix factorization with the self-paced regularization. Appl. Intell. 2023, 53, 15818–15835. [Google Scholar] [CrossRef]
- Li, X.b.; Yang, Y.p.; Zhang, W.d. Fault detection method for non-Gaussian processes based on non-negative matrix factorization. Asia-Pac. J. Chem. Eng. 2013, 8, 362–370. [Google Scholar] [CrossRef]
- Xiao, L.; Yang, X.; Yang, X. A graph neural network-based bearing fault detection method. Sci. Rep. 2023, 13, 5286. [Google Scholar] [CrossRef]
- Ren, Z.; Zhang, W.; Zhang, Z. A deep nonnegative matrix factorization approach via autoencoder for nonlinear fault detection. IEEE Trans. Ind. Inform. 2019, 16, 5042–5052. [Google Scholar] [CrossRef]
- Xiu, X.; Fan, J.; Yang, Y.; Liu, W. Fault detection using structured joint sparse nonnegative matrix factorization. IEEE Trans. Instrum. Meas. 2021, 70, 3513011. [Google Scholar] [CrossRef]
- Zhang, X.; Xiu, X.; Zhang, C. Structured joint sparse orthogonal nonnegative matrix factorization for fault detection. IEEE Trans. Instrum. Meas. 2023, 72, 2506015. [Google Scholar] [CrossRef]
- Ahmadian, S.; Berahmand, K.; Rostami, M.; Forouzandeh, S.; Moradi, P.; Jalili, M. Recommender Systems based on Non-negative Matrix Factorization: A Survey. IEEE Trans. Artif. Intell. 2025, 1–21. [Google Scholar] [CrossRef]
- Févotte, C.; Bertin, N.; Durrieu, J.L. Nonnegative matrix factorization with the Itakura-Saito divergence: With application to music analysis. Neural Comput. 2009, 21, 793–830. [Google Scholar] [CrossRef]
- Cichocki, A.; Lee, H.; Kim, Y.D.; Choi, S. Non-negative matrix factorization with α-divergence. Pattern Recognit. Lett. 2008, 29, 1433–1440. [Google Scholar] [CrossRef]
- Févotte, C.; Idier, J. Algorithms for nonnegative matrix factorization with the β-divergence. Neural Comput. 2011, 23, 2421–2456. [Google Scholar] [CrossRef]
- Yang, Z.; Zhang, H.; Yuan, Z.; Oja, E. Kullback-Leibler divergence for nonnegative matrix factorization. In Proceedings of the International Conference on Artificial Neural Networks, Espoo, Finland, 14–17 June 2011; Springer: Berlin/Heidelberg, Germany, 2011; pp. 250–257. [Google Scholar]
- Hien, L.T.K.; Gillis, N. Algorithms for nonnegative matrix factorization with the Kullback–Leibler divergence. J. Sci. Comput. 2021, 87, 93. [Google Scholar] [CrossRef]
- Zhang, L.; Liu, Z.; Pu, J.; Song, B. Adaptive graph regularized nonnegative matrix factorization for data representation. Appl. Intell. 2020, 50, 438–447. [Google Scholar] [CrossRef]
- Chen, K.; Che, H.; Li, X.; Leung, M.F. Graph non-negative matrix factorization with alternative smoothed L 0 regularizations. Neural Comput. Appl. 2023, 35, 9995–10009. [Google Scholar] [CrossRef]
- Zhang, G.; Wang, Y.; Lessard, L.; Grosse, R.B. Near-optimal local convergence of alternating gradient descent-ascent for minimax optimization. In Proceedings of the International Conference on Artificial Intelligence and Statistics—Proceedings of Machine Learning Research, Virtual, 28–30 March 2022; pp. 7659–7679. [Google Scholar]
- Harper, J.; Wells, D. Recent advances and future developments in PGD. Prenat. Diagn. 1999, 19, 1193–1199. [Google Scholar] [CrossRef]
- Hajinezhad, D.; Chang, T.H.; Wang, X.; Shi, Q.; Hong, M. Nonnegative matrix factorization using ADMM: Algorithm and convergence analysis. In Proceedings of the 2016 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Shanghai, China, 20–25 March 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 4742–4746. [Google Scholar]
- Lin, C.J. Projected gradient methods for nonnegative matrix factorization. Neural Comput. 2007, 19, 2756–2779. [Google Scholar] [CrossRef]
- Yin, S.; Ding, S.X.; Haghani, A.; Hao, H.; Zhang, P. A comparison study of basic data-driven fault diagnosis and process monitoring methods on the benchmark Tennessee Eastman process. J. Process Control 2012, 22, 1567–1581. [Google Scholar] [CrossRef]
- Lee, G.; Han, C.; Yoon, E.S. Multiple-fault diagnosis of the Tennessee Eastman process based on system decomposition and dynamic PLS. Ind. Eng. Chem. Res. 2004, 43, 8037–8048. [Google Scholar] [CrossRef]
- Zhang, C.; Guo, Q.; Li, Y. Fault detection in the Tennessee Eastman benchmark process using principal component difference based on k-nearest neighbors. IEEE Access 2020, 8, 49999–50009. [Google Scholar] [CrossRef]
- Wang, B.; Lei, Y.; Li, N. XJTU-SY bearing datasets. Github Github Repos. 2018. [Google Scholar]
- Wang, B.; Lei, Y.; Li, N.; Li, N. A hybrid prognostics approach for estimating remaining useful life of rolling element bearings. IEEE Trans. Reliab. 2018, 69, 401–412. [Google Scholar] [CrossRef]
- Xue, Y.; Yang, R.; Chen, X.; Tian, Z.; Wang, Z. A novel local binary temporal convolutional neural network for bearing fault diagnosis. IEEE Trans. Instrum. Meas. 2023, 72, 3525013. [Google Scholar] [CrossRef]

| PCA | NMF | NMF_KL | NMF_IS | GNMF | ONMF | SNMF | NMF_JS | ISGONMF | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| T2 | SPE | T2 | SPE | T2 | SPE | T2 | SPE | T2 | SPE | T2 | SPE | T2 | SPE | T2 | SPE | T2 | SPE | |
| IDV1 | 59.30 | 99.75 | 99.50 | 99.63 | 99.13 | 99.00 | 98.75 | 98.88 | 98.38 | 99.13 | 97.63 | 99.00 | 99.00 | 99.38 | 99.38 | 99.63 | 99.38 | 99.75 |
| IDV2 | 30.38 | 98.63 | 97.75 | 97.61 | 97.75 | 98.00 | 97.13 | 98.50 | 97.50 | 98.00 | 96.75 | 97.38 | 97.50 | 98.75 | 97.75 | 98.13 | 98.00 | 96.63 |
| IDV3 | 10.63 | 3.75 | 2.38 | 4.13 | 2.00 | 1.63 | 3.00 | 4.00 | 8.75 | 8.38 | 10.75 | 14.38 | 0.63 | 1.50 | 4.88 | 6.50 | 2.00 | 3.25 |
| IDV4 | 6.00 | 93.88 | 11.38 | 52.13 | 2.25 | 2.63 | 1.38 | 6.63 | 3.13 | 5.50 | 1.25 | 5.38 | 0.75 | 5.25 | 12.88 | 32.38 | 15.75 | 47.00 |
| IDV5 | 30.75 | 28.63 | 22.38 | 27.00 | 19.38 | 22.38 | 20.63 | 24.00 | 16.00 | 25.25 | 18.25 | 27.13 | 18.63 | 20.38 | 26.38 | 19.38 | 19.88 | 19.50 |
| IDV6 | 99.38 | 99.38 | 99.88 | 99.88 | 100.00 | 100.00 | 100.00 | 100.00 | 99.25 | 100.00 | 98.50 | 100.00 | 100.00 | 99.88 | 99.50 | 98.50 | 99.63 | 99.63 |
| IDV7 | 50.12 | 100.00 | 100.00 | 99.88 | 99.50 | 99.13 | 92.50 | 99.75 | 100.00 | 100.00 | 62.25 | 83.88 | 71.63 | 99.88 | 97.25 | 88.38 | 100.00 | 100.00 |
| IDV8 | 89.00 | 97.50 | 93.63 | 97.33 | 88.50 | 91.13 | 90.75 | 92.38 | 70.50 | 92.25 | 68.75 | 90.13 | 72.13 | 92.88 | 87.38 | 64.88 | 94.75 | 87.00 |
| IDV9 | 8.13 | 4.38 | 3.75 | 3.88 | 1.38 | 1.00 | 3.00 | 2.63 | 7.13 | 7.38 | 4.38 | 10.38 | 0.25 | 1.50 | 2.38 | 2.13 | 1.25 | 2.88 |
| IDV10 | 52.75 | 42.75 | 31.13 | 38.63 | 26.63 | 30.88 | 28.88 | 29.38 | 31.38 | 43.88 | 37.13 | 47.88 | 12.65 | 18.33 | 15.50 | 13.13 | 13.50 | 23.25 |
| IDV11 | 13.88 | 68.63 | 23.00 | 44.25 | 5.38 | 13.00 | 3.75 | 20.50 | 12.75 | 20.63 | 13.50 | 19.13 | 0.50 | 14.75 | 33.75 | 20.13 | 14.38 | 38.00 |
| IDV12 | 92.13 | 98.63 | 88.63 | 95.38 | 81.00 | 82.25 | 81.75 | 84.38 | 68.38 | 88.38 | 69.13 | 86.25 | 77.83 | 89.38 | 75.88 | 56.38 | 79.00 | 90.38 |
| IDV13 | 91.38 | 91.63 | 92.38 | 91.38 | 90.50 | 91.38 | 88.88 | 91.00 | 87.63 | 92.00 | 88.63 | 92.38 | 82.88 | 92.13 | 89.75 | 88.83 | 92.75 | 93.13 |
| IDV14 | 19.50 | 88.38 | 56.63 | 81.88 | 6.88 | 48.38 | 3.63 | 57.13 | 5.63 | 29.75 | 3.00 | 11.75 | 5.13 | 62.63 | 62.00 | 52.00 | 34.38 | 97.63 |
| IDV15 | 14.88 | 5.50 | 3.50 | 5.75 | 5.63 | 5.00 | 3.13 | 7.50 | 13.63 | 12.25 | 12.13 | 16.25 | 0.38 | 3.50 | 4.13 | 5.00 | 1.75 | 3.00 |
| IDV16 | 38.75 | 27.13 | 51.75 | 61.63 | 29.88 | 30.38 | 22.63 | 20.50 | 33.25 | 47.38 | 43.75 | 55.63 | 25.13 | 53.38 | 57.13 | 20.63 | 60.50 | 63.75 |
| IDV17 | 54.88 | 23.38 | 39.25 | 57.25 | 35.25 | 26.00 | 7.88 | 27.13 | 20.50 | 30.75 | 12.38 | 22.00 | 1.00 | 35.38 | 53.13 | 55.75 | 35.25 | 52.13 |
| IDV18 | 88.38 | 90.00 | 88.73 | 98.13 | 88.38 | 87.88 | 88.50 | 89.25 | 83.13 | 87.63 | 81.38 | 86.63 | 84.88 | 88.88 | 87.63 | 95.63 | 81.13 | 92.25 |
| IDV19 | 2.13 | 13.75 | 2.38 | 5.75 | 1.88 | 1.13 | 2.13 | 1.50 | 4.88 | 4.38 | 3.88 | 5.25 | 0.25 | 2.38 | 4.75 | 14.63 | 5.00 | 4.63 |
| IDV20 | 21.38 | 28.88 | 21.88 | 42.13 | 12.88 | 20.50 | 11.00 | 22.13 | 23.25 | 29.25 | 18.38 | 35.63 | 13.25 | 20.38 | 63.75 | 64.38 | 40.88 | 47.75 |
| IDV21 | 28.38 | 44.88 | 34.13 | 47.35 | 32.13 | 32.00 | 13.88 | 17.50 | 17.12 | 41.38 | 44.38 | 46.50 | 11.63 | 35.33 | 23.88 | 22.38 | 20.63 | 39.88 |
| avreage | 42.96 | 59.50 | 50.66 | 59.56 | 44.10 | 46.84 | 41.10 | 47.36 | 42.96 | 50.64 | 42.19 | 50.13 | 36.95 | 49.32 | 52.33 | 48.51 | 48.08 | 57.21 |
| PCA | NMF | NMF_KL | NMF_IS | GNMF | ONMF | SNMF | NMF_JS | ISGONMF | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| T2 | SPE | T2 | SPE | T2 | SPE | T2 | SPE | T2 | SPE | T2 | SPE | T2 | SPE | T2 | SPE | T2 | SPE | |
| IDV1 | 0.00 | 2.50 | 0.00 | 0.00 | 0.00 | 0.00 | 1.25 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.63 | 0.00 | 1.88 | 0.00 | 0.00 | 2.50 |
| IDV2 | 0.00 | 1.88 | 0.63 | 0.63 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 1.25 | 1.88 | 1.25 | 0.63 | 1.25 |
| IDV3 | 6.38 | 1.25 | 2.50 | 2.50 | 0.00 | 0.00 | 0.63 | 0.63 | 0.63 | 0.00 | 0.00 | 1.25 | 0.00 | 0.63 | 3.75 | 5.63 | 0.63 | 1.88 |
| IDV4 | 0.00 | 2.50 | 0.63 | 1.25 | 0.00 | 0.00 | 1.25 | 1.25 | 3.13 | 1.25 | 1.25 | 1.25 | 0.00 | 0.00 | 0.00 | 1.25 | 1.88 | 1.88 |
| IDV5 | 0.00 | 2.50 | 0.63 | 1.25 | 0.00 | 0.00 | 1.25 | 1.25 | 3.13 | 1.25 | 1.25 | 1.25 | 0.00 | 0.00 | 4.21 | 1.88 | 1.25 | 0.63 |
| IDV6 | 0.00 | 0.63 | 0.00 | 1.25 | 0.00 | 0.00 | 1.25 | 2.50 | 0.63 | 1.88 | 1.25 | 1.88 | 0.00 | 0.63 | 1.25 | 1.88 | 1.88 | 1.88 |
| IDV7 | 0.63 | 0.00 | 2.50 | 4.38 | 0.00 | 0.00 | 0.63 | 1.25 | 1.25 | 0.63 | 6.88 | 11.88 | 0.00 | 0.63 | 0.00 | 1.25 | 4.38 | 1.25 |
| IDV8 | 1.88 | 0.00 | 1.88 | 1.25 | 0.00 | 0.00 | 0.00 | 3.13 | 0.00 | 7.50 | 5.63 | 16.25 | 0.00 | 1.25 | 0.63 | 2.50 | 1.88 | 0.00 |
| IDV9 | 24.38 | 1.88 | 8.78 | 7.63 | 0.00 | 0.00 | 2.50 | 5.63 | 15.63 | 21.25 | 17.38 | 18.73 | 1.25 | 0.63 | 5.63 | 1.88 | 0.63 | 3.13 |
| IDV10 | 0.00 | 1.25 | 0.63 | 1.25 | 0.00 | 0.00 | 0.00 | 0.63 | 0.00 | 0.63 | 0.63 | 0.00 | 0.00 | 0.63 | 2.50 | 0.00 | 0.63 | 4.38 |
| IDV11 | 0.00 | 3.13 | 0.63 | 3.13 | 0.00 | 0.00 | 0.00 | 1.88 | 6.88 | 0.00 | 2.50 | 2.50 | 0.00 | 1.25 | 1.25 | 5.00 | 1.25 | 1.88 |
| IDV12 | 13.13 | 1.25 | 1.88 | 1.25 | 0.25 | 0.25 | 1.25 | 3.13 | 8.75 | 5.63 | 1.25 | 10.63 | 1.88 | 2.38 | 2.50 | 1.88 | 1.88 | 2.50 |
| IDV13 | 0.00 | 0.00 | 0.00 | 0.63 | 0.00 | 0.00 | 0.00 | 1.25 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 2.50 | 1.25 | 0.63 |
| IDV14 | 0.88 | 2.75 | 0.00 | 1.88 | 0.00 | 0.00 | 0.00 | 0.63 | 6.25 | 3.13 | 5.63 | 3.75 | 0.63 | 0.63 | 1.63 | 1.38 | 1.25 | 0.63 |
| IDV15 | 0.00 | 1.25 | 0.63 | 0.63 | 0.00 | 0.00 | 1.25 | 0.00 | 0.63 | 0.00 | 0.00 | 1.25 | 0.63 | 1.25 | 2.50 | 1.88 | 1.25 | 3.13 |
| IDV16 | 32.50 | 3.75 | 6.38 | 5.25 | 0.00 | 0.00 | 6.25 | 11.88 | 0.63 | 18.13 | 11.88 | 17.25 | 1.25 | 5.63 | 1.25 | 1.88 | 2.50 | 3.75 |
| IDV17 | 0.00 | 1.88 | 1.25 | 4.38 | 0.00 | 0.00 | 1.88 | 2.50 | 10.13 | 7.25 | 13.13 | 16.25 | 1.25 | 1.25 | 1.25 | 2.50 | 4.38 | 1.88 |
| IDV18 | 0.00 | 4.38 | 5.63 | 75.64 | 0.00 | 0.00 | 4.38 | 3.13 | 0.00 | 0.00 | 0.00 | 1.25 | 0.00 | 0.63 | 0.00 | 56.25 | 0.63 | 10.00 |
| IDV19 | 0.00 | 0.00 | 0.63 | 1.88 | 0.00 | 0.00 | 1.25 | 1.88 | 3.75 | 2.50 | 0.63 | 3.13 | 0.00 | 1.25 | 0.63 | 0.63 | 1.25 | 0.00 |
| IDV20 | 0.00 | 0.63 | 0.63 | 0.63 | 0.00 | 0.00 | 0.00 | 0.00 | 0.63 | 0.63 | 0.00 | 0.00 | 0.00 | 0.00 | 1.88 | 0.33 | 1.25 | 1.25 |
| IDV21 | 2.50 | 3.13 | 0.63 | 0.63 | 0.00 | 0.00 | 1.88 | 1.88 | 0.00 | 0.63 | 0.00 | 0.63 | 0.25 | 1.38 | 1.88 | 0.63 | 1.25 | 1.25 |
| avreage | 3.91 | 1.73 | 1.73 | 5.58 | 0.01 | 0.01 | 1.28 | 2.11 | 2.95 | 3.60 | 3.29 | 5.19 | 0.36 | 1.01 | 1.74 | 4.40 | 1.59 | 2.17 |
| PCA | NMF | NMF_KL | NMF_IS | GNMF | ONMF | SNMF | NMF_JS | ISGONMF | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| T2 | SPE | T2 | SPE | T2 | SPE | T2 | SPE | T2 | SPE | T2 | SPE | T2 | SPE | T2 | SPE | T2 | SPE | |
| Bearing 1-1 | 95.60 | 95.48 | 95.11 | 95.47 | 95.24 | 95.60 | 95.11 | 95.48 | 95.24 | 95.60 | 95.36 | 95.36 | 94.88 | 95.48 | 95.24 | 95.48 | 95.36 | 95.24 |
| Bearing 1-2 | 95.36 | 95.24 | 95.24 | 95.36 | 95.24 | 95.36 | 95.24 | 95.36 | 95.36 | 95.36 | 95.24 | 95.36 | 95.24 | 95.24 | 95.24 | 95.24 | 95.36 | 95.36 |
| Bearing 1-3 | 95.24 | 95.24 | 95.24 | 95.48 | 95.24 | 95.24 | 95.36 | 95.48 | 95.24 | 95.36 | 95.24 | 95.36 | 95.36 | 95.24 | 95.24 | 95.36 | 95.24 | 95.36 |
| Bearing 1-4 | 21.45 | 78.24 | 5.24 | 81.79 | 5.83 | 79.88 | 14.88 | 64.88 | 12.86 | 44.66 | 13.24 | 76.90 | 3.05 | 72.29 | 21.86 | 77.81 | 4.17 | 82.14 |
| Bearing 1-5 | 5.00 | 13.46 | 4.41 | 23.13 | 4.51 | 19.89 | 5.83 | 14.29 | 4.38 | 16.48 | 3.24 | 16.76 | 3.33 | 8.14 | 5.00 | 27.19 | 7.86 | 4.76 |
| Bearing 2-1 | 95.24 | 95.24 | 95.24 | 95.24 | 95.24 | 95.24 | 95.24 | 95.24 | 95.24 | 95.24 | 95.24 | 95.24 | 95.24 | 95.24 | 95.24 | 95.24 | 95.24 | 95.24 |
| Bearing 2-2 | 95.24 | 95.24 | 95.24 | 95.24 | 95.24 | 95.24 | 95.24 | 95.24 | 95.24 | 95.24 | 95.24 | 95.24 | 95.24 | 95.24 | 95.24 | 95.24 | 95.24 | 95.36 |
| Bearing 2-3 | 95.24 | 95.24 | 95.24 | 95.24 | 95.24 | 95.24 | 95.24 | 95.36 | 95.24 | 95.24 | 95.36 | 95.36 | 95.24 | 95.24 | 95.48 | 95.24 | 95.36 | 95.36 |
| Bearing 2-4 | 3.36 | 15.48 | 14.12 | 33.36 | 7.71 | 32.62 | 10.71 | 17.62 | 5.98 | 28.95 | 3.52 | 25.52 | 2.19 | 35.81 | 12.96 | 16.09 | 2.86 | 6.07 |
| Bearing 2-5 | 95.36 | 95.24 | 95.24 | 95.36 | 95.24 | 95.48 | 95.36 | 95.36 | 95.24 | 95.36 | 95.48 | 95.24 | 95.24 | 95.24 | 95.36 | 95.24 | 95.24 | 95.95 |
| Bearing 3-1 | 95.24 | 95.24 | 95.24 | 95.48 | 95.24 | 95.24 | 95.24 | 95.24 | 95.24 | 95.24 | 95.36 | 95.24 | 95.36 | 95.36 | 95.24 | 95.36 | 95.24 | 95.24 |
| Bearing 3-2 | 95.24 | 95.36 | 95.24 | 95.24 | 95.24 | 95.36 | 95.24 | 95.24 | 95.24 | 95.24 | 95.36 | 95.36 | 95.24 | 95.24 | 95.24 | 95.36 | 95.36 | 95.24 |
| Bearing 3-3 | 95.48 | 95.24 | 95.47 | 95.36 | 95.48 | 95.36 | 95.48 | 95.24 | 95.48 | 95.48 | 95.24 | 95.60 | 95.36 | 95.36 | 95.24 | 95.48 | 95.36 | 95.48 |
| Bearing 3-4 | 95.24 | 95.36 | 95.36 | 95.48 | 95.36 | 95.36 | 95.36 | 95.24 | 95.71 | 95.81 | 95.24 | 95.48 | 95.36 | 95.36 | 95.36 | 95.48 | 95.36 | 95.36 |
| Bearing 3-5 | 29.05 | 95.24 | 31.67 | 95.48 | 28.34 | 95.12 | 71.79 | 95.24 | 28.57 | 95.48 | 77.38 | 95.38 | 11.67 | 95.81 | 75.33 | 95.81 | 32.22 | 95.56 |
| avreage | 73.82 | 83.37 | 73.55 | 85.51 | 72.95 | 85.07 | 76.76 | 82.71 | 73.35 | 82.31 | 76.38 | 84.22 | 71.20 | 84.02 | 77.55 | 84.37 | 73.03 | 82.51 |
| PCA | NMF | NMF_KL | NMF_IS | GNMF | ONMF | SNMF | NMF_JS | ISGONMF | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| T2 | SPE | T2 | SPE | T2 | SPE | T2 | SPE | T2 | SPE | T2 | SPE | T2 | SPE | T2 | SPE | T2 | SPE | |
| Bearing 1-1 | 5.00 | 1.75 | 1.88 | 0.63 | 1.88 | 1.25 | 2.50 | 1.25 | 1.88 | 1.25 | 1.88 | 0.63 | 2.50 | 1.88 | 1.88 | 0.63 | 1.88 | 1.25 |
| Bearing 1-2 | 1.88 | 1.25 | 0.00 | 2.50 | 0.00 | 3.13 | 0.63 | 1.88 | 0.00 | 2.50 | 1.25 | 3.75 | 0.00 | 1.88 | 0.63 | 3.13 | 1.88 | 1.25 |
| Bearing 1-3 | 0.00 | 0.63 | 1.25 | 0.00 | 1.25 | 0.63 | 1.25 | 0.63 | 0.00 | 1.88 | 0.63 | 1.25 | 0.63 | 0.63 | 0.00 | 1.88 | 2.50 | 1.25 |
| Bearing 1-4 | 0.62 | 0.62 | 1.87 | 1.87 | 1.88 | 2.50 | 1.25 | 2.50 | 1.25 | 1.25 | 1.25 | 1.25 | 1.88 | 3.13 | 1.88 | 0.63 | 1.25 | 3.13 |
| Bearing 1-5 | 1.25 | 0.00 | 1.25 | 1.25 | 0.00 | 0.63 | 1.88 | 0.00 | 0.62 | 1.23 | 0.00 | 1.25 | 0.63 | 0.00 | 0.63 | 0.63 | 1.25 | 1.88 |
| Bearing 2-1 | 0.00 | 0.63 | 0.63 | 0.63 | 0.63 | 0.00 | 0.63 | 0.63 | 0.63 | 1.25 | 0.63 | 0.63 | 0.63 | 1.25 | 1.25 | 1.88 | 0.00 | 1.88 |
| Bearing 2-2 | 0.63 | 1.25 | 0.00 | 1.25 | 0.00 | 1.88 | 0.00 | 0.00 | 0.00 | 2.50 | 0.00 | 3.12 | 0.00 | 1.25 | 0.00 | 0.63 | 0.00 | 0.00 |
| Bearing 2-3 | 0.00 | 3.13 | 1.88 | 0.00 | 1.88 | 0.00 | 0.63 | 0.63 | 0.00 | 0.00 | 0.63 | 0.00 | 1.86 | 0.00 | 1.25 | 1.25 | 1.25 | 0.63 |
| Bearing 2-4 | 0.62 | 0.00 | 0.00 | 0.63 | 0.62 | 0.62 | 0.63 | 0.63 | 0.62 | 0.62 | 0.00 | 0.00 | 0.00 | 0.00 | 0.62 | 0.62 | 1.25 | 0.63 |
| Bearing 2-5 | 0.63 | 0.00 | 1.25 | 0.00 | 1.25 | 0.00 | 0.63 | 0.63 | 1.25 | 1.25 | 0.63 | 0.63 | 1.25 | 0.00 | 0.63 | 1.88 | 0.63 | 0.63 |
| Bearing 3-1 | 0.63 | 0.00 | 1.25 | 0.63 | 1.88 | 0.00 | 2.50 | 0.63 | 2.50 | 0.00 | 0.00 | 1.25 | 1.86 | 0.00 | 1.25 | 0.00 | 1.25 | 0.00 |
| Bearing 3-2 | 1.25 | 1.25 | 3.13 | 2.50 | 2.50 | 1.25 | 2.50 | 0.63 | 1.88 | 1.88 | 0.00 | 0.63 | 1.86 | 0.63 | 2.50 | 2.50 | 1.88 | 0.63 |
| Bearing 3-3 | 0.00 | 1.88 | 0.00 | 1.25 | 0.00 | 0.00 | 0.63 | 0.63 | 0.00 | 0.00 | 1.25 | 0.63 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.63 |
| Bearing 3-4 | 1.25 | 0.00 | 0.62 | 0.62 | 0.63 | 0.63 | 0.63 | 0.63 | 0.63 | 0.63 | 1.25 | 0.63 | 0.63 | 1.25 | 0.63 | 0.00 | 0.00 | 0.63 |
| Bearing 3-5 | 0.63 | 0.63 | 3.75 | 1.25 | 1.25 | 1.25 | 0.00 | 0.00 | 3.75 | 2.50 | 1.25 | 2.50 | 3.75 | 3.75 | 2.50 | 0.00 | 3.16 | 0.00 |
| avreage | 0.96 | 0.87 | 1.25 | 1.00 | 1.04 | 0.92 | 1.08 | 0.75 | 1.00 | 1.25 | 0.71 | 1.21 | 1.16 | 1.04 | 1.04 | 1.04 | 1.21 | 0.96 |
| Dataset | Model | FDR | FAR | ||
|---|---|---|---|---|---|
| (%) | SPE (%) | (%) | SPE (%) | ||
| TEP | ISGONMF | 48.08 | 57.21 | 1.59 | 2.17 |
| ISGNMF | 46.63 | 52.13 | 1.71 | 2.35 | |
| XJTU-SY | ISGONMF | 73.03 | 82.51 | 1.21 | 0.96 |
| ISGNMF | 72.11 | 81.95 | 0.89 | 1.12 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Wu, J.; Zhang, J.; Leung, M.-F. Graph-Regularized Orthogonal Non-Negative Matrix Factorization with Itakura–Saito (IS) Divergence for Fault Detection. Mathematics 2025, 13, 2343. https://doi.org/10.3390/math13152343
Liu Y, Wu J, Zhang J, Leung M-F. Graph-Regularized Orthogonal Non-Negative Matrix Factorization with Itakura–Saito (IS) Divergence for Fault Detection. Mathematics. 2025; 13(15):2343. https://doi.org/10.3390/math13152343
Chicago/Turabian StyleLiu, Yabing, Juncheng Wu, Jin Zhang, and Man-Fai Leung. 2025. "Graph-Regularized Orthogonal Non-Negative Matrix Factorization with Itakura–Saito (IS) Divergence for Fault Detection" Mathematics 13, no. 15: 2343. https://doi.org/10.3390/math13152343
APA StyleLiu, Y., Wu, J., Zhang, J., & Leung, M.-F. (2025). Graph-Regularized Orthogonal Non-Negative Matrix Factorization with Itakura–Saito (IS) Divergence for Fault Detection. Mathematics, 13(15), 2343. https://doi.org/10.3390/math13152343






