Abstract
The chiral nonlinear Schrödinger equation (CNLSE) serves as a simplified model for characterizing edge states in the fractional quantum Hall effect. In this paper, we leverage the generalization and parameter inversion capabilities of physics-informed neural networks (PINNs) to investigate both forward and inverse problems of 1D and 2D CNLSEs. Specifically, a hybrid optimization strategy incorporating exponential learning rate decay is proposed to reconstruct data-driven solutions, including bright soliton for the 1D case and bright, dark soliton as well as periodic solutions for the 2D case. Moreover, we conduct a comprehensive discussion on varying parameter configurations derived from the equations and their corresponding solutions to evaluate the adaptability of the PINNs framework. The effects of residual points, network architectures, and weight settings are additionally examined. For the inverse problems, the coefficients of 1D and 2D CNLSEs are successfully identified using soliton solution data, and several factors that can impact the robustness of the proposed model, such as noise interference, time range, and observation moment are explored as well. Numerical experiments highlight the remarkable efficacy of PINNs in solution reconstruction and coefficient identification while revealing that observational noise exerts a more pronounced influence on accuracy compared to boundary perturbations. Our research offers new insights into simulating dynamics and discovering parameters of nonlinear chiral systems with deep learning.
Keywords:
physics-informed neural networks; chiral nonlinear Schrödinger equations; data-driven solutions; parameters discovery MSC:
35Q55; 35R30; 65M99
1. Introduction
In recent decades, nonlinear partial differential equations (NPDEs) have emerged as indispensable mathematical frameworks for modeling and resolving the intricate dynamics underlying phenomena across fluid mechanics, quantum theory, optics, biology, finance, and others. Specifically, the renowned nonlinear Schrödinger (NLS) equation has been employed to describe physical phenomena, including quantum mechanical systems at microscopic scales [1], the dynamics of Bose–Einstein condensates [2], nonlinear wave propagation in diverse media such as optical fibers [3], shallow water media [4], and pulses [5]. Understanding the fundamental nature of nonlinear phenomena crucially depends on deriving solutions for NPDEs that govern these complex systems. This imperative has driven the development of sophisticated techniques to investigate exact solutions, such as the Hirota bilinear method [6], Darboux transformation [7], Bäcklund transformation [8], inverse scattering method [9], Lie group analysis [10], dynamical system approaches [11,12,13,14,15], and so on.
The advent of high-performance computing has spurred significant advancements in numerical algorithms for solving NPDEs, effectively mitigating the inherent limitations of traditional numerical methods, such as intricate implementation procedures and constrained applicability to high-dimensional or strongly nonlinear systems. More recently, neural network-based approaches have emerged as alternative tools for tackling NPDEs and other complex physical models [16,17,18,19,20]. Among these, the introduction of physics-informed neural networks (PINNs) has garnered significant scholarly interest [17], owing to PINNs’ unique ability to integrate physical laws into neural networks. In contrast to classical methods requiring structured meshes, the PINNs framework achieves grid independence through random sampling and incorporates automatic differentiation [21] for accurate evaluation of differential operators. On one hand, the PINNs method provides a framework for data-driven solutions of NPDEs by penalizing governing equation residuals and incorporating physical laws into the loss function. On the other hand, the PINNs method demonstrates particular efficacy in addressing inverse problems by leveraging observational data to identify unknown parameters.
Numerous renowned NPDEs have been investigated via the PINNs method. Specifically, the forward and inverse problems of the NLS equation [22] and the extended NLS equation, such as the derivative NLS equation [23], logarithmic, defocusing, fractional, and saturable NLS equations with potential [24,25,26,27], as well as high-order and high-dimensional NLS equations [28,29], were successfully addressed in terms of soliton, breather, or rogue wave solutions. Moreover, several optimization algorithms have been developed to enhance predictive accuracy and elucidate the dynamical behavior of solutions from the perspectives of loss function [30,31], hyperparameters [23,29,32,33,34], domain decomposition [35,36,37,38], conservation law [39,40], integrable property [41,42], and others [43,44,45]. Meanwhile, the error and convergence of the PINNs method were studied from both theoretical and experimental perspectives [46,47,48]. Nevertheless, it should be noted that PINNs cannot replace current numerical methods in solving well-posed low-dimensional forward problems, especially at angles of accuracy and generality [49]. Savović et al. [50] revealed that the standard explicit finite difference method (FDM) achieved better accuracy and a significant reduction in computational time compared to the PINNs approach in solving the Sine–Gordon equation. Grossmann et al. [51] compared the finite element method (FEM) and vanilla PINNs regarding computation time and accuracy across elliptic, parabolic, and hyperbolic PDEs. They discovered that FEM outperformed PINNs in computation time by 1-3 orders of magnitude, especially for lower-dimensional PDEs. For the 1D Poisson equation, the maximum accuracy achieved by the FEM surpasses that of PINNs by two orders of magnitude. Dong et al. [52] demonstrated that the performance of FEM is more efficient than that of PINNs in solving the 1D nonlinear Helmholtz equation and Burgers equation. The integration of certain concepts from conventional numerical methods with PINNs has also demonstrated promising results [53,54].
The chiral nonlinear Schrödinger equation (CNLSE) [55,56], renowned for its application in characterizing nonlinear wave propagation within chiral media (e.g., chiral materials and chiral molecules), plays a pivotal role in revealing the distinctive wave dynamics inherent to these systems. Specifically, the 1D CNLSE was derived as a simplified model to capture the essence of edge states observed in the fractional quantum Hall effect [57,58]. The 1D CNLSE is given by [55]
where denotes the complex field concerning the spatial variable x and temporal variable t, is a constant, and ∗ indicates the complex conjugate. Furthermore, the 2D CNLSE is written as [56]
where is a dispersion coefficient, and denote the coupling term’s coefficients. Here represents the complex solution in terms of variables x, y, and t. By means of the generalized auxiliary equation method [59], the Jacobi elliptic expansion method [60], and so on [61,62,63,64], numerous solutions of Equations (1) and (2) have been obtained.
To the best of our knowledge, a comprehensive exploration of the forward and inverse problems for the CNLSE using the deep learning method had not been discussed before. In this study, we aim to investigate data-driven solutions for 1D and 2D CNLSEs, while also uncovering the unknown parameters of these equations. The innovations of our work can be outlined as follows. A hybrid optimization strategy incorporating exponential learning rate decay is proposed to reconstruct the soliton and periodic solutions. Varying parameter configurations derived from the equations and their corresponding solutions are considered to evaluate the applicability of the PINNs framework. Several factors that can impact the robustness of the model in addressing inverse problems are investigated as well.
The remaining parts of this paper are organized as follows. In Section 2, we introduce the PINNs framework to address the forward and inverse problems of the CNLSEs in 1D and 2D cases. In Section 3, the real part, imaginary part, and modulus of the predicted bright soliton, dark soliton, and periodic solutions are reconstructed and analyzed. In Section 4, the coefficients of 1D and 2D CNLSEs are determined under varying levels of noise interference. We present some concluding remarks and discussions in Section 5.
2. Methods
In this section, to facilitate integration into the PINNs framework, we first apply a decomposition transform to separate the original complex equation into two coupled real-valued PDEs. Subsequently, we elaborate on the PINNs framework for addressing forward modeling and inverse parameter estimation tasks in the context of 1D and 2D CNLSEs.
2.1. Model Preprocessing
For the 1D case, the complex-valued solution of Equation (1) is decomposed into its real part and imaginary part as . Therefore, Equation (1) can be converted into
which corresponds to the following system of coupled PDEs
Analogously, for the 2D case, the complex solution of Equation (2) is decomposed as . Separating the real and imaginary components results in
Without loss of generality, we prioritize the CNLSE in 2D case as a representative scenario. The 2D CNLSE (2), defined over the computational domain , is supplemented with the following physical constraints:
where the functions and denote the initial conditions (). The boundary condition is composed of , , , and . is composed of , , , and . Particularly, the functions and denote the observational information () at a specific time , which are critical for identifying the parameters of the equation. A schematic of the PINNs framework for solving the 2D CNLSE (2) is illustrated in Figure 1.
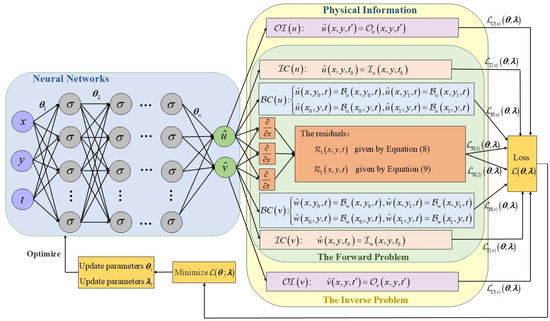
Figure 1.
Schematic of the PINNs framework tailored for addressing both forward and inverse problems of the 2D CNLSE with physical constraints (6).
2.2. Forward Problem
We leverage a fully-connected neural architecture comprising N layers, denoted as . Specifically, the input layer comprises three neurons to encode the spatial-temporal variables x, y, and t. Each hidden layer contains n neurons, with affine transformations given by , where denotes a nonlinear activation function, and and are the weight matrices, while are the bias vectors. The output layer possesses two neurons to generate the predicted solutions and , with the affine transformation , where and . The neural network iteratively updates the parameter set via automatic differentiation during backpropagation, minimizing the loss function over training iterations. In the forward problem, the loss usually comprises three components. The residuals of CNLSE, which measure the network’s compliance with the governing equation, are defined as
Thus, the losses and can be computed via automatic differentiation at collocation points , namely
where is the count of residual collocation points. The losses that come from initial and boundary conditions, ensuring adherence to prescribed initial states and domain boundaries, can be quantified through the initial value and boundary datasets and , namely
where and correspond to the count of the initial and boundary sampling points, respectively. The aggregate loss function is therefore formulated as
Finally, the optimizers Adam and L-BFGS will be used to minimize the loss (10) as much as possible by updating the parameters of the networks over a finite number of iterations. For smooth PDE solutions, the L-BFGS optimizer can converge to a satisfactory solution with fewer iterations compared to Adam. However, when dealing with stiff solutions, the L-BFGS optimizer is more prone to being trapped at a poor local minimum. In this study, our objective is to take advantage of hybrid optimizers to minimize the loss function. Therefore, the optimization process is structured in two stages: we first employ the Adam optimizer to train the model for M steps; then, the L-BFGS optimization algorithm is applied to refine the network parameters until convergence is achieved. Compared to the conventional Schrödinger equation, the introduction of chiral terms in Equations (1) and (2) may break the space-inversion symmetry, cause severe oscillations in the loss function, and trap the optimization path in a narrow valley. Thus, to overcome these challenges, an alternative approach is to implement an exponential decaying learning rate schedule instead of fixing the learning rate for the Adam optimizer (see Algorithm 1 for more details).
| Algorithm 1: Two-stage optimization with exponential learning rate decay. |
 |
2.3. Inverse Problem
Apart from the initial and boundary conditions mentioned above, we leverage observational data at specific spatial-temporal points (e.g., or ) to enhance the identification of unknown parameters . Specifically, we illustrate the methodology using observations at a fixed time , and the same approach applies analogously to observations at a fixed spatial position . With the incorporation of as undetermined parameters, the loss function must be adapted to incorporate these parameters. Importantly, should not be embedded directly into the neural network architecture, as they are external parameters to be adjusted alongside the network parameters . For observations at spatial-temporal points , we define the losses for and as
where is the number of observations. The total loss is minimized with respect to both and
In the next sections, numerical experiments are conducted to approximate the solutions and associated parameters for 1D and 2D CNLSEs. All implementations are developed in Python 3.8 with TensorFlow 2.8.0, executed on a computer configured with a 1.6 GHz eight-core i5 processor and 8 GB RAM.
3. Data-Driven Solutions of CNLSE
In this section, we leverage the PINNs method to explore data-driven solutions for 1D and 2D CNLSEs. The efficacy of PINNs is validated by examining the real part, imaginary part, and modulus of the learned solutions. Specifically, we consider bright soliton solution for 1D CNLSE, and bright, dark, as well as periodic solutions for 2D CNLSE. Particularly, different parameters of the equation and solution are adopted to highlight the applicability and robustness of the PINNs method.
3.1. Investigating the Data-Driven Soliton Solution of 1D CNLSE
By applying the sine-Gordon expansion method [58], the soliton solution of 1D CNLSE (1) is derived as
where k, c are real constants, and ensures the validity of the soliton. The spatial–temporal domain for Equation (1) is chosen as . Employing the formula and setting , and , the initial conditions for the real and imaginary parts of are given by
Analogously, the boundary conditions at for are written as
The neural network architecture employs two hidden layers, each containing 20 neurons with hyperbolic tangent (tanh) activation. The input layer processes the coordinates, while the output layer consists of two branches to predict the real and imaginary components of the solution. For training, we sample 10,000 random points within the to evaluate the PDE residuals. Furthermore, and points are allocated to satisfy the initial and boundary constraints, respectively. As summarized in Algorithm 1, we first optimize the network using Adam with exponential learning rate decay over 5000 epochs, and subsequently perform L-BFGS to refine the model. The network achieves an -norm error of after 14,577 iterations, with a total running time of 496.64 s.
Figure 2 illustrates the reconstructed soliton solution of the 1D CNLSE using physics-informed machine learning. For the real component , the 3D visualization and density map of the numerical are exhibited in Figure 2(a1,a2). The -norm error between the exact and predicted real parts is quantified as . Figure 2(a3) visualizes the absolute error distribution, revealing that the dynamic discrepancies are more pronounced near the spatial positions and compared to other regions. To further elucidate these localized deviations, Figure 2(a4) provides a comparative analysis of and specifically at and .
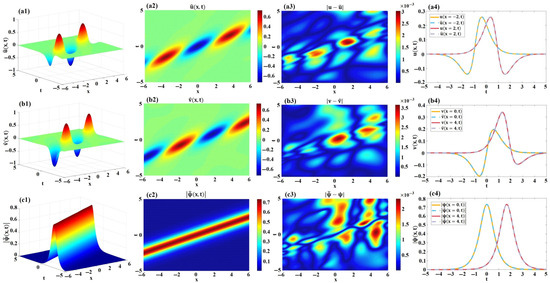
Figure 2.
The data-driven soliton solutions of the 1D CNLSE. (a1) 3D visualization of . (a2) Density map of . (a3) Absolute error distribution of . (a4) Spatiotemporal comparisons of exact and predicted real parts at and . (b1) 3D visualization of . (b2) Density map of . (b3) Absolute error distribution of . (b4) Spatiotemporal comparisons of exact and predicted imaginary parts at and . (c1) 3D visualization of . (c2) Density map of . (c3) Absolute error distribution of . (c4) Spatiotemporal comparisons of exact and predicted moduli at and .
Figure 2(b1,b2) exhibit the 3D profile and density plot of the numerically reconstructed for the imaginary part. The -norm error between the analytical reference solution and the approximation is computed as . A closer examination of the dynamic error distribution, illustrated in Figure 2(b3), reveals that the discrepancies are notably more significant near the spatial positions and compared to other regions. Therefore, we provide a comparison of the reference and the learned at the specific positions and in Figure 2(b4).
With regard to the solution modulus , Figure 2(c1,c2) display the 3D visualization and corresponding spatial intensity distribution of the machine learning-reconstructed modulus . The -norm error between the exact and predicted moduli is quantified as . The learned one-soliton solution exhibits a characteristic bell-shaped profile, with its propagation speed directly proportional to its amplitude. The dynamic error distribution for , illustrated in Figure 2(c3), underscores that the discrepancies are more pronounced near the spatial positions and compared to other regions. Accordingly, Figure 2(c4) provides a comparative analysis of the exact and numerically approximated moduli at and . This comparison reveals the soliton’s propagation along the positive t-axis as the spatial variable x evolves.
Notably, the close alignment between the solid and dashed lines in Figure 2(a4,b4,c4) indicates the efficacy of PINNs machine learning in accurately reconstructing and capturing the soliton solutions of 1D CNLSE. Since the curve-fitting results are relatively close, making it difficult to identify the variation of errors, three new plots are presented to illustrate the changes in errors over time. From Figure 3a–c, we can observe the dynamic behavior of errors varies at different spatial locations and shows no obvious regularity. Specifically, the errors in the learned real part of the solution (see Figure 3a) are more pronounced near and , with error amplitudes ranging between . The errors in the learned imaginary part (see Figure 3b) are more noticeable near and , and the error amplitudes are within . Furthermore, the amplitudes of the errors in the modulus of the solution (see Figure 3c) are within , and the errors are more significant near and , as well as near and .
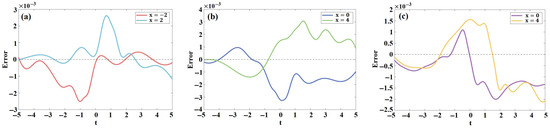
Figure 3.
Errors propagation at special position over time. (a) The errors of at spatial positions and . (b) The errors of at spatial positions and . (c) The errors of at spatial positions and .
To determine the optimal number of residual points, which are critical for training the network and minimizing PDE residuals, we conducted a series of experiments. The approximation performance of PINNs in data-driven solutions for the 1D CNLSE under varying numbers of residual points is shown in Table 1. As the number of residual points increased from 5000 to 20,000, the total iteration count fluctuated between 14,000 and 16,000. Notably, the runtime demonstrates a marked positive correlation with the quantity of residual points. However, simply augmenting residual points does not guarantee improved solution accuracy. In practical application scenarios, achieving optimal accuracy-efficiency trade-offs requires systematic experiments to identify the most suitable training point configuration.

Table 1.
Performance of PINNs in approximating data-driven solutions for the 1D CNLSE under varied residual points.
Table 2 presents the numerical results of solving Equation (1) under various parameter configurations. We can observe that the data-driven solutions remain consistently within the order of , underscoring the method’s robustness and accuracy across different parameter regimes. Furthermore, the results displayed in Table 2 elucidate a trend that training time generally increases with the number of iterations, but this relationship is not strictly linear. Specifically, the training duration does not scale proportionally with the iteration count, suggesting that other factors (e.g., network architecture, optimization dynamics, inherent problem complexity) may also play pivotal roles in influencing the training efficiency. This observation highlights the importance of a holistic approach when evaluating the performance of PINNs for solving complex nonlinear partial differential equations.

Table 2.
Performance of PINNs in approximating data-driven solutions for the 1D CNLSE under varied parameter configurations.
3.2. Investigating the Data-Driven Solution of 2D CNLSE
Building upon prior work on solving the 1D CNLSE, this subsection extends the application of PINNs to reconstruct bright soliton, dark soliton, and periodic solutions of the 2D CNLSE.
3.2.1. Data-Driven Bright Soliton Solution
The bright soliton solution for the 2D CNLSE was analytically obtained using the generalized auxiliary equation approach [59], resulting in the expression of
with the dispersion relations , and . To simulate the solution (16) for Equation (2), we select the computational domain as . The initial-boundary conditions are established through the method outlined in Section 3.1 by setting , , , , , , , and ; consequently, , and . 20,000 points are randomly sampled within the for enforcing the PDE residual. Furthermore, and points are employed to approximate the initial and boundary conditions, respectively. Other experimental conditions (e.g., network complexity, activation function, learning rate, optimization strategy) are identical to those specified in solving the 1D CNLSE case (see Section 3.1). The network achieves an -norm error of after 14,323 iterations, with a total learning time of 2047.85 s.
Figure 4 illustrates the learned real part of the data-driven bright soliton solution for the 2D CNLSE. The -norm error between the exact and predicted real parts is quantified as . The spatial–temporal evolution of the is visualized in Figure 4(a1,a2) for and , respectively. The corresponding density plots of at these time instances are shown in Figure 4(b1,b2). Furthermore, the error distributions between the exact and predicted real parts are depicted in Figure 4(c1,c2).
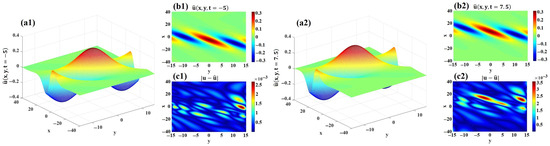
Figure 4.
The real part of the data-driven bright soliton solution for 2D CNLSE. (a1,a2) 3D visualizations of and . (b1,b2) 2D projections of and . (c1,c2) Error distributions of and .
For the imaginary part , the 3D visualizations and 2D projections of and are displayed in Figure 5(a1,a2) and Figure 5(b1,b2), respectively. The -norm error between the exact and predicted imaginary parts is computed as . Figure 5(c1,c2) illustrate the absolute error distributions for in and , respectively.
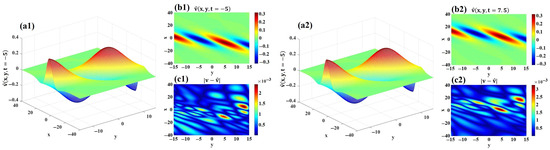
Figure 5.
The imaginary part of the data-driven bright soliton solution for 2D CNLSE. (a1,a2) 3D visualizations of and . (b1,b2) 2D projections of and . (c1,c2) Error distributions of and .
The modulus of the predicted bright soliton solution for the 2D CNLSE is analyzed in Figure 6. Specifically, the -norm error between the exact and predicted moduli is quantified as . The 3D profiles, 2D density diagrams, and dynamic error distributions of and are exhibited in Figure 6(a1,a2), Figure 6(b1,b2), and Figure 6(c1,c2), respectively. From Figure 6(b1,b2), it is evident that the bright soliton propagates along the positive x-direction during temporal evolution, consistent with the theoretical behavior of bright solitons in the 2D CNLSE.
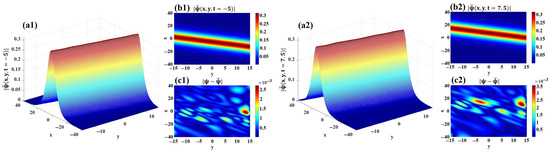
Figure 6.
The modulus of the data-driven bright soliton solution for 2D CNLSE. (a1,a2) 3D visualizations of and . (b1,b2) 2D projections of and . (c1,c2) Error distributions of and .
Furthermore, we conduct an investigation into the influence of neural network configurations on model performance by varying the number of layers and the quantity of neurons in each hidden layer. As presented in Table 3, it is evident that more intricate network architectures generally lead to an improvement in the model’s approximation accuracy for bright soliton solutions. In particular, a neural network with three layers and 20 neurons per hidden layer achieves a reasonable -norm error while mitigating excessive computational costs. Further increasing layers or neurons yields only marginal error reduction and may induce overfitting in complex networks, especially with scarce data.

Table 3.
-norm errors of the data-driven bright soliton solutions of 2D CNLSE under different numbers of network layers and neurons per hidden layer.
Table 4 provides a comparative analysis of numerical solutions for the 2D CNLSE across different coefficient configurations. The -norm errors associated with the predicted real part , imaginary part , and modulus remain bounded within , thereby validating the robustness and predictive capability of the PINNs method for solving the 2D CNLSE. Moreover, the running time reported in Table 4 demonstrates a notable increase compared to the data presented in Table 2, owing to the expanded deployment of collocation points used for enforcing the PDE residual and boundary-initial conditions.

Table 4.
Performance of PINNs in approximating data-driven solutions for the 2D CNLSE under varied coefficient selections.
In conclusion, when modeling bright solitons, PINNs are required to capture the peak position, amplitude, and waveform stability. Our experimental results demonstrate that, with errors on the order of , PINNs can successfully reproduce these key features, indicating their reliable performance in capturing the characteristics of bright solitons.
3.2.2. Data-Driven Dark Soliton Solution
For the dark soliton solution of the 2D CNLSE, we adopt the form given in [59]
where , . The computational domain , defined for Equation (2), is set as . To obtain the corresponding initial and boundary conditions, the parameter values are assigned as , , , , , , , and . Consequently, and . For the training process, we utilize random sampling points within to ensure that the PDE residual condition is met. Additionally, and points are employed to satisfy the initial and boundary conditions. All other experimental parameters are kept consistent with those specified for training the bright soliton solution. The network achieves an -norm error of after 20,000 iterations, with a total learning time of 2355.79 s.
For the real part , Figure 7(a1,a2) display the 3D visualizations, while Figure 7(b1,b2) show the 2D density plots of and . The -norm error between the exact and predicted real parts is calculated as . Furthermore, Figure 7(c1,c2) visualize the absolute error distributions of at these time instances.
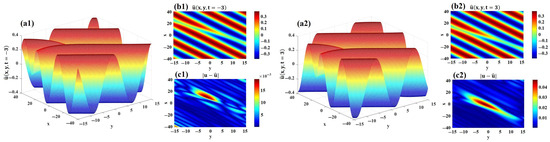
Figure 7.
The real part of the data-driven dark soliton solution for 2D CNLSE. (a1,a2) 3D visualizations of and . (b1,b2) 2D projections of and . (c1,c2) Error distributions of and .
The spatial–temporal evolution of the imaginary part is exhibited in Figure 8(a1,a2) for and . The -norm error between the exact and predicted imaginary parts is measured at . Corresponding density plots and absolute errors of at these time instances are presented in Figure 8(b1,b2) and Figure 8(c1,c2), respectively. These figures offer insights into the accuracy of the predictions across the domain.
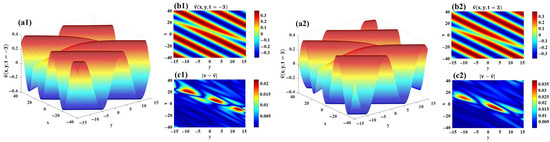
Figure 8.
The imaginary part of the data-driven dark soliton solution for 2D CNLSE. (a1,a2) 3D visualizations of and . (b1,b2) 2D projections of and . (c1,c2) Error distributions of and .
The modulus of the data-driven dark soliton solution for the 2D CNLSE is analyzed in Figure 9. The -norm error between the exact and predicted moduli is quantified as . Specifically, the 3D visualizations, 2D density plots, and dynamic error distributions of and are presented in Figure 9(a1,a2), Figure 9(b1,b2), and Figure 9(c1,c2), respectively. From Figure 9(b1,b2), it is evident that the dark soliton propagates along the negative x-axis as time progresses.
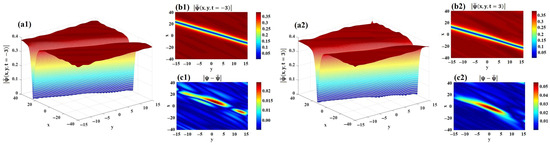
Figure 9.
The modulus of the data-driven dark soliton solution for 2D CNLSE. (a1,a2) 3D visualizations of and . (b1,b2) 2D projections of and . (c1,c2) Error distributions of and .
Table 5 illustrates the impact of different weight distributions in the loss function on the -norm errors, total number of iterations, and running time when solving the dark soliton solutions of the 2D CNLSE. Specifically, as the weights are gradually reduced from 1 to 0.1, a discernible upward trend is observed in the -norm errors associated with , , and . When examining the total number of iterations and the running time, no consistent pattern emerges across various weight configurations. Nevertheless, it becomes apparent that the model configured with all weights set to 1 demonstrates superior performance in accurately approximating the dark soliton solution of the 2D CNLSE.

Table 5.
Effect of weights distributions of the loss function for solving the dark soliton solution of 2D CNLSE.
In summary, when dealing with dark solitons, the key features encompass the width and depth of the dark region, as well as its contrast against the surrounding background. Since the simulation error of dark solitons is , there remains space for PINNs to improve their performance in capturing specific elements.
3.2.3. Data-Driven Periodic Solution
The periodic solution (also referred to as an exponential solution in the literature [59]) for the 2D CNLSE is written as
where , . The computational domain , defined for Equation (2), is set as . To derive the initial and boundary conditions, the parameters are assigned the values: , , , , , , , and . This yields and . The experimental parameters, including the network structure, allocation points, activation function, and optimization strategy, are kept consistent with those outlined in Section 3.2.1. The network achieves an -norm error of after 9212 iterations, with a total learning time of 1431.71 s.
Figure 10 illustrates the learned real part of the data-driven periodic solution for the 2D CNLSE. The -norm error between the exact and predicted real parts is measured at . The spatial–temporal evolution of is exhibited in Figure 10(a1,a2) for and . Additionally, the 2D density diagrams and absolute error distributions for at these two time points are depicted in Figure 10(b1,b2) and Figure 10(c1,c2), respectively.
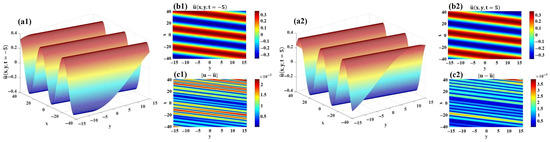
Figure 10.
The real part of the data-driven periodic solution for 2D CNLSE. (a1,a2) 3D visualizations of and . (b1,b2) 2D projections of and . (c1,c2) Error distributions of and .
For the imaginary part , the 3D visualizations and 2D projections of and are displayed in Figure 11(a1,a2) and Figure 11(b1,b2), respectively. The -norm error between the exact and predicted imaginary parts is computed as . Figure 11(c1,c2) illustrate the absolute error distributions for at and , respectively.
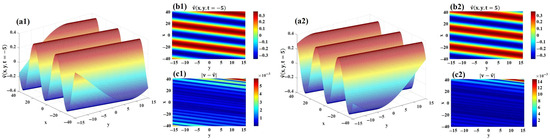
Figure 11.
The imaginary part of the data-driven periodic solution for 2D CNLSE. (a1,a2) 3D visualizations of and . (b1,b2) 2D projections of and . (c1,c2) Error distributions of and .
The modulus of the machine learning-generated periodic solution for the 2D CNLSE is analyzed in Figure 12. Specifically, the -norm error between the exact and predicted moduli is quantified as . The 3D profiles, 2D density diagrams, and dynamic error distributions of and are exhibited in Figure 12(a1,a2), Figure 12(b1,b2), and Figure 12(c1,c2), respectively.
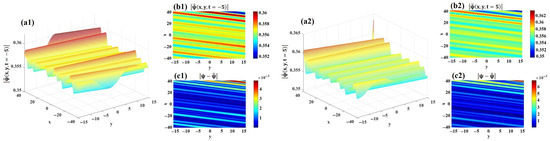
Figure 12.
The modulus of the data-driven periodic solution for 2D CNLSE. (a1,a2) 3D visualizations of and . (b1,b2) 2D projections of and . (c1,c2) Error distributions of and .
Table 6 provides a comprehensive summary of the -norm errors associated with diverse optimization schemes employed for solving the modulus of 1D and 2D CNLSEs. The single Adam optimizer, when executed for 10,000 steps with a constant learning rate of 0.001, yields an error magnitude on the order of . For the Adam optimizer incorporating exponential learning rate decay, referred to as Adam⋆ in Table 6, the first stage of Algorithm 1 is implemented to minimize the model over 10,000 steps. The data presented in the table clearly demonstrate that Adam⋆ outperforms the original Adam optimizer with a fixed learning rate, especially when dealing with 2D problems. The single L-BFGS optimizer, trained until convergence, exhibits better performance than Adam or Adam⋆. However, it is still inferior to the two-stage optimization approach that combines Adam and L-BFGS. In a comparative analysis of hybrid optimization strategies, the combination of the L-BFGS optimizer with Adam⋆ exhibits superior predictive performance in comparison to its pairing with the original Adam optimizer.

Table 6.
Performance of different optimization schemes for solving the CNLSEs.
In conclusion, when handling periodic solutions, PINNs have to accurately determine the period, amplitude, and phase. With a simulation error of , PINNs exhibit a remarkable capability in capturing the characteristics of periodic solutions.
4. Data-Derived Discovery of CNLSE
In the subsequent analysis, we employ the PINNs framework, as detailed in Section 2.3, to identify the coefficients of 1D and 2D CNLSEs. Particularly, we assess the network’s resilience by incorporating quantitative noise perturbations into both the initial-boundary conditions and the observed data, thereby examining the feasibility and practical applicability of the method under realistic conditions.
4.1. Recognizing the Coefficients Driven by Solution Data of the 1D CNLSE
The 1D CNLSE with unknown coefficients is given by
In this subsection, we consider the computational domain for Equation (19) defined by . Alongside the initial-boundary conditions specified in Equations (14) and (15), we incorporate observational data at the spatial position . These observations are expressed as
Specifically, we sample equidistant points in the temporal domain at the fixed spatial position . The observational data are then generated by substituting these points into Equation (20). Additionally, we initialize the unknown parameters with the guess . All other experimental conditions remain consistent with the forward problem setup described in Section 3.1. The network training completed in approximately 525.39 s after 13,462 iterations. The identified coefficients are and . The evolution of these coefficients from their starting values of 0.1 to the final estimates is visualized in Figure 13a. To better observe fluctuations in the training trajectory after 6000 iterations, Figure 13(a1) provides a detailed zoom of the training dynamics for and . As depicted in Figure 13(a1), the identified coefficients are observed to repeatedly touch and cross the standard values. This phenomenon is attributed to the multi-objective optimization task and some potential factors, such as the interactions among the parameters.
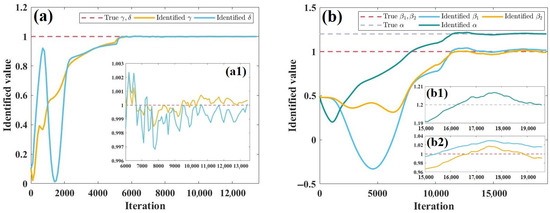
Figure 13.
The process of coefficients being determined from initial guesses to target values. (a) Driving data derive from the solution of the 1D CNLSE. (a1) Variation curve of prediction coefficients and over iterations 6000–13,462. (b) Driving data derive from the solution of the 2D CNLSE. (b1) Variation curve of prediction coefficient over iterations 15,000–19,581. (b2) Variation curve of prediction coefficients and over iterations 15,000–19,581.
To assess the robustness of neural networks, we conducted an investigation by incorporating Gaussian noise into the training dataset. For this purpose, our study generates zero-mean Gaussian noise characterized by independent and identically distributed samples and then superimposes it onto the training dataset. The procedure for introducing n% Gaussian noise into the clear data is outlined as follows:
- # add n% noise to Data(x)
- def NoisyData(x):
- sigma=n/100
- for i in range(x.size)
- NewData=Data(x) + random.gauss(0, sigma)
- return NewData
Here, Data(x) represents either a dataset or a function, and the dimension of x is arbitrary. We suppose that sigma denotes the standard deviation of the Gaussian distribution. By adding Gaussian noise, we obtain a new dataset NewData, and this process is defined as NoisyData(x). On the one hand, we consider the impact of initial and boundary perturbations on the predictive accuracy of the model. As shown in Table 7, even when a level of 3% initial and boundary noise is introduced into the training data, the error in identifying the coefficients and can be as small as . However, as the noise level escalates to 5%, the error in coefficient identification rises to . On the other hand, we further scrutinized the sensitivity of observation noise on the model. According to the results in Table 8, when 1% observation noise is added, the error in identifying both coefficients remains at the order of . When the observation noise level is increased to 3%, the error fluctuates between the order of and . Furthermore, when the observation noise reaches 5%, the error in coefficient identification once again climbs to . The results summarized in Table 7 and Table 8 highlight two key insights. Firstly, the PINNs method demonstrates remarkable proficiency in accurately recognizing the coefficients of the 1D CNLSE. Secondly, it becomes evident that observation noise exerts a more pronounced influence on the model’s accuracy compared to initial-boundary noise.

Table 7.
A comparison between the estimated coefficients of Equation (19) derived from solutions under varying initial-boundary noise levels.

Table 8.
A comparison between the estimated coefficients of Equation (19) derived from solutions under varying observation noise levels.
Furthermore, we conduct additional numerical experiments to investigate the scenarios in which the presented method begins to fail. In this study, we hypothesize that PINNs start to lose effectiveness when the accuracy of the predicted coefficients hits . Table 9 shows that the prediction accuracy of one of the coefficients increases to when the initial-boundary noise exceeds 3.2%. When the initial-boundary noise reaches 9%, the accuracy of both predicted coefficients rises to . When noise greater than 10% is introduced, the PINNs method becomes invalid. In contrast, Table 10 demonstrates that observational noise has a more pronounced impact on the model. When 2% observational noise is introduced, the prediction accuracy of one of the coefficients increases to . When the observational noise level is maintained between 3.5% and 8%, the prediction accuracy of both coefficients rises to . When the intensity of the observational noise exceeds 8. 5%, the PINNs method starts to fail.

Table 9.
Errors of the estimated coefficient of Equation (19) derived from solutions under varying initial-boundary noise levels.

Table 10.
Errors of the estimated coefficient of Equation (19) derived from solutions under varying observation noise levels.
4.2. Recognizing the Coefficients Driven by Solution Data of the 2D CNLSE
The 2D CNLSE with unknown coefficients is given by
In this subsection, we establish a fixed spatial domain defined by , which is set to . Subsequently, we embark on an investigation into the impact of altering the temporal range and the set of observation moments on the performance of PINNs. In the training process of the neural network, 10,000, , and random points are sampled from the respective domains for evaluating PDE residuals, initial conditions, and boundary conditions. Moreover, at each observation moment, points are acquired for further analysis. Regarding the selection of optimizers, we also employ the two-stage optimization strategy as described in Section 2.2. Specifically, we first optimize the network using Adam over 10,000 epochs, and subsequently utilize L-BFGS optimizer to further train the model. In addition, we provide an initial estimate for the unknown parameters, setting . All other experimental conditions remain consistent with those specified in Section 3.1.
To investigate the impacts of the temporal range and the observation moments on the model, we separately considered scenarios where the computational domain is symmetric about the origin and where the initial time instant is fixed at zero. Specifically, the selection of a time-axis computational domain symmetric about the origin is aimed at enhancing the model’s capability to capture the inherent symmetric physical laws in the equation solutions, thereby improving the accuracy and convergence rate of the solution. Maintaining a fixed initial time allows for a more straightforward view of how the distances between the observation moments and the initial time affect the model.
The results provided in Table 11 and Table 12 demonstrate that, when the temporal range is kept constant, the predictive error decreases significantly at later observation moments compared with earlier ones. In essence, the observation moment can be viewed as a calibration tool which serves to identify the PDE coefficients with greater precision. However, when the temporal range is expanded to a broader extent, relying solely on a single observation moment proves insufficient for accurately identifying all the parameters. Consequently, we incorporate additional observation moments to enhance the prediction accuracy.

Table 11.
Estimation coefficients from Equation (21) across varying temporal range and observation moments . The symbol “/” indicates unsuccessful parameter estimation (error ≥ 1).

Table 12.
Estimation coefficients from Equation (21) across varying temporal range and observation moments .
Particularly, with the temporal range set to and the observation moments specified as and , the model training consumed approximately 3991.76 s, and the optimal model was attained at the 19,581th iteration. The identified coefficients converged to the values , , and . We scaled and visualized the trajectory of these coefficients evolving from their initial guess values of 0.5 to their final values, as depicted in Figure 13b. To obtain a clearer view of the fluctuations in the coefficient curves beyond the 15,000th iteration, Figure 13(b1,b2) present the detailed training dynamics for and , , respectively, spanning iterations from 15,000 to 19,581.
5. Conclusions and Discussions
In this study, we extended the application of physics-informed neural networks (PINNs) to tackle forward modeling and inverse parameter estimation tasks for 1D and 2D chiral nonlinear Schrödinger equations (CNLSEs). The performance of PINNs was investigated and analyzed with respect to various influencing factors, including model parameter selection, network architecture, weight setting, noise intensity, temporal range, as well as the number of residual points and observation time instants.
For forward problems, data-driven soliton solutions of 1D and 2D CNLSEs were explored, achieving accuracies ranging from to . Numerical simulations visualized the real part, imaginary part, and modulus of the learned bright soliton, dark soliton, and periodic solutions. For inverse problems, remarkable results were obtained in coefficient identification. In the 1D CNLSE, two coefficients were identified with an accuracy of and . Even with 5% noise in initial and boundary data, the identification error remained at . Numerical experiments demonstrated that observation noise has a more pronounced impact on prediction accuracy than initial-boundary noise. For the 2D CNLSE, three coefficients were identified, achieving accuracies of and . When noise greater than 10% is introduced, the PINNs method becomes invalid. The results further indicate that, under fixed temporal ranges, errors at later observation instants were smaller than those at earlier instants, while larger temporal ranges required multiple observation instants for accurate parameter identification. In addition, we point out that the differences in computational costs of PINNs under various problem settings in this study primarily stem from the dimensionality of the equations and the number of configuration points. The derivative operations (especially high-order derivatives) based on the chain rule also significantly increase the computational cost.
However, there are still some aspects worth improving for the PINNs method. When the parameters c and k in Equation (13) satisfy or , the solution of the equation exhibits a highly localized spatial distribution. Consequently, PINNs begin to fail in accurately capturing the characteristic features of the solution. Future research will focus on introducing a neuron-wise locally adaptive activation function to better address these issues. Some non-intuitive strategies, such as combining PINNs with domain decomposition techniques and conservation law constraints, can be adopted to improve the model’s overall performance across diverse solution types. Moreover, we plan to integrate the advantages of PINNs and traditional numerical methods to provide more comprehensive and practical solutions. Investigating the impact of potential interactions among identified parameters on the model when tackling inverse problems is also a worthwhile task meriting thorough consideration.
The physics-informed deep learning approach provides a novel tool for simulating and reconstructing the intricate dynamics of nonlinear systems. Although it has certain limitations compared to traditional numerical methods in solving well-posed low-dimensional forward problems, as error and optimization theories keep evolving, deep learning is expected to produce more practical outcomes with major impacts.
Author Contributions
Conceptualization, Z.W., L.Z., X.H., and C.M.K.; methodology, Z.W., L.Z., X.H., and C.M.K.; software, Z.W.; validation, L.Z.; formal analysis, Z.W. and L.Z.; investigation, Z.W., L.Z., X.H., and C.M.K.; data curation, Z.W.; writing—original draft preparation, Z.W. and L.Z.; writing—review and editing, Z.W., L.Z., X.H., and C.M.K.; visualization, Z.W.; supervision, L.Z.; funding acquisition, L.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (12172199).
Data Availability Statement
Data will be made available upon request.
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Schrödinger, E. An undulatory theory of the mechanics of atoms and molecules. Phys. Rev. 1926, 28, 1049–1070. [Google Scholar] [CrossRef]
- Bludov, Y.V.; Konotop, V.V.; Akhmediev, N. Matter rogue waves. Phys. Rev. A 2009, 80, 033610. [Google Scholar] [CrossRef]
- Solli, D.R.; Ropers, C.; Koonath, P.; Jalali, B. Optical rogue waves. Nature 2007, 450, 1054–1057. [Google Scholar] [CrossRef] [PubMed]
- Chabchoub, A.; Hoffmann, N.P.; Akhmediev, N. Rogue wave observation in a water wave tank. Phys. Rev. Lett. 2011, 106, 204502. [Google Scholar] [CrossRef] [PubMed]
- Hasegawa, A.; Tappert, F. Transmission of stationary nonlinear optical pulses in dispersive dielectric fibers. I. Anomalous dispersion. Appl. Phys. Lett. 1973, 23, 142–144. [Google Scholar] [CrossRef]
- Hirota, R. The Direct Method in Soliton Theory; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Matveev, V.B.; Salle, M.A. Darboux Transformations and Solitons; Springer Press: Berlin/Heidelberg, Germany, 1991. [Google Scholar]
- Miura, R.M. Bäcklund Transformations, the Inverse Scattering Method, Solitons, and Their Applications; Springer Press: Berlin, Germany, 1978. [Google Scholar]
- Ablowitz, M.J.; Clarkson, P.A. Solitons, Nonlinear Evolution Equations and Inverse Scattering; Cambridge University Press: Cambridge, UK, 1991. [Google Scholar]
- Olver, P.J. Applications of Lie Groups to Differential Equations; Springer: New York, NY, USA, 1993. [Google Scholar]
- Zhang, L.J.; Wang, J.D.; Shchepakina, E.; Sobolev, V. New solitary waves in a convecting fluid. Chaos Solitons Fractals 2024, 183, 114953. [Google Scholar] [CrossRef]
- Li, J.B.; Liu, Z.R. Traveling wave solutions for a class of nonlinear dispersive equations. Chin. Ann. Math. 2002, 23, 397–418. [Google Scholar] [CrossRef]
- Zhang, L.J.; Zhao, Q.; Huo, X.W.; Khalique, C.M. Explicit Solutions to the n-dimensional Semi-stationary Compressible Stokes Problem. Int. J. Theor. Phys. 2025, 64, 49. [Google Scholar] [CrossRef]
- Liu, H.Z.; Li, J.B. Symmetry reductions, dynamical behavior and exact explicit solutions to the Gordon types of equations. J. Comput. Appl. Math. 2014, 257, 144–156. [Google Scholar] [CrossRef]
- Wang, J.D.; Zhang, L.J.; Li, J.B. New solitary wave solutions of a generalized BBM equation with distributed delays. Nonlinear Dyn. 2023, 111, 4631–4643. [Google Scholar] [CrossRef]
- Sirignano, J.; Spiliopoulos, K. DGM: A deep learning algorithm for solving partial differential equations. J. Comput. Phys. 2018, 375, 1339–1364. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Long, Z.C.; Lu, Y.P.; Dong, B. PDE-Net 2.0: Learning PDEs from data with a numeric-symbolic hybrid deep network. J. Comput. Phys. 2019, 399, 108925. [Google Scholar] [CrossRef]
- Lu, L.; Jin, P.Z.; Pang, G.F.; Zhang, Z.Q.; Karniadakis, G.E. Learning nonlinear operators via DeepONet based on the universal approximation theorem of operators. Nat. Mach. Intell. 2021, 3, 218–229. [Google Scholar] [CrossRef]
- Li, Z.Y.; Kovachki, N.; Azizzadenesheli, K.; Liu, B.; Bhattacharya, K.; Stuart, A.; Anandkumar, A. Fourier neural operator for parametric partial differential equations. arXiv 2020, arXiv:2010.08895. [Google Scholar]
- Baydin, A.G.; Pearlmutter, B.A.; Radul, A.A.; Siskind, J.M. Automatic differentiation in machine learning: A survey. J. Mach. Learn. Res. 2018, 18, 1–43. [Google Scholar]
- Pu, J.C.; Li, J.; Chen, Y. Soliton, breather, and rogue wave solutions for solving the nonlinear Schrödinger equation using a deep learning method with physical constraints. Chin. Phys. B 2021, 30, 060202. [Google Scholar] [CrossRef]
- Pu, J.C.; Li, J.; Chen, Y. Solving localized wave solutions of the derivative nonlinear Schrödinger equation using an improved PINN method. Nonlinear Dyn. 2021, 105, 1723–1739. [Google Scholar] [CrossRef]
- Zhou, Z.J.; Yan, Z.Y. Solving forward and inverse problems of the logarithmic nonlinear Schrödinger equation with -symmetric harmonic potential via deep learning. Phys. Lett. A 2021, 387, 127010. [Google Scholar] [CrossRef]
- Wang, L.; Yan, Z.Y. Data-driven rogue waves and parameter discovery in the defocusing nonlinear Schrödinger equation with a potential using the PINN deep learning. Phys. Lett. A 2021, 404, 127408. [Google Scholar] [CrossRef]
- Bo, W.B.; Wang, R.R.; Fang, Y.; Wang, Y.Y.; Dai, C.Q. Prediction and dynamical evolution of multipole soliton families in fractional Schrödinger equation with the -symmetric potential and saturable nonlinearity. Nonlinear Dyn. 2023, 111, 1577–1588. [Google Scholar] [CrossRef]
- Song, J.; Yan, Z.Y. Deep learning soliton dynamics and complex potentials recognition for 1D and 2D -symmetric saturable nonlinear Schrödinger equations. Physica D 2023, 448, 133729. [Google Scholar] [CrossRef]
- Zhang, Y.; Lv, X. Data-driven solutions and parameter discovery of the extended higher-order nonlinear Schrödinger equation in optical fibers. Physica D 2024, 468, 134284. [Google Scholar] [CrossRef]
- Tang, K.J.; Wan, X.L.; Yang, C. DAS-PINNs: A deep adaptive sampling method for solving high-dimensional partial differential equations. J. Comput. Phys. 2023, 476, 111868. [Google Scholar] [CrossRef]
- Yu, J.; Lu, L.; Meng, X.H.; Karniadakis, G.E. Gradient-enhanced physics-informed neural networks for forward and inverse PDE problems. Comput. Methods Appl. Mech. Eng. 2022, 393, 114823. [Google Scholar] [CrossRef]
- Li, J.H.; Chen, J.C.; Li, B. Gradient-optimized physics-informed neural networks (GOPINNs): A deep learning method for solving the complex modified KdV equation. Nonlinear Dyn. 2022, 107, 781–792. [Google Scholar] [CrossRef]
- Jagtap, A.D.; Kawaguchi, K.; Karniadakis, G.E. Adaptive activation functions accelerate convergence in deep and physics-informed neural networks. J. Comput. Phys. 2020, 404, 109136. [Google Scholar] [CrossRef]
- Hou, J.; Li, Y.; Ying, S.H. Enhancing PINNs for solving PDEs via adaptive collocation point movement and adaptive loss weighting. Nonlinear Dyn. 2023, 111, 15233–15261. [Google Scholar] [CrossRef]
- Wu, C.X.; Zhu, M.; Tan, Q.Y.; Kartha, Y.; Lu, L. A comprehensive study of non-adaptive and residual-based adaptive sampling for physics-informed neural networks. Comput. Methods Appl. Mech. Eng. 2023, 403, 115671. [Google Scholar] [CrossRef]
- Jagtap, A.D.; Kharazmi, E.; Karniadakis, G.E. Conservative physics-informed neural networks on discrete domains for conservation laws: Applications to forward and inverse problems. Comput. Methods Appl. Mech. Eng. 2020, 365, 113028. [Google Scholar] [CrossRef]
- Jagtap, A.D.; Karniadakis, G.E. Extended physics-informed neural networks (XPINNs): A generalized space-time domain de-composition based deep learning framework for nonlinear partial differential equations. Commun. Comput. Phys. 2020, 28, 2002–2041. [Google Scholar] [CrossRef]
- Pu, J.C.; Chen, Y. Complex dynamics on the one-dimensional quantum droplets via time piecewise PINNs. Phys. D 2023, 454, 133851. [Google Scholar] [CrossRef]
- Luo, D.; Jo, S.H.; Kim, T. Progressive Domain Decomposition for Efficient Training of Physics-Informed Neural Network. Mathematics 2025, 13, 1515. [Google Scholar] [CrossRef]
- Fang, Y.; Wu, G.Z.; Kudryashov, N.A.; Wang, Y.Y.; Dai, C.Q. Data-driven soliton solutions and model parameters of nonlinear wave models via the conservation-law constrained neural network method. Chaos Solitons Fractals 2022, 158, 112118. [Google Scholar] [CrossRef]
- Lin, S.N.; Chen, Y. A two-stage physics-informed neural network method based on conserved quantities and applications in localized wave solutions. J. Comput. Phys. 2022, 457, 111053. [Google Scholar] [CrossRef]
- Pu, J.C.; Chen, Y. Lax pairs informed neural networks solving integrable systems. J. Comput. Phys. 2024, 510, 113090. [Google Scholar] [CrossRef]
- Lin, S.N.; Chen, Y. Physics-informed neural network methods based on Miura transformations and discovery of new localized wave solutions. Physica D 2023, 445, 133629. [Google Scholar] [CrossRef]
- Yang, L.; Meng, X.H.; Karniadakis, G.E. B-PINNs: Bayesian physics-informed neural networks for forward and inverse PDE problems with noisy data. J. Comput. Phys. 2021, 425, 109913. [Google Scholar] [CrossRef]
- Song, J.; Zhong, M.; Karniadakis, G.E.; Yan, Z.Y. Two-stage initial-value iterative physics-informed neural networks for simulating solitary waves of nonlinear wave equations. J. Comput. Phys. 2024, 505, 112917. [Google Scholar] [CrossRef]
- Anand, R.; Manikandan, K.; Serikbayev, N. Exploring data driven soliton and rogue waves in symmetric and spatio-temporal potentials using PINN and SC-PINN methods. Eur. Phys. J. Plus 2025, 140, 214. [Google Scholar] [CrossRef]
- Lu, L.; Meng, X.H.; Mao, Z.P.; Karniadakis, G.E. DeepXDE: A deep learning library for solving differential equations. SIAM Rev. 2021, 63, 208–228. [Google Scholar] [CrossRef]
- Wang, S.F.; Yu, X.L.; Perdikaris, P. When and why PINNs fail to train: A neural tangent kernel perspective. J. Comput. Phys. 2022, 449, 110768. [Google Scholar] [CrossRef]
- Zhou, Z.J.; Yan, Z.Y. Is the neural tangent kernel of PINNs deep learning general partial differential equations always convergent. Phys. D 2024, 457, 133987. [Google Scholar] [CrossRef]
- Zhang, W.W.; Suo, W.; Song, J.H.; Cao, W.B. Physics Informed Neural Networks (PINNs) as intelligent computing technique for solving partial differential equations: Limitation and Future prospects. arXiv 2024, arXiv:2411.18240. [Google Scholar] [CrossRef]
- Savović, S.; Ivanović, M.; Drljača, B.; Simović, A. Numerical Solution of the Sine-Gordon Equation by Novel Physics-Informed Neural Networks and Two Different Finite Difference Methods. Axioms 2024, 13, 872. [Google Scholar] [CrossRef]
- Grossmann, T.G.; Komorowska, U.J.; Latz, J.; Schönlieb, C.B. Can physics-informed neural networks beat the finite element method? IMA J. Appl. Math. 2024, 89, 143–174. [Google Scholar] [CrossRef] [PubMed]
- Dong, S.C.; Li, Z.W. Local extreme learning machines and domain decomposition for solving linear and nonlinear partial differential equations. Comput. Methods Appl. Mech. Eng. 2021, 387, 114129. [Google Scholar] [CrossRef]
- Xiao, Y.; Yang, L.M.; Shu, C.; Dong, H.; Du, Y.J.; Song, Y.X. Least-square finite difference-based physics-informed neural network for steady incompressible flows. Comput. Math. Appl. 2024, 175, 33–48. [Google Scholar] [CrossRef]
- Tarbiyati, H.; Nemati Saray, B. Weight initialization algorithm for physics-informed neural networks using finite differences. Eng. Comput. 2024, 40, 1603–1619. [Google Scholar] [CrossRef]
- Nishino, A.; Umeno, Y.; Wadati, M. Chiral nonlinear Schrödinger equation. Chaos Solitons Fractals 1998, 9, 1063–1069. [Google Scholar] [CrossRef]
- Biswas, A. Chiral solitons in 1+2 dimensions. Int. J. Thror. Phys. 2009, 48, 3403–3409. [Google Scholar] [CrossRef]
- Aglietti, U.; Griguolo, L.; Jackiw, R.; Pi, S.Y.; Semirara, D. Anyons and chiral solitons on a line. Phys. Rev. Lett. 1996, 77, 4406. [Google Scholar] [CrossRef] [PubMed]
- Bulut, H.; Sulaiman, T.A.; Demirdag, B. Dynamics of soliton solutions in the chiral nonlinear Schrödinger equations. Nonlinear Dyn. 2018, 91, 1985–1991. [Google Scholar] [CrossRef]
- Akinyemi, L.; Inc, M.; Khater, M.M.A.; Rezazadeh, H. Dynamical behaviour of Chiral nonlinear Schrödinger equation. Opt. Quant. Electron. 2022, 54, 191. [Google Scholar] [CrossRef]
- Hosseini, K.; Mirzazadeh, M. Soliton and other solutions to the (1+2)-dimensional chiral nonlinear Schrödinger equation. Commun. Theor. Phys. 2020, 72, 125008. [Google Scholar] [CrossRef]
- Eslami, M. Trial solution technique to chiral nonlinear Schrödinger’s equation in (1+2)-dimensions. Nonlinear Dyn. 2016, 85, 813–816. [Google Scholar] [CrossRef]
- Raza, N.; Arshed, S. Chiral bright and dark soliton solutions of Schrödinger’s equation in (1+2)-dimensions. Ain Shams Eng. J. 2020, 11, 1237–1241. [Google Scholar] [CrossRef]
- Younis, M.; Cheemaa, N.; Mahmood, S.A.; Rizvi, S.T. On optical solitons: The chiral nonlinear Schrödinger equation with perturbation and Bohm potential. Opt. Quant. Electron. 2016, 48, 1–41. [Google Scholar] [CrossRef]
- Esen, H.; Ozdemir, N.; Secer, A. Solitary wave solutions of chiral nonlinear Schrödinger equations. Mod. Phys. Lett. B 2021, 35, 2150472. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).