Exploring Harmonic Evolute Geometries Derived from Tubular Surfaces in Minkowski 3-Space Using the RM Darboux Frame
Abstract
1. Introduction
2. Preliminaries
- X is called spacelike if or ,
- X is called timelike if ,
- X is called lightlike (or null) if and .
3. RM Darboux Frame in Minkowski 3-Space
4. Modeling Tubular Surfaces Through the RM Darboux Frame
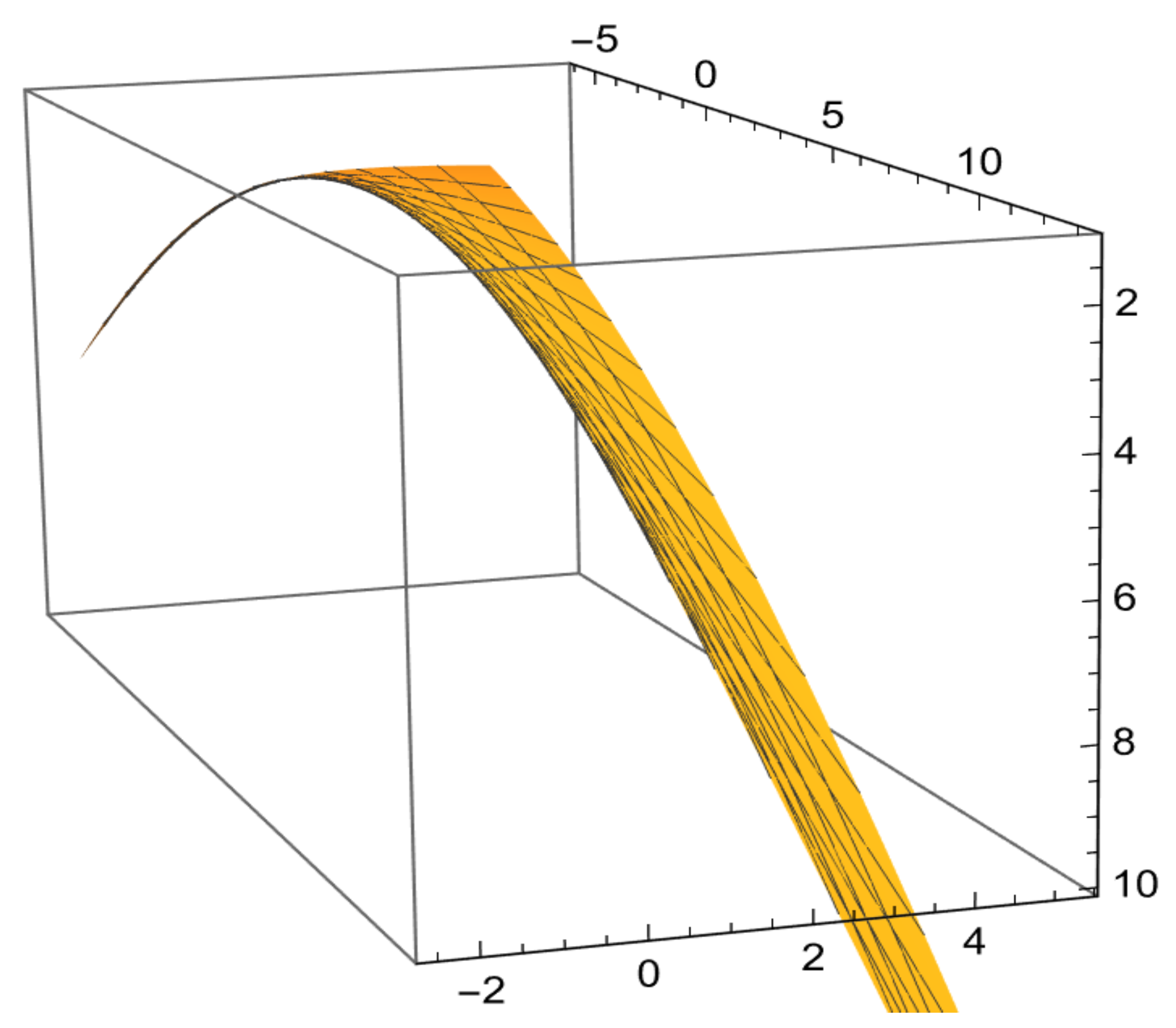
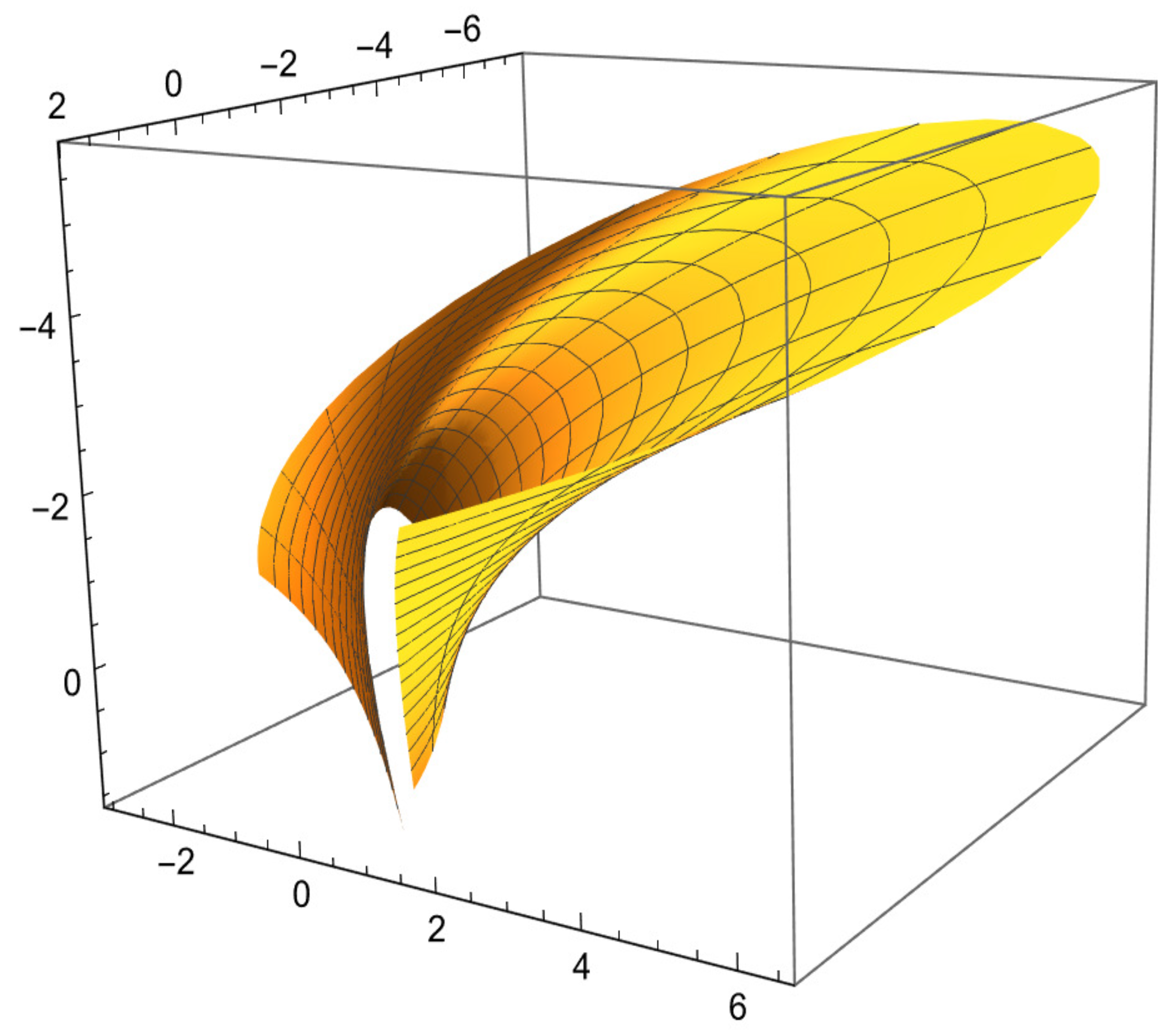
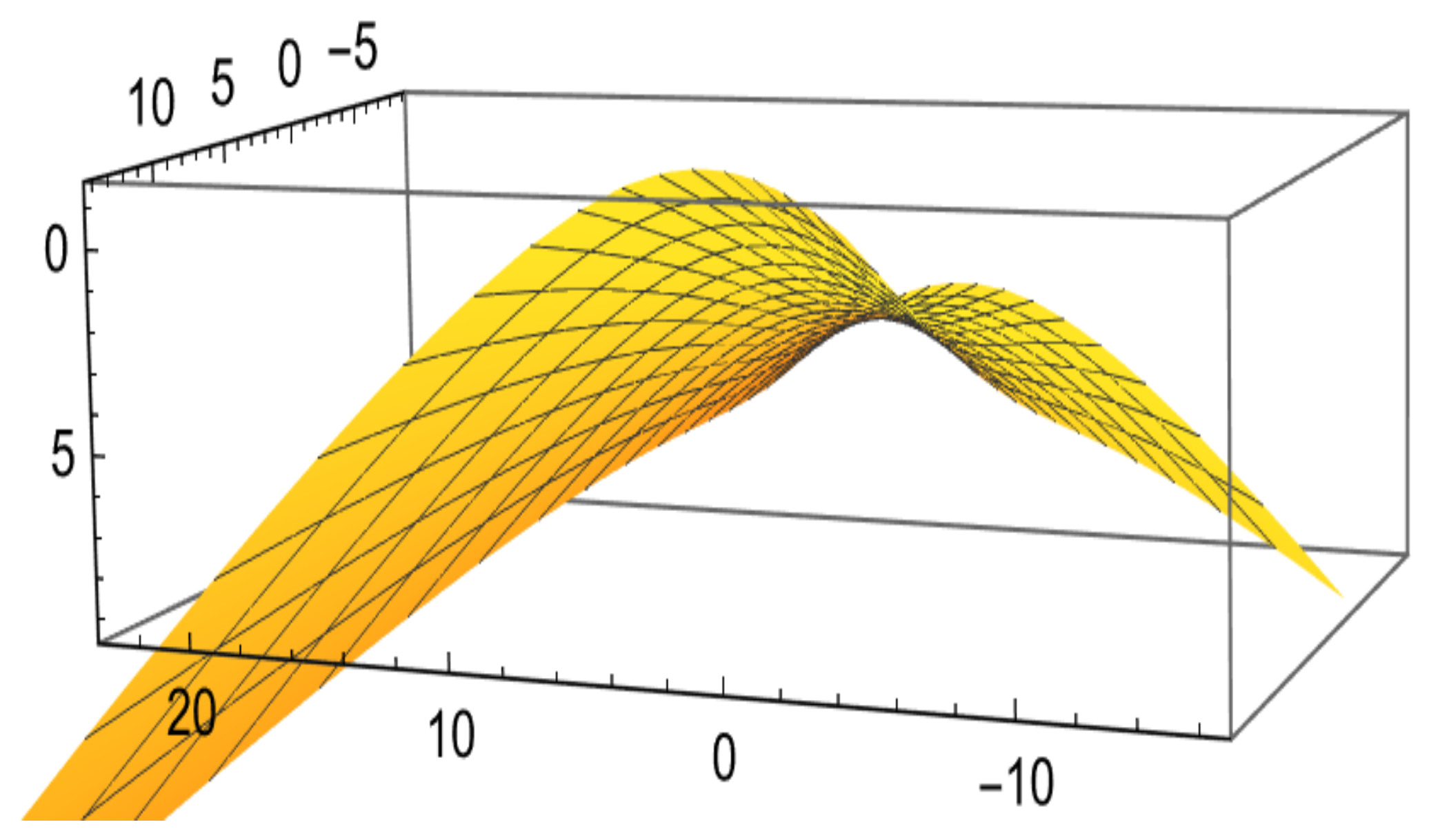
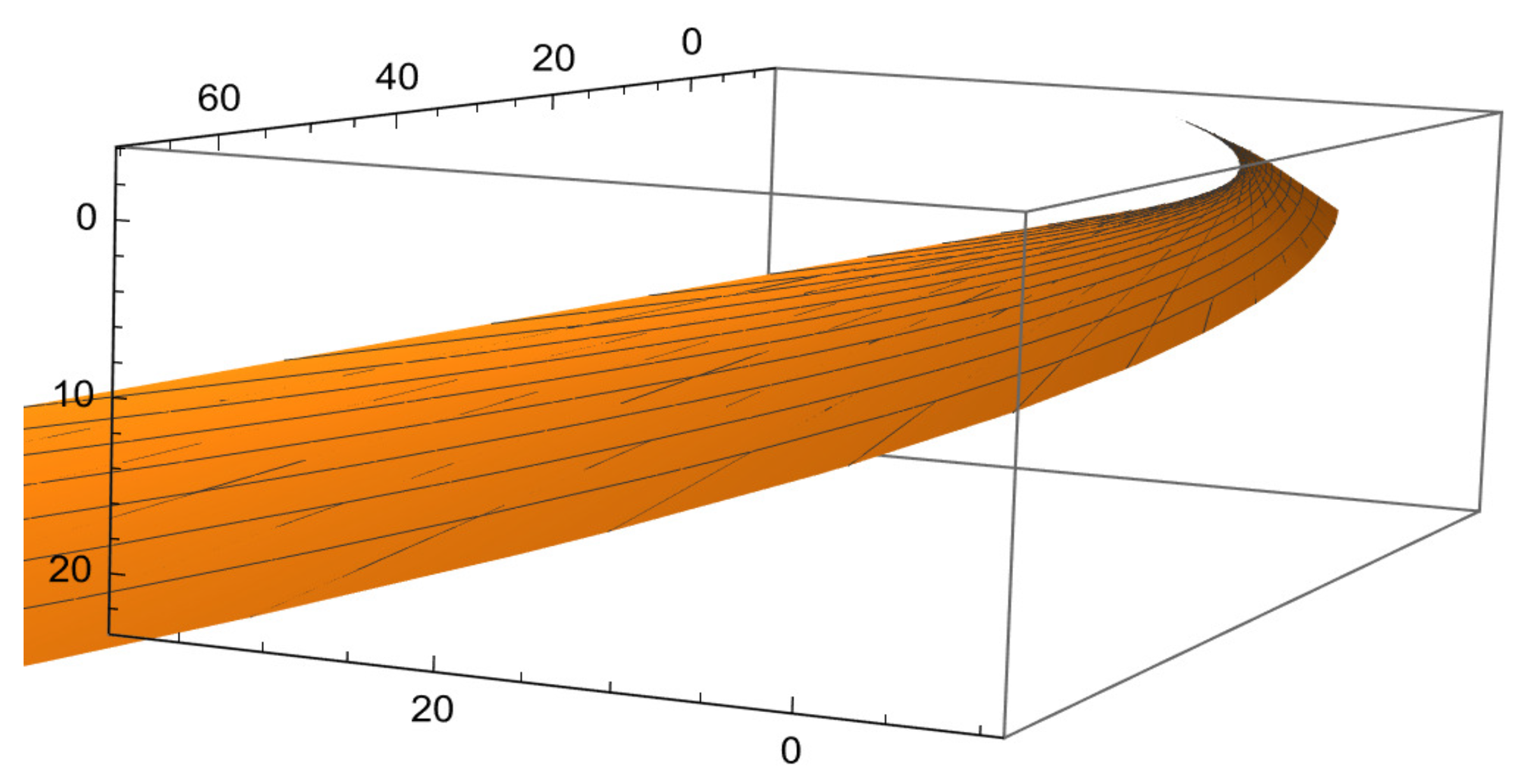
5. Building a Tubular Surface Harmonically Using the RM Darboux Frame
- 1.
- The r-parameter curves of cannot be asymptotic curves.
- 2.
- The υ-parameter curves of are asymptotic curves if and only if η satisfies the partial differential equation
- , this indicates the curves with r-parameters are not asymptotic.
- If and only if . Then, , which indicates the curves with υ-parameters are asymptotic.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Drachal, K.; Mishra, V.N. Some algebro–geometric aspects of spacetime c–boundary. Math. Aeterna 2016, 6, 561–572. [Google Scholar]
- Laurian-Ioan, P.; Mishra, V.N. Projective flatness of a new class of g-metrics. Georgian Math. J. 2017, 26, 133–139. [Google Scholar] [CrossRef]
- Yoon, D.W. Timelike Minimal Surfaces and Harmonic Maps in Minkowski 3-Space. Bull. Korean Math. Soc. 2022, 59, 1649–1662. [Google Scholar]
- Solouma, E.; Al-Dayel, I.A.; Abdelkawy, M.A. Ruled surfaces and their geometric invariants via the orthogonal modified frame in Minkowski 3-space. Mathematics 2025, 13, 940. [Google Scholar] [CrossRef]
- Aminian, M.B.; Kashani, S.M. Lk-biharmonic Hypersurfaces in Space Forms. Acta Math. Vietnam. 2017, 42, 471–490. [Google Scholar] [CrossRef]
- Park, S.; Pyo, J. Chern-Ricci harmonic functions on zero mean curvature surfaces in the three-dimensional Lorentz-Minkowski space and the rigidity of Enneper’s surface. J. Math. Anal. Appl. 2022, 514, 126371. [Google Scholar] [CrossRef]
- Elsharkawy, A.; Cesarano, C.; Tawfiq, A.; Ismail, A.A. The non-linear Schrödinger equation associated with the soliton surfaces in Minkowski 3-space. AIMS Math. 2022, 7, 17879–17893. [Google Scholar] [CrossRef]
- Bishop, L.R. There is more than one way to frame a curve. Am. Math. Monthly 1975, 82, 246–251. [Google Scholar] [CrossRef]
- Özdemir, M.; Tosun, M. Rotation Minimizing Frames in Lorentz-Minkowski 3-Space. Commun. Fac. Sci. Univ. Ank. Ser. A1 Math. Stat. 2021, 70, 757–770. [Google Scholar]
- Sipus, Z.M.; Volenec, V. The harmonic evolute of a surface in Minkowski 3-space. Math. Commun. 2014, 19, 43–55. [Google Scholar]
- Lopez, R.; Sipus, Z.M.; Gajcic, L.P.; Protrka, I. Harmonic evolutes of B-scrolls with constant mean curvature in Lorentz-Minkowski space. Int. J. Geom. Methods Mod. Phys. 2019, 16, 1950076. [Google Scholar] [CrossRef]
- García, R.; Jiménez, J. On the use of rotation minimizing frames for curves in Lorentzian spaces. Mathematics 2020, 8, 1412. [Google Scholar]
- Körpinar, T.; Kaymanli, G.U. On the harmonic evolute of quasi normal surfaces. J. Sci. Arts 2010, 1, 55–64. [Google Scholar]
- Solouma, E.M.; Al-Dayel, I. Harmonic Evolute Surface of Tubular Surfaces via F-Darboux Frame in Euclidean 3-Space. Adv. Math. Phys. 2021, 2021, 7. [Google Scholar] [CrossRef]
- Ali, A.T.; Turgut, M. Rotation Minimizing Darboux Frame and Applications to Surfaces in Minkowski Space. Results Math. 2023, 78, 153. [Google Scholar]
- Saad, M.K. On the harmonic evolute of time-like Hasimoto surfaces in Lorentz–Minkowski space. Int. J. Geom. Methods Mod. Phys. 2023, 20, 2350206. [Google Scholar] [CrossRef]
- Gladkov, S.O. To the question of Gauss’s curvature in n-dimensional Euclidian space. J. Math. Res. 2020, 12, 93–99. [Google Scholar] [CrossRef]
- Bektaş, M.; Akyiğit, M. Harmonic maps and RM frames on curves in Lorentzian spaces. Adv. Geom. 2021, 21, 489–503. [Google Scholar]
- Özdemir, M.; Yaylı, Y. On RM frame and tubular surfaces in Euclidean and Minkowski space forms. Turk. J. Math. 2022, 46, 684–699. [Google Scholar]
- Chen, B.Y.; Li, S. Harmonicity and evolute surfaces using Darboux frame fields in E3. Differ. Geom. Its Appl. 2023, 89, 101874. [Google Scholar]
- O’Neill, B. Semi-Riemannian Geometry With Applications to Relativity; Academic Press: New York, NY, USA, 1983. [Google Scholar]
- Do Carmo, M.P. Differential Geometry of Curves and Surfaces; Revised and Updated Second Edition; Courier Dover Publications: Mineola, NY, USA, 2016. [Google Scholar]
- Savci, U.Z.; Yilmaz, S. The Darboux rotation axis & special curves according to rotation minimizing frame in Minkowski 3- Space. Prespacetime J. 2018, 9, 232–244. [Google Scholar]
- Hu, S.; Wang, Z.; Tang, X. Tubular surfaces of center curves on spacelike surfaces in Lorentz-Minkowski 3-space. Math. Methods Appl. Sci. 2019, 42, 3136–3166. [Google Scholar] [CrossRef]
- Hu, G.; Cao, H.; Wu, J.; Wei, G. Construction of developable surfaces using generalized C-Bézier bases with shape parameters. Comput. Appl. Math. 2020, 39, 157. [Google Scholar] [CrossRef]
- Qian, J.; Liu, J.; Fu, X.; Jung, S.D. Geometric characterizations of canal surfaces with Frenet center curves. AIMS Math. 2021, 6, 9476–9490. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Solouma, E.; Saber, S.; Baskonus, H.M. Exploring Harmonic Evolute Geometries Derived from Tubular Surfaces in Minkowski 3-Space Using the RM Darboux Frame. Mathematics 2025, 13, 2329. https://doi.org/10.3390/math13152329
Solouma E, Saber S, Baskonus HM. Exploring Harmonic Evolute Geometries Derived from Tubular Surfaces in Minkowski 3-Space Using the RM Darboux Frame. Mathematics. 2025; 13(15):2329. https://doi.org/10.3390/math13152329
Chicago/Turabian StyleSolouma, Emad, Sayed Saber, and Haci Mehmet Baskonus. 2025. "Exploring Harmonic Evolute Geometries Derived from Tubular Surfaces in Minkowski 3-Space Using the RM Darboux Frame" Mathematics 13, no. 15: 2329. https://doi.org/10.3390/math13152329
APA StyleSolouma, E., Saber, S., & Baskonus, H. M. (2025). Exploring Harmonic Evolute Geometries Derived from Tubular Surfaces in Minkowski 3-Space Using the RM Darboux Frame. Mathematics, 13(15), 2329. https://doi.org/10.3390/math13152329






