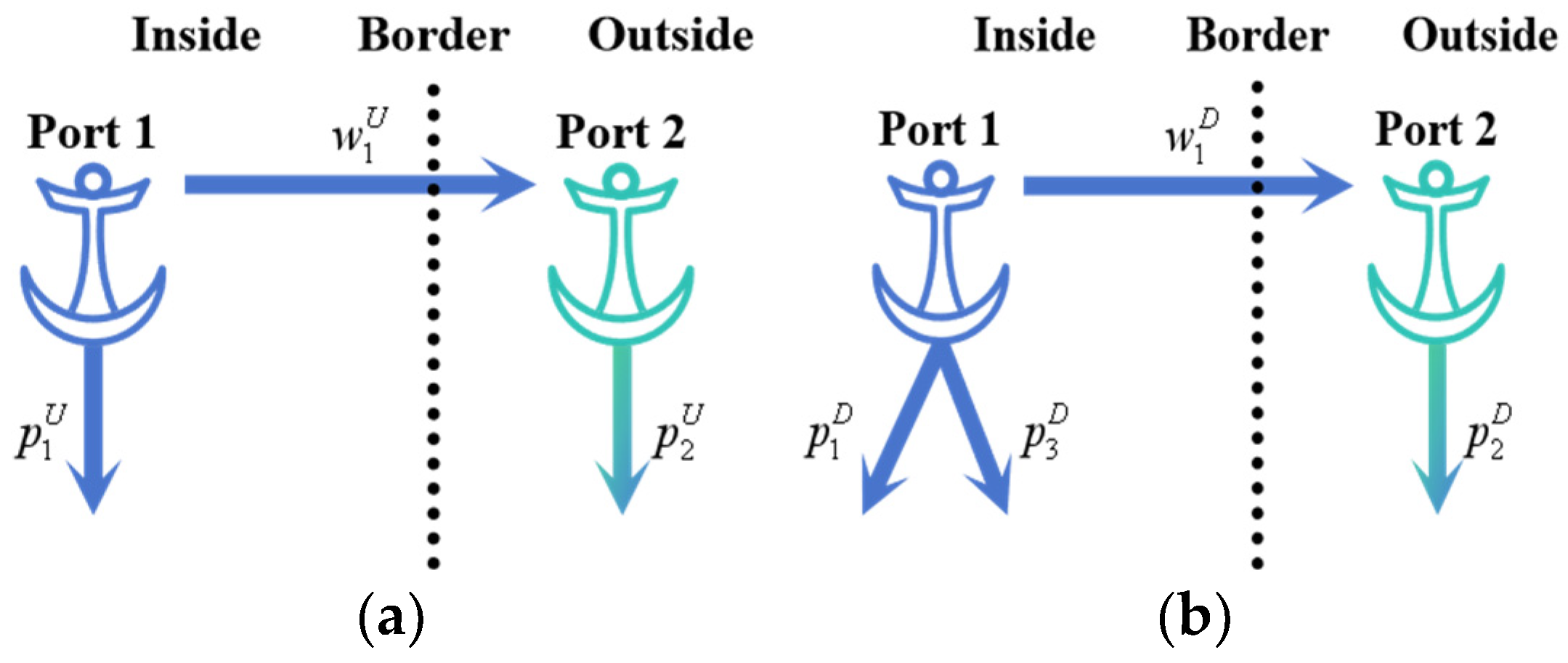
1. Introduction
Ports, as a basis for regional economic development, generally offer the value of increasing port throughput, which has broad economic impacts [
1,
2,
3,
4,
5]. To achieve a synergistic effect for ports in a specific region, different ports employ various methods to maximize benefits from the economy or environment, such as price adjustments or increased environmental benefits [
6,
7,
8]. For example, in China, the Guangdong–Hong Kong–Macao Greater Bay Area is in the process of integrating regional economic development, with frequent port activities and complex commercial relations. From this case, the unified market is being implemented in relevant policies [
9]. Then, in the port field, is it possible to realize a unified policy, such as the price strategy from the port? In particular, under the special circumstances of crossing the border, whether it is possible to achieve the rational operation of regional ports in a specific way is a realistic problem that needs to be considered urgently in the current policy of regional economic integration.
Additionally, the wave of digitalization is constantly empowering every link of port operation [
10,
11,
12,
13]. For example, blockchain technology not only enhances the transparency of port logistics and the security of data sharing but also automates workflow through smart contracts, significantly reducing human errors and delays, thereby improving overall operational efficiency [
14,
15,
16,
17]. At the same time, blockchain technology also helps the port cope with the increasingly complex international trade environment and volatile customer needs, ensuring the port’s core position in the global logistics network. Hence, as a port used for regional activity, it needs to consider how to utilize its technical superiority to enhance port service efficiency, such as data sharing through the support of blockchain technology, which helps to improve customer experience.
The existing literature on port operations has explored pricing strategies and operational strategies using game-theoretical models, laying the groundwork for understanding strategic interactions among ports. Blockchain technology, as an emerging technology, holds significant potential for enhancing data sharing and operational collaboration. Therefore, we aim to explore a potential solution for improving the service level of ports using blockchain technology in regional development. Additionally, this study addresses three questions:
- (1)
What is the equilibrium for the inside border port in the context of cross-border ports for regional rationalization development?
- (2)
What is the value of blockchain technology in facilitating data sharing between ports in across-border activity?
- (3)
What is the equilibrium strategy for inside border port, as an incumbent port, when facing different cases such as port congestion?
Through these discussions, we can show the research value in enhancing the level of port service and blockchain service while highlighting the unique features of studying port activities.
Based on these questions, we develop a game-theoretical model to investigate the equilibrium between inside and outside border ports, considering existing activities. Correspondingly, the analytical questions are shown below.
Firstly, we analyze the equilibrium strategy for competitive ports in the different zones. Specifically, we find that the equilibrium is a differentiated price strategy from the view of the inside border port due to its controllability in the local area. In this case, a differential price strategy can enhance the diversity of port services to obtain economic benefits for the inland border port.
Secondly, we explore the equilibrium strategy by supporting blockchain technology for competitive ports. Specifically, although it is an equilibrium strategy to use a differentiated price strategy, the empowerment of blockchain technology can realize the economic benefits of an inside border port under limited conditions, due to a controllable degree of port strategy in local zones, which also demonstrates the commercial value of blockchain in data sharing.
Finally, we discuss port congestion about the feature of port research. Specifically, we investigate the decision to expand the inside border port. The results suggest that the port manager should consider the economic benefits of expanding port capacity. Furthermore, we also analyze the environmental impact, tariff impact, and influence of port cooperation, which provides some management implications for ports located within the border (also referred to as incumbent ports).
Therefore, this study makes two contributions. On the one hand, our study proposes a management strategy. In this study, we develop a game-theoretical model to investigate the optimal strategy in the context of an across-border port, considering two pricing strategies: unified price and differential price. Specifically, we examine the influence of an inside border port with controllability on business strategy. The analytical results can be used as a reference for ports from the view of flexibility in the price decision and economic strategy. On the other hand, the results emphasize the importance of improving port operation efficiency by using the new technology. By introducing blockchain technology for data sharing, the operational efficiency of the local port can be significantly improved, costs can be reduced, and service quality can be enhanced. Moreover, the study proposes an analytical framework for integrating blockchain-enabled data sharing into a pricing strategy model for cross-border port interactions. Further discussion shows that it can be applied to actual situations in port management.
The paper is structured as follows:
Section 2 presents a literature review;
Section 3 describes the model setting, including scenario analysis and game-theoretical model setting;
Section 4 provides an analysis of service price, service quantity, firms’ profits and decisions, decision of data sharing by blockchain service, and decision of expansion for incumbent port;
Section 5 analyzes the environment impact, tariff impact, and influence of port cooperation; and
Section 6 presents the main findings and managerial implications.
Appendix A provides proof to support the propositions.
4. Basic Analysis
In the basic analysis, we discuss several aspects, including service price, service quantity, firms’ profits, the decision to share data via blockchain services, and capacity expansion.
4.1. Service Price
In this part, we analyze the service price of ports. Specifically, we compare the service price between Port 1 to Port 2 and the market prices of two ports, respectively. The findings are shown in Proposition 1.
Proposition 1. (Service price):
- (1)
;
- (2)
; ; .
Proposition 1 illustrates the service price for ports under the two cases of price strategy. Specifically, the first finding shows that the two pricing methods will not have a clear price size. Both Port 1 and Port 2 need to consider the transferred container quantity when determining their pricing strategy in relation to the upstream price. Note that the flexible upstream price refers to the changes in service price between Port 1 and Port 2 in a horizontal direction, which are uncertain.
Moreover, from the aspect of downstream price activity, Port 1’s price shows the same tendency. Note that the downstream price represents the service price changes in Port 1 and Port 2 in the market, moving in a vertical direction. Therefore, Port 1 has no clear pricing preference due to the uncertain upstream price. However, we find that unified pricing is higher than differentiated pricing as the latter is more flexible. In addition, unified pricing is equivalent to transferring low price to high price and high price to low price in a unified market, reaching a unified price in a market. Finally, we also found that unified pricing is more advantageous than differential pricing (). This case also reflects the value of a unified market in pricing.
Therefore, from the viewpoint of service price, we can deduce two aspects of management implications. On the one hand, the incumbent port (e.g., Port 1) could consider using a unified pricing strategy to attract the most customers, given the relatively low price level for customers. On the other hand, the incumbent port could determine the upstream service price according to the cooperation level of other ports due to their uncontrollable business behavior.
4.2. Service Quantity
In this part, we analyze the service quantity for ports between two price models. Specifically, we discuss the changes in container quantity in the U model and D model. Moreover, we also reflect the quantity changes for the incumbent port (e.g., Port 1), which are shown in Proposition 2.
Proposition 2. (Service quantity):
- (1)
; ; ;
- (2)
.
Proposition 2 shows the service quantity changes for two models. The strategy of differential price shows the quantity effect from Proposition 2(1). Although the incumbent port has no clear price strategy, the D model has high level quantity (). That is the differentiated pricing targets specific market segments, attracting more customers. One the one hand, the container quantity from Port 2 to Port 1 prefers the U model since a unified price strategy could reduce potential market risk (). This case is named the quantity effect in our study. On the other hand, shows that the sales quantity under unified pricing is lower than the average sales quantity under differentiated pricing for the incumbent port (e.g., Port 1). This is because the price acceptable to consumers in differentiated pricing reconciles the sales quantity when consumers choose unified pricing. In this case, from the view of customers, they prefer to use the low price (such as acceptable price ) to obtain more container quantity. However, shows the different results in general cognition. Therefore, from this view, we could point out that the U model is beneficial to some extent for the incumbent port (e.g., Port 1).
Therefore, from the perspective of the quantity effect, we can derive management implications. To meet customer requirements, the D model can offer a relatively low price and capture a substantial transferred quantity for the incumbent port (e.g., Port 1). Moreover, the incumbent port can consider adopting a new model to achieve a consistent choice between price and quantity strategies, such as implementing new technology to facilitate strategy changes.
4.3. Profit and Firm’s Decision
In this section, we analyze the profit and the firm’s decision in the U model and D model based on Proposition 3 to determine the optimal strategy.
Proposition 3. (Profit analysis): ; .
Proposition 3 reflects the profit changes between Port 1 and Port 2. Specifically, the result indicates that the optimal strategy of Port 1 is the D model. The potential reason has two aspects. On the one hand, the D model has a large market share compared to the U model, which can satisfy the needs of consumers, thus gaining the motivation of continuous investment and key support. On the other hand, the differentiated pricing scheme helps the port to optimize the service quality and quantity. By offering various levels of service to cater to the diverse needs of different customers, the port can utilize its resources more effectively and enhance operational efficiency. From the perspective of Port 2, as an outside border port, it is more willing to increase its benefits and capture a larger market share through a unified price. However, since Port 2 is located on the outside border, its optimal strategy does not need to be considered.
Therefore, we can obtain the two aspects of management implications. On the one hand, ports should pay attention to the importance of market segmentation and positioning. The port’s adoption of a differentiated price scheme first shows the importance of market segmentation. By deeply understanding the needs, preferences, and payment ability of different customers, ports can divide the market into different customer groups and provide customized services and prices for each group. This kind of market segmentation is helpful for ports to meet customers’ needs more accurately, improve customer satisfaction, and then increase market share and profits. On the other hand, ports also need to consider the level of price decision. In other words, ports need to constantly adjust prices according to market changes, customer demand, and competitive situations to ensure steady growth of benefits. This flexible pricing ability is very important for the long-term development of the port because it can help the port maintain its competitiveness in the complex and changing market environment.
4.4. Decision of Data Sharing by Blockchain Service
In this part, we consider adopting the blockchain service into the port decision. The motivation is that ports can increase the service experience by data sharing with blockchain services, such as information of cargo circulation or increasing supply chain activity. In this case, we use the blockchain service to increase consumer experience . Moreover, in order to improve the data cooperation between ports, an inside border port may choose to share certain data or information with an external border port (), but an outside port needs to pay related fees. In other words, the openness of data will have a direct bearing on the benefit of out-board ports. This case has the advantage of improving the service experience of the two ports and bringing higher service efficiency to consumers.
According to this setting, we can redesign the analytical model based on the basic model. Specifically, we adopt the new inverse demand functions and profit function as follows:
Based on these settings, we consider the new results between the new U-B model and the D model, which obtain the equilibrium strategy in Proposition 4 from Ports 1 and 2. Note that shows that the higher participation usually means lower marginal cost for Port 2, which also shows the value of technology maturity for technology investment of blockchain service. means the benefits of blockchain information opening. is the technical cost to be shared.
Proposition 4. (Decision of data sharing by blockchain service):
- (1)
; ;
- (2)
Proposition 4 shows the decision of data sharing using the blockchain service for ports. Specifically, we can find that the result is , which shows the value of the blockchain service between the U-B model and the D model. The result reveals that the openness of blockchain services can improve the efficiency of port services and the value of data. The potential reasons can be divided into two parts. For example, blockchain technology ensures that data is encrypted and stored on multiple nodes through distributed ledger technology, making it difficult to be tampered with or deleted, thereby providing a highly secure data sharing environment. At the same time, the openness of the blockchain enhances the transparency of the supply chain, allowing ports to access the status and information of goods in real-time. In addition, the blockchain also optimizes the cross-border trade process, reduces the detention time of goods in the port, and improves the logistics efficiency by simplifying document processing, realizing paperless trading, and accelerating customs clearance.
However, from the port’s perspective, the result shows that the equilibrium strategy is the D model. In other words, the D model is more flexible for port’s services. Although the D model is an equilibrium strategy between ports, the inside border port can better control a reasonable strategy. Therefore, the management implications of blockchain technology and differential price strategy for ports can be adopted in two aspects.
On the one hand, through the introduction of blockchain technology, ports within the border can establish a decentralized and tamper-proof data sharing platform, enabling ports, shipping companies, and other parties to share and update cargo information in real-time and accurately, thereby improving logistics efficiency. On the other hand, the differentiated pricing strategy can provide personalized service prices according to the needs of different customers and the characteristics of goods, which can not only attract more customers but also enhance the profitability of the port. By combining blockchain technology and differentiated pricing strategy, ports can achieve more efficient, flexible and safer operation and management, enhance competitiveness, and meet the diversified needs of the market.
4.5. Decision of Expansion for Incumbent Port
In this section, we consider the decision to expand an incumbent port. Specifically, we analyze the case where the incumbent port is located inside a border port (e.g., Port 1), which demonstrates the influence of port capacity on port activity based on the U-B model. Specifically, we adjust the term
to
, one of term
as the level of expansion level for Port 1. In addition, we can adopt the profit function for the U-BE model as follows:
Note that the term is the expansion cost of the port. According to the quantity changes for Port 1, we can obtain the term , which describes port congestion in the cases of the two models. Based on these changes for model setting in the new model, we can deduce Proposition 5 about the decision of expansion for an incumbent port.
Proposition 5. (Decision of expansion for incumbent port):
- (1)
The is small; the result is .
- (2)
The is the maximum for satisfying a specific condition; the result is .
Proposition 5 shows the decision of expansion for an incumbent port. Specifically, when the cost of port capacity expansion is small, we need to consider its impact from two aspects. On the one hand, a unified pricing strategy is the key to efficient port operation. It simplifies the port operation process, eliminates the complicated negotiations caused by price differences, and effectively relieves the port congestion problem. On the other hand, the application of blockchain technology has brought revolutionary changes to port management. Through real-time data sharing and the automatic execution of intelligent contracts, the port can accurately track cargo dynamics, optimize resource allocation, and maximize the utilization of port capacity.
When the cost of port capacity expansion is high, it is particularly necessary to choose a unified pricing scheme. On the one hand, the unified pricing scheme can effectively reduce the management and operational costs of ports, as it avoids the complicated negotiation and contract management associated with differentiated pricing. In the context of high expansion costs, this simplified operation method can help the port better control costs and improve economic benefits. On the other hand, unified pricing can also enhance the market competitiveness of ports, attract more customers, and stabilize market share by providing a consistent and transparent price system. Furthermore, the scheme can also reduce management risk, avoid uncertainty caused by price fluctuations and changes in market demand, and provide a guarantee for the stable operation of the port.
Therefore, we can adopt some management implications for ports. On the one hand, cost-effectiveness and decision-making flexibility are the elements that must be weighed when ports make strategic decisions. When the port faces capacity expansion, if the cost is low, we should actively adopt new technologies, such as blockchain, to promote innovation in port operations and improve service quality and efficiency. However, when the cost of expansion is high, it is necessary to consider cost-effectiveness more carefully and choose a more economical and less risky scheme, such as a unified pricing scheme, to ensure a return on investment and stable port operation.
On the other hand, technological innovation and market demand are the two driving forces for the sustainable development of ports. The introduction of blockchain and other technologies has brought unprecedented opportunities for port management, which can significantly improve the efficiency of data sharing and optimize resource allocation. However, the application of these technologies also needs to be closely combined with market demand to ensure that the technologies are in line with the actual business scenarios and to enhance the competitiveness and customer satisfaction of the port.
5. Further Analysis
5.1. Influence of Environment by Port Activity
In this part, we analyze the influence of the environment on port activity between the U model and the U-B model. According to some existing studies [
40,
41], we can adopt the quantity between two models to obtain the environment impact:
,
. This model can be understood as every unit of quantity having pollution emissions. Hence, we can obtain Proposition 6.
Proposition 6. (Influence of environment by port activity): .
Proposition 6 shows the environment impact by port activity between the U model and U-B model according to the above analysis. Specifically, we found that the result is . The potential reason has two aspects. On the one hand, the unified price strategy primarily focuses on pricing methods and market strategies and has a limited direct impact on the environment. It pays more attention to the economic benefits and market competition of enterprises and less directly involves the consumption and emission of environmental resources. Therefore, from this perspective, the environmental impact of the unified price strategy is not significant. On the other hand, the unified price strategy supported by blockchain technology, although enhanced by the high efficiency and transparency of blockchain technology, has an impact on the environment that is not single and stable. The operation of blockchain technology consumes a lot of energy and may produce certain carbon emissions. At the same time, the application of blockchain technology may also lead to an increase in hardware waste and a challenge to data storage, which will have a certain impact on the environment. However, the size of this impact depends on the specific implementation of blockchain technology and is related to energy-saving and emission-reduction measures.
Therefore, when developing a pricing strategy, a port should not only consider economic benefits and market competition, but also fully evaluate its impact on the environment. Port needs to realize that any business activity may have a direct or indirect impact on the environment. Therefore, environmental sustainability should be taken into consideration when formulating strategies to ensure that ports can contribute to environmental protection while pursuing economic benefits. Furthermore, when introducing new technologies such as blockchain, ports should not only focus on improving efficiency and transparency but also consider the environmental challenges it may bring. While promoting the application of technology, ports should take corresponding measures to reduce energy consumption, emissions, and waste management to minimize the adverse impact on the environment.
5.2. Influence of Tariffs on Incumbent Port
In this part, we adopt the tariff in the incumbent port, namely as an inside border port. Specifically, we redescribe the profit function based on the U model as follows:
In this case, Port 1 needs to pay the across-border fee from Port 2’s quantity. The case is based on a realistic situation. For example, Yantian Port and Kwai Tsing Port are combined modes of water and water transport. In order to improve the transportation efficiency, we can consider adopting the employment method to realize the circulation of goods between the two ports. At this time, it is equivalent to the state that the goods need to pass through customs and pay customs tariffs. Therefore, we can obtain Proposition 7 between the U model and U-T model.
Proposition 7. (Influence of tariffs on incumbent port): .
Proposition 7 shows the influence of tariffs on an incumbent port, which refers to the inside border port for Port 1. Specifically, first of all, the addition of tariffs may affect the cargo quantity of the port. If tariffs increase the import cost, the quantity of imported goods may decrease, thus reducing the cargo quantity of the port. However, if the addition of tariffs promotes the export of some commodities, the cargo quantity of the port may increase, which in turn will promote the port’s benefit. Secondly, the addition of tariffs may change the value of goods and the demand for services. High tariffs may lead to higher prices of imported goods, thus increasing the demand for high-value goods and services, such as stricter warehousing and logistics requirements. This may prompt the port to offer more professional and high-end services, thereby increasing the port’s revenue. Finally, the addition of tariffs may also affect the operational efficiency of the port. More complex processes and procedures often accompany the introduction of tariffs, and ports need to improve their operational efficiency to cope with these changes. If the port can optimize the process and improve service efficiency, it can maintain or even improve its benefits even under the challenge brought by tariffs.
Based on the above analysis, we can obtain the three aspects of management implication. First of all, port managers should pay close attention to the change in tariff policy and analyze its influence on cargo quantity, cargo value, and service demand, so as to adjust port operation strategy in time. Secondly, it is very important to improve the operational efficiency and service quality of the port. Under the tariff policy, ports need to optimize processes and improve service efficiency to cope with complex import and export procedures and higher service demand. Finally, the port should actively explore diversified development, reducing its dependence on a single source of trade by expanding into new business areas and service models, thereby enhancing its anti-risk ability and market competitiveness.
5.3. Influence of Port Cooperation on Incumbent Port
In this part, we analyze the port cooperation of Port 1 and Port 2, which aims to simulate the cooperation between regional ports, such as the same operational part (e.g., Hutchison Port Holdings in the Yantian Port and Kwai Tsing Port) or unified regional port policy (e.g., Shandong Port integration policy in China). Based on these cases in reality, we reset the model as , which means centralized decision-making in ports. Furthermore, we discuss the relationship between the new model U-J and the U model in Proposition 8.
Proposition 8. (Influence of port cooperation on incumbent port): .
Proposition 8 shows the influence of port cooperation on the incumbent port from Port 1, the inside border port. Specifically, the result is , which shows inconsistency of the results. The potential reasons may have three aspects. Firstly, centralized decision-making may bring a scale effect and increase market bargaining power, but it may also lead to regulatory pressure and limit pricing power due to market monopoly. Although the inside border port is small in terms of market size, it may maintain a certain market share due to its flexibility or special services. Secondly, although centralized decision-making helps to unify procurement and reduce cost, it may also lead to decreased efficiency due to increased management complexity. An inside border port may have lower operating costs or enjoy cost advantages due to geographical advantage. Thirdly, centralized decision-making binds the fate of the two ports together, which is riskier. Once the market changes or policies are adjusted, it may affect the whole system. An inside border port is more independent and adaptable and can adjust its strategies to cope with market changes more quickly.
Therefore, from a management implication perspective, we can identify two aspects. On the one hand, managers at the inside border port should recognize that flexibility should not be overlooked while pursuing economies of scale. Although centralized decision-making can bring advantages in scale, it may also slow down the response speed to market changes because it is too large. Therefore, managers need to find a balance between the two, not only to ensure economies of scale, but also to maintain sufficient flexibility to cope with market changes. On the other hand, whether centralized decision-making or local management (e.g., inside border port), risk management is very important. Centralized decision-making may bring greater risks because it involves more resources and interests. Therefore, managers need to establish a sound risk management system to identify, evaluate, and monitor potential risks to ensure the stability and sustainability of decision-making. At the same time, local management cannot ignore risk management, and it needs to be vigilant at all times to guard against various potential risks.
6. Conclusions
In this study, we analyze unified price or differential price in the port system, which discusses the possible strategy of competition and cooperation between regional ports. Moreover, we also show the technical value of blockchain services in the data sharing of market information between an inside border port and outside border port. Furthermore, the expansion of port capacity can reduce congestion at the internal border port to some extent under specific conditions. Finally, we also analyze some other cases, including the environmental impact, tariff impact, and influence of port cooperation, which further give some management implications for the inside border port (also called the incumbent port within).
Based on the above main points, we can further put forward some new management implications for the inside border port. On the one hand, from the perspective of the synergy strategy from within the port, the port can adopt a differential price strategy to increase its benefits. The strategic synergy is not only the pursuit of the scale effect, but more importantly, how to achieve differentiated competition through synergy. When the two ports make centralized decisions, they can jointly study market demand, formulate differentiated development strategies, and avoid homogenized competition, thereby giving full play to their respective advantages and enhancing their overall competitiveness. Inside border ports can also utilize their unique advantages, such as geographical location, policy differential superiority, or special services, to complement centralized decision-making ports and jointly explore the market.
On the other hand, in the face of a changing market environment, centralized decision-making for ports in different regions needs to pay attention to innovation management and technology application. By introducing new technologies (such as blockchain technology for data sharing) and optimizing management processes, the port operation efficiency can be improved, the cost can be reduced, and the service quality can be improved to meet the diversified needs of customers.
In this study, we mainly discussed two cases of price models with the empowerment of blockchain technology in different regions of the ports. Furthermore, we also discussed how the impact of digital upgrading on regional port services, especially when there are cross-border goods, will be more complicated to analyze. Furthermore, in the uncertain environment of an inside border port, we can use the asymmetry theory to explain the influence of competition and cooperation on ports. Moreover, future work could employ agent-based models to explore how pricing and blockchain adoption evolve in heterogeneous port networks or under learning-based decision frameworks. Finally, to increase the credibility and persuasiveness of the research conclusions, future studies can employ empirical tests to reflect the actual performance of port competition and cooperation.