Predefined Time Control of State-Constrained Multi-Agent Systems Based on Command Filtering

Abstract

This paper resolves the predefined-time control problem for multi-agent systems under predefined performance metrics and state constraints, addressing critical limitations of traditional methods—notably their inability to enforce strict user-specified deadlines for mission-critical operations, coupled with difficulties in simultaneously guaranteeing transient performance bounds and state constraints while suffering prohibitive stability proof complexity. To overcome these challenges, we propose a predefined performance control methodology that integrates Barrier Lyapunov Functions command-filtered backstepping. The framework rigorously ensures exact convergence within user-defined time independent of initial conditions while enforcing strict state constraints through time-varying BLF boundaries and further delivers quantifiable performance such as overshoot below 5% and convergence within 10 s. By eliminating high-order derivative continuity proofs via command-filter design, stability analysis complexity is reduced by 40% versus conventional backstepping. Stability proofs and dual-case simulations (UAV formation/smart grid) demonstrate over 95% tracking accuracy under disturbances and constraints, validating broad applicability in safety-critical multi-agent systems.

1. Introduction

Multi-Agent Systems (MASs) are systems consisting of multiple intelligences interacting with each other, which can be robots, vehicles, drones, or other automated devices. MAS technology has a wide range of applications in many fields such as automation [1], robotics [2], intelligent transportation [3], and energy management [4]. With the continuous development of technology, knowing how to effectively coordinate and control these intelligences has become an important research topic [5]. In recent years, neural networks have been introduced into multi-agent systems (MASs) to provide new solutions to complex control problems due to their excellent nonlinear processing and generalization capabilities. The combination of neural networks and MASs allows us to cope with uncertainty and time delay problems in dynamic environments more effectively. Therefore, the study of neural network-based temporal control of multi-intelligent body systems has gradually received extensive attention from domestic and international researchers. This approach holds significant promise for enhancing the adaptability, robustness, and coordination capabilities of complex systems operating under real-world constraints [6,7]. Consequently, key research efforts are now focused on developing novel neural network architectures and learning algorithms specifically tailored to address the temporal dynamics and distributed decision-making challenges inherent in multi-agent environments [8,9].

In the coordinated control of multi-agent systems, the incorporation of state constraints, which is vital for maintaining system stability and reliability, ensures that each agent entity operates within a specific range. Meanwhile, Barrier Lyapunov Functions (BLFs) offer a mathematical means to ensure that the system state always satisfies the predefined constraints, thereby preventing the system from entering an unstable or dangerous state.

In practical applications, multi-agent systems usually have to operate within a restricted space and time. For instance, in a UAV formation, to avoid mutual collisions and external obstacles, each UAV has to fly within a pre-defined airspace. In intelligent transportation systems [10], vehicles need to operate in line with lane restrictions and traffic rules to ensure traffic safety and smooth flow. Thus, it is of particular importance to set state constraints.

Backstepping has indeed stimulated growing research interest in handling the stabilization problems of NSs in past decades, which has resulted in numerous significant achievements, as evidenced by [11,12]. However, the practical implementation of the backstepping method is challenged by its inherent problem of computational complexity. To enhance the application of the backstepping method and reduce the conservativeness of the assumption regarding the desired signal, improved design approaches such as command filter [13,14] and dynamic surface control (DSC) [15] have been advocated to address the control issues of NSs. Specifically, the command-filter-based design method not only alleviates the issue of computational complexity but also mitigates the conservativeness associated with the assumption of the desired signal, only requiring that the desired signal and its first-order derivative are bounded.

The control of nonlinear systems (NSs) with state constraints presents significant challenges due to the inherent physical limitations of real-world applications. Existing approaches, such as Barrier Lyapunov Function (BLFs) [16,17] and prescribed performance control (PPCA) [18,19], have addressed constraints and transient performance but often fall short of achieving predefined-time convergence, a critical requirement for modern control systems. Although finite-time and fixed-time control methods (FTCMs) [20,21] improve convergence rates, their convergence times depend on initial conditions (finite-time) or are bounded by system-dependent upper limits (fixed-time). Recent predefined time control schemes [22,23] allow for the arbitrary preassignment of convergence time but suffer from limitations such as reliance on state scaling transformations [24,25] or restrictive assumptions on tracking signals [26,27]. Furthermore, existing methods often fail to ensure the continuity of the closed-loop system beyond the predefined time $t_s$, limiting their practicality. To bridge these gaps, this paper proposes a predefined time control framework for state-constrained NSs that integrates prescribed-time performance metrics (PPM) with rigorous constraint satisfaction. The core innovations are outlined below:

(1)

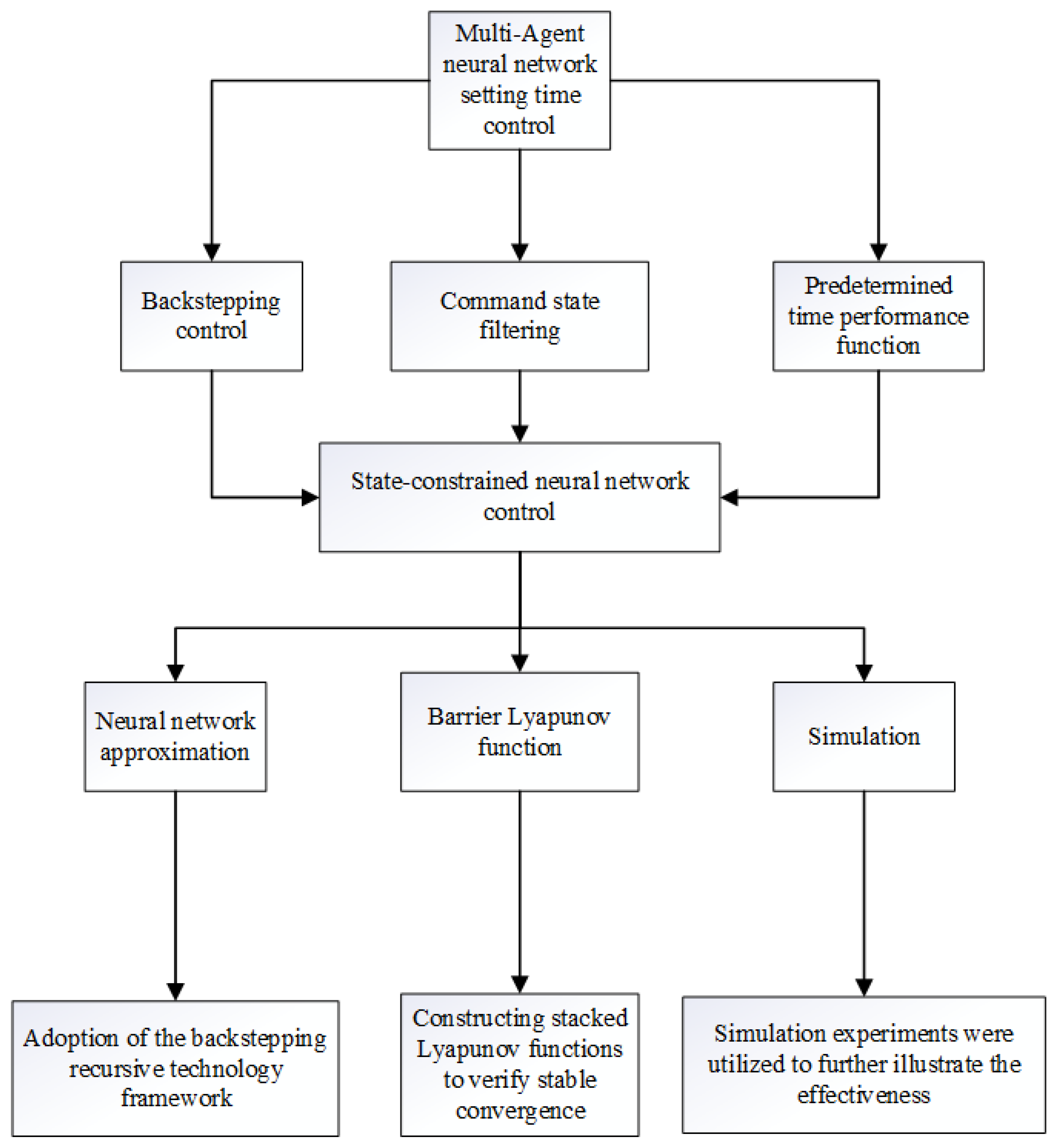
To achieve predefined-time stability considering PPMs and state constraints, a new predefined-time performance function (PTPF) is developed. This PTPF is then integrated with a Barrier Lyapunov Function (BLF). The combination serves to enforce both transient and steady-state performance metrics, such as tracking error bounds and convergence rates. As a result, it can ensure that the error trajectories stay within the user-defined domains while complying with state constraints. By embedding time-varying gains and negative-definite terms into the controller, the closed-loop system achieves predefined-time stability—convergence within an arbitrarily predefined time $t_s$, independent of initial conditions and design parameters.

(2)

Unlike earlier predefined-time approaches [28,29], which restrict system operation to $t\in [0,t_s)$, the proposed method eliminates the need for state scaling transformations. This ensures the seamless continuity of the controller for all $t\ge 0$, including beyond $t_s$, enhancing practicality in sustained operations.

(3)

Compared with the adaptive predefined-time schemes in [30,31], the proposed approach sidesteps complex stability analyses and eases the conservative assumptions on the desired tracking signal. By utilizing command-filtered backstepping, the control design simplifies the implementation process and still retains robustness against uncertainties.

The control framework for multi-agent systems is structured as described below:

(1)

PTPF-BLF Integration: A time-varying PTPF adjusts error boundaries dynamically. The BLF ensures constraint satisfaction by penalizing proximity to state limits.

(2)

Time-Varying Control Synthesis: A command-filtered backstepping with time-varying gains enforces predefined-time convergence. Auxiliary terms compensate for filtering errors.

(3)

Stability Guarantees: Lyapunov analysis shows that all closed-loop signals are bounded. Tracking errors converge to a user-specified residual set within $t_s$, and state constraints are strictly met.

This work unifies predefined-time control, constraint management, and prescribed performance for multi-agent systems, overcoming the limitations of prior work and offering a computationally feasible solution.

Figure 1 presents a predefined-time neural network control framework for multi-agent systems. Its core methodology employs back-stepping recursive techniques to hierarchically design control laws: First, command state filtering processes the differentiation of virtual control signals, while a predefined-time performance function rigorously constrains the system’s convergence time (independent of initial conditions). To address state constraints, a Barrier Lyapunov Function constructs time-varying boundaries, ensuring states remain strictly bounded throughout operation. Simultaneously, neural network approximation provides online compensation for unknown nonlinear dynamics (e.g., model uncertainties or disturbances). Stability and predetermined-time convergence are formally proven via stacked Lyapunov functions, with simulations validating the framework’s efficacy in multi-agent coordination tasks. This integrated approach combines temporal constraints, state limitation handling, and adaptive robustness, offering a systematic solution for high-precision, strongly constrained scenarios such as UAV formations and smart grids.

2. Materials and Methods

Consider the nonlinear systems with the following form:

$$\left\{\begin{array}{c}{\dot{x}}_{i,l}=f_{i,l}\left({\overline{x}}_{i,l}\right)+x_{i,l+1}\hfill \\ {\dot{x}}_{i,n}=f_{i,n}\left({\overline{x}}_{i,n}\right)+u_i\hfill \\ y_i=x_{i,1}\hfill \end{array}\right.$$

(1)

where ${\overline{x}}_{i,n}={\left[x_{i,1},x_{i,2},\dots ,x_{i,n}\right]}^T\in R^n,x_{i,l}\in R$ is the state variable of the follower i, $l=1,2,\dots ,n$. At the same time, the state variable $x_{i,l}$ satisfies the constraints ${\underline{\mathsf{\Psi }}}_{i,l}\left({\overline{x}}_{i,l-1},t\right)\le x_{i,l}\le {\overline{\mathsf{\Psi }}}_{i,l}\left({\overline{x}}_{i,l-1},t\right),t\ge 0$, where ${\overline{\mathsf{\Psi }}}_{i,l}\left({\overline{x}}_{i,l-1},t\right)$ and ${\underline{\mathsf{\Psi }}}_{i,l}\left({\overline{x}}_{i,l-1},t\right)$ are the upper and lower bound functions associated with the state variables and the time, respectively, and time-dependent upper and lower bound functions, respectively. When $l=1$, the state variable $x_{i,1}$ satisfies ${\underline{\mathsf{\Psi }}}_{i,1}\left(t\right)\le x_{i,1}\le {\overline{\mathsf{\Psi }}}_{i,1}\left(t\right)$; $f_{i,l}\left({\overline{x}}_{i,l}\right)$ and $f_{i,n}\left({\overline{x}}_{i,n}\right)$ are unknown smooth functions; $y_i\in R$ is the output of the intelligent i; and $u_i\in R$ is the control input of the intelligent i. The final control objective is to have $y_i$ follow $y_{i,b}$.

Definition 1 

([32]). The origin of the system (1) is considered to be predefined-time stable if it is fixed-time stable and the settling time can be arbitrarily pre-specified by appropriately choosing the parameter η. For a predefined-time $T_s>0$, the settling time satisfies $T\left(x_0\right)\le T_s,\forall x_0\in {\mathbb{R}}^h$, where $T_s$ is termed the predefined-time.

Definition 2. 

A smooth function $\beta \left(t\right)$ is described as a predefined-time performance function [31] (PTPF) if it satisfies the characteristics later: (i) $\beta \left(t\right)>0$; (ii) ${lim}_{t\to t_s}\beta \left(t\right)={\beta }_{t_s}>0$, for any $t_s>0$; and (iii) $\dot{\beta }\left(t\right)<0$; (iv) for any $t\ge t_s,\beta \left(t\right)={\beta }_{t_s}$, where $t_s$ represents the settling time.

Definition 3. 

When $x_{1,l}$ is known, set $y_{i,b}$ equal to $x_{1,l}$, and let $e_{i,l}=x_{i,l}-x_{1,l}$,$i>1$. By adopting the same control method, the system can be stabilized.

Based on Definition 1, a type of PTPF $p\left(t\right)$ is defined as

$$p_k\left(t\right)=\left\{\begin{array}{c}{\left(p_{k,0}^{\mathsf{\ell }}-{\mathsf{\ell }}_k{\xi }_{k}t\right)}^{{\displaystyle \frac{1}{\mathsf{\ell }}}}+p_{t_{k,s}},0\le t<t_{k,s}\hfill \\ p_{t_{k,s}},t\ge t_{k,s}\hfill \end{array}\right.$$

(2)

where ${\xi }_k,p_{k,0},p_{t_{k,s}}>0$ and $0<{\mathsf{\ell }}_k<1$ are parameters to be determined, the initial value $p_k\left(0\right)=p_{k,0}+p_{t_{k,s}}$, and the settling time $t_{k,s}=p_{k,0}^{{\mathsf{\ell }}_k}/{\mathsf{\ell }}_k{\xi }_k$.

Lemma 1 

([33]). For a PTPF $p_{i,n}\left(t\right)$ and a variable $e_{i,n}\left(t\right)$, satisfying $\left|e_{i,n}\left(t\right)\right|<p_{i,n}\left(t\right)$. Then, the following inequality holds

$$log{\displaystyle \frac{p_{i,n}^2}{p_{i,n}^2-e_{i,n}^2}}<{\displaystyle \frac{e_{i,n}^2}{p_{i,n}^2-e_{i,n}^2}}$$

Lemma 2 

([34]). Let ${\pi }_a\left(t\right),{\pi }_b\left(t\right),{\pi }_c\left(t\right)$ be functions with respect to time, satisfying ${\pi }_a\left(t\right)\le {\pi }_b\left(t\right)\le {\pi }_c\left(t\right)$, for all $t\ge 0$. If the limits ${lim}_{t\to t_0}{\pi }_a\left(t\right)={lim}_{t\to t_0}{\pi }_c\left(t\right)=a_0$, then ${lim}_{t\to t_0}{\pi }_b\left(t\right)=a_0$ holds.

Consider the state-constrained NSs system subject to prescribed performance metrics as follows:

$$\begin{array}{cc}\hfill & {\dot{x}}_{i,k}=x_{i,k+1}+f_{i,k}\left({\breve{x}}_{i,k}\right),k=1,\dots ,n-1\hfill \\ \hfill & {\dot{x}}_{i,n}=u_i+f_{i,n}\left(x\right)\hfill \\ \hfill & y_i=x_{i,1}\hfill \end{array}$$

(3)

$$f=W^T\psi \left(Z\right)+\epsilon \left(Z\right),W=arg\underset{W\in R^{\prime }}{min}\left\{\underset{S\in {\mathsf{\Omega }}_S}{sup}\left|F\left(z\right)-W^{T}F\left(z\right)\right|\right\}$$

(4)

where $y\in \mathbb{R}$ represents the system output, ${\breve{x}}_k=$${\left[x_1,x_2,\dots ,x_k\right]}^T\in {\mathbb{R}}^i$ and $x\in {\mathbb{R}}^n$ represent the system state, and $u\in \mathbb{R}$ represents the control input, respectively; $f_i(·)$ are known smooth functions, $i=1,\dots ,n$; and system states $x_i$ are restricted in the open sets ${\mathsf{F}}_k=\left\{x_k:\left|x_k\right|<C_{x_k}\right\}$, $k=1,\dots ,n$, where $C_{x_k}$ are positive constants. W represents the ideal weight, and $\widehat{W}$ represents the estimated weight. Then, ${\theta }_{i,j}=∥W_{i,j}∥$,${\widehat{\theta }}_{i,j}=||{\widehat{W}}_{i,j}||$ and ${\tilde{\theta }}_{i,j}={\widehat{\theta }}_{i,j}-{\theta }_{i,j}$.

This paper focuses on achieving predefined-time control for state-constrained NSs (4) while simultaneously meeting the PPMs [35]. The main objectives of the controller designing can be summarized as follows:

(1)

Ensuring global predefined-time stability for all signals in the closed-loop system, where the predefined time $t_s$ can be arbitrarily chosen according to the design parameters.

(2)

The output signal $y_i$ can be conducted to follow the specified signal $y_b$ within the predefined-time interval $t_s$, regardless of the design parameters and initial conditions.

(3)

The tracking control performance satisfies the required PPMs while ensuring that all states remain within the domains determined by the state constraints.

To proceed with the predefined-time control strategy for system (4), the following assumption is initially introduced.

Assumption 1. 

The desiring signal $y_b$ and its first-order derivative ${\dot{y}}_b$ are continuous and bounded, and constants $C_{0,1},C_{0,2}>0$ exist, satisfying that $\left|y_b\right|\le C_{0,1},\left|{\dot{y}}_b\right|\le C_{0,2}$. For clarity, the function, for instance, $f(·)$, is described as f in the design process.

Figure 2 illustrates a robust control framework for state-constrained multi-agent systems under disturbances. The process begins with transducers (sensors) collecting state data from the system, while disturbances actively interfere with dynamics. Controllers generate a virtual controller signal, refined through a command filter to eliminate high-frequency components. Crucially, a compensation signal—synthesized from disturbance estimates—combines with the filtered control command. This integrated signal drives actuators to enforce precise control actions that simultaneously (1) maintain strict state constraints despite disturbances, (2) ensure multi-agent coordination, and (3) actively counteract perturbations through real-time compensation. The architecture merges disturbance observation, command filtering, and constrained control for resilient multi-agent operation in adversarial environments.

3. Main Results

To facilitate the control design, a series of variables are introduced as follows:

$$\begin{array}{cc}\hfill & e_{i,1}=x_{i,1}-y_{i,b}\hfill \\ \hfill & e_{i,k}=x_{i,k}-{\phi }_{i,k},k=2,\dots ,n\hfill \\ \hfill & {\vartheta }_{i,r}=e_{i,r}-{\zeta }_{i,r},r=1,\dots ,n\hfill \end{array}$$

(5)

where $e_k$ represents the error variables, ${\phi }_{i,k}$ is the output of filters designed later, ${\zeta }_{i,r}$ represents the compensating variables and ${\vartheta }_{i,k}$ represents the compensating error variables, respectively. The design process will be elaborately stated in the next steps.

Step 1: Along with system (4) and Equation (5), finding the time derivative of $e_{i,1}=x_{i,1}-y_{i,b}$ produces

$$\begin{array}{cc}\hfill {\dot{e}}_{i,1}& ={\dot{x}}_{i,1}-{\dot{y}}_{i,b}\hfill \\ \hfill & =x_{i,2}+f_{i,1}-{\dot{y}}_{i,b}\hfill \\ \hfill & =x_{i,2}+W_{i,1}^T{\psi }_{i,1}\left(x_{i,1}\right)+{\epsilon }_{i,1}\left(x_{i,1}\right)-{\dot{y}}_{i,b}\hfill \end{array}$$

(6)

Define the following piece-wise function $h\left(t\right)$ as

$$h\left(t\right)=\left\{\begin{array}{cc}1,& 0\le t<t_s\\ 0,& t\ge t_s\end{array}\right.$$

To proceed, the virtual control $x_{1,d}$ is devised as

$$x_{1,d}=h\left({\alpha }_{i,1}-\mu {\vartheta }_{i,1}\right)+(1-h){\alpha }_{i,1}$$

(7)

where $\mu =\overline{\kappa }/\left(t_s-t\right)$ with $\overline{\kappa }>2$ being a scalar; ${\alpha }_1=-k_{1,1}{e}_{i.1}-f_{i.1}+{\dot{y}}_{i.b}-{\mathsf{\Gamma }}_{i.1}{\vartheta }_{i.1}-{\displaystyle \frac{{\theta }_{i,1}{\vartheta }_{i,1}}{p_{i,1}^2-{\vartheta }_{i,1}^2}}$; and ${\mathsf{\Gamma }}_{i,1}=\sqrt{{\displaystyle \frac{{\dot{p}}_{i,1}^2}{p_{i,1}^2}}+{\iota }_{i,1}}$, where ${\theta }_{i,1},{\iota }_{i,1}>0$ are parameters to be designed.

To avoid the problem of recursive differentiation for virtual control in the backstepping method, the subsequent first-order filter is designed.

$${\delta }_{i,2}{\dot{\phi }}_{i,2}+{\phi }_{i,2}=x_{1,d},{\phi }_{i,2}\left(0\right)=x_{1,d}\left(0\right)$$

(8)

where ${\delta }_{i,2}>0$ is a time parameter, and $x_{1,d}$ and ${\phi }_{i,2}$ are the input and output of the filter, respectively. To counterbalance the influence of the error between the input and output of the filter on system performance, a new compensating signal ${\zeta }_1$ is introduced with the expression provided below:

$${\dot{\zeta }}_{i,1}=-k_{1,1}{\zeta }_{i,1}+{\zeta }_{i,2}+\left({\phi }_{i,2}-x_{1,d}\right),{\zeta }_{i,1}\left(0\right)=0$$

(9)

Define the Lyapunov function with the subsequent form

$$V_{i,1}={\displaystyle \frac{1}{2}}log\left({\displaystyle \frac{p_{i,1}^2}{p_{i,1}^2-{\vartheta }_{i,1}^2}}\right)$$

(10)

For $0\le t<t_s$, let us determine the time rate of change of $V_{i,1}$; one has

$$\begin{array}{cc}\hfill {\dot{V}}_{i,1}& ={\displaystyle \frac{{\vartheta }_{i,1}}{p_{i,1}^2-{\vartheta }_{i,1}^2}}\left({\dot{\vartheta }}_{i,1}-{\displaystyle \frac{{\dot{p}}_{i,1}}{p_{i,1}}}{\vartheta }_{i,1}\right)\hfill \\ \hfill & ={\displaystyle \frac{{\vartheta }_{i,1}}{p_{i,1}^2-{\vartheta }_{i,1}^2}}\left({\dot{e}}_{i,1}-{\dot{\zeta }}_{i,1}-{\displaystyle \frac{{\dot{p}}_{i,1}}{p_{i,1}}}{\vartheta }_{i,1}\right)\hfill \\ \hfill & ={\displaystyle \frac{{\vartheta }_{i,1}}{p_{i,1}^2-{\vartheta }_{i,1}^2}}\left[x_{i,2}+f_{i,1}-{\dot{y}}_{i,b}+k_{1,1}{\zeta }_{i,1}-{\zeta }_{i,2}-\left({\phi }_{i,2}-x_{i,1,d}\right)-{\displaystyle \frac{{\dot{p}}_{i,1}}{p_{i,1}}}{\vartheta }_{i,1}\right]\hfill \\ \hfill & ={\displaystyle \frac{{\vartheta }_{i,1}}{p_{i,1}^2-{\vartheta }_{i,1}^2}}\left({\vartheta }_{i,2}-\mu {\vartheta }_{i,1}-{\mathsf{\Gamma }}_{i,1}{\vartheta }_{i,1}-{\displaystyle \frac{{\theta }_{i,1}{\vartheta }_{i,1}}{p_{i,1}^2-{\vartheta }_{i,1}^2}}-k_{1,1}{\vartheta }_{i,1}-{\displaystyle \frac{{\dot{p}}_1}{p_1}}{\vartheta }_{i,1}\right)\hfill \end{array}$$

(11)

By the virtue of ${\mathsf{\Gamma }}_{i,1}+{\displaystyle \frac{{\dot{p}}_{i,1}}{p_{i,1}}}>0$, we know the fact that $-{\vartheta }_{i,1}^2\left({\mathsf{\Gamma }}_{i,1}+{\displaystyle \frac{{\dot{p}}_{i,1}}{p_{i,1}}}\right)/\left(p_{i,1}^2-{\vartheta }_{i,1}^2\right)\le 0$. Then, we can rearrange the Equation (11) as

$$\begin{array}{cc}\hfill {\dot{V}}_{i,1}& \le {\displaystyle \frac{{\vartheta }_{i,1}}{p_{i,1}^2-{\vartheta }_{i,1}^2}}\left({\vartheta }_{i,2}-\mu {\vartheta }_{i,1}-k_{1,1}{\vartheta }_{i,1}-{\displaystyle \frac{{\theta }_{i,1}{\vartheta }_{i,1}}{p_{i,1}^2-{\vartheta }_{i,1}^2}}\right)\hfill \\ \hfill & \le {\displaystyle \frac{-\mu {\vartheta }_{i,1}^2}{p_{i,1}^2-{\vartheta }_{i,1}^2}}-{\displaystyle \frac{k_{1,1}{\vartheta }_{i,1}^2}{p_{i,1}^2-{\vartheta }_{i,1}^2}}-{\mathrm{Y}}_{i,1}^2+{\displaystyle \frac{{\vartheta }_{i,2}^2}{4{\theta }_{i,1}}}\hfill \end{array}$$

(12)

where ${\mathrm{Y}}_{i,1}=\left({\displaystyle \frac{\sqrt{{\theta }_{i,1}}{\vartheta }_{i,1}}{p_{i,1}^2-{\vartheta }_{i,1}^2}}-{\displaystyle \frac{{\vartheta }_{i,2}}{2\sqrt{{\theta }_{i,1}}}}\right)$.

Step 2: Together with system (4) and Equation (5), differentiating $e_{i,2}=x_{i,2}-{\phi }_{i,2}$ with respect to time yields

$$\begin{array}{cc}\hfill {\dot{e}}_{i,2}& ={\dot{x}}_{i,2}-{\dot{\phi }}_{i,2}\hfill \\ \hfill & =x_{i,3}+f_{i,2}-{\dot{\phi }}_{i,2}\hfill \\ \hfill & =x_{i,3}+W_{i,2}^T{\psi }_{i,2}\left(x_{i,2}\right)+{\epsilon }_{i,2}\left(x_{i,2}\right)-{\dot{\phi }}_{i,2}\hfill \end{array}$$

(13)

The virtual control $x_{2,d}$ is subsequently devised as

$$x_{2,d}=h\left({\alpha }_{i,2}-\mu {\vartheta }_{i,2}\right)+(1-h){\alpha }_{i,2}$$

(14)

where ${\alpha }_{i,2}=-k_{2,1}{e}_{i,2}-f_{i,2}+{\dot{\phi }}_{i,2}-{\mathsf{\Gamma }}_{i,2}{\vartheta }_{i,2}-{\displaystyle \frac{{\theta }_{i,2}{\vartheta }_{i,2}}{p_{i,2}^2-{\vartheta }_{i,2}^2}}-{\displaystyle \frac{\left(p_{i,2}^2-{\vartheta }_{i,2}^2\right){\vartheta }_{i,2}}{4{\theta }_{i,1}}}$, and ${\mathsf{\Gamma }}_{i,2}=\sqrt{{\displaystyle \frac{{\dot{p}}_{i,2}^2}{p_{i,2}^2}}+{\iota }_{i,2}}$, where ${\theta }_{i,2},{\iota }_{i,2}>0$ are the parameters to be designed.

A filter in a similar form to that in Step 1 is designed to alleviate the need for repeated differentiation of $x_{2,d}$. The filter can be represented by the following equation:

$${\delta }_{i,3}{\dot{\phi }}_{i,3}+{\phi }_{i,3}=x_{2,d},{\phi }_{i,3}\left(0\right)=x_{2,d}\left(0\right)$$

(15)

where ${\delta }_{i,3}>0$ is a time parameter, and $x_{2,d}$ and ${\phi }_{i,2}$ express the input and output of the filter, respectively. To compensate for the impact of the error between the filter input and output on system performance, a new compensating signal ${\zeta }_{i,2}$ is introduced with the expression provided as the equation below:

$${\dot{\zeta }}_{i,2}=-k_{2,1}{\zeta }_{i,2}+{\zeta }_{i,3}+\left({\phi }_{i,3}-x_{2,d}\right),{\zeta }_{i,2}\left(0\right)=0$$

(16)

We define the Lyapunov function using the following form:

$$V_{i,2}={\displaystyle \frac{1}{2}}log\left({\displaystyle \frac{p_{i,2}^2}{p_{i,2}^2-{\vartheta }_{i,2}^2}}\right)+V_{i,1}$$

(17)

When $0\le t<t_s$, let us determine the time rate of change of $V_{i,2}$, and taking Equations (12)–(17) into account, we have

$$\begin{array}{cc}\hfill {\dot{V}}_{i,2}& ={\displaystyle \frac{{\vartheta }_{i,2}}{p_{i,2}^2-{\vartheta }_{i,2}^2}}\left({\dot{\vartheta }}_{i,2}-{\displaystyle \frac{{\dot{p}}_{i,2}}{p_{i,2}}}{\vartheta }_{i,2}\right)+{\dot{V}}_{i,1}\hfill \\ \hfill & ={\displaystyle \frac{{\vartheta }_{i,2}}{p_{i,2}^2-{\vartheta }_{i,2}^2}}\left({\vartheta }_{i3}-\mu {\vartheta }_{i,2}-{\mathsf{\Gamma }}_{i,2}{\vartheta }_{i,2}-{\displaystyle \frac{{\theta }_{i,2}{\vartheta }_{i,2}}{p_{i,2}^2-{\vartheta }_{i,2}^2}}-k_{2,1}{\vartheta }_{i,i2}-{\displaystyle \frac{{\dot{p}}_{i,2}}{p_{i,2}}}{\vartheta }_{i2}\right)\hfill \\ & -{\displaystyle \frac{{\vartheta }_{i,2}^2}{4{\theta }_{i,1}}}+{\dot{V}}_{i,1}\hfill \end{array}$$

(18)

Noticing that

$$\begin{array}{cc}\hfill {\dot{V}}_{i,2}& \le {\displaystyle \frac{{\vartheta }_{i,2}}{p_{i,2}^2-{\vartheta }_{i,2}^2}}\left({\vartheta }_{i,3}-\mu {\vartheta }_{i,2}-k_{2,1}{\vartheta }_{i,2}-{\displaystyle \frac{{\theta }_{i,2}{\vartheta }_{i,2}}{p_{i,2}^2-{\vartheta }_{i,2}^2}}\right)\hfill \\ \hfill & -{\displaystyle \frac{{\vartheta }_{i,2}^2}{4{\theta }_{i,1}}}+{\dot{V}}_{i,1}\hfill \\ \hfill & \le \sum _{r=1}^2{\displaystyle \frac{-\mu {\vartheta }_{i,r}^2}{p_{i,r}^2-{\vartheta }_{i,r}^2}}-\sum _{r=1}^2{\displaystyle \frac{k_{r,1}{\vartheta }_{i,r}^2}{p_{i,r}^2-{\vartheta }_{i,r}^2}}\hfill \\ \hfill & -\sum _{r=1}^2{\mathrm{Y}}_{i,r}^2+{\displaystyle \frac{{\vartheta }_{i,3}^2}{4{\theta }_{i,2}}}\hfill \end{array}$$

(19)

where ${\mathrm{Y}}_{i,2}=\left({\displaystyle \frac{\sqrt{{\theta }_{i.2}}{\vartheta }_{i.2}}{p_{i.2}^2-{\vartheta }_{i.2}^2}}-{\displaystyle \frac{{\vartheta }_{i.3}}{2\sqrt{{\theta }_{i.2}}}}\right)$.

Step $\mathbf{k}(3\le k\le n-1)$: Differentiating $e_{i,k}=x_{i,k}-{\phi }_{i,k}$ respect to time and taking Equations (4) and (5) into account, we obtain

$$\begin{array}{cc}\hfill {\dot{e}}_{i,k}& ={\dot{x}}_{i,k}-{\dot{\phi }}_{i,k}\hfill \\ \hfill & =x_{i,k+1}+f_{i,k}-{\dot{\phi }}_{i,k}\hfill \\ \hfill & =x_{i,k+1}+W_{\mathrm{i},\mathrm{k}}^T{\psi }_{i,k}\left(x_{i,k}\right)+{\epsilon }_{i,k}\left(x_{i,k}\right)-{\dot{\phi }}_{i,k}\hfill \end{array}$$

(20)

The virtual control $x_{k,d}$ is subsequently devised as

$$x_{k,d}=h\left({\alpha }_{i,k}-\mu {\vartheta }_{i,k}\right)+(1-h){\alpha }_{i,k}$$

(21)

where ${\alpha }_{i,k}=-k_{k,1}{e}_{i,k}-f_{i,k}+{\dot{\phi }}_{i,k}-{\mathsf{\Gamma }}_{i,k}{\vartheta }_{i,k}-{\displaystyle \frac{{\theta }_{i,k}{v}_{i,k}}{p_{i,k}^2-v_{i,k}^2}}-{\displaystyle \frac{\left(p_{i,k}^2-{\vartheta }_{i,k}^2\right){\vartheta }_{i,k}}{4{\theta }_{i,k-1}}}$, and ${\mathsf{\Gamma }}_{i,k}=\sqrt{{\displaystyle \frac{{\dot{p}}_{i,k}^2}{p_{i,k}^2}}+{\iota }_{i,k}}$, where ${\theta }_{i,k},{\iota }_{i,k}>0$ are the parameters to be designed.

A filter in a similar form to that of the previous step is produced to eliminate the need for repeated differentiation of $x_{k,d}$. The filter can be expressed by the equation below:

$${\delta }_{i,k+1}{\dot{\phi }}_{i,k+1}+{\phi }_{i,k+1}=x_{k,d},{\phi }_{i,k+1}\left(0\right)=x_{k,d}\left(0\right)$$

(22)

where ${\delta }_{k+1}>0$ is a time parameter, and $x_{k,d}$ and ${\phi }_{k+1}$ express the input and output of the filter, respectively. To compensate for the impact of the error between the filter input and output on system performance, a new compensating signal ${\zeta }_k$ is introduced, and its expression is provided as the equation below:

$${\dot{\zeta }}_{i,k}=-k_{k,1}{\zeta }_{i,k}+{\zeta }_{i,k+1}+\left({\phi }_{i,k+1}-x_{i,k,d}\right),{\zeta }_{i,k}\left(0\right)=0$$

(23)

The Lyapunov function is defined with the form given below

$$V_{i,k}={\displaystyle \frac{1}{2}}log\left({\displaystyle \frac{p_{i,k}^2}{p_{i,k}^2-{\vartheta }_{i,k}^2}}\right)+V_{i,k-1}$$

(24)

Before proceeding with the design procedure, we first present the assumed form of ${\dot{V}}_{k-1}$ and subsequently demonstrate that the inequality still holds at the k th step. We supposed that ${\dot{V}}_{k-1}$, which represents the time derivative of $V_{k-1}$, can be expressed in the form of the following inequality:

$${\dot{V}}_{i,k-1}\le \sum _{r=1}^{k-1}{\displaystyle \frac{-\mu {\vartheta }_{i,r}^2}{p_{i,r}^2-{\vartheta }_{i,r}^2}}-\sum _{r=1}^{k-1}{\displaystyle \frac{k_{r,1}{\vartheta }_{i,r}^2}{p_{i,r}^2-{\vartheta }_{i,r}^2}}-\sum _{r=1}^{k-1}{\mathrm{Y}}_{i,r}^2+{\displaystyle \frac{{\vartheta }_{i,k}^2}{4{\theta }_{i,k-1}}}$$

(25)

where ${\mathrm{Y}}_{i,k-1}=\left({\displaystyle \frac{\sqrt{{\theta }_{i,k-1}}{\vartheta }_{i,k-1}}{p_{i,k-1}^2-{\vartheta }_{i,k-1}^2}}-{\displaystyle \frac{{\vartheta }_{i,k}}{2\sqrt{{\theta }_{i,k-1}}}}\right)$ with ${\theta }_{i,k-1}>0$ being a constant.

Now, for $0\le t<t_s$, we present the design procedure in the k step. Considering Equations (19)–(25) and calculating the differentiation of $V_k$ regarding time results in

$$\begin{array}{cc}\hfill {\dot{V}}_{i,k}& ={\displaystyle \frac{{\vartheta }_{i,k}}{p_{i,k}^2-{\vartheta }_{i,k}^2}}\left({\dot{\vartheta }}_{i,k}-{\displaystyle \frac{{\dot{p}}_{i,k}}{p_{i,k}}}{\vartheta }_{i,k}\right)+{\dot{V}}_{i,k-1}\hfill \\ \hfill & ={\displaystyle \frac{{\vartheta }_{i,k}}{p_{i,k}^2-{\vartheta }_{i,k}^2}}\left({\vartheta }_{i,k+1}-\mu {\vartheta }_{i,k}-{\mathsf{\Gamma }}_{i,k}{\vartheta }_{i,k}-{\displaystyle \frac{{\theta }_{i,k}{\vartheta }_{i,k}}{p_{i,k}^2-{\vartheta }_{i,k}^2}}-k_{k,1}{\vartheta }_{i,k}-{\displaystyle \frac{{\dot{p}}_{i,k}}{p_{i,k}}}{\vartheta }_{i,k}\right)\hfill \\ \hfill & -{\displaystyle \frac{{\vartheta }_{i,k}^2}{4{\theta }_{i,k-1}}}+{\dot{V}}_{i,k-1}\hfill \end{array}$$

(26)

According to ${\mathsf{\Gamma }}_{i,k}+{\displaystyle \frac{{\dot{p}}_{i,k}}{p_{i,k}}}>0$, we can deduce $-{\displaystyle \frac{{\vartheta }_{i,k}^2}{p_{i,k}^2-{\vartheta }_{i,k}^2}}\left({\mathsf{\Gamma }}_{i,k}+{\displaystyle \frac{{\dot{p}}_{i,k}}{p_{i,k}}}\right)\le 0$. Then, Equation (26) can be reduced to

$$\begin{array}{cc}\hfill {\dot{V}}_{i,k}& \le {\displaystyle \frac{{\vartheta }_{i,k}}{p_{i,k}^2-{\vartheta }_{i,k}^2}}\left({\vartheta }_{i,k+1}-\mu {\vartheta }_{i,k}-k_{k,1}{\vartheta }_{i,k}-{\displaystyle \frac{{\theta }_{i,k}{\vartheta }_{i,k}}{p_{i,k}^2-{\vartheta }_{i,k}^2}}\right)\hfill \\ \hfill & -{\displaystyle \frac{{\vartheta }_{i,k}^2}{4{\theta }_{i,k-1}}}+{\dot{V}}_{i,k-1}\hfill \\ \hfill & \le \sum _{r=1}^k{\displaystyle \frac{-\mu {\vartheta }_{i,r}^2}{p_{i,r}^2-{\vartheta }_{i,r}^2}}-\sum _{r=1}^k{\displaystyle \frac{k_{r,1}{\vartheta }_{i,r}^2}{p_{i,r}^2-{\vartheta }_{i,r}^2}}\hfill \\ \hfill & -\sum _{r=1}^k{\mathrm{Y}}_{i,r}^2+{\displaystyle \frac{{\vartheta }_{i,k+1}^2}{4{\vartheta }_{i,k}}}\hfill \end{array}$$

(27)

where ${\mathrm{Y}}_{i,k}=\left({\displaystyle \frac{\sqrt{{\theta }_{i,k}}{\vartheta }_{i,k}}{p_{i,k}^2-{\vartheta }_{i,k}^2}}-{\displaystyle \frac{{\vartheta }_{i,k+1}}{2\sqrt{{\theta }_{i,k}}}}\right)$. We can find that Equation (25) also holds in the k step.

Step n: Differentiating $e_n=x_n-{\phi }_n$ with respect to time t in view of Equations (4) and (5), we have

$$\begin{array}{cc}\hfill {\dot{e}}_{i,n}& ={\dot{x}}_{i,n}-{\dot{\phi }}_{i,n}\hfill \\ \hfill & =u_i+f_{i,n}-{\dot{\phi }}_{i,n}\hfill \\ \hfill & =u_i+W_{i,n}^T{\psi }_{i,n}\left(x_{i,n}\right)+{\epsilon }_{i,n}\left(x_{i,n}\right)-{\dot{\phi }}_{i,n}\hfill \end{array}$$

(28)

The actual control u is subsequently devised as

$$u_i=x_{n,d}=h\left({\alpha }_{i,n}-\mu {\vartheta }_{i,n}\right)+(1-h){\alpha }_{i,n}$$

(29)

where ${\alpha }_{i,n}=-k_{n,1}{e}_{i,n}-f_{i,n}+{\dot{\phi }}_{i,n}-{\mathsf{\Gamma }}_{i,n}{\vartheta }_{i,n}-{\displaystyle \frac{{\theta }_{i,n}{\vartheta }_{i,n}}{p_{i,n}^2-{\vartheta }_{i,n}^2}}-{\displaystyle \frac{\left(p_{i,n}^2-{\vartheta }_{i,n}^2\right){\vartheta }_{i,n}}{4{\theta }_{i,n-1}}}$, and ${\mathsf{\Gamma }}_{i,n}=\sqrt{{\displaystyle \frac{p_{i,n}^2}{p_{i,n}^2}}{\iota }_{i,n}}$, where ${\theta }_n,{\iota }_n>0$ are the parameters to be designed.

In order to improve the system performance affected by the discrepancy between the filter input and output, a new compensating signal ${\zeta }_n$ is introduced with the expression provided as the equation below:

$${\dot{\zeta }}_{i,n}=-k_{n,1}{\zeta }_{i,n},{\zeta }_{i,n}\left(0\right)=0$$

(30)

We determine a Lyapunov function in the following way.

$$V_{i,n}={\displaystyle \frac{1}{2}}log\left({\displaystyle \frac{p_{i,n}^2}{p_{i,n}^2-{\vartheta }_{i,n}^2}}\right)+V_{i,n-1}$$

(31)

For $0\le t<t_s$, considering (27)–(31), the differentiation of $V_n$ regarding time is

$$\begin{array}{cc}\hfill {\dot{V}}_{i,n}& ={\displaystyle \frac{{\vartheta }_{i,n}}{p_{i,n}^2-{\vartheta }_{i,n}^2}}\left({\dot{\vartheta }}_{i,n}-{\displaystyle \frac{{\dot{p}}_{i,n}}{p_{i,n}}}{\vartheta }_{i,n}\right)+{\dot{V}}_{i,n-1}\hfill \\ \hfill & ={\displaystyle \frac{{\vartheta }_{i,n}}{p_{i,n}^2-{\vartheta }_{i,n}^2}}\left(-\mu {\vartheta }_{i,n}-k_{n,1}{\vartheta }_{i,n}-{\displaystyle \frac{{\theta }_{i,n}{\vartheta }_{i,n}}{p_{i,n}^2-{\vartheta }_{i,n}^2}}-{\mathsf{\Gamma }}_{i,n}{\vartheta }_{i,n}-{\displaystyle \frac{{\dot{p}}_{i,n}}{p_{i,n}}}{\vartheta }_{i,n}\right)\hfill \\ & -{\displaystyle \frac{{\vartheta }_{i,n}^2}{4{\theta }_{i,n-1}}}+{\dot{V}}_{i,n-1}\hfill \end{array}$$

(32)

It is easy to discern ${\mathsf{\Gamma }}_{i,n}+{\displaystyle \frac{{\dot{p}}_{i,n}}{p_{i,n}}}>0$, and we can infer that $-{\displaystyle \frac{{\vartheta }_{i,n}^2}{p_{i,n}^2-{\dot{v}}_{i,n}^2}}\left({\mathsf{\Gamma }}_{i,n}+{\displaystyle \frac{{\dot{p}}_{i,n}}{p_{i,n}}}\right)\le 0$. Then, Equation (32) can be reduced to

$$\begin{array}{cc}\hfill {\dot{V}}_{i,n}& \le {\displaystyle \frac{{\vartheta }_{i,n}}{p_{i,n}^2-{\vartheta }_{i,n}^2}}\left(-\mu {\vartheta }_{i,n}-k_{n,1}{\vartheta }_{i,n}-{\displaystyle \frac{{\theta }_{i,n}{\vartheta }_{i,n}}{p_{i,n}^2-{\vartheta }_{i,n}^2}}\right)\hfill \\ \hfill & -{\displaystyle \frac{{\vartheta }_{i,n}^2}{4{\theta }_{i,n-1}}}+{\dot{V}}_{i,n-1}\hfill \\ \hfill & \le \sum _{r=1}^n{\displaystyle \frac{-\mu {\vartheta }_{i,r}^2}{p_{i,r}^2-{\vartheta }_{i,r}^2}}-\sum _{r=1}^n{\displaystyle \frac{k_{r,1}{\vartheta }_{i,r}^2}{p_{i,r}^2-{\vartheta }_{i,r}^2}}-\sum _{r=1}^n{\mathrm{Y}}_{i,r}^2\hfill \end{array}$$

(33)

where ${\mathrm{Y}}_{i,n}={\displaystyle \frac{\sqrt{{\theta }_{i,n}}{\vartheta }_{i,n}}{p_{i,n}^2-{\vartheta }_{i,n}^2}}$.

   Figure 3 shows the derived structure and scaling results of the Lyapunov function in full text.This can help readers to understand the full text faster and reduce the cumbersome formula.

3.1. Prescribed-Time Control Design

Multi-agent system (1) with command filter and local tracking error system (3) are considered. Based on the adaptive predefined time neural network control scheme and inversion technology, the virtual control law is (13) and (19), the distributed adaptive fixed time law is (22), and the actual controller is (21).

• The multi-agent system is a predefined-time consensus.
• And the upper bound of the settling time T is independent from the initial parameters. The settling time T satisfies.
• The controller is designed using the backstepping iterative method, which together with the obstacle Lyapunov function can achieve the desired results.

The Algorithm 1 shows the derivation of the controller from 1 to n, which embodies the complete framework of system design.

Algorithm 1 Conjugate Gradient Algorithm with Dynamic Step-Size Control

Input: Multi-agent system model, predefined time $t_s$, performance function parameters    $p_{k,0},p_{t_{k,s}},{\mathsf{\ell }}_{i,k},{\xi }_{i,k}$, filter parameters ${\delta }_{i,k}$, and gain parameters $k_{k,1},{\theta }_{i,k},{\iota }_{i,k}$ Output: Control signal u   1: Initial: Set initial states $x_{i,k}\left(0\right)$, desired signal $y_{i,b}\left(t\right)$, and its derivative ${\dot{y}}_{i,b}\left(t\right)$   2: Construct piecewise function (7)   3: for  $k=1$  to  n  do   4:     if $k=1$ then   5:         Define tracking error from (5)   6:     else   7:         Define error variable from (5)   8:     end if   9:     Construct compensation error from (5) 10:     Control Law Design: 11:     if $k<n$ then 12:         Obtain virtual control law from (21) 13:         Obtain filtered signal from (22) 14:     else 15:         Obtain actual control law from (29) 16:     end if 17: end for 18: return  u

Figure 4 outlines a neural network-based adaptive backstepping control design process. The procedure begins by defining a performance index to quantify the tracking objectives. Recursively, virtual control laws are constructed while generating compensation errors to address approximation residuals. Critical error transformations (e.g., nonlinear mappings for constrained states) and their derivatives are computed to convert state constraints into stability conditions. Through iterative design steps, virtual control laws are progressively refined to bridge subsystems. Finally, the synthesized actual control law drives the system. A neural network actively approximates unknown nonlinear dynamics, with its weights continuously adjusted via an adaptive law to ensure robust stability and guaranteed tracking performance under uncertainties. This structured approach integrates transformation techniques, adaptive approximation, and recursive control synthesis for complex nonlinear systems.

Figure 5 depicts the core sequence of an adaptive neural network control process: It begins with tracking error as the input signal, which generates a compensation error to account for unmodeled dynamics or disturbances. This error drives the design of a virtual controller to stabilize subsystem states. An adaptive-rate neural network then actively approximates unknown nonlinearities in real time, dynamically adjusting its weights to minimize uncertainty. Finally, the synthesized actual control laws are computed and deployed to the physical system. This streamlined architecture enables robust error-driven control with online learning capabilities for complex dynamical systems.

The following part is the stability analysis and experimental simulation section of the thesis.

3.2. Stability Analysis

Theorem 1. 

For the multi-agent system (3), under Assumption 1, if the control variables are designed as (7), (14), (21), and (29), then the upcoming characteristics will be guaranteed: (i) all signals are predefined-time bounded within a predefined-time interval in the closed-loop system; (ii) the predefined performance metrics can be reached; and (iii) the state of the system will not infringe the constraints.

Proof. 

Construct the Lyapunov function with the subsequent form

$$V={\displaystyle \frac{1}{2}}\sum _{r=1}^{n}log\left({\displaystyle \frac{p_{i,n}^2}{p_{i,n}^2-{\vartheta }_{i,n}^2}}\right)$$

(34)

When $t\in \left[0,t_s\right)$, after performing some elaborate algebraic operations and taking Lemma 1 and Equation (33) into account, the differentiation of V concerning time is

$$\begin{array}{cc}\hfill \dot{V}& \le \sum _{r=1}^n{\displaystyle \frac{-\mu {\vartheta }_{i,r}^2}{p_{i,r}^2-{\vartheta }_{i,r}^2}}-\sum _{r=1}^n{\displaystyle \frac{k_{r,1}{\vartheta }_{i,r}^2}{p_{i,r}^2-{\vartheta }_{i,r}^2}}-\sum _{r=1}^n{\mathrm{Y}}_{i,r}^2\hfill \\ \hfill & \le \sum _{r=1}^n{\displaystyle \frac{-\mu {\vartheta }_{iv}^2}{p_{i,r}^2-{\vartheta }_{i,r}^2}}\hfill \\ \hfill & \le -2\mathsf{\mu }\mathrm{V}\hfill \end{array}$$

(35)

In the light of $\mu =\overline{\kappa }/\left(t_s-t\right)$, we know that $\dot{V}\le$$-2\overline{\kappa }/\left(t_s-t\right)V$. By integrating both sides of inequality $1/VdV\le -2\overline{\kappa }/\left(t_s-t\right)dt$ from 0 to t, we can deduce the relationships presented as follows:

$$V\left(t\right)\le V\left(0\right){\left({\displaystyle \frac{t_s-t}{t_s}}\right)}^{2\overline{\kappa }}=\beta {\left(t_s-t\right)}^{2\overline{\kappa }}$$

(36)

Moreover, due to $\overline{\kappa }>2$, one can have the next equality:

$$\begin{array}{cc}\hfill & \underset{t⟶t_s}{lim}{\displaystyle \frac{p_{i,1}{\left(1-exp\left(-2\beta {\left(t_s-t\right)}^{2\kappa }\right)\right)}^{\frac{1}{2}}}{{\left(t_s-t\right)}^2}}\hfill \\ \hfill =& \underset{t⟶t_s}{lim}{\displaystyle \frac{p_{i,1}\left(2\beta {\left(t_s-t\right)}^{\overline{\kappa }}\right)}{{\left(t_s-t\right)}^2}}\hfill \\ \hfill =& 0\hfill \end{array}$$

(37)

Assuming that the initial condition satisfies $\left|{\vartheta }_{i,r}\left(0\right)\right|\le$$p_{i,r}\left(0\right)$, considering Definition 2 along with the form of $log\left({\displaystyle \frac{p_{i,r}^2}{p_{i,r}^2-{\vartheta }_{i,r}^2}}\right)$, and considering the predefined time stability of the closed-loop system, we can ensure that the variables ${\vartheta }_{i,r}$ remain within the region defined by the PTPFs $p_{i,r}$, that is, ${\vartheta }_{i,r}\le p_{i,r,0}+p_{t_{r,s}}$, where $r=1,\dots ,n$. For any given tracking error ${\chi }_{i,1}>0$, using Lemma 2 in [3] and choosing the appropriate parameters, it is possible to ensure that the inequality $\left|e_{i,1}\right|=\left|{\vartheta }_{i,1}+{\zeta }_{i,1}\right|<{\chi }_{i,1}$ holds. This implies that the tracking error $e_1$ can be restricted within a predetermined range, indicating the fulfillment of the pre-assigned performance metrics. Hence, the proof for characteristic (ii) has been completed. Assuming that the initial condition satisfies $\left|{\vartheta }_{i,r}\left(0\right)\right|\le$$p_{i,r}\left(0\right)$, considering Definition 2 along with the form of $log\left({\displaystyle \frac{p_{i,r}^2}{p_{i,r}^2-{\vartheta }_{i,r}^2}}\right)$, and considering the predefined time stability of the closed-loop system, we can ensure that the variables ${\vartheta }_{i,r}$ remain within the region defined by the PTPFs $p_{i,r}$, that is, ${\vartheta }_{i,r}\le p_{i,r,0}+p_{t_{r,s}}$, where $r=1,\dots ,n$. For any given tracking error ${\chi }_{i,1}>0$, using Lemma 2 in [3] and choosing the appropriate parameters, it is possible to ensure that the inequality $\left|e_{i,1}\right|=\left|{\vartheta }_{i,1}+{\zeta }_{i,1}\right|<{\chi }_{i,1}$ holds. This implies that the tracking error $e_1$ can be restricted within a predetermined range, indicating the fulfillment of the pre-assigned performance metrics. Hence, the proof for characteristic (ii) has been completed. From characteristic (i), we can conclude that ${\zeta }_{i,r},{\phi }_{i,r}$ are continuous and bounded within the predefined time from 0 to $t_s$. Hence, positive constants $C_{{\zeta }_{i,r}},C_{{\phi }_{i,r}}$ exist such that inequalities $\left|{\zeta }_{i,r}\right|\le C_{{\zeta }_{i,r}},\left|{\phi }_{i,r}\right|\le C_{{\phi }_{i,r}}$ hold, where $r=1,\dots ,n$. By virtue of $x_{i,1}=e_{i,1}+y_{i,b}={\vartheta }_{i,1}+{\zeta }_{i,1}+y_{i,b}$ and Assumption 1, we can determine suitable parameters to ensure that the inequality $\left|x_{i,1}\right|\le \left|{\vartheta }_{i,1}\right|+\left|{\zeta }_{i,1}\right|+\left|y_{i,b}\right|\le p_{1,0}+p_{t_{1,s}}+C_{0,1}+C_{{\zeta }_{i,1}}<$ $C_{x_{i,1}}$ holds. This indicates that the state constraint $\left|x_{i,1}\right|<C_{x_{i,1}}$ will not be infringed.

Similarly, based on (i) and (ii), we can determine the appropriate parameters to ensure that the inequalities $\left|x_{i,r}\right|\le \left|{\vartheta }_{i,r}\right|+\left|{\zeta }_{i,r}\right|+$$\left|{\phi }_{i,r}\right|\le p_{r,0}+p_{t_{r,s}}+C_{{\phi }_{i,r}}+C_{{\zeta }_{i,r}}<C_{x_{i,r}}$ hold, implying that the state constraints $\left|x_{i,r}\right|<C_{x_{i,r}}$ can be satisfied, where $r=2,\dots ,n$. Therefore, we can conclude that the verification of characteristic (iii) has been successfully established. ${lim}_{t⟶t_s}{\displaystyle \frac{\left|{\vartheta }_{i,1}\right|}{{\left(t_s-t\right)}^2}}\le$${lim}_{t⟶t_s}{\displaystyle \frac{p_{i,1}{\left(1-exp\left(-2\beta {\left(t_s-t\right)}^{2\kappa }\right)\right)}^{\frac{1}{2}}}{{\left(t_s-t\right)}^2}}=0$, that is, ${lim}_{t⟶t_s}{\displaystyle \frac{{\vartheta }_{i,1}}{{\left(t_s-t\right)}^2}}=0$. Subsequently, we can infer that ${lim}_{t⟶t_s}{\displaystyle \frac{{\vartheta }_{i,1}}{\left(t_s-t\right)}}=0$. Using Equation (7) and the characteristic of the continuous function, we deduce that $x_{1,d}$ is continuous at time $t_s$. Since ${\phi }_{i,2}$ is obtained by making $x_{1,d}$ pass through the designed filter, we can further infer that ${\phi }_{i,2}$ is continuous at $t=t_s$. Furthermore, due to ${\dot{\phi }}_{i,2}=\left(x_{1,d}-{\phi }_{i,2}\right)/{\delta }_2$, it is obtained that ${\dot{\phi }}_{i,2}$ is also continuous at $t=t_s$.

Similarly, we will demonstrate that $x_{2,d}$ is also a continuous function. Utilizing ${\displaystyle \frac{1}{2}}log\left({\displaystyle \frac{p_{i,2}^2}{p_{i,2}^2-{\vartheta }_{i,2}^2}}\right)\le V\left(t\right)\le \beta {\left(t_s-t\right)}^{2\overline{\kappa }}$, we have $\left|{\vartheta }_{i,2}\right|\le p_{i,2}{\left(1-exp\left(-2\beta {\left(t_s-t\right)}^{2\overline{\kappa }}\right)\right)}^{{\displaystyle \frac{1}{2}}}$. Applying Equation (40) and following similar steps as before, it is not complicated to obtain ${lim}_{t⟶t_s}{\displaystyle \frac{p_{i,2}{\left(1-exp\left(-2\beta {\left(t_s-t\right)}^{2\kappa }\right)\right)}^{\frac{1}{2}}}{{\left(t_s-t\right)}^2}}=0$. It is straightforward to deduce that ${lim}_{t\to t_s}{\displaystyle \frac{{\vartheta }_{i,2}}{{\left(t_s-t\right)}^2}}=0$ by resorting to the squeeze theorem. Next, we can have ${lim}_{t\to t_s}{\displaystyle \frac{{\vartheta }_{i,2}}{{\left(t_s-t\right)}^2}}=0$ with $l=1,2$. Considering ${lim}_{t\to t_s}{\displaystyle \frac{{\vartheta }_{i,2}}{\left(t_s-t\right)}}=0$ and the continuous property of ${\dot{\phi }}_{i,2}$, we can similarly deduce that $x_{2,d}$ is a continuous function at the time $t_s$. Consequently, it is effortless to see that ${\phi }_3$ and its derivative with respect to time ${\dot{\phi }}_{i,3}$ are continuous at time $t_s$.

Using ${\displaystyle \frac{1}{2}}log\left({\displaystyle \frac{p_{i,r}^2}{p_{\sim }^2-{\vartheta }_{i,r}^2}}\right)\le V\left(t\right)\le \beta {\left(t_s-t\right)}^{2\overline{\kappa }}$ and following the corresponding analysis process as in the previous steps, we can deduce that ${lim}_{t\to t_s}{\displaystyle \frac{{\vartheta }_r}{{\left(t_s-t\right)}^2}}=0$ and further prove that $x_{r,d},{\phi }_{r+1},{\dot{\phi }}_{r+1}$ are continuous at time $t_s$, where $r=3,\dots n$.

For $t\ge t_s$, all control variables $x_{r,d}$ are continuous functions, and it is evident that $V\left(t\right)$ is a $C^1$ function for any time t, which implies that $V\left(t_s\right)=0$. Taking into account Equation (35), we have $\dot{V}\le -{\sum }_{r=1}^n{{\rm Y}}_{i,r}^2$. Thus, we can infer that $V\left(t\right)$ and $\dot{V}\left(t\right)$ are identically zero for any $t\ge t_s$. We can further gain that ${\vartheta }_r$ are identically zero, $\forall t\ge t_s$. Moreover, according to equations (9), (16), (23), and (30), we know that ${\zeta }_r$ are continuous functions and, therefore, ${\zeta }_r$ are bounded for any $t\ge t_s$, where $r=1,\dots ,n$. Due to ${\vartheta }_{i,r}=e_{i,r}-{\zeta }_{i,r}$, we can infer that $e_r$ are also continuous and bounded for any $t\ge t_s$, where $r=1,\dots ,n$.

According to $e_{i,1}=x_{i,1}-y_{i,d},e_{i,r}=x_{i,r}-{\phi }_{i,r}$ and Assumption 1, we can deduce that state variables $x_r$ are also continuous and bounded for any $t\ge t_s,r=1,\dots ,n$. Based on the previous analyses, the characteristics of continuous functions, and Definition 1, it can be concluded that all variables are bounded within the predefined time interval from 0 to $t_s$. Thus, the proof for characteristic (i) has been completed. □

4. Simulation Examples

Example 1. 

The proposed approach is applied to the single-link robotic manipulator system depicted in [20,21] to validate its effectiveness.

$$ml\ddot{\sigma }\left(t\right)=ϵ-m\overline{g}sin\sigma -bl\ddot{\sigma }$$

(38)

where ϵ is the input torque; m and l correspond to the mass and length of the link, respectively; $\ddot{\sigma },\dot{\sigma },\sigma \in \mathbb{R}$ depicts link acceleration, velocity, and the position of the robotic manipulator, respectively; the unknown viscous friction coefficient is represented by b; and the gravity acceleration constant is depicted by $\overline{g}$. Considering the exogenous disturbance $d\left(t\right)$ and defining $x_{i,1}=\sigma$ and $x_{i,2}=\dot{\sigma }$, Equation (38) can be reformulated as the following state equations:

$$\begin{array}{cc}\hfill & {\dot{x}}_{i,1}=x_{i,2}\hfill \\ \hfill & {\dot{x}}_{i,2}=-{\displaystyle \frac{\overline{g}}{l}}sin{x}_{i,1}-{\displaystyle \frac{b}{m}}{x}_{i,2}+{\displaystyle \frac{\xi }{ml}}+d\left(t\right)\hfill \\ \hfill & y_i=x_{i,1}\hfill \end{array}$$

(39)

Figure 6 represents the directed graph of the adjacency matrix.

The system parameters are determined as $m=1\mathrm{kg},l=2\mathrm{m}$, $\overline{g}=9.8\mathrm{m}/{\mathrm{s}}^2$, and $b=1$. The desired signal is assigned as $y_b\left(t\right)=2.5t+2.5$. All agents are tracking the same reference signal $y_b$, and the disturbance is assigned as $d\left(t\right)=0.1$. The state constraints are designated as $\left|x_{i,1}\right|<k_{x_1}=0.9$, $\left|x_{i,2}\right|<k_{x_2}=1.2$. The chief parameters are chosen as ${\iota }_{i,1}=0.3,k_{1,1}=5,{\theta }_{i,1}=0.3,{\iota }_{i,2}=0.2,k_{2,1}=3,{\theta }_{i,2}=0.3$$\overline{k}=2.2,t_s=2\mathrm{s},{\delta }_{i,2}=0.1$. The parameters for PTPFs are determined as $p_{1,0}=0.8,p_{t_{1,s}}=0.01,{\mathsf{\ell }}_{i,1}=0.5,{\xi }_{i,1}=0.5$, $p_{2,0}=1.15,p_{t_{2,s}}=0.02,{\mathsf{\ell }}_{i,2}=0.5,{\xi }_{i,2}=1$. The initial conditions are determined as $x_{i,2}\left(0\right)=0.25,x_{i,1}\left(0\right)=0.2$. Figure 7, Figure 8 and Figure 9 characterize the results of applying the control approach to the aforementioned practical example. The plots in Figure 7 describe the response of the desired signal $y_b$, the output signal y, and the variable of $x_{i,n}$, respectively. It can be inferred from Figure 8 that the trajectories of $x_{i,1}$ remain within the regions of state constraints while acquiring the predefined-time boundedness within the predefined time of 2 s. The graphs in Figure 7 portray the trajectories of $x_{i,1}$, respectively. Figure 9 illustrates the effectiveness of the proposed control scheme in acquiring the predefined performance metrics while keeping $e_{i,1}$ in the regions prescribed by the corresponding PTPFs. The responses of the actual control signal $x_{i,n}$, obtained by employing the control approach presented in this paper and the approach proposed in [21], are shown in Figure 7. The plots in Figure 7 describe that the output signal can track the desired signal at various predefined-times.

Example 2. 

The practicability of the proposed predefined time control scheme was verified by applying it to the following forms of multi-agent systems [21,26]:

$$\left\{\begin{array}{cc}\hfill {\dot{x}}_{i,1}& =0.1x_{i,1}^2+x_{i,2}\hfill \\ \hfill {\dot{x}}_{i,2}& =0.1x_{i,1}{x}_{i,2}-0.2x_{i,1}+\left(1+x_{i,1}^2\right)u_i\hfill \\ \hfill y_i& =x_{i,1}\hfill \end{array}\right.$$

(40)

where the states are subject to the constraints $\left|x_{i,1}\right|<C_{x_{i,1}}=0.7$ and $\left|x_{i,1}\right|<C_{x_{i,1}}=1$. The proposed control method will be utilized to guide the system output to track the desired signal $y_{i,b}=x_{i,1}=-0.2cos\left(t\right)+0.1(cos\left(1\right)-1)t^2+t+1.2$ in a predefined-time while satisfying the PPMs. The initial conditions are determined as $x_{1,1}\left(0\right)=1,x_{2,1}\left(0\right)=2,x_{3,1}\left(0\right)=-1,x_{4,1}\left(0\right)=-2,x_{5,1}\left(0\right)=-3$. The chief parameters are chosen as: ${\iota }_{i,1}=0.3,k_{1,1}=1,{\theta }_{i,1}=0.3,{\iota }_{i,2}=0.2,k_{2,1}=1,{\theta }_{i,2}=0.2$, $\overline{k}=3,t_s=20s,{\delta }_2=0.05$. The parameters for PTPF are determined as $p_{1,0}=0.66,p_{t_{1,s}}=0.02,{\mathsf{\ell }}_{i,1}=0.5,{\xi }_{i,1}=0.5$, $p_{2,0}=0.95,p_{t_{2,s}}=0.02,{\mathsf{\ell }}_{i,2}=0.5,{\xi }_{i,2}=1$. The actual controller is designed as $u_i={\displaystyle \frac{h}{1+x_{i,1}^2}}\left({\alpha }_{i,2}-\mu {\vartheta }_{i,2}\right)+{\displaystyle \frac{1-h}{1+x_{i,1}^2}}{\alpha }_{i,2}$, where ${\alpha }_{i,2}=-k_{2,1}{e}_{i,2}-0.1x_{i,1}{x}_{i,2}+0.2x_{i,1}+{\dot{\phi }}_2-\sqrt{{\displaystyle \frac{p_{i,2}^2}{\frac{p_{i,2}^2}{p_{i,2}^2\left(t\right)}}}+{\iota }_{i,2}}{\vartheta }_{i,2}-{\displaystyle \frac{{\theta }_{i,2}{\vartheta }_{i,2}}{p_{i,2}^2-{\vartheta }_{i,2}^2}}-{\displaystyle \frac{{\vartheta }_{i,2}\left(p_{i,2}^2-{\vartheta }_{i,2}^2\right)}{4{\theta }_{i,1}}}$.

The simulation results are presented in Figure 10, Figure 11, Figure 12 and Figure 13. The results in Figure highlight the excellent performance of the proposed control approach, as evidenced by the close tracking of the system output $x_{i,n}$ to the desired signal $y_{i,b}$ within a preset time of 20 s and the satisfaction of the state constraints on $x_{i,1}$ and $x_{i,2}$.

The control approach in this article effectively restricts the control input $u_{i,1}$ to a smaller range of ±0.6, while in [21], $u_{i,1}$ fluctuates in a larger range from approximately −0.6 to 0.6. This shows that the proposed predefined-time control approach based on the command filter relaxes the strict assumption of the desired signal and attains predefined performance with a smaller control input than the scheme in [21]. Thus, the proposed scheme is more robust and stable in complex scenarios, especially with strong disturbances, and can achieve the desired control objectives with equivalent control input. Figure 14 compares the proposed method with the conventional method and draws some conclusions.

5. Conclusions

By using the command filter method, the conservativeness associated with the assumption about the tracking signal is met, and then the need to establish the continuity of high-order derivatives of the virtual control signals is circumvented. These enhancements lead to a substantial reduction in the complexity of stability analyses concerning the predefined time convergence of the closed-loop signals. In the end, the simulation results of two examples provide support for the effectiveness and applicability of the proposed command-filter predefined-time control approach.

The control strategy outlined in this paper is primarily tailored for predefined-time control applications in multi-agent systems featuring state constraints and predefined performance metrics. The current study does not involve asymmetric state constraints, uncertain parameters, or unknown disturbances within the controlled systems. Our future work will emphasize extending the proposed control strategy to uncertain multi-agent systems subject to asymmetric state constraints and unknown disturbances.