Enhanced Ratio-Type Estimators in Adaptive Cluster Sampling Using Jackknife Method
Abstract
1. Introduction
2. Adaptive Cluster Sampling
3. Proposed Estimators in Adaptive Cluster Sampling Using the Jackknife Method
- (1)
- First proposed estimator
- (2)
- Second proposed estimator
- (3)
- Third proposed estimator
4. Simulation Study and Discussion
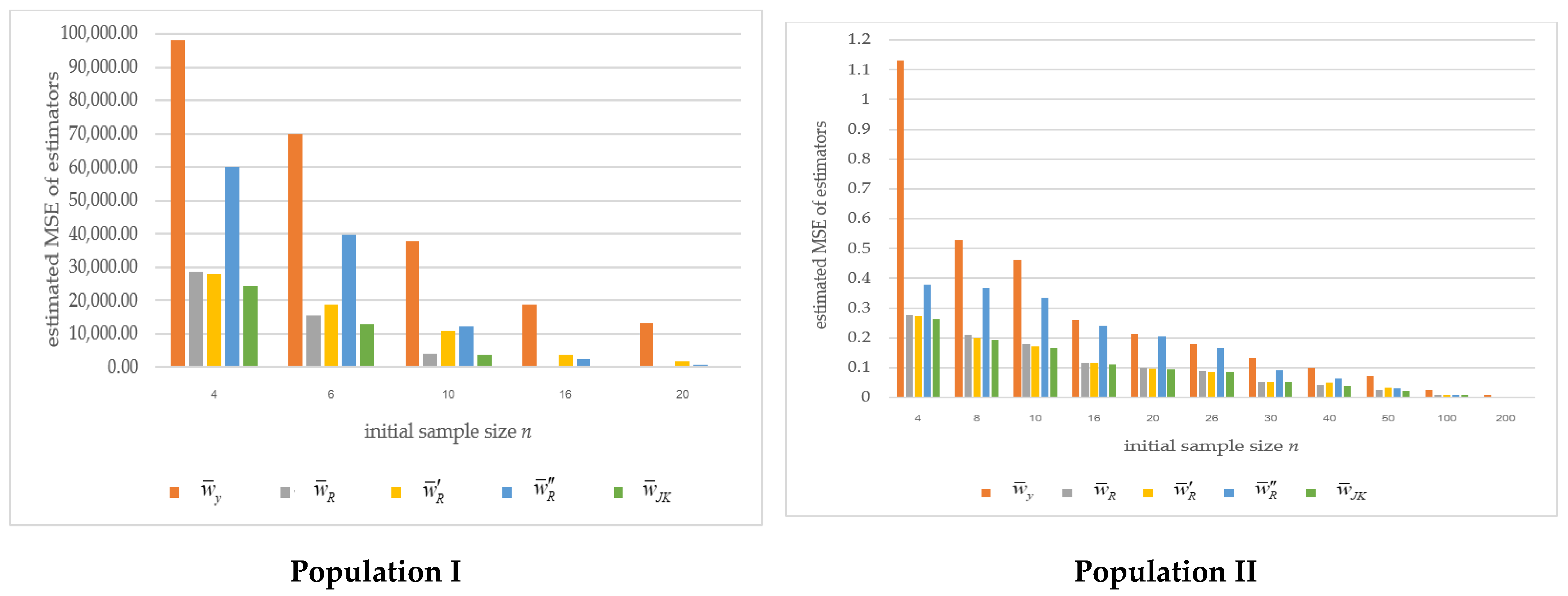
Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A



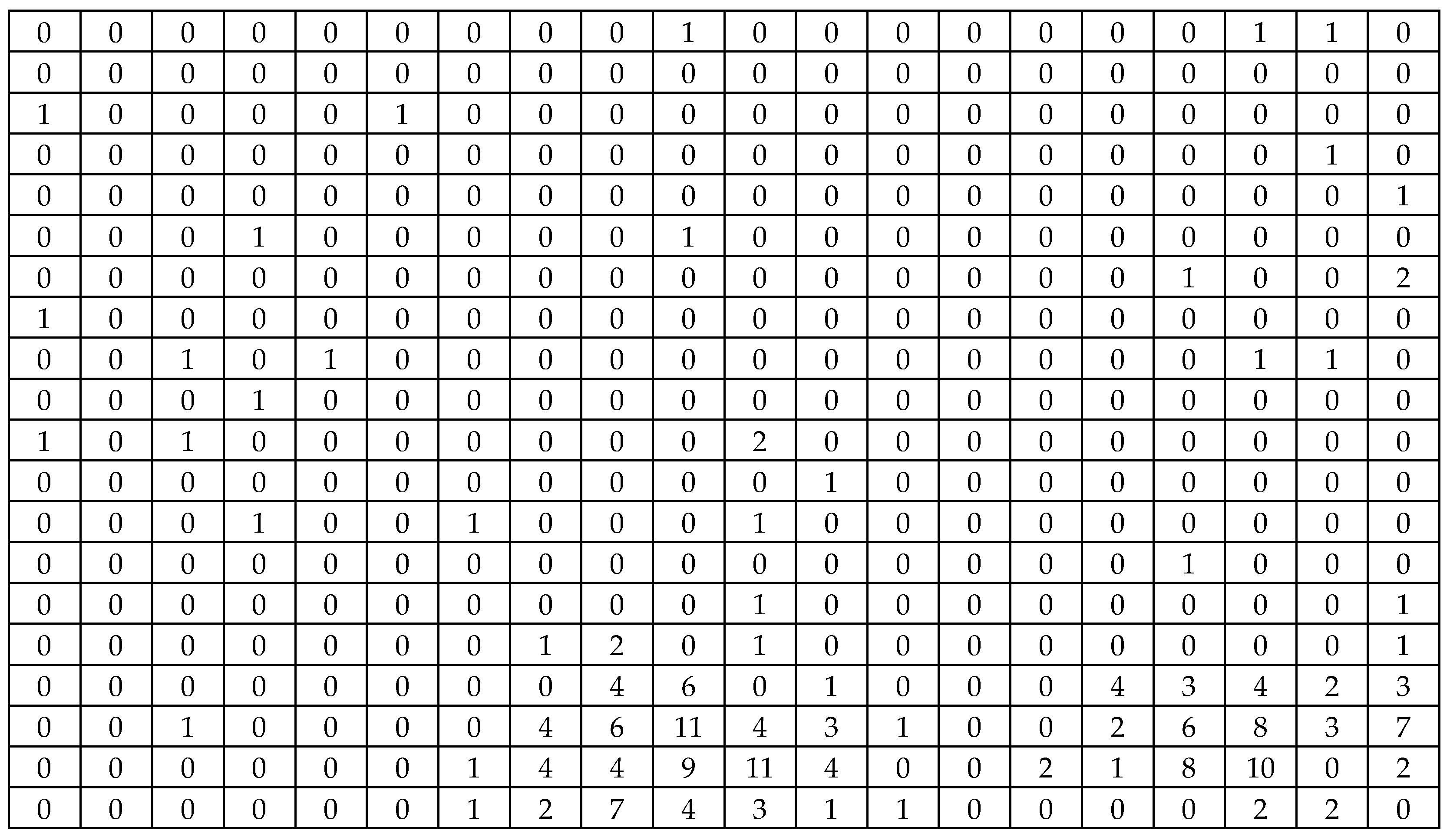
Appendix B
References
- Sisodia, B.V.S.; Dwivedi, V.K.A. Modified ratio Estimator Using Coefficient of Variation of Auxiliary Variable. J. Indian Soc. Agric. Stat. 1981, 33, 13–18. [Google Scholar]
- Singh, H.P.; Tailor, R. Use of Known Correlation Coefficient in Estimating the Finite Population Mean. Stat. Transit. 2003, 6, 553–560. [Google Scholar]
- Yadav, S.K.; Subramani, J.; Mishra, S.S.; Shukla, A.K. Improved Ratio-Cum-Product Estimators of Population Mean Using Known Population Parameters of Auxiliary Variables. Am. J. Oper. Res. 2016, 6, 48–54. [Google Scholar] [CrossRef]
- Jerajuddin, M.; Kishun, J. Modified Ratio Estimators for Population Mean Using Size of the Sample, Selected from Population. Int. J. Sci. Res. Sci. Eng. Technol. 2016, 2, 10–16. [Google Scholar] [CrossRef]
- Soponviwatkul, K.; Lawson, N. New Ratio Estimators for Estimating Population Mean in Simple Random Sampling using a Coefficient of Variation, Correlation Coefficient and a Regression Coefficient. Gazi Univ. J. Sci. 2017, 30, 610–621. [Google Scholar]
- Thompson, S.K. Adaptive cluster sampling. J. Am. Statist. Assoc. 1990, 85, 1050–1059. [Google Scholar] [CrossRef]
- Magnussen, S.; Kurz, W.; Leckie, D.G.; Paradine, D. Adaptive cluster sampling for estimation of deforestation rates. Eur. J. For. Res. 2005, 124, 207–220. [Google Scholar] [CrossRef]
- Noon, B.R.; Ishwar, N.M.; Vasudevan, K. Efficiency of adaptive cluster and random sampling in detecting terrestrial herpetofauna in a tropical rainforest. Wildl. Soc. Bull. 2006, 34, 59–68. [Google Scholar] [CrossRef]
- Sullivan, W.P.; Morrison, B.J.; Beamish, F.W.H. Adaptive cluster sampling: Estimating density of spatially autocorrelated larvae of the sea lamprey with improved precision. J. Great Lakes Res. 2008, 34, 86–97. [Google Scholar] [CrossRef]
- Smith, D.R.; Villella, R.F.; Lemarié, D.P. Application of adaptive cluster sampling to low-density populations of freshwater mussels. Environ. Ecol. Stat. 2003, 10, 7–15. [Google Scholar] [CrossRef]
- Conners, M.E.; Schwager, S.J. The use of adaptive cluster sampling for hydroacoustic surveys. ICES J. Mar. Sci. 2002, 59, 1314–1325. [Google Scholar] [CrossRef]
- Olayiwola, O.M.; Ajayi, A.O.; Onifade, O.C.; Wale-Orojo, O.; Ajibade, B. Adaptive cluster sampling with model based approach for estimating total number of Hidden COVID-19 carriers in Nigeria. Stat. J. IAOS 2020, 36, 103–109. [Google Scholar] [CrossRef]
- Chandra, G.; Tiwari, N.; Nautiyal, R. Adaptive cluster sampling-based design for estimating COVID-19 cases with random samples. Curr. Sci. 2021, 120, 1204–1210. [Google Scholar] [CrossRef]
- Stehlík, M.; Kiseľák, J.; Dinamarca, A.; Alvarado, E.; Plaza, F.; Medina, F.A.; Stehlíková, S.; Marek, J.; Venegas, B.; Gajdoš, A.; et al. REDACS: Regional emergency-driven adaptive cluster sampling for effective COVID-19 management. Stoch. Anal. Appl. 2022, 41, 474–508. [Google Scholar] [CrossRef]
- Hwang, J.; Bose, N.; Fan, S. AUV adaptive sampling methods: A Review. Appl. Sci. 2019, 9, 3145. [Google Scholar] [CrossRef]
- Giouroukis, D.; Dadiani, A.; Traub, J.; Zeuch, S.; Markl, V. A survey of adaptive sampling and filtering algorithms for the internet of things. In Proceedings of the 14th ACM International Conference on Distributed and Event- Based Systems, Montreal, QC, Canada, 13–17 July 2020; pp. 27–38. [Google Scholar] [CrossRef]
- Chao, C.T. Ratio estimation on adaptive cluster sampling. J. Chin. Stat. Assoc. 2004, 42, 307–327. [Google Scholar] [CrossRef]
- Dryver, A.L.; Chao, C.T. Ratio estimators in adaptive cluster sampling. Environmetric 2007, 18, 607–620. [Google Scholar] [CrossRef]
- Chutiman, N.; Kumphon, B. Ratio estimator using two auxiliary variables for adaptive cluster sampling. Thail. Stat. 2008, 6, 241–256. [Google Scholar]
- Chutiman, N. Adaptive cluster sampling using auxiliary variable. J. Math. Stat. 2013, 9, 249–255. [Google Scholar] [CrossRef]
- Yadav, S.K.; Misra, S.; Mishra, S. Efficient estimator for population variance using auxiliary variable. Am. J. Oper. Res. 2016, 6, 9–15. [Google Scholar] [CrossRef]
- Chaudhry, M.S.; Hanif, M. Generalized exponential-cum-exponential estimator in adaptive cluster sampling. Pak. J. Stat. Oper. Res. 2015, 11, 553–574. [Google Scholar] [CrossRef]
- Chaudhry, M.S.; Hanif, M. Generalized difference-cum-exponential estimator in adaptive cluster sampling. Pak. J. Stat. 2017, 33, 335–367. [Google Scholar]
- Bhat, A.A.; Sharma, M.; Shah, M.; Bhat, M. Generalized ratio type estimator under adaptive cluster sampling. J. Sci. Res. 2023, 67, 46–51. [Google Scholar] [CrossRef]
- Thompson, S.K. Sampling, 3rd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2012; pp. 319–337. [Google Scholar]
- Banerjie, J.; Tiwari, N. Improved ratio type estimator using jack-knife method of estimation. J. Reliab. Stat. Stud. 2011, 4, 53–63. [Google Scholar]
- Quenouille, M.H. Notes on Bias in Estimation. Biometrika 1956, 43, 353–360. [Google Scholar] [CrossRef]
- Smith, D.R.; Conroy, M.J.; Brakhage, D.H. Efficiency of adaptive cluster sampling for estimating density wintering waterfowl. Biometrics 1995, 51, 777–788. [Google Scholar] [CrossRef]
- Pochai, N. Double and Resampling in Adaptive Cluster Sampling. Doctoral Dissertation, National Institute of Development Administration, Bangkok, Thailand, 2006. [Google Scholar]


| Population I | ||||
| 4 | 9.6743 | 0.1089 | 0.3728 | 0.2151 |
| 8 | 13.3041 | 0.0209 | 0.2094 | 0.0584 |
| 10 | 18.9176 | 0.0160 | 0.0723 | 0.0138 |
| 16 | 25.2787 | 0.0074 | 0.0120 | 0.0087 |
| 20 | 28.5644 | 0.0009 | 0.0110 | 0.0014 |
| Population II | ||||
| 4 | 6.8705 | 0.5189 | 0.6967 | 0.6011 |
| 8 | 12.8042 | 0.2987 | 0.5419 | 0.3481 |
| 10 | 15.8498 | 0.2007 | 0.4472 | 0.2344 |
| 16 | 24.8431 | 0.0638 | 0.2750 | 0.0775 |
| 20 | 30.9154 | 0.0249 | 0.1920 | 0.0326 |
| 26 | 38.9001 | 0.0331 | 0.1360 | 0.0348 |
| 30 | 43.8715 | 0.0258 | 0.0978 | 0.0273 |
| 40 | 56.7309 | 0.0076 | 0.0381 | 0.0082 |
| 50 | 68.5383 | 0.0098 | 0.0268 | 0.0101 |
| 100 | 120.1685 | 0.0018 | 0.0082 | 0.0018 |
| 200 | 215.1886 | 0.0030 | 0.0004 | 0.0003 |
| Population I | |||||||
| n | Estimators without auxiliary variable information | Estimators utilizing auxiliary variable information | |||||
| 4 | 9.6743 | 460,161.8988 | 98,093.5592 | 28,660.4541 | 28,139.4430 | 60,246.5137 | 24,515.0587 |
| 8 | 13.3041 | 348,211.0954 | 69,903.2109 | 15,438.8033 | 18,899.7352 | 39,627.6046 | 12,953.4060 |
| 10 | 18.9176 | 181,110.7250 | 37,756.8454 | 4107.7002 | 10,795.4605 | 12,398.3285 | 3881.9643 |
| 16 | 25.2787 | 76,613.8482 | 18,963.6552 | 533.3519 | 3771.5275 | 2526.1157 | 512.5064 |
| 20 | 28.5644 | 46,482.3626 | 13,304.8071 | 85.8090 | 1804.1610 | 763.9441 | 82.4876 |
| Population II | |||||||
| 4 | 6.8705 | 10.8216 | 1.1305 | 0.2777 | 0.2730 | 0.3777 | 0.2625 |
| 8 | 12.8042 | 10.8059 | 0.5291 | 0.2115 | 0.1986 | 0.3679 | 0.1929 |
| 10 | 15.8498 | 10.7229 | 0.4623 | 0.1792 | 0.1705 | 0.3361 | 0.1649 |
| 16 | 24.8431 | 9.6113 | 0.2606 | 0.1158 | 0.1149 | 0.2407 | 0.1102 |
| 20 | 30.9154 | 9.2723 | 0.2122 | 0.0990 | 0.0962 | 0.2040 | 0.0938 |
| 26 | 38.9001 | 7.7315 | 0.1790 | 0.0873 | 0.0863 | 0.1665 | 0.0856 |
| 30 | 43.8715 | 6.9521 | 0.1315 | 0.0527 | 0.0521 | 0.0906 | 0.0517 |
| 40 | 56.7309 | 5.9159 | 0.1004 | 0.0406 | 0.0495 | 0.0651 | 0.0401 |
| 50 | 68.5383 | 4.7074 | 0.0717 | 0.0252 | 0.0322 | 0.0292 | 0.0215 |
| 100 | 120.1685 | 1.5727 | 0.0238 | 0.0078 | 0.0091 | 0.0080 | 0.0078 |
| 200 | 215.1886 | 0.2266 | 0.0076 | 0.0023 | 0.0027 | 0.0024 | 0.0023 |
| Population I | ||||||||||
| 4 | 9.6743 | 1 | 3.4226 | 3.4860 | 1.6282 | 4.0014 | 1 | 1.0185 | 0.4757 | 1.1691 |
| 8 | 13.3041 | 1 | 4.5278 | 3.6986 | 1.7640 | 5.3965 | 1 | 0.8169 | 0.3896 | 1.1919 |
| 10 | 18.9176 | 1 | 9.1917 | 3.4975 | 3.0453 | 9.7262 | 1 | 0.3805 | 0.3313 | 1.0581 |
| 16 | 25.2787 | 1 | 35.5556 | 5.0281 | 7.5070 | 37.0018 | 1 | 0.1414 | 0.2111 | 1.0407 |
| 20 | 28.5644 | 1 | 155.0514 | 7.3745 | 17.4159 | 161.2946 | 1 | 0.0476 | 0.1123 | 1.0403 |
| Population II | ||||||||||
| 4 | 6.8705 | 1 | 4.0712 | 4.1412 | 2.9929 | 4.3076 | 1 | 1.0172 | 0.7352 | 1.0579 |
| 8 | 12.8042 | 1 | 2.5014 | 2.6639 | 1.4384 | 2.7424 | 1 | 1.0650 | 0.5749 | 1.0964 |
| 10 | 15.8498 | 1 | 2.5794 | 2.7109 | 1.3755 | 2.7950 | 1 | 1.0510 | 0.5332 | 1.0867 |
| 16 | 24.8431 | 1 | 2.2500 | 2.2682 | 1.0826 | 2.3652 | 1 | 1.0078 | 0.4811 | 1.0508 |
| 20 | 30.9154 | 1 | 2.1424 | 2.2061 | 1.0398 | 2.2618 | 1 | 1.0291 | 0.4853 | 1.0554 |
| 26 | 38.9001 | 1 | 2.0506 | 2.0739 | 1.0754 | 2.0926 | 1 | 1.0116 | 0.5243 | 1.0199 |
| 30 | 43.8715 | 1 | 2.4950 | 2.5252 | 1.4516 | 2.5452 | 1 | 1.0115 | 0.5817 | 1.0193 |
| 40 | 56.7309 | 1 | 2.4740 | 2.0307 | 1.5437 | 2.5061 | 1 | 0.8202 | 0.6237 | 1.0125 |
| 50 | 68.5383 | 1 | 2.8456 | 2.2289 | 2.4582 | 3.3355 | 1 | 0.7826 | 0.8630 | 1.1721 |
| 100 | 120.1685 | 1 | 3.0606 | 2.6042 | 2.9650 | 3.0606 | 1 | 0.8571 | 0.9750 | 1.0000 |
| 200 | 215.1886 | 1 | 3.2479 | 2.8464 | 3.2340 | 3.2479 | 1 | 0.8519 | 0.9583 | 1.0000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wichitchan, S.; Nathomthong, A.; Guayjarernpanishk, P.; Chutiman, N. Enhanced Ratio-Type Estimators in Adaptive Cluster Sampling Using Jackknife Method. Mathematics 2025, 13, 2020. https://doi.org/10.3390/math13122020
Wichitchan S, Nathomthong A, Guayjarernpanishk P, Chutiman N. Enhanced Ratio-Type Estimators in Adaptive Cluster Sampling Using Jackknife Method. Mathematics. 2025; 13(12):2020. https://doi.org/10.3390/math13122020
Chicago/Turabian StyleWichitchan, Supawadee, Athipakon Nathomthong, Pannarat Guayjarernpanishk, and Nipaporn Chutiman. 2025. "Enhanced Ratio-Type Estimators in Adaptive Cluster Sampling Using Jackknife Method" Mathematics 13, no. 12: 2020. https://doi.org/10.3390/math13122020
APA StyleWichitchan, S., Nathomthong, A., Guayjarernpanishk, P., & Chutiman, N. (2025). Enhanced Ratio-Type Estimators in Adaptive Cluster Sampling Using Jackknife Method. Mathematics, 13(12), 2020. https://doi.org/10.3390/math13122020








