Stability Diagrams of Bed Evolution for Vertically Averaged and Moment (VAM) Models
Abstract
1. Introduction
1.1. Background
1.2. Study Objectives
- Baseline Case—Classical SVE Framework: The traditional Saint-Venant–Exner (SVE) equations, formulated under the hydrostatic pressure assumption and incorporating the standard Chezy resistance relation, serve as the reference model for subsequent comparisons.
- Case 1—Incorporation of Non-Hydrostatic Effects: The baseline SVE equations are extended by integrating non-hydrostatic pressure terms derived from the moment of momentum approach, allowing assessment of their influence on instability predictions.
- Case 2—Hydrostatic VAM Model: The hydrostatic form of the VAM equations is employed, incorporating a modified Chezy-type resistance formulation tailored to moment-based velocity distributions for improved bed shear stress estimation.
- Case 3—Fully Extended VAM Model: This configuration combines both the moment-based velocity representation and non-hydrostatic pressure effects, providing the most comprehensive modeling framework for evaluating bedform evolution mechanisms.
1.3. Paper Organization
2. Methodology
2.1. Perturbation Analysis
2.2. Linearization of Conventional Saint-Venant (SV) Equation (Reference Case)
3. Effect of SV Equation (SVE) Enhancements
3.1. Linearized Form of SVE with Non-Hydrostatic Terms (Case 1)
3.2. Linear Stability Formulation of the VAM-Hydrostatic Model (Case 2)
3.3. Linear Stability Formulation of the Non-Hydrostatic VAM Model (Case 3)
4. Results and Discussion
4.1. Migration Direction of Evolving Bedforms
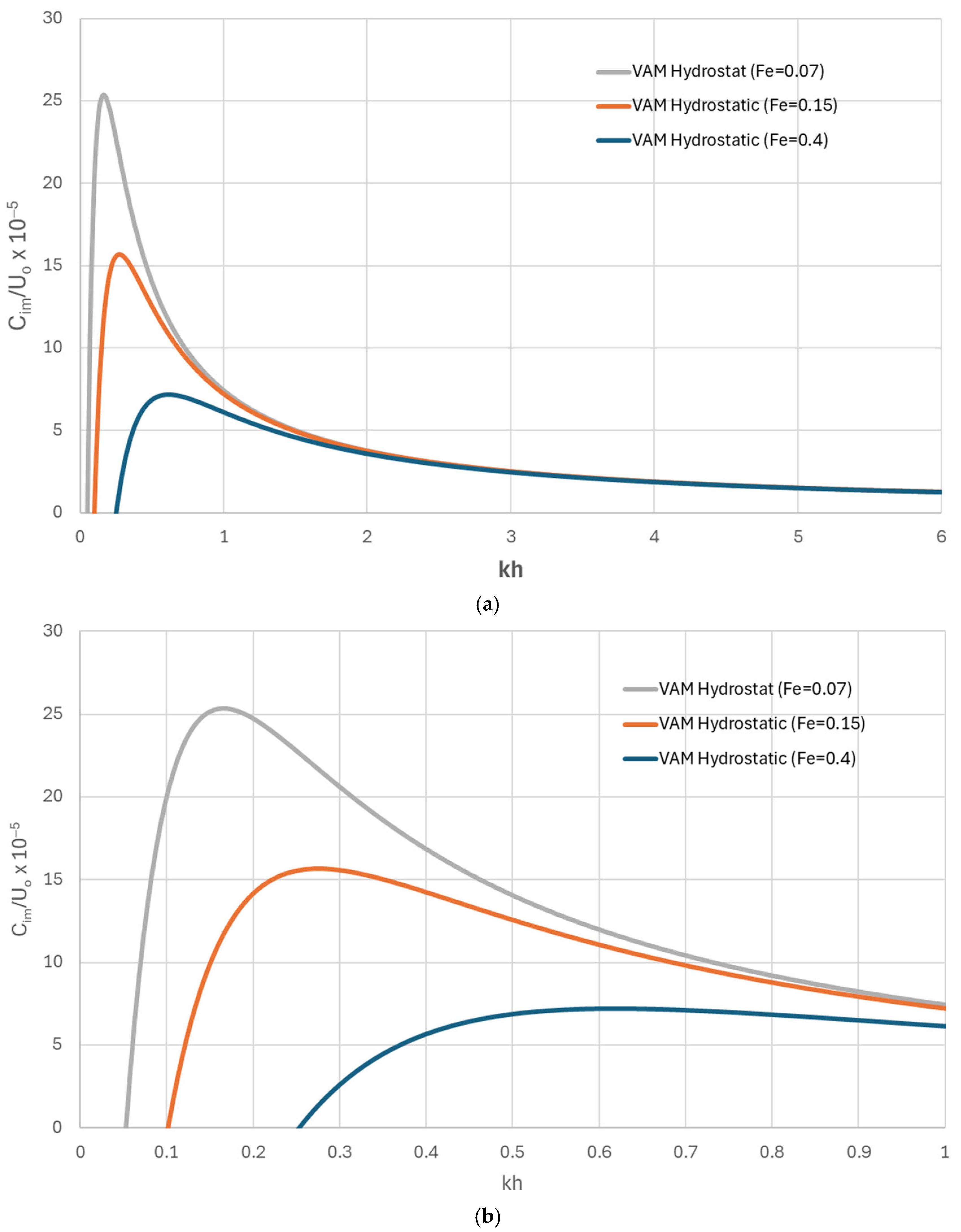
4.2. Bedform Evolution Analysis Based on the Hydrostatic VAM Model
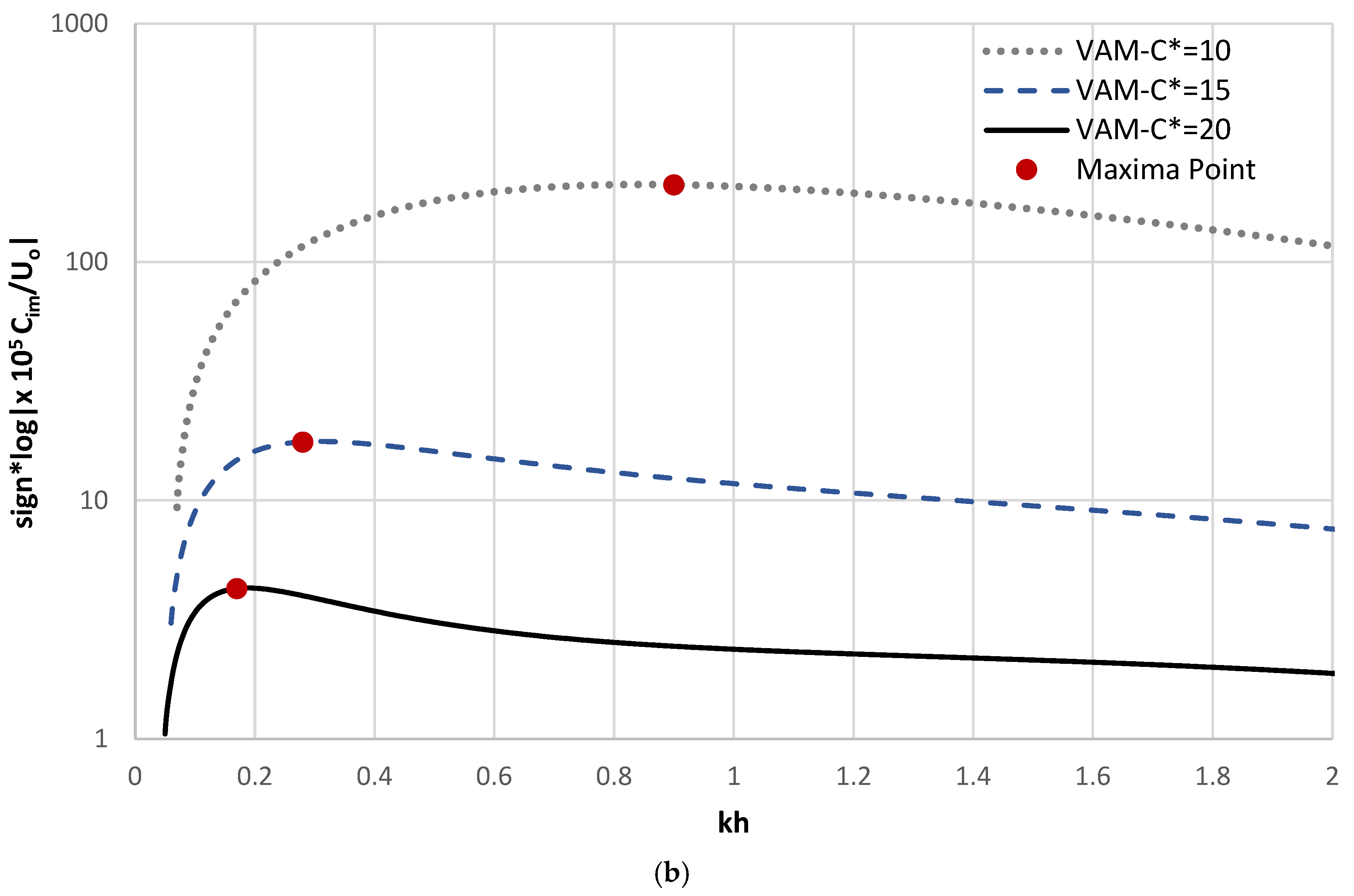
4.3. Bedform Evolution Analysis Based on Non-Hydrostatic VAM Formulation
4.4. Comparison with Bedform Measurements
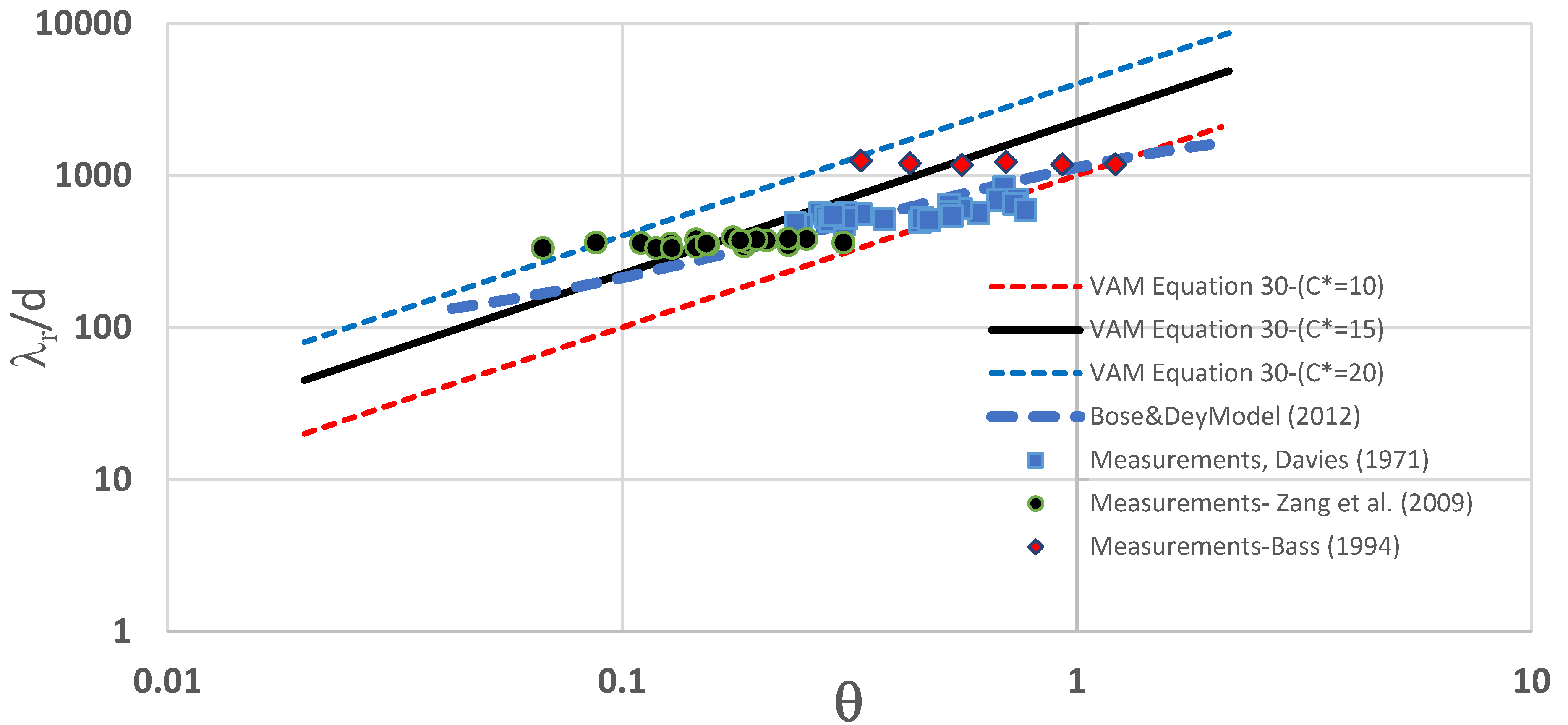
4.4.1. Dominant Wavelengths for Ripples
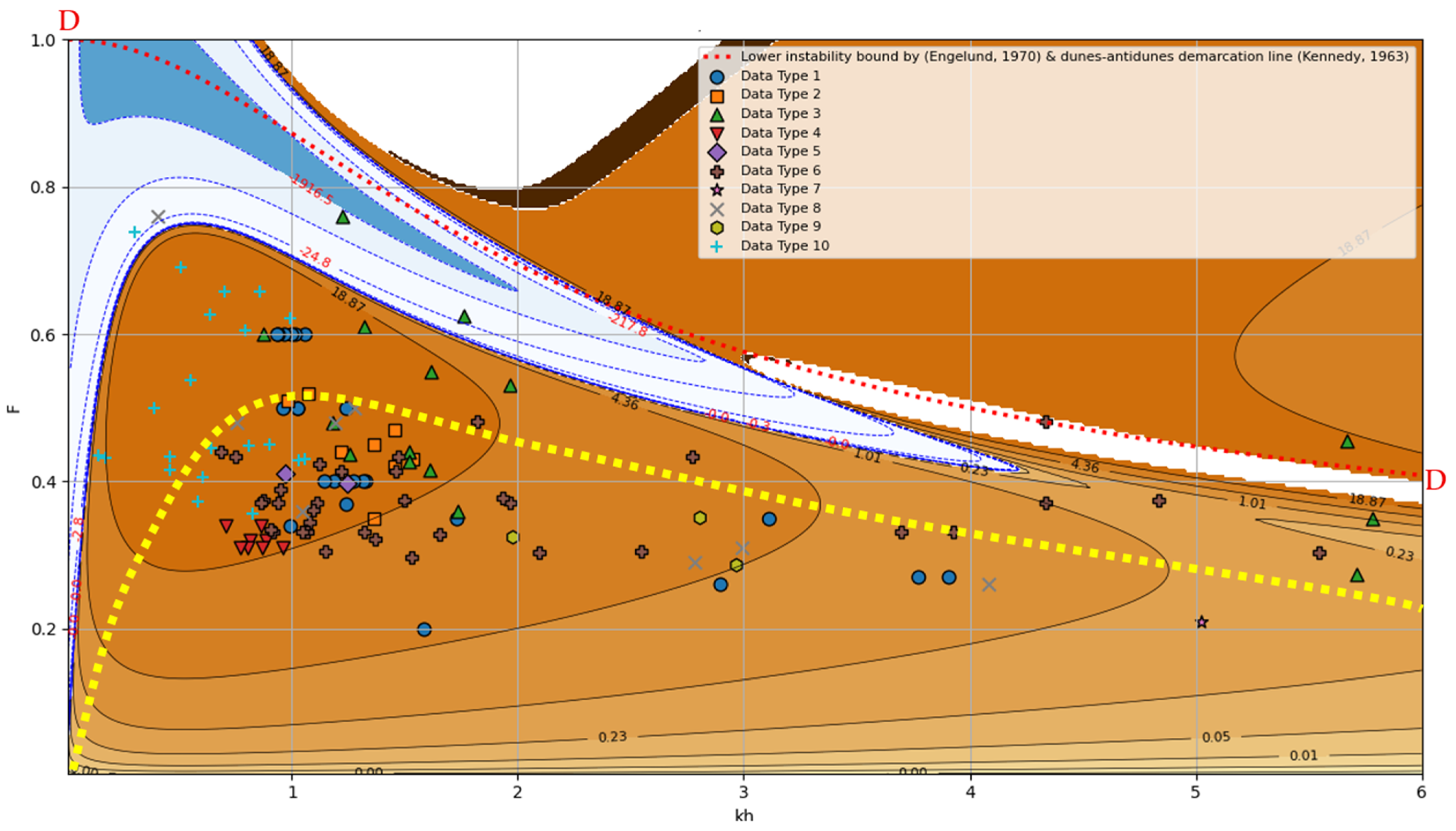
4.4.2. Dominant Wavelength for Dunes and Low-Flow Regime Sand Waves
4.5. Comparison with Colombini’s Analysis
5. Conclusions
6. Limitations and Outlook
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| b | Channel/flume bed width |
| C | Wave speed of bed perturbation |
| Creal | Real part of wave speed of bed perturbation |
| Cim | Imaginary part of wave speed of bed perturbation |
| C* | Dimensionless Chezy coefficient |
| C2 | Moment-based dimensionless Chezy coefficient |
| Cvi | A set of dimensionless coefficients for VAM model, refer to Appendix A.2 |
| Cdi | A set of dimensionless coefficients for VAM-hydrostatic model, refer to Appendix A.1 |
| F | Dimensionless Froude number |
| Fe | Eddy viscosity coefficient |
| g | Acceleration of gravity |
| h | Local water depth at distance x |
| i | . |
| Kr | Dimensionless calibration coefficient with a value ranging from about 1.45 to 2.7 |
| k | Turbulent kinetic energy per unit mass |
| kt | Coefficient based on sediment properties (used in Chang’s formula for bed load) |
| LSA | Linear stability analysis |
| n | Bed soil porosity |
| q | Specific discharge per unit width [m2/s] |
| q* | Dimensionless variable (refer to Equation (12)) |
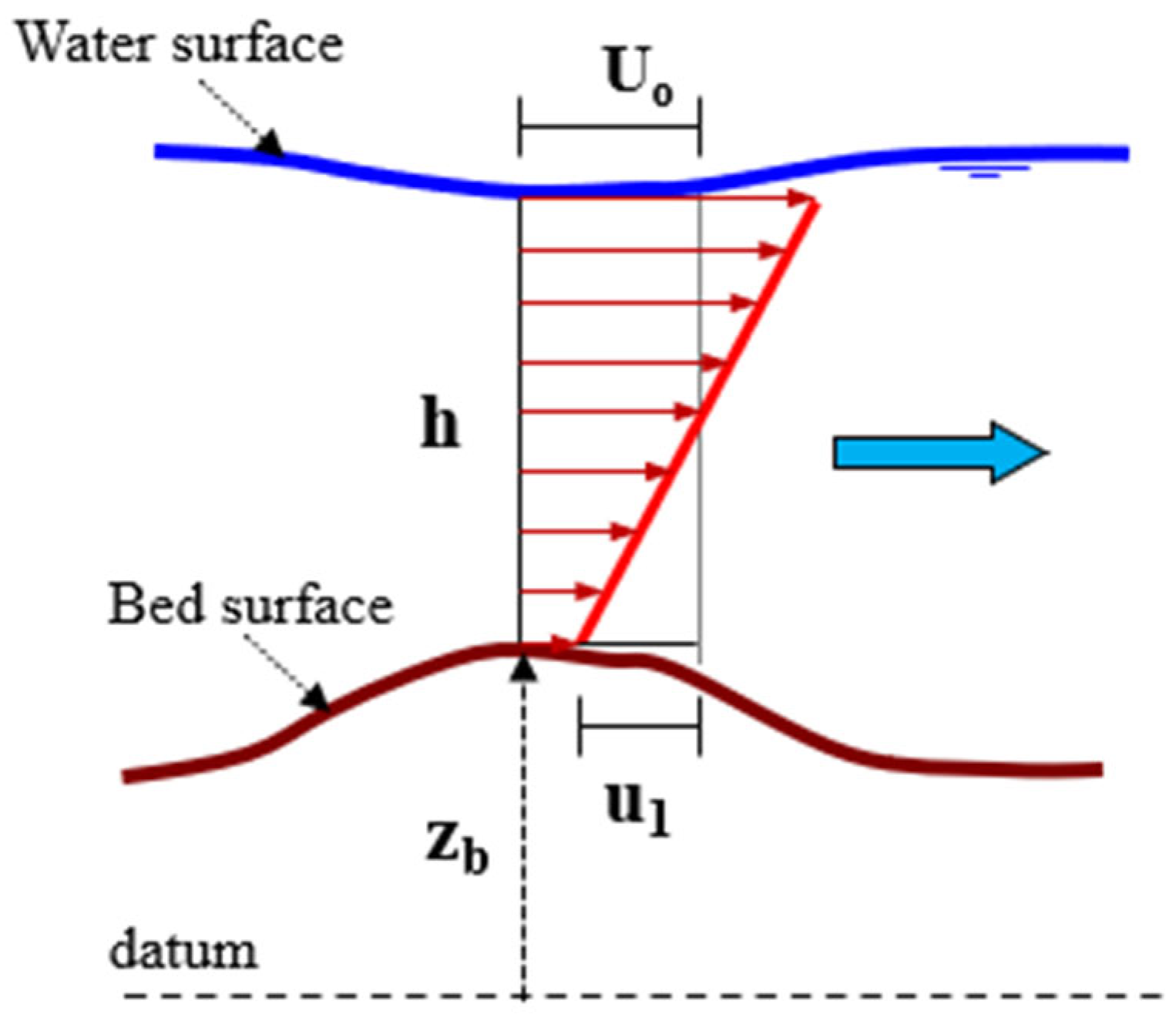
| u1 | Moment-based integral velocity scale along the flow x direction (refer to Figure 1) |
| Uo | Longitudinal depth-averaged velocity at location x |
| x | Horizontal coordinate in the flow direction |
| u1* | Normalized u1 value (Equation (2)) |
| x | Horizontal coordinate in the flow direction |
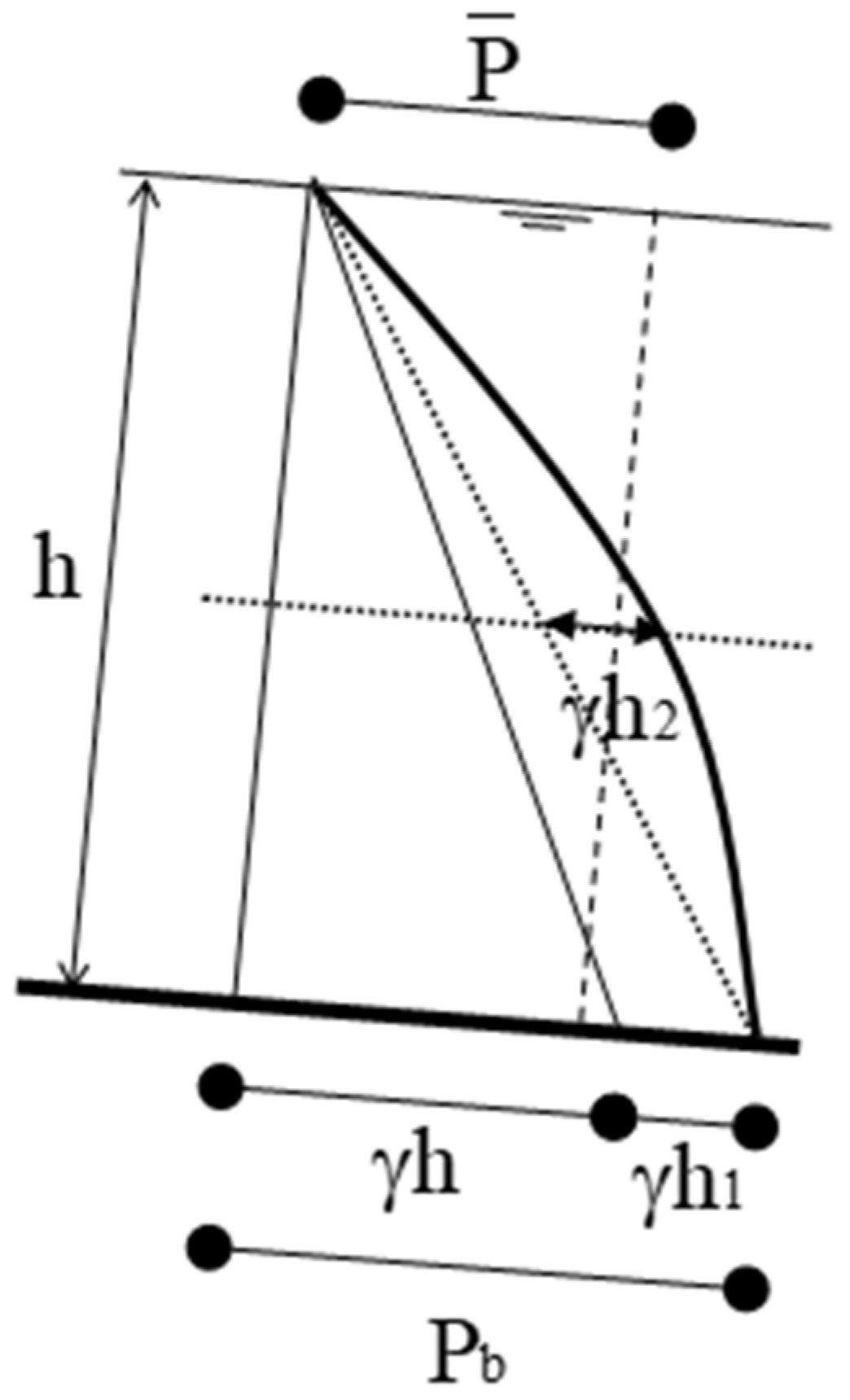
| z | Vertical distance from a given arbitrary horizontal datum up to an arbitrary point (refer to Figure 1) |
| zav | Vertical distance from a given arbitrary horizontal datum up to the mid-water depth |
| zb | Local bed level |
| MofM | Moment of momentum (refer to Figure 1) |
| SVE | Saint-Venant Equation |
| VA | Vertically averaged or depth averaged model |
| VAM | Vertically Averaged and Moment model |
| Δ | Bedform height |
| λ | Bedform wavelength |
| ν | Water kinematic viscosity |
| νt | Eddy viscosity |
| θcr | Dimensionless critical shear stress |
Appendix A. Coefficients of VAM Model
Appendix A.1. VAM-Hydrostatic Equations
Appendix A.2. VAM Equations
Appendix A.3. Coefficients of Velocity Profiles Approximations
Appendix B. Derivation of Creal and Cim for VAM-Hydrostatic Model
- (a)
- The first order continuity equation reads:
- (b)
- The moment-based Chezy formula for bed shear stress reads:
- (c)
- Considering (A62), the first-order x-momentum equation reads:
- (d)
- The first-order x-moment of momentum equation reads:
- (e)
- The bed load sediment flux formula reads:
- (f)
- Exner sediment mass balance formula reads:
References
- Dey, S.; Mahato, R.K.; Ali, S.Z. Linear and Weakly Nonlinear Instabilities of Sand Waves Caused by a Turbulent Flow. J. Hydraul. Eng. 2024, 150, 04024005. [Google Scholar] [CrossRef]
- Dey, S.; Ali, S.Z. Fluvial instabilities. Phys. Fluids 2020, 32, 061301. [Google Scholar] [CrossRef]
- Julien, P.Y.; Klaassen, G.J. Sand-Dune Geometry of Large Rivers during Floods. J. Hydraul. Eng. 1995, 121, 657–663. [Google Scholar] [CrossRef]
- Bradley, R.W.; Venditti, J.G. Reevaluating dune scaling relations. Earth-Sci. Rev. 2017, 165, 356–376. [Google Scholar] [CrossRef]
- Schippa, L.; Cilli, S.; Ciavola, P.; Billi, P. Dune contribution to flow resistance in alluvial rivers. Water 2019, 11, 2094. [Google Scholar] [CrossRef]
- Lefebvre, A.; Herrling, G.; Becker, M.; Zorndt, A.; Krämer, K.; Winter, C. Morphology of estuarine bedforms, Weser Estuary, Germany. Earth Surf. Process Landf. 2022, 47, 242–256. [Google Scholar] [CrossRef]
- Karim, F. Bed-Form Geometry in Sand-Bed Flows. J. Hydraul. Eng. 1999, 125, 1253–1261. [Google Scholar] [CrossRef]
- Richards, K.J. The formation of ripples and dunes on an erodible bed. J. Fluid. Mech. 1980, 99, 597–618. [Google Scholar] [CrossRef]
- Kennedy, J.F. The mechanics of dunes and antidunes in erodible-bed channels. J. Fluid. Mech. 1963, 16, 521–544. [Google Scholar] [CrossRef]
- Reynolds, A.J. Waves on the erodible bed of an open channel. J. Fluid. Mech. 1965, 22, 113–133. [Google Scholar] [CrossRef]
- Hayashi, T. Formation of Dunes and Antidunes in Open Channels. J. Hydraul. Div. 1970, 96, 357–366. [Google Scholar] [CrossRef]
- Hayashi, T. Erratum for ‘Formation of Dunes and Antidunes in Open Channels’. J. Hydraul. Div. 1971, 97, 1135–1136. [Google Scholar] [CrossRef]
- Chien, N.; Wan, Z. Mechanics of Sediment Transport; American Society of Civil Engineers: Reston, VA, USA, 1999. [Google Scholar]
- Di Cristo, C.; Iervolino, M.; Vacca, A. Linear stability analysis of a 1-D model with dynamical description of bed-load transport. J. Hydraul. Res. 2006, 44, 480–487. [Google Scholar] [CrossRef]
- Fourrière, A.; Claudin, P.; Andreotti, B. Bedforms in a Turbulent Stream. Part 2: Formation of Ripples by Primary Linear Instability and of Dunes by Non-Linear Pattern Coarsening. arXiv 2008, arXiv:0805.3417. [Google Scholar]
- Bradley, R.W.; Venditti, J.G. Mechanisms of Dune Growth and Decay in Rivers. Geophys. Res. Lett. 2021, 48, e2021GL094572. [Google Scholar] [CrossRef]
- Coleman, S.E.; Fenton, J.D. Potential-flow instability theory and alluvial stream bed forms. J. Fluid. Mech. 2000, 418, 101–117. [Google Scholar] [CrossRef]
- Engelund, F. Instability of erodible beds. J. Fluid. Mech. 1970, 42, 225–244. [Google Scholar] [CrossRef]
- Fredsøe, J. On the development of dunes in erodible channels. J. Fluid. Mech. 1974, 64, 1–16. [Google Scholar] [CrossRef]
- Colombini, M. Revisiting the linear theory of sand dune formation. J. Fluid. Mech. 2004, 502, 1–16. [Google Scholar] [CrossRef]
- Sumer, B.M.; Bakioglu, M. On the formation of ripples on an erodible bed. J. Fluid. Mech. 1984, 144, 177–190. [Google Scholar] [CrossRef]
- McLean, S. The stability of ripples and dunes. Earth Sci. Rev. 1990, 29, 131–144. [Google Scholar] [CrossRef]
- Ali, S.Z.; Dey, S. Linear stability of dunes and antidunes. Phys. Fluids 2021, 33, 094109. [Google Scholar] [CrossRef]
- Ohata, K.; Naruse, H.; Izumi, N. Linear-stability analysis of plane beds under flows with suspended loads. Earth Surf. Dyn. 2023, 11, 961–977. [Google Scholar] [CrossRef]
- Gradowczyk, M.H. Wave propagation and boundary instability in erodible-bed channels. J. Fluid. Mech. 1968, 33, 93–112. [Google Scholar] [CrossRef]
- Cui, Y.; Parker, G. Linear analysis of coupled equations for sediment transport. In Proceedings of the Congress of the International Association of Hydraulic Research, IAHR, San Francisco, CA, USA, 10–15 August 1997. [Google Scholar]
- Elgamal, M.; Steffler, P. Stability Analysis of Dunes Using 1-D Depth Averaged...—Google Scholar. 2nd IAHR Symposium on Rivers, Coastal and Estuarine Morpho-Dynamics. Available online: https://scholar.google.com/scholar?hl=en&as_sdt=0%2C5&q=Stability+Analysis+of+Dunes+Using+1-D+Depth+Averaged+Flow+Models&btnG= (accessed on 27 April 2025).
- Bose, S.K.; Dey, S. Reynolds averaged theory of turbulent shear flows over undulating beds and formation of sand waves. Phys. Rev. E Stat. Nonlin Soft Matter Phys. 2009, 80, 036304. [Google Scholar] [CrossRef]
- Bose, S.K.; Dey, S. Instability Theory of Sand Ripples Formed by Turbulent Shear Flows. J. Hydraul. Eng. 2012, 138, 752–756. [Google Scholar] [CrossRef]
- Yu, Q. Numerical Modeling of Fluvial Urban Floods: Implications for Flood Mitigation Strategies. Doctoral Dissertation, Université d’Ottawa | University of Ottawa, Ottawa, ON, Canada, 2025. Available online: https://ruor.uottawa.ca/items/4de5a89d-470b-484e-b400-e9d4b0c75f2b (accessed on 27 April 2025).
- Koyuncu, B.; Akerkouch, L.; Le, T. On the depth-averaged models of ice-covered flows. Environ. Fluid. Mech. 2024, 24, 1263–1289. [Google Scholar] [CrossRef]
- Steffler, P.M.; Yee-Chung, J. Depth averaged and moment equations for moderately shallow free surface flow. J. Hydraul. Res. 1993, 31, 5–17. [Google Scholar] [CrossRef]
- Elgamal, M. A moment-based chezy formula for bed shear stress in varied flow. Water 2021, 13, 1254. [Google Scholar] [CrossRef]
- Ghamry, H.K.; Steffler, P.M. Two dimensional vertically averaged and moment equations for rapidly varied flows. J. Hydraul. Res. 2002, 40, 579–587. [Google Scholar] [CrossRef]
- Steldermann, I.; Torrilhon, M.; Kowalski, J. Shallow Moments to Capture Vertical Structure in Open Curved Shallow Flow. J. Comput. Theor. Transp. 2023, 52, 475–505. [Google Scholar] [CrossRef]
- Ghamry, H.K.; Steffler, P.M.; Asce, A.M. Effect of Applying Different Distribution Shapes for Velocities and Pressure on Simulation of Curved Open Channels. J. Hydraul. Eng. 2002, 128, 969–982. [Google Scholar] [CrossRef]
- Albers, C.; Steffler, P. Estimating Transverse Mixing in Open Channels due to Secondary Current-Induced Shear Dispersion. J. Hydraul. Eng. 2007, 133, 186–196. [Google Scholar] [CrossRef]
- Elgamal, M. A Moment-Based Depth-Averaged K-ε Model for Predicting the True Turbulence Intensity over Bedforms. Water 2022, 14, 2196. [Google Scholar] [CrossRef]
- Elgamal, M. Mapping Mean Velocity Field over Bed Forms Using Simplified Empirical-Moment Concept Approach. Water 2023, 15, 3351. [Google Scholar] [CrossRef]
- Yang, C.T. Sediment Transport: Theory and Practice; McGraw-Hill: New York, NY, USA, 1996. [Google Scholar]
- Sanders, S.; Jafarinik, S.; Hernandez Moreira, R.; Johnson, R.; Balkus, A.; Ahmadpoor, M.; Fryson, B.; McQueen, B.; Fedele, J.; Viparelli, E. Influence of Sand Supply and Grain Size on Equilibrium Upper Regime Bedforms. J. Geophys. Res. Earth Surf. 2023, 128, e2022JF006820. [Google Scholar] [CrossRef]
- Guy, H.P.; Simons, D.B.; Richardson, E.V. Summary of Alluvial Channel Data from Flume Experiments, 1956–1961; Google Books; US Government Printing Office: Washington, DC, USA, 1966; Available online: https://books.google.com.eg/books?hl=en&lr=&id=3swyVPwkYFAC&oi=fnd&pg=PR1&dq=Summary+of+Alluvial+Channel+Data+From+Flume+Experiments&ots=N1c03CCA2Q&sig=43kU9nA6YFHKAw95b9yBD2Gg3jg&redir_esc=y#v=onepage&q=Summary%20of%20Alluvial%20Channel%20Data%20From%20Flume%20Experiments&f=false (accessed on 6 June 2025).
- Coleman, S.E.; Melville, B.W. Initiation of Bed Forms on a Flat Sand Bed. J. Hydraul. Eng. 1996, 122, 301–310. [Google Scholar] [CrossRef]
- Coleman, S.E.; Eling, B. Sand wavelets in laminar open-channel flows. J. Hydraul. Res. 2000, 38, 331–338. [Google Scholar] [CrossRef]
- Yalin, M.S. River Mechanics; Elsevier: Amsterdam, The Netherlands, 2015. [Google Scholar]
- Davies, T.R. Summary of Experimental Data for Flume Tests over Fine Sand; Rep. CE/3/71; Dept. of Civil Engineering, Univ. of Southampton: Southampton, UK, 1971. [Google Scholar]
- Baas, J.H. A flume study on the development and equilibrium morphology of current ripples in very fine sand. Sedimentology 1994, 41, 185–209. [Google Scholar] [CrossRef]
- Zhang, X.-D.; Tang, L.-M.; Xu, T.-Y. Experimental study of flow intensity influence on 2-D sand ripple geometry characteristics. Water Sci. Eng. 2009, 2, 52–59. [Google Scholar] [CrossRef]
- Leclair, S.F. Preservation of cross-strata due to the migration of subaqueous dunes: An experimental investigation. Sedimentology 2002, 49, 1157–1180. [Google Scholar] [CrossRef]
- Blom, A.; Ribberink, J.S.; De Vriend, H.J. Vertical sorting in bed forms: Flume experiments with a natural and a trimodal sediment mixture. Water Resour. Res. 2003, 39, 1–13. [Google Scholar] [CrossRef]
- Coleman, S.E.; Zhang, M.H.; Clunie, T.M. Sediment-Wave Development in Subcritical Water Flow. J. Hydraul. Eng. 2005, 131, 106–111. [Google Scholar] [CrossRef]
- Wren, D.G.; Kuhnle, R.A.; Wilson, C.G. Measurements of the relationship between turbulence and sediment in suspension over mobile sand dunes in a laboratory flume. J. Geophys. Res. Earth Surf. 2007, 112. [Google Scholar] [CrossRef]
- Kuhnle, R.A.; Wren, D.G. Size of suspended sediment over dunes. J. Geophys. Res. Earth Surf. 2009, 114. [Google Scholar] [CrossRef]
- Tuijnder, A. Sand in Short Supply: Modelling of Bedforms, Roughness and Sediment Tansport in Rivers Under Supply-Limited Conditions. Ph.D. Thesis, University of Twente, Enschede, The Netherlands, 2010. [Google Scholar] [CrossRef]
- Guala, M.; Singh, A.; Badheartbull, N.; Foufoula-Georgiou, E. Spectral description of migrating bed forms and sediment transport. J. Geophys. Res. Earth Surf. 2014, 119, 123–137. [Google Scholar] [CrossRef]
- Venditti, J.G.; Lin, C.Y.M.; Kazemi, M. Variability in bedform morphology and kinematics with transport stage. Sedimentology 2016, 63, 1017–1040. [Google Scholar] [CrossRef]
- Vah, M.; Jarno, A.; Marin, F.; Le Bot, S. Experimental Study on Sediment Supply-Limited Bedforms in a Coastal Context. In Estuaries and Coastal Zones in Times of Global Change: Proceedings of ICEC-2018; Springer: Singapore, 2020; pp. 647–664. [Google Scholar] [CrossRef]
- Geng, M.; Song, H.; Liu, S.; Zhang, Y.; Meng, L.; Yang, B.; Wang, L.; Gu, Y.; Rong, J.; Zhang, B. Characteristics and migration of subaqueous sand dunes influenced by internal solitary waves in the Dongsha Region, Northern South China Sea. Geomorphology 2024, 461, 109325. [Google Scholar] [CrossRef]
- Van Mierlo, M.C.L.M.; De Ruiter, J.C.C. Turbulence Measurements Above Artificial Dunes; Deltares (WL): Delft, The Netherlands, 1988. [Google Scholar]
- Englund, F.; Fredsoe, J. Sediment ripples and dunes. Annu. Rev. Fluid. Mech. 1982, 14, 13–37. [Google Scholar] [CrossRef]






| Run | Bed Slope (-) | h (cm) | Δ (cm) | λ (cm) | kh | C (cm/min) | Uo (m/s) | F | u∗ (cm/s) | Bed Configuration |
|---|---|---|---|---|---|---|---|---|---|---|
| 5-SS | 0.013 | 4.98 | 4.5 | 80 | 0.391 | −150 | 1.06 | 1.58 | 7.05 | u/s antidune |
| 6A-SS | 0.015 | 5.52 | 5.5 | 90 | 0.385 | – | 0.95 | 1.41 | 7.06 | u/s antidune |
| 6B-SS | 0.018 | 3.89 | 3 | 100 | 0.244 | – | 0.68 | 1.24 | 5.66 | u/s antidune |
| 7-SS | 0.011 | 5.92 | 1 | 55 | 0.676 | −18 | 0.89 | 1.24 | 6.67 | u/s antidune |
| 2-SJ | 0.011 | 6.16 | 1.5 | 30 | 1.290 | 60 | 1.28 | 1.76 | 6.74 | d/s antidune |
| 6-SJ | 0.0074 | 7.91 | 3.2 | 25 | 1.988 | 29 | 1 | 1.21 | 6.26 | d/s antidune |
| Data Type No. | Study (Author/Year) | No. of Runs | Water Depth (m) | Velocity (m/s) | Froude No.(F) | Bedform Height (Δ, mm) | Bedform Length (λ, mm) | Median Sediment Size (mm) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Min | Max | Min | Max | Min | Max | Min | Max | Min | Max | Min | Max | |||
| 1 | [49] | 23 | 0.150 | 0.900 | 0.400 | 0.840 | 0.20 | 0.60 | 43.2 | 137 | 710.0 | 1500.0 | 0.430 | 0.810 |
| 2 | [50] | 8 | 0.154 | 0.389 | 0.590 | 0.830 | 0.35 | 0.52 | 17.0 | 122 | 790.0 | 1790.0 | 0.650 | 2.820 |
| 3 | [51] | 15 | 0.085 | 0.170 | 0.264 | 0.806 | 0.27 | 0.76 | 9.7 | 42.5 | 104.5 | 717.6 | 0.230 | 0.820 |
| 4 | [52] | 8 | 0.192 | 0.208 | 0.660 | 0.680 | 0.31 | 0.34 | 57.0 | 70.0 | 1350.0 | 1710.0 | 0.530 | 0.530 |
| 5 | [53] | 2 | 0.219 | 0.224 | 0.590 | 0.600 | 0.40 | 0.41 | 56.0 | 61.0 | 1130.0 | 1420.0 | 0.500 | 0.503 |
| 6 | [54] | 35 | 0.150 | 0.300 | 0.460 | 0.675 | 0.30 | 0.48 | 6.0 | 95.0 | 260.0 | 1640.0 | 0.800 | 0.800 |
| 7 | [55] | 5 | 0.186 | 0.212 | 0.354 | 0.717 | 0.26 | 0.50 | 20.0 | 40.0 | 290.0 | 1030.0 | 0.800 | 1.800 |
| 8 | [56] | 3 | 0.134 | 0.152 | 0.433 | 0.867 | 0.36 | 0.76 | 38.8 | 65.7 | 906.0 | 2060.0 | 0.550 | 0.550 |
| 9 | [57] | 5 | 0.195 | 0.250 | 0.350 | 0.550 | 0.22 | 0.35 | 140.0 | 620.0 | 0.328 | 0.617 | ||
| 10 | [58] | 21 | 0.055 | 0.186 | 0.382 | 0.686 | 0.36 | 0.74 | 22.8 | 140. | 755.4 | 3486.2 | 0.830 | 0.830 |
| Total/Extreme Value | 125 | 0.085 | 0.9 | 0.167 | 0.867 | 0.10 | 0.76 | 6 | 137 | 104.5 | 2060 | 0.23 | 2.82 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elgamal, M.H.; Mumtaz, M.A. Stability Diagrams of Bed Evolution for Vertically Averaged and Moment (VAM) Models. Mathematics 2025, 13, 1997. https://doi.org/10.3390/math13121997
Elgamal MH, Mumtaz MA. Stability Diagrams of Bed Evolution for Vertically Averaged and Moment (VAM) Models. Mathematics. 2025; 13(12):1997. https://doi.org/10.3390/math13121997
Chicago/Turabian StyleElgamal, Mohamed Hassan, and Mohd Aamir Mumtaz. 2025. "Stability Diagrams of Bed Evolution for Vertically Averaged and Moment (VAM) Models" Mathematics 13, no. 12: 1997. https://doi.org/10.3390/math13121997
APA StyleElgamal, M. H., & Mumtaz, M. A. (2025). Stability Diagrams of Bed Evolution for Vertically Averaged and Moment (VAM) Models. Mathematics, 13(12), 1997. https://doi.org/10.3390/math13121997







