Nonlinear Shear Waves in Compressible Media: Occurrence of Strong Shocks
Abstract
1. Introduction
1.1. An Overview
1.2. Current Research
2. Principal Equations
2.1. Pure Shear
2.1.1. Displacement Field
2.1.2. Deformation Gradient
2.1.3. Left Cauchy–Green Deformation Tensor
2.2. Ogden–Hill Compressible Hyperelastic Potential
2.3. Principal Stresses
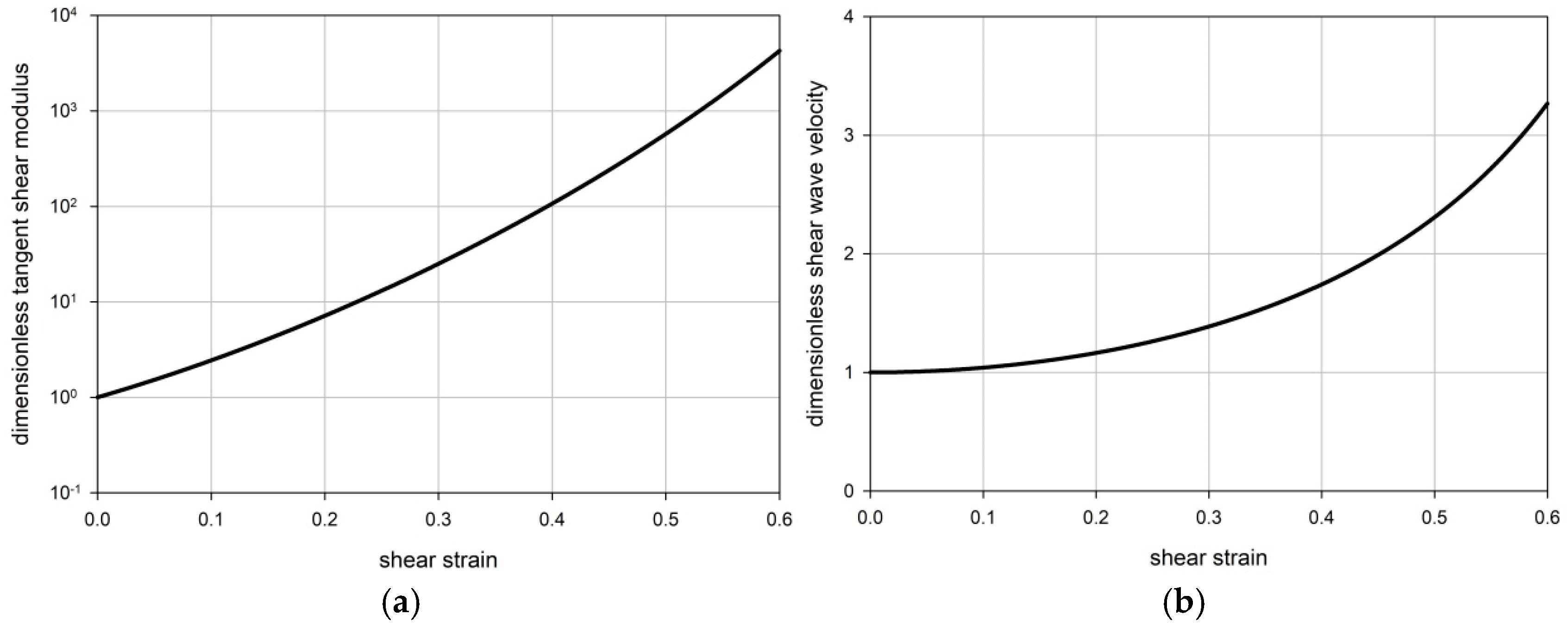
2.4. Tangent Modulus and Shear Wave Velocity
2.5. Equation of Motion
2.6. Initial and Boundary Conditions
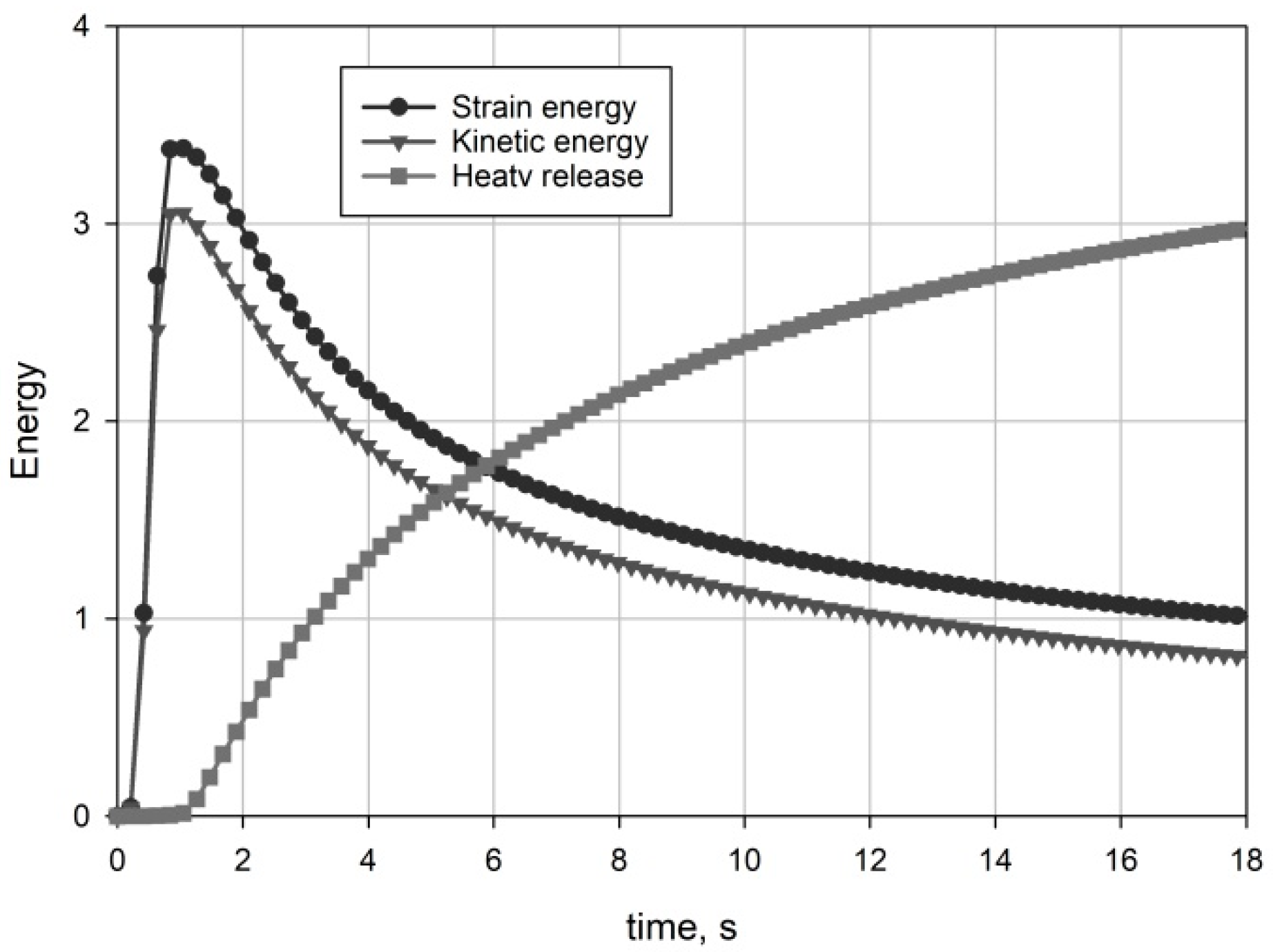
2.7. Equations of Energy Balance
2.8. Numerical Modelling
3. Numerical Analysis
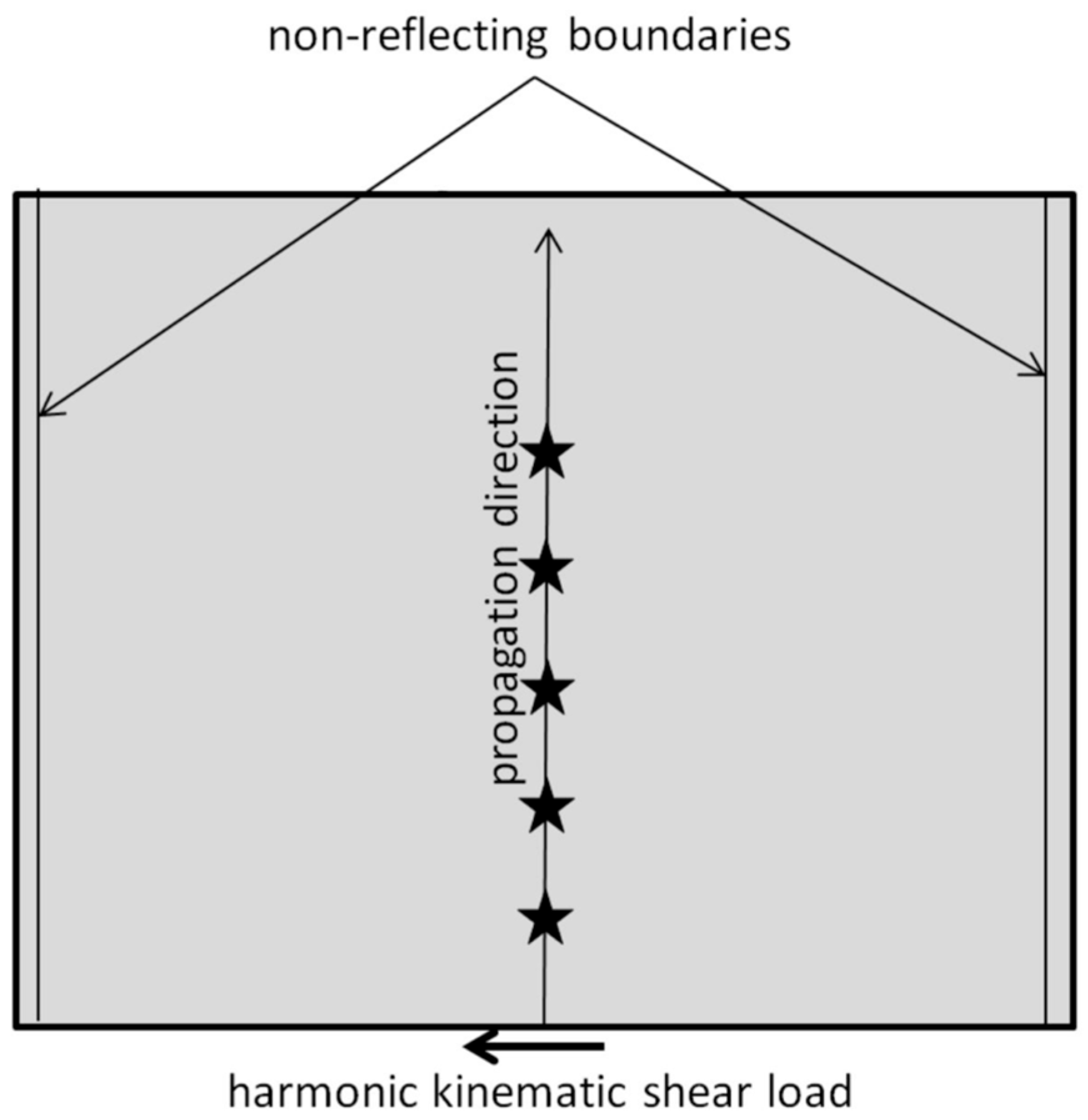
3.1. The Model
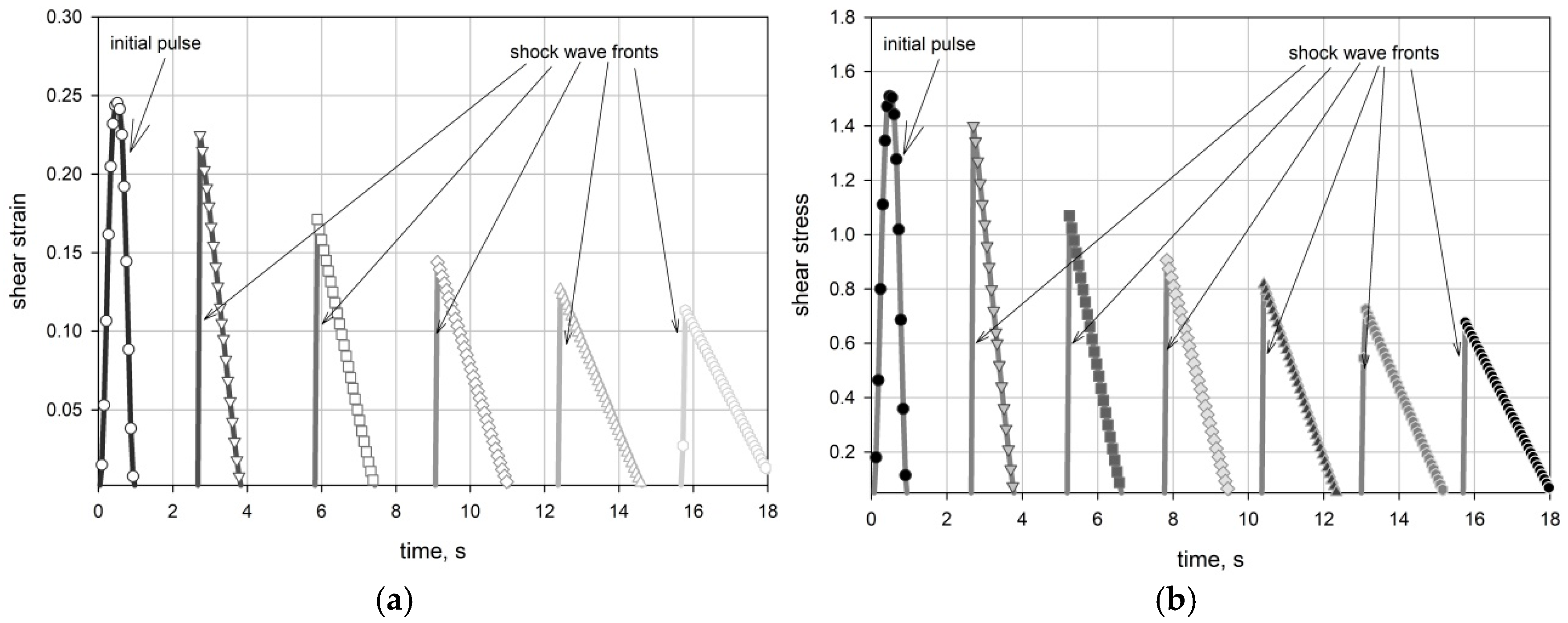
3.2. Shear Waves and Shear Shocks
4. Concluding Remarks
- (i)
- The appearance of discontinuities (shocks) in both strain and stress (Figure 2); the observed shocks are caused by the overtaking of slower moving parts of the delta-like pulse by faster ones.
- (ii)
- The decrease in strain and stress magnitudes of the propagating pulse with distance from the excitation source (Figure 2).
- (iii)
- Spreading out the pulse over distance caused by spatial dispersion (Figure 2).
- (iv)
- (v)
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cui, X. Shock waves: From gas dynamics to granular flows. Int. J. Aeronaut. Aerosp. Eng. 2019, 1, 7–9. [Google Scholar] [CrossRef]
- Gray, J.M.N.T.; Cui, X. Weak, strong and detached oblique shocks in gravity driven granular free-surface flows. J. Fluid Mech. 2007, 579, 113–136. [Google Scholar] [CrossRef]
- Graziani, F.; Moldabekov, Z.; Olson, B.; Bonitz, M. Shock physics in warm dense matter: A quantum hydrodynamics perspective. Contrib. Plasma Phys. 2021, 62, 202100170. [Google Scholar] [CrossRef]
- Menounou, P.; Blackstock, D.T. A new method to predict the evolution of the power spectral density for a finite-amplitude sound wave in a dissipative fluid. J. Acoust. Soc. Am. 2004, 115, 567–580. [Google Scholar] [CrossRef]
- Murata, S. New exact solution of the blast wave problem in gas dynamics. Chaos Solitons Fractals 2006, 28, 327–330. [Google Scholar] [CrossRef]
- Rankine, W.J.M. On the thermodynamic theory of waves of finite longitudinal disturbances. Philos. Trans. R. Soc. Lond. 1870, 160, 277–286. [Google Scholar]
- Resler, E.L.; Lin, S.C.; Kantrowitz, A. The production of high temperatures in shock tubes. J. App. Phys. 1952, 23, 1390–1399. [Google Scholar] [CrossRef]
- Salas, M. The curious events leading to the theory of shock waves. Shock Waves 2007, 16, 477–487. [Google Scholar] [CrossRef][Green Version]
- Sinclair, J.; Cui, X. A theoretical approximation of the shock standoff distance for supersonic flows around a circular cylinder. Phys. Fluids 2017, 29, 0261021. [Google Scholar] [CrossRef]
- Takabe, H. Shock Waves and Ablation Dynamics. In The Physics of Laser Plasmas and Applications—Volume 2; Springer Series in Plasma Science and Technology; Springer: Cham, Switzerland, 2024. [Google Scholar]
- Thomas, T.Y. The fundamental hydrodynamical equations and shock conditions for gases. Math. Mag. 1949, 22, 169–189. [Google Scholar] [CrossRef]
- Vieille, P. Etude sur le role des discontinuites dans les phenomenes de propagation. Meml. Poudres Salpetres 1900, 10, 177–260. [Google Scholar] [CrossRef]
- Whitham, G.B. On the propagation of shock waves through regions of non-uniform area or flow. J. Fluid Mech. 1958, 4, 337–360. [Google Scholar] [CrossRef]
- Woodward, P.; Colella, P. The numerical simulation of two-dimensional fluid flow with strong shocks. J. Comput. Phys. 1984, 54, 115–173. [Google Scholar] [CrossRef]
- Duran, A.V.; Ramazani, V.; Sundararaghavan, A. Multi-scale modeling of shock wave propagation in energetic solid-state composites. Int. J. Solids Struct. 2023, 285, 112535. [Google Scholar] [CrossRef]
- Goto, H.; Kaneko, Y.; Young, J.; Avery, H.; Damiano, L. Extreme accelerations during earthquakes caused by elastic flapping effect. Sci. Rep. 2019, 9, 1117. [Google Scholar] [CrossRef] [PubMed]
- Jones, R.M. Stress-strain relations for materials with different moduli in tension and compression. AIAA J. 1977, 15, 16–23. [Google Scholar] [CrossRef]
- Kuznetsova, M.; Khudyakov, M.; Sadovskii, V. Wave propagation in continuous bimodular media. Mech. Adv. Mater. Struct. 2021, 29, 3147–3162. [Google Scholar] [CrossRef]
- Tomar, S.K.; Kumar, S. Wave propagation in elastic–plastic material with voids. J. Appl. Phys. 2020, 127, 054901. [Google Scholar] [CrossRef]
- Bland, D.R. On shock structure in a solid. J. Inst. Math. Appl. 1965, 1, 56–75. [Google Scholar] [CrossRef]
- Gavrilov, S.N.; Herman, G.C. Wave propagation in a semi-infinite heteromodular elastic bar subjected to a harmonic loading. J. Sound Vib. 2012, 331, 4464–4480. [Google Scholar] [CrossRef]
- Jeffrey, A.; Teymur, M. Formation of shock waves in hyperelastic solids. Acta Mech. 1974, 20, 133–149. [Google Scholar] [CrossRef]
- Truesdell, C.; Toupin, R.A. The Classical Field Theories. In Principles of Classical Mechanics and Field Theory/Prinzipien der Klassischen Mechanik und Feldtheorie; Flügge, S., Ed.; Handbuch der Physik Encyclopedia of Physics; Springer: Berlin, Germany, 1960; Volume III/1, pp. 226–858. [Google Scholar]
- Cohen, T.; Durban, D. Longitudinal shock waves in solids: The piston shock analogue. Proc. R. Soc. A Math. Phys. Eng. Sci. 2014, 470, 2164. [Google Scholar] [CrossRef]
- Haddow, J.B.; Jiang, L. Finite amplitude spherically symmetric wave propagation in a prestressed hyperelastic shell. Int. J. Solids Struct. 1999, 36, 2793–2805. [Google Scholar] [CrossRef]
- Ilyashenko, A.V.; Kuznetsov, S.V. Theoretical aspects of applying Lamb waves in nondestructive testing of anisotropic media. Russ. J. Nondestruct. Test. 2017, 53, 243–259. [Google Scholar] [CrossRef]
- Landauer, A.; Li, X.; Franck, C.; Henann, D.L. Experimental characterization and hyperelastic constitutive modeling of open-cell elastomeric foams. J. Mech. Phys. Solids 2019, 133, 103701. [Google Scholar] [CrossRef]
- Lucchesi, M.; Pagni, A. Longitudinal oscillations of bimodular rods. Int. J. Struct. Stab. Dyn. 2005, 5, 37–54. [Google Scholar] [CrossRef]
- Nuñez-Labielle, A.; Cante, J.; Huespe, A.E.; Oliver, J. Towards shock absorbing hyperelastic metamaterial design. (I) Macroscopic scale: Computational shock-capturing. Comput. Meth. Appl. Mech. Eng. 2022, 393, 114732. [Google Scholar] [CrossRef]
- Predebon, W.W.; Nariboli, G.A. Shock waves in a hyperelastic medium. Z. Angew. Math. Mech. 1972, 52, 133–136. [Google Scholar] [CrossRef]
- Rushchitsky, J.J. On the types and number of plane waves in hypoelastic materials. Int. Appl. Mech. 2005, 41, 1288–1298. [Google Scholar] [CrossRef]
- Rushchitsky, J.J. Nonlinear Plane Waves in Hypoelastic Materials. In Nonlinear Elastic Waves in Materials. Foundations of Engineering Mechanics; Springer: Cham, Switzerland, 2014. [Google Scholar]
- Burgoyne, H.A.; Daraio, C. Elastic–plastic wave propagation in uniform and periodic granular chains. ASME J. Appl. Mech. 2015, 82, 081002. [Google Scholar] [CrossRef]
- Dequiedt, J.L.; Stolz, C. Propagation of a shock discontinuity in an elasto-plastic material: Constitutive relations. Arch. Mech. 2004, 56, 391–410. [Google Scholar]
- Howell, P.; Ockendon, H.; Ockendon, J.R. Mathematical modelling of elastoplasticity at high stress. Proc. R. Soc. A Math. Phys. Eng. Sci. 2012, 468, 3842–3868. [Google Scholar] [CrossRef]
- Von Karman, T.; Duwez, P. The propagation of plastic deformation in solids. J. Appl. Phys. 1950, 21, 987–994. [Google Scholar] [CrossRef]
- Molinari, A.; Ravichandran, G. Fundamental structure of steady plastic shock waves in metals. J. Appl. Phys. 2004, 95, 1718–1732. [Google Scholar] [CrossRef]
- Chockalingam, S.; Cohen, T. Shear shock evolution in incompressible soft solids. J. Mech. Phys. Solids 2020, 134, 103746. [Google Scholar] [CrossRef]
- Chu, B.-T. Transverse shock waves in incompressible elastic solids. J. Mech. Phys. Solids 1967, 15, 1–14. [Google Scholar] [CrossRef]
- Goldstein, R.V.; Dudchenko, A.V.; Kuznetsov, S.V. The modified Cam-Clay (MCC) model: Cyclic kinematic deviatoric loading. Arch. Appl. Mech. 2016, 86, 2021–2031. [Google Scholar] [CrossRef]
- Ned, C.R.; Caenen, A.; Nightingale, K.R. Phase and group velocities for shear wave propagation in an incompressible, hyperelastic material with uniaxial stretch. Phys. Med. Biol. 2022, 67, 095015. [Google Scholar]
- Catheline, S.; Gennisson, J.-L.; Tanter, M.; Fink, M. Observation of shock transverse waves in elastic media. Phys. Rev. Lett. 2003, 91, 164301. [Google Scholar] [CrossRef]
- Espindola, D.; Lee, S.; Pinton, G. Shear shock waves observed in the brain. Phys. Rev. Appl. 2017, 8, 044024. [Google Scholar] [CrossRef]
- Villani, V.; Lavallata, V. The theories of rubber elasticity and the goodness of their constitutive stress–strain equations. Physchem 2024, 4, 296–318. [Google Scholar] [CrossRef]
- Destrade, M.; Pucci, E.; Saccomandi, G. Generalization of the Zabolotskaya equation to all incompressible isotropic elastic solids. Proc. R. Soc. A Math. Phys. Eng. Sci. 2019, 475, 2227. [Google Scholar] [CrossRef]
- Saccomandi, G.; Vitolo, R. On the mathematical and geometrical structure of the determining equations for shear waves in nonlinear isotropic incompressible elastodynamics. J. Math. Phys. 2014, 55, 081502. [Google Scholar] [CrossRef]
- Chen, Q.; Cao, P.F.; Advincula, R.C. Mechanically robust, ultraelastic hierarchical foam with tuneable properties via 3D printing. Adv. Funct. Mater. 2018, 28, 1800631. [Google Scholar] [CrossRef]
- Ghahramani, P.; Behdinan, K.; Moradi-Dastjerdi, R.; Naguib, H.E. Development and modeling of an ultra-robust TPU-MWCNT foam with high flexibility and compressibility. Nanotechnol. Rev. 2024, 13, 20230219. [Google Scholar] [CrossRef]
- Reed, N.; Huynh, N.U.; Rosenow, B.; Manlulu, K.; Youssef, G. Synthesis and characterization of elastomeric polyurea foam. J. Appl. Polym. Sci. 2019, 137, 48839. [Google Scholar] [CrossRef]
- Tripathi, N.; Bag, D.S.; Dwivedi, M. A Review on auxetic polymeric materials: Synthetic methodology, characterization and their applications. J. Polym. Mater. 2024, 40, 227–269. [Google Scholar] [CrossRef]
- Caprini, D.; Battista, F.; Zajdel, P.; Di Muccio, G.; Guardiani, C.; Trump, B.; Carter, M.; Yakovenko, A.A.; Amayuelas, E.; Bartolomé, L.; et al. Bubbles enable volumetric negative compressibility in metastable elastocapillary systems. Nat. Commun. 2024, 15, 5076. [Google Scholar] [CrossRef]
- Kuznetsov, S.V. “Forbidden” planes for Rayleigh waves. Q. Appl. Math. 2002, 60, 87–97. [Google Scholar] [CrossRef]
- Lakes, R.; Wojciechowski, K.W. Negative compressibility, negative Poisson’s ratio, and stability. Phys. Status Solidi 2008, 245, 545–551. [Google Scholar] [CrossRef]
- Moore, B.; Jaglinski, T.; Stone, D.S.; Lakes, R.S. Negative incremental bulk modulus in foams. Philos. Mag. Lett. 2006, 86, 651–659. [Google Scholar] [CrossRef]
- Vakarin, E.V.; Duda, Y.; Badiali, J.P. Negative linear compressibility in confined dilatating systems. J. Chem. Phys. 2006, 124, 144515. [Google Scholar] [CrossRef]
- Ogden, R.W. Large deformation isotropic elasticity–on the correlation of theory and experiment for compressible rubberlike solids. Proc. R. Soc. Lond. A 1972, 328, 567–583. [Google Scholar]
- Ogden, R.W. Volume changes associated with the deformation of rubberlike solids. J. Mech. Phys. Solids 1976, 24, 323–338. [Google Scholar] [CrossRef]
- Ogden, R.W.; Saccomandi, G.; Sgura, I. Fitting hyperelastic models to experimental data. Comput. Mech. 2004, 34, 484–502. [Google Scholar] [CrossRef]
- Storåkers, B. On material representation and constitutive branching in finite compressible elasticity. J. Mech. Phys. Solids 1986, 34, 125–145. [Google Scholar] [CrossRef]
- Yao, Y.; Chen, S.; Huang, Z. A generalized Ogden model for the compressibility of rubber-like solids. Proc. R. Soc. A Math. Phys. Eng. Sci. 2022, 380, 20210320. [Google Scholar] [CrossRef] [PubMed]
- Yan, S.; Jia, D.; Yu, Y.; Wang, L.; Qiu, Y.; Wan, Q. Novel strategies for parameter fitting procedure of the Ogden hyperfoam model under shear condition. Eur. J. Mech. A/Solids 2021, 86, 104154. [Google Scholar] [CrossRef]
- Blatz, P.D.; Ko, W.L. Application of finite elasticity to the deformation of rubbery materials. Trans. Soc. Rheol. 1962, 6, 223–251. [Google Scholar] [CrossRef]
- Hill, R. Acceleration waves in solids. J. Mech. Phys. Solids 1962, 10, 1–16. [Google Scholar] [CrossRef]
- Hill, R. Aspects of invariance in solid mechanics. Adv. Appl. Mech. 1978, 18, 1–75. [Google Scholar]
- Truesdell, C. General and exact theory of waves in finite elastic strain. Arch. Ration. Mech. Anal. 1961, 8, 263–296. [Google Scholar] [CrossRef]
- Truesdell, C.; Noll, W.; Antman, S. The Non-Linear Field Theories of Mechanics; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Belytschko, T.; Liu, W.K.; Moran, B. Nonlinear Finite Elements for Continua and Structures; Wiley: New York, NY USA, 2000. [Google Scholar]
- Lax, P.D. Hyperbolic Systems of Conservation Laws and the Mathematical Theory of Shock Waves; SIAM: Philadelphia, PA, USA, 1972. [Google Scholar]
- Moreira, D.C.; Nunes, L.C.S. Comparison of simple and pure shear for an incompressible isotropic hyperelastic material under large deformation. Polym. Test. 2013, 32, 240–248. [Google Scholar] [CrossRef]
- Ogden, R.W. Nonlinear Elastic Deformations; Wiley: Dover, UK, 1984. [Google Scholar]
- Motaghian, S. Nonlinear eigenstrain analysis for compressible Blatz–Ko solids. Int. J. Non-Linear Mech. 2023, 155, 104448. [Google Scholar] [CrossRef]
- Auld, B.A. Acoustic Fields and Waves in Solids, 2nd ed.; Krieger Publishing Company: Malabar, FL, USA, 1990; Volume 2. [Google Scholar]
- Djeran-Maigre, I. Velocities, dispersion, and energy of SH-waves in anisotropic laminated plates. Acoust. Phys. 2014, 60, 200–207. [Google Scholar] [CrossRef]
- Scovazzi, G.; Song, T.; Zeng, X. A velocity/stress mixed stabilized nodal finite element for elastodynamics: Analysis and computations with strongly and weakly enforced boundary conditions. Comput. Meth. Appl. Mech. Eng. 2017, 325, 532–576. [Google Scholar] [CrossRef]
- Li, S.; Brun, M.; Djeran-Maigre, I. Explicit/implicit multi-time step co-simulation in unbounded medium with Rayleigh damping and application for wave barrier. Europ. J. Environ. Civ. Eng. 2020, 24, 2400–2421. [Google Scholar] [CrossRef]
- Li, S.; Brun, M.; Djeran-Maigre, I. Benchmark for three-dimensional explicit asynchronous absorbing layers for ground wave propagation and wave barriers. Comput. Geotech. 2021, 131, 103808. [Google Scholar] [CrossRef]
- Terentjeva, E.O. Planar internal Lamb problem: Waves in the epicentral zone of a vertical power source. Acoust. Phys. 2015, 61, 356–367. [Google Scholar]
- Rossi, A.; Bocchetta, G.; Botta, F.; Scorza, A. Accuracy characterization of a MEMS accelerometer for vibration monitoring in a rotating framework. Appl. Sci. 2023, 13, 5070. [Google Scholar] [CrossRef]
- Dudchenko, A.V. Vertical wave barriers for vibration reduction. Arch. Appl. Mech. 2020, 91, 257–276. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bratov, V.; Kuznetsov, S.V. Nonlinear Shear Waves in Compressible Media: Occurrence of Strong Shocks. Mathematics 2025, 13, 1991. https://doi.org/10.3390/math13121991
Bratov V, Kuznetsov SV. Nonlinear Shear Waves in Compressible Media: Occurrence of Strong Shocks. Mathematics. 2025; 13(12):1991. https://doi.org/10.3390/math13121991
Chicago/Turabian StyleBratov, Vladimir, and Sergey V. Kuznetsov. 2025. "Nonlinear Shear Waves in Compressible Media: Occurrence of Strong Shocks" Mathematics 13, no. 12: 1991. https://doi.org/10.3390/math13121991
APA StyleBratov, V., & Kuznetsov, S. V. (2025). Nonlinear Shear Waves in Compressible Media: Occurrence of Strong Shocks. Mathematics, 13(12), 1991. https://doi.org/10.3390/math13121991







