The Influence of the Mass Ratio and the Jacobi Constant on the Probability of Escape in the 3D (4+2)-Body Ring Problem

Abstract

The dynamics of escape in the $(N+2)$-body ring problem exhibits a limited supply of research that involves the investigation in the three-dimensional scenario. In this paper, we introduce a new method based on the use of a spherical surface of section to analyze the probability of escape in the $(4+2)$-body ring problem in three dimensions. Our analysis reveals perplexing results regarding the impact of the mass ratio, $\beta$, and the Jacobi constant, C, parameters on this escape probability. In order to delineate the different effects exerted by these parameters, we incorporate into the system three increasing values of $\beta$ and four values of C for each value of $\beta$, that show different behaviors in the distribution of the escaping orbits.

1. Introduction

Through many centuries, scientists have delved increasingly deeper into the motion of celestial bodies such as planetary rings or Trojan asteroids in the universe to understand the complex behavior of our Solar System. This interest persists to the present time, particularly in the well-known $(N+2)$-body problem, which is one of the issues that allows us to analyze the initial state of motion, besides the prediction of complex interactions between these celestial bodies. One of the restricted aforementioned problems that many researchers have taken into investigation is the $(N+2)$-body ring problem [1,2,3,4,5,6,7,8]. It refers to the motion of a particle of infinitesimal mass moving in space in a planar ring configuration, attracted by the gravitational pull of $N+1$ bodies (called primaries). Maxwell was the first to present this concept in his investigation of Saturn’s rings [9]. Further exploration has been carried out to precisely study the impact of the Jacobi constant, C, and the bifurcations of the mass ratio, $\beta$, on the geometry of the zero-velocity curves and surfaces [8,10].

On the other hand, the analysis of the escape of a particle from a dynamical system has captured significant interest in recent decades [11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28], and it is currently an active field of research, particularly within the framework of the three-body problem [29,30,31,32,33,34]. It is well known that the limiting curve of the basins of escape on a suitable surface of section is given by the stable manifolds to the Lyapunov-unstable periodic orbits that are located at the openings of the zero-velocity surfaces of the system. The use of surfaces of section permit researchers to concentrate their study of the escape on particular areas of interest within the phase space. This method was developed by Henri Poincaré [35], proving to be an impressive tool for determining the existence of stable or unstable regions, periodic orbits, or regions exhibiting chaotic behavior. Navarro and Martínez–Belda [36,37,38,39] have conducted various studies in the numerical exploration of the escape in the $(N+2)$-body ring problem, using multiple surfaces of section in two dimensions.

In recent years, several studies have looked into escape dynamics and orbital stability. For example, Sanchez et al. [40] investigated the ring system of the dwarf planet Haumea, a trans-Neptunian object known for its unique characteristics, including its two moons and a recently discovered ring. The study employs perturbation maps to analyze the behavior of particles within this ring, particularly focusing on their interactions and stability under various conditions. In [41], the authors analyze the influence of both the angle and the magnitude of velocity perturbations on trajectories emerging from equilibrium points in the circular restricted three-body problem.

In the present work, we maintain the same methodology and structure utilized in our prior work [42] while emphasizing an additional objective, which is the impact of the mass ratio and the Jacobi constant parameters on the probability of escape in the $3D$ $(4+2)$-body ring configuration. In order to unveil the complexities of this investigation, we carry out a numerical integration of the equations of motion with a proper selection of a surface of section, analyzing the data of the escaping orbits for three different values of $\beta$, specifically $\beta =2,10,20$ and four values of C for each of them.

Thus, this paper contributes to extending our previous analysis of the system into a probabilistic framework and opens promising directions for further research of the escape dynamics in high-dimensional systems.

The paper is organized in the following manner: in Section 2, we present a brief summary of the equations of motion of a test particle influenced by the gravitational force of a ring configuration. In Section 3, we provide a comprehensive description of the numerical integration technique used in our research and establish the interpretation of the escaping orbits for each case of $\beta =2,10,20$. Ultimately, our paper ends with Section 4, where the conclusions and findings of this investigation are detailed.

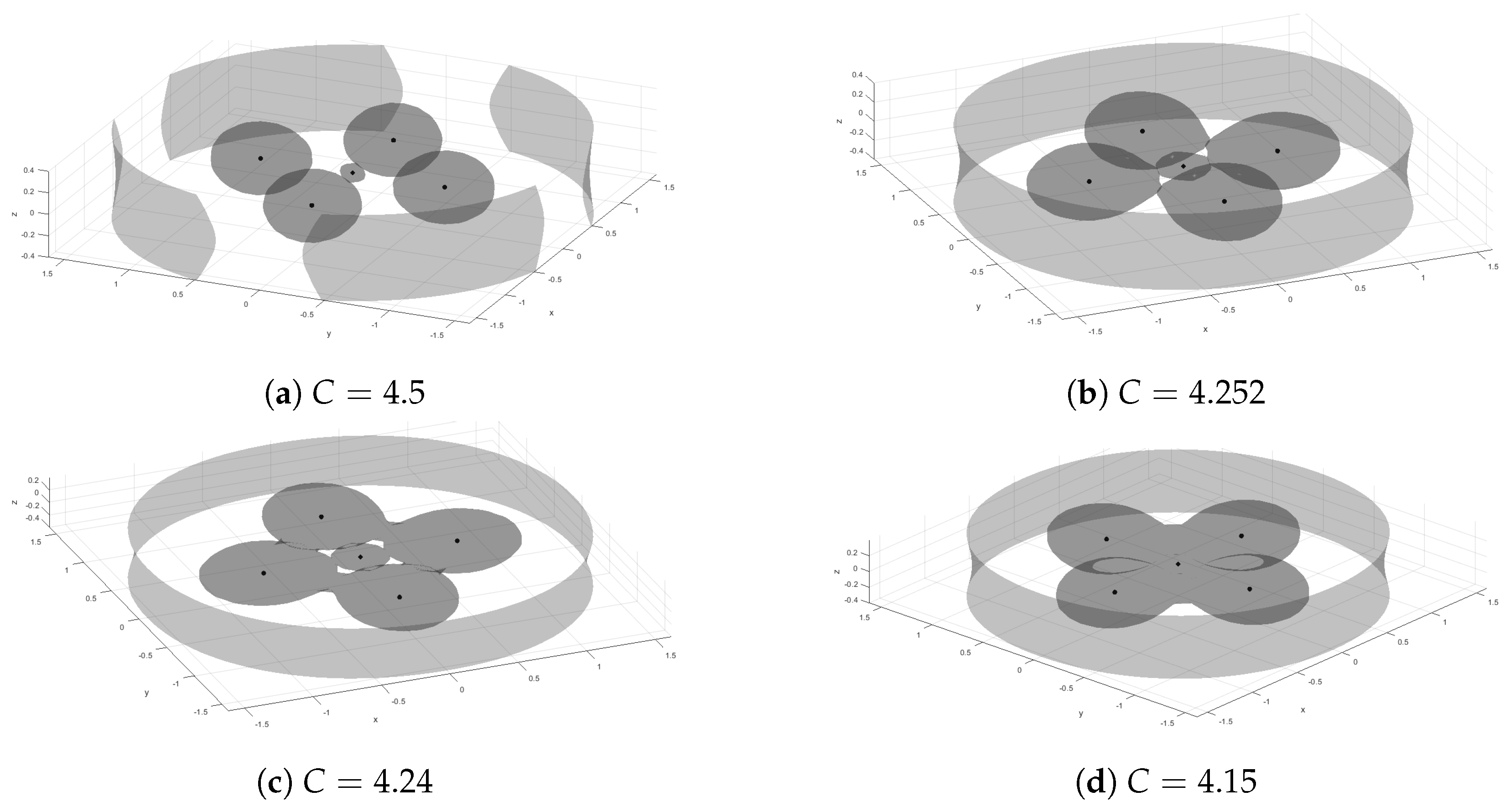
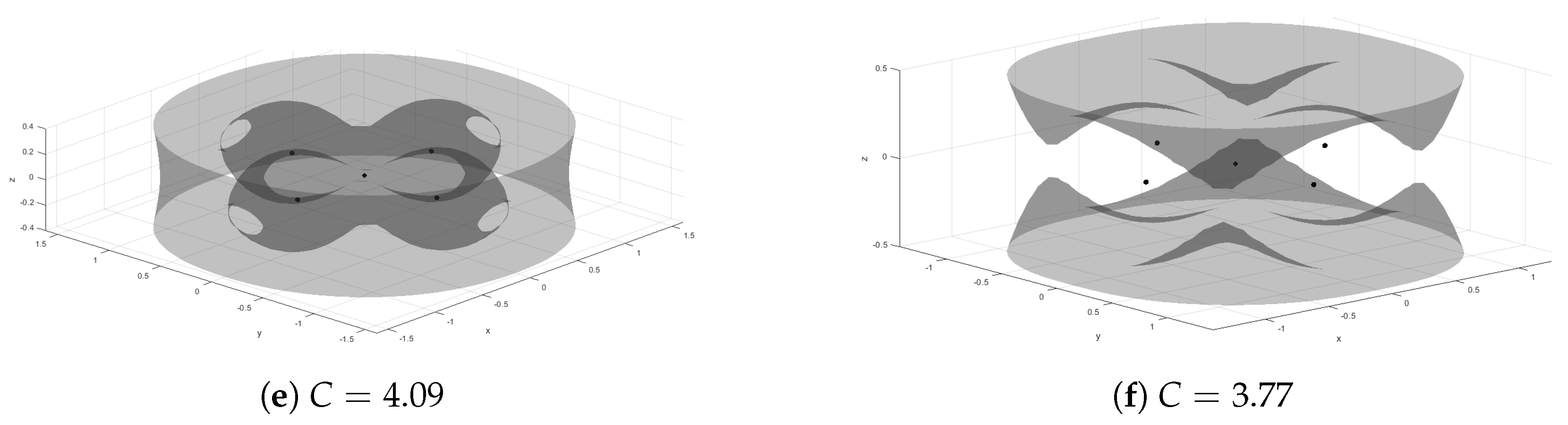
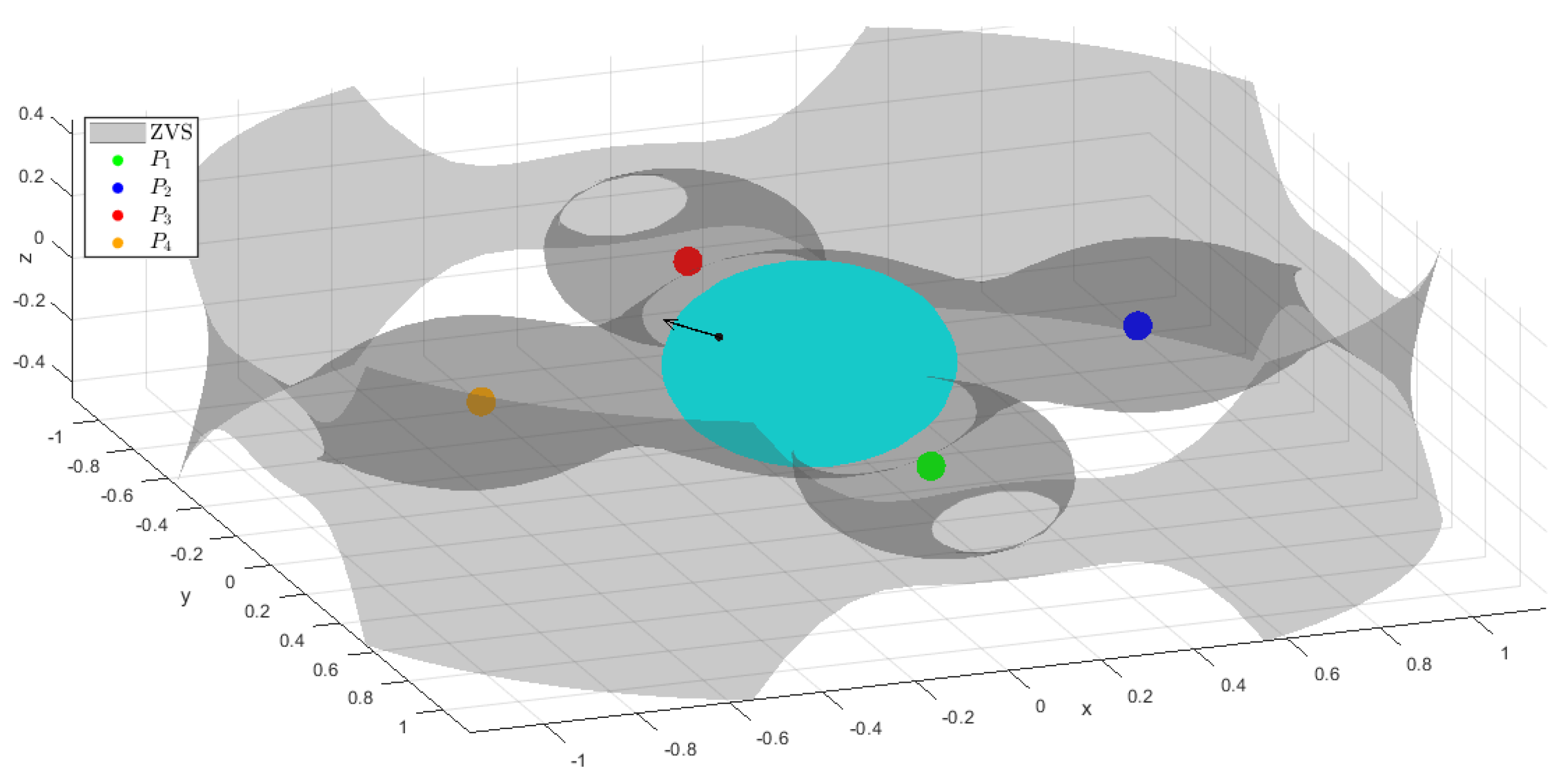
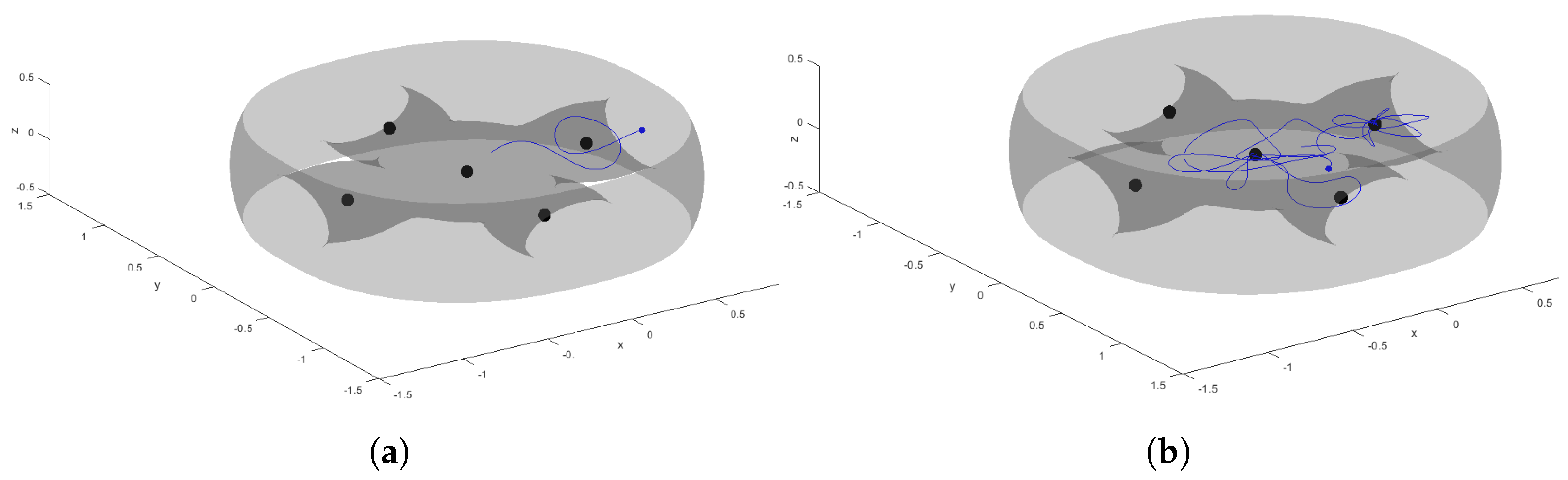
2. Equations of Motion

In the $3D$ $(4+2)$-body ring configuration, we assume that four spherical and homogeneous bodies $P_i$, $i=1,2,3,4$, with equal masses, $m_i=m$, $\forall i=1,2,3,4$, are in a 4-gon configuration attracted to each other, based on Newton’s law of gravitation. They are symmetrically distributed in a circular ring arrangement, spinning around a central body, $P_0$, which has a mass of $m_0$. These five bodies are usually named primaries. The sixth body, here denoted as S, is a particle that moves under the influence of the primaries and has a negligible mass compared to them. The motion of the test particle S can be represented using a barycentric synodic coordinate system, $Oxyz$, which revolves at the same constant angular velocity as the primaries. The succeeding dimensionless equations of motion of the particle S in space are given by (see, for instance, [4]):

$$\begin{array}{cc}\hfill \ddot{x}-2\dot{y}& ={\displaystyle \frac{\partial U}{\partial x}},\hfill \\ \hfill \ddot{y}+2\dot{x}& ={\displaystyle \frac{\partial U}{\partial y}},\hfill \\ \hfill \ddot{z}& ={\displaystyle \frac{\partial U}{\partial z}}.\hfill \end{array}$$

(1)

The potential function $U(x,y,z)$ is described by

$$U(x,y,z)={\displaystyle \frac{1}{2}}(x^2+y^2)+{\displaystyle \frac{1}{\Delta }}\left({\displaystyle \frac{\beta }{r_0}}+\sum _{i=1}^4{\displaystyle \frac{1}{r_i}}\right),$$

(2)

where $\beta =m_0/m$ represents the ratio of the central mass, $m_0$, with one of the peripheral masses, m;

$$r_0=\sqrt{x^2+y^2+z^2}$$

is the test particle’s distance from the central body; and

$$r_{\nu }=\sqrt{{(x-x_{\nu }^{\ast })}^2+{(y-y_{\nu }^{\ast })}^2+z},\mathrm{for}\nu =1,2,3,4,$$

are the distances between the test particle and the four peripheral primaries of the system, while the quantities $x_{\nu }^{\ast }$ and $y_{\nu }^{\ast }$ represent the positions of the peripheral bodies. An extended description of these equations can be found, for instance, in [3,4,5].

The set of Equation (1) has a Jacobi-type integral of motion, determined by

$$C=2U(x,y,z)-({\dot{x}}^2+{\dot{y}}^2+{\dot{z}}^2),$$

(3)

in which C is known as the constant of Jacobi.

The zero-velocity surfaces (ZVSs) are the regions where the particle, S, has zero velocity in all directions, so they are given by

$$C=2U(x,y,z).$$

(4)

The geometry of the ZVSs changes with the variation of some specific parameters, such as C and $\beta$. Each of these parameters is essential for defining the structure and evolution of these surfaces. On the one hand, for each value of N, there is a bifurcation value of the mass parameter, $\beta$, denoted as ${\beta }^{\ast }$, which produces a change in the number of stationary solutions in the system from $5N$ to $3N$, and also causes changes in the geometry of the ZVSs [43]. In Figure 1 and Figure 2, we illustrate several examples of the different ZVS shapes that may occur in the scenarios with $5N$ and $3N$ stationary solutions, respectively. Moreover, it is also known that there are more bifurcations or critical values of $\beta$ that affect the geometry of the ZVSs [8,10].

On the other hand, there exists a critical value of the Jacobi constant, represented as $C_e$, that governs the opening of the windows, allowing the test particle to possibly escape as it gets close to one of the exit channels, which are covered by an unstable Lyapunov periodic orbit, as previously mentioned. The stability of the configuration has already been studied and is well known, and it is established that ring configurations become linearly stable when $N\ge 7$ (see, for instance, [44]).

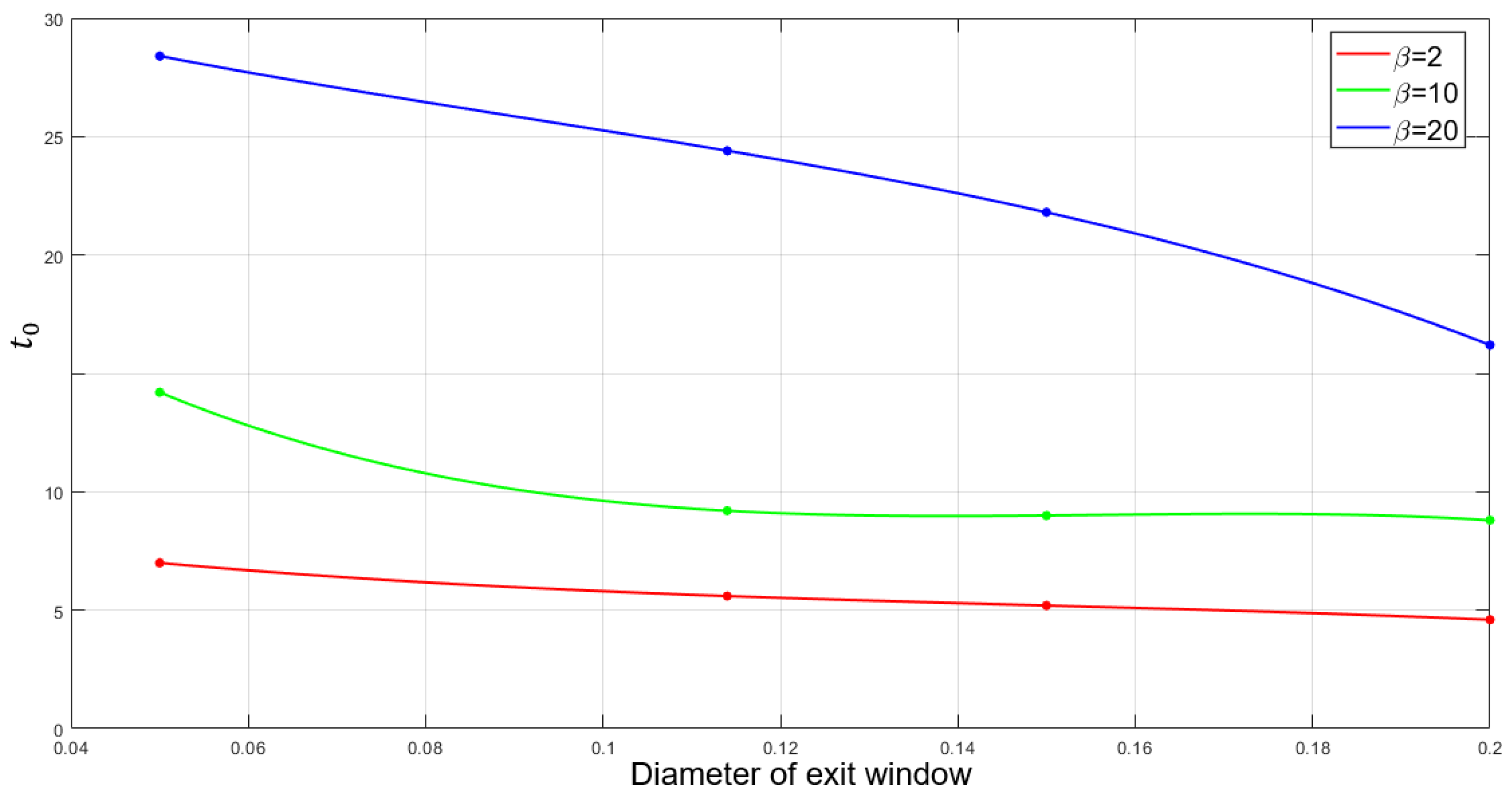
3. Numerical Analysis of the System

The methodology of the current study is based on performing a numerical integration of the equations of motion (1) by means of recurrent power series [45] for three fixed values of $\beta$ and four values of the constant of Jacobi for each of them, which are denoted as $C_{\beta ,k}$, $k=1,2,3,4$. These values of C are selected to provide a scenario where the ZVSs are open, as we are interested in analyzing the escape of the system, as well as to have exit channels (which have a circular shape) of approximately the same diameter, here denoted as $\psi$, for each triplet $(C_{2,k},C_{10,k},C_{20,k})$ (see

Table 1. Critical value of the Jacobi constant, $C_e$, values $C_{\beta ,i},i=1,2,3,4$, and diameter of the escaping channels for $N=4$ and $\beta =2,10,20$.

$\mathit{\beta }$	${\mathit{C}}_{\mathit{e}}$	${\mathit{C}}_{\mathit{\beta },1}$	${\mathit{C}}_{\mathit{\beta },2}$	${\mathit{C}}_{\mathit{\beta },3}$	${\mathit{C}}_{\mathit{\beta },4}$
2	$2.751296833$	$2.7505$	$2.7476$	$2.7449$	$2.7399$
10	$1.995422686$	$1.9943$	$1.99$	$1.9861$	$1.9787$
20	$1.814663302$	$1.8134$	$1.8085$	$1.804$	$1.7951$
$\psi$	0.0	0.05	0.114	0.15	0.2

).

The set of values $C_{\beta ,k}$ is kept the same as in a previous study [42], where an analysis of the geometry of escape of the system was carried out, revealing how the parameters $\beta$ and C alter the geometry of the basins of escape.

The sample of initial conditions is selected such that the initial positions lie on the surface of section defined by the boundary of a sphere inside the ZVS, with a fixed radius $\rho =0.3$, denoted here as $\mathbf{B}(\overrightarrow{0},\rho )$, and the initial velocity is assumed to be perpendicular to the tangent plane of the sphere for each initial position and such that its modulus is derived from the integral of Jacobi (Equation (3)). The set of initial positions is defined on a grid of $2048\times 2048$ points uniformly distributed in the region of the hyperplane $(\varphi ,\theta )$, where $\varphi \in [0,\pi ]$ and $\theta \in [0,2\pi )$ are the angles defined in spherical coordinates. Thus, the initial conditions, ${\mathbf{x}}_{\mathbf{0}}=(x_0,y_0,z_0),\dot{{\mathbf{x}}_{\mathbf{0}}}=(\dot{x_0},\dot{y_0},\dot{z_0})$, are taken in the following domain:

$$D=\left\{({\mathbf{x}}_{\mathbf{0}},\dot{{\mathbf{x}}_{\mathbf{0}}})\in {\mathbb{R}}^6\mid {\mathbf{x}}_{\mathbf{0}}\in \mathbf{B}(\overrightarrow{0},\rho ),\dot{{\mathbf{x}}_{\mathbf{0}}}=\sigma {\mathbf{x}}_{\mathbf{0}},\sigma =+{\displaystyle \frac{\sqrt{2U-C}}{\rho }}\right\}.$$

(5)

In Figure 3, we depict the set of initial positions chosen (colored in cyan), an example of the initial velocity for one particular position in the sphere, and the four primaries (colored in green, dark blue, red, and orange, respectively).

We carry out the numerical integration over $T_{max}={10}^2$ maximum time units to examine the distribution of the escape times of a test particle inside the system, according to Navarro et al. [39]. Then, orbits that do not escape after a numerical integration of $T_{max}={10}^2$ time units are assumed to be trapped orbits or non-escaping orbits. In Figure 4, we show two examples of orbits with different initial conditions in the domain D, one escaping through the first opening and the other one trapped inside the potential well.

Let us introduce $N_T$ to represent the total number of initial conditions integrated. As the chosen radius of the sphere, $\mathbf{B}(\overrightarrow{0},\rho )$, ensures that all of the initial conditions lie within the region of allowable motion, the value of $N_T$ is unvarying for any given values of C and $\beta$.

For each $\beta$ and C, we define the total number of orbits that escape from the potential well up to a maximum time $T_{max}$ as $N_{esc}(\beta ,C,T_{max})$. Furthermore, $N_{esc}(\beta ,C,t_1,t_2)$ represents the number of orbits that exit the potential well within a specific time interval, $t_1<t\le t_2$.

Thus, the total probability of escape is represented by

$$P(\beta ,C,T_{max})={\displaystyle \frac{N_{esc}(\beta ,C,T_{max})}{N_T}},$$

(6)

and the probability of escape within a specific time interval, $t_1<t\le t_2$, is given by

$$P(\beta ,C,t_1,t_2)={\displaystyle \frac{N_{esc}(\beta ,C,t_1,t_2)}{N_T}}.$$

(7)

In order to improve the comprehension and visibility of our data, we methodically organize the results of our integration in

Table 2. Number of escaping orbits, diameter of the exit windows, and probability of escape, considering $T_{max}={10}^2$, for each $C_{\beta ,k},k=1,2,3,4$.

$\mathbf{\beta }$	${\mathit{C}}_{\mathit{\beta },1}(\mathit{\psi }=0.05)$			${\mathit{C}}_{\mathit{\beta },2}(\mathit{\psi }=0.114)$			${\mathit{C}}_{\mathit{\beta },3}(\mathit{\psi }=0.15)$			${\mathit{C}}_{\mathit{\beta },4}(\mathit{\psi }=0.2)$
	2	10	20	2	10	20	2	10	20	2	10	20
$C_{\beta ,k}$	$2.7505$	$1.9943$	$1.8134$	$2.7476$	$1.99$	$1.8085$	$2.7449$	$1.9861$	$1.804$	$2.7399$	$1.9787$	$1.7954$
$N_{esc}(\beta ,C,T_{max})$	5199	6127	577	48,166	54,842	8666	99,329	96,201	19,488	194,647	165,908	34,892
$P(\beta ,C,T_{max})$	$0.0012$	$0.0015$	$0.0001$	$0.0115$	$0.0131$	$0.0021$	$0.0237$	$0.0229$	$0.0046$	$0.05$	$0.0396$	$0.0083$

, which describes the number of escaping orbits and the probability of escape that correspond to each case of $C_{\beta ,k}$, for $\beta =2,10,20$ and $k=1,2,3,4$, collected attending to the opening window’s diameter, $\psi$, and considering $T_{max}={10}^2$. These data allow us to examine how the escape of the test particle depends on both parameters $\beta$ and C.

Let us observe that in the cases of $C=C_{\beta ,1}$ and $C=C_{\beta ,2}$ that correspond to the smaller diameters of the exit windows, the probability of escape increases from $\beta =2$ to $\beta =10$ and decreases from $\beta =10$ to $\beta =20$, which indicates that there is not a monotonic variation with respect to the mass ratio $\beta$; while in the cases of $C=C_{\beta ,3}$ and $C=C_{\beta ,4}$ that correspond to the larger diameters of the exit windows, the probability of escape shows a monotonic decreasing variation with respect to the mass ratio $\beta$.

On the other hand, we also analyze the distribution of the times of fast escape from the system for which we consider a maximum time of escape of 30 units of time. Our investigation reveals the following findings:

-

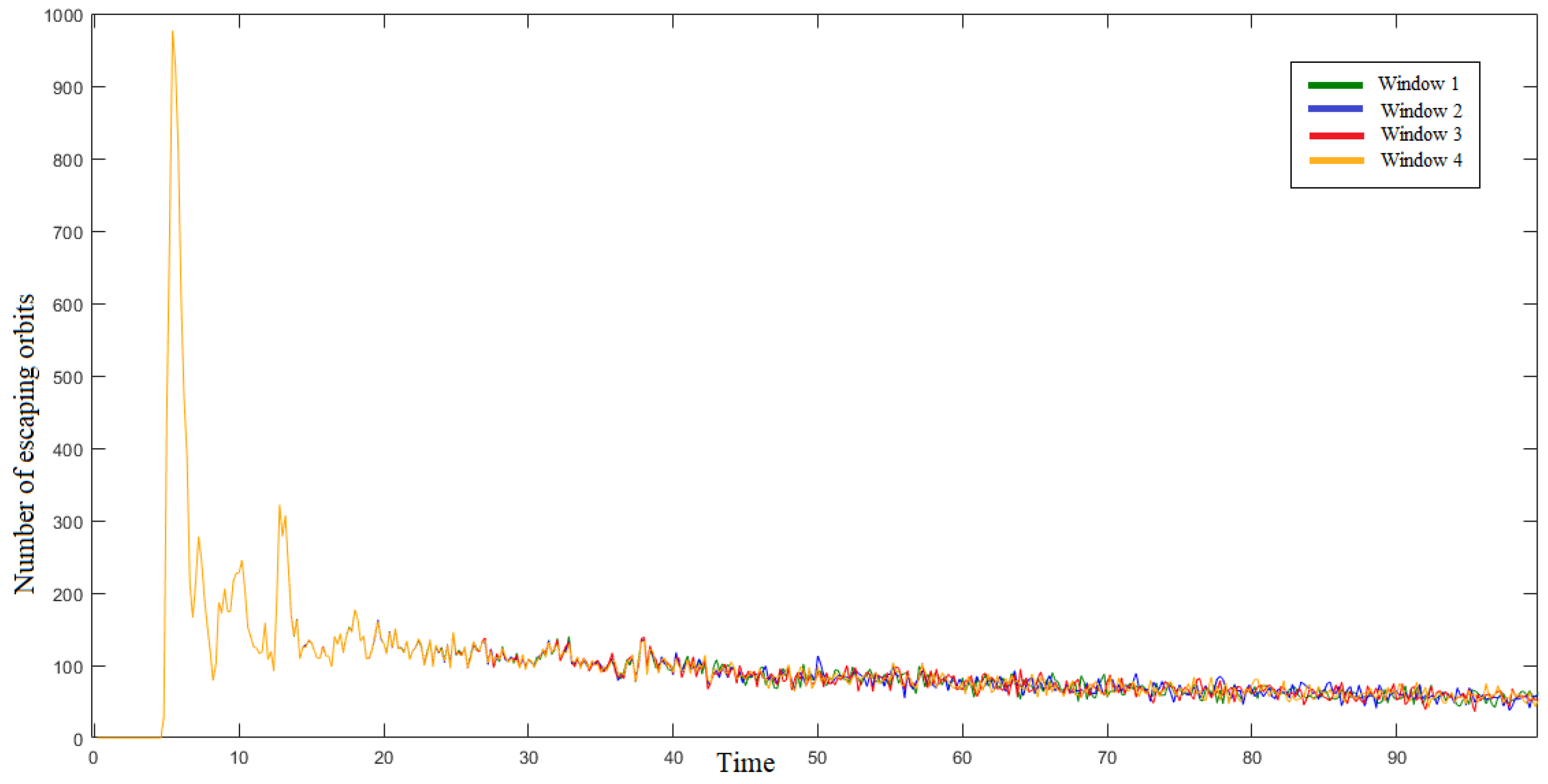
For $\beta =2$ and $C_{2,1}=2.7505$: In Figure 5a, there are a total of 1379 orbits that escape from the potential well. This leads to only $0.0329\%$ of orbits escaping. Upon thorough analysis of the presented data, it becomes apparent that none of the orbits escape within the interval ($0,7$]. The highest peak of 120 orbits is observed in the interval ($7.2,7.4$]. Afterwards, the number of escaping orbits decreases to 28 in the interval ($7.6,7.8$], and increases again with a secondary peak of 68 orbits in the interval ($7.8,8$]. For the next time intervals, the overall pattern of the escaping orbits corresponds approximately to a cyclical behavior, which is distinguished by repeated sequences of ascent and descent to zero with some periods of stability in the escape, in the following intervals: in the interval ($9.4,9.8$], there are 8 escaping orbits; we observe 16 escaping orbits in ($10.4,10.6$]; a total of 32 escaping orbits are identified in the interval $(12.8,13]$, and finally 8 escaping orbits are observed in the interval $(16.6,17.2]$.

-

For $\beta =2$ and $C_{2,2}=2.7476$: In Figure 5d, as the diameter of the escape windows increases slightly, we observe notable changes in behavior that correspond to an increase in the number of escaping orbits, with a total of 16,243 orbits. This leads to $0.3875\%$ of orbits escaping. In comparison to the previous patterns, the oscillations no longer display a pattern of decreasing to zero or having periods of stability per intervals of time. It is clear that no orbits escape over the interval ($0,5.6$].

Furthermore, we identify the highest peak of 716 orbits in the interval ($5.8,6$]. Afterwards, the number of escaping orbits decreases to 64 orbits in the interval ($7,7.2$], and right after that, the frequency of escaping orbits oscillates in a sequential way.

-

For $\beta =2$ and $C_{2,3}=2.7449$: In Figure 5g, we detect a total of 39,139 escaping orbits from the potential well. Thus, $0.9336\%$ of orbits escape. There are no escaping orbits on the interval ($0,5.2$]. We identify a highest peak of 1164 orbits in the interval ($5.6,8$]; after that, there is a sudden decline of 200 orbits in interval ($6.8,7$] and a secondary peak of 736 orbits in interval ($12.6,13$]. Subsequently, the number of escaping orbits per interval of time continues to show an oscillating pattern.

-

For $\beta =2$ and $C_{2,4}=2.7399$: In Figure 5j, which corresponds to the scenario with the largest diameter of the exit windows, we observe a total of 88,068 orbits that escape from the potential well. Thus, $2.1007\%$ of orbits escape. There are no orbits that escape over the interval ($0,4.6$]. We locate a main peak of 3908 orbits in the interval ($5.2,4$]. After a last peak of 1288 escaping orbits in the interval ($12.6,13.2$], we observe a notable gradual reduction in the behavior of oscillations, reaching barely a state of constancy.

-

For $\beta =10$ and $C_{10,1}=1.9943$: In Figure 5b, we identify a total of 279 orbits that escape from the potential well. Thus, $0.0067\%$ of orbits escape. There are no escaping orbits on the interval ($0,14.2$]. There is a highest peak of 64 orbits in interval ($15.8,16.2$] and two secondary peaks of 56 in the intervals ($16.6,16.8$] and ($17.4,17.6$], and the other peaks are in repeated phases of ascending and descending to zero escaping orbits. This particular case exhibits a strikingly distinct sequence with specific peaks that have the same number of orbits throughout various time intervals, i.e., ($19,20.2$], ($22.2,23$], ($23.4,24$] and ($24,24.6$].

-

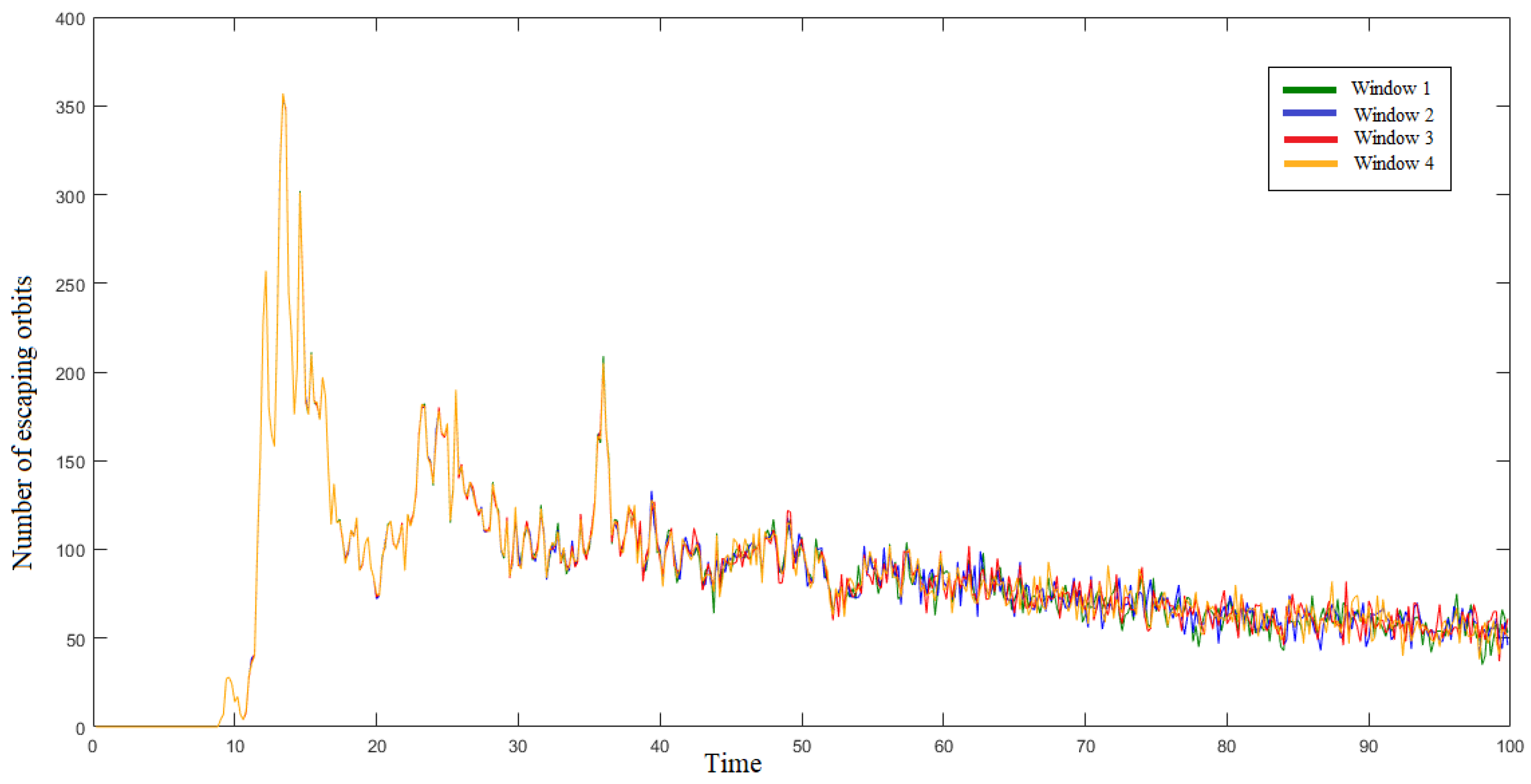
For $\beta =10$ and $C_{10,2}=1.99$: In Figure 5e, there are a total of 3603 escaping orbits. Thus, $0.0859\%$ of orbits escape. There are no escaping orbits on the interval ($0,9.2$]. After that time interval, smaller peaks begin to emerge, which gradually increase in height until they reach a main peak of 424 orbits in the interval ($14.8,15$]. Then, the other peaks decrease slowly till a sudden decline to the lowest peak of 24 orbits in the interval ($20.2,20.4$]. Afterwards, the pattern continues to oscillate.

-

For $\beta =10$ and $C_{10,3}=1.9861$: In Figure 5h, we detect a total of 7064 orbits escaping from the potential well. Thus, $0.1685\%$ of orbits escape. There are no escaping orbits on the interval ($0,9$]. The main peak consists of 641 escaping orbits in the interval ($14.4,14.6$]. We observe that the patterns of the peaks exhibit the same behavior shown in Figure 5e, with an increase in the number of escaping orbits related to the expansion of the diameter of the exit windows.

-

For $\beta =10$ and $C_{10,4}=1.9787$: In Figure 5k, there are a total of 13,877 of orbits that escape from the potential well. Therefore, $0.3310\%$ of orbits escape. There are no escaping orbits over the interval ($0,8.8$]. However, the pattern of peaks follows barely the same behavior as in Figure 5h, with a reveal of three discrete peaks, among which the highest peak has 1424 orbits in the interval ($13.2,13.4$].

-

For $\beta =20$ and $C_{20,1}=1.8134$: In Figure 5c, there are only two orbits that escape from the potential well in the interval ($28.4,28.6$]. We observe a larger interval with no escaping orbits until $28.6$ time units.

-

For $\beta =20$ and $C_{20,2}=1.8085$: In Figure 5h, we note that there are a total of 159 escaping orbits. Therefore, $0.0038\%$ of orbits escape. There are no escaping orbits over the intervals ($0,24.4$] and ($24.4,25.8$]. Then after that, there appear gradually increasing peaks until they reach the main one, with 64 escaping orbits in the interval ($27.2,27.4$]

-

For $\beta =20$ and $C_{20,3}=1.804$: In Figure 5i, there are a total of 706 orbits escaping from the potential well. Thus, $0.0168\%$ of orbits escape. We observe a decline in the time intervals that have no escaping orbits, limited only in ($0,21.8$] and ($22.8,23.4$]. The main peak has 228 orbits in the interval ($23.6,23.8$].

-

For $\beta =20$ and $C_{20,4}=1.7954$: In Figure 5l, there are a total of 1952 orbits that escape from the potential well. Thus, $0.0466\%$ of orbits escape. We observe the same pattern as in the previous Figure 5c,f,i with a decrease in the intervals of time that have no escaping orbits, limited in ($0,16.2$] and ($17.2,17.8$]. There appear to be four clearly emerging peaks, such that the highest one has 668 orbits in the interval ($25.8,26$].

A general overview of all the results evidences that when $\beta =2$, the highest peak increases directly and also declines suddenly to the lowest value, while for $\beta =10$, the increase in the highest peak and the decline occur gradually, accompanied by the emergence of many secondary peaks. However, for $\beta =20$, the peaks appear separately, following a sequential pattern.

In Figure 6, we depict an estimation for the initial time, $t_0$, at which the orbits start to escape from the potential well with the variation of the diameter of the opening windows, $\psi$, for each case of $\beta$, by means of a polynomial interpolation. We conclude that when the mass ratio, $\beta$, increases, the initial time of escaping, $t_0$, increases concurrently, which means that the orbits need more time to escape as the mass ratio increases. This behavior is directly related to the fact that $\beta$ is the ratio between the central mass and the peripheral masses. Furthermore, as the Jacobi constant decreases, the initial time, $t_0$, decreases. This fact obviously indicates that orbits start escaping faster because the diameter of the opening windows becomes larger. We can deduce that the mass ratio, $\beta$, and the Jacobi constant, C, generate distinct changes in the distribution of the escape.

In Figure 7, Figure 8 and Figure 9, we illustrate the number of orbits that escape from each of the four openings, for $\beta =2,10,20$ and $\psi =0.2$, such that the results of Windows 1, 2, 3 and 4 are colored in green, blue, red, and yellow, respectively. We can observe that for the pair $\beta =2$, $C_{2,4}=2.7399$, the four curves overlap in the interval of time $[0,20]$, and for $\beta =10$, $C_{10,4}=1.9787$, they overlap in the interval of time $[0,30]$, while for $\beta =20$ and $C_{20,4}=1.7951$, the interval of time is extended to $[0,50]$. It is evident that the time of fast escape for each case is significantly increased with the increase in $\beta$ and the decrease in C.

The percentage of the escaping orbits in each window converges to approximately $25\%$ from the total amount of them in each case, which means that the number of orbits escaping from each window is probably identical, and the observed variations are presumably attributable to propagation errors that may result from the numerical integration process. Therefore, we can conclude that no structural or energetic limitations favor one window over another. Thus, it is expected that the occurrence of escaping trajectories through each opening has an equivalent probability, so the four windows can be considered equiprobable. This equiprobability arises from the symmetry of the problem, leading to a balanced and consistent number of escapes through each window.

4. Conclusions

In this paper, we elucidate the impact of the Jacobi constant, C, and the mass ratio, $\beta$, on the probability of the escaping orbits in the $(4+2)$-body ring problem in three dimensions using a numerical integration on a grid of $2048\times 2048$ initial conditions that are evenly spaced and arranged along the boundary of a sphere with a radius of $\rho =0.3$. It is assumed that the initial velocity at each initial condition is perpendicular to the tangent plane of the sphere. In order to accomplish this analysis, we incorporate into the study three values of $\beta$, $\beta =2,10,20$. For each of these values, we choose four values of C, such that the diameter of the opening windows is identical.

The results that we obtain reveal that when we consider the Jacobi constant values associated with the opening that has the largest diameter, the probability of escape varies monotonically with respect to the mass ratio; conversely, with the opening that has the smallest diameter, the probability does not vary monotonically. Furthermore, significant variations take place in the distribution of the escaping orbits and the initial time of escape, $t_0$, as the mass ratio increases. It is evident, based on our findings, that the four windows can be considered equiprobable. While there are minor errors due to the numerical integration, the probabilities of escape through each window exhibit a substantial level of similarity in the interval time of fast escape, regardless their unequal distribution in the other intervals.

These results complement our previous research [42], where the repeating patterns observed in the regions facing the escape windows exhibited a consistent structure and identical coloring in four distinct regions, indicating similar dynamical behavior in each escape window. This structural symmetry is reinforced by the current result, which shows that the probability of escape through each of the four windows remains nearly equal during the interval of fast escape. Taken together, these outcomes point to an underlying symmetry in both the geometry and the escape dynamics of the system.

The insight acquired from this research serves as a starting point for subsequent investigations concerning the dynamic of escape in three dimensions. For more accuracy, it is possible to conduct an extensive examination that incorporates a larger range of mass ratio values and the Jacobi constant in order to determine the extent to which the behavior of escape probability is dependent on those parameters. Such sorts of endeavors have the potential to advance the field of celestial mechanics and reveal more profound explanations for the dynamic of orbital systems.