Abstract
Among searchable encryption techniques, multi-user dynamic searchable encryption (MUDSE) schemes are an important research direction. After the data owner transfers data to the cloud, it may be necessary to authorize different users to access some or all of the data while allowing for dynamic updates. Enabling dynamic data sharing in cloud storage while preserving users’ ability to search the data is crucial for promoting data flow and maximizing its value. This approach is particularly significant in addressing the data silo problem. However, existing security mechanisms remain imperfect, and most current scenarios assume that cloud servers are merely “curious but honest”. In reality, cloud servers may exhibit malicious behavior, such as returning incorrect or incomplete search results. Similarly, malicious users might falsify search results—for example, to avoid payment—or collude with cloud servers to steal other users’ search privacy. To address these challenges, this paper proposes an updatable multi-user dynamic searchable encryption scheme with bidirectional verification. The scheme enables secure dynamic data sharing in multi-user scenarios by constructing an index structure using homomorphic message authentication codes and bitmaps. This ensures secure updates to encrypted data without revealing the relationship between files and keyword search keys while providing forward and backward security. Regarding privilege management, the scheme employs updatable keys, ensuring that users can only generate valid search commands if they possess the latest encryption key. Additionally, blockchain technology is introduced to assist in verifying user honesty. Through actual testing and security analysis, the proposed solution demonstrates improved search speed over traditional methods while maintaining security. It also exhibits high adaptability for handling frequently changing cloud data.
Keywords:
multi-user dynamic searchable encryption; updatable keys; blockchain; bidirectional verification MSC:
68W01
1. Introduction
With the rapid growth of data volume, locally stored and processed data face limitations due to the restricted storage capacity and parallel computing capabilities of terminal devices [1]. As a result, average users struggle to meet the storage demands of ultra-large-scale datasets [2]. Meanwhile, cloud storage services have emerged as a popular alternative, attracting a vast number of users to upload substantial amounts of private data. However, due to weak data protection awareness, technical vulnerabilities, malicious attacks, and profit-driven motives, issues such as data leaks, unauthorized access, illegal data trading, and privacy breaches have become prevalent [3].
To mitigate these risks, encrypting uploaded data has become essential to prevent privacy violations. This ensures that even if adversaries compromise the cloud server, they cannot extract meaningful information from the ciphertext [4]. For robust security, users retain exclusive control over encryption keys, restricting the cloud server to accessing only ciphertext and preventing it from performing additional operations. Among these operations, data retrieval is the most fundamental, as it enables extracting specific information from large datasets, facilitating subsequent data integration and sharing [5]. Traditional encryption methods require downloading all data locally for encryption and decryption, which imposes high demands on system memory and encryption algorithms. Efficiently utilizing ciphertext data remains a critical challenge in information security and a key research focus in both academia and industry.
The emergence of searchable encryption (SE) [6] provides an innovative solution to this problem. This framework allows users to construct verifiable index structures on encrypted data, implemented in three key phases: First, salient keywords are extracted from the original documents, followed by the synchronized upload of encrypted documents and their associated indexes. Next, when initiating a search request, the user generates a specific trapdoor function and submits it to the server. Finally, the cloud server employs pattern-matching algorithms to return the qualified result set.
In the context of big data, the explosive growth of private data has become the norm [7], and cloud-stored ciphertexts undergo continuous additions and deletions, exhibiting dynamic characteristics. Thus, achieving fast and accurate retrieval from vast, dynamically changing datasets remains a critical challenge. Traditional methods involve downloading indexes, performing local updates, and re-uploading modified indexes—a process that is inefficient and burdensome under frequent updates. To address this, dynamic symmetric searchable encryption (DSSE) has emerged [8,9], enabling users to dynamically modify ciphertexts and indexes while maintaining consistency. This ensures secure and efficient updates to searchable ciphertexts. While existing SE techniques have preliminarily addressed secure queries in dynamic environments, they still face numerous challenges in handling massive datasets, including scalability, efficiency, and security trade-offs.
1.1. Related Works
Searchable encryption (SE) technology, as a pivotal solution in the field of ciphertext retrieval, primarily aims to achieve controlled query functionality over encrypted data. Based on cryptographic architectures, SE can be classified into public-key encryption with keyword search (PEKS) [6] and symmetric searchable encryption (SSE) [10].
In the public-key paradigm, Boneh et al. [6] pioneered the PEKS mechanism in 2004. While PEKS demonstrates advantages in multi-user collaborative scenarios, its practical adoption is hindered by the high computational complexity stemming from bilinear pairing operations, resulting in significant efficiency challenges. In contrast, symmetric searchable encryption (SSE) offers superior computational efficiency, making it more suitable for single-user-dominated data storage and retrieval scenarios. The foundation of SSE research dates back to 2000, when Song et al. [10] proposed a two-layer encryption framework, enabling cloud servers to perform ciphertext scanning through a specialized cryptographic structure.
In the field of multi-user searchable encryption, Curtmola et al. [11] pioneered the integration of broadcast encryption mechanisms [12] into the multi-user symmetric searchable encryption (MSSE) framework. Building upon this foundation, Bao et al. [13] innovatively proposed a distributed user management model, significantly enhancing the system scalability of the encryption scheme. Regarding the extension of search functionality, Jarecki [14] and Sun et al. [15] independently adapted Cash’s single-user scheme [16] for multi-user scenarios, constructing conjunctive keyword search models. To address security threats from malicious users, Popa et al. [17] introduced the multi-key searchable encryption (MKSE) architecture, achieving fine-grained access control through an authorization conversion mechanism. In pursuit of optimal security-practicality trade-offs, Hamlin et al. [18] proposed two innovative approaches: the first employs a data replica isolation strategy that eliminates cross-user leakage at the cost of O(n) storage overhead, while the second [19] constructs a lightweight index based on indistinguishability obfuscation. Subsequent improvements by Patel et al. [20] introduced dynamic obfuscation factors to control keyword leakage probability under a single-copy storage architecture, though this approach remains vulnerable to semantic leakage when honest and malicious users access overlapping documents. Wang et al. [21,22] achieved a refined balance between performance and security through a triple-optimization strategy: reducing cross-user leakage to negligible levels, optimizing search time complexity, and effectively defending against historical data backtracking attacks. This comprehensive approach represents significant advancement in secure multi-user searchable encryption systems.
In the field of dynamic searchable encryption, Kamara et al. [8] pioneered the use of an inverted index architecture, achieving a breakthrough solution that supports dynamic updates. While this scheme overcomes the functional limitations of static systems, it introduces additional overhead in storage efficiency and computational complexity, along with potential keyword information leakage during document insertion. A significant milestone in DSSE (dynamic searchable symmetric encryption) technology was marked by Cash et al. [23] in 2016 with their index optimization scheme. By constructing a two-layer hash index structure, they reduced storage overhead from the traditional O(n²) to O(n) while limiting information leakage to the operation type and the number of matched documents. This breakthrough achieved, for the first time, a balance between storage efficiency and privacy protection, with its leakage model later termed the “Minimal Leakage Principle” in subsequent research. To address the inherent information leakage risks in DSSE systems, Stefanov et al. [24] established a dynamic operation security framework in 2017, systematically defining forward security and backward security mechanisms. Forward security employs a layered encryption strategy to isolate update operations from historical data correlations, ensuring that newly added documents do not reveal prior search patterns. Backward security, on the other hand, utilizes logical deletion chains to eliminate residual index traces after deletion operations, effectively defending against historical data backtracking attacks.
Most existing schemes predominantly assume that cloud servers are honest but curious. This means cloud servers comply with protocol requirements, neither actively disrupting system operations nor altering data, while attempting to extract additional information from processed data. However, in real-world scenarios, when cloud servers are compromised or misconfigured, they may return erroneous search results, thereby compromising the accuracy of user queries. In recent years, blockchain-based verification schemes for searchable encryption [25,26] have demonstrated significant improvements in system security. These approaches substantially reduce reliance on intermediate entities and effectively prevent data tampering and theft by malicious adversaries, thereby ensuring the correctness and integrity of user search results.
1.2. Our Motivation and Contributions
Most existing searchable encryption schemes remain confined to the single-data-owner paradigm, where only the data uploader can perform search operations using specific trapdoors. However, as application scenarios continue to expand in both data scale and user base, multi-user data sharing and collaborative access have become essential requirements. Traditional single-user architectures can no longer adequately meet the functional demands of modern distributed systems. Against this backdrop, searchable encryption techniques supporting multi-user collaborative retrieval have emerged as a crucial research direction in cryptography. Although some of the research on searchable encryption technology has realized the data sharing function to a certain extent, it faces multidimensional security challenges in the dynamic data environment. First, with the real-time update of data resources and the complexity of application scenarios, the traditional static encryption model has found it difficult to cope with the security hazards arising from the dynamic updating process; specifically, the problem of forward privacy and backward privacy during the iteration of data versions needs to be solved urgently. Secondly, the dynamic management mechanism of access rights under multi-user collaboration scenarios has not yet been perfected, and there are systematic defects in key updating and access control policy adjustment in the process of rights change, which constitutes a key constraint in breaking the phenomenon of data silos and promoting the efficient circulation of data.
The first issue faced in this scenario is the management of user access rights, which refers to how the data owner controls which data users can access the data and which cannot. It is also necessary to consider changes in the access rights of data users, such as how to revoke the access rights of users when the rights of use purchased by them expire. To solve this problem, existing work combines a searchable encryption scheme with a broadcast encryption scheme to send a secret message to users with access rights using broadcast encryption. When a user is revoked, the secret message has to be regenerated and sent to all data users with access rights at the moment; however, this method does not support the data owner to update the data. Although the existing work can make use of the proxy server to manage the access rights of users, ensuring that only users in the legitimate access list can obtain the valid secret information returned by the proxy server when searching for data and complete the search for data. In most existing schemes, only forward security can be achieved, and backward security cannot be guaranteed when deleting data. This chapter further explores how to design a more efficient and secure solution that achieves both forward and backward security while also managing user access rights without the involvement of a proxy server.
It is worth noting that this technology also needs to deal with the credible challenges in the cloud service environment:driven by economic interests or system failures and other factors, the cloud service provider may return incomplete or biased search result sets, while private users may refuse to pay and thus return “dishonest” results, which will seriously threaten data availability and system reliability. Therefore, it is necessary to study multi-user dynamic searchable encryption that supports authentication.
To achieve secure multi-user dynamic ciphertext sharing with bidirectional verification, the core concept involves constructing a security-controlled sharing platform. This platform employs a bidirectional verification mechanism to ensure data update integrity while realizing dynamic access management through key update strategies. For the one-to-many sharing model of dynamic data, we utilize homomorphic message authentication codes (HMACs), binary bitmaps, and pseudo-random functions (PRFs) to construct a dynamic index structure. Each keyword corresponds to a bitmap matching the file count, where 1/0 markers indicate keyword–file associations. PRFs randomize bitmap position mapping, while HMACs combined with keyword-specific keys complete bitmap encryption.
During data updates, leveraging the homomorphic property, updated HMACs can be generated through linear combination of original authentication codes and differential authentication codes, thereby achieving synchronous key updates. For fine-grained access control, a key fragmentation mechanism enables dynamic permission granting and revocation. When a data owner authorizes access to a user, only the target keyword’s key and current-state differential HMACs are distributed. For permission revocation, the owner simply restricts the user’s access to subsequent differential HMACs without requiring a reconstruction of private key information.
Finally, leveraging blockchain’s tamper-proof characteristics, bidirectional verification is implemented: cloud server results undergo blockchain auditing, while user behavior authenticity is verified through HMAC. Formal security proofs and experimental evaluations demonstrate that our solution satisfies both forward security and backward security, while significantly reducing computational and communication overhead in multi-user scenarios.
To sum up, the main contributions are as follows:
- The scheme achieves dynamic search key updates, thereby enabling real-time adjustment of user data access privileges. It enables dynamic security maintenance of encrypted information during user searches, where updated ciphertexts become inaccessible to search operations using pre-update keys. This mechanism provides effective defense against file injection attacks during data addition operations while preventing sensitive information leakage during deletion processes.
- Capture forward security and backward security. When authorizing a user to access specific keywords, the data owner distributes the corresponding keyword-specific key and current differential HMACs to the target user. For permission revocation, the data owner neither needs to modify the master key nor reconstruct the cryptographic material; instead, it suffices to restrict the target user’s access to subsequent differential HMAC updates.
- The immutability property of blockchain is leveraged to verify the integrity of cloud-returned results, while user behavior authenticity is validated through HMAC-based authentication.
A comparison of our scheme with the existing schemes is given in Table 1.

Table 1.
A comparison of our scheme with the existing schemes.
1.3. Organization
Section 2 reviews some of the basic primitives used in this paper. Section 3 presents the security model and the specific structure of our proposed scheme. In Section 4, the security of this scheme is analyzed and proved. In Section 5, we compare and analyze the efficiency and feasibility of our scheme through simulation experiments. Finally, in Section 6, we conclude and look forward to future work.
2. Preliminaries
2.1. Notations
The notations are shown in Table 2.

Table 2.
Notation description.
2.2. Basic Primitives
2.2.1. Negligible Function
Assuming that an adversary is able to decipher an encryption scheme within polynomial time complexity poly(n), the encryption scheme is determined to be computationally insecure. Conversely, an encryption scheme is considered computationally secure when the probability of success of an adversary in deciphering the scheme within polynomial time complexity is less than . This probability threshold is defined as negligible probability. Its mathematical formalization is described as follows:
Definition 1
(Negligible Function). For any function , if for any polynomial function poly(n), , there exists a natural number such that for any , the following is satisfied:
Then, the function negl(x) is treated as negligible.
2.2.2. Pseudo-Random Function
A pseudo-random function (PRF) [31] is a cryptographic tool that simulates real random behavior through deterministic algorithms and has a wide range of applications in various cryptosystems. The method has a certain degree of randomness, but its essence is a family of mathematical functions built on the basis of deterministic algorithms. For any input pseudo-random function, the output is a random variable. Given a key (seed) and input, it is able to output seemingly random values but can reproduce the result with the same seed. The algorithm produces a fixed sequence based on the seed, and the same input must yield the same output. Under computational complexity theory, polynomial time algorithms cannot distinguish between the PRF outputs and the true random sequences. The security of the seed directly determines the unpredictability of the function’s outputs, and a leakage of the seed will lead to the exposure of the full sequence. The following is a formal definition of a pseudo-random function.
Definition 2
(Pseudo-random function). If a function is considered as a safe pseudo-random function, its dominance is defined for any polynomial time adversary A as follows: where negl(x) is a negligible function, , and f is a true random function mapping from X to Y.
2.2.3. Homomorphic Message Authentication Code
A homomorphic message authentication code (HMAC) is a new cryptographic tool that integrates homomorphic encryption and a message authentication mechanism. Its core function is to support the computational verification of ciphertext data, i.e., to verify the integrity and authenticity of remote computation results without decrypting the ciphertext. The technique has the synergy of pseudo-random functions and homomorphic encryption algorithms, allowing third parties to perform specific operations (e.g., addition, multiplication) on encrypted data, and the resulting computation results can still be verified.
In this paper, the role of homomorphic message authentication codes is mainly to verify whether the data have been tampered with or not. Since cloud servers are not always honest and trustworthy, users have to perform a lot of computational work on the data stored in cloud servers. In addition to key techniques, such as verifiable computation and storage proxies, homomorphic authentication-based methods have received much attention for authenticating the results of computation. Here, a more efficient homomorphic message authentication code proposed by Catalano and Fiore [32] is introduced, whose security relies solely on the existence of pseudo-random functions. The following is its formal definition.
Definition 3
(Homomorphic Message Authentication Code). A secure homomorphic message authentication code scheme contains the following four-stage polynomial time algorithm:
- Key generation: . This key generation algorithm inputs a security parameter λ and outputs a user private key sk and a user computation key ek.
- Authentication: . This authentication algorithm inputs a user private key sk, any message m in the message space M and its corresponding input label v, and it outputs the authentication label ω for this message m.
- Verification: . This authentication algorithm inputs a user private key sk, any message m in the message space M, a program and an authentication label ω for m. The output is either 1 or 0, where 1 means that the authentication has passed and 0 means that the authentication has failed.
- Evaluation: . This evaluation algorithm takes as input a computational key ek, a computational function F, and a vector with respect to the authentication tags, and it outputs a new authentication tag ω.
Note that this scheme is combinatorial; the authentication tags output by the computational algorithm can be used again as input to this computational algorithm. For example, the computational algorithm outputs , a total of n authentication labels corresponding to different authentication information , if the computational algorithm is fed again with and a program P to obtain a new authentication tag . The output obtained by the program P and outputs the obtained new message m. Then, due to the combinatorial nature of the program, it is made that is the authentication label of message m.
2.3. Symmetric Searchable Encryption
Symmetric searchable encryption (SSE) is constructed based on a symmetric encryption system and cryptographic primitives to support the retrieval operation of ciphertext data in non-trusted environments, aiming to ensure data privacy and security during the retrieval operation.
Definition 4
(Symmetric Searchable Encryption). A symmetric searchable encryption algorithm includes the following three specific algorithms:
- Initialization: : This algorithm takes the original database DB and the security parameter λ as inputs to generate the encrypted database EDB. The client transmits the generated EDB to the third-party cloud storage provider, while the key k and the system state α are securely stored locally.
- Search: : This protocol runs as an interactive process between the client and the cloud server. The client calls the locally securely stored encryption key, combines the keywords to be checked ω to generate the search token t, and updates the system state to . After receiving the token t, the cloud service provider executes the search operation based on the EDB, and finally returns the matching result r to the client. At the same time, it completes the update iteration of the encrypted database EDB.
- Update: : This protocol is implemented as a two-way communication mechanism between the client and the cloud server. The client performs symmetric encryption of the original database DB using key k, generates a new encrypted database EDB and updates the system state to . The newly encrypted data are transmitted over a secure channel to the cloud server for storage, and the cloud server thus completes the update iteration of the EDB.
3. Security Models and Construction of Our Proposed Scheme
In this section, we now introduce the security definition, the system framework and the scheme description.
3.1. Security Models
3.1.1. Adaptive Security
In the field of searchable encryption, most of the existing schemes allow a specific degree of privacy leakage in order to improve the retrieval efficiency as compared to high-cost techniques such as multi-party computation with full homomorphic encryption. The information leakage of dynamic searchable encryption (DSSE) schemes can be formally described as follows [24]: .
The model allows an attacker A to obtain system information by performing initialization, retrieval, and data update processes. The security of DSSE is formally verified through a framework of real-world and ideal-world experiments. This study has definitions for two games: denotes a game that simulates the operation of a real system, and denotes a game that operates in an ideal experimental environment. If the attacker is unable to distinguish between the two types of experiments, the scheme is judged to satisfy the security requirements.
In the real world, the system strictly follows the protocol specification: Firstly, the encrypted database EDB is generated by and transmitted to the attacker, who can select the keyword to initiate the query and can select the set of documents EDB to receive response. Then, the encrypted database outputs the adjudication bit 0,1.
In the ideal experiment, the simulator S reconstructs the system response based on the leakage function: the simulated EDB is generated using and transmitted to the attacker, who performs the retrieval and update operations based on the leakage functions and and ultimately outputs the judgment bit 0,1 in the simulated environment. In this case, op is an ‘add’ or ‘delete’ operation that dynamically updates data.
Definition 5
(Adaptive Security). A DSSE scheme satisfies the adaptive security requirement if and only if there exists a probabilistic polynomial time simulator S, such that for any probabilistic polynomial time attacker A both satisfy the following:
3.1.2. Forward and Backward Security
As the key indexes for evaluating the security of dynamic searchable encryption schemes, forward security and backward security [24,33] provide protection mechanisms for different operations, respectively. Forward security aims to ensure the security of the op=add operation of adding documents in dynamic searchable encryption, and schemes with forward security features can effectively prevent document injection attacks. Backward security, as a security standard for document deletion operations, is categorized into three levels of security strength based on the difference in the degree of information leakage. The next step is to define the formalization of forward and backward security.
Forward security means that the add document operation must not expose the correlation between the historical search keywords and the added document. The formalization for forward security is defined as follows:
Definition 6
(Forward Security). When a dynamic searchable encryption scheme can satisfy the definition of forward security, then its corresponding update leakage function needs to satisfy the following mathematical constraints:
The above definition indicates that if a dynamic searchable encryption scheme is forward secure, there is no way for the scheme to synchronize the exposure of the corresponding operator op, the document identifier id, and the number of keywords involved in the document update.
Backward security [24] requires dynamic searchable encryption schemes to prohibit the disclosure of any information related to an entry during the execution of a delete operation. However, such schemes may lead to a significant decrease in search efficiency. For this reason, Bost et al. proposed three gradations of backward security (BP-I, BP-II, and BP-III) based on the differences in the degree of information leakage to balance security and search efficiency. These three levels correspond to different tiers of leakage: BP-I has the lowest amount of information leakage, while BP-III has the highest. In order to systematically characterize these three leakage levels, partial functions need to be predefined.
Let the function Q denote the set of operations associated with each entry. In the entry retrieval process, define t as the timestamp and as the keyword to be queried.
The first function that is defined is the Time function, whose function is to return the keyword (t, id) associated with all the added operations, which is formally defined as follows:
The second function Update is used to extract the timestamp of the database update operation, which is formally defined as follows:
The third function, Delete, is used to return the set of timestamps corresponding to the delete operation, which is formally defined as follows:
Based on the above three functions, backward security can be formally defined as follows:
Definition 7
(Backward Security). If an adaptive dynamic searchable encryption scheme needs to satisfy backward security, it must fulfill the following conditions:
- BP-I level backward security (Backward Privacy type-I):
- BP-II level backward security (Backward Privacy type-II):
- BP-III backward security (Backward Privacy type-III):
Note that the functions L′ and L″ are both defined as stateless functions in such models.
3.2. System Framework
There are four core entities in this scheme: A data owner responsible for data encryption and authority management. A data user performing retrieval requests and decryption operations. A cloud server undertaking ciphertext storage and computation tasks. A blockchain supported by distributed ledger technology realizing operation auditing and key verification. These four core entities together constitute the system model of the program, which will be introduced in detail below. The scheme model architecture is shown in Figure 1.
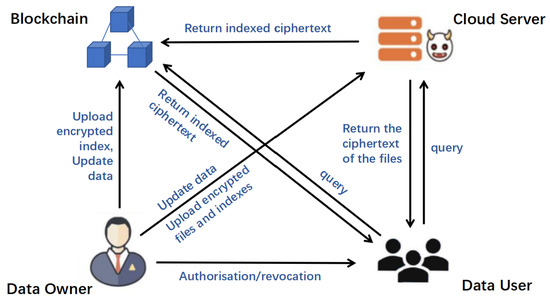
Figure 1.
The model architecture of the BVUMU-DSSE scheme.
- Data Owner:
As the controlling body of data resources, the core responsibility of a data owner includes encrypting the original data, extracting the feature keywords and generating the index structure from the original dataset, and then completing the index encryption operation, and finally transmitting the encrypted data collection to the cloud storage node securely. In the dynamic data change scenario, including the addition or removal of data items, the subject needs to synchronize the maintenance of the corresponding encrypted database and the update of the necessary parameters involving the key system to the authorized users to ensure that the retrieval operation is always performed based on the latest version of the data collection. The subject of this operation is preset to be fully trusted, and its behavioral pattern strictly follows the protocol specification of the scheme.
- Data User:
As the subject of authorized data access, data users are granted retrieval permission by the data owner and obtain key system related parameters for data query operations. When the subject initiates a retrieval request, the key parameters are utilized to transform the retrieval keyword into an encryption key, which is transmitted to the cloud server through a secure channel. The cloud server performs the retrieval operation and returns the corresponding dataset to the requesting party. When there is doubt about the returned dataset, the result can be verified through the data owner. The operation endpoint is preconfigured as a technical execution unit with limited trust attributes, and its behavioral pattern, while following established protocols, presents a potential risk of incomplete reliability.
- Cloud Server:
As a core component of the distributed computing architecture, the cloud server possesses superior computing performance and ample storage resources. Its core functions include securely storing encrypted databases submitted by data owners and providing retrieval services to authorized users. The entity keeps the encrypted dataset intact for both the initial submission and subsequent updates by the data owner. Upon receiving the query command from the data user, the system performs the retrieval operation by invoking the stored encrypted database and the search key, and it finally returns the processing result to the requesting party. This computing node is set to be semi-honest, and it may run the complete algorithmic protocol with incomplete or biased feedback information due to computational errors; at the same time, driven by interests, it may try to parse the sensitive information in the ciphertext database while following the protocol specifications, which happens from time to time in real scenarios.
- Blockchain:
A blockchain based on distributed ledger technology is naturally equipped with tamper-proof features and distributed fault-tolerant mechanisms. These core mechanisms provide infrastructure support for trusted data interactions. The network adopts a federated chain architecture, and its node access mechanism is limited to data controllers and authenticated member nodes. After completing a data sharing or version update operation, the data owner needs to synchronize the relevant auxiliary parameters to the blockchain. The architecture maintains an encrypted index library and returns the corresponding ciphertext dataset to the data requestor based on the authorization token. When receiving the update credentials from the data owner, the system performs the key rotation operation based on the update credentials. When an authorized user initiates a keyword search, they need to obtain the authentication-related parameters from the distributed ledger to perform the search and authentication process.
3.3. Scheme Description
For ease of presentation, we name the proposed updatable multi-user dynamic searchable encryption scheme with bidirectional authentication support BVUMU-DSSE, which contains six core algorithms, namely the initialization algorithm, the data update algorithm, the ciphertext search algorithm, the user authorization algorithm, the decryption algorithm, and the result verification algorithm. A flow chart of the scheme is shown in Figure 2. The initialization algorithm generates the system public parameters and the master private key based on the input security parameters, the update protocol regulates the data owner to perform the generation and maintenance of the ciphertext database, the ciphertext search algorithm contains the data user to generate the search key, and the cloud service provider performs the ciphertext retrieval process based on the key. The user authorization algorithm distributes the corresponding key to the authorized user, the decryption algorithm and the authentication algorithm are used to decrypt the retrieval results and verify the integrity of the results; at the same time, they are used verify the honesty of the user.
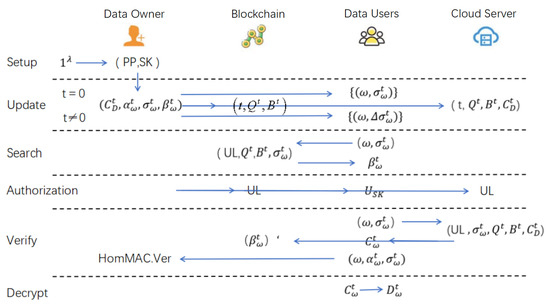
Figure 2.
A flow chart of the BVUMU-DSSE scheme.
- Setup: .
The data owner inputs the security parameters. Execute the initialization algorithm to generate the keys and hash functions that are required by the system according to the security parameters. In the specific implementation, the data owner will randomly select three keyed hash functions according to the security parameter , randomly select the hash function as well as two families of hash functions P and Q (used for the index generation and encryption operations), and generate the master key , and the file encryption key .
Finally, the output of this initialization algorithm outputs the public parameters and saves the private key .
- Update: .
The data owner generates or updates the ciphertext data with index at different time nodes t through a dynamic maintenance mechanism as follows. The update algorithm pseudo-code is shown in Table 3.

Table 3.
The update algorithm pseudo-code.
When t = 0, which corresponds to the initialization phase, this means the first instance of ciphertext database construction: The data owner assigns a column file encryption key to each column of the data and then assigns a unique column ordinal number p to each file through the hash function P. Then, it encrypts the file using the column file encryption key corresponding to this column identifier. For the files without assigned column identifiers, a file-equivalent random number is generated and encrypted as the padding ciphertext of this column file, which finally forms the file ciphertext collection . When constructing the index, the data owner extracts the file keyword collection and constructs an n bit-length bitmap for each keyword, and the bitmap is displayed as 1 only if the keyword exists in the column file to which it belongs; otherwise, it is displayed as 0. The plaintext is displayed as 1 only if the keyword exists in the column file to which it belongs. Otherwise, it is displayed as 0. After the plaintext index is constructed, the algorithm is called to generate a row encryption key, and is encrypted by using this key to obtain . Subsequently, a set of encrypted indexes is constructed by the hash function . Finally, the encrypted database generated at moment t is sent to the cloud server, and the auxiliary information such as is sent to the blockchain.
When , which is the database update phase, the data owner dynamically updates certain files, performs file addition and deletion operations, and selects a new hash function P from the function family P based on the temporal state. Moreover, it assigns new column keys and column identifiers to the files within the same operation as when the database was first constructed and performs encryption operations on the files. After that, the data owner will adjust the keyword set (add or delete keywords), generate keys for the new keywords according to the initialization rules, and then select a new function Q from the function family Q, reconstruct a new bitmap for each keyword and construct an encrypted index. At the same time, in order for users to search the ciphertext database normally to obtain the desired results, the data owner will proceed to calculate the difference corresponding to the same keyword and construct the difference label HMAC through . Eventually, the updated ciphertext database is sent to the cloud server, auxiliary information is sent to the blockchain, and the set of differential labels is distributed to authorized users.
- Search: .
The ciphertext search algorithm requires data users and blockchain nodes to collaborate to complete the operation process. The specific process is outlined below. The search algorithm pseudo-code is shown in Table 4.

Table 4.
The search algorithm pseudo-code.
For the data user, there are two states: the initial state and the update state. In the initial state, i.e., when t = 0, the initial tag set received by the legitimate user contains the search key parameter ; in the update state, i.e., when , the ciphertext database will be changed at this time, and the user will need to perform the calculation algorithm of the HMAC (homomorphic message authentication code) to regenerate the updated search key, . The updated key is eventually submitted to the blockchain network over a secure channel.
For the blockchain, after receiving the dataset containing the search request and the key, it is necessary to complete the verification of the membership in the authorization list. This search process should be terminated if it is verified that the user is not in this user list; if it is verified that the user is in this list, it is necessary to parse the set of ciphertext indexes corresponding to the keywords searched by the user by and then return the ciphertext index set to the data user who initiated the search.
- Authorization: .
The user authorization algorithm requires the data owner to perform a user authorization operation, add user u to the user authorization list, and then distribute the user private key to user u, which consists of and . Eventually, the data owner synchronizes the updated authorization list UL to the blockchain node with the cloud server to complete the update of the user list status.
- Verification:
This result verification algorithm is divided into two phases.
The first phase is the cloud server honesty verification phase, where the the data user submits the search key to the cloud server. After the cloud server receives the dataset containing the search request and the key, it needs to complete the verification of the membership in the authorization list first and terminate this search process if it is verified that the user is not in this user list. If the user is found to be in this list, it is necessary to use to reverse parse out the identifier of the ciphertext index corresponding to the keyword searched by the user to obtain ’ and carry out decryption. Then, it is necessary to increase all the files corresponding to component 1 to the final set of retrieval results . Ultimately, the collection of retrieval results should be sent to the user who initiated the search, and the collection of ciphertext indexes corresponding to the collection of retrieval results ′ should be sentto the blockchain. The blockchain compares ′ with its own calculated . If the comparison is consistent, the verification passes, indicating that the set of search results returned to the data user by the cloud server is correct; if the comparison is inconsistent, the verification fails, indicating that the cloud server returns an incorrect result.
The second stage is the user honesty verification stage. The data user decrypts the ciphertext index data returned by the blockchain to obtain ′, and then transmits to the data owner, who executes the verification algorithm in the homomorphic message authentication code. If the result of the algorithm is 1, this means that the result provided by the user is valid; otherwise, the user is deemed untrustworthy.
- Decryption:
After obtaining the search results, the data user deduces the encryption key of the corresponding column based on the position of 1 in the index and then decrypts the ciphertext returned by the cloud server by applying the key of this column, so as to recover the original plaintext file .
3.4. Correctness
When a user needs to retrieve a file containing a specific keyword at time t, they need to perform the operations in lines 1 to 9 of the ciphertext search algorithm to generate a search token for the keyword and transmit it to the cloud server. Since the ciphertext indexes of the cloud server are all constructed by the same pseudo-random function, this mechanism guarantees the accuracy of keyword retrieval. However, since the cloud server acts as a semi-honest participant in the index construction stage, the query results returned by it are not necessarily correct, so we compare and verify the ciphertext index collection in the search results through the blockchain, so as to confirm that the documents returned in the cloud server correspond to the ciphertext index collection, i.e., whether the returned documents are related to the search keywords.
3.5. Complexity Analysis
This subsection provides an analytical comparison between the BVUMU-DSSE scheme and some of the existing schemes in terms of complexity, as shown in Table 5, where the owner represents the data owner entity, |D| denotes the total number of documents in the document collection, N denotes the number of combinations between keywords and document identifiers, denotes the frequency of keyword addition operations, W is defined as the keyword collection, |W| denotes the number of keyword collections, m denotes the number of keywords, and denotes the collection of documents that contain a particular keyword .

Table 5.
A complexity comparison of our scheme with the existing schemes.
4. Security Analysis
We need to prove the following theorem.
Theorem 1.
If the pseudo-random functions satisfy the security conditions and the symmetric encryption scheme complies with the IND-CPA security standard while the homomorphic message authentication code has security, the BVUMU-DSSE scheme is said to be able to achieve forward and backward security.
Proof
Provenance: According to the threat model, the cloud server acts as a semi-honest attacker that steals sensitive information that should be kept confidential, despite performing operations according to the protocol specification. Assume that in a real scenario, challenger C responds to attacker A’s query with real data and algorithmic outputs; in the simulation scenario, simulator S generates an answer based on the information provided by leakage function L only. In the following, we will demonstrate, through a series of games, that the attacker is unable to differentiate between the environments in which it operates with non-negligible probability.
Game : This game is identical to the real world, i.e., we can treat it as if it were the real world, so we define .
Game : In this game, we assume that the system generates the keys for the columns by no longer calling the pseudo-random function H realistically, but by randomly selecting the values and depositing them in the key table. If column p has been interrogated, the simulator S reads the corresponding key from the key table directly; otherwise, it generates a new random value and updates the key table. Since the pseudo-random function is secure, it follows that the attacker A is unable to distinguish the two games and with non-negligible probability, or else it would be able to construct some other attacker , which would be able to invoke A to attack this pseudo-random function H. Therefore, we get ).
Game : The same operation as H is applied to the pseudo-random function P. As in the first game, if the attacker can distinguish the real pseudo-random function from P with indistinguishable probability, they can design a polynomial time algorithm to break its security assumption, so . With the same principle, we construct the game for the pseudo-random function and the game for the pseudo-random function . Then, we obtain and .
Game : This game is a modified update algorithm based on . Instead of performing the operations of the original update algorithm, the simulator S dynamically sets the corresponding keyword bitmap based on the leakage timestamp t, search result , search pattern and update operation. The bitmap of the queried keywords is generated according to the search result and the file position at the current moment, while the bitmap of the unqueried keywords is populated by random binary sequences, thus obtaining a ciphertext database EDB. When the ciphertext database EDB is updated, the simulator S adjusts the keyword update based on in the leakage function in the current state. Some keywords are not subject to the update operation. Adjust the bitmap based on the updated file order, thus ensuring the correct response to attacker A’s query both before and after the state update. In the following, we will prove four aspects that the attacker is unable to extract valid information from the encrypted database EDB and therefore cannot distinguish whether their interaction is still with the simulator S or with the challenger C.
- 1.
- The attacker is unable to extract any valid information from the encrypted file. Even if the columns in which the file is located are not displaced and the content of the file itself is not updated, the mechanism still guarantees the data confidentiality, which would otherwise break the IND-CPA security of the symmetric encryption scheme.
- 2.
- The probability of using the key for keyword to decrypt other keywords is negligible, because the decryption key is bound to a specific keyword and the corresponding bitmap state, which makes it difficult for an attacker to decrypt keyword ′ using the key for keyword . If such an attack succeeds, it will violate the authentication of the homomorphic message authentication code and the IND-CPA security of the symmetric encryption scheme at the same time.
- 3.
- Before and after the system update, the attacker cannot extract any data related to the keyword from the encrypted index; otherwise, it will violate the IND-CPA security property of the symmetric encryption scheme. If the attacker launches multiple queries for the same keyword, it is assumed that the two search keys are and , respectively. However, due to the synchronization change of the bitmap caused by the file sorting update, the attacker who does not hold the latest key cannot retrieve the updated data, and the key generated at the previous moment is invalid for the new version of data retrieval; otherwise, the authentication of the homomorphic message authentication code will be violated.
- 4.
- If the attacker A has the computational key , due to the difference label being transmitted through the public key encryption mechanism, this results in the attacker’s access being revoked and not able to obtain this updated difference label, thus losing the ability to generate the latest key with the ability to retrieve the updated data; otherwise, it will threaten the security of the public key encryption system.
Therefore, the attacker is unable to recognize the difference between the two games (, ) with non-negligible probability, thus satisfying . Since corresponds exactly to the environment generated by the simulator S through the leakage function, it can be obtained that .
Combining the above analyses, it finally follows that , where is a negligible function. It can be proved that the BVUMU-DSSE scheme has security in the L-adaptive security model. In addition, since the amount of information in the leakage function is strictly limited to the forward and backward security framework, it can be further inferred that the BVUMU-DSSE scheme satisfies the forward and backward security requirements.
The proof is complete. □
5. Scheme Simulation Experiment
This section focuses on analyzing and comparing the efficiency of the BVUMU-DSSE scheme with other existing schemes through simulation experiments, so as to prove that its performance is feasible in practical applications. Since the MFS [37] scheme is highly compatible with the proposed architecture in this study in terms of functionality and considering that its efficiency is significantly better than most of the existing schemes, the next simulation experiments of the BVUMU-DSSE scheme will choose the MFS [37] scheme as the benchmark comparison object.
5.1. Experimental Environment
In this subsection, the experimental equipment is configured as follows. We use a Linux system with a 2.4 GHz Intel Core i7 processor (Intel, Guangzhou, China), with 16 GB of RAM, running the Windows 10 operating system. This hardware environment provides standardized test benchmarks for scheme performance evaluation. In terms of algorithm implementation, the hash operation in the scheme is implemented using the HMAC module, the symmetric encryption and decryption is implemented using the AES algorithm, the public key encryption scheme is based on the RSA protocol, the bilinear pair operation is implemented using the 80-bit security parameter, and the length of the ciphertext is fixed at 512 bits. The above parameter settings ensure that the experimental results are reproducible and horizontally comparable.
5.2. Comparison of Performance Evaluation
In this subsection, we compare the performance of the BVUMU-DSSE scheme with the MFS [37] scheme.
The computational complexity of the index construction phase is positively correlated with the amount of keyword–document identifier association data, and the processing efficiency of the MFS scheme is directly affected by this parameter. The experiments set the initial data size as 500,000 sets of keyword–document identifier mapping relationships (k = ), the BVUMU-DSSE scheme adopts a test environment with a fixed document base of , and the average number of keyword associations in a single document is 50. Comparison and analysis of the index construction under the keyword sizes from 1 × to 1 × show the difference in time overhead. The results, displayed in Figure 3, show that the index construction efficiency of BVUMU-DSSE is significantly higher than that of the MFS scheme, mainly due to the fact that the latter needs to perform bilinear pair operations. Both schemes use the AES algorithm to realize document encryption, and the test document base maintains experimental consistency. The index construction time and keyword size show a linear growth relationship.
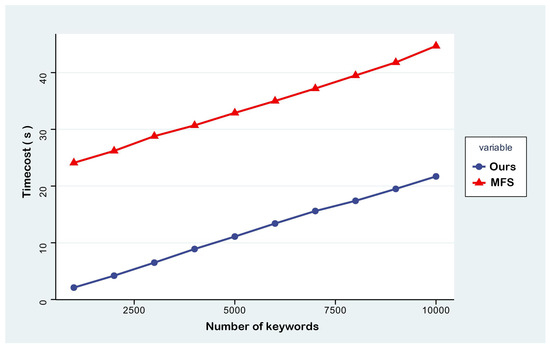
Figure 3.
Index generation time cost.
In terms of trapdoor generation efficiency, the trapdoor generation process of the MFS scheme relies on the cooperative computing resources of the proxy server. In order to accurately evaluate the total system time consumed, the computation of the cloud server is also included in the test scope. Tests for 1k to 10k trapdoor generation operations show that the trapdoor generation mode of BVUMU-DSSE is categorized into two computation paths according to the update status: a single public key encryption operation is required when there is no update, and homomorphic message authentication code computation is required to be superimposed when there is an update. The results are shown in Figure 4: the trapdoor generation efficiency of BVUMU-DSSE without trapdoor update operation is superior to the MFS scheme.
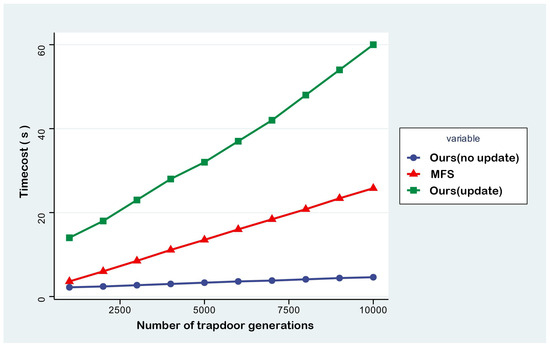
Figure 4.
Trapdoor generation time cost.
In terms of ciphertext retrieval efficiency, this study continuously examines two scenarios of the FBM-DSSE scheme in the presence or absence of updates. The horizontal axis of the MFS scheme characterizes the total number of documents returned for a query keyword, which is expressed as the retrieval of a single keyword, w, covering 100–1000 (keyword–document ID) combinations. The BVUMU-DSSE scheme corresponds to retrieving 100–1000 independent keywords, a feature that originates from the design principle that its bitmap indexing structure can obtain all the matching results through a single search. The experimental results are shown in Figure 5, which indicate that the BVUMU-DSSE scheme has better retrieval performance, and its execution efficiency is significantly better than the MFS scheme under the same data size.
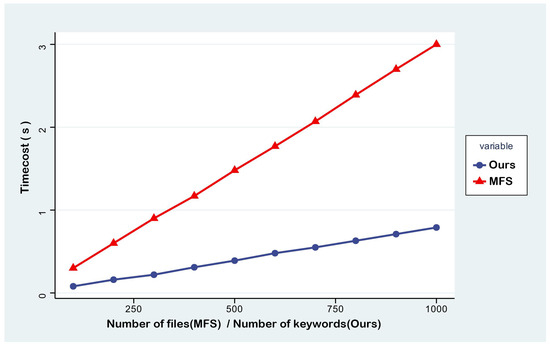
Figure 5.
Update time cost.
In terms of index updating, a comparison of the time overheads of the two schemes when implementing an extension equivalent to the existing index capacity is shown in Figure 6. The BVUMU-DSSE scheme needs to extend 1k to 10k keywords, and the overall time consumed exceeds the initial index generation phase due to the need to re-construct the keyword global mapping relationships. In contrast, the MFS scheme continuously appends 500k sets of (keyword–document ID) pairings, and the range of the corresponding keyword numbers is kept at 1k to 10k sets, which results in the time consumption being basically the same as that of the index creation cycle, since the updating mechanism of the scheme is little affected by the existing indexes. However, the experimental data show that the BVUMU-DSSE scheme still outperforms the MFS scheme.
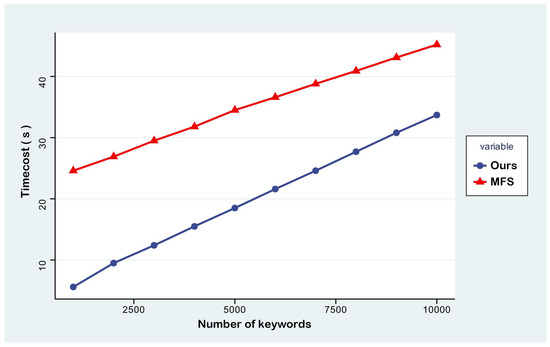
Figure 6.
Search time cost.
Comprehensive performance analysis shows that compared with the existing verifiable multi-user dynamic searchable schemes, this scheme achieves significant optimization in terms of computational resource consumption, transmission load, and storage requirements, which makes it more practical and efficient in multi-user application scenarios.
6. Conclusions
Facing the demand of dynamic encrypted data sharing, this study builds a security control system for dynamic multi-user scenarios, covering user rights’ management, ciphertext retrieval and dynamic update functions. In order to realize the verifiable dynamic update of encrypted data (which needs to satisfy the dual constraints of forward security and backward security), we need to simultaneously solve the security access control and privilege recovery mechanism of the authorized users on the incremental data under the security constraints. This study builds an index architecture with a state tracking capability by means of bitmap structure and homomorphic message authentication code technology, adopts key dynamic updating mechanism to synchronize forward and backward security and fine-grained privilege control, and utilizes blockchain technology to assist in completing the bidirectional authentication between the cloud server and the users.
However, some technical bottlenecks are found in the research process that still need to be explored in depth:
- 1.
- This study is currently limited to a single keyword search mode. In order to improve the applicability of practical scenarios, it is necessary to explore the expansion of search function sets in a multi-user collaborative environment, such as the support of Boolean logic composite queries, numerical range searches, and fuzzy matching based on edit distance and other core functions. Such extensions are of key value for medical data analysis, financial transaction auditing, and other scenarios, and new indexing structures need to be designed under the premise of ensuring forward security, such as combining Bloom filters and range trees to realize efficient range queries.
- 2.
- This study focuses on the dynamic data sharing problem under the one-to-many authorization paradigm. In the future, it is necessary to further explore the data sharing technology of many-to-many collaboration scenarios. At the permission management level, we need to construct a fine-grained permission control mechanism based on attribute encryption and optimize the security and performance of the scheme to promote the practical application of the scheme in distributed cloud environments. In addition, we are committed to exploring an integrated searchable encryption scheme that supports multimodal retrieval, data aggregation, and secure sharing. For example, in medical data sharing scenarios, we need to design encrypted retrieval protocols that support fuzzy matching and statistical analysis of gene sequences. This kind of research will advance searchable encryption technology from theoretical models to practical engineering applications.
Author Contributions
Conceptualization, Z.L.; methodology, Z.L.; software, Z.L.; validation, Z.L.; formal analysis, Z.L.; investigation, Z.L.; resources, Z.L.; data curation, Z.L.; writing—original draft preparation, Z.L.; writing—review and editing, Z.L. and B.W.; visualization, Z.L.; supervision, Z.L. and B.W.; project administration, Z.L. and B.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| PRF | Pseudo-random Function |
| DSSE | Dynamic Symmetric Searchable Encryption |
| HMAC | Homomorphic Message Authentication Code |
References
- Zhang, L.; Meng, X.; Choo, K.K.R.; Zhang, Y.; Dai, F. Privacy-preserving cloud establishment and data dissemination scheme for vehicular cloud. IEEE Trans. Dependable Secur. Comput. 2018, 17, 634–647. [Google Scholar] [CrossRef]
- Manthiramoorthy, C.; Khan, K.M.S. Comparing several encrypted cloud storage platforms. Int. J. Math. Stat. Comput. Sci. 2024, 2, 44–62. [Google Scholar] [CrossRef]
- Zhang, Q.; Cheng, L.; Boutaba, R. Cloud computing: State-of-the-art and research challenges. J. Internet Serv. Appl. 2010, 1, 7–18. [Google Scholar] [CrossRef]
- Shi, H.; Niu, L.; Sun, J. Construction of industrial internet of things based on MQTT and OPC UA protocols. In Proceedings of the 2020 IEEE International Conference on Artificial Intelligence and Computer Applications (ICAICA), Dalian, China, 27–29 June 2020; pp. 1263–1267. [Google Scholar]
- Ahsan, M.M.; Ali, I.; Bin Idris, M.Y.I.; Imran, M.; Shoaib, M. Countering statistical attacks in cloud-based searchable encryption. Int. J. Parallel Program. 2020, 48, 470–495. [Google Scholar] [CrossRef]
- Boneh, D.; Di Crescenzo, G.; Ostrovsky, R.; Persiano, G. Public key encryption with keyword search. In Proceedings of the International Conference on the Theory and Applications of Cryptographic Techniques, Interlaken, Switzerland, 2–6 May 2004; Springer: Berlin/Heidelberg, Germany, 2004; pp. 506–522. [Google Scholar]
- Abdul-Hussein, M.K.; ALRikabi, H.T. Secured Transfer and Storage Image Data for Cloud Communications. Int. J. Online Biomed. Eng. 2023, 19, 4. [Google Scholar]
- Kamara, S.; Papamanthou, C.; Roeder, T. Dynamic searchable symmetric encryption. In Proceedings of the 2012 ACM Conference on Computer and Communications Security, Raleigh, NC, USA, 16–18 October 2012; pp. 965–976. [Google Scholar]
- Kamara, S.; Papamanthou, C. Parallel and dynamic searchable symmetric encryption. In Financial Cryptography and Data Security: Proceedings of the 17th International Conference, FC 2013, Okinawa, Japan, 1–5 April 2013; Revised Selected Papers 17; Springer: Berlin/Heidelberg, Germany, 2013; pp. 258–274. [Google Scholar]
- Song, D.X.; Wagner, D.; Perrig, A. Practical techniques for searches on encrypted data. In Proceedings of the 2000 IEEE Symposium on Security and Privacy, S&P, Berkeley, CA, USA, 14–17 May 2000; pp. 44–55. [Google Scholar]
- Curtmola, R.; Garay, J.; Kamara, S.; Ostrovsky, R. Searchable symmetric encryption: Improved definitions and efficient constructions. In Proceedings of the 13th ACM Conference on Computer and Communications Security, Alexandria, VA, USA, 30 October–3 November 2006; pp. 79–88. [Google Scholar]
- Fiat, A.; Naor, M. Broadcast encryption. In Advances in Cryptology—CRYPTO’93: Proceedings of the 13th Annual International Cryptology Conference Santa Barbara, CA, USA, 22–26 August 1993; Proceedings 13; Springer: Berlin/Heidelberg, Germany, 1994; pp. 480–491. [Google Scholar]
- Bao, F.; Deng, R.H.; Ding, X.; Yang, Y. Private query on encrypted data in multi-user settings. In Proceedings of the International Conference on Information Security Practice and Experience, Sydney, Australia, 21–23 April 2008; Springer: Berlin/Heidelberg, Germany, 2008; pp. 71–85. [Google Scholar]
- Jarecki, S.; Jutla, C.; Krawczyk, H.; Rosu, M.; Steiner, M. Outsourced symmetric private information retrieval. In Proceedings of the 2013 ACM SIGSAC conference on Computer & Communications Security, Berlin, Germany, 4–8 November 2013; pp. 875–888. [Google Scholar]
- Sun, S.F.; Liu, J.K.; Sakzad, A.; Steinfeld, R.; Yuen, T.H. An efficient non-interactive multi-client searchable encryption with support for boolean queries. In Computer Security–ESORICS 2016: Proceedings of the 21st European Symposium on Research in Computer Security, Heraklion, Greece, 26–30 September 2016; Proceedings, Part I 21; Springer International Publishing: Cham, Switzerland, 2016; pp. 154–172. [Google Scholar]
- Cash, D.; Jarecki, S.; Jutla, C.; Krawczyk, H.; Roşu, M.C.; Steiner, M. Highly-scalable searchable symmetric encryption with support for boolean queries. In Advances in Cryptology–CRYPTO 2013: Proceedings of the 33rd Annual Cryptology Conference, Santa Barbara, CA, USA, 18–22 August 2013; Proceedings, Part I; Springer: Berlin/Heidelberg, Germany, 2013; pp. 353–373. [Google Scholar]
- Popa, R.A.; Zeldovich, N. Multi-Key Searchable Encryption. Cryptology ePrint Archive. 2013. Available online: https://eprint.iacr.org/2013/508 (accessed on 5 May 2025).
- Hamlin, A.; Shelat, A.; Weiss, M.; Wichs, D. Multi-key searchable encryption, revisited. In Public-Key Cryptography—PKC 2018: Proceedings of the 21st IACR International Conference on Practice and Theory of Public-Key Cryptography, Rio de Janeiro, Brazil, 25–29 March 2018; Proceedings, Part I 21; Springer International Publishing: Cham, Switzerland, 2018; pp. 95–124. [Google Scholar]
- Ishai, Y.; Pandey, O.; Sahai, A. Public-coin differing-inputs obfuscation and its applications. In Theory of Cryptography: Proceedings of the 12th Theory of Cryptography Conference, TCC 2015, Warsaw, Poland, 23–25 March 2015; Proceedings, Part II 12; Springer: Berlin/Heidelberg, Germany, 2015; pp. 668–697. [Google Scholar]
- Patel, S.; Persiano, G.; Yeo, K. Symmetric searchable encryption with sharing and unsharing. In Proceedings of the European Symposium on Research in Computer Security, Barcelona, Spain, 3–7 September 2018; Springer International Publishing: Cham, Switzerland, 2018; pp. 207–227. [Google Scholar]
- Wang, Y.; Papadopoulos, D. Multi-user collusion-resistant searchable encryption with optimal search time. In Proceedings of the 2021 ACM Asia Conference on Computer and Communications Security, Virtual Event, 7–11 May 2021; pp. 252–264. [Google Scholar]
- Wang, Y.; Papadopoulos, D. Multi-user collusion-resistant searchable encryption for cloud storage. IEEE Trans. Cloud Comput. 2023, 11, 2993–3008. [Google Scholar] [CrossRef]
- Cash, D.; Jaeger, J.; Jarecki, S.; Jutla, C.; Krawczyk, H.; Roşu, M.C.; Steiner, M. Dynamic Searchable Encryption in Very-Large Databases: Data Structures and Implementation. Cryptology ePrint Archive. 2014. Available online: https://www.ndss-symposium.org/ndss2014/ndss-2014-programme/dynamic-searchable-encryption-very-large-databases-data-structures-and-implementation/ (accessed on 5 May 2025).
- Stefanov, E.; Papamanthou, C.; Shi, E. Practical Dynamic Searchable Encryption with Small Leakage. Cryptology ePrint Archive. 2013. Available online: https://eprint.iacr.org/2013/832 (accessed on 5 May 2025).
- Wu, H.; Song, R.; Lei, K.; Xiao, B. Slicer: Verifiable, secure and fair search over encrypted numerical data using blockchain. In Proceedings of the 2022 IEEE 42nd International Conference on Distributed Computing Systems (ICDCS), Bologna, Italy, 10–13 July 2022; pp. 1201–1211. [Google Scholar]
- Zhang, D.; Wang, S.; Zhang, Q.; Zhang, Y. Attribute based conjunctive keywords search with verifiability and fair payment using blockchain. IEEE Trans. Serv. Comput. 2023, 16, 4168–4182. [Google Scholar] [CrossRef]
- Ghareh Chamani, J.; Papadopoulos, D.; Papamanthou, C.; Jalili, R. New constructions for forward and backward private symmetric searchable encryption. In Proceedings of the 2018 ACM SIGSAC Conference on Computer and Communications Security, Toronto, ON, Canada, 15–19 October 2018; pp. 1038–1055. [Google Scholar]
- Guo, Y.; Zhang, C.; Jia, X. Verifiable and forward-secure encrypted search using blockchain techniques. In Proceedings of the ICC 2020–2020 IEEE International Conference on Communications (ICC), Dublin, Ireland, 7–11 June 2020; pp. 1–7. [Google Scholar]
- He, K.; Chen, J.; Zhou, Q.; Du, R.; Xiang, Y. Secure dynamic searchable symmetric encryption with constant client storage cost. IEEE Trans. Inf. Forensics Secur. 2020, 16, 1538–1549. [Google Scholar] [CrossRef]
- Xu, P.; Susilo, W.; Wang, W.; Chen, T.; Wu, Q.; Liang, K.; Jin, H. ROSE: Robust searchable encryption with forward and backward security. IEEE Trans. Inf. Forensics Secur. 2022, 17, 1115–1130. [Google Scholar] [CrossRef]
- Katz, J.; Lindell, Y. Introduction to Modern Cryptography: Principles and Protocols; Chapman and Hall/CRC: Boca Raton, FL, USA, 2007. [Google Scholar]
- Catalano, D.; Fiore, D. Practical homomorphic message authenticators for arithmetic circuits. J. Cryptol. 2018, 31, 23–59. [Google Scholar] [CrossRef]
- Chang, Y.C.; Mitzenmacher, M. Privacy preserving keyword searches on remote encrypted data. In Proceedings of the International Conference on Applied Cryptography and Network Security, New York, NY, USA, 7–10 June 2005; Springer: Berlin/Heidelberg, Germany, 2005; pp. 442–455. [Google Scholar]
- Bost, R.; Minaud, B.; Ohrimenko, O. Forward and backward private searchable encryption from constrained cryptographic primitives. In Proceedings of the 2017 ACM SIGSAC Conference on Computer and Communications Security, Dallas, TX, USA, 30 October–3 November 2017; pp. 1465–1482. [Google Scholar]
- Li, J.; Huang, Y.; Wei, Y.; Lv, S.; Liu, Z.; Dong, C.; Lou, W. Searchable symmetric encryption with forward search privacy. IEEE Trans. Dependable Secur. Comput. 2019, 18, 460–474. [Google Scholar] [CrossRef]
- Zuo, C.; Sun, S.F.; Liu, J.K.; Shao, J.; Pieprzyk, J. Dynamic searchable symmetric encryption with forward and stronger backward privacy. In Proceedings of the European Symposium on Research in Computer Security, Luxembourg, 23–27 September 2019; Springer International Publishing: Cham, Switzerland, 2019; pp. 283–303. [Google Scholar]
- Wang, Q.; Guo, Y.; Huang, H.; Jia, X. Multi-user forward secure dynamic searchable symmetric encryption. In Network and System Security: Proceedings of the 12th International Conference, NSS 2018, Hong Kong, China, 27–29 August 2018; Proceedings 12; Springer International Publishing: Cham, Switzerland, 2018; pp. 125–140. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).