From Lagrange to Bernstein: Generalized Transfinite Elements with Arbitrary Nodes
Abstract
1. Introduction
2. General Formulation
2.1. State of the Art
2.2. Extension of the Projectors
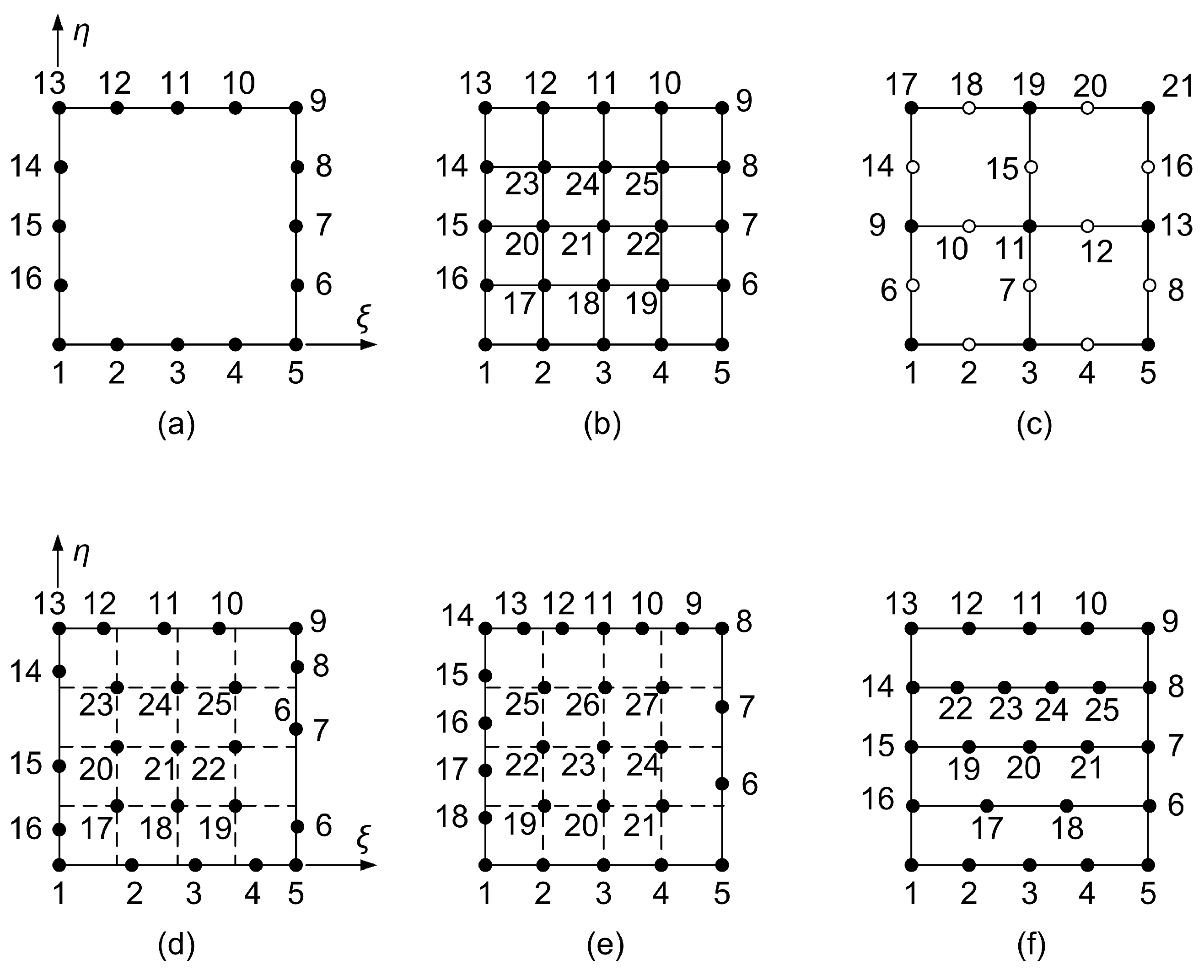
3. Construction of Transfinite Elements
- If a nodal point lies on the boundary but neither coincides with any of the four patch corners nor corresponds to an intersection between the boundary and another orthogonal station, then only one of the three associated projections remains active.
- If the nodal point lies at the intersection of two stations, and at least one of them shares the same discretization as the blending functions, then only one projection operator remains active.
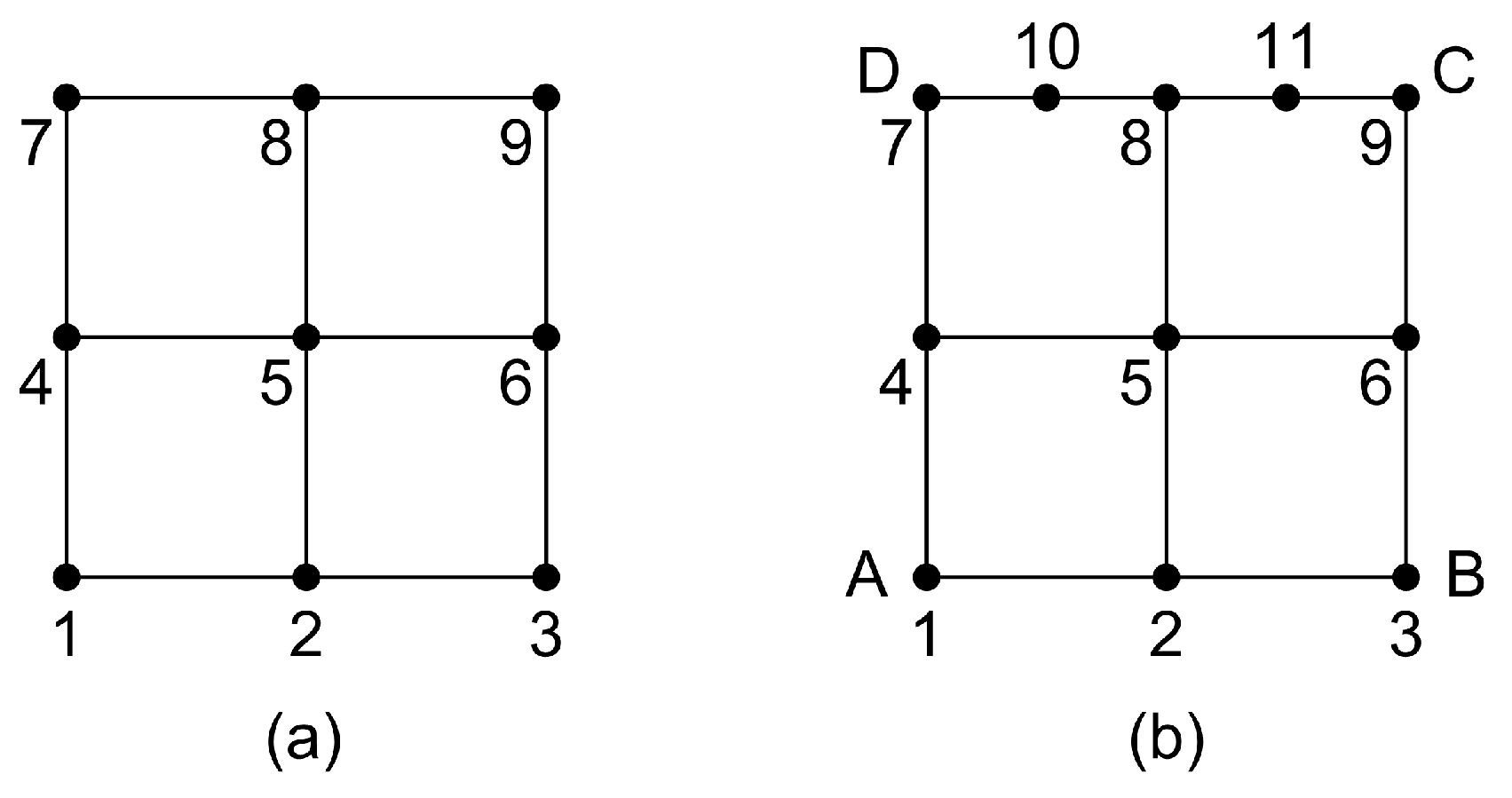
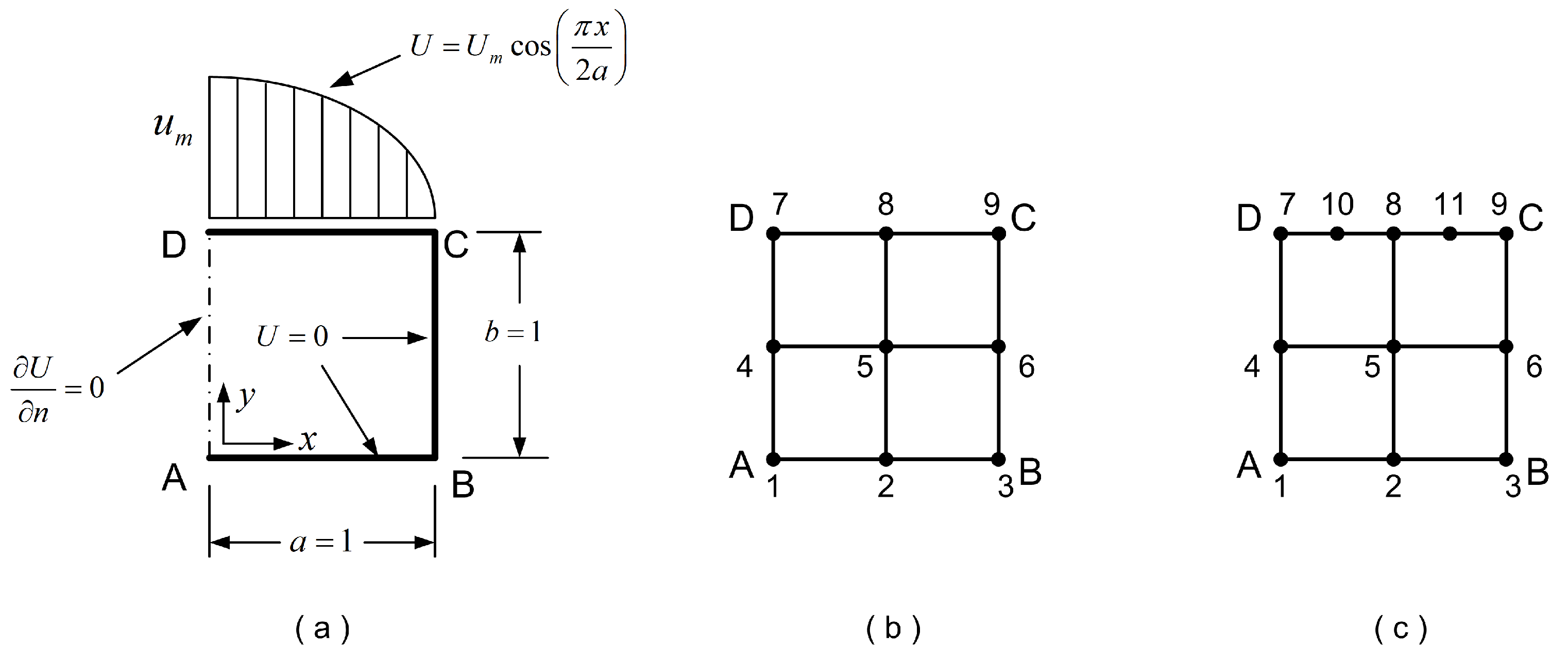
3.1. Tensor Product 9-Node Element
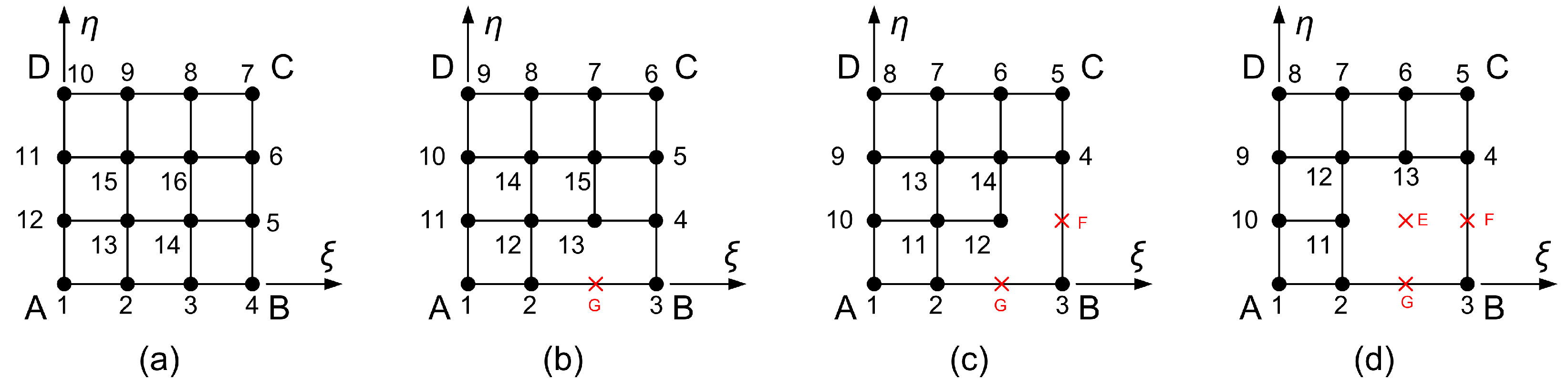
3.2. Transfinite 11-Node Element Described by Only One Projector
3.3. Element Formulation Based on Lagrange Polynomials
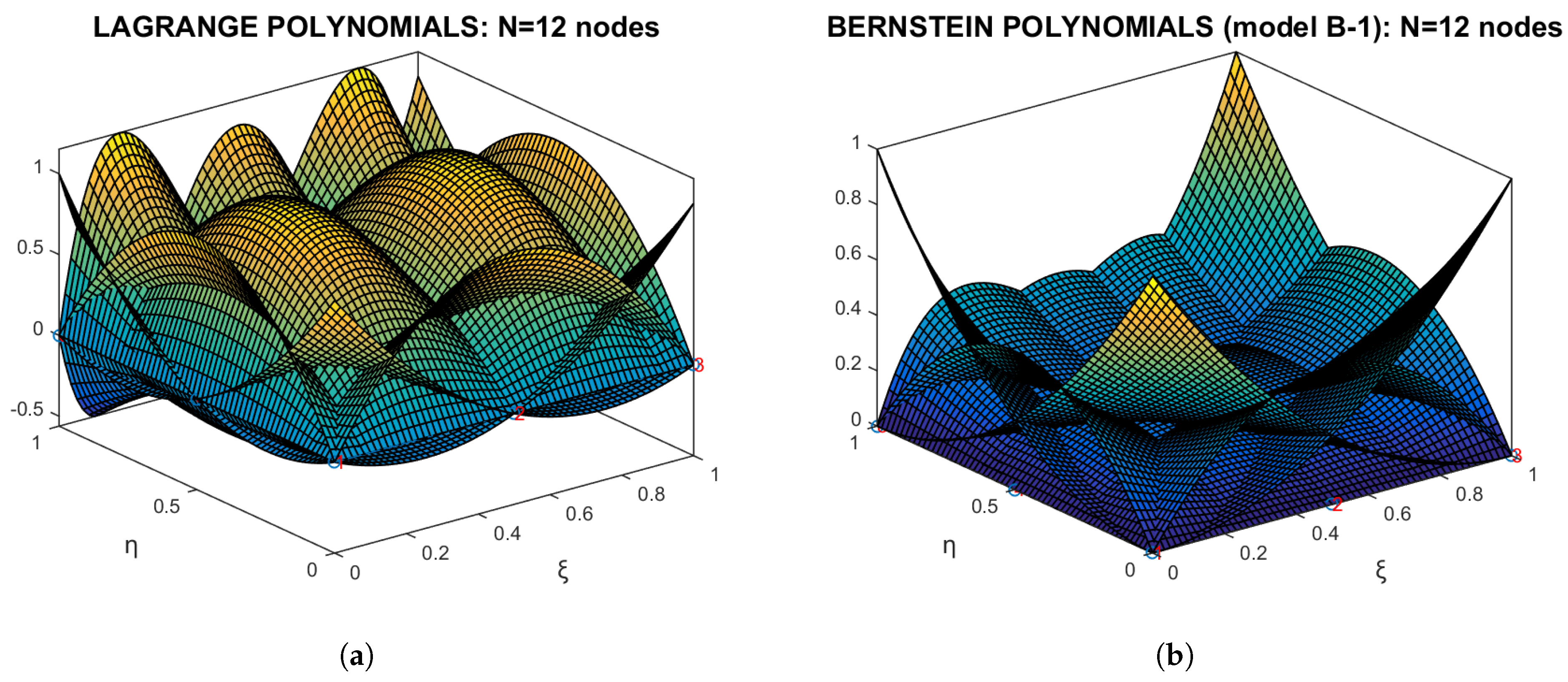
3.4. Element Formulation Based on Bernstein Polynomials
3.4.1. First Approach (Model B-1): Straight Forward (Blind) Replacement
- The functions are quadratic (degree ) and thus will be blindly substituted by the following three quadratic Bernstein polynomials: and .
- The functions are quadratic and thus will be blindly substituted by the following three quadratic Bernstein polynomials: , and .
- The functions are quartic (degree ) and thus will be blindly substituted by the following five quartic Bernstein polynomials: , and .
3.4.2. Second Approach (Model B-2): Accurate Process of Transfinite Interpolation Formula
- Moreover, the extreme nodal values are expressed in terms of the boundary coefficients, considering the transpose inverse of Equation (31) (see also Appendix A), i.e.,whence
- The internal nodal value is left as is.
- They both use the same univariate interpolation (Bernstein polynomials) on the four edges of the patch.
- Model B-1 considers Bernstein polynomials for blending functions.
- Model B-2 considers Lagrange-transformed-to-Bernstein polynomials for blending functions.
3.5. Proposed Automated Procedure for Arbitrary-Noded Transfinite Elements
3.5.1. Lagrange Polynomial Formulation
- Those shape functions associated with the boundary nodes which are intermediate to an edge are given in terms of trial and blending functions. For example, for the i-th nodal point on the edge (associated with blending function ), we have the following:where is the i-th Lagrange polynomial of degree on the edge .
- The shape functions associated with the four corner nodes are influenced by all the three projectors. For example, for the corner A, we have the following:
- Those shape functions associated with the internal nodes (at the position () are given in terms of tensor products of blending functions as follows:
3.5.2. Bernstein Polynomial Formulation (Model B-2)
3.6. 27-Node Transfinite Element
3.6.1. Lagrange–Based Formulation
3.6.2. Bernstein–Based Formulation: Model B-1
3.6.3. Bernstein–Based Formulation: Model B-2
3.7. Concluding Remark
3.8. Transitional Transfinite Elemenets
- Tensor product elements.
- Classical elements with stations holding a standard discretization per direction.
- Distorted tensor product elements.
- Elements with internal nodes in the pattern of a tensor product and arbitrary-noded boundaries.
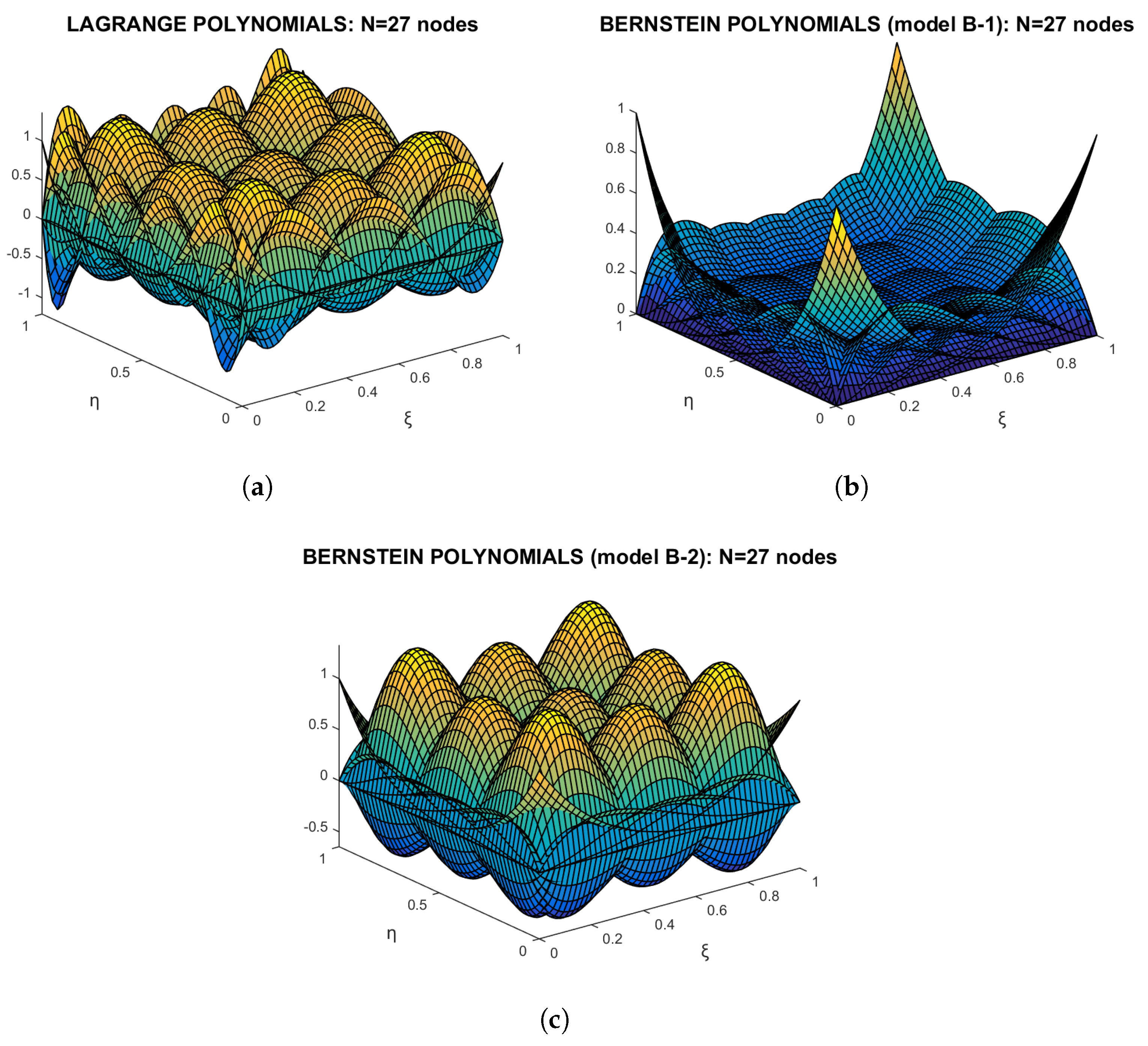
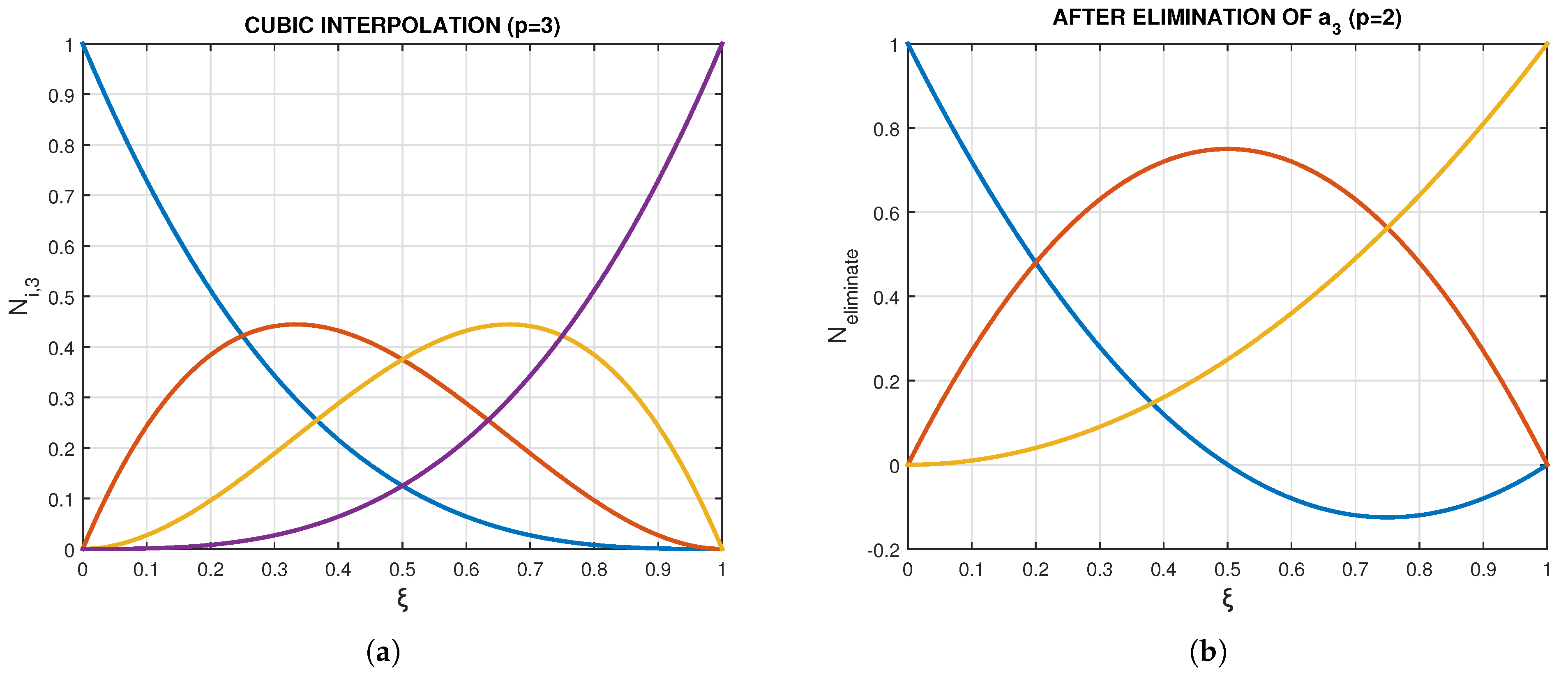
4. Reduction of Bernstein Polynomials
Non-Uniform Lagrange Polynomials
5. T-Mesh Elements
5.1. Simplified T-Elements
5.2. Boundary Nodes
5.2.1. The 13-, 14- and 15-Node Elements
5.2.2. 14-Node Element
5.2.3. 13-Node Element
5.3. Internal Nodes
- If the objective is to construct a Lagrange-based polynomial model, one begins with a tensor product of Lagrange polynomials, which is subsequently modified—through constraints—to account for any missing internal nodes. This issue has been previously discussed in full detail in Ref. [10].
- If the objective is to construct a Bernstein-based model, one begins with a tensor product of Bernstein polynomials, which is subsequently modified to account for any missing internal nodes. This is the main topic of this paper.
5.3.1. Lagrange Polynomials
- The elimination of the middle node along the horizontal station 16-17-18-6 (Figure 13b) is made either considering a non-uniform polynomial of degree 3 for which the transfinite interpoltion is , or by the following constraint:
- The elimination of the middle node along the vertical station (made of nodes 3-20-23-11) is made either considering a non-uniform polynomial of degree 3 for which the transfinite approximation is or using the following constraint:
- Alternatively, we may consider the average of the above two considerations for the eliminated DOF as follows:
5.3.2. Bernstein Polynomials
- When the bottom (horizontal) layer is considered as a non-uniform polynomial of degree 3, the approximation is . Alternatively, the associated constraint is as follows:
- When the middle (vertical) layer is considered as a non-uniform polynomial of degree 3, the approximation is . Alternatively, the associated constraint is as follows:
- When the average of the above two approximations is considered, the associated constraint is as follows:
6. Results
6.1. Small-Size Models with Fully Populated Interior
- Regarding the tensor product 9-node element (Figure 14b), using either Lagrange or Bernstein polynomials, the calculated error was found to be the same, equal to (see Table 2). The only difference in the two numerical solutions was the condition number of the equations’ matrix (of size ), which was found equal to 41.8 and 55.3 for Lagrange and Bernstein polynomials, respectively.
- Regarding the non-tensor product 11-node element (Figure 14c), the numerical results for the plate with cosine-like temperature, are shown in the last line of Table 2. One may observe that the Bernstein-based model B-2 (Equation (40)) is equivalent to the Lagrange-based model, where the Bernstein-based model B-1 (Equation (29)) is marginally better.
- Regarding the non-tensor product 12-node element (Figure 7a), the difference between Lagrange and Bernstein polynomials (model B-1) is minor, and thus, we attempted to develop model B-2.
- In all cases, as the model increases the accuracy improves.
6.2. Medium-Size Models
- When the bottom (horizontal) layer (made of nodes 16-17-18-6) is considered as a non-uniform polynomial of degree 3, the transfinite approximation becomes , and the error of the numerical solution is . The same result is obtained when inserting the constraint given by Equation (101) into the tensor product of Lagrange polynomials.
- When the middle (vertical) layer (made of nodes 3-20-23-11) is considered as a non-uniform polynomial of degree 3, the transfinite approximation is , and the numerical result is . The same result is obtained when inserting the constraint given by Equation (102) into the tensor product of Lagrange polynomials.
- When the average of the above two considerations was taken for the eliminated DOF according to Equation (103), the result was .
- Regarding tensor product solution (25 nodes), Lagrange polynomials led to the same numerical error equal to .
- When the bottom (horizontal) layer is considered as a non-uniform polynomial of degree 3, the approximation is , and the result is . The same result is obtained when inserting the constraint () of Equation (104) into the tensor product.
- When the middle (vertical) layer is considered as a non-uniform polynomial of degree 3, the approximation is and the result is . The same result is obtained when inserting the constraint () of Equation (105) into the tensor product.
- When the average of the above two considerations was taken for the eliminated DOF, i.e., () of Equation (106), the result was .
- Regarding tensor product solution (25 nodes), Bernstein polynomials led to the same numerical error equal to .
6.3. Large-Size Model
7. Discussion
8. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Substitution of Lagrange by Bernstein Polynomials on an Edge
Appendix B. Examples of a Single Constraint in Bernstein Polynomials
Appendix B.1. Quadratic
Appendix B.2. Cubic
Appendix B.3. Quartic
Appendix C. General Expression for a Constraint on Bernstein Polynomials
Appendix D. MATLAB Script for the Coefficient of xn
- clear all
- clc
- syms x
- n = 5; % You can change this to any degree
- % Define symbolic coefficients a_0, ..., a_n
- a = sym(’a’, [1 n+1]);
- % Initialize the full Bernstein sum
- f = 0;
- for i = 0:n
- Bi = nchoosek(n, i) ∗ x^i ∗ (1 - x)^(n - i); % B_i^n(x)
- f = f + a(i+1) ∗ Bi;
- end
- % Expand and collect terms
- f_expanded = expand(f);
- f_collected = collect(f_expanded, x);
- % Extract coefficient of x^n
- coeff_xn = coeffs(f_collected, x);
- % Get max power of x
- power_list = feval(symengine, ’degree’, f_collected, x);
- % Display coefficient of x^n
- fprintf(’Coefficient of x^%d:\n’, n);
- disp(coeff_xn(end)); % The last term corresponds to x^n
Appendix E. Basis Functions
Appendix E.1. Lagrange Polynomials
Appendix E.2. Bernstein Polynomials (Model B-1)
Appendix E.3. Bernstein Polynomials (Model B-2)
Appendix F. MATLAB Code for Basis Functions (Model B-2)
- %**************************************************************
- % SYMBOLIC MANIPULATION OF BASIS FUNCTIONS FOR 46-NODE T-MESH
- %**************************************************************
- clear all; clc;
- U = sym(’U’, [81 1]); %Nodal values
- A = sym(’A’, [81 1]); %Coefficients
- for k = 1:81 %For older MATLAB versions such as R2014
- assume(U(k), ’real’);
- assume(A(k), ’real’);
- end
- % BERNSTEIN POLYNOMIALS:
- syms B1x B2x B3x B4x B5x B6x B7x B8x B9x B1y B2y B3y B4y B5y B6y B7y B8y B9y
- syms Up Us Ap As %primary and secondary sets of variables.
- %--------------------------------------------------------------------
- % TRANSFORMATION MATRIX [T] (of size 81x81) in local numbering:
- nx=8; ny=8; %uniform subdivisions in x- and y-directions.
- dcs=1/nx; dht=1/ny; %steps
- nc1=0; %counter-1
- for j=1:9
- ht=(j-1)∗dht;
- for i=1:9
- nc1=nc1+1;
- cs=(i-1)∗dcs;
- BxVector(1,1:9)=[(1-cs)^8 , 8∗(1-cs)^7∗cs , 28∗(1-cs)^6∗cs^2,...
- 56∗(1-cs)^5∗cs^3, 70∗(1-cs)^4∗cs^4, 56∗(1-cs)^3∗cs^5,...
- 28∗(1-cs)^2∗cs^6, 8∗(1-cs) ∗cs^7, cs^8];
- ByVector(1,1:9)=[(1-ht)^8 , 8∗(1-ht)^7∗ht , 28∗(1-ht)^6∗ht^2,...
- 56∗(1-ht)^5∗ht^3, 70∗(1-ht)^4∗ht^4, 56∗(1-ht)^3∗ht^5,...
- 28∗(1-ht)^2∗ht^6, 8∗(1-ht) ∗ht^7, ht^8];
- nc2=0; %counter-2
- for jj=1:9
- for ii=1:9
- nc2=nc2+1;
- T(nc1,nc2)=BxVector(1,ii)∗ByVector(1,jj); %Eq.(109)
- end
- end
- end
- end
- %---INVERSE MATRIX:
- Tinv = inv(T);
- %----------------------------------------------------------------------
- %% CONSTRAINTS:
- U(51)= [-3/70 2/7 -4/5 6/5 2/5 -2/35 1/70]∗U([1 2 3 4 5 6 7]); %Station H1
- U(61)= [1/14 -3/7 1 -1 1 3/7 -1/14] ∗U([1 2 3 4 5 6 7]); %Station H1
- U(52)= [-3/70 2/7 -4/5 6/5 2/5 -2/35 1/70] ∗U([8 9 10 11 12 13 14]);
- U(62)= [1/14 -3/7 1 -1 1 3/7 -1/14] ∗U([8 9 10 11 12 13 14]);
- U(65)= [-9/28 15/14 1/2 -3/7 5/28] ∗U([1 8 28 33 40]);
- U(67)= [-2/7 5/7 1 -5/7 2/7] ∗U([1 8 28 33 40]);
- U(69)= [-9/70 2/7 6/5 -4/7 3/14]∗U([1 8 28 33 40]);
- U(79)= [1/28 -1/14 1/2 5/7 -5/28] ∗U([1 8 28 33 40]);
- U(66)= [-9/28 15/14 1/2 -3/7 5/28] ∗U([2 9 29 34 41]);
- U(68)= [-2/7 5/7 1 -5/7 2/7] ∗U([2 9 29 34 41]);
- U(70)= [-9/70 2/7 6/5 -4/7 3/14]∗U([2 9 29 34 41]);
- U(80)= [1/28 -1/14 1/2 5/7 -5/28] ∗U([2 9 29 34 41]);
- U(54)=[-1/14 16/35 -6/5 8/5 2/5 -8/35 3/70]∗U([67 68 20 21 22 23 24]);
- U(55)=[-1/14 3/7 -1 1 1 -3/7 1/14]∗U([67 68 20 21 22 23 24]);
- U(53)= [-3/70 2/7 -4/5 6/5 2/5 -2/35 1/70]∗U([65 66 15 16 17 18 19]);
- U(63)= [1/14 -3/7 1 -1 1 3/7 -1/14] ∗U([65 66 15 16 17 18 19]);
- U(50)= [5/112 -2/7 3/4 5/8 -1/4 1/7 -3/112]∗U([40 41 42 43 44 45 46]);
- U(60)= [-3/112 1/7 -1/4 5/8 3/4 -2/7 5/112]∗U([40 41 42 43 44 45 46]);
- U(49)= [5/112 -2/7 3/4 5/8 -1/4 1/7 -3/112]∗U([33 34 35 36 37 38 39]);
- U(59)= [-3/112 1/7 -1/4 5/8 3/4 -2/7 5/112]∗U([33 34 35 36 37 38 39]);
- U(72)=[-3/14 8/7 -12/5 12/5 4/35 -3/70]∗U([7 14 19 24 39 46]);
- U(75)=[ -3/7 15/7 -4 3 3/7 -1/7 ]∗U([7 14 19 24 39 46]);
- U(78)=[-5/14 12/7 -3 2 6/7 -3/14]∗U([7 14 19 24 39 46]);
- U(71)=[-3/14 8/7 -12/5 12/5 4/35 -3/70]∗U([6 13 18 23 38 45]);
- U(74)=[ -3/7 15/7 -4 3 3/7 -1/7 ]∗U([6 13 18 23 38 45]);
- U(77)=[-5/14 12/7 -3 2 6/7 -3/14]∗U([6 13 18 23 38 45]);
- U(47)=[5/112 -2/7 3/4 5/8 -1/4 1/7 -3/112]∗U([69 70 25 26 27 71 72]);
- U(56)=[-3/112 1/7 -1/4 5/8 3/4 -2/7 5/112]∗U([69 70 25 26 27 71 72]);
- U(73)=[3/28 -5/7 2 -3 5/2 1/7 -1/28]∗U([61 62 63 22 27 37 44]);
- U(76)=[5/28 -8/7 3 -4 5/2 4/7 -3/28]∗U([61 62 63 22 27 37 44]);
- U(48)=[5/112 -2/7 3/4 5/8 -1/4 1/7 -3/112]∗U([79 80 31 32 76 77 78]);
- U(81)=[1/56 -1/7 1/2 -1 5/4 1/2 -1/7 1/56]∗U([51 52 53 54 26 32 36 43]);
- U64A=[5/112 -2/7 3/4 5/8 -1/4 1/7 -3/112]∗U([28 29 30 81 73 74 75]);
- U64B=[1/56 -1/7 1/2 -1 5/4 1/2 -1/7 1/56]∗U([4 11 16 21 47 48 49 50]);
- U(64)=1/2∗(U64A+U64B);
- U57A=[-3/112 1/7 -1/4 5/8 3/4 -2/7 5/112]∗U([28 29 30 81 73 74 75]);
- U57B=[3/28 -5/7 2 -3 5/2 1/7 -1/28]∗U([5 12 17 55 56 59 60]);
- U(57)=1/2∗(U57A+U57B);
- U57A=[-3/112 1/7 -1/4 5/8 3/4 -2/7 5/112]∗U([28 29 30 81 73 74 75]);
- U57B=[3/28 -5/7 2 -3 5/2 1/7 -1/28]∗U([5 12 17 55 56 59 60]);
- U57=1/2∗(U57A+U57B
- U58A=[-3/112 1/7 -1/4 5/8 3/4 -2/7 5/112]∗U([79 80 31 32 76 77 78]);
- U58B=[5/28 -8/7 3 -4 5/2 4/7 -3/28]∗U([5 12 17 55 56 59 60]);
- U(58)=1/2∗(U58A+U58B);
- %--- SPLIT [U] IN PRIMARY AND SECONDARY (Eq. (112)):
- Up = U(1:46); %primary
- Us = U(47:81); %secondary
- %--- SPLIT [A] IN PRIMARY AND SECONDARY (Eq. (112)):
- Ap = A(1:46); %primary
- As = A(47:81); %secondary
- %---DETERMINE THE [Su]-MATRIX, see Eq.(111):
- for j=1:35
- p = Us(j);
- [coeffs_list, terms] = coeffs(p, Up);
- % Ensure all coefficients are displayed, including zero
- coefficients = zeros(1, length(Up));
- for i = 1:length(terms)
- index = find(Up == terms(i));
- coefficients(index) = coeffs_list(i);
- end
- Su(j,1:46)=coefficients; %Eq.(111)
- end
- %----------------------------------------------------------
- %% BASED ON THE ABOVE VARIABLES Ui’s, FIND Ai’s:
- Ucolumn=[...
- U(1) U(2) U(3) U(4) U(51) U(5) U(61) U(6) U(7) ...
- U(8) U(9) U(10) U(11) U(52) U(12) U(62) U(13) U(14) ...
- U(65) U(66) U(15) U(16) U(53) U(17) U(63) U(18) U(19) ...
- U(67) U(68) U(20) U(21) U(54) U(55) U(22) U(23) U(24) ...
- U(69) U(70) U(25) U(47) U(26) U(56) U(27) U(71) U(72) ...
- U(28) U(29) U(30) U(64) U(81) U(57) U(73) U(74) U(75) ...
- U(79) U(80) U(31) U(48) U(32) U(58) U(76) U(77) U(78) ...
- U(33) U(34) U(35) U(49) U(36) U(59) U(37) U(38) U(39) ...
- U(40) U(41) U(42) U(50) U(43) U(60) U(44) U(45) U(46)];
- Acolumn=[...
- A(1) A(2) A(3) A(4) A(51) A(5) A(61) A(6) A(7) ...
- A(8) A(9) A(10) A(11) A(52) A(12) A(62) A(13) A(14) ...
- A(65) A(66) A(15) A(16) A(53) A(17) A(63) A(18) A(19) ...
- A(67) A(68) A(20) A(21) A(54) A(55) A(22) A(23) A(24) ...
- A(69) A(70) A(25) A(47) A(26) A(56) A(27) A(71) A(72) ...
- A(28) A(29) A(30) A(64) A(81) A(57) A(73) A(74) A(75) ...
- A(79) A(80) A(31) A(48) A(32) A(58) A(76) A(77) A(78) ...
- A(33) A(34) A(35) A(49) A(36) A(59) A(37) A(38) A(39) ...
- A(40) A(41) A(42) A(50) A(43) A(60) A(44) A(45) A(46)];
- %% APPLY Eq.(113), for ALL VARIABLES (PRIMARY & SECONDARY):
- %---H1 (Bottom horizontal isoline, at eta=0):
- A(1) =Tinv(1,1:81)∗Ucolumn.’;
- A(2) =Tinv(2,1:81)∗Ucolumn.’;
- A(3) =Tinv(3,1:81)∗Ucolumn.’;
- A(4) =Tinv(4,1:81)∗Ucolumn.’;
- A(51)=Tinv(5,1:81)∗Ucolumn.’;
- A(5) =Tinv(6,1:81)∗Ucolumn.’;
- A(61)=Tinv(7,1:81)∗Ucolumn.’;
- A(6) =Tinv(8,1:81)∗Ucolumn.’;
- A(7) ;=Tinv(9,1:81)∗Ucolumn.’;
- %---H2 (Second horizontal isoline measured from bottom):
- A(8) =Tinv(10,1:81)∗Ucolumn.’;
- A(9) =Tinv(11,1:81)∗Ucolumn.’;
- A(10)=Tinv(12,1:81)∗Ucolumn.’;
- A(11)=Tinv(13,1:81)∗Ucolumn.’;
- A(52)=Tinv(14,1:81)∗Ucolumn.’;
- A(12)=Tinv(15,1:81)∗Ucolumn.’;
- A(62)=Tinv(16,1:81)∗Ucolumn.’;
- A(13)=Tinv(17,1:81)∗Ucolumn.’;
- A(14)=Tinv(18,1:81)∗Ucolumn.’;
- %---H3 (Third horizontal isoline measured from bottom):
- A(65)=Tinv(19,1:81)∗Ucolumn.’;
- A(66)=Tinv(20,1:81)∗Ucolumn.’;
- A(15)=Tinv(21,1:81)∗Ucolumn.’;
- A(16)=Tinv(22,1:81)∗Ucolumn.’;
- A(53)=Tinv(23,1:81)∗Ucolumn.’;
- A(17)=Tinv(24,1:81)∗Ucolumn.’;
- A(63)=Tinv(25,1:81)∗Ucolumn.’;
- A(18)=Tinv(26,1:81)∗Ucolumn.’;
- A(19)=Tinv(27,1:81)∗Ucolumn.’;
- %---H4 (Fourth horizontal isoline measured from bottom):
- A(67)=Tinv(28,1:81)∗Ucolumn.’;
- A(68)=Tinv(29,1:81)∗Ucolumn.’;
- A(20)=Tinv(30,1:81)∗Ucolumn.’;
- A(21)=Tinv(31,1:81)∗Ucolumn.’;
- A(54)=Tinv(32,1:81)∗Ucolumn.’;
- A(55)=Tinv(33,1:81)∗Ucolumn.’;
- A(22)=Tinv(34,1:81)∗Ucolumn.’;
- A(23)=Tinv(35,1:81)∗Ucolumn.’;
- A(24)=Tinv(36,1:81)∗Ucolumn.’;
- %---H5 (Fifth horizontal isoline measured from bottom):
- A(69)=Tinv(37,1:81)∗Ucolumn.’;
- A(70)=Tinv(38,1:81)∗Ucolumn.’;
- A(25)=Tinv(39,1:81)∗Ucolumn.’;
- A(47)=Tinv(40,1:81)∗Ucolumn.’;
- A(26)=Tinv(41,1:81)∗Ucolumn.’;
- A(56)=Tinv(42,1:81)∗Ucolumn.’;
- A(27)=Tinv(43,1:81)∗Ucolumn.’;
- A(71)=Tinv(44,1:81)∗Ucolumn.’;
- A(72)=Tinv(45,1:81)∗Ucolumn.’;
- %--H6 (Sixth horizontal isoline measured from bottom):
- A(28)=Tinv(46,1:81)∗Ucolumn.’;
- A(29)=Tinv(47,1:81)∗Ucolumn.’;
- A(30)=Tinv(48,1:81)∗Ucolumn.’;
- A(64)=Tinv(49,1:81)∗Ucolumn.’;
- A(81)=Tinv(50,1:81)∗Ucolumn.’;
- A(57)=Tinv(51,1:81)∗Ucolumn.’;
- A(73)=Tinv(52,1:81)∗Ucolumn.’;
- A(74)=Tinv(53,1:81)∗Ucolumn.’;
- A(75)=Tinv(54,1:81)∗Ucolumn.’;
- %---H7 (Seventh horizontal isoline measured from bottom):
- A(79)=Tinv(55,1:81)∗Ucolumn.’;
- A(80)=Tinv(56,1:81)∗Ucolumn.’;
- A(31)=Tinv(57,1:81)∗Ucolumn.’;
- A(48)=Tinv(58,1:81)∗Ucolumn.’;
- A(32)=Tinv(59,1:81)∗Ucolumn.’;
- A(58)=Tinv(60,1:81)∗Ucolumn.’;
- A(76)=Tinv(61,1:81)∗Ucolumn.’;
- A(77)=Tinv(62,1:81)∗Ucolumn.’;
- A(78)=Tinv(63,1:81)∗Ucolumn.’;
- %---H8 (Eighth horizontal isoline measured from bottom):
- A(33)=Tinv(64,1:81)∗Ucolumn.’;
- A(34)=Tinv(65,1:81)∗Ucolumn.’;
- A(35)=Tinv(66,1:81)∗Ucolumn.’;
- A(49)=Tinv(67,1:81)∗Ucolumn.’;
- A(36)=Tinv(68,1:81)∗Ucolumn.’;
- A(59)=Tinv(69,1:81)∗Ucolumn.’;
- A(37)=Tinv(70,1:81)∗Ucolumn.’;
- A(38)=Tinv(71,1:81)∗Ucolumn.’;
- A(39)=Tinv(72,1:81)∗Ucolumn.’;
- %---H9 (Ninth horizontal isoline measured from bottom, at eta=1):
- A(40)=Tinv(73,1:81)∗Ucolumn.’;
- A(41)=Tinv(74,1:81)∗Ucolumn.’;
- A(42)=Tinv(75,1:81)∗Ucolumn.’;
- A(50)=Tinv(76,1:81)∗Ucolumn.’;
- A(43)=Tinv(77,1:81)∗Ucolumn.’;
- A(60)=Tinv(78,1:81)∗Ucolumn.’;
- A(44)=Tinv(79,1:81)∗Ucolumn.’;
- A(45)=Tinv(80,1:81)∗Ucolumn.’;
- A(46)=Tinv(81,1:81)∗Ucolumn.’;
- %% SPLIT THE VECTOR {A} IN PRIMARY AND SECONDARY SUB-VECTORS:
- Ap = A(1:46);
- As = A(47:81);
- %---Position of primary DOFs in local (grid) numbering
- % (e.g., A5 is at 6th local position (in tensor-product grid),
- % A46 is at 81, etc):
- PrimaryDOF=[1 2 3 4 6 8 9 10 11 12 13 15 17 18 21 22 24 26 27 ...
- 30 31 34 35 36 39 41 43 46 47 48 57 59 64 65 66 68 70 71 72 ...
- 73 74 75 77 79 80 81];
- %---Position of secondary DOFs in local (grid) numbering
- % (e.g., A47 is at 40:
- SecondaryDOF=[40 58 67 76 5 14 23 32 33 42 51 60 69 78 ...
- 7 16 25 49 19 20 28 29 37 38 44 45 52 53 ...
- 54 61 62 63 55 56 50];
- %---Find sub-matrices, involved in Eq.(113):
- Tpp = Tinv(PrimaryDOF,PrimaryDOF);
- Tps = Tinv(PrimaryDOF,SecondaryDOF);
- Tsp = Tinv(SecondaryDOF,PrimaryDOF);
- Tss = Tinv(SecondaryDOF,SecondaryDOF);
- Sa = (Tsp+Tss∗Su)/(Tpp+Tps∗Su); %Eq.(117)
- %================
- clear A
- A = sym(’A’, [81 1]);
- for k = 1:81
- assume(A(k), ’real’);
- end
- %================
- %---PRIMARY:
- Ap=A(1:46);
- %---SECONDARY:
- A(47:81) = Sa(1:35,1:46)∗Ap; %Eq.(116)
- %--------------------------------------------------------------------
- %% TENSOR-PRODUCT OF BERNSTEIN POLYNOMIALS:
- Pxy = (B1x∗B1y)∗A(1) + (B2x∗B1y)∗A(2) + (B3x∗B1y)∗A(3) + (B4x∗B1y)∗A(4) ...
- + (B5x∗B1y)∗A(51)+ (B6x∗B1y)∗A(5) + (B7x∗B1y)∗A(61)+ (B8x∗B1y)∗A(6) +(B9x∗B1y)∗A(7) ...
- + (B1x∗B2y)∗A(8) + (B2x∗B2y)∗A(9) + (B3x∗B2y)∗A(10)+ (B4x∗B2y)∗A(11) ...
- + (B5x∗B2y)∗A(52)+ (B6x∗B2y)∗A(12)+ (B7x∗B2y)∗A(62)+ (B8x∗B2y)∗A(13)+(B9x∗B2y)∗A(14) ...
- + (B1x∗B3y)∗A(65)+ (B2x∗B3y)∗A(66)+ (B3x∗B3y)∗A(15)+ (B4x∗B3y)∗A(16) ...
- + (B5x∗B3y)∗A(53)+ (B6x∗B3y)∗A(17)+ (B7x∗B3y)∗A(63)+ (B8x∗B3y)∗A(18)+(B9x∗B3y)∗A(19) ...
- + (B1x∗B4y)∗A(67)+ (B2x∗B4y)∗A(68)+ (B3x∗B4y)∗A(20)+ (B4x∗B4y)∗A(21) ...
- + (B5x∗B4y)∗A(54)+ (B6x∗B4y)∗A(55)+ (B7x∗B4y)∗A(22)+ (B8x∗B4y)∗A(23)+(B9x∗B4y)∗A(24) ...
- + (B1x∗B5y)∗A(69)+ (B2x∗B5y)∗A(70)+ (B3x∗B5y)∗A(25)+ (B4x∗B5y)∗A(47) ...
- + (B5x∗B5y)∗A(26)+ (B6x∗B5y)∗A(56)+ (B7x∗B5y)∗A(27)+ (B8x∗B5y)∗A(71)+(B9x∗B5y)∗A(72) ...
- + (B1x∗B6y)∗A(28)+ (B2x∗B6y)∗A(29)+ (B3x∗B6y)∗A(30)+ (B4x∗B6y)∗A(64) ...
- + (B5x∗B6y)∗A(81)+ (B6x∗B6y)∗A(57)+ (B7x∗B6y)∗A(73)+ (B8x∗B6y)∗A(74)+(B9x∗B6y)∗A(75) ...
- + (B1x∗B7y)∗A(79)+ (B2x∗B7y)∗A(80)+ (B3x∗B7y)∗A(31)+ (B4x∗B7y)∗A(48) ...
- + (B5x∗B7y)∗A(32)+ (B6x∗B7y)∗A(58)+ (B7x∗B7y)∗A(76)+ (B8x∗B7y)∗A(77)+(B9x∗B7y)∗A(78) ...
- + (B1x∗B8y)∗A(33)+ (B2x∗B8y)∗A(34)+ (B3x∗B8y)∗A(35)+ (B4x∗B8y)∗A(49) ...
- + (B5x∗B8y)∗A(36)+ (B6x∗B8y)∗A(59)+ (B7x∗B8y)∗A(37)+ (B8x∗B8y)∗A(38)+(B9x∗B8y)∗A(39) ...
- + (B1x∗B9y)∗A(40)+ (B2x∗B9y)∗A(41)+ (B3x∗B9y)∗A(42)+ (B4x∗B9y)∗A(50) ...
- + (B5x∗B9y)∗A(43)+ (B6x∗B9y)∗A(60)+ (B7x∗B9y)∗A(44)+ (B8x∗B9y)∗A(45)+(B9x∗B9y)∗A(46);
- % Collect coefficients of A1 to A46:
- vars = A(1:46).’;
- [coefficients, terms] = coeffs(Pxy, vars);
- % Initialize a symbolic row vector
- coeff_vector = sym(zeros(1, length(vars))); %A47...A81 in terms of (A1...A46)
- % Store symbolic coefficients
- for i = 1:length(vars)
- idx = find(terms == vars(i));
- if ~isempty(idx)
- coeff_vector(i) = coefficients(idx); % Store the coefficient
- else
- coeff_vector(i) = 0; % If no coefficient exists, assign 0
- end
- end
- % Convert to numeric using vpa, if needed
- coeff_vector_numeric = vpa(coeff_vector);
- % Display the results
- disp(’Row vector of symbolic coefficients:’);
- disp(coeff_vector);
- disp(’Row vector of numeric coefficients:’);
- disp(coeff_vector_numeric);
- % Display coefficients
- format short
- for i = 1:length(vars)
- fprintf(’Coefficient of %s: %s\n’, ...
- char(vars(i)), char(coefficients(find(terms == vars(i)))));
- end
- return
References
- Rayleigh, L. Scientific Papers; Cambridge University Press: Cambridge, UK, 1900; Volume II. [Google Scholar]
- Ritz, W. Über eine neue Methode zur Lösung gewisser Variationsprobleme der mathematischen Physik [On a new method for the solution of certain variational problems of mathematical physics]. J. Reine Angew. Math. 1909, 135, 1–61. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C. The Finite Element Method, 3rd ed.; McGraw-Hill: London, UK, 1977. [Google Scholar]
- Bathe, K.J. Finite Element Procedures, 2nd ed.; Prentice-Hall: Englewood Cliffs, NJ, USA, 1996. [Google Scholar]
- Gordon, W.J.; Hall, C.A. Transfinite element methods: Blending-function interpolation over arbitrary curved element domains. Numer. Math. 1973, 21, 109–129. [Google Scholar] [CrossRef]
- Coons, S.A. Surfaces for Computer-Aided Design of Space Forms; MIT: Cambridge, MA, USA, 1967. [Google Scholar]
- Provatidis, C.G. Precursors of Isogeometric Analysis: Finite Elements, Boundary Elements, and Collocation Methods; Springer: Cham, Switzerland, 2019. [Google Scholar] [CrossRef]
- Provatidis, C. Transfinite patches for isogeometric analysis. Mathematics 2025, 13, 35. [Google Scholar] [CrossRef]
- Provatidis, C. Transfinite elements using Bernstein polynomials. Axioms 2025, 14, 433. [Google Scholar] [CrossRef]
- Provatidis, C.; Eisenträger, S. Macroelement analysis in T-patches using Lagrange polynomials. Mathematics 2025, 13, 1498. [Google Scholar] [CrossRef]
- Birkhoff, G.; Cavendish, J.C.; Gordon, W.J. Multivariate Approximation by Locally Blended Univariate Interpolants. Proc. Nat. Acad. Sci. USA 1974, 71, 3423–3425. [Google Scholar] [CrossRef] [PubMed]
- Sederberg, T.W.; Zheng, J.; Bakenov, A.; Nasri, A. T-splines and T-NURCCs. ACM Trans. Graph. (TOG) 2003, 22, 477–484. [Google Scholar] [CrossRef]
- Bazilevs, Y.; Calo, V.M.; Cottrell, J.A.; Evans, J.A.; Hughes, T.J.R.; Lipton, S.; Scott, M.A.; Sederberg, T.W. Isogeometric analysis using T-splines. Comput. Methods Appl. Mech. Eng. 2010, 199, 229–263. [Google Scholar] [CrossRef]
- Dörfel, M.R.; Jüttler, B.; Simeon, B. Adaptive isogeometric analysis by local h-refinement with T-splines. Comput. Methods Appl. Mech. Eng. 2010, 199, 264–275. [Google Scholar] [CrossRef]
- Wen, Z.; Pan, Q.; Zhai, X.; Kang, H.; Chen, F. Adaptive isogeometric topology optimization of shell structures based on PHT-splines. Comput. Struct. 2024, 305, 107565. [Google Scholar] [CrossRef]
- Chen, K.; Qiu, C.; Liu, Z.; Tan, J. A high-precision T-spline blade modeling method with 2D and 3D knot adaptive refinement. Adv. Eng. Softw. 2024, 194, 103684. [Google Scholar] [CrossRef]
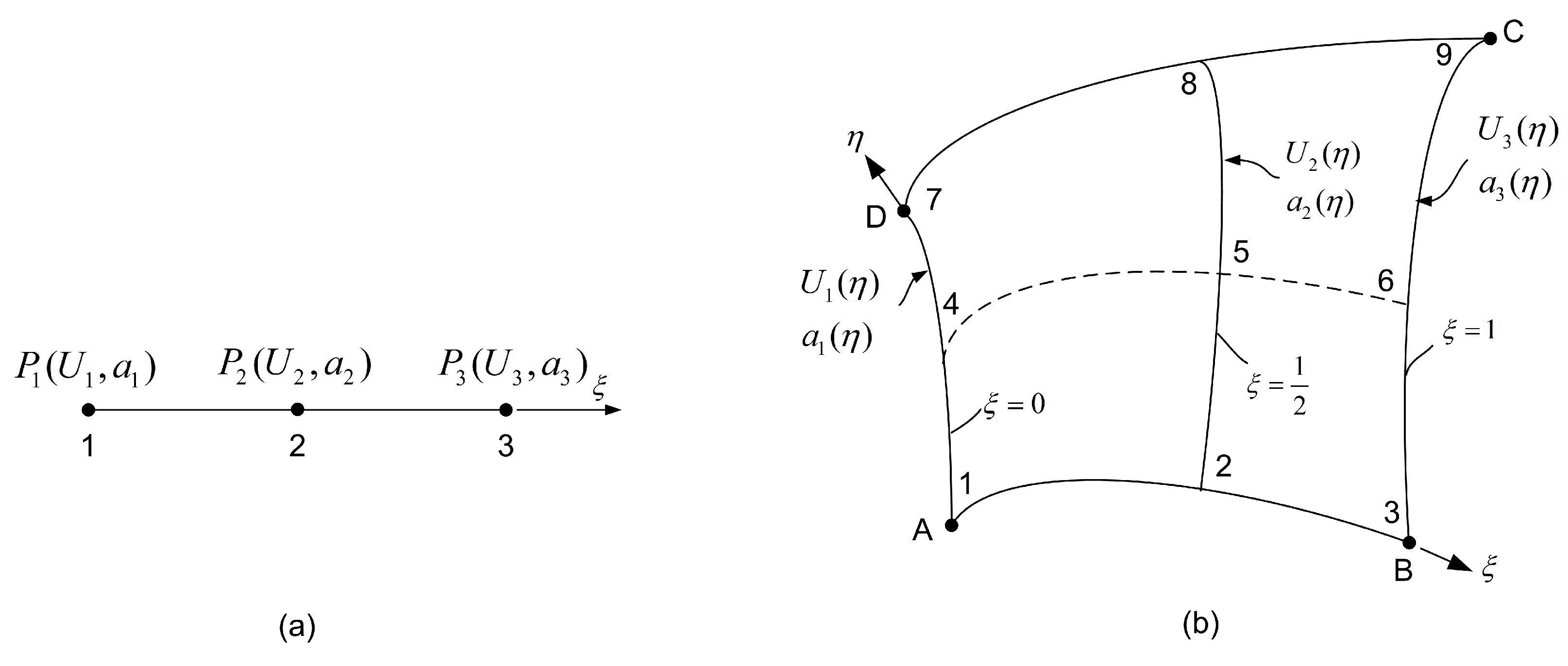





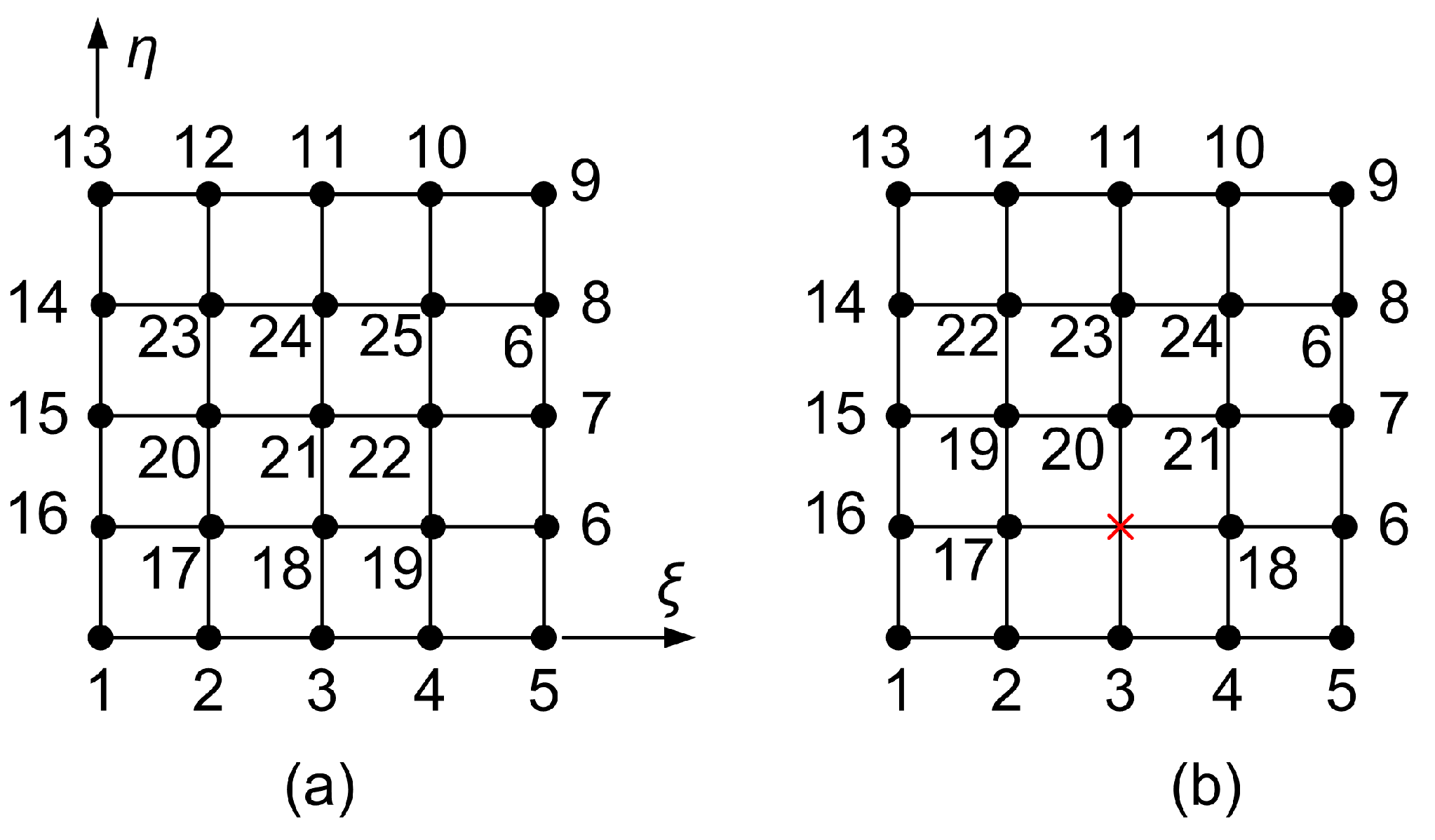

| Element Type | Lagrange Polynomials | Bernstein: Model B-1 | Bernstein: Model B-2 |
|---|---|---|---|
| Equation (22) | Equation (29) | Equation (40) | |
| 9-node | 21.2377 | 21.2377 | 21.2377 |
| 11-node | 21.2870 | 21.2879 | 21.2870 |
| 12-node | 21.2870 | 21.2870 | – |
| 18-node | 0.9024 | 0.9033 | – |
| Element Type | Lagrange Polynomials | Bernstein: Model B-1 | Bernstein: Model B-2 |
|---|---|---|---|
| Equation (22) | Equation (29) | Equation (40) | |
| 9-node | 3.2235 | 3.2235 | 3.2235 |
| 11-node | 2.8567 | 2.6875 | 2.8567 |
| 12-node | 2.6671 | 2.6655 | – |
| 18-node | 0.1638 | 0.1556 | – |
| Element Type | Lagrange Polynomials | Bernstein: Model B-1 | Bernstein: Model B-2 |
|---|---|---|---|
| Equation (22) | Equation (29) | Equation (40) | |
| 9-node | 3.1905 | 3.1905 | 3.1905 |
| 11-node | 2.9028 | 2.6920 | 2.9028 |
| 12-node | 2.6721 | 2.6691 | – |
| 18-node | 0.1641 | 0.1543 | – |
| Problem Type | Lagrange Polynomials | Bernstein: Model B-1 | Bernstein: Model B-2 |
|---|---|---|---|
| Equation (22) | Equation (29) | Equation (40) | |
| Example 2 | 0.0115 | 0.0072 | 0.0115 |
| Condition Number | |||
| Example 3 | 0.0225 | 0.0042 | 0.0225 |
| Condition Number |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Provatidis, C. From Lagrange to Bernstein: Generalized Transfinite Elements with Arbitrary Nodes. Mathematics 2025, 13, 1983. https://doi.org/10.3390/math13121983
Provatidis C. From Lagrange to Bernstein: Generalized Transfinite Elements with Arbitrary Nodes. Mathematics. 2025; 13(12):1983. https://doi.org/10.3390/math13121983
Chicago/Turabian StyleProvatidis, Christopher. 2025. "From Lagrange to Bernstein: Generalized Transfinite Elements with Arbitrary Nodes" Mathematics 13, no. 12: 1983. https://doi.org/10.3390/math13121983
APA StyleProvatidis, C. (2025). From Lagrange to Bernstein: Generalized Transfinite Elements with Arbitrary Nodes. Mathematics, 13(12), 1983. https://doi.org/10.3390/math13121983






