Abstract
Over the past two decades, substantial efforts have been made to develop survival models for gap times between recurrent events. An emerging approach involves considering rate models derived from a non-homogeneous Poisson process, thus allowing the conditional distribution of a gap time given the previous recurrence time to be deduced. Under this approach, some parametric rate models have been proposed, differing in their distributional assumptions on gap times. In particular, the extended exponential–Poisson, Weibull and extended Chen–Poisson distributions have been considered. Alternatively, a flexible rate model using restricted cubic splines is proposed here to capture complex non-monotonic rate shapes. Moreover, a comprehensive comparison of parametric rate models is presented. The maximum likelihood method is applied for parameter estimation in the presence of right-censoring. It is shown that some models include important special cases that allow testing of the independence assumption between a gap time and the previous recurrence time. The likelihood ratio test, as well as two information criteria, are discussed for model selection. Model fit is assessed using Cox–Snell residuals. Applications to two well-known clinical data sets illustrate the comparative performance of both the existing and proposed models, as well as their practical relevance.
Keywords:
gap times; non-homogeneous Poisson process; parametric models; rate function; recurrent events; restricted cubic splines; survival analysis MSC:
62F05; 62F12; 62H05; 62N01; 62N02; 62P10; 65C99
1. Introduction
Advances in scientific research, particularly in the health sciences, have been pivotal in driving substantial improvements in the average life expectancy of populations worldwide. Consequently, patients with longer survival times may experience certain clinical events more than once. For this reason, since the 1980s, there has been a growing effort to develop survival models to analyse multivariate time data [,], arising from the observation of several episodes of a particular event of interest. These episodes are referred to as recurrent events [] and are commonly observed in medical studies on cancer relapses, myocardial infarctions, asthma attacks and hospital readmissions. Furthermore, in scenarios where patients may recover after each occurrence, researchers (e.g., []) often focus on modelling the time elapsed between two consecutive events, known as the gap time.
As mentioned by Cook and Lawless [], there are two fundamental approaches to modelling recurrent events, which involve developing models based on event counts or gap times. Poisson processes are the canonical models for event counts, typically using the calendar time as the time scale. In contrast, the renewal process is the canonical framework when analysing gap times between recurrent events. Such a stochastic process relies on the assumption that gap times are independent and identically distributed (iid) random variables. Since this is a strong condition that holds only in a few cases, more general gap time models that account for within-individual dependence have been developed over the years using conditional distributions. These include various regression models for the assessment of covariates’ effects on a given function of interest (e.g., intensity, rate, hazard, mean or quantile functions) [,,,,,,,,], multistate models to capture transitions between different event states [,], gap time models with random effects to account for unobserved heterogeneity [,,] and copula-based models for the joint modelling of dependent gap times [,]. For a more in-depth overview of the topic, readers are referred to [].
Another approach in gap time modelling involves obtaining the conditional distribution of a gap time, given a previous recurrence time. This issue has been investigated by several authors [,,], who have proposed different non-parametric estimators of the conditional survival (or distribution) function that, in some way, are based on the Kaplan–Meier estimator of the survival function. From a different perspective, the conditional distribution of the gap times can be deduced under the classic assumption that the number of recurrent events up to a given time follows a non-homogeneous Poisson process (NHPP) []. In this setting, Zhao and Zhou [] developed an additive semiparametric model with a rate function derived from an NHPP. One advantage of this model is its ability to estimate covariate effects without assuming a specific parametric form for the baseline rate function, similarly to the well-known Cox-based models, which feature an unspecified baseline hazard function. However, this may present a limitation when estimating these functions is of primary interest, particularly in medicine, as it enables the evaluation of how the risk of disease occurrence evolves over time. As stated by Royston and Parmar [] and Jullum and Hjort [], using a parametric version of the Cox model, when appropriate, can provide more accurate survival probability estimates, enhancing the understanding of the phenomenon under study. Therefore, adopting a fully parametric model may be more suitable, a stance supported by Cox in [].
Following Zhao and Zhou [], a class of parametric rate models has emerged considering alternative specifications for the baseline rate function. Macera et al. [] and Louzada et al. [] studied a model based on the extended exponential–Poisson (EEP) distribution. Similarly, Louzada et al. [] and Sousa-Ferreira et al. [] studied the use of the Weibull form to specify the baseline rate, but the models were extended in different directions to account for the presence of zero-recurrence (cured) individuals. Both the EEP and Weibull rate models have been shown to include the classical homogeneous Poisson process (HPP) as a special case, a property that is useful for model-checking purposes. Nonetheless, these models only allow for monotonic rate functions and may fall short in capturing complex disease patterns over a patient’s lifetime. To overcome this limitation, Sousa-Ferreira et al. [] proposed a model based on the extended Chen–Poisson (ECP) distribution, whose rate function can accommodate non-monotonic shapes, including bathtub or unimodal.
Despite the variety of available parametric approaches, a comprehensive comparison of existing parametric rate models is still lacking. Thus, a more detailed study is justified to assess the strengths and limitations of different parametric rate models, providing a valuable understanding of their relative performance and applicability.
This paper is organised as follows. Section 2 provides an overview of the mathematical properties underlying the general rate model for gap times between recurrent events derived from an NHPP, followed by the formulation of existing parametric rate models that differ in terms of the distributional assumptions on gap times. A new model, based on restricted cubic splines (RCSs), is also introduced in this section. Section 3 outlines the inferential procedure based on the usual maximum likelihood (ML) method for right-censored data and addresses the likelihood ratio (LR) test for model selection. Section 4 illustrates the application of these models to two real data sets from the literature, namely bowel motility data and hospital readmission data. Finally, Section 5 presents some concluding remarks and directions for future work.
2. Parametric Rate Models for Gap Times Between Recurrent Events
Survival models for recurrent events can be formulated by defining the distribution of the number of events in an infinitesimal interval , given the process history up to time t. In general, fully specifying this distribution is unfeasible due to its complexity. As the interest often lies in marginal features of the recurrence process, Poisson process-based models focusing on the rate and mean functions have been developed [,].
Consider an individual whose recurrence process begins at time 0 for simplicity. Let be the continuous and non-negative random variables denoting the ordered times corresponding to episodes of a given event of interest, where () is the time from the beginning of the study until the occurrence of the kth episode. These times are realisations of a counting process, , which records the cumulative number of events in . An alternative representation of the same process is through the gap times, defined as , with .
Assuming that is a Poisson process, the intensity function is defined as
where is the increment over . A key assumption is that has independent increments. Therefore, Equation (1) is known as the rate function and represents the marginal (unconditional on the history) instantaneous probability of an event at time t []. Considering that the probability of more than one event over is negligible, it follows that and . Thus, an equivalent way to define this process is . The mean function (also called the cumulative rate function), defined as , describes the expected number of events at t. The process is called homogeneous if is a positive constant; otherwise, it is non-homogeneous.
The Poisson process is useful in deriving the conditional distribution of gap times, given the previous recurrence time []. Under the assumptions of an NHPP, the probability that no event occurs during a gap time of length y, given that the individual survived beyond time , is defined as
where is the baseline survival function. The expected value of , conditional on , takes the expression , which, by definition, corresponds to the mean residual life function of at time .
The conditional survival function (2) expresses the dependence structure among gap times within an individual but reduces to for the first gap time (). In general, gap times are not independent, except in the special case of an HPP, where and the gap times are iid exponential random variables with rate parameter .
The corresponding expected number of recurrences over the interval is equal to the conditional cumulative rate function
where is the baseline cumulative rate function. Then, the rate function of the recurrence process can be straightforwardly deduced from as
where is the baseline rate function.
During the past two decades, gap time models characterised by the rate function (4) have been developed. These models differ in the nature (non-parametric or parametric) of the baseline rate. The first model was proposed by Zhao and Zhou [], who considered a kernel estimation method to estimate the baseline rate non-parametrically. Subsequent models [,,,,] assumed a specific parametric form for based on a particular distribution. Moreover, a Poisson process can be generalised to incorporate covariates or random effect terms [], which has also been done by some authors (e.g., [,,]) under this approach. Here, however, the focus is exclusively on gap time modelling.
2.1. Extended Exponential–Poisson (EEP) Rate Model
Macera et al. [] and Louzada et al. [] proposed similar models, assuming that the baseline rate function has the same analytical form as the hazard function of the exponential–Poisson and Poisson–exponential distributions, respectively. These distributions, intended for single-event analysis, arise in competitive and complementary risk (CCR) problems, where the lifetime of each cause (which, in this case, follows an exponential distribution) is unobservable, and only the minimum or maximum lifetime across all possible causes can be observed. Ramos et al. [] showed that, if the number of causes follows a zero-truncated Poisson distribution with parameter , the distributions of the minimum and maximum can be unified into a single model by extending to , giving rise to the unified Poisson family of distributions. The expected number of latent causes is , approaching 1 as . The exponential–Poisson and Poisson–exponential distributions are particular cases of the EEP distribution for (distribution of the minimum) and (distribution of the maximum), respectively. Thus, the two parametric rate models of Macera et al. [] and Louzada et al. [] can likewise be merged, as discussed in [].
For the EEP rate model, the rate function of the recurrence process is
where and . Its shape is monotonically decreasing for and increasing for , stabilising at as the gap time tends to infinity. Since , the exponential rate model (HPP) with constant rate is a limiting case. While broadly applicable to recurrent gap time data, this model is especially useful in CCR problems as it yields a practical interpretation: for (or ), represents the minimum (or maximum) gap time among all competitive (or complementary) causes.
2.2. Extended Chen–Poisson (ECP) Rate Model
Sousa-Ferreira et al. [] deduced the conditional distribution of a gap time, given the previous recurrence time, assuming a baseline rate function with an ECP form []. Their work addresses a limitation of the EEP rate model, whose monotonic rate function may not be suitable for scenarios where the risk peaks and then declines, such as in disease progression. Based on the ECP distribution, the resulting parametric rate model accommodates non-monotonic rate shapes, offering a more accurate representation of real-world data. Similarly to the EEP distribution, the ECP distribution is a member of the unified Poisson family [] but, in this case, the lifetime of each unobservable cause follows a Chen distribution.
For the ECP rate model, the rate function of the kth gap time, , conditional on , takes the expression
where and . This function can adopt the same shapes as the hazard function of the ECP distribution [], including monotonic increasing, monotonic decreasing, unimodal, bathtub, increasing–decreasing–increasing and decreasing–increasing–decreasing–increasing. Since has the same analytical form as the hazard function of the Chen distribution, it follows that the ECP rate model reduces to the Chen rate model as . In CCR settings, retains its interpretation in terms of competing () or complementary () causes, enabling the estimation of the average number of latent causes.
2.3. Flexible Rate Model Based on Restricted Cubic Splines (RCSs)
Traditional distributions—such as the exponential, Weibull, gamma or other generalised exponential distributions—often lack the flexibility to capture rate functions that increase and decrease multiple times. For this reason, we propose using RCSs in this class of parametric rate models. A cubic spline is a smooth function defined by a set of third-degree polynomial functions joined at a predefined number of points, with continuous first and second derivatives. The first and last of these points are named boundary knots, and the remaining are internal knots. This function may also be constrained to be linear beyond the boundary knots, ensuring a sensible functional form in the tails [,], where data are typically sparse. These types of splines are known as RCSs and have been used in survival models [,].
For a predefined number m of internal knots, denoted by , with boundary knots and , the RCS function of an observation x can be written as
where is the vector of parameters and is the lth basis function (), defined as
with . The complexity of the curve is regulated by the number of degrees of freedom (df), given by . As m increases, the curve gains flexibility; however, it may become unstable if m is too large. By convention, df indicates that no internal knots are specified, so . Some authors [,] recommend modelling on the log time scale, i.e., with , as this strategy reduces the variation between curves with different df.
Following the approach of Royston and Parmar [], we propose to model the log-cumulative baseline rate function as an RCS function of log time, which yields analytically tractable functions. From (3), the flexible rate model has a cumulative rate function characterised by
where is the log-cumulative baseline rate function and is the RCS function (7) of . Therefore, the corresponding rate function of the recurrence process is
with the expression for available in Appendix A. This flexible rate function can capture rollercoaster shapes with multiple inflection points. Each choice of m internal knots defines a different parametric rate model. With no internal knots, the rate simplifies to , which means that follows a Weibull rate model, with scale parameter and shape parameter . This case, studied in [,] using a more common parametrisation, includes the HPP as a nested model when . All other cases correspond to an NHPP.
Considerations on the Use of Restricted Cubic Splines (RCSs)
The placement and number of internal knots are widely debated topics in the literature (e.g., [,]). Royston and Parmar [] discourage the use of data-driven optimisation methods to automatically select the location of each knot, arguing that such approaches may lead to overfitting by capturing minor features of the data. Instead, they recommend placing boundary knots at the minimum and maximum of uncensored log survival times, with internal knots set at equally spaced empirical quantiles (e.g., quartiles for three knots; see Table 1). From a practical perspective, these authors found that the location of the internal knots has a minimal impact on the overall shape of the estimated hazard function.

Table 1.
Placement of internal knots in the restricted cubic spline, depending on the number m of internal knots considered.
The automated selection of the number m is also discouraged for similar reasons. Note that RCS-based models are not necessarily nested, so the application of the LR test is generally inappropriate to compare models with different values of m. Royston and Parmar [] and Rutherford et al. [] found that little is gained by considering . Consequently, these authors suggested informally examining the observed values of the Akaike information criterion (AIC) and Bayesian information criterion (BIC) for models fitted with zero to three internal knots.
Rutherford et al. [] conducted a comprehensive simulation study on the use of RCSs to approximate complex hazard functions. Their findings revealed that, with a sufficient number of knots, the hazard function estimated via an RCS closely approximates the true simulated hazard function across a wide range of complex shapes. Moreover, they concluded that the hazard ratio values are largely insensitive to baseline hazard misspecification.
Although the primary objective of using RCSs is to accurately approximate the baseline hazard function, Royston and Parmar [] chose to model the log-cumulative baseline hazard function as an RCS function of log time, rather than modelling or directly, to obtain analytically tractable functions. By contrast, Crowther and Lambert [] modelled using RCSs, acknowledging the need for numerical integration to derive the survival and cumulative hazard functions, but highlighting its advantages when incorporating time-dependent covariates.
3. Statistical Inference
The inferential procedures are based on the usual ML approach and large sample properties, under a general right-censoring mechanism and within the framework of recurrent event analysis [], assuming that gap times are conditionally independent given the previous observed recurrence time.
Suppose that data are available from n independent individuals. Let be the pair associated with the kth recurrence of the ith individual, and , where is the observed gap time between two consecutive events, and is the censoring indicator, taking the value 1 if is completely observed and 0 if it is right-censored. Thus, represents the observed event times corresponding to the recurrences. In general, consider that the parametric rate model, characterised by the rate function (4), is known up to a vector of parameters . Assuming that the censoring mechanism is non-informative, the ML estimate of can be obtained by maximising the log-likelihood function, , given by
where is specified according to the parametric distributional assumption on the gap times, conditional on the previous recurrence time. If follows an EEP rate model, the rate function (5) is used; if it follows an ECP rate model, the rate function (6) is used; and if it follows a flexible rate model, the rate function (8) is used.
Large sample inference for the vector of parameters can be based on the corresponding ML estimates and their estimated standard errors, evaluated in the usual manner from the inverse of the observed information matrix. The confidence intervals (CIs) for the parameters can be constructed using the normal approximation. For computational implementation, the optim function available in the R [] statistical software (version 4.5.0) is applied to directly maximise the log-likelihood function (9) using standard numerical optimisation methods, such as the Broyden–Fletcher–Goldfarb–Shanno algorithm.
The goodness of fit comparison between the EEP and exponential rate models (and between the ECP and Chen rate models) involves testing the hypotheses versus . The LR test is commonly used for model selection between two nested models. The LR statistic is given by , where and are the maximised log-likelihoods under the null and alternative hypotheses, respectively. Note that the test is performed at the boundary of the parametric space of . Under this non-standard condition, we conjecture that the asymptotic distribution of the LR statistic is a 50:50 mixture of a degenerate distribution at zero and a chi-squared distribution with one degree of freedom, as suggested by the theoretical results of Chernoff [] and Self and Liang []. Simulation studies provide empirical support for the use of this asymptotic distribution of the LR statistic when testing the EEP and exponential rate models [,], as well as the ECP and Chen rate models [].
In addition, the exponential rate model is nested within the Weibull rate model. The LR test can again be carried out to evaluate the hypotheses versus . In this situation, the classical asymptotic distribution theory for the LR statistic remains valid, as the test is conducted within the interior of the parameter space of . Incorporating the exponential rate model as a sub-model is particularly valuable, as it corresponds to the special case of the HPP, where gap times are iid. Consequently, hypothesis testing allows for the assessment of the independence assumption between a gap time, , and the previous recurrence time, .
When comparing two or more models, not necessarily nested, an information criterion based on the maximised likelihood, such as the AIC or BIC, can be used for model selection. Furthermore, to verify that the assumptions underlying the fitted model are reasonable given the available data, a residual analysis can be performed to informally assess whether the observed times follow the specified parametric model. In this context, a generalised version of Cox–Snell residuals is useful in evaluating the overall goodness of fit of models for recurrent events []. These residuals are defined as , and , where is the estimated cumulative rate function of the fitted model. For the correct model, the graphical representation of the pairs yields a straight line through the origin with a unit slope, where is the Nelson–Aalen estimate of the cumulative rate function based on the residuals. Alternatively, plotting the pairs makes it easier to identify deviations from linearity.
4. Application to Real Data
4.1. Analysis of Bowel Motility Data
In the current subsection, the performance of parametric rate models is compared in the analysis of a well-known data set on small bowel motility during fasting, originally discussed and made available in Aalen and Husebye []. These data were also considered by Louzada et al. [] and Sousa-Ferreira et al. [] with the Poisson–exponential and ECP rate models, respectively. The study involved 19 healthy individuals who underwent continuous monitoring for 13 h and 40 min. A standard meal induced a fed state with irregular contractions (4 to 7 h), after which the fasting state began, characterised by cyclical motility. The event of interest is linked to the start of each motility cycle (migrating motor complex). A total of 99 gap times between cycles were recorded, with the last gap time censored for all individuals due to the end of the monitoring period. Table 2 shows the composition and evolution of the risk set for each bowel motility recurrence.

Table 2.
Summary of each recurrence in the bowel motility data.
Eight parametric rate models were fitted to the bowel motility data. The ML estimates, their corresponding 95% CIs, the negative of the maximised log-likelihood, the AIC and BIC values and the LR test are presented in Table 3. As outlined earlier, the exponential rate model (HPP) is a special case of the Weibull and EEP rate models, allowing testing of the independence assumption between a gap time and previous recurrence time under : and : , respectively. The results of the LR test ( in both cases) indicate significant dependence, highlighting the importance of accounting for it. This is an interesting result for the bowel motility data, as earlier studies [,] found no evidence of dependence between successive gap times, which supports the use of renewal process-based models. For example, Cook and Lawless [] fitted two extensions of the classical renewal process based on the log-normal distribution: one that allows for deducing the conditional distribution of a gap time given the previous gap time and another that incorporates a random effect. They concluded that both cases provide little evidence of an association between successive gap times. However, the models considered in our study (derived from a Poisson process) reveal that a gap time and the previous recurrence time are correlated.

Table 3.
Results from parameter estimation and goodness of fit assessment of parametric rate models fitted to bowel motility data.
The remaining parametric rate models also address this lack of independence. For the Chen and ECP rate models, the LR test is again applied to compare them under . As the resulting p-value is substantially low, there is strong evidence favouring the ECP rate model. For flexible rate models, the AIC and BIC are used to informally select the most appropriate number of internal knots. Among models with zero to three internal knots, the flexible rate model with (df ) internal knot yields the lowest AIC and BIC values. This also holds when compared to all other fitted models, making it the best performer overall.
The estimates of the rate function for some of the fitted models are depicted in Figure 1. While both the Weibull and EEP rate models suggest a monotonically increasing rate, the ECP rate model exhibits a unimodal shape, and the flexible rate models with and display an increasing–decreasing–increasing shape. The latter models, which have the smallest AIC values, likely achieve improved goodness of fit due to their ability to capture the non-monotonic shape of the rate function.
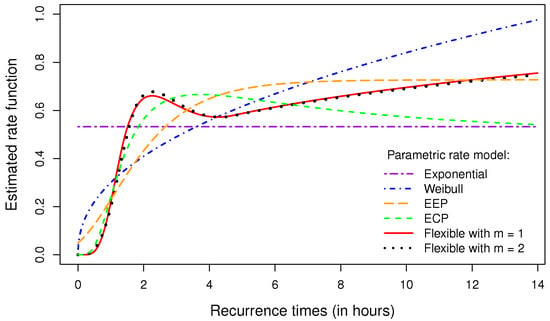
Figure 1.
Estimated rate functions of the exponential, Weibull, EEP, ECP and flexible rate models fitted to the bowel motility data.
Additionally, the Cox–Snell residuals are used to informally assess the model fit. Figure 2 illustrates the diagnostic plots on the log scale for the exponential and the best flexible rate models, allowing a direct comparison with the EEP and ECP models reported in []. Figure 2a confirms the very poor fit of the HPP model. Although Louzada et al. [] and Sousa-Ferreira et al. [] have described that the Cox–Snell residuals associated with the EEP and ECP rate models closely approximate the reference line, the flexible rate model with offers an even better fit to these data (see Figure 2b).
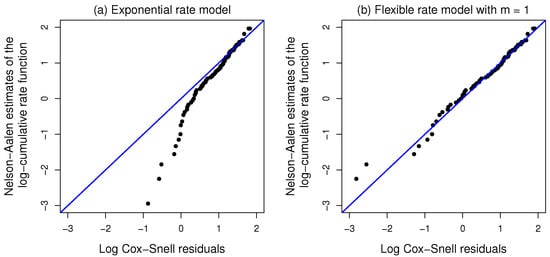
Figure 2.
Diagnostic plots based on Cox–Snell residuals for the evaluation of the adequacy of the (a) exponential and (b) flexible rate models fitted to the bowel motility data.
4.2. Analysis of Hospital Readmission Data
The same parametric rate models are now applied to hospital readmission data from 403 colorectal cancer patients, obtained from the prospective cohort study conducted by González et al. []. The first gap time refers to the time elapsed between the date of tumour resection surgery and the first admission related to colorectal cancer. Subsequent gap times are defined as the difference between a given readmission date and the preceding discharge date. A total of 861 readmissions were recorded, ranging from 1 to 22 per patient (mean: 2.3, median: 1.0). These data are available in the R library frailtypack. Table 4 summarises the evolution of the risk set for the first ten hospital readmissions.

Table 4.
Summary of the first ten recurrences in the readmission data.
After fitting eight parametric rate models to the readmission data, the results of parameter estimation and goodness of fit assessment are compiled in Table 5. LR tests comparing the Weibull and EEP rate models to the classical HPP model produced an extremely small p-value, rejecting the independence assumption. The ECP model also revealed a significantly better fit than its sub-model. Informal analysis based on the AIC and BIC further suggests that the ECP rate model outperforms those with exponential, Weibull, EEP and Chen baseline rates. Nevertheless, the flexible rate model with (df ) once again attains the smallest scores for both information criteria, as in the previous example, offering the best overall fit for the readmission data among all models considered here.

Table 5.
Results from parameter estimation and goodness of fit assessment of parametric rate models fitted to readmission data.
Figure 3 shows the estimated rate functions for some models. The Weibull and EEP rate models exhibit monotonically decreasing rates, whereas the ECP and flexible rate models (with and ) display positively skewed unimodal shapes. Remarkably, the RCS-based model is scarcely affected by the inclusion of additional internal knots. Based on the best-fitting model, the estimated readmission rate peaks at around 23 days post-discharge, identifying a high-risk period for targeted follow-up care that may improve outcomes and optimise resources.
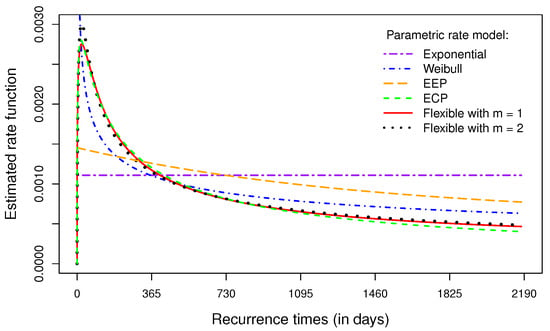
Figure 3.
Estimated rate functions of the exponential, Weibull, EEP, ECP and flexible rate models fitted to the readmission data.
In addition, the overall goodness of fit of the exponential, EEP, ECP and flexible rate models was informally assessed using Cox–Snell residual plots (see Figure 4). The upper panels show substantial deviations from linearity for the exponential and EEP rate models, indicating an inadequate fit. In contrast, the lower panels show exceptional alignment with the reference line for both the ECP and the best flexible rate models, corroborating their superior performance. Once again, the improved fit appears to be linked to the greater flexibility of the rate function in these models.
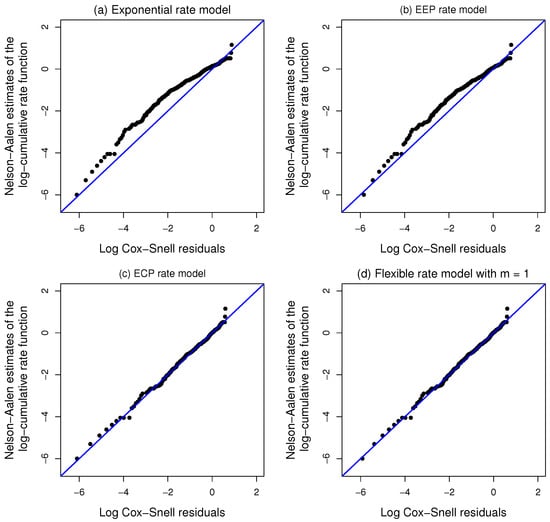
Figure 4.
Diagnostic plots based on Cox–Snell residuals for the evaluation of the adequacy of the (a) exponential, (b) EEP, (c) ECP and (d) flexible rate models fitted to the readmission data.
The readmission data were also used to illustrate the application of more general parametric rate models. In these studies, the Weibull rate model [,] was extended in different ways to incorporate covariates in the scale parameter; a proportion of zero-recurrence individuals, where the inclusion of covariates in this proportion was also explored via a logistic function; and a shared frailty term, acting additively on the rate function. The results from our comparative analysis suggest that a flexible baseline rate should be used when analysing the readmission data. This serves as a preliminary step before developing more complex parametric rate models that include fixed and random effect terms. It is crucial to ensure the correct specification of the distribution of a gap time given the previous recurrence time. Otherwise, the estimation of covariate effects may be compromised or, in some cases, unnecessary random effects may be included.
5. Concluding Remarks and Future Work
The main objective of our study was to provide a comprehensive comparison of parametric rate models for the analysis of gap times between recurrent events from theoretical and practical perspectives. The models differ in their distributional assumptions on the gap times but share the feature of having a rate function derived from an NHPP, enabling the conditional distribution of a gap time given the previous recurrence time to be obtained. An additional contribution of this work is the proposal of the flexible rate model, accompanied by a thorough discussion of its formulation and modelling strategy using RCS functions.
In the application to two well-known clinical data sets—the bowel data and the readmission data—our findings suggest that a model with a monotonic rate function (exponential, Weibull or EEP form) may fit data poorly when dependence is present, as shown by the result of the LR test. Both applications showed that the ECP and flexible rate models markedly improved the fit by capturing non-monotonic rate shapes, with the latter yielding the best overall goodness of fit. Curiously, the baseline cumulative rate function of the flexible rate model did not require great algebraic complexity, as only a single internal knot (df ) was sufficient in the spline part to achieve the lowest AIC and BIC values, while also exhibiting the best alignment with the reference line in the Cox–Snell residual plot. This highlights the advantage of modelling the log-cumulative baseline rate function as an RCS function of log time, particularly when no qualitative information is available to guide the selection of the most appropriate baseline distribution for the gap times.
At this stage of our research, no simulation study was conducted to assess the performance of the flexible rate model. This decision was motivated by the extensive literature supporting the use of RCS functions to approximate complex hazard shapes in survival analysis, as discussed throughout this work. In particular, when an adequate number of internal knots is specified, RCS-based models provide accurate approximations to the baseline hazard function. Nonetheless, we recognise that simulation studies could be pursued under the flexible rate model to evaluate the risk of overfitting in small samples and the impact of different degrees of dependence between a gap time and the previous recurrence time within an individual.
A promising avenue for future work would be to extend the existing parametric rate models to include covariates through the scale parameter, assuming a multiplicative effect on the rate function. Moreover, these models can also be generalised to incorporate a frailty term (random effect), aiming to represent unobserved or unmeasurable risk factors. Finally, we plan to develop an R package dedicated to the methodology discussed here.
Author Contributions
Conceptualisation, I.S.-F., A.M.A. and C.R.; methodology, I.S.-F., A.M.A. and C.R.; software, I.S.-F.; validation, I.S.-F., A.M.A. and C.R.; formal analysis, I.S.-F.; investigation, I.S.-F., A.M.A. and C.R.; writing—original draft preparation, I.S.-F.; writing—review and editing, A.M.A. and C.R.; visualisation, I.S.-F.; supervision, A.M.A. and C.R. All authors have read and agreed to the published version of the manuscript.
Funding
This work is partially financed by national funds through the FCT—Fundação para a Ciência e a Tecnologia—under the projects UID/00006/2025 and UIDB/00006/2020 (DOI: https://doi.org/10.54499/UIDB/00006/2020) (CEAUL—Centro de Estatística e Aplicações) and the projects UID/04674/2025 and UIDB/04674/2020 (DOI: https://doi.org/10.54499/UIDB/04674/2020) (Center for Research in Mathematics and Applications (CIMA) related to the Statistics, Stochastic Processes and Applications (SSPA) group). Additionally, part of this research was undertaken while I.S.-F. held the FCT PhD grant 2020.06459.BD (DOI: https://doi.org/10.54499/2020.06459.BD).
Data Availability Statement
The original data sets analysed in the study are openly available in [,].
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AIC | Akaike Information Criterion |
| BIC | Bayesian Information Criterion |
| CCR | Competitive and Complementary Risks |
| CI | Confidence Interval |
| EEP | Extended Exponential–Poisson |
| ECP | Extended Chen–Poisson |
| HPP | Homogeneous Poisson Process |
| LR | Likelihood Ratio |
| ML | Maximum Likelihood |
| NHPP | Non-Homogeneous Poisson Process |
| RCS | Restricted Cubic Spline |
Appendix A. Derivatives of the Restricted Cubic Spline (RCS) Function of Log Time
The RCS function is defined in (7). Since the flexible rate model described in this work is formulated on the log time scale, the focus is on the RCS function of log time, i.e., with . Thus, the first derivative of in order to t is given by
with defined for as
where . Hence, the second derivative is expressed as
with defined for as
References
- Andersen, P.K.; Gill, R.D. Cox’s regression model for counting processes: A large sample study. Ann. Stat. 1982, 10, 1100–1120. [Google Scholar] [CrossRef]
- Prentice, R.L.; Williams, B.J.; Peterson, A.V. On the regression analysis of multivariate failure time data. Biometrika 1981, 68, 373–379. [Google Scholar] [CrossRef]
- Cook, R.J.; Lawless, J.F. The Statistical Analysis of Recurrent Events; Springer Science & Business Media: New York, NY, USA, 2007. [Google Scholar]
- Aalen, O.O.; Husebye, E. Statistical analysis of repeated events forming renewal processes. Stat. Med. 1991, 10, 1227–1240. [Google Scholar] [CrossRef] [PubMed]
- Kelly, P.J.; Lim, L.L.Y. Survival analysis for recurrent event data: An application to childhood infectious diseases. Stat. Med. 2000, 19, 13–33. [Google Scholar] [CrossRef]
- Lawless, J.F.; Nadeau, C. Some simple robust methods for the analysis of recurrent events. Technometrics 1995, 37, 158–168. [Google Scholar] [CrossRef]
- Lawless, J.F.; Nadeau, C.; Cook, R.J. Analysis of mean and rate functions for recurrent events. In Proceedings of the First Seattle Symposium in Biostatistics, Melbourne, VIC, Australia, 20–21 November 1995; Lin, D.Y., Fleming, T.R., Eds.; Springer: New York, NY, USA, 1997; pp. 37–49. [Google Scholar] [CrossRef]
- Lin, D.Y.; Wei, L.J.; Ying, Z. Accelerated failure time models for counting processes. Biometrika 1998, 85, 605–618. [Google Scholar] [CrossRef]
- Lin, D.Y.; Wei, L.J.; Yang, I.; Ying, Z. Semiparametric regression for the mean and rate functions of recurrent events. J. R. Stat. Soc. B Stat. Methodol. 2000, 62, 711–730. [Google Scholar] [CrossRef]
- Liu, Y.; Wu, Y.; Cai, J.; Zhou, H. Additive–multiplicative rates model for recurrent events. Lifetime Data Anal. 2010, 16, 353–373. [Google Scholar] [CrossRef]
- Schaubel, D.E.; Zeng, D.; Cai, J. A semiparametric additive rates model for recurrent event data. Lifetime Data Anal. 2006, 12, 389–406. [Google Scholar] [CrossRef]
- Sun, X.; Peng, L.; Huang, Y.; Lai, H.J. Generalizing quantile regression for counting processes with applications to recurrent events. J. Am. Stat. Assoc. 2016, 111, 145–156. [Google Scholar] [CrossRef]
- Sun, L.; Tong, X.; Zhou, X. A class of Box-Cox transformation models for recurrent event data. Lifetime Data Anal. 2011, 17, 280–301. [Google Scholar] [CrossRef] [PubMed]
- Cook, R.J.; Lawless, J.F. Life history analysis with multistate models: A review and some current issues. Can. J. Stat. 2022, 50, 1270–1298. [Google Scholar] [CrossRef]
- Meira-Machado, L.; de Uña-Álvarez, J.; Cadarso-Suárez, C.; Andersen, P.K. Multi-state models for the analysis of time-to-event data. Stat. Methods Med. Res. 2009, 18, 195–222. [Google Scholar] [CrossRef] [PubMed]
- Box-Steffensmeier, J.M.; De Boef, S. Repeated events survival models: The conditional frailty model. Stat. Med. 2006, 25, 3518–3533. [Google Scholar] [CrossRef]
- Liu, X.R.; Pawitan, Y.; Clements, M.S. Generalized survival models for correlated time-to-event data. Stat. Med. 2017, 36, 4743–4762. [Google Scholar] [CrossRef]
- Barthel, N.; Geerdens, C.; Czado, C.; Janssen, P. Dependence modeling for recurrent event times subject to right-censoring with D-vine copulas. Biometrics 2019, 75, 439–451. [Google Scholar] [CrossRef]
- Lee, J.; Cook, R.J. Dependence modeling for multi-type recurrent events via copulas. Stat. Med. 2019, 38, 4066–4082. [Google Scholar] [CrossRef]
- Lin, D.; Sun, W.; Ying, Z. Nonparametric estimation of the gap time distribution for serial events with censored data. Biometrika 1999, 86, 59–70. [Google Scholar] [CrossRef]
- Moreira, A.; Araújo, A.; Meira-Machado, L. Estimation of the bivariate distribution function for censored gap times. Commun. Stat. Simul. Comput. 2017, 46, 275–300. [Google Scholar] [CrossRef]
- Schaubel, D.E.; Cai, J. Non-parametric estimation of gap time survival functions for ordered multivariate failure time data. Stat. Med. 2004, 23, 1885–1900. [Google Scholar] [CrossRef]
- Zhao, X.; Zhou, X. Modeling gap times between recurrent events by marginal rate function. Comput. Stat. Data Anal. 2012, 56, 370–383. [Google Scholar] [CrossRef]
- Royston, P.; Parmar, M.K. Flexible parametric proportional-hazards and proportional-odds models for censored survival data, with application to prognostic modelling and estimation of treatment effects. Stat. Med. 2002, 21, 2175–2197. [Google Scholar] [CrossRef] [PubMed]
- Jullum, M.; Hjort, N.L. What price semiparametric Cox regression? Lifetime Data Anal. 2019, 25, 406–438. [Google Scholar] [CrossRef]
- Reid, N. A conversation with Sir David Cox. Stat. Sci. 1994, 9, 439–455. [Google Scholar] [CrossRef]
- Macera, M.A.; Louzada, F.; Cancho, V.G.; Fontes, C.J.F. The exponential-Poisson model for recurrent event data: An application to a set of data on malaria in Brazil. Biom. J. 2015, 57, 201–214. [Google Scholar] [CrossRef]
- Louzada, F.; Macera, M.A.; Cancho, V.G. The Poisson-exponential model for recurrent event data: An application to bowel motility data. J. Appl. Stat. 2015, 42, 2353–2366. [Google Scholar] [CrossRef]
- Louzada, F.; Macera, M.A.; Cancho, V.G. A gap time model based on a multiplicative marginal rate function that accounts for zero-recurrence units. Stat. Methods Med. Res. 2017, 26, 2000–2010. [Google Scholar] [CrossRef]
- Sousa-Ferreira, I.; Abreu, A.M.; Rocha, C. An additive shared frailty model for recurrent gap time data in the presence of zero-recurrence subjects. In New Frontiers in Statistics and Data Science; Henriques-Rodrigues, L., Menezes, R., Machado, L.M., Faria, S., de Carvalho, M., Eds.; Springer Nature: Cham, Switzerland, 2025; pp. 27–42. [Google Scholar] [CrossRef]
- Sousa-Ferreira, I.; Rocha, C.; Abreu, A.M. The extended Chen–Poisson marginal rate model for recurrent gap time data. In Recent Developments in Statistics and Data Science; Bispo, R., Henriques-Rodrigues, L., Alpizar-Jara, R., de Carvalho, M., Eds.; Springer International Publishing: Cham, Switzerland, 2022; pp. 337–351. [Google Scholar] [CrossRef]
- Ramos, P.L.; Dey, D.K.; Louzada, F.; Lachos, V.H. An extended Poisson family of life distribution: A unified approach in competitive and complementary risks. J. Appl. Stat. 2020, 47, 306–322. [Google Scholar] [CrossRef]
- Sousa-Ferreira, I.; Abreu, A.M.; Rocha, C. The extended Chen-Poisson lifetime distribution. Revstat. Stat. J. 2023, 21, 173–196. [Google Scholar] [CrossRef]
- Durrleman, S.; Simon, R. Flexible regression models with cubic splines. Stat. Med. 1989, 8, 551–561. [Google Scholar] [CrossRef]
- Crowther, M.J.; Lambert, P.C. A general framework for parametric survival analysis. Stat. Med. 2014, 33, 5280–5297. [Google Scholar] [CrossRef] [PubMed]
- Herndon, J.E.; Harrell, F.E. The restricted cubic spline hazard model. Comm. Statist. Theory Methods 1990, 19, 639–663. [Google Scholar] [CrossRef]
- Royston, P.; Lambert, P.C. Flexible Parametric Survival Analysis Using Stata: Beyond the Cox Model; Stata Press: College Station, TX, USA, 2011. [Google Scholar]
- Rutherford, M.J.; Crowther, M.J.; Lambert, P.C. The use of restricted cubic splines to approximate complex hazard functions in the analysis of time-to-event data: A simulation study. J. Stat. Comput. Sim. 2015, 85, 777–793. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2025. [Google Scholar]
- Chernoff, H. On the distribution of the likelihood ratio. Ann. Math. Stat. 1954, 25, 573–578. [Google Scholar] [CrossRef]
- Self, S.; Liang, K. Asymptotic properties of maximum likelihood estimators and likelihood ratio tests under nonstandard conditions. J. Am. Stat. Assoc. 1987, 82, 605–610. [Google Scholar] [CrossRef]
- González, J.R.; Fernandez, E.; Moreno, V.; Ribes, J.; Peris, M.; Navarro, M.; Cambray, M.; Borràs, J.M. Sex differences in hospital readmission among colorectal cancer patients. J. Epidemiol. Community Health 2005, 59, 506–511. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).