Optimal Tuning of Robot–Environment Interaction Controllers via Differential Evolution: A Case Study on (3,0) Mobile Robots
Abstract
1. Introduction
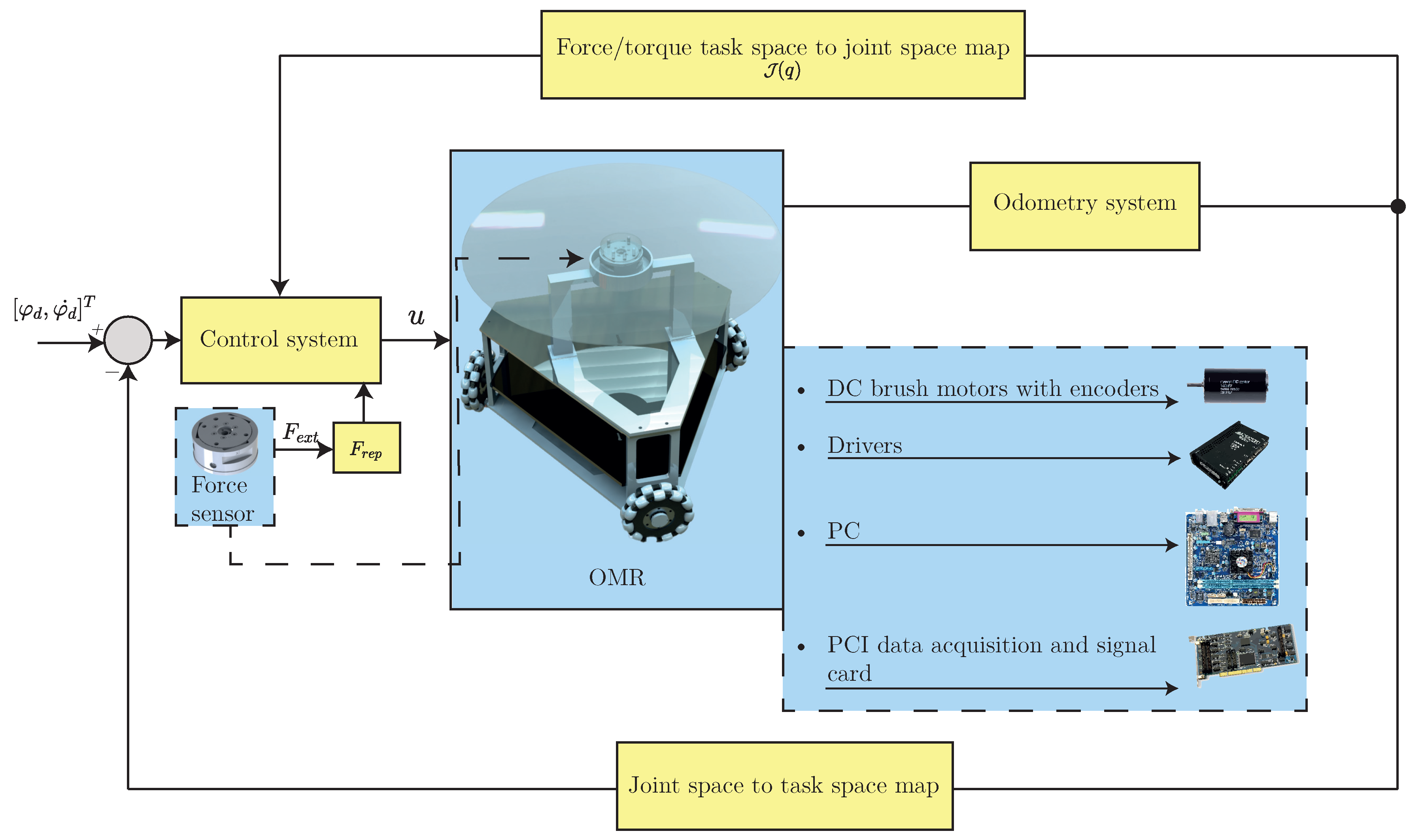
2. Controller Tuning Approach for Robot–Environment Interactions Based on Differential Evolution Optimizers
2.1. Robot Dynamics and Control System
- Stability Analysis
2.1.1. Repulsive Force as a Potential Field
2.1.2. Repulsive Potential Fields
2.2. Optimization Problem Formulation
2.3. Case Study: Application to Omnidirectional Mobile Robots
3. Optimization Techniques
| Algorithm 1 Pseudocode |
| Require: Maximum generations (), Population size (), Bounds (), Crossover rate (), Scaling factor (). Ensure: Best solution .
|
- Initialization
- Mutation
- Crossover
- Selection
| Nomenclature | Variant |
|---|---|
| DE/rand/1/bin | |
| DE/rand/1/exp | |
| DE/best/1/bin | |
| DE/best/1/exp | |
| DE/current-to-rand/1/bin |
4. Results
4.1. Optimization Process Conditions
4.2. Statistical Analysis of the Algorithm Performance
- The most promising algorithms are DE/best/1/bin and DE/best/1/exp among the DE variants. The inferential statistics indicate no significant difference (as shown by the overlap in the figure) and, thus, those algorithms perform similarly.
- DE/best/1/bin provides the best value through the particular thirty executions according to the descriptive statistics.
- The DE/rand/1/bin, DE/rand/1/exp, and DE/current-to-rand/1/bin perform similarly (those overlap in the figure), and those represent the worst algorithms for the particular controller tuning problem.
4.3. Validation of the Controller Tuning Approach for Robot–Environment Interactions
4.3.1. Simulation–Experimentation Results with Virtual External Force
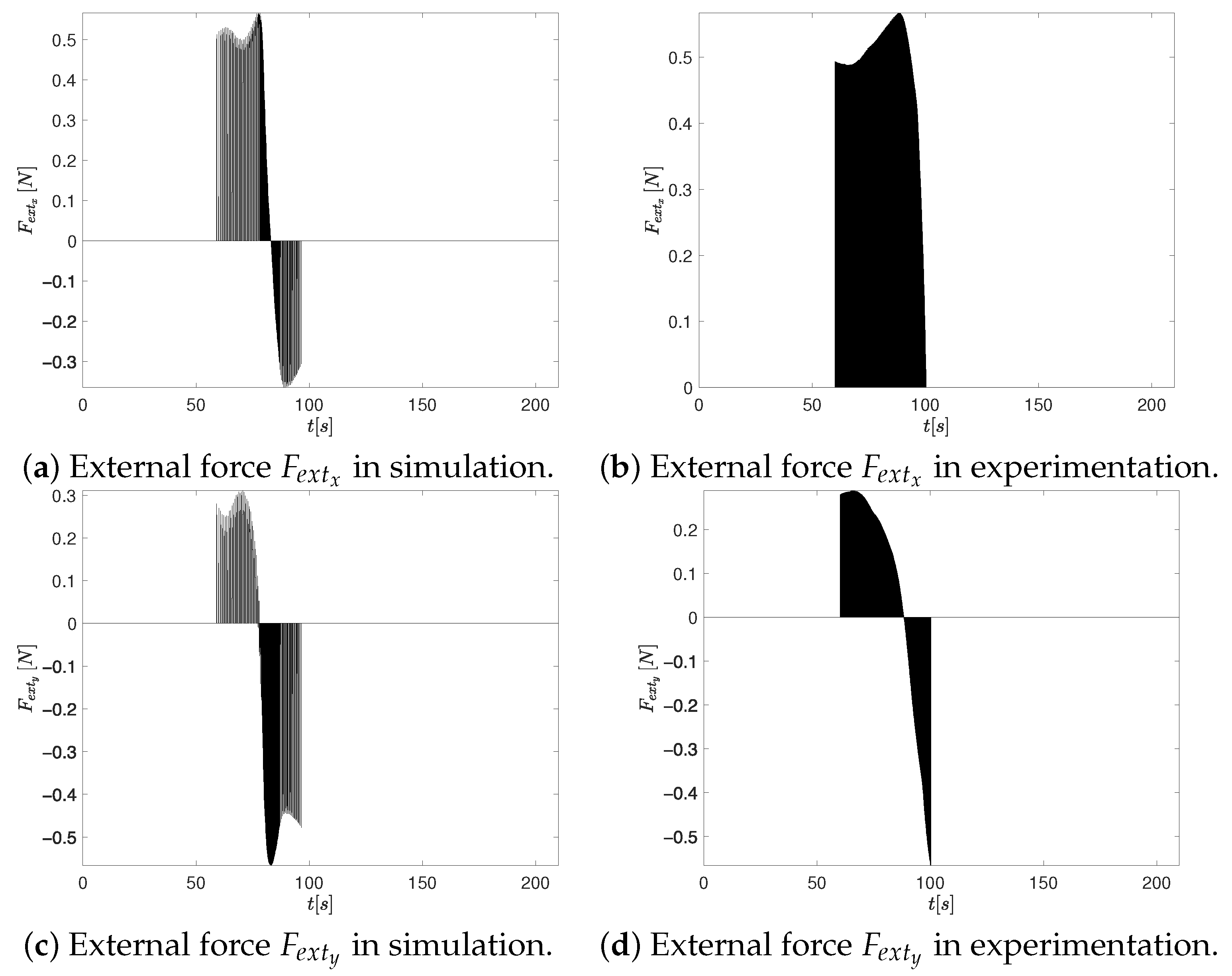
4.3.2. Comparative Results
- The tradeoff between the tracking error and the controller signal’s smoothness is an important factor to be considered in the robot–environment interaction task. It is observed that the proposed CTAwREI reduces the tradeoff related to the performance function J by in simulations concerning the CCTA (see J column). The experimental results reveal a reduction of in such a tradeoff.
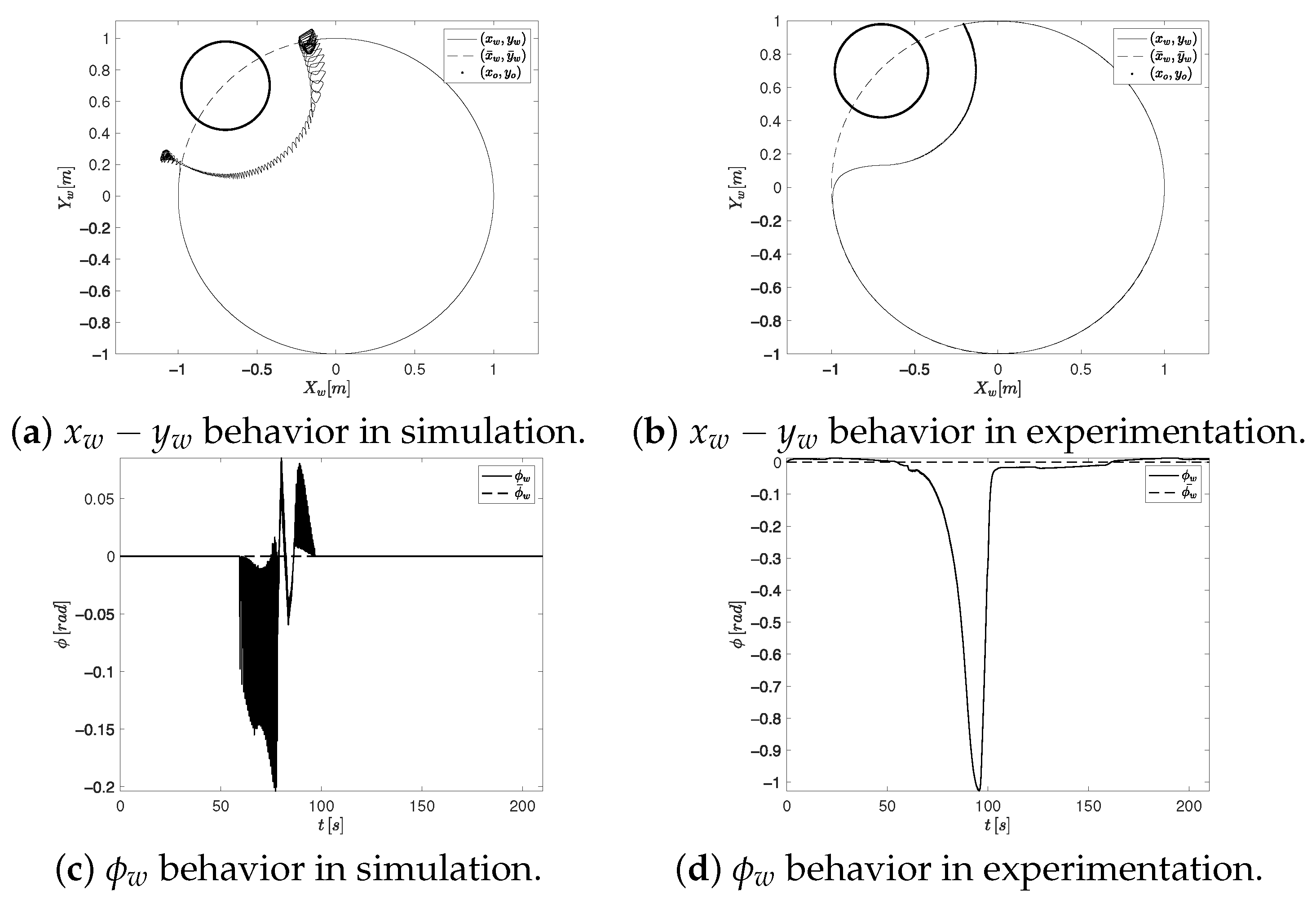
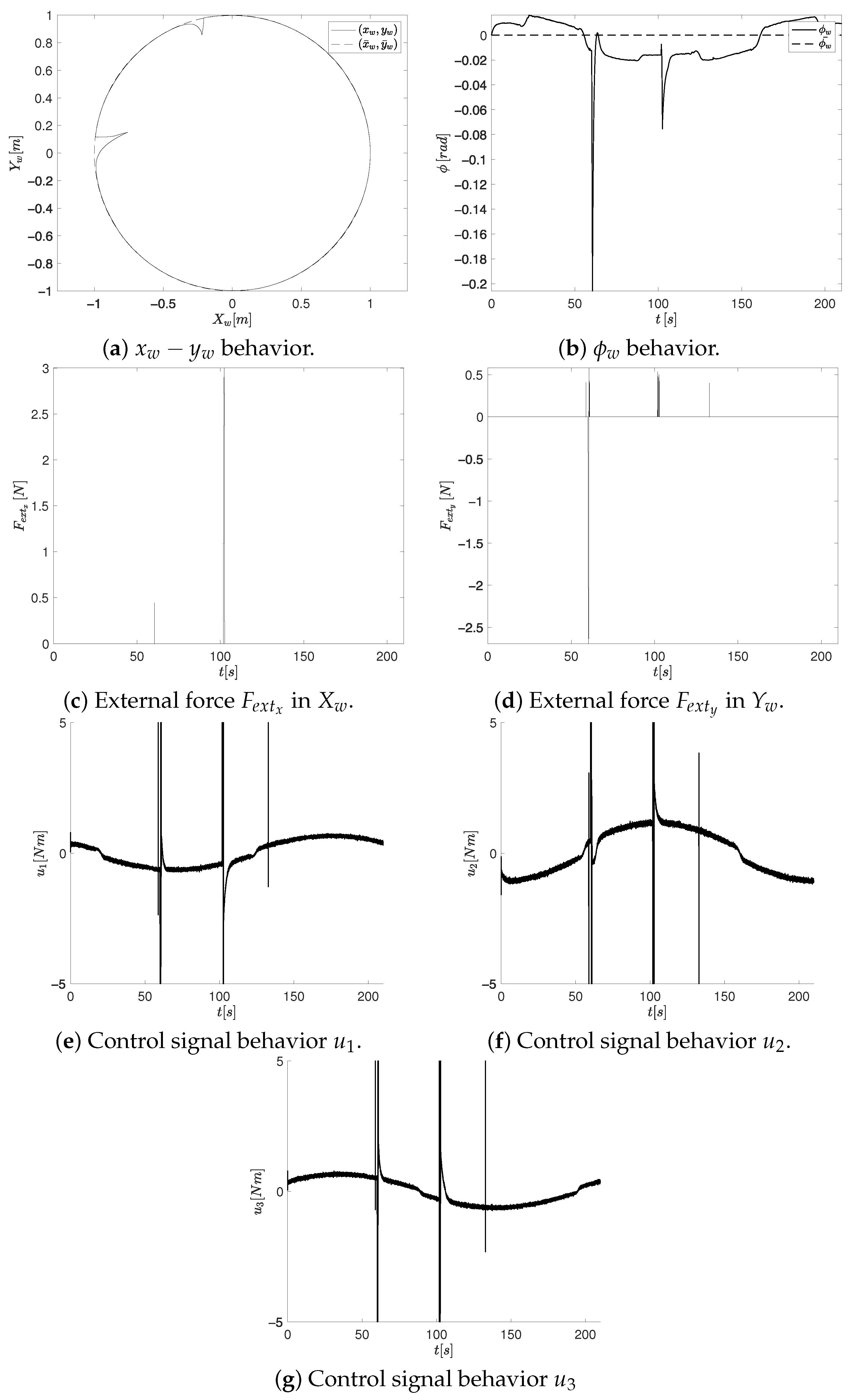
- Once the OMR moves beyond the obstacle, the proposed CTAwREI reduces the tracking error in the Cartesian position and orientation compared to CCTA by and , respectively. In the experimental results, the tracking reduction is around and , respectively. Those results can be visualized in the MEDwO column of Table 6. In Figure 10a,b and Figure 13a,b, these errors are also observed in the segments where the presence of the obstacle does not influence the OMR.
- The control signals of the proposal in the simulation are significantly smoother than the CCTA, as indicated in the ISDU column of Table 6 with a reduction of . This is also visualized in Figure 14, where the control signals commute between their limits. The lack of control smoothness in the controller tuning formulation of the comparative controller tuning approach could have an impact on the high vibration of the OMR and an increase in energy consumption. In the case of the experimental result, the reduction of the control signal is .
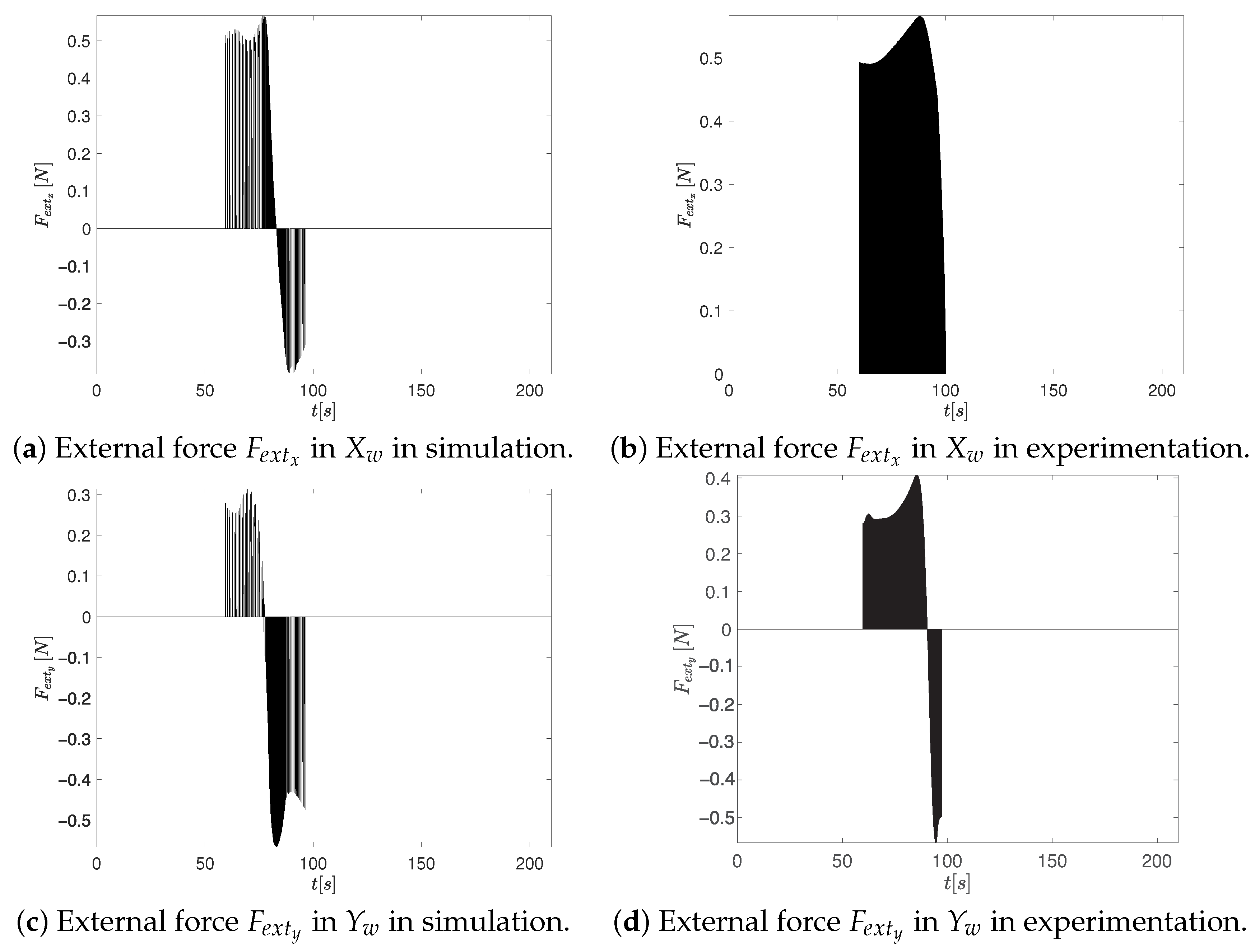
- Although both controller tuning approaches exhibit similar overall behavior in terms of external forces (see Figure 12 and Figure 15), a noticeable difference arises in the axis force component during experimentation. Specifically, the CTAwREI approach produces a slightly higher peak in of 0.4 N compared to 0.3 N in the CCTA approach. This increase can be attributed to a redistribution of the repulsive force components along the and directions, resulting from the interaction between the repulsive potential field and the optimized controller gains. While increases, a compensatory reduction in is observed, indicating that the overall external interaction force is not intensified but rather reoriented. It is important to note that the resultant external force is determined by both components, and . Despite the higher peak in , the RMS value of the resultant external force in CTAwREI is lower than in CCTA (see the experimentation in column RMS of Table 6). It is important to note that the RMS value of the resultant external force in CTAwREI is also reduced by in the simulation. This marginal reduction suggests a more balanced force distribution, which contributes to smoother control actions, enhanced stability during interaction, and potentially lower energy consumption.
- In a real-world scenario, the proposed approach, which incorporates the synergy between the tracking error and the controller signal smoothness, benefits from the fact that once disturbed by an obstacle, the robot can follow the path more precisely and smoothly (see the MEDwO column), positively affecting energy consumption. Despite the fact that the experimental improvements are smaller compared to those observed in simulation, in practice, even slight improvements observed in experimental testing can significantly impact the task execution, particularly in high-precision applications where even minimal deviations can lead to significant performance degradation.
4.3.3. Experimentation Results with an Actual Force System
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhu, J.; Lyu, L.; Xu, Y.; Liang, H.; Zhang, X.; Ding, H.; Wu, Z. Intelligent soft surgical robots for next-generation minimally invasive surgery. Adv. Intell. Syst. 2021, 3, 2100011. [Google Scholar] [CrossRef]
- Yang, L.; Zhang, Z.; Zhang, Z.; Lou, Y.; Han, S.; Liu, J.; Fang, L.; Zhang, S. Design of Heavy-Load Soft Robots Based on a Dual Biomimetic Structure. Biomimetics 2024, 9, 398. [Google Scholar] [CrossRef] [PubMed]
- Pan, L. Motion trajectory control system for production line robots based on variable domain fuzzy control. Adv. Multimed. 2022, 2022, 3893937. [Google Scholar] [CrossRef]
- Spong, M.W. Robot Dynamics and Control, 1st ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1989. [Google Scholar]
- Ogata, K. Modern Control Engineering, 4th ed.; Prentice Hall PTR: Hoboken, NJ, USA, 2001. [Google Scholar]
- Borase, R.P.; Maghade, D.; Sondkar, S.; Pawar, S. A review of PID control, tuning methods and applications. Int. J. Dyn. Control 2021, 9, 818–827. [Google Scholar] [CrossRef]
- Rodríguez-Molina, A.; Mezura-Montes, E.; Villarreal-Cervantes, M.G.; Aldape-Pérez, M. Multi-objective meta-heuristic optimization in intelligent control: A survey on the controller tuning problem. Appl. Soft Comput. 2020, 93, 106342. [Google Scholar] [CrossRef]
- Reeves, C.R. Heuristic search methods: A review. In Operational Research-Keynote Papers; Springer: Cham, Switzerland, 1996; pp. 122–149. [Google Scholar]
- Franceschi, P.; Castaman, N.; Ghidoni, S.; Pedrocchi, N. Precise Robotic Manipulation of Bulky Components. IEEE Access 2020, 8, 222476–222485. [Google Scholar] [CrossRef]
- Vignesh, C.; Uma, M.; Sethuramalingam, P. Development of rapidly exploring random tree based autonomous mobile robot navigation and velocity predictions using K-nearest neighbors with fuzzy logic analysis. Int. J. Interact. Des. Manuf. (IJIDeM) 2024, 18, 1–25. [Google Scholar] [CrossRef]
- Zhou, Q.; Feng, H.; Liu, Y. Multigene and Improved Anti-Collision RRT* Algorithms for Unmanned Aerial Vehicle Task Allocation and Route Planning in an Urban Air Mobility Scenario. Biomimetics 2024, 9, 125. [Google Scholar] [CrossRef]
- Sun, X.; Deng, S.; Tong, B.; Wang, S.; Zhang, C.; Jiang, Y. Hierarchical framework for mobile robots to effectively and autonomously explore unknown environments. ISA Trans. 2023, 134, 1–15. [Google Scholar] [CrossRef]
- Sharma, U.; Medasetti, U.S.; Deemyad, T.; Mashal, M.; Yadav, V. Mobile Robot for Security Applications in Remotely Operated Advanced Reactors. Appl. Sci. 2024, 14, 2552. [Google Scholar] [CrossRef]
- Taheri, H.; Zhao, C.X. Omnidirectional mobile robots, mechanisms and navigation approaches. Mech. Mach. Theory 2020, 153, 103958. [Google Scholar] [CrossRef]
- Achirei, S.D.; Mocanu, R.; Popovici, A.T.; Dosoftei, C.C. Model-predictive control for omnidirectional mobile robots in logistic environments based on object detection using CNNs. Sensors 2023, 23, 4992. [Google Scholar] [CrossRef] [PubMed]
- Tao, Y.; Li, M.; Cao, X.; Lu, P. Mobile robot collision avoidance based on deep reinforcement learning with motion constraints. IEEE Trans. Intell. Veh. 2024. [Google Scholar] [CrossRef]
- Mirsky, R.; Xiao, X.; Hart, J.; Stone, P. Conflict Avoidance in Social Navigation—A Survey. ACM Trans. Hum.-Robot. Interact. 2024, 13, 1–36. [Google Scholar] [CrossRef]
- Spiess, F.; Reinhart, L.; Strobel, N.; Kaiser, D.; Kounev, S.; Kaupp, T. People detection with depth silhouettes and convolutional neural networks on a mobile robot. J. Image Graph. 2021, 9, 135–139. [Google Scholar] [CrossRef]
- Zhang, J.; Lu, Y.; Che, L.; Zhou, M. Moving-distance-minimized PSO for mobile robot swarm. IEEE Trans. Cybern. 2021, 52, 9871–9881. [Google Scholar] [CrossRef]
- Rodriguez-Molina, A.; Solis-Romero, J.; Villarreal-Cervantes, M.G.; Serrano-Perez, O.; Flores-Caballero, G. Path-planning for mobile robots using a novel variable-length differential evolution variant. Mathematics 2021, 9, 357. [Google Scholar] [CrossRef]
- da Rocha Balthazar, G.; Silveira, R.M.F.; da Silva, I.J.O. How Do Escape Distance Behavior of Broiler Chickens Change in Response to a Mobile Robot Moving at Two Different Speeds? Animals 2024, 14, 1014. [Google Scholar] [CrossRef]
- Villani, L.; De Schutter, J. Force Control. In Springer Handbook of Robotics; Springer: Berlin/Heidelberg, Germany, 2016; pp. 195–220. [Google Scholar]
- Shin, H.; Kim, S.; Seo, K.; Rhim, S. A virtual pressure and force sensor for safety evaluation in collaboration robot application. Sensors 2019, 19, 4328. [Google Scholar] [CrossRef]
- Sharkawy, A.N.; Ma’arif, A.; Furizal; Sekhar, R.; Shah, P. A Comprehensive Pattern Recognition Neural Network for Collision Classification Using Force Sensor Signals. Robotics 2023, 12, 124. [Google Scholar] [CrossRef]
- Li, S.; Xu, J. Multiaxis Force/Torque Sensor Technologies: Design Principles and Robotic Force Control Applications: A Review. IEEE Sens. J. 2025, 25, 4055–4069. [Google Scholar] [CrossRef]
- Park, K.M.; Park, F.C. Collision Detection for Robot Manipulators: Methods and Algorithms; Springer: Berlin/Heidelberg, Germany, 2023. [Google Scholar]
- Yousefizadeh, S.; Bak, T. Unknown external force estimation and collision detection for a cooperative robot. Robotica 2020, 38, 1665–1681. [Google Scholar] [CrossRef]
- Liu, S.; Wang, L.; Wang, X.V. Sensorless force estimation for industrial robots using disturbance observer and neural learning of friction approximation. Robot. Comput.-Integr. Manuf. 2021, 71, 102168. [Google Scholar] [CrossRef]
- Zurlo, D.; Heitmann, T.; Morlock, M.; De Luca, A. Collision Detection and Contact Point Estimation Using Virtual Joint Torque Sensing Applied to a Cobot. In Proceedings of the 2023 IEEE International Conference on Robotics and Automation (ICRA), London, UK, 29 May–2 June 2023; pp. 7533–7539. [Google Scholar] [CrossRef]
- Rosales, A.; Heikkilä, T. Analysis and design of direct force control for robots in contact with uneven surfaces. Appl. Sci. 2023, 13, 7233. [Google Scholar] [CrossRef]
- Abbas, M.; Al Issa, S.; Dwivedy, S.K. Event-triggered adaptive hybrid position-force control for robot-assisted ultrasonic examination system. J. Intell. Robot. Syst. 2021, 102, 84. [Google Scholar] [CrossRef]
- Zhou, B.; Song, F.; Liu, Y.; Fang, F.; Gan, Y. Robust sliding mode impedance control of manipulators for complex force-controlled operations. Nonlinear Dyn. 2023, 111, 22267–22281. [Google Scholar] [CrossRef]
- Yoon, I.; Na, M.; Song, J.B. Assembly of low-stiffness parts through admittance control with adaptive stiffness. Robot. Comput.-Integr. Manuf. 2024, 86, 102678. [Google Scholar] [CrossRef]
- Tao, Q.; Liu, J.; Zheng, Y.; Yang, Y.; Lin, C.; Guang, C. Evaluation of an active disturbance rejection controller for ophthalmic robots with piezo-driven injector. Micromachines 2024, 15, 833. [Google Scholar] [CrossRef]
- Roveda, L.; Piga, D. Sensorless environment stiffness and interaction force estimation for impedance control tuning in robotized interaction tasks. Auton. Robot. 2021, 45, 371–388. [Google Scholar] [CrossRef]
- Abdullah Hashim, A.A.; Ghani, N.M.A.; Tokhi, M.O. Enhanced PID for pedal vehicle force control using hybrid spiral sine-cosine optimization and experimental validation. J. Low Freq. Noise Vib. Act. Control. 2025, 14613484251320723. [Google Scholar] [CrossRef]
- Chen, J.; Deng, L.; Hua, Z.; Ying, W.; Zhao, J. Bayesian optimization-based efficient impedance controller tuning for robotic interaction with force feedback. IEEE Trans. Instrum. Meas. 2023, 72, 1–10. [Google Scholar] [CrossRef]
- Yanyong, S.; Kaitwanidvilai, S. Experimental realization of PSO-based hybrid adaptive sliding mode control for force impedance control systems. Results Control. Optim. 2025, 19, 100548. [Google Scholar] [CrossRef]
- Zhai, J.; Zeng, X.; Su, Z. An intelligent control system for robot massaging with uncertain skin characteristics. Ind. Robot. Int. J. Robot. Res. Appl. 2022, 49, 634–644. [Google Scholar] [CrossRef]
- Shaw, J.S.; Lee, S.Y. Using genetic algorithm for drawing path planning in a robotic arm pencil sketching system. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2024, 238, 7134–7142. [Google Scholar] [CrossRef]
- Sun, C.; Zhu, H. Active Disturbance Rejection Control of Bearingless Permanent Magnet Slice Motor Based on RPROP Neural Network Optimized by Improved Differential Evolution Algorithm. IEEE Trans. Power Electron. 2024, 39, 3064–3074. [Google Scholar] [CrossRef]
- Ahmed, H.; As’arry, A.; Hairuddin, A.A.; Khair Hassan, M.; Liu, Y.; Onwudinjo, E.C.U. Online DE Optimization for Fuzzy-PID Controller of Semi-Active Suspension System Featuring MR Damper. IEEE Access 2022, 10, 129125–129138. [Google Scholar] [CrossRef]
- Meng, M.; Zhou, C.; Lv, Z.; Zheng, L.; Feng, W.; Wu, T.; Zhang, X. Research on a Method of Robot Grinding Force Tracking and Compensation Based on Deep Genetic Algorithm. Machines 2023, 11, 1075. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential Evolution—A Simple and Efficient Heuristic for global Optimization over Continuous Spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Serrano-Pérez, O.; Villarreal-Cervantes, M.G.; Rodríguez-Molina, A.; Serrano-Pérez, J. Offline robust tuning of the motion control for omnidirectional mobile robots. Appl. Soft Comput. 2021, 110, 107648. [Google Scholar] [CrossRef]
- Mousakazemi, S.M.H. Comparison of the error-integral performance indexes in a GA-tuned PID controlling system of a PWR-type nuclear reactor point-kinetics model. Prog. Nucl. Energy 2021, 132, 103604. [Google Scholar] [CrossRef]
- Tavazoei, M.S. Notes on integral performance indices in fractional-order control systems. J. Process. Control. 2010, 20, 285–291. [Google Scholar] [CrossRef]
- Reynoso-Meza, G.; Garcia-Nieto, S.; Sanchis, J.; Blasco, F.X. Controller Tuning by Means of Multi-Objective Optimization Algorithms: A Global Tuning Framework. IEEE Trans. Control. Syst. Technol. 2013, 21, 445–458. [Google Scholar] [CrossRef]
- Osyczka, A. Multicriterion Optimization in Engineering with FORTRAN Programs; Ellis Horwood Series in Engineering Science; E. Horwood: Chichester, UK, 1984. [Google Scholar]
- Villarreal-Cervantes, M.G.; Cruz-Villar, C.A.; Álvarez-Gallegos, J.; Portilla-Flores, E.A. Kinematic dexterity maximization of an omnidirectional wheeled mobile robot: A comparison of metaheuristic and sqp algorithms. Int. J. Adv. Robot. Syst. 2012, 9, 161. [Google Scholar] [CrossRef]
- Vázquez, J.; Velasco-Villa, M. Path-Tracking Dynamic Model Based Control of an Omnidirectional Mobile Robot. IFAC Proc. Vol. 2008, 41, 5365–5370. [Google Scholar] [CrossRef]
- Villarreal-Cervantes, M.G.; Alvarez-Gallegos, J. Off-line PID control tuning for a planar parallel robot using DE variants. Expert Syst. Appl. 2016, 64, 444–454. [Google Scholar] [CrossRef]
- Rojas-López, A.G.; Villarreal-Cervantes, M.G.; Rodríguez-Molina, A. Optimum Online Controller Tuning Through DE and PSO Algorithms: Comparative Study with BLDC Motor and Offline Controller Tuning Strategy. In Proceedings of the 2023 10th International Conference on Soft Computing & Machine Intelligence (ISCMI), Mexico City, Mexico, 25–26 November 2023; pp. 215–221. [Google Scholar] [CrossRef]
- Serrano-Pérez, O.; Villarreal-Cervantes, M.G.; González-Robles, J.C.; Rodríguez-Molina, A. Meta-heuristic algorithms for the control tuning of omnidirectional mobile robots. Eng. Optim. 2020, 52, 325–342. [Google Scholar] [CrossRef]
- Huang, C.; Li, Y.; Yao, X. A Survey of Automatic Parameter Tuning Methods for Metaheuristics. IEEE Trans. Evol. Comput. 2020, 24, 201–216. [Google Scholar] [CrossRef]
- Derrac, J.; García, S.; Molina, D.; Herrera, F. A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms. SWarm Evol. Comput. 2011, 1, 3–18. [Google Scholar] [CrossRef]
- Villarreal-Cervantes, M.G.; Guerrero-Castellanos, J.F.; Ramírez-Martínez, S.; Sánchez-Santana, J.P. Stabilization of a (3,0) mobile robot by means of an event-triggered control. ISA Trans. 2015, 58, 605–613. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, J.; Zhang, O.; Zhao, Y.; Chen, W.; Gao, Y. Adaptive Disturbance Observer-Based Fixed-Time Tracking Control for Uncertain Robotic Systems. IEEE Trans. Ind. Electron. 2024, 71, 14823–14831. [Google Scholar] [CrossRef]


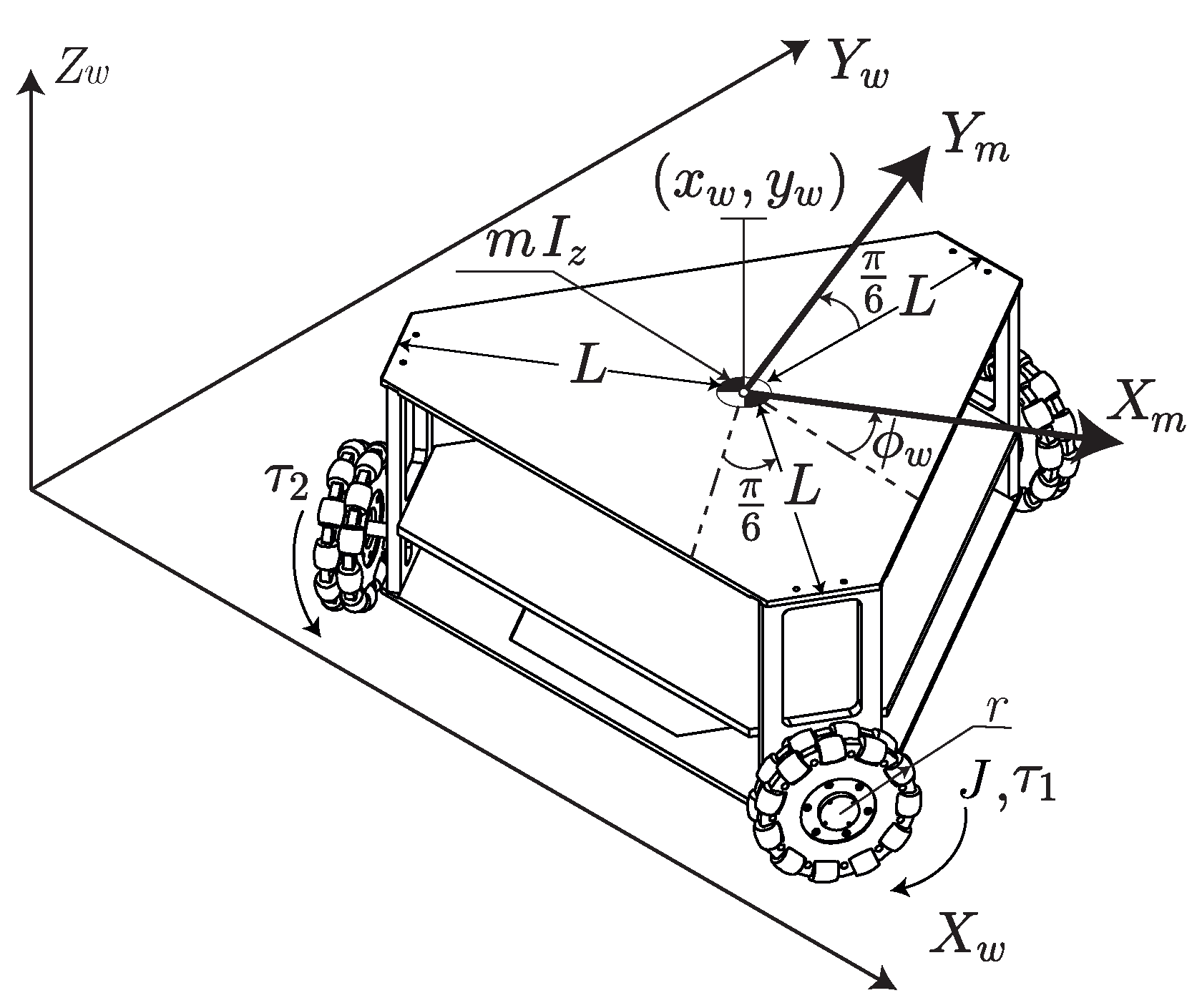








| Parameters | Description | Value | Units |
|---|---|---|---|
| r | Wheel radius | m | |
| L | Distance from the center of mass to the wheel | m | |
| m | Mass of the mobile robot | kg | |
| J | Wheel inertia | kgm | |
| Inertia of the mobile robot | kgm |
| DE Variant | Best | Worst | Average | Std. Dev. |
|---|---|---|---|---|
| DE/best/1/bin | 0.00017462 | 0.00017505 | 0.00017489 | |
| DE/best/1/exp | 0.00017463 | 0.00017507 | 0.00017488 | |
| DE/rand/1/bin | 0.00017473 | 0.0001752 | 0.00017504 | |
| DE/rand/1/exp | 0.00017474 | 0.00017517 | 0.00017502 | |
| DE/current-to-rand/1/bin | 0.00017473 | 0.00017515 | 0.00017501 |
| DE Variant | ISE | ISDU | J |
|---|---|---|---|
| DE/best/1/bin | 0.0235957 | 0.4987973 | 0.0001751 |
| DE/best/1/exp | 0.0235813 | 0.5029812 | 0.0001750 |
| DE/rand/1/bin | 0.0236669 | 0.4476411 | 0.0001754 |
| DE/rand/1/exp | 0.0236020 | 0.5284644 | 0.0001753 |
| DE/current-to-rand/1/bin | 0.0236105 | 0.4871172 | 0.0001752 |
| DE Variant | ||||||
|---|---|---|---|---|---|---|
| DE/best/1/bin | 49.57786 | 81.72389 | 99.87804 | 54.05250 | 80.16629 | 12.69077 |
| DE/best/1/exp | 49.04154 | 80.70653 | 99.65450 | 53.64447 | 80.41555 | 12.72143 |
| DE/rand/1/bin | 51.21167 | 84.04647 | 99.90994 | 51.47192 | 79.49911 | 12.76682 |
| DE/rand/1/exp | 47.62710 | 78.43357 | 99.78120 | 52.44649 | 82.91281 | 12.57076 |
| DE/current-to-rand/1/bin | 50.20748 | 83.57064 | 99.130624 | 50.92731 | 82.51137 | 12.51611 |
| Controller Tuning Approach | Sim/Exp | RMS | MEDwO | ISE | ISDU | J |
|---|---|---|---|---|---|---|
| CTAwREI | Sim | 0.124053 | 0.000149/0.000039 | 0.0236 | 0.5076 | 0.00017 |
| CCTA | Sim | 0.125882 | 0.012025/0.000397 | 0.0233 | 66.721 | 0.00045 |
| CTAwREI | Exp | 0.159726 | 0.019885/0.019022 | 0.0643 | 1.5526 | 0.00047 |
| CCTA | Exp | 0.159870 | 0.020182/0.020123 | 0.0646 | 1.5969 | 0.00048 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Paredes-Ballesteros, J.A.; Villarreal-Cervantes, M.G.; Benitez-Garcia, S.E.; Rodríguez-Molina, A.; Rojas-López, A.G.; Silva-García, V.M. Optimal Tuning of Robot–Environment Interaction Controllers via Differential Evolution: A Case Study on (3,0) Mobile Robots. Mathematics 2025, 13, 1789. https://doi.org/10.3390/math13111789
Paredes-Ballesteros JA, Villarreal-Cervantes MG, Benitez-Garcia SE, Rodríguez-Molina A, Rojas-López AG, Silva-García VM. Optimal Tuning of Robot–Environment Interaction Controllers via Differential Evolution: A Case Study on (3,0) Mobile Robots. Mathematics. 2025; 13(11):1789. https://doi.org/10.3390/math13111789
Chicago/Turabian StyleParedes-Ballesteros, Jesús Aldo, Miguel Gabriel Villarreal-Cervantes, Saul Enrique Benitez-Garcia, Alejandro Rodríguez-Molina, Alam Gabriel Rojas-López, and Victor Manuel Silva-García. 2025. "Optimal Tuning of Robot–Environment Interaction Controllers via Differential Evolution: A Case Study on (3,0) Mobile Robots" Mathematics 13, no. 11: 1789. https://doi.org/10.3390/math13111789
APA StyleParedes-Ballesteros, J. A., Villarreal-Cervantes, M. G., Benitez-Garcia, S. E., Rodríguez-Molina, A., Rojas-López, A. G., & Silva-García, V. M. (2025). Optimal Tuning of Robot–Environment Interaction Controllers via Differential Evolution: A Case Study on (3,0) Mobile Robots. Mathematics, 13(11), 1789. https://doi.org/10.3390/math13111789










