Abstract
As the number of objectives increases, the comprehensive processing performance of multi-objective optimization problems significantly declines. To address this challenge, this paper proposes an Angle-based dual-association Evolutionary Algorithm for Many-Objective Optimization (MOEA-AD). The algorithm enhances the exploration capability of unknown regions by associating empty subspaces with the solutions of the highest fitness through an angle-based bi-association strategy. Additionally, a novel quality assessment scheme is designed to evaluate the convergence and diversity of solutions, introducing dynamic penalty coefficients to balance the relationship between the two. Adaptive hierarchical sorting of solutions is performed based on the global diversity distribution to ensure the selection of optimal solutions. The performance of MOEA-AD is validated on several classic benchmark problems (with up to 20 objectives) and compared with five state-of-the-art multi-objective evolutionary algorithms. Experimental results demonstrate that the algorithm exhibits significant advantages in both convergence and diversity.
Keywords:
multi-objective optimization; angle; dual-association; evolutionary algorithm; hierarchical MSC:
68w50; 65K10; 90C29
1. Introduction
Many complex problems in the real world can be abstracted as multi-objective optimization problems (MaOPs) [1]. Such problems typically involve three or more conflicting objectives, which can be mathematically described as follows:
Here, is an n-dimensional decision variable in the decision space , and represents the m conflicting objective functions to be optimized simultaneously in the m-dimensional objective space. Due to the conflicts among these objectives, no solution exists that can optimize all objectives at the same time. In multi-objective optimization problems, an effective strategy involves producing a collection of Pareto-optimal solutions through balancing competing objectives [2]. Mathematically, solution x is considered to Pareto-dominate solution y (expressed as ) when x demonstrates equal or superior performance across all objective functions while exhibiting strictly better performance in at least one objective dimension.
A solution is considered Pareto optimal if no solution in set satisfies the condition . The aggregation of all such Pareto-optimal solutions in the decision space constitutes the Pareto-optimal set, with their corresponding objective vectors in the objective space forming the Pareto frontier.
In various practical domains, a wide range of complex real-world problems can be modeled as many-objective optimization problems (MaOPs). Typical examples include the optimal design of water distribution systems [3], search-based recommendation systems [4], and route planning problems [5]. The proven effectiveness of evolutionary algorithms (EA) in solving MaOPs in diverse application areas, such as magnetism research [6], supply chain optimization [7], task allocation in hierarchical multi-agent systems [8], wind-thermal economic emission dispatch [9], and vehicular navigation in road networks [3], has drawn considerable attention from the research community [10,11].
Despite these advances, recent empirical studies have shown that the performance of traditional multi-objective evolutionary algorithms (MOEAs) tends to degrade significantly as the number of objectives increases [12]. This degradation is primarily attributed to two major challenges as follows: First, the effectiveness of the Pareto dominance relation diminishes in high-dimensional objective spaces. As more objectives are considered, a large proportion of the population becomes non-dominated, which reduces the selection pressure toward the true Pareto front [13]. Consequently, the dominance-based sorting loses its discriminative power, making it difficult to guide the evolutionary process effectively.
As the number of objectives increases, many traditional metaheuristic algorithms, especially those based on Pareto front methods, face significant challenges in solving multi-objective optimization problems. These challenges primarily include the loss of selection pressure, difficulty in maintaining diversity, and imbalance between convergence and diversity. In high-dimensional objective spaces, traditional algorithms often fail to effectively explore sparse regions and tend to result in incomplete coverage of the solution space or premature convergence. To overcome these issues, we propose an angle-based evolutionary algorithm for addressing multi-objective optimization problems (MaOPs). Compared with existing reference point/vector based approaches, the main contributions of this paper are summarized as follows:
- (1)
- The proposed angle-based twofold association strategy incorporates null subspace consideration, establishing associations with the most fitness-appropriate solutions. This approach not only enhances the probability of exploring uncharted regions but also maintains convergence guarantees.
- (2)
- This paper presents a novel quality assessment scheme that has been developed to quantify solution quality within subspaces. This scheme initially evaluates both convergence and diversity metrics for each solution, with the diversity component further decomposed into global and local diversity measures. The incorporation of dynamic penalty coefficients serves to penalize solutions with inferior global diversity while preserving those located in sparse regions. Additionally, an adaptive two-phase sorting mechanism has been implemented to simultaneously maintain convergence and diversity characteristics.
- (3)
- To validate the efficacy of MOEA-AD, a comprehensive series of simulation experiments were conducted. The experimental results demonstrate that MOEA-AD outperforms existing MOEAs in addressing MaOPs, primarily attributed to its dual-phase sorting strategy. This innovative approach not only facilitates superior search space exploration and population diversity maintenance but also ensures robust convergence characteristics, thereby significantly enhancing the algorithm’s overall performance.
The remainder of this paper is organized as follows. Section 2 introduces the related work and background knowledge. Section 3 elaborates on the framework of the proposed algorithm and the specific implementation of its components. Section 4 presents the experimental results and provides detailed analysis and discussion. Finally, Section 5 concludes the paper.
2. Related Work and Background Knowledge
This section is divided into two main components. Section 2.1 examines the existing approaches and advancements in addressing MaOPs challenges. Section 2.2 outlines the essential background information on the relevant algorithms, facilitating a deeper understanding of the following discussions.
2.1. Related Work
The scalability of evolutionary algorithms in handling many-objective optimization problems (MaOPs) remains a major challenge due to the increasing number of objectives, which significantly reduces algorithmic effectiveness. Existing research efforts to address this issue can generally be categorized into four main strategies as follows: enhanced Pareto dominance mechanisms, problem simplification, objective reduction, and preference-driven optimization.
2.1.1. Enhanced Pareto Dominance Strategies
The first class of approaches seeks to improve Pareto dominance mechanisms to mitigate the declining selection pressure in high-dimensional objective spaces. As the number of objectives increases, most solutions tend to become non-dominated, which weakens the driving force toward convergence. To address this issue, various enhanced dominance techniques have been proposed.
For instance, Aguirre et al. [14] proposed an adaptive -ranking strategy, which performs fine-grained sorting after the initial Pareto classification, followed by randomized -dominance sampling to promote solution diversity. Jiang et al. [15] introduced a method that uses reference vectors and angle-penalized distances to balance convergence and diversity. Cai et al. [16] developed a dual-distance-based dominance relation leveraging the PBI (Penalty-based Boundary Intersection) function. Grid-based strategies have also proven effective; for example, Yang et al. [17] enhanced selection pressure through grid-based solution partitioning. Additionally, fuzzy logic has been incorporated into dominance assessment, where fuzzy dominance degrees allow for more nuanced fitness evaluation and ranking among solutions [18,19].
2.1.2. Problem Simplification Strategies
The second category focuses on simplifying MaOPs, particularly by identifying and eliminating redundant objectives. This dimensionality reduction helps to ease the computational burden while retaining solution quality.
Vijai et al. [20] proposed a federated learning-assisted NSGA-II framework that uses an optimal point set initialization strategy to enhance solution quality for simplified MaOPs. Meanwhile, Zhu et al. [21] introduced a neural network-based gradient descent method that decouples complex interdependencies between objectives, improving both convergence and diversity. However, simplification methods tend to lose effectiveness when applied to problems with inherently high-dimensional or complex Pareto fronts, limiting their practical scope to moderate-sized MaOPs.
2.1.3. Objective Reduction Strategies
Objective reduction techniques aim to decrease the dimensionality of the objective space by identifying essential objectives while discarding irrelevant or weakly contributing ones. These methods are especially useful in scenarios where many objectives are correlated or redundant.
A pioneering effort in this area is the PCA-NSGA-II algorithm by Deb and Saxena [22], which integrates Principal Component Analysis into the NSGA-II framework to filter out redundant objectives. Singh et al. [23] extended this idea by estimating the effective dimensionality of the Pareto front using extreme points, thereby constructing minimal yet representative objective subsets. Despite their merits, such strategies typically suffer performance degradation in highly complex or dynamic MaOPs, as they may omit crucial information during reduction.
2.1.4. Preference-Driven Optimization Strategies
The final category involves preference-driven approaches, which guide the search toward regions of interest on the Pareto front using decision-maker input. These methods significantly improve computational efficiency by narrowing the solution space according to predefined preferences.
Deb and Kumar [24] developed RD-NSGA-II, which incorporates reference direction guidance into the search process. Thiele et al. [25] proposed PBEA by integrating reference points into the IBEA framework. Further advancing this line of work, Wang et al. [26] introduced PICEA-g, which generates a complete Pareto approximation before integrating decision preferences. Although these approaches demonstrate strong performance in specific scenarios, over-reliance on preference information can cause premature convergence and hinder exploration, as noted by Bechikh et al. [27].
2.2. Basic Definition
Definition 1.
(Pareto dominance): Given two solutions, denoted as solution and solution , the following condition holds:
Then, it is said that dominates , or is dominated by , denoted as .
Definition 2.
(Pareto-optimal solution): The status of Pareto optimality is conferred upon a decision vector when the scenario is unattainable for any .
Definition 3.
(Pareto-optimal set): The ensemble encompassing every Pareto-optimal solution is delineated as follows:
Definition 4.
(): The ideal point is represented by the vector , with each denoting the minimal value within , where i ranges from 1 to m.
Definition 5.
(): The nadir point is represented by the vector , in which denotes the maximum value within , given that .
Definition 6.
(Reference vector generation): Reference vector partitions the objective space into N distinct subspaces. In this approach, reference vectors are drawn from the unit simplex, with their quantity being determined by the dimension m of the objective space and the number of segments H per objective axis, where . represents the reference vector corresponding to the i-th index.
3. The Proposed MOEA-AD
This section not only elaborates on the angle-based dual-association evolutionary algorithm framework and its components but also provides an in-depth analysis of the proposed innovations, thereby validating the uniqueness and originality of MOEA-AD.
3.1. The Main Framework of MOEA-AD
The overall structure of the MOEA-AD algorithm is outlined in Algorithm 1. The process begins by generating a set of predefined reference vectors. For cases where , Deb et al. [28] recommend using a two-layer reference vector structure with a reduced value of H, which enables a more uniform partitioning of the objective space into N distinct subregions. Subsequently, an initial population of size N is randomly generated. In the next phase, steps 3 and 4 compute the minimum and maximum values of each objective to identify the ideal point and the nadir point , respectively. The main loop of the algorithm (steps 6 to 27) is repeated until the termination criterion is met, which in this study is defined as a maximum of 10,000 function evaluations. In step 7, the offspring population is generated by applying genetic operators to the current parent population , including simulated binary crossover (SBX) [29] and polynomial mutation (PM) [30]. The parent population is then merged with the offspring population to form a new population . Step 8 performs non-dominated sorting on , followed by step 9, which updates the set of ideal points. To enhance computational efficiency, step 11 normalizes the objective values of all individuals. In step 12, a dual-association process is conducted to associate each solution with a reference vector. Then, in step 13, the solutions within each subregion are ranked using the evaluation strategy proposed in this study. The best-performing solution in each subregion is assigned to , while the remaining solutions are distributed into different levels (, , etc.), forming the set . From steps 14 to 18, adaptive selection is carried out in each subregion based on the progress of the iteration. The selected solutions are evaluated using an adaptive parameter K to determine whether to prioritize diversity ranking or convergence ranking. Finally, from steps 18 to 24, the solutions in are sequentially used to fill the new generation. If the population size N is not yet reached after all have been used, the remaining slots are filled by randomly selecting from the remaining candidate solutions to ensure population completeness. This mechanism effectively balances convergence and diversity throughout the evolutionary process. The following sections will provide a detailed explanation of the core components and implementation of MOEA-AD.
| Algorithm 1 The main framework of MOEA-AD |
| Input: N (Population size) Output: P (final population)
|
3.2. The Angle-Based Dual-Association Strategy
Once the entire objective space is divided into N distinct subspaces, the population spread across the objective space must be distributed among these subspaces. The approach of linking each solution in the normalized objective set to its nearest reference vector has been embraced in various recent studies, each with unique features and rationales. In the conventional association strategy [31], if a subspace lacks solutions, meaning it is empty, a solution is randomly picked and linked to that subspace. This implies that the randomly selected solution is allocated to the vacant subspace. This technique is referred to as random association. While random association aims to enhance the exploration of uncharted areas, the random selection of solutions might adversely affect the search process. In algorithms for subspace decomposition based on density [32], every non-dominated solution is linked to a subspace, with the density of each subspace being gauged by the count of solutions connected to it. Nonetheless, the existence of empty subspaces can result in flawed estimations. Moreover, certain approaches do not undertake additional measures and merely disregard these empty subspaces upon their appearance, potentially undermining the diversity of the solutions achieved. This technique of association is known as single association.
To more effectively explore uncharted areas and boost diversity, we have developed a dual association approach. Initially, akin to current techniques for linking empty subspaces [33], every reference vector creates a subspace, and each solution is linked to its nearest subspace. Yet, as previously mentioned, this can lead to empty subspaces and may not preserve the diversity of the solutions acquired. To address this limitation, we implement a secondary association phase. For every empty subspace, we link the nearest solution by employing the perpendicular Euclidean distance (between each solution and each reference vector) to gauge the distance between the solution and the subspace (denoted by the respective reference vector). This method markedly enhances the diversity of the solutions obtained, as elaborated subsequently.
Illustrated in Figure 1, the normalized population features vector as the normalization vector, where the origin o represents the ideal point, and u denotes the projection of onto the reference vector . Let denote the distance between the ideal point o and u, while represents the perpendicular Euclidean distance from to . The precise definitions of and are outlined as follows:
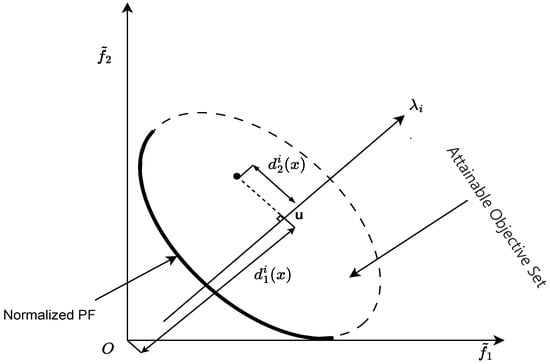
Figure 1.
Visual representation of distance and distance .
The initial association step aligns with the conventional methods as follows: for every solution , the perpendicular Euclidean distance between and each reference vector is computed, linking solution to the closest subspace. In the subsequent step, any empty subspaces lacking associated solutions are connected to the nearest solution through comparison . While the traditional dual association approach significantly enhances diversity, it exhibits somewhat limited convergence efficacy in addressing specific challenges. The angle-based dual association approach introduced in this study aims to mitigate this problem. During the initial phase, the solutions are connected following the conventional dual association technique. In particular, every solution within the collection is associated with its corresponding reference vector in the normalized objective space by means of the perpendicular Euclidean distance .
During the second phase (), we initially verify the presence of a solution set. Upon confirmation, we calculate the angle between every solution in and the reference vector of the vacant subspace, which is defined as follows:
In this context, functions as the fitness metric, while denotes the normalized distance between the candidate point and the origin within the objective space. Following this, the sine of is computed and then multiplied by the perpendicular Euclidean distance , resulting in . This product is utilized as the evaluation criterion in this study, as elaborated in Equation (8). It is employed to identify the optimal solution for linking with an unoccupied subspace. In the absence of an empty subspace, the secondary association phase is omitted. By combining distance and angular metrics, solutions more aligned with the empty subspace are prioritized. This method ensures population convergence while boosting diversity, thereby strengthening the algorithm’s robustness.
The angle-based dual-association strategy (Algorithm 2) aims to associate each solution in the normalized merged population with one of the predefined reference vectors in set W. First, all reference vectors are initialized with empty associated solution sets . Then, for each solution , the perpendicular Euclidean distance between its objective vector and each reference vector is calculated. The solution is associated with the reference vector that minimizes a penalty function , typically incorporating both distance and angle metrics. The solution is then added to the corresponding set .
| Algorithm 2 The angle-based dual-association strategy |
| Input: (The normalized merged population.), W (Reference vector set) Output: (Store all solutions associated with each reference vector)
|
3.3. Adaptive Evaluation Strategy
In order to holistically assess the potential of each solution, a novel quality evaluation function has been developed for solutions within each subspace . This function incorporates metrics for both convergence and diversity. The evaluation function for a solution x in subspace is defined as follows:
In this context, denotes the minimum perpendicular Euclidean distance between each solution x and the ideal point, serving as a metric to evaluate the convergence of solution x. A lower value of signifies the superior convergence properties of the algorithm. The minimal perpendicular Euclidean distance between each solution x and the reference vectors serves as a metric to assess the solution’s contribution to global diversity. A reduced value of reflects the enhanced diversity in the solution. denotes the mean distance between solution x and all other solutions within subspace . A lower value of reflects the greater diversity in solution x. u acts as a penalty function aimed at discouraging solutions in densely populated areas. The value of u increases with the number of solutions present in subspace . For this research, u is fixed at , while m denotes the count of problem objectives. With an increase in the number of objectives, the selection pressure intensifies significantly. Adaptively adjusting the weight of facilitates a more effective balance between convergence and diversity in high-dimensional scenarios.
3.4. Adaptive Two-Stage Sorting
After evaluating all solutions in Section 3.3, the solutions in subspace are sorted according to , resulting in . Following the sorting process, an appropriate number of solutions from are selected based on the adaptive formula, expressed as follows:
Select the top solutions from and compare them with k to choose a more suitable method for sorting the selected solutions. If , sort the solutions in based on . If , sort the solutions in based on to better balance convergence and diversity. Define k as the population size N divided by twice the number of objectives. In contrast to conventional selection methods, the dual-stage sorting introduced in this study adaptively organizes solutions according to iteration count and the number of problem objectives. This approach integrates both diversity and convergence metrics and enhances the preservation of solutions in sparsely populated areas, leading to an improved equilibrium between diversity and convergence.
3.5. Handling Multi-Objective Optimization Problems
To effectively address many-objective optimization problems (MaOPs), the proposed MOEA-AD adopts the following strategies:
- (1)
- Angle-based dual association: The algorithm assigns solutions to reference vectors by considering both perpendicular distance and the angular relationship, ensuring a well-spread distribution even in high-dimensional objective spaces.
- (2)
- Subspace-based quality evaluation: Each solution’s quality is evaluated not only by its convergence to the Pareto front but also by its diversity. The diversity is further categorized into the following: Global diversity, which measures the solution’s contribution to the overall spread. Local diversity, which maintains the distribution within subregions.
- (3)
- Dynamic penalty mechanism: A penalty is applied to solutions with poor global diversity, protecting sparse regions and promoting exploration in less explored areas.
- (4)
- Adaptive two-stage selection: To balance convergence and diversity, the algorithm uses a two-stage selection strategy. First, solutions are ranked based on their convergence and diversity scores; then, an adaptive mechanism selects the most representative solutions for the next generation.
These strategies collectively help MOEA-AD to maintain a balance between convergence and diversity, effectively tackling the challenges of solving MaOPs.
4. Experimental Study
This section outlines the experimental framework designed to evaluate the performance of the proposed MOEA-AD in addressing many-objective optimization challenges. Initially, a concise overview of the test problems and experimental configurations is provided. To ensure an equitable comparison, all competing algorithms are executed on the PlatEMO [34] platform (Matlab version: R2020b 64-bit), with the stipulation that the software must reside in the C drive to meet CPU specifications. Following this, the experimental outcomes are meticulously analyzed and deliberated to underscore the efficacy of the proposed MOEA-AD. Ultimately, ablation studies confirm the robust competitiveness of the introduced innovations.
4.1. Test Problems
To assess the performance of the six algorithms examined in this study, the DTLZ (DTLZ1-DTLZ7) [35] and WFG (WFG1-WFG9) [36] test suites were employed. These suites are extensively used as benchmarks in many-objective optimization. They feature a range of intricate properties, including degeneracy, bias, large-scale, non-separable, and partially separable decision variables in the decision space, along with linear, convex, concave, mixed geometric structures, and multimodal Pareto fronts (PF) in the objective space. These varied properties present considerable challenges to algorithm performance. Moreover, the objectives and decision variables in these test problems can be adjusted to any required scale.
In this experiment, the number of objectives for the test problems is set to range from 5 to 20, i.e., . For the DTLZ test suite, the number of decision variables is determined by the formula . The value of k may vary across different test problems. Following the recommendations in [29,35], the k value for DTLZ1 is set to 5; for DTLZ2 to DTLZ6, it is set to 10; and for DTLZ7, it is set to 20. For the WFG test suite, as suggested by [36,37], the number of decision variables for all test problems is set to 24, and the position-related parameter is set to .
4.2. Comparative Algorithms
To assess the effectiveness of the proposed MOEA-AD algorithm in addressing many-objective optimization problems (MaOPs), this research conducted comparative experiments with five prominent many-objective evolutionary algorithms (MaOEAs). NSGA-III [28] was selected as the benchmark algorithm, given its extensive application in solving MaOPs. ANSGA-III [38] was incorporated for its dynamic parameter and strategy adaptation, which enhances performance across diverse problems. SPEA/R [33], a decomposition-based algorithm that integrates Pareto dominance, was also included. Furthermore, the indicator-driven MaOEA-IGD [39] and the recently introduced MaOEA-IT [40] were part of the experiments, with MaOEA-IT utilizing novel techniques to favor solutions exhibiting strong convergence and diversity.
4.3. Experimental Settings
This subsection outlines the experimental configurations and details the parameter settings for each algorithm under comparison.
- (1)
- Execution and stopping condition: Every algorithm is run 20 times independently on each test case. The stopping condition for each execution is the attainment of the maximum function evaluations (MFEs). For the DTLZ1-7 and WFG1-9 test suites, the MFEs are configured as 99,960; 99,990; 100,100; 100,386; and 99,960 corresponding to objective counts m of 5, 8, 12, 16, and 20, respectively.
- (2)
- Statistical evaluation: The Wilcoxon rank-sum test is utilized to evaluate the statistical significance of the outcomes from MOEA-AD and the five other algorithms, with a significance threshold set at 0.05. In all tables, +, −, and ≈ indicate superior to, inferior to, and comparable to competing methods, respectively, while gray highlighting denotes the best value achieved on the current test problem.
- (3)
- Population size: The determination of population size N is governed by parameter H rather than being arbitrarily set. For problems involving 8, 12, 16, and 20 objectives, where , a two-tiered reference vector generation approach with reduced H values, as suggested in, is employed to generate intermediate reference vectors. Comparable configurations are applied to other algorithms. To maintain fairness in comparisons, identical population sizes are utilized across all algorithms.
- (4)
- Crossover and mutation parameters: All compared algorithms utilize SBX [29] and PM [30]. For SBX, the crossover probability is set to 1.0, and the distribution index is set to 20. For polynomial mutation, the distribution index and mutation probability are set to 20 and , respectively. More algorithm parameter settings are shown in Table 1.
 Table 1. Parameter settings of all compared algorithms.
Table 1. Parameter settings of all compared algorithms. - (5)
- Evaluation metrics: This paper employs two metrics, IGD and HV, to assess the diversity and convergence of the algorithms. IGD quantifies the average distance between the algorithm’s solutions and the sampled points on the true Pareto front (PF). A lower IGD value reflects superior convergence and diversity. Notably, solutions dominated by the reference point are omitted in HV calculations. HV is computed using PlatEMO [34], with a higher HV value indicating better algorithm performance.
4.4. Performance Comparison Analysis on the DTLZ Test Suite
The Wilcoxon rank-sum test results in Table 2 indicate that MOEA-AD achieves significantly superior IGD values compared to NSGA-III, ANSGA-III, SPEA/R, MaOEA-IGD, and MaOEA-IT across the 35 test instances. Specifically, MOEA-AD outperforms these algorithms in 17, 22, 21, 24, and 35 instances, respectively. In contrast, NSGA-III, ANSGA-III, SPEA/R, MaOEA-IGD, and MaOEA-IT exhibit better IGD results than MOEA-AD in only 11, 7, 10, 6, and 0 instances, respectively.

Table 2.
IGD results (mean and standard deviation) obtained by six algorithms on the DTLZ problems.
Similarly, the Wilcoxon rank-sum test results in Table 3 reveal that MOEA-AD demonstrates significantly better HV performance than NSGA-III, ANSGA-III, SPEA/R, MaOEA-IGD, and MaOEA-IT in the majority of the 35 test instances (15, 17, 21, 26, and 35 instances, respectively). Conversely, the HV results of NSGA-III, ANSGA-III, SPEA/R, MaOEA-IGD, and MaOEA-IT surpass those of MOEA-AD in only 12, 9, 12, 3, and 0 instances, respectively. These findings highlight MOEA-AD’s consistent dominance in both IGD and HV metrics across most test scenarios.

Table 3.
HV results (mean and standard deviation) obtained by six algorithms on the DTLZ problems.
In the DTLZ2 benchmark problem, MOEA-AD demonstrates superior performance in scenarios involving 16 and 20 objectives. For a clearer visualization of the outcomes from the six evaluated algorithms, Figure 2 illustrates the parallel coordinate plots of the ultimate solutions derived by each algorithm for the 20-objective DTLZ2 scenario. The figure reveals that MOEA-AD’s approximate Pareto Front (PF) showcases enhanced uniformity and convergence in the 20-objective DTLZ2 context, with SPEA/R trailing closely. Conversely, the remaining trio of algorithms fall short in achieving convergence to the authentic PF.
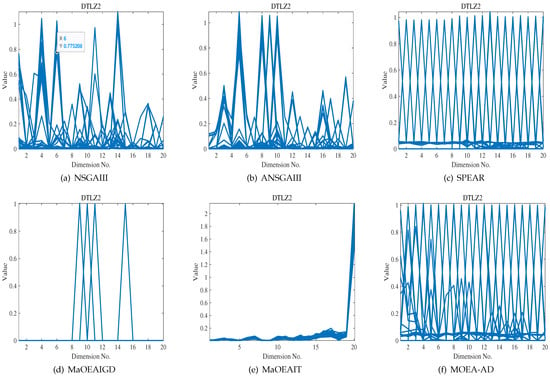
Figure 2.
Parallel coordinate visualization of the non-dominated solutions from six algorithms on the 20-objective DTLZ2 problem.
The DTLZ3 problem, characterized by its multimodal complexity, poses significant challenges. An analysis of the IGD and HV metrics, as emphasized in Table 2 and Table 3, indicates MOEA-AD’s dominance in 12- and 20-objective instances. MOEA-AD surpasses both MaOEA-IGD and MaOEA-IT, a success potentially linked to its dual-association strategy that ensures robust diversity among solutions.
The DTLZ5 and DTLZ6 benchmark problems exhibit degenerate Pareto Fronts (PFs); however, a non-degenerate segment emerges in the Pareto front when the objective count surpasses four. This characteristic significantly influences the performance of comparative algorithms in addressing degenerate multi-objective optimization problems (MaOPs). In the context of these two problems, MOEA-AD consistently delivers superior IGD values across instances with 5, 8, and 12 objectives, underscoring the robustness and versatility of its dual-association strategy. Regarding the HV metric, MOEA-AD outperforms competing algorithms in tackling such challenges, as its inherent collaborative mechanism ensures an optimal equilibrium between convergence and diversity.
A thorough examination of Table 2 and Table 3 and Figure 2 reveals that while MOEA-AD may not secure top results in certain objective test scenarios, it consistently excels across the majority of test problems. This consistent performance further validates MOEA-AD’s advantage over the five rival algorithms.
4.5. Performance Comparison Analysis on the WFG Test Suite
The statistical analysis of IGD and HV metrics, as presented in Table 4 and Table 5, demonstrates the superior performance of our proposed MOEA-AD over the other five algorithms in the majority of cases. Based on the Wilcoxon rank-sum test results in the final row of Table 4, MOEA-AD achieves significantly better IGD values than NSGA-III, ANSGA-III, SPEA/R, MaOEA-IGD, and MaOEA-IT across most of the 45 test instances (26, 25, 27, 41, and 45 instances, respectively). Conversely, the IGD results of NSGA-III, ANSGA-III, SPEA/R, MaOEA-IGD, and MaOEA-IT surpass those of MOEA-AD in only a limited number of instances (11, 8, 10, 0, and 0 instances, respectively).

Table 4.
IGD results (mean and standard deviation) obtained by six algorithms on the WFG problems.

Table 5.
HV results (mean and standard deviation) obtained by six algorithms on the WFG problems.
Similarly, the Wilcoxon rank-sum test results in the last row of Table 5 indicate that MOEA-AD’s HV values are significantly higher than those of NSGA-III, ANSGA-III, SPEA/R, MaOEA-IGD, and MaOEA-IT in the majority of the 45 test instances (25, 29, 29, 40, and 42 instances, respectively). In contrast, the HV results of NSGA-III, ANSGA-III, SPEA/R, MaOEA-IGD, and MaOEA-IT outperform those of MOEA-AD in only a small subset of instances (8, 8, 8, 0, and 0 instances, respectively).
For a more detailed comparative analysis between MOEA-AD and the five competing algorithms, Figure 3 illustrates the distribution of solutions generated by the six algorithms on the 16-objective WFG3 benchmark problem. The visualization clearly indicates that MaOEA-IGD and MaOEA-IT yield the least favorable results. On the other hand, NSGA-III, ANSGA-III, and SPEA/R demonstrate solutions that are relatively closer to the Pareto Front (PF) than those of MaOEA-IGD and MaOEA-IT. Nevertheless, MOEA-AD consistently achieves the closest proximity to the PF across the entire evaluation process, with a noticeable trend of continuous improvement. This observation further underscores the robust competitiveness of MOEA-AD. The following section will provide a comprehensive analysis of the experimental findings.
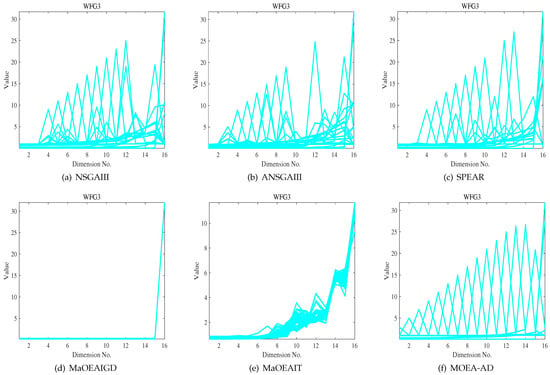
Figure 3.
Parallel coordinate visualization of the non-dominated solutions from six algorithms on the 16-objective WFG3 problem.
WFG3, a connected variant of WFG2, comprises multiple disjoint convex Pareto Front (PF) segments with non-separable variables. Its linear and degenerate PF presents a formidable challenge for reference vector-based algorithms. DAEA excels in 8-, 12-, 16-, and 20-objective test cases, with the exception of the 5-objective scenario, where NSGAIII and ANSGAIII outperform it. These findings underscore the efficacy of our proposed MOEA-AD in bolstering convergence and preserving diversity.
WFG4 through WFG9 feature a shared hyper-elliptical PF in the objective space, yet they exhibit distinct characteristics in the decision space. Notably, WFG4’s multimodal nature, characterized by “hill sizes”, serves as a litmus test for an algorithm’s ability to evade local optima. MOEA-AD holds a pronounced edge in 5-, 8-, 16-, and 20-objective cases, barring the 12-objective instance, where NSGAIII takes the lead. On WFG4, MOEA-AD secures the top HV values for all objectives.
WFG6, a non-separable and streamlined problem, sees DAEA leading in IGD values across all test instances, save for the 16-objective case, where SPEAR prevails. The HV metric reveals that SPEA/R’s performance is on par with MOEA-AD in 5- and 12-objective instances, highlighting MOEA-AD’s prowess in diversity and convergence, particularly in high-dimensional optimization challenges.
WFG7 to WFG9 incorporate specific biases to test algorithmic diversity. MOEA-AD consistently ranks first in all test instances, with SPEA/R, NSGA-III, and ANSGA-III trailing behind. In contrast, MaOEA-IGD and MaOEA-IT falter in these scenarios.
4.6. Performance Comparison Analysis on Real-World Problems
To further demonstrate the effectiveness of the proposed algorithm within the MOEA-D framework, five representative real-world benchmark problems were selected for comparative experiments. These include the following: the Disc Brake Design Problem (DBDP) [41], involving two objectives and four constraints; the Car Side Impact Design Problem (CSIDP) [42], characterized by three objectives and nine constraints; the Gear Train Design Problem (GTDP) [38], which focuses on optimizing gear parameters such as the number of teeth, module, and transmission ratio to satisfy criteria like efficiency, compactness, and cost; and two planar truss structures frequently used in engineering mechanics—the Four-Bar Plane Truss (FBPT) [11] and the Two-Bar Plane Truss (TBPT) [43]—where both the members and applied forces are confined to a single plane. Further details on these problems are available in the cited original references.
Since real-world problems lack a true Pareto front, the Hypervolume (HV) indicator is used to evaluate algorithm performance—a higher HV value indicates better performance. In Table 6, the HV values of six algorithms across five real-world problems are presented. Clearly, MOEA-AD outperforms NSGA-III, ANSGA-III, SPEAR, MaOEA-IGD, and MaOEA-IT on three, four, four, five, and three problems, respectively, and it also achieves the best HV value on three of the five test problems. This further demonstrates the strong practicality and competitiveness of MOEA-AD.

Table 6.
HV results (mean and standard deviation) obtained by six algorithms on the real-world case problems.
5. Conclusions
This paper proposes an Angle-based Dual-Association Evolutionary Algorithm (MOEA-AD) for many-objective optimization problems. The algorithm employs a dual-association strategy based on angular information to associate empty subspaces with the most suitable solutions, thereby promoting the exploration of unexplored regions while maintaining good convergence performance. In addition, a novel quality evaluation framework for subspace solutions is developed. This framework first assesses the convergence and diversity of each solution, with diversity further divided into global and local aspects.
- (1)
- To protect solutions in sparse regions, the framework introduces a dynamic penalty factor that penalizes solutions with insufficient global diversity.
- (2)
- The algorithm also adopts an adaptive two-stage sorting mechanism, which effectively balances convergence and diversity, leading to favorable optimization performance.
- (3)
- However, despite its innovative design, the efficiency of the proposed method decreases as the number of objectives increases.
Future research on MOEA-AD is expected to focus on several key directions aimed at comprehensively improving its performance and expanding its application scope. To address the challenges posed by high-dimensional objective spaces, effective dimensionality reduction techniques and diversity preservation strategies can be introduced to enhance solution distribution quality. In addition, by incorporating specialized constraint-handling mechanisms, the adaptability of MOEA-AD to constrained optimization problems can be further strengthened. Moreover, deploying the algorithm in real-world engineering and manufacturing applications, combined with adaptive parameter tuning, will not only improve its practical utility but also provide solid support for experimental validation and engineering implementation.
Author Contributions
Conceptualization, X.W. and J.C.; Data curation, X.W. and J.C.; Formal analysis, J.C.; Funding acquisition, W.W. and J.C.; Investigation, J.C.; Methodology, J.C.; Project administration, W.W. and J.C.; Resources, J.C.; Software, J.C.; Supervision, X.W. and J.C.; Validation, X.W. and J.C.; Visualization, X.W., H.W. and Z.T.; Writing—original draft, X.W., H.W., Z.T., W.W. and J.C.; Writing—review and editing, X.W., H.W., Z.T., W.W. and J.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
All experimental data in the article were obtained through testing experiments conducted on the test sets (WFG and DTLZ) of the PlatEMO 4.6 platform. The access link is https://github.com/BIMK/PlatEMO (accessed on 19 September 2023).
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Abbreviations
The following abbreviations are used in this manuscript:
| N | Population size |
| M | Number of objectives |
| Ideal point | |
| Nadir point | |
| Perpendicular distance to reference vector | |
| Angle between solution vector and reference vector | |
| Q | Quality score of a solution |
| Global Diversity | |
| Local Diversity | |
| Pareto Front | |
| Evolutionary Algorithms | |
| Many-objective Optimization Problems | |
| MOEA-AD | Angle-based dual-association Evolutionary Algorithm for Many-Objective Optimization |
| Multi-Objective Evolutionary Algorithm |
References
- Li, G.; Li, L.; Cai, G. A two-stage coevolutionary algorithm based on adaptive weights for complex constrained multiobjective optimization. Appl. Soft Comput. 2025, 173, 112825. [Google Scholar] [CrossRef]
- Chao, Y.; Chen, X.; Chen, S.; Yuan, Y. An improved multi-objective antlion optimization algorithm for assembly line balancing problem considering learning cost and workstation area. Int. J. Interact. Des. Manuf. (IJIDeM) 2025, 1–15. [Google Scholar] [CrossRef]
- Nuthakki, P.; T., P.K.; Alhussein, M.; Anwar, M.S.; Aurangzeb, K.; Gunnam, L.C. AI-Driven Resource and Communication-Aware Virtual Machine Placement Using Multi-Objective Swarm Optimization for Enhanced Efficiency in Cloud-Based Smart Manufacturing. Comput. Mater. Contin. 2024, 81, 4743–4756. [Google Scholar] [CrossRef]
- Guo, X.; Gong, R.; Bao, H.; Lu, Z. A multiobjective optimization dispatch method of wind-thermal power system. IEICE Trans. Inf. Syst. 2020, 103, 2549–2558. [Google Scholar] [CrossRef]
- Tian, W.; Zhang, Y.; Fang, Q.; Liu, W. A route network resource allocation method based on multi-objective optimization and improved genetic algorithm. J. Intell. Fuzzy Syst. 2024, 48, 1–13. [Google Scholar] [CrossRef]
- Di Barba, P.; Mognaschi, M.E.; Wiak, S. A method for solving many-objective optimization problems in magnetics. In Proceedings of the 2019 19th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering (ISEF), Nancy, France, 29–31 August 2019; pp. 1–2. [Google Scholar]
- Moncayo-Martínez, L.A.; Mastrocinque, E. A multi-objective intelligent water drop algorithm to minimise cost of goods sold and time to market in logistics networks. Expert Syst. Appl. 2016, 64, 455–466. [Google Scholar] [CrossRef]
- Li, M.; Wang, Z.; Li, K.; Liao, X.; Hone, K.; Liu, X. Task allocation on layered multiagent systems: When evolutionary many-objective optimization meets deep Q-learning. IEEE Trans. Evol. Comput. 2021, 25, 842–855. [Google Scholar] [CrossRef]
- Amorim, E.A.; Rocha, C. Optimization of wind-thermal economic-emission dispatch problem using NSGA-III. IEEE Lat. Am. Trans. 2021, 18, 1555–1562. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, J.; Lv, C. Multi-Stage and Multi-Objective Optimization of Solar Air-Source Heat Pump Systems for High-Rise Residential Buildings in Hot-Summer and Cold-Winter Regions. Energies 2024, 17, 6414. [Google Scholar] [CrossRef]
- Hao, L.; Peng, W.; Liu, J.; Zhang, W.; Li, Y.; Qin, K. Competition-based two-stage evolutionary algorithm for constrained multi-objective optimization. Math. Comput. Simul. 2025, 230, 207–226. [Google Scholar] [CrossRef]
- Bechikh, S.; Elarbi, M.; Ben Said, L. Many-objective optimization using evolutionary algorithms: A survey. In Recent Advances in Evolutionary Multi-Objective Optimization; Springer: Cham, Switzerland, 2017; pp. 105–137. [Google Scholar]
- Ishibuchi, H.; Tsukamoto, N.; Nojima, Y. Evolutionary many-objective optimization: A short review. In Proceedings of the 2008 IEEE Congress on Evolutionary Computation (IEEE World Congress on Computational Intelligence), Hong Kong, China, 1–6 June 2008; pp. 2419–2426. [Google Scholar]
- Gu, Q.; Li, K.; Wang, D.; Liu, D. A MOEA/D with adaptive weight subspace for regular and irregular multi-objective optimization problems. Inf. Sci. 2024, 661, 120143. [Google Scholar] [CrossRef]
- Jiang, B.; Dong, Y.; Zhang, Z.; Li, X.; Wei, Y.; Guo, Y.; Liu, H. Integrating a Physical Model with Multi-Objective Optimization for the Design of Optical Angle Nano-Positioning Mechanism. Appl. Sci. 2024, 14, 3756. [Google Scholar] [CrossRef]
- Cai, X.; Li, B.; Wu, L.; Chang, T.; Zhang, W.; Chen, J. A dynamic interval multi-objective optimization algorithm based on environmental change detection. Inf. Sci. 2025, 694, 121690. [Google Scholar] [CrossRef]
- Yang, S.; Li, M.; Liu, X.; Zheng, J. A grid-based evolutionary algorithm for many-objective optimization. IEEE Trans. Evol. Comput. 2013, 17, 721–736. [Google Scholar] [CrossRef]
- He, Z.; Yen, G.G.; Zhang, J. Fuzzy-based Pareto optimality for many-objective evolutionary algorithms. IEEE Trans. Evol. Comput. 2013, 18, 269–285. [Google Scholar] [CrossRef]
- Liu, S.; Lin, Q.; Tan, K.C.; Gong, M.; Coello, C.A.C. A fuzzy decomposition-based multi/many-objective evolutionary algorithm. IEEE Trans. Cybern. 2020, 52, 3495–3509. [Google Scholar] [CrossRef] [PubMed]
- Vijai, P.; P., B.S. A hybrid multi-objective optimization approach With NSGA-II for feature selection. Decis. Anal. J. 2025, 14, 100550. [Google Scholar] [CrossRef]
- Zhu, J.; He, Y.; Gao, Z. Wind power interval and point prediction model using neural network based multi-objective optimization. Energy 2023, 283, 129079. [Google Scholar] [CrossRef]
- Deb, K.; Saxena, D. Searching for Pareto-optimal solutions through dimensionality reduction for certain large-dimensional multi-objective optimization problems. In Proceedings of the World Congress on Computational Intelligence (WCCI-2006), Vancouver, BC, Canada, 16–21 July 2006; pp. 3352–3360. [Google Scholar]
- Singh, H.K.; Isaacs, A.; Ray, T. A Pareto corner search evolutionary algorithm and dimensionality reduction in many-objective optimization problems. IEEE Trans. Evol. Comput. 2011, 15, 539–556. [Google Scholar] [CrossRef]
- Deb, K.; Kumar, A. Interactive evolutionary multi-objective optimization and decision-making using reference direction method. In Proceedings of the 9th Annual Conference on Genetic and Evolutionary Computation, London, UK, 7–11 July 2007; pp. 781–788. [Google Scholar]
- Thiele, L.; Miettinen, K.; Korhonen, P.J.; Molina, J. A preference-based evolutionary algorithm for multi-objective optimization. Evol. Comput. 2009, 17, 411–436. [Google Scholar] [CrossRef]
- Wang, R.; Purshouse, R.C.; Fleming, P.J. Preference-inspired coevolutionary algorithms for many-objective optimization. IEEE Trans. Evol. Comput. 2012, 17, 474–494. [Google Scholar] [CrossRef]
- Bechikh, S. Incorporating Decision Maker’s Preference Information in Evolutionary Multi-Objective Optimization. Ph.D. Thesis, University of Tunis, Tunis, Tunisia, 2012. [Google Scholar]
- Deb, K.; Jain, H. An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, part I: Solving problems with box constraints. IEEE Trans. Evol. Comput. 2013, 18, 577–601. [Google Scholar] [CrossRef]
- Deb, K.; Agrawal, R.B. Simulated binary crossover for continuous search space. Complex Syst. 1995, 9, 115–148. [Google Scholar]
- Deb, K.; Goyal, M. A combined genetic adaptive search (GeneAS) for engineering design. Comput. Sci. Inform. 1996, 26, 30–45. [Google Scholar]
- Dai, C.; Wang, Y. A new multiobjective evolutionary algorithm based on decomposition of the objective space for multiobjective optimization. J. Appl. Math. 2014, 2014, 906147. [Google Scholar] [CrossRef]
- Li, K.; Deb, K.; Zhang, Q.; Kwong, S. An evolutionary many-objective optimization algorithm based on dominance and decomposition. IEEE Trans. Evol. Comput. 2014, 19, 694–716. [Google Scholar] [CrossRef]
- Jiang, S.; Yang, S. A strength Pareto evolutionary algorithm based on reference direction for multiobjective and many-objective optimization. IEEE Trans. Evol. Comput. 2017, 21, 329–346. [Google Scholar] [CrossRef]
- Tian, Y.; Cheng, R.; Zhang, X.; Jin, Y. PlatEMO: A MATLAB platform for evolutionary multi-objective optimization [educational forum]. IEEE Comput. Intell. Mag. 2017, 12, 73–87. [Google Scholar] [CrossRef]
- Deb, K.; Thiele, L.; Laumanns, M.; Zitzler, E. Scalable multi-objective optimization test problems. In Proceedings of the 2002 Congress on Evolutionary Computation, CEC’02 (Cat. No. 02TH8600), Honolulu, HI, USA, 12–17 May 2002; Volume 1, pp. 825–830. [Google Scholar]
- Huband, S.; Hingston, P.; Barone, L.; While, L. A review of multiobjective test problems and a scalable test problem toolkit. IEEE Trans. Evol. Comput. 2006, 10, 477–506. [Google Scholar] [CrossRef]
- Gómez, R.H.; Coello, C.A.C. MOMBI: A new metaheuristic for many-objective optimization based on the R2 indicator. In Proceedings of the 2013 IEEE Congress on Evolutionary Computation, Cancun, Mexico, 20–23 June 2013; pp. 2488–2495. [Google Scholar]
- Jain, H.; Deb, K. An evolutionary many-objective optimization algorithm using reference-point based nondominated sorting approach, part II: Handling constraints and extending to an adaptive approach. IEEE Trans. Evol. Comput. 2013, 18, 602–622. [Google Scholar] [CrossRef]
- Sun, Y.; Yen, G.G.; Yi, Z. IGD indicator-based evolutionary algorithm for many-objective optimization problems. IEEE Trans. Evol. Comput. 2018, 23, 173–187. [Google Scholar] [CrossRef]
- Sun, Y.; Xue, B.; Zhang, M.; Yen, G.G. A new two-stage evolutionary algorithm for many-objective optimization. IEEE Trans. Evol. Comput. 2018, 23, 748–761. [Google Scholar] [CrossRef]
- Osyczka, A.; Kundu, S. A genetic algorithm-based multicriteria optimization method. In Proceedings of the 1st World Congress on Structural and Multidisciplinary Optimization, Goslar, Germany, 28 May–2 June 1995; pp. 909–914. [Google Scholar]
- Ray, T.; Liew, K. A swarm metaphor for multiobjective design optimization. Eng. Optim. 2002, 34, 141–153. [Google Scholar] [CrossRef]
- Cheng, F.Y.; Li, X. Generalized center method for multiobjective engineering optimization. Eng. Optim. 1999, 31, 641–661. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).