Abstract
Missing data remain a challenge for researchers and decision-makers due to their impact on analytical accuracy and uncertainty estimation. Many studies on missing data are based on randomness, but randomness itself is problematic. This makes it difficult to identify missing data mechanisms and affects how effectively the missing data impacts can be minimized. The purpose of this paper is to examine a potentially simple test to diagnose whether the missing data are missing at random. Such a test is developed using an extended taxonomy of missing data mechanisms. A key aspect of the approach is the use of single mean imputation for handling missing data in the test development dataset. Changing this to random imputation from the same underlying distribution, however, has a negative impact on the diagnosis. This is aggravated by the possibility of high inter-variable correlation, confounding, and mixed missing data mechanisms. The verification step uses data from a high-quality real-world dataset and finds some evidence—in one case—that the data may be missing at random, but this is less persuasive in the second case. Confidence in these results, however, is limited by the potential influence of correlation, confounding, and mixed missingness. This paper concludes with a discussion of the test’s merits and finds that sufficient uncertainties remain to render it unreliable, even if the initial results appear promising.
Keywords:
missing data; survey nonresponse; generalized linear model; verification data; missing at random test; extended missing data taxonomy; confounding MSC:
62D10
1. Introduction
Missing data are frequently found in datasets, yet present a significant problem for analysis. Not only can they introduce bias [1] and generate misleading results [2], but they can even impact the ability to correctly select models [3]. Dealing effectively with missing data requires two separate steps, namely, correctly identifying the nature of the missing data mechanism, and then selecting a suitable treatment for that type of missing data [4]. Failure to correctly identify the type of missing data can result in the selection of an inappropriate treatment, which may introduce an additional source of error into the analysis [5,6]. This has been recognized for over 50 years, but the increased use of data in modern life has magnified the potential for harm from these omissions.
This paper investigates the possibility of a simple diagnostic test for missing at random (MAR) data. MAR data are the most likely to be identifiable directly from the data, owing to their inherent characteristics compared to those of other types of missing data, e.g., missing completely at random and missing not at random. Such a quick diagnostic would be of assistance to analysts who believe they are dealing with MAR but would value supporting evidence. To investigate this, first, we extend the missing data taxonomy to describe the different models that can result in the three types of missingness. A possible diagnostic test is then developed through the use of simulated data and assessed using real data. The use of a different approach in a key step of the test development process, however, raises concerns about the test’s accuracy. Additionally, there are fundamental issues that must be considered when examining the results. Although the test provides some evidence of potential success, it is subject to such a high degree of uncertainty that the overall approach remains unreliable.
Types of Missing Data
The most straightforward description of missing data is found in [7], which is followed here unless indicated otherwise. Let denote a rectangular data matrix, where represents the value on the row. The missing data indicator matrix indicates if the data point is missing or observed . Based on the randomness of the missing data, there are three basic types.
If the missingness of the data does not depend on the complete data, then they are considered to be missing completely at random (MCAR), as follows:
where Y represents the complete data, M denotes the missing data, and denotes an unknown parameter. Note that this does not mean that there is no pattern to the missingness of the data, just that it does not depend on the data values.
If the data missingness depends only on the observed and not the missing components of Y, it is called missing at random (MAR). That is, if represents the observed data components of Y and , the missing components, then the missing data are MAR if we have the following:
Finally, if the missingness of the data depends on all of Y, including the missing components , it is referred to as missing not at random (MNAR). Note that this missing component may also include unmeasured data. MNAR is the most problematic form of missing data and potentially the most damaging to statistical inference.
A brief review of approaches to dealing with missing data [8] highlights that the missingness mechanism can involve both MAR and MNAR. This is where two different missing data mechanisms are mixed in the same dataset. It gives the example of missing age data, where societal norms may mean that women may not wish to disclose their ages (an example of MAR data, in that missingness is determined by gender). In the same data sample, very low- or high-income individuals may also be unwilling to reveal their salaries (an example of MNAR, in that pay itself determines the disclosure of salary). Clearly, this mixing of missing data types complicates any analysis and imputation, in that one standard approach cannot be adopted for both missing data elements. In [9], the case of mixed MCAR, MAR, and MNAR missing data in the same data sample was discussed. The conclusion was that “model-based methods will provide estimates based on a model that is partially wrong for all participants with missing values, while ad-hoc methods that assume MCAR will provide estimates based on the wrong assumption for only some of the participants with missing values” (original author emphasis).
A concept often used to distinguish MAR from MNAR data is the ignorability of the missingness mechanism, which is used for likelihood-based inference from data with missing values [10]. The non-ignorability condition [7] considers observed values , where represents an observed data point, m denotes the missingness indicator, represents the parameter space, represent the parameters for the likelihood maximization and for the missingness, represent the maximum likelihood values for the full dataset, the ignored data, and the rest of the data, respectively, represents the recorded values, and denotes the index of missingness ([7]). The first, full likelihood equation (i.e., referring to all of the data, and ), considered as a function of the parameters , is as follows:
whereas the “ignorable likelihood” of —ignoring the missingness mechanism ([7], original author emphasis)—just referring to the observed data , is as follows:
Being ignorable, the model M does not appear in Equation (9). This shows that the following two conditions must apply if the missingness mechanism is to be ignorable (i.e., inference can be made on just the observed data, ):
- The parameter that determines whether a data point is missing () should be independent of the parameter being evaluated in the overall model (), that is, we have the following:
- the full likelihood should be factorizable.
- This likelihood-based approach has been refined further e.g., in [11,12].
MNAR is further subdivided in [9] into focused MNAR and diffuse MNAR. Focused MNAR occurs when the missingness depends solely on the missing values themselves, that is, we have the following:
In contrast, diffuse MNAR depends on both the observed and missing data and can be described as follows:
In both cases, the mechanism is MNAR, as is required to determine their values. Gomer and Yuan [9] also mention the impact of how influences missingness. Direct is where directly causes the missing values; in contrast, Indirect missingness is where influences another variable, say Z, which causes the missingness. Each time the underlying cause is , differing only in how direct the impact is.
In a review paper, Jamshidian and Yuan [13] examined an approach commonly used to identify missing data mechanisms, which is based on the similarity of means and/or covariances. The assumption here is that only MCAR data will have similar means and covariances before and after missing data imputation. They use simulated data based on MAR or MNAR processes to show that this similarity of mean and/or covariance can be present in non-MCAR data. This can result in several of the tests failing to reject the hypothesis of similarity, thereby misclassifying the missing data mechanism as MCAR when it is not. They also consider a test for the equality of parameters, which they find possible but “not simple”, and which also fails to identify whether the rejected data are MAR or MNAR. As many of these tests rely on the assumption of underlying normality, they also examine tests for multivariate kurtosis and skewness. However, they note that this is more of a rule of thumb, as real-world data rarely follow a truly normal distribution. This approach may also face challenges when dealing with MNAR data.
An important subdivision of MNAR analysis is between data that have missing covariates, missing response data, or a combination of both. This classification was outlined in a paper by Li and Yi [14], which described these missingness types as arising frequently in longitudinal studies. In an article on generalized linear models as an approach to MNAR data analysis, Zhao and Shao [15] also noted that many missing data techniques are designed to address either missing response or covariate data, but that less attention has been given to methods for handling both, particularly if the data are MNAR. The Li and Yi paper also introduced the use of the variable Z, which is completely observed (i.e., without any missing values), but which may influence covariate or response missingness.
2. Extending the Missing Data Taxonomy
As seen in Section 1, the classification of missing data mechanisms is more complex than the simple tripartite MCAR, MAR, and MNAR system would imply. Building upon [14], it appears possible to create a table of the combinations of responses and covariates that can be associated with a specific missing data mechanism. This, in turn, suggests that any missing data mechanism taxonomy should be designed to accommodate the multiplicity of potential elements that can influence the presence or otherwise of an item of data. This section examines such an extension.
Let the data missingness be denoted as m, and let the five components that can influence its missingness be denoted as ; these are described in Table 1. With the exception of and , these can be either individual variables or matrices ( and are always vectors). In this treatment, the single variable notation is used, but this does not exclude their being matrices (e.g., as opposed to ).

Table 1.
Description of elements in missing data mechanisms.
Combining these different elements yields for and , that is, the total number of element combinations summing to 32, as shown in Table 2.

Table 2.
Enumeration of possible MDM element combinations.
It may be possible, however, to simplify this structure by re-examining the x and y elements. In this case, both Y and X may be simplified as follows:
- The dependent variable Y is either evaluated as a complete set of observations, (i.e., ), or it is not, (). Although this means that there is no need to consider both and in combination, it still makes sense to consider them separately, as (the observed data) is associated with MAR missing data, whereas (all of the data, observed and missing) is associated with MNAR.
- The independent variable X is also evaluated on all its data (i.e., ) or it is not (). Unlike Y, however, as there is often more than one independent variable, these should be considered as separate elements. This means that it makes sense to include and in combination.
- The current structure has two independent variable representations, X and Z, where Z represents an independent variable that comprises a set of observations that is always fully recorded. Even though z and both represent independent variables, has missing values and so is not fully observed. The key distinction is between independent variables that are fully observed (e.g., a key study component, such as the presence of a specific condition) and independent variables that have missing observations.
These adjustments are shown in Table 3. This step has reduced the total number of possible combinations from 32 to 24. This abbreviated table can be reordered by the missing data mechanism, as shown in Table 4. As can be seen in Table 3 and Table 4, there are far more MNAR models than there are for MAR or MCAR.

Table 3.
Possible missing data mechanism element combinations when and are considered mutually exclusive.

Table 4.
Possible combinations of elements, grouped by missing data mechanism, when and are considered mutually exclusive.
In Table 5, the different numbers of functional forms, once and are considered mutually exclusive, are grouped together. Each option is associated with a standard missing data mechanism category (MCAR, MAR, or MNAR), depending on the elements present. Taking the MCAR category, for instance, the probability of missing data is, by definition, not associated with any of these five elements. It is, therefore, associated solely with a constant. In other words, for missing data to have an MCAR mechanism, we have the following:
where M denotes the binary indicator of missing data (1 if missing, 0 if present), Y denotes the set of all response variables, X denotes the set of all covariates that have missing data, Z denotes the set of all covariates that have no missing data, denotes the parameter associated with the missingness mechanism, and K denotes a constant. For the other missing data mechanisms (i.e., MAR and MNAR), there are multiple combinations of elements that can yield either MAR or MNAR missing data, with MNAR having the most possible combinations.

Table 5.
Number of functional forms for each missing data type when are considered mutually exclusive.
The seven possible forms of MAR missing data identified through this classification approach further illustrate the challenges analysts face in selecting appropriate methods for data imputation. These range from the simple univariate form, , to the complex multivariate version, .
As always, the greatest complexity is associated with MNAR data. To begin with, the 16 possible models for MNAR missing data highlight the difficulty that analysts face in imputing values for this type of missing data. There is also a range of possible functional forms that can yield MNAR data. These range from single-covariate forms (), for instance) to more complex formulations with four covariates ( or ). In addition, conditioning on the unobserved data presents a significant barrier to testing for an MNAR mechanism. This classification structure is also compatible with the Focused and Diffused classifications of MNAR data described in Section 1.
However, it should be noted that the number of possible functional forms for missing data mechanisms does not directly correspond to the probability of each type of missing data. In other words, just because only 1 of 24 possible missing data mechanisms corresponds to MCAR missing data does not in any way imply that only 1 in 24 occurrences of missing data is MCAR.
If the missing data are dominated by MAR-related elements (, and z) with only a few missing data elements belonging to or , it would explain why [11] found that MNAR techniques often failed to produce better outcomes than MAR models.
Note that the formulation described so far implicitly assumes a direct influence between the missing covariate or response variable and its missingness. As pointed out earlier in Section 1, it is also possible that a variable or response has an indirect influence on missingness, possibly through variables not included in the dataset. In this part of the study, the focus is on the direct effects; indirect effects will be considered later in Section 3.5.5 and in the Discussion (Section 5).
3. Direct Testing for MAR Missing Data
Having described the 24-model structure of missing data mechanisms, it is reasonable to ask if this can be used to assist in identifying the different missing data mechanisms. Gaining evidence to help with the identification of the missing data mechanism directly from the data would be of great assistance to analysts. Accordingly, the following sections look at the possibility of direct testing of the data to gather evidence for the missing data mechanism present.
3.1. The Inability to Test Directly for MCAR or MNAR Missing Data
On the face of it, the 24-model structure suggests the possibility of a direct test for MCAR missingness. This would require that the probability of missingness, , be constant irrespective of the variables in the conditional form , i.e., for every combination of , as listed in the final column of Table 4, we have the following:
As outlined in Section 1, however, MCAR missingness is driven by a random process. The inability to identify randomness as such and, indeed, the temptation to assign patterns to randomness is a well-understood phenomenon that has been extensively explored in the literature, for example, as described in [16,17,18]. This presents a significant barrier to the identification of MCAR missingness from the data alone. In addition, there is the risk that the set of variables under examination fails to include the independent variable that drives the missingness. In this way, model misspecification can be confused with an indicator of MCAR missingness. This is aggravated by the fact that the missingness may be driven by a spatial or temporal component that is not included in the dataset.
This is why the most common method of identifying MCAR involves comparing the means and distributions of the data with and without any imputed (missing) data; the mechanism is considered MCAR if no statistically significant difference is detected within the sets of means and distributions. However, it has been shown in [13], as described in Section 1, that the equality of means and distributions may be owing to other causes and not driven by an MCAR mechanism.
Similarly, there are formidable barriers to directly identifying an MNAR mechanism from the data. By definition, an MNAR dataset is missing the very components that drive the MNAR mechanism. This increases the likelihood of both type I and type II errors (identifying non-MNAR missingness as MNAR, and vice versa). Additionally, as can be seen from Section 2, there are far more MNAR models than for MCAR and MAR combined. This is compounded by the complexity of many of the MNAR models. Overall, these characteristics make the successful direct identification of MNAR missingness from the data highly unlikely.
3.2. Testing Directly for MAR Missing Data
Of the three types of missing data mechanisms, only MAR is theoretically identifiable through direct testing of the data. This is because MAR is associated with the observed data, not the missing data, in a given dataset. One complication is the existence of seven different MAR models, which may confuse this identification. Another concern is the possibility that MCAR—especially MNAR—missingness may be mistaken for MAR. Additionally, care must be taken to include all independent variables that may be influencing the MAR missingness mechanism. Nonetheless, it is worth evaluating whether direct testing can provide sufficient evidence to support the assumption of a MAR mechanism.
3.3. Simulating Missing Data
In order to assess the feasibility of direct diagnosis for MAR missingness, it is necessary to create simulated data for which the missing data mechanisms are known. This section describes how the simulated data are created for each of the missing data types (MCAR, MAR, and MNAR). The next sections look at the direct testing for these mechanisms and conclude with an examination of the experimental results. Data creation and analysis were carried out in R version 4.1.0.
The approach used to generate missing data is based on that of Ref. [19] as described in Appendix A of that paper. It has, however, been modified to allow for a greater range of individual forms of the missing data mechanisms, as described in Section 2. The following core data variables are created: Y, the dependent variable, X, the independent variable, which may also have missing data, and Z, an independent variable that is always completely observed. There is no predetermined relationship between the dependent variable Y and the independent variables X and Z, as all three are the products of random draws from a statistical distribution. This is to avoid possibly introducing bias into the diagnostic development. In addition, each X and Y variable has a correlated partner variable (denoted and ), which is used to generate the different missing data indicators, as described in the following sections. In combination, these 5 data variables generate 24 different models (as outlined in Section 2) that produce missing data. In each case, the different combinations of these variables, , and Z, are used to generate a missing data indicator, which has an index number that shows the type of missing data mechanism (MCAR, MAR, or MNAR) as well as the specific functional form, as described in Section 2 and detailed in Table 4. The missing data indicator is then used to delete the missing data from the Y variable (where 1 = missing data, 0 = observed data). Conversion to the terminology used elsewhere in this document is shown in Table 6.

Table 6.
Simulated data labels and their mathematical forms.
In order to identify the X variable missing data, it is necessary to create an additional missing data indicator series. This series, denoted as , is generated by random draws from a binomial distribution with a probability of 0.2.
An additional amendment to the original Gomer and Yuan approach [19] involves adding draws from a random normal distribution to the , and Z variables. This is to add a random error element to the original data series (these series are referred to as ‘dirty’ data) to replicate more realistic data conditions. Three such random error series are created in each case. For the normal distribution dataset, for instance, these comprise draws from N(0, 0.1), N(0, 0.5), and N(0, 1.0) distributions. A separate draw is created for each of the , and Z variables to avoid introducing an unwanted element of correlation between the variables.
The Z variable is created by generating 10,000 random draws from the same distribution used for , and .0
In order to generate the and variables, it is first necessary to create a correlation matrix that correlates Y to and X to . The Y, , X, and variables are generated using multinomial distributions, as in the original Gomer and Yuan paper. The random error variables for ‘dirtying’ the Y, , X, , and Z series are generated by random draws from a normal distribution with zero mean and an appropriate standard distribution. These random error factors are then added to the Y, , X, , and Z series. As the random error approaches the same magnitude as the original series, the correlation coefficients may need to be adjusted to maintain the (approximate) 0.3 correlation between the Y and and X and series.
The missing data mechanism indicator variable denotes which Y series data points need to be removed to create the relevant missing data. In contrast, the missing X data indicator, as described above, is used across all models to remove missing X data from the X series.
To avoid confusion, the term case will refer to the six different model classes tested, i.e., base case clean data; base case dirty data; clean missing data; dirty missing data 1; dirty missing data 2; and dirty missing data 3. The term model will refer to the 24 different functional forms tested in each case. The first two cases—base case clean data and base case dirty data—are only used to check the model construction and are not used in any of the analyses.
Three different distributions were used to generate the simulated data for the six different model cases, as shown in Table 7. These were chosen to represent distributions commonly encountered in real-world datasets [20], with normal representing continuous and Poisson, discrete distributions.

Table 7.
Distributions used to generate simulated data.
To create the MCAR data, a series of 10,000 draws from a binomial distribution with is generated. This gives a series (denoted as MCARi) that randomly allocates 20% of the Y variables as missing data. The data (represented by variable ) have entries that correspond to the missing data indicator (MCARi = 1) deleted.
MAR missing data mechanism indicators are generated by applying the functional forms listed in Table 4, using the same index numbers for identification. This generates three missing data mechanism indicators that have one variable each, three missing data indicators that have two variables each, and one missing data mechanism that is based on three variables. The details are given in Table 8.

Table 8.
MAR simulated missing data variants.
The data (represented by variable ) have entries that correspond to the appropriate missing data indicator deleted.
Having more than one element generating the missing data element means that the initial (one element) threshold levels used by Gomer and Yuan [19] in generating their simulated data no longer yield 20% of the total. As a result, the missing data thresholds for two- and three-element functional forms have lower threshold levels that yield approximately 20% missing data indicators. These were found through a trial-and-error process. This also applies to the threshold levels used to create MNAR models with greater than one missing data element.
MNAR missing data mechanism indicators are also generated by applying the functional forms listed in Table 4 and using the same index numbers for identification as in these tables. This generates two missing data mechanism indicators with one variable each, six with two variables each, six with three variables each, and two with four variables each. The details are provided in Table 9.

Table 9.
MNAR simulated missing data variants.
This time, the and data (represented by variables and Y) have entries that correspond to the appropriate missing data indicator deleted.
To create a more realistic dataset, a separate error series is generated for each of , and Z, and in each case, the error is added to the original series before any missing data deletions are carried out.
3.4. Testing for MAR Missingness
As the missing data can be represented as a dummy series (where 1 represents missing data and 0 represents observed data), a logical approach is to use a binary statistical test. In this case, a generalized linear regression (GLM) model using a logit link function is used as a test, and the output comprises the indicators of statistical fit as well as an ‘area under the curve’ (AUC) plot [21]. The missing data indicators generated during the simulated data creation process serve as the dummy variables. In a sense, this is just a reversal of the normal process of indicating missing data; for real data, the presence of missing data generates the dummy 1/0 missing data indicator series, whereas in this case, the missing data indicators generate the gaps in the data.
As previously mentioned, the analysis was carried out on four cases for each simulated data generation, as listed in Table 10, where “DD1”, “DD2”, and “DD3” refer to the different levels of random errors used with the distributions.

Table 10.
Models used in simulated data testing, where “DD” refers to the “dirty data” type.
As mentioned in Section 3.3, the first two cases—“Clean CC base case” and “Dirty CC base case”—are solely to check model construction. As these cases have complete data (even if one has a random error added), they should provide the strongest signals to identify the variables used to generate the missing data indicators.
For all tests, the statistically significant level was taken to be 0.001 to reduce the likelihood of random noise being taken as a signal. Any results at the 0.01 significance level were taken to be a partial signal and are distinguished in the tables in Appendix A and Appendix B by being represented by lowercase letters in parentheses. The Akaike information criteria (AIC) and area under the curve (AUC) diagnostics were also used to assess the returns, but these tables were omitted from the paper owing to the volume of material involved.
Although the tests were carried out on all 24 functional forms of the same case at the same time, the tests and results will be presented by missing data type.
Importantly, GLM tests cannot be carried out on data with missing values. As the missing data indicators are directly generated from the variables, it follows that deleting incomplete rows also eliminates the associated missing data indicators and makes testing impossible. To avoid this, it is necessary to fill in the missing data with substitute values. The purpose of this substitution is not to find values that have similar magnitudes to the original (missing) data but to fill in the gap without introducing unnecessary variation into the process. One approach is to use the arithmetic means of the Y and X variables, respectively, as substitutes for their missing values. This preserves the overall variable mean, and the impact of potentially reducing the variable’s standard deviation is acceptable as the least worst substitution option. An alternative is to use random values drawn from the same distribution as the models under test. Most other potential substitute values risk skewing the results or adding no new information (a normal distribution, for example, has a mean, median, and mode of 0, thereby eliminating three alternative substitutes). The results of the random-based tests are used to assess the accuracy of the single mean imputation results for cases 4, 5, and 6 (there is no missing data deletion for cases 1 and 2, and data without a random error are unlikely to be encountered with real data). The results of using these different substitutions are compared and discussed in Section 3.5.5.
For all six cases and seven MAR models, the GLM test was carried out using the relevant missing data indicator (MARii to MARviii) as the dependent variable and the five remaining variables (, and Z) as independent variables. A logit function was used as the GLM link function. For the test to provide evidence for the MAR missing data mechanism when using these data, the only statistically significant items should be the intercept and the variables used to generate the missing data indicator.
MCAR: For all six cases, the GLM test was carried out using MCARi (the random binomial draws) as the dependent variable and the five remaining variables (, and Z) as independent variables. A logit function was used as the GLM link function. For the test to provide evidence for the MCAR missing data mechanism with this dataset, the only statistically significant item at the 0.001 level should be the intercept.
For all six cases and sixteen MNAR models, the GLM test was carried out using the relevant missing data indicator (MNARix to MARxxix) as the dependent variable and the five remaining variables (, and Z) as independent variables. A logit function was used as the GLM link function. For the test to provide evidence for the MNAR missing data mechanism with this dataset, the only statistically significant items should be the intercept and the variables used to generate the missing data indicator.
3.5. Experimental Results from Testing with Simulated Data
This section focuses on examining the possibility of diagnosing MAR missingness directly from the data using this simple test. In order to do so successfully, it will also be necessary to contrast the results found for the MCAR and MNAR data to identify possibly confusing results. As mentioned in Section 3.4, this analysis is carried out using the single mean substitution data; the impact of changing this approach to random (from the same underlying distribution) infilling is assessed in Section 3.5.5.
There are results for 24 models for each of the four cases; this gives a total of 96 separate tests for each set of simulated data. Unsurprisingly, the test cases—clean complete case data and dirty complete case data—produced highly accurate results and will not be discussed further.
The results for each distribution are given in tables, which are to be found in n. These comprise Table A1, Table A3 and Table A5, which give the variables (in format) found significant for the Normal(0,1), Poisson(30), and Poisson(5) simulated data, respectively. In each case, the tables also indicate the relevant missing data mechanism and the functional form for each model. The data in the output test summaries from each of the model runs are also important for interpreting the results, but, owing to the large volume of material outputted, these are excluded from this paper. Following the structure used in the rest of this document, the results will be discussed by missing data mechanism type.
3.5.1. MAR Results
As the number of variables in each functional form affects the fit of the GLM test, they will be discussed separately.
- For all three distributions and four missing data cases, the tests on the one-variable functions (, or Z, that is, models MARii, MARiii, and MAR iv) resulted in the failure of the test and the warning messages ‘1: glm.fit: algorithm did not converge; and 2: glm.fit: fitted probabilities numerically 0 or 1 occurred’. In each case, the AUC had a value of 1, indicating a perfect fit. In these cases, the Akaike information criteria (AIC), a diagnostic statistic for assessing model fit (see Ref. [22]), is very low (12).
- Both of the two-variable functions containing (model MARv and MARvii) appear sensitive to the missing data; this was shown by the Y variable also being found significant. In contrast, this sensitivity was not found for the variable. In both combinations of variables that used to generate the missing data mechanism indicators ( and , models MARvi and MARvii), only the (not the X) variable was found to be statistically significant. The Z variable was correctly identified in all cases in which it was part of the model. The AUC values for all three two-variable functional forms were in the region of 0.95, ranging from 0.950 to 0.957. An examination of the model test summaries found that the correctly identified variables always had a positive z-score, and the intercept always had a negative z-score. In the cases where Y was incorrectly identified as a significant variable, it always had a negative z-score.
- As with the two-variable models, once the missing data were deleted, the three-variable model (model MARviii) also found the Y variable significant. Again, this sensitivity was not found for the variable, and the Z variable was only identified as significant when present in the model. The AUC values for the three-variable functional forms were in the region of 0.92, ranging from 0.915 to 0.931. As with the two-variable models, test summaries indicated that correctly identified variables always had positive z-scores, the intercept always had a negative z-score, and if Y was incorrectly identified as a significant variable, it always had a negative z-score.
The overall results for the MAR model tests across all four missing data cases and three distributions suggest that it may be possible to use these results to acquire evidence for MAR missingness. This would involve combining the variables found to be significant with the signs of their corresponding z-scores. This result appears robust, even in the presence of a substantial level of random data error.
Before these results can be fully accepted, however, it is necessary to contrast them with the results obtained for MCAR and MNAR data.
3.5.2. MCAR Results
For all three distributions and all four missing data cases, the GLM output for the MCAR model (MCARi) shows that the only statistically significant part of the fitted model is the intercept. This implies that , which is the expected result for MCAR missing data. The AUC results support this finding, in that all of the distributions and cases yield a value close to 0.5. This is a value that is consistent with a randomly generated data distribution.
These results do not overlap with any of the MAR results and so are unlikely to cause confusion. As discussed in Section 3.1, however, these results cannot be extrapolated beyond this simulated data.
3.5.3. MNAR Results
Again, as the number of variables in each functional form affects the fit of the GLM test, they will be discussed separately. The focus of the discussion is whether there is a possibility of confusion between the MAR and MNAR results.
- One-variable models: In the X-based models, both X and are found to be statistically significant, unlike in the MAR models, where X is never found to be significant. The Y-based models find both Y and to be significant, with Y consistently having a positive z-score. In contrast, the z-score for Y in MAR models is always negative. These characteristics help distinguish MNAR models from MAR models.
- Two-variable models: Z is found to be statistically significant only when it is present in a model. If X is in the model, X is always returned as significant, often along with . If Y is included, it is usually returned with , and Y has a positive z-score. If only is in the model, the Y z-score is negative. These MNAR models can be distinguished from MAR models because none of the MAR models found X to be significant, and Y in the MAR models has a negative z-score when found significant.
- Three-variable models: Z is found statistically significant only when present in the model. Y and are often returned together, but if Y is present in the model, it has a positive z-score; if it is not, it has a negative z-score. X is always correctly returned as significant, but sometimes accompanied by and vice versa. As before, it appears that the MNAR models can be distinguished from the MAR models because none of the MAR models find X to be significant, and Y in the MAR models has a negative z-score when it is found to be significant.
- Four-variable models: All five variables are returned as significant in both cases. They can be distinguished by the Y z-score, that is, positive if Y is in the model, negative if it is not. X and Y with positive z-scores are never found in MAR models; this can be used to distinguish between MAR and MNAR models.
In summary, tests on the single-variable MAR models failed to identify any significant variables, but the AUC of “1” suggested a perfect fit was present. As this was not found with any of the MCAR or MNAR models, this is a unique return for these MAR models. It may, however, be an artifact of the simulated data and unlikely to be encountered with real data. MCAR returns were distinctive but may not be found with real data.
It may also be possible to distinguish between MAR and MNAR missingness. For MAR, the X variable is never returned as statistically significant, whereas if the Y variable is returned as statistically significant, it has a negative z-score. In contrast, MNAR returns X as statistically significant if present in the model, and if Y is correctly returned as statistically significant, it always has a positive z-score. Z is always returned as statistically significant if present.
3.5.4. Out-of-Sample Testing
Having developed a series of tests to identify missing data mechanisms, the next step is to evaluate them against an out-of-sample dataset. The test data were created by following exactly the same procedure as used for the original simulation data (as described in Section 3.3) but using a different probability distribution and random error generators. This time, the Beta(1, 2) distribution was used with the three levels of random errors generated by N(1, 0.1), N(0, 0.2), and N(0, 0.3) random draws for cases 4, 5, and 6, respectively. The same six cases were created as before, and the results will be evaluated on their ability to identify the correct missing data mechanism. The variables found significant at the 0.001 level are given in Table A7, found in Appendix B. Again, the first two cases (which have no missing data) are omitted from this evaluation.
- MAR: The test for missing data under a one-variable MAR mechanism results in model failure, as indicated by the warning messages ‘1: glm.fit: algorithm did not converge; and 2: glm.fit: fitted probabilities numerically 0 or 1 occurred’. In each case, the AUC had a value of 1, indicating a perfect fit. This is exactly what is found with the Beta(1, 2) data in all cases and is found in no other models. For two-variable MAR models, the test is considered successful when the correct variables are returned as significant; these may also show Y as significant but with a negative z-score. For the Beta(1, 2) data, the only time Y as well as are returned as statistically significant, the associated Y z-scores are negative. All other variables identified as significant are correctly selected. For the three-variable MAR model, the expected result is that the correct variables are returned as significant; these may also be accompanied by Y but with a negative z-score. The Beta(1, 2) data return the correct variables as significant in all cases, and when Y is also returned as significant, it has a negative z-score.
- MCAR: Apart from case 3 (missing data with no random errors, which found no significant variables), only the intercept was found significant, and the AUC was close to or at 0.5. These results, however, were also returned for one of the MNAR models. This finding underlines the difficulty of directly identifying MCAR in the data. More significantly, none of these results can be confused with the MAR results.
- MNAR: These results are again grouped by the number of variables in each model and assessed in terms of their likelihood of being mistaken for MAR results.One-variable models: For the X-based model, the test always returns X and as significant. For the Y-based model, both Y and may be returned as significant, but the z-score for the Y variable is always positive. As noted in the MCAR discussion, the Beta(1, 2) results sometimes resemble those of MCAR. However, in no case do they resemble MAR results, either because of the specific variables identified as significant or the sign of the z-scores.Two-variable models: X is always returned as significant if correct, is only returned as significant if correct, Y is returned as significant with a positive z-score if correctly identified, and Z is always correctly identified.Three-variable models: X is always returned as significant if correct, Y is always returned as significant with a positive z-score if correct, and Z is always correctly returned as significant where present in the model.Four-variable models: All five variables are returned as statistically significant, with the models distinguishable by the sign of the Y z-score.Overall, it appears that the tests were successful in distinguishing between MAR and MNAR, as the MNAR results were different from those found for MAR.
3.5.5. Comparing the Impact of Using Random Value Missing Data Infilling on the Test and Its Results
The results so far suggest that success in using this diagnostic test to diagnose MAR missingness is a realistic option. Repeating this testing with a data series that uses random substitution, however, casts doubt on these results. As can be seen from Table A2, Table A4 and Table A6, the apparently clear signals for MAR broke down when faced with less orderly data. While the single-variable MAR models also failed with the same warning messages, the two- and three-variable models were not sufficiently differentiated from MNAR results to allow a clear distinction. For the two-variable models, both Y and were often returned, irrespective of whether was actually in the model. In addition, when Y was returned, it could have either a positive or a negative sign. This indicated that the clean Y-sign signal from the single mean replacement approach could no longer be taken as a reliable indicator of the missing data mechanism type. For the three-variable models, the correct model variables were returned, but Y was also identified as significant. In these model returns, the Y sign could also be either positive or negative. Finally, the MCAR and several MNAR returns also looked similar to the MAR returns, further reducing the likelihood of correctly identifying MAR missingness.
Taken together, these findings raise significant doubts about the ability of this test to diagnose MAR missingness directly from the data. Along with this is the possibility that there may be a high correlation between some of the variables within the dataset. This correlation can be the result of random chance, a direct relationship between the variables, or the presence of a confounder that influences two or more of the variables. Such a correlation could distort the test results and appear to identify MAR when it is not present.
There was also the possibility of the dataset containing mixed missingness. If more than one type of missing data mechanism was present, the impact on the test became unpredictable. It could, however, generate either type I or type II errors—incorrectly identifying MAR when it was not present, or vice versa.
4. Verification Testing with Real Data
Although the analysis so far has raised doubts about the viability of this diagnostic procedure, it is still worthwhile to see how it would perform with real-world data. Although the missingness is generally unknown for real-world data, its use in this direct testing may give further evidence regarding the value of this approach to identifying MAR data.
4.1. The Dataset
The data used in this study are the Financial Lives survey, 2020 (FLS) from the Financial Conduct Authority of the United Kingdom (FCA), sourced from the Consumer Data Research Centre, an Economic and Social Research Council (ESRC) Data Investment. It comprises responses to a 2020 survey on consumer attitudes, experiences, and holdings of financial products (see https://www.fca.org.uk/financial-lives (accessed on 9 August 2023) for further information on the data and the collection). The survey contains very high-quality data from 16,190 individuals across all four nations of the UK. Personally identifying data are not included in the dataset, and no attempt was made to identify individual contributors.
Owing to the high quality and the inclusion of sensitive personal details, including location information, the data are restricted, meaning that the licensing agreement prohibits the author from sharing or publishing any part of the dataset in any format.
In survey-based datasets, missing data can be of different types. “Unit nonresponse” is where a respondent fails to answer any questions. If every question is not answered, it is referred to as “item nonresponse”. With item nonresponse, the possible options are a blank entry and what is described in [23] as “I don’t know”, “I’m not sure”, and “I don’t want to answer”. They describe each as having different motivations and meanings; “I don’t want to answer” implies that an answer is known but the respondent is unwilling to share this information, “Don’t know” implies a lack of knowledge. Finally, “I’m not sure” is found in attitudinal questions when the respondent is genuinely uncertain about the response. Ref. [24] argued that “Don’t know” represents a valid response, and that treating these as missing data and imputing for them introduces a new form of error into the analysis. In contrast, Ref. [25] failed to find a difference in results irrespective of whether “Don’t know” and “Refused” (“Prefer not to say”) answers were combined or separated. It follows that any analysis of “Don’t know” and “Prefer not to say” missing data found in a survey needs to be treated carefully to avoid the possibility of introducing an additional potential source of error.
A list of the selected variables is presented in Table 11, which includes information on valid responses as well as nonresponse, categorized as either PNTS or DK. In the original data, some variables also contained blank entries, but for the purposes of this exercise, they were treated as PNTS. This separation allows DK to represent a valid survey response.

Table 11.
Financial Lives survey variables used in verification testing and their percentage of nonresponse by type.
The variables selected for this analysis were “Ethnicity” and “Sexuality”. These were chosen due to the absence of DK responses (thus, avoiding the issue of whether these should be treated as missing data) and because there is a plausible case that the other variables may influence their missingness, see [26,27]. The variables “Number of adults in household” and “Number of dependents at or under 17” act as proxies for social pressures, whereas the variable “Current residential property” acts as a proxy for social status.
The data variables representing characteristics were recoded to numeric levels, including one value for DK and another for PNTS and blank entries. Two new variables were also generated to represent missing data for both “Ethnicity” and “Sexuality”, where PNTS and blank entries were represented by ‘1’ and all other values by ‘0’. Similar to before, all tests were carried out using GLM regression with a logit link function. To mimic real-world conditions, PNTS and blank values in the independent variables were deleted prior to analysis, as substitute values for characteristic levels were not estimated (or, potentially, capable of estimation). Therefore, neither single mean nor random value substitution was used for the data under analysis.
4.2. Results
The results of the analysis for “Ethnic group” are given in Table 12. From this, it can be seen that four variables are at the required 0.001 level of significance (plus the intercept)—“Gender”, “Age”, “Highest qualification”, and “Sexuality”. All four are plausible candidates to drive missingness in the “Ethnic group” variable (see [27]), although the z-score for “Age” is negative. It is at this stage that domain knowledge would be required to assess the viability of these variables as candidates for MAR missingness, taking into account the structure of the survey, the population surveyed, and other contextual factors. Nonetheless, further insight may be gained by examining the AUC plot for this model, as shown in Figure 1. This plot suggests that MAR cannot be rejected as a plausible explanation for the “Ethnic group” missingness. Omitting “Age” changes the AIC slightly, from 1716.5 to 1698.4, but leaves the AUC unchanged at 0.883. For comparison, the “Null” (intercept only) model has a higher AIC at 2501.9 but an unchanged AUC at 0.883.

Table 12.
Output from the GLM analysis of the “Ethnic group”.
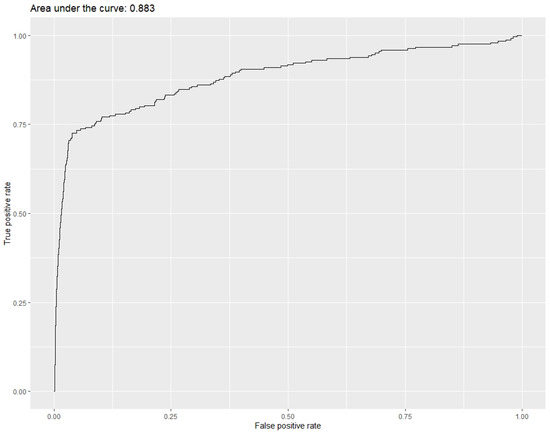
Figure 1.
AUC plot of direct testing for MAR missingness for the variable “Ethnic group”.
Taking into account the “random data” substitution-related concerns, however, suggests that these results need to be carefully reconsidered. As seen, the presence of a negative sign for “Age” does not necessarily indicate that it needs to be discarded from the model. At the same time, there is a risk of confounding from variables not included in the model, such as income or net wealth. While the test appears to identify MAR as present, this conclusion must be regarded as tentative due to the associated test and data complications.
The results of the analysis for “Sexuality” are given in Table 13. From this, it can be seen that five variables are at the required 0.001 level of significance (plus the intercept)—“Gender”, “Age”, “Number of dependents aged 17 or under”, “Highest qualification”, and “Ethnic group”. The sign of the z-score for “Age” and “Number of dependents at or under 17”, however, is negative. As before, all five are plausible candidates to drive “Sexuality” missingness.

Table 13.
Output from GLM analysis of “Sexuality”.
In this case, however, the AUC plot, which is shown in Figure 2, provides a less convincing case. Indeed, on the basis of this plot, the evidence for MAR missingness is not convincing, and it would be just as credible to argue that this is MNAR or even MCAR. Once again, the input of a domain expert is required to decide on how to proceed with the missing data. Omitting the negative z-score variables makes the situation worse. In this case, the AIC rises slightly, from 4690.8 to 4749.8, but the AUC falls from 0.708 to 0.695. For comparison, the “Null” (intercept only) model has an AIC of 5276.5 but an AUC of 0.500, a value that is consistent with the randomly generated data distribution. This adds to the evidence suggesting that a MAR model for this missing data may be suspect. Indeed, [28] found data that could potentially lead to discrimination, such as sexual orientation, to be a candidate for MNAR missingness. Along with this is the potential for confused signals, as demonstrated by the random-imputed test data findings, as well as the possibility of confounding and mixed missingness. Accordingly, whilst the data do not appear to be MAR, this cannot be ruled out with certainty.
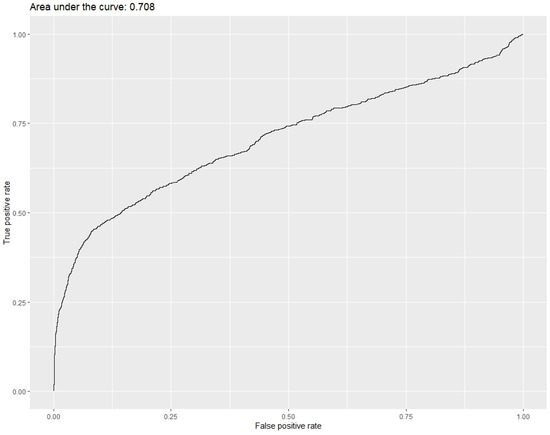
Figure 2.
AUC plot of direct testing for MAR missingness for variable “Sexuality”.
5. Discussion
This study aimed to develop a possible diagnostic test of MAR missingness via an extended missing data taxonomy, and to evaluate this diagnostic using real data. Following the introduction and background, Section 2 extended the missing data mechanism taxonomy to describe 24 possible missing data models. Simulated data (using single mean imputation for the missing data) were used in Section 3 to evaluate a possible diagnostic test for MAR missingness. This provided evidence supporting the viability of the test. Doubts were raised, however, in Section 3.5.5, following additional analyses using a random imputation method for the missing data. These doubts were magnified by concerns about the potential impact of high correlation among variables, confounding, and possible mixed missingness within the dataset. In Section 4, the diagnostic test was used with two variables from a real dataset, providing evidence that the missing data in one variable (“Ethnic group”) are MAR, whereas the evidence is less convincing for the other variable (“Sexuality”), which may well be MNAR. Considering the concerns arising from the random imputation-based analyses, as well as the other complicating factors, it becomes difficult to draw definite conclusions regarding the presence of MAR.
Additionally, it must be remembered that much of this analysis rests on the use of simulated data and, therefore, may not translate well to real-world datasets.
The potential impact of inter-variable correlations and confounding factors has already been mentioned. These correlations could be the result of random chance, a relationship between the variables, or the presence of confounders. The proposed diagnostic also assumes that all of the variables that influence the missingness are present in the analyzed dataset. These absent variables may include temporal or spatial components, which may not even be recorded in the data. As already highlighted, there is also no consideration of mixed missing data mechanisms or how these could impact the pattern of missingness.
The need to delete missing data in the real-world dataset may also affect the results. In addition, the real-world dataset used in this study is of very high quality with low levels of missingness, something that may not be true of other datasets. The associated increase in required deletions may further aggravate the impact on the diagnostic results.
This taxonomy does, however, highlight the escalating complexity of the basic missing data mechanisms. The simplest is MCAR, which represents a random process; the most complex is the self-referential MNAR, with MAR occupying a middle ground in terms of complexity. The number of models in this taxonomy should not, however, be considered a reflection of the relative frequency of the missing data mechanisms in real data. This is potentially unknowable, owing to the difficulties in identifying specific missing data mechanisms.
The nature of MAR data suggests that a direct diagnostic test may be possible. In this case, however, the diagnostic developed by means of the extended taxonomy proved not to be viable. Even the use of carefully crafted simulated data did not produce a set of results that could clearly identify MAR. Adding the uncertainties of real-world data, including inter-variable correlation, confounding variables, and possible mixed missingness, renders the results so unreliable that they cannot even be considered indicative.
Author Contributions
Conceptualization, D.S. and A.B.; methodology, D.S.; software, D.S.; validation, D.S., A.B. and Z.L.; formal analysis, D.S.; investigation, D.S.; resources, A.B.; data curation, D.S.; writing—original draft preparation, D.S.; writing—review and editing, A.B. and Z.L.; visualization, D.S.; supervision, A.B.; project administration, D.S.; funding acquisition, A.B. All authors have read and agreed to the published version of the manuscript.
Funding
The authors acknowledge the support from the UK Research and Innovation funding: Future Leaders Fellowships “Missing Data as Useful Data”, grant number MR/Y011856/1; Big Data- Good Data: Understanding Society by combining survey data and new forms of data, grant number 2815847; and Indicative Data: Extracting 3D Models of Cities from Unavailability and Degradation of Global Navigation Satellite Systems (GNSS), grant number MR/S01795X/2. For the purpose of open access, the author(s) have applied a Creative Commons Attribution (CC BY) license to any author-accepted manuscript version arising from this submission.
Data Availability Statement
The licensing agreement for the data used in the verification step specifically prohibits data sharing. The code required to generate the simulated data and carry out the testing, including verification testing, is available at https://drive.google.com/file/d/1OlN2U6O58h8WQRTNY5154eBIgqZdkZsY/view?usp=sharing (accessed on 21 May 2025).
Acknowledgments
The data for this research have been provided by the Consumer Data Research Centre, an ESRC Data Investment, under project ID CDRC 1434, ES/L011840/1; ES/L011891/1. The authors would like to thank Chris Brunsdon for his thoughts on the original concept for this work. The authors would also like to thank the two anonymous referees, whose valuable comments greatly improved the final paper.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AIC | Akaike information criterion |
| AUC | area under the curve |
| DK | don’t know |
| ESRC | Economic and Social Research Council |
| FCA | Financial Conduct Authority of the United Kingdom |
| FLS | Financial Lives survey |
| MAR | missing at random |
| MCAR | missing completely at random |
| MNAR | missing not at random |
| PNTS | prefer not to say |
Appendix A. Tables of Variables Found Significant for Binary Fitting of Simulated Missing Data

Table A1.
Variables found significant from testing for binary fitting of normally generated simulated data (single mean value substitution).
Table A1.
Variables found significant from testing for binary fitting of normally generated simulated data (single mean value substitution).
| Type | Model | Actual Model | Base Case Clean | Base Case Dirty, | Clean Missing | Dirty Missing, | Dirty Missing, | Dirty Missing, |
|---|---|---|---|---|---|---|---|---|
| MCAR | i | - | I | I | I | I | I | I |
| ii | Z | - | - | - | - | - | - | |
| iii | YR | - | - | - | - | - | - | |
| iv | XR | - | - | - | - | - | - | |
| MAR | v | Z, YR | I, Z, YR | I, Z, YR | I, Y, Z, YR | I, Y, Z, YR | I, Y, Z, YR | I, Y, Z, YR |
| vi | Z, XR | I, Z, XR | I, Z, XR | I, Z, XR | I, Z, XR | I, Z, XR | I, Z, XR | |
| vii | XR, YR | I, XR, YR | I, XR, YR | I, Y, XR, YR | I, Y, XR, YR | I, Y, XR, YR | I, Y, XR, YR | |
| viii | Z, XR, YR | I, Z, XR, YR | I, Z, XR, YR | I, Y, Z, XR, YR | I, Y, Z, XR, YR | I, Y, Z, XR, YR | I, Y, Z, XR, YR | |
| ix | Y | - | - | I, Y, YR | I, Y, YR | I, (y), YR | I, Y, YR | |
| x | X | - | - | I, X, XR | I, X, XR | I, X, XR | I, X, XR | |
| xi | Y, Z | I, Y, Z | I, Y, Z | I, Y, Z, YR | I, Y, Z, YR | I, Y, Z, YR | I, Y, Z, YR | |
| xii | X, Y | I, X, Y | I, X, Y | I, X, Y, YR | I, X, Y, (xr), YR | I, X, Y, (xr), YR | I, X, Y, (xr), YR | |
| xiii | X, YR | I, X, YR | I, X, YR | I, X, Y, XR, YR | I, X, Y, XR, YR | I, X, Y, XR, YR | I, X, Y, XR, YR | |
| xiv | X, Z | I, X, Z | I, X, Z | I, X, Z, (xr) | I, X, Z, (xr) | I, X, Z, XR | I, X, Z, XR | |
| xvi | Y, XR | I, Y, XR | I, Y, XR | I, Y, XR, YR | I, Y, XR, YR | I, Y, XR, YR | I, Y, XR, YR | |
| MNAR | xvii | X, XR | I, X, XR | I, X, XR | I, X, XR | I, X, XR | I, X, XR | I, X, XR |
| xviii | X, Y, Z | I, X, Y, Z | I, X, Y, Z | I, X, Y, Z, YR | I, X, Y, Z, YR | I, X, Y, Z, YR | I, X, Y, Z, YR | |
| xix | X, Z, YR | I, X, Z, YR | I, X, Z, YR | I, X, Y, Z, YR | I, X, Y, Z, (xr), YR | I, X, Y, Z, (xr), YR | I, X, Y, Z, XR, YR | |
| xxi | Y, Z, XR | I, Y, Z, XR | I, Y, Z, XR | I, Y, Z, XR, YR | I, Y, Z, XR, YR | I, Y, Z, XR, YR | I, Y, Z, XR, YR | |
| xxii | X, Z, XR | I, X, Z, XR | I, X, Z, XR | I, X, Z, XR | I, X, Z, XR | I, X, Z, XR | I, X, Z, XR | |
| xxiii | X, XR, YR | I, X, XR, YR | I, X, XR, YR | I, X, Y, XR, YR | I, X, Y, XR, YR | I, X, Y, XR, YR | I, X, Y, XR, YR | |
| xxvi | X, Y, XR | I, X, Y, XR | I, X, Y, XR | I, X, Y, XR, YR | I, X, Y, XR, YR | I, X, Y, XR, YR | I, X, Y, XR, YR | |
| xxviii | X, Y, Z, XR | I, X, Y, Z, XR | I, X, Y, Z, XR | I, X, Y, Z, XR, YR | I, X, Y, Z, XR, YR | I, X, Y, Z, XR, YR | I, X, Y, Z, XR, YR | |
| xxix | X, Z, XR, YR | I, X, Z, XR, YR | I, X, Z, XR, YR | I, X, Y, Z, XR, YR | I, X, Y, Z, XR, YR | I, X, Y, Z, XR, YR | I, X, Y, Z, XR, YR |

Table A2.
Variables found significant from testing for binary fitting of normally generated simulated data (random value substitution, dirty data only).
Table A2.
Variables found significant from testing for binary fitting of normally generated simulated data (random value substitution, dirty data only).
| Type | Model | Actual Model | Dirty Missing, | Dirty Missing, | Dirty Missing, |
|---|---|---|---|---|---|
| MCAR | i | - | I, Y, YR | I, Y, YR | I, Y, YR |
| ii | Z | - | - | - | |
| iii | YR | - | - | - | |
| iv | XR | - | - | - | |
| MAR | v | Z, YR | I, Y, Z, YR | I, Y, Z, YR | I, Y, Z, YR |
| vi | Z, XR | I, Y, Z, XR, YR | I, Y, Z, XR, YR | I, Y, Z, XR, YR | |
| vii | XR, YR | I, Y, XR, YR | I, Y, XR, YR | I, Y, XR, YR | |
| viii | Z, XR, YR | I, (y), Z, XR, YR | I, Y, Z, XR, YR | I, Y, Z, XR, YR | |
| ix | Y | - | I, Y, (xr) | I, Y, YR | |
| x | X | I, X, Y, XR, (yr) | I, X, Y, XR, YR | I, X, Y, XR | |
| xi | Y, Z | I, Y, Z | I, Y, Z, YR | I, Y, Z, YR | |
| xii | X, Y | I, X, Y, XR, YR | I, X, Y, XR, YR | I, X, Y, XR, YR | |
| xiii | X, YR | I, X, Y, XR, YR | I, X, Y, XR, YR | I, X, Y, XR, YR | |
| xiv | X, Z | I, X, Y, Z, YR | I, X, Y, Z, XR, YR | I, X, Y, Z, XR | |
| xvi | Y, XR | I, Y, XR, YR | I, Y, XR, YR | I, Y, XR, YR | |
| MNAR | xvii | X, XR | I, X, Y, XR | I, X, Y, XR, YR | I, X, Y, XR, YR |
| xviii | X, Y, Z | I, X, Y, Z, YR | I, X, Y, Z, XR, YR | I, X, Y, X, (xr), YR | |
| xix | X, Z, YR | I, X, Y, Z, (xr), YR | I, X, Y, Z, (xr), YR | I, X, Y, Z, XR, YR | |
| xxi | Y, Z, XR | I, Y, Z, XR | I, Y, Z, XR, YR | I, Y, Z, XR, YR | |
| xxii | X, Z, XR | I, X, Y, Z, XR, YR | I, X, Y, Z, XR, (yr) | I, X, Y, Z, XR, YR | |
| xxiii | X, XR, YR | I, X, Y, XR, YR | I, X, Y, XR, YR | I, X, Y, XR, YR | |
| xxvi | X, Y, XR | I, X, Y, XR, YR | I, X, Y, (z), XR, YR | I, X, Y, XR, YR | |
| xxviii | X, Y, Z, XR | I, X, Y, Z, XR | I, X, Y, Z, XR, YR | I, X, Y, Z, XR | |
| xxix | X, Z, XR, YR | I, X, Y, Z, XR, YR | I, X, Y, Z, XR, YR | I, X, Y, Z, XR, YR |

Table A3.
Variables found significant from testing for binary fitting of Poisson (mean 30)-generated simulated data (single mean value substitution).
Table A3.
Variables found significant from testing for binary fitting of Poisson (mean 30)-generated simulated data (single mean value substitution).
| Type | Model | Actual Model | Base Case Clean | Base Case Dirty, | Clean Missing | Dirty Missing, | Dirty Missing, | Dirty Missing, |
|---|---|---|---|---|---|---|---|---|
| MCAR | i | - | I | I | I | I | I | I |
| ii | Z | - | - | - | - | - | - | |
| iii | YR | - | - | - | - | - | - | |
| iv | XR | - | - | - | - | - | - | |
| MAR | v | Z, YR | I, Z, YR | I, Z, YR | I, Y, Z, YR | I, Y, Z, YR | I, Y, Z, YR | I, Y, Z, YR |
| vi | Z, XR | I, Z, XR | I, Z, XR | I, Z, XR | I, Z, XR | I, Z, XR | I, Z, XR | |
| vii | XR, YR | I, XR, YR | I, XR, YR | I, Y, XR, YR | I, Y, XR, YR | I, Y, XR, YR | I, Y, XR, YR | |
| viii | Z, XR, YR | I, Z, XR, YR | I, Z, XR, YR | I, Y, Z, XR, YR | I, Y, Z, XR, YR | I, Y, Z, XR, YR | I, Y, Z, XR, YR | |
| ix | Y | - | - | I, Y, YR | I, Y, YR | I, Y, YR | I, Y, YR | |
| x | X | - | - | I, X, XR | I, X, XR | I, X, XR | I, X, XR | |
| xi | Y, Z | I, Y, Z | I, Y, Z | I, Y, Z, YR | I, Y, Z, YR | I, Y, Z, YR | I, Y, Z, YR | |
| xii | X, Y | I, X, Y | I, X, Y | I, X, Y, XR, YR | I, X, Y, XR, YR | I, X, Y, (xr), YR | I, X, Y, YR | |
| xiii | X, YR | I, X, YR | I, X, YR | I, X, Y, XR, YR | I, X, Y, XR, YR | I, X, Y, YR | I, X, Y, YR | |
| xiv | X, Z | I, X, Z | I, X, Z | I, X, Z, XR | I, X, Z, XR | I, X, Z | I, X, Z | |
| xvi | Y, XR | I, Y, XR | I, Y, XR | I, Y, XR, YR | I, Y, XR, YR | I, Y, XR, YR | I, Y, XR, YR | |
| MNAR | xvii | X, XR | I, X, XR | I, X, XR | I, X, XR | I, X, XR | I, X, XR | I, X, XR |
| xviii | X, Y, Z | I, X, Y, Z | I, X, Y, Z | I, X, Y, Z, XR, YR | I, X, Y, Z, YR | I, X, Y, Z, (xr), YR | I, X, Y, Z, YR | |
| xix | X, Z, YR | I, X, Z, YR | I, X, Z, YR | I, X, Y, Z, XR, YR | I, X, Y, Z, (xr), YR | I, X, Y, Z, (xr), YR | I, X, Y, Z, YR | |
| xxi | Y, Z, XR | I, Y, Z, XR | I, Y, Z, XR | I, Y, Z, XR, YR | I, Y, Z, XR, YR | I, Y, Z, XR, YR | I, Y, Z, XR, YR | |
| xxii | X, Z, XR | I, X, Z, XR | I, X, Z, XR | I, X, Z, XR | I, X, Z, XR | I, X, Z, XR | I, X, Z, XR | |
| xxiii | X, XR, YR | I, X, XR, YR | I, X, XR, YR | I, X, Y, XR, YR | I, X, Y, XR, YR | I, X, Y, XR, YR | I, X, Y, XR, YR | |
| xxvi | X, Y, XR | I, X, Y, XR | I, X, Y, XR | I, X, Y, XR, YR | I, X, Y, XR, YR | I, X, Y, XR, YR | I, X, Y, XR, YR | |
| xxviii | X, Y, Z, XR | I, X, Y, Z, XR | I, X, Y, Z, XR | I, X, Y, Z, XR, YR | I, X, Y, Z, XR, YR | I, X, Y, Z, XR, YR | I, X, Y, Z, XR, YR | |
| xxix | X, Z, XR, YR | I, X, Z, XR, YR | I, X, Z, XR, YR | I, X, Y, Z, XR, YR | I, X, Y, Z, XR, YR | I, X, Y, Z, XR, YR | I, X, Y, Z, XR, YR |

Table A4.
Variables found significant from testing for binary fitting of Poisson (mean 30)-generated simulated data (random value substitution, dirty data only).
Table A4.
Variables found significant from testing for binary fitting of Poisson (mean 30)-generated simulated data (random value substitution, dirty data only).
| Type | Model | Actual Model | Dirty Missing, | Dirty Missing, | Dirty Missing, |
|---|---|---|---|---|---|
| MCAR | i | - | I, Y, YR | I, Y, YR | I, Y, YR |
| ii | Z | - | - | - | |
| iii | YR | - | - | - | |
| iv | XR | - | - | - | |
| MAR | v | Z, YR | I, Y, Z, YR | I, Y, Z, YR | I, Y, Z, YR |
| vi | Z, XR | I, Y, Z, XR, YR | I, Y, Z, XR, YR | I, Y, Z, XR | |
| vii | XR, YR | I, Y, XR, YR | I, (x), Y, XR, YR | I, Y, XR, YR | |
| viii | Z, XR, YR | I, Y, Z, XR, YR | I, Y, Z, XR, YR | I, Y, Z, XR, YR | |
| ix | Y | I, Y, YR | I, YR | I, Y, YR | |
| x | X | I, X, Y, XR, YR | I, X, Y, XR, YR | I, X, Y, XR, YR | |
| xi | Y, Z | I, Y, Z, YR | I, Y, Z, YR | I, Y, Z, YR | |
| xii | X, Y | I, X, Y, XR, YR | I, X, Y, XR, YR | I, X, Y, (xr), YR | |
| xiii | X, YR | I, X, Y, XR, YR | I, X, Y, XR, YR | I, X, Y, (xr), YR | |
| xiv | X, Z | I, X, Y, Z, XR, YR | I, X, Y, Z, XR, YR | I, X, Y, Z, YR | |
| xvi | Y, XR | I, Y, XR, YR | Y, XR, YR | I, Y, XR, YR | |
| MNAR | xvii | X, XR | I, X, Y, XR, YR | I, X, Y, XR, YR | I, X, Y, XR, YR |
| xviii | X, Y, Z | I, X, Y, Z, XR, YR | I, X, Y, Z, YR | I, X, Y, Z, YR | |
| xix | X, Z, YR | I, X, Y, Z, XR, YR | I, X, Y, Z, (xr), YR | I, X, Y, Z, (xr), YR | |
| xxi | Y, Z, XR | I, Y, Z, XR, YR | I, Y, Z, XR, YR | I, Y, Z, XR, YR | |
| xxii | X, Z, XR | I, X, Y, Z, XR | I, X, Y, Z, XR, YR | I, X, Y, Z, XR, YR | |
| xxiii | X, XR, YR | I, X, Y, XR, YR | I, X, Y, XR, YR | I, X, Y, XR, YR | |
| xxvi | X, Y, XR | I, X, Y, XR, YR | I, X, Y, XR, YR | I, X, Y, XR, YR | |
| xxviii | X, Y, Z, XR | I, X, Y, Z, XR, YR | I, X, Y, Z, XR, YR | I, X, Y, Z, XR, YR | |
| xxix | X, Z, XR, YR | I, X, Y, Z, XR, YR | I, X, Y, Z, XR, YR | I, X, Y, Z, XR, YR |

Table A5.
Variables found significant from testing for binary fitting of Poisson (mean 5)-generated simulated data (single mean value substitution).
Table A5.
Variables found significant from testing for binary fitting of Poisson (mean 5)-generated simulated data (single mean value substitution).
| Type | Model | Actual Model | Base Case Clean | Base Case Dirty, | Clean Missing | Dirty Missing, | Dirty Missing, | Dirty Missing, |
|---|---|---|---|---|---|---|---|---|
| MCAR | i | - | I | I | I | I | I | I |
| ii | Z | - | - | - | - | - | - | |
| iii | YR | - | - | - | - | - | - | |
| iv | XR | - | - | - | - | - | - | |
| MAR | v | Z, YR | I, Z, YR | I, Z, YR | I, Y, Z, YR | I, Y, Z, YR | I, (x), Y, Z, YR | I, Y, Z, YR |
| vi | Z, XR | I, Z, XR | I, Z, XR | I, Z, XR | I, Z, XR | I, Z, XR | I, Z, XR | |
| vii | XR, YR | I, XR, YR | I, XR, YR | I, Y, XR, YR | I, Y, XR, YR | I, Y, XR, YR | I, Y, XR, YR | |
| viii | Z, XR, YR | I, Z, XR, YR | I, Z, XR, YR | I, Y, Z, XR, YR | I, Y, Z, XR, YR | I, X, Y, Z, XR, YR | I, Y, Z, XR, YR | |
| ix | Y | - | - | I, Y, YR | I, Y, YR | I, YR | I, YR | |
| x | X | - | - | I, X, XR | I, X, XR | I, X, XR | I, X, XR | |
| xi | Y, Z | I, Y, Z, (yr) | I, Y, Z | I, Y, Z, YR | I, Y, Z, YR | I, Y, Z, YR | I, Y, Z, YR | |
| xii | X, Y | I, X, Y | I, X, Y | I, X, Y, XR, YR | I, X, Y, XR, YR | I, X, Y, XR, YR | I, X, Y, YR | |
| xiii | X, YR | I, X, YR | I, X, YR | I, X, Y, XR, YR | I, X, Y, XR, YR | I, X, Y, XR, YR | I, X, Y, YR | |
| xiv | X, Z | I, X, Z | I, X, Z | I, X, Z, XR | I, X, Z, (xr) | I, X, Z, XR | I, X, Z, (xr) | |
| xvi | Y, XR | I, Y, XR | I, Y, XR | I, Y, XR, YR | I, Y, XR, YR | I, Y, XR, YR | I, Y, XR, YR | |
| MNAR | xvii | X, XR | I, X, XR | I, X, XR | I, X, XR | I, X, (z), XR | I, X, XR | I, X, XR |
| xviii | X, Y, Z | I, X, Y, Z, (yr) | I, X, Y, Z, XR | I, X, Y, Z, XR, YR | I, X, Y, Z, (xr), YR | I, X, Y, Z, XR, YR | I, X, Y, Z, YR | |
| xix | X, Z, YR | I, X, Z, YR | I, X, Z, (xr), YR | I, X, Y, Z, XR, YR | I, X, Y, Z, YR | I, X, Y, Z, (xr), YR | I, X, Y, Z, YR | |
| xxi | Y, Z, XR | I, Y, Z, XR, YR | I, Y, Z, XR | I, Y, Z, XR, YR | I, (x), Y, Z, XR, YR | I, (x), Y, Z, XR, YR | I, Y, Z, XR, YR | |
| xxii | X, Z, XR | I, X, Z, XR | I, X, Z, XR | I, X, Z, XR | I, X, Z, XR | I, X, Z, XR | I, X, Z, XR | |
| xxiii | X, XR, YR | I, X, XR, YR | I, X, XR, YR | I, X, Y, XR, YR | I, X, Y, XR, YR | I, X, Y, XR, YR | I, X, Y, XR, YR | |
| xxvi | X, Y, XR | I, X, Y, XR | I, X, Y, XR | I, X, Y, XR, YR | I, X, Y, XR, YR | I, X, Y, XR, YR | I, X, Y, XR, YR | |
| xxviii | X, Y, Z, XR | I, X, Y, Z, XR | I, X, Y, Z, XR | I, X, Y, Z, XR, YR | I, X, Y, Z, XR, YR | I, X, Y, Z, XR, YR | I, X, Y, Z, XR, (yr) | |
| xxix | X, Z, XR, YR | I, X, Z, XR, YR | I, X, Z, XR, YR | I, X, Y, Z, XR, YR | I, X, Y, Z, XR, YR | I, X, Y, Z, XR, YR | I, X, Y, Z, XR, YR |

Table A6.
Variables found significant from testing for binary fitting of Poisson (mean 5)-generated simulated data (random value substitution, dirty data only).
Table A6.
Variables found significant from testing for binary fitting of Poisson (mean 5)-generated simulated data (random value substitution, dirty data only).
| Type | Model | Actual Model | Dirty Missing, | Dirty Missing, | Dirty Missing, |
|---|---|---|---|---|---|
| MCAR | i | - | Y, YR | I, Y, (yr) | I, (y) |
| ii | Z | - | - | - | |
| iii | YR | - | - | - | |
| iv | XR | - | - | - | |
| MAR | v | Z, YR | I, Y, Z, YR | I, X, Y, Z, YR | I, Y, Z, YR |
| vi | Z, XR | I, Y, Z, XR, YR | I, Y, Z, XR, YR | I, Y, Z, XR, YR | |
| vii | XR, YR | I, Y, XR, YR | I, Y, XR, YR | I, Y, XR, YR | |
| viii | Z, XR, YR | I, Y, Z, XR, YR | I, Y, Z, XR, YR | I, Z, XR, YR | |
| ix | Y | I, Y, YR | I, Y, YR | I, Y, YR | |
| x | X | I, X, Y, XR | I, X, Y, XR | I, X, Y, XR, YR | |
| xi | Y, Z | I, Y, Z, YR | I, Y, Z, YR | I, Y, Z, YR | |
| xii | X, Y | I, X, Y, XR | I, X, Y, XR, YR | I, X, Y, YR | |
| xiii | X, YR | I, X, Y, XR, YR | I, X, Y, XR, YR | I, X, Y, (xr), YR | |
| xiv | X, Z | I, X, Y, Z, XR | I, X, Y, Z, XR, (yr) | I, X, Y, Z, XR, YR | |
| xvi | Y, XR | I, Y, XR, YR | I, Y, XR, YR | I, Y, XR, YR | |
| MNAR | xvii | X, XR | I, X, Y, XR, YR | I, X, Y, XR, YR | I, X, Y, XR |
| xviii | X, Y, Z | I, X, Y, Z, XR, YR | I, X, Y, Z, XR, YR | I, X, Y, Z, YR | |
| xix | X, Z, YR | I, X, Y, Z, YR | I, X, Y, Z, YR | I, X, Y, Z, YR | |
| xxi | Y, Z, XR | I, (x), Y, Z, XR | I, Y, Z, XR, YR | I, Y, Z, XR, YR | |
| xxii | X, Z, XR | I, X, Y, Z, XR, YR | I, X, Y, Z, XR, YR | I, X, Y, Z, XR, YR | |
| xxiii | X, XR, YR | I, X, Y, XR, YR | I, X, XR, YR | I, X, Y, XR, YR | |
| xxvi | X, Y, XR | I, X, Y, XR, YR | I, X, Y, XR, YR | I, X, Y, XR, YR | |
| xxviii | X, Y, Z, XR | I, X, (y), Z, XR, YR | I, X, Y, Z, XR, YR | I, X, Y, Z, XR | |
| xxix | X, Z, XR, YR | I, X, Y, Z, XR, YR | I, X, Y, Z, XR, YR | I, X, Z, XR, YR |
Appendix B. Table of Variables Found Significant for Binary Fitting of Simulated Out-of-Sample Missing Data

Table A7.
Variables found significant from testing for binary fitting of Beta(1, 2)-generated simulated data.
Table A7.
Variables found significant from testing for binary fitting of Beta(1, 2)-generated simulated data.
| Type | Model | Actual Model | Base Case Clean | Base Case Dirty, | Clean Missing | Dirty Missing, | Dirty Missing, | Dirty Missing, |
|---|---|---|---|---|---|---|---|---|
| MCAR | i | - | I | - | I | I | I | I |
| ii | Z | - | - | - | - | - | - | |
| iii | YR | - | - | - | - | - | - | |
| iv | XR | - | - | - | - | - | - | |
| MAR | v | Z, YR | I, Z, YR | I, Z, YR | Y, Z, YR | I, Z, YR | I, Z, YR | I, Z, YR |
| vi | Z, XR | I, Z, XR | I, Z, XR | I, Z, XR | I, Z, XR | I, Z, XR | I, Z, XR | |
| vii | XR, YR | I, XR, YR | I, XR, YR | I, Y, XR, YR | I, XR, YR | I, XR, YR | I, XR, YR | |
| viii | Z, XR, YR | I, Z, XR, YR | I, Z, XR, YR | I, Y, Z, XR, YR | I, Z, XR, YR | I, Z, XR, YR | I, Z, XR, YR | |
| ix | Y | - | - | Y, YR | I, (yr) | I, (x) | I | |
| x | X | - | - | I, X, XR | I, X | I, X | I, X | |
| xi | Y, Z | I, Y, Z | I, Y, Z | I, Y, Z, YR | I, Y, Z | I, Y, Z | I, Y, Z | |
| xii | X, Y | I, X, Y | I, X, Y | I, X, Y, YR | I, X, Y, (yr) | I, X, Y | I, X, Y | |
| xiii | X, YR | I, X, YR | I, X, YR | I, X, Y,(xr), YR | I, X, YR | I, X, YR | I, X, YR | |
| xiv | X, Z | I, X, Z | I, X, Z, (xr) | I, X, Z | I, X, Z | I, X, Z | I, X, Z | |
| xvi | Y, XR | I, Y, XR | I, (x), Y, XR | I, Y, XR, YR | I, Y, XR, (yr) | I, Y, XR | I, Y XR | |
| MNAR | xvii | X, XR | I, X, XR | I, X, XR | I, X, XR | I, X, XR | I, X, XR | I, X, XR |
| xviii | X, Y, Z | I, X, Y, Z | I, X, Y, Z | I, X, Y, Z, YR | I, X, Y, Z | I, X, Y, Z | I, X, Y, Z | |
| xix | X, Z, YR | I, X, Z, YR | I, X, Z, YR | I, X, Y, Z, YR | I, X, Z, YR | I, X, Z, YR | I, X, Z, YR | |
| xxi | Y, Z, XR | I, Y, Z, XR | I, Y, Z, XR | I, Y, Z, XR, YR | I, Y, Z, XR | I, Y, Z, XR | I, Y, Z, XR | |
| xxii | X, Z, XR | I, X, Z, XR | I, X, Z, XR | I, X, Z, XR | I, X, Z, XR, (yr) | I, X, Z, XR | I, X, Z, XR | |
| xxiii | X, XR, YR | I, X, XR, YR | I, X, XR, YR | I, X, Y, XR, YR | I, X, XR, YR | I, X, XR, YR | I, X, XR, YR | |
| xxvi | X, Y, XR | I, X, Y, XR | I, X, Y, XR | I, X, Y, XR, YR | I, X, Y, XR | I, X, Y, XR | I, X, Y, XR | |
| xxviii | X, Y, Z, XR | I, X, Y, Z, XR | I, X, Y, Z, XR | I, X, Y, Z, XR, YR | I, X, Y, Z, XR | I, X, Y, Z, XR | I, X, Y, Z, XR | |
| xxix | X, Z, XR, YR | I, X, Z, XR, YR | I, X, Z, XR, YR | I, X, Y, Z, XR, YR | I, X, Z, XR, YR | I, X, Z, XR, YR | I, X, Z, XR, YR |
References
- Olteanu, A.; Castillo, C.; Diaz, F.; Kiciman, E. Social Data: Biases, Methodological Pitfalls, and Ethical Boundaries. Front. Big Data 2019, 2, 13. [Google Scholar] [CrossRef] [PubMed]
- Lin, X.; Genest, C.; Banks, D.L.; Molenberghs, G.; Scott, D.W.; Wang, J.L. Past, Present, and Future of Statistical Science; CRC Press LLC: London, UK, 2014. [Google Scholar]
- Cohen, N.; Berchenko, Y. Normalized Information Criteria and Model Selection in the Presence of Missing Data. Mathematics 2021, 9, 2474. [Google Scholar] [CrossRef]
- Rehman, N.U.; Contreras, I.; Beneyto, A.; Vehi, J. The Impact of Missing Continuous Blood Glucose Samples on Machine Learning Models for Predicting Postprandial Hypoglycemia: An Experimental Analysis. Mathematics 2024, 12, 1567. [Google Scholar] [CrossRef]
- Griffith, D.A.; Liau, Y.T. Imputed spatial data: Cautions arising from response and covariate imputation measurement error. Spat. Stat. 2021, 42, 100419. [Google Scholar] [CrossRef]
- Li, F.; Sun, H.; Gu, Y.; Yu, G. A Noise-Aware Multiple Imputation Algorithm for Missing Data. Mathematics 2023, 11, 73. [Google Scholar] [CrossRef]
- Little, R.; Rubin, D. Statistical Analysis with Missing Data; Wiley Series in Probability and Statistics; Wiley: Hoboken, NJ, USA, 2019. [Google Scholar]
- Silva, L.O.; Zárate, L.E. A brief review of the main approaches for treatment of missing data. Intell. Data Anal. 2014, 18, 1177–1198. [Google Scholar] [CrossRef]
- Gomer, B.; Yuan, K.H. A Realistic Evaluation of Methods for Handling Missing Data When There is a Mixture of MCAR, MAR, and MNAR Mechanisms in the Same Dataset. Multivar. Behav. Res. 2022, 58, 988–1013. [Google Scholar] [CrossRef]
- Little, R.J.; Rubin, D.B.; Zangeneh, S.Z. Conditions for Ignoring the Missing-Data Mechanism in Likelihood Inferences for Parameter Subsets. J. Am. Stat. Assoc. 2017, 112, 314–320. [Google Scholar] [CrossRef]
- Little, R.J. Missing Data Assumptions. Annu. Rev. Stat. Its Appl. 2021, 8, 89–107. [Google Scholar] [CrossRef]
- Doretti, M.; Geneletti, S.; Stanghellini, E. Missing Data: A Unified Taxonomy Guided by Conditional Independence. Int. Stat. Rev. 2018, 86, 189–204. [Google Scholar] [CrossRef]
- Jamshidian, M.; Yuan, K.H. Examining missing data mechanisms via homogeneity of parameters, homogeneity of distributions, and multivariate normality. Wiley Interdiscip. Rev. Comput. Stat. 2014, 6, 56–73. [Google Scholar] [CrossRef]
- Li, H.; Yi, G.Y. Missing Data Mechanisms for Analysing Longitudinal Data with Incomplete Observations in Both Responses and Covariates. Aust. New Zealand J. Stat. 2016, 58, 377–396. [Google Scholar] [CrossRef]
- Zhao, J.; Shao, J. Approximate Conditional Likelihood for Generalized Linear Models with General Missing Data Mechanism. J. Syst. Sci. Complex. 2017, 30, 139–153. [Google Scholar] [CrossRef]
- Taleb, N. Fooled by Randomness: The Hidden Role of Chance in Life and in the Markets, 2nd ed.; Penguin Books: London, UK, 2007. [Google Scholar]
- Williams, J.J.; Griffiths, T.L. Why Are People Bad at Detecting Randomness? A Statistical Argument. J. Exp. Psychology. Learn. Mem. Cogn. 2013, 39, 1473–1490. [Google Scholar] [CrossRef] [PubMed]
- Almlöf, J.; Vall Llosera, G.; Arvidsson, E.; Björk, G. Creating and detecting specious randomness. EPJ Quantum Technol. 2023, 10, 1. [Google Scholar] [CrossRef]
- Gomer, B.; Yuan, K.H. Subtypes of the Missing Not at Random Missing Data Mechanism. Psychol. Methods 2021, 26, 559–598. [Google Scholar] [CrossRef]
- Coskun, A.; Oosterhuis, W.P. Statistical distributions commonly used in measurement uncertainty in laboratory medicine. Biochem. Medica 2020, 30, 5–17. [Google Scholar] [CrossRef]
- Hoo, Z.H.; Candlish, J.; Teare, D. What is an ROC curve? Emerg. Med. J. EMJ 2017, 34, 357–359. [Google Scholar] [CrossRef]
- Snipes, M.; Taylor, D.C. Model selection and Akaike Information Criteria: An example from wine ratings and prices. Wine Econ. Policy 2014, 3, 3–9. [Google Scholar] [CrossRef]
- Montagni, I.; Cariou, T.; Tzourio, C.; González-Caballero, J.L. “I don’t know”, “I’m not sure”, “I don’t want to answer”: A latent class analysis explaining the informative value of nonresponse options in an online survey on youth health. Int. J. Soc. Res. Methodol. 2019, 22, 651–667. [Google Scholar] [CrossRef]
- Kroh, M. Taking ‘don’t knows’ as valid responses: A multiple complete random imputation of missing data. Qual. Quant. 2006, 40, 225–244. [Google Scholar] [CrossRef]
- Yan, T.; Curtin, R. The Relation Between Unit Nonresponse and Item Nonresponse: A Response Continuum Perspective. Int. J. Public Opin. Res. 2010, 22, 535–551. [Google Scholar] [CrossRef]
- Kim, H.J.; Fredriksen-Goldsen, K.I. Nonresponse to a Question on Self-Identified Sexual Orientation in a Public Health Survey and Its Relationship to Race and Ethnicity. Am. J. Public Health 2013, 103, 67–69. [Google Scholar] [CrossRef] [PubMed]
- Ahlmark, N.; Algren, M.H.; Holmberg, T.; Norredam, M.L.; Nielsen, S.S.; Blom, A.B.; Bo, A.; Juel, K. Survey nonresponse among ethnic minorities in a national health survey—A mixed-method study of participation, barriers, and potentials. Ethn. Health 2015, 20, 611–632. [Google Scholar] [CrossRef]
- Joinson, A.N.; Paine, C.; Buchanan, T.; Reips, U.D. Measuring self-disclosure online: Blurring and non-response to sensitive items in web-based surveys. Comput. Hum. Behav. 2008, 24, 2158–2171. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).