Abstract
Sound-based predictive maintenance (PdM) is a critical enabler for ensuring operational continuity and productivity in industrial systems. Due to the diversity of equipment types and the complexity of working environments, numerous feature engineering methods and anomaly diagnosis models have been developed based on sound signals. However, existing reviews focus more on the structures and results of the detection model, while neglecting the impact of the differences in feature engineering on subsequent detection models. Therefore, this paper aims to provide a comprehensive review of the state-of-the-art feature extraction methods based on sound signals. The judgment standards in the sound detection models are analyzed from empirical thresholding to machine learning and deep learning. The advantages and limitations of sound detection algorithms in varied equipment are elucidated through detailed examples and descriptions, providing a comprehensive understanding of performance and applicability. This review also provides a guide to the selection of feature extraction and detection methods for the predictive maintenance of equipment based on sound signals.
MSC:
68T01; 68T10
1. Introduction
Predictive maintenance (PdM) is a critical strategy to ensure the reliable operation of industrial equipment in the manufacturing, energy, and transportation sectors [1,2,3,4]. Unscheduled equipment shutdown can cause substantial economic losses and pose risks to operator safety, prompting manufacturing companies to allocate considerable manpower and resources to equipment safety inspection [5,6,7,8]. However, unnecessary or improper maintenance activities consume up to one-third of the total maintenance budget in manufacturing firms [9,10].
Recently, sound-based PdM methods have attracted considerable interest in academic and industrial communities due to the non-invasive sensing and the ability to capture high-dimensional information [11]. As an inherent characteristic of equipment operation, sound can precisely detect subtle changes during operation, including friction, impact, and resonance [12]. These changes often reflect early-stage faults, enabling the PdM of industry equipment. Saucedo et al. [13] demonstrated that mechanical acoustic emission signals can accurately characterize critical fault modes, such as bearing wear, gear tooth breakage, and rotor imbalance [14].
The sound PdM system includes online/training and offline/testing processes [15,16]. The general flow of sound anomaly detection is shown in Figure 1. In each part, the analysis processing of the sound signal involves two steps: the acoustic feature engineering and the anomalous sound detection. On the one hand, the construction of feature engineering for sound signals forms the foundation of predictive maintenance systems, ensuring that the extracted features reflect subtle changes in the operation of the equipment. The feature extraction methods transform the one-dimensional raw sound signals into high-dimensional feature vectors, which can represent the operational state of the target equipment. Therefore, the existing feature extraction methods are classified into statistical parameters, waveform decomposition, and spectrogram analysis.
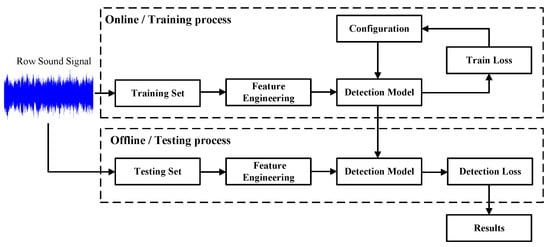
Figure 1.
The general flow of sound anomaly detection for the PdM system.
On the other hand, anomaly detection serves as the core component, responsible for accurately identifying abnormal events from the extracted features. Driven by the rapid progress of intelligent detection, equipment sound analysis has progressed from empirical threshold-based methods to feature-driven machine learning, then to data-centric deep learning, and is now approaching physics-integrated paradigms as a future direction. The development trend of sound anomaly detection for the PdM system is shown in Figure 2. The traditional experience-driven model has the highest detection efficiency, but the interference from complex external noise makes experience unable to meet the current needs of predictive maintenance for complex equipment. Thereby, feature-driven Support Vector Machine (SVM) models determine anomalies by detecting the distance between features. The data-driven convolutional neural networks (CNNs) extract latent information from raw sound signals. Feature and data-driven models have become the mainstream of current sound detection methods for improving the robustness and accuracy. The main feature extraction methods and detection models in recent sound-based industrial PdM are summarized in Table 1.
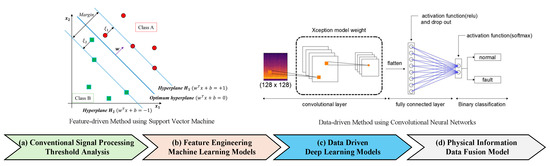
Figure 2.
The development trend of sound anomaly detection for the PdM system. The feature-driven SVM method reproduced from [17] with permission. Copyright Sensors. The data-driven CNN method reproduced from [18] with permission. Copyright Electronics.

Table 1.
Summary of sound equipment anomaly detection methods in recent years.
Nevertheless, acoustic diagnostics still face challenges such as insufficient transferability across devices [49], lack of robustness in feature extraction under extreme noise conditions [50], and the trade-off between real-time performance and accuracy for lightweight edge deployment [51]. Existing reviews focus more on the structures and results of the detection model, while neglecting the impact of differences in feature engineering on subsequent detection models. Therefore, this paper starts with the sound feature engineering for guiding the selection of sound feature extraction methods in different equipment and environments. Further, the judgment standards in the sound detection models are analyzed from the empirical threshold to machine learning and deep learning.
This study provides a comprehensive analysis of the evolution of acoustic diagnostic technologies, identifying the technical bottlenecks associated with noise suppression, feature generalization, and cross-device transferability. Additionally, it discusses next-generation solutions propelled by the fusion of artificial intelligence and physical modeling to offer theoretical support for the transition and standardization framework within this research area. Thus, this study aims to explore the theoretical foundations and application processes of sound signal analysis in the context of predictive maintenance for equipment.
The paper is divided into four sections. Section 2 focuses on the feature engineering of sound signals with statistical parameters, waveform decomposition, and spectrogram analysis. Section 3 reports on anomalous sound detection and classification methods. The last section is devoted to a discussion and conclusion.
2. Acoustic Feature Engineering
Acoustic feature engineering plays a vital role in the PdM of equipment [52]. Feature extraction methods transform the one-dimensional sound signal into a high-dimensional and interpretable feature vector [53]. The extracted feature vectors are then used to diagnose the operating state of the target equipment using the anomalous sound detection model. With the differences in the processes and routes of more feature extraction methods, this paper classifies the existing sound feature engineering methods into statistical parameters, waveform decomposition, and spectrogram analysis. The classification of acoustic feature engineering in the PdM of equipment systems is shown in Figure 3. This section explores the principles and application scenarios of these methods.
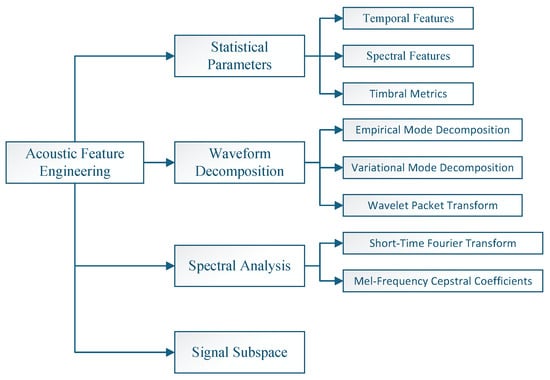
Figure 3.
The classification of acoustic feature engineering in the PdM of the equipment system.
2.1. Statistical Parameters
Statistical parameter extraction is a straightforward approach to describing the characteristics of equipment sounds because changes in waveform and energy occur when a device malfunctions [54,55]. Typically, statistical features are not applied independently. All statistical parameters are calculated from a finite-length sound sequence. To improve the real-time performance of the device’s prognostic system, the acquired sound signals are segmented into frame signals of equal length by a slip window. The framing process of a sound signal is shown below:
where n is the time variant of the sampling point, i is the position variant of the frame, records the amplitude value of the sound signal in the frame i, is the window function, s is the increased distance between the windows, and N is the length of the frame and the slipping window.
According to the different statistical targets and analysis methods, the statistical parameters are classified into temporal features, spectral features, and timbral metrics. The equations of statistical parameters applied in equipment sound detection are summarized in Table 2.

Table 2.
The summary of statistical parameters in equipment sound detection.
Given the prolonged operation of stable transformers, acoustic signals often exhibit significant variations in amplitude and frequency compared to normal conditions. Based on this operational environment, the purpose of feature extraction for transformer equipment is to detect shock signals in the acoustic signal. Therefore, Yu et al. [20] utilized the Short-Time Energy (STE) and Zero-Crossing Rate (ZCR) as foundational metrics for the preliminary assessment of acoustic signatures in power transformers.
Cao et al. [38] proposed an ensemble classifier to diagnose railway point machines with the temporal and spectral features. The recorded sound signals are decomposed into 15-level Intrinsic Mode Functions (IMFs) by the EMD method. Then, the entropy and statistical parameters are extracted from the obtained IMFs. In the feature engineering process, time and frequency domain statistical parameters are extracted as the raw discrimination features from each IMF. The extracted features include 10-dimensional time-domain statistical parameters, 4-dimensional frequency-domain statistical parameters, and 8-dimensional energy entropy. Finally, the feature matrix is sent into the proposed classifier.
In [25], based on the frequency domain signal, the traditional spectral features include the spectral envelope slope, spectrum mass center, and peak amplitude crest. Meanwhile, some temporal features can also be used in the frequency domain, such as peak value, skewness, and kurtosis. In [40], six sound features are selected and sent into the unsupervised learning model. Extracted sound features include the RMS, crest factor, peak value, peak frequency, median frequency, and relative peak.
Yasuji and Masashi [47] proposed a method that employs timbral metrics to extract and analyze fault features from machine sounds. The timbral metrics include sharpness, boominess, brightness, depth, and roughness. These timbral metrics are tailored to specific machine types based on their fault-related sound impressions. The theoretical foundations and computational models of these metrics are illustrated as follows: Sharpness is a quantification of the sensation of a sound being sharp or shrill. Roughness describes the perception of a sound as buzzing, harsh, or raspy. Boominess quantifies the sensation of low-frequency vibration or resonance. Brightness is associated with the perception of high-frequency energy in a sound. Depth, as a timbral attribute, reflects the prominence of low-frequency components in a sound.
The applied statistical parameters in different detection frameworks and applications are recorded in Table 3.

Table 3.
The summary of statistical parameters in different detection frameworks.
2.2. Waveform Decomposition
Waveform decomposition serves as a critical signal decoupling technique in equipment predictive maintenance. It effectively identifies latent failure signatures by applying standardized computational frameworks to separate single-channel acoustic signals into multi-layer components. Current industrial implementations predominantly adopt Empirical Mode Decomposition (EMD), Variational Mode Decomposition (VMD), and Wavelet Packet Transform (WPT) [56]. The pros and cons of the waveform decomposition methods are summarized in Table 4.
2.2.1. Empirical Mode Decomposition
Empirical Mode Decomposition (EMD), a non-stationary signal processing, decomposes complex signals into a set of Intrinsic Mode Functions (IMFs) [57]. The algorithm proceeds as follows:
Step 1: Extrema Identification. Detect all local maxima and minima points in the target signal.
Step 2: Envelope Construction. Generate upper and lower envelopes via cubic spline interpolation using the identified extrema.
Step 3: Mean Envelope Calculation. Compute the instantaneous mean envelope by averaging the lower and upper envelopes.
Step 4: IMF Extraction. Subtract from the original signal to derive a candidate IMF . Verify if satisfies the IMF criteria [58]. And then, the IMF component is saved in memory If unsatisfied, iteratively refine by treating it as the new input for Steps 1–3 until convergence. The iteration terminates when
where is an empirical parameter , which is used to control the distance between IMFs, and records the number of the iterations.
Step 5: Residual Computation. Update the residual signal , where is the number of the IMFs. This residual component is treated as new data and is subjected to the same processes described previously to calculate the next IMF component [59].
Step 6: Termination Condition. Repeat the process until the residual is monotonic or envelope amplitudes fall below a predefined threshold.
Shi et al. [27] introduced a dual-phase fusion framework integrating acoustic and vibration signals to improve rolling bearing fault detection. This methodology suppresses ambient noise interference while augmenting system state characterization through synergistic signal fusion. EMD is employed to refine fused signals by temporal smoothing and adaptive decomposition based on intrinsic time-scale features.
Delgado et al. [60] implement Complete Ensemble Empirical Mode Decomposition (CEEMD) [61], a noise-augmented approach, to isolate fault-induced frequency components within IMFs without compromising temporal fidelity. Post-decomposition, Gabor transform frequency margins are analyzed to derive discriminative spectral signatures from IMFs.
2.2.2. Variational Mode Decomposition
Variational Mode Decomposition (VMD) [62] operates through iterative optimization to partition signals into bandwidth-limited modal components [63]. This technique effectively resolves frequency overlap while addressing inherent limitations of traditional methods, including boundary distortion and modal aliasing, establishing its prominence in mechanical fault diagnostics [64].
The objective of VMD is to determine a collection of IMFs that collectively reduce total bandwidth expenditure while maintaining signal reconstruction fidelity. Bandwidth quantification utilizes the squared norm of gradient-modulated signals.
Step 1: Analytical Signal Derivation. Compute the analytic signal of each mode via the Hilbert transform to obtain its single-sided spectrum:
where is the Dirichlet function, and ∗ is the convolution symbol.
Step 2: Frequency Demodulation. Shift the spectrum of each mode to the baseband by mixing with its pre-estimated center frequency:
where represents the center frequency, denotes the IMF component, represents a impulse function and ∗ is the convolution calculation.
Step 3: Bandwidth Optimization. Estimate the bandwidth of each mode using the squared norm of the demodulated signal gradient. The constrained variational model is formulated as
where K is the number of modal components, , and are shorthand notations for the set of all modes and their center frequencies.
Step 4: Introducing the quadratic penalty factor and Lagrange multiplication operator. To transform the constrained problem into an unconstrained problem, the augmented Lagrange function is expressed as follows:
where is the penalty factor, is the multiplication operator, represents the -norm, and ⟨⟩ means the operation of the inner product.
The augmented Lagrangian method converts the constrained problem into an unconstrained form. However, the algorithm exhibits high computational complexity , limiting its applicability to real-time scenarios.
Lou et al. [34] introduce a hybrid feature extraction framework combining FFT and VMD. Spectral analysis and multi-scale temporal decomposition enable the capture of complementary frequency–energy distributions and transient characteristics. The integrated preprocessing strategy attenuates noise interference while preserving critical time–frequency signatures, enhancing neural networks’ ability to discern subtle fault patterns.
Yin et al. [35] devise a non-invasive fault identification system utilizing VMD and Support Vector Machines (SVMs). To overcome the degradation of fault diagnosis accuracy caused by IMFs with multiple feature sets. Six scale-invariant statistical metrics (including kurtosis and impulse factor) are computed from these IMFs, serving as discriminative inputs for SVM-based classification.
Xiao et al. [65] engineer a sealing strip acoustic assessment device coupled with an enhancement algorithm. The combination of Wiener filtering and VMD (WF-VMD) is proposed to enhance weak acoustic signals. The sound signal is divided into four IMFs () with the penalty constraint .
Lei et al. [66] present a novel denoising method integrating metaheuristic-optimized VMD with wavelet thresholding to address these challenges. The core innovation lies in the coati optimization algorithm (COA)-driven parameter selection for VMD, which adaptively determines the optimal decomposition mode count K and penalty factor , thereby overcoming the empirical parameterization limitations of conventional VMD. Subsequent cross-correlation analysis filters out low-frequency drift and high-frequency artifacts, achieving multi-stage noise suppression.
Li et al. [42] develop a Sparrow Search Algorithm-optimized VMD (SSA-VMD) model paired with enhanced wavelet thresholding. Leveraging the Sparrow Search Algorithm [67], the framework minimizes envelope entropy to optimize VMD parameters, preserving high-frequency transient features often lost in conventional methods. Experimental validation confirms superior noise attenuation and signal fidelity, particularly in scenarios involving intermittent fault impulses.
2.2.3. Wavelet Packet Transform
The Wavelet Packet Transform (WPT) extends signal decomposition capabilities by recursively partitioning high-frequency sub-bands [68], enabling refined frequency-band segmentation throughout the analyzed spectrum [69]. This hierarchical decomposition mechanism improves the spectral resolution, particularly in localized time–frequency regions [70]. In the context of sound detection, Discrete Wavelet Transform (DWT) generalizes the decomposition process by applying the wavelet function , mathematically expressed as
where is the scale factor, and is the shift factor.
In [23], 1D-DWT with 4 levels and 4 low-pass filter subbands is proposed to decompose the engine sounds. Proposed multileveled 1D-DWT applies wavelet filters to both low- and high-frequency components, mathematically expressed as
where represents the frequency-band signal at the i level. . J indicates the total number of decomposed frequency-band signals and equals . , with I denoting the decomposition depth. is the low-pass filter, and is the high-pass filter.
For recognizing power system equipment based on sound signals, Bai et al. [19] carry out the WT to obtain the wavelet coefficient–time diagram, where the mean square integrable space is applied as the basic wavelet and mother wavelet. The extracted diagram is transformed into an image by the structural similarity image processing method and then sent to the machine learning classifier.
In [31], the multi-resolution wavelet transform is used to decompose the engine’s sound signal based on the microphone. Both a 5-level DWT and a 4-level Wavelet Packet Analysis (WPA) are used to measure noise signals for extracting fault features of the engine using the Daubechies wavelet function. The Daubechies wavelet function is defined by a set of finite-length filter coefficients [71].
For detecting the rolling bearing of the belt conveyor, the sound signals are divided into four levels of the IFMs by the WPT method [26]. The Teager Energy Operator (TEO) is used to strengthen the weak shock component of the original signal [72]. For a digital signal , the operator can be approximated in the time domain, which is expressed as follows:

Table 4.
The pros and cons of the waveform decomposition methods.
Table 4.
The pros and cons of the waveform decomposition methods.
| Methods | Pros | Cons | Ref. |
|---|---|---|---|
| EMD | Adaptive decomposition | Severe mode mixing issues. | [27,59] |
| without basis functions. | Highly sensitive to noise. | ||
| Suitable for non-stationary. | |||
| CEEMD | Suppresses mode mixing | Doubled computational complexity | [60] |
| Better detail preservation | Requires manual noise amplitude selection | ||
| EEMD | Reduces mode mixing through | Ensemble size requires empirical selection. | [73] |
| noise-assisted decomposition. | Influenced by the type of noise introduced. | ||
| Anti-noise Interference. | |||
| More reproducible and consistent. | |||
| VMD | Variational framework | Requires preset mode number K | [34,35,65] |
| ensures unique decomposition | |||
| WF-VMD | Wiener-filtered enhancement | Latency Per Frame | [65] |
| COA-VMD | Auto-optimizes K and | Increased computation time for optimization | [66] |
| SSA-VMD | Effective for multi-fault coexistence detection | Requires large iterations | [42] |
| WT | Flexible basis function selection | Energy leakage | [19,68] |
| DWT | Efficient implementation with filter banks | Limited shift-invariance | [31] |
| WPT + TEO | Quickly capture the resonant frequency | Manual threshold setting | [26] |
| bands of fault characteristics. |
2.3. Spectrogram Analysis
As a time–frequency analysis method, spectrogram analysis transforms the one-dimensional sound sequence into a two-dimensional spectrogram. The existing spectrogram analysis methods include Short-time Fourier Transform (STFT) and Mel-Frequency Cepstral Coefficients (MFCCs) [74,75]. The spectrogram is spliced by multiple frequencies transformed from the framed sound signals along the time axis. The framing process of the spectrogram is expressed in Figure 4. Therefore, the spectrogram can effectively represent the operational state of the target equipment. The frame parameters of the spectrogram analysis are summarized in Table 5.
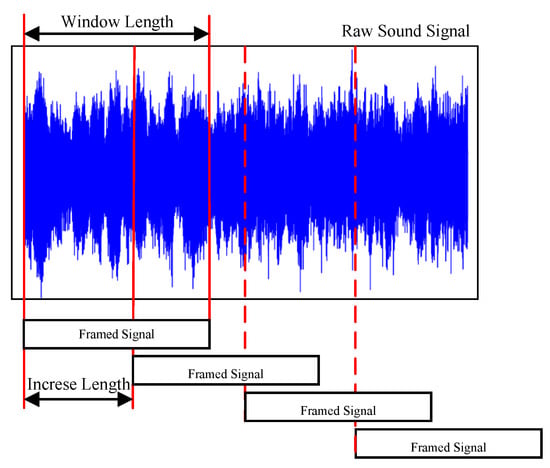
Figure 4.
The framing process of raw sound signal.
2.3.1. Short-Time Fourier Transform
STFT is one of the basic sound analysis methods that extracts potential feature information by framing, windowing, and frequency transforming. Furthermore, sound frequency signals are widely used as inputs to the model. STFT is constrained by the time–frequency resolution of the window function, and the time–frequency resolution is fixed [64].
In [76], the STFT transforms a 1D sound signal into a 2D frequency matrix. The extracted matrix is sent into the deep learning model to diagnose bearing faults. Based on a single-channel off-the-shelf microphone, Behnam et al. [36] convert the real-time collected time-domain signals of construction site operation sounds into the frequency domain by the STFT. The one-dimensional sound data are transformed into two-dimensional image data, and then the image data are sent into the convolutional neural network.
2.3.2. Mel-Frequency Cepstral Coefficient
Mel-Frequency Cepstral Coefficients (MFCCs) constitute a perceptually motivated feature set derived from cepstral analysis in the Mel-scaled frequency domain. These coefficients quantitatively characterize the energy distribution of acoustic signals across critical frequency bands, encapsulating both low-frequency spectral envelopes and high-frequency fine structures within the cepstral domain [77]. The Mel scale operates as a psychoacoustic frequency scaling system that emulates human auditory frequency sensitivity, nonlinearly compressing higher frequencies to align with biological perception mechanisms [41]. The workflow of the MFCC is shown in Figure 5. Meanwhile, the frame parameters of the FFT process in MFCC are recorded in Table 5.
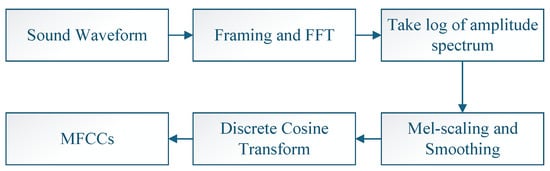
Figure 5.
The workflow of the MFCC.
Firstly, the calculation process for MFCC is based on the frequency signal . The spectral energy of the framed frequency signal is shown as follows:
where K is the number of the frequency sample rate in the FFT, and k denotes the frequency-position variable.
Secondly, the energy spectrum of a frame in the frequency domain is filtered by the Mel filter bank [45]. The parameters of the MFCC are expressed as follows:
where represents the Mel filters bank, and N is the number of Mel filters. The calculation process of the Mel filters [78] is illustrated as follows:
where M is the Mel frequency and f is the frequency:
where is the scale value in the linear frequency domain, which is obtained through the inverse operation of the Mel frequency.
Finally, the logarithms of Mel filter energy are calculated and processed by the discrete cosine transform for MFCC, which is expressed as follows:
To eliminate the effect of noise on sound anomaly detection, Yu et al. [20] use the MFCC method to extract the sound feature information.
For detecting the click sound event of the automobile car engine, Espinosa et al. [32] apply five extraction methods to represent the feature vector. The MFCC method is used to identify and track timbre fluctuations. The chromogram is calculated to represent pitch classes and harmony based on the STFT method. Spectral Centroid (SC) provides complementary rich information with MFCC for sound discrimination tasks [79]. Tonnetz representation (TR) measures the tonal centroid of a sound based on harmonic changes [80]. The extracted 1D vector has 213 dimensions, which include MFCCs (60 dimensions), chromogram (12 dimensions), Mel-scaled spectrogram (128 dimensions), SC (7 dimensions), and TR (6 dimensions).

Table 5.
The summary of the frequency frame parameters and applications.
Table 5.
The summary of the frequency frame parameters and applications.
| Sample Rate | Window Function | Window Length | Increase Length | Applications | Ref. |
|---|---|---|---|---|---|
| 8820 | Hanning | 819 | 205 | Multiple-equipment Recognition | [36] |
| 1920 | Hamming | 1920 | 960 | Underground Pipeline Damage | [41] |
| 256 | Hanning | 4096 | 2048 | Excavation Equipment | [81] |
| 1024 | - | 1024 | 512 | DCASE 2020 Task 2 | [45] |
| 2048 | Hamming | 2048 | 512 | Rotating Machinery | [33] |
2.4. Signal Subspace
Different from the feature engineering of the single-channel sound signal, the signal subspace methods focus on analyzing the interactions between array signals [82]. By transforming multi-channel array signals into a matrix, this method aims to achieve sound source localization and feature dimensionality reduction. The signal subspace methods are applied to analyze the microphone array signal [83].
Mahyub et al. [84] propose the Signal Latent Subspace method to classify environmental sound. In [85], the multichannel signals recorded are first preprocessed using the Principal Component Analysis (PCA) method to monitor the liquid–gas pipe. The PCA is used to identify the subspace in the sound signal that has the maximum variance. The multi-channel sound signal matrix is inputted, where denotes the number of the sound vector, and N is the number of the microphones. The calculation process of the transformed matrix Y is expressed as follows:
where is the mean value of the sound signal matrix:
where is a matrix that consists of orthonormal eigenvectors, and denotes a diagonal matrix:
where represents an orthonormal transformation matrix, and . Therefore, the applied PCA method reduces the vector dimension of the array sound signals, thus improving the computational efficiency.
3. Anomalous Sound Detection
The identification of anomalous acoustic signatures is emerging as an increasingly complex challenge across diverse industrial applications. The timely recognition of such deviations enables preventive measures to mitigate potential equipment failures, catastrophic breakdowns, or safety hazards. Contemporary methodologies leverage advanced feature extraction techniques and machine learning architectures to develop intelligent diagnostic frameworks. According to the scale and complexity of the model, the current state-of-the-art equipment sound anomaly detection models can be classified into experience-based thresholding analysis, feature-driven machine learning, and data-driven deep learning. These systems facilitate the evolution of predictive maintenance strategies by correlating sound feature engineering with incipient fault conditions, thereby transforming reactive maintenance paradigms into data-driven prognostic approaches. The classification of anomalous sound detection methods is shown in Figure 6. These approaches enhance system adaptability across diverse operating scenarios and requirements, effectively meeting the needs of predictive maintenance while improving operational efficiency and safety. Therefore, the model structures and anomaly judgments, such as empirical thresholds, feature distances, and loss functions, are illustrated in this section.
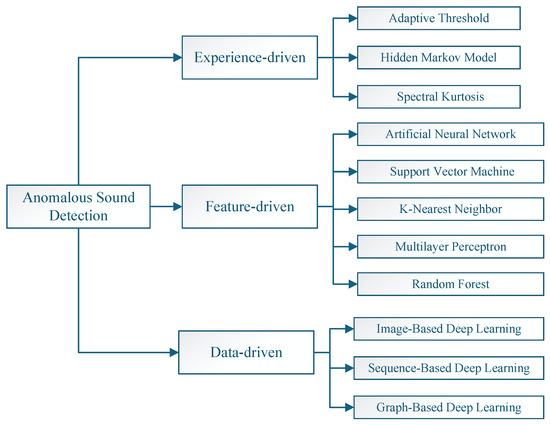
Figure 6.
The classification of anomalous sound detection methods.
3.1. Experience-Driven Thresholding Analysis
Experience-based thresholding analysis is the most fundamental and quickest method for detecting sound anomalies. The distinction between normal and abnormal sounds is derived from manual empirical judgment. The process of setting thresholds uses statistical methods without neural networks. Common threshold analysis methods include the Hidden Markov Model (HMM) and adaptive thresholding.
In [20], the sound signals of the power transformer are recorded by a single-channel microphone. To detect the impulse events of the power transform, the HMM is trained and applied based on the temporal features (Short-Time Energy and zero-crossing rate) and spectrogram features (MFCCs). Temporal thresholds are set by multiple statistical experiments, which are expressed as follows:
where and are set through multiple statistical experiments, represents the ratio of abnormal Short-Time Energy to total frames, and represents the ratio of abnormal zero-crossing rate to total frames.
Yu et al. [20] use the HMM to set thresholds [86] based on the results of the MFCC method. The diagnosis process is illustrated as follows:
where denotes the results of the MFCC method, T is the number of the IMF components, G is the state number, and the is calculated as follows:
where denotes the transition probability from state i to state j at time t, and is the probability of observing in state j:
where M refers to the matching degree.
The fault diagnosis methodology employs kurtosis-driven component selection, where Intrinsic Mode Functions (IMFs) are quantitatively assessed through a kurtosis thresholding scheme to identify components containing critical fault signatures [27]. These optimized IMF subsets undergo selective reconstruction, effectively amplifying rolling bearing defect characteristics in the composite signal.
A novel Teager Energy Spectral Kurtosis (TESK) index is developed through a four-stage process [26]. Firstly, the sound signal is decomposed via WPT. Secondly, sub-band energy is demodulated using the Teager operator [72]. Thirdly, time–frequency is mapped into two-dimensional spectral information. Finally, comprehensive TESK distribution is generated via spectral kurtosis computation across time–frequency planes. This hybrid approach enables simultaneous resolution in both temporal and spectral domains, effective for detecting transient bearing faults under variable operating conditions.
3.2. Feature-Driven Machine Learning
Unlike conventional threshold analysis, machine learning utilizes neural network architectures to fit normal data patterns, allowing for the detection of anomalies and outliers. To increase the speed of detection and to enable the running of sound detection models with limited storage space, the machine learning methods based on feature engineering have widely been applied to detect equipment sounds in recent years [87]. The pipeline frameworks include the Artificial Neural Network (ANN), K-Nearest Neighbor (KNN) [23], Multilayer Perceptron (MLP) [88], Support Vector Machine (SVM) [89], and Random Forest (RF) [90]. These methods have been successfully applied in various applications.
For diagnosis engine faults based on array microphone and accelerometer, Wang et al. [31] propose a three-layer artificial neural network (ANN). The recorded sounds are preprocessed into 4 parts, in the wavelet packet analysis illustrated in Section 2.3. The input feature matrix is defined by 21 blocks in 9 signals. The calculation process of the proposed ANN-based detection model is illustrated as follows:
where i, j, and k represent the number of dimensions in the output layer, the hidden layer, and the input layer. is the output result. is a pure linear function. represents the log-sigmoid function.
The mean squared error is used as the loss function for updating the trained parameters and , which is shown as follows:
where is the desired output, and is the cardinality of the learning dataset.
This approach demonstrates robust capabilities in processing both stationary and non-stationary signals, making it highly suitable for engine fault diagnosis. The model’s versatility extends beyond vehicle engine fault diagnosis, offering potential applications in various sound-related engineering fault detection domains.
To recognize the damaged bearing, Pacheco et al. [25] design and compare three supervised machine learning methods.
In method 1, the multi-domain feature extraction with SVM classifier (MFE-SVM) is designed. Time, frequency, and time–frequency parameters (14 dimensions) are extracted as a vector. Then, the vectors are categorized by a binary classifier using the SVM, which is expressed as follows:
where is the input vector, l is the training sample number, is the Lagrange multiplier, refers to the kernel function, and represents the bias value.
Method 2 calculates the relative energy share based on the 8-level DWT method, where the Daubechies 8 and Biorthogonal 3.7 are used as the mother wavelet functions, and then the decomposed sound signals are classified by the Random Forest (RF) classifier with cross-validation.
In method 3, time-spectral features extraction and reduction with linear discriminant analysis (TSFDR-LDA) combine temporal and spectral features to perform classification. The LDA method obtains classified vectors by the KNN and GMM models.
Experiments show that TSFDR-LDA performs optimally in combining acoustic and vibration signals, which is suitable for scenarios with high accuracy requirements; MFE-SVM and RWE outperform in single signals (especially acoustic) and are suitable for non-invasive or resource-constrained scenarios; and acoustic signals outperform vibration signals in most methods, validating their potential as a low-cost, non-contact monitoring solution.
For pipeline leakage localization in municipal water systems based on a microphone unit, Notani et al. [40] develop a clustering framework employing One-Class Support Vector Machines (OC-SVMs) to process hydroacoustic signatures. This unsupervised technique constructs an optimal hyperplane in kernel space that maximizes the margin between normalized acoustic data points and the coordinate origin, effectively isolating leak-induced acoustic patterns from background noise.
Yin et al. [91] introduce an ensemble diagnostic architecture combining EMD with multi-feature SVM classification for automotive component monitoring. Based on the decomposed IMFs, the kurtosis and skewness are selected as the fusion features of fault signals according to the Pearson correlation coefficient. Then, the extracted features are sent into the SVM model to detect the sound of the automobile rearview mirror folding. The proposed method significantly improves the accuracy of fault diagnosis compared to single-feature detection methods.
Liu et al. [41] present a sound monitoring system for the prevention of underground pipeline damage caused by construction. The temporal features (including STE and ZCR) and spectrogram features based on the MFCC are extracted and then sent into the designed Random Forest (RF) model.
In [32], this study builds and trains five classical machine learning classifiers and a CNN classifier to detect the sound event. The 213-dimensional feature vector is extracted in the feature engineering process, which includes five extraction methods illustrated in Section 2.3.2. Compared with SVM, KNN, MLP, and RF classifiers, the MLP classifier is selected and optimized for the sound detection of click-event assembled harnesses. The MLP contains three parts: an input layer, hidden layers, and an output layer. Each layer is connected by neurons with a simple activation function. Meanwhile, the structure of the proposed CNN contains sparse interaction, parameter sharing, and quasi-variant representation [92].
3.3. Data-Driven Deep Learning
The data-driven methodology has emerged as a pivotal factor in predictive maintenance paradigms. By enabling the proactive identification of potential failures, this approach significantly mitigates operational downtime, reduces costs associated with redundant maintenance activities, and optimizes resource allocation in maintenance scheduling. Consequently, extensive research efforts in recent years have been dedicated to the development and refinement of advanced anomaly detection systems, with notable advancements in algorithmic robustness and operational efficiency [93]. According to the different input data types, the existing depth-based methods for detecting abnormal sounds in devices are categorized into image-based methods [94], sequence-based methods [95], and graph-based methods [96]. The data-driven deep learning methods with different input data types are summarized in Table 6.

Table 6.
The summary of the data-driven deep learning methods with different input data types.
3.3.1. Image-Based Deep Learning
Image-based deep learning methods aim to detect the anomalous sound signals using image analysis technologies. The 1D sound signals are transformed into a 2D image, which includes temporal and spectral information.
To detect bearing failures in rotating machinery based on the array microphone, Liu et al. [33] propose the lightweight fault diagnosis network called MPNet. The recorded sound signals are transformed into a frequency image using the STFT method. The extracted frequency image includes temporal information and frequency information. The proposed MPNet model contains three parts: the multibranch feature fusion module, the residual attention pyramid module, and the classifier. The multibranch feature fusion module is used to obtain multi-scale information by multi-scale convolutional branches. Then, the residual attention pyramid module, containing 4-level attention networks, is designed to extract deep fault features and enhance network representation ability. The cross-entropy loss is applied to optimize the detection framework, which is expressed as follows:
where represents the element of the true fault category, and represents the probability.
The MPNet can accurately, and in real-time, diagnose typical faults of bearings and belt conveyor idlers with fewer network parameters and faster computational efficiency. Compared with other detection models, the proposed model has higher accuracy and robustness under noise.
Due to the overlapping feature distributions and limited separability of subtle anomalies, unsupervised anomalous sound detection faces inherent challenges related to ambiguous decision boundaries. To address these limitations, Wu et al. [44] integrate the ArcFace classifier and GMM to enhance feature discriminability and model complex decision boundaries in unsupervised settings. The proposed framework includes two parts: the pre-training process and the detection process.
The CNN is trained using the ArcFace loss function [98] to extract the hidden features in the pre-training process. The extracted features are mapped into a high-dimensional arc space to maximize inter-class distances while ensuring intra-class compactness. The Arcface loss function is expressed as follows:
where M is the batch size, is the number of vector elements, denotes the angle of the label, and is the angle between the hidden feature vector and the weight vector.
The process of the ArcFace loss-based classification neural network is shown in Figure 7.
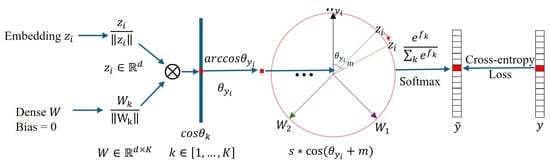
Figure 7.
Training of the ArcFace loss-based classification neural network. Reproduced from [43] with permission. Copyright IEEE access.
In the detection process, the two-dimensional spectrogram transformed from the recorded sound signal is sent into the trained deep classification network. Then, the designed GMM model is classified as a binary output. The anomaly score is expressed as follows:
where represents the GMM function, and is the output result from the deep classification network.
The framework is validated by experiments on the ToyADMOS datasets [93] and MIMII datasets. The method effectively trains the distribution boundaries of different classes of data, and the extracted hidden features have high separability, thus improving the detection performance [44].
Liu et al. [45] adopt a self-supervised classification strategy based on the spectral–temporal fusion feature (STgram) and MobileFaceNet (MFN) [99]. The STgram is a fusion of the Tgram and the MFCC spectrogram . The Tgram is obtained by the TgramNet, which contains a 1D convolution with a smaller kernel size. The proposed framework applies the ArcFace loss function [98] rather than the cross-entropy error as the loss function.
To obtain more information from the raw sound signal and MFCCs, Kong et al. [43] fuse the Tgram, Wgram, MFCC spectrogram, and Sgram into the multi-features. Then, the obtained sound feature is sent into the Squeeze-and-Excitation MobileFaceNet (SE-MFN). The designed framework is shown in Figure 8. The Tgram is calculated from the raw sound signal using the TgramNet [45]. The Wgram is extracted from the raw signal based on the WaveNet [100] utilizing dilated causal convolutional networks. The Sgram is extracted from the STFT spectrogram using SpecNet as a convolutional neural network.
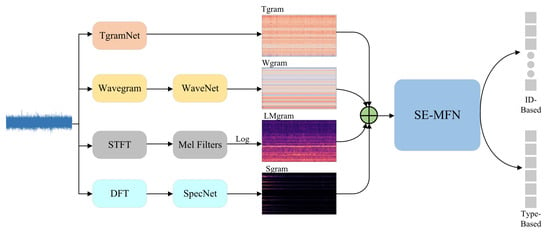
Figure 8.
The framework of the proposed method for anomalous sound detection. Reproduced from [43] with permission. Copyright IEEE Access.
In this study, loss functions are designed with the ArcFace loss function () [44] and the combined loss function (). The combined loss function
where is a balancing weight, represents the classification loss function based on the machine type, and denotes the loss function of the machine ID.
In addressing the challenge of simultaneously recognizing activities of multiple heavy construction equipment based on the microphone, Sherafat et al. [36] propose a multi-label and multilevel sound classification method based on STFT and CNN, utilizing single-channel microphones as input. The model architecture leverages STFT for feature extraction and CNN for classification, with the output being the identification of activities from multiple equipment. To enhance robustness, a data augmentation technique is developed to simulate real-world sound mixtures. The method is tested on both synthetic and real-world equipment sound mixtures, demonstrating its effectiveness in accurately identifying activities of multiple pieces of equipment on construction sites without the need for prior sound signal separation.
To address the challenge of sensor data noise interference in predictive maintenance for industrial equipment, Priscile et al. [22] propose a noise-robust predictive maintenance framework. Focusing on milling machines and motors, the research collects multi-modal sensor data, including sound, vibration, and ultrasonic signals, and constructs two novel datasets. Three models are proposed: a deep neural network (DNN), a deep convolutional neural network (DCNN), and an ensemble model (RFC + KNN + SVC). To enhance robustness, a Gaussian noise layer is introduced into the DCNN, and a training strategy with progressively reduced noise levels is implemented. Experimental results demonstrate that the noise-convolutional deep learning method significantly improves model robustness, offering a new solution for industrial equipment condition monitoring.
Cheng et al. [101] propose a hybrid model combining Generative Adversarial Networks (GANs) and the unsupervised CNN model for acoustic anomaly detection. The proposed GAN model aims to reduce the difference between normal samples and anomalous samples. The extracted features, as abnormal samples, are sent into the training process of the sound detection model.
3.3.2. Sequence-Based Deep Learning
Different from the image discrete detection method, the sequence-based deep learning methods focus on the causality of the input signal in time. The common sequence-based deep learning structures include the Recurrent Neural Network (RNN) [30], Temporal Convolutional Networks (TCNs), and AutoEncoder (AE) [24].
In [46], both MFCC and statistical features are sent into the Deep Diagnosis AutoEncoder (DDAE) to improve the accuracy of equipment anomaly diagnosis in high-noise environments. The proposed DDAE model contains two types of architectures. On the one hand, dimensionality reduction coding is performed for MFCC features to map the 128-dimensional MFCC features to 8 dimensions; on the other hand, dimensionality enhancement coding is performed for dimensional statistical features to map the 8-dimensional statistical features to 128 dimensions. The calculation processes of the encoder and decoder layers in the proposed DDAE model are expressed as follows:
where h is the result of the encoder, x is the input data, means the activation function, W is the trainable parameter to control the output dimension of the encoder layer, and b is the biases:
where is the result of the decoder, is the trainable parameter to control the output dimension of the decoder layer, and is the biases in the decoder.
Further, the mean squared error is applied as the loss function when assessing the outcomes, which is shown as follows:
The experimental results show that the proposed methodology affords an average area under the curve performance improvement of approximately 18% based on the MIMII dataset [102].
Park et al. [97] propose a sound anomaly detection model named Fast Adaptive RNN Encoder–Decoder (FARED) for improving the fast adaptive capability of sound detection. The designed model is composed of a recurrent neural network (RNN) architecture, where each cell employs a Long Short-Term Memory (LSTM). To handle variations in longitudinal feature dimensions, the model adopts an autoencoder framework, and its architecture is illustrated in Figure 9. The real-time equipment sound signal is framed into a sequential input spectrum. Each LSTM cell has three types of gates and two types of states as follows:
where is the framed sound signal at time t, is the input gate, means the output gate, is the forget gate, is the cell state vector, is the output result, and W, U, and b are trainable parameters in the LSTM cells.
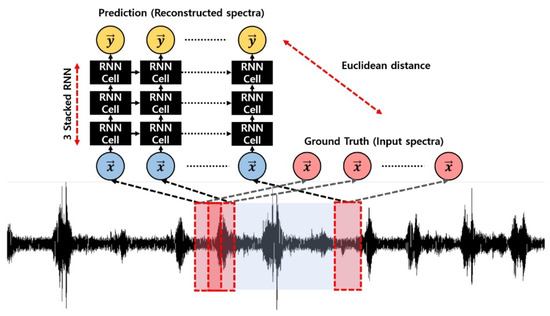
Figure 9.
The architecture of the RNN framework, where x represents the framed sound signal, and y is the reconstructed result through the encoder and decoder. Reproduced from [97] with permission. Copyright Sensors.
Further, the Euclidean distance is used to determine anomalies. An experimental evaluation is conducted on a set of datasets from the SMD assembly machine. Results show cutting-edge performance with fast adaptation.
To ensure the functionality of the sound anomaly detection model on various devices, Emanuele et al. [48] propose a joint framework using the ID Conditioned Network (ID-CN), LSTM, encoder, and decoder. The output of the joint framework is shown below:
where is the domain related to the latent representation of input X produced by the encoder. represents the domain of latent samples reconstructed by the decoder. H is the condition function.
Considering the input ID number, the classical autoencoder loss is not enough in the training process. To address this problem, an arbitrary value C is added to the distance loss, which is shown below:
In the offline detection part, the threshold for judging anomalies is generated from the built error of the training samples or based on the ROC curves.
Validated on the MIMII dataset, which simulates real-world industrial acoustic scenarios, the framework achieves a 17.61% improvement in partial AUC (pAUC) over non-conditioned counterparts and baseline methods.
To achieve early fault detection in belt conveyor systems, Alharbi et al. [28] propose an Intelligent fault detection method using the Yet Another Audio Mobilenet Network (YAMNet) using Bidirectional Long Short Term Memory (BiLSTM) and Bidirectional Gated Recurrent Units (BiGRUs). The designed framework enhances detection capabilities by extracting temporal features from generated embeddings with a soft attention mechanism. Further, the categorical hinge loss is employed to compute the classification outcomes for distinct sound categories.
In [34], spectral and temporal features are extracted from the sound signals of the rotating machine using the FFT and VMD methods. Further, a parallel network model with the LSTM and Bidirectional Temporal Convolutional Network (BiTCN) is employed to obtain multi-dimensional information. To extract the latent sound information based on the feature engineering, the frequency sequence signals are inputted into the LSTM model. Meanwhile, the results of the VMD method are sent into the BiTCN model:
where represents the output of the j layer in the block, and is the convolutional function.
Further, Lou et al. [34] propose a detection model using the cross-attention mechanism to fuse the latent features ( and ) extracted by the BiTCN and LSTM, which embeds the multi-information into Binary classification. The cross-attention mechanism is expressed as follows:
where is the query vectors, is the key vectors, and is the value vectors. , , and are trainable parameters. is the dimension of .
The proposed framework enriches the feature representation of rotating machine sound signals. The proposed framework performs well in processing rotating machine sound signals with a low signal-to-noise ratio (SNR), yielding evaluation metrics that surpass those of traditional methods and providing an effective approach for abnormal sound detection in rotating machines.
However, sequence-based methods may not be optimal for every machine type and working condition, particularly when the sound characteristics of machines exhibit high similarity and when the training and test sets are relatively unbalanced. Future research should focus on exploring multimodal information fusion methods with stronger generalization capabilities for machine abnormal sound detection (ASD) under a broader range of working conditions.
3.3.3. Graph-Based Deep Learning
In recent years, Graph Convolutional Networks (GCNs) have offered a promising alternative for detecting dynamic sequences, excelling in contextual relationship analysis within discrete sequences independently of feature numbers [103]. The extracted sound features are transformed into a graph G. A graph structure is defined as follows:
where V represents a set of vertices for recording the result of the feature engineering, E denotes a set of edges connecting two nodes, and A is the adjacency matrix.
Compared with the traditional CNN, the GCN model focuses on the relationship between the target features. The aggregation operation of GCNs inherently has a smoothing effect on noise, making it particularly suitable for low signal-to-noise ratio environments. The message passing mechanism of GCNs allows nodes to aggregate information from multi-hop neighbors while preserving local details and global patterns.
The Deep Graph Convolutional Network (DGCN) proposed by Zhang et al. [29] leverages graph theory and spectral graph convolution to enable the acoustic-based fault diagnosis of roller bearings. The architecture begins by transforming raw acoustic signals into graph-structured data, where each 3600-point signal is mapped into a 60 × 60 matrix. Nodes represent signal points, and edges encode Euclidean distances between neighboring vertices.
The DGCN employs multiple graph convolutional blocks, each comprising a spectral convolution layer using Chebyshev polynomial approximations of graph Laplacian filters, a graph coarsening layer (via multilevel clustering to group similar nodes), and a graph pooling layer (via balanced binary tree rearrangement for 1D pooling). The final network structure (depth = 3, layer widths = 64/256/32) feeds extracted features into a Fully Connected layer and SoftMax classifier. The Chebyshev calculation of the GCN convolutional layer is shown as follows:
where and mean the output results at the and l layers of the GCN. is the sum of the adjacency matrix A and self-loop matrix I. is the degree of . is the trainable parameter.
While the loss function is not explicitly stated, cross-entropy loss is inferred due to the classification task and backpropagation-based optimization. Key advantages include superior classification accuracy over conventional methods, robustness to noise and variable speeds, and end-to-end learning without manual feature engineering. However, limitations include reliance on laboratory data (untested in real-world industrial environments), sensitivity to graph construction methods (fixed Euclidean edge weights), computational overhead from graph coarsening, and empirical parameter tuning (e.g., optimal Chebyshev kernel length = 7). The DGCN demonstrates promising potential for intelligent fault diagnosis but requires further validation under operational conditions and the exploration of adaptive graph topologies for broader applicability.
Yan et al. [39] extend this paradigm with Unsuper-TDGCN, combining Transformer-based time–frequency feature extraction, Dynamic GCN (DyGCN) for domain-shift-aware dependency modeling, and a Domain Self-adaptive Network (DSN) for covariance alignment. This framework achieves state-of-the-art performance in unsupervised machine anomalous sound detection under domain shifts, demonstrating superior generalization and efficiency. Both works underscore the efficacy of GNNs in capturing geometric relationships and domain-invariant features, yet face limitations in real-world validation and computational overhead. To achieve unsupervised anomalous sound detection, a fusion loss is designed as follows:
where is the loss function of the IDT-GCN model, is the loss function of the VDT-GCN model, is the second-order covariance distance, is the Additive Angular Margin (AAM) loss function, and is the poly loss function. The loss function of the IDT-GCN model is shown as follows:
where means the Fully Connected (FC) layer and is the features computed by the IDT-GCN model.
The loss function of the IDT-GCN model is shown as follows:
where is the features computed by the VDT-GCN model, and represents category labels.
While DGCN excels in structured fault diagnosis, Unsuper-TDGCN pioneers adaptive graph learning for broader industrial applications, though the scalability to other modalities remains unexplored. Collectively, these studies advance intelligent fault detection by harmonizing graph theory, spectral analysis, and domain adaptation, yet emphasize the need for lightweight architectures and cross-domain validation.
4. Opportunities
The evolution of acoustic-based predictive maintenance will be propelled by the synergistic integration of generative networks and physics-informed learning paradigms. Generative adversarial networks [104] and diffusion models are poised to address data scarcity through synthetic fault sound generation with domain-adversarial training, enabling robust anomaly detection under low-fault-sample regimes [105]. Concurrently, physics-informed neural networks (PINNs) [106] will bridge data-driven models with first-principle constraints, enhancing feature interpretability and extrapolation capability for novel failure modes [107]. Emerging hybrid architectures, such as physics-embedded GANs, will unify synthetic data augmentation with mechanism-driven feature learning, achieving cross-domain fault diagnosis. Edge deployment will benefit from neuromorphic computing for real-time acoustic processing. Future breakthroughs demand the co-design of generative physics-aware models and standardized validation protocols across industrial ecosystems.
5. Conclusions
Sound-based predictive maintenance has emerged as a pivotal technology for industrial equipment health monitoring, offering non-invasive sensing, cost-effectiveness, and high-dimensional information capture. This review systematically outlines the evolution of acoustic diagnostic methodologies, spanning foundational signal processing techniques to advanced deep learning frameworks. The suggestions of the feature engineering methods in different equipment and environments are recorded in Table 7. In fields with high real-time requirements, it is crucial to analyze the potential features within sound signals. When dealing with constant power devices, statistical features can effectively detect abnormal fluctuations and impacts. In complex noise environments, signal decomposition can significantly reduce noise and improve the signal-to-noise ratio. Furthermore, when facing variable power devices, spectral analysis can quickly obtain the operating status of the equipment. Subspace analysis can achieve sound source localization and signal enhancement.

Table 7.
The suggestions of the feature engineering methods in different equipment and environments.
By integrating physical propagation models with data-driven approaches, these methods address critical challenges such as non-stationarity, noise interference, and sparse fault samples. Key advancements include adaptive feature engineering for interpretable fault signatures, noise-robust architectures, and edge-compatible models for real-time deployment. However, persistent limitations of SNR in harsh environments, cross-device generalization gaps, and the trade-off between computational efficiency and accuracy hinder large-scale industrial adoption. Future research should prioritize interdisciplinary innovations, such as physics-informed neural networks for mechanism-aligned learning, lightweight architectures for edge intelligence, and multimodal fusion with vibration or thermal data. Standardized evaluation benchmarks and self-supervised learning paradigms will further enhance robustness in data-scarce scenarios. Ultimately, the convergence of domain knowledge, advanced algorithms, and industrial digitization will drive the next generation of intelligent maintenance systems, enabling proactive fault mitigation and sustainable operational excellence in Industry 4.0 ecosystems.
Author Contributions
Conceptualization L.Y.; Data curation, T.Y. and T.P.; Date analysis, T.Y. and L.Y.; Resources, L.Y.; Validation, T.Y. and T.P.; Writing—original draft, T.Y.; Writing—review and editing L.Y. and T.P.; Revision, L.Y. and T.P. All authors have read and agreed to the published version of the manuscript.
Funding
Research Institute for Advanced Manufacturing (no. 1-CD9F and 1-CDK3); the Startup fund (no. 1-BE9L), The Hong Kong Polytechnic University; and the National Natural Science Foundation of China (no. 51475001 and 61170060).
Data Availability Statement
No new data were created or analyzed in this study.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| PdM | Predictive Maintenance |
| SVM | Support Vector Machine |
| CNN | Convolutional Neural Network |
| WT | Wavelet Transform |
| MFCC | Mel-Frequency Cepstral Coefficient |
| HMM | Hidden Markov Model |
| DT | Decision Tree |
| DCNN | Deep Convolutional Neural Network |
| KNN | K-Nearest Neighbor |
| DWT | Discrete Wavelet Transform |
| STFT | Short-Time Fourier Transform |
| VMD | Variational Mode Decomposition |
| EMD | Empirical Mode Decomposition |
| AE | AutoEncoder |
| RF | Random Forest |
| LDA | Linear Discriminant Analysis |
| WPT | Wavelet Packet Transform |
| BiLSTM | Bi-directional Long Short-Term |
| BiGRU | Bidirectional Gated Recurrent Unit |
| DGCN | Deep Graph Convolutional Network |
| LSTM | Long Short-Term Memory |
| ANN | Artificial Neural Network |
| MLP | Multilayer Perceptron |
| BiTCN | Bi-directional Temporal Convolutional Network |
| TDGCN | Unsuper-Transformer and Dynamic Graph Convolution |
| GMM | Gaussian Mixture Model |
| FFT | Fast Fourier Transform |
| STE | Short-Time Energy |
| ZCR | Zero-Crossing Rate |
| IMF | Intrinsic Mode Function |
| CEEMD | Complete Ensemble Empirical Mode Decomposition |
| COA | Coati Optimization Algorithm |
| SSA | Sparrow Search Algorithm |
| WPA | Wavelet Packet Analysis |
| TEO | Teager Energy Operator |
| SC | Spectral Centroid |
| TR | Tonnetz representation |
| PCA | Principal Component Analysis |
| TESK | Teager Energy Spectral Kurtosis |
| TSFDR-LDA | Time-spectral features extraction |
| and reduction with linear discriminant analysis | |
| YAMNet | Yet Another Audio Mobilenet Network |
| DSN | Domain Self-adaptive Network |
| GAN | Generative Adversarial Network |
| PINN | Physics-informed Neural Network |
References
- Mennilli, R.; Mazza, L.; Mura, A. Integrating Machine Learning for Predictive Maintenance on Resource-Constrained PLCs: A Feasibility Study. Sensors 2025, 25, 537. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Yang, D.; Wang, H. Data-Driven Methods for Predictive Maintenance of Industrial Equipment: A Survey. IEEE Syst. J. 2019, 13, 2213–2227. [Google Scholar] [CrossRef]
- Tiago, Z.; Cristiano, A.D.; Rodrigo, D.; Miromar, J.d.; Eduardo, S.D.; Guann Pyng, L. Predictive maintenance in the Industry 4.0: A systematic literature review. Comput. Ind. Eng. 2020, 150, 106889. [Google Scholar]
- Pech, M.; Vrchota, J.; Bednář, J. Predictive maintenance and intelligent sensors in smart factory. Sensors 2021, 21, 1470. [Google Scholar] [CrossRef]
- Chan, T.K.; Chin, C.S. A Comprehensive Review of Polyphonic Sound Event Detection. IEEE Access 2020, 8, 103339–103373. [Google Scholar] [CrossRef]
- Amrit, S.; Chiranjeev, K.; Preetam, S. Early detection of mechanical malfunctions in vehicles using sound signal processing. Appl. Acoust. 2022, 188, 108578. [Google Scholar]
- Rihi, A.; Baïna, S.; Mhada, F.Z.; El Bachari, E.; Tagemouati, H.; Guerboub, M.; Benzakour, I.; Baïna, K.; Abdelwahed, E.H. Innovative predictive maintenance for mining grinding mills: From LSTM-based vibration forecasting to pixel-based MFCC image and CNN. Int. J. Adv. Manuf. Technol. 2024, 135, 1271–1289. [Google Scholar] [CrossRef]
- Yousuf, M.; Alsuwian, T.; Amin, A.A.; Fareed, S.; Hamza, M. IoT-based health monitoring and fault detection of industrial AC induction motor for efficient predictive maintenance. Meas. Control 2024, 57, 1146–1160. [Google Scholar] [CrossRef]
- Yong-Cheol, L.; Moeid, S.; Abbas, R.; Hyun Woo, L. Evidence-driven sound detection for prenotification and identification of construction safety hazards and accidents. Autom. Constr. 2020, 113, 103127. [Google Scholar]
- An, Q.; Zang, J.; Zhang, Z.; Gao, L.; Wang, G.; Xue, C. Integrated Acoustic-Vibratory Sensor Inspired by the Ear Bones of Sea Turtles for Heart Sound Detection. IEEE Sens. J. 2024, 24, 15865–15874. [Google Scholar] [CrossRef]
- Xiong, W.; Xu, X.; Chen, L.; Yang, J. Sound-Based Construction Activity Monitoring with Deep Learning. Buildings 2022, 12, 1947. [Google Scholar] [CrossRef]
- Ye, T.; Peng, T.; Li, J. A sound frequency ridge positioning model oriented to mine equipment. J. Vib. Control 2024, 30, 3402–3413. [Google Scholar] [CrossRef]
- Saucedo-Espinosa, M.A.; Escalante, H.J.; Berrones, A. Detection of defective embedded bearings by sound analysis: A machine learning approach. J. Intell. Manuf. 2017, 28, 489–500. [Google Scholar] [CrossRef]
- Chen, Y.; Chang, R.; Guo, J. Emotion recognition of EEG signals based on the ensemble learning method: AdaBoost. Math. Probl. Eng. 2021, 2021, 8896062. [Google Scholar] [CrossRef]
- Srinivasan, R.; Tamzeed Islam, M.; Islam, B.; Wang, Z.; Sookoor, T.; Gnawali, O.; Nirjon, S. Preventive maintenance of centralized HVAC systems: Use of acoustic sensors, feature extraction, and unsupervised learning. In Proceedings of the Building Simulation 2017, San Francisco, CA, USA, 7–9 August 2017; Volume 15, pp. 2518–2524. [Google Scholar]
- Zhang, T.; Lee, Y.C.; Scarpiniti, M.; Uncini, A. A supervised machine learning-based sound identification for construction activity monitoring and performance evaluation. In Proceedings of the Construction Research Congress 2018, New Orleans, LA, USA, 2–4 April 2018; pp. 358–366. [Google Scholar]
- Lee, J.; Choi, H.; Park, D.; Chung, Y.; Kim, H.Y.; Yoon, S. Fault detection and diagnosis of railway point machines by sound analysis. Sensors 2016, 16, 549. [Google Scholar] [CrossRef] [PubMed]
- Jung, H.; Choi, S.; Lee, B. Rotor fault diagnosis method using CNN-Based transfer learning with 2D sound spectrogram analysis. Electronics 2023, 12, 480. [Google Scholar] [CrossRef]
- Bai, K.; Zhou, Y.; Cui, Z.; Bao, W.; Zhang, N.; Zhai, Y. HOG-SVM-Based Image Feature Classification Method for Sound Recognition of Power Equipments. Energies 2022, 15, 4449. [Google Scholar] [CrossRef]
- Yu, Z.; Wei, Y.; Niu, B.; Zhang, X. Automatic Condition Monitoring and Fault Diagnosis System for Power Transformers Based on Voiceprint Recognition. IEEE Trans. Instrum. Meas. 2024, 73, 1–11. [Google Scholar] [CrossRef]
- Ayhan, A.; Ferhat, Y.; Orhan, Y. A sound based method for fault detection with statistical feature extraction in UAV motors. Appl. Acoust. 2021, 183, 108325. [Google Scholar]
- Suawa, P.F.; Halbinger, A.; Jongmanns, M.; Reichenbach, M. Noise-Robust Machine Learning Models for Predictive Maintenance Applications. IEEE Sens. J. 2023, 23, 15081–15092. [Google Scholar] [CrossRef]
- Yaman, O. An automated faults classification method based on binary pattern and neighborhood component analysis using induction motor. Measurement 2021, 168, 108323. [Google Scholar] [CrossRef]
- Yun, H.; Kim, H.; Jeong, Y.H.; Jun, M.B. Autoencoder-based anomaly detection of industrial robot arm using stethoscope based internal sound sensor. J. Intell. Manuf. 2023, 34, 1427–1444. [Google Scholar] [CrossRef]
- Josué, P.C.; Jesús, A.F.D.; Froylán, C.S.; Luz, M.; David, I.I.Z. Bearing fault detection with vibration and acoustic signals: Comparison among different machine leaning classification methods. Eng. Fail. Anal. 2022, 139, 106515. [Google Scholar]
- Zhang, X.; Wan, S.; He, Y.; Wang, X.; Dou, L. Teager energy spectral kurtosis of wavelet packet transform and its application in locating the sound source of fault bearing of belt conveyor. Measurement 2021, 173, 108367. [Google Scholar] [CrossRef]
- Shi, H.; Li, Y.; Bai, X.; Zhang, K.; Sun, X. A two-stage sound-vibration signal fusion method for weak fault detection in rolling bearing systems. Mech. Syst. Signal Process. 2022, 172, 109012. [Google Scholar] [CrossRef]
- Alharbi, F.; Luo, S.; Zhao, S.; Yang, G.; Wheeler, C.; Chen, Z. Belt Conveyor Idlers Fault Detection Using Acoustic Analysis and Deep Learning Algorithm With the YAMNet Pretrained Network. IEEE Sens. J. 2024, 24, 31379–31394. [Google Scholar] [CrossRef]
- Zhang, D.; Stewart, E.; Entezami, M.; Roberts, C.; Yu, D. Intelligent acoustic-based fault diagnosis of roller bearings using a deep graph convolutional network. Measurement 2020, 156, 107585. [Google Scholar] [CrossRef]
- Yan, H.; Bai, H.; Zhan, X.; Wu, Z.; Wen, L.; Jia, X. Combination of VMD mapping MFCC and LSTM: A new acoustic fault diagnosis method of diesel engine. Sensors 2022, 22, 8325. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, N.; Guo, H.; Wang, X. An engine-fault-diagnosis system based on sound intensity analysis and wavelet packet pre-processing neural network. Eng. Appl. Artif. Intell. 2020, 94, 103765. [Google Scholar] [CrossRef]
- Espinosa, R.; Ponce, H.; Gutiérrez, S. Click-event sound detection in automotive industry using machine/deep learning. Appl. Soft Comput. 2021, 108, 107465. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, Y.; Li, X.; Zhou, X.; Wu, D. MPNet: A lightweight fault diagnosis network for rotating machinery. Measurement 2025, 239, 115498. [Google Scholar] [CrossRef]
- Luo, Y.; Wang, M.; Luo, L.; Liu, Z.; Zhao, J. Optimized LSTM-BiTCN parallel network model for anomalous sound detection in rotating machinery. Meas. Sci. Technol. 2025, 36, 046110. [Google Scholar] [CrossRef]
- Yin, X.; He, Q.; Zhang, H.; Qin, Z.; Zhang, B. Sound Based Fault Diagnosis Method Based on Variational Mode Decomposition and Support Vector Machine. Electronics 2022, 11, 2422. [Google Scholar] [CrossRef]
- Sherafat, B.; Rashidi, A.; Asgari, S. Sound-based multiple-equipment activity recognition using convolutional neural networks. Autom. Constr. 2022, 135, 104104. [Google Scholar] [CrossRef]
- Eleni, T.; Andreas, P.; Maria, S. Monitoring, profiling and classification of urban environmental noise using sound characteristics and the KNN algorithm. Energy Rep. 2020, 6, 223–230. [Google Scholar]
- Cao, Y.; Sun, Y.; Xie, G.; Li, P. A Sound-Based Fault Diagnosis Method for Railway Point Machines Based on Two-Stage Feature Selection Strategy and Ensemble Classifier. IEEE Trans. Intell. Transp. Syst. 2022, 23, 12074–12083. [Google Scholar] [CrossRef]
- Yan, J.; Cheng, Y.; Wang, Q.; Liu, L.; Zhang, W.; Jin, B. Transformer and Graph Convolution-Based Unsupervised Detection of Machine Anomalous Sound Under Domain Shifts. IEEE Trans. Emerg. Top. Comput. Intell. 2024, 8, 2827–2842. [Google Scholar] [CrossRef]
- Notani, K.; Hayashi, T.; Mori, N. Abnormal Sound Detection in Pipes Using a Wireless Microphone and Machine Learning. Mater. Trans. 2022, 63, 1622–1630. [Google Scholar] [CrossRef]
- Liu, Z.; Li, S. A sound monitoring system for prevention of underground pipeline damage caused by construction. Autom. Constr. 2020, 113, 103125. [Google Scholar] [CrossRef]
- Li, S.; Zhao, Q.; Liu, J.; Zhang, X.; Hou, J. Noise Reduction of Steam Trap Based on SSA-VMD Improved Wavelet Threshold Function. Sensors 2025, 25, 1573. [Google Scholar] [CrossRef]
- Kong, D.; Yu, H.; Yuan, G. Multi-Spectral and Multi-Temporal Features Fusion with SE Network for Anomalous Sound Detection. IEEE Access 2024, 12, 167262–167277. [Google Scholar] [CrossRef]
- Wu, J.; Yang, F.; Hu, W. Unsupervised anomalous sound detection for industrial monitoring based on ArcFace classifier and gaussian mixture model. Appl. Acoust. 2023, 203, 109188. [Google Scholar] [CrossRef]
- Liu, Y.; Guan, J.; Zhu, Q.; Wang, W. Anomalous Sound Detection Using Spectral-Temporal Information Fusion. In Proceedings of the ICASSP 2022—2022 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Singapore, 22–27 May 2022; pp. 816–820. [Google Scholar]
- Kim, S.M.; Soo Kim, Y. Enhancing Sound-Based Anomaly Detection Using Deep Denoising Autoencoder. IEEE Access 2024, 12, 84323–84332. [Google Scholar] [CrossRef]
- Ota, Y.; Unoki, M. Anomalous Sound Detection for Industrial Machines Using Acoustical Features Related to Timbral Metrics. IEEE Access 2023, 11, 70884–70897. [Google Scholar] [CrossRef]
- Emanuele, D.; Antonino, F.; Antonio, G.; Vincenzo, M.; Giancarlo, S. An anomalous sound detection methodology for predictive maintenance. Expert Syst. Appl. 2022, 209, 118324. [Google Scholar]
- Ren, J.; Hu, C.; Shang, Z.; Li, Y.; Zhao, Z.; Yan, R. Learning Interpretable and Transferable Representations via Wavelet-constrained Transformer for Industrial Acoustic Diagnosis. IEEE Trans. Instrum. Meas. 2025, 74, 3512312. [Google Scholar] [CrossRef]
- Majasan, J.O.; Robinson, J.B.; Owen, R.E.; Maier, M.; Radhakrishnan, A.N.; Pham, M.; Tranter, T.G.; Zhang, Y.; Shearing, P.R.; Brett, D.J. Recent advances in acoustic diagnostics for electrochemical power systems. J. Phys. Energy 2021, 3, 032011. [Google Scholar] [CrossRef]
- Fang, H.; An, J.; Liu, H.; Xiang, J.; Zhao, B.; Dunkin, F. A lightweight transformer with strong robustness application in portable bearing fault diagnosis. IEEE Sens. J. 2023, 23, 9649–9657. [Google Scholar] [CrossRef]
- Suraj, G.; Akhilesh, K.; Jhareswar, M. A critical review on system architecture, techniques, trends and challenges in intelligent predictive maintenance. Saf. Sci. 2024, 177, 106590. [Google Scholar]
- Wang, X.; Mao, D.; Li, X. Bearing fault diagnosis based on vibro-acoustic data fusion and 1D-CNN network. Measurement 2021, 173, 108518. [Google Scholar] [CrossRef]
- Mian, T.; Choudhary, A.; Fatima, S. An efficient diagnosis approach for bearing faults using sound quality metrics. Appl. Acoust. 2022, 195, 108839. [Google Scholar] [CrossRef]
- Ono, Y.; Onishi, Y.; Koshinaka, T.; Takata, S.; Hoshuyama, O. Anomaly detection of motors with feature emphasis using only normal sounds. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013; pp. 2800–2804. [Google Scholar]
- Peng, Y.; Li, Z.; He, K.; Liu, Y.; Li, Q.; Liu, L. Broadband mode decomposition and its application to the quality evaluation of welding inverter power source signals. IEEE Trans. Ind. Electron. 2019, 67, 9734–9746. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Li, R.; He, D. Rotational machine health monitoring and fault detection using EMD-based acoustic emission feature quantification. IEEE Trans. Instrum. Meas. 2012, 61, 990–1001. [Google Scholar] [CrossRef]
- Amarnath, M. andPraveen Krishna, I. Local fault detection in helical gears via vibration and acoustic signals using EMD based statistical parameter analysis. Measurement 2014, 58, 154–164. [Google Scholar] [CrossRef]
- Delgado-Arredondo, P.A.; Morinigo-Sotelo, D.; Osornio-Rios, R.A.; Avina-Cervantes, J.G.; Rostro-Gonzalez, H.; de Jesus Romero-Troncoso, R. Methodology for fault detection in induction motors via sound and vibration signals. Mech. Syst. Signal Process. 2017, 83, 568–589. [Google Scholar] [CrossRef]
- Torres, M.E.; Colominas, M.A.; Schlotthauer, G.; Flandrin, P. A complete ensemble empirical mode decomposition with adaptive noise. In Proceedings of the 2011 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Prague, Czech Republic, 22–27 May 2011; pp. 4144–4147. [Google Scholar]
- Gai, J.; Shen, J.; Hu, Y.; Wang, H. An integrated method based on hybrid grey wolf optimizer improved variational mode decomposition and deep neural network for fault diagnosis of rolling bearing. Measurement 2020, 162, 107901. [Google Scholar] [CrossRef]
- Chen, B.; Zhang, W.; James, X.; Song, D.; Cheng, Y.; Zhou, Z.; Gu, F.; Andrew, D.B. Product envelope spectrum optimization-gram: An enhanced envelope analysis for rolling bearing fault diagnosis. Mech. Syst. Signal Process. 2023, 193, 110270. [Google Scholar] [CrossRef]
- Xu, B.; Zhou, F.; Li, H.; Yan, B.; Liu, Y. Early fault feature extraction of bearings based on Teager energy operator and optimal VMD. ISA Trans. 2019, 86, 249–265. [Google Scholar] [CrossRef]
- Xiao, Y.; Feng, X.; Lv, J.; Shen, Y.; Zhou, S.; Zhou, N.; Du, Z. Sealing strip acoustic performance evaluation using WF-VMD based signal enhancement method. Appl. Acoust. 2024, 217, 109860. [Google Scholar] [CrossRef]
- Lei, W.; Guo, W.; Wan, B.; Min, Y.; Wu, J.; Li, B. High voltage shunt reactor acoustic signal denoising based on the combination of VMD parameters optimized by coati optimization algorithm and wavelet threshold. Measurement 2024, 224, 113854. [Google Scholar] [CrossRef]
- Gharehchopogh, F.S.; Namazi, M.; Ebrahimi, L.; Abdollahzadeh, B. Advances in sparrow search algorithm: A comprehensive survey. Arch. Comput. Methods Eng. 2023, 30, 427–455. [Google Scholar] [CrossRef]
- Chen, L.J.; Lin, W.M.; Tsao, T.P.; Lin, Y.H. Study of Partial Discharge Measurement in Power Equipment Using Acoustic Technique and Wavelet Transform. IEEE Trans. Power Deliv. 2007, 22, 1575–1580. [Google Scholar] [CrossRef]
- Lou, X.; Loparo, A.K. Bearing fault diagnosis based on wavelet transform and fuzzy inference. Mech. Syst. Signal Process. 2004, 18, 1077–1095. [Google Scholar] [CrossRef]
- Wang, Y. Sound quality estimation for nonstationary vehicle noises based on discrete wavelet transform. J. Sound Vib. 2009, 324, 1124–1140. [Google Scholar] [CrossRef]
- Vonesch, C.; Blu, T.; Unser, M. Generalized Daubechies wavelet families. IEEE Trans. Signal Process. 2007, 55, 4415–4429. [Google Scholar] [CrossRef]
- Bozchalooi, I.S.; Liang, M. Teager energy operator for multi-modulation extraction and its application for gearbox fault detection. Smart Mater. Struct. 2010, 19, 075008. [Google Scholar] [CrossRef]
- Yang, Z.X.; Zhong, J.H. A hybrid EEMD-based SampEn and SVD for acoustic signal processing and fault diagnosis. Entropy 2016, 18, 112. [Google Scholar] [CrossRef]
- Jung, S.Y.; Liao, C.H.; Wu, Y.S.; Yuan, S.M.; Sun, C.T. Efficiently classifying lung sounds through depthwise separable CNN models with fused STFT and MFCC features. Diagnostics 2021, 11, 732. [Google Scholar] [CrossRef]
- Ramalingam, A.; Krishnan, S. Gaussian mixture modeling of short-time Fourier transform features for audio fingerprinting. IEEE Trans. Inf. Forensics Secur. 2006, 1, 457–463. [Google Scholar] [CrossRef]
- He, M.; He, D. Deep Learning Based Approach for Bearing Fault Diagnosis. IEEE Trans. Ind. Appl. 2017, 53, 3057–3065. [Google Scholar] [CrossRef]
- Singh, M.K.; Kumar, S.; Nandan, D. Faulty voice diagnosis of automotive gearbox based on acoustic feature extraction and classification technique. J. Eng. Res. 2023, 11, 100051. [Google Scholar] [CrossRef]
- Liu, X.; Pei, D.; Lodewijks, G.; Zhao, Z.; Mei, J. Acoustic signal based fault detection on belt conveyor idlers using machine learning. Adv. Powder Technol. 2020, 31, 2689–2698. [Google Scholar] [CrossRef]
- Le, P.N.; Ambikairajah, E.; Epps, J.; Sethu, V.; Choi, E.H. Investigation of spectral centroid features for cognitive load classification. Speech Commun. 2011, 53, 540–551. [Google Scholar] [CrossRef]
- Harte, C.; Sandler, M.; Gasser, M. Detecting harmonic change in musical audio. In Proceedings of the 1st ACM Workshop on Audio and Music Computing Multimedia, Santa Barbara, CA, USA, 23–27 October 2006; pp. 21–26. [Google Scholar]
- Cao, J.; Huang, W.; Zhao, T.; Wang, J.; Wang, R. An enhance excavation equipments classification algorithm based on acoustic spectrum dynamic feature. Multidimens. Syst. Signal Process. 2017, 28, 921–943. [Google Scholar] [CrossRef]
- Yadav, S.K.; Tyagi, K.; Shah, B.; Kalra, P.K. Audio Signature-Based Condition Monitoring of Internal Combustion Engine Using FFT and Correlation Approach. IEEE Trans. Instrum. Meas. 2011, 60, 1217–1226. [Google Scholar] [CrossRef]
- Sarradj, E. A fast signal subspace approach for the determination of absolute levels from phased microphone array measurements. J. Sound Vib. 2010, 329, 1553–1569. [Google Scholar] [CrossRef]
- Mahyub, M.; Souza, L.S.; Batalo, B.; Fukui, K. Signal latent subspace: A new representation for environmental sound classification. Appl. Acoust. 2024, 225, 110181. [Google Scholar] [CrossRef]
- Lawal, A.; Iqbal, N.; Zerguine, A.; Noui-Mehidi, M.N.; Zeghlache, M.L.; Al-Shaikhi, A.A. A Novel PCA-Based Slug Flow Characterization Using Acoustic Sensing. IEEE Access 2024, 12, 42849–42859. [Google Scholar] [CrossRef]
- Rabiner, L.R. A tutorial on hidden Markov models and selected applications in speech recognition. Proc. IEEE 1989, 77, 257–286. [Google Scholar] [CrossRef]
- Lang, R.; Lu, R.; Zhao, C.; Qin, H.; Liu, G. Graph-based semi-supervised one class support vector machine for detecting abnormal lung sounds. Appl. Math. Comput. 2020, 364, 124487. [Google Scholar] [CrossRef]
- Sack, S.; Åbom, M. Acoustic plane-wave decomposition by means of multilayer perceptron neural networks. J. Sound Vib. 2020, 486, 115518. [Google Scholar] [CrossRef]
- Sabillon, C.A.; Rashidi, A.; Samanta, B.; Cheng, C.F.; Davenport, M.A.; Anderson, D.V. A productivity forecasting system for construction cyclic operations using audio signals and a Bayesian approach. In Proceedings of the Construction Research Congress 2018, New Orleans, LA, USA, 2–4 April 2018; pp. 295–304. [Google Scholar]
- Sun, Z.; Tao, W.; Gao, M.; Zhang, M.; Song, S.; Wang, G. Broiler health monitoring technology based on sound features and random forest. Eng. Appl. Artif. Intell. 2024, 135, 108849. [Google Scholar] [CrossRef]
- Yin, X.; He, Q.; Peng, S.; Zhang, Y.; Zhang, B. A Fault Diagnosis Method Based on EMD-SVM with Multi-Feature Fusion via Sound Signals. In Proceedings of the 2022 IEEE International Conference on Real-time Computing and Robotics (RCAR), Guiyang, China, 17–22 July 2022; pp. 540–544. [Google Scholar]
- Grossberg, S. Nonlinear neural networks: Principles, mechanisms, and architectures. Neural Netw. 1988, 1, 17–61. [Google Scholar] [CrossRef]
- Koizumi, Y.; Saito, S.; Uematsu, H.; Kawachi, Y.; Harada, N. Unsupervised Detection of Anomalous Sound Based on Deep Learning and the Neyman–Pearson Lemma. IEEE/ACM Trans. Audio Speech Lang. Process. 2019, 27, 212–224. [Google Scholar] [CrossRef]
- Koizumi, Y.; Saito, S.; Uematsu, H.; Harada, N. Optimizing acoustic feature extractor for anomalous sound detection based on Neyman-Pearson lemma. In Proceedings of the 2017 25th European Signal Processing Conference (EUSIPCO), Kos Island, Greece, 28 August–2 September 2017; pp. 698–702. [Google Scholar]
- Yun, E.; Jeong, M. Acoustic Feature Extraction and Classification Techniques for Anomaly Sound Detection in the Electronic Motor of Automotive EPS. IEEE Access 2024, 12, 149288–149307. [Google Scholar] [CrossRef]
- Ruff, L.; Kauffmann, J.R.; Vandermeulen, R.A.; Montavon, G.; Samek, W.; Kloft, M.; Dietterich, T.G.; Müller, K.R. A Unifying Review of Deep and Shallow Anomaly Detection. Proc. IEEE 2021, 109, 756–795. [Google Scholar] [CrossRef]
- Park, Y.; Yun, I.D. Fast Adaptive RNN Encoder–Decoder for Anomaly Detection in SMD Assembly Machine. Sensors 2018, 18, 3573. [Google Scholar] [CrossRef]
- Deng, J.; Guo, J.; Xue, N.; Zafeiriou, S. ArcFace: Additive Angular Margin Loss for Deep Face Recognition. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 4685–4694. [Google Scholar]
- Chen, S.; Liu, Y.; Gao, X.; Han, Z. Mobilefacenets: Efficient cnns for accurate real-time face verification on mobile devices. In Proceedings of the Chinese Conference on Biometric Recognition, Urumqi, China, 11–12 August 2018; pp. 428–438. [Google Scholar]
- Van Den Oord, A.; Dieleman, S.; Zen, H.; Simonyan, K.; Vinyals, O.; Graves, A.; Kalchbrenner, N.; Senior, A.; Kavukcuoglu, K. Wavenet: A generative model for raw audio. arXiv 2016, arXiv:1609.03499. [Google Scholar]
- Cheng, T.; Guo, F. Machine anomalous sound detection based on audio synthesis generative adversarial network. J. Phys. Conf. Ser. 2024, 2816, 012041. [Google Scholar] [CrossRef]
- Purohit, H.; Tanabe, R.; Ichige, K.; Endo, T.; Nikaido, Y.; Suefusa, K.; Kawaguchi, Y. MIMII Dataset: Sound dataset for malfunctioning industrial machine investigation and inspection. arXiv 2019, arXiv:1909.09347. [Google Scholar]
- Jiang, Y.; Dai, P.; Fang, P.; Zhong, R.Y.; Cao, X. Electrical-STGCN: An electrical spatio-temporal graph convolutional network for intelligent predictive maintenance. IEEE Trans. Ind. Inform. 2022, 18, 8509–8518. [Google Scholar] [CrossRef]
- Madhu, A.; K, S. EnvGAN: A GAN-based augmentation to improve environmental sound classification. Artif. Intell. Rev. 2022, 55, 6301–6320. [Google Scholar] [CrossRef]
- Premachandra, C.; Kunisada, Y. GAN Based Audio Noise Suppression for Victim Detection at Disaster Sites with UAV. IEEE Trans. Serv. Comput. 2024, 17, 183–193. [Google Scholar] [CrossRef]
- Olivieri, M.; Karakonstantis, X.; Pezzoli, M.; Antonacci, F.; Sarti, A.; Fernandez-Grande, E. Physics-informed neural network for volumetric sound field reconstruction of speech signals. EURASIP J. Audio Speech Music Process. 2024, 2024, 42. [Google Scholar] [CrossRef]
- Koyama, S.; Ribeiro, J.G.; Nakamura, T.; Ueno, N.; Pezzoli, M. Physics-Informed Machine Learning for Sound Field Estimation: Fundamentals, state of the art, and challenges [Special Issue on Model-Based and Data-Driven Audio Signal Processing]. IEEE Signal Process. Mag. 2025, 41, 60–71. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).