The Development of Fractional Black–Scholes Model Solution Using the Daftardar-Gejji Laplace Method for Determining Rainfall Index-Based Agricultural Insurance Premiums
Abstract
1. Introduction
2. The Standard and Fractional Black–Scholes Models
- (1)
- The option under consideration is a European option, which can only be exercised at maturity.
- (2)
- Stock prices follow a stochastic process with a lognormal distribution, assuming a constant variance in stock returns.
- (3)
- The risk-free interest rate is constant.
- (4)
- There is no dividend payment on the stock during the option term.
- (5)
- There are no taxes or transaction costs in the process of buying or selling options.
3. Lie Symmetry Analysis of the Fractional Black–Scholes Partial Differential Equation
4. Solution of the Fractional Black–Scholes Model Using the Daftardar-Gejji Laplace Method
5. Identification of Long-Term Effects and Estimation of Fractional Order Parameter
5.1. Rescaled Range Statistics Method
5.2. Geweke and Porter-Hudak Method
- (1)
- Determine the harmonic frequency for each observation and the optimal bandwidth
- (2)
- Determine the periodogram valuewhere represents the autocovariance value at lag .
- (3)
- Determine the response variable using Equation (56) and the predictor variable
- (4)
- Determine the fractional order parameter using the Ordinary Least Squares (OLS) method.
5.3. Significance Test for the Fractional Order Estimator
- (the fractional order parameter is not significant for the model).
- (the fractional order parameter is significant for the model).
6. Materials and Methods
6.1. Materials
6.2. Methods
6.2.1. Historical Burn Analysis Method
- (1)
- Determine the insured period or index windowThe selection of the index window period was based on the strongest correlation coefficient between the variables. The focus of this study was on seasonal rainfall and corn production data. Therefore, the index window period was determined through direct discussions with farmers to identify the periods required to be covered by insurance. The Pearson product–moment correlation coefficient was subsequently calculated using the following formula:where is the correlation coefficient between variables and , is the -th independent variable (rainfall), is the -th dependent variable (corn production), and is the number of data points. The movement of the correlation coefficient towards +1 or −1 shows a strong relationship but the movement toward 0 is a representation of a weak relationship.
- (2)
- Determine the Cap threshold value for ten days (dasarian) periods.The Cap threshold represents the maximum amount of rainfall calculated for every dasarian. The Cap value was determined based on the daily potential evapotranspiration value. This is in line with the submission of Allen et al. [58], according to which potential evapotranspiration represents the energy required by an environment or agricultural area from solar radiation, with due consideration for other factors such as temperature and air humidity. The average potential evapotranspiration values are presented in Table 1.
- (3)
- Calculate the dasarian rainfall based on the index windowThe dasarian rainfall in the index window period was calculated monthly as follows:where is the rainfall data for the -th day,. For months with 28, 29, or 31 days, the calculation was conducted starting from the 21st day until the last day of the month. The index window period that spans more than one month requires the index to be continued as . In a situation where is a multiple of 3, was calculated up to the last day of the month.
- (4)
- Determine the dasarian adjusted rainfallThe dasarian adjusted rainfall was calculated based on the following assumptions:
- The adjusted rainfall is set as equal to the Cap value when the dasarian rainfall exceeds the Cap value.
- The adjusted rainfall value equals the actual dasarian rainfall when the dasarian rainfall is less than or equal to the Cap value.
- (5)
- Calculate the average total dasarian adjusted rainfallThe average total dasarian adjusted rainfall was computed as follows:where is the number of dasarian periods.
- (6)
- Arrange the average total dasarian adjusted rainfall in increasing order
- (7)
- Determine the exit and trigger rainfall indices.The exit rainfall index was obtained from the lowest value of the sorted average total adjusted rainfall data as follows:The trigger rainfall index was derived from the percentile value of the average total adjusted rainfall data as follows:where is an integer which is less than 100.
6.2.2. The Standard and Fractional Black–Scholes Models for Agricultural Insurance
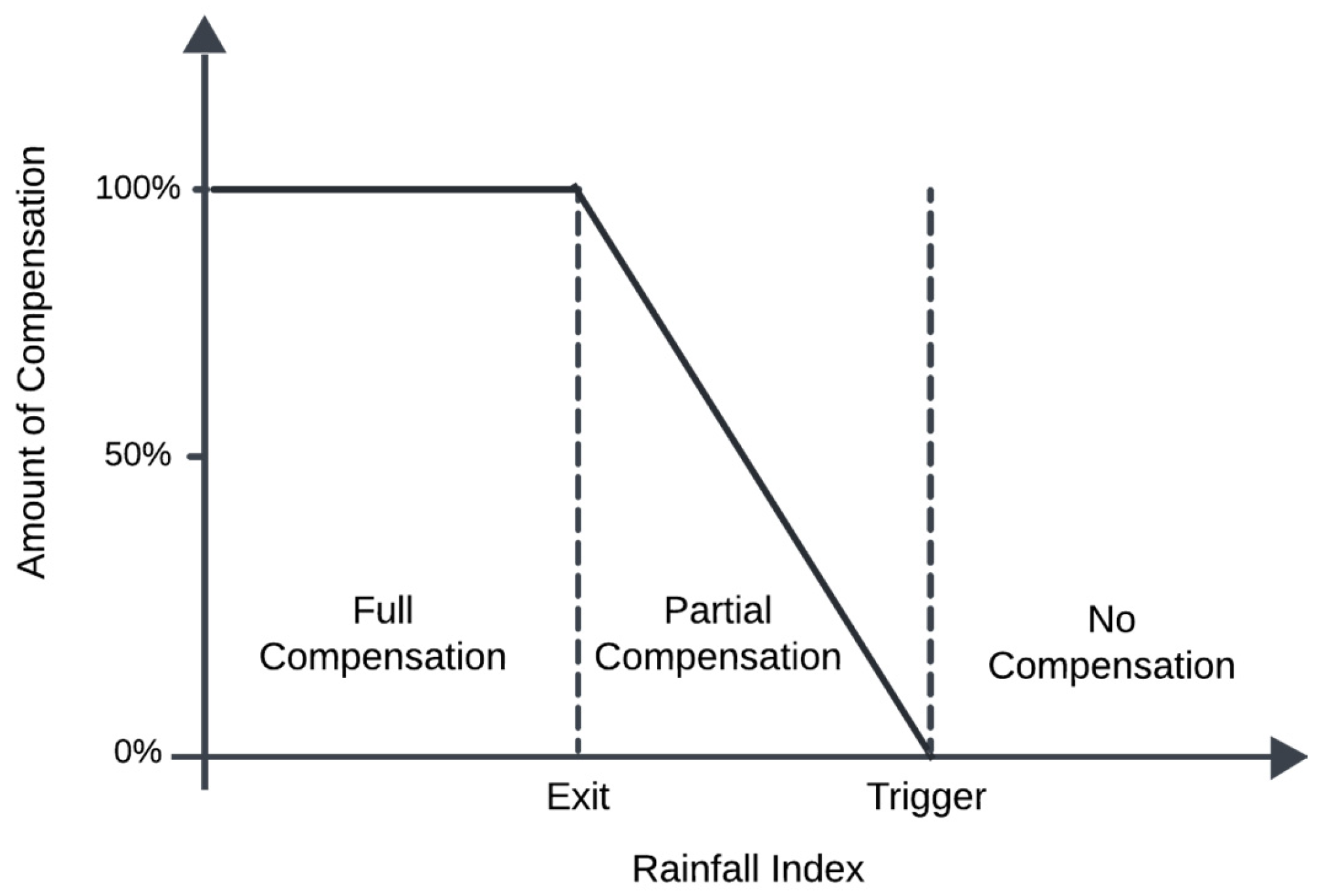
6.2.3. Agricultural Insurance Compensation Amount
7. Results
7.1. Corn Production and Rainfall Data
7.2. Determination of Exit and Trigger Rainfall Indices Using Historical Burn Analysis
7.2.1. Determination of the Index Window
7.2.2. Determination of Cap Threshold Value
7.2.3. Calculation of Dasarian Rainfall
7.2.4. Determination of Dasarian Adjusted Rainfall
- = 99 mm was greater than the Cap value of 50 mm and the adjusted rainfall value was set to 50 mm.
- = 150 mm was greater than the Cap value of 50 mm and the adjusted rainfall value was set to 50 mm.
- = 120 mm was greater than the Cap value of 50 mm and the adjusted rainfall value was set to 50 mm.
| Month | j | (mm) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 2016 | 2017 | 2018 | 2019 | 2020 | 2021 | 2022 | 2023 | ||
| September | 1 | 50 | 1 | 50 | 1.8 | 37.7 | 8 | 49 | 0 |
| 2 | 50 | 1 | 11 | 2.2 | 1 | 50 | 50 | 0.3 | |
| 3 | 50 | 50 | 50 | 2.4 | 50 | 50 | 50 | 0 | |
| October | 1 | 50 | 50 | 5 | 2.8 | 50 | 13 | 50 | 1.5 |
| 2 | 50 | 50 | 13 | 3.2 | 50 | 48.7 | 50 | 0 | |
| 3 | 50 | 28 | 50 | 0 | 50 | 50 | 50 | 22 | |
| November | 1 | 50 | 50 | 50 | 50 | 50 | 50 | 50 | 33.7 |
| 2 | 50 | 50 | 50 | 50 | 50 | 50 | 50 | 7.2 | |
| 3 | 50 | 42.4 | 50 | 26.8 | 50 | 50 | 50 | 50 | |
| December | 1 | 50 | 39 | 50 | 50 | 50 | 46.1 | 22.4 | 50 |
| 2 | 50 | 50 | 59 | 50 | 50 | 23.4 | 36 | 0 | |
| 3 | 0 | 15 | 46 | 50 | 0 | 50 | 35.8 | 28.2 | |
7.2.5. Calculation of Average Total Dasarian Adjusted Rainfall
7.2.6. Arrangement of Average Total Dasarian Adjusted Rainfall
7.2.7. Determination of the Exit and Trigger Rainfall Indices
7.3. Calculation of Premiums Using the Standard and Fractional Black–Scholes Models
7.3.1. Calculation of Premiums Using the Standard Black–Scholes Model
7.3.2. Calculation of Premiums Using the Fractional Black–Scholes Model
7.4. Determination of Agricultural Insurance Compensation Using Historical Burn Analysis
8. Discussion
9. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kraus, K.; Kraus, N.; Pochenchuk, G. Principles, Assessment and Methods of Risk Management of Investment Activities of the Enterprise. VUZF Rev. 2021, 6, 45–58. [Google Scholar] [CrossRef]
- Giudice, M.D.; Evangelista, F.; Palmaccio, M. Defining the Black and Scholes Approach: A First Systematic Literature Review. J. Innov. Entrep. 2015, 5, 5. [Google Scholar] [CrossRef]
- Gupta, S.L. Financial Derivatives: Theory, Concepts and Problems; PHI Learning Private Limited: Delhi, India, 2017. [Google Scholar]
- Higham, D.J. An Introduction to Financial Option Valuation; Cambridge University Press: New York, NY, USA, 2004. [Google Scholar]
- Guo, C.; Fang, S.; He, Y. Derivation of Fractional Black-Scholes Equations Driven by Fractional G-Brownian Motion and Their Application in European Option Pricing. Int. J. Math. Comput. Sci. 2021, 15, 24–30. [Google Scholar]
- Meng, L.; Wang, M. Comparison of Black-Scholes Formula with Fractional Black-Scholes Formula in the Foreign Exchange Option Market with Changing Volatility. Asia-Pac. Financ. Mark. 2010, 17, 99–111. [Google Scholar] [CrossRef]
- He, X.J.; Lin, S. A Fractional Black-Scholes Model with Stochastic Volatility and European Option Pricing. Expert Syst. Appl. 2021, 178, 114983. [Google Scholar] [CrossRef]
- Sun, Y.; Gong, W.; Dai, H.; Yuan, L. Numerical Method for American Option Pricing under the Time-Fractional Black–Scholes Model. Math. Probl. Eng. 2023, 74, 55–72. [Google Scholar] [CrossRef]
- Flint, E.; Maré, E. Fractional Black–Scholes Option Pricing, Volatility Calibration and Implied Hurst Exponents in South African Context. S. Afr. J. Econ. Manag. Sci. 2017, 20, a1532. [Google Scholar] [CrossRef]
- Muhammad, A.; Aliu, J.N.; Micah, E.E.M.; Taiwo, I.; Abasido, A.U.; Adesugba, A.K. Fractional Stochastic Calculus and Multifractional Processes: Applications in Financial Modeling. Polac. Int. J. Econs MGT Sci. 2024, 10, 79–86. [Google Scholar]
- Khan, W.; Ansari, F. European Option Pricing of Fractional Black-Scholes Model Using Sumudu Transform and its Derivatives. Gen. Lett. Math. 2016, 1, 74–80. [Google Scholar] [CrossRef]
- Ahmad, M.; Mishra, R.; Jain, R. Time Fractional Black–Scholes Model and Its Solution Through Sumudu Transform Iterative Method. Comput. Econ. 2025, 1–20. [Google Scholar] [CrossRef]
- Kumar, S.; Yildirim, A.; Khan, Y.; Jafari, H.; Sayevand, K.; Wei, L. Analytical solution of fractional Black-Scholes european option pricing equation by using Laplace transform. J. Fract. Calc. Appl. 2012, 2, 1–9. [Google Scholar]
- Owoyemi, A.E.; Sumiati, I.; Rusyaman, E.; Sukono, S. Laplace Decomposition Method for Solving Fractional Black-Scholes European Option Pricing Equation. Int. J. Quant. Res. Model. 2020, 1, 194–207. [Google Scholar] [CrossRef]
- Johansyah, M.D.; Sumiati, I.; Rusyaman, E.; Sukono; Muslikh, M.; Mohamed, M.A.; Sambas, A. Numerical Solution of the Black-Scholes Partial Differential Equation for the Option Pricing Model Using the ADM-Kamal Method. Nonlinear Dyn. Syst. Theory 2023, 23, 295–309. [Google Scholar]
- Yavuz, M.; Ozdemir, N. A Quantitative Approach to Fractional Option Pricing Problems with Decomposition Series. Konuralp J. Math. 2018, 6, 102–109. [Google Scholar]
- Kanth, A.S.V.R.; Aruna, K. Solution of time fractional Black-Scholes European option pricing equation arising in financial market. Nonlinear Eng. 2016, 5, 269–276. [Google Scholar] [CrossRef]
- Batiha, B.; Ghanim, F.; Alayed, O.; Hatamleh, R.; Heilat, A.S.; Zureigat, H.; Bazighifan, O. Solving Multispecies Lotka-Volterra Equations by the Daftardar-Gejji and Jafari Method. Int. J. Math. Math. Sci. 2022, 2022, 1839796. [Google Scholar] [CrossRef]
- Sugandha, A.; Rusyaman, E.; Sukono; Carnia, E. A New Solution to the Fractional Black–Scholes Equation Using the Daftardar-Gejji Method. Mathematics 2023, 11, 4887. [Google Scholar] [CrossRef]
- Khuri, S.A. A Laplace Decomposition Algorithm Applied to a Class of Nonlinear Differential Equations. J. Appl. Math. 2001, 1, 141–155. [Google Scholar] [CrossRef]
- Prabowo, A.; Zakaria, Z.A.; Mamat, M.; Riyadi, S.; Bon, A.T. Determination of Agricultural Insurance Premium Prices Based on Rainfall Index with Formula Cash-or-Nothing Put Option. In Proceedings of the 2nd African International Conference on Industrial Engineering and Operations Management Harare, Harare, Zimbabwe, 7–10 December 2020. [Google Scholar]
- Nnadi, F.N.; Chikaire, J.; Echetama, J.A.; Ihenacho, R.A.; Umunnakwe, P.C.; Utazi, C.O. Agricultural Insurance: A Strategic Tool for Climate Change Adaptation in the Agricultural Sector. Net J. Agric. Sci. 2013, 1, 1–9. [Google Scholar]
- Dick, W.J.A.; Wang, W. Government Interventions in Agricultural Insurance. Agric. Agric. Sci. Procedia 2010, 1, 4–12. [Google Scholar] [CrossRef]
- Adeyinka, A.A.; Kath, J.; Nguyen-Huy, T.; Mushtaq, S.; Souvignet, M.; Range, M.; Barratt, J. Global Disparities in Agricultural Climate Index-based Insurance Research. Clim. Risk Manag. 2022, 35, 100394. [Google Scholar] [CrossRef]
- Nagaraju, D.; Venkatareddy, B.; Kotreshwar, G. Innovative Alternatives for Crop Insurance: Rainfall-Index-Based Insurance and Futures. Int. J. Banking Risk Insur. 2021, 9, 12–19. [Google Scholar]
- Coble, K.H.; Hanson, T.; Miller, J.C.; Shaik, S. Agricultural Insurance as an Environmental Policy Tool. J. Agric. Appl. Econ. 2003, 35, 391–405. [Google Scholar] [CrossRef]
- Chicaíza, L.; Cabedo, D. Using the Black-Scholes Method for Estimating High-cost Illness Insurance Premiums in Colombia. Innovar Rev. Ciencias Adm. Soc. 2009, 19, 119–130. [Google Scholar]
- Weber, R.; Fecke, W.; Moeller, I.; Musshoff, O. Meso-level Weather Index Insurance: Overcoming Low Risk Reduction Potential of Micro-level Approaches. Agric. Financ. Rev. 2015, 75, 31–46. [Google Scholar] [CrossRef]
- Filiapuspa, M.H.; Sari, S.F.; Mardiyati, S. Applying Black Scholes Method for Crop Insurance Pricing. In AIP Conference Proceedings, Depok, Indonesia, 30–31 October 2018; AIP Publishing: Melville, NY, USA, 2019; p. 020042. [Google Scholar] [CrossRef]
- Paramita, A.; Sari, F.; Kusumaningrum, D.; Sutomo, V.A. Pure Premium Calculation of Dry Weather-Based Insurance for Wonogiri Farmers. In AIP Conference Proceedings, Tangerang, Indonesia, 2–3 November 2021; AIP Publishing: Melville, NY, USA, 2023; p. 030005. [Google Scholar] [CrossRef]
- Luenberger, D.G. Investment Science; Oxford University Press: New York, NY, USA, 1998. [Google Scholar]
- Janková, Z. Drawbacks and Limitations of Black-Scholes Model for Options Pricing. J. Financ. Stud. Res. 2018, 1–7. [Google Scholar] [CrossRef]
- Zhu, M.; Wang, M.; Wu, J. An Option Pricing Formula for Active Hedging Under Logarithmic Investment Strategy. Mathematics 2024, 12, 3784. [Google Scholar] [CrossRef]
- Hull, J.C. Options, Futures, and Other Derivatives; Prentice Hall: Upper Saddle River, NJ, USA, 2002. [Google Scholar]
- Schoenmakers, J.G.M.; Kloeden, P.E. Robust Option Replication for a Black-Scholes Model Extended with Nondeterministic Trends. J. Appl. Math. Stoch. Anal. 1999, 12, 113–120. [Google Scholar] [CrossRef]
- Önalan, Ö. Time-changed generalized mixed fractional Brownian motion and application to arithmetic average Asian option pricing. Int. J. Appl. Math. Res. 2017, 6, 85–92. [Google Scholar] [CrossRef]
- Björk, T.; Hult, H. A note on Wick products and the fractional Black-Scholes model. Financ. Stoch. 2005, 9, 197–209. [Google Scholar] [CrossRef]
- Duncan, T.E.; Hu, Y.Z.; Pasik-Duncan, B. Stochastic calculus for fractional Brownian motion. I Theory SIAM J. Control Optim. 2000, 38, 582–612. [Google Scholar] [CrossRef]
- Yaozhong, H.; Oksendal, B. Fractional white noise calculus and application to finance. Infin. Dimens. Anal. 2000, 6, 1–32. [Google Scholar]
- Necula, C. Option Pricing in a Fractional Brownian Motion Environment. DOFIN Acad. Econ. Stud. Buchar. Rom. 2002, 1–19. [Google Scholar] [CrossRef]
- Kinani, E.H.E.; Ouhadan, A. Lie symmetry analysis of some time fractional partial differential equations. Int. J. Mod. Phys. Conf. Ser. 2015, 38, 1560075. [Google Scholar] [CrossRef]
- Yourdkhany, M.; Nadjafikhah, M. Symmetries, similarity invariant solution, conservation laws and exact solutions of the time-fractional Harmonic Oscillator equation. J. Geom. Phys. 2020, 153, 103661. [Google Scholar] [CrossRef]
- Yu, J.C.; Feng, Y.Q. Group classification of time fractional Black-Scholes equation with time-dependent coefficients. Fract. Calc. Appl. Anal. 2024, 27, 2335–2358. [Google Scholar] [CrossRef]
- Chatibi, Y.; Kinani, E.H.E.; Ouhadan, A. Lie symmetry analysis and conservation laws for the time fractional Black-Scholes equation. Int. J. Geom. Methods Mod. Phys. 2020, 17, 2050010. [Google Scholar] [CrossRef]
- Gazizov, R.K.; Kasatkin, A.A.; Lukashchuk, S.Y. Continuous transformation groups of fractional differential equations. Comput. Appl. Math. 2007, 9, 125–135. [Google Scholar] [CrossRef]
- Jafari, H.; Ncube, M.N.; Makhubela, L. Natural Daftardar-Jafari Method for Solving Fractional Partial Differential Equations. Nonlinear Dyn. Syst. Theory 2020, 20, 299–306. [Google Scholar]
- Schiff, J.L. The Laplace Transform: Theory and Applications; Springer: New York, NY, USA, 1999. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: London, UK, 1999. [Google Scholar]
- Gorenflo, R.; Kilbas, A.A.; Mainardi, F.; Rogosin, S.V. Mittag-Leffler Functions, Related Topics and Applications; Springer: Heidelberg, Germany, 2014. [Google Scholar]
- Hurst, H.E. Long-term Storage Capacity of Reservoirs. Trans. Am. Soc. Civ. Eng. 1951, 116, 770–799. [Google Scholar] [CrossRef]
- Geweke, J.; Porter-Hudak, S. The Estimation and Application of Long Memory Time Series Models. J. Time Ser. Anal. 1983, 4, 221–238. [Google Scholar] [CrossRef]
- Johnson, D.H. The Insignificance of Statistical Significanca Testing. J. Wildl. Manag. 1999, 63, 763–772. [Google Scholar] [CrossRef]
- Hidayat, A.S.E.; Sembiring, A.C. Application of the Historical Burn Analysis Method in Determining Rainfall Index for Crop Insurance Premium Using Black-Scholes. J. Actuar. Financ. Risk Manag. 2023, 2, 1–9. [Google Scholar] [CrossRef]
- Azka, M.; Fauziyyah; Hasanah, P.; Dinata, S.A.W. Designing Rainfall Index Insurance for Rubber Plantation in Balikpapan. J. Phys. Conf. Ser. 2021, 1863, 012018. [Google Scholar] [CrossRef]
- Prabowo, A.; Sukono; Mamat, M. Determination of the Amount of Premium and Indemnity in Shallot Farming Insurance. Univers. J. Agric. Res. 2023, 11, 322–335. [Google Scholar] [CrossRef]
- Hellmuth, M.E.; Osgood, D.E.; Hess, U.; Moorhead, A.; Bhojwani, H. Index Insurance and Climate Risk. In Climate and Society No. 2; International Research Institute for Climate and Society (IRI); Columbia University: New York, NY, USA, 2009. [Google Scholar]
- Sholiha, A.; Fatekurohman, M.; Tirta, I.M. Application of Black Scholes Method in Determining Agricultural Insurance Premium Based on Climate Index Using Historical Burn Analysis Method. Berk. Sainstek 2021, 9, 103–108. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration-Guildelines for Computing Crop Water Requirements. In FAO Irrigation and Drainage Paper No. 56; Food and Agriculture Organization of the United Nation: Rome, Italy, 1998; pp. 1–300. [Google Scholar]
- Ariyanti, D.; Riaman, R.; Irianingsih, I. Application of Historical Burn Analysis Method in Determining Agricultural Premium Based on Climate Index Using Black Scholes Method. JTAM (J. Teor. Dan Apl. Matematika) 2020, 4, 28–38. [Google Scholar] [CrossRef]
- Azahra, A.S.; Johansyah, M.D.; Sukono. Agricultural Insurance Premium Determination Model for Risk Mitigation Based on Rainfall Index: Systematic Literature Review. Risks 2024, 12, 205. [Google Scholar] [CrossRef]
- Baškot, B.; Stanić, S. Parametric crop insurance against floods: The case of Bosnia and Herzegovina. Econ. Ann. 2020, 65, 83–100. [Google Scholar] [CrossRef]
- Wati, T.; Kusumaningtyas, S.D.A.; Aldrian, E. Study of Season Onset based on Water Requirement Assessment. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2019; p. 012042. [Google Scholar] [CrossRef]
- Rasyid, A.R.; Arifin, M.; Rochma, M.A.F.; Asfan, L.M.; Yanti, S.A. Towards a water-senstive city: Level of regional damage to floods in Makassar City (case study: Manggala District). In IOP Conference Series: Earth and Enviromental Science; IOP Publishing: Bristol, UK, 2020; p. 012085. [Google Scholar] [CrossRef]


| Region | Average Daily Temperature | ||
|---|---|---|---|
| Cold | Moderate | Warm | |
| Tropical and Subtropical | |||
| Humid and Sub-Humid | |||
| Dry and Semi-Dry | |||
| Moderate | |||
| Humid and Sub-Humid | |||
| Dry and Semi-Dry | |||
| Year | Corn Production (Ton) | Rainfall (mm) | ||||
|---|---|---|---|---|---|---|
| Season I | Season II | Season III | Season I | Season II | Season III | |
| 2016 | 38,224.33 | 37,620.49 | 31,733.05 | 1589.00 | 1181.00 | 1583.00 |
| 2017 | 27,032.93 | 10,402.79 | 51,949.46 | 1830.00 | 478.00 | 1619.40 |
| 2018 | 46,886.57 | 22,485.70 | 40,693.74 | 1069.30 | 282.20 | 1098.00 |
| 2019 | 22,592.43 | 21,365.82 | 13,346.48 | 1343.20 | 168.80 | 649.20 |
| 2020 | 25,273.73 | 48,144.17 | 20,969.97 | 1188.00 | 708.60 | 1237.90 |
| 2021 | 10,342.91 | 12,045.55 | 13,308.55 | 853.00 | 506.90 | 750.90 |
| 2022 | 5593.91 | 5286.51 | 13,515.13 | 879.40 | 550.20 | 957.00 |
| 2023 | 20,785.31 | 4205.02 | 5838.12 | 565.30 | 434.20 | 269.00 |
| Corn Production | Season I | Season II | Season III | |
|---|---|---|---|---|
| Rainfall | ||||
| Season I | 0.44 | 0.39 | 0.76 | |
| Season II | 0.15 | 0.51 | 0.13 | |
| Season III | 0.45 | 0.49 | 0.82 | |
| Month | j | (mm) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 2016 | 2017 | 2018 | 2019 | 2020 | 2021 | 2022 | 2023 | ||
| September | 1 | 99 | 1 | 81 | 1.8 | 37.7 | 8 | 49 | 0 |
| 2 | 150 | 1 | 11 | 2.2 | 1 | 60 | 141 | 0.3 | |
| 3 | 120 | 181 | 77 | 2.4 | 152.8 | 115 | 92.9 | 0 | |
| October | 1 | 180 | 251 | 5 | 2.8 | 186.8 | 13 | 105 | 1.5 |
| 2 | 77 | 223 | 13 | 3.2 | 130.2 | 48.7 | 93.9 | 0 | |
| 3 | 151 | 28 | 67 | 0 | 101.5 | 72.1 | 60.3 | 22 | |
| November | 1 | 65 | 174 | 294 | 114.6 | 185.6 | 123.1 | 104.5 | 33.7 |
| 2 | 249 | 467 | 104 | 50.4 | 113.2 | 125.1 | 89.7 | 7.2 | |
| 3 | 193 | 42.4 | 199 | 26.8 | 99.8 | 57 | 126.5 | 62.5 | |
| December | 1 | 116 | 39 | 140 | 162.2 | 114.3 | 46.1 | 22.4 | 113.6 |
| 2 | 83 | 197 | 61 | 179.6 | 115 | 23.4 | 36 | 0 | |
| 3 | 0 | 15 | 46 | 148.2 | 0 | 59.4 | 35.8 | 28.2 | |
| Year | (mm) | (mm) | |||
|---|---|---|---|---|---|
| 2016 | 1 | 45.8333 | 2023 | 8 | 16.0750 |
| 2017 | 2 | 35.5333 | 2019 | 4 | 24.1000 |
| 2018 | 3 | 39.5833 | 2017 | 2 | 35.5333 |
| 2019 | 4 | 24.1000 | 2018 | 3 | 39.5833 |
| 2020 | 5 | 40.7250 | 2020 | 5 | 40.7250 |
| 2021 | 6 | 40.7667 | 2021 | 6 | 40.7667 |
| 2022 | 7 | 45.2667 | 2022 | 7 | 45.2667 |
| 2023 | 8 | 16.0750 | 2016 | 1 | 45.8333 |
| Percentile | Trigger () | Percentile | Trigger () |
|---|---|---|---|
| 1% | 16.6368 | ||
| 5% | 18.8838 | 55% | 40.5537 |
| 10% | 21.6925 | 60% | 40.7333 |
| 15% | 24.6717 | 65% | 40.7479 |
| 20% | 28.6733 | 70% | 40.7625 |
| 25% | 32.6750 | 75% | 41.8917 |
| 30% | 35.9383 | 80% | 43.4667 |
| 35% | 37.3558 | 85% | 45.0417 |
| 40% | 38.7733 | 90% | 45.4367 |
| 45% | 39.7546 | 95% | 45.6350 |
| 50% | 40.1542 | 100% | 45.8333 |
| No | Rainfall (mm/day) | Criteria |
|---|---|---|
| 1 | 0.5–20 | Light Rain |
| 2 | 20–50 | Moderate Rain |
| 3 | 50–100 | Heavy Rain |
| 4 | 100–150 | Very Heavy Rain |
| 5 | 150 | Extreme Rain |
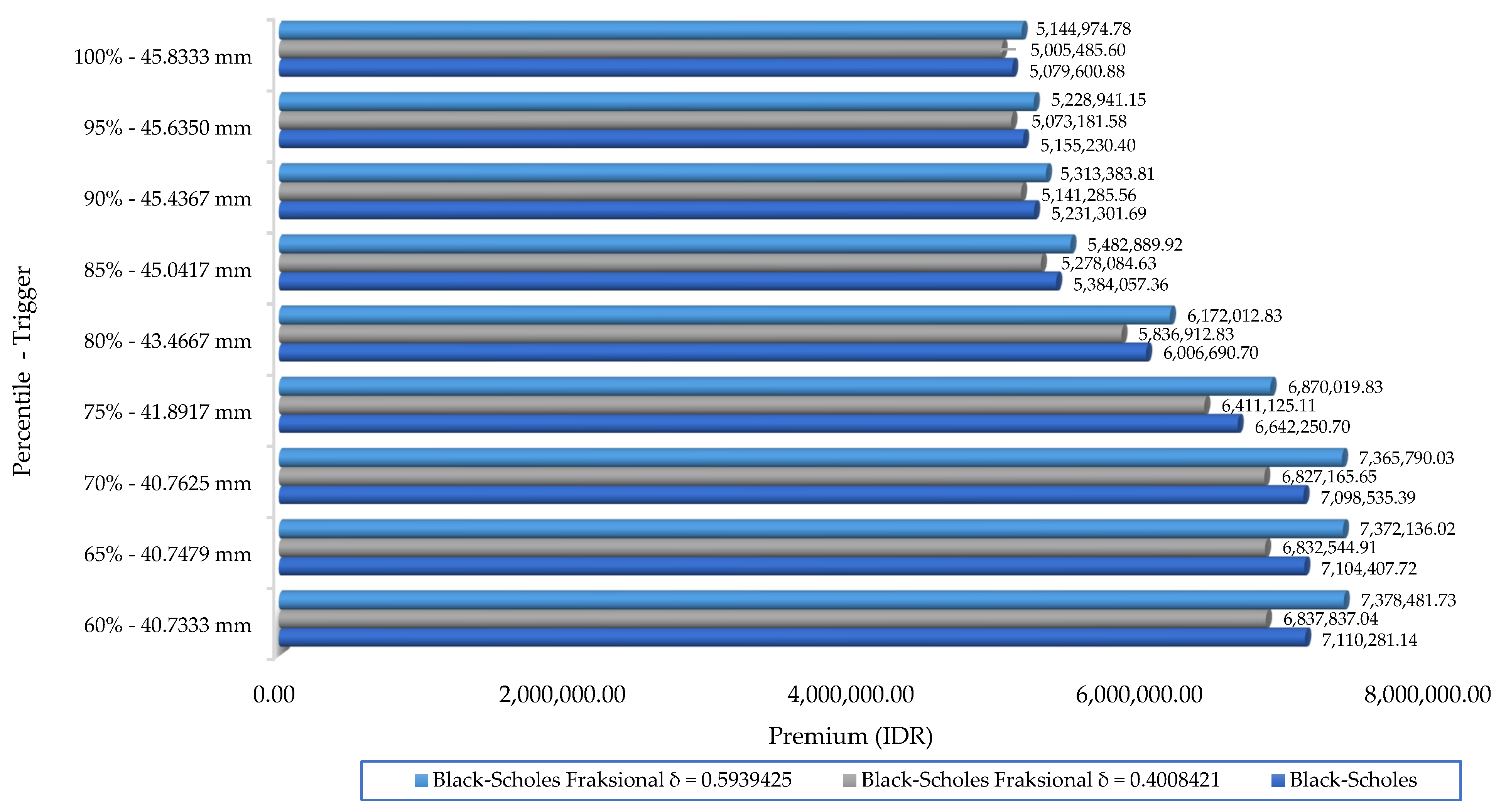
| Percentile | Trigger (mm) | Premium (IDR) | |
|---|---|---|---|
| 60% | 40.7333 | 0.642583 | 7,110,281.14 |
| 65% | 40.7479 | 0.642025 | 7,104,407.72 |
| 70% | 40.7625 | 0.641522 | 7,098,535.39 |
| 75% | 41.8917 | 0.600285 | 6,642,250.70 |
| 80% | 43.4667 | 0.542847 | 6,006,690.70 |
| 85% | 45.0417 | 0.486578 | 5,384,057.36 |
| 90% | 45.4367 | 0.472773 | 5,231,301.69 |
| 95% | 45.6350 | 0.465898 | 5,155,230.40 |
| 100% | 45.8333 | 0.459063 | 5,079,600.88 |
| No | Rainfall (mm/day) | Criteria |
|---|---|---|
| 1 | 1.000 | Very Dry |
| 2 | 1.001–2.000 | Dry |
| 3 | 2.001–3.000 | Moderate |
| 4 | 3.001–4.000 | Wet |
| 5 | 4.000 | Very Wet |
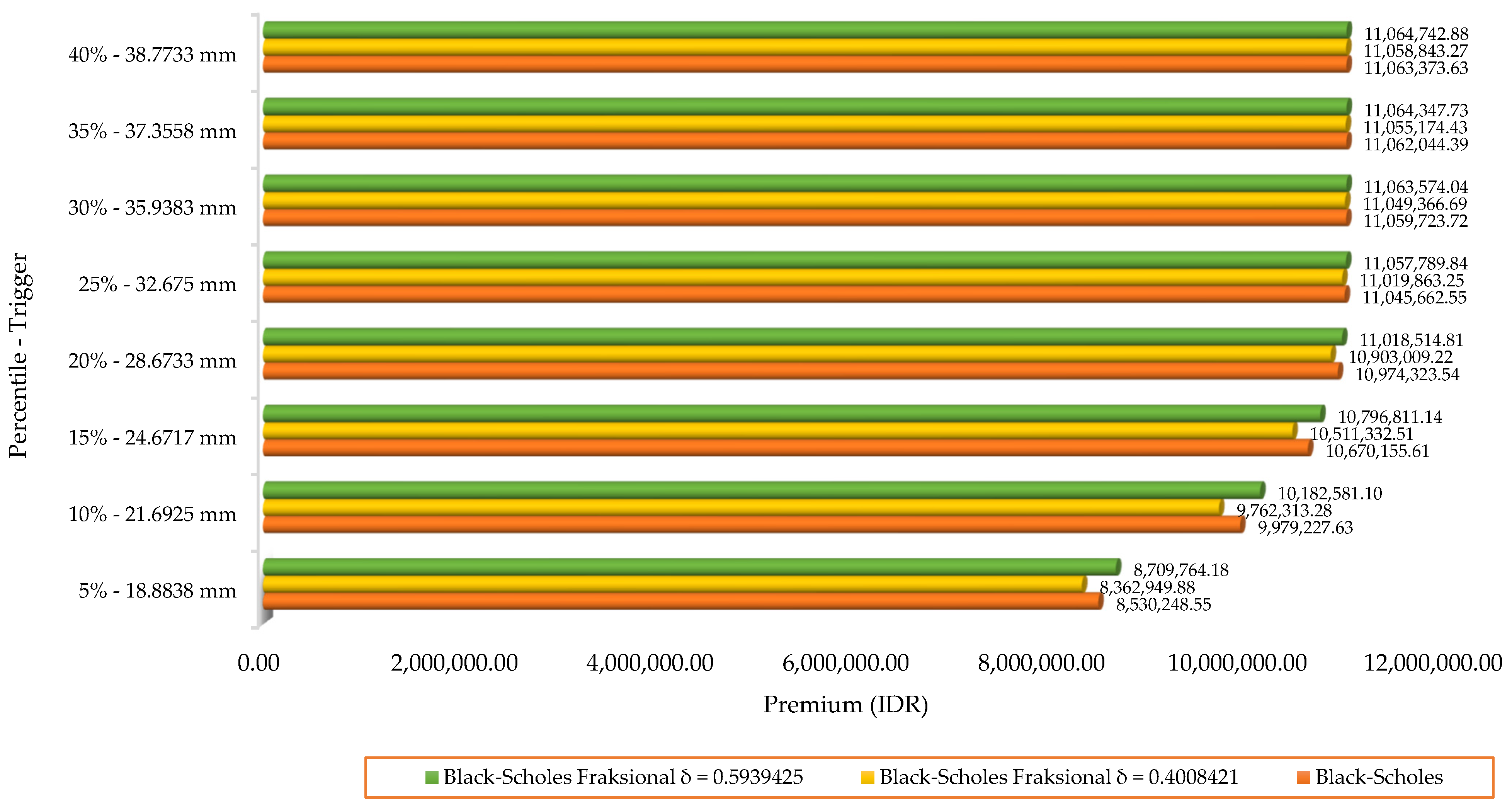
| Percentile | Trigger (mm) | Premium (IDR) | |
|---|---|---|---|
| 5% | 18.8838 | 0.770927 | 8,530,248.55 |
| 10% | 21.6925 | 0.901851 | 9,979,227.63 |
| 15% | 24.6717 | 0.964296 | 10,670,155.61 |
| 20% | 28.6733 | 0.991789 | 10,974,323.54 |
| 25% | 32.6750 | 0.998238 | 11,045,662.55 |
| 30% | 35.9383 | 0.999509 | 11,059,723.72 |
| 35% | 37.3558 | 0.999719 | 11,062,044.39 |
| 40% | 38.7733 | 0.999839 | 11,063,373.63 |
| Percentile | Trigger (mm) | ||||
|---|---|---|---|---|---|
| Premium (IDR) | Premium (IDR) | ||||
| 60% | 40.7333 | 0.617969 | 6,837,837.04 | 0.666808 | 7,378,481.73 |
| 65% | 40.7479 | 0.617476 | 6,832,544.91 | 0.666236 | 7,372,136.02 |
| 70% | 40.7625 | 0.616990 | 6,827,165.65 | 0.665663 | 7,365,790.03 |
| 75% | 41.8917 | 0.579392 | 6,411,125.11 | 0.620860 | 6,870,019.83 |
| 80% | 43.4667 | 0.527500 | 5,836,912.83 | 0.557782 | 6,172,012.83 |
| 85% | 45.0417 | 0.476999 | 5,278,084.63 | 0.495507 | 5,482,889.92 |
| 90% | 45.4367 | 0.464636 | 5,141,285.56 | 0.480188 | 5,313,383.81 |
| 95% | 45.6350 | 0.458481 | 5,073,181.58 | 0.472556 | 5,228,941.15 |
| 100% | 45.8333 | 0.452363 | 5,005,485.60 | 0.464969 | 5,144,974.78 |
| Percentile | Trigger (millimeter) | ||||
|---|---|---|---|---|---|
| Premium (IDR) | Premium (IDR) | ||||
| 5% | 18.8838 | 0.755792 | 8,362,949.88 | 0.787124 | 8,709,764.18 |
| 10% | 21.6925 | 0.882250 | 9,762,313.28 | 0.920228 | 10,182,581.10 |
| 15% | 24.6717 | 0.949943 | 10,511,332.51 | 0.975743 | 10,796,811.14 |
| 20% | 28.6733 | 0.985344 | 10,903,009.22 | 0.995783 | 11,018,514.81 |
| 25% | 32.6750 | 0.995906 | 11,019,863.25 | 0.999334 | 11,057,789.84 |
| 30% | 35.9383 | 0.998572 | 11,049,366.69 | 0.999863 | 11,063,574.04 |
| 35% | 37.3558 | 0.999098 | 11,055,174.43 | 0.999927 | 11,064,347.73 |
| 40% | 38.7733 | 0.999430 | 11,058,843.27 | 0.999963 | 11,064,742.88 |
| Percentile | Exit | Trigger | Rainfall Index (mm) | Compensation (IDR) |
|---|---|---|---|---|
| 60% | 16.0750 | 40.7333 | 16.0750 | 0 |
| 17.075 | 451,368.71 | |||
| 18.075 | 902,737.41 | |||
| 19.075 | 1,354,106.12 | |||
| 21.075 | 2,256,843.53 | |||
| 23.075 | 3,159,580.94 | |||
| 26.075 | 4,513,687.06 | |||
| 28.075 | 5,416,424.47 | |||
| 30.075 | 6,319,161.88 | |||
| 32.075 | 7,221,899.29 | |||
| 34.075 | 8,124,636.70 | |||
| 36.075 | 9,027,374.11 | |||
| 38.075 | 9,930,111.52 | |||
| 39.075 | 10,381,480.23 | |||
| 40.075 | 10,832,848.94 | |||
| 40.7333 | 11,130,000 |
| Percentile | Exit | Trigger | Rainfall Index (mm) | Compensation (IDR) |
|---|---|---|---|---|
| 5% | 16.0750 | 18.8838 | 16.0750 | 11,130,000 |
| 16.575 | 9,148,691.59 | |||
| 17.075 | 7,167,383.18 | |||
| 17.575 | 5,186,074.77 | |||
| 18.075 | 3,204,766.36 | |||
| 18.575 | 1,223,457.94 | |||
| 18.8838 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Azahra, A.S.; Johansyah, M.D.; Sukono. The Development of Fractional Black–Scholes Model Solution Using the Daftardar-Gejji Laplace Method for Determining Rainfall Index-Based Agricultural Insurance Premiums. Mathematics 2025, 13, 1725. https://doi.org/10.3390/math13111725
Azahra AS, Johansyah MD, Sukono. The Development of Fractional Black–Scholes Model Solution Using the Daftardar-Gejji Laplace Method for Determining Rainfall Index-Based Agricultural Insurance Premiums. Mathematics. 2025; 13(11):1725. https://doi.org/10.3390/math13111725
Chicago/Turabian StyleAzahra, Astrid Sulistya, Muhamad Deni Johansyah, and Sukono. 2025. "The Development of Fractional Black–Scholes Model Solution Using the Daftardar-Gejji Laplace Method for Determining Rainfall Index-Based Agricultural Insurance Premiums" Mathematics 13, no. 11: 1725. https://doi.org/10.3390/math13111725
APA StyleAzahra, A. S., Johansyah, M. D., & Sukono. (2025). The Development of Fractional Black–Scholes Model Solution Using the Daftardar-Gejji Laplace Method for Determining Rainfall Index-Based Agricultural Insurance Premiums. Mathematics, 13(11), 1725. https://doi.org/10.3390/math13111725







