Cholesterol Particle Interaction with the Surface of Blood Vessels

Abstract

A numerical experiment on the dynamics of the cholesterol particle is presented. This work is devoted to the analysis of how cholesterol accumulates on the surface of the blood vessel. To get acquainted with the effect of cholesterol accumulation in the vessel, it is important to understand the behavior of individual cholesterol particles. As a first step, the study is carried out by examining the ability of a particle of cholesterol to interact with the surface of the vessel, taking into account the influence of the action of various forces. For this, the experiment is divided into three parts, each of which is important for understanding how different forces act on the interaction of cholesterol with the surface of the vessel. To present the results of the motion of cholesterol particles, the figures of force, displacement, and time are provided. The results show the ability of cholesterol particles to interact and adhere to the blood vessel surface.

1. Introduction

Cholesterol types. There are different types of cholesterol, including high-density lipoprotein (HDL), low-density lipoprotein (LDL), very-low-density lipoprotein (VLDL), and triglycerides (TGs). The main focus here is on low-density lipoproteins.

Importance of investigation and cholesterol. A review of cholesterol as a metabolically important molecule is given by Schade et al. [1]. They mention that cholesterol’s unique structure gives it the ability to influence many cellular functions and is one reason that every cell in the body can synthesize cholesterol for its own use. Reducing cholesterol, mortality, and the significance of taking into account the initial level of risk is given by Smith et al. [2]. They mention that in a combined analysis, any pure benefit from the point of view of total mortality from cholesterol was observed only during testing, including patients with a very high initial risk of coronary heart disease. Longevity, statins, and cholesterol from age 70 to 90 years are discussed by Jacobs et al. [3].

Physical experiments with cholesterol. Most physical experiments are dedicated to the analysis of possibilities to lower excessive accumulated cholesterol levels in organisms. The effects of probiotics and prebiotics to reduce cholesterol, an overview of the research results in vivo and in vitro, is given by Ooi and Liong [4]. They note that some probiotic strains and prebiotic types show cholesterol-lowering properties. The feasibility and clinical relevance of in vivo cholesterol crystal detection using optical coherence tomography are presented by Katayama et al. [5]. They note that cholesterol crystallization penetrating the fibrous cap is often associated with subsequent acute myocardial infarctions and plaque ruptures. Tsai et al. [6] describe the cholesterol-lowering potential of lactic acid bacteria based on bile salt hydrolase activity and the effects of potent strains on cholesterol metabolism in vivo and in vitro. They note that the probiotic strains isolated and characterized in their study have great potential as cholesterol-lowering therapies. An in vivo evaluation of the efficacy of Lactobacillus plantarum in lowering cholesterol levels in adults with normal or moderately hypercholesterolemic levels is presented by Costabile et al. [7]. They note that Lactobacillus plantarum is a well-tolerated natural probiotic that can be used as an alternative or adjunct to existing therapies to reduce cardiovascular risk. A preliminary probiotic and technological characterization of the Pediococcus pentosaceus strain and in vivo cholesterol-lowering activity evaluation were presented by Damodharan et al. [8]. They mention that P. pentosaceus shows cholesterol-lowering activity in vivo and has essential properties that make it a potential probiotic.

Numerical simulation. Molecular dynamics simulations of model biological membranes with cholesterol are given by Berkowitz [9]. They note that, to observe raft self-assembly in simulations, it is necessary to conduct multi-scale simulations in which information from detailed molecular simulations is transferred to coarse-grained simulations to allow larger, longer-term simulations. The effect of cholesterol on the non-polar region of the phosphatidylcholine bilayer, a molecular modeling study, is presented by Róg and Pasenkiewicz-Gierula [10]. Their investigation provides insight into the coexistent region properties of the partial phase diagram for dimyristoylphosphatidylcholine-cholesterol bilayers. Molecular dynamics simulations of phospholipid bilayers with cholesterol are presented by Hofsass et al. [11]. The size of the systems modeled in their work provides an illustration of the molecular-level effects of cholesterol molecules intercalated into lipid bilayers. A molecular dynamics study taking into account the interaction of cholesterol and sphingomyelin is presented by Róg and Pasenkiewicz-Gierula [12]. They note that cholesterol affects both the interface and core of the stearoylsphingomyelin bilayer. Robinson et al. [13] conducted a molecular dynamics study of the behavior of cholesterol and its influence on headgroup and chain conformations in lipid bilayers. They note that cholesterol is not strongly related to lipids and is relatively mobile within its region in the lipid bilayer.

Human aging and cholesterol. Auley et al. [14] present a mathematical model of cholesterol metabolism and its age-related dysregulation. They note that cholesterol metabolism is a complex multicomponent system, and changes in this system as a result of aging can lead to high plasma cholesterol levels. Mathematical modeling of cholesterol metabolism dynamics and aging is also investigated by Morgan et al. [15]. Their work shows that computational systems biology has an important role to play in improving the understanding of health span and lipid metabolism. An evaluation of cholesterol metabolism computational models is presented by Paalvast et al. [16]. They emphasize that cholesterol metabolism can be modeled using relatively simple computational models.

Future investigations. Khera and Rader [17] provide guidance on future therapeutic directions in the reverse cholesterol transport. Their review discusses the fundamental importance of quantifying RCT flux. The regulation of cholesterol homeostasis in health and disease is presented by Duan et al. [18]. They note that impaired cholesterol homeostasis plays a critical role in the development of many diseases, including cardiovascular diseases, cancer, and neurodegenerative diseases, but particularly cardiovascular diseases in which the accumulation of lipids in macrophages/foam cells under the endothelial layer ultimately leads to the formation of atherosclerotic lesions. Pownall et al. [19] analyze reverse cholesterol transport, atherogenesis, and high-density lipoproteins. They note that not only do the low-lipid particles LpA-IV, γ-LpE, and preβ1-LpA-I account for the important residual cholesterol efflux capacity of HDL-deficient plasma, but they also play important functions in the reverse cholesterol transport of normal plasma.

2. Problem Formulation

It is known that biological material cholesterol has the property of accumulating on the surface of a blood vessel, and that excessive accumulation of cholesterol can cause blockage of blood vessels. The task is related to the study of the adhesion of cholesterol particles and the numerical modeling of the attachment of these particles to the inner surface of a blood vessel.

The problem remains of selecting the initial data, describing the process of interaction, and assessing the ability of a particle of cholesterol to stick to a surface. It became important to analyze/predict how fast these particles are attracted to the surface.

The question is how cholesterol reaches the surface of the inner vessel. This question arises because the influence of the blood and the electrostatic double-layer force on the small particle is very strong. To represent the acting forces on a particle of cholesterol, the Methodology section is provided.

In this paper, the discrete element method (DEM) is considered for modeling a cholesterol particle. The DEM is based on the description of forces that simultaneously (resultant force) act on a particle. Using them (acting forces), it is possible to calculate velocities and displacements of particles, according to Jasevičius [16]. The movement of the particle and the resultant force influence on it are not stationary. The problem is associated with the analysis of dynamics (not kinematics) when the mass of the cholesterol particle and its deformation (a nonlinear Hertz model) are considered.

Further studies are needed to model the effects of fluid/blood on cholesterol particles and to analyze tangential interaction. When considering computational fluid dynamics (CFD) in conjunction with the discrete element method (DEM), the lattice Boltzmann method (LBM), the Navier–Stokes equations, and the Euler–Lagrange approach are usually used, as seen in Kravets et al. [20], Schulz et al. [21], Vollmari et al. [22], and Kruggel-Emden et al. [23]. In this case, two separate computing programs (CFD/DEM) are combined to simultaneously calculate the problem.

The available COMSOL multiphysics software (software version 6.2; developer location: 100 District Avenue, Burlington, MA, USA) can also be used to simulate the effects of fluids, as in Brusokas et al. [24] and Tofan et al. [25].

For fluid flow modeling, geometric potential analysis may be considered (see Milman et al.) [26]. In mathematical physics, potential theory is an analysis of harmonic functions. Geometric potential evaluation can be an alternative for future analysis in evaluating fluid flow and the pressure field for the cholesterol particle system. The geometric potential theory for two-dimensional flows was analyzed by Dimitriou [27]. The author noted that the main goal of this study was to combine the kinematics of two-dimensional incompressible flow with its topology. Potential flow theory should also be considered, according to Kaushik [28], e.g., velocity potential analysis and fluid flow/stream function analysis, as should the calculation of potential flow around arbitrary bodies (cholesterol agglomerates of different shapes), per Hess and Smith [29]. Therefore, this requires new research, which may be a future task.

In the presented work, the problem is focused on creating an interaction model for a cholesterol particle, taking into account the DEM, in order to study the particle system in the future. In the next section, the methodology for calculating the dynamics of a nanosized cholesterol particle will be presented.

3. Methodology

The methodology is based on the discrete element method (DEM), which was originally used to simulate the motion of a system of particles. When using the DEM method, it is important to describe the interaction model of the particle (in this case, the cholesterol particle). Newton’s second law is applied to describe the movement of a cholesterol particle, per Jasevičius [16]:

$$m_i{\displaystyle \frac{{{\mathrm{d}}^2\mathit{x}}_i}{\mathrm{d}{t}^2}}={\mathit{F}}_i\left(t\right)$$

(1)

where $m_i$ and vector ${\mathit{x}}_i$ are the mass and position of the i-th cholesterol particle, and vector ${\mathit{F}}_i\left(t\right)=\sum _j{\mathit{F}}_{i,j}\left(t\right)$ corresponds to the resultants of forces added up and acting on the center of a cholesterol particle i during a possible interaction.

The integration of Equation (1) for a particle at time $t+∆t$ (where $∆t$ is the time step) is performed numerically by applying a fifth-order Gear’s predictor-corrector scheme (see Allen and Tildesley) [30]. Gear’s predictor-corrector scheme represents a two-step procedure, prediction ${\mathit{y}}^p\left(t+\Delta t\right)$ and correction ${\mathit{y}}^c\left(t+\Delta t\right)$. In this scheme, the time-dependent variables are denoted as position $\mathit{x}\left(t\right)$, velocities $\mathit{\upsilon }\left(t\right)=\mathrm{d}\mathit{x}/\mathrm{d}t$, and acceleration $\mathit{a}\left(t\right)={\mathrm{d}}^2\mathit{x}/\mathrm{d}{t}^2$, as well as the higher time derivatives ${\mathit{b}}_3\left(t\right)={\mathrm{d}}^3\mathit{x}/\mathrm{d}{t}^3$, ${\mathit{b}}_4\left(t\right)={\displaystyle \frac{{\mathrm{d}}^4\mathit{x}}{\mathrm{d}{t}^4}},$ and ${\mathit{b}}_5\left(t\right)={\mathrm{d}}^5\mathit{x}/\mathrm{d}{t}^5$ of the cholesterol by the vector $\mathit{y}={\left\{\mathit{x},\mathit{\upsilon },\mathit{a},{\mathit{b}}_3,{\mathit{b}}_4,{\mathit{b}}_5\right\}}^T$. The new value variables at the time increment $t+\Delta t$ are predicted by a simple series expansion up to a desired order of accuracy ${\mathit{y}}^p\left(t+\Delta t\right)=\mathit{y}\left(t\right)+{\mathit{y}}^p\left(\Delta t\right)$. Here, the incremental vector ${\mathit{y}}^p\left(\Delta t\right)$ presents the required terms of the expansion series. Then, according to the new positions and velocities, the cholesterol forces and accelerations are corrected, and the acceleration increment $\Delta \mathit{a}$ is updated. Finally, the vector of the cholesterol variables is corrected as follows ${\mathit{y}}^c\left(t+\Delta t\right)={\mathit{y}}^p\left(t+\Delta t\right)+{\mathit{y}}^c\left(c_j,\Delta t,\Delta \mathit{a}\right)$. Here, the correction vector ${\Delta \mathit{y}}^c$ is calculated by using the given integration constant $c_j$. For this simulation, cholesterol motion is limited to normal direction, position $x\left(t\right),$ which is presented here as displacement $h\left(t\right)$.

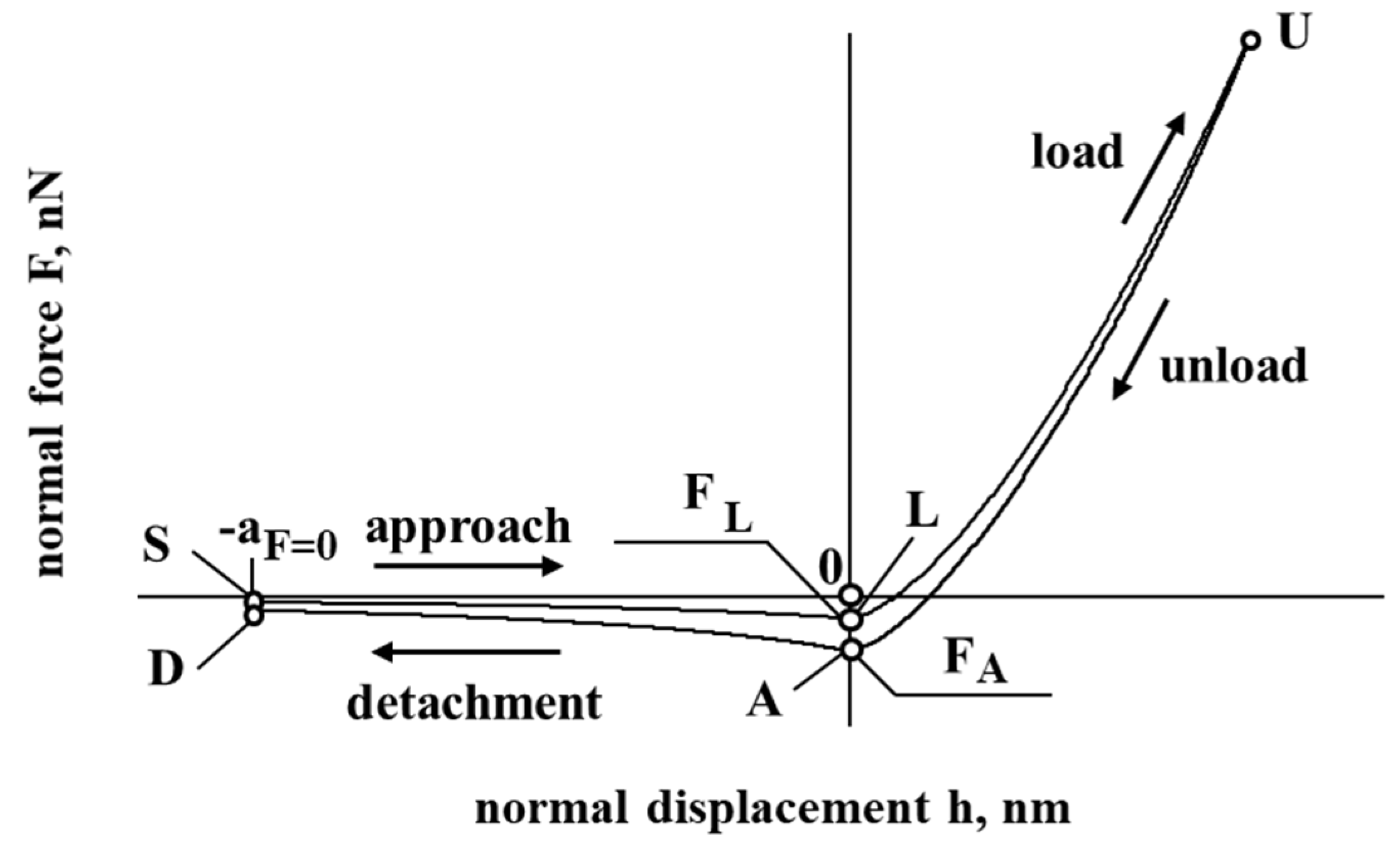
Figure 1 presents a model of the interaction of cholesterol particles. The negative displacement (SL and DA) corresponds to the case when a particle of cholesterol is at a distance from the interacting surface, while a positive displacement (LU and AU) corresponds to the contact/deformation of the particle of cholesterol. In Figure 1, the negative force corresponds to the resultant force, which has an attraction effect, while a positive force corresponding to the resultant force has a repulsion effect on the interaction of cholesterol particles with the vessel surface.

The forces acting on a cholesterol particle can be described by the following general expression:

$$F\left(t\right)=F_{adh}\left(t\right)+F_{el}+F_{diss}+F_{dl}\left(t\right){+F}_{drag}\left(t\right)$$

(2)

here $F_{adh}\left(t\right)$ is the adhesion force, $F_{dl}\left(t\right)$ is the electrostatic double-layer force, $F_{drag}\left(t\right)$ is the drag force, $F_{el}\left(t\right)$ is the elastic force, and $F_{diss}\left(t\right)$ is the energy dissipation force.

For cholesterol particles, the adhesion force $F_{adh}$ plays an important role, especially when we talk about the agglomeration of cholesterol particles. In this paper, the work of adhesion is considered based on the Tomas model, as seen in Tomas [31,32,33]. The cholesterol particle is considered a nanosized object to which the Derjaguin, Müller, and Toporov (DMT) model is applied. This model predicts that half of the interaction force $F_{adh,DMT}/2$ occurs outside in the annular area, which is located at the perimeter closed by the contact, considering the effective radius $R_{eff}$, per Tomas [31,32,33] and Jasevičius et al. [34,35].

$$F_{adh,DMT}=4\cdot \pi \cdot {\sigma }_{sls}\cdot R_{eff}$$

(3)

The median adhesion force $F_{adh,DMT}$ of a direct spherical particle contact can be expressed in terms of the work of adhesion $W_A$, conventional surface energy ${\gamma }_A$ or surface tension ${\sigma }_{sls}$; see Tomas [31,32,33].

$$W_A=2\cdot {\gamma }_A=2\cdot {\sigma }_{sls}$$

(4)

The index sls means particle surface-adsorption layers (with liquid equivalent mechanical behavior)—particle surface interaction. This surface tension ${\sigma }_{sls}$ equals half the energy needed to separate two flat surfaces from an equilibrium contact distance $a_{F=0}$ to infinity, per Tomas [31,32,33]:

$${\sigma }_{sls}=-{\displaystyle \frac{1}{2}}\cdot {\int }_{a_{F=0}}^{\mathrm{\infty }}{p}_{vdW}\left(a\right)\mathrm{d}a={\displaystyle \frac{C_{H,sls}}{24\cdot \pi \cdot a_{F=0}^2}}$$

(5)

The adhesion force per unit area of a flat surface or the attractive pressure $p_{vdW}$ (the index vdW means van der Waals), which is used here to describe the van der Waals interactions in contact, is equivalent to the theoretical bond strength (considering the Hamaker constant $C_{H,sls}$) and can be calculated as (Tomas [31,32,33]):

$$p_{vdW}={\displaystyle \frac{C_{H,sls}}{6\cdot \pi \cdot a_{F=0}^3}}={\displaystyle \frac{4\cdot {\sigma }_{sls}}{a_{F=0}}}$$

(6)

A characteristic adhesion separation for direct contact is on a molecular scale (atomic distance from the center-to-center) and can be evaluated for the equilibrium of force $F=-\mathrm{d}U/\mathrm{d}a$ molecular attraction and repulsion potentials, $a=a_{F=0}$ (Tomas [31,32,33]). This separation of the interaction potential minimum amounts is at least about $a_{F=0}\approx 20 \mathrm{n}\mathrm{m}$ in a liquid medium. It is assumed that the minimum center separation $a_{F=0}$ is constant during loading and unloading, per Tomas [31,32,33].

After approaching from an infinite distance $-\infty$ to this minimum center separation $a_{F=0}$, the interacting surface contact is formed without any contact deformation by the attractive short-range adhesion force $F_{adh,0}$ (the so-called “jump in”). As a response, from $F_{adh,0}$, the contact is elastically compacted, forming an approximated circular contact area (Tomas [31,32,33]).

Considering the unload and detachment curve (Figure 1), the contribution of the work of adhesion $W_{A, separation}$ is considered to detach the flattened contact surfaces from the center approach $\approx h_U$ to infinity $-\infty$ (to separate particles), according to Tomas [31,32,33]:

$$W_{A,separation}=F_{adh,0}\cdot a_{F=0}$$

(7)

3.1. Approach

The movement of the cholesterol particle at a certain distance towards the vessel’s inner surface can be described as follows:

$$F\left(t\right)=F_{adh}\left(t\right)+F_{dl}\left(t\right){+F}_{drag}\left(t\right)$$

(8)

here $F_{adh}\left(t\right)$ is the adhesion force, $F_{dl}\left(t\right)$ is the electrostatic double-layer force, and $F_{drag}\left(t\right)$ is the drag force. The adhesion force $F_{adh}\left(t\right)$ for a cholesterol particle is described as follows:

$$F_{adh}\left(t\right)={\displaystyle \frac{F_{adh,L}{a}_{F=0}^2}{{\left(a_{F=0}+\left|h\left(t\right)\right|\right)}^2}}$$

(9)

The considered member $F_{adh,L}$ is the adhesion force ($F_{adh,L}$ = $F_{adh,0}$, Tomas [31,32,33]) when the cholesterol’s surface is in contact with the interacting surface (at point $L$, where ${h=h}_L=0$):

$$F_{dl}\left(t\right)=4\pi R_{eff}\epsilon {\epsilon }_0{\psi }_i{\psi }_j{\lambda }_D^{-1}\cdot e^{{\displaystyle \frac{h\left(t\right)}{{\lambda }_D}}}$$

(10)

here $\psi$ is the surface potential, ${\epsilon }_0$ is the permittivity of the free space, and $\epsilon$ is the dielectric constant of water. The Debye length can be calculated as follows:

$${\lambda }_D=0.304/\sqrt{c}$$

(11)

here $c$ is the concentration of the electrolyte expressed in Molar. The effective radius $R_{eff}$ is described as follows:

$$R_{eff}={\left({\displaystyle \frac{1}{R_i}}+{\displaystyle \frac{1}{R_j}}\right)}^{-1}$$

(12)

The drag force is described as follows:

$$F_{drag}\left(t\right)=6\cdot \pi ·\eta ·R_H·{\upsilon }_{relative}\left(t\right)$$

(13)

here $\eta$ is viscosity and $R_H$ is the hydrodynamic radius. The relative velocity can be described as follows:

$${\upsilon }_{relative}\left(t\right)={\upsilon }_i\left(t\right)-{\upsilon }_{blood}\left(t\right)$$

(14)

here ${\upsilon }_i$ is cholesterol particle velocity and ${\upsilon }_{blood}$ is blood velocity.

3.2. Contact and Loading

When a cholesterol particle touches the surface, the contact begins. During the contact, the loading process is described as follows:

$$F\left(t\right)=F_{adh}\left(t\right)+F_{el}\left(t\right)+F_{dl,L}{+F}_{drag}\left(t\right)$$

(15)

here $F_{adh}\left(t\right)$ is the adhesion force, $F_{dl}\left(t\right)$ is the electrostatic double-layer force, $F_{drag}\left(t\right)$ is the drag force, $F_{el}\left(t\right)$ is the elastic force, and $F_{diss}\left(t\right)$ is the energy dissipation force.

The deformation of the cholesterol particle is described as elastic using the Hertz model:

$$F_{el}={\displaystyle \frac{4}{3}}·{\displaystyle \frac{E_i{E}_j}{E_i\left(1-{\nu }_j^2\right)+E_j\left(1-{\nu }_i^2\right)}}{R}_{eff}^{0.5}{h}_{ij}^{1.5}$$

(16)

${\nu }_i$ and ${\nu }_j$ are the Poisson’s ratios of the cholesterol particle and the vessel’s inner surface, respectively; $E_i$ and $E_j$ are the modulus of elasticity of the cholesterol particle and the inner vessel surface, respectively.

It is considered that the cholesterol particle has a radius $R_i$, while the interacting surface is flat. This assumption can be made considering that the interacting surface is many times bigger than the cholesterol particle itself, $R_j\gg R_i$, enough to consider it a flat surface with the radius $R_j=\mathrm{\infty }$, which gives $R_{eff}=R_i$. The double-layer force $F_{dl,L}$, which acts during the contact, is described as follows:

$$F_{dl,L}=4\pi R_{eff}\epsilon {\epsilon }_0{\psi }_i{\psi }_j{\lambda }_D^{-1}$$

(17)

3.3. Contact and Unloading

When, during the contact, the cholesterol particle reaches maximum displacement $h_U$, it will start unloading. This process can be described as follows:

$$F\left(t\right)=F_{adh}\left(t\right)+F_{dl}\left(t\right){+F}_{drag}\left(t\right)+F_{el}\left(t\right)+F_{diss}\left(t\right)$$

(18)

Here, $F_{adh}\left(t\right)$ is the adhesion force, $F_{dl}\left(t\right)$ is the electrostatic double-layer force, $F_{drag}\left(t\right)$ is the drag force, $F_{el}\left(t\right)$ is the elastic force, and $F_{diss}\left(t\right)$ is the energy dissipation force. Energy dissipation due to a change in the adhesion representative dissipative force is described as follows:

$$F_{adh,diss}\left(t\right)=-{\displaystyle \frac{2W_{ad,diss}}{h_U+a_{F=0}}}\cdot \overline{h}\left(t\right)$$

(19)

Here $\overline{h}\left(t\right)$ is the normal strain, which depends on maximum displacement $h_U$:

$$\overline{h}\left(t\right)={\displaystyle \frac{h_U-h\left(t\right)}{h_U}}$$

(20)

The amount of dissipated energy during the contact is calculated as follows, per Jasevičius et al. [34,35]:

$$W_{adh,diss}=k_H\cdot \left|F_{L,adh}\cdot a_{F=0}\right|$$

(21)

The coefficient $k_H$ estimates the different amount of energy dissipated due to the influence of adhesion. In this simulation, this coefficient is $k_H=1$.

3.4. Detachment

The detachment starts when the cholesterol particle physically detaches from the surface. It could be described as follows:

$$F\left(t\right)=F_{adh}\left(t\right)+F_{dl}\left(t\right){+F}_{drag}\left(t\right)+F_{diss}\left(t\right)$$

(22)

Here, $F_{adh}\left(t\right)$ is the adhesion force, $F_{dl}\left(t\right)$ is the electrostatic double-layer force, $F_{drag}\left(t\right)$ is the drag force, and $F_{diss}$ is the energy dissipation force. The Van der Waals force $F_{adh}\left(t\right)$ of the cholesterol particle, which is obtained during particle detachment, is as follows:

$$F_{adh}\left(t\right)={\displaystyle \frac{F_{A,adh}{a}_{F=0}^2}{{\left(a_{F=0}+\left|h\left(t\right)\right|\right)}^2}}$$

(23)

Adhesion for point A:

$$F_{A,adh}\left(t\right)=F_{L,adh}+F_{adh,diss}$$

(24)

The mass of the cholesterol particle can be calculated as follows:

$$m_i={\displaystyle \frac{4}{3}}\pi {\rho }_i{R}_i^3$$

(25)

where $R_i$ is the radius of the cholesterol particle and ${\rho }_i$ is the density of the cholesterol particle:

$$m_{eff}=m_i$$

(26)

4. Results

For modelling, LDL (low-density lipoprotein) is considered a spherical biological nanoparticle. In

Table 1. Initial data.

Objects	Initial Parameters	Values	References, Source
LDL Cholesterol	$\mathrm{Diameter} \mathrm{range}, d$	$21.4\pm 1.3 \mathrm{n}\mathrm{m}$	Rajman et al. [36] Sacks and Campos et al. [37]
	$\mathrm{Considered} \mathrm{diameter}, d_i$	22.7 nm	Gan et al. [38]
	$\mathrm{Radius}, R_i$	$11.35 \mathrm{n}\mathrm{m}$	-
	$\mathrm{Initial} \mathrm{interaction} \mathrm{distance}, h_S$  $(h_S=a_{F=0})$	$20 \mathrm{n}\mathrm{m}$	Jasevičius et al. [35]
	$\mathrm{Initial} \mathrm{velocity}, {\upsilon }_0$	$-0.010783 \mathrm{c}\mathrm{m}/\mathrm{s}$	Jasevičius et al. [35]
	$\mathrm{Mass}, m_i$	$\approx 6.4·{10}^{-21} \mathrm{k}\mathrm{g}$	Equation (25)
	$\mathrm{Density}, {\rho }_i$	$\approx 1.045 \mathrm{g}/{\mathrm{c}\mathrm{m}}^3$ $(\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{g}\mathrm{i}\mathrm{n}\mathrm{g} \mathrm{b}\mathrm{e}\mathrm{t}\mathrm{w}\mathrm{e}\mathrm{e}\mathrm{n} 1.024 \mathrm{a}\mathrm{n}\mathrm{d}$ $1.045 \mathrm{g}/{\mathrm{c}\mathrm{m}}^3$)	Chen and Kane [39]
	$\mathrm{Young}’\mathrm{s} \mathrm{modulus}, E_i$	20 MPa (native)	Wang et al. [40]
	$\mathrm{Poisson}’\mathrm{s} \mathrm{ratio}, {\mathsf{\nu }}_i$	0.4	Wang et al. [41]
	$\mathrm{Surface} \mathrm{potential}, {\psi }_i$	$-14.3 \mathrm{m}\mathrm{V}$ $(\mathrm{ranging} \mathrm{between}-4.3$$\mathrm{and}-14.3 \mathrm{m}\mathrm{V}$)	Desrumaux et al. [42]
	$\mathrm{The} \mathrm{adhesion} \mathrm{force} (\mathrm{point} \mathrm{L}), F_{L,adh}$	$-0.19 \mathrm{n}\mathrm{N}$	Gan et al. [38]
	$\mathrm{Adhesive} \mathrm{dissipative} \mathrm{energy}, W_{adh,diss}$$(F_{L,adh}$$, a_{F=0}$$, k_H$)	$3.8·{10}^{-18 }\mathrm{J}$	Equation (16)
Vessel cell (endothelium)	$\mathrm{Density}, {\rho }_j$	$1.03 \mathrm{g}/{\mathrm{c}\mathrm{m}}^3$	Nees et al. [43]
	$\mathrm{Young}’\mathrm{s} \mathrm{modulus}, E_j$	$5.0 \mathrm{k}\mathrm{P}\mathrm{a}$	Zeng et al. [44]
	$\mathrm{Poisson} \mathrm{ratio}, {\nu }_j$	$0.5$	Jasevičius [45]
	$\mathrm{Surface} \mathrm{potential}, {\psi }_j$	$-48.3 \mathrm{m}\mathrm{V}$	Nakashima et al. [46]
Blood	PH	$7.4$	Wilschut [47]
	$\mathrm{Temperature}, T_{temp}$	$36.8 °\mathrm{C}$	Jasevičius [45]
	$\mathrm{The} \mathrm{permittivity} \mathrm{of} \mathrm{the} \mathrm{free} \mathrm{space}, {\epsilon }_0$	$8.854\cdot {10}^{-12} {\mathrm{C}}^2{\mathrm{J}}^{-1}{\mathrm{m}}^{-1}$	Jasevičius [45]
	$\mathrm{Debye} \mathrm{length}, {\lambda }_D$ $\mathrm{A} \mathrm{dielectric} \mathrm{constant} \mathrm{of} \mathrm{water}, \epsilon$	$0.785$ nm 74.5	Jasevičius [45] Butt et al. [48]
	$\mathrm{Blood} \mathrm{flow} \mathrm{velocity}, {\upsilon }_{max,blood}^T$	$-3.0 \mathrm{c}\mathrm{m}/\mathrm{s}$	Nagaoka and Yoshida [49]
	$\mathrm{Blood} \mathrm{flow} \mathrm{velocity} \mathrm{at} a_{F=0}=20 \mathrm{n}\mathrm{m}$$\mathrm{Distance} \mathrm{in} \mathrm{normal} \mathrm{direction}, {\upsilon }_S$	$-0.010783 \mathrm{c}\mathrm{m}/\mathrm{s}$	Jasevičius [45]
	$\mathrm{Viscosity}, {\eta }_f$	$0.003 \mathrm{P}\mathrm{a}·\mathrm{s}$	Nacev et al. [50]
Blood Vessel	$\mathrm{Diameter}, d_{blood vessel}$	$100 \mathsf{\mu }\mathrm{m}$	Nagaoka and Yoshida [49]

are given the main initial data for the simulation of this particle interaction. Also, initial mechanical parameters of the blood vessels as well as the blood are presented, which are needed for the particle mechanical interaction with the inner vessel surface simulation. In order to conduct a simulation, the main parameters from the physical experiments available from the known literature were considered; however, because it is an object of a biological nature, it is not excluded that mechanical parameters may vary depending on various parameters such as particle size, biological composition, and so on.

The essence of the study is to analyze the interaction of cholesterol particles. Because it is a numerical experiment, the influence of each of the forces assessed on each cholesterol particle is further investigated. Different estimated forces include adhesion, elasticity, the electrostatic double layer, and drag/fluid resistance. To this end, the investigation was divided into three parts. Each part reveals the different influences of acting forces. In Figure 2, Figure 3 and Figure 4, the negative displacement h < 0 means distance to the surface of the interaction. Positive displacement when h > 0 means physical contact. Negative resultant force F < 0 means attraction, while positive resultant force F > 0 means repulsion.

In the first part of the study, the interaction was examined without an assessment of the electrostatic double-layer force $F_{dl}$ or the drag/liquid resistance force $F_{drag}$. The second part leaves out only the drag/fluid resistance force $F_{drag}$. In the third part, all forces applied in this work are evaluated.

Now, let us look at the results of the first part of the investigation, presented in Figure 2. Figure 2a presents a force–displacement curve. During the interaction of the cholesterol particle and the inner surface of the blood vessel, a hysteresis of the force–displacement curve is observed during the unloading of a particle of cholesterol. Hysteresis is a loss of energy, and it is necessary to attach this particle to the cell surface. In addition, as a result, during unloading, a particle of cholesterol that stops its further movement (unloading) can be considered to be reloading and at the beginning of the sticking process for the particle.

Figure 2. The interaction of the particle of cholesterol without evaluating the electrostatic double layer and the drag forces. The first part of the study. Dependence of force on displacement (a) and time (b); dependence of displacement on time (c).

Figure 2. The interaction of the particle of cholesterol without evaluating the electrostatic double layer and the drag forces. The first part of the study. Dependence of force on displacement (a) and time (b); dependence of displacement on time (c).

Figure 2b presents a force–time curve. It was observed that the duration of the interaction between the cholesterol particle and the vascular cell is quite short, which indicates that the sticking itself occurs very quickly. The maximum reached repulsion force is about 0.3 nN (nano Newton scale).

Figure 2c presents a displacement–time curve. During the sticking process, the displacement of the cholesterol particle was relatively high, which indicates that the particle could stick firmly or even penetrate during this interaction, an idealistic case when there is no liquid between the soft cell and the cholesterol particle.

Figure 3a presents a force–displacement curve. After assessing the influence of the electrostatic double-layer force, as in the case of Figure 2a, a hysteresis is formed in the force–displacement curve. Nevertheless, a particle of cholesterol has already stopped during the detachment/separation, when it was properly distant from the interacting surface. Further movement is a return to the surface of the interaction and the beginning of the sticking process. In addition, it should be mentioned that in both cases presented in Figure 2 and Figure 3 (with electrostatic double-layer force and without it), a particle of cholesterol will stick.

Figure 3. The interaction of the particle of cholesterol without evaluating the drag force. The second part of the study. Dependence of force on displacement (a) and time (b); dependence of displacement on time (c).

Figure 3. The interaction of the particle of cholesterol without evaluating the drag force. The second part of the study. Dependence of force on displacement (a) and time (b); dependence of displacement on time (c).

Figure 3b presents a force–time curve. Here, the achieved maximum resultant force, unlike in Figure 2b, increased by about 10 times. Looking at the Figure 3b time scale, the duration of the interaction decreased by less than 8 times.

Figure 3c presents a displacement–time curve. Regarding the displacement parameter, the shift decreased by about 250 times. Also, based on the results, the electrostatic double-layer force prevents penetration into the cell, forming a “protective” barrier that prevents the penetration of a cholesterol particle.

Figure 4 shows the interaction that evaluates the drag force of the liquid. The effect of the resistance of the liquid significantly changes the entire course of the interaction. Both the overall force effect and the displacement/penetration of the particles are significantly reduced. In either case, the movement of the cholesterol particle during the interaction was stopped at the cell surface with a small displacement, while the cholesterol particle remained attached.

Figure 4a presents a force–displacement curve. The influence of fluid drag force has very suddenly reduced the influence of adhesion and electrostatic double layer forces. Nevertheless, the effects of attraction/adhesion were sufficient for the cholesterol particle to approach the cell surface and adhere to it.

Figure 4b presents a force–time curve. Due to the influence of fluid, the duration of the interaction increased significantly compared to previous cases (Figure 2 and Figure 3), 10 and 70 times, respectively.

Figure 4c presents a displacement–time curve. The cholesterol particle was stuck with little deformation and immediately stopped.

Further investigation will be conducted with the intent to analyze the sticking process of the cholesterol particle.

Figure 4. Interaction of a cholesterol particle, taking into account all the acting forces presented in this work. The third part of the study. Dependence of force on displacement (a) and time (b); dependence of displacement on time (c).

Figure 4. Interaction of a cholesterol particle, taking into account all the acting forces presented in this work. The third part of the study. Dependence of force on displacement (a) and time (b); dependence of displacement on time (c).

5. Conclusions

It is important to describe cholesterol particle interaction (how it interacts) because the cholesterol particle plays one of the essential roles in vascular diseases. Excessive cholesterol levels can have serious consequences, from which many people suffer today (for example, type II diabetes, high blood pressure, and so on). In order to understand the effects of cholesterol, it is important to understand its behavior at each moment in time. It is expected that the presented model will allow for modeling the dynamics of the cholesterol particle and predicting the behavior of cholesterol particles when their accumulation forms on the surface of the blood vessel. In this work, the interaction of the cholesterol particle with the surface of the blood vessel was studied. An LDL cholesterol particle was chosen. An attempt was made to simulate its ability to attach. The results of the study showed that due to its small dimensions, the cholesterol particle, already under the influence of adhesion forces, can relatively quickly approach the surface of the blood vessel (within about 150 ns) and initiate the adhesion process.

The next step of the research is to complicate the interaction model to describe the sticking process and also to describe the movement of the cholesterol particle in a tangential direction. The model may also include computational fluid dynamics and geometrical potential theory analysis. Using numerical modeling to understand the formation of stable cholesterol structures, it is necessary to evaluate the interactions between cholesterol particles over a longer period of time (including the sticking process), which will allow for the description of cholesterol accumulation and provide insight into plaque formation over time. This can be one of the important topics for continuing research direction in this area.