Stiffness Regulation of Cable-Driven Redundant Manipulators Through Combined Optimization of Configuration and Cable Tension
Abstract
1. Introduction
- (1)
- A dual-level stiffness regulation strategy is proposed, combining configuration and cable tension optimization. This integrated approach offers enhanced flexibility and a broader range of stiffness regulation.
- (2)
- Motion-level and tension-level factors are introduced into the respective optimization models. These factors serve as control variables, effectively manipulating the configuration and tension solutions to achieve stiffness regulation.
2. Related Work
3. Stiffness Model of CDRMs
3.1. Stiffness Model
3.2. Stiffness Analysis
4. Stiffness Regulation Method
4.1. Configuration Optimization
4.1.1. Configuration Optimization Model
4.1.2. Optimization Objective Function
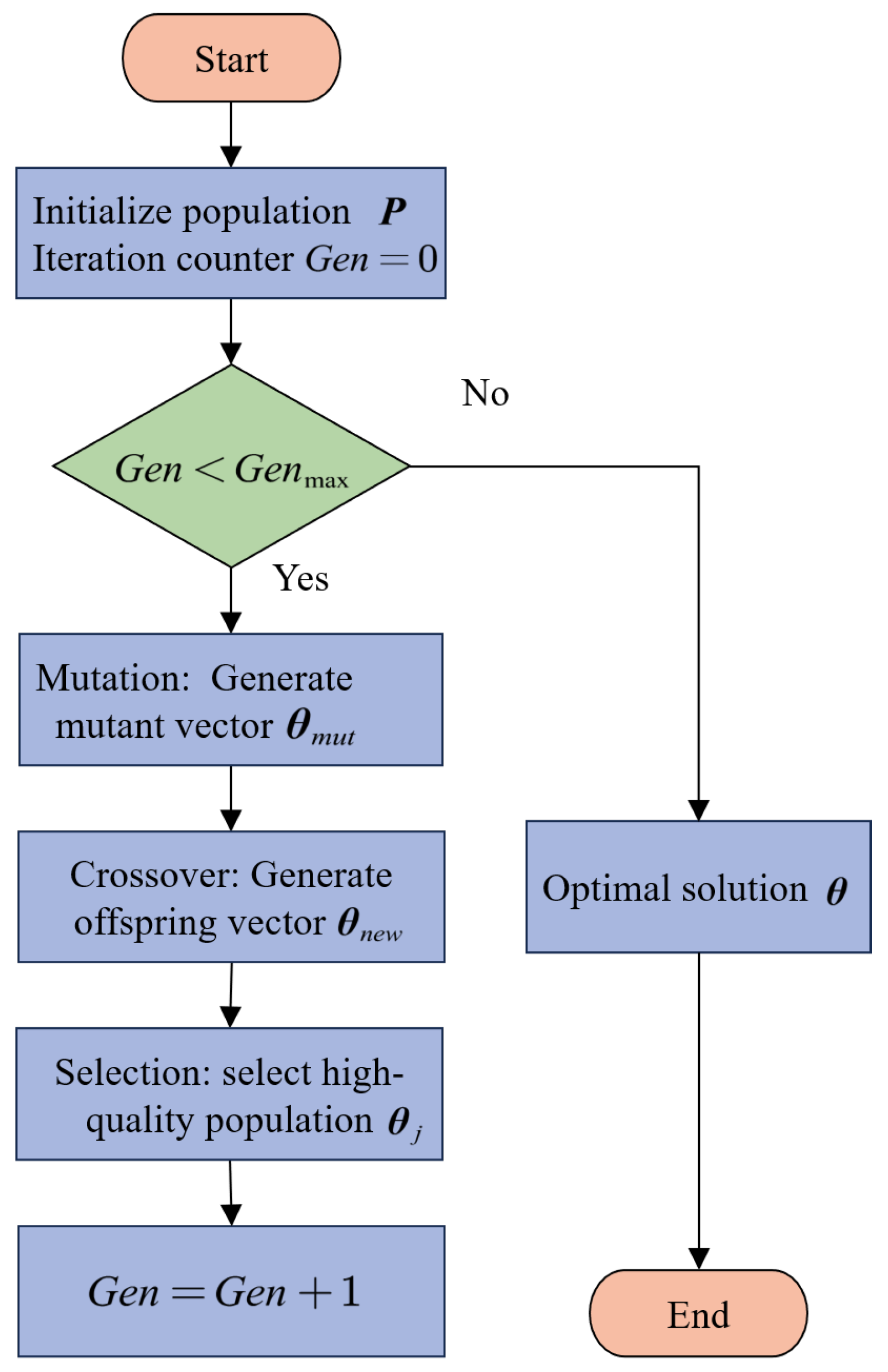
4.1.3. Configuration Optimization Algorithm
| Algorithm 1 Configuration optimization based on improved DE algorithm |
|
4.2. Cable Tension Optimization
4.2.1. Tension Optimization Model
4.2.2. Optimization Objective Function
4.2.3. Tension Optimization Algorithm
| Algorithm 2 Cable tension optimization based on modified GPM |
|
5. Case Study Example
5.1. Structure of the Planar CDRM
5.2. Kinematic Model
5.3. Kinetostatic Model
| Algorithm 3 Kinetostatic model of CDRMs |
|
5.4. Stiffness Regulation
5.4.1. Configuration Optimization
5.4.2. Cable Tension Optimization
6. Numerical Simulation
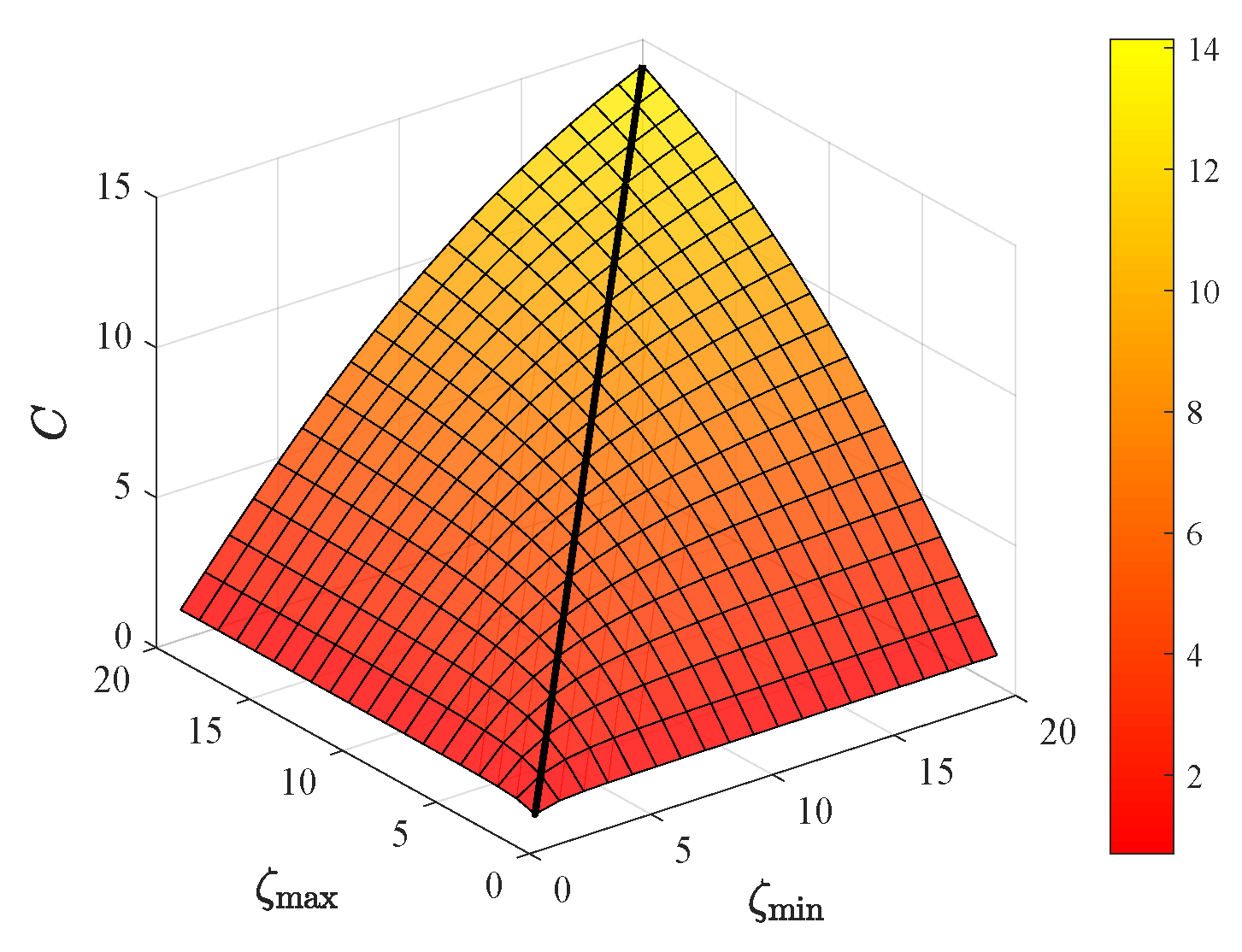
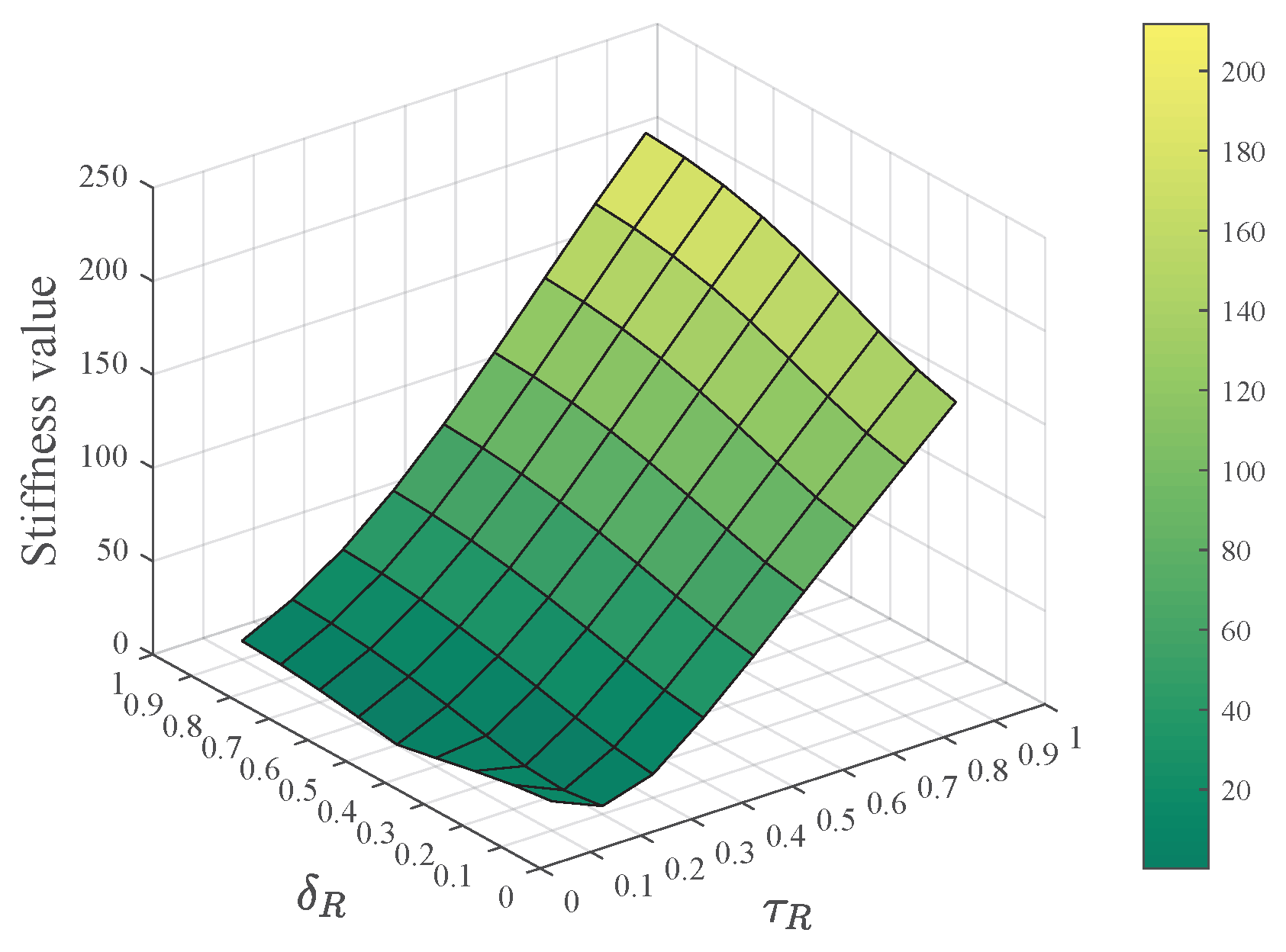
6.1. Stiffness Evaluation Metrics
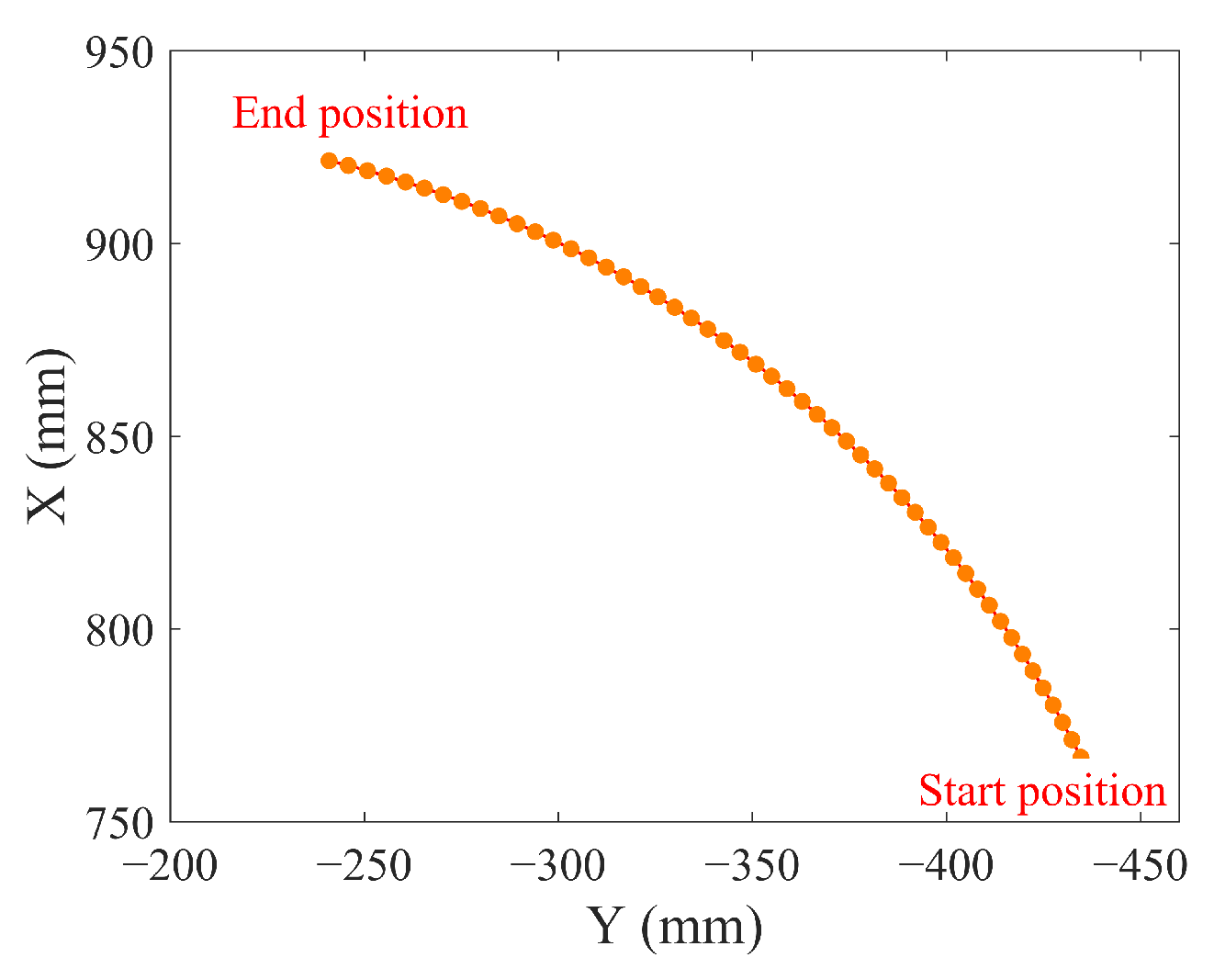
6.2. Configuration Optimization
6.3. Cable Tension Optimization
6.4. Combined Optimization of Configuration and Cable Tension
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| CDRM | Cable-Driven Redundant Manipulator |
| DOF | Degree of Freedom |
| DE | Differential Evolution |
| GA | Genetic Algorithms |
| PSO | Particle Swarm Optimization |
| GPM | Gradient Projection Method |
| RSR | Range Span Ratio |
Appendix A. Kinetostatic Model
- (1)
- Determine the Unit Screws of Twists and Reciprocal Wrenches
- (2)
- Calculate the passive joint torques
- (3)
- Calculate the active joint torques
- (4)
- Determine the Static Equilibrium Equation
References
- Li, W.S.; Huang, X.; Yan, L.; Cheng, H.Y.; Liang, B.; Xu, W.F. Force Sensing and Compliance Control for a Cable-Driven Redundant Manipulator. IEEE-ASME Trans. Mechatron. 2024, 29, 777–788. [Google Scholar] [CrossRef]
- Xu, W.F.; Liu, T.L.; Li, Y.M. Kinematics, Dynamics, and Control of a Cable-Driven Hyper-Redundant Manipulator. IEEE-ASME Trans. Mechatron. 2018, 23, 1693–1704. [Google Scholar] [CrossRef]
- Omisore, O.M.; Han, S.P.; Xiong, J.; Yang, J.; Li, Z.; Wang, L. A Review on Flexible Robotic Systems for Minimally Invasive Surgery. IEEE Trans. Syst. Man Cybern.-Syst. 2022, 52, 631–644. [Google Scholar] [CrossRef]
- Hong, W.Z.; Xie, L.; Liu, J.H.; Sun, Y.J.; Li, K.Y.; Wang, H.S. Development of a Novel Continuum Robotic System for Maxillary Sinus Surgery. IEEE-ASME Trans. Mechatron. 2018, 23, 1226–1237. [Google Scholar] [CrossRef]
- Seyfi, N.S.; Khalaji, A.K. Robust control of a cable-driven rehabilitation robot for lower and upper limbs. ISA Trans. 2022, 125, 268–289. [Google Scholar] [CrossRef] [PubMed]
- Mao, Y.; Agrawal, S.K. Design of a cable-driven arm exoskeleton (carex) for neural rehabilitation. IEEE Trans. Robot. 2012, 28, 922–931. [Google Scholar] [CrossRef]
- Lou, Y.N.; Di, S.C. Design of a cable-driven auto-charging robot for electric vehicles. IEEE Access 2020, 8, 15640–15655. [Google Scholar] [CrossRef]
- Wang, M.F.; Dong, X.; Ba, W.M.; Mohammad, A.; Axinte, D.; Norton, A. Design, modelling and validation of a novel extra slender continuum robot for in-situ inspection and repair in aeroengine. Robot. Comput.-Integr. Manuf. 2021, 67, 102054. [Google Scholar] [CrossRef]
- Endo, G.; Horigome, A.; Palmer, D.; Takata, A. Super dragon: A 10-m-long-coupled tendon-driven articulated manipulator. IEEE Robot. Autom. Lett. 2019, 4, 934–941. [Google Scholar] [CrossRef]
- Pang, S.X.; Shang, W.W.; Dai, S.Q.; Deng, J.; Zhang, F.; Zhang, B.; Cong, S. Stiffness optimization of cable-driven humanoid manipulators. IEEE/ASME Trans. Mechatron. 2024, 29, 4168–4178. [Google Scholar] [CrossRef]
- Lang, G.D.; Gao, Y.S.; Luo, Z.W.; Liang, G.L.; Zhu, Y.H.; Zhao, J. Kinematic analysis for the spatial interlocking 3-uu mechanism with the wide range of motion. IEEE Robot. Autom. Lett. 2024, 9, 3926–3931. [Google Scholar] [CrossRef]
- Xu, H.J.; Meng, D.S.; Li, Y.N.; Wang, X.Q.; Liang, B. A novel cable-driven joint module for space manipulators: Design, modeling, and characterization. IEEE/ASME Trans. Mechatron. 2024, 29, 2044–2055. [Google Scholar] [CrossRef]
- Gao, Y.M.; Lv, G.K.; Zhao, S.; Ding, N.; Mu, Z.G. An analytical variable-stiffness method for the fine control of concentric cable-driven manipulators. IEEE Trans. Syst. Man Cybern. Syst. 2024, 54, 5434–5443. [Google Scholar] [CrossRef]
- Sanjeevi, N.S.S.; Vashista, V. Stiffness modulation of a cable-driven leg exoskeleton for effective human-robot interaction. Robotica 2021, 39, 2172–2192. [Google Scholar] [CrossRef]
- Ramadoss, V.; Sagar, K.; Ikbal, M.S.; Zlatanov, D.; Zoppi, M. Modeling and stiffness evaluation of tendon-driven robot for collaborative human-robot interaction. In Proceedings of the 2021 IEEE International Conference on Intelligence and Safety for Robotics (IEEE-ISR), Electr Network, Nagoya, Japan, 4–6 March 2021; pp. 233–238. [Google Scholar]
- Sanjeevi, N.S.S.; Vashista, V. Stiffness modulation of a cable-driven serial-chain manipulator via cable routing alteration. J. Mech. Robot. 2023, 15, 021009. [Google Scholar] [CrossRef]
- Yang, K.S.; Yang, G.L.; Chen, S.L.; Wang, Y.; Zhang, C.; Fang, Z.J.; Zheng, T.J.; Wang, C.C. Study on stiffness-oriented cable tension distribution for a symmetrical cable-driven mechanism. Symmetry 2019, 11, 1158. [Google Scholar] [CrossRef]
- Yang, K.S.; Yang, G.L.; Wang, Y.; Zhang, C.; Chen, S.L. Stiffness-oriented cable tension distribution algorithm for a 3-dof cable-driven variable-stiffness module. In Proceedings of the 2017 IEEE ASME International Conference on Advanced Intelligent Mechatronics (AIM), Munich, Germany, 3–7 July 2017; pp. 454–459. [Google Scholar]
- Lim, W.B.; Yeo, S.H.; Yang, G.L. Optimization of tension distribution for cable-driven manipulators using tension-level index. IEEE/ASME Trans. Mechatron. 2014, 19, 676–683. [Google Scholar] [CrossRef]
- Abdolshah, S.; Zanotto, D.; Rosati, G.; Agrawal, S.K. Optimizing stiffness and dexterity of planar adaptive cable-driven parallel robots. J. Mech. Robot. 2017, 9, 031004. [Google Scholar] [CrossRef]
- Orekhov, A.L.; Simaan, N. Directional stiffness modulation of parallel robots with kinematic redundancy and variable stiffness joints. J. Mech. Robot. 2019, 11, 051003. [Google Scholar] [CrossRef]
- Chen, S.T.; Zhou, G.Z.; Li, D.C.; Song, Z.A.; Chen, F.F. Soft robotic joints with anisotropic stiffness by multiobjective topology optimization. IEEE/ASME Trans. Mechatron. 2024, 29, 1064–1075. [Google Scholar] [CrossRef]
- Hong, W.Z.; Feng, F.; Xie, L.; Yang, G.Z. A two-segment continuum robot with piecewise stiffness for maxillary sinus surgery and its decoupling method. IEEE/ASME Trans. Mechatron. 2022, 27, 4440–4450. [Google Scholar] [CrossRef]
- Yeo, S.H.; Yang, G.; Lim, W.B. Design and analysis of cable-driven manipulators with variable stiffness. Mech. Mach. Theory 2013, 69, 230–244. [Google Scholar] [CrossRef]
- Liu, T.L.; Xu, W.F.; Yang, T.W.; Li, Y.M. A hybrid active and passive cable-driven segmented redundant manipulator: Design, kinematics, and planning. IEEE/ASME Trans. Mechatron. 2021, 26, 930–942. [Google Scholar] [CrossRef]
- Zhao, B.; Zeng, L.Y.; Wu, Z.H.; Xu, K. A continuum manipulator for continuously variable stiffness and its stiffness control formulation. Mech. Mach. Theory 2020, 149, 103746. [Google Scholar] [CrossRef]
- Ma, N.; Yu, J.J.; Dong, X.; Axinte, D. Design and stiffness analysis of a class of 2-dof tendon driven parallel kinematics mechanism. Mech. Mach. Theory 2018, 129, 202–217. [Google Scholar] [CrossRef]
- Pang, S.X.; Shang, W.W.; Zhang, F.; Zhang, B.; Cong, S. Design and stiffness analysis of a novel 7-dof cable-driven manipulator. IEEE Robot. Autom. Lett. 2022, 7, 2811–2818. [Google Scholar] [CrossRef]
- Huang, J.L.; Clement, R.; Sun, Z.H.; Wang, J.Z.; Zhang, W.J. Global stiffness and natural frequency analysis of distributed compliant mechanisms with embedded actuators with a general-purpose finite element system. Int. J. Adv. Manuf. Technol. 2013, 65, 1111–1124. [Google Scholar] [CrossRef]
- Alamdari, A.; Haghighi, R.; Krovi, V. Stiffness modulation in an elastic articulated-cable leg-orthosis emulator: Theory and experiment. IEEE Trans. Robot. 2018, 34, 1266–1279. [Google Scholar] [CrossRef]
- Zhang, L.Y.; Gao, Y.M.; Mu, Z.G.; Yan, L.; Li, Z.X.; Gao, M.W. A variable-stiffness planning method considering both the overall configuration and cable tension for hyper-redundant manipulators. IEEE-ASME Trans. Mechatron. 2024, 29, 659–667. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Liang, J.; Lin, H.Y.; Yue, C.T.; Yu, K.J.; Guo, Y.; Qiao, K.J. Multiobjective differential evolution with speciation for constrained multimodal multiobjective optimization. IEEE Trans. Evol. Comput. 2023, 27, 1115–1129. [Google Scholar] [CrossRef]
- Cai, Z.H.; Gao, S.C.; Yang, X.; Zhou, M.C. Multiselection-based differential evolution. IEEE Trans. Syst. Man Cybern.-Syst. 2024, 54, 7318–7330. [Google Scholar] [CrossRef]
- Tsafarakis, S.; Zervoudakis, K.; Andronikidis, A.; Altsitsiadis, E. Fuzzy self-tuning differential evolution for optimal product line design. Eur. J. Oper. Res. 2020, 287, 1161–1169. [Google Scholar] [CrossRef]
- Hielscher, T.; Hadigheh, S.A. Optimizing memory-efficient multimodal networks for image classification using differential evolution. Appl. Soft Comput. 2025, 171, 112714. [Google Scholar] [CrossRef]
- Dinh, Q.V.; Dinh, V.N.; Leahy, P.G. A differential evolution model for optimising the size and cost of electrolysers coupled with offshore wind farms. Int. J. Hydrogen Energy 2025, 124, 318–330. [Google Scholar] [CrossRef]
- Haro, E.H.; Oliva, D.; Beltrán, L.A.; Casas-Ordaz, A. Enhanced differential evolution through chaotic and euclidean models for solving flexible process planning. Knowl.-Based Syst. 2025, 314, 113189. [Google Scholar] [CrossRef]
- Ji, S.T.; Karlovsek, J. Optimized differential evolution algorithm for solving dem material calibration problem. Eng. Comput. 2023, 39, 2001–2016. [Google Scholar] [CrossRef]
- Das, S.; Mullick, S.S.; Suganthan, P.N. Recent advances in differential evolution—An updated survey. Swarm Evol. Comput. 2016, 27, 1–30. [Google Scholar] [CrossRef]
- Das, S.; Abraham, A.; Chakraborty, U.K.; Konar, A. Differential evolution using a neighborhood-based mutation operator. IEEE Trans. Evol. Comput. 2009, 13, 526–553. [Google Scholar] [CrossRef]
- Wang, X.; Yang, D.S.; Dolly, D.R.J.; Chen, S.; Alassafi, M.O.; Alsaadi, F.E. Opposition-based differential evolution for synchronized control of multi-agent systems with uncertain nonlinear dynamics. Appl. Soft Comput. 2024, 150, 111044. [Google Scholar] [CrossRef]
- Chin, V.J.; Salam, Z.; Ishaque, K. An accurate and fast computational algorithm for the two-diode model of PV module based on a hybrid method). IEEE Trans. Ind. Electron. 2017, 64, 6212–6222. [Google Scholar] [CrossRef]
- Xie, Z.T.; Jin, L.; Luo, X.; Sun, Z.B.; Liu, M. Rnn for repetitive motion generation of redundant robot manipulators: An orthogonal projection-based scheme. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 615–628. [Google Scholar] [CrossRef] [PubMed]
- Cheng, M.; Li, L.A.; Ding, R.Q.; Xu, B.; Jiang, P.; Mattila, J. Prioritized multitask flow optimization of redundant hydraulic manipulator. IEEE-ASME Trans. Mechatron. 2024, 29, 487–498. [Google Scholar] [CrossRef]
- Mustafa, S.K.; Agrawal, S.K. On the force-closure analysis of n-DOF cable-driven open chains based on reciprocal screw theory. IEEE Trans. Robot. 2012, 28, 22–31. [Google Scholar] [CrossRef]
- Liang, Z.; Jiang, B.; Quan, P.K.; Lin, H.Y.; Lou, Y.N.; Di, S.C. Force-closure analysis of multilink cable-driven redundant manipulators considering cable coupling and friction effects. IEEE-ASME Trans. Mechatron. 2024, 29, 3324–3335. [Google Scholar] [CrossRef]
- Xi, F.F.; Zhang, D.; Mechefske, C.M.; Lang, S.Y.T. Global kinetostatic modelling of tripod-based parallel kinematic machine. Mech. Mach. Theory 2004, 39, 357–377. [Google Scholar] [CrossRef]
- Ceccarelli, M.; Carbone, G. A stiffness analysis for capaman (cassinoparallel manipulator). Mech. Mach. Theory 2002, 37, 427–439. [Google Scholar] [CrossRef]

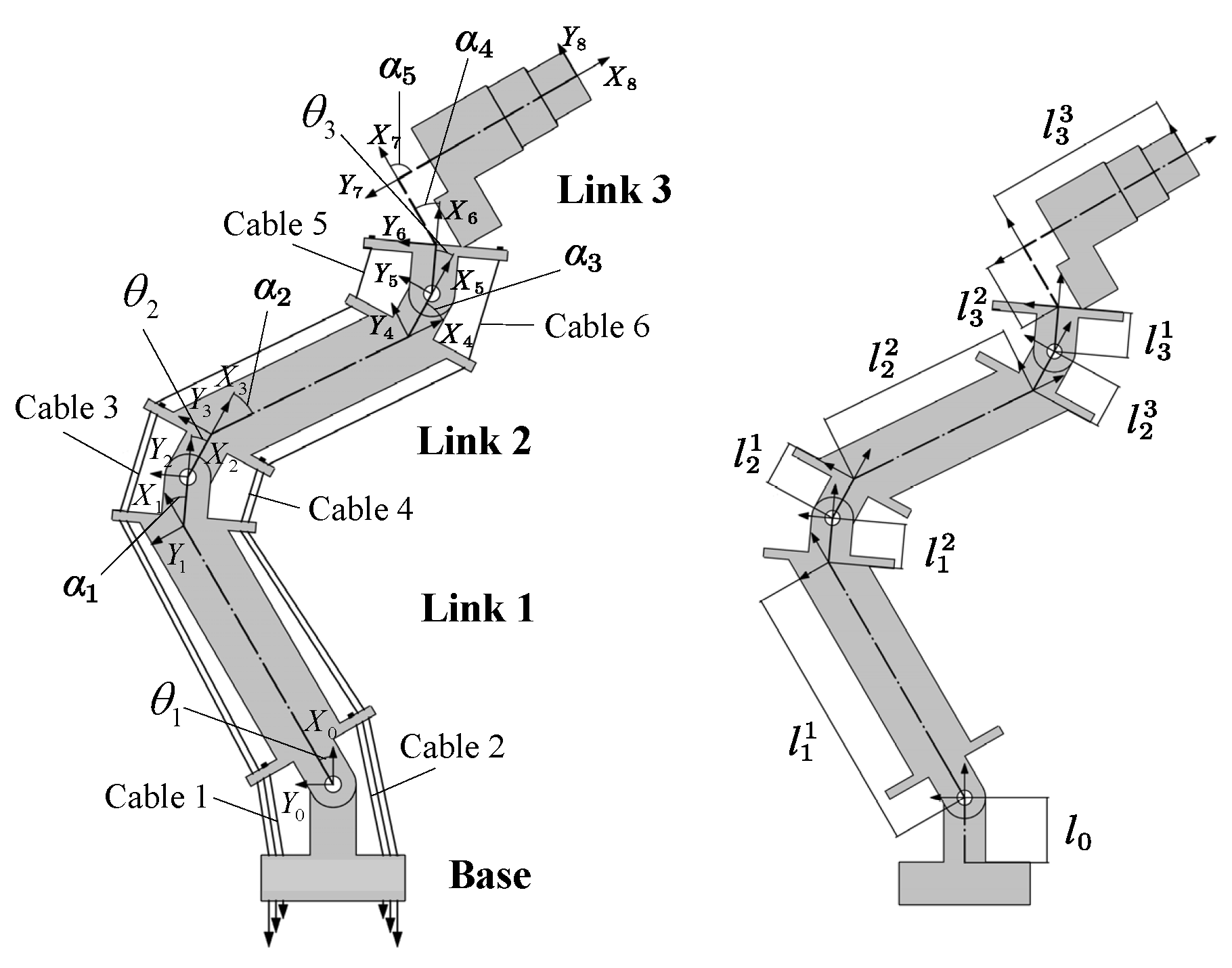

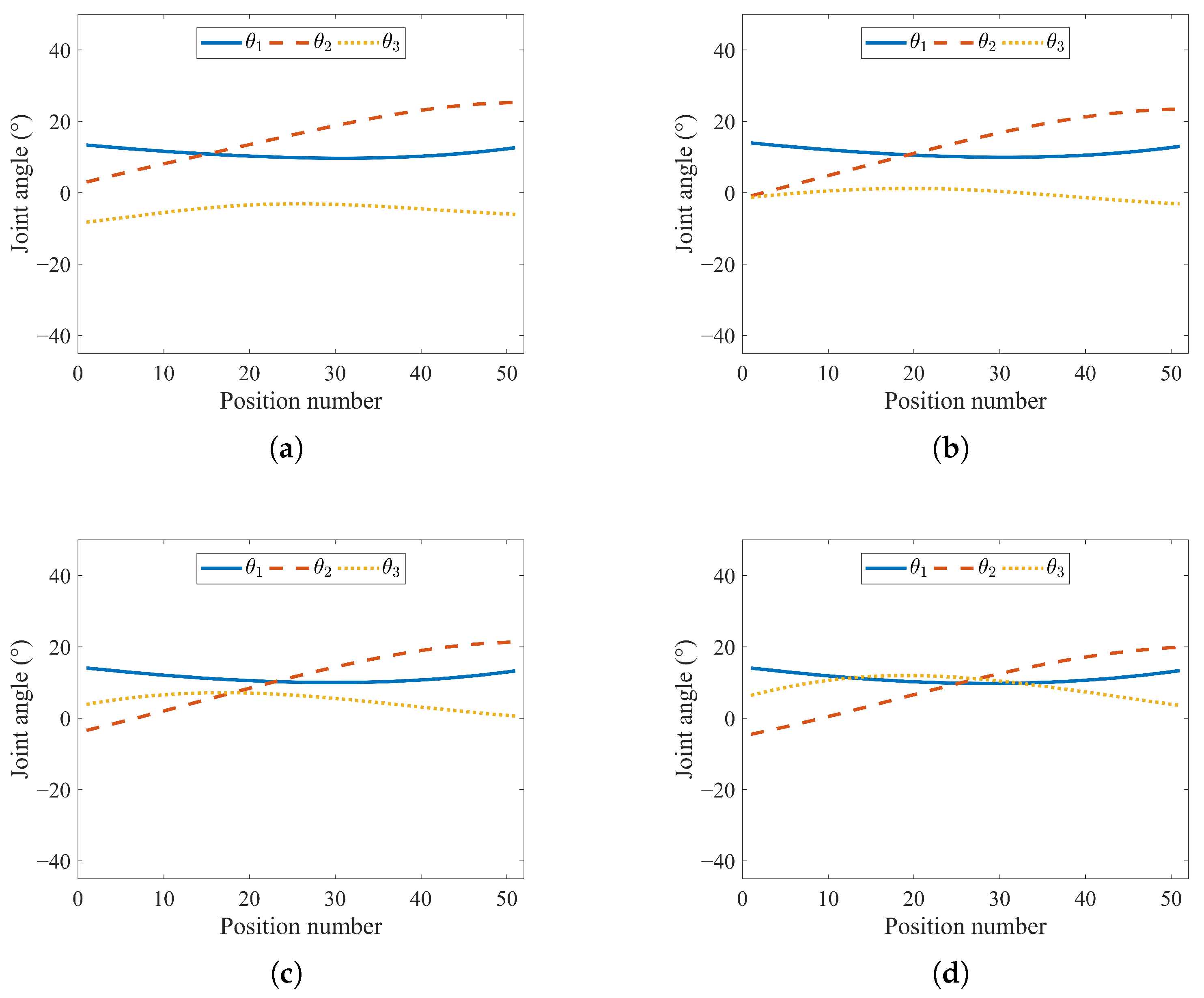
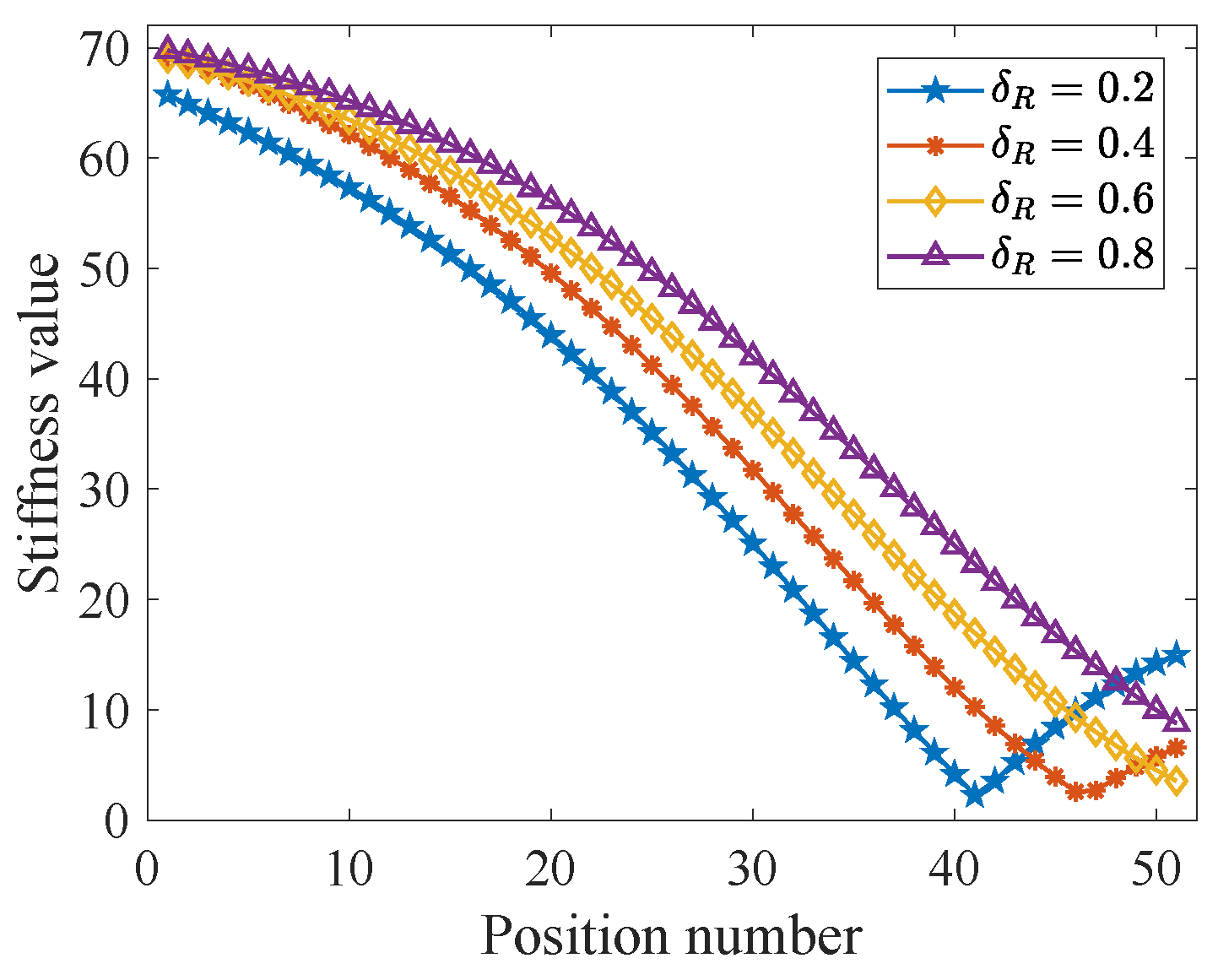
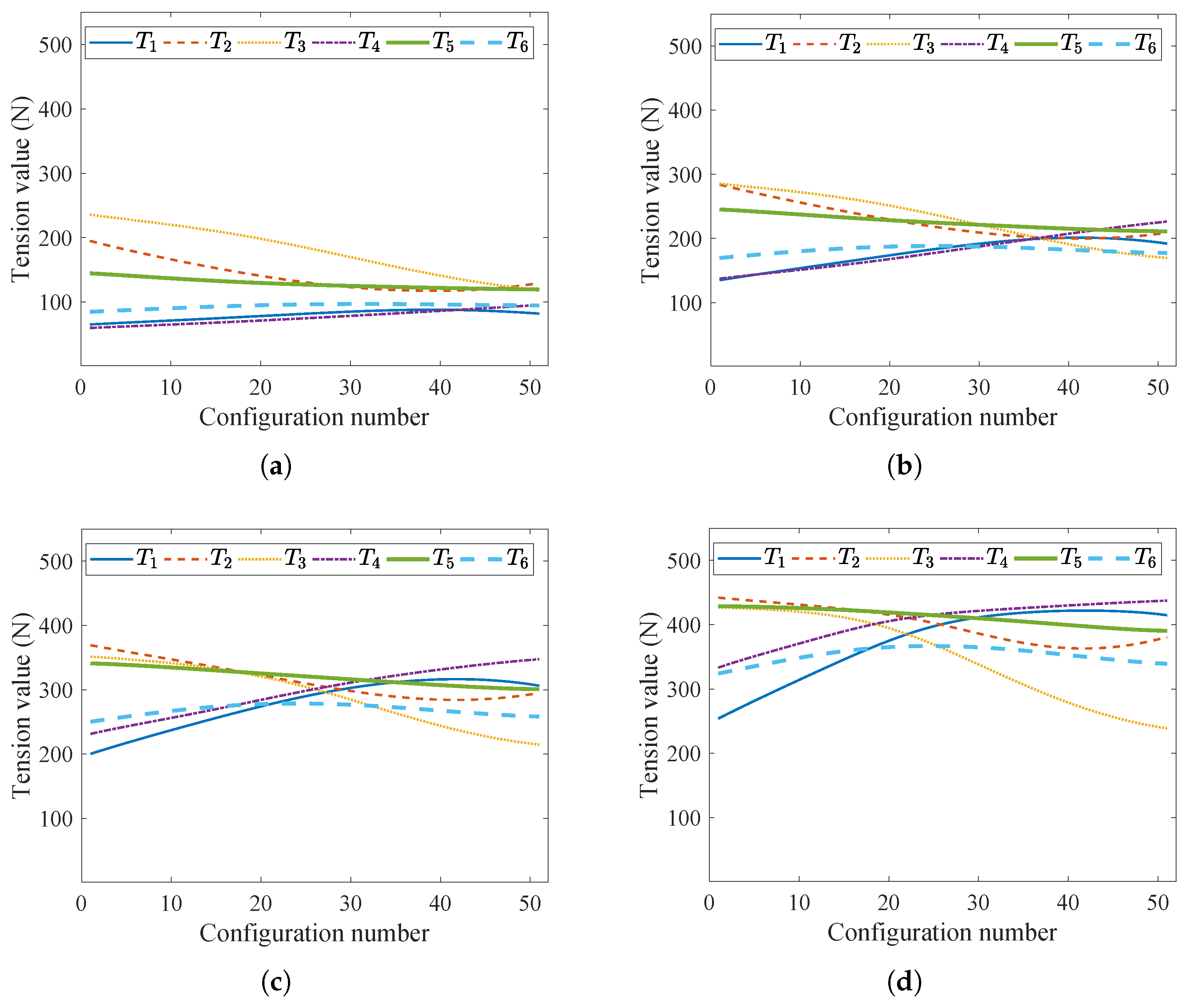
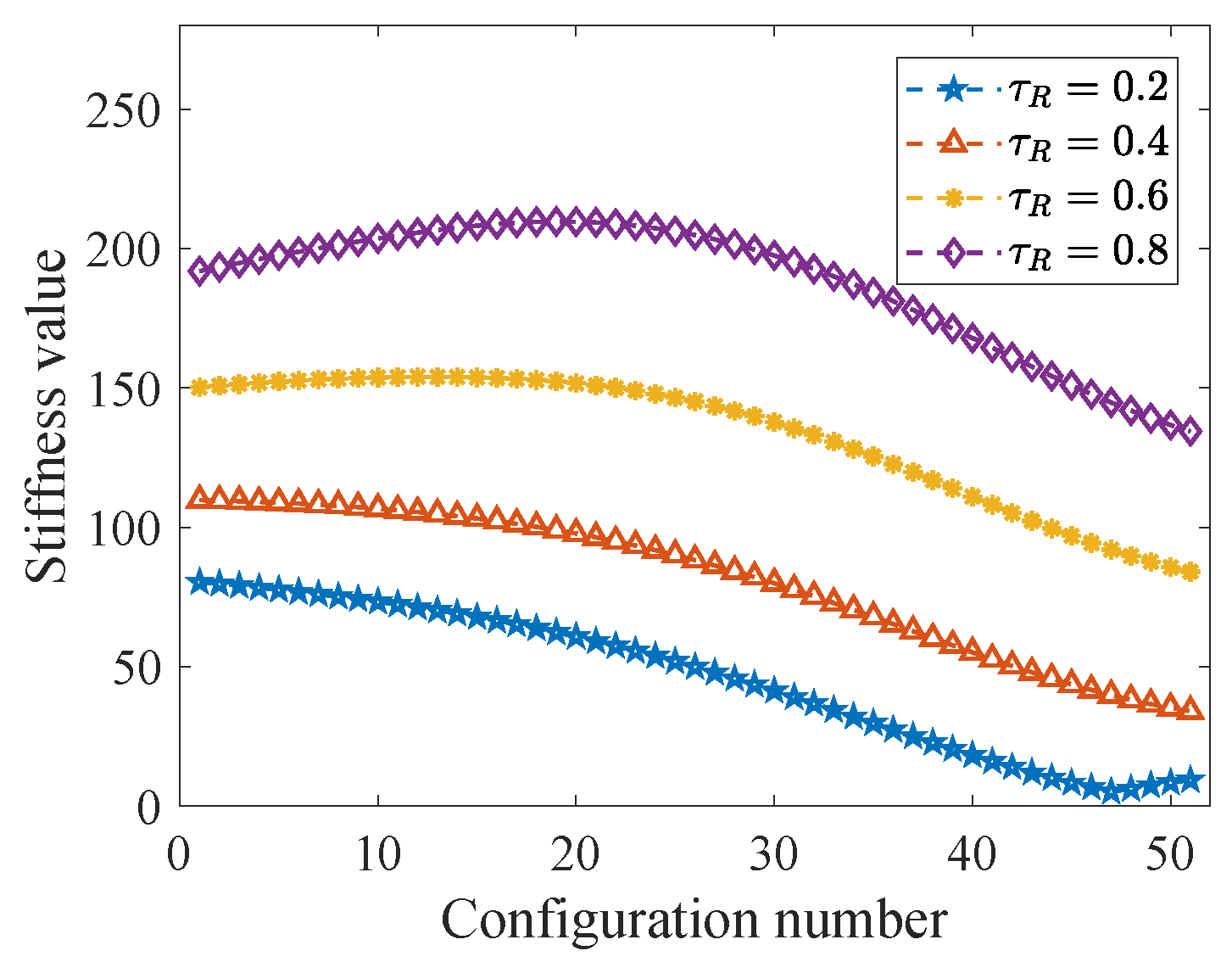
| Symbol | Value | Symbol | Value |
|---|---|---|---|
| 75 mm | |||
| 301 mm | |||
| 55 mm | |||
| 55 mm | |||
| 257 mm | |||
| 55 mm | kg | ||
| 55 mm | kg | ||
| 85.26 mm | kg | ||
| 231.31 mm |
| Position | Configuration Opt. | Cable Tension Opt. | Combined Opt. |
|---|---|---|---|
| 1 | |||
| 5 | |||
| 10 | |||
| 15 | |||
| 20 | |||
| 25 | |||
| 30 | |||
| 35 | |||
| 40 | |||
| 45 | |||
| 50 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, Z.; Quan, P.; Di, S. Stiffness Regulation of Cable-Driven Redundant Manipulators Through Combined Optimization of Configuration and Cable Tension. Mathematics 2025, 13, 1714. https://doi.org/10.3390/math13111714
Liang Z, Quan P, Di S. Stiffness Regulation of Cable-Driven Redundant Manipulators Through Combined Optimization of Configuration and Cable Tension. Mathematics. 2025; 13(11):1714. https://doi.org/10.3390/math13111714
Chicago/Turabian StyleLiang, Zhuo, Pengkun Quan, and Shichun Di. 2025. "Stiffness Regulation of Cable-Driven Redundant Manipulators Through Combined Optimization of Configuration and Cable Tension" Mathematics 13, no. 11: 1714. https://doi.org/10.3390/math13111714
APA StyleLiang, Z., Quan, P., & Di, S. (2025). Stiffness Regulation of Cable-Driven Redundant Manipulators Through Combined Optimization of Configuration and Cable Tension. Mathematics, 13(11), 1714. https://doi.org/10.3390/math13111714





