Spin-Wheel: A Fast and Secure Chaotic Encryption System with Data Integrity Detection

Abstract

The increasing demand for real-time multimedia communications has driven the need for highly secure and computationally efficient encryption schemes. In this work, we present a novel chaos-based encryption system that provides remarkable levels of security and performance. It leverages the benefits of applying fast-to-evaluate chaotic maps, along with a 2-Dimensional Look-Up Table approach (2D-LUT), and simple but powerful periodic perturbations. The foundation of our encryption system is a Pseudo-Random Number Generator (PRNG) that consists of a fully connected random graph with M vertices representing chaotic maps that populate the 2D-LUT. In every iteration of the system, one of the M chaotic maps in the graph and the corresponding trajectories are randomly selected from the 2D-LUT using an emulated spin-wheel picker game. This approach exacerbates the complexity in the event of an attack, since the trajectories may come from the same or totally different maps in a non-sequential time order. We additionally perform two levels of perturbation, at the map and trajectory level. The first perturbation (map level) produces new trajectories that are retrieved from the 2D-LUT in non-sequential order and with different initial conditions. The second perturbation applies a p-point crossover scheme to combine a pair of trajectories retrieved from the 2D-LUT and used in the ciphering process, providing higher levels of security. As a final process in our methodology, we implemented a simple packet-based data integrity scheme that detects with high probability if the received information has been modified (for example, by a man-in-the-middle attack). Our results show that our proposed encryption scheme is robust to common cryptanalysis attacks, providing high levels of security and confidentiality while supporting high processing speeds on the order of gigabits per second. To the best of our knowledge, our chaotic cipher implementation is the fastest reported in the literature.

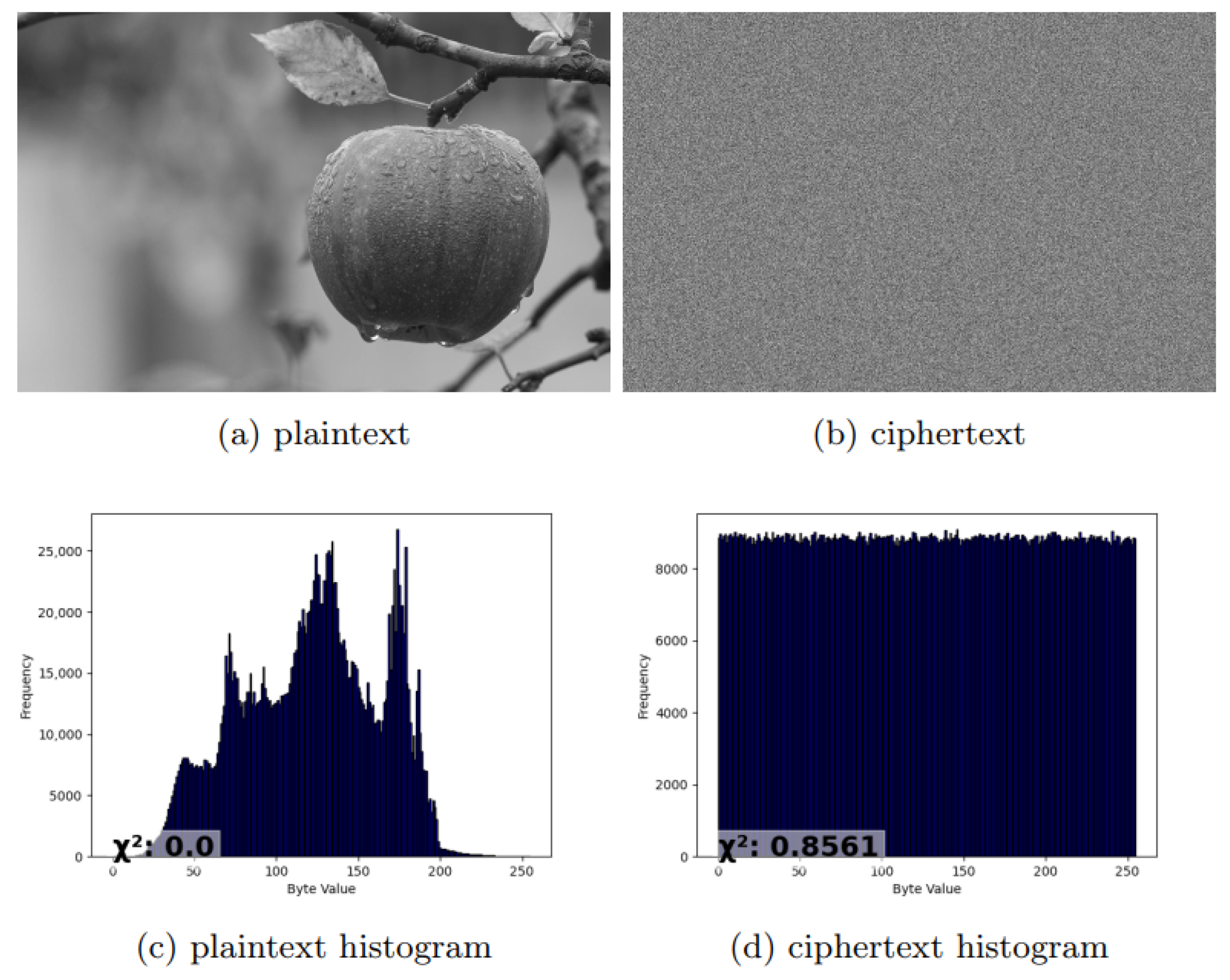
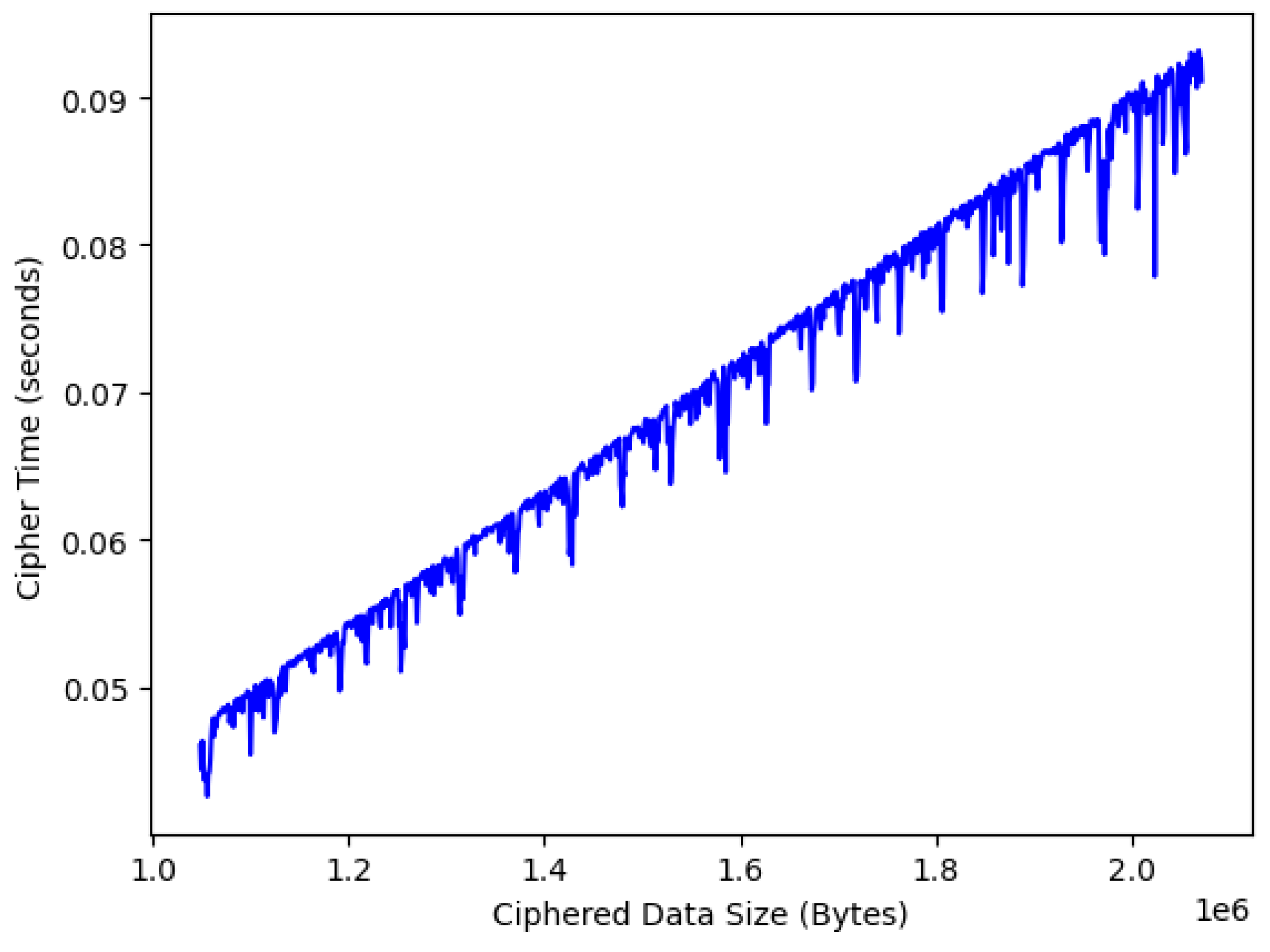
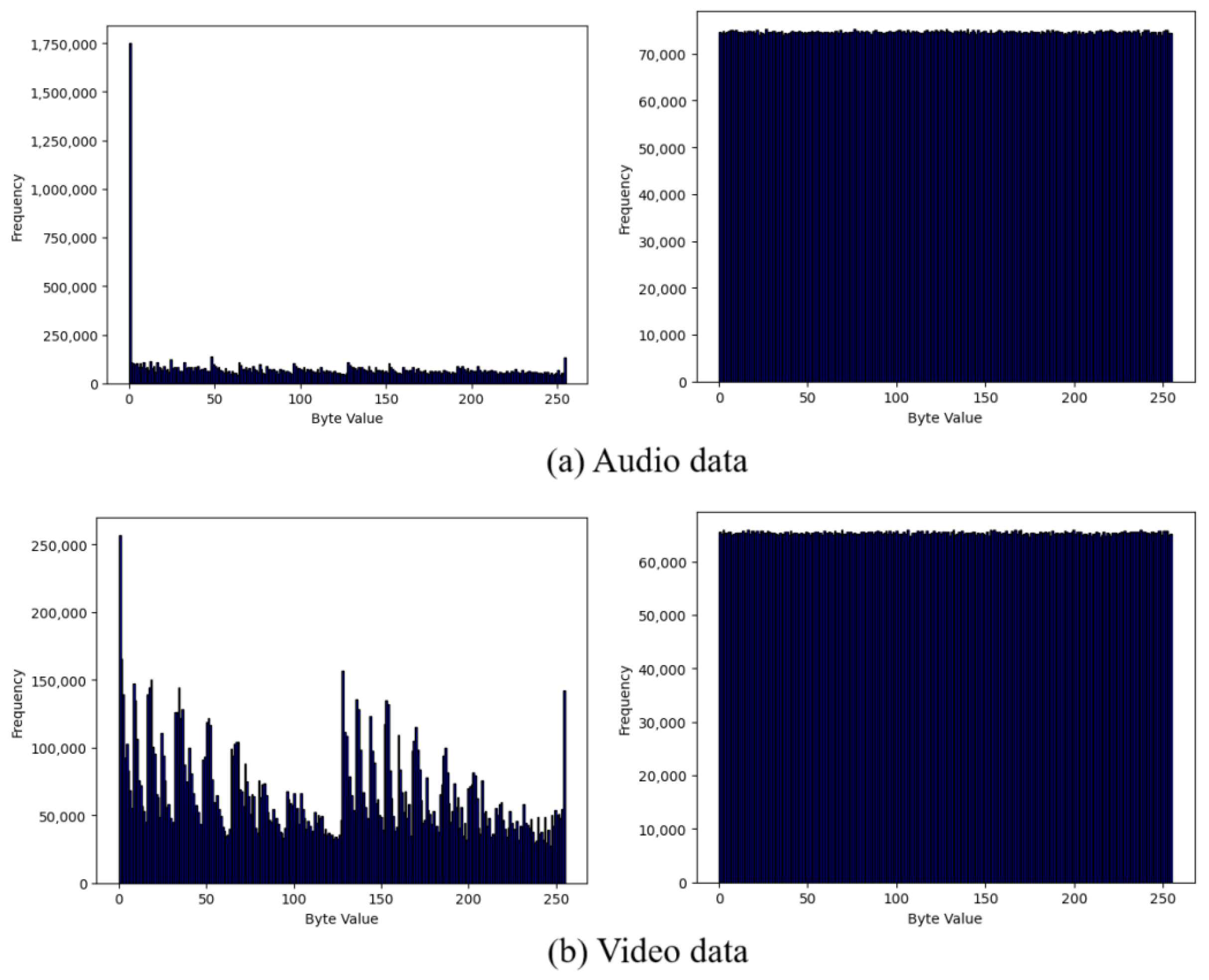
1. Introduction

Video streaming (on-demand and real-time) has revolutionized our communication culture in all aspects of our lives (social, healthcare, entertainment, business, education, etc.), accounting for 65% of total Internet traffic [1], and it is projected to increase to 82% during 2025 [2]. Among video streaming applications, live or real-time streaming is one of the most popular media transmitted over the Internet (27% more views per video compared to video on demand [3]), allowing for virtual interactions among geographically separated individuals. This increasing demand in video communications has consequently driven the need for users’ right to privacy and consequently propelled the development of highly secure and computationally efficient encryption schemes.

Although the security of current encryption standards is paramount, good performance and low power consumption are equally important aspects that chaos-based encryption schemes can offer [4,5,6]. Previous studies [7,8] have shown that chaos-based block ciphers can consume 150% less energy and be 200% faster than current implementations of the Advanced Encryption Standard (AES) [9] on various platforms, such as desktops, laptops, and smartphones. These promising results open up new possibilities for the development of competitive chaotic encryption schemes on very different platforms, ranging from high-end workstations to mobile devices, including low-performance Internet of Things (IoT) technologies.

However, Chaos-Based Cryptography (CBC) still faces some major challenges, including security, computational complexity, and floating-point precision. The security of CBC schemes depends on the appropriate choice of the underlying chaotic dynamical systems. These systems must have good dynamical properties, such as long cycles, high sensitivity to initial conditions, and an appropriate (uniform) probability distribution. The computational complexity of CBC schemes must be efficient in meeting the demands of modern multimedia applications, especially on power and energy-constrained mobile devices. Lastly, most CBC schemes require floating-point precision calculations, which can introduce rounding errors and affect the probability distribution of generated trajectories, introducing vulnerabilities to the system [10,11]. Despite these challenges, various techniques have been proposed to improve the security and efficiency of CBC schemes, focusing on extending the cycle length at the expense of increasing their computational complexity. Among the most important techniques for this work are multiple maps and perturbation schemes [7,12,13,14,15,16,17], High-Dimensional Chaotic Systems (HDCSs) [18,19,20,21], and LookUp Table (LUT) approaches [22,23]. In particular, the use of LUTs, initially controversial [24,25], is now an excellent solution for robust chaos-based cryptography, as described in Section 2.

The idea behind multiple chaotic maps is to increase both the cycle length and the robustness of the overall system. In this way, an attacker must face the task of breaking a network of chaotic maps rather than a single map. When combined with periodic perturbations, the level of security increases considerably. We are convinced that both the cryptographic strategy itself and the use of multiple low-dimensional chaotic maps should work together to ensure the security of the system. Moreover, the vulnerabilities of chaotic maps should be independent of the overall scheme itself. That is, the scheme should have the ability to overcome these vulnerabilities when they arise.

In [26], a simple Coupled Map Lattice (CML) is proposed for color image encryption, consisting of interacting elements (chaotic maps) through a coupling parameter. Every trajectory produced by the CML is influenced by all maps, providing greater security than single map schemes. A similar but more complex and robust image encryption scheme is proposed in [27]. The authors mixed different chaotic maps (Logistic, Sine and Tent maps) into the CML and applied a Z-scrambling method at a bit level to increase the security of the encryption scheme. A CML variant is presented in [7], in which the N interacting maps are iterated into smaller subgroups rather than collectively. A moving window of size $1<w<N$ is defined, and only the maps falling within w are sequentially iterated a random number of times. The window moves periodically along the CML, grouping different maps in such a way that, in the end, all maps are equally iterated. A three-level perturbation scheme is also proposed [7], which modifies the map’s variables, parameters, and the initial key to increase the cycle length of the CML.

Although HDCS offer greater complexity, this often results in a significant decrease in performance [28,29], resulting in slower schemes. Excess complexity is the main cause of speed limitations in many chaos-based schemes [28,30,31]. In [32], the authors propose a multi-channel image encryption algorithm that makes use of pixel reorganization and hyperchaotic maps. Their algorithm employs two hyperchaotic maps to jointly generate chaotic sequences to obtain better randomness. Then, two rounds of scrambling and diffusion operations are applied and coupled with one round of substitution operations to the high 4-bit components of the image. For the 4-bit low components, one round of substitution and diffusion operations is conducted. In [33], an encryption algorithm is proposed, using a new Pseudo-Random Number Generator (PRNG) based on mixing three-dimensional variables of a cat chaotic map. A uniformly distributed chaotic sequence by a logistic map is also used during a pixel mixing step. The core of the algorithm is to use the sequence generated by the PRNG to achieve the disruption and diffusion of the image pixels and produce an effect of obfuscation and encryption of the image content. Hyperchaos and biological systems such as DNA sequence merging have been proposed for robust image encryption [23,34,35,36,37]. The authors in [34] transform the input image into a binary matrix, then carry out DNA encoding, and they perform the DNA sequence complement operation using two logistic maps. olor image encryption based on the DNA and double chaos system is proposed [35]. After the input image is scrambled, three sets of chaotic sequences are generated using Lorenz chaotic mapping and fourth-order Rossler hyperchaotic to transform the chaotic component images and chaotic sequences into DNA sequences. They applied the DNA coding rules and three DNA operation rules for the final image encryption.

The use of chaotic maps along with dynamic LUT models has been shown to generate fast and secure encryption systems with an excellent avalanche effect (ciphertexts from slightly different plaintexts differ significantly), as described in [38]. An LUT can be seen as a transformation function in which the input value produces an index to be used in the encryption process. The beginning of LUT models can be traced back to Baptista (1998) [39], who proposed an iterative chaotic encryption scheme where the phase space is divided into M equal-sized subintervals corresponding to the number of elements in the plaintext alphabet. Each plaintext alphabet is assigned to one subinterval and encrypted as the number of iterations on the logistic map needed to visit the corresponding subinterval departing from a private initial condition. Baptista´s scheme and variants stayed in the eye of the hurricane for more than 10 years due to security flaws and low speed performance [40]. A different and improved LUT approach is proposed in [38], in which the M subintervals are represented by indices pointing to chaotic trajectories stored (initially) in sequential order. Since the indices are randomly chosen, the encryption process is performed using non-sequential trajectories that may be far apart (in time) from each other, increasing the security and speed of the system.

Our goal is to develop a system that is not only secure but also highly efficient and adaptable to the needs of modern real-time multimedia applications. In contrast to previously mentioned approaches that use high-dimensional or multiple chaotic maps sequentially iterated, in this research, we propose a simpler and more efficient structure based on the concept of a random graph of chaotic maps (representing the vertices), wherein maps are randomly selected via a spin-wheel-like procedure. This random selection, combined with a new two-dimensional lookup table of trajectories and random perturbations, allows for a higher degree of diffusion and confusion in the ciphertext, increasing resistance to cryptanalysis attacks. Finally, a fast and robust scheme is incorporated after the encryption process to establish the integrity of the encrypted plaintext at the recipient’s end [41]. The overall goal of this research is to develop an encryption scheme that provides an optimal balance between security and performance, focusing on applications that require a high level of confidentiality and low latency.

2. Proposed Scheme

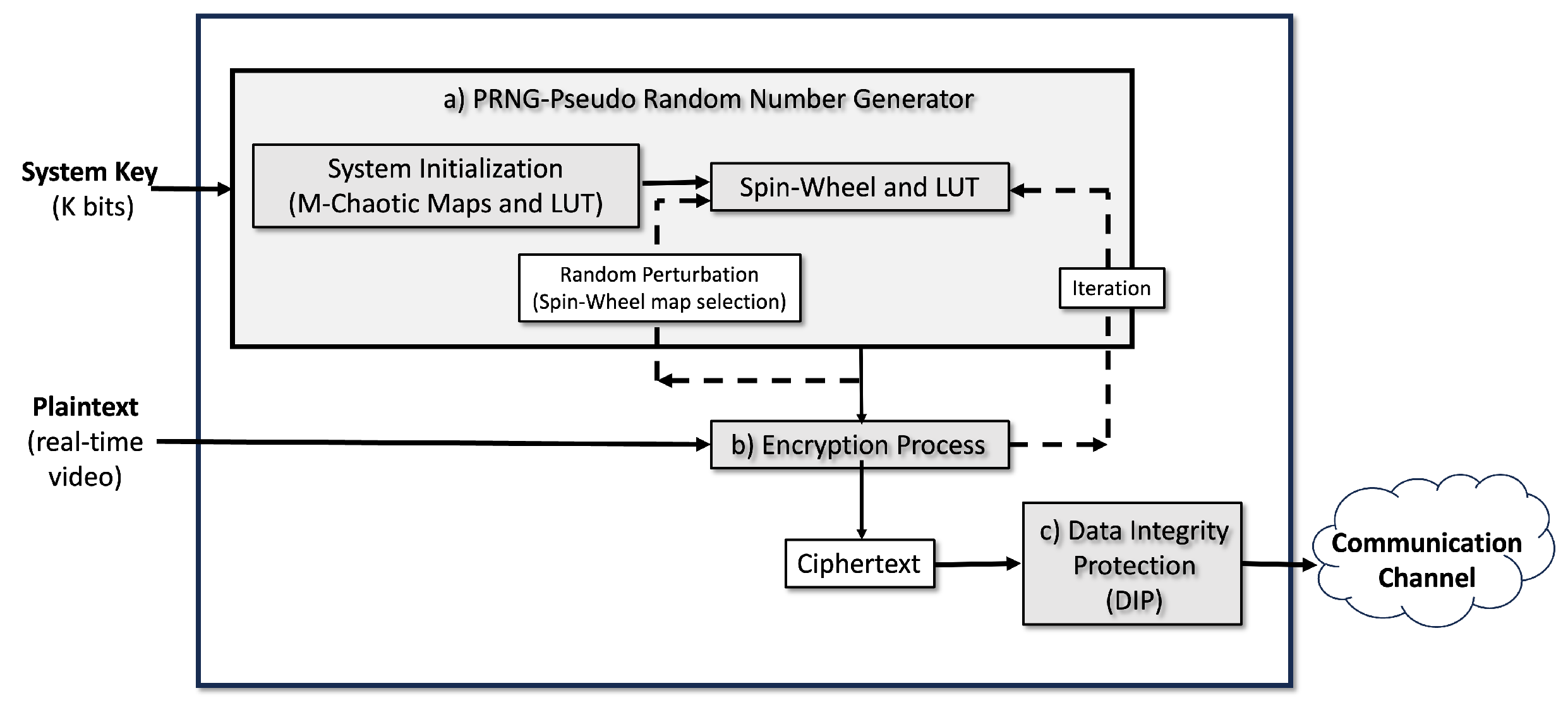
Our proposed encryption algorithm can be applied to any type of multimedia data, including text, audio, images, and video, in a compressed or uncompressed domain. It is independent of the compression method and can be applied as full or selective encryption [4,37,42,43,44], depending on the level of security required by the application. Broadly speaking, our encryption system consists of three main modules (see Figure 1): (a) A Pseudo-Random Number Generator (PRNG), the core algorithm in the encryption process; (b) Encryption Process; and (c) Data Integrity Protection (DIP), a mechanism for detecting ciphertext manipulation or attacks during the communication process. Each module is described in detail in the following subsections.

2.1. Pseudo-Random Number Generator (PRNG)

Our PRGN is based on the concept of a random graph or random network of M chaotic maps and a 2-Dimensional LUT (2D-LUT) of size $NxM$ that stores N trajectories per map. Each map and corresponding trajectories are randomly selected on the basis of the Spin-Wheel Picker (SWP) game. The SWP generates two random indices, one for the selection of the chaotic map and the other for the corresponding map trajectory within the 2D-LUT. In this way, every system iteration generates random trajectories from different maps without a predefined temporal order (older trajectories may be randomly used before newer ones within the selected map), which increases the robustness of the system against various attacks such as brute-force, plaintext, ciphertext, etc. Each requested trajectory is replaced by a new one coming from the sequential iterative process of the corresponding selected map. Each component of the PRNG is described in detail in the following sub-sections.

2.1.1. Chaotic Map: Digitized Renyi Map

An important decision that must be made in any chaos-based encryption is the choice of the chaotic map (i.e., the core function of the system). Since our interest lies in developing a fast and highly secure encryption system, we choose a digitized version of the Renyi map [45], defined as follows:

$$x_k=\mathsf{\Phi }\left(x_{k-1}\right)=(\beta x_{k-1}+(x_{k-1}\gg n))mod{2}^{PR}$$

(1)

where $\mathsf{\Phi }$ is the Renyi map function, k is the iteration index, $\beta \in Z^{>0}$ and $1\le n\le 8$ are control parameters, $PR$ is the CPU bit-precision (32 or 64 bits), and $x_0\in Z^{>0}$ is the initial condition. $\mathsf{\Phi }$ is defined over the integer domain and generates trajectories with much higher speed than the corresponding chaotic maps with floating-point arithmetic. However, as a digitized chaotic map, it presents degraded dynamic properties caused by the limited precision of computers (see [15]). In consequence, its statistical properties and cycle length are severely degraded compared to their analog representation, resulting in trajectories with poor random behavior. Furthermore, the trajectories of the Renyi map follow a linear process (see Equation (1)), increasing until they exceed the computer precision and the wrap-around occurs. Having consecutive trajectories of this map significantly reduces the number of possible parameters, making it partially predictable to an attacker. Ideal chaotic behavior has been shown not to be necessary from the chosen map, as long as the proposed scheme provides the mechanisms or strategies to improve randomness, mitigate cycles, overcome fixed points, and generate a uniform distribution [38]. Our proposed scheme is intended to provide all the necessary protection to avoid exposing the identity of chaotic maps.

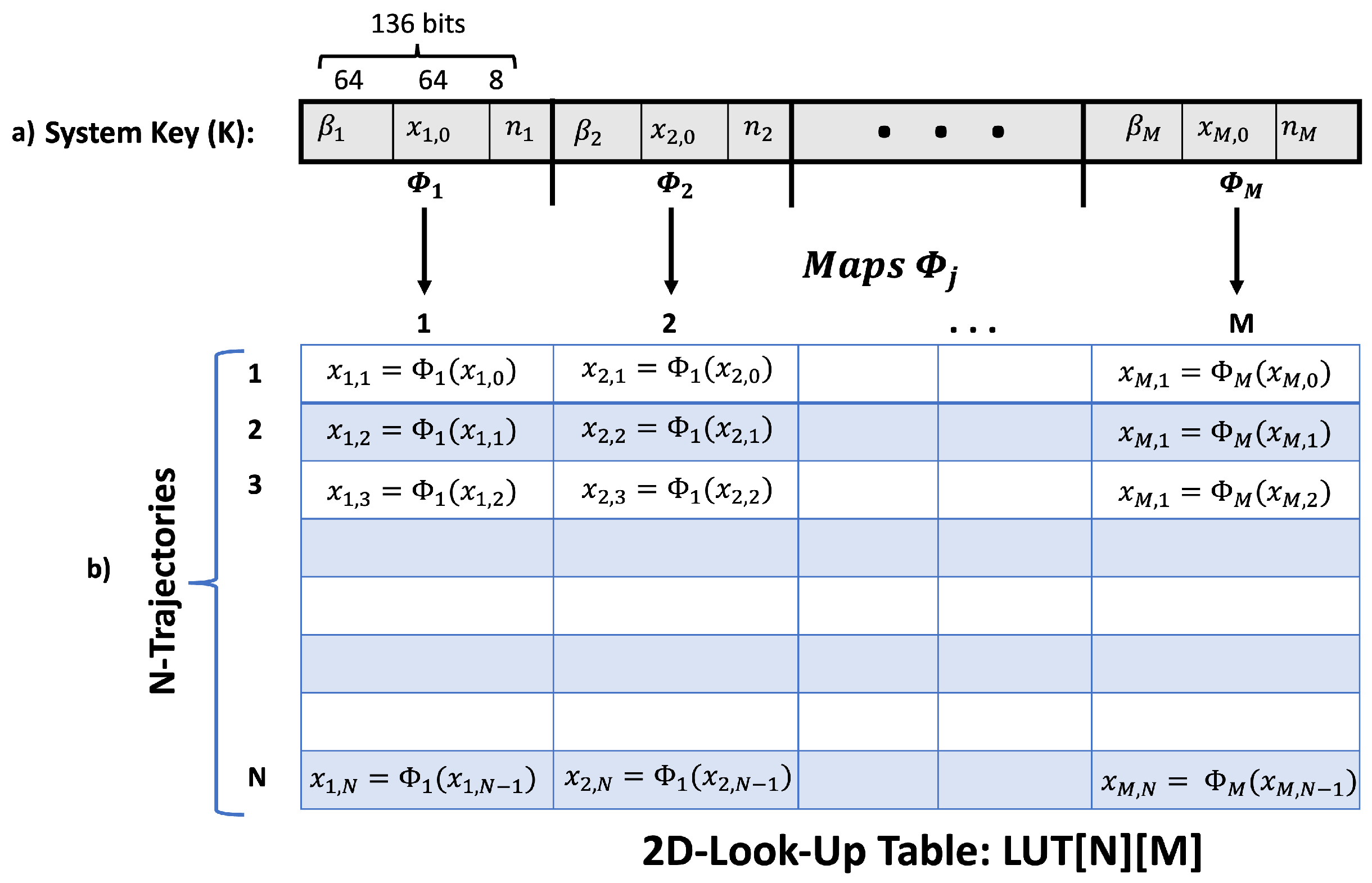
2.1.2. PRNG Initialization

The initialization process (Algorithm 1) begins by assigning random values to each map parameter and initial variable, according to a predefined seed or system key K, as shown in Figure 2a. $\beta$ and $x_0$ are represented by $PR=64$ bits (see

Table 1. Size in bits of chaotic map’s parameters for $PR$ of 64 bits. For a different PR, $\beta$ and $x_0$ match the PR value, while the size of n remains at 8 bits. Note: Event though n uses 8 bits, only 6 are used for $PR=64$ since $2^6=64$.

Parameter	$\mathit{\beta }$	${\mathit{x}}_0$	n
Size (bits)	64	64	8 (6 effectively)

), while n is represented by 8 bits; therefore, 136 bits are taken from the cipher key $\left(K\right)$ to initialize each map in sequential order (from 1 to M). The longer the encryption key, the greater the number of chaotic maps involved in the system. For M maps, a key length of 136 × M bits is required; however, if K is shorter, a bit overlap strategy of at most $PR/2$ bits can be used to initialize each map to avoid the same or similar control parameters. The M maps are represented as follows:

$$x_{m,k}={\mathsf{\Phi }}_m\left(x_{m,k-1}\right)=({\beta }_m{x}_{m,k-1}+(x_{m,k-1}\gg n_j))\left(mod{2}^{PR}\right)$$

(2)

where $8\le m\le M$ is the current map index and $M\le 16$ is the total number of maps as a function of $1088\le K\le 2176$ bits (without map overlapping). For every cipher session, different system’s seeds are employed; that is, K is a random variable in both value and length (and thus M). An associated matrix (2D-LUT) is then built and fed with N sequential trajectories from each map to form an $N\times M$ initial matrix (Figure 2b). It is worth mentioning that this is the only step in which the trajectories for each map (or column) are inserted in order in the 2D-LUT; during plaintext encryption, the trajectories are inserted randomly for additional security (as explained later in Section 2.1.1).

Algorithm 1 Initialization

1: Parameters, X_initials = PRNG_SEED   2: H = 0 // Perturbation Term   3: Maps = [ Map(Parameter,X) for Parameter,X in Parameters, X_initials ]   4: for i in 0…N do // Fill the the trajectories 2D-LUT   5:      for j in 0…M do   6:           2D-LUT[i][j] = Maps[i].next() // this also updates Maps[i].X   7:      end for   8: end for   9: $T_{LAST}$ = 2D-LUT[i][j] // Sets the last value entered into the 2D-LUT 10: iteration = 0 11: for m in 0…M do 12:      H = H ⨁ Matrix[N][M] 13: end for

Once the look-up table has been populated, a system perturbation variable (to be used during ciphering) is initialized as follows:

$${\displaystyle H_{i=0}=\underset{m=1}{\overset{M}{⨁}}2\mathrm{D}\text{-}\mathrm{LUT}[N,m]}$$

(3)

where i represents the system iteration index, and $H_{i=0}$ represents the XOR (⨁) operation of the last inserted trajectories in the 2D-LUT per map; that is, all map trajectories along the $N^{th}$ row (Figure 2b). $H_{i>0}$ is updated on an iteration basis using the most recently inserted trajectory. The main function of $H_i$ during the encryption process is to randomly perturb individual maps with contributions from all maps (as explained in the following subsection), modifying in this way the future behavior and dynamics of the encryption system. Finally, $T_{LAST}=2\mathrm{D}\text{-}\mathrm{LUT}[N,M]$ is the last trajectory inserted in the lookup-table and used by the SWP for the selection of a map ($T_{LAST}$ varies on an iteration basis).

2.1.3. Spin-Wheel and Crossover Process

The goal of our proposed PRNG is to create complex and mutual interactions between maps to lengthen the encryption system cycle. Our strategy is to avoid using consecutive trajectories of the same map or a predefined sequence of maps; otherwise, chaotic parameters could be inferred and used to predict future values of the sequence. Our PRNG consists of two schemes (Figure 3):

Spin-Wheel Picker (SWP): The first step in the PRNG is the random selection of the map and corresponding trajectory within the 2D-LUT employing the SWP strategy (Figure 3a). The SWP generates two random indices, one for the selection of the map (column index) and another for the selection of its corresponding trajectory (row index) in the 2D-LUT. In the first case (map index), the SWP is simulated by putting together the M maps in a circular array and using the module operation as follows:

$$m_i=\left(T_{LSB}(i-1)modM\right)+1;$$

(4)

where $m_i$ is the selected map index in the 2D-LUT at global or system iteration i, and $T_{LSB}$ is the Least Significant Byte (LSB) of $T_{LAST}$. The corresponding trajectory or row index ($t_i$) is obtained in a similar way as in Equation (4), except that we now use the Most Significant Byte (MSB) of $T_{LAST}$, named $T_{MSB}$:

$$t_i=\left(T_{MSB}(i-1)modN\right)+1;$$

(5)

The corresponding random trajectory $T_{m_i}=LUT[t_i,m_i]$ becomes the seed for generating the final trajectories to be used in the ciphering process (described in Section 2.2).

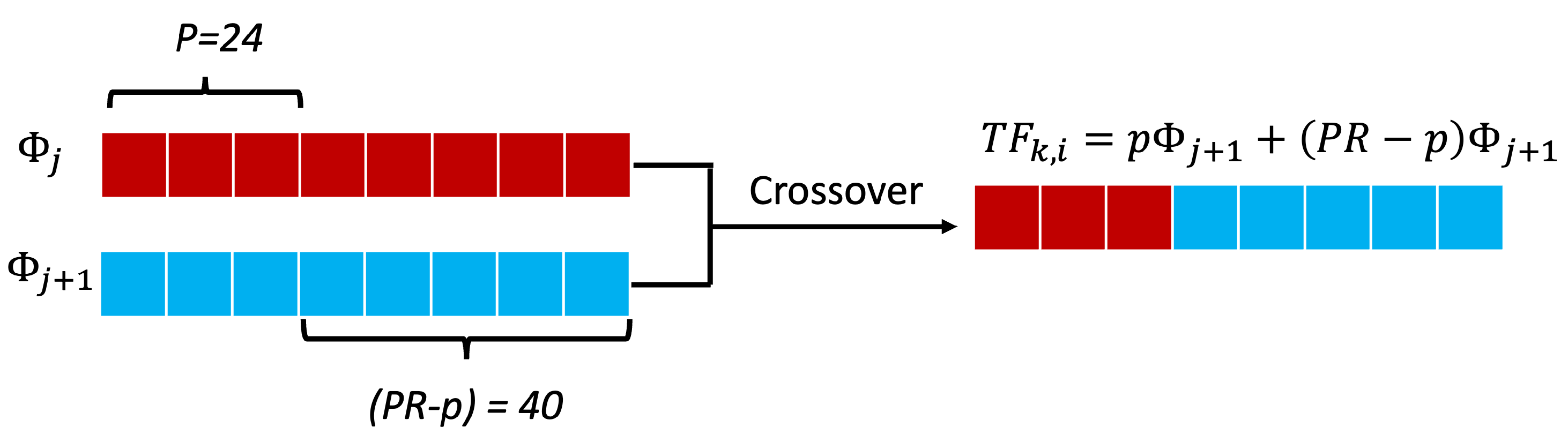
Crossover Strategy: In our second step, three additional trajectories are generated through a p-point crossover operation between the selected trajectories $T_{m_i}$ and its adjacent trajectory $T_{m_i+1}=LUT[t_i,m_{i+1}]$ (Figure 3b). During crossover, a random bit position $p=\left(T_{LAST}mod(PR-15)\right)+8$ is calculated so that the first $8\le p\le (PR-8)$ bits of $T_{m_i}$ and the $PR-p$ bits of $T_{m_i+1}$ are combined to generate the first final trajectory (out of three) of the $i^{th}$ iteration $T{F}_{1,i}$, as shown in Figure 4. After this process, the bits used in $T_{m_i}$ and $T_{m_i+1}$ are replaced by the next trajectory of the selected chaotic map. The ${\mathsf{\Phi }}_{m_i}$ map is first perturbed with the following expression:

$$x_{m,k}^{\prime }={\mathsf{\Phi }}_{m_i}\left(x_{m_i,k-1}\right)+\left(H_{i}modϵ\right);$$

(6)

where ($H_{i}modϵ$) is the perturbation mechanism and $ϵ$ is an arbitrary 3-bit value obtained from the crossover variable $T{F}_{1,i}$. The new perturbed trajectory $x_{m_i,k}^{\prime }$ is now inserted in $LUT[m_i,t_i]$. Henceforth, the 2D-LUT holds original and perturbed trajectories in the same column (or map) in a nonsequential order, and both are available to be randomly picked for future iterations. $T_{m+1,i}$ is simply replaced by the next iterated trajectory $LUT[t_i,m_{i+1}]=x_{m_{i+1},k}={\mathsf{\Phi }}_{m_{i+1}}\left(x_{m_{i+1},k-1}\right)$, which is also involved in the new values of $T_{LAST}=x_{m_{i+1},k}$ and $H_i=H_{i-1}⨁T_{LAST}$.

Similarly, to compute the second final trajectory, new indices $m_i$ and $t_i$ are calculated from the SWP (Equations (4) and (5)) based on the least and most significant bytes of the new $T_{LAST}$, respectively. The new adjacent and randomly selected trajectories $T_{m_i}$ and $T_{m_{i+1}}$ are retrieved from the 2D-LUT to go through the p-point crossover operation to obtain $T{F}_{2,i}$. In a similar fashion as in $T{F}_{1,i}$, $T_{m_i}$ and $T_{m_i+1}$ are replaced by new trajectories from their corresponding maps, and $T_{LAST}$ and $H_i$ are updated, respectively. The same operation is performed to obtain $T{F}_{3,i}$. As can be seen, only those trajectories selected by the SWP are perturbed; the corresponding adjacent trajectories (which become the actual $T_{LAST}$) are used as pointers to the new indices for the next trajectory.

It is worth noting that the described approach ensures that it is not possible to know which trajectory corresponds to each map at a given time. As a result, even if an attacker obtains consecutive trajectories used in the ciphering processing, he cannot easily determine the parameters of an individual map because the trajectories are masked (crossover process) and do not necessarily belong to the same map consecutively. The random selection of maps and trajectories breaks the continuity of the entire system.

The process used to generate a single random number is explained in Algorithm 2.

Algorithm 2 Random Number Generation

1: // SWP random selection of the map and trajectory indices   2: $m_i=T_{LSB}mod$ M   3: $t_i=T_{MSB}modN$   4: selected_trajectory = 2D-LUT[$t_i$,$m_i$]   5: selected_trajectory_secondary = 2D-LUT[$t_i$, $m_i$ + 1 mod M]   6: // Crossover Strategy   7: p = ($T_{LAST}$ mod (PR − 15)) + 8   8: TF = crossover(selected_trajectory, selected_trajectory_secondary, p)   9: // before returning the random number we have to replace the random bits used 10: // $ϵ$ & H adds the perturbation term 11: $T_{LAST}$ = Maps[$m_i$].next() + $ϵ$ & H 12: H = H ⨁$T_{LAST}$ 13: // —————————– 14: // this will replace only the bits used to generate the random number 15: selected_trajectory = crossover($T_{LAST}$, selected_trajectory, p) 16: selected_trajectory_secondary = crossover(selected_trajectory_secondary, $T_{LAST}$, p) 17: // —————————– 18: return TF

2.2. Ciphertext and Data Integrity

A resistant encryption scheme along with a simple mechanism to verify and detect data integrity at the receiver’s end is proposed. For each cipher block i, three final trajectories ($T{F}_{l,i}$ ($1\le l\le 3$)) are generated by the PRNG (Section 2.1) and combined in a block-cipher as follows:

$$C_i=E\left(P_i\right):=\left\{\begin{array}{cc}\left(P_i+T{F}_{1,i}\right)\oplus T{F}_{2,i}\oplus {\mathsf{\Phi }}_{M+1}\left(T{F}_{3,i}\right)\hfill & \mid i=1\hfill \\ \left(P_i+T{F}_{1,i}\right)\oplus T{F}_{2,i}\oplus {\mathsf{\Phi }}_{M+1}\left(C_{i-1}\oplus T{F}_{3,i}\right)\hfill & \mid i>1\hfill \end{array}\right.$$

(7)

$P_i$ is the plaintext of length PR bits, $C_i$ is the corresponding ciphertext, and ${\mathsf{\Phi }}_{M+1}$ is a new Renyi map with parameters $\beta =T{F}_{1,1}\oplus T{F}_{2,1}\oplus H_i$ and $n=\left(T{F}_{3,1}mod8\right)$. ${\mathsf{\Phi }}_{M+1}$ is independent of the PRNG and only participates in the cipher as a feedback transformation function between previous ciphertext ($C_{i-1}$) and the actual final trajectory $T{F}_{3,i}$. It creates ciphertext dependencies in each iteration, making the system more sensitive to changes in the plaintext and corresponding key. As described in Section 3 (Performance Analysis), due to feedback transformation, it is difficult to determine the individual values of $T{F}_{1,i}$, $T{F}_{2,i}$, $T{F}_{3,i}$, $C_{i-1}$, and ${\mathsf{\Phi }}_{M+1}$ parameters ($\beta$ and n). Moreover, it is practically impossible to determine the original trajectories and corresponding parameters of the $\left(M\right)$ Renyi maps for the following reasons: (a) trajectories may have gone through multiple perturbations; and (b) trajectories in the LUT are taken randomly.

A severe disadvantage of adding feedback to the cipher is that a single bit error in the received bitstream impedes deciphering of all remaining data. To solve this, packets (transmitted over the Internet) are ciphered independently; that is, feedback is reset on a packet basis, eliminating all dependencies among them (the dependency is only intra-packet). If a packet is lost, the rest of the information can still be deciphered. In the case of an attack, such as Man-in-the-Middle, the intruder positions himself between two-party communication and may divert and/or alter original messages, taking control of the communication. The mechanism for verifying data integrity is simple and lightweight; it does not have an impact on the encryption/decryption speed or the information transfer time. The scheme is based on a predefined SHA-256 key, known by both the sender and receiver. Each byte of the SHA-256 key (32 bytes long), represented by $SHA{8}_i$$(1\le i\le 32)$, is transformed according to the ciphertext content of each packet as follows:

$$D{I}_p={\mathsf{\Phi }}_{M+1}((BYTE\_SUM\left(P_p\right))\oplus \mathrm{SHA}{8}_{b=\left(pmod32\right)+1})$$

(8)

The resulting byte $D{I}_p$ is appended to the corresponding cipher-packet as an identifier of data integrity. $D{I}_p$ (where p is the packet number) is obtained by adding all bytes in the last plaintext of the processing packet ($BYTE\_SUM\left(P_p\right)$) and XORed with the $b^{th}$ byte of $SHA{8}_b$, and the result is transformed by ${\mathsf{\Phi }}_{M+1}$.

The decryption process consists of performing the inverse operations; therefore, the inverse transformation is expressed as follows:

$$P_i=D\left(C_i\right):=\left\{\begin{array}{cc}\left(C_i\oplus T{F}_{2,i}\oplus \mathsf{\Phi }\left(T{F}_{3,i}\right)\right)-T{F}_{1,i}\hfill & \mid i=1\hfill \\ \left(C_i\oplus T{F}_{2,i}\oplus \mathsf{\Phi }\left(C_{i-1}\oplus T{F}_{3,i}\right)\right)-T{F}_{1,i}\hfill & \mid i>0\hfill \end{array}\right.$$

(9)

where Equation (8) remains unmodified. The operations performed are practically the same as during encryption, so in contrast to other encryption algorithms such as AES, the encryption and decryption speeds should be the same.

After processing the ciphertext, the last deciphered text should coincide with the original plaintext $P_p$, which is then used to compute a candidate byte $SHA{8}_b^{\prime }$. The computed candidate byte is compared with the real $SHA{8}_b$; if they coincide, then the package is considered legitimate; otherwise, the packet has been tampered with.

3. Performance Analysis

In this section, the performance of the proposed scheme is analyzed based on the following cryptosystem properties: (1) PRNG randomness test; (2) map selection randomness; (3) PRNG seed sensitivity; (4) ciphertext distribution; (5) correlation analysis; (6) cryptographics attack; and (7) speed performance. The scheme is applied to various plaintext formats (see

Table 2. Sample files for testing the proposed encryption system.

File	Format	Size (MB)
Video [46]	MPEG-4	15.9
Audio [47]	mp3	18.2
Image [48]	PGM	7.8
(Uncompressed)
NIST-Manual [49]	pdf	7.4

) using different number of maps ($8\le M\le 16$) and, consequently, different system key lengths ($1088\le K\le 2176$).

3.1. PRNG Randomness Test

To characterize the effectiveness of our PRNG, we applied the random test suite developed by the National Institute of Standards and Technology (NIST) [49], with parameters specified in

Table 3. Standard parameters in the NIST test suite [49]. M represents the number of bits in a substring (block) being tested.

Parameter	Value
Bit stream length	$1\times {10}^6$
Number of bit streams	100
Significance level	0.01
Block frequency test—block length (M)	128
Non-overlapping template test—block length (M)	9
Overlapping template test—block length (M)	9
Approximate entropy test—block length (M)	10
Serial test—block length (M)	16
Linear complexity test—block length (M)	500

.

By applying the proposed SWP approach with Renyi maps, our proposed PRNG successfully passes the NIST tests, as shown in

Table 4. NIST randomness test results, * p-value resulting from applying the chi-squared test to the frequency of the p-values obtained by the randomness tests, ** Proportion of binary sequences that passed the randomness test.

Test	p-Value *	Proportion of Success **
Frequency	0.816537	98/100	Success
CumulativeSums	0.366918	98/100	Success
Runs	0.019188	99/100	Success
LongestRun	0.739918	99/100	Success
Rank	0.996335	98/100	Success
FFT	0.971699	99/100	Success
NonOverlappingTemplate	0.964295	99/100	Success
OverlappingTemplate	0.137282	100/100	Success
Universal	0.798139	99/100	Success
ApproximateEntropy	0.350485	100/100	Success
RandomExcursions	0.517442	65/65	Success
RandomExcursionsVariant	0.063482	64/65	Success
Serial	0.699313	100/100	Success
LinearComplexity	0.816537	100/100	Success

, demonstrating a uniform distribution and robust randomness suitable for cryptographic applications. The success of this approach, in passing the tests, can be primarily attributed to the random selection of maps and the coupling term between different trajectories (crossover process). This coupling term acts as “noise” that masks the calculation errors in digitized maps and diversifies the values, achieving a more ideal random behavior.

3.2. Map Selection Randomness

Another aspect investigated is the efficiency of the number of chaotic maps in the SWP. Although the overall randomness of the PRNG has been verified with randomness tests (Section 3.1), it is important to ensure that the selection of maps is done optimally (unbiased) and does not generate unnecessary computational resources. In this sense, the present analysis focuses on evaluating the efficiency of the SPW in the random selection of chaotic maps. For this, we created an occurrence table to record each time a chaotic map is selected and analyzed the frequency distribution using both the ${\chi }^2$ test and the Quantile–Quantile plot (QQ-plot), which represent a graphical tool to help us assess whether a set of data plausibly came from some theoretical distribution, such as the uniform distribution in this case.

Figure 5 shows the evolution of the ${\chi }^2$ uniformity test with a significance level of $\alpha =0.1$ for different numbers of maps. It can be seen that the number of maps used in the generation process within the range $8\le M\le 16$ is above the significance level, which means that there is enough evidence to conclude that the distribution is uniform (all maps have the same probability of being visited during the encryption process). It is worth noting that, when the number of maps is a power of 2, the significance level is asymptotically close to 1. A QQ-plot and histogram visualization reveal that no matter the number of maps, the uniformity test is confirmed, as shown in Figure 6.

3.3. PRNG Seed Sensitivity

A systematic approach to evaluate the sensitivity of the PRNG to the initial seed is conducted using the Hamming distance (number of bit positions at which the corresponding symbols are different). By analyzing the distribution of the calculated Hamming distances, insights into the sensitivity of the PRNG to the initial seed are obtained. First, an initial random seed is selected as a starting point. This seed is then subject to systematic modifications by changing a single bit and generating a sequence of random numbers using the PRNG. Subsequently, the Hamming distance between the encrypted sequence generated with the original seed and the sequence generated with the modified seed is calculated. We perform this process for every single bit in K, and the results obtained indicate a high sensitivity of the PRNG to the initial seed. The average Hamming distance was found to be close to 0.5 (see Figure 7), suggesting that, on average, half of the bits in the random sequences differ when a single bit of the seed is modified. This confirms that small changes in the initial seed produce significant changes in the generated random number sequences. In other words, our PRNG fulfills a fundamental requirement for randomness and security: the impossibility of predicting the random number sequence from a similar seed or the inability to perform a local search starting from a seed that produces a similar sequence. Additionally, the high sensitivity to the seed provides significant resistance against brute-force attacks, enhancing the security of the PRNG.

3.4. Ciphertext Distribution

A fundamental requirement for a secure encryption scheme is to produce ciphertext with a uniform distribution, regardless of the plaintext’s distribution. This ensures that each symbol in the ciphertext has an equal probability of occurrence, thwarting attempts by attackers to identify statistically significant patterns. Such patterns could potentially reveal information about the underlying plaintext. By rendering a ciphertext that is indistinguishable from random noise, the proposed encryption scheme effectively masks the characteristics of the original data.

Figure 8 illustrates the effectiveness of the proposed encryption scheme. The plaintext image, when encrypted, undergoes a significant transformation, resulting in a ciphertext image that is visually indistinguishable from random noise. This is evident in the histograms of the plaintext and ciphertext images. The plaintext histogram exhibits distinct peaks and valleys, reflecting the non-uniform distribution of pixel intensities. In contrast, the ciphertext histogram shows a nearly flat distribution, indicating that the encryption process has successfully randomized the pixel values. This uniform distribution is a key characteristic of a strong encryption scheme, as it makes it difficult for attackers to extract any meaningful information from the ciphertext. Figure 9 shows original and encrypted histograms for audio and video data, respectively, wherein the same uniform ciphertext pattern as in Figure 8 is obtained. Therefore, our encryption system provides uniform ciphertexts independently of the data type and compression scheme.

3.5. Correlation Analysis

We now present the effect of two different system keys on the resultant ciphertext for the same plaintext. For this, we make use of Pearson’s correlation coefficient. This statistical measure allows us to determine the relationship between pairs of ciphertexts generated with slightly different keys. It quantifies the linear relationship between two variables; that is, it indicates how well the data fit into a straight line. The correlation coefficient can take values between $-1$ and 1 and is defined as follows:

$$r_{xy}={\displaystyle \frac{n\sum x_i{y}_i-\sum x_i\sum y_i}{\sqrt{n\sum x_i^2-{(\sum x_i)}^2}\sqrt{n\sum y_i^2-{(\sum y_i)}^2}}}$$

(10)

If the correlation is high (close to 1 or $-1$), it means that a small change in the key produces a predictable change in the ciphertext, indicating a weakness in the cipher. Conversely, if the correlation is low (close to 0), it indicates that the cipher is resistant to key changes, producing significant and unpredictable changes in the ciphertext. To evaluate the sensitivity of the encryption algorithm to key modifications, we modify the most significant, least significant, and middle bits. By analyzing the correlation coefficients obtained for each file type and each key modification (see

Table 5. Correlation coefficients between ciphertext with an original key and ciphertext with a modified bit in the original key. video file corresponds to [46]; audio file corresponds to [47]; image file corresponds to [48]; and book file corresponds to [49].

File	Bit	Bit	Bit
	Least Significant	Middle	Most Significant
video.mp4	0.0002	$-0.0016$	$-0.0011$
audio.mp3	0.0008	$4.4\times {10}^{-5}$	0.0002
image.pgm	0.0011	0.0007	0.0029
NIST-Manual.pdf	$-9.9\times {10}^{-5}$	$-0.0001$	0.0015

), it was consistently observed that the values were close to zero (we have included a pdf book in our current test).

3.6. Cryptographic Attack

With the aim of determining the strength of our encryption scheme, we evaluate the computational complexity of recovering the random numbers or trajectories involved in the ciphering process. This is evaluated based on the following cryptanalysis techniques: brute force, chosen ciphertext, and chosen plaintext attacks.

In brute-force attacks, the main objective is to infer the system key K. In our case, it requires $\left(2^{1088\le K\le 2176}\right)$ operations to break the entire system, becoming a practically impossible task with current computer performance. Since we allow an overlapping system-key (additional maps can be created by reusing a portion of K), the order of the attack becomes even higher since we have more unknown number maps than the original key length can provide (see Section 2.1 System Initialization). With key overlapping, the total brute force attack becomes $2^{1088\le K\le 2176}+2^{N(PR=64)/2}$, where N is the number of additional maps derived from K.

In chosen ciphertext attack, the attacker can generate the corresponding plaintext $P_i$ from the selected ciphertext $C_i$). By analyzing this relationship, the attacker may be able to deduce the key. For this, it is necessary to first determine the values of the final trajectories $T{F}_{1,i}$, $T{F}_{2,i}$, and $\varphi (c_{i-1}\oplus T{F}_{3,i})$ on an iteration basis (see Equation (9)). Given that PRNG and ciphertext have a uniform distribution and considering that each packet is independently encrypted with an average length of 720 bytes (it contains 90 ciphertexts requiring 3 × 64 bit final trajectories), then the chosen ciphertext attack becomes $2^{90\times (3\times 64)=17,280}$ (for only one packet). It is better but still hard to guess the 90 64-bit plaintexts in each packet ($2^{90\times 64=5720}$). If, on the other hand, the target attack is to find the parameters and initial condition of the M maps, it becomes again an impossible task. It is necessary to find the inverse process of the entire cipher system, i.e., $T{F}_{(1,2,3),i}$, $\varphi \left(\right)$, the inverse of the crossover, the trajectory used for selecting a map by the $SWP$, etc. Finally, for a chosen plaintext attack, in which the attacker can choose specific messages (plaintexts) and the corresponding ciphetext to analyze correspondences, the same inverse process (as in the chosen ciphertext attack) needs to be performed. As can be seen, the best option to attack the system is brute force. The proposed PRNG is robust enough for currently known attacks.

The integrity of the received ciphertext information (or packets) may also be subject to attacks using, for example, a man-in-the-middle attack (see Section 2.2). In this attack, an intruder may be eavesdropping on private communication between the sender and receiver, sometimes altering or replacing messages to disrupt the conversation. To simulate this attack, we performed a random permutation of bits within a packet, randomly toggled random bits in the ciphertext sequence, then deciphered into plaintext and checked whether the integrity byte matched the correct value. The experiment was repeated one million times, and the collisions were counted and compared for the full number of experiments. Our results show a probability of 0.0039 that an integrity attack would pass undetected.

3.7. Speed Performance

Encryption speed is a critical factor in many applications, especially those that require real-time processing of large volumes of data, such as video streaming. This section presents the speed performance of the encryption algorithm on two different platforms, as shown in

Table 6. Our cipher speed comparison against state-of-the-art schemes. * The speed in [23] is approximated.

Algorithm	Operating System	Processor	RAM	Speed (Gbps)
Our Scheme	Windows 11	Intel Core i5-11400H	16 GB	5.9981
AES	Windows 11	Intel Core i5-11400H	16 GB	1.6113
Wang [23]	Windows 11	Intel Core i5-13400F	8 GB	0.745 *
Feng [32]	Not reported	Intel E3-1232 v3	8 GB	0.0609
Shi [33]	Not reported	Not reported (3.6 GHz)	8 GB	0.4531

.

To compare the efficiency of our proposed scheme against AES and other state-of-the-art chaotic ciphers, a performance experiment was conducted. In each test, a random 1 GB file was generated and encrypted using each of the algorithms. To ensure an accurate measurement of the encryption time, the initialization time of the algorithm was excluded. The results obtained were expressed in terms of encryption speed, measured in gigabits per second. To ensure a fair comparison between the algorithms, only software implementations of AES provided by the OpenSSL library (version 3.0.7) were used.

As shown in Table 6, the proposed encryption scheme was found to be significantly faster than the rest. A noteworthy observation is that the Roulette scheme has virtually the same encryption and decryption speed, whereas AES has a higher encryption speed. We consider this property to be of great importance for real-time communications, as if encryption is faster, the source may send messages faster than the destination can process them, introducing additional latency between messages.

To further characterize the performance of the developed cipher system, the relationship between the size of the data being ciphered and the corresponding cipher processing time was investigated. Figure 10 illustrates this dependency for 1KB data size increments, showing an overall positive linear correlation between ciphered data size and cipher time. In general, this indicates that our proposed cipher algorithm processes the data in a consistent manner, taking a relatively constant amount of time per byte.

4. Conclusions

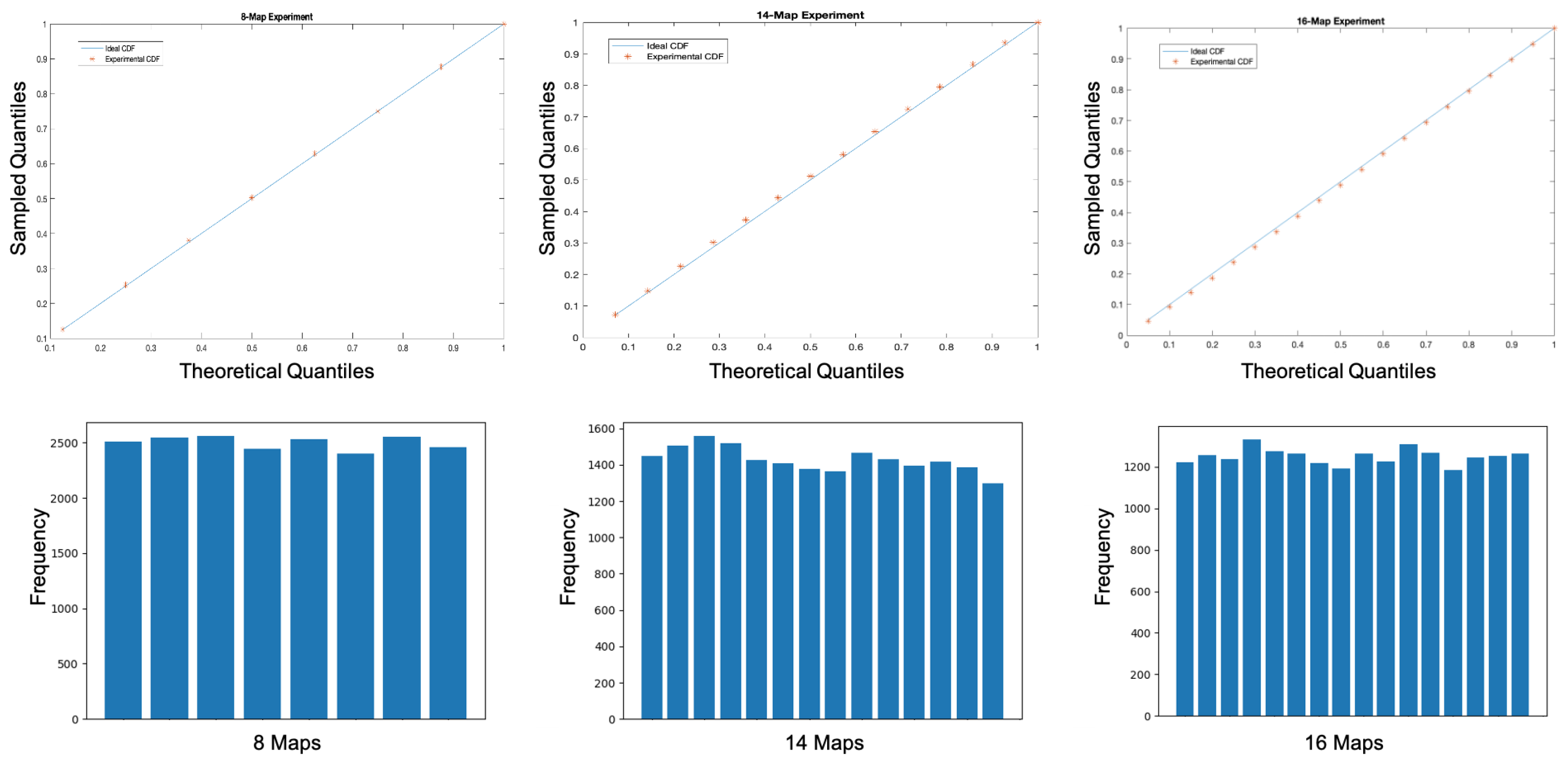
The proposed scheme is based on a random roulette method for selecting and iterating through a graph composed of M chaotic maps and an $N\times M$ lookup table, with N precalculated trajectories initially ordered in temporal order for each map M. Three random values are involved in the encryption process: (1) selection of the map $M_i$ through the random roulette; (2) selection of the trajectory of the map $i^{th}$ map $(M_i,j)$ in the lookup table; and (3) random selection of the variable $0\le Offset<8$, which indicates the position of the byte within the selected map trajectory from which the trajectory will start for the encryption process (each trajectory consists of 8 bytes). Point (2) indicates that the trajectories of each map are not used sequentially or in temporal order, while point (3) indicates that the final trajectory selected within the lookup table may come from up to two contiguous maps $M_i$ and $M_{i+1}$, containing the first bytes of $M_i$ and the last of $M_{i+1}$, which significantly increases the security of the system in case of attacks. Experimental analysis demonstrates that the developed scheme is completely random in terms of trajectory generation and selection of maps or nodes in the chaotic map graph, showing a uniform distribution in both cases. There is an equal probability of visiting any map within the graph, offering high security against both system and brute-force attacks. According to the reported encryption speeds, the proposed scheme is theoretically capable of serving hundreds of real-time video communications without affecting performance. Based on our state-of-the-art literature review, we can confirm that our proposed encryption scheme is the fastest reported in the literature.

Since our proposed scheme exhibits a very high performance, the main target applications are real-time multimedia communications (audio, image, and video). In the context of video conferencing, the implementation of this scheme would enable higher concurrent participants without perceptible degradation in the stream quality. This capability holds significant implications for applications which require secure communication for sensitive domains, including governmental and corporate sectors, remote medical consultations, or financial exchanges.