A Novel Multi-Channel Image Encryption Algorithm Leveraging Pixel Reorganization and Hyperchaotic Maps

Abstract

Chaos-based encryption is promising for safeguarding digital images. Nonetheless, existing chaos-based encryption algorithms still exhibit certain shortcomings. Given this, we propose a novel multi-channel image encryption algorithm that leverages pixel reorganization and hyperchaotic maps (MIEA-PRHM). Our MIEA-PRHM algorithm employs two hyperchaotic maps to jointly generate chaotic sequences, ensuring a larger key space and better randomness. During the encryption process, we first convert input images into two fused matrices through pixel reorganization. Then, we apply two rounds of scrambling and diffusion operations, coupled with one round of substitution operations, to the high 4-bit matrix. For the low 4-bit matrix, we conduct one round of substitution and diffusion operations. Extensive experiments and comparisons demonstrate that MIEA-PRHM outperforms many recent encryption algorithms in various aspects, especially in encryption efficiency.

1. Introduction

With the advent of the digital era and the rapid evolution of emerging technologies such as artificial intelligence (AI), cloud computing, and big data, digital images have found increasingly widespread use across diverse industries. Constantly, a vast number of digital images are generated, originating from a multitude of sensors, smartphones, and other terminal devices. These images are then distributed and stored through various channels, including intranets and the Internet [1]. During their transmission and storage, digital images face a growing spectrum of security threats, encompassing data breaches and unauthorized access. These threats not only jeopardize personal privacy but also pose significant risks to the information security of diverse industries. As a result, the challenge of ensuring the efficient and secure safeguarding of image data has risen to the forefront as a critical issue requiring immediate attention [2].

As an effective means of safeguarding image data, image encryption technology is gaining increasing favor. This technology transforms digital images into unrecognizable, quasi-noise images, rendering it impossible for unauthorized parties to obtain meaningful information, thereby effectively ensuring the security of image data [3]. Notably, digital images are characterized by strong pixel correlation, significant data redundancy, and vast data volume. This renders text-oriented traditional algorithms, such as advanced encryption standard (AES), inappropriate for encrypting image data [4]. Thus, to achieve higher encryption efficiency and security, researchers are continually exploring various techniques and methodologies to devise image encryption algorithms. Among these are chaotic systems [5,6,7,8,9,10], quantum computing [11,12,13], deoxyribonucleic acid (DNA) sequence operations [14,15,16], compressed sensing [17,18,19], neural networks [20,21,22,23,24,25], optical transformations [26,27], and numerous others [28,29,30,31]. Additionally, a notable trend in the field of image encryption is that chaotic systems are increasingly adopted [2,32].

In fact, this trend is by no means accidental. Chaotic systems are highly regarded because of their remarkable characteristics, which are extremely suitable for developing cryptographic systems. Specifically, chaotic systems have the characteristics of ergodicity, unpredictability, randomness, and extreme sensitivity to initial conditions. In recent years, the academic community has continued to deepen and advance the research on chaos-based image encryption. There is a large number of image encryption algorithms that have been proposed in the past few years [5,6,7,8,9,33,34,35,36,37]. However, many recently reported encryption algorithms still exhibit certain weaknesses in terms of practicality or security [38,39,40].

With a 2D hyperchaotic map formed by coupling multiple seed maps, Nan et al. [33] presented an encryption algorithm based on compressed sensing and S-box. The algorithm exhibits commendable encryption results due to the inherent randomness of chaotic sequences. Nevertheless, the complex structure of their map leads to poor encryption efficiency. Furthermore, their algorithm brings data loss, rendering it impractical for encrypting images with intricate details.

Wang et al. [34] devised an encryption algorithm based on a 1D chaotic map, which employs a common permutation and diffusion framework. To bolster the algorithm’s ability to resist plaintext attacks, they utilized the image’s hash value directly to obtain the initial inputs of the adopted chaotic map. Such a design poses practical challenges in terms of key management. Furthermore, given that the chaotic map employed features just a single control parameter, the algorithm’s effective key space is actually small.

Employing a 2D combined hyperchaotic map, Etoundi et al. [35] built an efficient encryption algorithm. This algorithm achieves the encryption of the input image by conducting substitution and scrambling operations. Since no diffusion mechanism is introduced, it is actually unable to effectively resist various differential attacks.

In [36], Liu et al. introduced an encryption algorithm that leverages a spatiotemporal chaotic system and DNA sequence operations. Due to its dual-bit encryption approach, the algorithm’s encryption efficiency fails to satisfy the demands of practical applications. In addition, the algorithm exploits hash values to generate the initial inputs of the chaotic system, which also leads to the dilemma of key management.

To address the deficiencies in existing algorithms and achieve higher encryption efficiency and security, we propose a novel multi-channel image encryption algorithm that leverages hyperchaotic maps and pixel reorganization (MIEA-PRHM). Distinct from numerous encryption algorithms reported in recent years [3,4,5,7,8,9,14,15,16,17,23,29,31,33,34,35,41,42,43,44,45,46,47,48,49,50,51,52,53,54], our MIEA-PRHM incorporates several novel designs aimed at enhancing encryption efficiency and bolstering security.

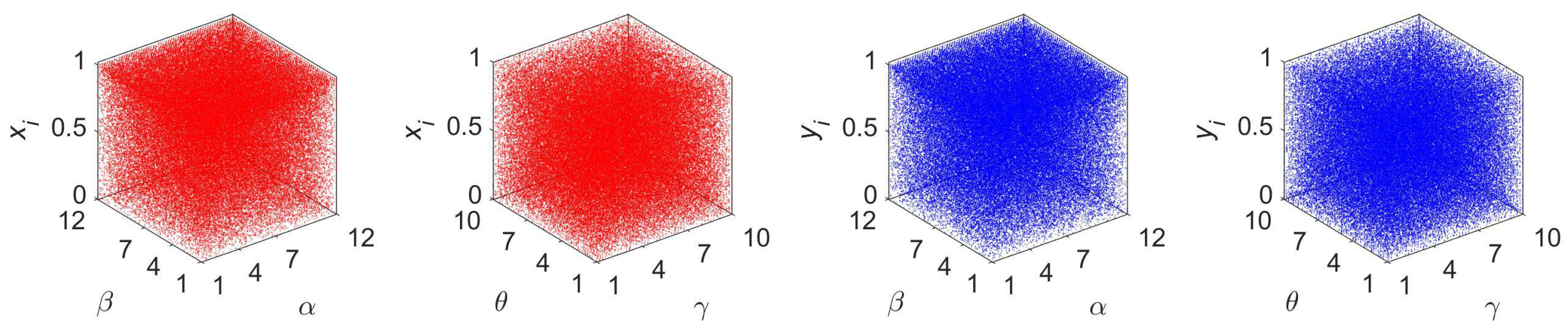
Firstly, we adopt two recently reported robust hyperchaotic maps, the 2D sinusoidally constrained polynomial hyperchaotic map (2D-SCPM) [46] and the 2D enhanced logistic modular map (2D-ELMM) [47]. These two hyperchaotic maps are used to jointly generate chaotic sequences. This not only expands the key space but also helps to enhance the non-periodicity and randomness of the generated chaotic sequences.

Secondly, we optimize the utilization of hash values. In our MIEA-PRHM algorithm, rather than being employed as secret keys, hash values are utilized solely to bolster the dynamism of the encryption process. This optimization not only enhances the sensitivity to plaintext, but also addresses the practical issues related to key management.

Thirdly, we apply pixel reorganization to encrypt the high 4-bit and low 4-bit components of image pixels with varying intensities. By leveraging pixel fusion and differentiated encryption, this design can reduce the computational overhead of subsequent encryption operations by roughly three-quarters.

Lastly, the encryption process of MIEA-PRHM encompasses multiple rounds of vector-level scrambling, diffusion, and substitution operations, which are not only computationally efficient but also exhibit dynamic characteristics.

In summary, our research contributes in the following aspects:

• Utilizing two robust hyperchaotic maps, 2D-SCPM and 2D-ELMM, we propose a novel multi-channel image encryption algorithm called MIEA-PRHM.
• Our proposed MIEA-PRHM algorithm utilizes 2D-SCPM and 2D-ELMM to jointly generate chaotic sequences, which can not only expand the key space but also enhance the randomness of chaotic sequences.
• Pixel reorganization achieves differentiated encryption by splitting and fusing image pixels. This can significantly reduce the computational amount in the entire encryption process and thus improve encryption efficiency.
• Dynamic vector-level encryption operations guarantee that MIEA-PRHM delivers exceptional security and encryption efficiency. Experimental results and performance analyses demonstrate that MIEA-PRHM possesses notable advantages in various aspects, particularly in terms of encryption efficiency.

We organize the remainder of this paper as follows: Section 2 briefly describes the two hyperchaotic maps and the SHA-256 hash function. Section 3 provides a detailed introduction to the entire encryption process of MIEA-PRHM. Section 4 evaluates and analyzes the performance of MIEA-PRHM through a series of experiments and comparisons. In the final section, we conclude the paper.

2. Preliminaries

Herein, we will first introduce two recently reported hyperchaotic maps employed in MIEA-PRHM, followed by a concise overview of the SHA-256 hash function.

2.1. The 2D-SCPM and 2D-ELMM

At present, chaotic maps are extensively employed in image encryption. For image encryption algorithms, the chaotic performance of the employed chaotic maps, alongside their efficiency in generating chaotic sequences, holds significant importance. Consequently, we opt for two recently introduced robust 2D hyperchaotic maps, distinguished by their simplicity, ease of implementation, and remarkable efficiency in generating chaotic sequences. Furthermore, these maps exhibit exceptional chaotic behavior, characterized by uniformly distributed state values, consistently high Lyapunov exponents, and broad, continuous hyperchaotic ranges. Notably, they surpass most counterparts in common chaotic performance metrics, and the chaotic sequences they produce meet the rigorous standards of randomness tests.

Among the two robust hyperchaotic maps mentioned above, we first introduce 2D-SCPM [46]. It is a polynomial map constrained by the sine function, and its specific definition is as follows:

$$\left\{\begin{array}{c}{x}_k=sin({10}^{\alpha }{x}_{k-1}{y}_{k-1}+{10}^{\beta }{y}_{k-1}),\hfill \\ y_k=sin({10}^{\beta }{x}_{k-1}{y}_{k-1}+{10}^{\alpha }{x}_{k-1}),\hfill \end{array}\right.$$

(1)

where $k=1,2,3,\dots$ represents the iteration number of 2D-SCPM, $(x_{k-1},y_{k-1})$ is the input of each iteration, and $(x_k,y_k)$ represents the corresponding output. $\alpha$ and $\beta$ are the two control parameters of 2D-SCPM. When $(a,b)\in [1,12]$, 2D-SCPM is always in a hyperchaotic state.

Another hyperchaotic map employed in our study is 2D-ELMM [47]. This hyperchaotic map also boasts a straightforward structure and outstanding chaotic performance. In detail, its definition is articulated as follows:

$$\left\{\begin{array}{c}{x}_i=e^{\gamma }{x}_{i-1}(e^{\theta }{y}_{i-1}-1)mod1,\\ y_i=e^{\theta }{y}_{i-1}(e^{\gamma }{x}_{i-1}-1)mod1,\end{array}\right.$$

(2)

where $i=1,2,3,\dots$ is the iteration number of 2D-ELMM, $(x_{i-1},y_{i-1})$ represents the input of each iteration, and $(x_i,y_i)$ denotes the corresponding output. $\gamma$ and $\theta$ stand for the two control parameters of 2D-ELMM. When $(\gamma ,\theta )\in [1,10]$, 2D-ELMM is always in a hyperchaotic state.

2.2. Mathematical Features of Hyperchaotic Maps

The two hyperchaotic maps utilized in our MIEA-PRHM possess mathematical features that perfectly align with the demands of image encryption. Firstly, their state value distributions are exceptionally uniform, characterized by boundedness and ergodicity. Encrypting digital images with their state values helps eliminate the prominent distribution characteristics of plaintext pixels as shown in Figure 1 and Section 4.7. Secondly, they exhibit extreme sensitivity to minute variations in their initial state values and control parameters. Utilizing these initial state values and control parameters as components of the secret key ensures exceptionally high key sensitivity as demonstrated in Section 4.2. Furthermore, they possess favorable intrinsic randomness and complexity. Employing them for designing image encryption algorithms not only generates highly random noise-like ciphertext images but also effectively resists numerous attacks targeting the secret key or statistical characteristics. Lastly, their complex and random chaotic behaviors are deterministic. Anyone possessing the correct secret key can losslessly decrypt indistinguishable noise-like ciphertext images back to original plaintext images. For more information on the mathematical features of these two hyperchaotic maps, please refer to [46,47].

2.3. NIST SP-800 Randomness Test

The NIST SP-800 randomness test constitutes a widely adopted collection of statistical methodologies aimed at assessing the quality of random and pseudorandom number generations [46]. To showcase the superiority of our chaotic sequence generation strategy, we subject the chaotic sequences employed within our MIEA-PRHM to the NIST SP-800 randomness test. Additionally, we conduct tests on chaotic sequences generated exclusively using either 2D-SCPM or 2D-ELMM. Given that the NIST SP-800 randomness test is tailored for binary sequences, we convert the resulting floating-point chaotic sequences into integers and then into binary form, following the method described in Equation (8).

According to the requirements of the NIST SP-800 randomness test, we utilize random inputs to generate a total of 60 sets of binary sequences, each with a length of 1,000,000 bits. For each test item, if the obtained p-value exceeds the threshold of 0.01, the test item is deemed to have been passed. Our final test results are presented in

Table 1. Results of the NIST SP-800 randomness test.

Test Item	2D-SCPM		2D-ELMM		Ours
	Pass/All	%	Pass/All	%	Pass/All	%
Frequency (Bit)	20/20	100%	20/20	100%	20/20	100%
Frequency (Block)	19/20	95%	20/20	100%	20/20	100%
Run	20/20	100%	20/20	100%	20/20	100%
Longest Run	20/20	100%	20/20	100%	20/20	100%
Binary Matrix Rank	20/20	100%	18/20	90%	20/20	100%
Discrete Fourier Transform	20/20	100%	20/20	100%	20/20	100%
Non-Overlapping Temp.	19/20	95%	20/20	100%	20/20	100%
Overlapping Temp.	20/20	100%	20/20	100%	20/20	100%
Universal Statistical	20/20	100%	20/20	100%	20/20	100%
Linear Complexity	20/20	100%	20/20	100%	20/20	100%
Serial 1	20/20	100%	19/20	95%	20/20	100%
Serial 2	19/20	95%	20/20	100%	20/20	100%
Appr. Entropy	20/20	100%	20/20	100%	20/20	100%
Cummu. Sums Forward	20/20	100%	20/20	100%	20/20	100%
Cummu. Sums Reverse	20/20	100%	20/20	100%	20/20	100%
Random Excur. ($x=-1$)	20/20	100%	20/20	100%	20/20	100%
Random Excur. ($x=+1$)	20/20	100%	20/20	100%	20/20	100%
Random Excur. Var. ($x=-1$)	20/20	100%	19/20	95%	20/20	100%
Random Excur. Var. ($x=+1$)	20/20	100%	20/20	100%	20/20	100%

. It can be observed that when generating binary sequences using 2D-SCPM or 2D-ELMM alone, a small number of sequences fail to pass all the test items. In contrast, all binary sequences generated by the joint generation strategy of MIEA-PRHM pass the test. This shows that our design is effective and can better ensure the randomness of chaotic sequences.

2.4. SHA-256 Hash Function

The SHA-256 hash function is devised by the National Security Agency (NSA) of the United States [54]. It processes input data in chunks, generating a 256-bit hash value through a series of mathematical operations. SHA-256 is characterized by its irreversibility, uniqueness, high security, and input sensitivity. No one can deduce the original data from the hash value. Different inputs yield nearly unique hash values, exhibiting high collision resistance. Any minor modification to the input data results in significant changes to the hash value. SHA-256 is extensively utilized in digital signatures, password storage, data integrity verification, blockchain, and other fields.

Currently, many image encryption algorithms utilize plaintext hash values to boost their sensitivity to plaintext. However, most of their methods for leveraging the hash values are impractical, posing significant challenges in key management. As a result, in our MIEA-PRHM, we solely utilize plaintext hash values to enhance the encryption process’s dynamism, rather than using them directly as secret keys or to create chaotic sequences. Specifically, we initially input two fused pixel matrices, ${\mathbf{F}}^{\left(1\right)}$ and ${\mathbf{F}}^{\left(2\right)}$, into the SHA-256 algorithm to obtain a 256-bit hash value $\tilde{h}$. For further details regarding ${\mathbf{F}}^{\left(1\right)}$ and ${\mathbf{F}}^{\left(2\right)}$, please refer to Section 3.1. Subsequently, we convert the hash value $\tilde{h}$ into a byte vector $\mathbf{v}$ of size $1\times 32$. Ultimately, these hash value bytes are transformed into a plaintext-related vector $\mathbf{V}$ of size $1\times 8$, which is utilized in the encryption process:

$$\mathbf{V}={\mathbf{v}}_{\mathbf{4}\times \mathbf{i}-\mathbf{3}}\times {\mathbf{v}}_{\mathbf{4}\times \mathbf{i}-\mathbf{2}}\times {\mathbf{v}}_{\mathbf{4}\times \mathbf{i}-\mathbf{1}}\times {\mathbf{v}}_{\mathbf{4}\times \mathbf{i}},$$

(3)

where $i=1,2,\dots ,8$.

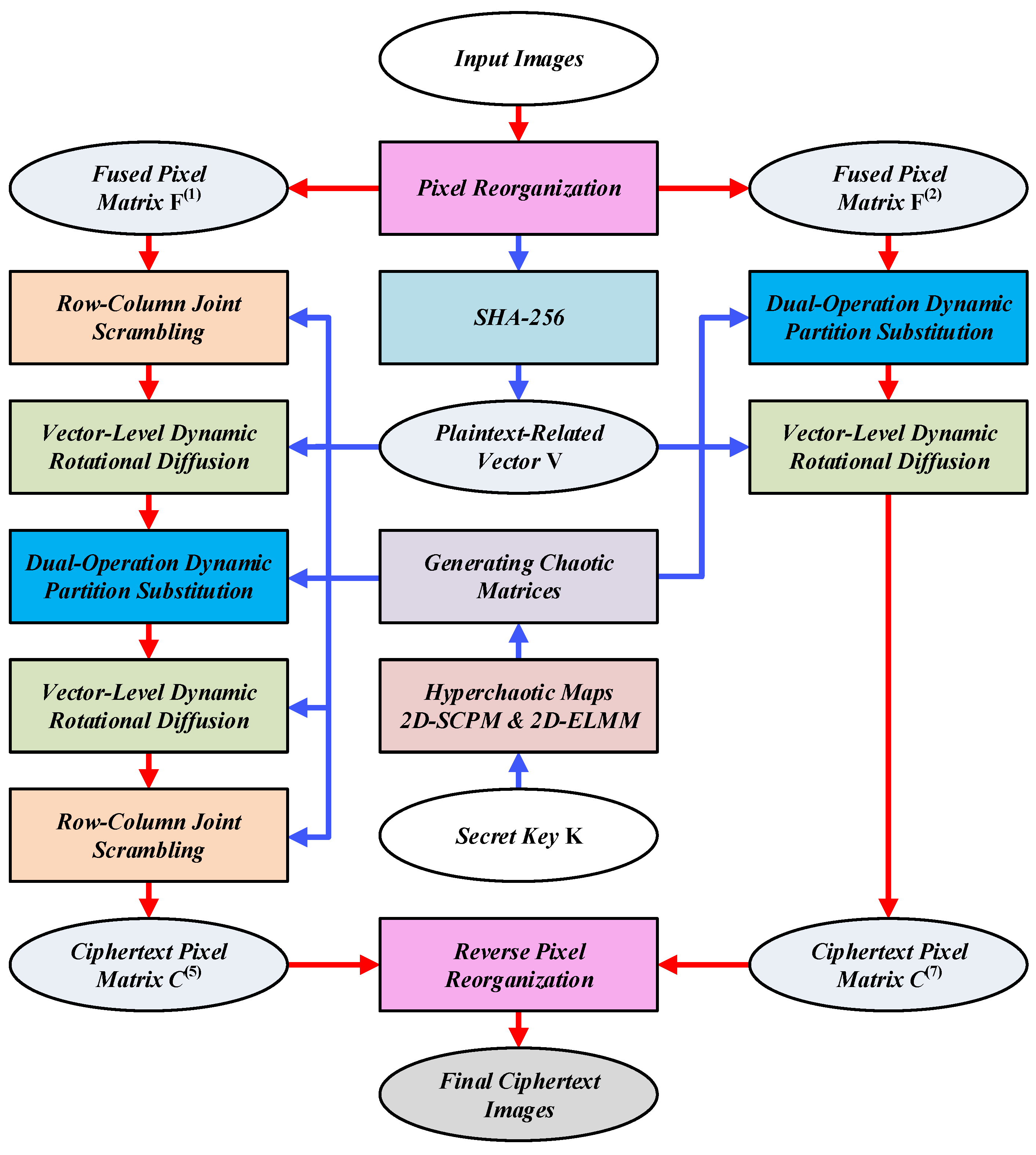
3. Proposed MIEA-PRHM

This section introduces the encryption steps and the complete encryption process of our proposed MIEA-PRHM algorithm. In this novel chaotic image encryption algorithm, there are five distinct encryption steps, which are pixel reorganization, generating chaotic sequences, row–column joint scrambling, vector-level dynamic rotational diffusion, and dual-operation dynamic partition substitution. As shown in Figure 2, some of these encryption steps are performed once, while others are performed twice or three times. Next, we introduce these encryption steps in detail one by one.

3.1. Pixel Reorganization

In this encryption step, we split the image pixels that require encryption into high 4-bit and low 4-bit components. Subsequently, separate pixel fusion operations are conducted on these components. The purpose of pixel splitting is to facilitate the application of different encryption intensities to the high 4-bit and low 4-bit components in subsequent encryption steps. Meanwhile, pixel fusion aims to more fully exploit the computational capabilities of the processor. Consequently, both approaches contribute to improving the encryption efficiency of MIEA-PRHM. Specifically, pixel reorganization encompasses the following steps:

• Step 1: For one or multiple input images that require encryption, aggregate them into a 3D pixel matrix ${\mathbf{T}}^{\left(1\right)}$ with dimensions of $\widehat{H}\times \widehat{W}\times N$. Here $\widehat{H}\times \widehat{W}$ signifies the channel dimensions of these images, and N signifies the total number of channels across these input images. In this context, a grayscale image is deemed a single channel image, whereas a color image is considered a three channel image, comprising the red (R), green (G), and blue (B) channels.
• Step 2: Reshape ${\mathbf{T}}^{\left(1\right)}$ into a 3D pixel matrix ${\mathbf{T}}^{\left(2\right)}$ with dimensions of $H\times W\times 8$, where $H=\widehat{H}/2$ and $W=(\widehat{W}\times N)/4$. If $\widehat{H}/2$ or $\widehat{W}/4$ is not an integer, ${\mathbf{T}}^{\left(1\right)}$ is filled with zero-value pixels to ensure that $H/2$ or $\widehat{W}/4$ becomes the smallest integer greater than itself.
• Step 3: Mathematically split ${\mathbf{T}}^{\left(2\right)}$ into a high 4-bit component ${\mathbf{T}}^{\left(3\right)}$, and a low 4-bit component ${\mathbf{T}}^{\left(4\right)}$:

  $$\left\{\begin{array}{c}{\mathbf{T}}^{\left(3\right)}=⌊{\mathbf{T}}^{\left(2\right)}/16⌋,\hfill \\ {\mathbf{T}}^{\left(4\right)}={\mathbf{T}}^{\left(2\right)}mod16,\hfill \end{array}\right.$$

  (4)

  where $⌊•⌋$ yields the largest integer that does not exceed its operand.
• Step 4: Sequentially superimpose each of the eight planes within ${\mathbf{T}}^{\left(3\right)}$ to obtain a fused 2D pixel matrix ${\mathbf{F}}^{\left(1\right)}$ with dimensions $H\times W$:

  $${\mathbf{F}}^{\left(1\right)}={\sum }_{k=1}^8\left({\mathbf{T}}^{\left(3\right)}(:,:,k)\times {16}^{8-k}\right).$$

  (5)
• Step 5: Analogously, each plane of size $H\times W$ within ${\mathbf{T}}^{\left(4\right)}$ is accumulated to yield another fused 2D pixel matrix ${\mathbf{F}}^{\left(2\right)}$.

  $${\mathbf{F}}^{\left(2\right)}={\sum }_{k=1}^8\left({\mathbf{T}}^{\left(4\right)}(:,:,k)\times {16}^{8-k}\right).$$

  (6)

3.2. Generating Chaotic Matrices

In our proposed MIEA-PRHM, the secret key comprises eight components, denoted as $\mathbf{K}=\{x_0^{\left(1\right)},y_0^{\left(1\right)},\alpha ,\beta ,x_0^{\left(2\right)},y_0^{\left(2\right)},\gamma ,\theta \}$. Among these eight components, the first four serve as inputs for 2D-SCPM, while the latter four are utilized as inputs for 2D-ELMM. In our proposed MIEA-PRHM, the chaotic sequences ${\tilde{\mathbf{Q}}}^{\left(1\right)}$ and ${\tilde{\mathbf{Q}}}^{\left(2\right)}$ generated by these two hyperchaotic maps are first superimposed to ensure that the resultant chaotic sequence ${\tilde{\mathbf{Q}}}^{\left(3\right)}$ exhibits enhanced aperiodicity and randomness. Subsequently, ${\tilde{\mathbf{Q}}}^{\left(3\right)}$ is further partitioned and transformed into four chaotic matrices ${\mathbf{R}}^{\left(1\right)}$, ${\mathbf{R}}^{\left(2\right)}$, ${\mathbf{R}}^{\left(3\right)}$, and ${\mathbf{R}}^{\left(4\right)}$, which are utilized in the subsequent encryption steps. Specifically, the generation processes of ${\mathbf{R}}^{\left(1\right)}$, ${\mathbf{R}}^{\left(2\right)}$, ${\mathbf{R}}^{\left(3\right)}$, and ${\mathbf{R}}^{\left(4\right)}$ are as follows:

• Step 1: Input $x_0^{\left(1\right)}$, $y_0^{\left(1\right)}$, $\alpha$, and $\beta$ into 2D-SCPM and subsequently perform iterations on it. The two chaotic state values obtained in each iteration are sequentially appended to ${\tilde{\mathbf{Q}}}^{\left(1\right)}$, continuing this process until the length of ${\tilde{\mathbf{Q}}}^{\left(1\right)}$ reaches $2\times H\times (H+W-1)$. Here, H and W are the height and width, respectively, of the two fused pixel matrices ${\mathbf{F}}^{\left(1\right)}$ and ${\mathbf{F}}^{\left(2\right)}$.
• Step 2: Input $x_0^{\left(2\right)}$, $y_0^{\left(2\right)}$, $\gamma$, and $\theta$ into 2D-ELMM and perform iterations on it. The two chaotic state values obtained in each iteration are sequentially appended to ${\tilde{\mathbf{Q}}}^{\left(2\right)}$, continuing this process until the length of ${\tilde{\mathbf{Q}}}^{\left(2\right)}$ reaches $2\times H\times (H+W-1)$.
• Step 3: Conduct a mathematical superposition on ${\tilde{\mathbf{Q}}}^{\left(1\right)}$ and ${\tilde{\mathbf{Q}}}^{\left(2\right)}$ to derive ${\tilde{\mathbf{Q}}}^{\left(3\right)}$:

  $${\tilde{\mathbf{Q}}}^{\left(3\right)}=({\tilde{\mathbf{Q}}}^{\left(1\right)}+{\tilde{\mathbf{Q}}}^{\left(2\right)})mod1.$$

  (7)
• Step 4: Conduct the following partitioning and transformation operations on ${\tilde{\mathbf{Q}}}^{\left(3\right)}$ to obtain the required four chaotic matrices:

  $$\left\{\begin{array}{c}{\mathbf{R}}^{\left(1\right)}=reshape({\widehat{\mathbf{Q}}}^{\left(3\right)}(1:H\times L),H,L),\hfill \\ {\mathbf{R}}^{\left(2\right)}=reshape(floor({\widehat{\mathbf{Q}}}^{\left(3\right)}(H\times L+1:H\times L+H\times W)\times 2^{32}),H,W),\hfill \\ {\mathbf{R}}^{\left(3\right)}=reshape({\widehat{\mathbf{Q}}}^{\left(3\right)}(H\times L+1:2\times H\times L),H,L),\hfill \\ {\mathbf{R}}^{\left(4\right)}=reshape(floor({\widehat{\mathbf{Q}}}^{\left(3\right)}(1:H\times W)\times 2^{32}),H,W),\hfill \end{array}\right.$$

  (8)

  where $L=H+W-1$.

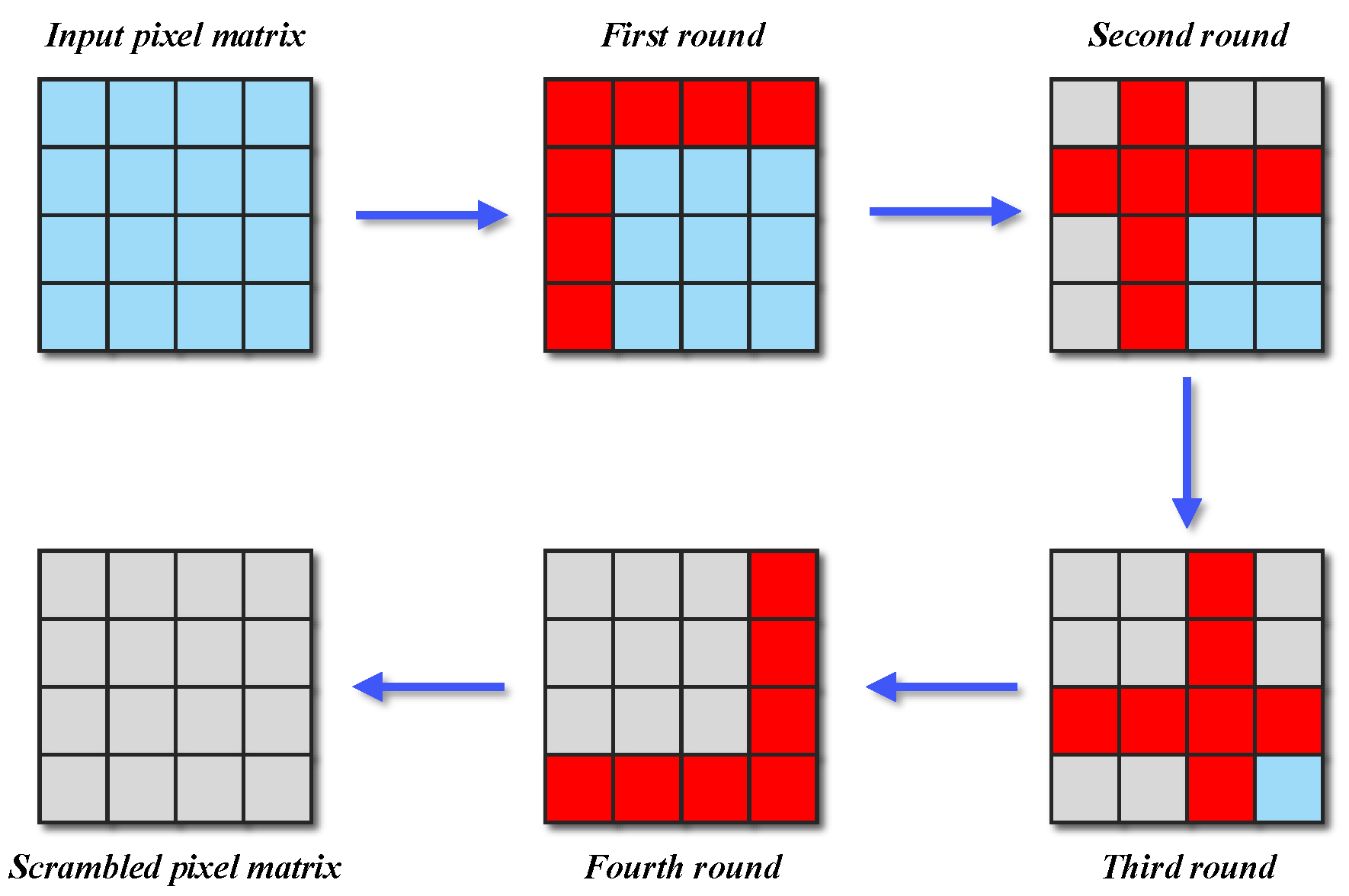
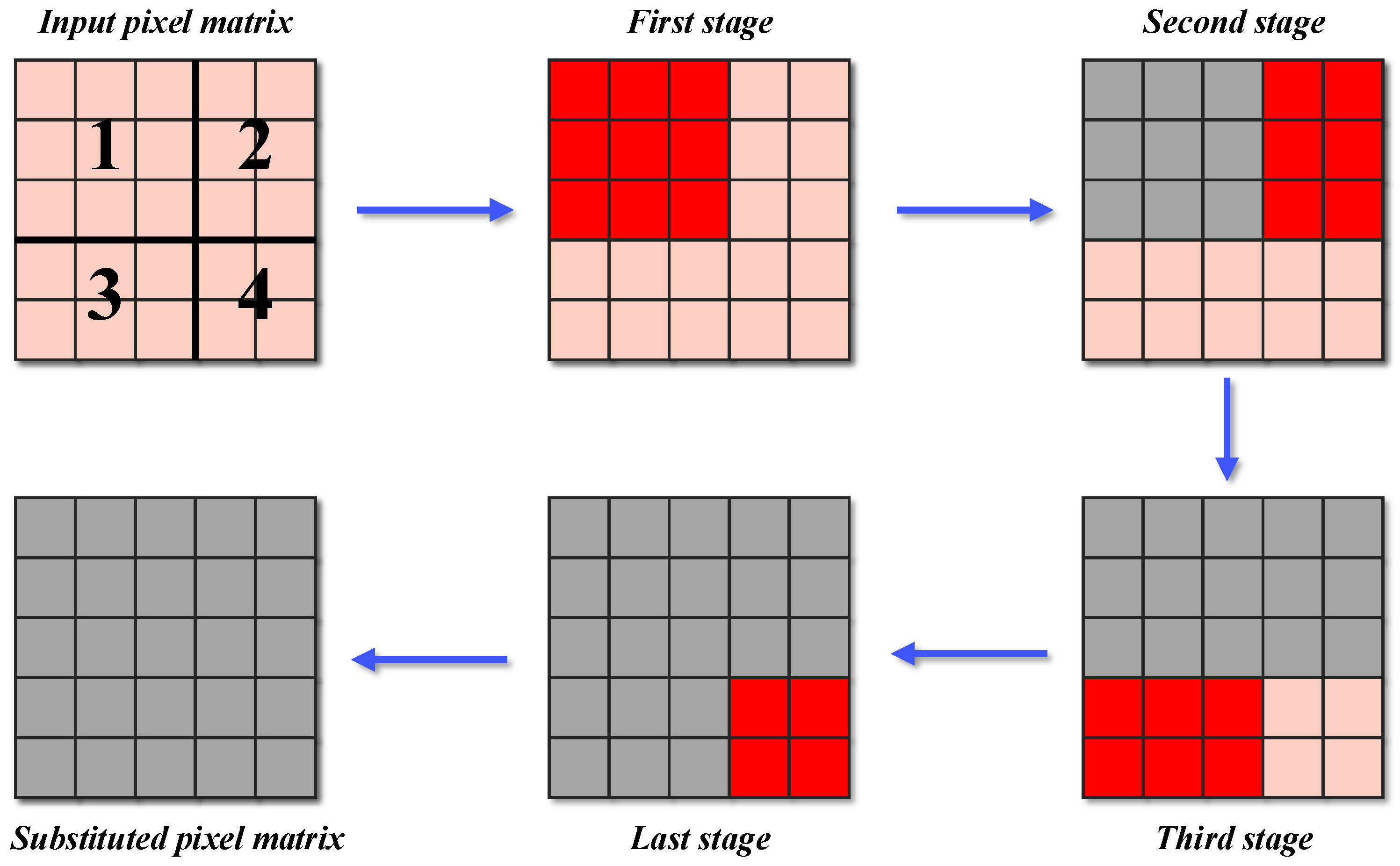
3.3. Row–Column Joint Scrambling

Scrambling or permutation operations constitute a pivotal component in modern cryptographic systems. In the context of image encryption algorithms, scrambling not only aids in reducing the correlation between adjacent pixels but also obscures the relationship between plaintext and ciphertext pixels, thereby enhancing the key sensitivity of image encryption algorithms [49]. Consequently, within our proposed MIEA-PRHM, we have devised an encryption step termed row–column joint scrambling. Below, we introduce this novel scrambling operation with a simple illustrative example as depicted in Figure 3.

This example demonstrates the row–column joint scrambling process for a $4\times 4$ input pixel matrix. It can be observed that the scrambling process consists of a total of four rounds. Initially, the pixels in the first row and first column are scrambled together. These seven pixels undergo permutation collectively. Subsequently, the seven pixels in the second row and second column are scrambled. Immediately thereafter, the pixels in the third row and third column are scrambled as well. Finally, the pixels in the fourth row and fourth column undergo scrambling. As shown in Figure 2, our proposed MIEA-PRHM performs row–column joint scrambling twice during the encryption process. Apart from the difference in input, there are no actual distinctions between these two scrambling steps. Therefore, we only provide the pseudocode for the first scrambling here as presented in Algorithm 1.

Algorithm 1 Row–column joint scrambling of MIEA-PRHM.

Input:   The fused pixel matrix ${\mathbf{F}}^{\left(1\right)}$ of size $H\times W$ and the chaotic matrix ${\mathbf{R}}^{\left(1\right)}$ of size $H\times (H+W-1)$.   1: $iter\_num=min(H,W)$;   2: for $i=1$ to $iter\_num$ do   3:    $left\_part={\mathbf{F}}^{\left(1\right)}(i,1:i-1)$;   4:    $mid\_part={\mathbf{F}}^{\left(1\right)}{(:,i)}^{\prime }$;   5:    $right\_part={\mathbf{F}}^{\left(1\right)}(i,i+1:W)$;   6:    $tmp\_px1=[left\_partmid\_partright\_part]$;   7:    $[\sim ,sort\_idx]=sort\left({\mathbf{R}}^{\left(1\right)}(i,:)\right)$;   8:    $tmp\_px2=tmp\_px1(sort\_idx)$;   9:     ${\mathbf{F}}^{\left(1\right)}(i,1:i-1)=tmp\_px2(1:i-1)$; 10:     ${\mathbf{F}}^{\left(1\right)}(:,i)=tmp\_px2{(i:i+H-1)}^{\prime }$; 11:     ${\mathbf{F}}^{\left(1\right)}(i,i+1:col)=tmp\_px2(i+H:H+W-1)$; 12: end for 13: ${\mathbf{C}}^{\left(1\right)}={\mathbf{F}}^{\left(1\right)}$; Output:  The scrambled pixel matrix ${\mathbf{C}}^{\left(1\right)}$.

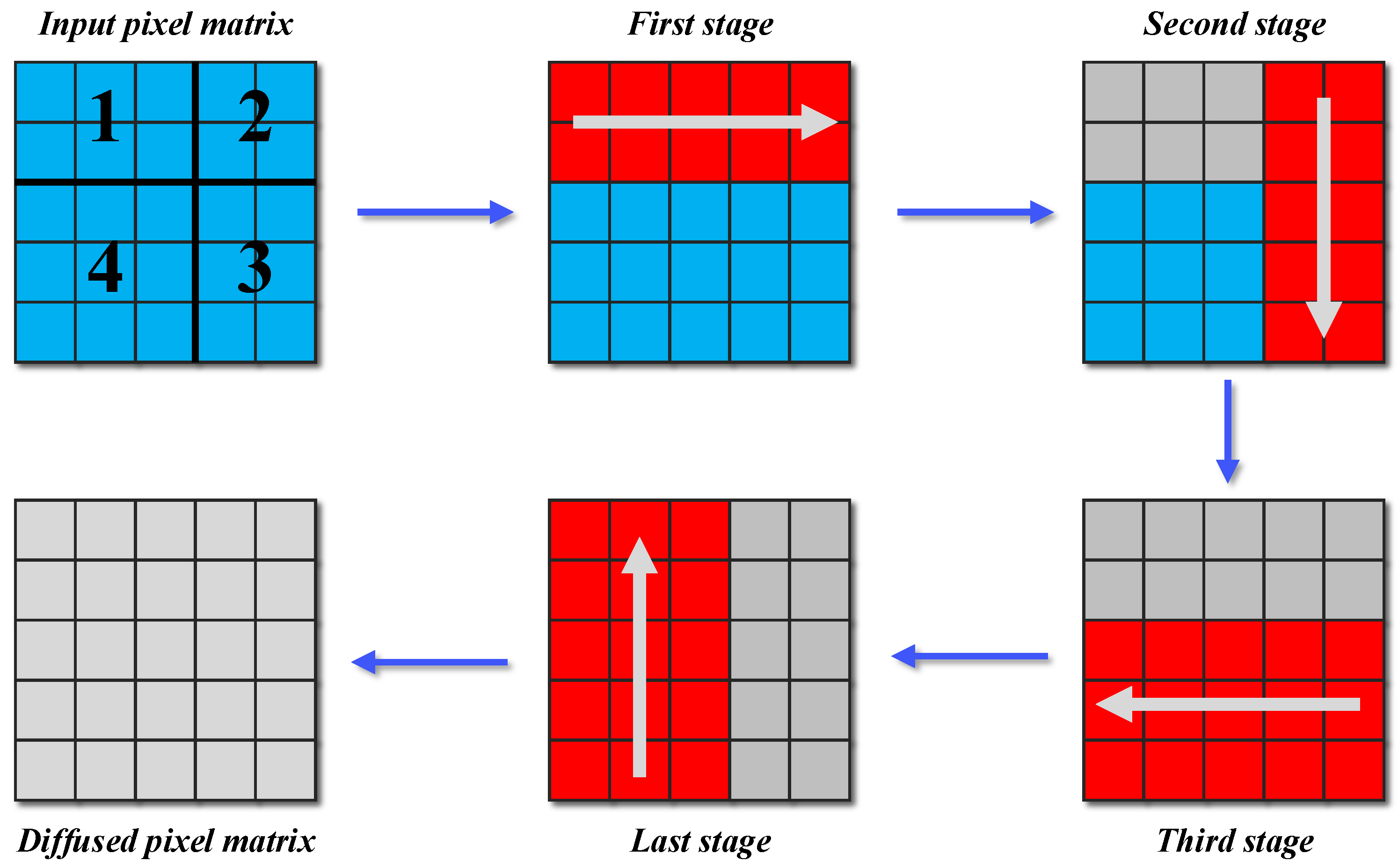
3.4. Vector-Level Dynamic Rotational Diffusion

Similarly to confusion, diffusion is one of the two fundamental principles advocated by Shannon for the design of cryptographic systems. Consequently, diffusion operations are indispensable in the design of image encryption algorithms. A well-designed diffusion operation will enhance the plaintext sensitivity and key sensitivity of the image encryption algorithm [49]. In light of this, we have devised an encryption step named vector-level dynamic rotational diffusion within our MIEA-PRHM. In comparison to the diffusion operations employed in some recent image encryption algorithms, our diffusion operation has several notable advantages. Firstly, it operates at the vector level, facilitating a more efficient pixel diffusion process, thereby enhancing encryption efficiency. Secondly, the dynamism of it, which is contingent upon image sizes, plaintext-related parameters, and chaotic sequence values, significantly increases the difficulty for attackers to launch successful differential attacks. Lastly, during the rotational diffusion of pixels, the mathematical operations employed vary depending on the diffusion directions. This design fosters a more complex nonlinear relationship between ciphertext and plaintext pixels, which similarly facilitates the thwarting of various differential attacks, including plaintext attacks.

In Figure 4, we provide a straightforward example to demonstrate the proposed vector-level dynamic rotational diffusion. Before initiating the diffusion process, we first determine a partitioning coordinate based on the input pixel matrix’s size, plaintext-related parameters, and chaotic sequence values. Specifically, in this example, the partitioning coordinate is $(2,3)$. Consequently, the input pixel matrix can be logically partitioned into four sub-blocks, named for convenience as logical sub-block 1, logical sub-block 2, logical sub-block 3, and logical sub-block 4. Subsequently, the diffusion of all pixels proceeds in four phases. In the first phase, the pixels within logical sub-blocks 1 and 2 are initially diffused. These pixels undergo horizontal diffusion from left to right in the form of column vectors. During the second phase, diffusion occurs in the regions occupied by logical sub-blocks 2 and 3, where pixels are vertically diffused from top to bottom in the form of row vectors. In the third phase, the pixels in logical sub-blocks 3 and 4 undergo diffusion in a manner similar to the first phase but with the opposite direction. During the final stage, the pixels within logical sub-blocks 1 and 4 are diffused in a bottom-to-top manner. As shown in Figure 2, our proposed MIEA-PRHM algorithm performs row–column joint scrambling third times during the encryption process.

As can be seen in Figure 2, our MIEA-PRHM algorithm incorporates three identical vector-level dynamic rotational diffusion steps in the encryption process, differing only in their input. Hence, we provide only the pseudocode for the initial diffusion step here, which is presented in Algorithm 2.

Algorithm 2 Vector-level dynamic rotational diffusion of MIEA-PRHM.

Input:  The scrambled pixel matrix ${\mathbf{C}}^{\left(1\right)}$ of size $H\times W$, the chaotic matrix ${\mathbf{R}}^{\left(2\right)}$ of size $H\times W$, and the plaintext-related vector $\mathbf{V}$ of size $1\times 8$.   1: Perform XOR operations on all elements of $\mathbf{V}$ and save the result to $h\_xor$;   2: $h\_idx$ = $mod(h\_xor,W-1)+1$;   3: $\tilde{x}=floor(H/2)+mod({\mathbf{R}}^{\left(2\right)}(1,h\_idx)+h\_xor,floor(H/8))$;   4: $\tilde{y}=floor(W/2)+mod({\mathbf{R}}^{\left(2\right)}(1,h\_idx+1)+h\_xor,floor(W/8))$;   5: ${\mathbf{M}}^{\left(1\right)}(1:\tilde{x},1)=mod({\mathbf{C}}^{\left(1\right)}(1:\tilde{x},1)+{\mathbf{C}}^{\left(1\right)}(1:\tilde{x},W)+{\mathbf{C}}^{\left(1\right)}(1:\tilde{x},W-1),2^{32})$;   6: ${\mathbf{M}}^{\left(1\right)}(1:\tilde{x},2)=mod({\mathbf{C}}^{\left(1\right)}(1:\tilde{x},2)+{\mathbf{M}}^{\left(1\right)}(1:\tilde{x},1)+{\mathbf{C}}^{\left(1\right)}(1:\tilde{x},W),2^{32})$;   7: for $i=3$ to W do   8:    ${\mathbf{M}}^{\left(1\right)}(1:\tilde{x},i)=mod({\mathbf{C}}^{\left(1\right)}(1:\tilde{x},i)+{\mathbf{M}}^{\left(1\right)}(1:\tilde{x},i-1)+{\mathbf{M}}^{\left(1\right)}(1:\tilde{x},i-2),2^{32})$;   9: end for 10: ${\mathbf{M}}^{\left(2\right)}(1,\tilde{y}+1:W)=bitxor({\mathbf{M}}^{\left(1\right)}(1,\tilde{y}+1:W),{\mathbf{M}}^{\left(1\right)}(H,\tilde{y}+1:W))$; 11: for $i=2$ to H do 12:    ${\mathbf{M}}^{\left(2\right)}(i,\tilde{y}+1:W)=bitxor({\mathbf{M}}^{\left(1\right)}(i,\tilde{y}+1:W),{\mathbf{M}}^{\left(2\right)}(i-1,\tilde{y}+1:W))$; 13: end for 14: ${\mathbf{M}}^{\left(3\right)}(\tilde{x}+1:H,W)=mod({\mathbf{M}}^{\left(2\right)}(\tilde{x}+1:H,W)+{\mathbf{M}}^{\left(2\right)}(\tilde{x}+1:H,1)+{\mathbf{M}}^{\left(2\right)}(\tilde{x}+1:H,2),2^{32})$; 15: ${\mathbf{M}}^{\left(3\right)}(\tilde{x}+1:H,W-1)=mod({\mathbf{M}}^{\left(3\right)}(\tilde{x}+1:H,W)+{\mathbf{M}}^{\left(2\right)}(\tilde{x}+1:H,W-1)+{\mathbf{M}}^{\left(2\right)}(\tilde{x}+1:H,1),2^{32})$; 16: for $i=W-2$ to 1 do 17:    ${\mathbf{M}}^{\left(3\right)}(\tilde{x}+1:H,i)=mod({\mathbf{M}}^{\left(2\right)}(\tilde{x}+1:H,i)+{\mathbf{M}}^{\left(3\right)}(\tilde{x}+1:H,i+1)+{\mathbf{M}}^{\left(3\right)}(\tilde{x}+1:H,i+2),2^{32})$; 18: end for 19: ${\mathbf{C}}^{\left(2\right)}(H,1:\tilde{y})=bitxor({\mathbf{M}}^{\left(3\right)}(H,1:\tilde{y}),{\mathbf{M}}^{\left(3\right)}(1,1:\tilde{y}))$; 20: for $i=H-1$ to 1 do 21:    ${\mathbf{C}}^{\left(2\right)}(i,1:\tilde{y})=bitxor({\mathbf{M}}^{\left(3\right)}(i,1:\tilde{y}),{\mathbf{C}}^{\left(2\right)}(i+1,1:\tilde{y}))$; 22: end for Output:  The diffused pixel matrix ${\mathbf{C}}^{\left(2\right)}$.

3.5. Dual-Operation Dynamic Partition Substitution

Like permutation and diffusion operations, substitution operations play a crucial role in the construction of modern cryptographic systems. They significantly contribute to enhancing the nonlinearity of the encryption process [49]. In numerous image encryption algorithms that rely on chaotic systems, substitution operations are typically carried out using single fixed mathematical operations. According to current cryptanalysis studies, such designs are vulnerable to plaintext attacks launched by attackers. Therefore, to further bolster the nonlinearity and security of the encryption process, we introduce an encryption step named dual-operation dynamic partition substitution in our MIEA-PRHM. Unlike some existing substitution operations, this encryption step possesses dynamic behavior that depends on both the plaintext and chaotic sequences. Additionally, it operates on partitioned sub-blocks while incorporating two mathematical operations. These features collectively reinforce the security of MIEA-PRHM, effectively safeguarding it against various potential attacks, especially the most threatening plaintext attacks.

Similarly, we illustrate our dual-operation dynamic partition substitution with a simple example as depicted in Figure 5. First, we determine a partitioning coordinate based on the input chaotic sequence values and plaintext parameters. Utilizing this coordinate, the input pixel matrix is logically divided into four sub-blocks. Subsequently, these four sub-blocks will undergo substitution in distinct phases and manners. In our proposed MIEA-PRHM, we perform a total of two dual-operation dynamic partition substitutions as demonstrated in Figure 2. Since the only distinction between these two substitution operations is the input parameters, we only provide the pseudocode for the substitution operation on ${\mathbf{C}}^{\left(2\right)}$ in Algorithm 3.

Algorithm 3 Dual-operation dynamic partition substitution of MIEA-PRHM.

Input:   The diffused pixel matrix ${\mathbf{C}}^{\left(2\right)}$ of size $H\times W$, the chaotic matrix ${\mathbf{R}}^{\left(2\right)}$ of size $H\times W$, and the plaintext-related vector $\mathbf{V}$ of size $1\times 8$.   1: $h\_sum=sum\left(\mathbf{V}\right(:\left)\right)$;   2: $h\_idx$ = $mod(h\_sum,H-1)+1$;   3: $\tilde{x}=floor(H/2)+mod({\mathbf{R}}^{\left(2\right)}(h\_idx,1)+h\_sum,floor(H/8))$;   4: $\tilde{y}=floor(W/2)+mod({\mathbf{R}}^{\left(2\right)}(h\_idx+1,1)+h\_sum,floor(W/8))$;   5: ${\mathbf{C}}^{\left(3\right)}(1:\tilde{x},1:\tilde{y})=mod({\mathbf{C}}^{\left(2\right)}(1:\tilde{x},1:\tilde{y})+{\mathbf{R}}^{\left(2\right)}(1:\tilde{x},1:\tilde{y})+h\_sum,2^{32})$;   6: ${\mathbf{C}}^{\left(3\right)}(1:\tilde{x},\tilde{y}+1:W)=bitxor(bitxor({\mathbf{C}}^{\left(2\right)}(1:\tilde{x},\tilde{y}+1:W),{\mathbf{R}}^{\left(2\right)}(1:\tilde{x},\tilde{y}+1:W)),h\_sum)$;   7: ${\mathbf{C}}^{\left(3\right)}(\tilde{x}+1:H,1:\tilde{y})=mod({\mathbf{C}}^{\left(2\right)}(\tilde{x}+1:H,1:\tilde{y})+{\mathbf{R}}^{\left(2\right)}(\tilde{x}+1:H,1:\tilde{y})+h\_sum,2^{32})$;   8: ${\mathbf{C}}^{\left(3\right)}(\tilde{x}+1:H,\tilde{y}+1:W)=bitxor(bitxor({\mathbf{C}}^{\left(2\right)}(\tilde{x}+1:H,\tilde{y}+1:W),{\mathbf{R}}^{\left(2\right)}(\tilde{x}+1:H,\tilde{y}+1:W)),h\_sum)$; Output:  The substituted pixel matrix ${\mathbf{C}}^{\left(3\right)}$.

3.6. Entire Encryption and Decryption Process of MIEA-PRHM

Below, we provide a concise description of the entire encryption and decryption process, aiming to clearly illustrate the execution sequence for all encryption steps, along with their corresponding input and output. Let us consider a scenario where Alice (the sender) and Bob (the receiver) wish to transmit a batch of images over an insecure communication channel. The secret key that they have mutually agreed upon is $\mathbf{K}=\{x_0^{\left(1\right)},y_0^{\left(1\right)},\alpha ,\beta ,x_0^{\left(2\right)},y_0^{\left(2\right)},\gamma ,\theta \}$. Initially, Alice proceeds with the encryption of the images as follows:

• Step 1: Perform pixel reorganization on the input images to obtain two fused 2D pixel matrices ${\mathbf{F}}^{\left(1\right)}$ and ${\mathbf{F}}^{\left(2\right)}$. For more information about pixel reorganization, please refer to Section 3.1.
• Step 2: Input the fused pixel matrices ${\mathbf{F}}^{\left(1\right)}$ and ${\mathbf{F}}^{\left(2\right)}$ into the SHA-256 algorithm to generate a 256-bit hash value $\tilde{h}$. Then, convert the hash value $\tilde{h}$ into a plaintext-related vector $\mathbf{V}$. More details on generating the plaintext-related vector $\mathbf{V}$ can be found in Section 2.4.
• Step 3: Utilize the secret key $\mathbf{K}$ to generate the four chaotic matrices ${\mathbf{R}}^{\left(1\right)}$, ${\mathbf{R}}^{\left(2\right)}$, ${\mathbf{R}}^{\left(3\right)}$, and ${\mathbf{R}}^{\left(4\right)}$. For more information about generating chaotic matrices, please refer to Section 3.2.
• Step 4: Employ the chaotic matrix ${\mathbf{R}}^{\left(1\right)}$ to perform row–column joint scrambling on the fused pixel matrix ${\mathbf{F}}^{\left(1\right)}$ to obtain the scrambled pixel matrix ${\mathbf{C}}^{\left(1\right)}$. More details on row–column joint scrambling can be found in Section 3.3.
• Step 5: Utilize the plaintext-related vector $\mathbf{V}$ and the chaotic matrix ${\mathbf{R}}^{\left(2\right)}$ to perform vector-level dynamic rotational diffusion on the scrambled pixel matrix ${\mathbf{C}}^{\left(1\right)}$. The output obtained is the diffused pixel matrix ${\mathbf{C}}^{\left(2\right)}$. For more information about vector-level dynamic rotational diffusion, please refer to Section 3.4.
• Step 6: Employ the plaintext-related vector $\mathbf{V}$ and the chaotic matrix ${\mathbf{R}}^{\left(2\right)}$ to perform dual-operation dynamic partition substitution on the diffused pixel matrix ${\mathbf{C}}^{\left(2\right)}$. The output obtained is the substituted pixel matrix ${\mathbf{C}}^{\left(3\right)}$. More details on perform dual-operation dynamic partition substitution can be found in Section 3.5.
• Step 7: Utilize the plaintext-related vector $\mathbf{V}$ and the chaotic matrix ${\mathbf{R}}^{\left(2\right)}$ to perform vector-level dynamic rotational diffusion on the substituted pixel matrix ${\mathbf{C}}^{\left(3\right)}$. The output obtained is the diffused pixel matrix ${\mathbf{C}}^{\left(4\right)}$.
• Step 8: Employ the chaotic matrix ${\mathbf{R}}^{\left(3\right)}$ to perform row–column joint scrambling on the diffused pixel matrix ${\mathbf{C}}^{\left(4\right)}$ to obtain the scrambled pixel matrix ${\mathbf{C}}^{\left(5\right)}$.
• Step 9: Utilize the plaintext-related vector $\mathbf{V}$ and the chaotic matrix ${\mathbf{R}}^{\left(4\right)}$ to perform dual-operation dynamic partition substitution on the fused pixel matrix ${\mathbf{F}}^{\left(1\right)}$. The output obtained is the substituted pixel matrix ${\mathbf{C}}^{\left(6\right)}$.
• Step 10: Employ the plaintext-related vector $\mathbf{V}$ and the chaotic matrix ${\mathbf{R}}^{\left(4\right)}$ to perform vector-level dynamic rotational diffusion on the substituted pixel matrix ${\mathbf{C}}^{\left(6\right)}$. The output obtained is the diffused pixel matrix ${\mathbf{C}}^{\left(7\right)}$.
• Step 11: Perform inverse pixel reorganization on the two ciphertext pixel matrices ${\mathbf{C}}^{\left(5\right)}$ and ${\mathbf{C}}^{\left(7\right)}$ to obtain the final ciphertext images.

Subsequently, Alice sends the final ciphertext images, along with the hash value $\tilde{h}$, to Bob via the insecure communication channel. Upon receiving them, Bob proceeds to decrypt the ciphertext images according to the decryption process depicted in Figure 6, ultimately acquiring the necessary decrypted images. By examining Figure 6, one can clearly see that the decryption process of MIEA-PRHM is the mirror image of its encryption process. Each decryption step corresponds directly to an encryption step, and is essentially the reverse of its counterpart. Since there are no significant differences, we will, for brevity’s sake, omit the redundant description of these decryption steps here.

4. Experiments and Performance Analyses

This section will demonstrate and analyze the performance of MIEA-PRHM in terms of security and efficiency. These analyses cover ten aspects, including visual assessment, key space, key sensitivity, plaintext sensitivity, and so on. The employed test images are sourced from common benchmark databases, which are USC-SIPI (http://sipi.usc.edu/database/, accessed on 1 November 2024) and CVG-UGR (https://ccia.ugr.es/cvg/dbimagenes/index.php, accessed on 1 November 2024). The hardware platform is a PC with an Intel CPU E3-1231 v3 and 8 GB of RAM. MATLAB R2017a serves as the simulation software. Unless specified, randomly generated secret keys are adopted to ensure the generality and objectivity of our performance analyses.

4.1. Visual Assessment

To ensure the robust safeguarding of various digital images, a proposed image encryption algorithm must possess the capacity to transform them into unrecognizable forms akin to random noise [51]. In this subsection, three grayscale images (5.1.09, 5.2.09, and boat.512) and three color images (4.1.07, avion, and beeflowr) undergo encryption and subsequent decryption processes utilizing our MIEA-PRHM algorithm. Notably, all twelve images undergo concurrent encryption and decryption, thereby demonstrating the exceptional multi-image encryption and decryption capabilities of our MIEA-PRHM. Inspection of Figure 7 reveals a compelling transformation: upon application of MIEA-PRHM, six images that were originally rich in detail are encrypted into indistinguishable, noise-like patterns. Crucially, upon decryption, these unrecognizable images are successfully restored to their pristine states without any loss of detail. This outcome underscores the exceptional encryption and decryption proficiency of MIEA-PRHM, thereby affirming its potential as an effective measure for safeguarding digital images.

4.2. Key Space

Brute-force attack is a prevalent attack methodology favored by adversaries. Its foundation lies in the exhaustive search paradigm, where every possible secret key within the key space is systematically scrutinized until the correct one is found. Consequently, the dimension of the key space is indispensable for thwarting brute-force attacks. Presently, the prevailing consensus believes that a suggested image encryption algorithm must possess a key space of at least $2^{128}$ [55,56]. A failure to meet this criterion would render the algorithm susceptible to brute-force attacks, thereby compromising its security.

The secret key $\mathbf{K}$ of MIEA-PRHM is comprised of eight constituents: $x_0^{\left(1\right)}$, $y_0^{\left(1\right)}$, $\alpha$, $\beta$, $x_0^{\left(2\right)}$, $y_0^{\left(2\right)}$, $\gamma$, and $\theta$. We delineate their respective permissible value ranges as $x_0^{\left(1\right)}\in (0,1)$, $y_0^{\left(1\right)}\in (0,1)$, $\alpha \in [1,12]$, $\beta \in [1,12]$, $x_0^{\left(2\right)}\in (0,1)$, $y_0^{\left(2\right)}\in (0,1)$, $\gamma \in [1,10]$, and $\theta \in [1,10]$. Moreover, we establish a minimum precision for each constituent, which is ${10}^{-15}$. Given these stipulations, we can readily ascertain the size of $\mathbf{K}$ for MIEA-PRHM as follows:

$$\begin{array}{cc}\hfill S^{\left(\mathbf{K}\right)}& =S^{x_0^{\left(1\right)}}\times S^{y_0^{\left(1\right)}}\times S^{\alpha }\times S^{\beta }\times S^{x_0^{\left(2\right)}}\times S^{y_0^{\left(2\right)}}\times S^{\gamma }\times S^{\theta }\hfill \\ \hfill & =9.8010\times {10}^{123}\approx 2^{412}.\hfill \end{array}$$

(9)

Apparently, $S^{\left(\mathbf{K}\right)}$ far surpasses the minimal threshold $2^{128}$ typically mandated for the size of the key space. Consequently, it is evident that our proposed MIEA-PRHM possesses an exceedingly vast key space, thereby rendering it highly efficacious in resisting brute-force attacks.

4.3. Key Sensitivity

Key sensitivity constitutes a pivotal attribute of image encryption algorithms, necessitating that minute variations in the secret key elicit substantial disparities in the resultant ciphertext [56]. An image encryption algorithm that possesses exceptionally high key sensitivity signifies its formidable resilience against various statistical or analytical attacks pertinent to the secret key. To ascertain the key sensitivity of MIEA-PRHM, we initially encrypt the test image 5.2.08 using a randomly generated secret key

$$bf\widehat{K}=\left\{\begin{array}{c}{\widehat{x}}_0^{\left(1\right)}=0.360017466884543,\hfill \\ {\widehat{y}}_0^{\left(1\right)}=0.322741310342732,\hfill \\ \widehat{\alpha }=10.638285158199237,\hfill \\ \widehat{\beta }=8.385277595506832,\hfill \\ {\widehat{x}}_0^{\left(2\right)}=0.540588294762065,\hfill \\ {\widehat{y}}_0^{\left(2\right)}=0.105110255236755,\hfill \\ \widehat{\gamma }=4.901907916370962,\hfill \\ \widehat{\theta }=9.782868288753209.\hfill \end{array}\right.$$

(10)

Subsequently, we introduce single minimal alterations to each component of $\widehat{\mathbf{K}}$ (incrementing each by ${10}^{-15}$) and utilize these modified secret keys to encrypt the identical image. Ultimately, we compute the differential images between these newly generated ciphertext images and the original one. Figure 8 delineates the pertinent experimental results. It is evident that even a minimal variation in the secret key elicits an exceedingly comprehensive ciphertext change. More crucially, all differential images display a strong resemblance to noise images, possessing a high degree of randomness. Consequently, our proposed MIEA-PRHM algorithm possesses exceptional key sensitivity, rendering it highly resilient against various statistical or analytical attacks pertinent to the secret key.

4.4. Plaintext Sensitivity

Differential attacks generally exploit the ciphertext disparities resulting from minimal plaintext changes to launch targeted attacks. Hence, to effectively withstand various differential attacks, suggested image encryption algorithms must possess exceptionally high plaintext sensitivity [52]. This entails any pixel bit change in the input digital image eliciting extremely noticeable ciphertext changes. To showcase the sensitivity of MIEA-PRHM to minimal plaintext alterations, we deliberately modify two pixel bits in the test image 2.1.05, positioned at its top-left and bottom-right corners. The second and third columns of the first row of Figure 9 show the two modified images. Visually, no discernible differences can be observed among the three plaintext images. Subsequently, we encrypt these three images using MIEA-PRHM and compute the differential images between the resultant ciphertext images. Observing Figure 9, one can ascertain that all encrypted images and differential images resemble noise patterns. This underscores that the single pixel bit variations, upon processing by MIEA-PRHM, elicit thorough, near-random ciphertext transformations. Consequently, MIEA-PRHM possesses extremely high plaintext sensitivity.

To rigorously and precisely validate the performance of MIEA-PRHM in plaintext sensitivity, we conduct pertinent quantitative analyses. There are two indices for quantifying plaintext sensitivity [52]. The first one is the normalized pixel change rate (NPCR), which can measure the proportion of pixels that differ between two images. The second is the unified average changing intensity (UACI), which can assess the average magnitude of pixel changes. Given two images ${\mathbf{I}}^{\left(\mathbf{1}\right)}$ and ${\mathbf{I}}^{\left(\mathbf{2}\right)}$ with dimensions $M\times N$, we can quantitatively evaluate the pixel changes between them using the following two equations:

$$NPCR({\mathbf{I}}^{\left(1\right)},{\mathbf{I}}^{\left(2\right)})={\sum }_{\alpha =1}^M{\sum }_{\beta =1}^N\mathbf{D}(\alpha ,\beta )/(M\times N)\times 100\%,$$

(11)

$$UACI({\mathbf{I}}^{\left(1\right)},{\mathbf{I}}^{\left(2\right)})={\sum }_{\alpha =1}^M{\sum }_{\beta =1}^N\left|{\mathbf{I}}^{\left(1\right)}(\alpha ,\beta )-{\mathbf{I}}^{\left(2\right)}(\alpha ,\beta )\right|/(255\times M\times N)\times 100\%.$$

(12)

In the aforementioned equation defining NPCR, $\mathbf{D}(\alpha ,\beta )$ takes a value of either 0 or 1. This depends on whether the pixel values at the identical coordinates are the same. If the pixel values match, $\mathbf{D}(\alpha ,\beta )$ is assigned a value of 1.

Table 2. NPCR experimental results (%) of six image encryption algorithms.

Image Size	Test Image	MIEA-PRHM	[53]	[45]	[49]	[47]	[50]
$256\times 256$	5.1.09	99.6124	99.5895	99.6338	99.6082	99.6246	99.6078
	5.1.11	99.5960	99.5926	99.6140	99.6298	99.5850	99.5819
	5.1.13	99.6155	99.5743	99.6048	99.6101	99.6033	99.6047
	5.1.14	99.6010	99.5865	99.5850	99.5884	99.5972	99.6292
$512\times 512$	5.2.09	99.5972	99.6292	99.6109	99.5975	99.6155	99.6170
	7.1.01	99.6262	99.6353	99.6429	99.6078	99.6292	99.6109
	7.1.03	99.6063	99.5834	99.5697	99.6155	99.5850	99.6032
	boat.512	99.6155	99.6445	99.5758	99.6239	99.6002	99.6078
$1024\times 1024$	5.3.01	99.6231	99.6155	99.6185	99.6181	99.6094	99.6262
	5.3.02	99.5941	99.6246	99.6353	99.6117	99.6155	99.6078
	7.2.01	99.6094	99.6185	99.6002	99.6071	99.5926	99.5864
	testpat.1k	99.6181	99.5895	99.6155	99.6006	99.6292	99.6139
	Avg	99.6096	99.6070	99.6089	99.6099	99.6072	99.6081
	Std. Dev.	0.0108	0.0235	0.0232	0.0113	0.0159	0.0138

and

Table 3. UACI experimental results (%) of six image encryption algorithms.

Image Size	Test Image	MIEA-PRHM	[53]	[45]	[49]	[47]	[50]
$256\times 256$	5.1.09	33.4845	33.3685	33.4223	33.4518	33.4847	33.3783
	5.1.11	33.4955	33.5111	33.3398	33.4329	33.4137	33.5601
	5.1.13	33.4224	33.4419	33.4388	33.5177	33.4525	33.4732
	5.1.14	33.4525	33.5885	33.4009	33.3714	33.4424	33.4905
$512\times 512$	5.2.09	33.4997	33.5932	33.5688	33.4583	33.4631	33.4716
	7.1.01	33.4965	33.5071	33.4418	33.5758	33.5157	33.3701
	7.1.03	33.4568	33.4755	33.5168	33.5422	33.3914	33.3884
	boat.512	33.5051	33.3798	33.5253	33.4603	33.4053	33.3365
$1024\times 1024$	5.3.01	33.4625	33.4009	33.3672	33.4915	33.4583	33.5294
	5.3.02	33.4478	33.3388	33.5134	33.4538	33.5248	33.3473
	7.2.01	33.4480	33.4569	33.4040	33.3529	33.4218	33.5224
	testpat.1k	33.3984	33.5242	33.5231	33.4404	33.5121	33.5067
	Avg	33.4641	33.4655	33.4552	33.4624	33.4572	33.4479
	Std. Dev.	0.0333	0.0833	0.0725	0.0639	0.0449	0.0788

present the NPCR and UACI assessment results obtained through our extensive experiments. In these experiments, each test image also undergoes only a single bit alteration. Notably, the experimental results achieved by MIEA-PRHM are remarkably close to the ideal values of 99.6094% and 33.4635% for NPCR and UACI, respectively. Furthermore, compared to the five recently reported image encryption algorithms, MIEA-PRHM not only demonstrates closer proximity to the ideal values but also exhibits superior stability. This underscores the exceptionally superior plaintext sensitivity of our proposed MIEA-PRHM algorithm.

4.5. Pixel Correlation

Within natural digital images, there are obvious discernible correlations among neighboring pixels. Consequently, to mitigate the potential security risks stemming from these correlations, robust image encryption algorithms must efficiently eradicate them [51]. To evaluate the capability of MIEA-PRHM in this regard, we encrypt two test images, which are 2.1.02 and 4.2.03. Thereafter, we generate twelve correlation analysis plots for these images, furnishing a vivid and intuitive depiction of the ability of MIEA-PRHM to disrupt the correlations and thereby bolster image security.

Figure 10 demonstrates the significant changes in pixel correlations across horizontal, vertical, and diagonal orientations. These analysis plots reveal an initially high degree of pixel correlations in all three orientations. However, upon application of MIEA-PRHM, there are no discernible pixel correlations across all orientations in encrypted images. This substantiates the superior capability of MIEA-PRHM in effectively removing the correlations among neighboring pixels.

Furthermore, we conduct a more objective numerical analysis of the capacity of MIEA-PRHM to eliminate the pixel correlation in all orientations. The evaluation metric employed here is the correlation coefficient (CC) [52]. Mathematically, one can compute the CC value for digital images using the following equation:

$$CC=E(({\nu }_{\alpha }-E\left({\nu }_{\beta }\right))\times ({\nu }_{\alpha }-E\left({\nu }_{\beta }\right)))/\sqrt{D\left({\nu }_{\alpha }\right)\times D\left({\nu }_{\beta }\right)}.$$

(13)

In the aforementioned equation, ${\nu }_{\alpha }$ and ${\nu }_{\beta }$ denote pixel values. $E\left({\nu }_{\alpha }\right)$ and $E\left({\nu }_{\beta }\right)$ represent expectations, while $D\left({\nu }_{\alpha }\right)$ and $D\left({\nu }_{\beta }\right)$ indicate variances.

Table 4. CC values of twelve test images and their ciphertext images.

Image Size	Test Image	CC Values (Plaintext)			CC Values (Ciphertext)
		Horizontal	Vertical	Diagonal	Horizontal	Vertical	Diagonal
$256\times 256$	5.1.09	0.9398	0.9053	0.9115	−0.0006	−0.0011	−0.0008
	5.1.11	0.9454	0.9555	0.8991	0.0016	−0.0013	−0.0011
	5.1.13	0.8567	0.8714	0.7895	0.0008	−0.0013	0.0007
	5.1.14	0.9035	0.9463	0.8621	0.0013	−0.0019	0.0003
$512\times 512$	5.2.09	0.8665	0.8975	0.7937	0.0019	0.0011	0.0005
	7.1.01	0.9173	0.9610	0.9026	0.0009	−0.0018	0.0002
	7.1.03	0.9288	0.9456	0.9021	0.0014	0.0010	−0.0012
	boat.512	0.9688	0.9411	0.9191	−0.0003	−0.0014	0.0006
$1024\times 1024$	5.3.01	0.9825	0.9773	0.9665	0.0017	−0.0004	−0.0002
	5.3.02	0.9020	0.9137	0.8632	−0.0011	−0.0005	0.0015
	7.2.01	0.9498	0.9639	0.9462	−0.0019	0.0005	−0.0008
	testpat.1k	0.8128	0.7840	0.7015	0.0002	0.0019	0.0001

presents the experimental outcomes obtained. Notably, all images demonstrate high CC values across various directions and channels. Nevertheless, subsequent to encryption using MIEA-PRHM, these CC values significantly diminish to exceptionally low levels. This underscores the MIEA-PRHM algorithm’s exceptional capability in eliminating pixel correlations.

4.6. Information Entropy

Owing to its capacity to gauge the overall randomness of pixels, information entropy is commonly invoked to scrutinize the security performance of proposed image encryption algorithms. Typically, a larger entropy value signifies that the ciphertext pixels exhibit a heightened level of randomness, accompanied by a more consistent distribution [54]. Mathematically, the determination of the entropy value can be achieved through the following definition:

$$\xi \left(\mathbf{v}\right)=-{\sum }_{\alpha =1}^{Q}p\left({\mathbf{v}}_{\alpha }\right)\times {log}_{2}p\left({\mathbf{v}}_{\alpha }\right),$$

(14)

where Q signifies the quantity of pixel values denoted as $\mathbf{v}$, and $p\left({\mathbf{v}}_{\alpha }\right)$ embodies the probabilistic measure of ${\mathbf{v}}_{\alpha }$. According to the formulation stipulated in Equation (14), for an 8-bit ciphertext image, the zenith of its entropy attains a value of 8.

Utilizing our MIEA-PRHM, we encrypt twelve common test images and proceed to compute the entropy outputs pertaining to these test images. An examination of the data presented in

Table 5. Information entropy assessment results for MIEA-PRHM.

Image Size	Test Image	Entropy (Plaintext)	Entropy (Ciphertext)
$512\times 512$	5.2.09	6.9940	7.9994
	7.1.04	6.1074	7.9993
	7.1.08	5.0534	7.9993
	boat.512	7.1914	7.9994
	avion	6.5768	7.9993
	beeflowr	3.0720	7.9994
$1024\times 1024$	2.2.01	7.3508	7.9998
	2.2.03	5.6627	7.9998
	2.2.05	7.0896	7.9998
	2.2.07	5.9199	7.9998
	5.3.01	7.5237	7.9998
	testpat.1k	4.4077	7.9999

elucidates that the entropy outputs associated with the original test images are comparatively modest. Conversely, subsequent to the encryption process, the entropy outputs corresponding to the resultant ciphertext images manifest a proximity to the ideal value of 8, indicating a significant enhancement in the informational randomness. From this observation, it is manifest that the ciphertext images outputted by our MIEA-PRHM possess exceptional randomness of a preeminent nature.

As detailed in

Table 6. Comparative outcomes of information entropy for six image encryption algorithms.

Algorithm	Entropy
MIEA-PRHM	7.9994
[43]	7.9976
[44]	7.9984
[45]	7.9992
[47]	7.9993
[54]	7.9993
[48]	7.9993

, we conduct a comparative analysis of our MIEA-PRHM against a selection of recently prominent image encryption algorithms. Upon scrutinizing the results, it becomes apparent that the information entropy metric attained by MIEA-PRHM approximates the optimal value of 8 with remarkable proximity. Consequently, MIEA-PRHM exhibits distinct advantages in terms of the randomness and uniformity of distribution pertaining to the ciphertext pixels, thereby affirming its superiority.

4.7. Pixel Distribution

The pixel distribution within natural digital images typically exhibits considerable heterogeneity with prominent features as depicted in the first and third rows of Figure 11. It is unequivocally evident that a secure and trustworthy image encryption algorithm must effectively nullify these distinctive attributes to robustly withstand diverse pixel-distribution-based attacks [53]. To validate the performance of our MIEA-PRHM in this context, we concurrently encrypt two color test images, which are 4.2.06 and 4.2.07. Subsequently, we generate 3D pixel distribution plots for the resultant images. It is manifest that the pixels, which are initially unevenly distributed across any of the three color channels (red, green, and blue), become remarkably uniform following encryption with MIEA-PRHM. This underscores the exceptional proficiency of MIEA-PRHM in eradicating the distribution characteristics of input pixels, thereby effectively mitigating various attacks that capitalize on such characteristics.

To achieve a more granular evaluation of the pixel distribution performance, we conduct an additional analysis by encrypting twelve test images and subsequently subject the resultant ciphertext images to a chi-square test. The chi-square statistic for a given ciphertext image can be mathematically formulated as delineated below:

$${\chi }^2={\sum }_{\alpha =1}^Q{\displaystyle \frac{{\gamma }_{\alpha }-M\times N\times \theta }{M\times N\times \theta }}.$$

(15)

In the equation presented above, ${\gamma }_{\alpha }$ signifies the quantity of ciphertext pixels possessing a value of $\alpha -1$. The variable Q denotes the maximal quantity of pixel values. For an 8-bit image, $Q=2^8$ and $\theta =1/Q$. Furthermore, M and N represent the vertical and horizontal dimensions of the encrypted image, respectively. Subsequently, one can ascertain the threshold value ${\chi }_{0.05}^2\left(255\right)$ of the chi-square test at a significance level of 0.05, which computes to 293.2478 [46]. Should the chi-square metric of an encrypted image fall beneath this threshold, it may be deemed to have successfully passed the test. This signifies that the pixel distribution within the encrypted image approximates a uniform distribution in a statistically significant manner.

Table 7. Results of the chi-square test obtained for MIEA-PRHM.

Image Size	Test Image	${\mathit{\chi }}^2$ Value	Passed or Not
		Threshold (293.2478)
$256\times 256$	5.1.09	268.8516	Yes
	5.1.11	219.4766	Yes
	5.1.13	265.6875	Yes
	5.1.14	264.7734	Yes
$512\times 512$	5.2.09	241.1348	Yes
	7.1.01	214.6758	Yes
	7.1.03	247.2500	Yes
	boat.512	243.1680	Yes
$1024\times 1024$	5.3.01	226.1406	Yes
	5.3.02	251.3809	Yes
	7.2.01	244.5845	Yes
	testpat.1k	265.4116	Yes

delineates the results of our chi-square test on the proposed MIEA-PRHM. Inspection reveals that all twelve encrypted images successfully meet the criteria of the chi-square test. This further substantiates that the encrypted images generated by MIEA-PRHM exhibit an exceptionally uniform pixel distribution.

4.8. Robustness Analysis

It is conceivable that during the transmission or storage of encrypted images, their ciphertext pixels may be subject to loss or corruption. Consequently, a robust image encryption algorithm ought to possess the capability to withstand a certain degree of ciphertext pixel loss or corruption [54]. To verify the robustness of the MIEA-PRHM, we conduct an array of evaluation experiments on the encrypted images it generates.

To emulate scenarios where ciphertext pixels are subjected to noise corruption, we introduce various intensities of salt and pepper noise (SPN) into an encrypted image of the test image 4.2.07 as depicted in the top row of Figure 12. Subsequently, we decrypt these corrupt images. The bottom row of Figure 12 displays the resultant decrypted images. Upon visual inspection, it becomes evident that, at relatively low noise intensities, the decrypted images exhibit no significant visual divergence from the original image. As the noise intensity escalates, the decrypted images progressively degrade in sharpness. Even so, when the noise intensity attains a magnitude as high as 0.05, a preponderance of meaningful visual information remains discernible within the decrypted images. This observation underscores the commendable robustness of the MIEA-PRHM in defending against noise attacks.

Analogously, we simulate scenarios of data loss by removing some pixels from an encrypted image of the test image 4.2.03. The first row of Figure 13 displays these ciphertext images with partially missing pixels. Their corresponding decrypted images are enumerated in the second row of Figure 13. It is observable that the quality of the decrypted images correlates with the number of missing pixels. When the number of missing pixels is relatively small, the decrypted images closely resemble the test image 4.2.03. As the number of missing pixels increases, the decrypted images progressively degrade in sharpness. Notably, even with the loss of up to $160\times 160\times 3$ pixels, a substantial amount of meaningful visual information remains discernible in the decrypted images. Consequently, MIEA-PRHM features excellent robustness against data loss.

4.9. Efficiency Analysis

Considering the prominent features of current digital image communications, including substantial data volume and high throughput, a practical image encryption algorithm must demonstrate exceptional encryption efficiency. Failure to do so renders a suggested image encryption algorithm unsuitable for practical application requirements [56]. During the design of MIEA-PRHM, various strategies are employed to enhance encryption efficiency. Firstly, plaintext pixels are split into high 4-bit and low 4-bit components. Given that most image information resides in the high 4-bit, the encryption process for the low 4-bit is simplified without compromising security. Secondly, pixel fusion is applied to both high and low 4-bit encryptions, reducing the overall computational load. Furthermore, the two hyperchaotic maps adopted possess relatively simple structures, enabling the efficient generation of chaotic sequences. Lastly, the extensive use of vector-level operations during encryption further contributes to improved efficiency.

We conduct an extensive array of experiments to validate and showcase the efficiency advantages of MIEA-PRHM. Cognizant of the potential disparities in efficiency that may arise from variations in hardware and software configurations, we opt to conduct these experiments on MIEA-PRHM and other recently reported image encryption algorithms under identical experimental conditions.

Table 8. Average times (Sec.) required by seven image encryption algorithms to encrypt one or more images.

Algorithm	$256\times 256\times 3$	$256\times 256\times 6$	$512\times 512\times 3$	$512\times 512\times 6$	$1024\times 1024\times 3$	$1024\times 1024\times 6$
[51]	0.2452	0.5014	1.1634	2.3861	4.7792	10.1742
[52]	0.2197	0.4677	0.9417	1.8929	3.8712	8.0234
[43]	0.4497	0.9057	1.8927	3.8468	7.6805	15.4763
[53]	0.1223	0.2576	0.5684	1.2404	2.6734	5.4156
[47]	0.0622	0.1332	0.2767	0.5636	1.1461	2.4245
[54]	0.1253	0.2579	0.4932	1.0353	2.1363	4.4000
MIEA-PRHM	0.0240	0.0485	0.0977	0.1970	0.3993	0.8152

presents the experimental results we obtain, while

Table 9. Corresponding throughputs (Mbps) achieved by seven image encryption algorithms.

Algorithm	$256\times 256\times 3$	$256\times 256\times 6$	$512\times 512\times 3$	$512\times 512\times 6$	$1024\times 1024\times 3$	$1024\times 1024\times 6$	Average
[51]	6.1175	5.9832	5.1573	5.0291	5.0218	4.7178	5.3378
[52]	6.8275	6.4144	6.3715	6.3395	6.1996	5.9825	6.3558
[43]	3.3356	3.3124	3.1701	3.1195	3.1248	3.1015	3.1940
[53]	12.2649	11.6460	10.5559	9.6743	8.9773	8.8633	10.3303
[47]	24.1158	22.5225	21.6841	21.2917	20.9406	19.7979	21.7254
[54]	11.9713	11.6324	12.1655	11.5908	11.2344	10.9091	11.5839
MIEA-PRHM	62.5000	61.8557	61.4125	60.9137	60.1052	58.8813	60.9447

enumerates the corresponding throughput values. It is evident from the results that, across various input sizes, MIEA-PRHM exhibits strikingly apparent efficiency advantages. Specifically, MIEA-PRHM requires merely 0.8152 s to encrypt image data with dimensions of $1024\times 1024\times 6$, which equates to six $1024\times 1024$ grayscale images or two color images of the same size. Moreover, the average throughput achieved by MIEA-PRHM is an impressive 60.9447 Mbps. This outstanding performance is ample to satisfy the real-time encryption requirements of various practical applications.

5. Conclusions

To address the security concerns, efficiency issues, and practical limitations identified in some recently reported encryption algorithms, we have meticulously designed a novel multi-channel image encryption algorithm called MIEA-PRHM. This encryption algorithm utilizes two robust hyperchaotic maps, 2D-SCPM and 2D-ELMM, to jointly generate chaotic sequences. This design enables MIEA-PRHM to possess a larger key space and better output randomness. Subsequently, a series of dynamic vector-level encryption steps, including row–column joint scrambling, vector-level dynamic rotational diffusion, and dual-operation dynamic partition substitution, further transform these matrices into indistinguishable noise-like ciphertext images.

We have conducted extensive experiments and analyses to evaluate the encryption performance of MIEA-PRHM. Our proposed MIEA-PRHM exhibits outstanding performance across a range of performance evaluation metrics, including key space ($2^{412}$), plaintext sensitivity (99.6096% and 33.4641%), pixel correlation (<0.002), information entropy (>7.999), pixel distribution (<293.2478), and encryption efficiency (60.9447 Mbps). Numerous experimental results and comparative analyses demonstrate that MIEA-PRHM outperforms many recently reported encryption algorithms, offering higher security and excellent encryption efficiency.

In the future, we will continue to optimize MIEA-PRHM and introduce more new techniques and methodologies to make it more secure and efficient. Furthermore, we will also endeavor to apply MIEA-PRHM to other multimedia data requiring protection, such as audio and video.