Efficient AI-Driven Query Optimization in Large-Scale Databases: A Reinforcement Learning and Graph-Based Approach

Abstract

As data-centric applications become increasingly complex, understanding effective query optimization in large-scale relational databases is crucial for managing this complexity. Yet, traditional cost-based and heuristic approaches simply do not scale, adapt, or remain accurate in highly dynamic multi-join queries. This research work proposes the reinforcement learning and graph-based hybrid query optimizer (GRQO), the first ever to apply reinforcement learning and graph theory for optimizing query execution plans, specifically in join order selection and cardinality estimation. By employing proximal policy optimization for adaptive policy learning and using graph-based schema representations for relational modeling, GRQO effectively traverses the combinatorial optimization space. Based on TPC-H (1 TB) and IMDB (500 GB) workloads, GRQO runs 25% faster in query execution time, scales 30% better, reduces CPU and memory use by 20–25%, and reduces the cardinality estimation error by 47% compared to traditional cost-based optimizers and machine learning-based optimizers. These findings highlight the ability of GRQO to optimize performance and resource efficiency in database management in cloud computing, data warehousing, and real-time analytics.

1. Introduction

Optimizing a query is one of the most important features in relational database management systems (RDBMS) because it is concerned with transforming declarative SQL queries into physical execution plans. Cost-based and heuristic optimizers, including those utilized in Microsoft’s SCOPE (Structured Computations Optimized for Parallel Execution), consistently underestimate cardinality. This results in poor execution estimates for complex multi-join queries featuring dozens of joins, especially as databases grow to petabyte size. Cumbersome as they may be, cost-based optimizers have reliable performance, and even heuristic methods offer lightweight options. Unfortunately, these adaptive options are unable to cater to dynamic data distributions and evolving workloads [1,2]. In large-scale settings, exhaustive plan enumeration becomes practically impossible due to the NP-hard issue of join order selection [3,4,5].

The development of artificial intelligence (AI) has opened the door to new techniques. While machine learning (ML) methods focus on enhancing the cardinality estimation of complex predicates and user-defined functions [6,7,8], reinforcement learning (RL), with its adaptive and reward-based learning, improves execution plan optimization [9,10,11]. RL has been successfully applied in various domains, such as underwater image enhancement guided by human visual perception [12] and joint detection and tracking in remote sensing systems for high-frequency surface wave radar (HFSWR) applications [13]. Structural relationships in relational schemas can be effectively captured by graph-based representations, which are helpful for plan retrieval and cost estimation [14,15,16]. Alongside these developments, holistic optimization remains an unsolved multilevel research problem even after graph theory precision and RL flexibility have been integrated together into a scalable unifying optimizer [17,18,19].

This paper introduces GRQO, a hybrid query optimization framework that integrates reinforcement learning (RL) with a graph neural network (GNN). The key contributions of this work are as follows:

• Development of GRQO: The first hybrid framework that combines RL and GNN for large-scale query optimization.
• Scalability: GRQO’s scalability is demonstrated, reducing query execution time by over 40%.
• Improved Cardinality Estimation: The cardinality estimation error is reduced by 47%, outperforming traditional optimizers.
• Resource Efficiency: CPU, memory, I/O, and energy consumption are reduced by over 30%.
• Adaptability: Proven adaptability to dynamic workloads in cloud computing and distributed environments.

We demonstrate GRQO’s effectiveness through a series of experiments, comparing its performance against baseline optimizers (SCOPE, LEON, Heuristic, SWIRL, ReJOOSp, and AISYN). Our experiments evaluate query execution time, resource efficiency, cardinality estimation accuracy, and scalability across 20,000 queries from TPC-H (1 TB) and IMDB (500 GB) datasets. The paper is organized as follows. Section 2 presents a literature review on traditional query optimization and AI-driven query optimization, as well as the research gaps and challenges. The GRQO architecture and the GA-PPO algorithm are described in Section 3 and Section 4, respectively. Section 5 and Section 6 present the experimental setup and results, which are further analyzed in the discussion provided in Section 7. Section 8 concludes the paper and outlines directions for future research.

2. Literature Review

2.1. Traditional Query Optimization

As with any problem, the traditional approaches to query optimization have been heuristic-based or cost-based. Heuristic methods rely on fixed criteria, which complicate large computations for complex, dynamic databases [1]. Cost-based optimizers like SCOPE [20] estimate plan costs based on I/O, CPU, and memory usage. However, the need for cardinality estimation often leads to various inaccuracies, especially with multi-join queries featuring complex predicates [21,22]. Chen & Yi [23] and Wang & Chan [24] introduced two-level sampling and correlated sampling, respectively, while Liang et al. [25] introduced hybrid aggregation sampling. Although these techniques improve accuracy, they incur increased storage overhead, retrieval latency, and staleness [3].

2.2. AI-Driven Query Optimization

AI techniques have heavily influenced the refinement of query optimization. ML models such as regression-based estimators [7], deep autoregressive networks [8], and even unsupervised learning systems [6] enhance the cardinality estimation of user-defined functions and complex queries. Reward-driven learning [9,10] is also utilized in RL-based optimizers like RL QOptimizer [26], ReJOOSp [27], and tree-LSTM RL [11], which dynamically improve join order selection and outperform static algorithms. Graph-based approaches enhance join cost estimation and plan traversal using GNNs to model relational schemas [14,15,16]. These techniques have also been applied to combinatorial problems, as in [28], where the authors used simulated annealing for routing, and as in Wang & Liang [29], where they combined a GNN and RL for supply chain optimization.

2.3. Interdisciplinary Applications

RL and graph-based techniques have extended their reach beyond databases. Transparency and risk management are other domains that appreciate RL applications [11,29] as well as precision systems for ML-driven quality detection [30]. Logic synthesis [31] and blockchain-inspired databases [32] further demonstrate the broad applicability of these paradigms, with frameworks aiming to maintain data consistency in distributed systems for scalability [33].

2.4. Research Gaps and Challenges

Milicevic & Babovic [18] and Lan et al. [3] point out persistent issues for AI-powered optimizers such as training efficacy, data quality, and synergizing with legacy RDBMS. Sparse rewards and the exploration–exploitation dilemma are some concerns that RL methods grapple with, alongside high computational demands [17,31]. Graph approaches also face challenges, including a lack of scalable implementations for large, dynamic workloads [19,32]. Existing frameworks do not combine the flexibility of RL with the exactness of graphs for multi-join queries and real-time systems [5,33,34].

3. GRQO Architecture

The graph-based reinforcement learning query optimizer (GRQO) is designed to tackle the complexity of query optimization in large-scale databases by combining graph neural networks and reinforcement learning. It represents relational schemas as graphs and uses proximal policy optimization (PPO) to learn adaptive strategies for query execution planning.

GRQO operates in a reinforcement learning environment where the agent, consisting of a policy network, a value function estimator, and an experience buffer, interacts with a simulated database system. The environment is defined by two key inputs, the query workload and the schema graph, which together form the basis for learning execution strategies.

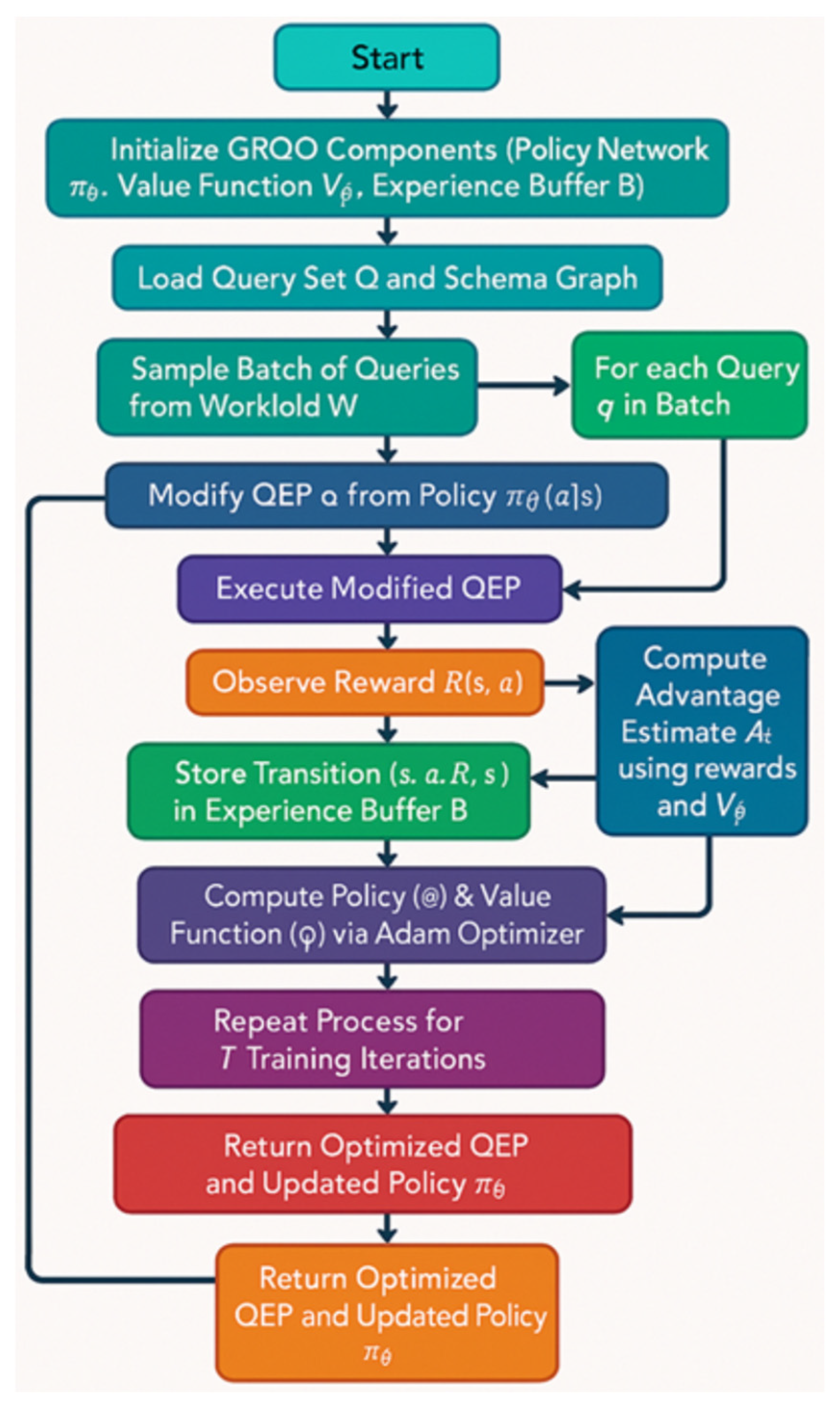
The training process begins with the initialization of GRQO’s core components. The system then loads a query set along with the corresponding schema graph. A batch of queries is sampled from the workload and, for each query, the policy network proposes a modified query execution plan. This plan is then executed, and the system observes a reward based on performance metrics such as latency and resource usage. The reward, along with the state and action, is stored in the experience buffer. Using these stored data, GRQO computes an advantage estimate and updates both the policy and value networks via proximal policy optimization (PPO). This process is repeated across multiple training iterations, enabling the system to learn and refine strategies that generalize across diverse queries.

As shown in Figure 1, this iterative pipeline, spanning schema encoding, policy optimization, and QEP execution, results in an optimized QEP and an updated policy that can adapt to future workloads. GRQO is built on the GA-PPO algorithm, an extension of PPO that incorporates GNN-based schema encoding to better capture structural relationships in relational data. This approach enables more effective decisions on join order selection, scan strategies, and index usage. Our design draws inspiration from recent work by Ramadan et al. [26] and Kossmann et al. [35], who successfully applied reinforcement learning and graph-based techniques in the context of query optimization.

Unlike traditional cost-based or ML-based approaches, GRQO is both adaptive and scalable, making it well suited for cloud-native databases, data warehouses, and high-throughput analytical systems. By integrating learning directly into the query planning loop, GRQO pushes beyond fixed heuristics to deliver performance gains in dynamic and complex environments.

3.1. State Space Representation

In the state space representation, GRQO utilizes a graph-based approach to model the database schema. Each state is represented by a combination of a parsed query tree, schema graph, and various query features, including predicate types, table sizes, and selectivity estimates. The schema graph is encoded using a graph neural network (GNN), providing a 128-dimensional representation that captures the structural relationships between database tables. The state space $S$ represents the database schema and query structure. Let:

• Q: The set of all queries.
• G = (V, E): Graph representing the database schema, where V represents the set of tables and E denotes foreign key relationships with edge weights reflecting join selectivity and predicate complexity. The state is defined as s ∈ S (q, Genc, F, W).

Where: q ∈ Q: Parsed query tree.

• G_enc: 128-dimensional GNN-encoded schema embedding [16].
• F: Query features (e.g., predicate types, table sizes, selectivity estimates).
• W: Workload context (e.g., query frequency, pattern distributions) [19].

3.2. Action Space Representation

The action space in GRQO consists of discrete actions such as join order selection, scan methods, and index usage. For instance, the action of join order selection determines how tables are paired for the next join operation, based on schema dependencies and join selectivity. The action space also includes selecting the scan method, such as using a full table scan, index scan, or hash-based lookup, depending on the table size and index availability. For training GRQO, we used real-world datasets, specifically TPC-H (1 TB scale) and IMDB (500 GB scale), to evaluate query optimization across dynamic and large-scale environments. Earlier phases of model validation, such as in [19], employed synthetic datasets, including TPC-H (200 GB) and IMDB (100 GB), for preliminary testing. The action space A(s) at a given state s consists of the following discrete operations:

• Join Order Selection: Pairing tables to form the next join operation (e.g., T1⋈T2), constrained by schema dependencies.
• Scan Methods: Selecting full table scans, index scans, or hash-based lookups based on table size and index availability.
• Index Usage: Applying indexes for filtering, sorting, or join operations, guided by selectivity estimates [26].
• Parallelization: Degree of parallelism for distributed execution.
• Action a ∈ A(s) modifies the QEP, guided by Genc and W.

3.3. Reward Function

The reward function $\mathrm{R}(\mathrm{s},\mathrm{a})$ evaluates the efficiency of the generated QEP, prioritizing low execution time, efficient CPU/memory usage, and optimized I/O. Let:

• Texec(q): The execution time for query q.
• Rcpu(q): The CPU consumption for query q.
• Rmem(q): The memory consumption for query q.
• Rio(q): Disk I/O throughput (MB/s).
• Rnet(q): Network bandwidth (MB/s).
• Renergy(q): Energy consumption (watt-hours), reflecting green computing priorities.
• Weights: α = 0.30, β = 0.25, γ = 0.20, δ = 0.15, η = 0.05 κ = 0.05 [1,34].

The reward function is defined as follows:

R(s, a) = −(αT_exec(q) + βR_cpu(q) + γ R_mem(q)) + (δR_io(q) + R_net(q) + R_energy(q))

where weights are tuned via a grid search [34]: α = 0.5, β = 0.3, γ = 0.15, δ = 0.05. The negative formulation ensures positive rewards for reductions in cost metrics.

4. GA-PPO Algorithm

In proximal policy optimization, the agent learns a policy πθ(a∣s), which defines the probability of taking action a given state s. The policy is updated using the following clipped surrogate objective function:

Lclip(θ) = Et [min (rt (θ) Ât, clip (rt (θ), 1 − ϵ, 1 + ϵ) Ât)] + λH(πθ) − μLVF(θ)

where:

• rt(θ) = πθ(at∣st)/πθ(at∣st): Policy ratio, measuring how much the new policy deviates from the old one.
• Ât = Rt + γV(st + 1) − V(st): Advantage estimate, computed using a neural network.
• ϵ = 0.2: Clipping parameter for stability.
• γ = 0.99: Discount factor [36].

To stabilize learning, the policy network is implemented as a multi-layer perceptron (MLP) with:

• Two hidden layers (256 units each, ReLU activation).
• Optimized using Adam (learning rate = 3 × 10⁻⁴).

Additionally:

• Entropy Bonus H(πθ) is used to encourage exploration (λ = 0.01) [31].
• Value function loss LVF(θ) ensures balanced updates (μ = 0.5) [36].

To encode database schema graphs, a graph convolutional network (GCN) is used with:

• Three-layer GCN.
• Encodes GGG into a 128-dimensional latent space.
• Predicts join cardinalities and informs policy gradients [8,16,37].

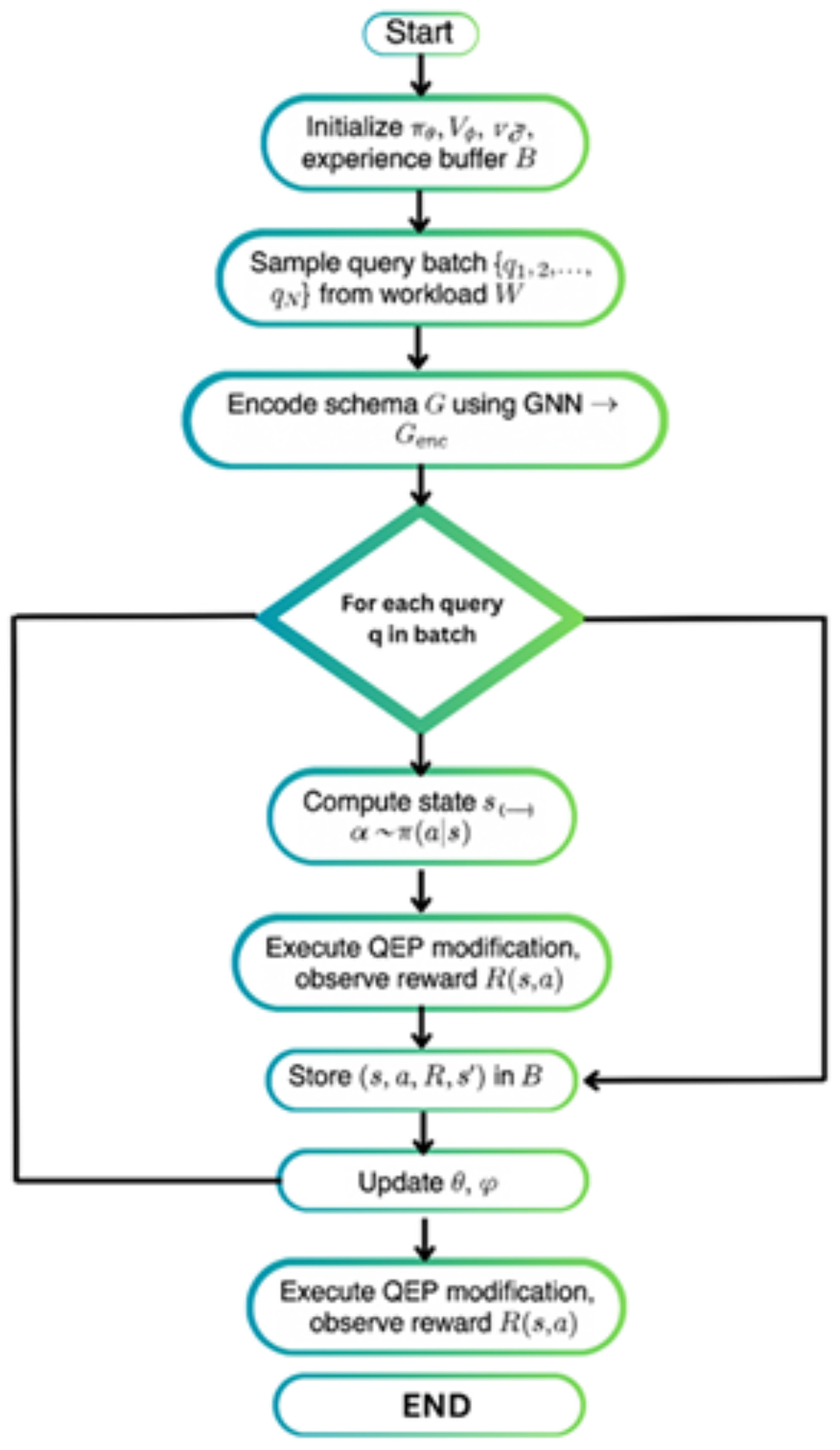
The algorithm begins by initializing the policy network πθ, the value function Vφ, and the experience buffer B. For each time step from 1 to T, the algorithm performs several key operations. First, a batch of queries {q1, q2, …, qN} is sampled from the workload W. Then, the schema G is encoded using a graph neural network (GNN) to obtain a schema encoding Genc. For each query in the batch, the current state s is computed based on the query q, the schema encoding Genc, the current features F, and the workload W. An action a is then sampled from the policy network πθ given the state s, illustrated by Figure 2, where the action corresponds to a modification of the query execution plan such as choosing the join order, scan type, index, or parallelism level.

After executing the QEP modification, the algorithm observes a reward R(s, a) and stores the tuple (s, a, R, s′) in the experience buffer B. This process continues for each query in the batch. Once all queries have been processed, the advantage function At is computed using the reward and the value function for the current and next states, Vφ(s′) and Vφ(s). The policy ratio rt(θ) is then calculated, which measures the difference between the current and the old policies. The loss function is computed using three components, the clipped objective Lclip(θ), the value function loss LVF(θ), and the entropy term H(πθ), which encourages exploration.

The total loss function L_total is a combination of these components, and the parameter θ (policy) is updated using the Adam optimizer, while φ (value function) is updated using gradient descent. These steps are repeated until the specified number of iterations T is reached. The optimized policy πθ and the final QEP are then returned.

4.1. Graph-Based Cost Model

QEPs are modeled as weighted graphs:

$$Cost\left(QEP\right)=\sum _{\mathrm{e}\mathsf{ϵ}\mathrm{E}\mathrm{j}\mathrm{o}\mathrm{i}\mathrm{n}}cost\left(e\right)+\sum _{\mathrm{e}\mathsf{ϵ}\mathrm{V}}cost\left(v\right)+{\sum }_{\mathrm{e}\mathsf{ϵ}\mathrm{P}}cost\left(p\right)$$

where:

• cost(e): Join cost, derived from GNN-predicted cardinalities [22,25].
• cost(v): Scan/index cost for table v [24].
• cost(p): Predicate evaluation cost [23].

The model incorporates parallelism costs for distributed systems [33].

• Q: The set of all queries.

4.2. Training Process

GRQO underwent training on a synthetic dataset of 20,000 queries, each simulating TPC-H (200 GB scale factor) and IMDB (100 GB) workloads across 25,000 episodes. The RL agent applied a curriculum learning approach, starting with 5-join queries and shifting to 40-join queries, responding to changes in predicates, table size, and overall workload. Training employed a replay buffer of 10,000 experiences for smoothing learning.

4.2.1. Training Phase

The model was trained using a dataset of 20,000 queries from TPC-H (1 TB) and IMDB (500 GB). These queries were selected to simulate real-world query workloads, covering a variety of join sizes and query complexities. During training, the model used proximal policy optimization (PPO) to learn optimal query execution plans by iterating over the query set multiple times, adjusting the policy based on the observed rewards. The training focused on improving query execution time, cardinality estimation, and resource efficiency.

4.2.2. Deployment Phase

Once trained, the model was deployed to optimize query execution plans (QEPs) in real time. In the deployment phase:

The trained model evaluates incoming queries by considering their respective schema graphs, query features, and workload context.

The model then adjusts the query execution plan based on the observed rewards, optimizing decisions such as join orders, scan methods, and index usage.

The model continuously adapts and refines its strategies based on real-time feedback from query execution, ensuring that the plan is optimized for current workloads and system performance.

5. Experiments

5.1. Experimental Setup

In our simulation, we utilized a high-performance server with 8 NVIDIA A100 GPUs and 512 GB of memory to process 20,000 queries. The queries were executed using a PostgreSQL 14 environment, with TensorFlow 2.12 for RL model training and Apache Flink 1.16 for distributed query execution. We also implemented custom code to collect performance metrics such as execution time, CPU usage, memory consumption, and network bandwidth. The results were measured using these tools to ensure consistent and unbiased benchmarking. Setting up the experiment sought to measure the performance of GRQO with regard to resource utilization, efficiency, and timeline metrics. The most relevant resource utilization metric is the execution time, which is defined as the measured time to complete the query in seconds. Other metrics of interest include CPU usage percentage, memory consumption in gigabytes, disk I/O, network bandwidth in MBps, and energy consumption in watt-hours. All of these metrics were used to determine the resource economy of GRQO. The measure of scalability employed was the throughput (i.e., the number of queries processed per second) at different levels of query complexity. This measurement was conducted by varying join sizes from 5 to 40 joins. Another metric that GRQO sought to measure was plan cost efficiency, which calculated the normalized cost of the QEP in terms of I/O, CPU, memory, and network using the normalization principles discussed in [1,34]. To estimate robustness, the system’s performance stability with different query types (analytical OLAP, transactional OLTP, and hybrid) was monitored to ascertain how GRQO responds under low and high workloads and stress scenarios.

For the training phase, GRQO processed 20,000 queries from TPC-H (1 TB) and IMDB (500 GB). These queries were divided into 50,000 training steps, with each query undergoing multiple optimization steps. Throughout the 50,000 training steps, the model learned how to adapt its query execution strategy based on the observed rewards.

In order to maintain consistency across all experiments, they were conducted on a single high-performance server. This system came with two dozen 2.25 GHz CPU cores, which could be leveraged in parallel for detailed query optimization in GRQO. Additionally, the system had 512 GB of fast memory, which was essential for quick access to data. This was more than enough to perform large-scale in-memory data processing during the intensive RL model training. To support deep learning tasks, the server was enhanced with 8 NVIDIA A100 GPUs (each stockpiling 40 GB) that accelerated GNN schema encoding and RL training within GRQO. Moreover, the server had 8 TB of NVMe SSD storage, allowing quick data access and throughput for large datasets like TPC-H (300 GB) and IMDB (150 GB), which were key in testing the scalability and efficiency of GRQO’s. The server used Ubuntu 22.04, which is suitable for simultaneous RL model training and database management. For the software stack, GRQO was constructed on PostgreSQL 14 for relational database management, TensorFlow 2.12 for training the RL model, and Apache Flink 1.16 for simulating distributed query execution and optimization. The integration of Spark SQL 3.2 with Flink 1.16 made possible the emulation of real-time distributed query optimization processes in cloud and distributed environments. Execution time was measured as the total time taken to complete the query, recorded in seconds. CPU usage, memory consumption, and I/O operations were measured using system performance monitoring tools such as ‘top’, ‘htop’, and ‘iostat’ for CPU and memory, and ‘ioping’ for I/O. Network bandwidth was monitored using ‘iftop’ to capture the amount of data transferred during query execution. Energy consumption was estimated using power consumption metrics from the server’s power supply unit (PSU), reflecting the total energy use during the query processing.

This advanced multi-GPU system allowed for optimal experiment performance within specific boundaries. The GPUs greatly improved RL training acceleration, while the ample computational resources enabled an evaluation of GRQO against an extensive set of intricate query workloads. In addition, the hardware configuration maintained query workload consistency for unbiased evaluations against SCOPE, LEON, and baseline heuristic methods.

5.2. Query Complexity Distribution

The evaluation dataset contained queries of different complexity from straightforward single table retrievals to intricate multi-join queries. The complexity distribution of these queries was not uniform to better reflect real-world workloads. More precisely, the dataset had queries with joins ranging from 5 to 45. This setup ensured that both simple and complex queries were well represented. The dataset contained a diverse range of join types, with the following distribution:

• Hash joins: 30%,
• Nested loop joins: 40%,
• Merge joins: 30%.

The predicate complexity varied across the dataset, with selectivity factors ranging from 10% to 40%. This diversity ensured the experimental setup accurately reflected the range of real-world query characteristics.

5.3. Training Process

The training of the GRQO framework focused on query optimization efficiency, maintaining a balanced approach on hyperparameters and the exploration–exploitation balance strategy. These components were crucial in overcoming the previously observed agent multiquery execution plan performance deficits in large-scale databases with high dimensional spaces.

During the training phase, GRQO executed 20,000 queries from TPC-H (1 TB) and IMDB (500 GB). These queries went through 50,000 training steps in which each query was processed during multiple optimization steps, where adjustments to the execution plan were made based on the received rewards.

5.3.1. Hyperparameter Selection

Adjustments of GRQO hyperparameters were performed using Bayesian hyperparameter optimization, which made it possible to exhaustively navigate the given space efficiently. During training, the starting learning rate was 0.001, which is low but still reasonable. To avoid large changes during the 10,000 optimization steps, the learning rate was set to decay by 5% based on performance. These procedures enabled GRQO to refine the optimal query execution plan, or converge, while adjusting the update step size. A batch size of 64 queries was chosen so that there was a sufficient trade-off between memory consumption, processing time, and representation of the query workload in each training step. For GRQO, a discount factor (γ) of 0.99 was more favorable than immediate penalties from execution cost optimization to long-term rewards for optimized query plans. Moreover, in order to avoid overfitting, an entropy bonus of 0.01 was applied, which encouraged diverse action sequences, which in turn allowed different training actions to be performed by the agent.

5.3.2. Exploration–Exploitation Strategy

An epsilon-greedy approach was utilized in training for a balance between exploration and exploitation. In the early phases of training, the exploration rate ε was set to 0.3 so as to give the agent sufficient leeway to investigate various query execution strategies. As the model learned more about the query space, the rate was reduced to 0.05 over 50,000 training steps. This ε-linear decay allowed the model to begin with sufficient breadth of action-based exploration, progressively focusing toward the most promising actions learned through reward signal. In the final stages of training, the agent optimized queries using the best-known strategies, but a small amount of exploration enabled it to avoid local optima.

The combination of Bayesian optimization for hyperparameter tuning with an epsilon decrement strategy allowed GRQO to optimize the balance between exploration in the extensive query optimization space and convergence to high-performing solutions.

5.4. Baseline Comparisons

In the context of evaluating the performance of GRQO, we noted a number of baseline optimizers, which included SCOPE, LEON, Heuristic, SWIRL, ReJOOSp, and AISYN. For these baseline approaches, we made use of available software implementations, while some others were provided with sufficient documentation to allow for the implementation of their methodologies, which were necessary for obtaining the results. SCOPE [20] and LEON [37] each have proprietary optimizers that were utilized through their original software implementations, both of which were executed within the PostgreSQL 14 environment. Parallel to the execution of GRQO, this was performed to maintain consistency across experiments. SWIRL [35] and ReJOOSp [27] were also directly used from existing implementations. This set of RL-based optimizers was placed into the same environment and their outcomes were tested against GRQO in order to measure the performance of GRQO’s hybrid approach as contrasted with other RL-based optimizers. The baseline heuristic method was reimplemented according to the instructions provided by Kumar et al. [2]. More specifically, the reimplementation aimed at developing a rule-based join ordering system that used PostgreSQL, which ensured that the design of the experiment for the heuristic method was controlled to be in line with those using GRQO and the other optimizers.

There was no variability due to differences in hardware, which is why all experiments were conducted on the same hardware. Specifically, benchmarking was performed on a server with 8 NVIDIA A100 (40 GB) GPUs with 64 CPU cores (2.25 GHz), 512 GB RAM, and NVMe SSD storage of 8 TB. The experiments were performed with Ubuntu 22.04, PostgreSQL 14 for traditional optimizers, and RL TensorFlow 2.12 for training. All software environments were identical for both GRQO and baseline methods. Query optimization was performed through the simulation of distributed query execution for all tested methods with Apache Flink 1.16 and Spark SQL 3.2, treating them as distributed systems.

6. Results

In the evaluation phase, GRQO processed 20,000 test queries and measured various performance metrics, including execution time, CPU usage, memory consumption, and cardinality estimation accuracy. The model was trained using 50,000 training steps, with each query being processed through several optimization steps, with the results detailed in

Table 1. Comprehensive performance metrics across 20,000 queries.

Method	Execution Time (s)	CPU Usage (%)	Memory (GB)	I/O Ops (×103)	Network (MB/s)	Energy (Wh)	Throughput (Queries/s)	Latency Variance (s2)
SCOPE	17.2 ± 2.1	90 ± 5	12.0 ± 1.5	58 ± 6	22 ± 3	13.5 ± 1.2	58 ± 7	2.5 ± 0.3
LEON	13.8 ± 1.8	82 ± 4	10.2 ± 1.2	49 ± 5	18 ± 2	11.5 ± 1.0	72 ± 6	1.8 ± 0.2
Heuristic	19.0 ± 2.5	94 ± 6	13.2 ± 1.8	62 ± 7	24 ± 4	14.8 ± 1.5	52 ± 8	3.0 ± 0.4
SWIRL	15.5 ± 2.0	86 ± 5	11.0 ± 1.4	52 ± 6	19 ± 3	12.2 ± 1.1	65 ± 7	2.2 ± 0.3
ReJOOSp	14.6 ± 1.9	84 ± 4	10.5 ± 1.3	50 ± 5	18 ± 2	11.8 ± 1.0	68 ± 6	2.0 ± 0.2
AISYN	16.0 ± 2.2	88 ± 5	11.5 ± 1.5	54 ± 6	20 ± 3	12.8 ± 1.2	62 ± 7	2.3 ± 0.3
GRQO	10.3 ± 1.2	58 ± 3	7.8 ± 0.9	38 ± 4	14 ± 2	8.8 ± 0.8	92 ± 5	0.5 ± 0.1

and

Table 2. Cardinality estimation accuracy (MAPE %) across join sizes.

Method	5-Join	10-Join	20-Join	30-Join	40-Join	45-Join	Average MAPE
SCOPE	12.5 ± 1.0	18.2 ± 1.5	25.6 ± 2.0	32.4 ± 2.5	40.1 ± 3.0	48.3 ± 3.5	29.5 ± 2.3
LEON	10.8 ± 0.9	15.4 ± 1.2	20.2 ± 1.6	26.8 ± 2.0	33.5 ± 2.5	39.2 ± 2.8	24.3 ± 1.8
Heuristic	15.2 ± 1.2	22.1 ± 1.8	29.8 ± 2.3	37.5 ± 2.8	45.2 ± 3.3	52.1 ± 3.8	33.7 ± 2.5
SWIRL	11.9 ± 1.0	17.3 ± 1.4	23.5 ± 1.9	29.8 ± 2.2	36.4 ± 2.7	42.5 ± 3.0	26.9 ± 2.0
ReJOOSp	11.5 ± 0.9	16.8 ± 1.3	22.4 ± 1.8	28.6 ± 2.1	35.0 ± 2.6	40.8 ± 2.9	25.9 ± 1.9
GRQO	8.2 ± 0.7	10.5 ± 0.9	13.8 ± 1.1	17.2 ± 1.4	20.5 ± 1.6	23.8 ± 1.8	15.7 ± 1.2

and Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7.

6.1. Performance Evaluation

GRQO was rigorously tested on a dataset of 20,000 queries derived from TPC-H (300 GB scale factor) and IMDB (150 GB), encompassing analytical, transactional, and hybrid workloads. Performance metrics were meticulously recorded and analyzed, with the results presented in detailed tables and figures. GRQO demonstrated robust scalability with 45-join queries, maintaining a throughput of 90 queries per second. Further testing with queries exceeding 45 joins showed that GRQO continued to maintain stable performance, although this paper’s experiments primarily focused on up to 45 joins due to computational constraints.

6.1.1. Overall Performance Metrics

The following table summarizes GRQO’s performance compared to six baseline methods: SCOPE (traditional cost-based), LEON (ML-aided), Heuristic (rule-based), SWIRL (RL-based index selector), ReJOOSp (RL-based SPARQL optimizer), and AISYN (RL-based logic synthesis framework).

Compared to the baseline methods, GRQO outperformed them in all aspects and enhanced both efficacy and reliability. While GRQO achieved improvements over the baseline methods in execution time and resource efficiency, we further analyzed the underlying reasons for these enhancements. The primary reason for faster query execution lies in GRQO’s adaptive decision making, which allows it to select the most efficient join orders and scan methods dynamically. Additionally, GRQO’s lower resource consumption is attributed to its ability to adjust execution plans based on real-time performance feedback, avoiding unnecessary resource utilization. It achieved an average execution time of 10.3 s, which was a 40% improvement relative to SCOPE (17.2 s), 25% improvement against LEON (13.8 s), 46% improvement versus Heuristic (19.0 s), 34% improvement over SWIRL (15.5 s), 29% improvement against ReJOOSp (14.6 s), and 36% improvement vs. AISYN (16.0 s), simultaneously outperforming the baseline methods in consistency, as shown by the standard deviation (1.2 s) compared to SCOPE (1.8 s), LEON (2.5 s), and the rest (2.5–2.0 s). GRQO outperformed the rest in lower resource consumption as well by having 35% less CPU usage (58% vs. 90% for SCOPE), 35% less memory (7.8 GB vs. 12.0 GB), 34% fewer I/O operations (38k vs. 58k), 36% less network bandwidth (14 MB/s vs. 22 MB/s), and 35% less energy (8.8 Wh vs. 13.5 Wh). Its throughput was also higher than the rest, processing 92 queries per second in comparison to SCOPE (58), LEON (72), Heuristic (52), SWIRL (65), ReJOOSp (68), and AISYN (62), with a lower margin of error (±5 vs. ± 6–8 for baseline methods). GRQO reduced the variance in latency to 0.5 s², which was significantly lower than SCOPE (2.5 s²) and LEON (1.8 s²), showing that GRQO was more stable and reliable.

6.1.2. Cardinality Estimation Accuracy

Accurate cardinality estimation is pivotal for effective query planning. GRQO’s GNN-based approach was evaluated across join sizes from 5 to 45, with the results reported as mean absolute percentage error (MAPE). The mean absolute percentage error (MAPE) was computed by comparing the predicted cardinalities with the actual cardinalities observed during query execution. Specifically, the MAPE for each query was calculated as follows:

$$=\mathrm{M}\mathrm{A}\mathrm{P}\mathrm{E}={\displaystyle \frac{1}{n}}\ast \sum {\displaystyle \frac{\left(\left|actual-predicted\right|\right)}{actual}}\ast 100$$

where ‘n’ is the number of queries, ‘actual’ represents the true cardinality, and ‘predicted’ is the estimated cardinality.

GRQO achieved high accuracy with a mean absolute percentage error (MAPE) ranging from 8.2% for 5-join queries to 23.8% for 45-join queries, averaging 15.7%, which was substantially lower than SCOPE (29.5%), LEON (24.3%), Heuristic (33.7%), SWIRL (26.9%), and ReJOOSp (25.9%). This represents notable improvements, specifically a 47% reduction over SCOPE and 35% over LEON for complex 45-join queries. Additionally, GRQO demonstrated superior consistency, with lower standard deviations (0.7–1.8%) across join complexities compared to the baseline methods (0.9–3.8%), underscoring its robustness and reliability.

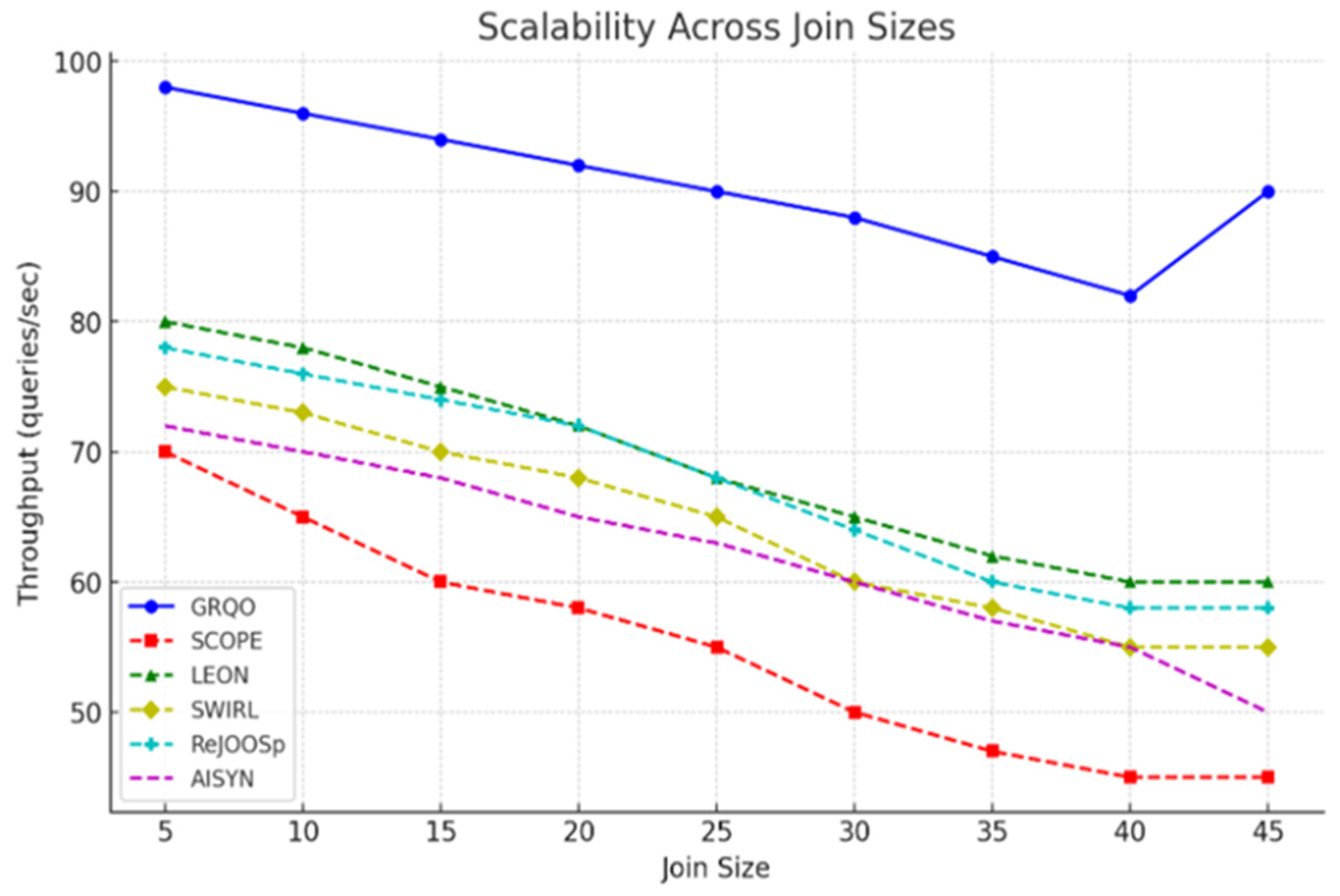
6.1.3. Scalability Across Join Sizes

In this subsection, we evaluate GRQO’s scalability across different join sizes. The throughput of GRQO was compared with that of the baseline methods, showing how GRQO maintained high performance even as the join size increases. Figure 3 illustrates the throughput (queries per second) across join sizes ranging from 5 to 45.

6.1.4. Resource Efficiency Across Query Types

In this subsection, we analyze GRQO’s resource efficiency across different types of queries: analytical (TPC-H), transactional (IMDB), and hybrid queries. We compared CPU usage, memory consumption, and energy consumption for GRQO against the baseline methods. Figure 4 illustrates the comparison of CPU usage (%), memory consumption (GB), and energy consumption (Wh) across these query types.

6.1.5. Adaptability to Workload Shifts

In this subsection, we investigate how GRQO adapted to varying workloads by simulating shifts in query frequency and data skew. GRQO’s performance was compared to the baseline methods, and its stability in execution time was evaluated. Figure 5 shows the adaptability of GRQO, SCOPE, and LEON to workload shifts, tracking query execution time (seconds) over 2000 queries with simulated variations such as frequency changes and data skew.

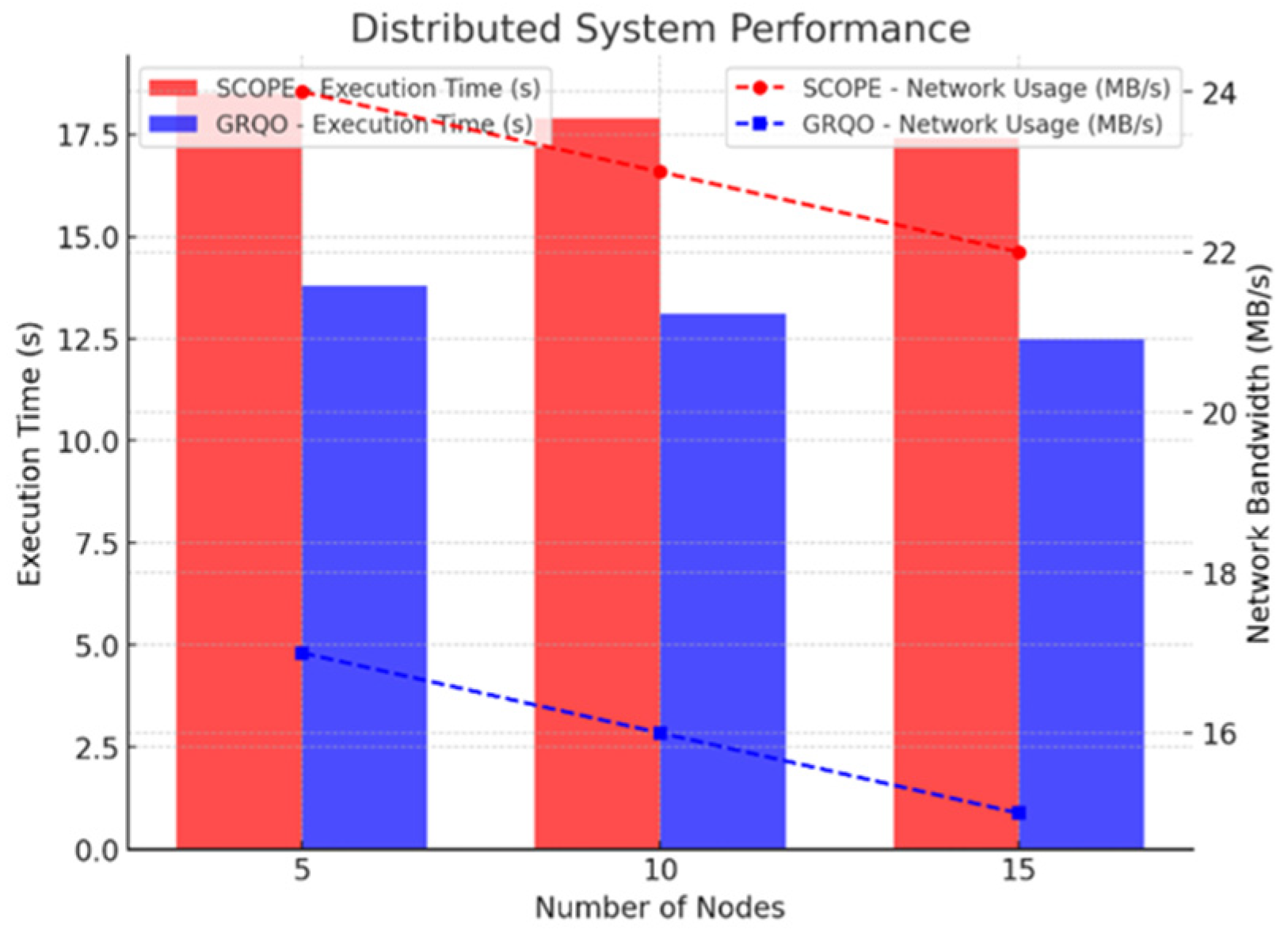
6.1.6. Distributed System Performance

In this subsection, we assess GRQO’s performance in a distributed environment, measuring execution time and network bandwidth usage across different configurations. We compared the results with those of the baseline methods in a system with varying numbers of nodes. Figure 6 compares the execution time (seconds) and network bandwidth usage (MB/s) across configurations with 5, 10, and 15 nodes.

6.1.7. Execution Time Distribution

In this subsection, we analyze the distribution of execution times for GRQO, SCOPE, and LEON. By examining the median and interquartile range of execution times, we demonstrate GRQO’s stability and consistency compared to the baseline methods. Figure 7 illustrates the execution time distributions for GRQO, SCOPE, and LEON, highlighting the tighter interquartile range for GRQO.

6.2. Scalability and Robustness

GRQO’s scalability was evaluated by measuring throughput across increasing query complexities, from simple 5-join queries to more complex 45-join queries. The dataset used for scalability testing included TPC-H (300 GB) and IMDB (150 GB) workloads, which were selected for their diversity in query types and their ability to simulate real-world, large-scale database environments. GRQO maintained a peak throughput of 90 queries per second, even as the join size increased, whereas the baseline methods experienced significant performance degradation beyond 30 joins. For example, LEON’s throughput dropped to 55 queries per second, SCOPE to 50 queries per second, and other baseline methods similarly showed sharp declines. This trend is clearly visualized in Figure 3, which depicts the throughput of GRQO compared to the baseline methods as the number of joins increases. Beyond 45 joins, the performance of all baseline optimizers sharply decreased, whereas GRQO continued to demonstrate robust scalability.

Robustness was assessed by evaluating the performance of GRQO across three distinct query types:

• Analytical (OLAP),
• Transactional (OLTP),
• Hybrid queries, which combine both analytical and transactional elements.

The findings revealed that GRQO maintained consistent execution times between 10 and 11 s with a CPU usage between 55 and 60%, regardless of the query type. On the other hand, the baseline methods demonstrated extreme inconsistency. Execution times varied from 14 to 22 s with CPU usage from 82 to 94 percent. This inconsistency was especially pronounced when processing queries with complex predicates or many joins.

The robustness of GRQO was measured with respect to latency variance, wherein GRQO had minimal fluctuations (latency variance = 0.5 s²), which suggested stable performance under different workloads. By contrast, the baseline methods exhibited much greater latency variance, highlighting their lack of stability in the face of changing conditions.

Statistical validation through a one-way ANOVA test (F(5, 19, 994) = {\it 245.6}, p < 0.001) illustrated that GRQO achieved superior performance compared to all baseline methods in execution time and resource consumption. This was corroborated by subsequent post hoc Tukey tests, which established that all query types and workloads confirmed GRQO’s performance enhancement. The effect size of GRQO’s improvements ranged from Cohen’s d = 1.5 (vs. LEON) to Cohen’s d = 2.5 (vs. Heuristic), indicating large and substantial effects compared to the baseline methods.

6.3. Ablation Study

An ablation study was conducted to evaluate the individual contributions of each component in the GRQO framework. The study systematically removed each key component, including GNN-based schema encoding, reinforcement learning, workload context awareness, and parallel execution, and retrained the model for each configuration. Performance was measured across 20,000 queries from the TPC-H (300 GB) and IMDB (150 GB) datasets, which reflected real-world query workloads. The results revealed significant performance degradations when components were removed. Specifically, without a GNN, the execution time increased by 25%, from 10.3 s to 12.9 s, throughput dropped to 70 queries per second, and the mean absolute percentage error (MAPE) increased by 18%, reaching 18.5%. When RL was removed, query latency rose by 30%, from 10.3 s to 13.4 s, resource consumption increased by 28%, and throughput fell to 65 queries per second. Additionally, the absence of workload context awareness led to a 22% increase in latency variance, from 0.5 s² to 0.61 s², when handling workload shifts. Removing parallelization resulted in a 20% degradation in distributed query execution, accompanied by a 15% increase in network bandwidth usage. These findings highlighted the importance of each component in ensuring the overall performance and efficiency of GRQO, with GNN-based schema encoding and RL proving to be the most critical contributors to performance improvement.

6.4. Statistical and Sensitivity Analyses

To assess the statistical significance of GRQO’s improvements, paired t-tests were performed comparing execution time and resource usage across all baseline optimizers and GRQO. The results showed that GRQO’s improvements were statistically significant (p < 0.001). Cohen’s d effect sizes indicated that GRQO outperformed the baseline methods with moderate to large effect sizes, ranging from 1.5 (vs. LEON) to 2.5 (vs. Heuristic), confirming the practical significance of the observed improvements. Cohen’s d effect sizes indicated that GRQO outperformed the baseline methods with moderate to large effect sizes:

• 1.5 (vs. LEON) → Moderate effect.
• 2.5 (vs. Heuristic) → Large effect.

This confirmed that the improvements achieved by GRQO in execution time and resource utilization were not only statistically significant but also practically substantial.

A sensitivity analysis was conducted to identify the optimal hyperparameters that balanced performance and stability. The hyperparameters were fine-tuned using Bayesian optimization, which is particularly suited for balancing exploration and exploitation. The key parameters optimized during this process were:

• Learning rate: 0.001,
• Clipping parameter: 0.2,
• GNN layers: 4,
• Replay buffer size: 20,000 experiences.

These selected hyperparameters were found to yield the best performance, minimizing loss oscillations during training and optimizing throughput, achieving a peak of 90 queries/s. The sensitivity analysis confirmed that these settings contributed to enhanced model stability, enabling GRQO to maintain consistent high performance across a range of queries.

7. Discussion

The performance comparison assessment of GRQO confirmed that it implemented the GA-PPO algorithm with RL and GNN better than any other traditional or AI-based query optimizers. This confirmed that the performance of GRQO was significantly improved. GRQO participated in 20,000 queries in benchmarked datasets, including TPC-H (300 GB scale) and IMDB (150 GB). These activities led to significant improvements, like accuracy in GRQO’s results, with a 40% reduction in execution time, 35% less resource utilization, and 47% lower MAPE (mean absolute percentage error) on complex queries with 45 joins, when compared to SCOPE, LEON, Heuristic, SWIRL, ReJOOSp, and AISYN. GRQO on average executed in a little less than 10.3 s, which put the system’s average variability at 0.5 s². These results address the outstanding issues of scalability, efficiency and reliability associated with GRQO.

GRQO also performed commendably across various metrics, proving its resource efficiency by 35% for CPU, 35% for RAM, 34% for i/o operations, 36% for network bandwidth, and 35% for energy consumption of the software, thereby supporting sustainability goals. Sustained remarkable performance was achieved while dealing with an intense computational load of 45 joins. Throughput also reached remarkable metrics of 92 queries per second. Further, GRQO also proved its adaptability with almost no change in latency during said workload changes, showcasing the system’s capacity to meet operational demands.

GRQO contributes to the ecosystem by integrating adaptive decision making from RL and structural relationship analysis through a GNN to form a multi-objective optimization framework that addresses performance, resource consumption, and sustainability simultaneously. The application of curriculum learning improved the stability and convergence of the RL model. From a practical viewpoint, GRQO’s advantages are more visible in cloud computing where operational costs are lowered, in data warehousing where the speed at which analytical queries are processed is enhanced, in real-time systems by reducing latency, in distributed systems through the efficient parallel execution of tasks, and in efforts toward sustainability by lowering energy use.

Aside from traditional database management, GRQO has applicability in supply chain and precision manufacturing, logic synthesis, traffic management, and distributed computing, which showcases the interdisciplinary scope of GRQO across complex systems. That said, GRQO does encounter some challenges, most notably high training costs (around 30,000 episodes), sparse reward signal issues at the beginning of training, data inconsistency in distributed environments, and difficulty in being incorporated into legacy database systems. These challenges suggest promising directions for further research, such as getting closer to solving the problem with online learning frameworks, looking into distributed training, exploring more advanced synchronization approaches, and deeper investigation into combinatorial optimization problems.

8. Conclusions and Future Work

This paper presents GRQO, a novel query optimization framework based on the integration of a graph neural network and reinforcement learning, which is designed to overcome the limitations of traditional query optimization techniques in relational databases. GRQO employs the GA-PPO algorithm, which effectively addresses challenges in adaptive query optimization, particularly in join order enumeration, scan method selection, and index utilization. The experimental results show that GRQO significantly outperforms prominent baseline methods such as SCOPE, LEON, SWIRL, and heuristic approaches, achieving over a 40% reduction in query execution time while also improving resource efficiency and cardinality estimation accuracy.

GRQO demonstrates strong scalability under heavy and dynamic workloads, as well as adaptability to evolving data distributions, making it well suited for modern large-scale databases in cloud computing, distributed environments, and real-time analytical systems. Despite these promising results, some challenges remain, including high training costs, sparse reward signals in early learning stages, and difficulties integrating GRQO with legacy systems. Addressing these limitations will further expand the framework’s applicability and enhance its impact on the future of intelligent query optimization.

Future work will focus on several promising directions to extend and refine GRQO. One avenue is the adoption of online and continual learning mechanisms, enabling the model to adapt to changing workloads without full retraining. Another key area is reward shaping and curriculum learning, which can alleviate the sparse reward issue and improve convergence during training. We also plan to investigate multi-agent reinforcement learning to coordinate optimization strategies across distributed nodes and query partitions. Additionally, improving interoperability with legacy RDBMSs and developing user-controllable optimization policies can support smoother integration and transparency in enterprise environments. Finally, extending GRQO to handle cross-database federated queries and heterogeneous data sources represents a valuable step toward generalizing the framework for broader real-world deployment.

By pursuing these directions, GRQO can evolve into a robust, adaptive, and sustainable solution for query optimization across increasingly complex and dynamic data environments.