Abstract
Several attacks on the well-known RSA cryptosystem that can be extended to a multi-prime version of RSA reveal that it is preferable to use the modulus having more prime factors. On the contrary, the larger the number of prime factors of the modulus, the greater the risk of its factorization, due to the reduced size of its prime factors. In this paper, we derive an optimal value of the number of prime factors in a multi-prime RSA modulus and introduce the notion of the “safest-value” and determine such safest-values for moduli of different sizes. By utilizing this concept, we propose an enhanced version of our Generalized Multi-Moduli RSA (GMMRSA), which is now secure against even more attacks than its previous version.
MSC:
11T71; 94A60
1. Introduction
The popular RSA Public Key Cryptosystem (PKC) [1], introduced in 1977, is still considered one of the most secure and efficient cryptosystems in today’s digital world. This cryptosystem is based on a hard problem of finding prime factors of a large positive integer, known as the integer factorization problem. Since the publication of RSA, many researchers have tried to mount various attacks on it, most of which have merely improved its security in practice by imposing various precautions. An excellent survey of various attacks on RSA given in [2] concludes that almost all the attacks that can be mounted on RSA are due to technical and practical factors, namely low public exponent, low private exponent, known partial factorization, etc. These attacks can be avoided if adequate care is taken during the implementation and utilization of the RSA. This survey was updated in [3] in 2019 with the same conclusion as [2].
For the sake of improvement in security and efficiency of RSA, many researchers have also suggested different modifications like incorporating padding, multi-prime RSA, applying the Chinese Remainder Theorem (CRT), homomorphic RSA, etc. Some recent advancements along this line are a hybrid Diffie–Hellman–RSA (DH–RSA) cryptosystem [4], a novel backdoor idea [5], using elliptic curves ([6,7]) etc.
One of these approaches, in particular, includes using more than two prime factors of the modulus in the cryptosystem, popular as multi-prime RSA. The motivation behind multi-prime RSA arises from the fact that the security of the RSA cryptosystem is primarily dependent on the factorization of a large integer. A magazine article in 1996 [8] advised to use three primes in an RSA modulus. It exhibited that using multiple prime factors can significantly increase the time-efficiency of RSA. It was also argued that the increased number of prime factors can compensate for their reduced size in terms of security. However, it is not always the case. A year later, the patent for the multi-prime RSA cryptosystem was filed [9], which we shall describe later in this article.
Published in 2008, [10] extends the attacks given in [2] on multi-prime RSA. It is evident that the majority of these attacks have less effect on multi-prime RSA compared to the RSA. In fact, it can also be deduced that the intensity of many attacks diminishes with the increasing number of primes. However, in the same paper, it is also stated that, on the contrary, the risk of factorization of the modulus rises with the number of its prime factors, thereby making the system less secure.
Some recent cryptanalytic research on RSA and its variants include cryptanalysis of RSA using small prime difference method [11], partial key exposure attack on an RSA variant [12], partial key exposure attack on a family of RSA-like cryptosystems [13], factorization and malleability of RSA moduli using elliptic curves [14], partial key known MSB attacks on RSA-CRT keys [15], a cryptanalysis using common modulus [16], cryptanalysis of prime power RSA with two private exponents [17] etc.
In this paper, we explore the attacks given in [10] briefly and understand their effects on multi-prime RSA. For better understanding, we discuss the factoring attacks separately from the other attacks to distinguish their contradicting effects. This necessitates determining a threshold value of the number of prime factors of a multi-prime RSA modulus, which provides optimal security against both these kinds of attacks. We introduce the notion of this threshold as the “safest-value” of the number of prime factors in multi-prime RSA modulus. Ultimately, we improvise our Generalized Multi-Moduli RSA (GMMRSA) cryptosystem [18] using this concept of safest-value and discuss its security advantage over other prevalent cryptosystems including GMMRSA.
2. Preliminaries
In this section, we describe the RSA cryptosystem and its multi-prime variants.
2.1. The RSA PKC
The RSA PKC comprises three distinct phases, namely key generation, encryption, and decryption. Setting up the RSA includes choosing two distinct secret primes and by the receiver and computing their product . In the key generation step, firstly, an integer e coprime to is chosen, where . Consequently, e has an inverse modulo , say d. Finally, the integer e along with N is made public by the receiver, while the values of and d are kept private. During the encryption, the sender converts the message, also known as the plaintext, M into the ciphertext C using the public key as and sends C to the receiver. During the decryption, the receiver utilizes their private key d to retrieve the plaintext M from C by computing
Based on the context of their usage, the public key e is also known as the encryption exponent and the private key d is also known as the decryption exponent. Furthermore, the product N is addressed as the RSA modulus or sometimes simply the modulus.
What makes the RSA cryptosystem function is the fact that given any large integer N, which is a product of two large primes—it is very difficult to obtain the prime factorization of N. This underlying problem is known as the “Integer Factorization Problem”. Breaking an RSA encryption amounts to determining the modular inverse d of the public exponent e modulo . It is well known that finding d is equivalent to factorizing the modulus N, a proof of which is provided in ([2] §1.1, fact 1). There are various algorithms that can factor a large integer in a feasible time. Among them, two well-known algorithms are Pollard’s factorization algorithm [19] and Lenstra’s Elliptic curve factorization algorithm [20]. Both of them are more efficient when either or has small prime factors. Lenstra’s Elliptic Curve Factorization algorithm (ECF) employs elliptic curves in the calculation process. The current best known method to efficiently factorize a large integer is Number Field Sieve (NFS). These methods are discussed in detail in Section 4.
According to the survey given in [2], attacks on RSA can be classified into four categories as (i) basic attacks utilizing deliberate misuse of the system, (ii) low private exponent attacks, (iii) low public exponent attacks, and (iv) attacks due to poor implementation. Attacks based on low private and public exponents are considered quite serious, and it is advised to avoid such exponents in practice. Despite many severe attacks, it was concluded in [2] that keeping all the necessary safety measures in mind while implementation, the RSA cryptosystem is reliable enough to be put in regular practice.
As previously discussed, attempts to strengthen the RSA cryptosystem against factoring attacks sprouted an improvisation of the RSA, commonly referred to as multi-prime RSA. Next, we describe a multi-prime RSA cryptosystem.
2.2. Multi-Prime RSA Cryptosystem
In the patented multi-prime RSA [9], k distinct primes are chosen by the receiver and the RSA modulus is their product .
Key Generation. Euler totient of RSA modulus N is computed as . Similar to RSA, a public key e is chosen to be relatively prime to and its modular inverse d is calculated modulo . The pair is published as the public key, whereas the k primes and d are kept private. The encryption and decryption processes are carried out in the same way as in RSA.
Encryption. The sender encrypts the plaintext message M, and sends ciphertext to the receiver using the public key pair of the receiver.
Decryption. The receiver retrieves the plaintext M from the ciphertext C using the knowledge of the private key d as .
When multi-prime RSA was introduced, it was anticipated that the reduction in the size of prime factors would be compensated by the necessity to factorize additional prime factors instead of merely one (refer [9]). Furthermore, as an additional benefit, the key generation and the decryption process can be made faster using the Chinese Remainder Theorem, enhancing the time-efficiency of the system.
Since the multi-prime RSA was introduced, many researchers have proposed various modifications to strengthen security or improve the time efficiency. One of these modifications suggested the use of two privately shared secret keys a and b [21], with encryption process as . So, the decryption process would also require the knowledge of a and b. Another modification is a generalized -prime RSA [22] with n different pairs of encryption and decryption exponents modulo instead of just one, where N is the product of all primes.
Remark 1.
It is intuitive that increasing the size of primes, and consequently the size of the RSA modulus, makes the system more secure. However, this leads to higher computational cost associated with the key generation, the encryption, and the decryption. Aiming the feasibility of these operations for practical implementation, depending on the average computing power, it becomes necessary to decide an optimal size for the RSA modulus. According to the current norms, a 2048-bit RSA modulus is considered secure and is widely used. However, for multi-prime RSA, limiting the size of the RSA modulus would imply that as the number of prime factors increases, their sizes are bound to decrease, which in turn makes the system vulnerable against factoring attacks. Further details are discussed in Section 4. To overcome this security concern in multi-prime RSA, it is advisable and beneficial to distribute these primes among more than one modulus rather than using a single modulus. Building on this idea, in [18], the authors proposed a Generalized Multi-Moduli RSA (GMMRSA) cryptosystem, and demonstrated that in comparison with a multi-prime RSA with -primes, it provides a much higher security advantage at just n-times the computational cost. For the sake of completion of the paper and making it self-contained, below we describe the GMMRSA with n moduli, where each modulus is a product of two primes.
2.3. The Generalized Multi-Moduli RSA (GMMRSA) [18]
Let and be distinct primes and let for .
Key Generation. The receiving party chooses n encryption exponents such that each is co-prime with , , where . Corresponding to each , an integer is calculated, satisfying
Now, the n pairs are made public while the integers are kept confidential.
Encryption. The encryption is carried out in n recursive steps, summed up as
where is the sender’s plaintext M and is the final ciphertext C to be sent to the receiver.
Decryption. The decryption process is also carried out recursively in n steps, but in the reverse order of the encryption. Summarizing the steps,
where i runs down from n to 1. Here again, is taken to be the received ciphertext C and the final result is the plaintext M.
The rationale behind devising this recursive approach in the GMMRSA [18] is that the computations involved in the encryption and the decryption processes are distributed over multiple moduli rather than a single modulus. Furthermore, this intuitive design of the algorithm does not resort to the Chinese remainder theorem which makes it different and efficient from other existing multi-prime RSA schemes. Hence, the recursive encryption and decryption proves to be a more appropriate implementation.
Remark 2.
As previously specified, the GMMRSA was proposed to counter the factoring attacks on multi-prime RSA. However, there are many other attacks that can be mounted on multi-prime RSA, which should be taken into consideration. As the number of prime factors in the modulus increases, the severity of these attacks decreases. We describe some of these attacks given in [10] in the succeeding section.
3. Impact of the Number of Primes in Various Attacks Mounted on Multi-Prime RSA
The effects of various attacks on RSA considered in [2] were studied for multi-prime RSA in [10] which are summarized below.
3.1. Small Private Exponent Attacks
Using the public key, sometimes it is possible to recover the private key given that it is sufficiently small. Given below is a tabular representation explaining the effect of this attack on multi-prime RSA, as extended in [23]. The required value of the private exponent d in the following table indicates its maximum value for which it can be computed in a polynomial time of . In other words, the required time depends on the number of bits in the RSA modulus N, rather than its actual numerical value. This makes the algorithm much faster under the given conditions.
Table 1 provides a tabular representation of the effect of Wiener’s continued fraction attack [24] on multi-prime RSA. The table suggests that the restriction on the value of d becomes stricter with the increment in r. As a result, the attack is less effective for multi-prime RSA than for the classic RSA cryptosystem.

Table 1.
Maximum value of the private exponent d based on the number of primes [24].
A lattice-based attack on RSA was given in [25], which was simplified in [26], and further extended to multi-prime RSA in [23]. This attack gives a bound on d which, again as before, decreases with the increase in the number of prime factors.
3.2. Partial Key Exposure Attacks (Known LSB)
In certain cases, if some least significant bits, say , of a private key d are known, then it is possible to recover d entirely. Here, . The attack in focus was given in [27] and extended on multi-prime RSA in [28]. Here, such that . If a real number such that message satisfies
then the recovery of the decryption exponent d is only a matter of polynomial complexity in and under the assumption of algebraic independence, i.e., there is no algebraic expression involving them. A condition on can also be derived from the expression (1) when either the private exponent is very small or the public exponent is very small .
3.3. Partial Key Exposure Attacks (Known MSB)
Assume that an eavesdropper can approximate the most significant bits of the private key d. Let be a real number such that . In other words, suppose they know such that , for some . In this case, two lattice-based attacks given in [27] are applicable which are extended to multi-prime RSA in [28]. One of these attacks produces the same condition on as expression (1), while the other attack gives different bounds for under different conditions, which is given in detail in [10].
Here, we mainly weigh on the fact that all such conditions on for these attacks weaken with the increment in r. This further implies that these attacks are harder to mount on multi-prime RSA as compared to the standard RSA.
3.4. Partial Key Exposure Attacks (Known Partial Factorization)
Suppose an eavesdropper knows some of the least (or most) significant bits of one or more prime factors of the modulus, along with none or some of the least (or most) significant bits of the private exponent.
A lattice-based factoring method for composite integers of the form was presented in [29]. This method was generalized to factor composite integers with the same form as multi-prime RSA moduli in [28].
The following is the table as given in [28].
Table 2 illustrates the fraction of bits of the unknown prime factors required to factor an RSA modulus N having different number of prime factors under this specific attack scenario, as detailed in [28]. Here, s primes from the total of r prime factors of N are of unknown value, with some of their bits being known. The attack gives a minimum number of bits required to efficiently factorize the modulus. For and , we obtain the Coppersmith bound [30], which states that an RSA modulus (with two prime factors) can be efficiently factorized given the of the bits of one of its prime factors. This bound increases with increment in the value of r. The similar observation can be made about other values of known primes, i.e., . In conclusion, like the attacks discussed above, this attack also becomes weaker on multi-prime RSA. Other attacks mentioned in [10] give different bounds on which show the same nature as previously mentioned bounds.

Table 2.
Fraction of bits required to factor N, according to [28].
3.5. Chinese Remainder Theorem Attack
In order to maximize the decryption efficiency, Chinese Remainder Theorem (CRT) can be used in the multi-prime RSA. In this version of multi-prime RSA, we initially select k CRT exponents such that , which are subsequently utilized in decryption. The decryption exponent d is calculated using the Chinese Remainder Theorem, which can be used to compute the encryption exponent e by inverting it modulo . Now, one may find that it is convenient to use smaller values of , where , to expedite the computations. If all but one of the values of are taken to be small, a factorization attack can be mounted. This attack, as described in [23], proves that if the second largest CRT-exponent is then the runtime required to factorize the modulus N is , where r denotes the number of prime factors of the RSA modulus N. The conclusion drawn in [10] is that each should be chosen sufficiently large such that it would not be easier to factorize the RSA modulus as compared to factorizing it using the methods discussed in Section 4.
Remark 3.
It is evident that regarding multi-prime RSA, all the attacks mentioned in this section exhibit a similar tendency. As the number of primes in an RSA modulus increases, these attacks become more challenging to execute on the system. However, this is not always the case. In the following section, we describe the factoring attacks and their effect on multi-prime RSA. We see that the usage of too many primes in a single RSA modulus poses some crucial security threats due to the factorization attacks.
4. Number of Primes in a Modulus: The Safest-Value
As specified in the preceding section, increasing the number of primes in an RSA modulus makes it more resilient against the various attacks described above. But, the risk of factorizing the modulus increases with the rise in the number of its prime factors. These contrasting security-demands necessitate determining an optimum number of prime factors of an RSA modulus which renders the system resilient against both these types of attacks, including the factoring attacks. Along this thought, in this section, we determine an optimal value for the number of primes in the RSA modulus.
We examine the impact of two of the most popular and efficient factorization algorithms, namely Number Field Sieve (NFS) and Lenstra’s Elliptic Curve Factorization (ECF) algorithm, on a multi-prime RSA cryptosystem. [20] conjectures a runtime for both these algorithms in terms of “big-” notation. However, for the sake of simplicity and comparative calculations, we shall consider the expressions given in [10], and modify them in the terms of bit-size of the RSA modulus and the prime factor. The expected runtime for the best method of factorization, NFS, can be given by
where n is the bit-size of RSA modulus. Judging solely from this expression, it appears that the expected runtime to factorize an n-bit 2-prime RSA modulus should be the same as an n-bit r-prime RSA modulus for any with balanced primes. This is, however, only true when using NFS for factorization and not in general. Again, as in [10], expected runtime for Lenstra’s ECF method to find the prime factor of bit-size p of the RSA modulus of bit-size n is given by
It is apparent from the above expression that the expected runtime to factorize an n-bit 2-prime RSA modulus should be greater than n-bit r-prime RSA modulus for any with balanced primes, as the size of primes will be smaller.
Since NFS is considered the best factorization method, it must be ensured that the runtime for Lenstra’s ECF method is not less than that of NFS. Otherwise, the number of prime factors in the RSA modulus cannot be considered safe anymore. More precisely, we introduce the following notion.
Definition 1.
The maximum number of primes in an RSA modulus with balanced primes for which the expected runtime for NFS is less than that of the Lenstra’s ECF method is said to be the safe value of prime factors for the modulus of given size.
The minimum time required for factorizing an RSA modulus stays constant for all the values of prime factors up to the “safe value”, as it is the time required for NFS. Hence, it can be concluded that the security of an n-bit r-prime RSA system will remain the same for any value of r up to the “safe value”, as far as factorization attacks are concerned. Although, such systems will still be vulnerable to the attacks described in the Section 3. On the other hand, as the number of primes exceeds the “safe value”, the system becomes vulnerable against factorization with Lenstra’s ECF method. By combining these both results, one can understand how the derived “safe value” is an optimum value for the number of prime factors in a multi-prime RSA modulus. Now, we shall calculate the expected runtime for both the methods using given expressions (2) and (3) for different modulus sizes with varying size of its prime factors. Consider the following example.
Example 1.

Consider the RSA modulus having balanced prime distribution, i.e., , where r is the number of primes and p is the bit-size of its prime factor to be found. We shall calculate the runtime for 2048-bit and 4096-bit RSA modulus. The runtime for NFS does not vary with the number of prime factors, while we calculate the runtime for Lenstra’s ECF method for a modulus having two, three, four, and five prime factors.
In Table 3, the shaded cells denote the condition for which Lenstra’s ECF method requires less time than NFS to factorize the modulus.

Table 3.
Runtime (in seconds) for NFS and Lenstra’s ECF method for different modulus sizes.
It is apparent from the below Table 3 that when a 2048-bit RSA modulus is a product of four or more primes, it becomes significantly easier to factorize it using Lenstra’s ECF method than the NFS. Hence, by our definition, the “safe value” of primes for a 2048-bit modulus with balanced primes turns out to be 3. Similarly, the “safe value” for a 4096-bit modulus is 4.
In the table that follows, p indicates the average bit-size of primes according to the modulus size, i.e., .
In Table 4, the column with bit-size p of prime factor indicates the “safe value” for various modulus sizes. In practice, for additional security, let us assume that the primes are distributed in such a fashion that the smallest prime factor is approximately of the size of p. In this case, we can define the safest-value of primes to be used in the RSA modulus of given size as follows.

Table 4.
Safe value of primes to be used in a multi-prime modulus depending on the modulus size and varying size of prime factors. Here the highlighted column indicates the “safest-value” for the number of prime factors of the modulus of different sizes.
Definition 2.
Let us assume that in a multi-prime RSA system, the bit-size of the smallest prime factor is about the 90% of the average bit-size of prime factors. In this case, the “safe value” of primes to be used in the RSA modulus can be defined as the safest-value. Equivalently, the maximum number of primes in an RSA modulus with its prime factors distributed in such a manner that the smallest prime factor is roughly the 90% of the average bit-size, for which the expected runtime for NFS is less than that of the Lenstra’s ECF method is said to be the safest-value of prime factors for the modulus of given size.
While introducing the definition of “safest-value”, to take care of the practical implementation, we allow for a flaw that the primes are not distributed in a perfectly balanced manner, where each prime is about the size as their average bit-size. We use the term “safest” because while a practical implementation may not have a drastic difference between the size of the smallest prime factor and the average bit-size of prime factors, they are also less likely to have been distributed in a perfectly balanced pattern. Here we consider that the smallest prime factor is of nearly 90% size of their average bit-size. Then we apply the similar calculations as mentioned earlier to find the “safe value” for this case, to derive a “safest-value” for the given modulus size. The values in the other columns in the Table 4 are derived using the similar calculations. The “safest-value” for some modulus size is given in the highlighted column of Table 4. Moreover, when the number of prime factors are greater than the maximum “safe value” or the “safest-value” given in Table 4, the multi-prime RSA cryptosystem is no longer considered safe. We can also observe that when the size of the prime factor to be found using ECF is significantly smaller than the average bit-size, it easily becomes vulnerable to the factoring attacks. This serves as a motivation to use balanced primes in any RSA cryptosystem.
In conclusion, it is advisable to use “safest-value” of primes in an RSA modulus in order to protect it against all known attacks on RSA. Also, it is clear from the expressions (2) and (3) and the given example that as far as factorization attacks are taken into consideration, the security remains the same for all the numbers up to the “safest-value” and decreases further with each increment in the number of prime factors beyond that.
Now, we use the concept of “safest-value” of primes in an RSA modulus to refine the GMMRSA cryptosystem [18].
5. Improved Generalized Multi-Moduli RSA with Safest-Value
Finally, we improvise the GMMRSA cryptosystem [18] utilizing the concept of “safest-value” introduced in the preceding section.
Let us consider n integers . Here, each is composed of primes . Here, is the ‘safest-value’ of prime corresponding to the bit-size of the modulus .
Given that , the Euler totient of is calculated as
Key generation and other operations are carried out the same way as GMMRSA, as explained in Section 2.3. However, we shall still explain them in brief here.
Key generation initiates with the receiver choosing n encryption exponents , where each relatively prime to . Private decryption exponents are computed as
The n pairs are published, and the decryption exponents are kept secret along with all the primes used in the system.
Encryption is also the same as GMMRSA, in n steps, given by
Decryption is also carried out in n steps in the reverse order of encryption as
Notice that identical to GMMRSA [18], the encryption and decryption are carried out in n consecutive iterations. Furthermore, this improvised version of GMMRSA is an “enhanced” version of the former. We discuss and prove this in the following section.
6. Discussion and Security Analysis
The ideas presented in this article aid in solving the security concerns regarding multi-prime RSA. The GMMRSA cryptosystem, introduced in [18] suggested that the primes should be divided among multiple moduli such that each modulus consists of two prime factors. The reason behind this was to make the system secure against factorization attack posed by Lentra’s ECF method. However, many other attacks discussed in [10], which are also mentioned in Section 3 of this article, are more effective on a modulus with two prime factors, and become weaker with increment in the number of prime factors. As a solution to this quandary of conflicting security requirements, we introduced, in this paper, the notion of the “safest-value”. This “safest-value” provides an optimum number of prime factors an RSA modulus should have in order to achieve maximum security advantage against various attacks.
Here we give detailed calculation used to achieve the “safest-value” in Table 4 i.e., the highlighted column where bit-size of prime factors to be found is , i.e., .
Table 5 represents how the runtime for NFS stays constant regardless of the number of prime factors, while the runtime for Lenstra’s ECF decreases as the number of prime factors increase. The highlighted cells in the below table indicate the value of number of prime factors which are considered unsafe according to our criteria.

Table 5.
Runtime (in seconds) for NFS and Lenstra’s ECF method for different modulus sizes. Here the size of the smallest prime factor is , where p is the average bit-size of prime factors.
For the visualization of the concept of the “safest-value”, we provide comparative line charts for a fixed modulus size. Here we have considered a logarithmic scale on the Y-axis for a better visual comprehension.
Figure 1, Figure 2, Figure 3, Figure 4 and Figure 5 convey the trend in focus quite clearly. Furthermore, Table 5 as well as Figure 1, Figure 2, Figure 3, Figure 4 and Figure 5 support the findings presented in Table 4.
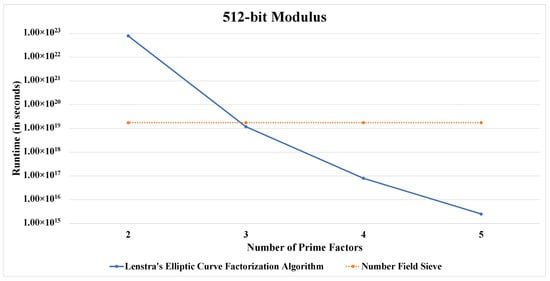
Figure 1.
Runtime comparison between both algorithms for a 512-bit modulus.
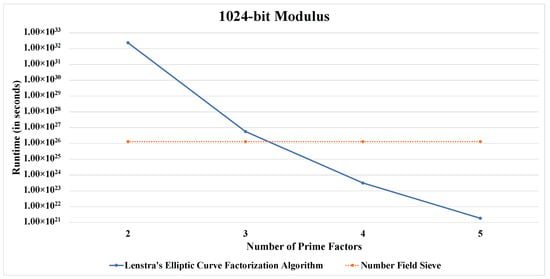
Figure 2.
Runtime comparison between both algorithms for a 1024-bit modulus.
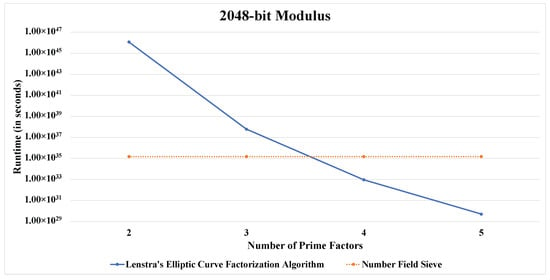
Figure 3.
Runtime comparison between both algorithms for a 2048-bit modulus.
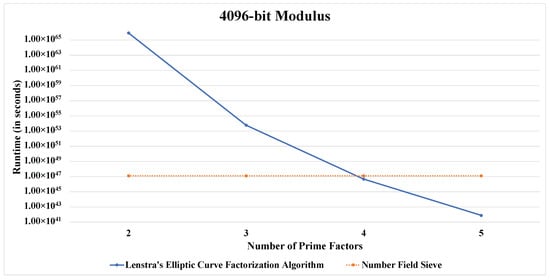
Figure 4.
Runtime comparison between both algorithms for a 4096-bit modulus.
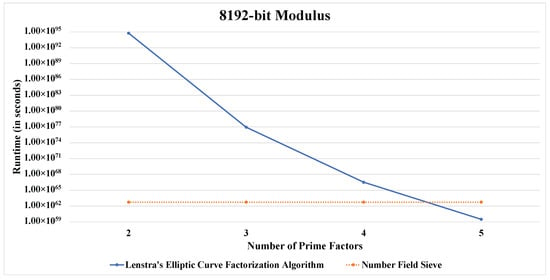
Figure 5.
Runtime comparison between both algorithms for a 8192-bit modulus.
The idea behind the introduction of the “safest-value” is quite intuitive. We observe that, as provided in [10], the heuristic runtime for the Number Field Sieve (NFS) does not depend on the size of primes involved in the system (see (2)). On the contrary, according to (3), the runtime for Lenstra’s Elliptic curve factorization (ECF) method relies heavily on the size of the prime factor to be found. Consequently, as we observe in the Table 5, with the increment in the number of primes, the factorization using Lenstra’s ECF method becomes easier. We also notice that after a certain value of number of prime factors, factorization using Lenstra’s ECF becomes quite easier than using NFS. For a balanced prime distribution case, we call this value the “safe value” according to the Definition 1. However, here in the case of Table 5, we have considered primes to be distributed in such a trend that the smallest prime is about the of the average bit-size. This is done to take care of the practical irregularities. For this scenario, we use the term “safest-value”, as defined in Definition 2.
Now, we turn our discussion to the security analysis of the proposed improvised GMMRSA cryptosystem and its advantages compared to other modern RSA cryptosystems, mainly multi-prime RSA. We discuss some attributes of the improvised GMMRSA below. Firstly, we discuss that its security strength is n-fold compared to the classical RSA. Secondly, we emphasize the security advantage of the improvised GMMRSA over multi-prime RSA variants with a single modulus. Finally, we discuss how it is an enhanced adaptation of the GMMRSA.
- In ([18] § 4), it was shown that the GMMRSA with -primes has an advantageous n-fold security compared to the classical RSA because of the recursive approach implemented in the encryption and the decryption processes in n-iterations. Due to the similar approach being devised in the improvised GMMRSA scheme, it also offers n-fold security fortification compared to the classical RSA.
- One of the main concerns in the RSA and its variants is its resilience against the factorization attack. As far as the factorization is concerned, as discussed in Section 4, any modulus, whether it is a product of two primes or a product of multiple primes up to the “safest-value”, possesses the same level of security. The only difference between the GMMRSA and the improvised GMMRSA is that each modulus in the former is a product of exactly two primes, whereas the number of prime factors of each modulus in the latter is precisely the “safest-value”. Therefore, the GMMRSA and its improvised version considered in this paper are equally secure against any factorization attacks. Evidently, as in [18], the improvised GMMRSA also is more resilient against the factorizations attacks as compared to multi-prime variants of RSA with a single modulus.
- Ultimately, we argue how the improvised GMMRSA is an “enhanced” version of the GMMRSA given by the authors [18]. Based on the conclusions of Section 3, certain attacks exhibit difficulty to mount on an RSA variant having modulus consisting of multiple prime factors rather than just two prime factors. In actuality, their impact reduces as the modulus’s prime factor count rises. We introduced the concept of the “safest-value” of the number of prime factors of a modulus, which is the maximum secure value against all the concerning attacks covered in this paper. The improvised GMMRSA is designed using this concept of the safest-value as compared to its two-prime multi-moduli counterpart. Therefore, the improvised GMMRSA offers enhanced security against the attacks described in Section 3 in comparison to the GMMRSA. Hence, the improvised GMMRSA, we proposed here, is indeed, an enhanced version of the GMMRSA.
The above discussion remarkably suggests that the improvised GMMRSA cryptosystem is advantageous and recommendable over not only the classical RSA but also multi-prime variants of RSA, including the multi-moduli variant GMMRSA.
7. Conclusions
The Generalized Multi-Moduli RSA (GMMRSA) cryptosystem [18] was proposed in order to overcome the security concern caused by factoring attacks on multi-prime RSA with a single modulus, in which using only two primes in an RSA modulus was recommended over multiple primes. However, it is evident that many attacks on multi-prime RSA actually become less effective with the increment in the number of primes in an RSA modulus. To balance these opposing phenomena, here we derived an optimal value of the number of prime factors in an RSA modulus such that the security of the system is not compromised when several known attacks are mounted. To achieve this, we introduced the concept of “safest-value” of prime factors in an RSA modulus. Using this novel concept, we refined our GMMRSA cryptosystem, which enhances the security of our previously proposed GMMRSA against the attacks described in Section 3, as these attacks are harder to apply on an RSA modulus with multiple prime factors.
Author Contributions
Conceptualization, J.M. and H.R.; Methodology, H.R.; Investigation, J.M. and H.R.; Writing—original draft, H.R.; Writing—review & editing, H.R. Supervision, J.M.; Project administration, J.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding authors.
Acknowledgments
The second author acknowledges the financial support of CSIR-HRDG in the form of Junior Research Fellowship. The authors thank Pushparajsinh Parmar for his valuable suggestions on a draft of this paper. The authors are extremely grateful to the anonymous referees whose valuable suggestions and insights improved the quality of this paper.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| GMMRSA | Generalized Mullti-Moduli RSA |
| NFS | Number Field Sieve |
| ECF | Elliptic Curve Factorization |
| LSB | Least Significant Bits |
| MSB | Most Significant Bits |
References
- Rivest, R.L.; Shamir, A.; Adleman, L. A method for obtaining digital signatures and public-key cryptosystems. Commun. ACM 1978, 21, 120–126. [Google Scholar] [CrossRef]
- Boneh, D. Twenty years of attacks on the RSA cryptosystem. Not. Am. Math. Soc. 1999, 46, 203–213. [Google Scholar]
- Mumtaz, M.; Ping, L. Forty years of attacks on the RSA cryptosystem: A brief survey. J. Discret. Math. Sci. Cryptogr. 2019, 22, 9–29. [Google Scholar] [CrossRef]
- Mehta, J. (Department of Mathematics, Sardar Patel University, Vallabh Vidyanagar, India); Parmar, P. (Department of Mathematics, Sardar Patel University, Vallabh Vidyanagar, India). A New Cryptosystem with Enhanced RSA Security and Forward Secrecy: A Hybrid Approach. Personal Communications, 2025. [Google Scholar]
- Cesati, M. A New Idea for RSA Backdoors. Cryptography 2023, 7, 45. [Google Scholar] [CrossRef]
- Koyama, K.; Maurer, U.M.; Okamoto, T.; Vanstone, S.A. New Public-Key Schemes Based on Elliptic Curves over the Ring Zn. In Advances in Cryptology—CRYPTO ’91; Feigenbaum, J., Ed.; Springer: Berlin/Heidelberg, Germany, 1992; pp. 252–266. [Google Scholar]
- Boudabra, M.; Nitaj, A. A New RSA Variant Based on Elliptic Curves. Cryptography 2023, 7, 37. [Google Scholar] [CrossRef]
- Nemo, C. RSA Moduli Should Have 3 Prime Factors. Scientific Bulgarian Magazine. 1996. Available online: http://fgrieu.free.fr/CaptainNemo.pdf (accessed on 20 May 2025).
- Collins, T.; Hopkins, D.; Langford, S.; Sabin, M. Public Key Cryptographic Apparatus and Method. U.S. Patent 5,848,159, 8 December 1998. Available online: https://patents.google.com/patent/US5848159A/en (accessed on 20 May 2025).
- Hinek, M.J. On the security of multi-prime RSA. J. Math. Cryptol. 2008, 2, 117–147. [Google Scholar] [CrossRef]
- Kamel Ariffin, M.R.; Abubakar, S.I.; Yunos, F.; Asbullah, M.A. New Cryptanalytic Attack on RSA Modulus N = pq Using Small Prime Difference Method. Cryptography 2019, 3, 2. [Google Scholar] [CrossRef]
- Rahmani, M.; Nitaj, A.; Ziane, M. Partial Exposure Attacks on a New RSA Variant. Cryptography 2024, 8, 44. [Google Scholar] [CrossRef]
- Teşeleanu, G. Partial Exposure Attacks Against a Family of RSA-like Cryptosystems. Cryptography 2025, 9, 2. [Google Scholar] [CrossRef]
- Dieulefait, L.V.; Urroz, J. Factorization and Malleability of RSA Moduli, and Counting Points on Elliptic Curves Modulo N. Mathematics 2020, 8, 2126. [Google Scholar] [CrossRef]
- Abd Ghafar, A.H.; Kamel Ariffin, M.R.; Md Yasin, S.; Sapar, S.H. Partial Key Attack Given MSBs of CRT-RSA Private Keys. Mathematics 2020, 8, 2188. [Google Scholar] [CrossRef]
- Adenan, N.N.H.; Kamel Ariffin, M.R.; Sapar, S.H.; Abd Ghafar, A.H.; Asbullah, M.A. New Jochemsz–May Cryptanalytic Bound for RSA System Utilizing Common Modulus N = p2q. Mathematics 2021, 9, 340. [Google Scholar] [CrossRef]
- Wang, S.; Sun, M. New Cryptanalysis of Prime Power RSA with Two Private Exponents. Mathematics 2024, 12, 3411. [Google Scholar] [CrossRef]
- Mehta, J.; Rana, H. A multi-moduli approach towards enhancing the security of multi-prime RSA. J. Discret. Math. Sci. Cryptogr. 2025; accepted. [Google Scholar]
- Pollard, J.M. Theorems on factorization and primality testing. Math. Proc. Camb. Philos. Soc. 1974, 76, 521–528. [Google Scholar] [CrossRef]
- Lenstra, H.W., Jr. Factoring integers with elliptic curves. Ann. Math. 1987, 126, 649–673. [Google Scholar] [CrossRef]
- Kamardan, M.G.; Aminudin, N.; Che-Him, N.; Sufahani, S.; Khalid, K.; Roslan, R. Modified Multi Prime RSA Cryptosystem. J. Phys. Conf. Ser. 2018, 995, 012030. [Google Scholar] [CrossRef]
- Shah, T.; Zohaib, M.; Xin, Q.; Almutairi, B.; Sajjad, M. Generalization of RSA cryptosystem based on 2n primes. AIMS Math. 2023, 8, 18833–18845. [Google Scholar] [CrossRef]
- Hinek, M.J.; Low, M.K.; Teske, E. On some attacks on multi-prime RSA. In Selected Areas in Cryptography, Proceedings of the 9th Annual International Workshop, SAC 2002, St. John’s, NL, Canada, 15–16 August 2002; Revised Papers 9; Springer: Berlin/Heidelberg, Germany, 2003; pp. 385–404. [Google Scholar] [CrossRef]
- Wiener, M. Cryptanalysis of short RSA secret exponents. IEEE Trans. Inf. Theory 1990, 36, 553–558. [Google Scholar] [CrossRef]
- Boneh, D.; Durfee, G. Cryptanalysis of RSA with private key d less than N/sup 0.292/. IEEE Trans. Inf. Theory 2000, 46, 1339–1349. [Google Scholar] [CrossRef]
- Blömer, J.; May, A. Low Secret Exponent RSA Revisited. In Cryptography and Lattices, Proceedings of the CaLC 2001, Providence, RI, USA, 29–30 March 2001; Silverman, J.H., Ed.; Springer: Berlin/Heidelberg, Germany, 2001; pp. 4–19. [Google Scholar]
- Ernst, M.; Jochemsz, E.; May, A.; de Weger, B. Partial Key Exposure Attacks on RSA up to Full Size Exponents. In Advances in Cryptology—EUROCRYPT 2005, Proceedings of the 24th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Aarhus, Denmark, 22–26 May 2005; Cramer, R., Ed.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 371–386. [Google Scholar]
- Hinek, M.J. On the Security of Some Variants of RSA. Ph.D. Thesis, University of Waterloo, Waterloo, ON, Canada, 2007. [Google Scholar]
- Boneh, D.; Durfee, G.; Howgrave-Graham, N. Factoring N = prq for Large r. In Advances in Cryptology—CRYPTO’ 99, Proceedings of the 19th Annual International Cryptology Conference, Santa Barbara, CA, USA, 15–19 August 1999; Wiener, M., Ed.; Springer: Berlin/Heidelberg, Germany, 1999; pp. 326–337. [Google Scholar]
- Coppersmith, D. Finding a Small Root of a Bivariate Integer Equation; Factoring with High Bits Known. In Advances in Cryptology—EUROCRYPT ’96, Proceedings of the International Conference on the Theory and Application of Cryptographic Techniques Saragossa, Spain, 12–16 May 1996; Maurer, U., Ed.; Springer: Berlin/Heidelberg, Germany, 1996; pp. 178–189. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).