Abstract
In the control of robot manipulators, input torque constraints and system nonlinearities present significant challenges for precise trajectory tracking. However, fuzzy adaptive logic control (FALC) often fails to generate the optimal membership functions or function intervals. This paper proposes a modified greater cane rat algorithm (MGCRA) to optimize a fuzzy adaptive logic controller (FALC) for minimizing input torques during trajectory tracking tasks. The main innovation lies in integrating the improved MGCRA with FALC, which enhances the controller’s adaptability and performance. For benchmarking, several state-of-the-art swarm intelligence algorithms—including particle swarm optimization (PSO), artificial bee colony (ABC), ant colony optimization (ACO), gray wolf optimization (GWO), covariance matrix adaptation evolution strategy (CMA-ES), adaptive guided differential evolution (AGDE), the basic greater cane rat algorithm (GCRA), and a trial-and-error method—are compared under identical conditions. Experimental results show that the MGCRA-tuned FALC achieves lower input torques and improved trajectory tracking accuracy compared to other methods. The findings demonstrate the effectiveness and potential of the proposed MGCRA-FALC framework for advanced robotic manipulator control.
Keywords:
fuzzy adaptive logic control (FALC); swarm intelligence; modified greater cane rat algorithm (MGCRA); friction compensation; robot manipulators MSC:
93C42; 93C85
1. Introduction
Robot manipulators have dramatically enhanced productivity and improved efficiency in industrial applications and intelligent agricultural engineering [1]. In the last decade, robot manipulators have been recreated and expanded into various subdivided industrial and agriculture fields [2,3]. Since robot manipulators are typically designed to grasp and operate objects in a working environment, increasing attention has been drawn to their tracking control problem.
Only if the model is known and no external disturbance exists, a combination of PID control and feedforward compensation control can meet the requirements of manipulator trajectory control. However, the working environment of a robot manipulator is always complicated; in practical terms, there is no manipulator system completely free from external disturbance [4]. On the other hand, the PID controller has poor adaptability to nonlinear, time-variant plants, and meanwhile, its parameters cannot be tuned online for continuous load variations. These drawbacks place various restrictions on the trajectory tracking control of robot manipulators by the PID technique. The fuzzy control method has been widely applied in the optimization of complex systems, achieving significant results in the fuzzy adaptive energy management strategy for agricultural tractors [5]. Similar approaches can also be utilized to improve robotic manipulation systems. Since robots have to confront various uncertainties in the working environment, achieving the desired control performance by using control algorithms solely based on the dynamic robot model is relatively difficult.
To deal with these problems, unceasing efforts have been stimulated to promote the tracking control techniques of robot manipulators with uncertainties. Under these circumstances, sliding mode control theory [6] and adaptive control theory have been proposed and extensively studied for the tracking control of robot manipulators [7,8]. Moreover, with the development of computer technology, artificial neural network (ANN) technology has gradually been applied to the trajectory tracking problem of robot manipulators [9]. Another advanced trajectory control technique is fuzzy logical control theory, which shows outstanding advantages for nonlinear systems with large time delay and time variation characteristics [10,11]. The fuzzy logic control technique mainly comprises two methods: one is to use it as a controller to realize direct control, and the other is to use it for system identification to realize the indirect control of the robot. Fuzzy logic controllers (in Figure 1) usually have quite a lot of fuzzy rule parameters to be adjusted. The rule parameters of the fuzzy inference system (FIS) used to be tuned by expert experience or conventional optimization algorithms, for example, the least square method and the maximum likelihood method. It has been observed that fuzzy adaptive logic control (FALC) often fails to adaptively generate optimal membership functions or function intervals.
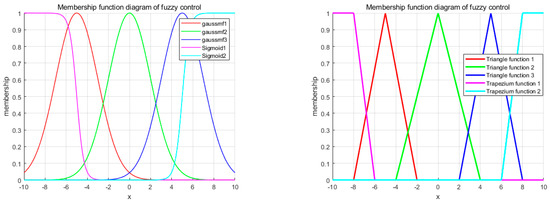
Figure 1.
Membership function diagram of fuzzy control.
In the recent decade, swarm intelligence optimization algorithms have shown their superiority in the field of optimization compared to conventional optimization algorithms. Swarm intelligence often abstracts the living habits of various animal and plant species, such as particle swarm optimization (PSO) [12], the genetic algorithm (GA) [13], differential evolution (DE), the ant colony optimization algorithm, the cuckoo search algorithm (CSA), the artificial bee colony algorithm (ABC) [14], the ant colony algorithm (ACO) [15], monarch butterfly optimization (MBO), social spider optimization (SSO) [16], the whale optimization algorithm (WOA), gray wolf optimization (GWO) [17], the firefly algorithm (FA), Harmony Search Optimization (HSO) [18], the sparrow search algorithm (SSA) [19,20], the covariance matrix adaptive evolutionary strategy (CMA) [21], the adaptive guided differential evolution (AGDE) algorithm [22], etc. Some swarm intelligence techniques have been already utilized to optimize the rule parameters of the fuzzy logic controller. For example, Bingul and Karahan employed PSO to tune the membership functions of antecedent/consequent fuzzy parameters [23], and for a two-link planar robot, there were a total of 60 parameters to optimize in their study. Qais et al. extended the whale optimization algorithm to the fuzzy logic controller for fault detection wind generators [24]. Al-Dabbagh et al. introduced the application of a DE algorithm to the identification of the barycentric parameters of the CRS A456 robot manipulator [25]. Bernal et al. compared the optimization performance between the galactic swarm optimization and the FA for type-2 fuzzy logic controller [26]. Rajeswari and Santhi investigated the application of FPA in programmable n-level inverters using fuzzy logic [27]. Swarm intelligence techniques have paved new insights into fuzzy logic controllers and drawn increasing interest for robot trajectory control.
Due to the time-consuming nature and complexity of tuning the rule parameters of fuzzy logical controllers, it is necessary to obtain a suitable FALC technique. FALC can be constructed by a combination of adaptive law schemes and FISs [28,29,30,31]. In a fuzzy adaptive logical controller, usually only the consequent parameters of the FIS are obtained via the adaptive law; however, FALC’s antecedent parameters are usually designed by expert experience or the trial-and-error method [32,33].
It is noted that the selection of membership functions in fuzzy parameters are likely to provide poor performance. Despite being time-consuming, the trial-and-error method unlikely results in the optimal antecedent parameters of FALC and the controller’s performance. Through our preliminary investigations, we found that the antecedent parameters significantly impact the maximum input torque and total performance of FALC. To promote the control performance, as will be seen later, we introduce swarm intelligence optimization algorithms into FALC to obtain its optimal input membership functions.
Recently, a new swarm intelligence algorithm, greater cane rat algorithm (GCRA), inspired by the ingenious foraging patterns exhibited by greater cane rats, both during and outside of their mating season, has been proposed [34]. Moreover, by comparison with dozens of the most recent optimization algorithms, the GCRA has shown considerable competitiveness for solving different engineering problems. However, only a few limited fields of applications of the GCRA have so far been conducted. For example, the trajectory tracking of robot manipulators is an ongoing research focus, yet no related research based on the GCRA has been discussed to the best of our knowledge.
To enlarge the application of the GCRA in solving the trajectory tracking problem of robot manipulators, an FALC scheme was employed to control a two-link robot manipulator with unknown frictions, in which the input membership functions, also called the antecedent fuzzy parameters, were to be optimized by swarm intelligence algorithms. Furthermore, in the present work, we proposed a modified greater cane rat algorithm (MGCRA) based on the standard GCRA. As will be illustrated later, the simulation results indicate the effectiveness and reliability of the MGCRA method on the optimization of FALC over other trial-and-error approaches, surpassing the limitations of the existing state-of-the-art algorithms for the trajectory control of robot manipulators.
2. Fuzzy Adaptive Logic Controller (FALC) for Robot Manipulators
In the present study, we particularly focus on the application of swarm intelligence in FALC, which consists of a fuzzy adaptive logic scheme and sliding mode control technique. This control technology has shown great potential in agricultural engineering, such as in the development of intelligent pollination robotic arms. Relevant research indicates that intelligent pollination robotic arms, through high-precision control, can significantly enhance pollination efficiency and quality while reducing labor costs [35]. This highlights the practical application value of FALC in agricultural robots as well as its effectiveness and adaptability in complex agricultural settings. On this foundation, this study further explores the application of swarm intelligence algorithms in optimizing FALC parameters. The goal is to improve the trajectory tracking performance of robot manipulators and provide technical support for agricultural automation and intelligent development.
2.1. Dynamic Model of Robot Manipulators
The n-link robot manipulator can be denoted by the following dynamic equation:
where is the vector of generalized coordinates, is the inertia matrix, is the vector of centrifugal and Coriolis forces, is the gravity vector, and is the input torque. is the unknown friction.
2.2. Sliding Mode Controller
The aim of the tracking target of the robot manipulator is to make output q track designed trajectory qd under proposed controller τ as time passes by.
The tracking error can be expressed as
We define the sliding mode function as
where Λ is a positive definite matrix.
We let
We define the Lyapunov function as
where is the ideal parameter.
The derivative of the Lyapunov function can be obtained by
2.3. Fuzzy Adaptive Compensation with Unknown Friction
Fuzzy compensation for the unknown friction is considered for the trajectory control of robot manipulators. Since friction is usually determined by the joint speed [36], it can be described by . The FIS used to approximate friction can be expressed as
where is the fuzzy compensation of friction . The fuzzy approximation error regarding friction can be expressed as
Eventually, the FALC law is designed as
where ; the convergence rate of the system depends on .
Substituting the control law (9) into the derivative of the Lyapunov function (6) yields
The adaptive laws are designed as
Then, the derivative of the Lyapunov function can be obtained by the following formula
Since . > 0 and w is the minimum approximation error, by designing proper fuzzy parameters , can be sufficiently smaller than ; thus, .
3. Modified Greater Cane Rat Algorithm (MGCRA)
The GCRA optimization process is inspired by the intelligent foraging behavior of cane rats during and outside the timeframe of mating seasons. They are highly nocturnal animals and leave traces when foraging in reeds and grass, which subsequently lead to sources of food, water, and shelter. This algorithm has shown to have superiority over several other algorithms as it is simple yet powerful.
3.1. Greater Cane Rat Algorithm
The GCRA includes three main procedures: (i) Initialization: a procedure that generates the search agents in the search space; (ii) Exploration: a procedure that explores the entire search space to seek diverse solutions; and (iii) Exploitation: a procedure that seeks improved solutions near the local optima.
Initialization phase: Similarly to other swarm intelligence algorithms, the initialization of the search agent is randomly generated, as denoted in Equation (13).
where d and n represent the dimensionality of the variables and the number of search agents, respectively. For instance, Xnd is the coordinate of the nth search agent in dth dimension.
Exploration phase: Cane rats construct their shelters (nests or burrows) around their territory (swamps, riverbanks, and cultivated land). They leave their different shelters to forage, either following paths to previous food sources or seeking new ones and leaving traces behind. The updating rule of the exploration phase can be described by
where , , , is the current iteration, and is the maximum iteration. And represents the updated GCR position, represents the current GCR position, and denotes the dominant male in the jth dimension.
Exploitation phase: The breeding season varies depending on the habitat and typically occurs during the rainy season. It is well known that, to increase genetic diversity, males disperse from the group during the breeding season. It is assumed that once the group disperses, foraging activities concentrate in areas abundant with food sources. The exploitation process implements the updating rule as follows:
3.2. Modified Greater Cane Rat Algorithm (MGCRA)
In the MGCRA, Latin hypercube sampling is applied to the initialization process and can be described as follows:
where represents a random permutation from 1 to n, and denotes a uniform and random distribution on the interval [0,1].
Latin hypercube sampling initialization has the advantage over random initialization in that it covers the parameter space more uniformly, facilitating a faster search for the global optimum and helping to avoid getting stuck in local optima.
The GCRA enters the exploration or exploitation phase based on the switch value of ρ. In the GCRA, the value of ρ is fixed at 0.5. However, in the MGCRA, we employ a strategy with a variable value of ρ, which can be suggested by
where is a constant that indicates the maximum value of the switch threshold. expresses the maximum number of iterations.
The maximum value of the switching threshold is an important parameter affecting the search ability of the MGCRA. If the parameter is set too large, the algorithm will easily fall into local optimization, and if the parameter is set too small, an inaccurate solution will be obtained. Via a sensitivity analysis of the parameter, we found that when the value of is set to 0.6, the algorithm can better balance its ability in local and global searches.
It can be known from Equation (17) that in the early stage of the iterative process, the switching threshold is small, and the global search ability of the algorithm is strong. After the iterative process carries on for a period of time, the switching threshold gradually converges to plateau ; at this stage, the local search ability of the algorithm is strong. After the plateau period, the switching threshold reduces, which is beneficial for the algorithm to maintain the diversity of the population and stop the algorithm from prematurely falling into a local optimum.
4. Simulation Results
4.1. Optimization of Input Membership Functions of FALC with MGCRA
In this section, a control system simulation model is presented. The system uses a trajectory planning module to set the reference trajectory and applies it to a two-link planar robotic manipulator (Figure 2) through a motion control module. This example illustrates the effectiveness of the MGCRA method. Finally, the motion trajectory of the end-effector of the two-link planar robotic manipulator model and the trajectory error are displayed by the oscilloscope module. The fuzzy controller adjusts the PID parameters based on the error and its rate.
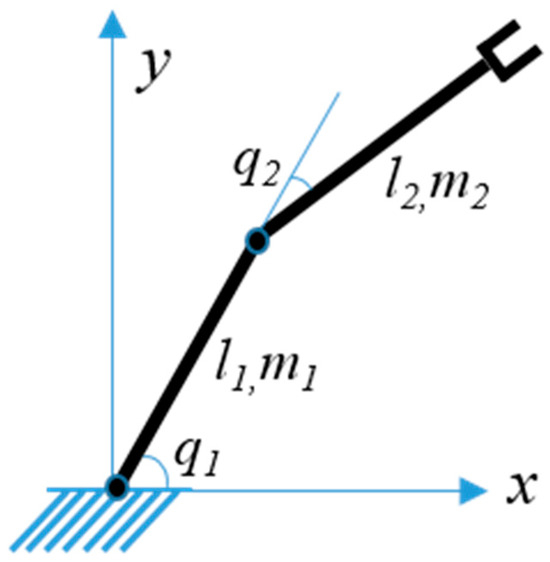
Figure 2.
A schematic diagram of the two-link planar robot manipulator.
To verify the effectiveness of the MGCRA in adaptive logic controllers, this paper conducted multiple experimental simulations to test the performance of the controller optimized by the MGCRA compared to that using traditional trial-and-error methods in several aspects, including convergence speed, error stability, and robustness.
The simulation results show that the controller using the MGCRA can reach the set target state within 5 s, while the trial-and-error method takes over 10 s. This indicates that the MGCRA demonstrates higher efficiency in real-time tuning.
In tests of dynamic environmental adaptability, the MGCRA-optimized controller maintains low error fluctuations, with a standard deviation of approximately 0.01, while the trial-and-error method exhibits larger error fluctuations, with a standard deviation of 0.05. This suggests that the MGCRA can effectively enhance the system’s stability in parameter adaptive tuning.
When external disturbances are introduced, the adaptive controller employing the MGCRA can quickly adjust its parameters to return to a stable state. In contrast, the recovery time for the traditional trial-and-error method is significantly prolonged, indicating insufficient robustness.
We assume that the structural parameters of the two-link planar robot model are known, and all state variables are measurable. They can be presented as [37]
where the structural parameters are listed in Table 1, and g is the gravity acceleration.

Table 1.
The structural parameters of the two-link robot manipulator.
The parameters of FALC are designed as , , I is the unit matrix, and . A simple sine signal was applied to demonstrate the effectiveness of the trajectory tracking technique for the robot manipulator, as follows:
where the initial state of the system is set to .
In order to prevent the input variables from exceeding the fuzzy domain in the presence of friction, when designing the membership functions of antecedent fuzzy parameters, we employ Sigmoid membership functions at both sides and Gaussian membership functions in the middle, as below.
where , and are the Gaussian membership functions; and are Sigmoid membership functions. In this context, joint 1 has four undetermined parameters of fuzzy parameters, i.e., n1, n2, n3, and n4, and so does joint 2. Hence, there are a total of eight parameters to be determined.
In the simulation, we employ the MGCRA for the optimization of the membership functions of the antecedent fuzzy parameters of FALC. A sketch map of the training process of FALC parameters with the MGCRA is illustrated in Figure 3. In the training process, the MGCRA is employed to optimize parameters n1~n8 to obtain the minimum of the input torques.
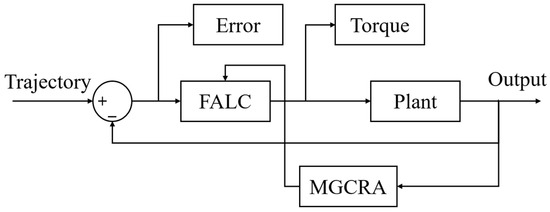
Figure 3.
Training process of FALC parameters with MGCRA.
Since the operating torque range always significantly influences the overall performance of robot manipulators, this study mainly focuses on the minimum of the maximum input torque of the robot manipulator. Therefore, the cost function designed herein is the sum of the maximum absolute of the input torques (SMAT), which can be written as follows:
To ensure the convergence accuracy when obtaining the minimum of the maximum input torque, the sum of squared error (SSE) is employed to evaluate the convergence error, namely
where N is the total number of test data, is the value of the ith input torque and is the ith error of the lth link of the robot manipulator.
When dealing with noise and irrelevant features, the L1 norm in SAMT can effectively drive the weights of irrelevant features toward zero, making the model more stable and less sensitive to noise. In certain applications of robotic arms, the primary concern is to avoid large errors (e.g., in industrial control, robotic path planning, etc.). In such cases, using the maximum absolute error as a cost function is very suitable. By minimizing the maximum error, this ensures that the model’s predictions do not exceed the allowed error range, avoiding anomalies in the model’s output. The L2 norm in the SSE helps reduce excessively large parameter values (i.e., penalizing overly complex models). Without regularization, a model may overfit the noise in the training data. By introducing the penalty of squared errors, the model becomes smoother in fitting the data, thereby helping to avoid overfitting.
In the meantime, for the purpose of comparison, we adopt the trial-and-error method and other swarm intelligence algorithms to test the performance of FALC with different antecedent parameters of fuzzy parameters. Specifically, in the trial-and-error method, five cases of undetermined antecedent parameters were employed for simulation, respectively. Case 1: n1 = n2 = … = n8 = 2; case 2: n1 = n2 = … = n8 = 4; case 3: n1 = n2 = … = n8 = 6; case 4: n1 = n2 = … = n8 = 8; and case 5: n1 = n2 = … = n8 = 10. And the swarm intelligence algorithms for comparison are, respectively, PSO, ABC, ACO, GWO, the CMA, AGDE, and the basic GCRA.
In the procedure of the simulation experiment, a pair of desired joint angle signals are input to the manipulator system at first. Then, the simulation process is launched using the MGCRA, PSO, ABC, ACO, GWO, CMA, AGDE and the basic GCRA methods. After three independent trials, each algorithm takes the mean performance value as a result. Overall, the population of these swarm intelligence algorithms is 30, and the maximum iterations are 20. Specifically, in the PSO method, the learning factors are set to 1.2 and 1.5, and the weight coefficient decreases linearly from 0.9 to 0.1. In the ABC method, the number of onlooker bees equals the entire population, the abandonment limit coefficient is set to 0.6, and the acceleration coefficient is set to 1. In the ACO method, the intensification factor is set to 0.4, and the deviation distance ratio is set to 1. In the GWO method, the coefficient of decreases linearly from 2 to 0 along with the iterations. In the CMA and AGDE methods, the algorithm parameters are consistent with the parameters described in [19,20]. After the simulation process, we can obtain optimal parameters n1~n8. Moreover, we can also obtain the output signal for the errors, torques, angles, angular velocities, etc.
4.2. Comparison of Results
In control system design, adaptive tuning plays a critical role in enhancing the overall performance of the system. An adaptive logic controller adjusts control parameters in real time to respond to unforeseen environmental changes and system dynamics. In recent years, the application of the modified greater cane rat algorithm (MGCRA) methods in adaptive control systems has received widespread attention. This paper analyzes the effectiveness of the MGCRA in adaptive tuning through simulation results and compares these methods to traditional trial-and-error methods.
The membership functions of antecedent fuzzy parameters are trained by the MGCRA and other swarm intelligence algorithms, with the goal of obtaining the minimum value of the cost function SMAT. The results of the input torque using different methods are listed in Table 2 and Table 3. And the membership functions for joint 1 and joint 2 after training with SMAT by the MGCRA are shown in Figure 4. It should be pointed out that this work adopts a symmetrical way to design the five membership functions; one can also design asymmetric or more membership functions of antecedent fuzzy parameters, which may result in better performance.

Table 2.
The performance of FALC by the trial-and-error method and MGCRA.

Table 3.
The performance of FALC by the MGCRA and other swarm intelligence algorithms.
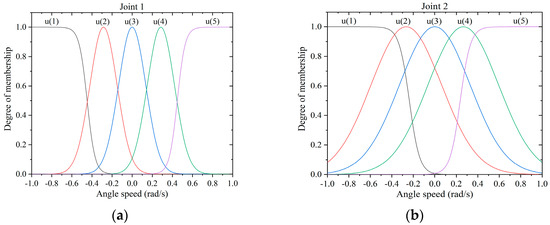
Figure 4.
Input membership functions for (a) joint 1 and (b) joint 2 after training with SMAT by the MGCRA.
It can be seen from Table 2 that the antecedent fuzzy parameters have a significant impact on SMAT values. Among the trial-and-error methods, case 5 and case 3 have the largest difference in SMAT by 19.0%. The results of case 2 and case 3 are the closest and almost equal. Moreover, the membership function parameters determined by the MGCRA are n1 = 5.5050; n2 = 5.2263; n3 = 6.3501; n4 = 5.2548; n5 = 5.9196; n6 = 2.1520; n7 = 5.2320; and n8 = 9.9616. Compared to the MGCRA and trial-and-error methods, the MGCRA resulted in a remarkable reduction in the input torques, which were reduced by 13.2% compared to case 2 and reduced by 34.9% compared to case 5.
It can be seen from Table 3 that the SMAT values obtained by different swarm intelligence algorithms are close to each other but smaller than those obtained via the trial-and-error method. In other words, the performance of all the swarm intelligence algorithms can easily exceed the trial-and-error method. Specifically, the MGCRA has the best convergence accuracy compared to the trial-and-error method and other swarm intelligence algorithms. In addition, from Table 2 and Table 3, we can see that the SSE values obtained by all the methods are close to each other. This is due to the fact that the convergence accuracy of the system mainly depends on the sliding mode control technique and the adaptive law.
To compare the performance of these swarm intelligence algorithms on the cost function SMAT, convergence curves are illustrated in Figure 5. In general, for the problem in this work, all the swarm intelligence algorithms are at the same level, and the convergence performance of the MGCRA has a slight advantage over the other swarm intelligence algorithms.
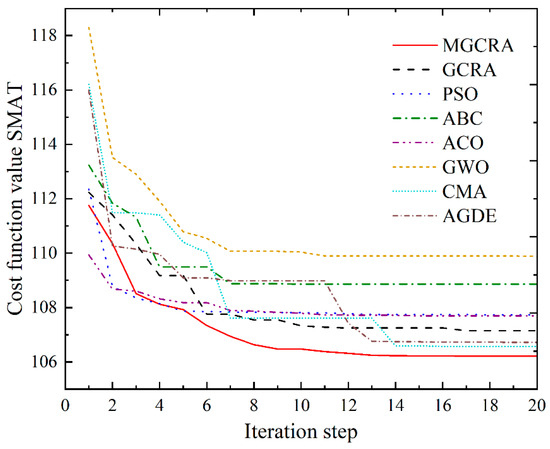
Figure 5.
A convergence curve of the swarm intelligence algorithms on the cost function.
The friction and fuzzy compensation of (a) joint 1 and (b) joint 2 by the MGCRA are demonstrated in Figure 6. We can see that although there is a high-frequency transformation in the friction torque, the fuzzy compensation torque of the friction torque is relatively smooth and no chattering occurs, which is a good situation.
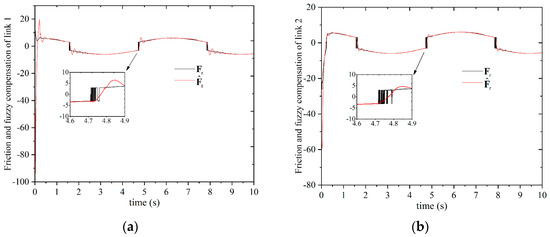
Figure 6.
The friction and fuzzy compensation of (a) joint 1 and (b) joint 2 by the MGCRA.
The input torques of joint 1 and joint 2 with antecedent fuzzy parameters designed by the trial-and-error method (case 1 to case 5) and MGCRA are illustrated in Figure 7. We can see that under different antecedent fuzzy parameters, the maximum absolute values of the input torque of joint 1 and joint 2 both occur in the initial stage, and after 0.6 s, the input torques of both joints gradually converge. For joint 1 in Figure 7a, the maximum absolute value occurs when the torque is positive; for joint 2 in Figure 7b, the maximum absolute value occurs when the torque is negative. In addition, remarkable chattering can be observed in case 4 for both joint 1 and joint 2. Compared to case 1 to case 5 of the trial-and-error method and the MGCRA, the input torques under the MGCRA method are the smallest and smoothest, so it is ultimately beneficial to the FALC performance for the trajectory tracking of robot manipulator systems.
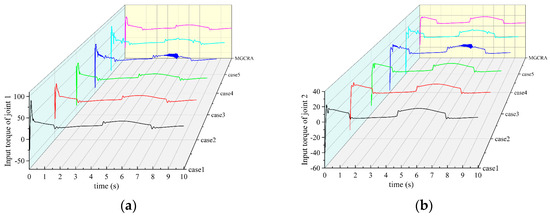
Figure 7.
Input torques of (a) joint 1 and (b) joint 2 with different antecedent fuzzy parameters.
5. Conclusions
In this paper, the MGCRA is advanced based on the basic GCRA, and then it is utilized in FALC to achieve the minimum input torques required for the trajectory tracking of robot manipulators. The trial-and-error method and other existing methods such as PSO, ABC, ACO, GWO, the CMA, AGDE and the basic GCRA method are adopted as comparative studies thereafter.
The simulation results demonstrate that the obtained torques of FALC by using swarm intelligence algorithms are significantly better than those using the trial-and-error method. Furthermore, the MGCRA provides comparative accuracy and has a slight advantage over the other swarm intelligence algorithms.
In short, by using the MGCRA to optimize the antecedent fuzzy parameters of FALC, the manipulator exhibits a significant decrease in the maximum input torques, resulting in better performance regarding the trajectory tracking technique. The practical application value of robot control research is not only limited to industrial production but also extends to agricultural engineering. Similarly to the development of automated systems for agricultural tasks, previous research has shown the effectiveness of robotic systems in enhancing efficiency and precision in greenhouse seedling transplantation [38]. For instance, in the field of agricultural harvesting robots, precise control strategies are crucial for reducing mechanical damage to fruits during the harvesting process, thereby improving the quality of agricultural products and enhancing economic benefits [39]. This cross-domain application potential further highlights the importance and broad prospects of robot control technology. Future advancements in robot control technology are expected to play an increasingly significant role in optimizing production processes and improving product quality across various industries.
Author Contributions
Conceptualization, J.S.; Methodology, J.S.; Software, J.S. and S.W.; Validation, S.W.; Formal analysis, S.W. and J.C.; Investigation, J.C., X.L., Z.W. and W.P.; Resources, J.C. and X.L.; Data curation, Z.W.; Writing—original draft, Z.W.; Writing—review & editing, R.X.; Visualization, R.X., W.P. and Y.Z.; Supervision, Y.Z.; Project administration, Y.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work is financially supported by the Manufacturing of Fujian Education Institutions [grant No. AMICM202203].
Data Availability Statement
No underlying data were collected or produced in this study.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Jin, Y.; Liu, J.; Xu, Z.; Yuan, S.; Li, P.; Wang, J. Development status and trend of agricultural robot technology. Int. J. Agric. Biol. Eng. 2021, 14, 1–19. [Google Scholar] [CrossRef]
- Roveda, L.; Maroni, M.; Mazzuchelli, L.; Praolini, L.; Shahid, A.A.; Bucca, G.; Piga, D. Robot End-Effector Mounted Camera Pose Optimization in Object Detection-Based Tasks. J. Intell. Robot. Syst. 2022, 104, 16. [Google Scholar] [CrossRef]
- Zubiete, E.D.; Nakahata, K.; Imamoglu, N.; Sekine, M.; Sun, G.; Gomez, I.; Yu, W. Evaluation of a Home Biomonitoring Autonomous Mobile Robot. Comput. Intell. Neurosci. 2016, 2016, 9845816. [Google Scholar]
- Benevides, J.; Paiva, M.; Simplício, P.; Inoue, R.; Terra, M. Disturbance observer-based robust control of a quadrotor subject to parametric uncertainties and wind disturbance. IEEE Access 2022, 10, 7554–7565. [Google Scholar] [CrossRef]
- Zhu, Z.; Zeng, L.; Chen, L.; Zou, R.; Cai, Y. Fuzzy adaptive energy management strategy for a hybrid agricultural tractor equipped with HMCVT. Agriculture 2022, 12, 1986. [Google Scholar] [CrossRef]
- Du, X.; Huang, J.; Zhu, L.-M. Sliding mode control with third-order contour error estimation for free-form contour following. Precis. Eng. 2020, 66, 282–294. [Google Scholar] [CrossRef]
- Asar, M.F.; Elawady, W.M.; Sarhan, A.M. ANFIS-based an adaptive continuous sliding-mode controller for robot manipulators in operational space. Multibody Syst. Dyn. 2019, 47, 95–115. [Google Scholar] [CrossRef]
- Ren, C.E. Adaptive Fuzzy Disturbance Observer-Based Control for Nonlinear Uncertain Systems with General Exogenous Disturbances. Int. J. Fuzzy Syst. 2021, 23, 1453–1461. [Google Scholar] [CrossRef]
- Parra, A.; Zubizarreta, A.; Pérez, J. An energy efficient intelligent torque vectoring approach based on fuzzy logic controller and neural network tire forces estimator. Neural Comput. Appl. 2021, 33, 9171–9184. [Google Scholar] [CrossRef]
- Castro, J.R.; Castillo, O.; Melin, P.; Rodríguez-Díaz, A. A hybrid learning algorithm for a class of interval type-2 fuzzy neural networks. Inf. Sci. 2009, 179, 2175–2193. [Google Scholar] [CrossRef]
- Lagunes, M.L.; Castillo, O.; Soria, J.; Valdez, F. Optimization of a fuzzy controller for autonomous robot navigation using a new competitive multi-metaheuristic model. Soft Comput. 2021, 25, 11653–11672. [Google Scholar] [CrossRef]
- Balasamy, K.; Ramakrishnan, S. An intelligent reversible watermarking system for authenticating medical images using Wavelet and PSO. Clust. Comput. 2019, 22, 4431–4442. [Google Scholar] [CrossRef]
- Tao, Y.; Wen, Y.; Gao, H.; Wang, T.; Wan, J.; Lan, J. A Path-Planning Method for Wall Surface Inspection Robot Based on Improved Genetic Algorithm. Electronics 2022, 11, 1192. [Google Scholar] [CrossRef]
- Toktas, A.; Stün, D.; Erdoan, N.B. Pioneer Pareto artificial bee colony algorithm for three-dimensional objective space optimization of composite-based layered radar absorber. Appl. Soft Comput. 2020, 96, 106696. [Google Scholar] [CrossRef]
- Karami, M.; Tavakolpour-Saleh, A.R.; Norouzi, A. Optimal Nonlinear PID Control of a Micro-Robot Equipped with Vibratory Actuator Using Ant Colony Algorithm: Simulation and Experiment. J. Intell. Robot. Syst. 2020, 99, 773–796. [Google Scholar] [CrossRef]
- Anter, A.; Hassanien, A.; ElSoud, M.; Kim, T. Feature selection approach based on social spider algorithm: Case study on abdominal CT liver tumor. In Proceedings of the 2015 Seventh International Conference on Advanced Communication and Networking (ACN), Kota Kinabalu, Malaysia, 8–11 July 2015; IEEE: Piscataway, NJ, USA, 11 July 2015; pp. 59–94. [Google Scholar]
- Nadimi-Shahraki, M.H.; Taghian, S.; Mirjalili, S. An improved grey wolf optimizer for solving engineering problems. Expert Syst. Appl. 2020, 166, 113917. [Google Scholar] [CrossRef]
- Valdez, F.; Castillo, O.; Peraza, C. Fuzzy Logic in Dynamic Parameter Adaptation of Harmony Search Optimization for Benchmark Functions and Fuzzy Controllers. Int. J. Fuzzy Syst. 2020, 22, 1198–1211. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. A novel swarm intelligence optimization approach: Sparrow search algorithm. Syst. Sci. Control. Eng. Open Access J. 2020, 8, 22–34. [Google Scholar] [CrossRef]
- Li, X.; Gu, J.; Sun, X.; Li, J.; Tang, S. Parameter identification of robot manipulators with unknown payloads using an improved chaotic sparrow search algorithm. Appl. Intell. 2022, 52, 10341–10351. [Google Scholar] [CrossRef]
- Hansen, N.; Müller, S.D.; Koumoutsakos, P. Reducing the time complexity of the derandomized evolution strategy with covariance matrix adaptation (CMA-ES). Evol. Comput. 2003, 11, 1–18. [Google Scholar] [CrossRef]
- Mohamed, A.W.; Mohamed, A.K. Adaptive guided differential evolution algorithm with novel mutation for numerical optimization. Int. J. Mach. Learn. Cybern. 2019, 10, 253–277. [Google Scholar] [CrossRef]
- Bingul, Z.; Karahan, O. A Fuzzy Logic Controller tuned with PSO for 2 DOF robot trajectory control. Expert Syst. Appl. 2011, 38, 1017–1031. [Google Scholar] [CrossRef]
- Qais, M.H.; Hasanien, H.M.; Alghuwainem, S. Whale optimization algorithm-based Sugeno fuzzy logic controller for fault ride-through improvement of grid-connected variable speed wind generators. Eng. Appl. Artif. Intell. 2020, 87, 103328.1–103328.13. [Google Scholar] [CrossRef]
- Al-Dabbagh, R.D.; Kinsheel, A.; Mekhilef, S.; Baba, M.S.; Shamshirband, S. System identification and control of robot manipulator based on fuzzy adaptive differential evolution algorithm. Adv. Eng. Softw. 2014, 78, 60–66. [Google Scholar] [CrossRef]
- Bernal, E.; Lagunes, M.L.; Castillo, O.; Soria, J.; Valdez, F. Optimization of Type-2 Fuzzy Logic Controller Design Using the GSO and FA Algorithms. Int. J. Fuzzy Syst. 2021, 23, 42–57. [Google Scholar] [CrossRef]
- Rajeswari, C.; Santhi, M. Modified flower pollination algorithm for optimizing FOPID controller and its application with the programmable n-level inverter using fuzzy logic. Soft Comput. 2021, 25, 2615–2633. [Google Scholar] [CrossRef]
- Yang, T.; Sun, N.; Fang, Y. Adaptive fuzzy control for a class of MIMO underactuated systems with plant uncertainties and actuator deadzones: Design and experiments. IEEE Trans. Cybern. 2021, 52, 8213–8226. [Google Scholar] [CrossRef]
- Ahanda, J.; Achille, M.; Essimbi, B. Adaptive Fuzzy Finite-Time Command-Filtered Backstepping Control of Flexible-Joint Robots. Robotica 2020, 39, 1081–1100. [Google Scholar]
- Abadlia, I.; Hassaine, L.; Beddar, A.; Abdoune, F.; Bengourina, M.R. Adaptive fuzzy control with an optimization by using genetic algorithms for grid connected a hybrid photovoltaic-hydrogen generation system-ScienceDirect. Int. J. Hydrogen Energy 2020, 45, 22589–22599. [Google Scholar] [CrossRef]
- Kluska, J. Adaptive Fuzzy Control of State-Feedback Time-Delay Systems With Uncertain Parameters. Inf. Sci. 2020, 540, 202–220. [Google Scholar] [CrossRef]
- Lin, G.; Yu, J.; Liu, J. Adaptive fuzzy finite-time command filtered impedance control for robotic manipulators. IEEE Access 2021, 9, 50917–50925. [Google Scholar] [CrossRef]
- Ganesh, E.N.; Bettyjane, J. Simulation and synthesis of TS fuzzy system using parallel distribution compensation technique. Int. J. Inf. Technol. 2020, 12, 1443–1449. [Google Scholar] [CrossRef]
- Agushaka, J.O.; Ezugwu, A.E.; Saha, A.K.; Pal, J.; Abualigah, L.; Mirjalili, S. Greater Cane Rat Algorithm (GCRA): A Nature-Inspired Metaheuristic for Optimization Problems. Heliyon 2024, 10, e31629. [Google Scholar] [CrossRef]
- Wu, P.; Lei, X.; Zeng, J.; Qi, Y.; Yuan, Q.; Huang, W.; Ma, Z.; Shen, Q.; Lyu, X. Research progress in mechanized and intelligentized pollination technologies for fruit and vegetable crops. Int. J. Agric. Biol. Eng. 2024, 17, 11–21. [Google Scholar] [CrossRef]
- Pennestrì, E.; Rossi, V.; Salvini, P.; Valentini, P.P. Review and comparison of dry friction force models. Nonlinear Dyn. 2016, 83, 1785–1801. [Google Scholar] [CrossRef]
- Jin, J.; Gans, N. Parameter identification for industrial robots with a fast and robust trajectory design approach. Robot Comput. Integer. Manuf 2015, 31, 21–29. [Google Scholar] [CrossRef]
- Pi, J.; Liu, J.; Zhou, K.; Qian, M. An octopus-inspired bionic flexible gripper for apple grasping. Agriculture 2021, 11, 1014. [Google Scholar] [CrossRef]
- Ji, W.; Qian, Z.; Xu, B.; Tang, W.; Li, J.; Zhao, D. Grasping damage analysis of apple by end-effector in harvesting robot. J. Food Process Eng. 2017, 40, e12589. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).