Hybrid Chebyshev-Type Methods for Solving Nonlinear Equations
Abstract
1. Introduction
2. Local Analysis of Method (5)
- (H1)
- There exists a CNDF such that the equation has an SPS. Denote such a solution by Set
- (H2)
- There exists a CNDF for function defined by the following:such that the equation has an SPS in the interval Denote such a solution by
- (H3)
- For the function defined by the equation has an SPS in ). Denote such a solution byDenote the functions and by the following:andNote, that in practice, we select the smallest of the two versions of the functions and The real functions and are used to majorize the error distances appearing in Theorem 1 that follows.
- (H4)
- The equation has an SPS in Denote such a solution by Setand It follows by these definitions that for all ,andThere exists a relationship between the functions and w with the operators on method (5).
- (H5)
- There exists a solution of the equation and an invertible operator such that for eachSet The notation denotes the open ball with a center at and a radius Moreover, is its closure.
- (H6)
- for eachand
- (H7)
- (i)
- The parameter r is shown to be a radius of convergence for the sequence given by formula (5) in Theorem 1.
- (ii)
- Some choices for M can be where I is the identity operator on X or In the latter case, is a simple solution. Note, that this is not assumed or necessarily implied by conditions (H1)–(H2). Consequently, method (5) can be used to find solutions of a multiplicity greater than one. Other choices for M are also possible, provided that criteria (H5) and (H6) hold such that where is an auxiliary point [11].
- (iii)
- The smaller of the two versions of the function is used. However, if these versions cross on the interval say, e.g., asfor andfor where then we choose
3. Semi-Local Analysis of Method (5)
- (C1)
- There exists a CNDF such that the equation has an SPS. Denote such a solution by Set
- (C2)
- There exists a CNDFDefine the sequence for some , and all by the following:and:The scalar sequence is shown to be majorizing for in Theorem 2. However, let us present a convergence criterion for it.
- (C3)
- There exists such that for all ,It follows by this condition and (26) that for all ,and there exists such that The limit point is the unique least upper bound of the sequence Notice that if the function is strictly increasing, and then we can take As in the local analysis, the real functions and v relate to the operators on method (5).
- (C4)
- There exist and an invertible operator such that for allNote, that Hene, and we can set Set
- (C5)
- for alland
- (C6)
- (i)
- The limit point can be exchanged by in condition (C6).
- (ii)
- if all conditions (C1)–(C6) hold, then one can take and in Proposition 2.
4. Local Analysis of Method (6)
- (H1)’ = (H1).
- (H2)’ There exists and a CNDF such that for the function defined by the following:the equation has an SPS in the interval Denote such a solution by
- (H3)’ For the function defined by the following:the equation has an SPS in the interval Denote such a solution by
- (H4)’ The equation has an SPS. Denote such a solution by SetandIt follows by these definitions that for all :and
- (H5)’ There exist a solution of the equation and an invertible operator such that for all :Set
- (H6)’ for all
- (H7)’ and set for all
5. Semi-Local Analysis for Method (6)
- (C1)’ = (C1).
- (C2)’ There exists a CNDF Define the sequence for some , and all by the following:andA convergence criterion is needed for the sequence
- (C3)’ There exists such that for all and It follows by this criterion and (46) that for all , and there exists such that
- (C4)’ There exist and an invertible operator such that for allSet
- (C5)’ for alland
- (C6)’ where for all
6. Numerical Examples
7. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Argyros, I.K.; George, S. On the complexity of extending the convergence region for Traub’s method. J. Complex. 2020, 56, 101423. [Google Scholar] [CrossRef]
- Ben-Israel, A.; Greville, T.N.E. Generalized Inverses: Theory and Applications; John Wiley and Sons: New York, NY, USA, 1974. [Google Scholar]
- Moore, R.H.; Nashed, M.Z. Approximations to generalized inverses of linear operators. SIAM J. Appl. Math. 1974, 27, 1–16. [Google Scholar] [CrossRef]
- Nashed, M.Z. Generalized Inverses and Applications; Academic Press: New York, NY, USA, 1976. [Google Scholar]
- Padcharoen, A.; Kumam, P.; Chaipunya, P.; Shehu, Y. Convergence of inertial modified Krasnoselskii-Mann iteration with application to image recovery. Thai J. Math. 2020, 18, 126–142. [Google Scholar]
- Proinov, P.D.; Petkova, M.D. Local and semilocal Convergence of a family of Multi-point Weierstrass-type Root-Finding Methods. Mediterr. J. Maths. 2020, 17, 107. [Google Scholar] [CrossRef]
- Regmi, S.; Argyros, I.K.; George, S.; Argyros, C.I. Extended Convergence of Three Step Iterative Methods for Solving Equations in Banach Space with Applications. Symmetry 2022, 14, 1484. [Google Scholar] [CrossRef]
- Häubler, W.M. A Kantorovich-type convergence analysis for the Gauss-Newton-method. Numer. Math. 1986, 48, 119–125. [Google Scholar]
- Argyros, I.K.; George, S.; Shakhno, S.; Regmi, S.; Havdiak, M.; Argyros, M.I. Asymptotically Newton-Type Methods without Inverses for Solving Equations. Mathematics 2024, 12, 1069. [Google Scholar] [CrossRef]
- Kantorovich, L.V.; Akilov, G. Functional Analysis in Normed Spaces; Fizmatgiz: Moscow, Russia, 1959; (German translation, Akademie-Verlag: Berlin, Germany, 1964): (English translation (2nd edition), Pergamon Press: London, UK, 1981), (1964). [Google Scholar]
- Ezquerro, J.A.; Hernandez-Veron, M.A. Domains of global convergence for Newtons’s method from auxiliary points. Appl. Math. Lett. 2018, 85, 48–56. [Google Scholar] [CrossRef]
- Ezquerro, J.A.; Hernandez-Veron, M.A. Newton’s Method: An Updated Approach of Kantorovich’s Theory; Birkhauser: Basel, Switzerland, 2017. [Google Scholar]
- Krasnoselskij, M.A. Two remarks on the method of successive approximations. Uspehi Mat. Nauk. 1995, 10, 123–127. (In Russian) [Google Scholar]
- Traub, J.F.; Wozniakowsi, H. Convegence and complexity of Newton iteration for operator equations. J. Assoc. Comput. March. 1979, 26, 250–258. [Google Scholar] [CrossRef]
- Proinov, P.D. New general convergence theory for iterative processes and its applications to Newton- Kantarovich type theorems. J. Complex. 2010, 25, 3–42. [Google Scholar] [CrossRef]
- Ostrowski, A.M. Solution of Equations in Euclidean and Banach Spaces; Academic Press: New York, NY, USA, 1973. [Google Scholar]
- Yamamoto, T. A convergence theorem for Newton-like methods in Banach spaces. Numer. Math. 1987, 51, 545–557. [Google Scholar] [CrossRef]
- Berinde, V. Iterative Approximation of Fixed Points; Springer: New York, NY, USA, 2007. [Google Scholar]
- Deuflhard, P. Newton Methods for Nonlinear Problems. Affine Invariance and Adaptive Algorithms; Springer Series in Computational Mathematics; Springer: Berlin/Heidelberg, Germany, 2004; Volume 35. [Google Scholar]
- Ezquerro, J.A.; Gutierrez, J.M.; Hernandez, M.A.; Romero, N.; Rubio, M.J. The Newton Method: From Newton to Kantorovich. Gac. R. Soc. Mat. Esp. 2010, 13, 53–76. (In Spanish) [Google Scholar]
- Rheinboldt, W.C. A unified convergence theory for a class of iterative process. SIAM J. Numer. Anal. 1968, 5, 42–63. [Google Scholar] [CrossRef]
- Catinas, E. The inexact, inexact perturbed, and quasi-Newton methods are equivalent models. Math. Comp. 2005, 74, 291–301. [Google Scholar] [CrossRef]
- Potra, F.A. Sharp error bounds for a class of Newton-like methods. Lib. Math. 1985, 5, 71–84. [Google Scholar]
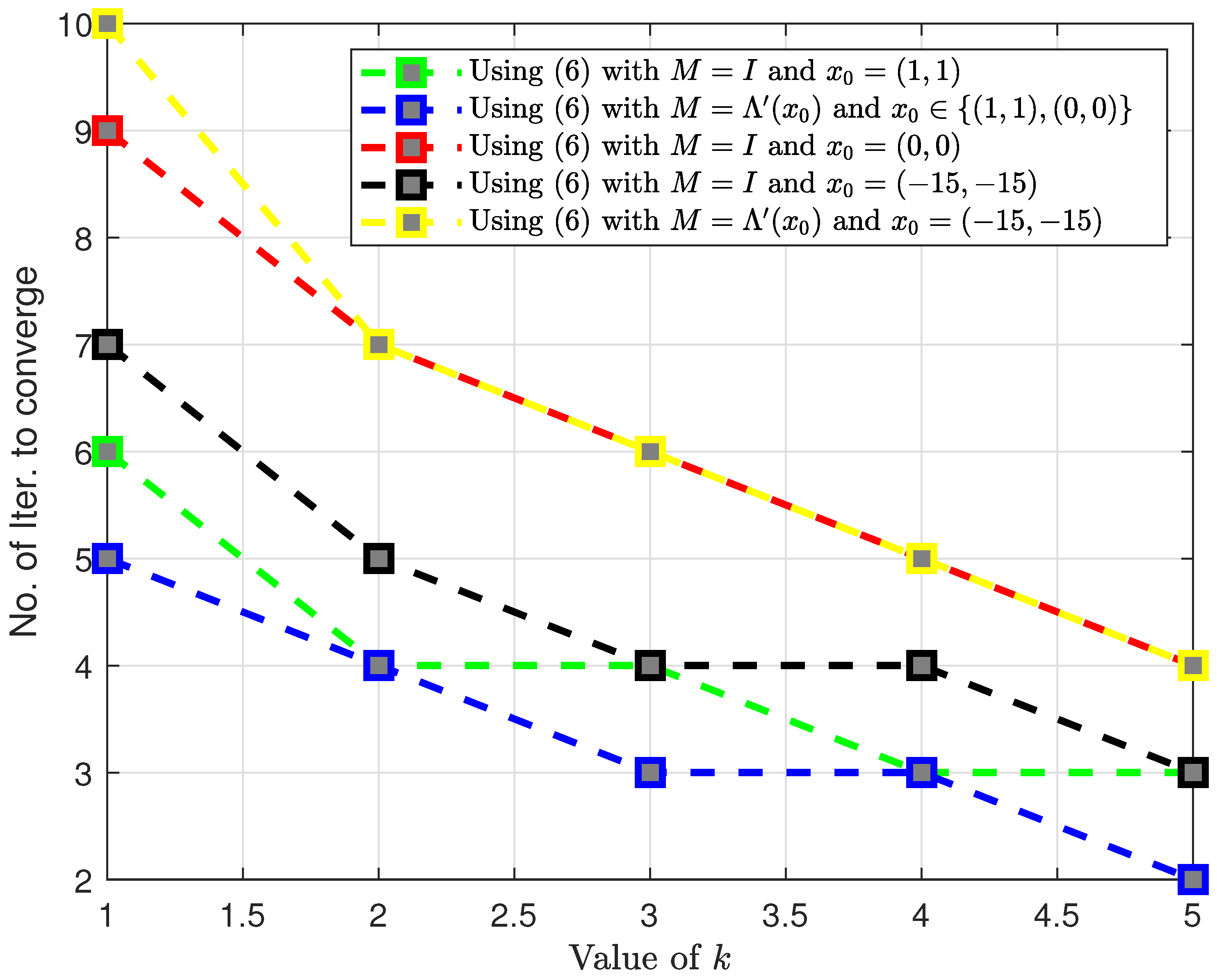
| Method | Iterations | Method | Iterations |
|---|---|---|---|
| Equation (5) | 3 | Equation (5) | 3 |
| Equation (50), | 6 | Equation (55), | 9 |
| Equation (51), | 4 | Equation (55), | 7 |
| Equation (52), | 4 | Equation (55), | 6 |
| Equation (53), | 3 | Equation (55), | 5 |
| Equation (54), | 3 | Equation (55), | 4 |
| Method | Iterations | Method | Iterations |
|---|---|---|---|
| Equation (5) | 2 | Equation (5) | 2 |
| Equation (50), | 5 | Equation (55), | 9 |
| Equation (51), | 4 | Equation (55), | 7 |
| Equation (52), | 3 | Equation (55), | 6 |
| Equation (53), | 3 | Equation (55), | 5 |
| Equation (54), | 2 | Equation (55), | 4 |
| Method | Iterations | Method | Iterations |
|---|---|---|---|
| Equation (5) | 3 | Equation (5) | 3 |
| Equation (50), | 7 | Equation (55), | 10 |
| Equation (51), | 5 | Equation (55), | 7 |
| Equation (52), | 4 | Equation (55), | 6 |
| Equation (53), | 4 | Equation (55), | 5 |
| Equation (54), | 3 | Equation (55), | 4 |
| Method | Iterations | Method | Iterations |
|---|---|---|---|
| Equation (5) | 3 | Equation (5) | 3 |
| Equation (50), | 9 | Equation (55), | 12 |
| Equation (51), | 6 | Equation (55), | 8 |
| Equation (52), | 5 | Equation (55), | 7 |
| Equation (53), | 4 | Equation (55), | 6 |
| Equation (54), | 4 | Equation (55), | 5 |
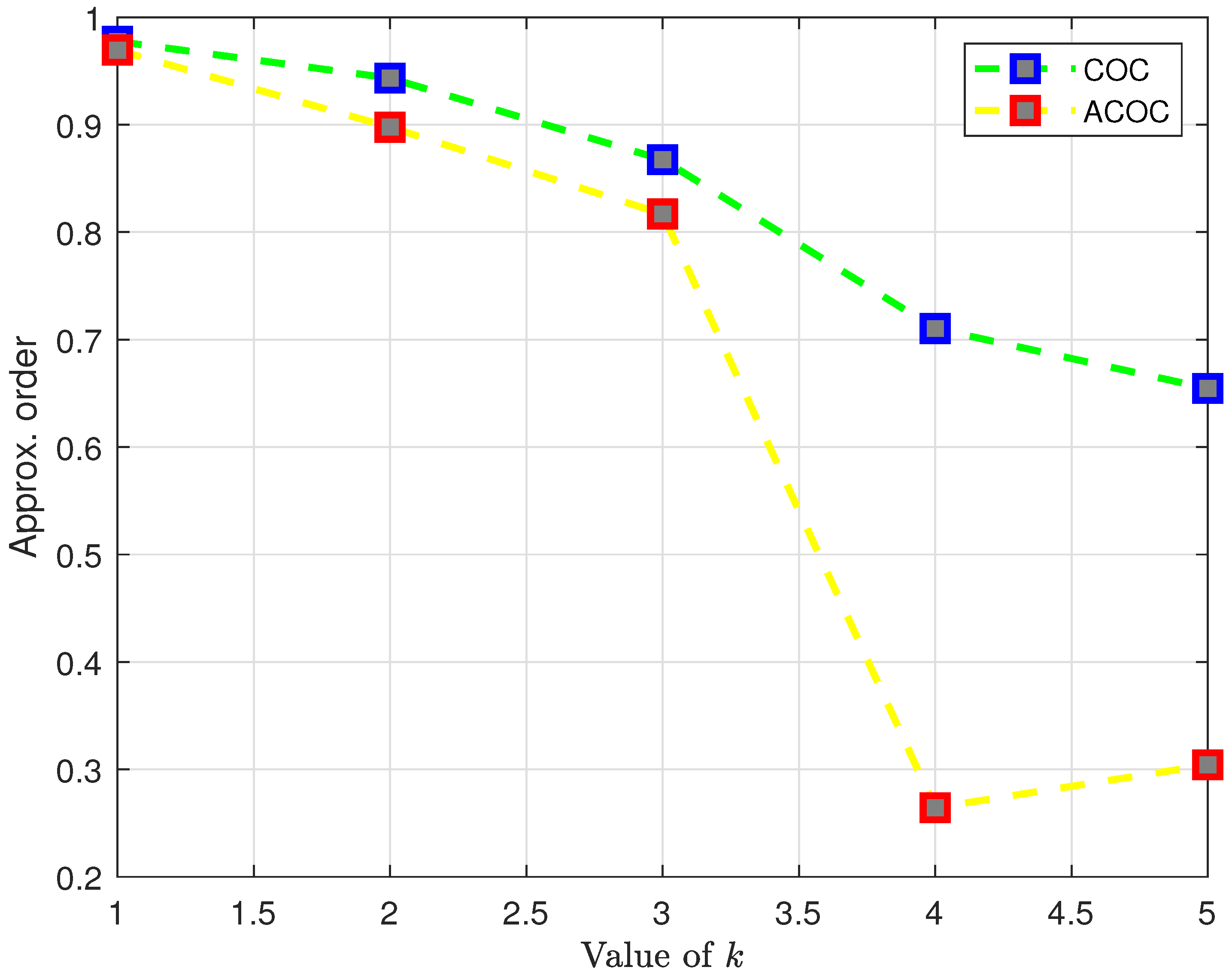
| Method | COC | ACOC |
|---|---|---|
| Equation (5) | 1.0 | NA |
| Equation (50), | 0.977468 | 0.969404 |
| Equation (51), | 0.943378 | 0.897736 |
| Equation (52), | 0.867463 | 0.816881 |
| Equation (53), | 0.710293 | 0.264330 |
| Equation (54), | 0.654524 | 0.304212 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Argyros, I.K.; George, S. Hybrid Chebyshev-Type Methods for Solving Nonlinear Equations. Mathematics 2025, 13, 74. https://doi.org/10.3390/math13010074
Argyros IK, George S. Hybrid Chebyshev-Type Methods for Solving Nonlinear Equations. Mathematics. 2025; 13(1):74. https://doi.org/10.3390/math13010074
Chicago/Turabian StyleArgyros, Ioannis K., and Santhosh George. 2025. "Hybrid Chebyshev-Type Methods for Solving Nonlinear Equations" Mathematics 13, no. 1: 74. https://doi.org/10.3390/math13010074
APA StyleArgyros, I. K., & George, S. (2025). Hybrid Chebyshev-Type Methods for Solving Nonlinear Equations. Mathematics, 13(1), 74. https://doi.org/10.3390/math13010074







