Exploration of Soliton Solutions to the Special Korteweg–De Vries Equation with a Stability Analysis and Modulation Instability
Abstract
1. Introduction
2. Presentation of Methods
2.1. Hirota Bilinear Method
2.2. Summary of Function Method
2.3. Description of the Sardar Sub-Equation Method
3. Breather Wave Soliton
4. Soliton Solutions
4.1. 1-Soliton Solutions
4.2. 2-Soliton Solutions
4.3. New Three-Wave Soliton
4.4. New Periodic-Wave
5. Exact Wave Solutions
5.1. Exact Siliton Solutions by Function Method
5.2. Exact Soliton Results via the Sardar Sub-Equation Method
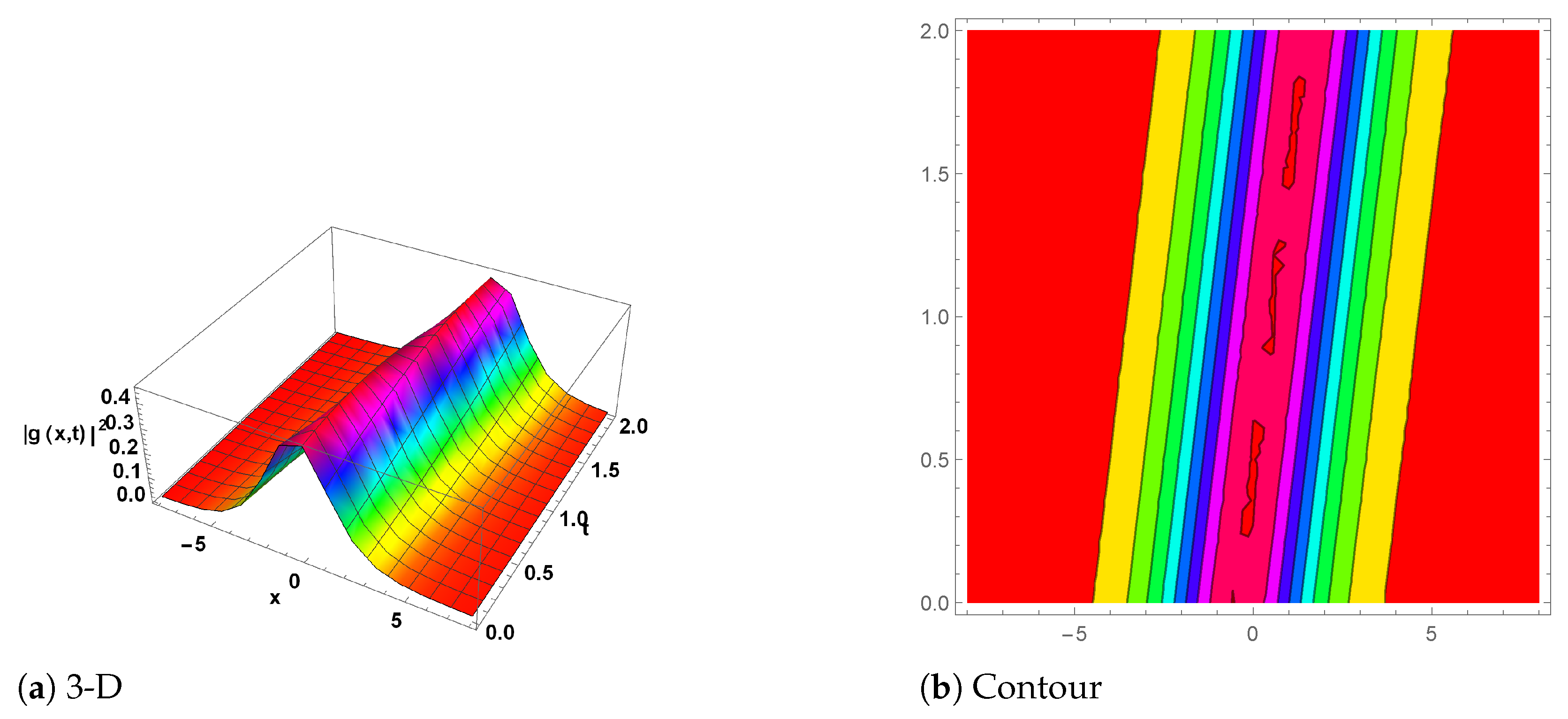
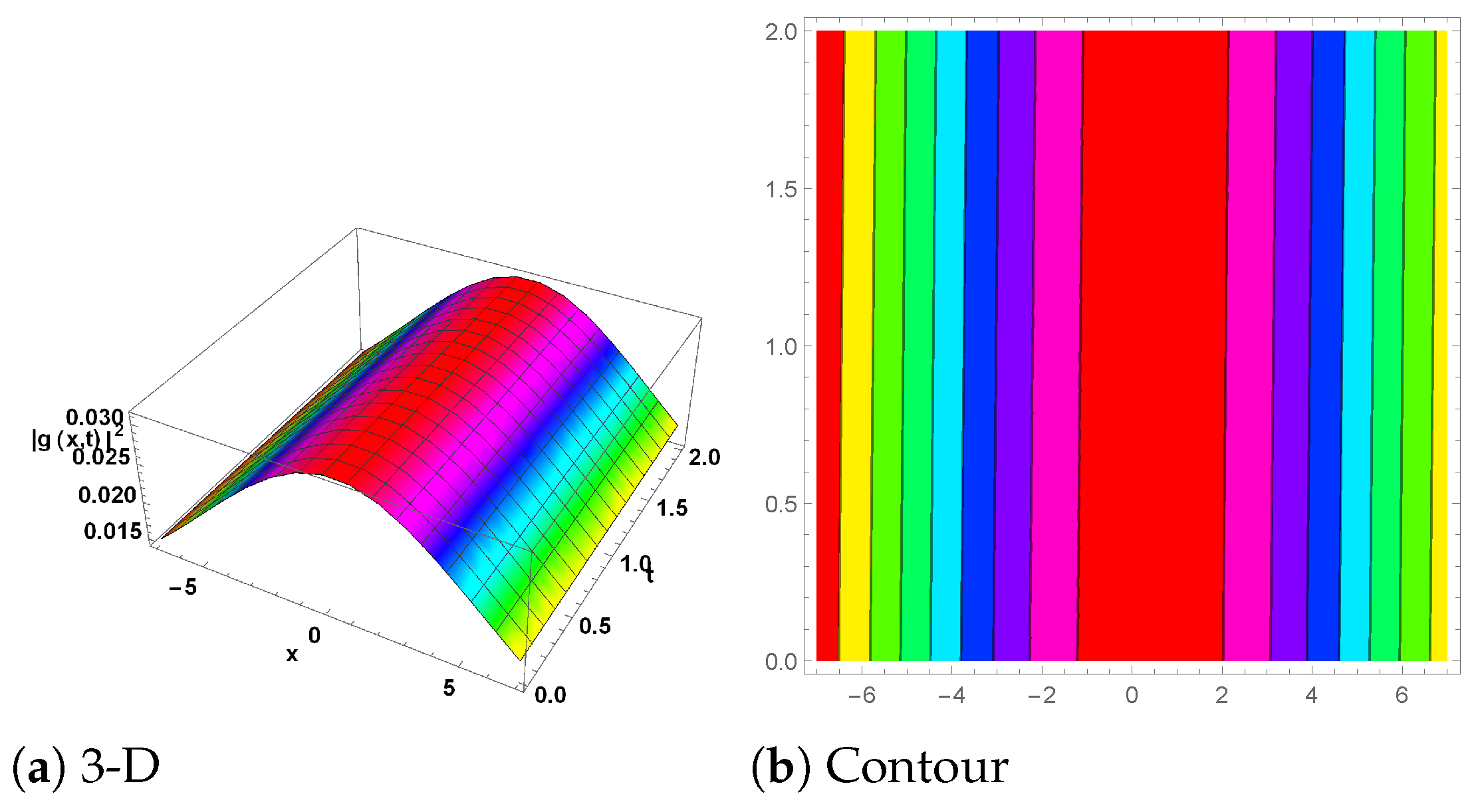
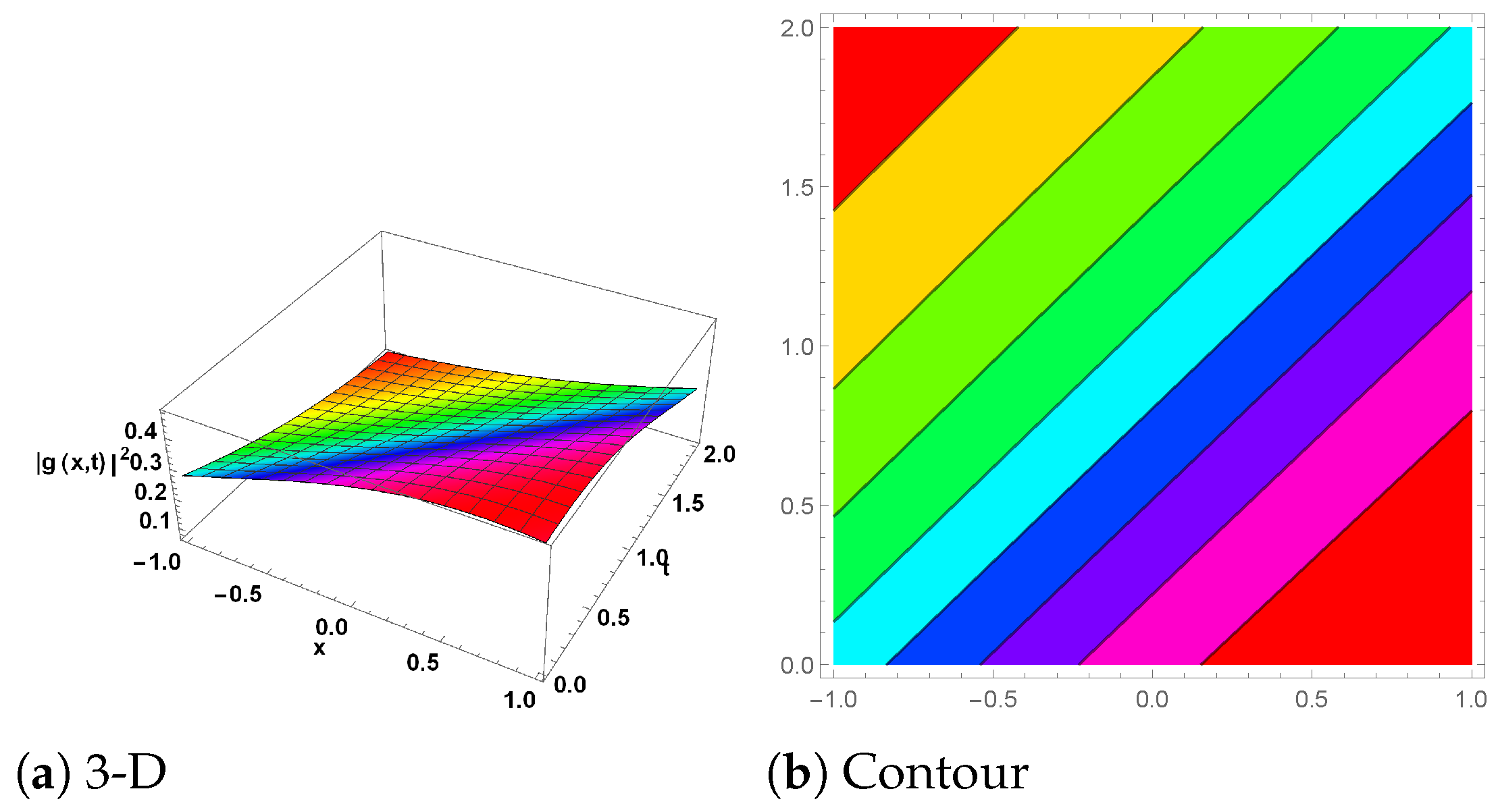
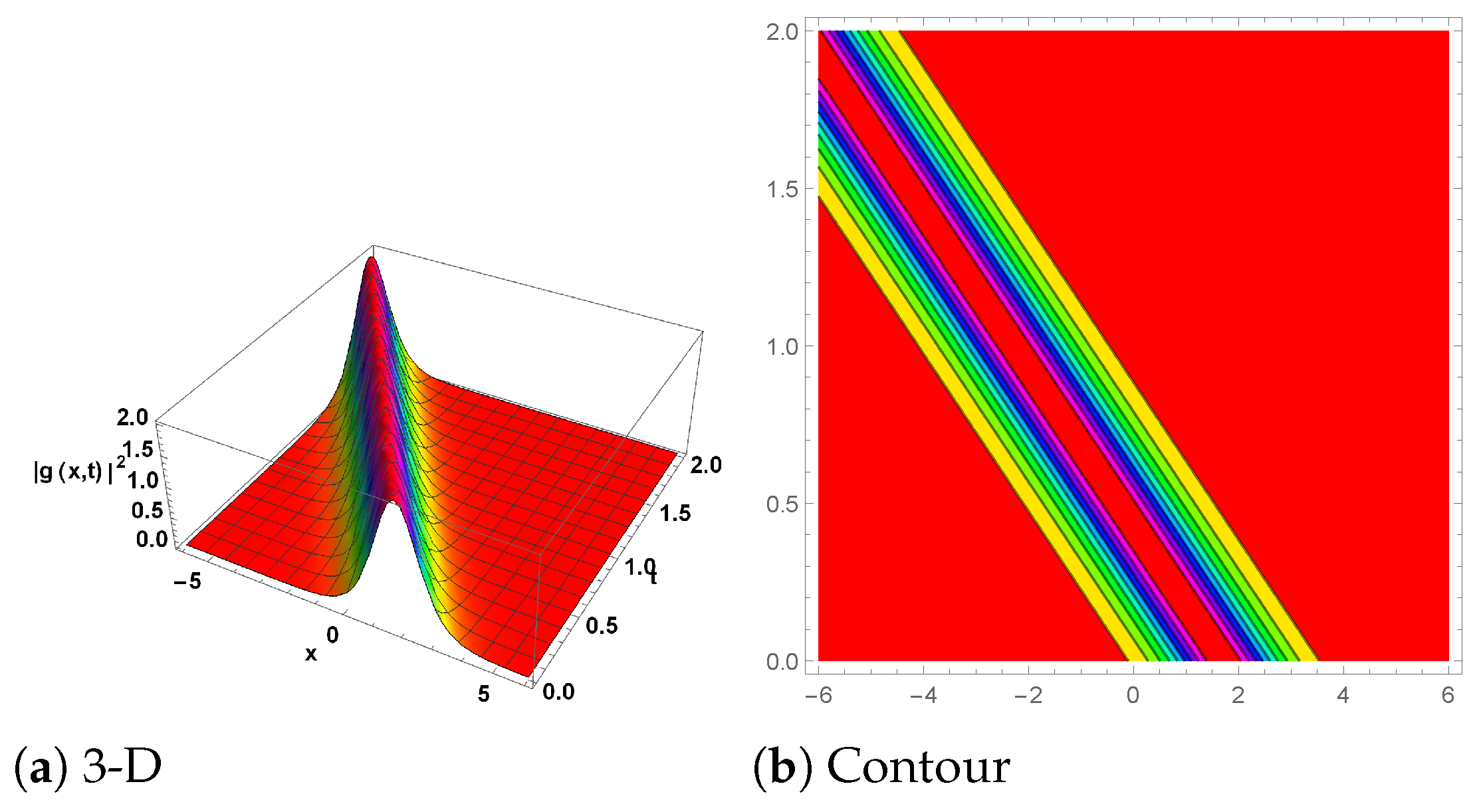
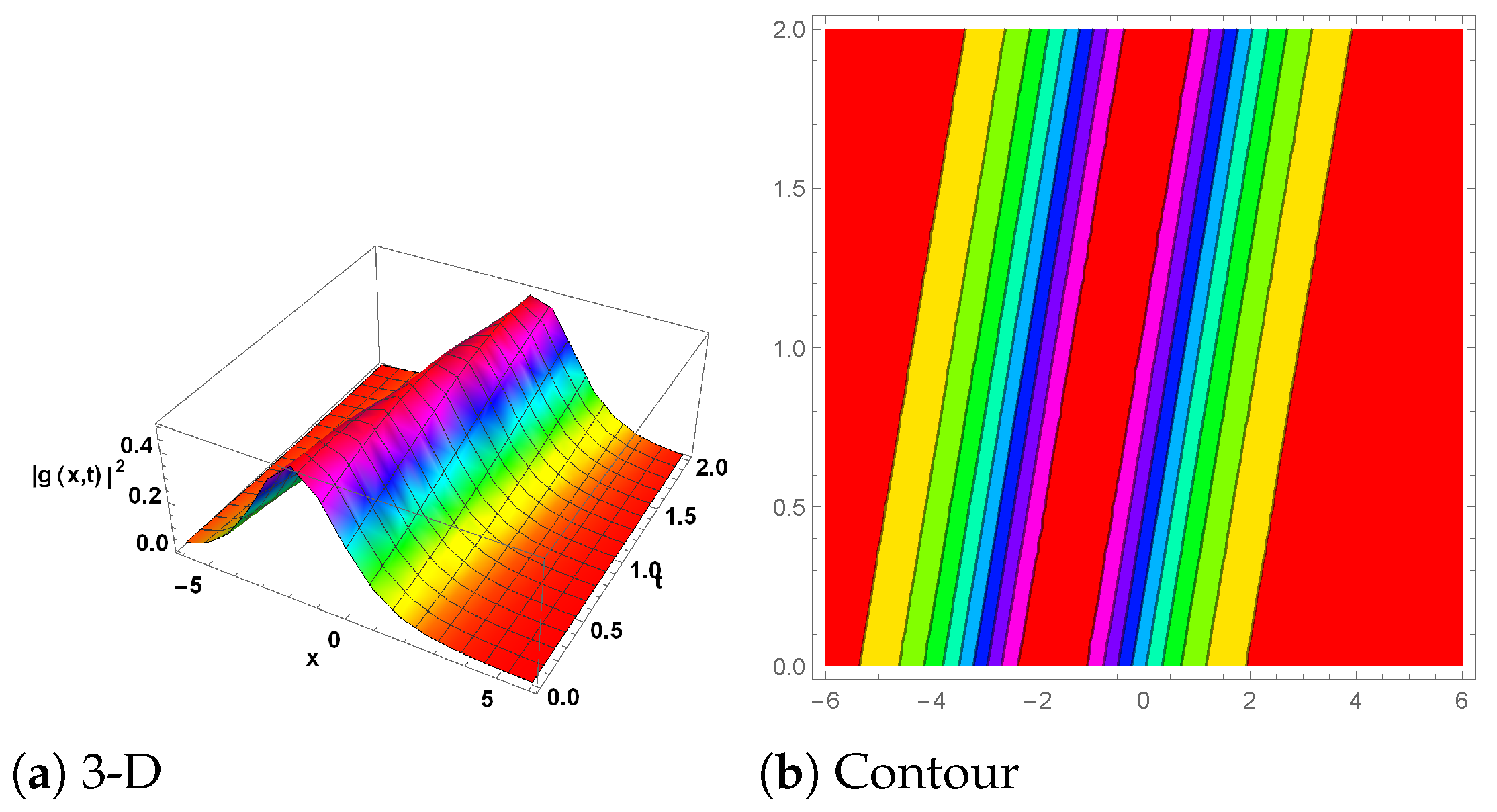
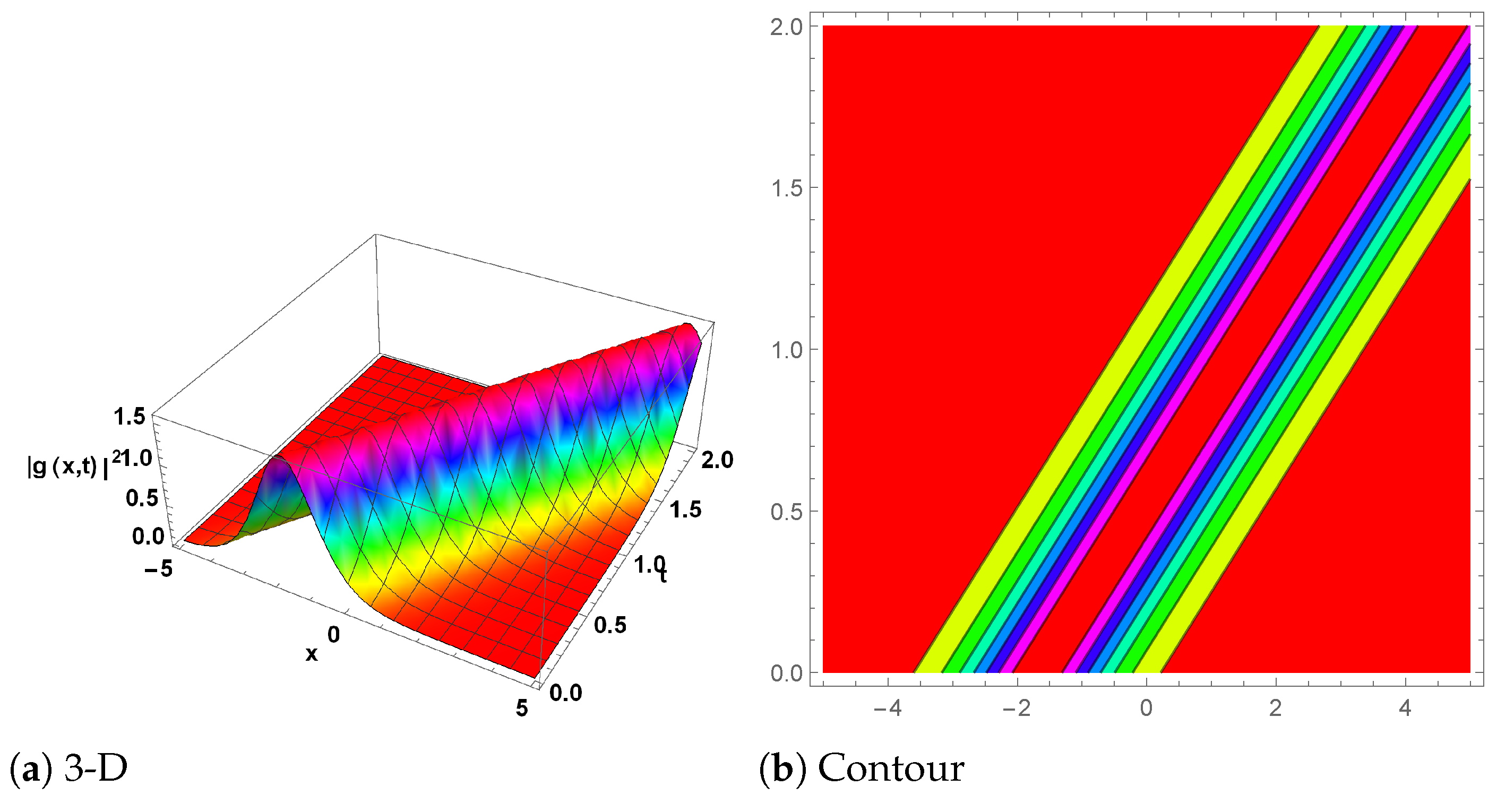
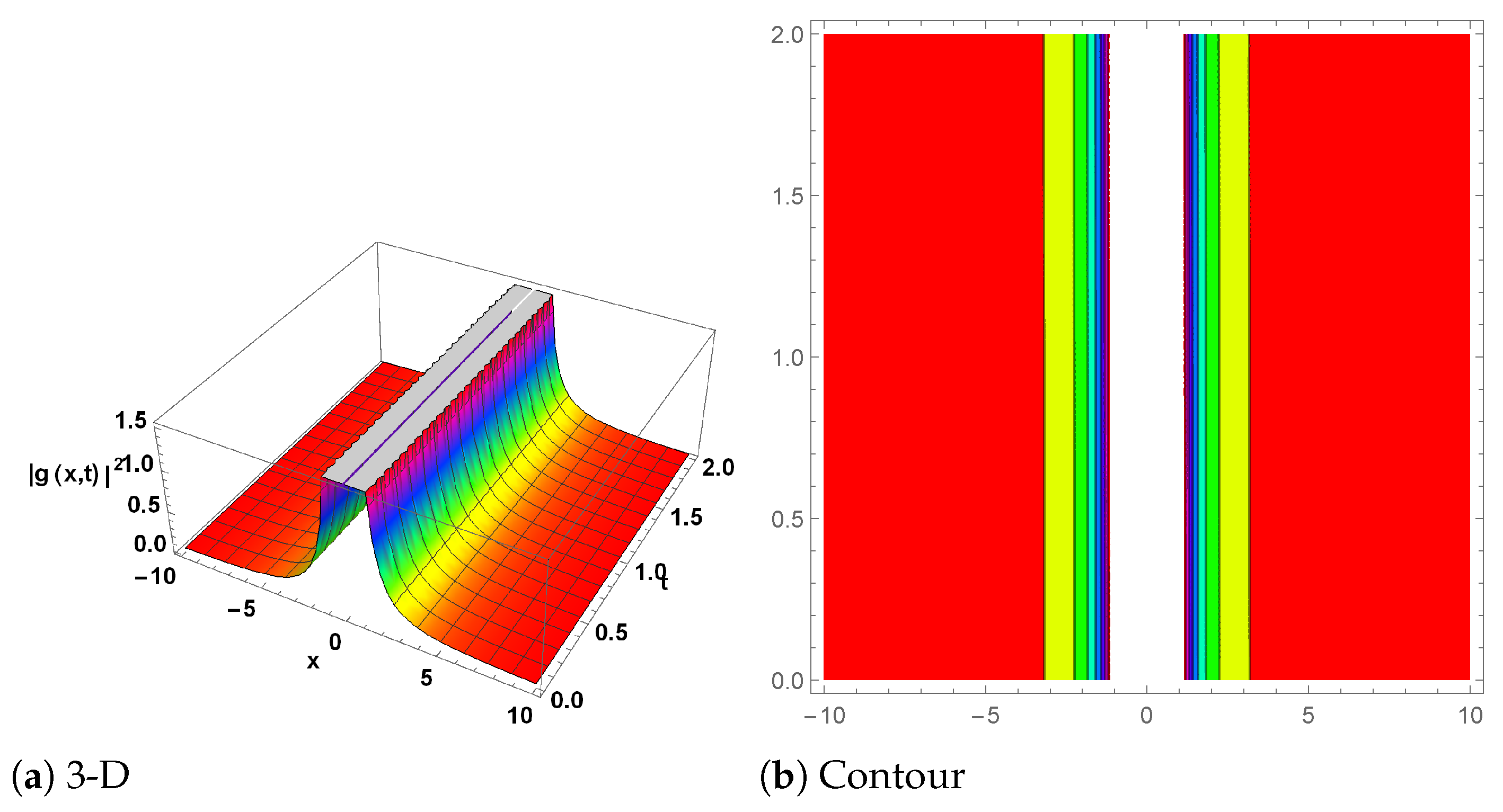
6. Graphical Explanation
7. Stability Analysis
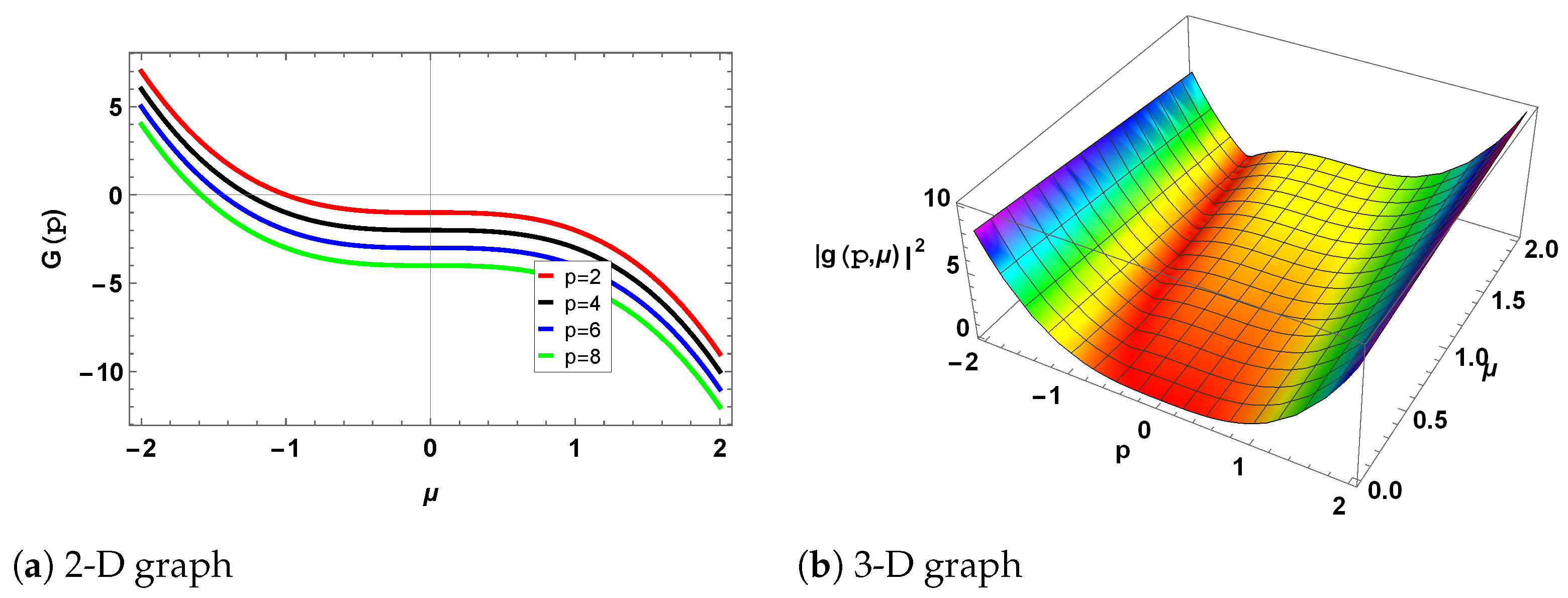
8. Modulation Instability (MI)
9. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hyder, A.-A.; Soliman, A.H. Analytical manner for abundant stochastic wave solutions of extended KdV equation with conformable differential operators. Math. Methods Appl. Sci. 2022, 45, 8600–8612. [Google Scholar] [CrossRef]
- Shakeel, M.; Alaoui, M.K.; Zidan, A.M.; Shah, N.A. Closed form solutions for the generalized fifth-order KDV equation by using the modified exp-function method. J. Ocean. Eng. Sci. 2022, in press. [Google Scholar]
- Islam, S.M.R.; Khan, K.; Akbar, M.A. Exact solutions of unsteady Korteweg–de Vries and time regularized long wave equations. SpringerPlus 2015, 4, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Khatun, M.M.; Akbar, M.A.; Fayazova, Z.K.; İlhan, O.A. Various wave solutions to the nonlinear fractional Korteweg–de Vries Zakharov-Kuznetsov equation by a new approach to the two-variable expansion scheme. Phys. Scr. 2024, 99, 035218. [Google Scholar] [CrossRef]
- AlQahtani, S.A.; Alngar, M.E.M. Soliton Solutions for Coupled Nonlinear Generalized Zakharov Equations with Anti-cubic Nonlinearity Using Various Techniques. Int. J. Appl. Comput. Math. 2024, 10, 9. [Google Scholar] [CrossRef]
- Pandir, Y.; Ekin, A. New solitary wave solutions of the Korteweg–de Vries (KdV) equation by new version of the trial equation method. Electron. J. Appl. Math. 2023, 1, 101–113. [Google Scholar] [CrossRef]
- Seadawy, A.R. New exact solutions for the KdV equation with higher order nonlinearity by using the variational method. Comput. Math. Appl. 2011, 62, 3741–3755. [Google Scholar] [CrossRef]
- Raheel, M.; Zafar, A.; Liu, J.-G. New periodic-wave, periodic-cross-kink wave, three wave and other analytical wave solitons of new (2 + 1)-dimensional KdV equation. Eur. Phys. J. Plus 2024, 139, 50. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, D. Multisoliton solutions of a (2 + 1)-dimensional variable-coefficient Toda lattice equation via Hirota’s bilinear method. Can. J. Phys. 2014, 92, 184–190. [Google Scholar] [CrossRef]
- Cao, R.; Zhao, Q.; Gao, L. Bilinear approach to soliton and periodic-wave solutions of two nonlinear evolution equations of Mathematical Physics. Adv. Differ. Equations 2019, 2019, 156. [Google Scholar] [CrossRef]
- Zhang, L.-L.; Lü, X.; Zhu, S.-Z. Painlevé analysis, Bäcklund transformation and soliton solutions of the (2 + 1)-dimensional variable-coefficient Boussinesq equation. Int. J. Theor. Phys. 2024, 63, 160. [Google Scholar] [CrossRef]
- Lü, X.; Zhang, L.L.; Ma, W.-X. Oceanic shallow-water description with (2 + 1)-dimensional generalized variable-coefficient Hirota–Satsuma–Ito equation: Painlevé analysis, soliton solutions, and lump solutions. Phys. Fluids 2024, 36, 6. [Google Scholar] [CrossRef]
- Qawaqneh, H.; Zafar, A.; Raheel, M.; Zaagan, A.A.; Zahran, E.H.M.; Cevikel, A.; Bekir, A. New soliton solutions of M-fractional Westervelt model in ultrasound imaging via two analytical techniques. Opt. Quantum Electron. 2024, 56, 737. [Google Scholar] [CrossRef]
- Altalbe, A.; Taishiyeva, A.; Myrzakulov, R.; Bekir, A.; Zaagan, A.A. Effect of truncated M-fractional derivative on the new exact solitons to the Shynaray-IIA equation and stability analysis. Results Phys. 2024, 57, 107422. [Google Scholar] [CrossRef]
- Razzaq, W.; Zafar, A.; Raheel, M. Searching the new exact wave solutions to the beta-fractional Paraxial nonlinear Schrödinger model via three different approaches. Int. J. Mod. Phys. 2024, 38, 2450132. [Google Scholar] [CrossRef]
- Alsharidi, A.K.; Bekir, A. Discovery of new exact wave solutions to the M-fractional complex three coupled Maccari’s system by Sardar sub-equation scheme. Symmetry 2023, 15, 1567. [Google Scholar] [CrossRef]
- Chou, D.; Ur Rehman, H.; Amer, A.; Amer, A. New solitary wave solutions of generalized fractional Tzitzéica-type evolution equations using Sardar sub-equation method. Opt. Quantum Electron. 2023, 55, 1148. [Google Scholar] [CrossRef]
- Ma, W.-X. Soliton solutions by means of Hirota bilinear forms. Partial. Differ. Equations Appl. Math. 2022, 5, 100220. [Google Scholar] [CrossRef]
- Matsutani, S. On real hyperelliptic solutions of focusing modified KdV equation. Math. Phys. Anal. Geom. 2024, 27, 19. [Google Scholar] [CrossRef]
- Miah, M.M.; Meia, M.A.A.; Sarker, M.M.R.; Hasan, A. Adequate Closed Form Wave Solutions to the Generalized KdV Equation in Mathematical Physics. J. Appl. Math. Phys. 2024, 12, 2069–2082. [Google Scholar] [CrossRef]
- Iqbal, M.; Faridi, W.A.; Algethamie, R.; Alomari, F.A.H.; Murad, M.A.S.; Alsubaie, N.E.; Seadawy, A.R. Extraction of newly soliton wave structure to the nonlinear damped Korteweg–de Vries dynamical equation through a computational technique. Opt. Quantum Electron. 2024, 56, 1189. [Google Scholar] [CrossRef]
- Bayrakci, U.; Demiray, S.T.; Yildirim, H. Obtaining new soliton solutions of the fractional generalized perturbed KdV equation. Phys. Scr. 2024, 99, 125202. [Google Scholar] [CrossRef]
- Ali, A.T.; Hassan, E.R. General Expa-function method for nonlinear evolution equations. Appl. Math. Comput. 2010, 217, 451–459. [Google Scholar] [CrossRef]
- Zayed, E.M.E.; Al-Nowehy, A.G. Generalized kudryashov method and general expa function method for solving a high order nonlinear schrödinger equation. J. Space Explor. 2017, 6, 1–26. [Google Scholar]
- Hosseini, K.; Ayati, Z.; Ansari, R. New exact solutions of the Tzitzéica-type equations in non-linear optics using the expa function method. J. Mod. Opt. 2018, 65, 847–851. [Google Scholar] [CrossRef]
- Zafar, A. The expa function method and the conformable time-fractional KdV equations. Nonlinear Eng. 2019, 8, 728–732. [Google Scholar] [CrossRef]
- Bashar, M.H.; Islam, S.M.R.; Kumar, D. Construction of traveling wave solutions of the (2+1)-dimensional Heisenberg ferromagnetic spin chain equation. Partial. Differ. Equations Appl. Math. 2021, 4, 100040. [Google Scholar] [CrossRef]
- Zafar, A.; Ali, K.K.; Raheel, M.; Nisar, K.S.; Bekir, A. Abundant M-fractional optical solitons to the pertubed Gerdjikov–Ivanov equation treating the mathematical nonlinear optics. Opt. Quantum Electron. 2022, 54, 1–17. [Google Scholar] [CrossRef]
- Zafar, A.; Bekir, A.; Raheel, M.; Rezazadeh, H. Investigation for optical soliton solutions of two nonlinear Schrödinger equations via two concrete finite series methods. Int. J. Appl. Comput. Math. 2020, 6, 1–13. [Google Scholar] [CrossRef]
- Ullah, N.; Asjad, M.I.; Awrejcewicz, J.; Muhammad, T.; Baleanu, D. On soliton solutions of fractional-order nonlinear model appears in physical sciences. Aims Math. 2022, 7, 7421–7440. [Google Scholar] [CrossRef]
- Lü, J.; Bilige, S.; Gao, X.; Bai, Y.; Zhang, R. Abundant Lump Solutions and Interaction Phenomena to the Kadomtsev-Petviashvili-Benjamin-Bona-Mahony Equation. J. Appl. Math. Phys. 2018, 6, 1733–1747. [Google Scholar] [CrossRef][Green Version]
- Yue, Y.; Huang, L.; Chen, Y. N-solitons, breathers, lumps and rogue wave solutions to a (3 + 1)-dimensional nonlinear evolution equation. Comput. Math. Appl. 2017, 12, 22. [Google Scholar] [CrossRef]
- Liu, J.; Du, J.; Zeng, Z.; Nie, B. New three-wave solutions for the (3 + 1)-dimensional Boiti–Leon–Manna–Pempinelli equation. Nonlinear Dyn. 2017, 88, 655–661. [Google Scholar] [CrossRef]
- Ilhan, O.A.; Manafian, J. Periodic type and periodic cross-kink wave solutions to the (2 + 1)-dimensional breaking soliton equation arising in fluid dynamics. Mod. Phys. Lett. B 2019, 33, 1950277. [Google Scholar] [CrossRef]
- Tariq, K.U.; Wazwaz, A.-M.; Javed, R. Construction of different wave structures, stability analysis and modulation instability of the coupled nonlinear Drinfel’d-Sokolov-Wilson model. Chaos Solitons Fractals 2023, 166, 112903. [Google Scholar] [CrossRef]
- Zulfiqar, H.; Aashiq, A.; Tariq, K.U.; Ahmad, H.; Almohsen, B.; Aslam, M.; Rehman, H.U. On the solitonic wave structures and stability analysis of the stochastic nonlinear Schrödinger equation with the impact of multiplicative noise. Optik 2023, 289, 171250. [Google Scholar] [CrossRef]
- ur Rehman, S.; Ahmad, J. Modulation instability analysis and optical solitons in birefringent fibers to RKL equation without four wave mixing. Alex. Eng. J. 2021, 60, 1339–1354. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alomair, A.; Al Naim, A.S.; Bekir, A. Exploration of Soliton Solutions to the Special Korteweg–De Vries Equation with a Stability Analysis and Modulation Instability. Mathematics 2025, 13, 54. https://doi.org/10.3390/math13010054
Alomair A, Al Naim AS, Bekir A. Exploration of Soliton Solutions to the Special Korteweg–De Vries Equation with a Stability Analysis and Modulation Instability. Mathematics. 2025; 13(1):54. https://doi.org/10.3390/math13010054
Chicago/Turabian StyleAlomair, Abdulrahman, Abdulaziz S. Al Naim, and Ahmet Bekir. 2025. "Exploration of Soliton Solutions to the Special Korteweg–De Vries Equation with a Stability Analysis and Modulation Instability" Mathematics 13, no. 1: 54. https://doi.org/10.3390/math13010054
APA StyleAlomair, A., Al Naim, A. S., & Bekir, A. (2025). Exploration of Soliton Solutions to the Special Korteweg–De Vries Equation with a Stability Analysis and Modulation Instability. Mathematics, 13(1), 54. https://doi.org/10.3390/math13010054






