Abstract
This work is concerned with Hirota bilinear, function, and Sardar sub-equation methods to find the breather-wave, 1-Soliton, 2-Soliton, three-wave, and new periodic-wave results and some exact solitons of the special (1 + 1)-dimensional Korteweg–de Vries (KdV) equation. The model of concern is a partial differential equation that is used as a mathematical model of waves on shallow water surfaces. The results are attained as well as verified by Mathematica and Maple softwares. Some of the obtained solutions are represented in three-dimensional (3-D) and contour plots through the Mathematica tool. A stability analysis is performed to verify that the results are precise as well as accurate. Modulation instability is also performed for the steady-state solutions to the governing equation. The solutions are useful for the development of corresponding equations. This work shows that the methods used are simple and fruitful for investigating the results for other nonlinear partial differential models.
Keywords:
special (1 + 1)-dimensional KdV equation; Hirota bilinear method; expa function method; Sardar-subequation method; analytical and other solutions; stability analysis; modulation instability MSC:
35C07; 35C08; 37K40; 83C15
1. Introduction
Partial differential equations (PDEs) are a form of natural phenomena. PDEs are models used in the various areas of science and engineering, for example, the extended KdV equation [1], generalized fifth-order KdV equation [2], and unsteady KdV equation [3]. Many methods have been created to obtain results for PDEs, like the two-variable expansion method [4], the extended trial function method [5], the trial equation method [6], and the variational method [7].
In this work, three different methods are utilized: the Hirota bilinear method, the function method, and the Sardar subequation method. The techniques of concern have been used to obtain results for the various models. For example, the Hirota bilinear technique is applied to achieve a new periodic wave, a three wave, and some kinds of solutions for new (2 + 1)-dimensional KdV equations [8]. Furthermore, 1-soliton, 2-soliton, and 3-soliton solutions of (2 + 1)-dimensional variable-coefficient Toda lattice equations are achieved by the Hirota bilinear scheme [9]; soliton and periodic-wave solutions of the two nonlinear evolution equations are gained by applying the Hirota bilinear scheme [10]; 1-soliton, 2-soliton solutions of the (2 + 1)-dimensional variable-coefficient Boussinesq equation are obtained by using the Hirota bilinear scheme along with Bäcklund transformations [11]; and one-soliton, two-soliton solutions and the lump solutions of the (2 + 1)-dimensional generalized variable-coefficient Hirota–Satsuma–Ito equations are gained by utilizing the Hirota bilinear scheme [12]. Some kinds of soliton results of the Westervelt equation are gained by using the function method [13]; various analytical results for the Shynaray–IIA equation are achieved [14], and exact wave results for the Paraxial nonlinear Schrödinger model are achieved [15]. Various kinds of wave results for complex three-coupled Maccari’s systems are gained by using the Sardar sub-equation method [16], and some types of results for generalized fractional Tzitzéica-kinds evolution models are attained in [17].
Consider the (1 + 1)-dimensional Korteweg–de Vries (KdV) equation given as follows:
where is a nonzero constant.
The Korteweg–De Vries (KdV) equation is a partial differential equation (PDE) that serves as a mathematical model of waves on shallow water surfaces. A model equation for any physical system, the Korteweg–de Vries (KdV) equation, commonly credited to Korteweg and de Vries (1895), governs the propagation of weakly dispersive, weakly nonlinear water waves and serves as a model equation for any physical system for which the dispersion relation for frequency versus wave number.
In our research, we consider the special case of the above Equation (1). We consider the special (1 + 1)-D Korteweg–de Vries (KdV) equation [18] given as follows:
where indicates a wave function that depends on the components x and t. Equation (2) has many features; for example, it is originally modeled shallow water waves, describing the balance between nonlinearity and dispersion. This equation supports soliton solutions, which are stable, localized waves that maintain their shape. The KdV equation also describes ion-acoustic waves in plasmas. The KdV equation has several connections to physical problems, including shallow-water waves with weakly non-linear restoring forces, long internal waves in a density-stratified ocean, ion-acoustic waves in a plasma, acoustic waves on a crystal lattice, and many others. There are different types of KdV equations, including the modified KdV equation [19], the generalized KdV equation [20], the damped KdV equation [21], and the generalized perturbed KdV equation [22].
Basically, Equation (2) is obtained from the general form of the KdV equation, given as
by considering and . As we consider the specific values of and , we can say that Equation (2) is a special form of the general KdV equation. For Equation (2), breather-wave, 1-soliton, 2-soliton, new three waves, new periodic waves, and some analytical wave solutions based on the Hirota bilinear, function, and Sardar sub-equation methods do not exist in the literature.
The fundamental aim of this research is to determine the breather-wave, 1-soliton, 2-soliton, new three wave, new periodic-wave, and some analytical wave solutions based on the Hirota bilinear, function, and Sardar sub-equation methods. The used methods may applied to other nonlinear partial differential equations. Furthermore, dynamical analyses are discussed in the form of stability analysis and modulation instability.
The motivation of our work is to explore the breather-wave, 1-soliton, 2-soliton, new three wave, new periodic-wave, and some analytical wave solutions based on the Hirota bilinear, function, and Sardar sub-equation methods. Hirota bilinear method provides different types of soliton solutions, including breather-wave, 1-soliton, 2-soliton, new wave, and new periodic wave. The function method provides rational wave solutions, while Sardar sub-equation method provides various types of analytical solutions, including dark, bright, singular, dark-bright, and periodic. These three methods are also reliable, effective, and fruitful for other nonlinear partial differential equations in science and engineering. Additionally, stability analysis and modulation instability analysis are performed to check the stability and accuracy of the obtained solutions.
This paper has different sections. Section 2 presents a description of methodologies; Section 3 presents results of the Hirota bilinear method; Section 4 provides a mathematical analysis of the equation and its exact soliton solutions, Section 5 provides a graphical representation; Section 6 presents stability analysis; Section 7 shows modulation instability; and Section 8 is the conclusion.
2. Presentation of Methods
2.1. Hirota Bilinear Method
2.2. Summary of Function Method
In this subsection, we will explain the method of concern [23,24,25,26,27,28,29].
Assuming a nonlinear PDE,
Equation (12) changes into a nonlinear ordinary differential equation (ODE):
Using a traveling wave transformation,
Supposing the solutions for Equation (13) are
Here, and are unknowns. The value of m is determined by a homogeneous balance approach in Equation (13). Putting Equation (15) into Equation (13) yields
By putting into Equation (16) equal to zero, a set of equations is obtained:
In this way, we can attain the results for Equation (12).
2.3. Description of the Sardar Sub-Equation Method
Here, we will mention the main steps of this method [30] by assuming a nonlinear PDE:
where denotes the wave function. Assume the transformation given as
This results in the non-linear ODE:
Consider a result of Equation (20), given as
where satisfies the ODE:
where and are the parameters.
Next, we proceed by first putting Equations (21) and (22) into Equation (20) and collecting the coefficients of each term of . As a result, we obtain a system of equations. By solving the system, we obtain the given sets. Type 1: if and , then
where, ,
Type 2: if and , we have
where, ,
Type 3: if and , then
where, ,
Type 4: if and , then
where, ,
3. Breather Wave Soliton
Consider the given relation to gain breather wave results [31].
Put Equation (37) into Equation (11) and sum up coefficients of every order of x,t,, equal to 0. By solving the system, we obtain
Set 1:
Set 2:
Set 3:
4. Soliton Solutions
In this part, we study the (1 + 1)-dimensional KdV equation of soliton solutions in Equation (11). The 1-soliton, 2-soliton, and three-wave solutions will be achieved.
4.1. 1-Soliton Solutions
For the 1-soliton result, we assume the transformation given as [32].
Putting Equation (44) into Equation (11), we obtain a system by collecting coefficients of equal to 0. By solving the system, we achieve
Set:
4.2. 2-Soliton Solutions
For 2-soliton solutions, we consider the relation given as [32].
Put Equation (47) into Equation (11), and collect coefficients of each order of , , and , taking it as equal to 0. By solving the system, we achieve
Set:
4.3. New Three-Wave Soliton
For new three-wave solutions, we assume a relation [33].
Put Equation (50) into Equation (11), collect coefficients of each order of , , and , and take it as equal to 0. Solving the system yields
Set 1:
Set 2:
Set 3:
Set 4:
4.4. New Periodic-Wave
For new periodic wave results, consider a relation [34]:
Insert Equation (59) into Equation (11), collect coefficients of each order of , ,, , and take it as equal to 0. By solving the system, we obtain
Set 1:
Set 2:
5. Exact Wave Solutions
Consider a traveling wave transformation;
By putting Equation (64) into Equation (2), we gain an ordinary differential equation given as follows:
Using homogenous balance scheme into Equation (65) yields . Now, we will obtain some new exact wave results for Equation (65).
5.1. Exact Siliton Solutions by Function Method
For , Equation (15) transforms into
Putting Equation (66) into Equation (65) and solving the system of equations yields
Set 1:
Set 2:
5.2. Exact Soliton Results via the Sardar Sub-Equation Method
For m = 2, Equation (21) changes to
Put Equation (71) into Equation (65) along with Equation (22). Collect coefficients of every order of equal to 0. Solving the system yields
Set 1:
Type 1: if and , we have
Type 2: if and , we have
Type 3: if and , we have
Type 4: if and , we have
6. Graphical Explanation
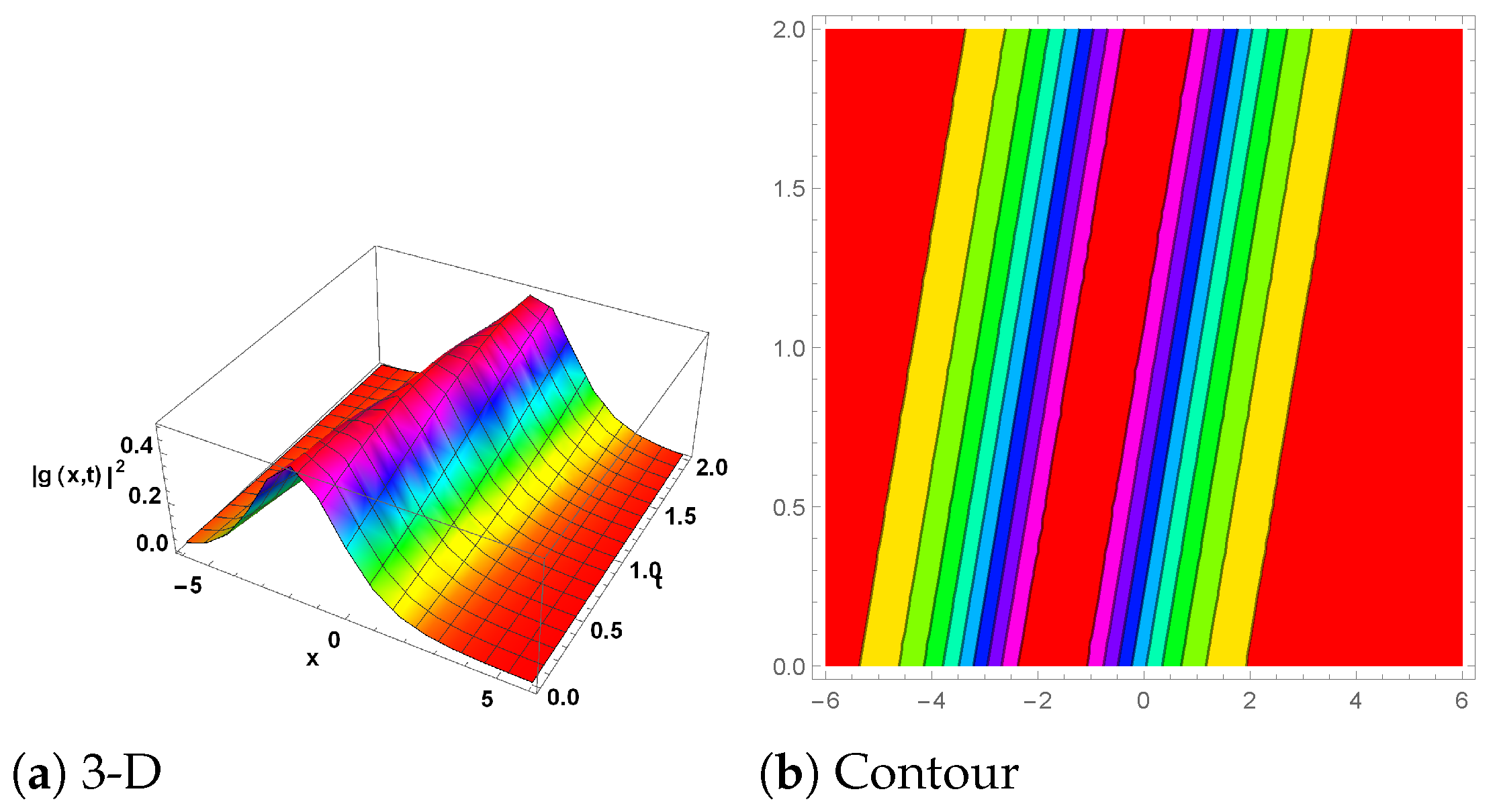
Here, we will represent some of the solutions gained graphically in 3D and contour (see Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7).
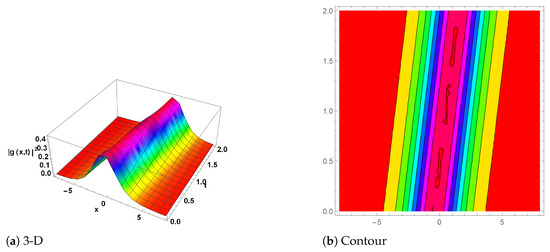
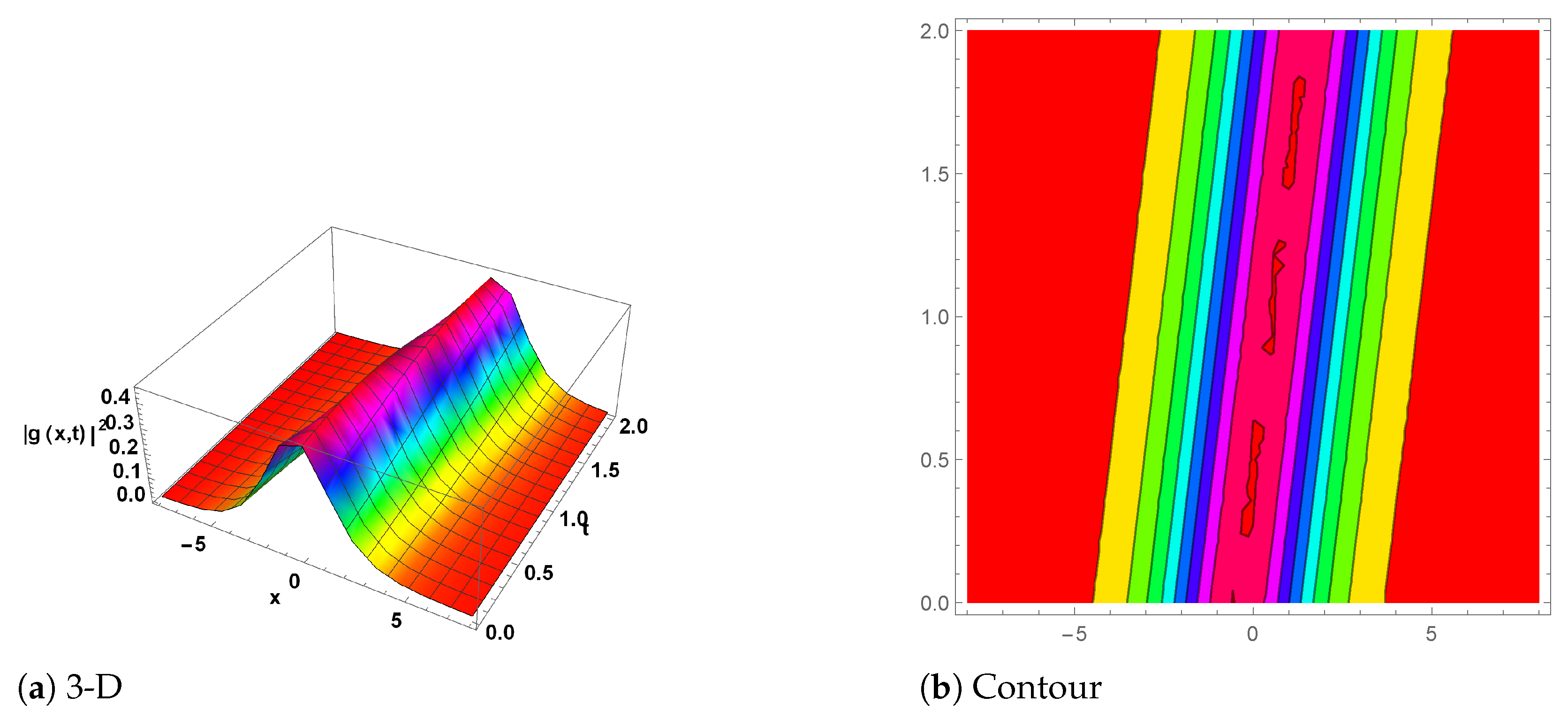
Figure 1.
(Breather wave) The plot for is shown in Equation (41) with the parameter values , and . (a) shows the 3D plot, while (b) represents the contour plot.
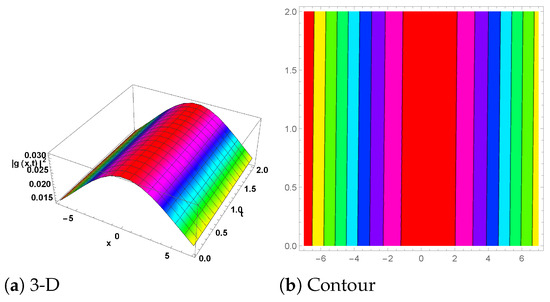
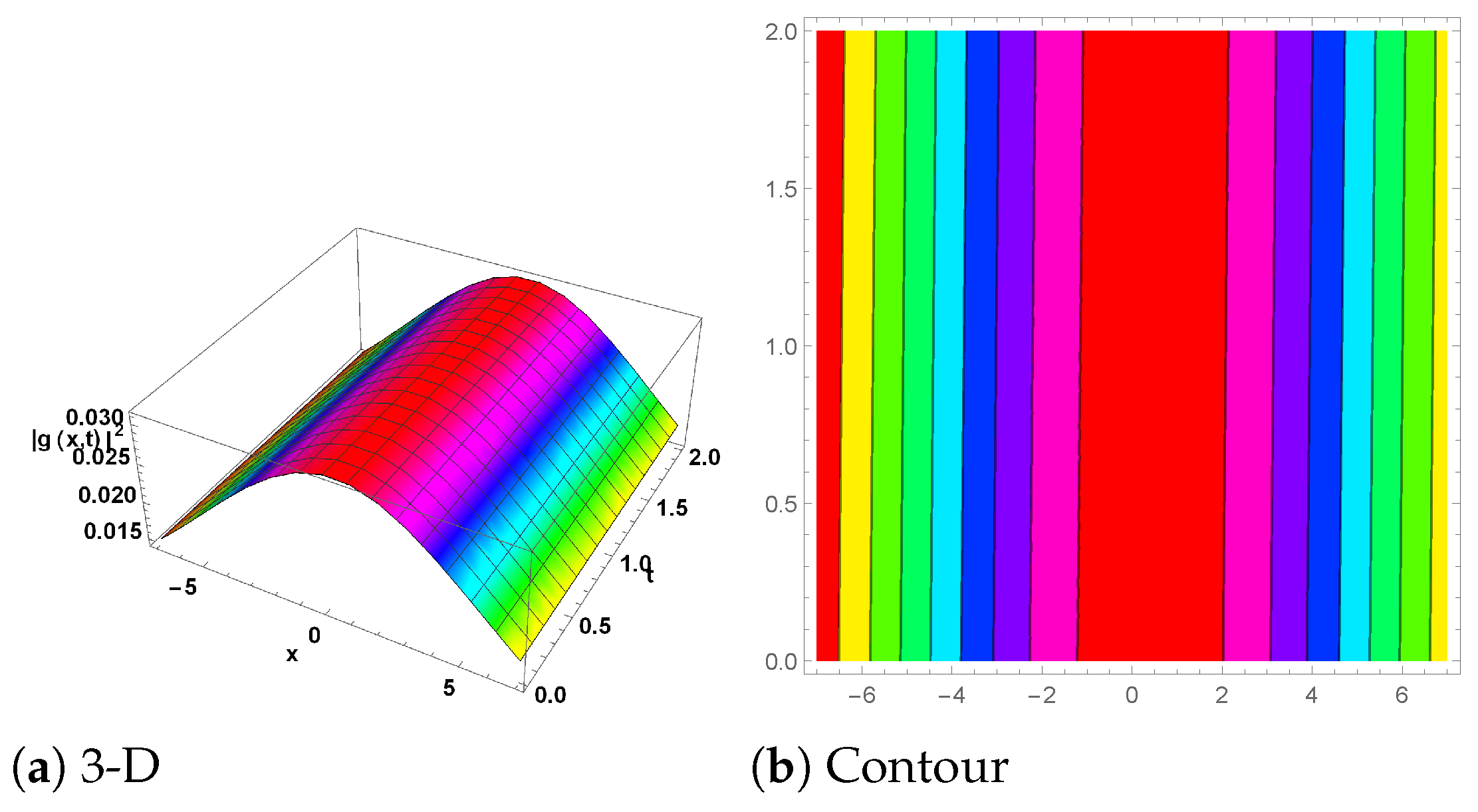
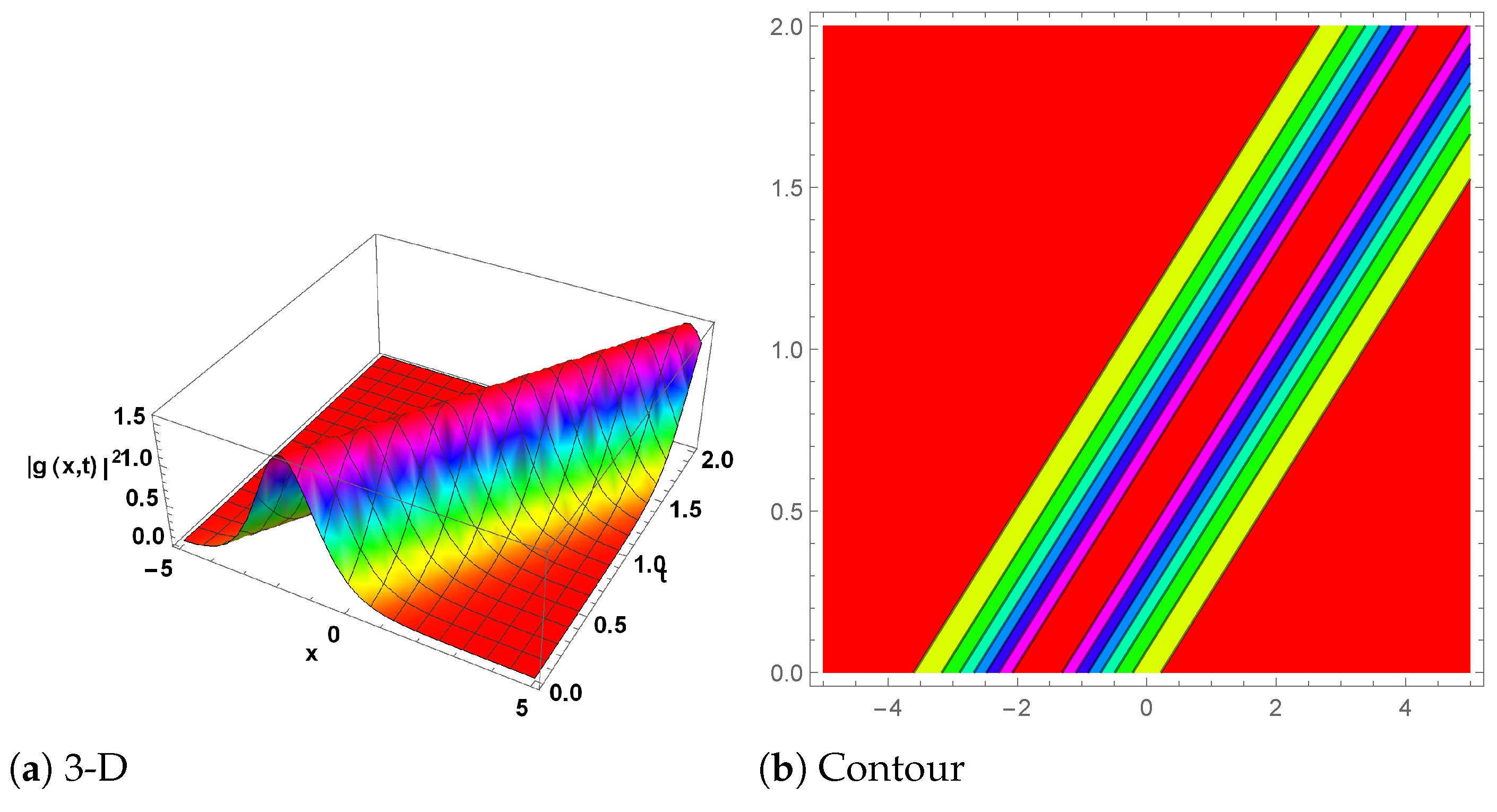
Figure 2.
(1-Soliton solution) The plot for is shown in Equation (46) with the parameter values , and . (a) shows the 3D plot, while (b) represents the contour plot.
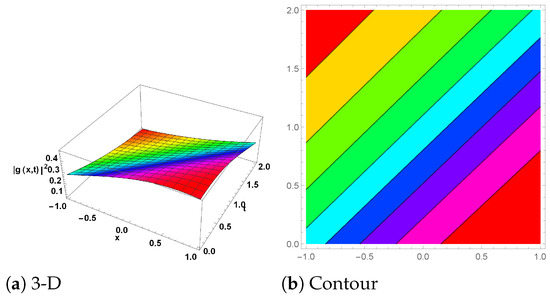
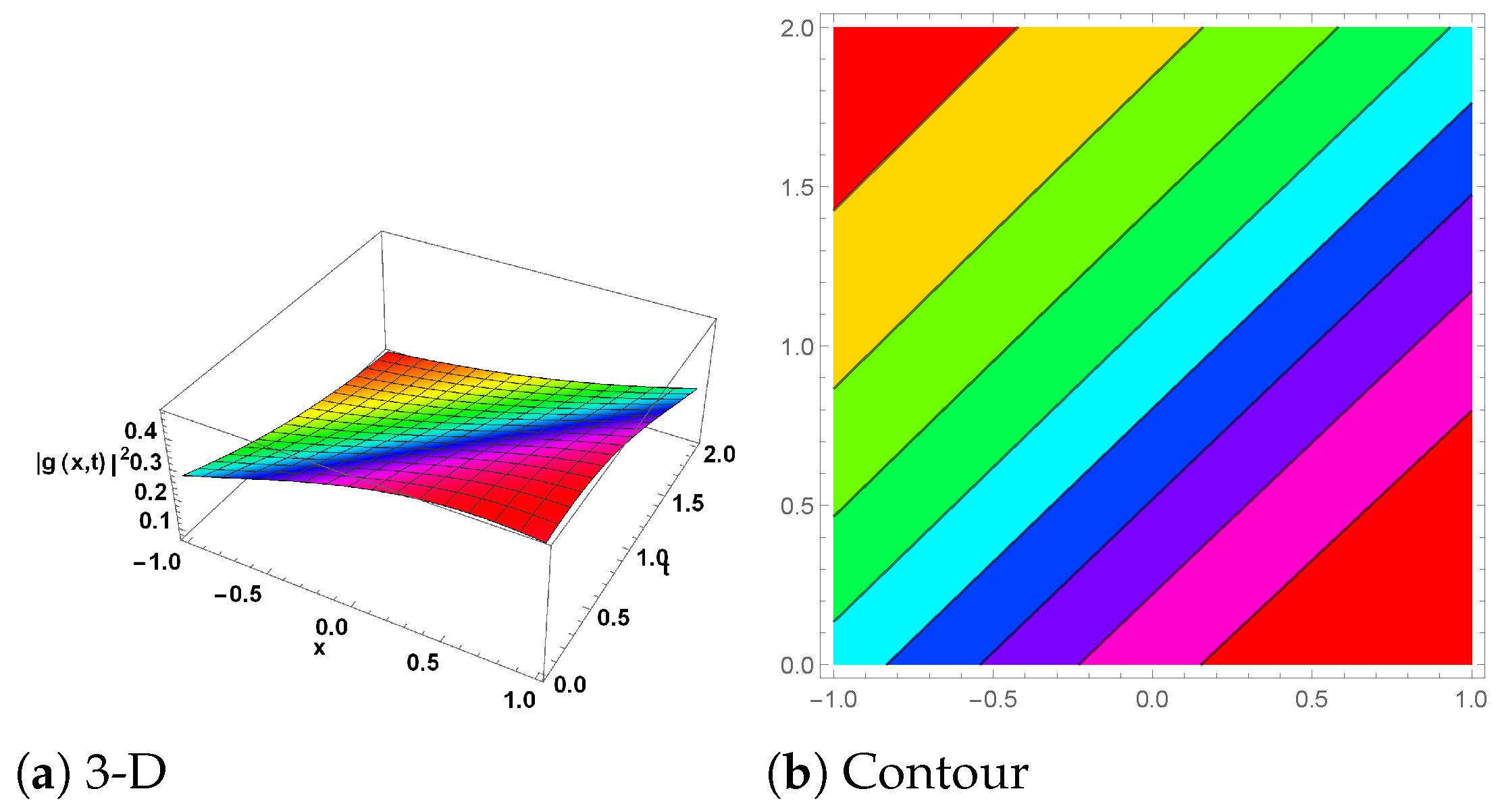
Figure 3.
(2-Soliton solution) The plot for is shown in Equation (49) with the parameter values , and . (a) shows the 3D plot, while (b) represents the contour plot.
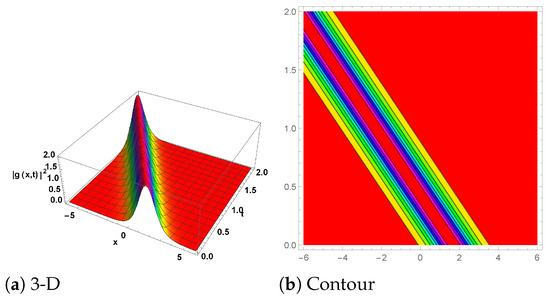
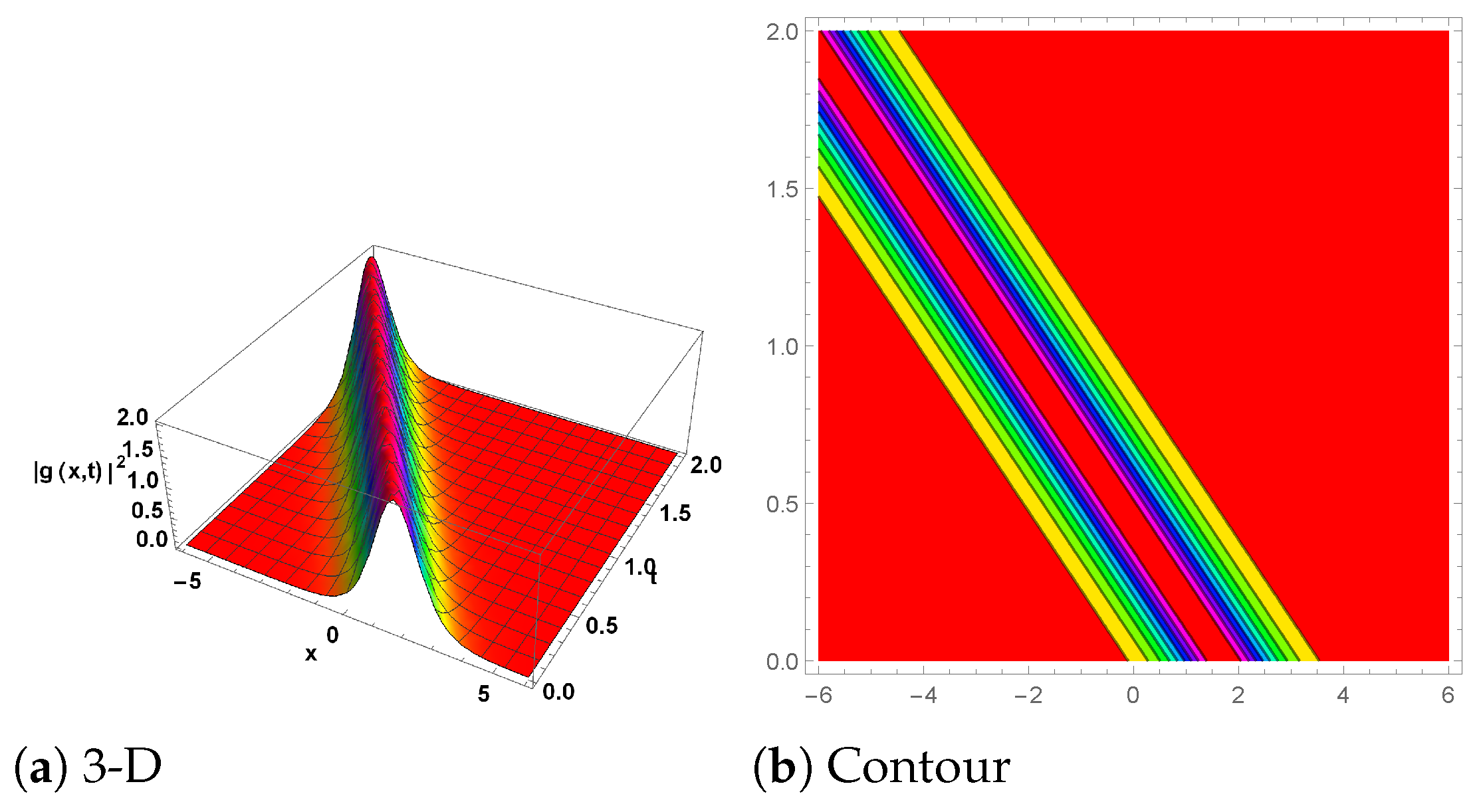
Figure 4.
(New three-wave solution) The plot for is shown in Equation (52) with the parameter values , and . (a) shows the 3D plot, while (b) represents the contour plot.
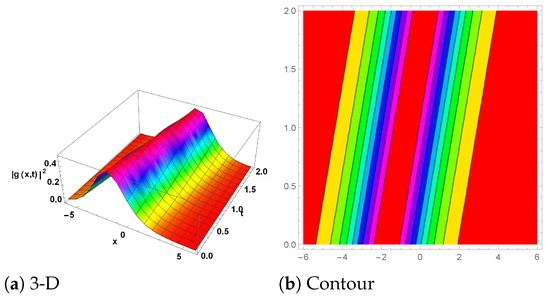
Figure 5.
(New periodic-wave solution) The plot for is represented by Equation (61) with the parameter values , and . (a) shows the 3D plot, while (b) represents the contour plot.
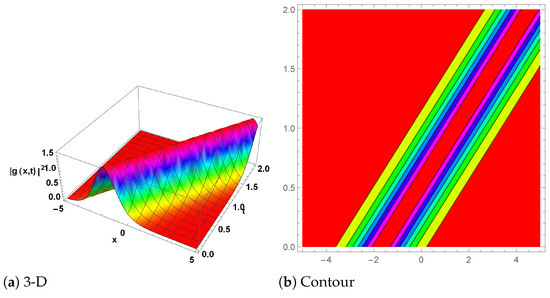
Figure 6.
(Rational wave solution) The plot for is represented by Equation (68) with the parameter values , and . (a) shows the 3D plot, while (b) represents the contour plot.
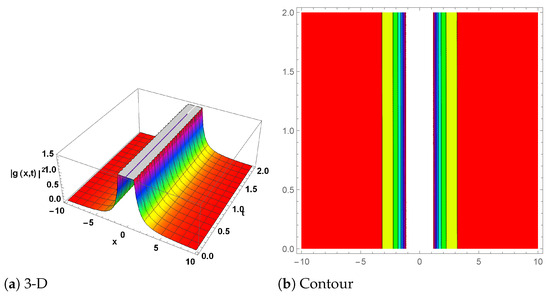
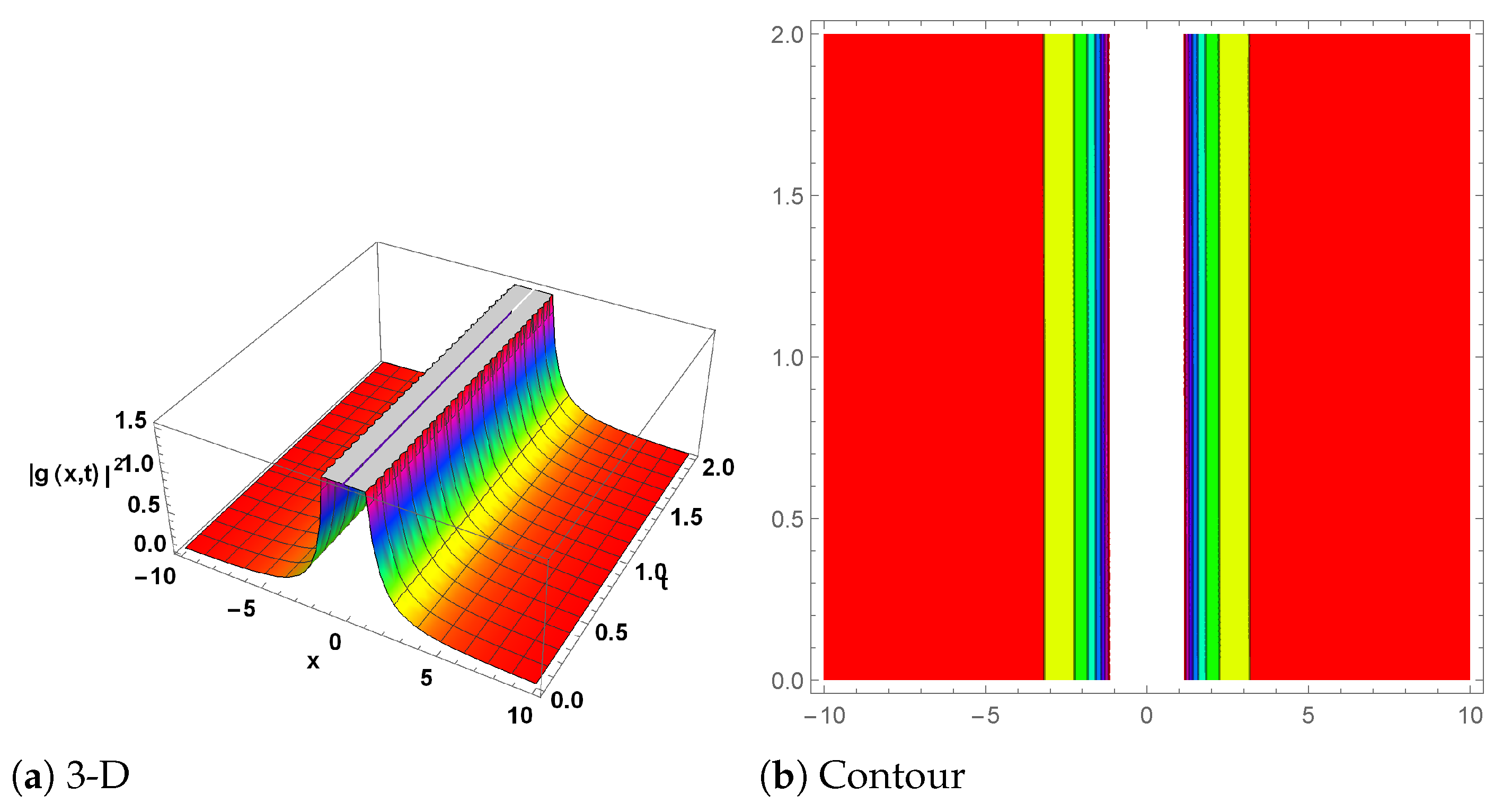
Figure 7.
(Singular wave solution) The plot for is represented by Equation (74) with the parameter values , and . (a) shows the 3D plot, while (b) represents the contour plot.
7. Stability Analysis
In this section, we discuss the stability analysis of the equation of concern. It is applied for many equations, like [35,36]. For the Equation (2) stability analysis, we use the Hamiltonian transformation,
where represents a momentum factor, where indicates the possibility power. The necessary criterion for the stable solution is shown as
where denotes a soliton velocity, and substituting Equation (74) in Equation (87) yields
by using the criterion given in Equation (88), we obtain
Hence, Equation (2) indicates that a stable nonlinear model provides the condition is fulfilled.
8. Modulation Instability (MI)
Dispersive and unsteady components of nonlinear systems have the ability to reduce the stability of the results. Modulating instabilities, or nonlinear factors interacting via the dispersion notion, are frequently the cause of instabilities for the stable solution of a new equation for partial differential equations fitting the optic transmission concept. In a nonlinear dispersion medium, a continuous surface wave causes modulation instability (MI), which results in the self-modulation of the phase and intensity. Assume the given relation to obtain the steady state solution of the (1 + 1)-dimensional special KdV equation is given as [37]
Here, shows the normalized optical power. Insert Equation (91) into Equation (2). By linearizing, one obtains
Consider the result of Equation (92) is given as
where q and p indicate the perturbation frequency and normalization wave number. Insert the Equation (93) in Equation (92). By collecting each coefficient of and , we obtain a dispersion relation by solving the determinant of the coefficient matrix.
Finding the dispersion result of Equation (94) for q yields
The achieved dispersion relation denotes the stable steady-state solution. When q is not real, then the steady-state result will be unstable because the perturbation grows gradually. When q is real, then the steady state changes to a stable one due to small perturbations. A steady-state solution is unstable if
The modulation instability gain spectrum is obtained:
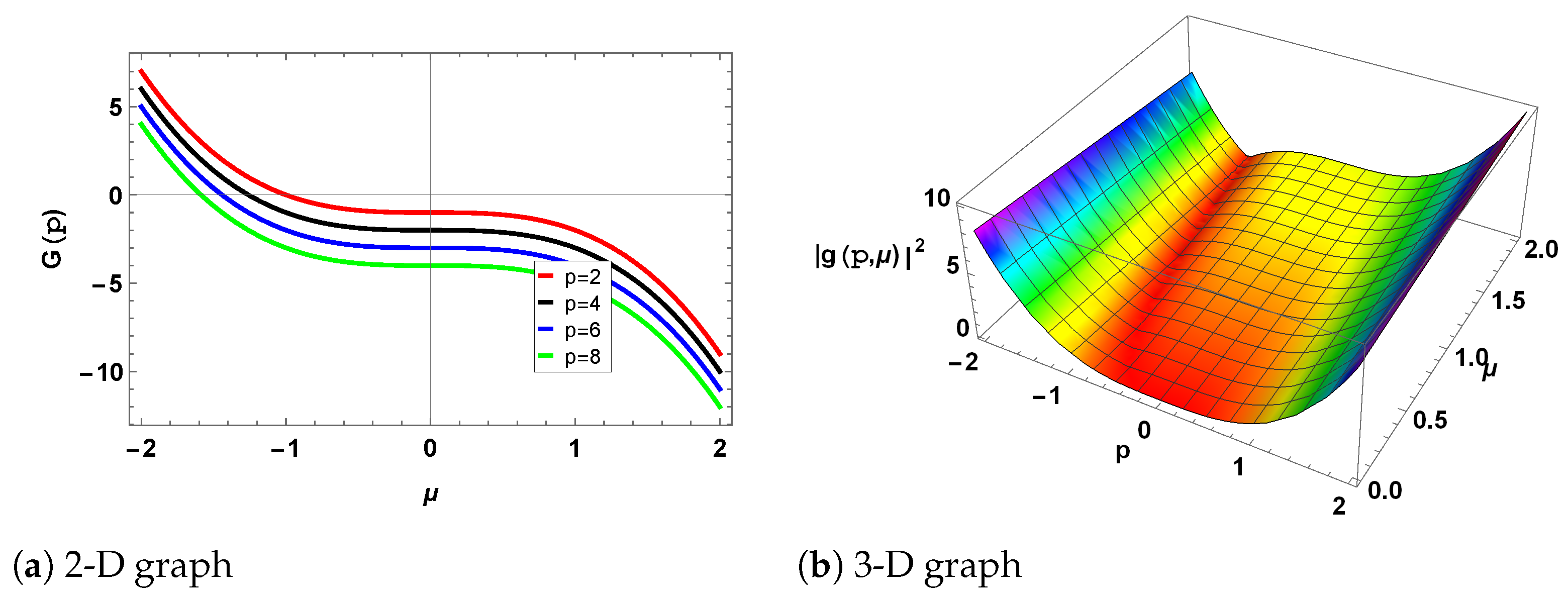
See Figure 8
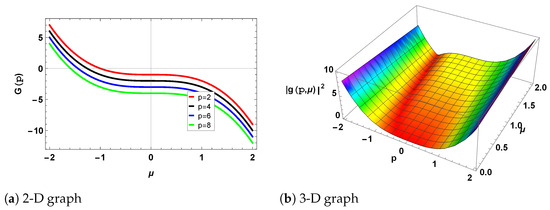
Figure 8.
The gain spectrum of MI for different values of , and . In the 2D graph, red curve is for , the black curve is for , the blue curve is for , and the green curve is for . (a) shows the 2D graph, while (b) represents the 3D graph.
9. Conclusions
In this paper, successful breather-wave, 1-soliton, 2-soliton, new three-wave, new periodic-wave, and some exact soliton results of special (1 + 1)-dimensional KdV equations are achieved by applying the Hirota bilinear, function, and Sardar sub-equation methods. Some of the results are shown in 3D and contour plots. All the obtained solutions were verified by Mathematica software. The results are useful for the development of governing equations. This research shows that the methods used are simple and fruitful for other partial differential equations.
Moreover, a stability analysis and the modulation instability of the governing model were conducted to verify the stability and precision of the obtained solutions. The methods utilized are not only straightforward but also exceptionally effective in solving nonlinear partial differential equations (PDEs). Furthermore, these techniques prove to be valuable for addressing higher-order NLPDEs and larger systems of equations. The findings presented here offer substantial insights and potential applications across various scientific and engineering areas. The solutions obtained by these methods are useful for optical fibers, telecommunications, plasma physics, fluid dynamics, and many more. In the end, it is concluded that the techniques used are reliable and provide useful results. Nowadays, exact solutions, especially soliton-like solutions, have gained much importance because this has become a special topic in nonlinear science. Soliton theory has gained importance because of the exceptional properties of solitons. Solitons maintain their shape and velocity after interaction and stability.
Author Contributions
A.A.: Writing, funding, review and editing, conceptualization, methodology, project administration; A.S.A.N.: Writing—review and editing, conceptualization, methodology; A.B.: Writing—original draft, conceptualization, methodology; review and editing, formal analysis; supervision. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Deanship of Scientific Research, Vice Presidency for Graduate Studies and Scientific Research, King Faisal University, Saudi Arabia [KFU242750].
Data Availability Statement
The datasets generated during and/or analyzed during the current study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare that they have no competing interests.
References
- Hyder, A.-A.; Soliman, A.H. Analytical manner for abundant stochastic wave solutions of extended KdV equation with conformable differential operators. Math. Methods Appl. Sci. 2022, 45, 8600–8612. [Google Scholar] [CrossRef]
- Shakeel, M.; Alaoui, M.K.; Zidan, A.M.; Shah, N.A. Closed form solutions for the generalized fifth-order KDV equation by using the modified exp-function method. J. Ocean. Eng. Sci. 2022, in press. [Google Scholar]
- Islam, S.M.R.; Khan, K.; Akbar, M.A. Exact solutions of unsteady Korteweg–de Vries and time regularized long wave equations. SpringerPlus 2015, 4, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Khatun, M.M.; Akbar, M.A.; Fayazova, Z.K.; İlhan, O.A. Various wave solutions to the nonlinear fractional Korteweg–de Vries Zakharov-Kuznetsov equation by a new approach to the two-variable expansion scheme. Phys. Scr. 2024, 99, 035218. [Google Scholar] [CrossRef]
- AlQahtani, S.A.; Alngar, M.E.M. Soliton Solutions for Coupled Nonlinear Generalized Zakharov Equations with Anti-cubic Nonlinearity Using Various Techniques. Int. J. Appl. Comput. Math. 2024, 10, 9. [Google Scholar] [CrossRef]
- Pandir, Y.; Ekin, A. New solitary wave solutions of the Korteweg–de Vries (KdV) equation by new version of the trial equation method. Electron. J. Appl. Math. 2023, 1, 101–113. [Google Scholar] [CrossRef]
- Seadawy, A.R. New exact solutions for the KdV equation with higher order nonlinearity by using the variational method. Comput. Math. Appl. 2011, 62, 3741–3755. [Google Scholar] [CrossRef]
- Raheel, M.; Zafar, A.; Liu, J.-G. New periodic-wave, periodic-cross-kink wave, three wave and other analytical wave solitons of new (2 + 1)-dimensional KdV equation. Eur. Phys. J. Plus 2024, 139, 50. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, D. Multisoliton solutions of a (2 + 1)-dimensional variable-coefficient Toda lattice equation via Hirota’s bilinear method. Can. J. Phys. 2014, 92, 184–190. [Google Scholar] [CrossRef]
- Cao, R.; Zhao, Q.; Gao, L. Bilinear approach to soliton and periodic-wave solutions of two nonlinear evolution equations of Mathematical Physics. Adv. Differ. Equations 2019, 2019, 156. [Google Scholar] [CrossRef]
- Zhang, L.-L.; Lü, X.; Zhu, S.-Z. Painlevé analysis, Bäcklund transformation and soliton solutions of the (2 + 1)-dimensional variable-coefficient Boussinesq equation. Int. J. Theor. Phys. 2024, 63, 160. [Google Scholar] [CrossRef]
- Lü, X.; Zhang, L.L.; Ma, W.-X. Oceanic shallow-water description with (2 + 1)-dimensional generalized variable-coefficient Hirota–Satsuma–Ito equation: Painlevé analysis, soliton solutions, and lump solutions. Phys. Fluids 2024, 36, 6. [Google Scholar] [CrossRef]
- Qawaqneh, H.; Zafar, A.; Raheel, M.; Zaagan, A.A.; Zahran, E.H.M.; Cevikel, A.; Bekir, A. New soliton solutions of M-fractional Westervelt model in ultrasound imaging via two analytical techniques. Opt. Quantum Electron. 2024, 56, 737. [Google Scholar] [CrossRef]
- Altalbe, A.; Taishiyeva, A.; Myrzakulov, R.; Bekir, A.; Zaagan, A.A. Effect of truncated M-fractional derivative on the new exact solitons to the Shynaray-IIA equation and stability analysis. Results Phys. 2024, 57, 107422. [Google Scholar] [CrossRef]
- Razzaq, W.; Zafar, A.; Raheel, M. Searching the new exact wave solutions to the beta-fractional Paraxial nonlinear Schrödinger model via three different approaches. Int. J. Mod. Phys. 2024, 38, 2450132. [Google Scholar] [CrossRef]
- Alsharidi, A.K.; Bekir, A. Discovery of new exact wave solutions to the M-fractional complex three coupled Maccari’s system by Sardar sub-equation scheme. Symmetry 2023, 15, 1567. [Google Scholar] [CrossRef]
- Chou, D.; Ur Rehman, H.; Amer, A.; Amer, A. New solitary wave solutions of generalized fractional Tzitzéica-type evolution equations using Sardar sub-equation method. Opt. Quantum Electron. 2023, 55, 1148. [Google Scholar] [CrossRef]
- Ma, W.-X. Soliton solutions by means of Hirota bilinear forms. Partial. Differ. Equations Appl. Math. 2022, 5, 100220. [Google Scholar] [CrossRef]
- Matsutani, S. On real hyperelliptic solutions of focusing modified KdV equation. Math. Phys. Anal. Geom. 2024, 27, 19. [Google Scholar] [CrossRef]
- Miah, M.M.; Meia, M.A.A.; Sarker, M.M.R.; Hasan, A. Adequate Closed Form Wave Solutions to the Generalized KdV Equation in Mathematical Physics. J. Appl. Math. Phys. 2024, 12, 2069–2082. [Google Scholar] [CrossRef]
- Iqbal, M.; Faridi, W.A.; Algethamie, R.; Alomari, F.A.H.; Murad, M.A.S.; Alsubaie, N.E.; Seadawy, A.R. Extraction of newly soliton wave structure to the nonlinear damped Korteweg–de Vries dynamical equation through a computational technique. Opt. Quantum Electron. 2024, 56, 1189. [Google Scholar] [CrossRef]
- Bayrakci, U.; Demiray, S.T.; Yildirim, H. Obtaining new soliton solutions of the fractional generalized perturbed KdV equation. Phys. Scr. 2024, 99, 125202. [Google Scholar] [CrossRef]
- Ali, A.T.; Hassan, E.R. General Expa-function method for nonlinear evolution equations. Appl. Math. Comput. 2010, 217, 451–459. [Google Scholar] [CrossRef]
- Zayed, E.M.E.; Al-Nowehy, A.G. Generalized kudryashov method and general expa function method for solving a high order nonlinear schrödinger equation. J. Space Explor. 2017, 6, 1–26. [Google Scholar]
- Hosseini, K.; Ayati, Z.; Ansari, R. New exact solutions of the Tzitzéica-type equations in non-linear optics using the expa function method. J. Mod. Opt. 2018, 65, 847–851. [Google Scholar] [CrossRef]
- Zafar, A. The expa function method and the conformable time-fractional KdV equations. Nonlinear Eng. 2019, 8, 728–732. [Google Scholar] [CrossRef]
- Bashar, M.H.; Islam, S.M.R.; Kumar, D. Construction of traveling wave solutions of the (2+1)-dimensional Heisenberg ferromagnetic spin chain equation. Partial. Differ. Equations Appl. Math. 2021, 4, 100040. [Google Scholar] [CrossRef]
- Zafar, A.; Ali, K.K.; Raheel, M.; Nisar, K.S.; Bekir, A. Abundant M-fractional optical solitons to the pertubed Gerdjikov–Ivanov equation treating the mathematical nonlinear optics. Opt. Quantum Electron. 2022, 54, 1–17. [Google Scholar] [CrossRef]
- Zafar, A.; Bekir, A.; Raheel, M.; Rezazadeh, H. Investigation for optical soliton solutions of two nonlinear Schrödinger equations via two concrete finite series methods. Int. J. Appl. Comput. Math. 2020, 6, 1–13. [Google Scholar] [CrossRef]
- Ullah, N.; Asjad, M.I.; Awrejcewicz, J.; Muhammad, T.; Baleanu, D. On soliton solutions of fractional-order nonlinear model appears in physical sciences. Aims Math. 2022, 7, 7421–7440. [Google Scholar] [CrossRef]
- Lü, J.; Bilige, S.; Gao, X.; Bai, Y.; Zhang, R. Abundant Lump Solutions and Interaction Phenomena to the Kadomtsev-Petviashvili-Benjamin-Bona-Mahony Equation. J. Appl. Math. Phys. 2018, 6, 1733–1747. [Google Scholar] [CrossRef][Green Version]
- Yue, Y.; Huang, L.; Chen, Y. N-solitons, breathers, lumps and rogue wave solutions to a (3 + 1)-dimensional nonlinear evolution equation. Comput. Math. Appl. 2017, 12, 22. [Google Scholar] [CrossRef]
- Liu, J.; Du, J.; Zeng, Z.; Nie, B. New three-wave solutions for the (3 + 1)-dimensional Boiti–Leon–Manna–Pempinelli equation. Nonlinear Dyn. 2017, 88, 655–661. [Google Scholar] [CrossRef]
- Ilhan, O.A.; Manafian, J. Periodic type and periodic cross-kink wave solutions to the (2 + 1)-dimensional breaking soliton equation arising in fluid dynamics. Mod. Phys. Lett. B 2019, 33, 1950277. [Google Scholar] [CrossRef]
- Tariq, K.U.; Wazwaz, A.-M.; Javed, R. Construction of different wave structures, stability analysis and modulation instability of the coupled nonlinear Drinfel’d-Sokolov-Wilson model. Chaos Solitons Fractals 2023, 166, 112903. [Google Scholar] [CrossRef]
- Zulfiqar, H.; Aashiq, A.; Tariq, K.U.; Ahmad, H.; Almohsen, B.; Aslam, M.; Rehman, H.U. On the solitonic wave structures and stability analysis of the stochastic nonlinear Schrödinger equation with the impact of multiplicative noise. Optik 2023, 289, 171250. [Google Scholar] [CrossRef]
- ur Rehman, S.; Ahmad, J. Modulation instability analysis and optical solitons in birefringent fibers to RKL equation without four wave mixing. Alex. Eng. J. 2021, 60, 1339–1354. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).