Abstract
A Hertz radiator’s Sommerfeld boundary value problem is considered for the case when its electric moment is directed horizontally relative to the plane interface between two media with different values of magnetic permeability. An integral representation of the exact expression for the Hertz potential, which generalizes the classical solution for non-magnetic media, both in cylindrical and spherical coordinate systems, is obtained. The corresponding expressions for the scattered wave fields are given in the form of Sommerfeld integrals. It is shown that the potential components can be represented as the sum of an infinite series in powers of the Green function.
Keywords:
Maxwell’s equations; convolution; Green function; electromagnetic wave scattering; Hertz dipole; Sommerfeld integrals MSC:
28A10; 28A25; 30B10; 30D10; 41A60; 78A02; 78A40
1. Introduction
The famous Sommerfeld half-space problem [1,2] was solved by Sommerfeld a century ago using the Hertz vector in terms of integrals, which are now called Sommerfeld integrals.
A detailed analysis of the horizontal electric dipole in a conducting half-space was conducted in the works of Banos and Wesley [3] and Lien [4], in which the calculation of the Sommerfeld integral was reduced to a form convenient for numerical calculation.
It should be noted that the advantage of analytical methods of solving the problem over numerical ones is, first of all, transparency and an adequate picture of physical processes. On the other hand, numerical methods cannot always compete in the accuracy of calculations with rigorous analytical methods. Therefore, the analytical outcomes can be used in semi-numerical methods for solving more complex problems.
Although there are many papers devoted to the Sommerfeld problem on a half-space, it still requires a specific solution in many areas of science and technology. The importance of the Sommerfeld half-space problem for modern technology is thoroughly described in the remarkable review article [5]. As an example, one can note the original work of Michalski [6] on an alternative formulation of the vector potential, which additionally uses a scalar potential, on which his previous works are based, as a gauge function corresponding to a monopole.
However, it is noted that the scalar potentials of single point charges in Sommerfeld’s formulation do not become identical in one of the special cases, when they are located, for example, above an ideal surface ([6], p. 57).
We suppose that the vector potential does not have the advantage of a gauge relation over the Hertz potential , as the auxiliary scalar potential is rigidly connected through the divergence operation with the sought potential . The above can be confirmed by the following transformations of potentials
which directly follow from expression (1) according to the formula
Hence, the proportionality of potentials and brings up a natural question about the uniqueness of the solution to the boundary value problem, as the expressions, for example, for the magnetic field in a cylindrical coordinate system, corresponding to each of the potentials ( and ), must be identical.
In contrast to his approach using the additional scalar potential , the posed Sommerfeld boundary value problem is solved in a standard way and its solution in Sommerfeld’s formulation is applicable to all special cases and limit transitions. Moreover, the components of the Hertz potential for each half-space, as well as the expressions for the fields in the form of expansion in powers of a spherical wave, have a simpler and more convenient form for users.
Unfortunately, there is still no solution to the Sommerfeld problem on a half-space for magnetic media in the form of a Hertz potential, as well as simple calculation formulas for fields.
The aim of this paper is to solve the Helmholtz equation with boundary conditions on a plane interface between two media with different values of magnetic permeability, where the electric moment of the Hertzian radiator is located above it in parallel.
The second section provides preliminary general expressions for a stationary electromagnetic field obtained using the Hertz potential.
The third section is devoted to a boundary value problem with boundary conditions and its solution in the form of Sommerfeld integrals.
In the fourth section, the components of the vector potential are considered in cylindrical and spherical coordinate systems.
In the fifth and sixth sections, the electromagnetic field of scattered waves is expressed by means of Sommerfeld integrals in cylindrical and spherical coordinate systems.
In the seventh section, the method of expanding the Sommerfeld integral into an infinite series in powers of the GF [7] is applied for calculating the fields of reflected waves.
2. General Expressions for Stationary Fields of Electromagnetic Waves
In this section, we will study stationary fields that depend on time according to the harmonic-time law, and then the factor , where is the wave circular frequency, will be omitted. Stationary solutions of Maxwell’s equations can be generally represented through a vector Hertz potential [8]
where , denotes a convolution of the current density with GF
It is obvious that the potential must satisfy the equation
as it is defined by the convolution in (2).
It is expedient to look for the components of the potential in the Cartesian coordinate system through the integral representation of GF
which follows from the Fourier inversion
in the cylindrical coordinate system (see Figure 1).
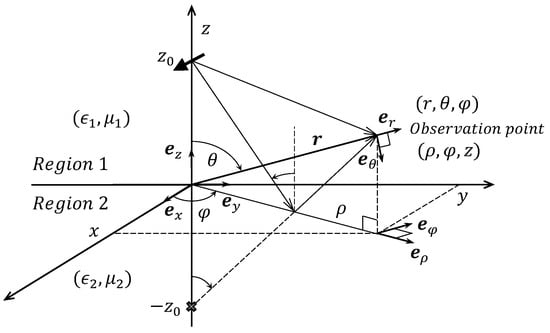
Figure 1.
A horizontal dipole and coordinate systems.
Let us first express the components of the fields in (1) through and
which we need to formulate the boundary conditions.
The vector potential of a point horizontal dipole can be expressed through GF
where the dipole moment , located at the point , corresponds to the current density
with its Fourier transform
3. Solution of the Boundary Value Problem
The index “1” in the above expressions corresponds to the upper half-space and “2”—to the lower half-space
Let us require that the boundary conditions for the tangential components of the magnetic and electric fields be satisfied in (6) and (7) for
The solution of the system (13) in the form (for )
is similar to the representation of GF in (4) or in (9), where the sought integrands do not depend on the spatial coordinates .
Further, we will keep in mind that
as the Hankel function depends only on .
From Equation (13a), it follows that
as there is a derivative of the Hankel function in (15) and (17).
Then, Equation (13b) can be written as
It is obvious that (13d) implies the equation
which, when taken into account, transforms Equation (13c) into
Substituting and from (14) and (16) into (21) and (23), we obtain a system of equations
which has the following solution
4. Hertz Vector Potential
Taking into account the solutions obtained in (25) and (26), we can write the components
in the upper half-space , as well as in the lower half-space
4.1. Potential in the Cylindrical Coordinate System
Expressions for the electromagnetic field of scattered waves in a cylindrical coordinate system can be calculated directly through the vector potential, or can be found by transforming fields from one coordinate system to another.
Further, we will consider the transformation of the potential from a Cartesian to a cylindrical coordinate system using the transformation of the basis vectors
As a result, we obtain the components of the potential in the cylindrical coordinate system
Interestingly, the Hertz potential in the cylindrical coordinate system consists of three components, whereas the vector potential in [6] has only two. This indicates that the vector potential probably corresponds to an approximate solution due to the uniqueness of the solution mentioned in the Introduction.
4.2. Potential in the Spherical Coordinate System
The vector in the spherical coordinate system is defined similarly
due to the transformation of the basis vectors
5. Expressions for Scattered Wave Fields in the Cylindrical Coordinate System
Substituting the components of the potential (34) into the curl (1), we obtain expressions for the magnetic field in the upper half-space
and in the lower half-space ()
Similarly, we obtain expressions for the electric field
where the identity holds ()
6. Expressions for Scattered Wave Fields in the Spherical Coordinate System
Having opened the curl, we find the components of the magnetic and electric fields ()
Here, in the expressions for the electric field, there are no second derivatives, because we used the Helmholtz equation in the spherical coordinate system.
7. Electromagnetic Field of a Horizontal Dipole
7.1. Dipole in the Cylindrical Coordinate System
The fields of a Hertzian point radiator can be conveniently obtained directly from the above expressions (36)–(38)
It is meant here that ().
7.2. Dipole in the Spherical Coordinate System
The Hertzian radiator fields in a spherical system can be obtained directly from (45)
and its electric field can be obtained from (46)
8. Asymptotic Expansion of the Potential Components
The components of the potential in the upper half-space can be expanded into an infinite series in powers of the Green’s function using the auxiliary integral [7]
where is a slowly oscillating function, is the root of the equation
Indeed, the final expressions in (30) and (31) can be easily represented in a concise form, both for the component
and for
For instance, the main expansion terms of Hertz potential’s components for reflected waves in a spherical coordinate system are
In order for the series to converge, the height of the source must be much greater than the wavelength .
9. Discussion
It should be noted that the solutions (30)–(33), in the case of non-magnetic media (), coincide with previously known expressions for the components of the Hertz potential, obtained, for example, in [4,9,10].
The same expressions for the magnetic field in a cylindrical coordinate system (36)–(41), obtained through the components of the potentials , can be obtained by transforming the Cartesian components of the magnetic field
taking into account the rules of differentiation of (18) and (19) in (6)
The validity of the expressions for the electric field (42)–(44) is easily verified using Maxwell’s equation
directly through magnetic field curl calculations in (36)–(41).
Similarly, we can show the validity of expressions (45a), (45b) for the magnetic field in a spherical coordinate system, using the previously obtained field components in a cylindrical coordinate system
and the change of the vector basis
Based on geometric considerations, the azimuthal component of the vector must remain the same in both the spherical (45c) and the cylindrical coordinate systems (37). In order to verify the identity of these expressions, it is sufficient to make the following substitutions in (37)
The expressions for the azimuthal component of the electric field in the expressions (46c) and (43) should also coincide, which is easily verified, due to simple relations
Note that unlike other coordinate systems, the expressions for the electric field (46) in the spherical coordinate system contain only first-order derivatives.
10. Conclusions
A general solution of the Hertz potential for non-magnetic media, both in cylindrical and spherical coordinate systems, is obtained in the form of Sommerfeld integrals.
Expressions for the fields of reflected and refracted waves at the interface between two media are found through Sommerfeld integrals.
The validity of the Hertz potential is verified by comparing the expressions for the fields obtained directly through it and by transforming the fields from one coordinate system to another. Moreover, the components of the Hertz potential in the particular case coincide with the previously known expressions for non-magnetic media in the Cartesian coordinate system [4,9,10].
The potential components for reflected waves are represented as the sum of an infinite series in powers of the Green’s function using the technique described in our previous paper [7].
This problem is the initial stage in finding a rigorous solution to the problem of transmitted waves in the second medium, as well as an analysis of surface waves, which still require more careful consideration. As some difficulties arise in solving problems with refracted waves, they will be discussed in detail in the other paper.
Author Contributions
Conceptualization, S.S.; methodology, S.S.; investigation, S.S. and M.S.; writing—original draft preparation, S.S. and M.S.; writing—review and editing, S.S. and M.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Science Committee of the Ministry of Education and Science of the Republic of Kazakhstan (Grant No. AP19676900).
Data Availability Statement
Data are contained within the article.
Acknowledgments
The authors are grateful to L.E. Strautman for her help in translating the text into English.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| SI | Sommerfeld integral |
| GF | Green function |
References
- Sommerfeld, A. Über die Ausbreitung der Wellen in der drahtlosen Telegraphie. Ann. Phys. 1926, 386, 1135–1153. [Google Scholar] [CrossRef]
- Sommerfeld, A. Partial Differential Equations in Physics; Academic Press: New York, NY, USA, 1949. [Google Scholar]
- Baños, A.; Wesley, J. The Horizontal Dipole in a Conducting Half-Space; University of California, Marine Physical Laboratory: San Diego, CA, USA, 1953. [Google Scholar]
- Lien, R.H. Radiation from a horizontal dipole in a semi-infinite dissipative medium. J. Appl. Phys. 1953, 24, 1–4. [Google Scholar] [CrossRef]
- Michalski, K.; Mosig, J. The Sommerfeld half-space problem revisited: From radio frequencies and Zenneck waves to visible light and Fano modes. J. Electromagn. Waves Appl. 2016, 30, 1–42. [Google Scholar] [CrossRef]
- Michalski, K.A. On the Alternative Vector Potential Formulation of the Sommerfeld Half-Space Problem. IEEE Antennas Wirel. Propag. Lett. 2018, 17, 54–57. [Google Scholar] [CrossRef]
- Sautbekov, S.; Sautbekova, M.; Baisalova, K.; Pshikov, M. Calculation of Sommerfeld Integrals in Dipole Radiation Problems. Mathematics 2024, 12, 298. [Google Scholar] [CrossRef]
- Sautbekov, S. The generalized solutions of a system of Maxwell’s equations for the uniaxial anisotropic media. Electromagn. Waves Propag. Complex Matter 2011, 1, 3–24. [Google Scholar]
- Michalski, K.A.; Lin, H.I. On the far-zone electromagnetic field of a horizontal electric dipole over an imperfectly conducting half-space with extensions to plasmonics. Radio Sci. 2018, 53, 62–82. [Google Scholar] [CrossRef]
- Moore, R.; Blair, W. Dipole radiation in a conducting half-space. J. Res. NBS 1961, 65, 547–563. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).