Exponential Stability and ℒ1-Gain Performance for Positive Sampled-Data Control Systems
Abstract
1. Introduction
2. Preliminaries
3. Main Results
3.1. Stability Analysis
3.2. -Gain Performance Analysis
3.3. Controller Design
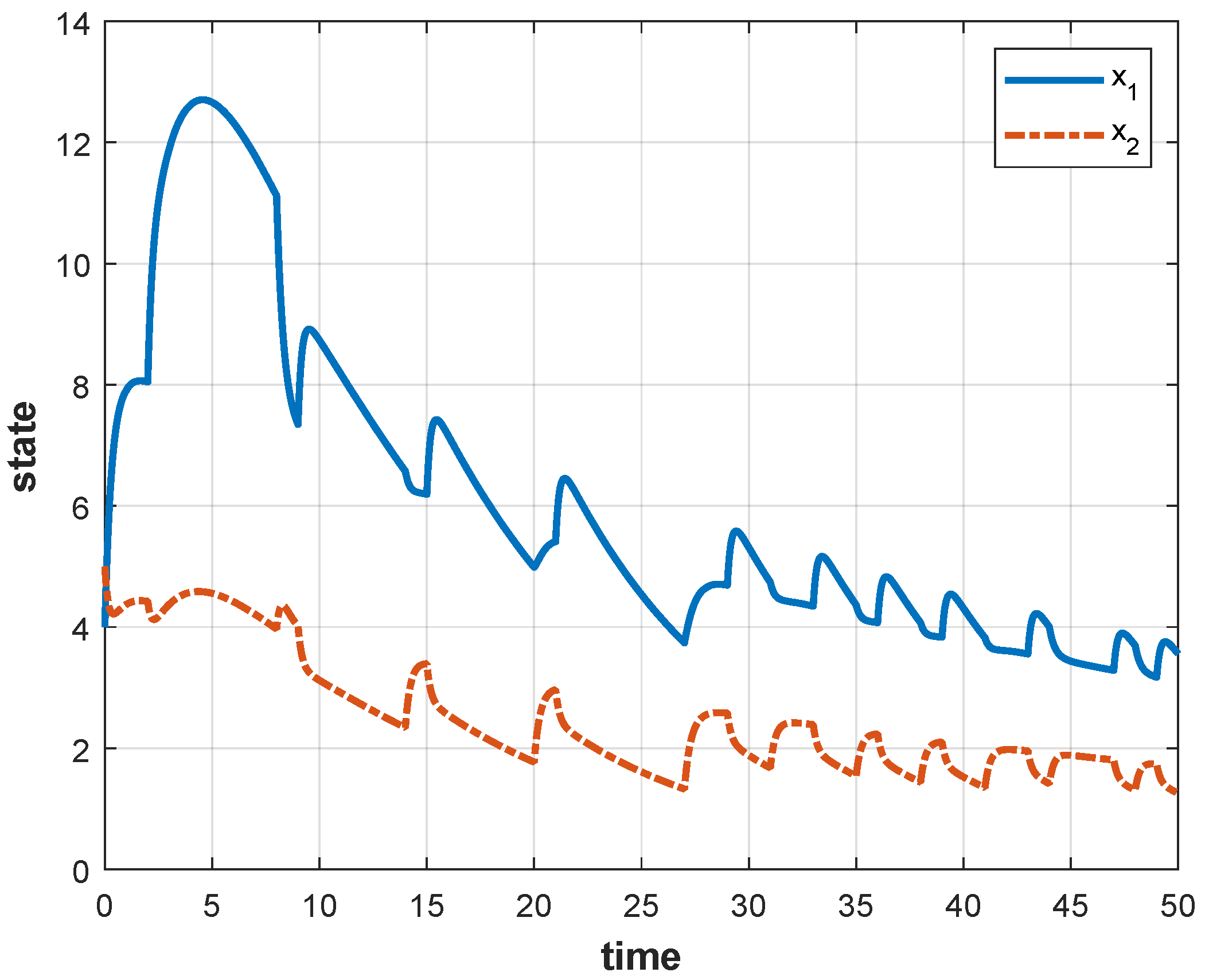
4. Numerical Example
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mariton, M. Jump Linear Systems in Automatic Control. In Marcel Dekker; CRC Press: New York, NY, USA, 1990. [Google Scholar]
- Ji, Y.; Chizeck, H.J. Controllability, stabilizability, and continuous-time Markovian jumping linear quadratic control. IEEE Trans. Autom. Control 1990, 35, 777–788. [Google Scholar] [CrossRef]
- Kaczorek, T. Stabilization of positive linear systems. In Proceedings of the IEEE Conference on Decision & Control, Tempa, FL, USA, 18 December 1998; IEEE: Piscataway, NJ, USA, 1999. [Google Scholar]
- Zhao, P. Practical stability, controllability and optimal controls of stochastic Markovian jump systems with time-delays. Automatica 2008, 44, 3120–3125. [Google Scholar] [CrossRef]
- Ackermann, J. Sampled-Data Control Systems: Analysis and Synthesis, Robust System Design; Springer: Berlin/Heidelberg, Germany; New York, NY, USA; Tokyo, Japan, 1985. [Google Scholar]
- Zhang, Y.; Wang, X. Sampled-data control for Markov jump systems with application to networked control systems. IEEE Trans. Autom. Control. 2022, 67, 1234–1245. [Google Scholar]
- Fridman, E. A refined input delay approach to sampled-data control. Automatica 2010, 46, 421–427. [Google Scholar] [CrossRef]
- Yu, X.; Lin, W. Sampled-data feedback stabilization in mean square for stochastic homogeneous systems. IEEE Trans. Autom. Control. 2024, 69, 6805–6820. [Google Scholar] [CrossRef]
- Bolzern, P.; Colaneri, P.; Nicolao, D.G. Stochastic stability of positive Markov jump linear systems. Automatica 2014, 50, 1181–1187. [Google Scholar] [CrossRef]
- Zhou, X.; Zhang, J.; Jia, X.; Feng, Y. Hybrid event-triggered dynamic control of positive Markovian jump systems. IEEE Trans. Circuits Syst. Ii: Express Briefs 2023, 70, 2122–2126. [Google Scholar] [CrossRef]
- Bolzern, P.; Colaneri, P. Positive Markov jump linear systems. Found. Trends Syst. Control 2015, 2, 275–427. [Google Scholar] [CrossRef]
- Hien, L.V. An LP approach to full-order and reduced order state estimations of positive Markov jump systems with delay. Int. J. Syst. Sci. 2017, 48, 2534–2543. [Google Scholar] [CrossRef]
- Rami, M.A.; Bokharaie, V.S.; Mason, O.; Wirth, F.R. Stability criteria for SIS epidemiological models under switching policies. Discret. Contin. Dyn.-Syst.-Ser. B 2014, 19, 2865–2887. [Google Scholar]
- Su, F.X.; Zhang, W.H.; Jiang, X.S. Stability analysis for positive Markov jump systems in p-th moment sense: Necessary and sufficient conditions. J. Frankl. Inst. 2024, 361, 106682. [Google Scholar] [CrossRef]
- Qi, W.H.; Park, J.H.; Cheng, J.; Kao, Y.G.; Gao, X.W. Exponential stability and L1-gain analysis for positive time-delay Markovian jump systems with switching transition rates subject to average dwell time. Inf. Sci. 2018, 424, 224–234. [Google Scholar] [CrossRef]
- Zhu, S.; Han, Q.L.; Zhang, C. L1-stochastic stability and L1-gain performance of positive Markov jump linear systems with time-delays: Necessary and sufficient conditions. IEEE Trans. Autom. Control 2017, 62, 3634–3639. [Google Scholar] [CrossRef]
- Lian, J.; Wang, R.K. Stochastic stability of positive Markov jump linear systems with fixed dwell time. Nonlinear Anal. Hybrid Syst. 2021, 40, 101014. [Google Scholar] [CrossRef]
- Guo, Y. Stabilization of positive Markov jump systems. J. Frankl. Inst. 2016, 353, 3428–3440. [Google Scholar] [CrossRef]
- Li, S.; Li, L.; Xiang, Z.; Tian, J.M.; Ghous, I. Event-triggered finite-time L1 control for positive Markov jump systems with partly known transition probability. J. Frankl. Inst. 2023, 360, 10018–10040. [Google Scholar] [CrossRef]
- Yin, K.; Yang, D. Sampled-data-based dynamic event-triggered asynchronous control of continuous-time positive Markov jump systems. Chaos Solitons Fractals 2023, 169, 113254. [Google Scholar] [CrossRef]
- Lamnabhi-Lagarrigue, F.; Loria, A.; Panteley, E. Advanced Topics in Control Systems Theory: Lecture Notes From FAP 2005; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Zakian, V.; Ono, T. Design of a sampled-data control system. In Control Systems Design; Springer: London, UK, 2005; pp. 165–189. [Google Scholar]
- Hu, M.J.; Shi, X.C.; Sun, Z.Q. Stability analysis and L1-gain characterization of positive sampled-data systems. Trans. Inst. Meas. Control 2024, 46, 1500–1506. [Google Scholar] [CrossRef]
- Du, S.L.; Qiao, J.F. Stability analysis and L1-gain controller synthesis of switched positive T-S fuzzy systems with time-varying delays. Neurocomputing 2018, 27, 2616–2623. [Google Scholar] [CrossRef]
- Zong, G.; Qi, W.; Karimi, H.R. L1 Control of positive semi-Markov jump systems with state delay. IEEE Trans. Syst. Man Cybern. Syst. 2020, 51, 7569–7578. [Google Scholar] [CrossRef]
- Li, S.; Xiang, Z.; Karimi, H.R. Stability and L1-gain controller design for positive switched systems with mixed time-varying delays. Appl. Math. Comput. 2013, 222, 507–518. [Google Scholar]
- Zhang, J. Sampled-data control of switched linear systems. In Proceedings of the 2012 3rd International Conference on System Science, Engineering Design and Manufacturing Informatization, Chengdu, China, 20–21 October 2012; IEEE: Piscataway, NJ, USA, 2012. [Google Scholar]
- Xiang, M.; Xiang, Z. Stability, L1-gain and control synthesis for positive switched systems with time-varying delay. Nonlinear Anal. Hybrid Syst. 2013, 9, 9–17. [Google Scholar] [CrossRef]
- Liu, L.J.; Xu, N.; Zhao, X.D. Stability and L1-gain analysis of nonlinear positive Markov jump systems based on a switching transition probability. ISA Trans. 2022, 121, 86–94. [Google Scholar] [CrossRef] [PubMed]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, P.; Niu, B. Exponential Stability and ℒ1-Gain Performance for Positive Sampled-Data Control Systems. Mathematics 2025, 13, 110. https://doi.org/10.3390/math13010110
Zhao P, Niu B. Exponential Stability and ℒ1-Gain Performance for Positive Sampled-Data Control Systems. Mathematics. 2025; 13(1):110. https://doi.org/10.3390/math13010110
Chicago/Turabian StyleZhao, Ping, and Ben Niu. 2025. "Exponential Stability and ℒ1-Gain Performance for Positive Sampled-Data Control Systems" Mathematics 13, no. 1: 110. https://doi.org/10.3390/math13010110
APA StyleZhao, P., & Niu, B. (2025). Exponential Stability and ℒ1-Gain Performance for Positive Sampled-Data Control Systems. Mathematics, 13(1), 110. https://doi.org/10.3390/math13010110





