The Boyle–Romberg Trinomial Tree, a Highly Efficient Method for Double Barrier Option Pricing

Abstract

Oscillations in option price convergence have long been a problematic aspect of tree methods, inhibiting the use of repeated Richardson extrapolation that could otherwise greatly accelerate convergence, a feature integral to some of the most efficient modern methods. These oscillations are typically caused by the fluctuating positions of nodes around the discontinuities in the payoff function or its derivatives. Our paper addresses this crucial gap that typically prohibits the use of lattice methods when high efficiency is needed. Focusing on double barrier options, we develop a trinomial tree in which the positions of the nodes are precisely adjusted to align with these discontinuities throughout the option’s lifespan and across various time steps. This alignment enables the use of repeated extrapolation to achieve high order convergence, including near barriers, a well-known challenge in many tree methods. Maintaining the inherent simplicity and adaptability of tree methods, our approach is easily applicable to other models and option types.

1. Introduction

Significant interest and numerous recent papers have focused on the pricing of double barrier and discrete double barrier options in the Black–Scholes framework. Various methods have been proposed for this purpose, many of which demonstrate high efficiency, often due to their capability to utilize repeated Richardson extrapolations. Although tree methods are among the simplest, most popular, and versatile for option pricing, their convergence speed is typically slow, reaching an order of $1/\sqrt{n}$, or at best, $1/n$ in the case of double barrier options. Additionally, oscillations in convergence hinder and limit the use of linear extrapolation. To our knowledge, repeated Richardson extrapolation has not been achieved for barrier options evaluated with lattice methods. This paper seeks to bridge this gap.

The primary issue that impedes smooth convergence, and prevents the use of repeated extrapolation when evaluating options with trees, stems from the fact that, in the log-space, the spacing between two nodes is constant, regardless of the price of the underlying asset, and solely depends on the number of time steps. Consequently, barriers and/or the strike price often fall between grid nodes. As the number of time steps changes, the distance to the nearest node fluctuates. As shown in prior studies (e.g., [1,2]), this triggers oscillations in the convergence of option prices, thereby preventing repeated extrapolation. To address this challenge, we introduce the Boyle–Romberg trinomial tree, an extension of Boyle’s original model (see [3,4]). This tree enables repeated Richardson extrapolation with an approximate Romberg sequence. In our tree, both barriers, the strike, and the stock price can be positioned at the exact location of a node throughout the life of the option. This is achieved by constructing the grid corresponding to the position of the underlying asset in the log-space in such a way that the spacing between two consecutive nodes varies, being stretched differently across various regions. The stretching parameters can remain constant, even when the number of time-steps changes. This ensures smooth convergence and enables repeated extrapolation, resulting in a high-order convergence speed.

Now we review some recent papers on the pricing of double barrier options in the Black–Scholes (BS) setting. We first consider articles that do not rely on tree-based approaches. In [5], a finite element method is applied to obtain highly accurate numerical values of the price of discrete double barrier options under the Black–Scholes model. In [6], a numerical method is proposed to compute the price of barrier options in the BS model where the parameters are time dependent. In [7], four different recombining quadrature methods are introduced. In [8], an accelerated Monte Carlo method is presented using a novel variance reduction technique. In [9], an efficient and fast numerical method for pricing the discrete double barrier option by the projection method is developed. In [10], a numerical method for pricing the discrete double barrier option by Legendre multiwavelet is proposed. In [11], a numerical method for pricing the discrete double barrier option by Chebyshev polynomials is developed. In [12], an orthogonal projection method is used. In [13], it is shown that the finite difference method for double barrier option pricing can be strongly enhanced by applying both a repeated Richardson extrapolation technique and a mesh optimization procedure in the Black–Scholes model. In [14,15], numerical methods are presented for pricing, respectively, double piecewise linear barrier options and step barrier options. The methods are based on probabilities that an underlying process does not cross the given barriers. In [16], a continuity correction method is established to provide an analytical approximation for the price of discrete barrier options under the Black–Scholes model. In [17], Lagrange interpolation on the Jacobi polynomials node is used to price discrete barrier options.

For tree methods, the literature is broad, and a variety of trees have been introduced. The convergence of tree-computed option prices to their limits has long been established in [18] for European/American and path-dependent options. See also [19] for a different approach. On the one hand, the computation of these option prices can be made more efficient by employing combinatorial techniques, as shown in [20,21], leveraging Catalan numbers as explored in [22], or using spectral methods, as demonstrated in [23,24]. On the other hand, for barrier options, the convergence speed of option prices is typically of order $1/\sqrt{n}$ for most tree-based models, where n is the number of time steps. Yet, a convergence speed of $1/n$ is achieved in [20,25] and a convergence speed of $1/n^{3/2}$ is obtained in [26] for single barrier options. Certainly, this is a far cry from the efficiency that can result from using repeated extrapolation.

Now, we review recent papers using trees to price barrier options in the Black–Scholes model or its generalizations. In addition to the papers previously referenced, we mention [27], where a Lagrange four-point interpolation technique is employed to price barrier options and address the near-barrier problem. In [28], probabilities are chosen to match local densities in trees capable of evaluating barrier options in local volatility models. In [29], willow trees are used to efficiently calculate moving average barrier option prices. In [30], multinomial trees based on saddle-point approximation are used to value barrier options in Lévy models. In [31], double-barrier options are priced using a bino-trinomial tree adapted to local volatility models. In [32], barrier option prices in stochastic volatility models are evaluated using a willow tree. In [33], a lattice-based approach is developed to price barrier options under mean-reverting regime-switching models. In [34], the bino-trinomial tree is used to price implied barriers and moving-barrier options.

In this paper, we introduce a tree method designed to precisely match the values of the barrier(s), the strike, and, indeed, any number of points of interest $A_1,\dots ,A_F$, which we refer to as the fixed points of the tree. The fixed points typically consist of those values where the payoff function or its derivatives are discontinuous. Our approach allows stretching parameters ${\Delta }_0,\dots ,{\Delta }_F$ to modulate the spacing between option prices over the various regions determined by these fixed points. These stretching parameters remain constant for varying numbers of time steps $N_0,\dots ,N_M$ approximating the Romberg sequence. Through numerical illustrations, we verify that repeated Richardson extrapolation can then be effectively employed, yielding high-order convergence. To the best of our knowledge, this is the first instance of achieving high-order option price convergence with trees, excluding the case of plain vanilla European options (see [35,36]). Our method is characterized by its simplicity and flexibility, and it can be extended to other options and models. We also address the well-known near-barrier problem, where the convergence speed of numerical methods is significantly dampened when the value of the spot price $S_0$ is near a barrier.

2. Description of the Model

First, we define the generalized Boyle trinomial model to be used. In each period in the Boyle trinomial model, the current stock price S changes to $Su$, $Sm$, $Sd$ with respective probabilities

$$p_u=\frac{md-M\left(m+d\right)+M^{2}V}{\left(u-d\right)\left(u-m\right)},p_d=\frac{um-M\left(m+u\right)+M^{2}V}{\left(u-d\right)\left(m-d\right)},p_m=1-p_u-p_d,$$

(1)

where

$$m=1,M=exp\left(rT/n\right),V=exp\left({\sigma }^{2}T/n\right).$$

In the generalized model the quantities u and d depend on S, as

$$u=e^{{\Delta }_u\left(S\right)\sqrt{\Delta t}},d=e^{-{\Delta }_d\left(S\right)\sqrt{\Delta t}},$$

where $\Delta t=T/n$ and ${\Delta }_u\left(S\right),{\Delta }_d\left(S\right)\ge \lambda \sigma$ for some $\lambda >1$.

In our case, let $A_1<$$\dots$$<A_F$ be the points that we want to be nodes in the tree. We call these points the fixed points. Then, we take

$${\Delta }_u\left(S\right)=\left\{\begin{array}{cccc}{\Delta }_0\hfill & & \mathrm{if}\hfill & S<A_1\hfill \\ {\Delta }_i\hfill & & \mathrm{if}\hfill & A_i\le S<A_{i+1},i=1,\dots ,F-1\hfill \\ {\Delta }_F\hfill & & \mathrm{if}\hfill & A_F\le S\hfill \end{array}\right.$$

and

$${\Delta }_d\left(S\right)=\left\{\begin{array}{cccc}{\Delta }_0\hfill & & \mathrm{if}\hfill & S\le A_1\hfill \\ {\Delta }_i\hfill & & \mathrm{if}\hfill & A_i<S\le A_{i+1},i=1,\dots ,F-1\hfill \\ {\Delta }_F\hfill & & \mathrm{if}\hfill & A_F<S\hfill \end{array}\right.$$

where the stretching parameters ${\Delta }_0,\dots ,{\Delta }_F$ are determined as follows:

• Set ${\Delta }_0={\Delta }_F=\lambda \sigma$ where $\lambda >1$.
• For $i=1,\dots ,F-1$, let $n_i$ be the smallest integer value of n such that

  $$\sqrt{n}\ge {\gamma }_i,\mathrm{where}{\gamma }_i=\frac{\lambda \sigma \sqrt{T}}{ln(A_{i+1}/A_i)}.$$
• Let

  $$\alpha ={\left(\sum _{i=1}^{F-1}\frac{ln(A_{i+1}/A_i)}{\lambda \sigma \sqrt{T}}\right)}^2.$$

  (2)
  Choose any integer number of time steps $N_0\ge max(\alpha ,n_1,...,n_{F-1})$, and for $i=1,\dots ,F-1$, set

  $${\Delta }_i=\frac{\lambda \sigma \sqrt{N_0}}{{\gamma }_i{\ell }_i}\mathrm{where}{\ell }_i=\mathrm{floor}(\sqrt{N_0}/{\gamma }_i)\ge 1.$$

  (3)

Now, we explain the choice of the ${\Delta }_i$ and the requirement that the number of time steps, $N_0$, is at least as large as $max(\alpha ,n_1,\dots ,n_{F-1})$. Note that the ${\Delta }_i$ depend on the choice of $N_0$. Note also that integer $n_i$ is the smallest integer n such that

$$A_{i+1}\ge A_i{e}^{\lambda \sigma \sqrt{T/n}}.$$

Our aim is to have all the $A_i$ as nodes, and we want the spacing between nodes in the log-space to be at least $\lambda \sigma \sqrt{T/N_0}$. Then, if $A_i$ is already a node and we want $A_{i+1}$ to be a node, then $N_0$ must be at least as large as $n_i$ and thus, n must be at least as large as $max(n_1,\dots ,n_{F-1})$. Next, since ${\ell }_i$ is the integer satisfying

$$A_i{e}^{{\ell }_i\lambda \sigma \sqrt{T/N_0}}\le A_{i+1}<A_i{e}^{({\ell }_i+1)\lambda \sigma \sqrt{T/N_0}},$$

we replace $\lambda \sigma$ by ${\Delta }_i$ in such a way that

$$A_{i+1}=A_i{e}^{{\ell }_i{\Delta }_i\sqrt{T/N_0}}.$$

The requirement that $N_0$ must be at least as large as $\alpha$ ensures that all the $A_i$ are nodes of the $N_0$-period tree, as demonstrated in Theorem 1 below. Furthermore, Theorem 1 proves that for any integer $k\ge 1$, if we increase the number of time steps from $N_0$ to $N_k=N_0{k}^2$, while maintaining the stretching parameters ${\Delta }_i$ unchanged, then the $A_i$ continue to be nodes of the $N_k$-period tree.

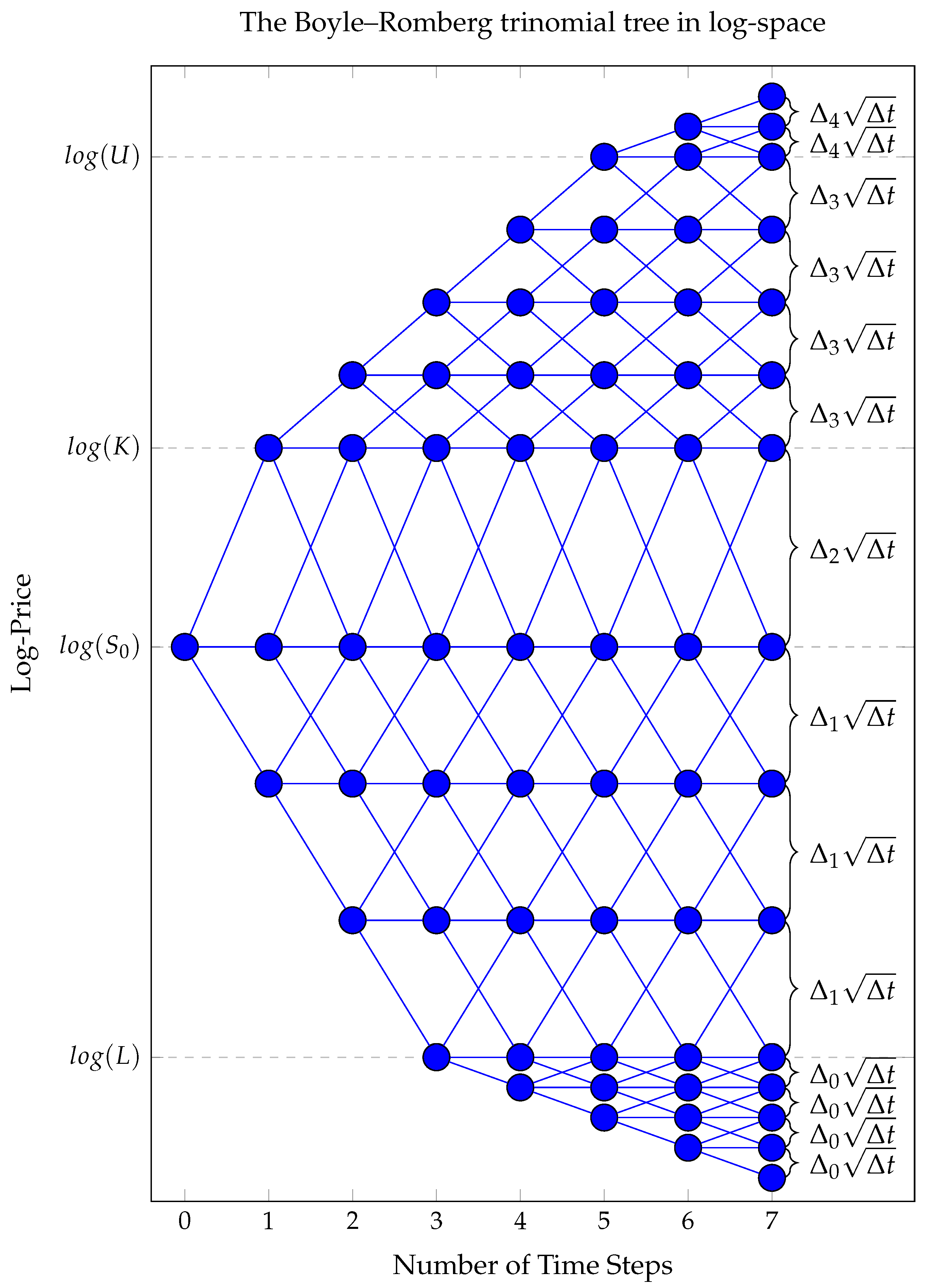
Observe that in the tree with $N_k$ time steps, the nodes smaller than $A_1$ can be expressed as $A_1{e}^{-j{\Delta }_0\sqrt{T/N_k}}$ for $j=1,2,\dots$. Those between $A_1$ and $A_F$ have the form $A_i{e}^{j{\Delta }_i\sqrt{T/N_k}}$ for $j=0,\dots ,{\ell }_{i}k$ or equivalently $A_{i+1}{e}^{-j{\Delta }_i\sqrt{T/N_k}}$ for $j=0,\dots ,{\ell }_{i}k$. Those larger than $A_F$ can be written as $A_F{e}^{j{\Delta }_F\sqrt{T/N_k}}$ for $j=1,2,\dots$. These points create a grid (not equally spaced), and the definition of $u,m$ and d ensures that each node connects to itself as well as its two immediate neighbors on the grid. Figure 1 illustrates the structure of the Boyle-Romberg tree.

We employ the Boyle–Romberg tree method in conjunction with repeated extrapolation techniques to achieve high efficiency. Typically, for such purposes, one would calculate the option price for varying numbers of time steps along the Romberg sequence $N_0,2N_0,\dots ,2^M{N}_0$. However, this approach would necessitate adjustments to the values of ${\Delta }_i$ for each time step. Since the coefficients in the price error expansion depend on the values of the ${\Delta }_i$, changing these values would hinder the applicability of repeated extrapolation because it requires those coefficients to remain constant.

Given the parameters $r,\sigma ,T,\lambda$ and the fixed points $A_1,\dots ,A_F$, we choose an initial number of time steps $N_0\ge max(\alpha ,n_1,\dots ,n_{F-1})$ and determine the stretching parameters ${\Delta }_1,\dots ,{\Delta }_F$ accordingly. With all parameters held constant, we compute the option prices $C_{N_0},\dots ,C_{N_M}$ for a various number of time steps $N_0,\dots ,N_M$ approximating the Romberg sequence. The $N_j$ are chosen to have the form $N_0{k}^2$ to ensures that the $A_i$ always remain nodes of the tree. The specific values of the $N_j$ and the repeated extrapolation procedure will be detailed in Section 3 below.

Theorem 1. 

Let integer $N_0\ge max(\alpha ,n_1,\dots ,n_{F-1})$. Consider the Boyle–Romberg tree starting at $S_0=A_q\in \{A_1,\dots ,A_F\}$ when the number of time steps is $n=N_0{k}^2$ for some integer $k\ge 1$ and the stretching parameters ${\Delta }_i$ are determined by $N_0$ as in Equation (3). Then, all of the values $A_1,\dots ,A_F$ are nodes in the n-period tree.

Proof. 

Recall that, when $n=N_0$, the number of up movements needed to reach $A_{i+1}$ starting from $A_i$ is ${\ell }_i$. Now let $N_k=N_0{k}^2$, and consider the tree with $N_k$ time steps. The number of up movements needed to reach $A_{i+1}$ starting from $A_i$ is ${\ell }_{i}k$ since

$$A_{i+1}=A_i{e}^{{\ell }_i{\Delta }_i\sqrt{T/N_0}}=A_i{e}^{{\ell }_{i}k{\Delta }_i\sqrt{T/N_k}}.$$

In the same manner, the number of down movements needed to reach $A_i$ starting from $A_{i+1}$ is ${\ell }_{i}k$. Since $S_0=A_q$, the node $A_F$ can be reached after ${\ell }_{q}k+$…$+{\ell }_{F-1}k$ up movements when starting from $S_0$. Analogously, the node $A_1$ can be reached after ${\ell }_{q-1}k+$…$+{\ell }_{1}k$ down movements when starting from $S_0$. Certainly, starting from $S_0$, fewer than $N_k$ movements are needed to reach any of the $A_i$ if

$$\sum _{i=1}^{F-1}{\ell }_{i}k\le N_0{k}^2.$$

This condition holds whenever

$$k\ge \frac{{\sum }_{i=1}^{F-1}{\ell }_i}{N_0}.$$

However,

$$\frac{{\sum }_{i=1}^{F-1}{\ell }_i}{N_0}\le \frac{{\sum }_{i=1}^{F-1}\frac{1}{{\gamma }_i}}{\sqrt{N_0}}=\frac{1}{\sqrt{N_0}}\sum _{i=1}^{F-1}\frac{ln(A_{i+1}/A_i)}{\lambda \sigma \sqrt{T}}\le 1,$$

because

$$N_0\ge \alpha ={\left(\sum _{i=1}^{F-1}\frac{ln(A_{i+1}/A_i)}{\lambda \sigma \sqrt{T}}\right)}^2.$$

Thus, the fixed points $A_1,\dots ,A_F$ are nodes in the $N_k$-period tree for any integer $k\ge 1$. □

2.1. Positivity of the Probabilities

In our generalized Boyle trinomial model, at each node S in the tree the probabilities are as in (1) with $u=e^{{\Delta }_u\left(S\right)\sqrt{\Delta t}}$, $d=e^{-{\Delta }_d\left(S\right)\sqrt{\Delta t}}$. Then,

$$\begin{array}{cc}\hfill p_u& =\frac{{\sigma }^2}{{\Delta }_u\left(S\right)({\Delta }_u\left(S\right)+{\Delta }_d\left(S\right))}+O\left(\sqrt{\Delta t}\right),\hfill \\ \hfill p_d& =\frac{{\sigma }^2}{{\Delta }_d\left(S\right)({\Delta }_u\left(S\right)+{\Delta }_d\left(S\right))}+O\left(\sqrt{\Delta t}\right),\hfill \\ \hfill p_m& =1-p_u-p_d=1-\frac{{\sigma }^2}{{\Delta }_u\left(S\right){\Delta }_d\left(S\right)}+O\left(\sqrt{\Delta t}\right).\hfill \end{array}$$

Because

$${\Delta }_u\left(S\right)\ge \lambda \sigma ,{\Delta }_d\left(S\right)\ge \lambda \sigma \mathrm{for}\mathrm{all}S,$$

for some $\lambda >1$, we see that for n large the three probabilities are positive.

2.2. Consistency with Black–Scholes Model

The probabilities $p_u$, $p_m$ and $p_d$ in (1) are defined so that

$$\begin{array}{cc}\hfill & p_u+p_m+p_d=1,p_{u}u+p_{m}m+p_{d}d=M=e^{r\Delta t},\hfill \\ \hfill & p_u{u}^2+p_m{m}^2+p_d{d}^2=M^{2}V=e^{(2r+{\sigma }^2)\Delta t}.\hfill \end{array}$$

Then, if $S_t$ is the stock price at the current node, and $S_{t+\Delta t}$ is the stock price at the end of the period,

$$\begin{array}{cc}\hfill E\left(S_{t+\Delta t}\right)& =p_u{S}_{t}u+p_m{S}_{t}m+p_d{S}_{t}d=S_t{e}^{r\Delta t},\hfill \\ \hfill E\left(S_{t+\Delta t}^2\right)& =p_u{S}_t{u}^2+p_m{S}_t{m}^2+p_d{S}_t{d}^2=S_t{e}^{(2r+{\sigma }^2)\Delta t}.\hfill \end{array}$$

Now, if $S_t$ satisfies $d{S}_t=r{S}_{t}dt+\sigma S_{t}d{W}_t$, as in the risk-neutral Black–Scholes model, then $log(S_{t+\Delta t}/S_t)$ is normally distributed with mean $(r-{\sigma }^2/2)\Delta t$ and variance ${\sigma }^2\Delta t$ so that

$$E\left(S_{t+\Delta t}\right)=S_t{e}^{r\Delta t},E\left(S_{t+\Delta t}^2\right)=S_t{e}^{(2r+{\sigma }^2)\Delta t}.$$

So, the generalized Boyle’s model matches the first and second moments of the risk neutral Black–Scholes model at any time $j\Delta t$ for $j=1,2,\dots ,n$. This happens regardless of how ${\Delta }_u$ and ${\Delta }_d$ are defined.

3. Repeated Extrapolation with an Approximate Romberg Sequence

Let K represent the strike price and S, the underlying asset’s price at expiration. Throughout this paper, we will use the term vanilla options to refer to options with payoff functions $max(S-K,0)$ for calls and $max(K-S,0)$ for puts. In contrast, digital options describe options with payoff functions $1_{[K,\infty )}\left(S\right)$ for calls and $1_{(-\infty ,K]}\left(S\right)$ for puts. Hence, in this paper, the terminology ’vanilla option’ and ’digital option’ precisely delineates two broad categories of options, encompassing sub-types like double knock-out vanilla call options, double knock-in digital put options, etc. This paper is mainly interested in double barrier vanilla options and double barrier digital options. The former are equipped with vanilla payoff functions, characterizing traditional options within the double barrier framework, with $max(S-K,0)$ for calls and $max(K-S,0)$ for puts. Conversely, the latter employ digital payoff functions, integrating the distinct binary outcome feature of digital options within the double barrier condition, with $1_{[K,\infty )}\left(S\right)$ for calls and $1_{(-\infty ,K]}\left(S\right)$ for puts.

Suppose we consider, for example, a double barrier call or put option with strike K, lower barrier L, and upper barrier U. Then, if, for instance, $S_0<K<U$, we would take $A_1=L<A_2=S_0<A_3=K<A_4=U$. For a single barrier call or put there would be $A_1<A_2<A_3$ and for a standard call or put there would be $A_1<A_2$.

Note that in our description above of the Boyle–Romberg tree, the choice of ${\Delta }_0$ and ${\Delta }_F$ is arbitrary, and we could have selected ${\Delta }_0={\Delta }_1$ and ${\Delta }_F={\Delta }_{F-1}$ instead of ${\Delta }_0=\lambda \sigma ={\Delta }_F$. In the case where $F=2$, this gives ${\Delta }_0={\Delta }_1={\Delta }_2$. This is Boyle’s model [3,4]. Then, for call options, the conjecture below follows from the Edgeworth expansions described in [2].

Conjecture 1. 

Consider vanilla and digital calls and puts, vanilla and digital single barriers calls and puts, and vanilla and digital double barrier calls and puts in the Black–Scholes world with interest rate r, volatility σ and maturity T. In the n-period Boyle–Romberg trinomial model, where $n=N_0{k}^2$ for integer $k=1,2,\dots$ there exist constants $c_1,c_2,\dots$ such that for all $M\ge 1$, the price $C_n$ calculated by this model satisfies

$$C_n=C_{BS}+\frac{c_1}{n^{{\gamma }_1}}+\frac{c_2}{n^{{\gamma }_2}}+\dots +\frac{c_M}{n^{{\gamma }_M}}+o\left(\frac{1}{n^{{\gamma }_M}}\right),$$

(4)

where ${\gamma }_j=\gamma +(j-1)\beta$ with $\gamma =1,\beta =1/2$ for vanilla options, and $\gamma =\beta =1/2$ for digital options. The constants $c_i$ depend only $r,\sigma ,T$, and the parameters of the trinomial tree, $\lambda ,A_1,\dots ,A_F,{\Delta }_0,\dots ,{\Delta }_F$.

Following Schmidt’s [37], we can re-write Equation (4) as

$$x\left(h\right)=z+c_1{h}^{{\gamma }_1}+c_2{h}^{{\gamma }_2}+\dots +c_M{h}^{{\gamma }_M}+o\left(h^{{\gamma }_M}\right),$$

(5)

where $z=C_{BS}$ and $h=1/n$. Schmidt has the parameter h run through a strictly decreasing sequence $h_0,$ $\dots ,$ $h_{M-1}$ such that $0<h_{i+1}\le b{h}_i$, where $0<b<1$. Then, he calculates two triangular arrays $x_{i,m}$, $y_{i,m}$, $m=0,\dots ,M-1$, $i=0,\dots ,M-m-1$, as follows. First, he calculates the first column of each array:

$$x_{i,0}=x\left(h_i\right),y_{i,0}=h_i^{\beta -\gamma },i=0,\dots ,M-1.$$

Then, he calculates the succeeding columns recursively. That is, for $m=1,\dots ,M-1$, he calculates

$$\begin{array}{cc}\hfill x_{i,m}& =x_{i+1,m-1}+\frac{x_{i+1,m-1}-x_{i,m-1}}{y_{i+1,m-1}{h}_i^{1/\beta }-y_{i,m-1}{h}_{i+m}^{1/\beta }}{y}_{i,m-1}{h}_{i+m}^{1/\beta },\hfill \\ \hfill y_{i,m}& =y_{i+1,m-1}+\frac{y_{i+1,m-1}-y_{i,m-1}}{h_i^{1/\beta }-h_{i+m}^{1/\beta }}{h}_{i+m}^{1/\beta },i=0,\dots ,M-m-1.\hfill \end{array}$$

Note that the y-array is used just to calculate the x-array. Schmidt shows the estimate

$$x_{i,m}=z+{\tilde{h}}_i^{{\gamma }_m}\frac{c_{m+1}+o\left(1\right)}{\left(\genfrac{}{}{0pt}{}{-\alpha }{m}\right)},$$

where $h_{i+m}<{\tilde{h}}_i<h_i$, $\alpha =\gamma /\beta$ and $\left(\genfrac{}{}{0pt}{}{-\alpha }{m}\right)={(-1)}^m\alpha (\alpha +1)\dots (\alpha +m-1)/m!$. In particular,

$$x_{0,M-1}=z+{\tilde{h}}_0^{{\gamma }_M}\frac{c_M+o\left(1\right)}{\left(\genfrac{}{}{0pt}{}{-\alpha }{M-1}\right)},$$

where $h_{M-1}<{\tilde{h}}_0<h_0$. Hence,

$$\left|x_{0,M-1}-z\right|\le h_0^{{\gamma }_M}\frac{|c_M|+o\left(1\right)}{|\left(\genfrac{}{}{0pt}{}{-\alpha }{M-1}\right)|}=O\left(h_0^{M/2+1/2}\right).$$

For the Boyle–Romberg tree, we set $x_{i,0}=C_{N_i}$, $z=C_{BS}$, and choose $h_i=1/N_i$, where $N_i=N_0{k}_i^2$, ensuring that the sequence $N_0,N_1,N_2,\dots$ approximates the Romberg sequence $N_0,2N_0,4N_0,\dots$. For this purpose, we set $\left(k_0,\dots ,k_4\right)=\left(1,\dots ,5\right)$, and for $i>4$ we choose $k_i$ to be the nearest integer to $2^{i/2}$. The first values of $k_i$ are: $1,2,3,4,5,6,8,11,16,23$. Certainly $\left|k_i-2^{i/2}\right|\le 1/2$ for $i>4$ and, therefore,

$$\frac{h_{i+1}}{h_i}={\left(\frac{k_i}{k_{i+1}}\right)}^2\le {\left(\frac{2^{i/2}+1/2}{2^{(i+1)/2}-1/2}\right)}^2\to \frac{1}{2}$$

as $i\to \infty$. It is easy to see that

$$\frac{h_{i+1}}{h_i}\le {\left(\frac{5}{6}\right)}^2$$

for all integer $i\ge 0$.

Remark 1. 

For a vanilla option, Equation (5) can be reformulated as:

$$x\left(h\right)=z+a_1{h}^1+a_2{h}^{3/2}+\dots +a_M{h}^{(M+1)/2}+o\left(h^{(M+1)/2}\right).$$

For a digital option, it simplifies to:

$$x\left(h\right)=z+a_1{h}^{1/2}+a_2{h}^1+\dots +a_M{h}^{M/2}+o\left(h^{M/2}\right).$$

The constants $a_i$ differ between the vanilla and digital cases. Note that, in Schmidt’s algorithm, when $\gamma =\beta$, the quantities $y_{i,m}$ are all equal to 1, making the algorithm identical to that described in [38,39].

4. Numerical Experiment

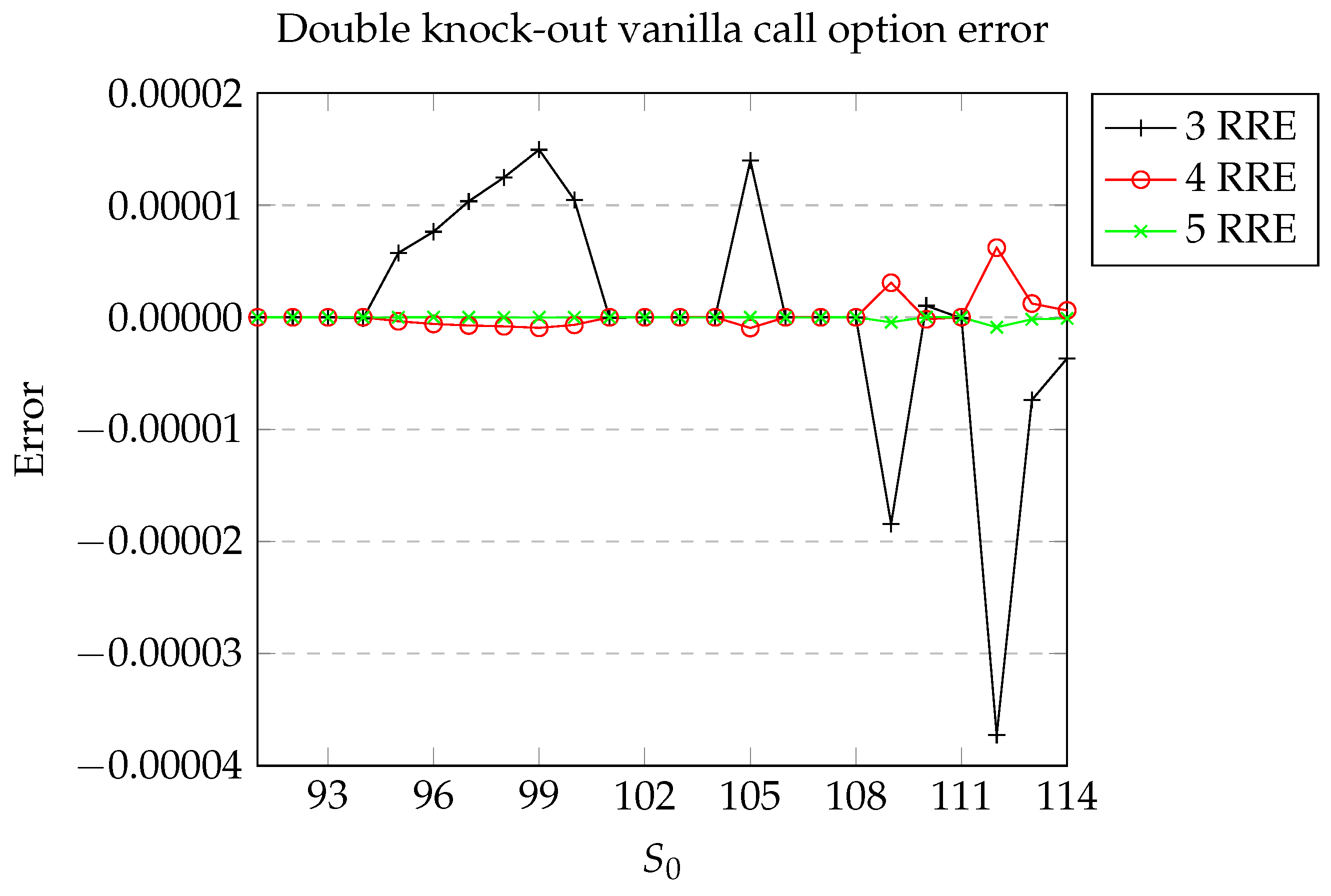
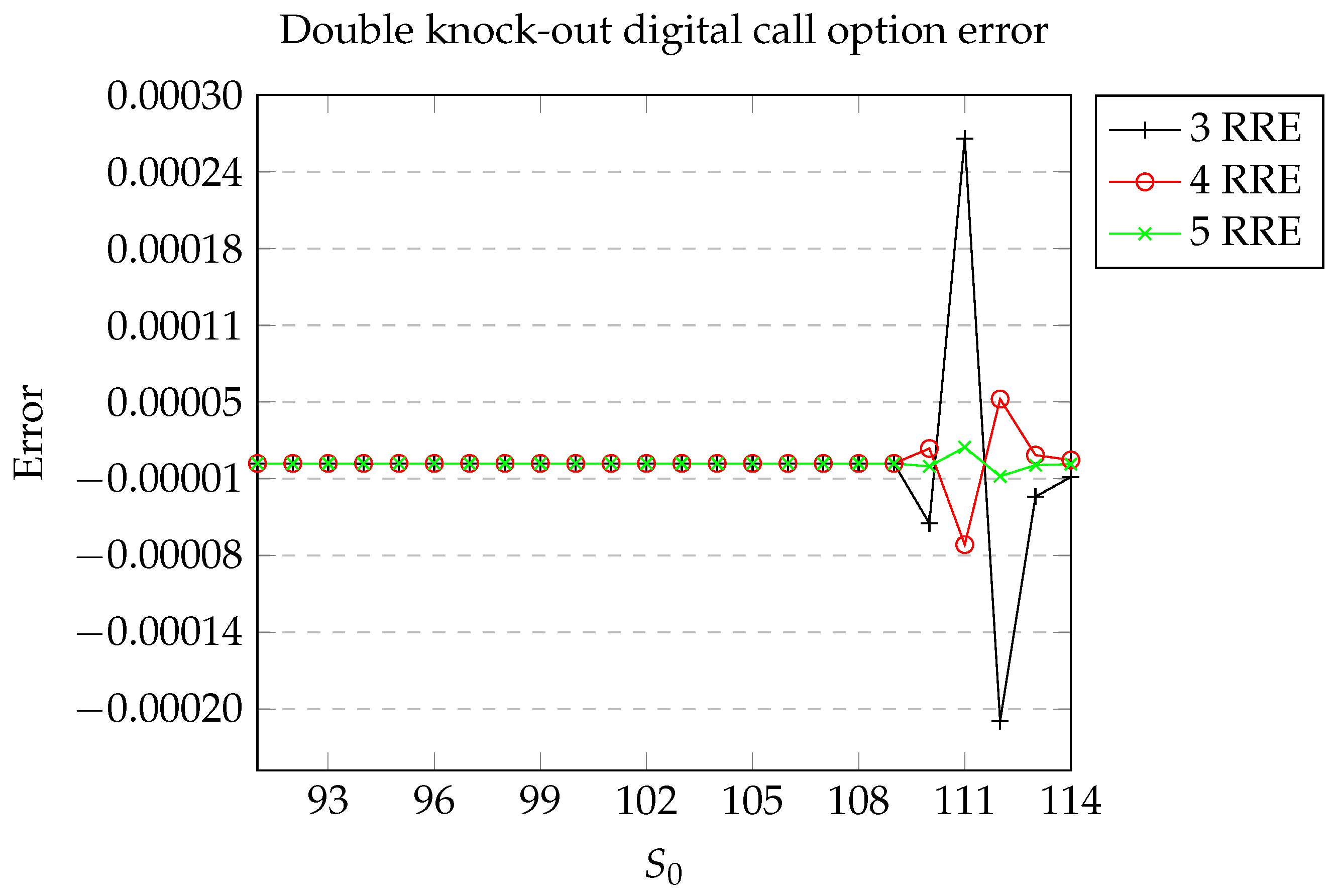
Here, we consider both a digital and a vanilla double knock-out call option with a strike $K=105$, lower barrier $L=90$, upper barrier $U=115$, risk-free rate $r=0.05$, volatility $\sigma =0.2$, and time to maturity $T=1$. We analyze the option price errors resulting from using the Boyle–Romberg trinomial tree, with values of $S_0$ ranging from 91 to 114. The number of time steps, $N_0$, is determined by $max(m_0,\alpha ,n_1,n_2,n_3)$, and the number of repeated extrapolations varies from 3 to 5. The value of $\lambda$ is set to $1.2$. For the vanilla option, we set a minimum of $m_0=25$ time steps, whereas for the digital option, a minimum of $m_0=100$ time steps is targeted.

Note that the case $N_0>m_0$ typically occurs when $S_0$ is near a barrier or the strike. Concretely, in our example, $N_0$ is as high as 30 when the distance between $S_0$ and $\{L,K,U\}$ is 5, it is as high as 42 when the distance is 4, 83 when it is 3, and, respectively, 188 and 756 for a distance of 2 and 1. In the other cases, $N_0=m_0$. The reason for this behavior is that $n_i\approx {(\lambda \sigma \sqrt{T}/ln(A_{i+1}/A_i))}^2$. Practically, this means that $N_0$ is proportional to the inverse of the square of the distance between $S_0$ and its closest fixed point neighbor in the log-space. Certainly, this makes the computations impracticable when $S_0$ is very close yet distinct from the strike or a barrier. This is the near strike/barrier problem, which we address in the next section.

We observe in Figure 2 that for certain values of $S_0$, the error is very small and nearly indistinguishable from the x-axis. The most significant errors are observed when $S_0=112$. In this case, $N_0=83$, and the errors are approximately $-3.7\times {10}^{-5}$, $6.2\times {10}^{-6}$, and $-8.9\times {10}^{-7}$ when the number of repeated extrapolations is 3, 4, and 5, respectively. These results are consistent with the findings of Schmidt [37] discussed earlier, where the errors are determined to be of magnitude $1/{83}^2$, $1/{83}^{2.5}$, and $1/{83}^3$, respectively, which is of magnitude approximately ${10}^{-4}$, ${10}^{-5}$, and ${10}^{-6}$. Unsurprisingly, the greater the number of extrapolations, the smaller the error. Implemented in C++, each computation is completed in a fraction of a second. In Figure 3, we illustrate the price error for the same option in the digital case. Furthermore, we specify a minimum of $m_0=100$ time steps. The behavior observed here corresponds to that reported in the vanilla case.

Remark 2. 

Typically, a double-precision floating-point number has a precision of approximately 15 to 17 decimal digits. It can naturally be assumed that a few dozen ordinary calculations would not significantly compromise this precision. However, in the specific case where $u=exp\left(\lambda \sigma \sqrt{\Delta t}\right)$, $d=exp(-\lambda \sigma \sqrt{\Delta t})$, $\lambda =1.10075$, $\sigma =0.2$, $r=0.05$, and $\Delta t=0.0001$, the computation of $p_m\approx 0.17$ using the formula $p_m=1-p_u-p_d$ or its equivalent

$$p_m=\frac{M(d+u)-du-M^{2}V}{(m-d)(u-m)},$$

yields results in C++ that differ by approximately $3\times {10}^{-10}$. We bear in mind that, as pointed out in [40], in the typical scenario of numerical approximations with finite decimal precision, the computation error tends to decrease until it reaches an optimal value, and then it starts to increase as the roundoff and condition errors dominate. Our calculations suggest that, for the Boyle–Romberg tree, the optimal error is typically of a magnitude of ${10}^{-9}$ to ${10}^{-11}$, depending on the values of the parameters. Near a barrier or the strike, this can sometimes slightly deteriorate to ${10}^{-8}$.

5. The Near Strike/Barrier Problem

It has long been observed that numerical methods for pricing barrier options often exhibit poor convergence speed when the spot price $S_0$ is in close proximity to a barrier. For a discussion on this topic, see [27], among others. In the trinomial tree described above, the minimal number of time steps required by the method, $N_0$, increases as $S_0$ approaches, yet remains distinct from a barrier or the strike price. Indeed, the minimum value of $N_0$ is given by $max(\alpha ,n_1,\dots ,n_{F-1})$, where

$$n_i\approx {\left(\frac{\lambda \sigma \sqrt{T}}{ln(A_{i+1}/A_i)}\right)}^2,\alpha ={\left(\sum _{i=1}^{F-1}\frac{ln(A_{i+1}/A_i)}{\lambda \sigma \sqrt{T}}\right)}^2\approx {\left(\sum _{i=1}^{F-1}\frac{1}{\sqrt{n_i}}\right)}^2\le F^2.$$

Given that $1<\lambda$ is an arbitrary constant, the term ${\lambda }^2{\sigma }^{2}T$ does not significantly contribute to the minimal value of $N_0$. For practical purposes, we assume that neither $L/U\approx 1$ nor $K/L\approx 1$ or $K/U\approx 1$ holds, unless K coincides with a barrier. The other cases are not considered very realistic. However, over the life of the option, the price of the underlying asset may become very close to a barrier or the strike, thereby causing a significant increase in the value of $N_0$, when the option’s price needs to be evaluated in such scenarios. This is known as the near barrier/strike problem. We explain here how to address this issue.

In the classical Boyle model and the Boyle–Romberg model introduced herein, an additional parameter, $\lambda >1$, is required for the construction of the tree. It can be observed that $\lambda$ should not be too close to 1, as otherwise, $p_m\approx 0$. Conversely, large values of $\lambda$ compromise the tree’s precision. Apart from these considerations, the value of $\lambda >1$ is arbitrary. Boyle obtained good results with $\lambda =1.2$, a value we have adopted in our calculations. Here, we confine our Boyle–Romberg tree to values of $\lambda$ in the interval $1.16\le \lambda <2$. This interval is chosen for a specific purpose: it ensures that probabilities ${\tilde{p}}_{i,d}$, ${\tilde{p}}_{i,m}$, and ${\tilde{p}}_{i,u}$ defined below are all greater than 0.

We assume that time steps $N_0,N_1,\dots ,N_M$ have been selected with a low or moderate value of $N_0\ge \alpha$, where $\alpha$ is as in (2). Let X be the strike price or one of the barriers. The problem to address here is that, when $S_0$ is very close to X, yet distinct from X, the number of time steps required to evaluate the option can become excessive. We assume that $S_0\ne X$ and, as we address the scenario where $S_0$ is near X, that the ratio $A_{i+1}/A_i$ is minimized for the pair $\{A_i,A_{i+1}\}=\{S_0,X\}$. Define $i_0$ such that $\{A_{i_0},A_{i_0+1}\}=\{S_0,X\}$, and let $q_i$ be the real number satisfying $X/S_0=exp\left(q_i\lambda \sigma \sqrt{\Delta t_i}\right)$, where $\Delta t_i=T/N_i$. We say that $S_0$ is near X if $\left|q_M\right|\le 0.5$. This means that, in the log-space with $N_M$ time steps, $log{S}_0$ is closer to $logX$ than any other node of the tree. Because $0<|q_0|<|q_1|<\dots <|q_M|$, the same is true for all $i=0,\dots ,M$.

In this definition, any $S_0$ that is very close to X will be considered near X. Conversely, if $S_0$ is not near X according to this definition, then $A_{i_0}exp\left(\lambda \sigma \sqrt{T/N_0^{*}}\right)\le A_{i_0+1}$, where $N_0^{*}=4N_M$. This leads to

$$\frac{\lambda \sigma \sqrt{T}}{ln(A_{i_0+1}/A_{i_0})}\le \sqrt{N_0^{*}},$$

resulting in $n_{i_0}\le N_0^{*}$. Given that $A_{i+1}/A_i$ is minimized for $A_{i_0+1}/A_{i_0}$, it follows that $n_i\le n_{i_0}$ for $i=1,\dots ,F-1$. Hence, the minimum number of time steps required to construct the Boyle–Romberg tree is $n_{i_0}\le N_0^{*}$. Considering that $N_0$ is either low or moderate, we regard the upper bound $N_0^{*}$ as not excessive, thereby enabling the application of the method described in Section 3. For instance, in the example treated earlier where the parameters are $\lambda =1.2$, $\sigma =0.2$, $K=105$, $L=90$, $U=115$, and $N_0=25$, seeking three repeated extrapolations results in a worst-case scenario of $N_0^{*}=1600$.

5.1. The Near Strike Case

Now suppose that $S_0$ is near the strike and $S_0\ne K$. To calculate the value of the option at $S_0$ and prevent the explosion of the minimal number of time steps $N_0$ when $S_0\to K$, we first construct a Boyle–Romberg trinomial tree, for which the root is set exactly at K. Then, we introduce a new root, $S_0$, which at time $\Delta t$ connects to the nodes $Kd$, K, and $Ku$ of this tree with specially defined probabilities ${\tilde{p}}_d$, ${\tilde{p}}_m$, and ${\tilde{p}}_u$, described below.

To be specific, for $i=0,\dots ,M$, we construct a Boyle–Romberg trinomial tree with $N_i$ time steps when the underlying asset value at time zero is equal to K, and we denote by $C_{N_i}\left(\Delta t_i,x\right)$ the option’s value calculated by this Boyle–Romberg trinomial tree at time $\Delta t_i=T/N_i$, when there are $N_i$ time steps and the underlying asset price is x. Recall that $N_i=N_0{k}_i^2$, where $k_i^2$ approximate the Romberg sequence. Then, the value $C_{N_i}\left(0,S_0\right)$ of the option at time zero, when the underlying asset value is $S_0$, is obtained as

$$C_{N_i}\left(0,S_0\right)=e^{-r\Delta t_i}E\left(C_{N_i}\left(\Delta t_i,S_{\Delta t_i}\right)\right),$$

where $S_{\Delta t_i}$ takes the values $S_0{\tilde{u}}_i$, $S_0{\tilde{m}}_i$, $S_0{\tilde{d}}_i$ with respective probabilities

$$\begin{array}{cc}\hfill {\tilde{p}}_{i,u}& =\frac{\tilde{m}{\tilde{d}}_i-M\left({\tilde{m}}_i+{\tilde{d}}_i\right)+M^{2}V}{\left({\tilde{u}}_i-{\tilde{d}}_i\right)\left({\tilde{u}}_i-{\tilde{m}}_i\right)},{\tilde{p}}_{i,d}=\frac{{\tilde{u}}_i{\tilde{m}}_i-M\left({\tilde{m}}_i+{\tilde{u}}_i\right)+M^{2}V}{\left({\tilde{u}}_i-{\tilde{d}}_i\right)\left({\tilde{m}}_i-{\tilde{d}}_i\right)},\hfill \\ \hfill {\tilde{p}}_{i,m}& =1-{\tilde{p}}_{i,u}-{\tilde{p}}_{i,d},\hfill \end{array}$$

where

$${\tilde{m}}_i=\frac{K}{S_0},{\tilde{d}}_i=\frac{K}{S_0}{e}^{-{\Delta }_d\left(K\right)\sqrt{\Delta t_i}},{\tilde{u}}_i=\frac{K}{S_0}{e}^{{\Delta }_u\left(K\right)\sqrt{\Delta t_i}}.$$

We suppose that an asymptotic expansion of $C_{N_i}(\Delta t_i,x)$ in powers of $1/\sqrt{N_i}$ exists. Note that in the framework of vanilla European options in Boyle’s model, this can be proved through the use of Edgeworth expansions as described in [2]. Specifically, the expansion is given by

$$C_{N_i}\left(\Delta t_i,x\right)=C_{BS}\left(\Delta t_i,x\right)+\sum _{k=1}^M\frac{a_k\left(\Delta t_i,x\right)}{{\sqrt{N_i}}^k}+o\left(\frac{1}{{\sqrt{N_i}}^M}\right),$$

where the coefficient $a_k\left(\Delta t_i,x\right)$ of $1/{\sqrt{N_i}}^k$ is an infinitely differentiable function of $\left(\Delta t_i,x\right)$ for which a Taylor expansion exists around any point $\left(\Delta t_i,x\right)$ such that $0\le \Delta t_i<T$ and $0<x$. Furthermore, for double barrier vanilla options, $a_1\left(\Delta t_i,x\right)=0$. The o-term is also assumed to be valid uniformly over closed bounded subsets of these intervals. Let $a_0\left(\Delta t_i,x\right)=C_{BS}\left(\Delta t_i,x\right)$. Taking the Taylor expansions of the functions $a_k(\Delta t_i,x)$ around the point $(0,S_0)$ and collecting like terms, we obtain a sum of terms of the form

$$\frac{b_{j,\ell }}{{\sqrt{N_i}}^{\ell }}{(x-S_0)}^j,$$

where $b_{j,\ell }$ is a constant depending only on $\lambda ,r,\sigma ,T,A_1,\dots ,A_F$ and ${\Delta }_0,\dots ,{\Delta }_F$. Note that $b_{0,0}=C_{BS}(0,S_0)$. Then $C_{N_i}\left(0,S_0\right)$ is a weighted sum of expectations of the form

$$e^{-r\Delta t_i}E\left({\left(S_{\Delta t_i}-S_0\right)}^j\right)/{\sqrt{N_i}}^{\ell },$$

plus the o-term. Note that, for double barrier vanilla options, $\ell \ne 1$. Additionally, since all components of these expectations have expansions in powers of $1/\sqrt{N_i}$, with constant coefficients, it is clear that the same holds true for $C_{N_i}(0,S_0)$.

In order to use Schmidt’s algorithm for repeated extrapolation as described above, we need to show that, for double barrier vanilla options, the smallest non-zero power of $1/\sqrt{N_i}$ in the expansion of $C_{N_i}(0,S_0)$ is $1/N_i$. Since $S_{\Delta t_i}-S_0=O\left(\sqrt{\Delta t_i}\right)$, we only need to consider the term $e^{-r\Delta t_i}E(S_{\Delta t_i}-S_0)$. However, risk neutrality gives

$$e^{-r\Delta t_i}E\left(S_{\Delta t_i}-S_0\right)=S_0\left(1-e^{-r\Delta t_i}\right)=O\left(\Delta t_i\right),$$

as wanted.

It remains to prove the positivity of the probabilities ${\tilde{p}}_{i,d}$, ${\tilde{p}}_{i,m}$, and ${\tilde{p}}_{i,u}$. Note that ${\Delta }_i=\lambda \sigma +O\left(\sqrt{\Delta t_0}\right)$ and recall that $1.16\le \lambda <2$ and $K/S_0=e^{q_i\lambda \sigma \sqrt{\Delta t_i}}$ with $|q_i|\le 1/2$. Then, it is easy to see that

$$\begin{array}{cc}\hfill {\tilde{p}}_{i,u}& ={\displaystyle \frac{q_i^2{\lambda }^2-q_i{\lambda }^2+1}{2{\lambda }^2}}+O\left(\sqrt{\Delta t_0}\right),{\tilde{p}}_{i,d}={\displaystyle \frac{q_i^2{\lambda }^2+q_i{\lambda }^2+1}{2{\lambda }^2}}+O\left(\sqrt{\Delta t_0}\right),\hfill \\ \hfill {\tilde{p}}_{i,m}& =1-q_i^2-\frac{1}{{\lambda }^2}+O\left(\sqrt{\Delta t_0}\right).\hfill \end{array}$$

Suppose that $q_i\ge 0$. The case $q_i<0$ follows by symmetry. We can see that $q_i^2{\lambda }^2-q_i{\lambda }^2+1>0$ for every value of $q_i$ unless ${\lambda }^2-4\ge 0$. However, the requirement $1.16\le \lambda <2$ guarantees that this cannot happen. Next, $q^2{\lambda }^2+q{\lambda }^2+1>0$, because $q_i,\lambda \ge 0$. Finally, $1-q_i^2-1/{\lambda }^2>0$ providing that $\left|q_i\right|<\sqrt{1-1/{\lambda }^2}$. However, this always holds since $1.16\le \lambda$ and $\left|q_i\right|\le 0.5$. Thus, when $\Delta t_0$ is sufficiently small, ${\tilde{p}}_{i,d}$, ${\tilde{p}}_{i,m}$, and ${\tilde{p}}_{i,u}$ are all greater than 0, as desired.

In

Table 1. Error near the strike for double knock-out vanilla and digital call options.

Option Type	RRE$\setminus {\mathit{S}}_0$	104.9	104.99	104.999	105.001	105.01	105.1
Vanilla	3	1.4 × 10−5	1.4 × 10−5	1.4 × 10−5	1.4 × 10−5	1.4 × 10−5	1.4 × 10−5
	4	−9.4 × 10−7	−9.5 × 10−7	−9.5 × 10−7	−9.5 × 10−7	−9.5 × 10−7	−9.7 × 10−7
	5	4.8 × 10−7	8.7 × 10−9	8.7 × 10−9	8.7 × 10−9	8.7 × 10−9	−2.0 × 10−9
Digital	3	−6.6 × 10−8	−6.9 × 10−8	−6.9 × 10−8	−7.3 × 10−8	−6.9 × 10−8	−6.9 × 10−8
	4	3.9 × 10−9	7.7 × 10−10	7.7 × 10−10	−2.4 × 10−9	7.7 × 10−10	7.7 × 10−10
	5	3.4 × 10−9	2.6 × 10−10	2.5 × 10−10	−2.9 × 10−9	2.5 × 10−10	2.5 × 10−10

Here, $L=90$, $U=115$, $K=105$, $r=0.05$, $\sigma =0.2$, and $T=1$. We report the error of the Boyle–Romberg trinomial tree with $\lambda =1.2$ against the BS price for various values of $S_0$ near the barrier. For the vanilla option, we use $N_0=25$ time steps, and for the digital option, we use $N_0=100$ time steps. We consider three, four, and five repeated Richardson extrapolations (RRE).

, we analyze a double knock-out vanilla call option and a double knock-out digital call option, respectively, reporting the error of the Boyle–Romberg tree method against the Black–Scholes model when $S_0$ approaches the strike. We use $N_0=25$ time steps for the vanilla option and $N_0=100$ time steps for the digital option, with different RRE counts ranging from 3 to 5. All calculations were completed in a fraction of a second.

5.2. The Near Barrier Case

Now, let X be a barrier and assume that $S_0$ is near X. For the purpose of this section, consider that $N_i=2^i{N}_0$. The method described above may not work very well because the Taylor expansions may not be valid across the barrier. However, the price can still be efficiently calculated as described below. For simplicity, we will suppose that $X=L$, as the case $X=U$ can be treated in an analogous manner.

We wish to use the Boyle–Romberg tree with $N_0$ time steps and $M\ge 1$ repeated extrapolations. First, we construct a Boyle–Romberg trinomial tree with $N_0$ time steps, setting the root of the tree at X. We denote by $X_{N_0}$ the immediate upper neighbor of X in this tree. We utilize the Boyle–Romberg trinomial tree with ${\mathcal{R}}_0$ repeated extrapolations to estimate the barrier option’s price $C_{BS}\left(X_{N_0}\right)$ when the underlying asset price is $X_{N_0}$. Note that the error in Schmidt’s algorithm is $O(\Delta t_0^{({\mathcal{R}}_0+1)/2})$. Therefore, we choose ${\mathcal{R}}_0$ to be the smallest integer such that $\Delta t_0^{({\mathcal{R}}_0+1)/2}\le \epsilon$, where $\epsilon$ is a specified precision level. We then repeat this procedure, substituting $N_0$ with $N_1,N_2,\dots$, thereby obtaining option prices $C_{BS}\left(X_{N_i}\right)$ corresponding to the spot prices $X_{N_i}$, for $i=0,\dots ,M$. However, when calculating $C_{BS}\left(X_{N_i}\right)$, we reduce the number of repeated extrapolations from ${\mathcal{R}}_0$ to ${\mathcal{R}}_i$. Here, ${\mathcal{R}}_i$ is defined as the smallest integer such that $\Delta t_i^{({\mathcal{R}}_i+1)/2}\le \epsilon$. Finally, we utilize Schmidt’s algorithm to calculate $C_{BS}\left(S_0\right)$, setting ${\gamma }_i=i$, $h_i=ln(X_{N_i}/X)-ln(S_0/X)$, and $x\left(h_i\right)=C_{BS}(0,X_{N_i})$, for $i=0,\dots ,M$. Observe that

$$ln(X_{N_i}/X)={\Delta }_u\left(X\right)\sqrt{\Delta t_i}=\lambda \sigma \sqrt{\Delta t_i}+O(\Delta t_0).$$

It is not difficult to see that

$$\frac{h_{i+1}}{h_i}\le \sqrt{\frac{\Delta t_{i+1}}{\Delta t_i}}+O(\Delta t_0)\le \sqrt{\frac{1}{2}}+O(\Delta t_0)<1,$$

for $N_0$ sufficiently large, justifying the use of Schmidt’s method.

In this context, we select $\epsilon ={10}^{-10}$ as our precision level, since it approximates the reliable precision of machine calculations and is sufficiently precise for our purposes. In

Table 2. Error near the barriers for double knock-out vanilla and digital call options.

Option Type	RRE$\setminus {\mathit{S}}_0$	90.1	90.01	90.001	114.9	114.99	114.999
Vanilla	3	−2.4 × 10−5	−2.8 × 10−5	−2.8 × 10−5	−2.5 × 10−5	−2.7 × 10−5	−2.7 × 10−5
	4	1.1 × 10−6	1.4 × 10−6	1.4 × 10−6	3.3 × 10−6	3.8 × 10−6	3.9 × 10−6
	5	−7.0 × 10−9	−7.6 × 10−9	−7.6 × 10−9	8.7 × 10−9	1.1 × 10−8	1.1 × 10−8
Digital	3	−3.0 × 10−7	−2.9 × 10−7	−2.2 × 10−7	1.9 × 10−8	2.6 × 10−8	2.7 × 10−8
	4	3.1 × 10−8	3.0 × 10−8	4.9 × 10−8	1.7 × 10−8	2.4 × 10−8	2.4 × 10−8
	5	4.6 × 10−8	4.2 × 10−8	1.8 × 10−7	−1.8 × 10−9	−1.9 × 10−9	−1.9 × 10−9

Here, $L=90$, $U=115$, $K=105$, $r=0.05$, $\sigma =0.2$, and $T=1$. We report the error of the Boyle–Romberg trinomial tree with $\lambda =1.2$ against the BS price for various values of $S_0$ near the barrier. For the vanilla option, we use $N_0=25$ time steps, and for the digital option, we use $N_0=100$ time steps. We consider three, four, and five repeated Richardson extrapolations (RRE).

, we respectively analyze a double knock-out vanilla call option and a double knock-out digital call option, comparing the price of the Boyle–Romberg tree method with the Black–Scholes price when $S_0$ approaches the barriers. All calculations were executed in a fraction of a second.

6. Conclusions

In this paper, we introduce the Boyle–Romberg trinomial tree, a new tree with the property that, throughout the entire life of the option and for various numbers of time steps, nodes can be precisely located at the points where the payoff function or its derivatives exhibit discontinuities, providing that there are finitely many of these discontinuities. This characteristic effectively eliminates the oscillations of the convergence commonly associated with tree methods, thus allowing repeated extrapolation. In the case of double barrier option valuation in the Black–Scholes model, a subject of several recent publications, we have empirically demonstrated that option prices computed using our tree can be highly efficient when used in conjunction with Schmidt’s algorithm for repeated extrapolation. This is significant because it is a key component for achieving arbitrarily fast convergence, a feature that, until now, had been realized with tree methods only in the case of European vanilla options. Our tree method is simple and can readily be adapted to other models and options. Our future work will focus on exploring this potential, aiming to harness the inherent efficiency and simplicity of our tree in a variety of models and options.