Hybrid Sine Cosine and Particle Swarm Optimization Algorithm for High-Dimensional Global Optimization Problem and Its Application

Abstract

Particle Swarm Optimization (PSO) is facing more challenges in solving high-dimensional global optimization problems. In order to overcome this difficulty, this paper proposes a novel PSO variant of the hybrid Sine Cosine Algorithm (SCA) strategy, named Velocity Four Sine Cosine Particle Swarm Optimization (VFSCPSO). The introduction of the SCA strategy in the velocity formulation ensures that the global optimal solution is found accurately. It increases the flexibility of PSO. A series of experiments are conducted on the CEC2005 test suite with compositional algorithms, algorithmic variants, and good intelligent algorithms. The experimental results show that the algorithm effectively improves the overall performance of compositional algorithms; the Friedman test proves that the algorithm has good competitiveness. The algorithm also performs better in PID parameter tuning. Therefore, the VFSCPSO is able to solve the high-dimensional global optimization problems in a better way.

1. Introduction

Over the past half century, human beings have taken inspiration from biological behavior and natural phenomena and proposed a variety of intelligent algorithms. Intelligent algorithms have been deeply applied in different fields. Intelligent algorithms show better global search capability and adaptability. These algorithms are able to adapt more successfully to a variety of optimization problems and overcome many limitations of traditional optimization algorithms. Therefore, intelligent algorithms outperform traditional optimization algorithms in many optimization problems, making them more effective and feasible choices.

Intelligent algorithms can be roughly divided into the following four types according to different classification standards: Firstly, evolutionary algorithms are a class of intelligent algorithms proposed by modeling the substantive abstraction of evolutionary law, these include Genetic Algorithm (GA) [1], Differential Evolution (DE) [2], Dandelion Optimizer (DO) [3], and Biogeography-Based Optimization (BBO) [4]. Secondly, swarm intelligent optimization algorithms are a class of intelligent algorithms that integrates the characteristics of biological groups into the solution of optimization problems, and include Particle Swarm Optimization (PSO) [5], Shuffled Frog Leaping Algorithm (SFLA) [6], Firefly Algorithm (FA) [7], Mayfly Algorithm (MA) [8], and Peafowl Optimization Algorithm (POA) [9]. Thirdly, physics-based algorithms are a class of intelligent algorithms formed by introducing the laws of nature into the solution of optimization problems, these include the Simulated Annealing (SA) [10] algorithm and the Sine Cosine Algorithm (SCA) [11]. Fourth, human-based algorithms are a class of intelligent algorithms that introduces human behavior characteristics, such as Student Psychology-Based Optimization (SPBO) [12] and the Optical Microscope Algorithm (OMA) [13].

PSO [14] is an optimization technique based on evolution and iteration, and the algorithm is used in various fields to solve real optimization problems, such as path planning problems [15], parameter identification problems [16], image processing problems [17], biomedical technologies problems [18], and other optimization problems. The advantages of PSO can be found mainly in the following four aspects. Firstly, the PSO emulates the characteristics of biological behavior, its theory and structure are relatively simple, the number of control parameters are few so that a large number of parameters do not need to be adjusted, and it is relatively easy to adjust the parameters according to the optimization problems [19]. Secondly, PSO has a strong global search ability, through cooperation and information sharing it can search for potential optimal solutions quickly in a wide scope and help the algorithm to approach the global optimal solution. Thirdly, PSO does not rely on the objective function’s gradient information, so it has certain advantages in solving complex optimization problems, and it is more flexible than traditional optimization algorithms and can solve large-scale problems. Fourthly, PSO performs well in dealing with continuous optimization problems and usually finds high-quality solutions. Based on the above discussion, we can find that PSO has more obvious advantages than other intelligent algorithms in solving high-dimensional optimization problems. Therefore, based on the unique advantages of PSO, we opt to employ PSO in order to obtain the effective resolution of high-dimensional optimization problems.

Similar to other intelligent algorithms, PSO has some disadvantages, such as a slow convergence velocity, premature convergence, and falling into local optima. Researchers have carried out many improvements. Among the current inertia weight selection strategies, the most popular one is still that of Shi et al. [20], who proposed a linear dynamic decreasing inertia weight strategy, which increases the exploration and exploitation capability in the process of evolution. Liu et al. [21] proposed Adaptive Weighted Particle Swarm Optimization (AWPSO) to improve the convergence velocity of the algorithm. Ahmed et al. [22] proposed a novel tracking technique based on Self-Tuning Particle Swarm Optimization (ST-PSO). This method maximizes power output from the power generated by a proton-exchange membrane fuel cell. Zhang et al. [23] proposed a corrective strategy, combining the characteristics of two strategies to propose Particle Swarm Optimization with Self-Corrective and Dimension-by-Dimension Learning Capabilities (SCDLPSO), which is more competitive in different dimensional optimization problems. Xue et al. [24] gave a strategy pool consisting of four strategies in solving high-dimensional feature selection problems. In addition, the introduction of other intelligent algorithm’s features can result in hybrid algorithms with better performance: Kaseb et al. [25] added the crossover and mutation operators of GA to PSO, which further balanced the exploration and exploitation capability of the algorithm, and improved its ability to deal with wind conditions in cities. Shams et al. [26] proposed a hybrid Dipper-Throated Optimization and Particle Swarm Optimization (DTPSO), combining the advantages of the Dipper-Throated Optimization algorithm and PSO for hepatocellular carcinoma prediction. Despite the existence of a large number of improvement studies, there is still space for the PSO [27] to enhance its overall performance, and improving the shortcomings of the PSO [28] while maintaining its advantages still requires further work by researchers. Although PSO performs well on many problems, it still has some limitations, such as easily falling into local optimal solutions and its slow convergence velocity. Meanwhile, different optimization problems have different characteristics and requirements, the PSO variant applicable to a certain problem may not be applicable to other problems, and cannot satisfy a broader range of application scenarios. Making improvements to PSO can not only increase the overall performance of the algorithm, but also adapt it to new research trends and requirements. Therefore, although the classical PSO method has many types of variants, it still has many aspects that can be improved and optimized. The improvement of PSO is still an important research direction, which can promote algorithmic innovation and development, and bring new ideas to the field of optimization algorithms.

SCA is an optimization technique based on objective laws, the algorithm performs a search based on the circular properties of the sine–cosine function, which can be applied to engineering design optimization problems [29], neural network problems [30], path planning problems [31], and others. SCA has the following three obvious advantages. Firstly, SCA can make full use of the circular property of the sine–cosine function in order to balance the exploration and exploitation capability of the algorithm and make the algorithm have better overall performance. Secondly, SCA does not rely on gradient information [32] and has a wide range of applicability. Thirdly, SCA has fewer adjustment parameters, which reduces the tedious work of tuning parameters and makes the algorithm more convenient to use. SCA performs well in many optimization problems. As the complexity of the optimization problem increases, it may take more time to find the optimal solution. Researchers have made improvements to SCA. Zhou et al. [33] used Gaussian mutation to increase the diversity of SCA, and the proposed FGSCA became a powerful tool. Ma et al. [34] used a nonlinear strategy and added a hill-climbing strategy in the local search part. The ISCA optimized the learning rate of GRU and the number of hidden layer neurons to further accurately predict the storage and utilization of solar energy by photovoltaic power generation. Hamad et al. [35] proposed QLESCA, which is an algorithm that has obtained superior fitness values. Although SCA has shown excellent performance in many optimization problems, as the complexity of optimization problems increases, more computer resources may be required to find the best strategy. Based on the aforementioned advantages, we selected SCA as our hybrid algorithmic strategy.

Most of the current intelligent algorithms cannot effectively solve large-scale problems [36]. Hence, enhancing the capability of intelligent algorithms to tackle high-dimensional global optimization problems [37] is a highly valuable research area. Problems with more than 100 dimensions are considered high-dimensional optimization problems. These include large-scale problems. Large-scale problems are abstracted from complex real-world optimization problems and have gradually become a hot research topic in optimization problems. As the number of decision variables increases, the computational complexity of calculating the objective function value and constraint increases dramatically, making the solution more difficult. The solution space of such a problem is very large and contains a massive number of potential solutions, but only a small portion of them are feasible and meaningful. At this point, it is easy to fall into local optimal solutions, and efficient algorithms are required for global search. Xu et al. [38] constructed a pool of selection strategies from PSO variants and deduced new PSO strategy sets. The algorithm was found to ultimately improve the overall performance of PSO in solving large-scale problems. Wang et al. [39] proposed a PSO based on a reinforcement learning layer, which adopts a hierarchical number-controlled reinforcement learning strategy and introduces a level competition mechanism, which effectively improves the PSO convergence in large-scale problems. Yi et al. [40] improved a GA variant to achieve good performance in large-scale problems based on human electroencephalography signal processing. The complexity of the problems faced by human beings is increasing. The algorithms in the above studies show some improvement in performance for solving large-scale problems, but can only solve problems with at most a thousand dimensions. Solving large-scale problems is a challenging task that requires a combination of knowledge, a suitable algorithm, and computational resource to obtain a feasible solution. Therefore, in this context, it is still necessary to improve the existing intelligent algorithms to solve high-dimensional global optimization problems.

With the increasing degree of automation, the real-life requirements for motor control are also increasing. Servo motor systems usually choose a PID controller as the executor to adjust the behavior of the entire system by tuning parameters. Since Ziegler and Nichols proposed the Ziegler–Nichols rectification method [41] in 1942, many classical parameter rectification methods have emerged. Selecting appropriate PID parameters is a critical step in the control process, and PID controllers based on intelligent algorithms can play an important role after parameter tuning. Most of the intelligent algorithms are suitable for optimizing the PID controller parameters of servo motors, helping the PID controller to determine the optimal parameter and significantly improving the performance of the whole control system. GA finds the best parameter combinations by selecting and mutating between different PID parameter sets [42] in order to minimize the performance metrics, such as system errors or vibrations, and thus, the system exhibits a good response characteristic. SA [43] discovers more appropriate PID parameters by progressively decreasing the probability of accepting a worse solution in the search solution space. The improved FA [44] self-tunes the PID parameters by introducing inertia weights and tuning factors, which ultimately improves the capability of the PID controller. While the application of intelligent algorithms in PID parameter tuning is relatively mature, this problem has not been perfectly solved. There is still room for further enhancement of this application with improved intelligent algorithms.

Over the past three decades, PSO has continuously enriched its theoretical material. Although PSO has been widely used in different fields, most of the PSO variants can only solve global optimization problems, but relatively little research has been carried out in the field of high-dimensional problems, especially large-scale problems, and a large number of complex optimization problems need to be solved urgently nowadays. Existing PSO variants are not able to solve them efficiently. SCA is a novel intelligent algorithm, introducing the advantages of SCA into PSO, which can open up more possibilities in the field of optimization. The obtained hybrid algorithm has better performance and solves optimization problem in a more efficient way. PSO suffers from the disadvantage of a worse local search ability, and SCA suffers from the disadvantage of the lower stability of the algorithm and lower adaptability in high-dimensional environments. Although there has been a great deal of research, there is no best algorithm, only better ones. In order to cope with this challenge, this paper proposes a new method, the Velocity Four Sine Cosine Particle Swarm Optimization (VFSCPSO) algorithm. VFSCPSO introduces the influence of SCA strategy on the basis of PSO. This new algorithm has high optimization accuracy and stability, effectively solving optimization problems. The primary contributions of this paper are summarized as follows:

• A new SCA strategy is proposed, this strategy is highly flexible by regulating the search range through the periodic variation of the sine–cosine function.
• A novel framework of PSO is proposed, which is more efficient than the original PSO algorithm. Meanwhile, VFSCPSO does not increase the computational complexity compared to PSO.
• The ductability of VFSCPSO in solving large-scale problems is verified through 10,000-dimensional numerical experiments on the CEC2005 test suite. The robustness of VFSCPSO in the PID parameter-tuning problem is verified through simulation experiments.

The rest of this paper is summarized as follows. Section 2 provides preliminary knowledge of the standard PSO and SCA. Section 3 presents the VFSCPSO and analyzes its complexity. Section 4 comprises the experiments and analysis. Finally, the conclusions are presented in Section 5.

2. Standard PSO and SCA

2.1. Particle Swarm Optimization (PSO)

In 1995, Eberhart and Kennedy collaborated to propose PSO, which is a swarm intelligence algorithm that abstracts the foraging behavior of bird communities into a mathematical model. In the standard PSO [45], a set of random solutions is first obtained by assuming that there a total of N particles, and the information of particle i is represented as a D-dimensional vector, where the position $x_i$ of particle i can be denoted as $x={(x_{i1},x_{i2},\dots ,x_{iD})}^T$, the velocity can be denoted $v_i$ as $v={(v_{i1},v_{i2},\dots ,v_{iD})}^T$, the individual extreme position can be denoted as $pbes{t}_i={(pbes{t}_1,pbes{t}_2,\dots ,pbes{t}_N)}^T$, and the global extreme position of the population can be denoted as $gbest$, and the formula for updating the velocity and position of the particle i in the ($k+1$)th iteration is denoted as

$$v_{id}^{k+1}=w{v}_{id}^k+c_1{r}_1\left(pbes{t}_i^k-x_{id}^k\right)+c_2{r}_2\left(gbes{t}^k-x_{id}^k\right)$$

(1)

The velocity update formula Equation (1) is one of the core formulas of the standard PSO. Where w is the inertia weight, this parameter maintains the motion inertia of the particle and reflects the degree of inheritance of the origin velocity. When the kth iteration is performed, $v_{id}$ denotes the velocity of particle i in the dth dimension of the search space; $x_{id}$ denotes the position of particle i in the dth dimension of the search space; $pbes{t}_i$ denotes the individual extreme position of particle i; $gbest$ denotes the global extreme position of the whole population. $c_1$ and $c_2$ are the learning factors, and $r_1$ and $r_2$ are random numbers between $[0,1]$.

$$x_{id}^{k+1}=x_{id}^k+v_{id}^{k+1}$$

(2)

From the other core formula of the PSO, Equation (2), the position equation consists of two key components. The first part is the position $x_{id}$ of particle i, corresponding to the candidate solution when the kth iteration is performed; the second part determines the adjustment of the position of particle i when the ($k+1$)th iteration is performed, i.e., the direction of particle i’s motion $v_{id}$. The two parts interact with each other to ultimately determine the position of the particle to select the solution when the ($k+1$)th iteration is performed. The formula for the velocity and position boundary conditions of particle i in the ($k+1$)th iteration is denoted as

$$v_i^k=\left\{\begin{array}{cc}{v}_i^k,\hfill & v_{min}\le v_i^k\le v_{max}\hfill \\ v_{max},\hfill & v_i^k>v_{max}\hfill \\ v_{min},\hfill & v_i^k<v_{min}\hfill \end{array}\right.$$

(3)

$$x_i^k=\left\{\begin{array}{cc}{x}_i^k,\hfill & x_{min}\le x_i^k\le x_{max}\hfill \\ x_{max},\hfill & x_i^k>x_{max}\hfill \\ x_{min},\hfill & x_i^k<x_{min}\hfill \end{array}\right.$$

(4)

In Equations (3) and (4), before updating the position of particle i at the kth iteration, it is judged whether the current velocity within the given velocity range is exceeded. If it is, the current velocity is replaced by the velocity boundary value. The same is true for the judgment of the current position pair. The boundary conditions are used to improve the particle searching ability and efficiency, to avoid the population dispersion caused by the particles jumping out of the searching range. The individual, global position update formula is denoted as

$$pbes{t}_i^{k+1}=\left\{\begin{array}{cc}pbes{t}_i^k,\hfill & f\left(x_i^k\right)\le f\left(pbes{t}_i^k\right)\hfill \\ x_i^{k+1},\hfill & f\left(x_i^k\right)>f\left(pbes{t}_i^k\right)\hfill \end{array}\right.$$

(5)

$$gbes{t}^{k+1}=\left\{\begin{array}{cc}gbes{t}^k,\hfill & f\left(pbes{t}_i^k\right)\le f\left(gbes{t}^k\right)\hfill \\ pbes{t}_i^k,\hfill & f\left(pbes{t}_i^k\right)>f\left(gbes{t}^k\right)\hfill \end{array}\right.$$

(6)

In Equations (5) and (6), updating the individual extreme value $pbes{t}_i$ and global extreme value $gbest$ in the particle population according to function f can guide the particle population to perform iterative optimization search in the direction of the global optimal solution. The termination condition is usually set to reach the maximum number of iterations in comparison experiments. The pseudocode of PSO is shown in Algorithm 1.

Algorithm 1 Particle Swarm Optimization

Input: Initialize population N, dimension D, iteration K, learning factors $c_1$, $c_2$, inertia weight w, velocity boundaries $v_{max}$, $v_{min}$, position boundaries $x_{max}$, $x_{min}$ Output: Optimal fitness value 1: The initialization population is randomly generated via Equations (1)–(4) and the position and velocity of the initialized particles $v_{id}$ and $x_{id}$ 2: Calculate the fitness value 3: Individual and global optimal positions $pbes{t}_i$ and $gbest$ are generated by equations Equations (5) and (6) 4: while$k<K$do 5:    for $i=0$ to N do 6:        Calculate the $v_{id}$ by Equations (1) and (3) 7:        Calculate the $x_{id}$ by Equations (2) and (4) 8:        Update $pbes{t}_i$ and $gbest$ by Equations (5) and (6) 9:    end for 10:   $k=k+1$ 11: end while

2.2. Sine Cosine Algorithm (SCA)

Mirjalili proposed SCA in 2016, inspired by the properties of the sine–cosine function, whose central idea is to find the optimal solution by using the periodic law of variation of the sine–cosine function in the search space combined with a random search strategy. Firstly, a set of candidate solutions are randomly initialized in the search space, the fitness of each candidate solution is calculated and the current optimal solution is recorded. In the exploration phase, due to the high random ratio, SCA makes the change in the solutions in the solution set more obvious, and imposes large fluctuations to control the current solutions in the solution space in order to search the unknown region in the solution space rapidly. In the exploitation phase, the degree of random solution variation is smaller, and weak random perturbations are applied to the obtained solution set to fully search the neighborhood of the current solution. Its optimal process is divided into two phases, exploration and exploitation, and the position update formula of SCA is denoted as

$$x_i^{k+1}=\left\{\begin{array}{cc}{x}_i^k+s_{1}sin\left(s_2\right)\left|s_3{P}_i^k-x_i^k\right|,\hfill & s_4<0.5\hfill \\ x_i^k+s_{1}cos\left(s_2\right)\left|s_3{P}_i^k-x_i^k\right|,\hfill & s_4\ge 0.5\hfill \end{array}\right.$$

(7)

The position of the solution is updated using the mathematical expression defined in Equation (7), which is the core formula of SCA. $x_i$ is the position of the current particle i at the kth iteration; $P_i$ is the historical individual optimal solution; $s_1$ is an adaptive parameter; $s_2$, $s_3$, and $s_4$ are random numbers; and “$\left|\right|$” denotes the absolute value.

The role of $s_1$ is to balance the range of variation of the sine and cosine to control the shift of the algorithm from global to local search gradually; a larger $s_1$ improves the global search capability of the algorithm, and on the contrary a smaller $s_1$ facilitates the local exploitation of the algorithm; $s_2$ is a random number in the range $[0,2]$ that is used to adjust the update solution to lie in or outside the solution space of the current and optimal solutions, defining the direction of the target of the solution and the extreme value of the iterative step size that can be achieved; $s_3$ is a random number in the range $[0,2]$ that gives a random weight for the current optimal solution, randomly emphasizing or weakening the influence of the target point, which defines the effect level of the candidate solution when it goes a distance away; $s_4$ is a random number in the range $[0,1]$ that is used to determine the sine or cosine updating formula, which helps to balance out the randomness in switching between sine and cosine to remove the connection that exists between iterative step size and direction.

$$s_1=a-a\frac{k}{K}$$

(8)

Equation (8) is the formula for the random number $s_1$, which adjusts the change in the position of the solution by making the phase change of the sine–cosine function change gradually with iterations to indicate the direction of the next solution’s movement, and thus, adjust the change in the position of the solution. The value of a determines the distance that a particle moves in the search space and is used to control the phase change of the sine–cosine function. Usually, the value of a is taken as a constant value of 2. The value of $k/K$ affects the change in amplitude, and as the number of iterations increases, the amplitude of the change in phase decreases gradually. Therefore, a reasonable choice of $s_1$ is crucial for the algorithm’s performance and convergence. The SCA pseudocode is shown in Algorithm 2.

Algorithm 2 Sine Cosine Algorithm

Input: Initialize dimension D, iteration K, constant parameter a Output: Optimal fitness value 1: Initialize a set of randomly generated solutions 2: while$k<K$do 3:    Evaluate the fitness value 4:    Update current optimal solution $pbes{t}_i$ 5:    Update parameter $s_1$ by Equation (8) and update parameters $s_2$-$s_4$ 6:    Update the position of the current solution by Equation (7) 7:     $k=k+1$ 8: end while

3. Proposed Method

3.1. Proposed SCA Strategy

SCA inherently benefits from high exploration, thus avoiding local optimality, and the adaptive range of the sine–cosine function allows for a smooth transition from exploration to exploitation when the algorithm utilizes the sine–cosine term to explore different regions of the search space. At the same time, the current solution always updates its position around the current best solution, and during the optimization process the solution moves towards the most promising region in the search space. The current optimal solution is stored in a variable as a target point and is retained during the optimization process, resulting ultimately in a global optimal value. Here, the current optimal solution is replaced with the global optimum solution. This means that more particles are focused on searching around the global optimal solution, which enables faster convergence to the global optimal solution. Firstly, the particles are guided by collective intelligence. The global optimal solution represents the best position of the whole population, introducing it into the SCA strategy amounts to introducing more collective wisdom, which makes the SCA strategy make better usage of the global information. Secondly, the global optimal solution corresponds to a better position in the solution space, using it as a guiding element can help SCA avoid falling into local optima, which improves the global search ability. The SCA strategy can effectively avoid falling into local optima. Thirdly, integrating the global optimal solution into the SCA strategy implies that the information exchange is enhanced, which makes the particles more likely to search along the direction of the global optimal solution, which strengthens the information exchange in populations, and it benefits them in finding the global optimal solution more rapidly. Finally, the introduction of the global optimal solution into SCA can accelerate the convergence process of the SCA strategy, increasing the efficiency of the algorithm and accelerating the search process. To sum up, changing the current optimal solution position of SCA to the global optimal solution not only enhances the global search capability and information exchange, but also can accelerate the convergence process and avoid falling into local optima, which improves the performance and efficiency of the algorithm. In this case, the SCA strategy proposed is denoted as

$$S=\left\{\begin{array}{c}{c}_3{r}_3\left(s_{1}sin\left(s_2\right)\left(s_{3}gbes{t}^k-x_{id}^k\right)\right),s_4<0.5\hfill \\ c_3{r}_3\left(s_{1}cos\left(s_2\right)\left(s_{3}gbes{t}^k-x_{id}^k\right)\right),s_4\ge 0.5\hfill \end{array}\right.$$

(9)

In Equation (9), $c_3$ stands for the learning factor, $r_3$ is a random number that takes values in the range of $[0,1]$, $s_1$ and $s_2$ are random numbers that control the direction in which the particles move, $s_{1}sin\left(s_2\right)$ and $s_{1}cos\left(s_2\right)$ determine the region where the solution will be located, $s_3$ controls the degree of influence of the global optimal solution $gbest$, and $s_4$ ensures that the velocity update switches equally between the sine–cosine function. Parameter $c_3$ is a random number in the range $[0,1]$ and a is a constant number, 2. $c_3{r}_3\left(s_{1}sin\left(s_2\right)\left(s_{3}gbes{t}^k-x_{id}^k\right)\right)$ and $c_3{r}_3\left(s_{1}cos\left(s_2\right)\left(s_{3}gbes{t}^k-x_{id}^k\right)\right)$ are composed of SCA influence terms.

3.2. Proposed Velocity Four Sine Cosine Particle Swarm Optimization (VFSCPSO)

The velocity formula Equation (1) is the core formula of the PSO, which is used to guide the particle to move in the direction of the global optimal solution. When updating the particle velocity, the particle is affected by two parts, the individual cognitive part and the group cognitive part, by adjusting the individual historical optimal and group historical optimal term in order to balance the exploration and exploitation in the optimization process, and ultimately converge to the global optimal solution in a rapid way. PSO has a strong global search ability, but the ability to jump out of a local optimal value at a later stage of the algorithm’s search is poor, which is due to the failure to take into account the possible influence of other factors on the particles. In order to improve the diversity of the algorithm and avoid local optima, other reasonable influence factors are integrated into the velocity updating process to improve the performance of the algorithm. We introduce the influence factors of SCA during the velocity updating to improve the diversity of the PSO in the whole searching process, which can make the particles more flexible in searching for the global optimum solution, increase the searching capability of the particles, and further guide the particles to move towards the direction of the global optimal solution. This paper proposes a Velocity Four Sine Cosine Particle Swarm Optimization (VFSCPSO) algorithm. Accordingly, the velocity update formula for the ($k+1$)th iteration in VFSCPSO is denoted as

$$v_{id}^{k+1}=w{v}_{id}^k+c_1{r}_1\left(pbes{t}_i^k-x_{id}^k\right)+c_2{r}_2\left(gbes{t}^k-x_{id}^k\right)+S$$

(10)

Equation (10) is the velocity update formula for the VFSCPSO algorithm model. $w{v}_{id}^k+c_1{r}_1\left(pbes{t}_i^k-x_{id}^k\right)+c_2{r}_2\left(gbes{t}^k-x_{id}^k\right)$ is the velocity formula Equation (1) for PSO. S is the SCA strategy. The other steps and formulas of VFSCPSO remain unchanged, therefore will not be further described here. VFSCPSO proposes a new algorithmic framework based on the PSO framework in combination with the SCA strategy, which ultimately improves PSO’s flexibility. The main steps of VFSCPSO can be described as follows:

Step 1: Input the required parameters such as particle population size N, particle search space dimension D, iteration K, inertia weight w, learning factors $c_1$, $c_2$, $c_3$, velocity boundaries $v_{max}$, $v_{min}$, position boundaries $x_{max}$, $x_{min}$, SCA constant parameter a, and so on;

Step 2: Randomly initialize the velocity and position of the particles through Equation (10), using Equations (2)–(6) to update the initial individual and global optimal positions, and individual and global fitness values;

Step 3: Update the SCA parameter $s_1$, inertia weights w, and other parameters after entering the iterative loop;

Step 4: Update the velocity of each particle after entering an iterative loop through Equation (10), and Equations (2)–(4), and determine whether the velocity crosses the boundary. If it crosses the boundary, change the velocity value to the boundary velocity value. Similarly the position update and judgment is applied;

Step 5: Calculate the fitness value;

Step 6: Update the individual and global optimal fitness values and positions by judging the conditional formulas in Equations (5) and (6);

Step 7: Update the parameters such as the iteration K;

Step 8: Determine whether the termination condition is reached or not, otherwise return to step 3;

Step 9: Output the result when the termination condition is reached.

Based on the main steps, the flowchart of VFSCPSO shown in Figure 1 can be obtained.

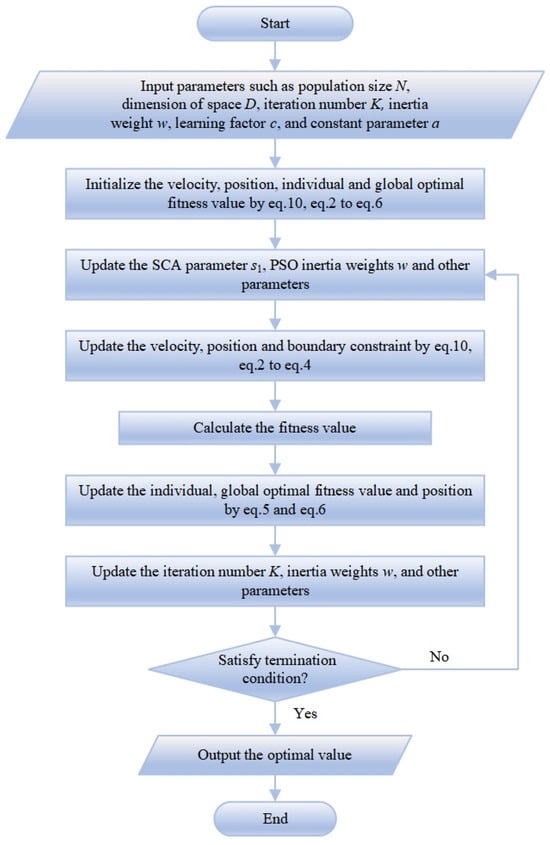
Figure 1. Flowchart of VFSCPSO.

Finally, the VFSCPSO algorithm pseudocode Algorithm 3 is shown below.

Algorithm 3 Velocity Four Sine Cosine Particle Swarm Optimization

Input: Initialize population N, dimension D, iteration K, learning factors $c_1$, $c_2$, $c_3$, inertia weight w, velocity boundaries $v_{max}$, $v_{min}$, position boundaries $x_{max}$, $x_{min}$ constant parameter a Output: Optimal fitness value 1: The initialization population is randomly generated via Equations (4)–(10) and the position and velocity of the initialized particles $v_{id}$ and $x_{id}$ 2: Calculate the fitness value 3: Individual and global optimal positions $pbes{t}_i$ and $gbest$ are generated by equations Equations (5) and (6) 4: while$k<K$do 5:    Update parameter $s_1$, inertia weights w 6:    for $i=0$ to N do 7:        Update random numbers $r_1$, $r_2$, $r_3$ 8:        Calculate the $v_{id}$ by Equations (3) and (10) 9:        Calculate the $x_{id}$ by Equations (2) and (4) 10:       Update $pbes{t}_i$ and $gbest$ by Equations (5) and (6) 11:    end for 12:    $k=k+1$ 13: end while

3.3. Complexity Discussion

In this subsection, we delve into the computational complexity of the VFSCPSO. The complexity of the VFSCPSO is compared with those of the standard PSO and SCA. We use O to denote an incremental upper bound on the time complexity. The population size of VFSCPSO is set to be N, the dimension of the optimization problem is D, the maximum number of iterations is T, and the required time to compute the fitness function is $f\left(D\right)$. The complexity of VFSCPSO is calculated as follows:

Step 1: The initialization phase takes time to set the parameters of the algorithm; the time complexity of this phase should be $O\left(1\right)$.

Step 2: It takes time $O(N·D)$ to randomly generate the positions and velocities of the individuals of the population particles, time $O(N·f(D\left)\right)$ to compute the values of the fitness function, and time $O\left(N\right)$ to find the optimal solution individual setups and record them, so the time complexity of this phase should be $O(D·N+N·f(D)+N)$.

Step 3: It takes time $t_2$ to record the initialization values and initialize the SCA adaptive parameter $s_1$, inertia weight w, and other parameters, and the time complexity of this phase should be $O\left(1\right)$.

Step 4: The optimization takes the same total time $O(N·D)$ as PSO and the time complexity of this phase should be $O(N·D)$.

Step 5–step 9: The computation, update, judgment, and output take a constant time $t_3$ and the time complexity is $O\left(1\right)$.

To sum up, the computational complexity of VFSCPSO can be expressed as

$$\left\{\begin{array}{c}T·O(1+(D+f\left(D\right)+1)·N)+1+D·N+1),s_4<0.5\hfill \\ T·O(1+(D+f\left(D\right)+1)·N)+1+D·N+1),s_4\ge 0.5\hfill \end{array}\right.$$

(11)

The random number $s_4$ ensures that the sine–cosine function is selected with approximately equivalent probability, and the complexity of the upper and lower equations in Equation (11) is the same, which results in the time complexity of VFSCPSO being $O(T·N·D)$. In order to objectively compare the quality of the algorithms, the time complexity of PSO and SCA is $O(T·N·D)$, the complexity of the VFSCPSO is only increased by an order of magnitude compared to that of PSO and SCA. In this paper, we verify the possibility of the implementation of the VFSCPSO through experiments, and VFSCPSO can converge to higher-quality values faster, which gives it a greater application value in reality.

4. Experiment and Analysis

4.1. Experimental Settings

The experimental environment was configured as Intel(R) Core(TM) i7-10700 CPU @ 2.90 GHz, and the software environment was MATLAB 2021b. In order to ensure the comparative effectiveness and fairness of the experiments, we selected the Competition on Evolutionary Computation 2005 (CEC2005) [46] test suite for comprehensive validation. The CEC2005 test suite was a test suite for the Optimization Algorithm Domain Competition, which provides 23 benchmark functions, aiming at comparing and evaluating the performance and efficiency of different algorithms through a series of benchmark functions to reveal the strengths and weaknesses of different algorithms on different optimization problems. In summary, the CEC2005 test suite is an important resource for evaluating the performance of optimization algorithms, and by testing and comparing algorithms on these functions, researchers are able to gain a more comprehensive understanding of the strengths and limitations of different algorithms. Details of the CEC2005 test suite are presented in Table 1 and Appendix A.

Table 1. CEC2005 test suite information.

Problem	Name	Dimensions	Search Space	$\mathit{f}\left({\mathit{x}}^{*}\right)$
$f1$	Sphere Function	30	${[-100,100]}^D$	0
$f2$	Schwefel’s Problem 2.22	30	${[-10,10]}^D$	0
$f3$	Schwefel’s Problem 1.2	30	${[-100,100]}^D$	0
$f4$	Schwefel’s Problem 2.21	30	${[-100,100]}^D$	0
$f5$	Generalized Rosenbrock’s Function	30	${[-30,30]}^D$	0
$f6$	Step Function	30	${[-100,100]}^D$	0
$f7$	Quartic Function, i.e., Noise	30	${[-1.28,1.28]}^D$	0
$f8$	Generalized Schwefel’s Problem 2.26	30	${[-500,500]}^D$	−12,569.5
$f9$	Generalized Rastrigin’s Function	30	${[-5.12,5.12]}^D$	0
$f10$	Ackley’s Function	30	${[-32,32]}^D$	0
$f11$	Generalized Griewank’s Function	30	${[-600,600]}^D$	0
$f12$	Generalized Penalized Function 1	30	${[-50,50]}^D$	0
$f13$	Generalized Penalized Function 2	30	${[-50,50]}^D$	0
$f14$	Shekel’s Foxholes Function	2	${[-65.536,65.536]}^D$	0.998003838
$f15$	Kowalik’s Function	4	${[-5,5]}^D$	0.0003075
$f16$	Six-Hump Camel-Back Function	2	${[-5,5]}^D$	−1.03162845
$f17$	Branin Function	2	$[-5,10][0,15]$	0.397887358
$f18$	Goldstein Price Function	2	${[-2,2]}^D$	3
$f19$	Hartman’s Family 1	3	${[0,1]}^D$	−3.86278215
$f20$	Hartman’s Family 2	6	${[0,1]}^D$	−3.32199517
$f21$	Shekel’s Family 1	4	${[0,10]}^D$	−10.1531997
$f22$	Shekel’s Family 2	4	${[0,10]}^D$	−10.4029406
$f23$	Shekel’s Family 3	4	${[0,10]}^D$	−10.5364

To make VFSCPSO more convincing, the comparison experiment covers a total of 12 intelligent algorithms, including the classical algorithms GA [1] and DE [2], the compositional algorithms PSO [5] and SCA [11] to verify the validity of the hybrid algorithm VFSCPSO, and the novel similar algorithm variants AWPSO [21] and SCDLPSO [23], which have better performance; these are selected to verify the superiority of the hybrid algorithm VFSCPSO. AWPSO is cited from “IEEE TCYB”. AWPSO and SCDLPSO are more representative PSO variants. These algorithms has high influence, convergence accuracy, overall performance, and scope of application and low reproduction error. In addition, the more novel and better performing algorithms SFLA [6] and BBO [4], and the advanced algorithms MA [8], POA [9], DO [3], and OMA [13], which were proposed between 2020 and 2023, respectively, are included to verify the advancement of VFSCPSO, having the values of references, and the specific parameter settings are taken from the original studies. The parameter values of VFSCPSO are based on the settings in Section 3. Meanwhile, the evaluation indexes use the best, mean, worst, and standard deviation (std), where the best results are shown in bold. Finally, the performance of the proposed VFSCPSO is further demonstrated by the Friedman test.

The Friedman test is a simple, flexible, and widely applicable statistical method, especially for situations where three or more related samples need to be compared. This method is also effective for data that do not follow a normal distribution or have a skewed distribution. Compared with other parametric tests, the Friedman test requires a relatively small sample size and can produce reliable results with small sample sizes. The Friedman test is one of the most commonly used methods in experimental design and data analysis. A detailed tutorial on using this nonparametric statistical test to compare the strengths and weaknesses of intelligent algorithms can be found in [47]. The following is the Friedman test process:

Step 1: Gather observed results for each algorithm/problem pair.

Step 2: For each problem i, rank values from 1 (best result) to k (worst result). Denote these ranks as $r_i^j(1\le j\le k)$.

Step 3: For each algorithm j, average the ranks obtained in all problems to obtain the final rank $R_j=\frac{1}{n}{\sum }_i{r}_i^j$.

Reasonable experimental design, cross validation, and evaluation methods are important steps to verify the overall performance of the hybrid algorithm; a series of numerical experiments are carried out, along with a detailed analysis of the results. The maximum number of function evaluations (MNFEs) is used as a termination condition for more accurate comparison of algorithmic performance. Compared with the other 12 comparison algorithms, VFSCPSO does not have an additional number of function evaluations, and the same number of iterations means the same MNFEs, so the maximum number of iterations is set to 1000 as the termination condition. To avoid the influence of chance on the results, each algorithm was run independently for 30 runs on each benchmark function separately.

4.2. Experimental Results and Analysis

4.2.1. Performance of Algorithm in Standard Environment

This series of experiments aims to assess the efficacy of VFSCPSO by conducting a comparative analysis with 11 other algorithms. The evaluation includes the determination of best, mean, worst, and std values. The corresponding experimental and test results are presented in Table 2, Table 3, Table 4 and Table 5.

Table 2. Experimental results and Friedman test results of VFSCPSO on CEC2005 test suite $f1$–$f15$.

Problem	Metric	GA	DE	PSO	SCA	AWPSO	SCDLPSO	VFSCPSO
$f1$	best	3.24E+00	1.82E−10	4.15E−02	1.37E−48	6.77E−23	4.40E−46	3.63E−74
	mean	6.63E+00	3.23E−10	6.12E−01	6.32E−33	9.66E−18	1.59E−38	1.69E−69
	worst	1.19E+01	4.69E−10	2.00E+00	1.88E−31	2.65E−16	4.57E−37	4.54E−68
	std	2.27E+00	7.16E−11	4.67E−01	3.43E−32	4.83E−17	8.35E−38	8.27E−69
$f2$	best	6.38E−01	5.19E−07	9.08E−01	1.32E−32	1.47E−11	3.33E−21	6.24E−39
	mean	8.37E−01	9.29E−07	1.08E+01	9.33E−28	5.28E−08	3.33E−01	7.44E−37
	worst	1.04E+00	1.28E−06	3.12E+01	1.85E−26	5.11E−07	1.00E+01	6.17E−36
	std	1.20E−01	1.79E−07	8.84E+00	3.38E−27	1.25E−07	1.83E+00	1.25E−36
$f3$	best	6.62E+03	1.63E+04	1.44E+03	8.50E+03	3.76E+02	8.09E+01	8.66E−02
	mean	1.38E+04	2.87E+04	5.54E+03	1.72E+04	1.09E+03	1.43E+03	3.06E+03
	worst	3.31E+04	3.93E+04	3.66E+04	2.46E+04	2.71E+03	6.31E+03	5.24E+04
	std	5.82E+03	6.31E+03	6.92E+03	4.04E+03	5.10E+02	1.81E+03	1.38E+04
$f4$	best	3.31E+00	3.89E+00	8.15E−01	6.70E−11	4.68E−04	5.69E−01	1.89E−32
	mean	4.98E+00	4.86E+00	1.93E+00	2.97E+00	2.10E−03	1.42E+00	6.45E−30
	worst	6.55E+00	5.76E+00	3.24E+00	1.95E+01	6.04E−03	3.67E+00	6.49E−29
	std	6.92E−01	4.81E−01	7.09E−01	5.52E+00	1.33E−03	6.40E−01	1.42E−29
$f5$	best	1.61E+02	3.68E+01	3.01E+01	2.60E+01	7.40E+00	9.90E−04	6.34E−02
	mean	4.39E+02	5.31E+01	6.94E+01	2.65E+01	2.84E+01	3.56E+01	6.15E−01
	worst	2.35E+03	8.46E+01	2.97E+02	2.69E+01	7.86E+01	8.14E+01	4.07E+00
	std	4.35E+02	1.31E+01	5.97E+01	2.28E−01	1.67E+01	2.84E+01	8.61E−01
$f6$	best	1.00E+00	0.00E+00	1.00E+00	0.00E+00	0.00E+00	0.00E+00	0.00E+00
	mean	7.97E+00	0.00E+00	1.71E+01	0.00E+00	1.77E+00	6.33E−01	0.00E+00
	worst	1.60E+01	0.00E+00	3.40E+01	0.00E+00	1.00E+01	7.00E+00	0.00E+00
	std	3.22E+00	0.00E+00	6.96E+00	0.00E+00	2.60E+00	1.56E+00	0.00E+00
$f7$	best	2.00E−02	1.68E−02	2.27E−03	3.46E−04	3.09E−03	9.75E−03	1.45E−05
	mean	6.53E−02	2.85E−02	8.35E−03	3.24E−03	6.40E−03	1.25E−01	9.41E−05
	worst	1.34E−01	4.34E−02	1.79E−02	1.37E−02	1.44E−02	2.70E+00	5.07E−04
	std	2.67E−02	6.71E−03	4.77E−03	2.78E−03	2.71E−03	4.88E−01	1.08E−04
$f8$	best	−1.26E+04	−1.26E+04	−1.00E+04	−6.93E+03	−4.11E+03	−1.06E+04	−1.26E+04
	mean	−1.26E+04	−1.26E+04	−8.49E+03	−5.76E+03	−3.33E+03	−8.58E+03	−1.25E+04
	worst	−1.25E+04	−1.26E+04	−5.17E+03	−5.26E+03	−2.79E+03	−7.28E+03	−1.22E+04
	std	5.39E+00	3.82E−05	1.01E+03	3.19E+02	3.41E+02	8.80E+02	7.89E+01
$f9$	best	1.38E+00	1.84E+01	3.25E+01	0.00E+00	1.69E+01	1.09E+01	0.00E+00
	mean	2.63E+00	2.39E+01	9.38E+01	1.78E−16	3.13E+01	3.15E+01	0.00E+00
	worst	4.13E+00	3.00E+01	1.54E+02	5.33E−15	5.87E+01	7.16E+01	0.00E+00
	std	7.44E−01	2.63E+00	3.41E+01	9.73E−16	9.35E+00	1.71E+01	0.00E+00
$f10$	best	9.94E−01	5.95E−06	4.47E−01	4.44E−15	1.74E−12	3.24E−14	8.88E−16
	mean	1.39E+00	9.18E−06	2.34E+00	8.80E+00	3.87E−01	5.19E−01	3.14E−15
	worst	1.87E+00	2.25E−05	3.94E+00	2.01E+01	2.32E+00	1.90E+00	4.44E−15
	std	2.13E−01	3.12E−06	9.03E−01	1.00E+01	7.97E−01	6.90E−01	1.74E−15
$f11$	best	1.02E+00	1.78E−09	2.26E−01	0.00E+00	1.51E+01	7.40E−03	0.00E+00
	mean	1.06E+00	1.61E−08	5.83E−01	1.29E−09	2.20E+01	1.20E−01	0.00E+00
	worst	1.10E+00	1.02E−07	9.60E−01	3.87E−08	2.57E+01	4.07E−01	0.00E+00
	std	1.98E−02	2.44E−08	2.13E−01	7.06E−09	2.48E+00	9.44E−02	0.00E+00
$f12$	best	7.48E−03	7.22E−12	5.97E−02	2.20E−03	2.04E−24	8.40E−23	8.56E−06
	mean	2.80E−02	1.34E−11	9.14E−01	4.18E−03	1.38E−01	2.02E−01	2.21E−04
	worst	8.77E−02	2.88E−11	4.15E+00	7.35E−03	8.30E−01	2.98E+00	5.71E−04
	std	1.81E−02	4.71E−12	9.53E−01	1.50E−03	2.18E−01	5.59E−01	1.42E−04
$f13$	best	1.38E−01	2.11E−11	8.58E−01	3.34E−02	1.82E−25	1.35E−32	2.89E−04
	mean	3.84E−01	4.44E−11	2.57E+00	1.91E−01	3.20E−21	6.95E−03	2.49E−03
	worst	7.05E−01	8.25E−11	5.09E+00	4.91E−01	3.83E−20	5.48E−02	7.32E−03
	std	1.47E−01	1.48E−11	1.32E+00	1.24E−01	8.89E−21	1.27E−02	1.90E−03
$f14$	best	9.98E−01	9.98E−01	9.98E−01	9.98E−01	9.98E−01	9.98E−01	9.98E−01
	mean	9.98E−01	9.98E−01	9.98E−01	9.98E−01	9.98E−01	9.98E−01	9.98E−01
	worst	9.98E−01	9.98E−01	9.98E−01	9.98E−01	9.98E−01	9.98E−01	9.98E−01
	std	2.23E−10	3.39E−16	3.39E−16	5.14E−12	3.39E−16	3.34E−16	1.08E−13
$f15$	best	6.01E−04	5.02E−04	3.07E−04	3.24E−04	3.07E−04	3.07E−04	3.07E−04
	mean	2.06E−03	6.70E−04	2.55E−03	5.82E−04	1.05E−03	8.44E−03	1.26E−03
	worst	2.04E−02	7.78E−04	2.04E−02	1.22E−03	2.04E−02	2.04E−02	2.25E−03
	std	3.52E−03	8.38E−05	5.05E−03	1.94E−04	3.66E−03	9.91E−03	8.35E−04

Table 3. Experimental results and Friedman test results of VFSCPSO on CEC2005 test suite $f16$–$f23$.

Problem	Metric	GA	DE	PSO	SCA	AWPSO	SCDLPSO	VFSCPSO
$f16$	best	−1.03E+00	−1.03E+00	−1.03E+00	−1.03E+00	−1.03E+00	−1.03E+00	−1.03E+00
	mean	−1.03E+00	−1.03E+00	−1.03E+00	−1.03E+00	−1.03E+00	−1.03E+00	−1.03E+00
	worst	−1.03E+00	−1.03E+00	−1.03E+00	−1.03E+00	−1.03E+00	−1.03E+00	−1.03E+00
	std	7.62E−06	6.78E−16	6.78E−16	9.74E−09	6.78E−16	6.78E−16	1.83E−09
$f17$	best	3.98E−01	3.98E−01	3.98E−01	3.98E−01	3.98E−01	3.98E−01	3.98E−01
	mean	3.98E−01	3.98E−01	3.98E−01	3.98E−01	3.98E−01	3.98E−01	3.98E−01
	worst	3.98E−01	3.98E−01	3.98E−01	3.98E−01	3.98E−01	3.98E−01	3.98E−01
	std	4.11E−05	0.00E+00	0.00E+00	1.36E−06	0.00E+00	0.00E+00	1.09E−07
$f18$	best	3.00E+00	3.00E+00	3.00E+00	3.00E+00	3.00E+00	3.00E+00	3.00E+00
	mean	3.00E+00	3.00E+00	3.00E+00	3.00E+00	3.00E+00	3.00E+00	3.00E+00
	worst	3.00E+00	3.00E+00	3.00E+00	3.00E+00	3.00E+00	3.00E+00	3.00E+00
	std	5.31E−05	1.73E−15	1.32E−15	2.32E−07	9.69E−16	1.32E−15	1.78E−07
$f19$	best	−3.86E+00	−3.86E+00	−3.86E+00	−3.86E+00	−3.86E+00	−3.86E+00	−3.86E+00
	mean	−3.86E+00	−3.86E+00	−3.86E+00	−3.86E+00	−3.86E+00	−3.86E+00	−3.86E+00
	worst	−3.86E+00	−3.86E+00	−3.85E+00	−3.86E+00	−3.86E+00	−3.86E+00	−3.85E+00
	std	1.07E−06	2.71E−15	2.73E−03	7.53E−05	2.71E−15	2.71E−15	1.45E−03
$f20$	best	−3.32E+00	−3.32E+00	−3.32E+00	−3.32E+00	−3.32E+00	−3.32E+00	−3.32E+00
	mean	−3.27E+00	−3.32E+00	−3.18E+00	−3.30E+00	−3.25E+00	−3.22E+00	−3.20E+00
	worst	−3.20E+00	−3.32E+00	−2.95E+00	−3.20E+00	−3.14E+00	−3.13E+00	−3.02E+00
	std	6.03E−02	1.36E−15	7.85E−02	4.60E−02	6.37E−02	5.14E−02	9.50E−02
$f21$	best	−1.03E+01	−1.03E+01	−1.03E+01	−1.03E+01	−1.03E+01	−1.03E+01	−1.03E+01
	mean	−5.25E+00	−1.03E+01	−9.29E+00	−9.94E+00	−7.58E+00	−9.63E+00	−1.03E+01
	worst	−2.66E+00	−1.03E+01	−5.10E+00	−5.10E+00	−2.66E+00	−5.09E+00	−1.03E+01
	std	3.46E+00	3.39E−06	2.13E+00	1.32E+00	3.30E+00	1.81E+00	5.81E−05
$f22$	best	−1.06E+01	−1.06E+01	−1.06E+01	−1.06E+01	−1.06E+01	−1.06E+01	−1.06E+01
	mean	−6.19E+00	−1.06E+01	−1.04E+01	−1.06E+01	−6.74E+00	−9.74E+00	−1.06E+01
	worst	−2.24E+00	−1.06E+01	−5.34E+00	−1.04E+01	−2.91E+00	−5.34E+00	−1.06E+01
	std	3.55E+00	4.51E−05	9.65E−01	3.58E−02	3.50E+00	2.00E+00	5.62E−05
$f23$	best	−1.07E+01	−1.07E+01	−1.07E+01	−1.07E+01	−1.07E+01	−1.07E+01	−1.07E+01
	mean	−5.28E+00	−1.07E+01	−1.07E+01	−1.07E+01	−6.57E+00	−9.58E+00	−1.07E+01
	worst	−2.28E+00	−1.07E+01	−1.07E+01	−1.07E+01	−3.02E+00	−5.19E+00	−1.07E+01
	std	2.34E+00	1.44E−03	4.21E−04	1.68E−02	2.16E+00	1.97E+00	1.65E−15
Count		0	9	4	2	6	4	11
Avg. rank		5.695652174	2.652173913	4.782608696	3.782608696	3.565217391	3.782608696	2.608695652
Overall rank		7	2	6	4	3	4	1

Table 4. Experimental results and Friedman test results of VFSCPSO on CEC2005 test suite $f1$–$f15$.

Problem	Metric	SFLA	BBO	MA	POA	DO	OMA	VFSCPSO
$f1$	best	2.38E−14	9.56E−01	4.22E+04	4.58E−16	2.28E−12	2.35E−02	3.63E−74
	mean	3.79E−13	2.84E+00	5.93E+04	9.08E−15	1.23E−11	7.37E−02	1.69E−69
	worst	3.33E−12	6.33E+00	7.05E+04	5.39E−14	4.81E−11	2.56E−01	4.54E−68
	std	5.97E−13	1.35E+00	6.16E+03	1.17E−14	9.27E−12	4.95E−02	8.27E−69
$f2$	best	1.75E−07	3.81E−01	2.16E+02	3.05E−10	8.65E−07	2.13E−03	6.24E−39
	mean	1.82E−03	5.41E−01	9.61E+09	2.41E−09	2.01E−06	4.31E−03	7.44E−37
	worst	5.09E−02	7.88E−01	1.33E+11	1.00E−08	6.50E−06	2.44E−02	6.17E−36
	std	9.28E−03	9.60E−02	2.91E+10	2.07E−09	1.05E−06	4.19E−03	1.25E−36
$f3$	best	8.30E+03	8.47E+03	9.27E+04	4.06E+03	4.89E+02	3.93E+03	8.66E−02
	mean	2.43E+04	1.76E+04	5.91E+05	9.68E+03	2.38E+03	7.39E+03	3.06E+03
	worst	4.89E+04	3.88E+04	1.74E+06	1.54E+04	4.66E+03	1.35E+04	5.24E+04
	std	1.01E+04	6.87E+03	3.48E+05	3.12E+03	1.10E+03	2.63E+03	1.38E+04
$f4$	best	5.88E−01	4.44E+00	5.40E+01	1.28E−01	1.45E−03	7.37E+00	1.89E−32
	mean	5.47E+00	5.61E+00	7.83E+01	1.47E+00	4.25E−03	1.02E+01	6.45E−30
	worst	1.20E+01	7.64E+00	9.06E+01	5.90E+00	1.08E−02	1.36E+01	6.49E−29
	std	3.08E+00	8.21E−01	8.13E+00	1.40E+00	2.08E−03	1.37E+00	1.42E−29
$f5$	best	1.07E+01	1.09E+02	1.27E+08	1.70E+01	2.40E+01	8.61E+01	6.34E−02
	mean	7.93E+01	3.60E+02	2.12E+08	4.22E+01	2.65E+01	1.67E+02	6.15E−01
	worst	3.03E+02	3.07E+03	2.72E+08	1.59E+02	9.04E+01	2.78E+02	4.07E+00
	std	7.24E+01	5.41E+02	3.58E+07	3.32E+01	1.21E+01	5.68E+01	8.61E−01
$f6$	best	0.00E+00	1.00E+00	4.45E+04	0.00E+00	0.00E+00	4.00E+00	0.00E+00
	mean	6.00E−01	2.57E+00	5.89E+04	0.00E+00	0.00E+00	2.59E+01	0.00E+00
	worst	3.00E+00	7.00E+00	7.23E+04	0.00E+00	0.00E+00	1.26E+02	0.00E+00
	std	8.14E−01	1.50E+00	5.87E+03	0.00E+00	0.00E+00	2.28E+01	0.00E+00
$f7$	best	1.47E−02	8.58E−03	3.55E+01	7.55E−03	6.16E−04	1.39E−02	1.45E−05
	mean	3.33E−02	2.79E−02	9.33E+01	1.69E−02	2.82E−03	3.26E−02	9.41E−05
	worst	4.84E−02	5.41E−02	1.37E+02	2.97E−02	5.52E−03	6.42E−02	5.07E−04
	std	9.29E−03	9.86E−03	2.48E+01	6.16E−03	1.13E−03	1.22E−02	1.08E−04
$f8$	best	−6.50E+03	−1.26E+04	−3.43E+03	−1.11E+04	−1.10E+04	−8.99E+03	−1.26E+04
	mean	−4.84E+03	−1.26E+04	−2.72E+03	−9.12E+03	−1.00E+04	−7.16E+03	−1.25E+04
	worst	−3.59E+03	−1.26E+04	−2.05E+03	−7.09E+03	−9.08E+03	−5.48E+03	−1.22E+04
	std	8.04E+02	2.77E+00	3.48E+02	1.10E+03	4.17E+02	9.65E+02	7.89E+01
$f9$	best	7.07E+01	5.75E−01	3.34E+02	1.89E+01	6.72E−12	2.39E+01	0.00E+00
	mean	1.11E+02	1.23E+00	3.80E+02	4.40E+01	7.27E+00	5.45E+01	0.00E+00
	worst	2.05E+02	2.68E+00	4.34E+02	8.36E+01	1.70E+01	1.00E+02	0.00E+00
	std	3.18E+01	4.58E−01	3.06E+01	1.38E+01	5.52E+00	2.29E+01	0.00E+00
$f10$	best	3.59E−05	5.32E−01	1.88E+01	5.59E−07	2.73E−07	2.09E+00	8.88E−16
	mean	2.55E+00	7.24E−01	2.01E+01	1.66E+01	7.54E−07	3.76E+00	3.14E−15
	worst	4.34E+00	1.14E+00	2.07E+01	2.00E+01	1.18E−06	6.07E+00	4.44E−15
	std	1.09E+00	1.69E−01	4.04E−01	7.55E+00	2.01E−07	9.32E−01	1.74E−15
$f11$	best	6.93E−13	7.84E−01	2.72E+02	3.33E−16	3.60E−11	3.34E−02	0.00E+00
	mean	1.49E−02	9.84E−01	5.12E+02	1.36E−02	1.29E−02	9.86E−02	0.00E+00
	worst	4.41E−02	1.05E+00	6.37E+02	3.44E−02	4.89E−02	2.36E−01	0.00E+00
	std	1.29E−02	6.46E−02	7.69E+01	1.19E−02	1.41E−02	5.16E−02	0.00E+00
$f12$	best	2.05E−09	2.43E−03	2.93E+08	2.51E−15	1.51E−09	1.00E−05	8.56E−06
	mean	1.66E+00	1.50E−02	4.60E+08	5.53E−02	5.49E−09	4.31E−01	2.21E−04
	worst	6.51E+00	1.15E−01	6.26E+08	5.19E−01	1.69E−08	1.42E+00	5.71E−04
	std	1.82E+00	2.17E−02	9.20E+07	1.08E−01	3.27E−09	4.37E−01	1.42E−04
$f13$	best	6.84E−13	4.72E−02	4.63E+08	6.99E−16	2.54E−08	7.97E−03	2.89E−04
	mean	2.95E+00	1.35E−01	9.03E+08	4.39E−03	7.69E−08	7.71E+00	2.49E−03
	worst	3.69E+01	2.24E−01	1.25E+09	1.10E−02	1.39E−07	3.09E+01	7.32E−03
	std	8.46E+00	4.33E−02	1.87E+08	5.47E−03	2.67E−08	9.65E+00	1.90E−03
$f14$	best	9.98E−01	9.98E−01	3.04E+01	9.98E−01	9.98E−01	9.98E−01	9.98E−01
	mean	9.98E−01	9.98E−01	3.75E+02	9.98E−01	9.98E−01	9.98E−01	9.98E−01
	worst	9.98E−01	9.98E−01	5.00E+02	9.98E−01	9.98E−01	9.98E−01	9.98E−01
	std	3.71E−16	5.01E−07	1.75E+02	3.39E−16	2.44E−16	3.39E−16	1.08E−13
$f15$	best	3.08E−04	5.54E−04	4.63E−03	3.07E−04	3.07E−04	3.07E−04	3.07E−04
	mean	5.72E−04	1.58E−03	4.09E−02	7.65E−04	3.38E−04	4.33E−04	1.26E−03
	worst	1.38E−03	3.28E−03	1.47E−01	1.22E−03	1.22E−03	2.50E−03	2.25E−03
	std	2.70E−04	6.48E−04	3.31E−02	4.66E−04	1.67E−04	4.29E−04	8.35E−04

Table 5. Experimental results and Friedman test results of VFSCPSO on CEC2005 test suite $f16$–$f23$.

Problem	Metric	SFLA	BBO	MA	POA	DO	OMA	VFSCPSO
$f16$	best	−1.03E+00	−1.03E+00	−1.00E+00	−1.03E+00	−1.03E+00	−1.03E+00	−1.03E+00
	mean	−1.03E+00	−1.03E+00	−5.05E−01	−1.03E+00	−1.03E+00	−1.03E+00	−1.03E+00
	worst	−1.03E+00	−1.03E+00	3.80E−01	−1.03E+00	−1.03E+00	−1.03E+00	−1.03E+00
	std	5.98E−16	5.66E−04	3.99E−01	6.78E−16	6.65E−15	6.78E−16	1.83E−09
$f17$	best	3.98E−01	3.98E−01	4.23E−01	3.98E−01	3.98E−01	3.98E−01	3.98E−01
	mean	3.98E−01	3.99E−01	1.21E+00	3.98E−01	3.98E−01	3.98E−01	3.98E−01
	worst	3.98E−01	4.05E−01	4.85E+00	3.98E−01	3.98E−01	3.98E−01	3.98E−01
	std	0.00E+00	1.62E−03	9.24E−01	0.00E+00	3.27E−13	0.00E+00	1.09E−07
$f18$	best	3.00E+00	3.00E+00	3.74E+00	3.00E+00	3.00E+00	3.00E+00	3.00E+00
	mean	3.00E+00	3.00E+00	2.60E+01	3.00E+00	3.00E+00	3.00E+00	3.00E+00
	worst	3.00E+00	3.04E+00	9.87E+01	3.00E+00	3.00E+00	3.00E+00	3.00E+00
	std	2.06E−15	7.03E−03	1.98E+01	1.34E−15	2.70E−10	1.98E−15	1.78E−07
$f19$	best	−3.86E+00	−3.86E+00	−3.84E+00	−3.86E+00	−3.86E+00	−3.86E+00	−3.86E+00
	mean	−3.86E+00	−3.86E+00	−3.57E+00	−3.86E+00	−3.86E+00	−3.86E+00	−3.86E+00
	worst	−3.86E+00	−3.86E+00	−2.95E+00	−3.86E+00	−3.86E+00	−3.86E+00	−3.85E+00
	std	2.51E−15	1.21E−04	2.49E−01	2.71E−15	5.15E−10	2.70E−15	1.45E−03
$f20$	best	−3.32E+00	−3.32E+00	−2.87E+00	−3.32E+00	−3.32E+00	−3.32E+00	−3.32E+00
	mean	−3.25E+00	−3.28E+00	−2.13E+00	−3.24E+00	−3.26E+00	−3.32E+00	−3.20E+00
	worst	−3.20E+00	−3.20E+00	−1.37E+00	−3.20E+00	−3.20E+00	−3.32E+00	−3.02E+00
	std	5.92E−02	5.83E−02	4.45E−01	5.54E−02	6.03E−02	1.79E−15	9.50E−02
$f21$	best	−1.03E+01	−1.03E+01	−1.61E+00	−1.03E+01	−1.03E+01	−1.03E+01	−1.03E+01
	mean	−7.36E+00	−8.74E+00	−8.48E−01	−8.68E+00	−7.90E+00	−9.41E+00	−1.03E+01
	worst	−2.66E+00	−2.66E+00	−3.60E−01	−2.66E+00	−2.66E+00	−5.09E+00	−1.03E+01
	std	3.54E+00	2.87E+00	3.31E−01	2.60E+00	2.89E+00	1.64E+00	5.81E−05
$f22$	best	−1.06E+01	−1.06E+01	−2.35E+00	−1.06E+01	−1.06E+01	−1.06E+01	−1.06E+01
	mean	−6.79E+00	−8.00E+00	−1.09E+00	−9.51E+00	−8.85E+00	−1.06E+01	−1.06E+01
	worst	−2.91E+00	−2.91E+00	−5.59E−01	−3.94E+00	−5.13E+00	−1.06E+01	−1.06E+01
	std	3.28E+00	3.31E+00	3.92E−01	2.27E+00	2.55E+00	5.12E−03	5.62E−05
$f23$	best	−1.07E+01	−1.07E+01	−3.79E+00	−1.07E+01	−1.07E+01	−1.07E+01	−1.07E+01
	mean	−7.05E+00	−6.44E+00	−1.50E+00	−7.43E+00	−7.55E+00	−7.62E+00	−1.07E+01
	worst	−3.17E+00	−4.24E+00	−8.86E−01	−5.19E+00	−5.19E+00	−6.84E+00	−1.07E+01
	std	2.80E+00	2.34E+00	6.40E−01	2.46E+00	2.54E+00	1.28E+00	1.65E−15
Count		3	1	0	5	5	6	12
Avg. rank		4.130434783	4.652173913	7	2.956521739	2.695652174	3.47826087	2.47826087
Overall rank		5	6	7	3	2	4	1

Based on the findings presented in Table 2 and Table 3, it is evident that GA demonstrates suboptimal performance across various benchmark function tests when compared to other algorithms. GA exhibits a notably high best value and a relatively low worst value, especially in functions such as $f1$ and $f2$, showing a significant performance gap compared to alternative algorithms. Additionally, GA displays a relatively large std, with substantial fluctuations in performance. DE exhibits commendable performance in some functions, with low fitness values observed in functions like $f6$, $f8$, and $f15$–$f20$. However, its performance is average on other functions, suggesting that DE is more suited for optimization problems with a smaller number of dimensions. PSO performs moderately well across most functions, with its best, mean, and worst values falling in the middle range compared to other algorithms, and performs relatively consistently, with a small std. SCA also performs moderately well in optimization problems with a small number of dimensions, particularly excelling in single-peak function $f1$ and multi-peak function $f6$. However, the larger std of SCA indicates lower stability. Considering the convergence accuracy and stability of PSO and SCA, their effective combination could result in a hybrid algorithm with enhanced performance. AWPSO performs well across most function tests, significantly improving on the performance of PSO and inheriting its advantage of higher stability with a smaller std value. SCDLPSO achieves relatively good results in functions such as $f1$ and $f2$, displaying a low fitness value. However, SCDLPSO exhibits a larger std value compared to AWPSO on functions like $f3$ and $f8$, indicating a higher performance fluctuation. While SCDLPSO enhances the accuracy of PSO, it compromises the stability. VFSCPSO demonstrates superior values of best, mean, and worst on functions such as $f1$, $f2$, $f6$, and $f14$. It outperforms the other compared algorithms, boasting a relatively small std value and high stability. In summary, each comparison algorithm exhibits varying performance across different functions, and no single algorithm excels in all scenarios. VFSCPSO, in the comprehensive series of experiments, emerges as a better solution relative to other algorithms. It excels in both single-peak and multi-peak functions, and shows superior global search ability and stability. While achieving favorable results in functions $f21$–$f23$, its performance in other fixed-dimensional functions is relatively poorer, possibly due to the lower dimensionality of fixed-dimensional functions. VFSCPSO may be better suited for high-dimensional optimization problems. The Friedman test results in Table 3 show that VFSCPSO has an average rank of 2.60 on the 23 tested functions and ranks first in the overall ranking, indicating that the VFSCPSO algorithm performs better overall. GA has an average rank of 5.69 and ranks seventh in the overall ranking, performing the worst in this group of environments. DE has an average rank of 2.65. This indicates that DE performs better as well, but is not the best algorithm. PSO is ranked sixth in the overall ranking and its average ranking is at the back of the pack. This indicates that VFSCPSO has a large improvement on the performance of the PSO algorithm, but is average in other metrics. SCA and SCDLPSO are ranked fourth in the overall ranking, with their average ranking in the middle of the pack. This indicates that SCA and SCDLPSO perform between VFSCPSO and GA. AWPSO ranks third in the overall ranking and is in the middle of the average ranking. This suggests that AWPSO may perform better overall.

The mean convergence curve is produced based on the results of 30 optimizations of the seven algorithms on the 23 benchmark functions in the CEC2005 test suite, and is used to compare the convergence performance of the algorithms, as shown in Figure 2.

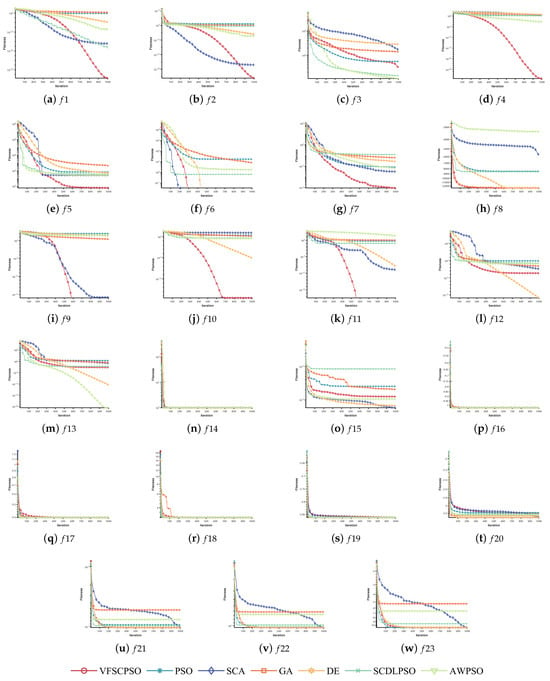
Figure 2. Convergence curves of VFSCPSO, PSO, SCA, GA, DE, SCDLPSO, and AWPSO on the CEC2005 test suite.

From Figure 2 it is evident that each algorithm displays substantial differences on $f1$–$f13$, showing their distinct advantages. In contrast, for $f14$–$f23$, each comparison algorithm experiences rapid declines during the initial phase and converges similarly in the iterative termination conditions. Notably, exceptions include $f15$, $f21$, and $f23$, where the algorithms exhibit minimal differences. This can be attributed to $f14$–$f23$ being fixed-dimensional functions, characterized by relatively lower difficulty. The majority of the compared algorithms effectively solve simpler optimization problems. GA and PSO show a slower decreasing trend and lack competitive superiority. DE performs relatively well on $f6$, $f8$, and $f10$–$f13$, as corroborated by Table 2 and Table 3, where it excels on fixed-dimensional functions. However, Figure 2 reveals that the performance of DE fails to significantly distinguish itself from other algorithms, and its advantages are less pronounced compared to VFSCPSO. SCA exhibits diverse performance across different functions, for instance, it performs well on $f2$ but comparatively worse on $f3$. This suggests that the effectiveness of SCA varies, with a relatively slower descent velocity observed on the fixed-dimensional functions $f20$–$f23$, resulting in poorer performance. The variants of PSO, namely, AWPSO and SCDLPSO, surpass classical algorithms such as GA and DE, as well as their component algorithms PSO and SCA, in the majority of optimization search processes. Notably, both algorithm variants demonstrate faster descent velocities on $f3$ and $f4$, with relatively small performance differences on $f5$ and $f12$. This indicates that both improved algorithms exhibit enhanced competitiveness.

Based on the insights derived from the experimental results detailed in Table 4 and Table 5, diverse algorithmic performances are observed. SFLA demonstrates moderate performance across all metrics, displaying an average performance on functions $f1$–$f5$ without a discernible advantage. BBO exhibits suboptimal performance on most functions, except for $f8$, where it outperforms the other algorithms with notably low values for best, mean, and worst, coupled with a relatively low std, indicating enhanced stability. BBO appears more suitable for addressing complex optimization problems. MA performs poorly across all metrics, particularly struggling on $f1$ and $f6$. It exhibits weaker performance, a relatively larger std, and poorer stability, suggesting that MA may be less versatile and better suited for a specific class of optimization problem. POA and DO display comparable performance with results on $f2$, featuring relatively low best, mean, and worst values. Additionally, both algorithms perform well on $f6$ and $f7$, with low mean values. Normal performance is observed on $f1$, $f3$, and $f4$ with higher mean values. POA exhibits relatively higher stability and proves applicable to various optimization problems, while DO is slightly less stable. OMA performs moderately well on most functions, boasting relatively high best and mean values along with low worst values. Although overall performance is suboptimal on $f1$ and $f2$, it excels on $f14$–$f23$, showing its suitability for lower-dimensional optimization problems. VFSCPSO stands out with excellent performance on most functions, featuring low values for best, mean, worst, and std. Notably, it excels on multi-peak functions such as $f9$–$f11$, demonstrating superior convergence accuracy and stability compared to other algorithms. The Friedman test results in Table 5 show that VFSCPSO has an average rank of 2.47 and ranks first in the overall ranking, and the overall performance of the VFSCPSO algorithm is still optimal. BBO has an average rank of 4.65 and it ranks sixth in the overall ranking, which is poor in this group of environments. MA has an average rank of 7, which suggests that MA has a poor overall performance and is likely to be less efficient in practical applications. POA, DO, and OMA are ranked in the middle in the overall ranking and their average rank is also in the middle. This indicates that the performance of the novel algorithms is more prominent. In summary, VFSCPSO excels, especially in multi-peak functions. The performance of other algorithms varies significantly across different objective functions, emphasizing the problem-specific nature of optimization algorithms. The selection of algorithms should consider the characteristics and applicability of each algorithm to specific problem types.

Mean convergence diagrams were produced based on the results of 30 optimizations of the seven algorithms on the 23 benchmark functions on the CEC2005 test suite. These were used to compare the convergence performance of the algorithms, and are shown in Figure 3.

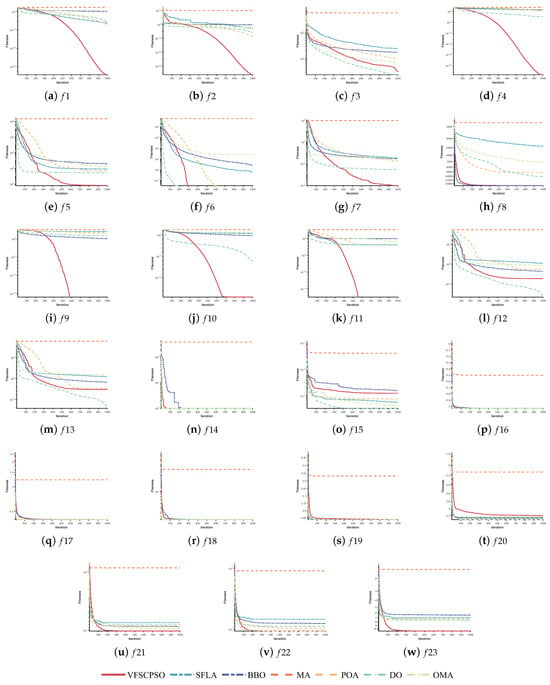
Figure 3. Convergence curves of VFSCPSO, SFLA, BBO, MA, POA, DO, and OMA on the CEC2005 test suite.

In Figure 3, the convergence curves of VFSCPSO on the single-peak functions $f1$, $f2$, $f4$, $f5$, and $f7$ and the multi-peak functions $f9$–$f11$ demonstrate a notably rapid descent, highlighting a distinct advantage over other comparative algorithms. Moreover, the convergence velocity of DO surpasses VFSCPSO on functions $f3$, $f6$, $f12$, and $f13$, implying its competitiveness in these specific contexts. Remarkably, POA exhibits swift convergence on $f6$. In addressing the intricate optimization challenge posed by $f8$, both VFSCPSO and BBO manifest robust competitiveness, indicating their suitability for solving complex optimization problems. Nevertheless, it is recognized that no algorithm can universally dominate all problem instances. Notably, VFSCPSO exhibits relative weakness on $f15$ and $f20$. Conversely, on $f22$ and $f23$, VFSCPSO demonstrates conspicuous advantages, suggesting its applicability not only to demanding optimization scenarios like $f8$ but also to simpler cases. The overall performance of VFSCPSO is superior across various problem complexities. In contrast, MA consistently grapples with falling into local optima across all convergence curves, revealing its inferior competitiveness compared to other algorithms.

4.2.2. Performance of Algorithms in High-Dimensional Environment

This series of experiments verifies the performance of VFSCPSO in a high-dimensional environment. In real life, addressing real optimization problem places heightened demands on algorithm performance, necessitating swift convergence to efficiently tackle high-dimensional challenges within predefined time constraints. The ensuing analysis includes the computation and documentation of the mean and std derived from this experimental set. The detailed experimental outcomes are encapsulated in Table 6, Table 7, Table 8, Table 9 and Table 10, while the corresponding Friedman test results are presented in Table 8 and Table 11.

Table 6. Experimental results of VFSCPSO on CEC2005 test suite $f1$–$f10$ (D = 50, 100, and 500).

Problem	Dimensions	Metric	GA	DE	PSO	SCA	AWPSO	SCDLPSO	VFSCPSO
$f1$	50	mean	7.88E+00	7.88E−10	5.25E−01	3.15E−32	4.52E−17	9.37E−43	1.19E−69
		std	2.66E+00	2.01E−10	3.41E−01	1.72E−31	2.43E−16	3.26E−42	6.30E−69
	100	mean	5.74E+00	1.48E−09	6.74E−01	1.86E−38	1.29E−18	8.49E−41	5.24E−70
		std	1.59E+00	4.28E−10	4.65E−01	7.36E−38	4.29E−18	4.53E−40	1.48E−69
	500	mean	7.41E+00	2.56E−09	6.55E−01	1.36E−37	7.96E−19	4.76E−41	7.48E−70
		std	3.04E+00	6.65E−10	6.17E−01	5.09E−37	3.45E−18	2.05E−40	1.76E−69
$f2$	50	mean	8.68E−01	3.70E−06	1.24E+01	2.25E−26	4.83E−08	3.33E−01	1.04E−36
		std	1.33E−01	6.52E−07	1.30E+01	7.76E−26	1.86E−07	1.83E+00	1.73E−36
	100	mean	9.06E−01	1.82E−04	1.31E+01	1.06E−26	1.24E−07	3.34E−01	7.17E−37
		std	1.74E−01	3.59E−05	9.41E+00	3.11E−26	4.85E−07	1.83E+00	9.86E−37
	500	mean	1.73E+35	8.60E+81	1.24E+01	5.32E−26	3.58E−08	9.99E−01	7.91E−37
		std	9.45E+35	4.70E+82	1.28E+01	1.66E−25	1.01E−07	3.05E+00	1.19E−36
$f3$	50	mean	1.59E+04	2.65E+04	4.70E+03	1.69E+04	1.05E+03	1.56E+03	2.81E+03
		std	6.69E+03	4.08E+03	4.49E+03	3.39E+03	4.69E+02	3.52E+03	1.43E+04
	100	mean	1.21E+04	2.61E+04	7.95E+03	1.67E+04	9.58E+02	8.89E+02	2.39E+03
		std	4.27E+03	5.77E+03	9.77E+03	3.77E+03	4.53E+02	7.42E+02	1.19E+04
	500	mean	1.44E+04	2.62E+04	8.23E+03	1.71E+04	1.32E+03	8.70E+02	2.53E+03
		std	6.25E+03	6.32E+03	1.54E+04	4.96E+03	7.04E+02	1.03E+03	1.23E+04
$f4$	50	mean	2.05E+01	2.51E+01	3.50E+00	4.91E+01	3.86E−01	4.16E+00	1.14E−28
		std	1.45E+00	1.21E+00	1.05E+00	1.16E+01	2.52E−01	1.28E+00	2.17E−28
	100	mean	5.01E+01	6.92E+01	5.68E+00	8.16E+01	3.63E+00	8.99E+00	4.24E−28
		std	1.23E+00	2.38E+00	1.50E+00	4.64E+00	5.33E−01	1.50E+00	1.48E−27
	500	mean	8.85E+01	9.89E+01	1.26E+01	9.84E+01	8.10E+00	1.75E+01	9.66E−27
		std	4.30E−01	2.58E−01	2.99E+00	3.67E−01	4.61E−01	1.95E+00	2.45E−26
$f5$	50	mean	3.43E+02	6.84E+01	1.79E+02	2.65E+01	2.52E+01	3.34E+01	2.09E+00
		std	1.63E+02	1.95E+01	5.58E+02	2.40E−01	9.52E+00	2.58E+01	6.72E+00
	100	mean	3.19E+02	6.19E+01	1.04E+02	2.64E+01	2.46E+01	3.03E+03	3.43E+00
		std	1.21E+02	1.87E+01	1.95E+02	2.19E−01	1.03E+01	1.64E+04	8.08E+00
	500	mean	3.27E+02	7.67E+01	3.14E+03	2.66E+01	2.85E+01	2.74E+01	5.40E−01
		std	1.28E+02	1.98E+01	1.64E+04	2.37E−01	1.66E+01	2.44E+01	5.34E−01
$f6$	50	mean	7.33E+00	0.00E+00	1.75E+01	0.00E+00	1.37E+00	4.67E−01	0.00E+00
		std	2.01E+00	0.00E+00	8.14E+00	0.00E+00	2.06E+00	6.81E−01	0.00E+00
	100	mean	8.63E+00	0.00E+00	1.94E+01	0.00E+00	1.33E+00	5.33E−01	0.00E+00
		std	3.58E+00	0.00E+00	1.12E+01	0.00E+00	1.42E+00	1.20E+00	0.00E+00
	500	mean	7.13E+00	0.00E+00	7.00E+01	0.00E+00	2.23E+00	1.37E+00	0.00E+00
		std	2.37E+00	0.00E+00	9.18E+01	0.00E+00	3.68E+00	4.63E+00	0.00E+00
$f7$	50	mean	6.03E−02	3.05E−02	1.88E−01	3.85E−03	7.10E−03	3.62E−02	9.79E−05
		std	2.06E−02	4.84E−03	6.80E−01	3.33E−03	2.56E−03	2.24E−02	1.11E−04
	100	mean	6.76E−02	3.18E−02	9.43E−03	3.05E−03	6.50E−03	2.10E−01	1.32E−04
		std	1.94E−02	6.36E−03	6.02E−03	1.62E−03	2.35E−03	6.86E−01	1.04E−04
	500	mean	6.27E−02	3.32E−02	3.67E−01	3.63E−03	6.72E−03	1.26E−01	1.22E−04
		std	2.39E−02	6.19E−03	1.54E+00	2.61E−03	2.40E−03	5.00E−01	1.19E−04
$f8$	50	mean	−1.26E+04	−1.26E+04	−8.74E+03	−5.66E+03	−3.41E+03	−8.83E+03	−1.24E+04
		std	3.98E+00	3.09E−05	1.07E+03	3.00E+02	3.90E+02	9.55E+02	3.56E+02
	100	mean	−1.26E+04	−1.26E+04	−8.54E+03	−5.84E+03	−3.35E+03	−9.01E+03	−1.22E+04
		std	5.61E+00	2.47E−05	1.29E+03	3.74E+02	3.15E+02	1.38E+03	4.93E+02
	500	mean	−1.26E+04	−1.26E+04	−8.55E+03	−5.71E+03	−3.31E+03	−8.90E+03	−1.22E+04
		std	5.11E+00	1.84E−05	1.05E+03	2.53E+02	4.19E+02	9.99E+02	4.80E+02
$f9$	50	mean	2.51E+00	1.61E+01	9.22E+01	2.25E−15	3.48E+01	2.76E+01	0.00E+00
		std	8.36E−01	2.39E+00	3.05E+01	7.85E−15	1.26E+01	1.21E+01	0.00E+00
	100	mean	2.45E+00	8.82E+00	8.81E+01	6.65E−10	3.09E+01	3.01E+01	0.00E+00
		std	7.64E−01	2.52E+00	3.56E+01	2.68E−09	8.79E+00	1.39E+01	0.00E+00
	500	mean	2.42E+00	4.27E+00	8.79E+01	3.64E−10	3.24E+01	3.38E+01	0.00E+00
		std	9.77E−01	2.39E+00	3.14E+01	1.99E−09	6.16E+00	2.03E+01	0.00E+00
$f10$	50	mean	1.31E+00	1.41E−05	2.42E+00	9.02E+00	7.10E−01	4.55E−01	3.61E−15
		std	2.74E−01	4.29E−06	7.49E−01	9.90E+00	1.12E+00	7.47E−01	1.53E−15
	100	mean	1.27E+00	1.78E−05	2.33E+00	8.70E+00	5.23E−01	7.72E−01	2.55E−15
		std	2.70E−01	4.20E−06	9.26E−01	1.01E+01	1.03E+00	8.77E−01	1.80E−15
	500	mean	1.27E+00	2.14E−05	1.91E+00	8.02E+00	2.94E−01	4.73E−01	3.14E−15
		std	2.86E−01	4.53E−06	8.21E−01	9.99E+00	7.77E−01	7.60E−01	1.74E−15

Table 7. Experimental results of VFSCPSO on CEC2005 test suite $f11$–$f13$ (D=50, 100, and 500).

Problem	Dimensions	Metric	GA	DE	PSO	SCA	AWPSO	SCDLPSO	VFSCPSO
$f11$	50	mean	1.06E+00	4.14E−08	5.11E−01	3.29E−12	2.09E+01	1.19E−01	0.00E+00
		std	2.37E−02	4.37E−08	1.98E−01	1.55E−11	3.72E+00	8.47E−02	0.00E+00
	100	mean	1.06E+00	7.20E−08	5.47E−01	1.72E−10	2.09E+01	1.31E−01	0.00E+00
		std	2.45E−02	1.02E−07	1.82E−01	9.21E−10	2.65E+00	1.24E−01	0.00E+00
	500	mean	1.07E+00	1.81E−07	5.19E−01	3.11E−15	2.12E+01	1.22E−01	0.00E+00
		std	2.27E−02	2.83E−07	2.33E−01	1.70E−14	2.22E+00	1.06E−01	0.00E+00
$f12$	50	mean	2.89E−02	2.75E−11	6.58E−01	4.04E−03	1.14E−01	1.27E−01	2.87E−04
		std	1.89E−02	7.92E−12	6.50E−01	1.58E−03	2.79E−01	2.12E−01	2.07E−04
	100	mean	3.82E−02	4.71E−11	7.31E−01	4.52E−03	1.45E−01	2.78E−01	2.24E−04
		std	3.35E−02	1.26E−11	7.72E−01	2.22E−03	1.92E−01	4.70E−01	1.41E−04
	500	mean	3.89E−02	7.76E−11	6.81E−01	3.91E−03	1.73E−01	2.08E−01	2.29E−04
		std	3.89E−02	2.62E−11	8.50E−01	1.61E−03	2.44E−01	3.06E−01	1.33E−04
$f13$	50	mean	3.70E−01	9.58E−11	2.56E+00	1.85E−01	4.64E−20	7.66E−03	3.86E−03
		std	1.41E−01	2.68E−11	1.55E+00	1.07E−01	1.66E−19	1.96E−02	3.90E−03
	100	mean	3.86E−01	1.83E−10	2.94E+00	1.74E−01	1.72E−20	4.03E−03	4.38E−03
		std	1.31E−01	6.34E−11	1.67E+00	1.18E−01	4.08E−20	8.89E−03	5.55E−03
	500	mean	4.00E−01	3.20E−10	2.74E+00	2.13E−01	3.04E−20	4.76E−03	2.94E−03
		std	1.36E−01	8.15E−11	1.32E+00	1.49E−01	1.07E−19	1.14E−02	1.67E−03

Table 8. Results of Friedman test for Table 6 and Table 7.

Dimension	Metrics	GA	DE	PSO	SCA	AWPSO	SCDLPSO	VFSCPSO
50	count	0	1	0	3	2	0	9
	Ave.rank	5.923076	3.76923	5.230769	3.461538	3.846153	4	1.538461
	Total.rank	7	3	6	2	4	5	1
100	count	0	1	0	3	1	1	9
	Ave.rank	5.615384	3.76923	5.153846	3.461538	3.846153	4.307692	1.615384
	Total.rank	7	3	6	2	4	5	1
500	count	0	1	0	3	1	1	9
	Ave.rank	5.846153	3.615384	5.076923	3.76923	3.923076	4	1.538461
	Total.rank	7	2	6	3	4	5	1

Table 9. Experimental results and Friedman test results of VFSCPSO on CEC2005 test suite $f1$–$f10$ (D = 50, 100, and 500).

Problem	Dimensions	Metric	SFLA	BBO	MA	DO	OMA	POA	VFSCPSO
$f1$	50	mean	3.42E+02	2.40E+00	5.64E+04	1.23E−11	7.40E−02	9.60E−15	1.19E−69
		std	8.12E+02	6.76E−01	8.83E+03	7.78E−12	3.47E−02	1.27E−14	6.30E−69
	100	mean	6.12E+03	2.96E+00	5.92E+04	1.29E−11	1.49E−01	5.95E−15	5.24E−70
		std	2.89E+03	1.24E+00	7.71E+03	8.22E−12	3.40E−01	7.08E−15	1.48E−69
	500	mean	3.93E+04	2.90E+00	5.81E+04	1.12E−11	7.27E−02	9.73E−15	7.48E−70
		std	2.74E+03	1.19E+00	6.44E+03	7.88E−12	4.21E−02	2.16E−14	1.76E−69
$f2$	50	mean	1.61E+03	5.46E−01	1.02E+19	2.14E−06	2.94E−03	1.39E−08	1.04E−36
		std	8.73E+03	8.74E−02	5.56E+19	9.23E−07	7.20E−04	1.31E−08	1.73E−36
	100	mean	1.43E+13	5.72E−01	2.19E+38	1.94E−06	3.27E−03	2.27E+00	7.17E−37
		std	7.55E+13	1.10E−01	1.20E+39	1.48E−06	3.94E−03	6.85E+00	9.86E−37
	500	mean	2.98E+239	7.91E−01	6.02E+190	1.73E−06	1.44E−03	4.54E+83	7.91E−37
		std	6.55E+04	1.31E−01	6.55E+04	6.93E−07	4.62E−04	2.48E+84	1.19E−36
$f3$	50	mean	2.47E+04	2.48E+04	5.86E+05	2.35E+03	7.91E+03	9.04E+03	2.81E+03
		std	1.28E+04	1.10E+04	4.28E+05	1.23E+03	2.77E+03	4.12E+03	1.43E+04
	100	mean	2.54E+04	1.93E+04	5.70E+05	2.08E+03	7.86E+03	1.13E+04	2.39E+03
		std	1.05E+04	1.16E+04	4.04E+05	1.06E+03	2.46E+03	3.90E+03	1.19E+04
	500	mean	7.77E+04	2.23E+04	6.00E+05	2.06E+03	7.58E+03	1.23E+04	2.53E+03
		std	2.37E+04	8.37E+03	4.06E+05	1.09E+03	2.44E+03	3.94E+03	1.23E+04
$f4$	50	mean	3.48E+01	1.33E+01	8.37E+01	5.87E−01	1.21E+01	7.44E+01	1.14E−28
		std	5.03E+00	1.79E+00	6.81E+00	3.87E−01	1.43E+00	7.86E+00	2.17E−28
	100	mean	4.26E+01	3.17E+01	8.97E+01	2.86E+01	1.35E+01	8.85E+01	4.24E−28
		std	9.77E−01	2.38E+00	3.89E+00	7.00E+00	9.86E−01	1.64E+00	1.48E−27
	500	mean	9.46E+01	7.81E+01	9.51E+01	9.03E+01	1.76E+01	9.70E+01	9.66E−27
		std	2.62E−01	1.27E+00	2.49E+00	2.00E+00	1.14E+00	3.82E−01	2.45E−26
$f5$	50	mean	3.41E+04	2.72E+02	1.94E+08	2.42E+01	1.54E+02	4.23E+01	2.09E+00
		std	8.02E+04	3.26E+02	4.29E+07	1.60E−01	6.21E+01	3.54E+01	6.72E+00
	100	mean	2.40E+06	2.13E+02	2.02E+08	2.43E+01	1.90E+02	5.09E+01	3.43E+00
		std	1.58E+06	9.18E+01	3.42E+07	2.06E−01	8.84E+01	3.71E+01	8.08E+00
	500	mean	8.25E+07	3.49E+02	1.99E+08	2.42E+01	1.61E+02	3.90E+01	5.40E−01
		std	1.80E+07	4.54E+02	3.49E+07	3.30E−01	7.71E+01	2.83E+01	5.34E−01
$f6$	50	mean	4.48E+01	2.63E+00	5.90E+04	0.00E+00	3.34E+01	0.00E+00	0.00E+00
		std	8.31E+01	1.73E+00	6.14E+03	0.00E+00	2.97E+01	0.00E+00	0.00E+00
	100	mean	6.63E+03	2.97E+00	5.76E+04	0.00E+00	3.84E+01	0.00E+00	0.00E+00
		std	2.98E+03	2.31E+00	7.27E+03	0.00E+00	3.32E+01	0.00E+00	0.00E+00
	500	mean	3.81E+04	2.33E+00	5.82E+04	0.00E+00	3.70E+01	0.00E+00	0.00E+00
		std	3.21E+03	1.52E+00	8.55E+03	0.00E+00	3.17E+01	0.00E+00	0.00E+00
$f7$	50	mean	3.03E−01	2.59E−02	8.72E+01	2.89E−03	3.75E−02	1.44E−02	9.79E−05
		std	2.78E−01	9.10E−03	2.74E+01	2.16E−03	1.18E−02	5.16E−03	1.11E−04
	100	mean	1.75E+00	2.71E−02	9.31E+01	3.46E−03	3.47E−02	1.49E−02	1.32E−04
		std	7.25E−01	9.06E−03	2.13E+01	1.48E−03	1.11E−02	5.74E−03	1.04E−04
	500	mean	4.07E+01	2.88E−02	8.56E+01	2.89E−03	3.33E−02	1.28E−02	1.22E−04
		std	5.36E+00	9.54E−03	1.72E+01	1.00E−03	1.21E−02	4.12E−03	1.19E−04
$f8$	50	mean	−3.96E+03	−1.26E+04	−2.69E+03	−1.00E+04	−7.11E+03	−8.98E+03	−1.24E+04
		std	5.45E+02	2.31E+00	4.33E+02	6.20E+02	8.19E+02	8.15E+02	3.56E+02
	100	mean	−3.88E+03	−1.26E+04	−2.79E+03	−1.02E+04	−7.18E+03	−8.62E+03	−1.22E+04
		std	3.04E+02	3.12E+00	5.64E+02	3.79E+02	9.82E+02	7.28E+02	4.93E+02
	500	mean	−4.47E+03	−1.26E+04	−2.61E+03	−1.01E+04	−7.21E+03	−8.78E+03	−1.22E+04
		std	3.17E+02	2.12E+00	3.99E+02	5.94E+02	8.83E+02	8.40E+02	4.80E+02
$f9$	50	mean	1.16E+02	1.26E+00	3.81E+02	8.50E+00	4.67E+01	3.86E+01	0.00E+00
		std	4.11E+01	4.43E−01	3.69E+01	7.26E+00	1.88E+01	1.02E+01	0.00E+00
	100	mean	1.21E+02	1.14E+00	3.85E+02	7.54E+00	5.84E+01	3.94E+01	0.00E+00
		std	5.30E+01	3.73E−01	2.08E+01	6.75E+00	2.60E+01	1.12E+01	0.00E+00
	500	mean	3.29E+02	1.04E+00	3.94E+02	7.14E+00	4.90E+01	4.11E+01	0.00E+00
		std	1.68E+01	3.49E−01	3.08E+01	5.35E+00	2.20E+01	1.05E+01	0.00E+00
$f10$	50	mean	4.87E+00	7.11E−01	2.01E+01	7.39E−07	4.14E+00	1.66E+01	3.61E−15
		std	3.10E+00	1.75E−01	3.15E−01	2.57E−07	1.14E+00	7.54E+00	1.53E−15
	100	mean	1.31E+01	7.56E−01	2.01E+01	7.97E−07	3.84E+00	1.79E+01	2.55E−15
		std	2.25E+00	1.86E−01	3.45E−01	2.86E−07	7.40E−01	6.08E+00	1.80E−15
	500	mean	1.96E+01	7.03E−01	2.00E+01	8.11E−07	4.04E+00	1.85E+01	3.14E−15
		std	1.97E−01	2.09E−01	5.60E−01	2.36E−07	8.67E−01	5.04E+00	1.74E−15

Table 10. Experimental results and Friedman test results of VFSCPSO on CEC2005 test suite $f11$–$f13$ (D = 50, 100, and 500).

Problem	Dimensions	Metric	SFLA	BBO	MA	DO	OMA	POA	VFSCPSO
$f11$	50	mean	2.87E+00	9.95E−01	5.26E+02	1.41E−02	1.32E−01	9.92E−03	0.00E+00
		std	7.45E+00	4.80E−02	4.13E+01	1.94E−02	7.10E−02	1.32E−02	0.00E+00
	100	mean	6.07E+01	9.99E−01	5.23E+02	1.75E−02	1.33E−01	9.27E−03	0.00E+00
		std	2.60E+01	3.95E−02	7.46E+01	2.26E−02	9.25E−02	1.05E−02	0.00E+00
	500	mean	3.46E+02	1.01E+00	5.37E+02	9.10E−03	1.59E−01	1.39E−02	0.00E+00
		std	3.67E+01	2.88E−02	5.04E+01	1.33E−02	1.05E−01	1.64E−02	0.00E+00
$f12$	50	mean	1.25E+03	1.59E−02	4.36E+08	5.88E−09	4.13E−01	8.31E−02	2.87E−04
		std	4.76E+03	1.76E−02	1.12E+08	3.06E−09	6.26E−01	2.31E−01	2.07E−04
	100	mean	1.76E+05	2.03E−02	4.26E+08	5.87E−09	4.82E−01	6.22E−02	2.24E−04
		std	2.01E+05	2.77E−02	8.97E+07	2.09E−09	6.15E−01	1.00E−01	1.41E−04
	500	mean	1.49E+08	1.81E−02	4.36E+08	5.63E−09	2.64E−01	6.58E−02	2.29E−04
		std	3.45E+07	1.94E−02	8.58E+07	2.27E−09	3.96E−01	1.65E−01	1.33E−04
$f13$	50	mean	2.50E+04	1.45E−01	8.70E+08	7.43E−08	6.73E+00	3.66E−03	3.86E−03
		std	1.03E+05	7.32E−02	2.11E+08	2.24E−08	8.44E+00	5.27E−03	3.90E−03
	100	mean	2.30E+06	1.20E−01	8.24E+08	6.92E−08	1.10E+01	3.66E−03	4.38E−03
		std	1.84E+06	3.26E−02	1.61E+08	3.56E−08	1.18E+01	5.27E−03	5.55E−03
	500	mean	3.47E+08	1.29E−01	9.08E+08	6.74E−08	6.40E+00	3.66E−03	2.94E−03
		std	5.39E+07	4.61E−02	1.99E+08	3.12E−08	9.00E+00	5.27E−03	1.67E−03

Table 11. Results of Friedman’s test for Table 9 and Table 10.

Dimensions	Metric	SFLA	BBO	MA	DO	OMA	POA	VFSCPSO
50	Count	0	1	0	4	0	1	9
	Avg. rank	5.76923	3.923076	7	2.076923	4.307692	3.307692	1.384615
	Overall rank	6	4	7	2	5	3	1
100	Count	0	1	0	4	0	1	9
	Avg. rank	5.846153	3.76923	7	2.076923	4.153846	3.538461	1.384615
	Overall rank	6	4	7	2	5	3	1
500	Count	0	1	0	4	0	1	9
	Avg. rank	6	3.692307	6.846153	2.076923	4.153846	3.692307	1.307692
	Overall rank	6	3	7	2	5	3	1

Based on the experimental results from Table 6 and Table 7, the evaluation across 50, 100, and 500 dimensions reveals distinctive algorithmic performances. GA demonstrates relatively good performance on $f8$ but exhibits poorer efficacy on other functions. SCA displays superior performance on $f2$, $f6$, $f7$, $f9$, and $f11$. Particularly noteworthy is its excellence on $f6$, which is inherited by VFSCPSO. DE holds a clear advantage on $f6$, $f8$, and $f12$. However, its overall performance is slightly lower compared to SCA. The introduction of the sine–cosine strategy in SCA contributes significantly to this advantage. AWPSO performs well on $f3$, $f4$, $f7$, and $f13$, demonstrating better overall performance and remarkable algorithmic stability. SCDLPSO excels on $f3$ and performs relatively well on $f1$, indicating its suitability for addressing single-peak problems. In terms of generality, AWPSO outperforms SCDLPSO. VFSCPSO exhibits a lower mean across different dimensions and relatively poorer performance on $f13$. However, it outperforms other comparison algorithms, especially on $f1$, $f4$, $f9$, and $f11$, with significantly better performance and lower std, indicating superior global search ability and stability. Despite a higher average ranking in higher dimensions, the removal of fixed-dimensional functions from the experiment affirms VFSCPSO’s suitability for complex optimization problem in higher dimensions. AWPSO and SCDLPSO exhibit better performance on functions such as $f3$ and $f4$ compared to GA and DE, thereby demonstrating specific advantages and the efficacy of the algorithm variants. From the Friedman test results in Table 8, GA and PSO still receive lower rankings. The competitiveness of DE diminishes compared to SCA after the dimensionality increase, suggesting that SCA is more suitable for solving high-dimensional optimization problems. The two algorithm variants, AWPSO and SCDLPSO, exhibit comparable performances with competitive outcomes. In summary, VFSCPSO proves effective, particularly in complex optimization problems of higher dimensions, demonstrating improved global search ability and stability.

Mean convergence diagrams were produced based on the results of 30 optimizations of the seven algorithms on the 12 benchmark functions on the CEC2005 test suite in high-dimensional environments, which are used to compare the algorithms’ convergence performance. They are shown in Figure 4.

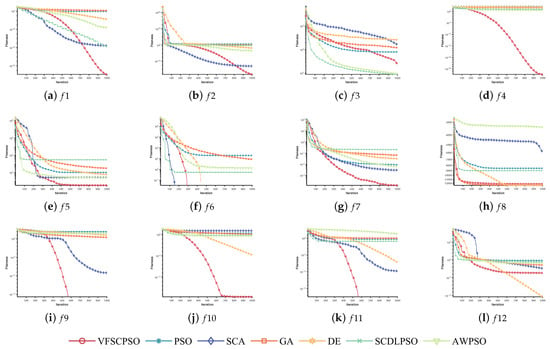
Figure 4. Convergence curves of VFSCPSO, PSO, SCA, GA, DE, SCDLPSO, and AWPSO on the CEC2005 test suite (D = 100).

As can be seen from Figure 4, it is evident that, compared to the standard CEC2005 test environment, the convergence rates of each algorithm remain relatively stable when elevated to 100 dimensions. Specific observations can be made for individual functions. On $f1$, the search accuracy of SCA diminishes, falling short of the performance achieved by SCDLPSO after the dimensionality increase. For $f2$ and $f7$, VFSCPSO demonstrates improved search accuracy despite the higher dimensionality. On $f3$, while the search accuracy of the variant AWPSO surpasses that of SCDLPSO, the overall convergence accuracy decreases compared to the experiment with 30 dimensions. On $f4$, all algorithms, excluding VFSCPSO, experience a decline in search accuracy. For $f5$, SCDLPSO exhibits reduced capability to escape local optima, indicating its unsuitability for high-dimensional optimization problems. Regarding $f8$, DE exhibits a degree of competitiveness, but a notable decrease in optimal search on $f11$ is observed. SCA achieves slightly higher search accuracy on $f9$, indicating that algorithmic search performance is influenced to varying degrees based on problem characteristics and changes in dimensionality. There is no significant change in the convergence velocity of each comparison algorithm on $f10$ and $f12$. VFSCPSO, notably, does not show significant accuracy degradation; instead, an improvement in the optimization search of individual functions is observed. This suggests that VFSCPSO is well suited for solving optimization problems with higher dimensionality.

According to the experimental results presented in Table 9 and Table 10, the overall performance of SFLA is generally satisfactory, demonstrating relative stability, particularly on $f4$. MA exhibits slightly inferior performance compared to SFLA across various functions. BBO performs suboptimally on single-peak functions such as $f1$, $f3$, and $f5$, but excels on multi-peak functions, particularly achieving the best performance on $f8$. DO outperforms others on $f3$, $f6$, $f12$, and $f13$, demonstrating competitiveness but still falling short compared to VFSCPSO. OMA displays strong competitiveness on $f4$, but its overall performance is subpar in other tests. POA stands out, with strong competitiveness on $f6$ and commendable performance on $f1$. In contrast, VFSCPSO consistently attains optimal performance across all test functions and dimensions, characterized by a small std, indicating remarkable stability. In summary, algorithmic performance varies significantly across different test functions and dimensions, demonstrating successes for the best value and challenges that necessitate problem-specific considerations. The Friedman test results in Table 11 show that MA continues to exhibit a lack of overall advantage, suggesting its potential suitability for specific problem types rather than high-dimensional optimization. The advantage of POA becomes more pronounced, elevating its ranking from third to second. DO and BBO struggle to adapt to the high-dimensional optimization environment, resulting in drops from second to fifth and third to sixth in the ranking, respectively. The change in OMA’s ranking is not substantial. VFSCPSO consistently maintains its first rank throughout the entire series of experiments, clearly distinguishing itself from other algorithms and proving highly suitable for high-dimensional optimization problems.

Mean convergence curves were made based on the results of 30 optimizations of the seven algorithms on the 12 benchmark functions on the CEC2005 test suite in a high-dimensional environment, and are used to compare the algorithms’ convergence performance. They are shown in Figure 5.

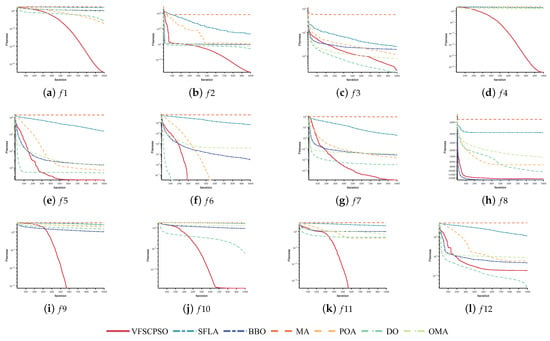
Figure 5. Convergence curves of VFSCPSO, SFLA, BBO, MA, POA, DO, and OMA on the CEC2005 test suite (D = 100).

As depicted in Figure 5, the comparison of this series of experiments with 30 dimensions reveals notable alterations in the search velocity and accuracy of SFLA across various functions, such as $f1$, $f5$, $f6$, $f7$, $f8$, and $f11$. Particularly on $f5$, $f6$, and $f12$, the decrease in performance is conspicuous. In contrast, VFSCPSO exhibits a substantial improvement in convergence accuracy on $f2$, whereas other algorithms show minimal variations. While slight performance declines are observed on $f12$, the search velocity remains relatively stable for each algorithm, and no significant changes occur on individual functions, such as $f3$. DO, however, undergoes significant performance changes on $f4$. In summary, SFLA experiences more pronounced alterations in convergence velocity and accuracy with rising dimensions. In contrast, for other algorithms, convergence rates do not exhibit significant changes when progressing to 100 dimensions, showing only marginal decreases. VFSCPSO consistently outperforms in all search aspects, highlighting its superior convergence performance in more complex optimization problems.

4.2.3. Performance of Algorithms in Large-Scale Environment

This series of experiments verifies the performance of VFSCPSO in a large-scale environment. Finally, the mean and std of this set of experiments are calculated and recorded. Table 12, Table 13, Table 14, Table 15 and Table 16 show the experimental results and Table 14 and Table 17 show the Friedman test results.

Table 12. Experimental results and Friedman test results of VFSCPSO on CEC2005 test suite $f1$–$f10$ (D = 1000, 2000, and 5000).

Problem	Dimensions	Metric	GA	DE	PSO	SCA	AWPSO	SCDLPSO	VFSCPSO
$f1$	1000	mean	7.22E+00	2.66E−09	5.71E−01	1.30E−33	7.45E−19	2.05E−39	1.24E−70
		std	2.36E+00	7.86E−10	5.03E−01	4.99E−33	1.68E−18	1.12E−38	3.04E−70
	2000	mean	6.94E+00	2.93E−09	5.61E−01	3.86E−34	1.35E−18	1.42E−38	6.89E−70
		std	2.13E+00	6.40E−10	4.12E−01	1.35E−33	3.81E−18	4.67E−38	1.72E−69
	5000	mean	7.13E+00	3.30E−09	4.40E−01	8.30E−38	3.10E−18	4.46E−42	5.15E−70
		std	2.15E+00	9.43E−10	2.61E−01	2.61E−37	1.16E−17	1.09E−41	1.16E−69
$f2$	1000	mean	6.55E+04	6.55E+04	2.82E+00	6.55E+04	4.50E+01	9.60E−05	1.39E−36
		std	Nan	Nan	2.98E+00	Nan	4.39E+01	3.30E−04	2.12E−36
	2000	mean	6.55E+04	6.55E+04	4.62E+00	6.55E+04	6.55E+04	4.59E−13	4.50E−36
		std	Nan	Nan	1.98E+00	Nan	Nan	2.05E−12	7.65E−36
	5000	mean	6.55E+04	6.55E+04	6.55E+04	6.55E+04	6.55E+04	6.55E+04	4.77E−30
		std	Nan	Nan	Nan	Nan	Nan	Nan	1.49E−29
$f3$	1000	mean	1.73E+04	2.65E+04	9.31E+03	1.88E+04	1.27E+03	1.03E+03	2.80E+03
		std	8.51E+03	4.88E+03	1.87E+04	4.60E+03	6.18E+02	1.07E+03	1.72E+03
	2000	mean	1.58E+04	2.74E+04	4.79E+03	1.70E+04	1.03E+03	1.66E+03	2.59E+03
		std	8.06E+03	4.56E+03	6.65E+03	4.33E+03	4.08E+02	1.47E+03	1.86E+03
	5000	mean	1.42E+04	2.64E+04	3.75E+03	1.61E+04	8.68E+02	7.41E+02	2.67E+03
		std	6.21E+03	6.09E+03	4.00E+03	4.56E+03	4.42E+02	6.15E+02	1.97E+03
$f4$	1000	mean	9.41E+01	9.95E+01	1.47E+01	9.93E+01	9.37E+00	2.15E+01	1.65E−25
		std	1.97E−01	1.22E−01	2.43E+00	1.44E−01	3.21E−01	2.18E+00	5.94E−25
	2000	mean	9.70E+01	9.97E+01	1.89E+01	9.97E+01	1.07E+01	2.35E+01	1.15E−24
		std	1.22E−01	5.85E−02	3.00E+00	8.35E−02	3.72E−01	1.34E+00	3.25E−24
	5000	mean	9.88E+01	9.99E+01	2.42E+01	9.99E+01	1.26E+01	2.79E+01	8.03E−24
		std	5.01E−02	1.60E−02	3.74E+00	4.93E−02	2.62E−01	2.25E+00	1.41E−23
$f5$	1000	mean	3.46E+02	7.32E+01	1.01E+02	2.64E+01	2.44E+01	3.18E+01	3.92E+00
		std	1.44E+02	1.94E+01	1.38E+02	1.86E−01	1.11E+01	2.92E+01	9.17E+00
	2000	mean	3.33E+02	6.68E+01	3.09E+03	2.65E+01	2.97E+01	2.09E+02	1.33E+00
		std	1.46E+02	1.73E+01	1.64E+04	2.35E−01	1.97E+01	6.77E+02	4.84E+00
	5000	mean	3.75E+02	6.47E+01	1.36E+02	2.65E+01	2.24E+01	1.83E+01	4.04E−01
		std	1.57E+02	1.61E+01	1.91E+02	2.60E−01	3.05E+00	2.46E+01	2.99E−01
$f6$	1000	mean	8.33E+00	0.00E+00	1.97E+01	0.00E+00	1.70E+00	7.67E−01	0.00E+00
		std	3.21E+00	0.00E+00	1.16E+01	0.00E+00	1.93E+00	1.38E+00	0.00E+00
	2000	mean	7.50E+00	0.00E+00	2.02E+01	0.00E+00	1.50E+00	5.00E−01	0.00E+00
		std	2.61E+00	0.00E+00	7.96E+00	0.00E+00	1.36E+00	6.88E−01	0.00E+00
	5000	mean	7.80E+00	0.00E+00	2.12E+01	0.00E+00	1.93E+00	1.33E−01	0.00E+00
		std	2.96E+00	0.00E+00	8.35E+00	0.00E+00	1.87E+00	3.52E−01	0.00E+00
$f7$	1000	mean	6.13E−02	3.34E−02	3.70E−01	3.91E−03	7.36E−03	3.09E−02	1.10E−04
		std	1.84E−02	6.56E−03	1.16E+00	2.86E−03	1.94E−03	1.36E−02	8.58E−05
	2000	mean	6.51E−02	3.36E−02	4.57E−01	3.40E−03	7.00E−03	3.31E−02	7.92E−05
		std	2.53E−02	7.33E−03	1.42E+00	1.92E−03	2.35E−03	1.51E−02	5.14E−05
	5000	mean	5.05E−02	3.53E−02	1.48E−02	3.82E−03	7.60E−03	3.89E−01	1.20E−04
		std	2.00E−02	4.80E−03	8.59E−03	2.40E−03	2.69E−03	1.38E+00	9.93E−05
$f8$	1000	mean	−1.26E+04	−1.26E+04	−8.32E+03	−5.70E+03	−3.28E+03	−9.15E+03	−1.22E+04
		std	4.68E+00	2.87E−05	1.05E+03	3.54E+02	3.97E+02	1.01E+03	5.32E+02
	2000	mean	−1.26E+04	−1.26E+04	−8.62E+03	−5.79E+03	−3.28E+03	−9.23E+03	−1.24E+04
		std	8.24E+00	1.66E−05	1.02E+03	3.58E+02	3.32E+02	1.12E+03	3.20E+02
	5000	mean	−1.26E+04	−1.26E+04	−8.71E+03	−5.62E+03	−3.16E+03	−8.87E+03	−1.24E+04
		std	6.55E+00	2.06E−05	1.10E+03	2.72E+02	3.88E+02	1.22E+03	1.62E+02
$f9$	1000	mean	2.48E+00	3.95E+00	9.09E+01	1.14E−05	2.92E+01	2.92E+01	0.00E+00
		std	7.17E−01	2.32E+00	3.37E+01	6.26E−05	1.00E+01	1.28E+01	0.00E+00
	2000	mean	2.59E+00	3.65E+00	8.10E+01	7.65E−11	2.61E+01	2.98E+01	0.00E+00
		std	8.62E−01	2.65E+00	3.23E+01	3.66E−10	8.00E+00	1.28E+01	0.00E+00
	5000	mean	2.37E+00	3.11E+00	8.17E+01	0.00E+00	3.36E+01	3.96E+01	0.00E+00
		std	8.56E−01	2.23E+00	3.84E+01	0.00E+00	1.04E+01	2.08E+01	0.00E+00
$f10$	1000	mean	1.21E+00	2.31E−05	2.23E+00	1.00E+01	4.28E−01	6.18E−01	3.02E−15
		std	1.85E−01	4.94E−06	8.08E−01	1.02E+01	8.77E−01	8.19E−01	1.77E−15
	2000	mean	1.15E+00	2.08E−05	2.38E+00	1.14E+01	8.72E−01	4.86E−01	2.90E−15
		std	2.33E−01	3.85E−06	6.31E−01	1.01E+01	1.44E+00	6.56E−01	1.79E−15
	5000	mean	1.32E+00	2.54E−05	1.98E+00	1.00E+01	1.27E−01	7.07E−01	3.73E−15
		std	2.92E−01	5.67E−06	1.06E+00	1.06E+01	4.91E−01	7.60E−01	1.50E−15

Table 13. Experimental results and Friedman test results of VFSCPSO on CEC2005 test suite $f11$–$f13$ (D = 1000, 2000, and 5000).

Problem	Dimensions	Metric	GA	DE	PSO	SCA	AWPSO	SCDLPSO	VFSCPSO
$f11$	1000	mean	1.07E+00	1.25E−07	4.78E−01	9.86E−11	2.16E+01	1.46E−01	0.00E+00
		std	1.62E−02	1.45E−07	2.24E−01	5.40E−10	3.00E+00	1.06E−01	0.00E+00
	2000	mean	1.06E+00	8.15E−08	5.19E−01	5.92E−17	2.09E+01	1.27E−01	0.00E+00
		std	2.55E−02	6.74E−08	1.82E−01	2.23E−16	3.17E+00	1.25E−01	0.00E+00
	5000	mean	1.08E+00	1.73E−07	5.33E−01	7.77E−17	2.02E+01	1.43E−01	0.00E+00
		std	2.77E−02	1.80E−07	2.25E−01	2.46E−16	2.46E+00	1.06E−01	0.00E+00
$f12$	1000	mean	3.82E−02	7.68E−11	9.59E−01	3.74E−03	1.35E−01	2.80E−01	2.07E−04
		std	3.52E−02	2.89E−11	1.12E+00	1.79E−03	1.83E−01	4.57E−01	1.50E−04
	2000	mean	4.07E−02	6.60E−11	7.61E−01	4.06E−03	1.14E−01	1.34E−01	2.55E−04
		std	3.70E−02	1.80E−11	1.05E+00	2.04E−03	1.50E−01	2.91E−01	2.07E−04
	5000	mean	2.88E−02	8.07E−11	7.17E−01	4.58E−03	2.07E−01	3.04E−01	3.38E−04
		std	1.36E−02	1.82E−11	5.85E−01	1.82E−03	3.82E−01	4.16E−01	1.47E−04
$f13$	1000	mean	3.57E−01	3.09E−10	3.67E+00	2.44E−01	3.66E−04	5.12E−03	2.59E−03
		std	1.03E−01	1.06E−10	2.35E+00	1.69E−01	2.01E−03	1.07E−02	1.70E−03
	2000	mean	3.87E−01	2.87E−10	2.90E+00	2.42E−01	3.71E−19	2.75E−03	3.72E−03
		std	1.30E−01	7.50E−11	1.98E+00	1.59E−01	1.52E−18	4.88E−03	3.25E−03
	5000	mean	4.12E−01	3.42E−10	2.38E+00	2.55E−01	2.49E−22	2.20E−03	3.93E−03
		std	1.27E−01	1.42E−10	2.27E+00	1.37E−01	3.97E−22	4.55E−03	5.45E−03

Table 14. Results of Friedman’s test for Table 12 and Table 13.

Dimensions	Problem	GA	DE	PSO	SCA	AWPSO	SCDLPSO	VFSCPSO
1000	Count	0	1	0	4	0	1	9
	Avg. rank	5.615385	3.923077	5.153846	3.615385	4	3.692308	1.538462
	Overall rank	7	4	6	2	5	3	1
2000	Count	0	1	0	3	2	0	9
	Avg. rank	5.692308	3.769231	5	3.538462	3.923077	3.769231	1.615385
	Overall rank	7	3	6	2	5	3	1
5000	Count	0	2	0	3	1	1	9
	Avg. rank	5.307692	3.692308	4.923077	3.461538	3.769231	3.769231	1.615385
	Overall rank	7	3	6	2	4	4	1

Table 15. Experimental results and Friedman test results of VFSCPSO on CEC2005 test suite $f1$–$f10$ (D = 1000, 2000, and 5000).

Problem	Dimensions	Metric	SFLA	BBO	MA	DO	OMA	POA	VFSCPSO
$f1$	1000	mean	3.86E+04	2.48E+00	5.88E+04	1.46E−11	8.33E−02	5.98E−15	1.24E−70
		std	3.33E+03	1.10E+00	8.76E+03	9.50E−12	4.69E−02	7.73E−15	3.04E−70
	2000	mean	4.00E+04	2.79E+00	5.77E+04	1.37E−11	8.54E−02	5.95E−15	6.89E−70
		std	2.97E+03	1.36E+00	6.89E+03	6.85E−12	4.83E−02	9.53E−15	1.72E−69
	5000	mean	3.82E+04	2.05E+00	5.64E+04	1.40E−11	6.77E−02	7.34E−15	5.15E−70
		std	3.71E+03	7.78E−01	8.85E+03	6.97E−12	3.75E−02	1.20E−14	1.16E−69
$f2$	1000	mean	6.55E+04	6.55E+04	6.55E+04	6.55E+04	6.55E+04	6.55E+04	1.39E−36
		std	Nan	Nan	Nan	Nan	Nan	Nan	2.12E−36
	2000	mean	6.55E+04	6.55E+04	6.55E+04	6.55E+04	6.55E+04	6.55E+04	4.50E−36
		std	Nan	Nan	Nan	Nan	Nan	Nan	7.65E−36
	5000	mean	6.55E+04	6.55E+04	6.55E+04	6.55E+04	6.55E+04	6.55E+04	4.77E−30
		std	Nan	Nan	Nan	Nan	Nan	Nan	1.49E−29
$f3$	1000	mean	7.38E+04	2.26E+04	5.85E+05	2.44E+03	8.25E+03	1.21E+04	2.80E+03
		std	2.24E+04	7.97E+03	3.20E+05	1.28E+03	3.21E+03	6.56E+03	1.72E+03
	2000	mean	7.33E+04	2.01E+04	6.12E+05	1.99E+03	8.00E+03	1.31E+04	2.59E+03
		std	1.93E+04	1.24E+04	3.88E+05	9.75E+02	2.81E+03	4.65E+03	1.86E+03
	5000	mean	5.72E+04	2.62E+04	6.65E+05	1.80E+03	7.96E+03	1.60E+04	2.67E+03
		std	2.10E+04	8.79E+03	5.38E+05	1.10E+03	2.65E+03	4.21E+03	1.97E+03
$f4$	1000	mean	9.80E+01	8.83E+01	9.65E+01	9.57E+01	1.90E+01	9.85E+01	1.65E−25
		std	1.34E−01	7.79E−01	1.39E+00	7.60E−01	1.10E+00	1.57E−01	5.94E−25
	2000	mean	9.92E+01	9.40E+01	9.76E+01	9.82E+01	2.05E+01	9.91E+01	1.15E−24
		std	6.99E−02	3.40E−01	9.93E−01	3.68E−01	9.22E−01	1.08E−01	3.25E−24
	5000	mean	9.97E+01	9.76E+01	9.83E+01	9.94E+01	2.25E+01	9.96E+01	8.03E−24
		std	2.54E−02	2.24E−01	5.56E−01	1.23E−01	6.30E−01	3.45E−02	1.41E−23
$f5$	1000	mean	9.78E+07	2.24E+02	1.97E+08	2.42E+01	1.71E+02	5.96E+01	3.92E+00
		std	1.31E+07	1.01E+02	3.42E+07	2.46E−01	8.53E+01	5.08E+01	9.17E+00
	2000	mean	8.91E+07	3.20E+02	1.99E+08	2.43E+01	1.54E+02	4.84E+01	1.33E+00
		std	1.43E+07	3.38E+02	3.68E+07	2.28E−01	4.60E+01	2.93E+01	4.84E+00
	5000	mean	8.54E+07	2.70E+02	1.82E+08	2.43E+01	1.95E+02	4.96E+01	4.04E−01
		std	1.60E+07	1.41E+02	3.56E+07	2.80E−01	7.38E+01	4.18E+01	2.99E−01
$f6$	1000	mean	3.94E+04	3.13E+00	5.65E+04	0.00E+00	4.43E+01	0.00E+00	0.00E+00
		std	4.51E+03	1.78E+00	5.35E+03	0.00E+00	3.14E+01	0.00E+00	0.00E+00
	2000	mean	4.00E+04	2.85E+00	6.16E+04	0.00E+00	3.48E+01	0.00E+00	0.00E+00
		std	3.60E+03	1.95E+00	5.63E+03	0.00E+00	2.50E+01	0.00E+00	0.00E+00
	5000	mean	3.86E+04	3.60E+00	5.80E+04	0.00E+00	3.07E+01	0.00E+00	0.00E+00
		std	2.74E+03	1.84E+00	6.89E+03	0.00E+00	2.14E+01	0.00E+00	0.00E+00
$f7$	1000	mean	4.38E+01	2.87E−02	8.73E+01	3.03E−03	3.31E−02	1.32E−02	1.10E−04
		std	6.81E+00	9.19E−03	2.11E+01	1.52E−03	1.15E−02	4.26E−03	8.58E−05
	2000	mean	4.08E+01	2.65E−02	9.02E+01	2.75E−03	3.35E−02	1.43E−02	7.92E−05
		std	8.05E+00	8.82E−03	2.13E+01	1.24E−03	9.93E−03	6.04E−03	5.14E−05
	5000	mean	3.85E+01	2.52E−02	9.44E+01	4.22E−03	3.21E−02	1.40E−02	1.20E−04
		std	8.03E+00	7.27E−03	2.98E+01	3.08E−03	7.21E−03	4.00E−03	9.93E−05
$f8$	1000	mean	−4.41E+03	−1.26E+04	−2.74E+03	−9.84E+03	−7.39E+03	−8.69E+03	−1.22E+04
		std	3.61E+02	3.39E+00	4.13E+02	5.43E+02	1.19E+03	7.09E+02	5.32E+02
	2000	mean	−4.32E+03	−1.26E+04	−2.66E+03	−1.01E+04	−7.49E+03	−8.35E+03	−1.24E+04
		std	3.02E+02	3.32E+00	3.01E+02	6.63E+02	1.14E+03	9.00E+02	3.20E+02
	5000	mean	−4.50E+03	−1.26E+04	−2.79E+03	−1.01E+04	−7.27E+03	−8.62E+03	−1.24E+04
		std	3.25E+02	3.94E+00	4.65E+02	6.18E+02	1.05E+03	5.29E+02	1.62E+02
$f9$	1000	mean	3.34E+02	1.19E+00	3.88E+02	8.87E+00	5.18E+01	3.90E+01	0.00E+00
		std	1.38E+01	5.13E−01	3.05E+01	6.49E+00	2.19E+01	9.08E+00	0.00E+00
	2000	mean	3.33E+02	1.28E+00	3.88E+02	1.16E+01	5.03E+01	3.75E+01	0.00E+00
		std	1.46E+01	4.90E−01	3.77E+01	8.83E+00	2.02E+01	1.05E+01	0.00E+00
	5000	mean	3.27E+02	1.25E+00	4.03E+02	9.30E+00	4.59E+01	3.48E+01	0.00E+00
		std	1.19E+01	3.97E−01	4.29E+01	6.10E+00	1.58E+01	1.03E+01	0.00E+00
$f10$	1000	mean	1.96E+01	7.09E−01	2.01E+01	8.32E−07	4.20E+00	1.86E+01	3.02E−15
		std	2.39E−01	1.85E−01	3.38E−01	2.63E−07	9.80E−01	5.05E+00	1.77E−15
	2000	mean	1.96E+01	7.10E−01	2.00E+01	7.40E−07	3.81E+00	1.69E+01	2.90E−15
		std	1.94E−01	1.73E−01	2.71E−01	2.77E−07	1.01E+00	7.30E+00	1.79E−15
	5000	mean	1.95E+01	6.40E−01	2.01E+01	7.51E−07	3.96E+00	1.86E+01	3.73E−15
		std	3.44E−01	1.58E−01	3.84E−01	2.71E−07	1.13E+00	5.15E+00	1.50E−15

Table 16. Experimental results and Friedman test results of VFSCPSO on CEC2005 test suite $f11$–$f13$ (D = 1000, 2000, and 5000).

Problem	Dimensions	Metric	SFLA	BBO	MA	DO	OMA	POA	VFSCPSO
$f11$	1000	mean	3.51E+02	1.00E+00	5.33E+02	1.13E-02	1.59E-01	1.97E-02	0.00E+00
		std	3.00E+01	3.03E-02	4.56E+01	1.81E-02	8.94E-02	2.26E-02	0.00E+00
	2000	mean	3.64E+02	1.00E+00	5.24E+02	2.59E-02	1.13E-01	1.10E-02	0.00E+00
		std	2.67E+01	4.19E-02	5.96E+01	2.94E-02	4.27E-02	1.07E-02	0.00E+00
	5000	mean	3.50E+02	1.00E+00	5.41E+02	1.28E-02	1.27E-01	8.86E-03	0.00E+00
		std	3.40E+01	6.12E-02	7.51E+01	1.96E-02	6.31E-02	8.91E-03	0.00E+00
$f12$	1000	mean	1.53E+08	1.75E-02	3.86E+08	6.22E-09	4.13E-01	7.26E-02	2.07E-04
		std	3.19E+07	1.90E-02	1.07E+08	3.29E-09	5.70E-01	1.34E-01	1.50E-04
	2000	mean	1.57E+08	1.18E-02	4.40E+08	4.65E-09	5.00E-01	3.63E-02	2.55E-04
		std	3.49E+07	1.01E-02	9.30E+07	1.75E-09	4.83E-01	6.95E-02	2.07E-04
	5000	mean	1.30E+08	1.67E-02	4.82E+08	4.48E-09	2.98E-01	1.38E-02	3.38E-04
		std	1.87E+07	1.25E-02	1.15E+08	2.37E-09	4.02E-01	5.35E-02	1.47E-04
$f13$	1000	mean	3.62E+08	1.21E-01	9.07E+08	7.28E-08	1.45E+01	3.30E-03	2.59E-03
		std	8.35E+07	3.59E-02	1.65E+08	3.78E-08	1.45E+01	5.12E-03	1.70E-03
	2000	mean	3.68E+08	1.33E-01	9.23E+08	8.00E-08	5.49E+00	3.30E-03	3.72E-03
		std	7.66E+07	4.09E-02	1.28E+08	3.21E-08	8.12E+00	5.17E-03	3.25E-03
	5000	mean	3.28E+08	1.47E-01	9.12E+08	6.51E-08	5.22E+00	3.66E-03	3.93E-03
		std	5.95E+07	3.90E-02	1.75E+08	2.20E-08	7.12E+00	5.36E-03	5.45E-03

Table 17. Results of Friedman’s test for Table 15 and Table 16.

Dimensions	Metric	SFLA	BBO	MA	DO	OMA	POA	VFSCPSO
1000	Count	0	1	0	4	0	1	9
	Avg. rank	5.692308	3.538462	6.461538	2.076923	4.076923	3.461538	1.307692
	Overall rank	6	4	7	2	5	3	1
2000	Count	0	1	0	4	0	1	9
	Avg. rank	5.769231	3.538462	6.384615	2.230769	4.076923	3.230769	1.384615
	Overall rank	6	4	7	2	5	3	1
5000	Count	0	1	0	4	0	1	9
	Avg. rank	5.769231	3.615385	6.384615	2.230769	4.076923	3.153846	1.384615
	Overall rank	6	4	7	2	5	3	1

The experimental results presented in Table 12 and Table 13 show substantial variations in algorithmic performance across functions and dimensions, spanning from $f1$ to $f13$. The algorithm ranking on $f1$ produces no significant change as the number of dimensions changes. At 1000 dimensions, VFSCPSO emerges as the best performer, with the smallest mean and std, indicative of enhanced stability. GA excels in mean performance, while both GA and PSO exhibit relatively poorer results. The results for 2000 dimensions are similar to those for 1000 dimensions, but the differences are more pronounced at higher numbers of dimensions. At 5000 dimensions VFSCPSO performs well on the mean, alongside competitive performances by SCDLPSO and SCA. All algorithms demonstrate a relatively small std on $f1$ at this number of dimensions. While the compared algorithms struggle with dimensionality, VFSCPSO maintains its robust performance, as is particularly evident on $f2$ at 5000 dimensions. On both $f1$ and $f2$, SCA and GA perform relatively poorly and show instability. On $f3$, VFSCPSO does not have a competitive advantage, and the best performer is AWPSO. VFSCPSO pulls away from the other comparison algorithms on $f4$, with the AWPSO performing better on the mean and VFSCPSO performing best for 1000 and 2000 dimensions. On $f5$, DE and AWPSO consistently perform admirably on the mean, with relatively minor stds across all dimensions. There are still three algorithms SCA, DE, and VFSCPSO that can converge to the global optimum on $f6$. Additionally, DE and AWPSO lead on $f7$ in mean performance, while PSO and SCA consistently deliver commendable mean values on $f8$. Across various functions $f1$–$f2$, $f4$–$f7$, $f9$–$f11$, VFSCPSO consistently attains optimal results, showing stability across all dimensions. DE performs well on the mean, and the std is relatively small and performs well on some functions. On $f10$ and $f11$, DE performs well on the mean for 1000 and 2000 dimensions, while AWPSO has a relatively small mean for 5000 dimensions. SCA and AWPSO are more competitive on $f12$ and $f13$. AWPSO, SCDLPSO, and VFSCPSO perform well and are relatively stable under several functions and dimensions, and can be used as alternative algorithms for large-scale optimization problems. PSO is affected by dimensionality in some cases. The Friedman test results in Table 14 show that VFSCPSO consistently achieves optimal outcomes, which is similar to the results produced in the 50-, 100-, and 500-dimensional settings.

Mean convergence diagrams were produced based on the results of 30 optimizations of the seven algorithms on the 12 benchmark functions on the CEC2005 test suite in a large-scale environment, which are used to compare the algorithms’ convergence performance. They are shown in Figure 6.

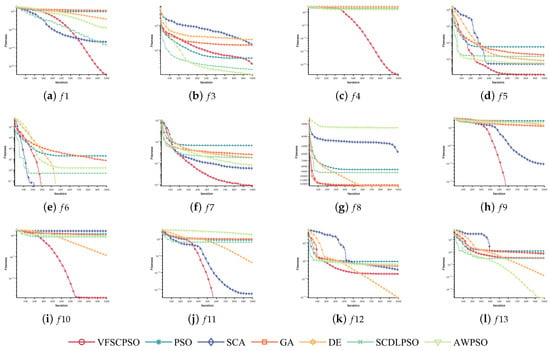
Figure 6. Convergence curves of VFSCPSO, PSO, SCA, GA, DE, SCDLPSO, and AWPSO on the CEC2005 test suite (D = 2000).

As can be seen from Figure 6, the impact of increasing the number of dimensions on the algorithmic convergence accuracy is evident. Notably, as the dimensionality rises, the convergence accuracy of SCA on $f1$ notably lags behind that of AWPSO. This discrepancy suggests that AWPSO may be better suited for tackling large-scale optimization problem. The convergence accuracy on $f3$ experiences a collective decrease among all algorithms, with SCA and PSO demonstrating the most significant declines. A certain differences is observable in the performances of algorithmic variants, with VFSCPSO showing relatively superior results, though the differences are not obvious. While the convergence accuracy decreases on $f4$ for all algorithms, the convergence velocity remains relatively stable. Noteworthy is the pronounced decrease in the search rate of PSO on $f5$, while $f6$ and $f9$–$f13$ exhibit minimal changes. On $f7$, the performance of PSO directly descends to the lowest rank, showing a diminished convergence velocity and accuracy compared to low-dimensional searches. A similar significant decline is observed in the performance of SCDLPSO. On $f8$, VFSCPSO demonstrates heightened competitiveness with increasing dimensionality. In summary, VFSCPSO excels in overall performance and maintains significant competitiveness in addressing large-scale problems.

The experimental results in Table 15 and Table 16 demonstrate the better performance of the VFSCPSO across all dimensions on $f1$, exhibiting advantage in the mean and std metrics and showing good stability. POA demonstrates aptitude for handling $f1$, likely due to its consistent performance even with the rise in dimensionality. In contrast, other algorithms witness a relative decline in performance as the number of dimensions increases, reaffirming VFSCPSO’s sustained leadership. For $f2$, the performance of all algorithms, excluding VFSCPSO, fails to diminish, highlighting the unique effectiveness of VFSCPSO in tackling this function. On $f3$, DO emerges as the top performer in mean, indicating its suitability for addressing $f3$ across diverse dimensions. VFSCPSO not only competes better but also maintains superior performance stability. Conversely, MA lags in mean performance. $f5$, $f8$, $f9$, $f10$, $f11$, and $f12$ underscore VFSCPSO’s consistent superiority in mean and standard deviation metrics across varying dimensions. VFSCPSO exhibits particular aptitude for handling $f5$. In the case of $f6$ and $f13$, the DO excels in both metrics, showing its adaptability to these functions. VFSCPSO, while maintaining competitive performance, also exhibits enhanced stability. The algorithms perform differently in different environments. The SFLA, BBO, MA, DO, OMA, and POA algorithms perform better in some specific contexts, but the VFSCPSO algorithm is relatively more competitive, especially in terms of mean and std. The selection of the most suitable algorithm still needs to consider the characteristics of the specific problem and practical application requirements. The Friedman test results in Table 17 show that the VFSCPSO algorithm has the first overall ranking under all dimensions and performs the best. The DO algorithm has the next best overall ranking under 2000 and 5000 dimensions, coming in second and also higher. The BBO and POA algorithms also perform better in the overall rankings, coming in third and fourth. VFSCPSO has the highest counts under all the dimensions, suggesting that it achieves the best performance under each dimension. The DO does not achieve the best performance under 1000 dimensions. However, it performs well under all other dimensions. Other algorithms did not achieve the best performance under some dimensions, and overall the VFSCPSO and DO algorithms performed relatively well in all dimensions.

Mean convergence curves were produced based on the results of 30 optimizations of the seven algorithms on the 12 benchmark functions on the CEC2005 test suite in a large-scale environment for comparing the algorithms’ convergence performance, as shown in Figure 7. Since there is no decrease on $f2$ except VFSCPSO, the convergence curve of $f2$ is not shown.

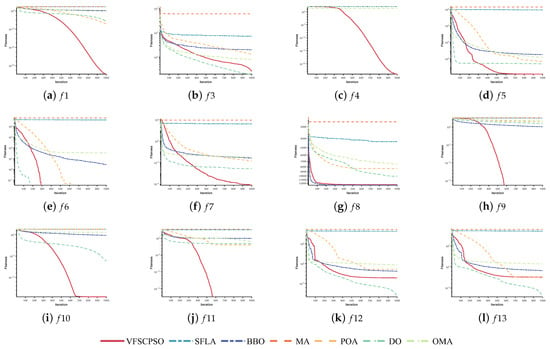
Figure 7. Convergence curves of VFSCPSO, SFLA, BBO, MA, POA, DO, and OMA on the CEC2005 test suite (D = 2000).

From Figure 7, it can be seen that as the dimension increases, the convergence trend of each algorithm on $f1$–$f5$ is almost the same as that in 100 dimension, and on $f6$ although some algorithms are able to iterate to the global optimum, the number of iterations of DO and POA increases in the search of global optimum, and the number of iterations of the VFSCPSO is almost unchanged. SFLA has a change in convergence trend on some functions, the accuracy on $f3$, $f5$–$f7$, $f10$–$f12$ shows a decreasing trend, the other algorithms do not change significantly, the accuracy of convergence velocity on $f13$ decreases more obviously. DO also has some competitiveness, the convergence velocity on $f6$ is fast and the number of iterations needed to converge to the global optimum is the least, although it does not converge to the global optimum on $f13$, but it achieves the best result among the comparative algorithms. The convergence trend of the convergence curve of the VFSCPSO algorithm is almost the same as that in 100 dimensions, and it achieves the first place in the overall rankings.

4.2.4. Performance of Algorithm in Ultra-Large-Scale Environment

In order to compare and analyze the performance of the hybrid algorithm in solving large-scale optimization problems in a deeper way and to demonstrate the superiority of the hybrid algorithm VFSCPSO proposed in this paper, this series of experiments verifies the performance of the VFSCPSO in an ultra-large-scale environment with D = 10,000. Finally, the best, mean, worst, and std of this series of experiments are calculated and recorded. Table 18 and Table 19 show the experimental results and Friedman test results.

Table 18. Experimental results and Friedman test results of VFSCPSO on CEC2005 test suite $f1$–$f13$ (D = 10,000).

Problem	Metric	GA	DE	PSO	SCA	AWPSO	SCDLPSO	VFSCPSO
$f1$	best	5.03E+00	1.89E−09	7.25E−02	1.87E−45	1.76E−21	2.79E−47	5.73E−73
	mean	7.10E+00	2.83E−09	7.90E−01	1.20E−36	5.80E−19	3.42E−38	6.16E−70
	worst	9.79E+00	3.91E−09	1.84E+00	6.97E−36	3.65E−18	3.40E−37	5.44E−69
	std	1.52E+00	6.70E−10	5.94E−01	2.51E−36	1.14E−18	1.07E−37	1.7E−69
$f2$	best	6.55E+04	6.55E+04	5.11E+00	6.55E+04	8.20E+01	3.35E−12	2.05E−36
	mean	6.55E+04	6.55E+04	6.55E+04	6.55E+04	6.55E+04	6.55E+04	1.66E−30
	worst	6.55E+04	6.55E+04	6.55E+04	6.55E+04	6.55E+04	6.55E+04	1.64E−29
	std	Nan	Nan	Nan	Nan	Nan	Nan	5.17E−30
$f3$	best	8.77E+03	1.51E+04	2.95E+02	1.04E+04	4.28E+02	1.67E+02	1.07E−01
	mean	1.33E+04	2.91E+04	5.57E+03	1.76E+04	1.18E+03	9.88E+02	1.04E+04
	worst	1.86E+04	4.00E+04	2.13E+04	2.55E+04	2.16E+03	3.55E+03	6.99E+04
	std	4.22E+03	8.11E+03	5.94E+03	3.86E+03	5.25E+02	1.10E+03	1.44E+04
$f4$	best	9.94E+01	9.99E+01	2.11E+01	9.99E+01	1.36E+01	2.85E+01	8.02E−27
	mean	9.94E+01	9.99E+01	2.84E+01	1.00E+02	1.40E+01	3.18E+01	1.32E−21
	worst	9.94E+01	1.00E+02	3.43E+01	1.00E+02	1.44E+01	3.44E+01	1.20E−20
	std	2.02E−02	1.78E−02	4.10E+00	7.58E−03	2.54E−01	2.12E+00	3.77E−21
$f5$	best	1.87E+02	3.86E+01	2.98E+01	2.62E+01	7.21E+00	1.27E+01	5.06E−03
	mean	3.22E+02	7.23E+01	5.75E+01	2.64E+01	2.11E+01	4.95E+01	5.65E−01
	worst	4.81E+02	1.03E+02	1.83E+02	2.70E+01	2.74E+01	1.05E+02	1.67E+00
	std	8.36E+01	1.98E+01	4.64E+01	2.18E−01	5.22E+00	3.41E+01	5.63E−01
$f6$	best	2.00E+00	0.00E+00	0.00E+00	0.00E+00	0.00E+00	0.00E+00	0.00E+00
	mean	6.30E+00	0.00E+00	1.57E+01	0.00E+00	1.30E+00	2.50E+00	0.00E+00
	worst	1.00E+01	0.00E+00	3.80E+01	0.00E+00	3.00E+00	1.00E+01	0.00E+00
	std	2.54E+00	0.00E+00	1.18E+01	0.00E+00	1.06E+00	3.78E+00	0.00E+00
$f7$	best	4.61E−02	2.82E−02	4.09E−03	1.46E−03	4.08E−03	2.50E−02	1.98E−05
	mean	6.59E−02	3.44E−02	8.23E−03	3.56E−03	2.76E−01	3.63E−02	6.67E−05
	worst	7.95E−02	4.39E−02	2.06E−02	6.13E−03	2.69E+00	4.84E−02	1.92E−04
	std	1.17E−02	4.83E−03	5.36E−03	1.53E−03	8.49E−01	7.52E−03	5.50E−05
$f8$	best	−1.26E+04	−1.26E+04	−1.01E+04	−6.25E+03	−3.44E+03	−1.05E+04	−1.26E+04
	mean	−1.26E+04	−1.26E+04	−8.37E+03	−5.70E+03	−3.13E+03	−8.97E+03	−1.23E+04
	worst	−1.25E+04	−1.26E+04	−7.32E+03	−5.18E+03	−2.81E+03	−6.27E+03	−1.15E+04
	std	5.29E+00	1.12E−05	9.60E+02	3.48E+02	1.97E+02	1.29E+03	3.66E+02
$f9$	best	1.04E+00	4.06E−01	0.00E+00	0.00E+00	1.79E+01	1.19E+01	0.00E+00
	mean	2.49E+00	2.41E+00	3.36E+01	0.00E+00	2.99E+01	2.48E+01	0.00E+00
	worst	4.33E+00	7.38E+00	1.35E+02	0.00E+00	4.18E+01	4.97E+01	0.00E+00
	std	9.98E−01	2.02E+00	4.78E+01	0.00E+00	7.91E+00	1.07E+01	0.00E+00
$f10$	best	7.96E−01	1.78E−05	2.13E+00	4.44E−15	3.29E−12	4.31E−14	8.88E−16
	mean	1.36E+00	2.27E−05	2.56E+00	8.03E+00	1.13E+00	4.00E−01	2.31E−15
	worst	1.77E+00	2.96E−05	3.19E+00	2.01E+01	3.09E+00	1.50E+00	4.44E−15
	std	3.27E−01	3.41E−06	3.47E−01	1.04E+01	1.24E+00	6.49E−01	1.83E−15
$f11$	best	1.04E+00	2.64E−08	3.98E−01	0.00E+00	1.72E+01	2.70E−02	0.00E+00
	mean	1.06E+00	9.74E−08	6.45E−01	5.55E−17	2.01E+01	1.21E−01	0.00E+00
	worst	1.10E+00	3.26E−07	8.51E−01	5.55E−16	2.26E+01	3.32E−01	0.00E+00
	std	1.55E−02	8.96E−08	1.50E−01	1.76E−16	1.85E+00	8.98E−02	0.00E+00
$f12$	best	1.15E−02	5.50E−11	0.00E+00	0.00E+00	5.90E−24	1.57E−32	0.00E+00
	mean	3.67E−02	8.46E−11	2.70E−01	1.25E−03	2.28E−01	2.95E−01	7.03E−05
	worst	1.02E−01	1.22E−10	2.87E+00	5.84E−03	8.32E−01	2.54E+00	4.58E−04
	std	2.83E−02	1.89E−11	6.17E−01	1.76E−03	2.76E−01	7.90E−01	1.37E−04
$f13$	best	2.17E−01	1.82E−10	1.74E+00	7.85E−02	1.68E−24	1.35E−32	8.58E−04
	mean	3.81E−01	3.54E−10	3.68E+00	2.23E−01	4.57E−20	6.50E−03	3.35E−03
	worst	6.29E−01	5.96E−10	7.57E+00	3.93E−01	2.58E−19	2.10E−02	6.47E−03
	std	1.21E−01	1.16E−10	1.70E+00	1.20E−01	8.15E−20	7.47E−03	1.70E−03
Count		0	3	0	2	1	1	9
Avg. rank		5	3.307692	5	3.692308	4.076923	3.846154	1.615385
Overall rank		6	2	6	3	5	4	1

Table 19. Experimental results and Friedman test results of VFSCPSO on CEC2005 test suite $f1$–$f13$ (D = 10,000).

Problem	Metric	SFLA	BBO	MA	DO	OMA	POA	VFSCPSO
$f1$	best	3.23E+04	1.49E+00	5.26E+04	2.18E−12	2.97E−02	7.88E−16	5.73E−73
	mean	3.72E+04	2.83E+00	6.07E+04	1.85E−11	7.90E−02	3.50E−15	6.16E−70
	worst	4.07E+04	4.47E+00	6.43E+04	6.82E−11	2.34E−01	1.48E−14	5.44E−69
	std	3.12E+03	8.98E−01	3.80E+03	1.88E−11	6.04E−02	4.35E−15	1.7E−69
$f2$	best	6.55E+04	6.55E+04	6.55E+04	6.55E+04	6.55E+04	6.55E+04	2.05E−36
	mean	6.55E+04	6.55E+04	6.55E+04	6.55E+04	6.55E+04	6.55E+04	1.66E−30
	worst	6.55E+04	6.55E+04	6.55E+04	6.55E+04	6.55E+04	6.55E+04	1.64E−29
	std	Nan	Nan	Nan	Nan	Nan	Nan	5.17E−30
$f3$	best	4.29E+04	8.03E+03	9.37E+04	4.31E+02	4.74E+03	6.91E+03	1.07E−01
	mean	6.07E+04	1.84E+04	5.89E+05	2.46E+03	8.21E+03	1.40E+04	1.04E+04
	worst	7.77E+04	2.84E+04	1.88E+06	3.94E+03	1.14E+04	1.91E+04	6.99E+04
	std	1.27E+04	7.01E+03	5.55E+05	1.16E+03	2.25E+03	4.11E+03	1.44E+04
$f4$	best	9.98E+01	9.86E+01	9.80E+01	9.97E+01	2.26E+01	9.97E+01	8.02E−27
	mean	9.99E+01	9.87E+01	9.91E+01	9.97E+01	2.37E+01	9.98E+01	1.32E−21
	worst	9.99E+01	9.88E+01	9.97E+01	9.99E+01	2.58E+01	9.98E+01	1.20E−20
	std	1.10E−02	5.57E−02	6.02E−01	5.16E−02	9.51E−01	2.38E−02	3.77E−21
$f5$	best	7.18E+07	1.31E+02	1.47E+08	2.41E+01	1.02E+02	2.50E+01	5.06E−03
	mean	7.67E+07	2.11E+02	2.02E+08	2.43E+01	1.63E+02	6.20E+01	5.65E−01
	worst	8.15E+07	2.89E+02	2.58E+08	2.45E+01	2.56E+02	9.57E+01	5.65E−01
	std	6.83E+06	5.77E+01	3.21E+07	1.40E−01	5.22E+01	3.18E+01	5.63E−01
$f6$	best	2.93E+04	0.00E+00	5.25E+04	0.00E+00	6.00E+00	0.00E+00	0.00E+00
	mean	3.17E+04	1.80E+00	6.07E+04	0.00E+00	3.02E+01	0.00E+00	0.00E+00
	worst	3.40E+04	3.00E+00	7.12E+04	0.00E+00	7.20E+01	0.00E+00	0.00E+00
	std	3.31E+03	9.19E−01	6.40E+03	0.00E+00	2.09E+01	0.00E+00	0.00E+00
$f7$	best	3.12E+01	1.42E−02	8.83E+01	7.93E−04	1.77E−02	5.36E−03	1.98E−05
	mean	3.41E+01	2.75E−02	1.04E+02	2.32E−03	3.31E−02	1.42E−02	6.67E−05
	worst	3.70E+01	3.86E−02	1.24E+02	4.19E−03	5.11E−02	2.76E−02	1.92E−04
	std	4.06E+00	7.74E−03	1.06E+01	1.11E−03	1.10E−02	6.80E−03	5.50E−05
$f8$	best	−4.49E+03	−1.26E+04	−4.25E+03	−1.10E+04	−7.82E+03	−9.36E+03	−1.26E+04
	mean	−4.32E+03	−1.26E+04	−2.76E+03	−1.03E+04	−7.03E+03	−8.15E+03	−1.23E+04
	worst	−4.14E+03	−1.26E+04	−1.95E+03	−9.33E+03	−6.13E+03	−6.73E+03	−1.15E+04
	std	2.50E+02	1.47E+00	6.52E+02	4.82E+02	5.99E+02	8.31E+02	3.66E+02
$f9$	best	3.30E+02	5.83E−01	3.37E+02	4.99E−12	2.49E+01	2.19E+01	0.00E+00
	mean	3.32E+02	1.20E+00	3.77E+02	4.98E+00	4.04E+01	3.40E+01	0.00E+00
	worst	3.33E+02	1.69E+00	4.11E+02	1.99E+01	6.47E+01	4.68E+01	0.00E+00
	std	2.37E+00	3.92E−01	2.30E+01	7.30E+00	1.30E+01	8.45E+00	0.00E+00
$f10$	best	1.93E+01	4.77E−01	1.95E+01	4.04E−07	3.37E+00	3.99E−07	8.88E−16
	mean	1.95E+01	6.44E−01	2.02E+01	7.28E−07	4.30E+00	1.80E+01	2.31E−15
	worst	1.97E+01	8.68E−01	2.05E+01	1.03E−06	5.89E+00	2.00E+01	4.44E−15
	std	2.80E−01	1.43E−01	2.96E−01	2.03E−07	8.45E−01	6.31E+00	1.83E−15
$f11$	best	2.93E+02	9.53E−01	4.74E+02	7.42E−11	5.07E−02	1.55E−15	0.00E+00
	mean	3.12E+02	1.01E+00	5.48E+02	1.74E−02	1.37E−01	1.82E−02	0.00E+00
	worst	3.31E+02	1.03E+00	6.42E+02	7.30E−02	3.21E−01	6.61E−02	0.00E+00
	std	2.71E+01	2.67E−02	5.74E+01	2.66E−02	8.52E−02	2.22E−02	0.00E+00
$f12$	best	1.37E+08	5.14E−03	2.63E+08	3.08E−09	2.32E−04	3.36E−16	0.00E+00
	mean	1.54E+08	9.97E−03	4.29E+08	5.34E−09	5.24E−01	5.18E−02	7.03E−05
	worst	1.72E+08	2.19E−02	6.61E+08	9.00E−09	1.46E+00	2.07E−01	4.58E−04
	std	2.46E+07	4.69E−03	1.17E+08	1.92E−09	5.48E−01	7.33E−02	1.37E−04
$f13$	best	2.36E+08	4.93E−02	6.26E+08	3.03E−08	1.19E−02	2.51E−15	8.58E−04
	mean	3.04E+08	1.36E−01	8.71E+08	5.75E−08	2.60E+00	4.39E−03	3.35E−03
	worst	3.72E+08	2.12E−01	1.13E+09	1.16E−07	1.14E+01	1.10E−02	6.47E−03
	std	9.59E+07	4.63E−02	1.64E+08	2.38E−08	4.00E+00	5.67E−03	1.70E−03
Count		0	1	0	4	0	1	9
Avg. rank		5.76923	3.538461	6.384615	2.153846	4	3.384615	1.384615
Overall rank		6	4	7	2	5	3	1

According to the experimental results in Table 18 and Table 19, the other twelve comparative algorithms show significant differences in the 10,000-dimensional environment. VFSCPSO achieves the best results in each of the metrics on $f1$, $f2$, $f4$, $f6$, $f7$, $f9$, $f10$, $f11$, and $f12$, which means that VFSCPSO performs well on most of the test functions. It is highly competitive in most cases, can be applied to different environments, shows diversity and adaptability, and has high convergence and stability. On $f2$, only the VFSCPSO algorithmic model is able to descend, and the comparative algorithms are all caught in the dilemma of being severely unable to descend, and this hybrid algorithmic model has a better global searchability even when it is difficult to optimize, and a relatively good solution can be found. On $f6$, the DE, SCA, DO, POA, and VFSCPSO algorithms are still able to converge to the global optimal solution. The different algorithms show their advantages under different benchmark functions and metrics. PSO and SCA perform well on some functions, but as constituent algorithms do not perform as well as VFSCPSO in most cases. VFSCPSO in 10,000 dimensions still does not produce significant changes on the 12 benchmark functions, with small fluctuations in the solution accuracy, high stability, and good performance consistency across different runs. This further proves that the VFSCPSO has excellent comprehensive performance in dealing with ultra-large-scale optimization problems, and is able to effectively cope with the challenges in large-scale environments. The Friedman test results show that VFSCPSO has the best performance and can be used for solving large-scale optimization problems. In the Friedman test results in Table 18, GA and PSO are relatively balanced and at a disadvantage, which may not be applicable to ultra-large-scale problems. DE is ranked second in the overall ranking, similar to the results of previous experiments, indicating that DE is more stable. SCA and SCDLPSO are ranked in the middle of the list, which is a better overall performance, but not as good as VFSCPSO. AWPSO ranked fifth in overall rank and average rank and the overall performance declined faster, indicating that the algorithm is less stable. According to the analysis results, VFSCPSO ranks first in both the overall ranking and the average ranking, and its performance is still excellent. In the Friedman test results in Table 19, SFLA, MA, and OMA have a high average rank and a low overall rank. These algorithms may not be applicable to ultra-large-scale problems. BBO, POA, and OMA have moderate overall performance in the ranking, with no particularly outstanding performance, and are relatively well balanced to each other. DO has a higher average rank of 2.15 and an overall rank of 2. It performs well on the overall ranking and has a more outstanding performance. VFSCPSO has an average rank of 1.38 and an overall rank of 1, with the highest ranking, indicating that its performance is excellent on all indicators. The average rank is the best performing algorithm on the overall ranking, with the most outstanding performance, and is most suitable for solving ultra-large-scale optimization problems. This is attributed to the SCA strategy that increases the flexibility of the algorithm and avoids the algorithm from falling into local optima, and the 10,000 dimensions run reflects the advantages of VFSCPSO more.

In order to demonstrate the performance of VFSCPSO, the convergence curves of VFSCPSO on the benchmark functions in 100, 500, 1000, 2000, 5000, and 10,000 dimensions were produced. They are shown in Figure 8.

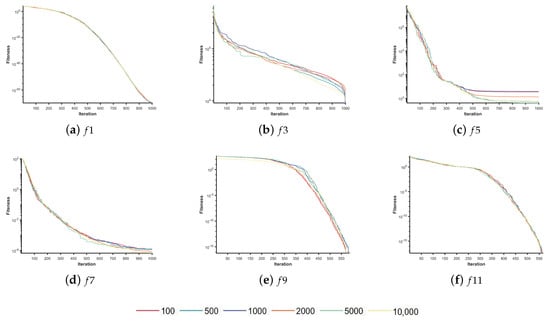
Figure 8. Convergence curves of VFSCPSO in different dimensions of the CEC2005 test suite.

As can be seen from Figure 8, the convergence curves of the hybrid algorithm VFSCPSO are basically the same as the number of dimensions increases. There is no obvious separation of the convergence curves as the number of dimensions continues to rise. Therefore, the VFSCPSO has strong search capability and extensibility, and the performance is basically unaffected by the number of dimensions, meaning it can effectively solve ultra-large-scale problems.

4.2.5. Application in PID Parameter Tuning

Optimization problems includes four elements. These elements are described in the following example of PID parameter tuning.

• Variables: In optimization problems, variables are quantities that can be adjusted or changed. They represent the decision variables or parameters of the optimal solution sought by the optimization method. In problems in engineering, science, or economics, variables can be various adjustable parameters such as size, velocity, temperature, etc. In the PID parameter-tuning problem, the variables usually are the parameters of the PID controller, i.e., the proportionality coefficients, the integration time, and the differentiation time. The response characteristics of the PID controller are controlled by tuning these parameters.
• Objective function: The objective function is the quantity to be maximized or minimized in an optimization problem. It represents the objective of the optimization. The form of the objective function depends on the specific problem; it can represent cost, benefit, efficiency, distance, or any other metric to be optimized. The objective is to bring these performance metrics to their optimal values or to satisfy certain requirements. In PID parameter-tuning problems, the objective function is usually the performance metric of the control system.
• Constraints: Constraints are conditions or restrictions that must be satisfied so that the solution is considered feasible or acceptable. Constraints define the space of feasible solutions and within this space the optimal solution is sought. Constraints usually come from physical limitations, technical limitations, regulations, or other constraints. In the case of PID parameter-tuning problems, constraints may come from the stability requirements of the control system. There may also be engineering constraints from practical applications, such as the range of PID parameter values or the performance requirements of the control system. The constraints are handled using a penalty function approach in this paper. There may also be engineering constraints from practical applications, such as the range of PID parameter values or the performance requirements of the control system. The constraints are handled using a penalty function approach in the paper. By introducing a penalty function, the constraints are incorporated into the objective function, thus transforming the original problem into an unconstrained optimization problems.
• Optimization method: An optimization method is a technique used to search for optimal solutions that minimize or maximize an objective function. The selection of an appropriate optimization method depends on the nature of the problem, constraints, objective function, and the availability of computational resources. The optimization method described in Section 1 can be used in the PID parameter-tuning problem, and therefore, will not be repeated here.

Understanding these elements is essential to understanding and solving optimization problems. These elements together shape the nature of the optimization problem and the possibilities for its solution, and so the impact of each element needs to be carefully considered and analyzed when undertaking the research and solution of the optimization problem. The structural diagram of PID tuning based on intelligent algorithms is shown in Figure 9.

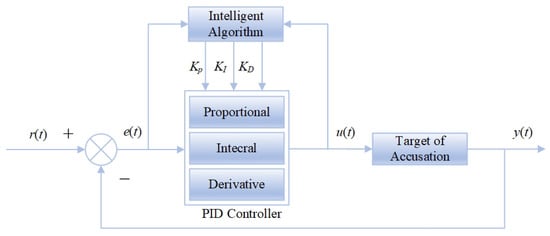
Figure 9. Structural diagram of PID tuning.

The main goal of the optimal design of PID controller parameters is to optimize certain performance indicators of the control system. It is difficult for a single error performance index to simultaneously meet the needs of the control system for speed, stability, and robustness, etc. Therefore, the integral of absolute error (IAE) is used as an adaptation function. The IAE criterion takes into account the dynamic nature of the iterative process and measures the integral of the absolute value of the error in the system response with time, which is used to quantify the tracking performance of the system with respect to a setting or target value. The parameters are then optimized using an intelligent algorithm. The IAE is used as the objective function f to obtain the demand of dynamic characteristics to satisfy the transition process, and the squared term of the control input is added to f to avoid too much control, and the final objective function is chosen as Equation (12):

$$f={\int }_0^{\infty }\left({\omega }_1\left|e\left(t\right)\right|+{\omega }_2{u}^2\left(t\right)\right)dt$$

(12)

In Equation (12), $e\left(t\right)$ is the system deviation, which is the error between the input and output values, and $u^2\left(t\right)$ is the squared term of the PID controller input, which is the control value. The weights ${\omega }_1$ and ${\omega }_2$ take values in $[0,1]$. Normally, ${\omega }_1$ = 0.999 and ${\omega }_2$ = 0.001 are taken, in addition, a penalty function is necessary to avoid overshooting, and once overshooting is generated, the systematic deviation is used as an item of the optimality index, at which point Equation (13) is chosen as the f that introduces the overshooting term:

$$f={\int }_0^{\infty }\left({\omega }_1\left|e\left(t\right)\right|+{\omega }_2{u}^2\left(t\right)+{\omega }_3\left|e\left(t\right)\right|\right)dt,e\left(t\right)<0$$

(13)

In Equation (13), ${\omega }_3$ is also a weight, ${\omega }_3>>{\omega }_1$, which is usually taken as ${\omega }_3$ = 100. ${\omega }_3\left|e\left(t\right)\right|$ is the penalty term. By combining the penalty function and IAE, the control performance of the system can be considered more comprehensively, and the PID parameter tuning carried out to achieve more stable and accurate control.

This paper introduces the basic concepts of servo motor systems and PID controllers and also describes the basic model of a servo motor system. The system performance can be significantly improved by adjusting and selecting appropriate PID controller parameters. A PID controller is a feedback control algorithm commonly used in control systems and its parameters need to be adjusted in order to optimize the performance of the system. VFSCPSO has a good adaptability in optimization problems and can be used to solve the problem of optimizing the PID control parameters of a servo motor. In this experiment, the maximum number of iterations is set to 20, the population size is 30, and the variable dimension is 3. In addition, the other parameters in VFSCPSO are set in accordance with numerical experiments, and for other algorithms we refer to the original studies.

The parameter tuning of the PID controller is a key part of the control system design, which usually needs to determine the values of $K_p$, $K_i$, and $K_d$ according to the characteristics of the controlled process. Since the PID controller was proposed, many parameter-tuning methods with excellent performance have emerged, but mankind has always been in pursuit of higher effectiveness. VFSCPSO is able to improve the shortcomings of poor adaptivity, complex control processes, and insufficient accuracy in PID control parameter optimization more effectively than traditional methods. In addition to the fitness value $f_{min}$, the following metrics are selected:

The overshoot $\sigma$ is the percentage of the steady-state value $y_s$ accounted for by the difference between the output step response peak $y_m$ and the steady-state value $y_s$, $\sigma \%=\left(y_m-y_s\right)/y_s$. The adjustment time $t_s$ refers to the time when the output step response enters steady state and starts to arrive at and remain in steady state within the specified error range, and it is the moment corresponding to the range of the steady-state value $y_s\pm \Delta$ error band, which is generally taken to be $\Delta =0.02$ or $\Delta =0.05$.

In order to objectively evaluate the effect of using these five intelligent algorithms in optimizing the PID control system of direct current servo motors, the following three evaluation metrics are selected based on the fitness function: best fitness value $f_{min}$, overshoot $\sigma$, and tuning time $t_s(2\%)$. The experimental results are shown in Table 20.

Table 20. System performance parameters tuned by the five algorithms.

Metric	VFSCPSO	PSO	SCA	FA	GA
$f_{min}$	39.26745	39.57185	39.83905	40.26736	48.93632
$\sigma$	0.012408	0.016805	0.023350	0.02546	0.007273
$t_s$	1.012408	1.016805	1.023350	1.02546	1.007273

From the simulation results shown in Table 20 and Figure 10, it can be seen that the PID controller optimized by VFSCPSO fully integrates the advantages and characteristics of proportional, integral, and differential control methods. Intelligent algorithms improve the performance of the direct current servo motor system to a greater extent, making the step response of the whole system optimal in terms of stability, velocity, and accuracy. Adjusting $K_d$ is conducive to accelerating the response velocity of the system and increasing the stability of the system, and adjusting $K_p$ can accelerate the response velocity of the system and improve the response velocity of the system. On the $f_{min}$ metric, the quality of the optimal solution found during the VFSCPSO search is the best, followed by PSO and SCA. FA and GA have relatively high values and relatively poor performance in finding the optimal parameters. On the $\sigma$ metric, GA has a smaller amount of overshooting, indicating better control performance, VFSCPSO is second, and FA has a larger amount of overshooting, requiring more time to reach stability. On $t_s$ metrics, VFSCPSO takes less time to adjust from the initial state to the steady state and the system responds faster, while FA has a longer adjustment time. In the comparison experiments of the five algorithms, the response curve of FA is the most unstable, and the response curve of GA is smoother but slower in response. Meanwhile, the overall performance of VFSCPSO is better than the two constituent algorithms, achieving the best overall performance.

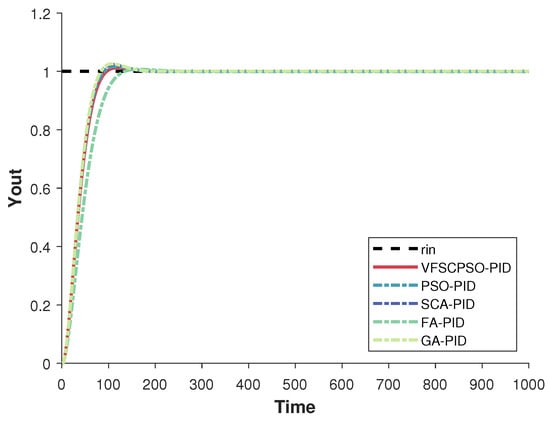
Figure 10. PID simulation result diagram.

As can be seen from the convergence curves in Figure 11, the convergence curve of the VFSCPSO algorithm decreases faster than those of the two algorithms GA and FA, which indicates that VFSCPSO is able to achieve better results than the other intelligent algorithms for this type of problem. SCA achieves worse results at the time of initialization but performs better at the later stage, which is exactly the opposite of PSO. In summary, VFSCPSO combines the advantages of the two compositional algorithms, with higher accuracy and faster convergence in the PID parameter-tuning problem, indicating that VFSCPSO has greater feasibility in practical engineering optimization problems.

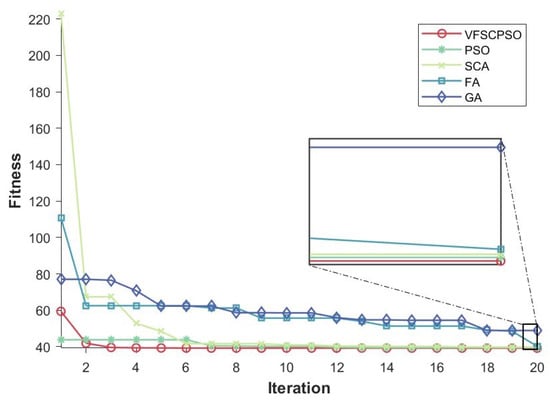
Figure 11. Convergence curves of five algorithms in PID parameter tuning of direct current servo motor.

4.2.6. Analysis of VFSCPSO’s Exploration and Exploitation

Exploration is the global search capability, exploring the entire search space. Exploitation is the local search capability, which adjusts the particle position within the local neighborhood. In intelligent algorithms, global search and local search will give full play to their respective advantages. Algorithms that are able to utilize both exploration and exploitation searches in an integrative manner can be more effective in finding excellent solutions. In this paper, the exploration and exploitation are obtained using dimension-wise diversity measurements presented in [48]. This subsection provides a test of the exploration and exploitation capabilities of the VFSCPSO. The method uses the following formulas:

$$\left\{\begin{array}{c}{Div}_j=\frac{1}{NP}\sum _{i=1}^{NP}\left|median\left(j\right)-x_i\left(j\right)\right|\hfill \\ Div=\frac{1}{D}\sum _{j=1}^D{Div}_j\hfill \end{array}\right.$$

(14)

In Equation (14), $median\left(j\right)$ denotes the median of dimension j in the population, $x_i\left(j\right)$ denotes the dimension j of individual i, $NP$ is the population size, and D is the number of variables in the optimization problems. A rise in the average of individual dimensional distances within the population in Equation (14) signifies exploration, whereas a decline in the average denotes exploitation. The percentage of exploration or exploitation can be calculated by the following formulas:

$$\left\{\begin{array}{c}\mathrm{Exploration}\%=\frac{Div}{Di{v}_{max}}\times 100\%,\hfill \\ \mathrm{Exploitation}\%=\frac{\left|Div-Di{v}_{max}\right|}{Di{v}_{max}}\times 100\%\hfill \end{array}\right.$$

(15)

In Equation (15), $Di{v}_{max}$ denotes the maximum population diversity during the iterative process. $Div$ is calculated from Equation (14). The values for exploration and exploitation calculated from Equation (15) are contradictory and supplement each other. Figure 12 shows the exploration and exploitation proportion of VFSCPSO on the CEC2005 test suite.

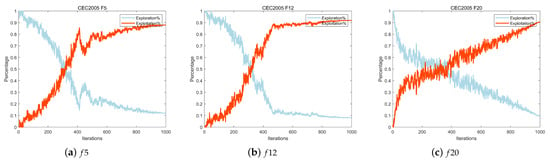
Figure 12. VFSCPSO tendency in exploration and exploitation on CEC2005 test suite.

From Figure 12, it can be seen that the exploitation and exploration tendency curves of VFSCPSO in different types of CEC2005 benchmark functions have their own characteristics, while the number of iterations in which exploration is equal to exploitation is different. The proportion of exploitation eventually reaches about $0.9$ and the proportion of exploration eventually reaches about $0.1$ in the later evolutionary period, which indicates the dominant capability of exploitation in the later iterations. This is due to the fact that the hybrid sine cosine strategy of the VFSCPSO enables exploration and exploitation to reach a balanced state in the end. Therefore, VFSCPSO can maintain a balance between exploitation and exploration.

4.2.7. Analysis of VFSCPSO’s Disadvantages

In the realm of algorithms, perfection remains an elusive concept. Every algorithm has its disadvantages. Although VFSCPSO exhibits remarkable efficacy in solving high-dimensional optimization problems, it also has some unconcealed disadvantages. Therefore, we must scrutinize its shortcomings and acknowledge them.

In this paper, the main limitation of VFSCPSO is parameter tuning. In Section 3.2, the optimal value of a is constant, 2. This is the standard SCA decision. But for most cases, not all. When the value of a is different, VFSCPSO may maintain different convergence accuracy. This means that a may be different for different problems. Moreover, we did not perform a grid search for a, which may have an exact optimal value.

In addition, VFSCPSO did not achieve full excellence in comparison with other good algorithms. For example, as shown in Table 8, VFSCPSO has worse results than AWPSO for individual benchmark functions. Therefore, the competitiveness of VFSCPSO may be increased by adding other effective strategies.

Finally, from the results of VFSCPSO challenging other good algorithms, VFSCPSO still has not effectively solved all complex problems. This shows that VFSCPSO cannot search effectively in the solution space of these problems. Therefore, it may be that the convergence performance of VFSCPSO can be further improved through other technologies.

5. Conclusions

In this paper, after deeply analyzing the advantages and drawbacks of PSO and SCA, a hybrid algorithm VFSCPSO is proposed. The framework of VFSCPSO mainly integrates the SCA strategy into the original PSO framework. It enables the algorithm to flexibly switch between local and global search, adapting to both high-dimensional global problems and engineering optimization problems. Then, to further show the advantages of VFSCPSO in large-scale environments, performance comparisons are conducted in the CEC2005 test suite in 50, 100, 500, 1000, 2000, 5000, and 10,000 dimensions. VFSCPSO shows efficient performance in solving large-scale problems, with the capability to solve global optimization problems up to 10,000 dimensions. In order to verify the advantages of VFSCPSO in solving engineering optimization problems, the experimental results of combining VFSCPSO with the comparative algorithms in the PID parameter-tuning problem show that the overall performance of VFSCPSO is the best. With the rapid development of modern society, problems in daily life have increasingly high requirements for algorithms. A good algorithm needs to serve human life, which is also our pursuit. Therefore, the next step will be to further study the defects of VFSCPSO, improve its optimization ability, and fully enhance the algorithm’s search performance. In the future, VFSCPSO will be applied to solve more complex real-world optimization problems, such as the vehicle path problem, data mining, environmental monitoring, and so on.

Appendix A.1. Sphere Function

$$\begin{array}{c}f1\left(x\right)=\sum _{i=1}^n{x}_i^2\hfill \end{array}$$

(A1)

Appendix A.2. Schwefel’s Problem 2.22

$$\begin{array}{c}f2\left(x\right)=\sum _{i=1}^n\left|x_i\right|+\prod _{i=1}^n\left|x_i\right|\hfill \end{array}$$

(A2)

Appendix A.3. Schwefel’s Problem 1.2

$$\begin{array}{c}f3\left(x\right)=\sum _{i=1}^n{\left(\sum _{j=1}^i{x}_j\right)}^2\hfill \end{array}$$

(A3)

Appendix A.4. Schwefel’s Problem 2.21

$$\begin{array}{c}f4\left(x\right)=\underset{i}{max}\left\{\left|x_i\right|,1\le i\le n\right\}\hfill \end{array}$$

(A4)

Appendix A.5. Generalized Rosenbrock’s Function

$$\begin{array}{c}f5\left(x\right)=\sum _{i=1}^{n-1}\left[100{\left(x_{i+1}-x_i^2\right)}^2+{\left(x_i-1\right)}^2\right]\hfill \end{array}$$

(A5)

Appendix A.6. Step Function

$$\begin{array}{c}f6\left(x\right)=\sum _{i=1}^n{\left(\left[x_i+0.5\right]\right)}^2\hfill \end{array}$$

(A6)

Appendix A.7. Quartic Function i.e., Noise

$$\begin{array}{c}f7\left(x\right)=\sum _{i=1}^{n}i{x}_i^4+random[0,1)\hfill \end{array}$$

(A7)

Appendix A.8. Generalized Schwefel’s Problem 2.26

$$\begin{array}{c}f8\left(x\right)=\sum _{i=1}^n-x_{i}sin\left(\left|x_i\right|\right)\hfill \end{array}$$

(A8)

Appendix A.9. Generalized Rastrigin’s Function

$$\begin{array}{c}f9\left(x\right)=\sum _{i=1}^n\left[x_i^2-10cos\left(2\pi x_i\right)+10\right]\hfill \end{array}$$

(A9)

Appendix A.10. Ackley’s Function

$$\begin{array}{c}f10\left(x\right)=\sum _{i=1}^n-20exp\left(-0.2\sqrt{\frac{1}{n}{\sum }_{i=1}^n{x}_i^2}\right)-exp\left(\frac{1}{n}\sum _{i=1}^{n}cos\left(2\pi x_i\right)\right)+20+e\hfill \end{array}$$

(A10)

Appendix A.11. Generalized Griewank’s Function

$$\begin{array}{c}f11\left(x\right)=\frac{1}{4000}\sum _{i=1}^n{x}_i^2-\prod _{i=1}^{n}cos\left(\frac{x_i}{\sqrt{i}}\right)+1\hfill \end{array}$$

(A11)

Appendix A.12. Generalized Penalized Function 1

$$\begin{array}{l}f12\left(x\right)=\frac{\pi }{n}\left\{10{sin}^2\left(\pi y_1\right)+\sum _{i=1}^n{\left(y_i-1\right)}^2\left[1+10{sin}^2\left(\pi y_i+1\right)\right]+{\left(y_n-1\right)}^2\right\}\hfill \\ +\sum _{i=1}^{n}u\left(x_i,10,100,4\right)\hfill \\ y_i=1+\frac{x_i+1}{4}\\ u(x_i, a, k, m)=\{\begin{array}{c}k{\left(x_i-a\right)}^m,x_i>a,\hfill \\ 0,-a\le x_i\le a,\hfill \\ k{\left(-x_i-a\right)}^m,x_i<-a.\hfill \end{array}\end{array}$$

(A12)

Appendix A.13. Generalized Penalized Function 2

$$\begin{array}{c}\hfill \begin{array}{c}f13\left(x\right)=0.1\left\{{sin}^2\left(\pi x_1\right)+\sum _{i-1}^n{\left(x_i-1\right)}^2\left[1+{sin}^2\left(3\pi y{x}_{i+1}\right)\right]+{\left(x_n-1\right)}^2\left[1+{sin}^2\left(2\pi x_n\right)\right]\right\}\hfill \\ +\sum _{i-1}^{n}u\left(x_i,5,100,4\right)\hfill \end{array}\end{array}$$

(A13)

Appendix A.14. Shekel’s Foxholes Function

$$\begin{array}{c}f14\left(x\right)={\left(\frac{1}{500}+\sum _{j=1}^{25}\frac{1}{j+{\sum }_{i=1}^2{\left(x_i-a_{ij}\right)}^6}\right)}^{-1}\hfill \end{array}$$

(A14)

Appendix A.15. Kowalik’s Function

$$\begin{array}{c}f15\left(x\right)=\sum _{i=1}^{11}{\left[a_i-\frac{x_i\left(b_i^2+b_i{x}_2\right)}{b_i^2+b_i{x}_3+x_4}\right]}^2\hfill \end{array}$$

(A15)

Appendix A.16. Six-Hump Camel-Back Function

$$\begin{array}{c}f16\left(x\right)=4x_1^2-2.1x_1^4+\frac{1}{3}{x}_1^6+x_1{x}_2-4x_2^2+4x_2^4\hfill \end{array}$$

(A16)

Appendix A.17. Branin Function

$$\begin{array}{c}f17\left(x\right)={\left(x_2-\frac{5.1}{4{\pi }^2}{x}_1^2+\frac{5}{\pi }{x}_1-6\right)}^2+10\left(1-\frac{1}{8\pi }\right)cos{x}_1+10\hfill \end{array}$$

(A17)

Appendix A.18. Goldstein Price Function

$$\begin{array}{c}f18\left(x\right)=\left[1+{\left(x_1+x_2+1\right)}^2\left(19-14x_1+3x_1^2-14x_1+6x_1{x}_2+3x_2^2\right)\right]\hfill \end{array}$$

(A18)

Appendix A.19. Hartman’s Family 1

$$\begin{array}{c}f19\left(x\right)=-\sum _{i=1}^n{c}_{i}exp\left(-\sum _{j=1}^3{a}_{ij}{\left(x_j-p_{ij}\right)}^2\right)\hfill \end{array}$$

(A19)

Appendix A.20. Hartman’s Family 2

$$\begin{array}{c}f20\left(x\right)=-\sum _{i=1}^n{c}_{i}exp\left(-\sum _{j=1}^6{a}_{ij}{\left(x_j-p_{ij}\right)}^2\right)\hfill \end{array}$$

(A20)

Appendix A.21. Shekel’s Family 1

$$\begin{array}{c}f21\left(x\right)=-\sum _{i=1}^5{\left[\left(x-a_i\right){(x-ai)}^T+ci\right]}^{-1}\hfill \end{array}$$

(A21)

Appendix A.22. Shekel’s Family 2

$$\begin{array}{c}f22\left(x\right)=-\sum _{i=1}^7{\left[\left(x-a_i\right){\left(x-a_i\right)}^T+c_i\right]}^{-1}\hfill \end{array}$$

(A22)

Appendix A.23. Shekel’s Family 3

$$\begin{array}{c}f23\left(x\right)=-\sum _{i=1}^{10}{\left[\left(x-a_{\mathrm{i}}\right){\left(x-a_i\right)}^T+c_i\right]}^{-1}\hfill \end{array}$$

(A23)