Leader-Following Consensus of Discrete-Time Nonlinear Multi-Agent Systems with Asymmetric Saturation Impulsive Control

Abstract

Impulsive control is an effective approach for coordinating multi-agent systems in practical environments due to its high robustness and low cost. However, impulsive control exhibits characteristics such as high amplitude and rapid variation, potentially presenting threats to the equipment. Additionally, multi-agent systems are constrained by input saturation due to limitations in physical controller structures and information-processing capabilities. These saturation constraints may be asymmetrical. Therefore, it is necessary to consider the saturation constraint when implementing impulsive control, as it can also mitigate the threats posed by the impulse to agents. This paper investigates the leader-following consensus for a class of discrete-time nonlinear multi-agent systems, proposing an asymmetric saturation impulsive control protocol to reduce the energy consumption and damage to the equipment. Regarding the handle of asymmetric saturation, an approach is proposed that eliminates the need for transformation from the asymmetric case to the symmetric case, which retains the saturation function and directly introduces the sector condition to deal with saturation nonlinearity. Furthermore, based on Lyapunov stability theory and matrix theory, sufficient conditions for leader-following consensus in discrete-time nonlinear multi-agent systems under asymmetric saturation impulsive control are established, and the admissible region of the system is estimated. Finally, numerical simulations are provided to verify the validity of the theoretical results.

1. Introduction

In recent years, distributed cooperative control problems of multi-agent systems have attracted extensive research and been widely applied in modern industrial fields such as smart city construction and multi-robot coordination [1,2,3,4]. Cooperative control in multi-agent systems includes consensus control [5], containment control [6], and formation control [7], etc. Among them, consensus control is regarded as an indispensable and foundational cooperative requisite, rendering it a vital area of investigation in multi-agent systems. Consensus control refers to the coordination achieved by agents through control protocols, culminating in the identical state [8].

Modeling methods for multi-agent systems are diverse, including continuous, discrete, or hybrid approaches, while system dynamics can be linear or nonlinear. However, the prevailing research on consensus control in multi-agent systems has predominantly relied on continuous-time models, as elucidated in [9,10,11]. When contemplating communication constraints and energy conservation, discrete-time systems appear more pragmatic. Consequently, more and more researchers tend to explore the consensus problem for discrete-time multi-agent systems. For instance, reference [12] studied the problem of secure output consensus in linear discrete-time multi-agent systems subjected to certain types of network attacks. Reference [13] analyzed the event-triggered related issues in linear discrete-time multi-agent systems. It is noteworthy that, in reality, systems frequently encounter nonlinear dynamics, sensor noise, non-ideal environmental variables, etc. Therefore, most practical multi-agent systems are nonlinear [14,15,16].

In practical environments, the evolution process of numerous systems may be affected by an abundance of disturbing factors that lead to sudden change. Consequently, impulsive control methods have received considerable attention in recent years [17,18,19]. Presently, impulsive control has become an effective tool for handling the coordination of multi-agent systems due to its robust performance and cost-effectiveness [20,21,22]. For example, reference [23] used event-triggered impulsive control to study the leader-following mean square consensus of stochastic multi-agent systems to make better use of limited communication resources. Impulsive control is triggered when the expected value of the trigger function of the agent during an event time interval is not negative. Research on the secure consensus problem of multi-agent systems under deception attacks through impulsive control is presented in [24]. Based on a dynamic event, reference [25] analyzed the output consensus problem of linear heterogeneous multi-agent systems under impulsive control. Impulsive control exhibits the characteristics of high amplitude and rapid variation, which may potentially endanger agent devices [26]. However, there is a scarcity of studies that have considered the effects of these characteristics on multi-agent systems.

Meanwhile, saturation constraints are very common, largely due to limitations in the physical controller structure and information processing capabilities. Therefore, it is necessary to consider the input saturation in the control system so that the input changes within a limited range to reduce the impact of these limitations. Input saturation is highly prevalent in specific control systems [27,28,29]. Dealing with saturation is challenging, mainly because saturation constraints often manifest as nonlinear, which complicates the control tasks. If saturation nonlinearity is ignored when designing the controller, it can lead to unstable or unpredictable system responses. In general, there are three main approaches to addressing saturation. One approach is to directly consider the saturation effects in the design process, and see the convex hull representation in [30], and the other is after the previous design is performed without regard to saturation conditions, and saturation effects are addressed in the second step, as can be seen in [31]. Another method is the low-gain feedback method.

In multi-agent systems, there is also a lot of research on input saturation. Reference [32] explores the consensus of linear multi-agent systems subject to input saturation based on the Q-learning method, which leverages the low-gain feedback theory to avoid saturation. Reference [33] studied the problem of input saturation and additive stable perturbations consensus in discrete-time linear multi-agent systems through dynamic output feedback in conjunction with the low-gain feedback method. For linear multi-agent systems with input saturation, reference [34] proposes a framework for addressing the semiglobal tracking cooperative control problem in multi-agent systems with switching communication topologies, which a key element in the proposed approach is the development of the low-gain feedback consensus protocol. However, refs. [32,33,34] adopt a low-gain feedback method to mitigate saturation, which requires the multi-agent system to be relatively simple and predominantly linear. The low-gain feedback method may fail to achieve dynamic consensus if the system exhibits nonlinear characteristics. The above analysis shows that accounting for a saturation constraint is imperative when implementing impulsive control, as it can also mitigate the threats posed by the impulse to agents. At present, only a few studies have focused on the saturation problem under impulsive control. Reference [35] proposed an impulsive consensus protocol for a class of continuous-time nonlinear multi-agent systems with input symmetric saturation. In the consensus problem of continuous-time nonlinear multi-agent systems, in [36], the input and state symmetric saturation are discussed. Reference [37] analyzes and studies the impulsive consensus problem in time-delay continuous-time multi-agent systems, incorporating the input symmetric saturation constraint into the design of an impulsive control protocol. The treatment of saturation in [35,36,37] considers saturation nonlinearity during the preliminary stages of controller construction and describes saturation mapping as a convex hull representation. Even though the domain of attraction estimated by convex hull representation is less conservative, the computational complexity of convex hull representation is $2^{\mathrm{m}}$ [38], thereby escalating the computational burden exponentially. When dealing with multi-agent systems with a high number of input dimensions, there is a risk of excessive computational load.

The mention of a crucial hypothesis in most of the above studies highlights an important consideration in the field of control systems and multi-agent systems coordination. The hypothesis being discussed is that saturation constraints are often assumed to be symmetric. In other words, it is commonly assumed that the limitations imposed on control inputs or outputs are the same in both the positive and negative directions. However, the article recognizes that, in many real systems, this assumption of symmetry in saturation constraints may not hold. Asymmetric saturation constraints can arise due to various factors, such as differences in sensor performance, communication limitations, or other system-specific characteristics. These asymmetries add a layer of complexity to the control design process, as the control strategy must now account for and adapt to different saturation levels in different directions. Considering the asymmetry saturation, reference [39] addresses the stabilization problem for discrete-time linear systems with unsymmetric saturation. To account for the structural properties of the unsymmetric saturation nonlinearity, the transformation from the symmetric case to the unsymmetric case is described. Reference [40] primarily investigates the stability of discrete-time linear systems when subjected to asymmetric saturation impulsive inputs. The analysis involves formulating discrete-time linear systems with a saturated impulse mechanism. Reference [41] proposes an innovative anti-windup scheme for linear systems experiencing asymmetric input saturation. The approach involves a coordinate transformation that converts the system subjected to asymmetric saturation into an equivalent one exhibiting symmetric saturation. To address asymmetric saturation, refs. [39,40,41] adopt a transformation from the asymmetric case to the symmetric case. This paper will give a method to deal with asymmetric saturation directly, which eliminates the need for transformation from the asymmetric case to the symmetric case. To our knowledge, the problem of asymmetric saturation has yet to be studied for nonlinear multi-agent systems. Therefore, this article investigates the leader-following consensus problem of discrete-time nonlinear multi-agent systems based on asymmetric saturation impulsive control. Among them, the asymmetric saturation impulsive control protocol is designed to reduce energy consumption and damage to the equipment of the system. We deal with saturation nonlinearity by directly considering the saturation effect, preserving the saturation function, and introducing the sector condition, which can reduce the computational cost. Then, based on Lyapunov stability theory and matrix theory, sufficient conditions for the leader-following consensus of discrete-time nonlinear multi-agent systems are established. The protocol designed can allow all followers to track the leader under asymmetric saturation, thus achieving a gradual consensus of the state. This research direction is expected to provide new perspectives and methods for understanding and controlling the consensus problem of discrete-time nonlinear multi-agent systems. The main contributions of this article are summarized as follows.

(1)

Compared to saturation mapping as a convex hull representation in [35,36,37], this paper retains the saturation function and directly introduces the sector condition to deal with saturation nonlinearity, which can reduce the computational cost.

(2)

Amidst asymmetric saturation, we propose an approach that eliminates the need for transformation from the asymmetric case to the symmetric case compared to methods in [39,40,41].

(3)

An asymmetric saturation impulsive control protocol is proposed to analyze the leader-following consensus of discrete-time nonlinear multi-agent systems, which can reduce energy consumption and damage to the equipment. Sufficient conditions are obtained for the leader-following consensus of nonlinear multi-agent systems, and the admissible region of the system is estimated.

The remainder of this paper is arranged as follows. Section 2 introduces the preliminaries and problem formulation. Section 3 provides sufficient conditions for leader-following consensus in multi-agent systems under asymmetric saturation impulsive control and estimates the admissible region. In Section 4, two numerical illustrations are provided to demonstrate the validity of the results. Section 5 constitutes the conclusion and future work of this article.

2. Preliminaries and Problem Formulation

2.1. Notations

Let $\mathbb{R}$ stand for the set of real numbers, $\mathbb{N}$ for the set of positive integers, and use ${\mathbb{R}}^{x\times y}$ and ${\mathbb{R}}^x$ to denote $x\times y$ real matrices and x-dimensional Euclidean space, respectively. The symbol $I_x$ stands for the $x\times x$ identity matrix. For a matrix A, $A^T$ represents its transpose, ${\lambda }_{max}\left(A\right)$ denotes its maximum eigenvalue, and ${\lambda }_{min}\left(A\right)$ represents its minimum eigenvalue. Additionally, let $A_{\left(i\right)}$ denotes the ith row of matrix A, and $A_{(i,j)}$ represents the element in row i and column j of matrix A. The ith component of the vector x is represented as $x_{\left(i\right)}$. The notations $|·|$ and $\left|\right|·\left|\right|$ mean the absolute value of a number and the standard Euclidean norm, respectively. $diag(x_1,x_2,\dots ,x_n)$ represents a diagonal matrix, where $x_i$ corresponds to the ith diagonal element. $min(i,j)$ refers to the minimum value between i and j. For a given constant $\beta >0$ and an $n\times n$ symmetric positive definite matrix P, the ellipsoid $\Im (P,\beta )$ is defined as $\Im (P,\beta )=\{e\left(k\right)\in \mathbb{R}{ }^{Nn}:e^T\left(k\right)(I_N\otimes P)e\left(k\right)\le \beta \}$, where $Nn$ denotes the product of N and n.

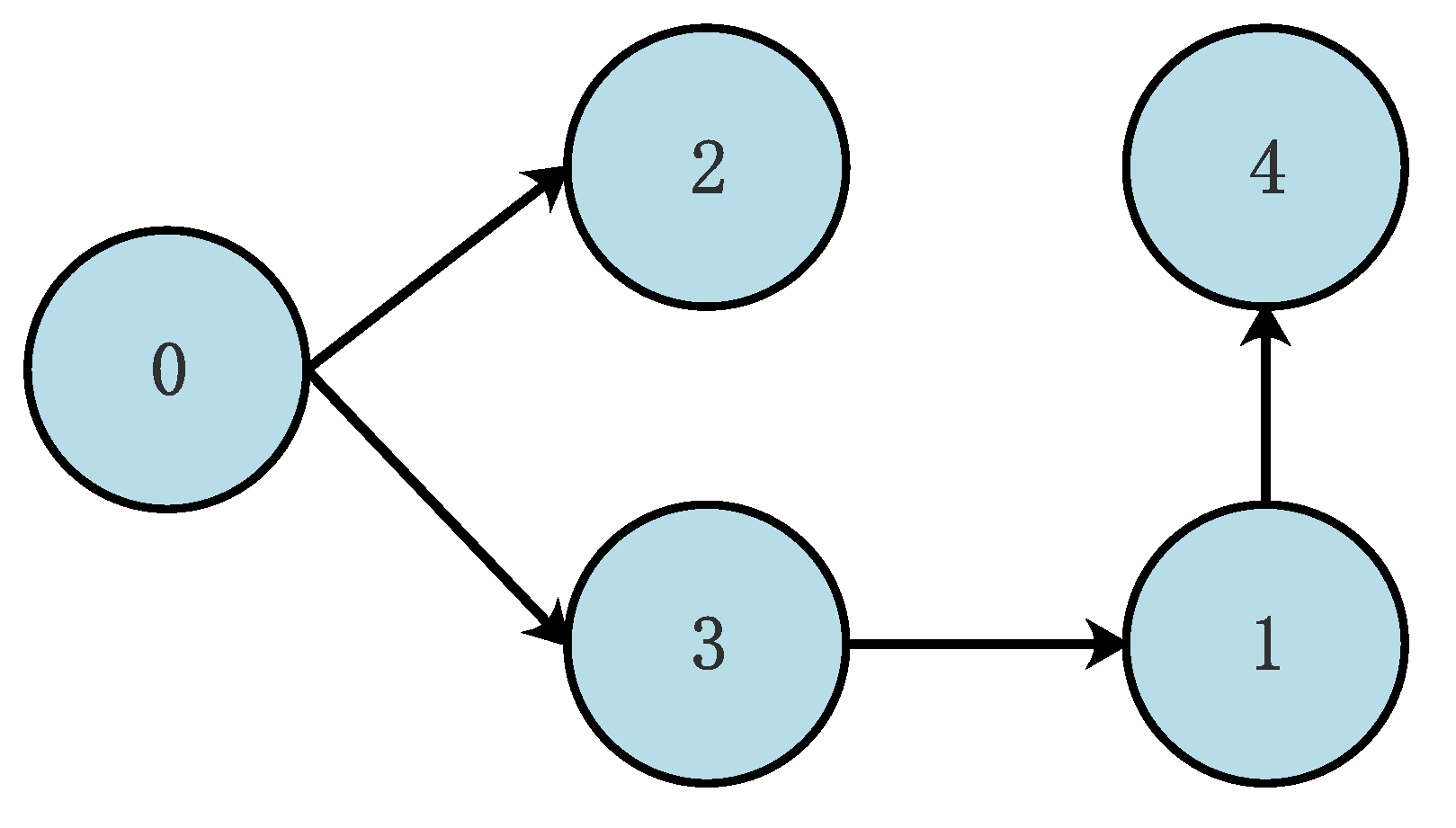
2.2. Algebraic Graph Theory

To denote a weighted directed graph comprising N follower agents, we use the notation $G=(V,\epsilon ,\phi )$, where $V=(v_1,v_2,\dots ,v_N)$ stands for the set of vertices, each corresponding to a follower agent. $\epsilon \subseteq V\times V$ denotes the edge set, and $\phi =\left[a_{ij}\right]\in {\mathbb{R}}^{N\times N}$ is a weighted adjacency matrix with $a_{ij}\ge 0$ for $i\ne j$, where $a_{ii}=0$. In the directed graph G, a directed edge ${\epsilon }_{ij}=(v_i,v_j)$ represents an edge from vertex $v_j$ to vertex $v_i$. If ${\epsilon }_{ij}\in \epsilon$, then $a_{ij}>0$. If ${\epsilon }_{ij}\notin \epsilon$, then $a_{ij}=0$. In this case, vertex $v_j$ is referred to as a neighbor of vertex $v_i$, meaning that vertex $v_i$ can receive information from vertex $v_j$. The Laplacian matrix L corresponding to the directed graph G is defined as $L=D-\phi$, where $D=diag\left({\sum }_{j=1}^N{a}_{1j},{\sum }_{j=1}^N{a}_{2j},\dots ,{\sum }_{j=1}^N{a}_{Nj}\right)$.

The leader agent is denoted as $v_0$, and similarly, communication between the leader agent $v_0$ and follower agents is directional. We define the leader adjacency matrix as $B=diag(b_1,b_2,\dots ,b_N)$. If vertex $v_0$ is a neighbor of vertex $v_i$, then $b_i>0$, and otherwise $b_i=0$ [42].

2.3. Problem Formulation

In this paper, the dynamics of leader is defined as

$$x_0(k+1)=A{x}_0\left(k\right)+f\left(x_0\left(k\right)\right),$$

(1)

where $x_0\left(k\right)\in {\mathbb{R}}^n$ is the state vector of leader, and A is the real matrix with appropriate dimensions. $f\left(x_i\left(k\right)\right)={[f_1\left(x_{i\left(1\right)}\left(k\right)\right),f_2\left(x_{i\left(2\right)}\left(k\right)\right),\dots ,f_n\left(x_{i\left(n\right)}\left(k\right)\right)]}^T$ represents the nonlinear vector function.

The dynamics of all followers are described by the following equations

$$\left\{\begin{array}{c}{x}_i(k+1)=A{x}_i\left(k\right)+f\left(x_i\left(k\right)\right),k\ne k_m,\hfill \\ \Delta x_i\left(k_m\right)=U_i\left(k_m\right),k=k_m,\hfill \\ U_i\left(k\right)=sat\left(u_i\left(k\right)\right),\hfill \end{array}\right. i=1,2,\dots ,N,$$

(2)

where $x_i\left(k\right)\in {\mathbb{R}}^n$ represents the state of the ith follower agent, and $U_i\left(k\right)\in {\mathbb{R}}^n$ are called impulsive control protocol. The impulsive time sequence $\left\{k_m,m\in \mathbb{N}\right\}$ needs to meet conditions $0=k_0<k_1<···<k_m<k_{m+1}<···,\underset{m\to +\infty }{lim}{k}_m=+\infty$, with the impulsive time interval $\tau =k_{m+1}-k_m>1$. We denote $\Delta x_i\left(k_m\right)=x_i(k_m+1)-x_i\left(k_m\right)$ and $\Delta x_i\left(k_m\right)$ represents the status of each follower being updated at the impulsive instant $k_m$. The input saturation function $sat\left(u_i\left(k\right)\right)$ is defined as $sat\left(u_i\left(k\right)\right)={[sat\left(u_{i\left(1\right)}\left(k\right)\right),\dots ,sat\left(u_{i\left(n\right)}\left(k\right)\right)]}^T$, with 

$$sat\left(u_{i\left(s\right)}\left(k\right)\right)=\left\{\begin{array}{c}{\psi }_{i\left(s\right)},u_{i\left(s\right)}\left(k\right)>{\psi }_{i\left(s\right)},\hfill \\ u_{i\left(s\right)}\left(k\right),-{\zeta }_{i\left(s\right)}\le u_{i\left(s\right)}\left(k\right)\le {\psi }_{i\left(s\right)}, s=1,\dots ,n,\hfill \\ -{\zeta }_{i\left(s\right)},u_{i\left(s\right)}\left(k\right)<-{\zeta }_{i\left(s\right)},\hfill \end{array}\right.$$

(3)

where ${\psi }_{i\left(s\right)},{\zeta }_{i\left(s\right)}\ge 0$. The upper and lower bounds of the saturation function are denoted, respectively. At the same time, we define $\psi ={[{\psi }_1^T,\dots ,{\psi }_N^T]}^T,\zeta ={[{\zeta }_1^T,\dots ,{\zeta }_N^T]}^T$ for later use.

Remark 1.

The impulsive signal can instantly change the state of the system and transition the system from one state to another. Motivated by [22], this paper argues that when the impulsive control signal is input into each agent, the status of the follower can be updated at the impulsive time. $x_i(k_m+1)$ represents the status of the follower after receiving the impulse at time $k_m$.

Design

$$u_i\left(k\right)=-C\left(\sum _{j=1}^N{a}_{ij}[x_i\left(k\right)-x_j\left(k\right)]+b_i[x_i\left(k\right)-x_0\left(k\right)]\right),$$

(4)

where matrix C is the control gain, $a_{ij}$ is the element at the $(i,j)$ position of adjacency matrix $\phi$, $b_i$ is the diagonal element of the ith row of the leader adjacency matrix B. By combining Equation (4) with Equation (2), we can re-describe the relationship as

$$\left\{\begin{array}{c}{x}_i(k+1)=A{x}_i\left(k\right)+f\left(x_i\left(k\right)\right),k\ne k_m,\hfill \\ \Delta x_i\left(k_m\right)=sat\left[-C\left({\displaystyle \sum _{j=1}^N}{a}_{ij}[x_i\left(k_m\right)-x_j\left(k_m\right)]+b_i[x_i\left(k_m\right)-x_0\left(k_m\right)]\right)\right],m\in \mathbb{N}.\hfill \end{array}\right.$$

(5)

We define the error state as $e_i\left(k\right)=x_i\left(k\right)-x_0\left(k\right)$. With this definition, and by combining systems (1) and (5), the error system can be expressed as

$$\left\{\begin{array}{c}{e}_i(k+1)=A{e}_i\left(k\right)+f\left(x_i\left(k\right)\right)-f\left(x_0\left(k\right)\right),k\ne k_m,\hfill \\ \Delta e_i\left(k_m\right)=sat\left[-C\left({\displaystyle \sum _{j=1}^N}{a}_{ij}[e_i\left(k_m\right)-e_j\left(k_m\right)]+b_i\left(e_i\left(k_m\right)\right)\right)\right],m\in \mathbb{N}.\hfill \end{array}\right.$$

(6)

The error system (6) of the multi-agent system can be rewritten in matrix form as

$$\left\{\begin{array}{c}e(k+1)=\left(I_N\otimes A\right)e\left(k\right)+F\left(k\right),k\ne k_m,\hfill \\ \Delta e\left(k_m\right)=sat\left(-(E\otimes C)e\left(k_m\right)\right),m\in \mathbb{N},\hfill \end{array}\right.$$

(7)

where $e\left(k\right)={[e_1^T\left(k\right),\cdots ,e_N^T\left(k\right)]}^T,F\left(k\right)={[{(f\left(x_1\left(k\right)\right)-f\left(x_0\left(k\right)\right))}^T,\cdots ,{(f\left(x_N\left(k\right)\right)-f\left(x_0\left(k\right)\right))}^T]}^T$, and $E=L+B$, where L is the Laplacian matrix.

Consider a matrix $G\in {\mathbb{R}}^{Nn\times Nn}$, defining the following set

$$S\left(G\right)=\{e\left(k\right)\in {\mathbb{R}}^{Nn},|G_{\left(i\right)}e\left(k\right)|\le min({\psi }_{\left(i\right)},{\zeta }_{\left(i\right)}),i=1,\dots ,Nn\}.$$

(8)

Lemma 1

([31]). There is a matrix F, and for any diagonal positive definite matrix $H\in {\mathbb{R}}^{Nn\times Nn}$. If $e\left(k\right)\in S\left(G\right)$, then the relation

$${(Fe\left(k\right)-sat\left(Fe\left(k\right)\right))}^{T}H(Ge\left(k\right)-sat\left(Fe\left(k\right)\right))\le 0.$$

(9)

Proof. 

When $F_{\left(i\right)}e\left(k\right)>{\psi }_{\left(i\right)}$, then $F_{\left(i\right)}e\left(k\right)-sat\left(F_{\left(i\right)}e\left(k\right)\right)>0$. Since $e\left(k\right)\in S\left(G\right)$, if either ${\psi }_{\left(i\right)}\le {\zeta }_{\left(i\right)}$, there is $G_{\left(i\right)}e\left(k\right)\le {\psi }_{\left(i\right)}$, then $G_{\left(i\right)}e\left(k\right)-sat\left(F_{\left(i\right)}e\left(k\right)\right)\le 0$, or ${\psi }_{\left(i\right)}>{\zeta }_{\left(i\right)}$, there is $G_{\left(i\right)}e\left(k\right)\le {\zeta }_{\left(i\right)}<{\psi }_{\left(i\right)}$, then $G_{\left(i\right)}e\left(k\right)-sat\left(F_{\left(i\right)}e\left(k\right)\right)<0$. It follows that ${(F_{\left(i\right)}e\left(k\right)-sat\left(F_{\left(i\right)}e\left(k\right)\right))}^T{H}_{(i,i)}(G_{\left(i\right)}e\left(k\right)-sat\left(F_{\left(i\right)}e\left(k\right)\right))\le 0.$

When $-{\zeta }_{\left(i\right)}\le F_{\left(i\right)}e\left(k\right)\le {\psi }_{\left(i\right)}$, then $F_{\left(i\right)}e\left(k\right)-sat\left(F_{\left(i\right)}e\left(k\right)\right)=0$, and it follows that ${(F_{\left(i\right)}e\left(k\right)-sat\left(F_{\left(i\right)}e\left(k\right)\right))}^T{H}_{(i,i)}(G_{\left(i\right)}e\left(k\right)-sat\left(F_{\left(i\right)}e\left(k\right)\right))=0.$

When $F_{\left(i\right)}e\left(k\right)<-{\zeta }_{\left(i\right)}$, then $F_{\left(i\right)}e\left(k\right)-sat\left(F_{\left(i\right)}e\left(k\right)\right)<0$. Since $e\left(k\right)\in S\left(G\right)$, if either ${\psi }_{\left(i\right)}\le {\zeta }_{\left(i\right)}$, there is $-{\zeta }_{\left(i\right)}\le -{\psi }_{\left(i\right)}\le G_{\left(i\right)}e\left(k\right)\le {\psi }_{\left(i\right)}$, then $G_{\left(i\right)}e\left(k\right)-sat\left(F_{\left(i\right)}e\left(k\right)\right)\ge 0$, or ${\psi }_{\left(i\right)}>{\zeta }_{\left(i\right)}$, there is $-{\zeta }_{\left(i\right)}\le G_{\left(i\right)}e\left(k\right)\le {\zeta }_{\left(i\right)}$, then $G_{\left(i\right)}e\left(k\right)-sat\left(F_{\left(i\right)}e\left(k\right)\right)\ge 0$. It follows that ${(F_{\left(i\right)}e\left(k\right)-sat\left(F_{\left(i\right)}e\left(k\right)\right))}^T{H}_{(i,i)}(G_{\left(i\right)}e\left(k\right)-sat\left(F_{\left(i\right)}e\left(k\right)\right))\le 0.$

Lemma 1 is thus proved.    □

Remark 2.

The difference between the Proof of Lemma 1 and reference [31] is that the condition proven in reference [31] is to model a linear system with deadzone nonlinearity under symmetric saturation. This article proves that the (9) relationship based on condition (8) holds under asymmetric saturation.

Lemma 2

([43]). For any vector $X,Y\in {\mathbb{R}}^n$, and positive definite matrix $Z\in {\mathbb{R}}^{n\times n}$, there exists a constant $\mu >0$, and the following inequality holds

$$2X^{T}Y\le \mu X^{T}ZX+\frac{1}{\mu }{Y}^T{Z}^{-1}Y.$$

(10)

Definition 1

([44]). The multi-agent systems (1) and (2) can achieve leader-following consensus if the following condition is satisfied

$$\underset{k\to \infty }{lim}∥x_i-x_0∥=0,i=1,2,\dots ,N.$$

(11)

Definition 2.

The systems (7) can reach local exponential stability if there are constants $x>0$ and $y\ge 1$, and a set ℑ containing the origin, such that for all initial values $e\left(k_0\right)\in \Im ,∥e\left(k\right)∥\le yexp\left\{-x\left(k-k_0\right)\right\}∥e\left(k_0\right)∥,\forall k\ge k_0$, where ℑ can be used as a system (7) that estimates the domain of attraction.

Remark 3.

Through the model transformation of the above system, the consensus problem of the systems (1) and (2) is transformed into the stability problem of the error system (7). The estimation of the domain of attraction in the system (7) can be used as the estimation of the admissible region of the systems (1) and (2).

Assumption 1.

At least one follower is connected to the leader and can receive information from the leader.

Assumption 2.

The nonlinear function $f_j(·):\mathbb{R}\to \mathbb{R}$ is continuous if there exists a constant $l_j>0,j=1,\dots ,n$ such that

$$|f_j\left({\upsilon }_1\right)-f_j\left({\upsilon }_2\right)|\le l_j|{\upsilon }_1-{\upsilon }_2|,\forall {\upsilon }_1,{\upsilon }_2\in \mathbb{R}.$$

(12)

Meanwhile, we define $\Lambda =diag\left(l_j\right)$ for later use.

3. Main Results

In this section, we will provide sufficient conditions for achieving leader-following consensus in the multi-agent systems (1) and (2) under asymmetric saturation impulsive control. Additionally, an estimate of the admissible region will be presented.

Theorem 1.

If a constant exists such that $\beta >0$, a positive definite matrix $Z\in {\mathbb{R}}^{Nn\times Nn}$ and a symmetric positive definite matrix $P\in {\mathbb{R}}^{n\times n}$, for given constants $\mu >0$, $\alpha >0$, $0<\rho <{(\alpha +1)}^{1-\tau }$, and $1<\tau$, the matrix G and the diagonal positive definite matrix H satisfy

$$\left[\begin{array}{cc}\Xi & I_N\otimes \left(A^T{P}^T\right)\\ \ast & -\mu Z\end{array}\right]<0,$$

(13)

$$\left[\begin{array}{cc}{I}_N\otimes P& G_{\left(j\right)}^T\\ \ast & {\beta }^{-1}{(1+\alpha )}^{-\tau }min{({\psi }_{\left(j\right)},{\zeta }_{\left(j\right)})}^2\end{array}\right]\ge 0,j=1,\dots ,Nn,$$

(14)

$$Y=\left[\begin{array}{cc}{Y}_1& Y_2\\ \ast & I_N\otimes P-2H\end{array}\right]\le 0,$$

(15)

where $\Xi =I_N\otimes \left(A^{T}PA\right)+\mu (I_N\otimes {\Lambda }^T)Z(I_N\otimes \Lambda )+(I_N\otimes {\Lambda }^T)(I_N\otimes P)(I_N\otimes \Lambda )-(1+\alpha )(I_N\otimes P)$, $Y_1=(1-\rho )(I_N\otimes P)+{(E\otimes C)}^{T}HG+G^T{H}^T(E\otimes C)$ and $Y_2=I_N\otimes P-{(E\otimes C)}^{T}H+G^T{H}^T$. Then, for $\forall e\left(k_0\right)\in \Im (P,\beta )$, the multi-agent systems (1) and (2) can achieve leader-following consensus, and the estimate of the admissible region is $\Im (P,\beta )$.

Proof. 

Consider the following Lyapunov function

$$V\left(k\right)=e^T\left(k\right)(I_N\otimes P)e\left(k\right).$$

(16)

When the impulse does not occur, let $\Delta V\left(k\right)=V(k+1)-V\left(k\right)$, according to the system (7), we can obtain

$$\begin{array}{cc}\hfill \Delta V\left(k\right)& =e^T(k+1)(I_N\otimes P)e(k+1)-e^T\left(k\right)(I_N\otimes P)e\left(k\right)\hfill \\ \hfill & ={\left[\left(I_N\otimes A\right)e\left(k\right)+F\left(k\right)\right]}^T(I_N\otimes P)\left[\left(I_N\otimes A\right)e\left(k\right)+F\left(k\right)\right]-e^T\left(k\right)(I_N\otimes P)e\left(k\right)\hfill \\ \hfill & =e^T\left(k\right)\left(I_N\otimes \left(A^{T}PA\right)-I_N\otimes P\right)e\left(k\right)+2F^T\left(k\right)\left(I_N\otimes \left(PA\right)\right)e\left(k\right)+F^T\left(k\right)(I_N\otimes P)F\left(k\right).\hfill \end{array}$$

(17)

According to the Lemma 2, it can be concluded that there a positive definite matrix $Z\in {\mathbb{R}}^{Nn\times Nn}$ and a constant $\mu >0$ exist that satisfy the following inequalities

$$\begin{array}{cc}\hfill & 2F^T\left(k\right)\left(I_N\otimes \left(PA\right)\right)e\left(k\right)+F^T\left(k\right)(I_N\otimes P)F\left(k\right)\hfill \\ \hfill & \le \mu F^T\left(k\right)ZF\left(k\right)+\frac{1}{\mu }{\left(\left(I_N\otimes \left(PA\right)\right)e\left(k\right)\right)}^T{Z}^{-1}\left(I_N\otimes \left(PA\right)\right)e\left(k\right)\hfill \\ \hfill & +F^T\left(k\right)(I_N\otimes P)F\left(k\right)\hfill \\ \hfill & \le \mu e^T\left(k\right)(I_N\otimes {\Lambda }^T)Z(I_N\otimes \Lambda )e\left(k\right)+\frac{1}{\mu }{e}^T\left(k\right)\left(I_N\otimes \left(A^T{P}^T\right)\right)Z^{-1}\left(I_N\otimes \left(PA\right)\right)e\left(k\right)\hfill \\ \hfill & +e^T\left(k\right)(I_N\otimes {\Lambda }^T)(I_N\otimes P)(I_N\otimes \Lambda )e\left(k\right)\hfill \\ \hfill & =e^T\left(k\right)(\mu (I_N\otimes {\Lambda }^T)Z(I_N\otimes \Lambda )+\frac{1}{\mu }(I_N\otimes \left(A^T{P}^T\right))Z^{-1}(I_N\otimes \left(PA\right))\hfill \\ \hfill & +(I_N\otimes {\Lambda }^T)(I_N\otimes P)(I_N\otimes \Lambda ))e\left(k\right).\hfill \end{array}$$

(18)

By combining Equations (13), (17), and (18), we can derive the relationship

$$\Delta V\left(k\right)\le \alpha V\left(k\right),$$

(19)

then

$$V(k+1)\le \alpha V\left(k\right)+V\left(k\right),k\in [k_m+1,k_{m+1}+1).$$

(20)

This indicates that when $k\in [k_m+1,k_{m+1}+1)$, it follows that

$$\begin{array}{cc}\hfill V\left(k\right)& \le (1+\alpha )V(k-1)\hfill \\ \hfill & \le {(1+\alpha )}^{2}V(k-2)\hfill \\ \hfill & \le \cdots \hfill \\ \hfill & \le {(1+\alpha )}^{k-k_m-1}V(k_m+1).\hfill \end{array}$$

(21)

For $k\in [k_0,k_1+1)$, we have

$$V\left(k\right)\le {(1+\alpha )}^{k-k_0}V\left(k_0\right),$$

(22)

which means

$$V\left(k_1\right)\le {(\alpha +1)}^{k_1-k_0}V\left(k_0\right)\le {(\alpha +1)}^{\tau }V\left(k_0\right).$$

(23)

For $\forall e\left(k_0\right)\in \Im (P,\beta )$, it can be deduced from Equation (14) that

$$e\left(k_1\right)\in S\left(G\right).$$

(24)

According to Lemma 1, we make the matrix $F=-(E\otimes C)$, and it holds that

$${(-(E\otimes C)e\left(k_1\right)-sat(-(E\otimes C)e\left(k_1\right)))}^{T}H(Ge\left(k_1\right)-sat(-(E\otimes C)e\left(k_1\right)))\le 0,$$

(25)

when $k=k_1$ and the impulse occurs,

$$\begin{array}{cc}\hfill V(k_1+1)& =e^T(k_1+1)(I_N\otimes P)e(k_1+1)\hfill \\ \hfill & \le {(e\left(k_1\right)+sat(-(E\otimes C)e\left(k_1\right)))}^T(I_N\otimes P)(e\left(k_1\right)\hfill \\ \hfill & +sat(-(E\otimes C)e\left(k_1\right)))-2(-(E\otimes C)e\left(k_1\right)\hfill \\ \hfill & -sat(-(E\otimes C)e\left(k_1\right)){)}^{T}H(Ge\left(k_1\right)-sat(-(E\otimes C)e\left(k_1\right))).\hfill \end{array}$$

(26)

Define $\Omega \left(k\right)={[e^T\left(k\right),sa{t}^T(-(E\otimes C)e\left(k\right))]}^T$, which is obtained by (15)

$$\begin{array}{cc}\hfill V(k_1+1)& \le {\Omega }^T\left(k_1\right)Y\Omega \left(k_1\right)+\rho e^T\left(k_1\right)(I_N\otimes P)e\left(k_1\right)\hfill \\ \hfill & \le \rho V\left(k_1\right).\hfill \end{array}$$

(27)

From (21) and (27), when $k\in [k_1+1,k_2+1)$, there exists $0<\rho <{(\alpha +1)}^{1-\tau }$ satisfying

$$\begin{array}{cc}\hfill V\left(k\right)& \le {(\alpha +1)}^{k-k_1-1}V(k_1+1)\hfill \\ \hfill & \le {(\alpha +1)}^{k-k_1-1}\rho V\left(k_1\right)\hfill \\ \hfill & \le {(\alpha +1)}^{k-k_1-1}\rho {(\alpha +1)}^{\tau }V\left(k_0\right)\hfill \\ \hfill & \le {(\alpha +1)}^{k-k_1}V\left(k_0\right),\hfill \end{array}$$

(28)

which means

$$V\left(k_2\right)\le {(\alpha +1)}^{\tau }V\left(k_0\right).$$

(29)

Therefore, one can easily obtain $e\left(k_2\right)\in S\left(G\right)$, and similarly to (27), we have $V(k_2+1)\le \rho V\left(k_2\right)$. When $k\in [k_2+1,k_3+1)$, one has

$$\begin{array}{cc}\hfill V\left(k\right)& \le {(\alpha +1)}^{k-k_2-1}V(k_2+1)\hfill \\ \hfill & \le {(\alpha +1)}^{k-k_2-1}\rho V\left(k_2\right)\hfill \\ \hfill & \le {(\alpha +1)}^{k-k_2-1}\rho {(\alpha +1)}^{\tau }V\left(k_0\right)\hfill \\ \hfill & \le {(\alpha +1)}^{k-k_2}V\left(k_0\right).\hfill \end{array}$$

(30)

Thus, when $k=k_3$, then $e\left(k_3\right)\in S\left(G\right)$, it can be obtain $V(k_3+1)\le \rho V\left(k_3\right)$. And, so on, when $k\in [k_{m-1}+1,k_m+1),m\ge 4$, we have $V\left(k\right)\le {(\alpha +1)}^{k-k_{m-1}}V\left(k_0\right)$. It leads to $V\left(k_m\right)\le {(\alpha +1)}^{\tau }V\left(k_0\right)$, and it can also obtain $e\left(k_m\right)\in S\left(G\right)$. Analogously, we can obtain inequalities $V(k_m+1)\le \rho V\left(k_m\right)$. Based on mathematical induction, the following conclusions can be drawn

$$V(k_m+1)\le \rho V\left(k_m\right),m\in \mathbb{N}.$$

(31)

When $k\in [k_m+1,k_{m+1}+1)$, one can have

$$\begin{array}{cc}\hfill V\left(k\right)& \le {(1+\alpha )}^{k-k_m-1}V(k_m+1)\hfill \\ \hfill & \le \rho {(1+\alpha )}^{k-k_m-1}V\left(k_m\right)\hfill \\ \hfill & \le \rho {(1+\alpha )}^{k-k_m-1+1}V(k_m-1)\hfill \\ \hfill & \le \rho {(1+\alpha )}^{k-k_m-1+k_m-k_{m-1}-1}V(k_{m-1}+1)\hfill \\ \hfill & \le {\rho }^2{(1+\alpha )}^{k-k_m-1+k_m-k_{m-1}-1}V\left(k_{m-1}\right)\hfill \\ \hfill & \le ···\hfill \\ \hfill & \le {\rho }^{m+1}{(1+\alpha )}^{k-k_0-m-1}V\left(k_0\right),\hfill \end{array}$$

(32)

since $k\le k_{m+1}$, then $k-k_0\le k_{m+1}-k_0=k_{m+1}-k_m+···+k_1-k_0\le (m+1)\tau$, and it can be obtained that

$$m+1\ge \frac{k-k_0}{\tau }.$$

(33)

Then

$$\begin{array}{cc}\hfill V\left(k\right)& \le exp\left\{\left(ln(1+\alpha )-\frac{1}{\tau }ln(1+\alpha )+\frac{1}{\tau }ln\rho \right)\left(k-k_0\right)\right\}V\left(k_0\right)\hfill \\ \hfill & =exp\left\{\frac{(\tau -1)ln(1+\alpha )+ln\rho }{\tau }\left(k-k_0\right)\right\}V\left(k_0\right).\hfill \end{array}$$

(34)

According to (16), we have

$$e^T\left(k\right)(I_N\otimes P)e\left(k\right)\le exp\left\{\frac{(\tau -1)ln(1+\alpha )+ln\rho }{\tau }(k-k_0)\right\}{e}^T\left(k_0\right)(I_N\otimes P)e\left(k_0\right).$$

(35)

Since the matrix P is a symmetric positive definite, it follows that

$$\begin{array}{cc}\hfill \left|\right|e\left(k\right)|{|}^2{\lambda }_{min}\left(P\right)& \le e^T\left(k\right)(I_N\otimes P)e\left(k\right)\hfill \\ \hfill & \le exp\left\{\frac{(\tau -1)ln(1+\alpha )+ln\rho }{\tau }(k-k_0)\right\}{e}^T\left(k_0\right)(I_N\otimes P)e\left(k_0\right)\hfill \\ \hfill & \le exp\left\{\frac{(\tau -1)ln(1+\alpha )+ln\rho }{\tau }(k-k_0)\right\}\left|\right|e\left(k_0\right)|{|}^2{\lambda }_{max}\left(P\right).\hfill \end{array}$$

(36)

Finally, we obtain that, for all $k\ge k_0$,

$$\left|\right|e\left(k\right)\left|\right|\le \sqrt{\frac{{\lambda }_{max}\left(P\right)}{{\lambda }_{min}\left(P\right)}}exp\left\{\frac{(\tau -1)ln(1+\alpha )+ln\rho }{2\tau }\left(k-k_0\right)\right\}\left|\right|e\left(k_0\right)\left|\right|.$$

(37)

This completes the proof.    □

Remark 4.

Theorem 1 provides sufficient conditions for multi-agent systems (1) and (2) under impulsive control to achieve leader-following consensus, where asymmetric saturation is fully considered. The algorithm supporting these conditions is outlined in Algorithm 1. From the proof of Theorem 1, for any $\forall e\left(k_0\right)\in \Im (P,\beta )$, the state trajectory before the impulse of the system (7) is estimated to be $\Im (P,\beta {(1+\alpha )}^{\tau })$. While, after the impulse, the state trajectory will go back to $\Im (P,\beta )$. But the ellipsoid $\Im (P,\beta )\subseteq \Im (P,\beta {(1+\alpha )}^{\tau })$, so the admissible region $\Im (P,\beta )$ cannot be an invariant set.

Algorithm 1 Leader-Following Consensus of Discrete-Time Nonlinear Multi-Agent Systems Based on the Asymmetric Saturation Impulsive Control Strategy

Input: Connection topology between agents, dynamic functions of agents, initial state of leader and followers $x_i\left(0\right)$ for $i=0,1,\dots ,n$, and parameters $\alpha ,\beta ,G$. Output: Parameters P and C satisfying the conditions specified in the theorem and assumptions. 1: Determine the impulsive time interval $\tau$; 2: while$k\ne 0$do 3:     if $k\ne k_m$ then 4:         Calculate the state $x_i\left(k\right)$ using Equation (13); 5:     else 6:         while Asymmetric saturation constraint do 7:            Determine the error state $e_i\left(k_m\right)\in S\left(G\right)$ using Equation (14); 8:            Deal with saturation nonlinearity using sector condition (9) and calculate the state $x_i\left(k\right)$ using Equation (15); 9:            Compute $P,C$ based on (13), (14) and (15). 10:         end while 11:     end if 12: end while

Remark 5.

From the proof, it becomes evident that we maintain the saturation function. The sector condition (9) is employed to deal with saturation nonlinearity. Compared to addressing saturated nonlinearity using the convex hull representation, although the sector condition reduces computational costs, the convex hull representation is less conservative than the sector condition. This is due to the convex hull representation method introducing a convex hull to analyze the saturation term, obviating the need to introduce additional sector inequality conditions in the analysis.

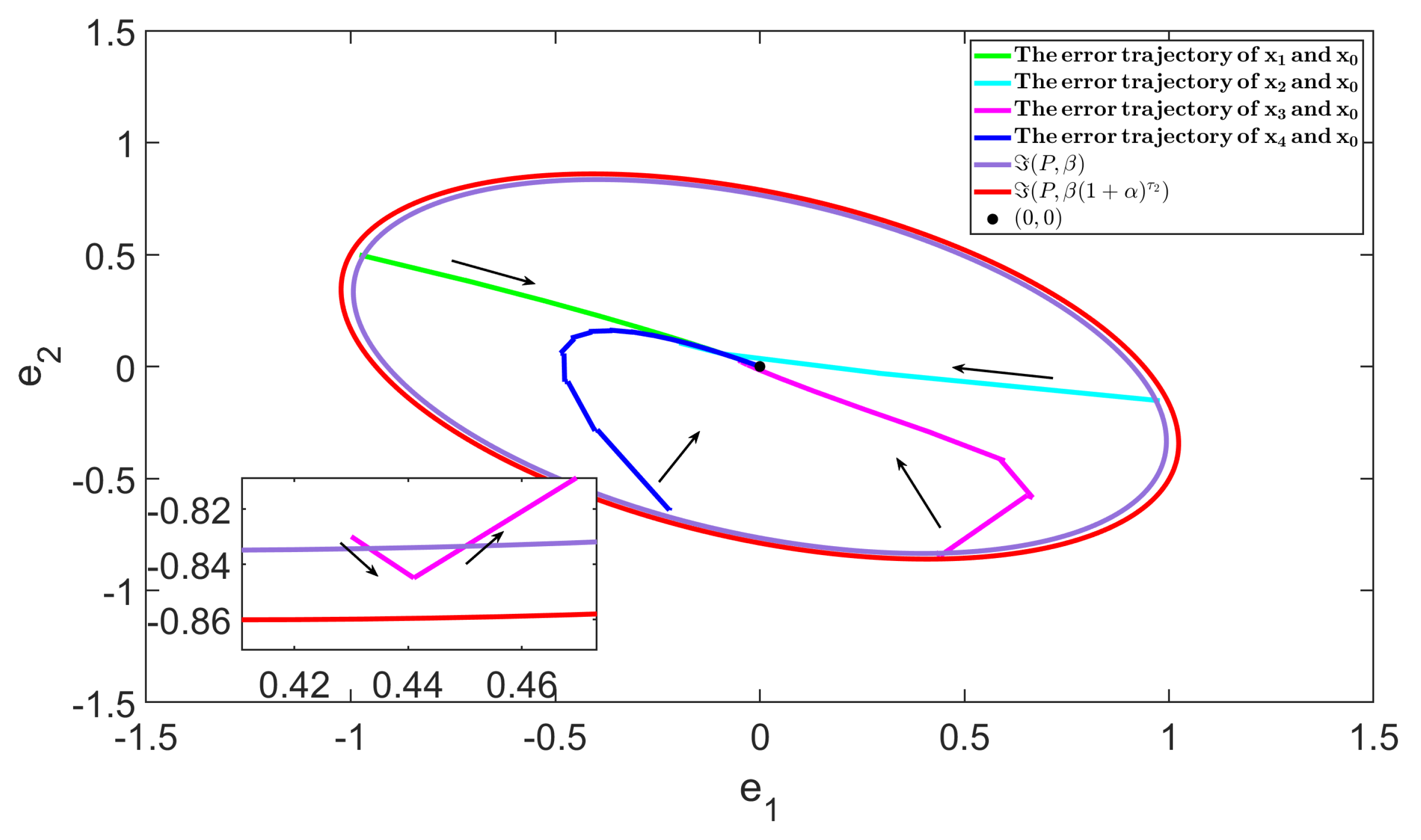
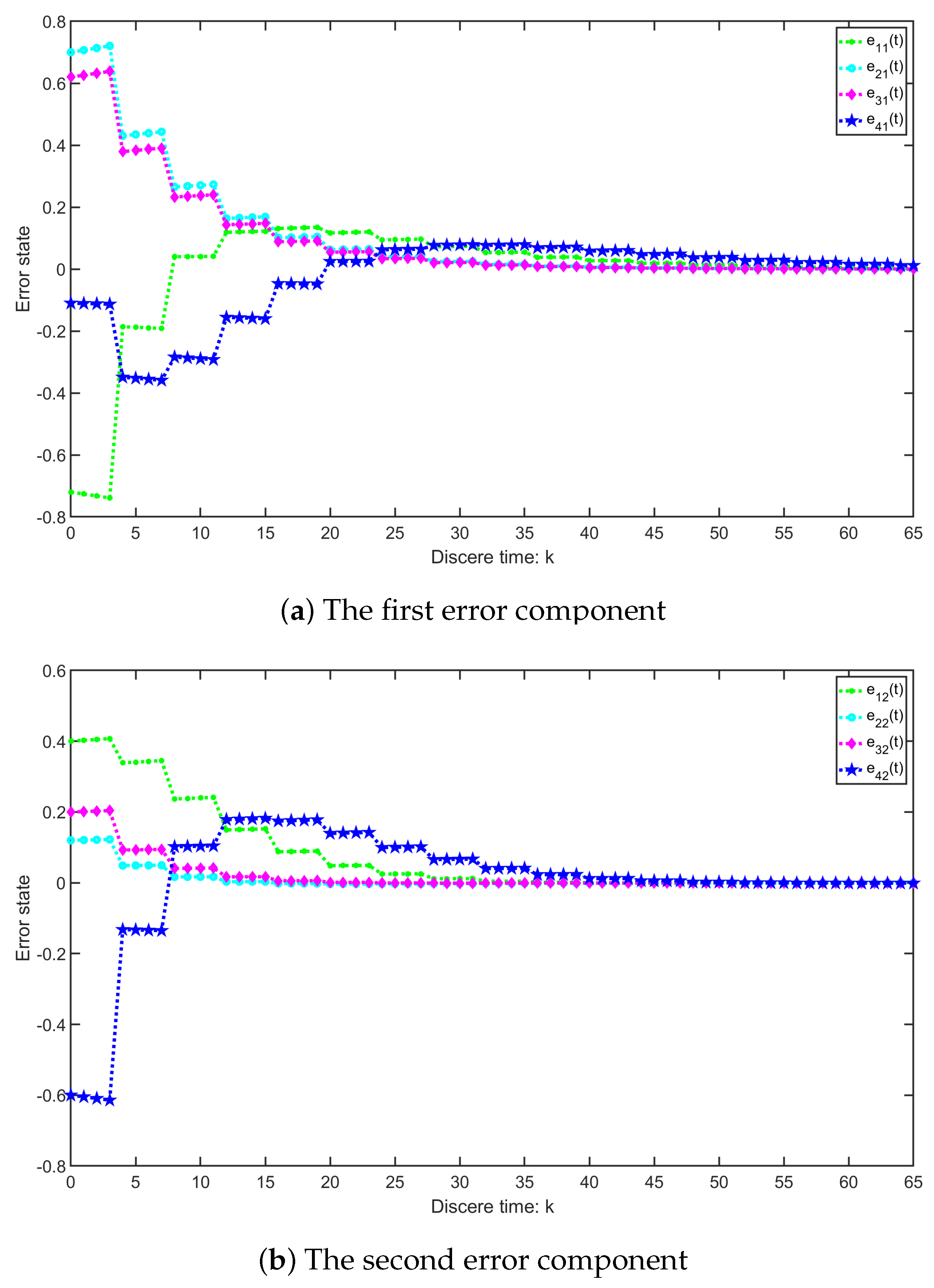
4. Numerical Simulation

In this section, we provide two numerical examples to validate the effectiveness of the theoretical results in this article.

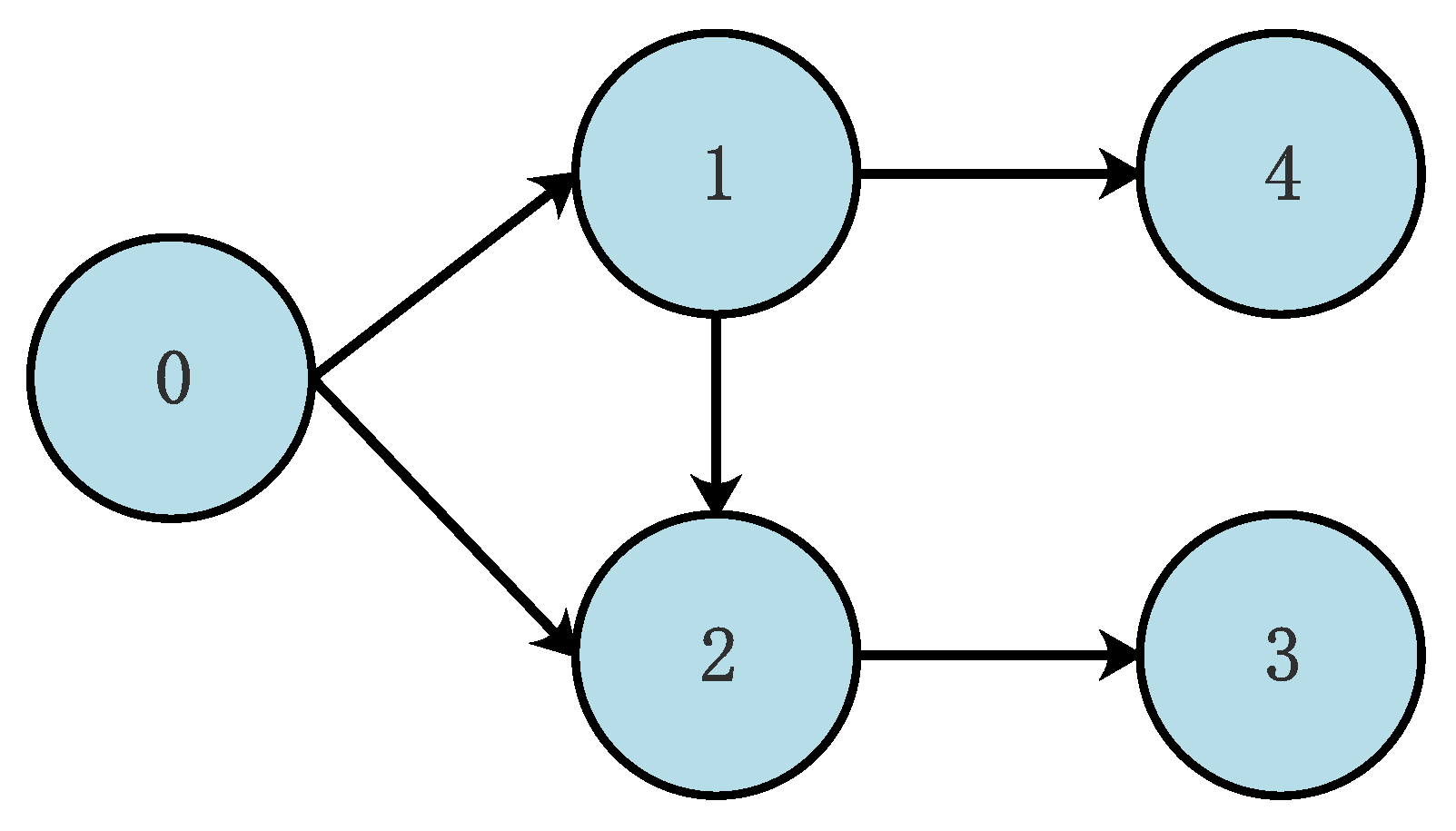
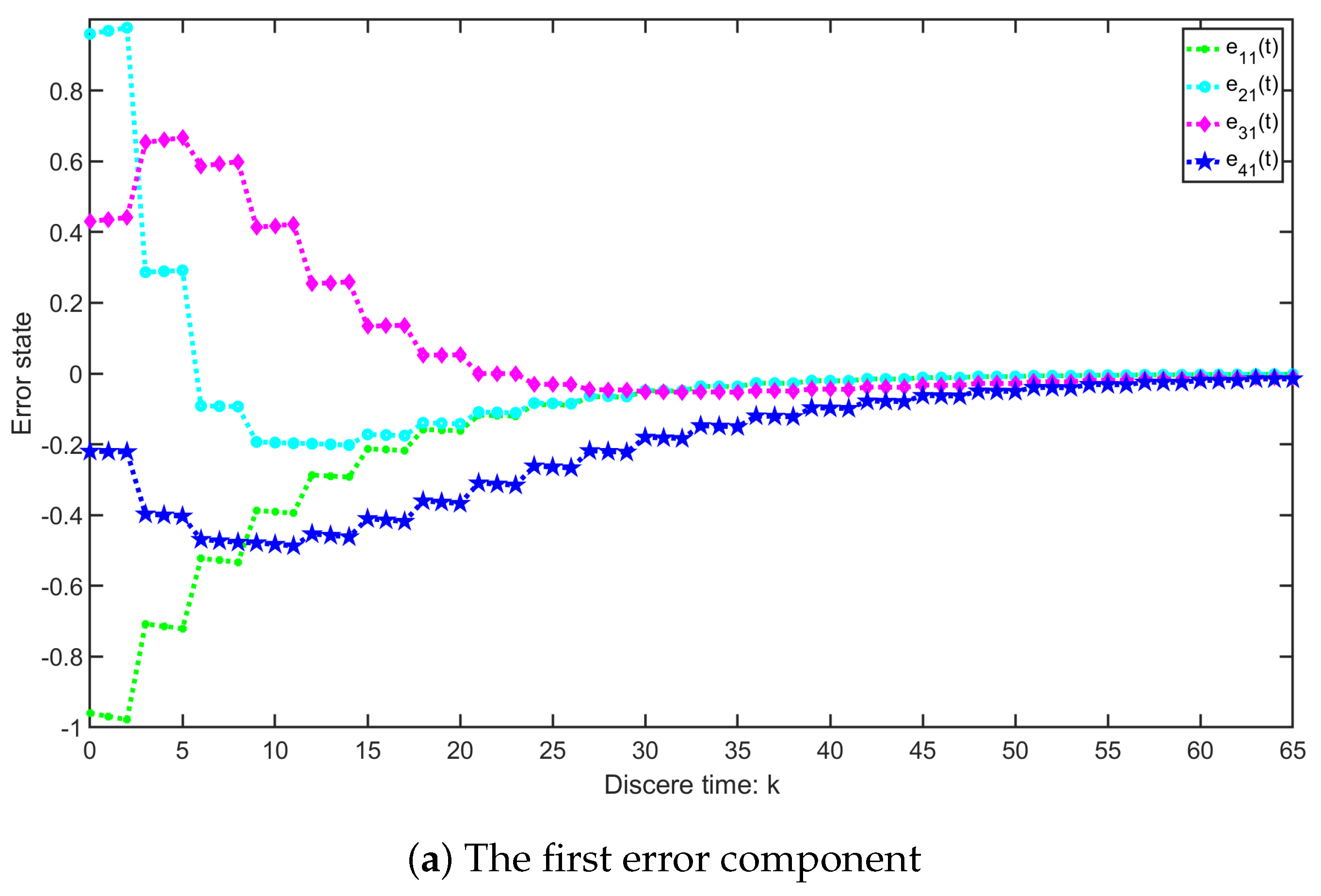
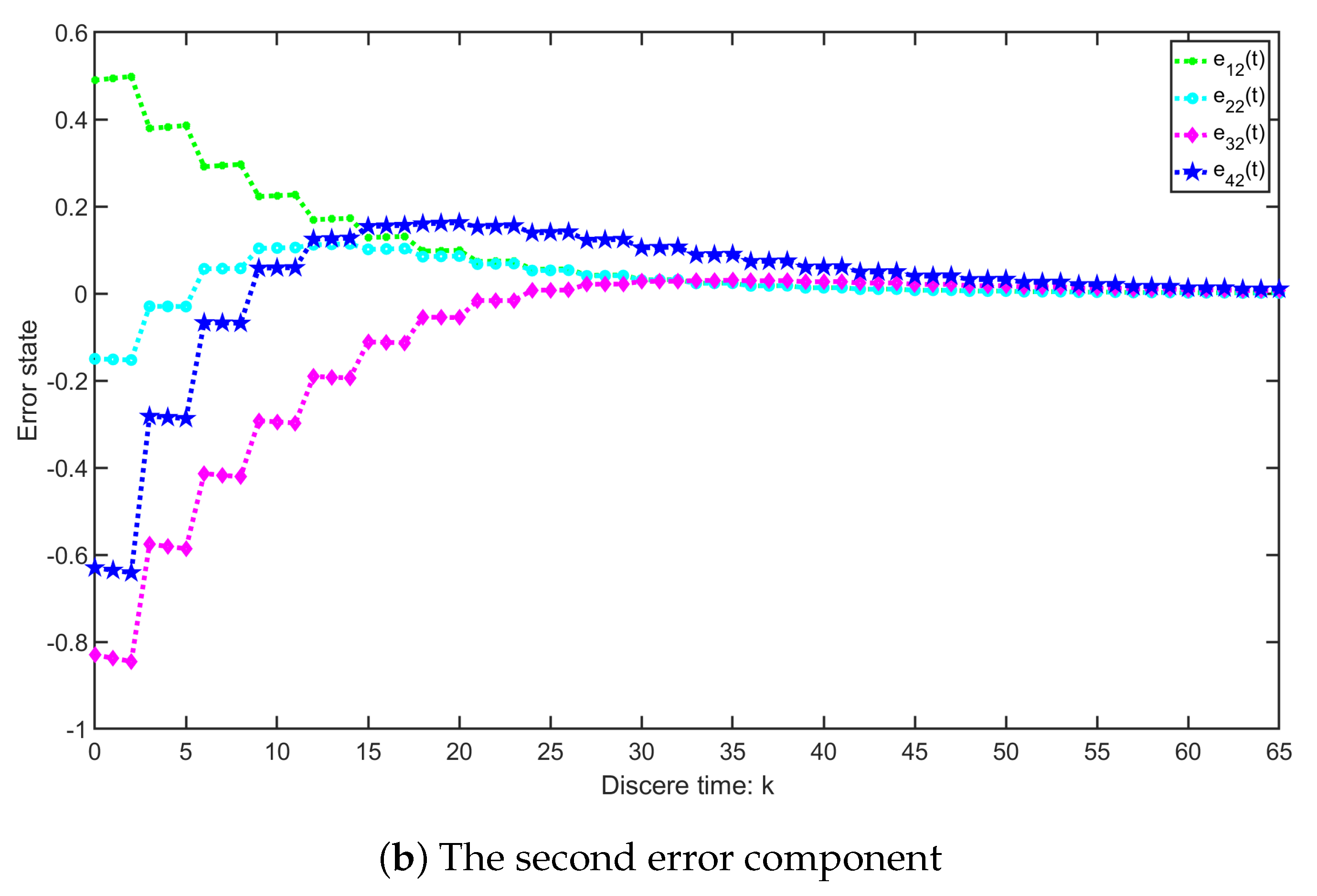
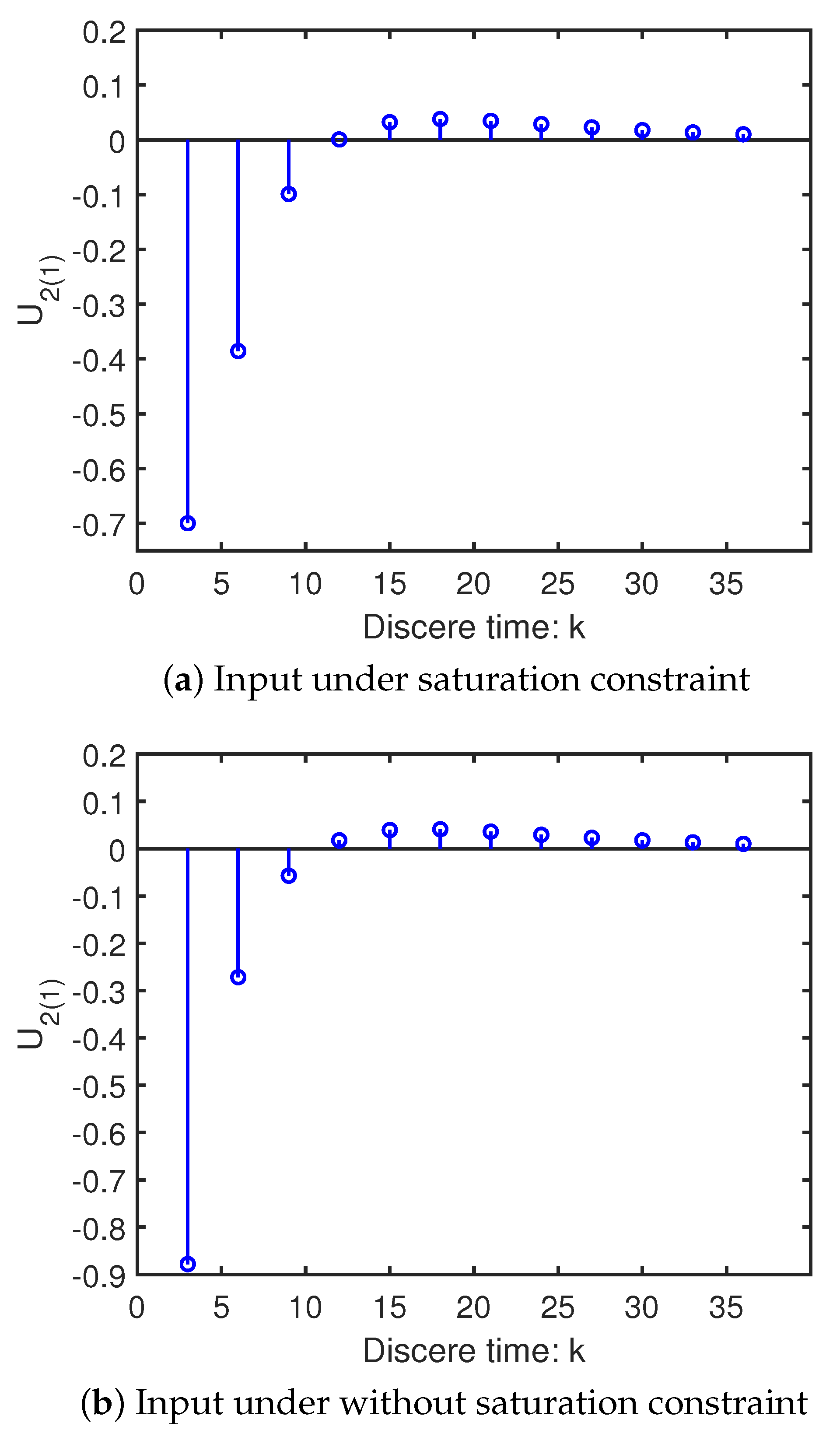
4.1. Example 1

Consider a multi-agent system consisting of four followers and one leader, whose communication topology is shown in Figure 1. The agent marked 0 is the leader, and the agents marked 1, 2, 3, and 4 are the followers.

Assume that the weight of all directed edges in the communication topology is 1. As shown in Figure 1, the Laplace matrix L and the leader adjacency matrix B are, respectively,

$$L=\left[\begin{array}{cccc}0\hfill & 0& 0& 0\\ -1\hfill & 1& 0& 0\\ 0\hfill & -1& 1& 0\\ -1\hfill & 0& 0& 1\end{array}\right],B=\left[\begin{array}{cccc}1\hfill & 0& 0& 0\\ 0\hfill & 1& 0& 0\\ 0\hfill & 0& 0& 0\\ 0\hfill & 0& 0& 0\end{array}\right].$$

Consider the system isolated and dispersed with a sampling time of 0.01, where $A=\left[\begin{array}{cc}0.78& -0.2\\ 0& 0.8\end{array}\right],f\left(x_i\left(k\right)\right)=\left[\begin{array}{c}{f}_1\left(x_{i\left(1\right)}\left(k\right)\right)\\ f_2\left(x_{i\left(2\right)}\left(k\right)\right)\end{array}\right]=\left[\begin{array}{c}0.1sin\left(x_{i\left(1\right)}\left(k\right)\right)\\ 0.1sin\left(x_{i\left(2\right)}\left(k\right)\right)\end{array}\right],i=0,1,2,3,4.$ Based on the nonlinear term, we can obtain $\Lambda =\left[\begin{array}{cc}0.1& 0\\ 0& 0.1\end{array}\right]$. Other parameters are given $\mu =1,\beta =0.6,\alpha =0.02,\rho =0.9,H=I_4\otimes \left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right],G=I_4\otimes \left[\begin{array}{cc}-0.60& -0.32\\ -0.21& -0.77\end{array}\right],{\psi }_i={[0.7,1.2]}^T,{\zeta }_i={[0.8,0.7]}^T,i=1,2,3,4.$ When $\tau =3$, we can find that

$$P=\left[\begin{array}{cc}0.7228& 0.3433\\ 0.3433& 1.0235\end{array}\right],C=\left[\begin{array}{cc}0.3116& 0.0549\\ 0.0549& 0.3540\end{array}\right].$$

The initial state of selecting the leader and followers are $x_0={[-0.29,0.51]}^T,x_1={[-1.25,1.00]}^T,$$x_2={[0.67,0.36]}^T,x_3={[0.14,-0.32]}^T,x_4={[-0.51,-0.12]}^T$. Figure 2 shows the evolution of the error $e_i\left(k\right)$ between the leader and the follower over time, and the results show that the multi-agent system can achieve the leader-following consensus. Figure 3 shows the impulsive control input for the first component of the follower marked 2 with and without saturation. Figure 4 shows that the ellipsoid $\Im (P,\beta )$ is not an invariant set. The trajectories from $\Im (P,\beta )$ might be outside $\Im (P,\beta )$. $\Im (P,\beta )$ is an estimate of the domain of attraction of the system (7) and an estimate of the admissible region of the multi-agent system (1) and (2).

4.2. Example 2

Consider the communication topology in Figure 5. Similarly, all directed edges in the communication topology have a weight of 1. The Laplace matrix L and the leader adjacency matrix B are, respectively,

$$L=\left[\begin{array}{cccc}1\hfill & 0& -1& 0\\ 0\hfill & 0& 0& 0\\ 0\hfill & 0& 0& 0\\ -1\hfill & 0& 0& 1\end{array}\right],B=\left[\begin{array}{cccc}0\hfill & 0& 0& 0\\ 0\hfill & 1& 0& 0\\ 0\hfill & 0& 1& 0\\ 0\hfill & 0& 0& 0\end{array}\right].$$

Suppose the system is isolated and dispersed over a 0.01 sample time interval. Consider parameters $A=\left[\begin{array}{cc}0.5& 0\\ 0& 0.3\end{array}\right],f\left(x_i\left(k\right)\right)=\left[\begin{array}{c}{f}_1\left(x_{i\left(1\right)}\left(k\right)\right)\\ f_2\left(x_{i\left(2\right)}\left(k\right)\right)\end{array}\right]=\left[\begin{array}{c}0.5tanh\left(x_{i\left(1\right)}\left(k\right)\right)\\ 0.5tanh\left(x_{i\left(2\right)}\left(k\right)\right)\end{array}\right],i=0,1,2,3,4,$ Obviously, $\Lambda =\left[\begin{array}{cc}0.5& 0\\ 0& 0.5\end{array}\right]$. Other parameters are given $\mu =1,\beta =0.4,\alpha =0.01,\rho =0.9,H=I_4\otimes \left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right],G=I_4\otimes \left[\begin{array}{cc}-0.60& -0.32\\ -0.21& -0.77\end{array}\right],{\psi }_i={[0.6,1.5]}^T,{\zeta }_i={[0.8,0.6]}^T,i=1,2,3,4.$ By selecting the value of $\tau =4$, we obtain the value of

$$P=\left[\begin{array}{cc}0.6762& 0.2311\\ 0.2311& 0.9622\end{array}\right],C=\left[\begin{array}{cc}0.4053& 0.0203\\ 0.0203& 0.4854\end{array}\right]$$

The initial states of selecting the leader and followers are specified as $x_0={[-0.20,0.50]}^T,$$x_1={[-0.92,0.90]}^T,x_2={[0.50,0.62]}^T,x_3={[0.42,0.70]}^T,x_4={[-0.31,-0.10]}^T.$ Figure 6 shows the state of the leader and followers will tend to be consensus. Figure 7 shows that the invariant set of the system is $\Im (P,\beta {(1+\alpha )}^{\tau })$.

5. Conclusions and Future Work

In this article, the leader-following consensus of a class of discrete-time nonlinear multi-agent systems with asymmetric saturation impulsive control has been investigated. Firstly, the consensus protocol has been designed using algebraic graph theory and impulsive system stability theory to reduce the energy consumption and damage to the equipment of the system. We have dealt with saturation nonlinearity for asymmetric saturation by directly considering the saturation effect, preserving the saturation function, and introducing the sector condition. Then, based on Lyapunov stability theory and matrix theory, sufficient conditions for the leader-following consensus of discrete-time nonlinear multi-agent systems have been established. The protocol designed can allow all followers to track the leader under asymmetric saturation, thus achieving a gradual consensus of the state. Finally, some examples are used to verify our conclusions. In future work, we will further study the consensus control of multi-agent systems with saturation constraints under impulsive disturbance.