Some New Notions of Continuity in Generalized Primal Topological Space
Abstract
1. Introduction
2. Preliminaries
- 1.
- Assume that , is a . Let be any subset of . is generalized semi-open if there is a -open set in such that ⊆ (), or, appropriately, if ()).
- 2.
- A generalized semi-closed set is the complement of a generalized semi-open set. The family of all generalized semi-open sets in . is indicated as -SO.
- 3.
- The union of all generalized semi-open sets of contained in is the generalized semi-interior of (briefly, ()).
- 4.
- Generalized semi-closure of (briefly, ()) is the intersection of all generalized semi-closed sets of containing .
- 1.
- Consider , as a . A subset of is generalized semi-generalized closed (briefly, -closed) if Cl ⊆ whenever ⊆ and is generalized semi-open in . Similarly, -closed) is generalized semi-generalized open, and is indicated as -open.
- 2.
- The generalized semi-generalized interior (briefly, ) of is specified as the union of all -open sets of contained in .
- 3.
- Assuming a subset of , , the generalized semi-generalized closure (briefly, ) of is termed as the intersection of all -closed sets in containing .
- 1.
- ∉.
- 2.
- For , ⊆ has ⊆ such that ∉ if ∉ .
- 3.
- For , ⊆ ; then, ∩ ∉ whenever ∉ and ∉ .
- 1.
- Assume that , , is a . A subset of , , is generalized primal semi-open if there exists a -open set in such that ⊆ ⊆ , or equivalently if Int.
- 2.
- The generalized primal semi-closed set is the complement of the generalized primal semi-open set. Thus, , , is the collection of all generalized primal semi-open sets in , , .
- 3.
- The , semi-interior of (briefly, , sInt) is the union of all generalized primal semi-open sets of contained in .
- 4.
- The intersection of all generalized primal semi-closed sets of containing is , (semi-closure of , briefly , sCl).
3. Main Results
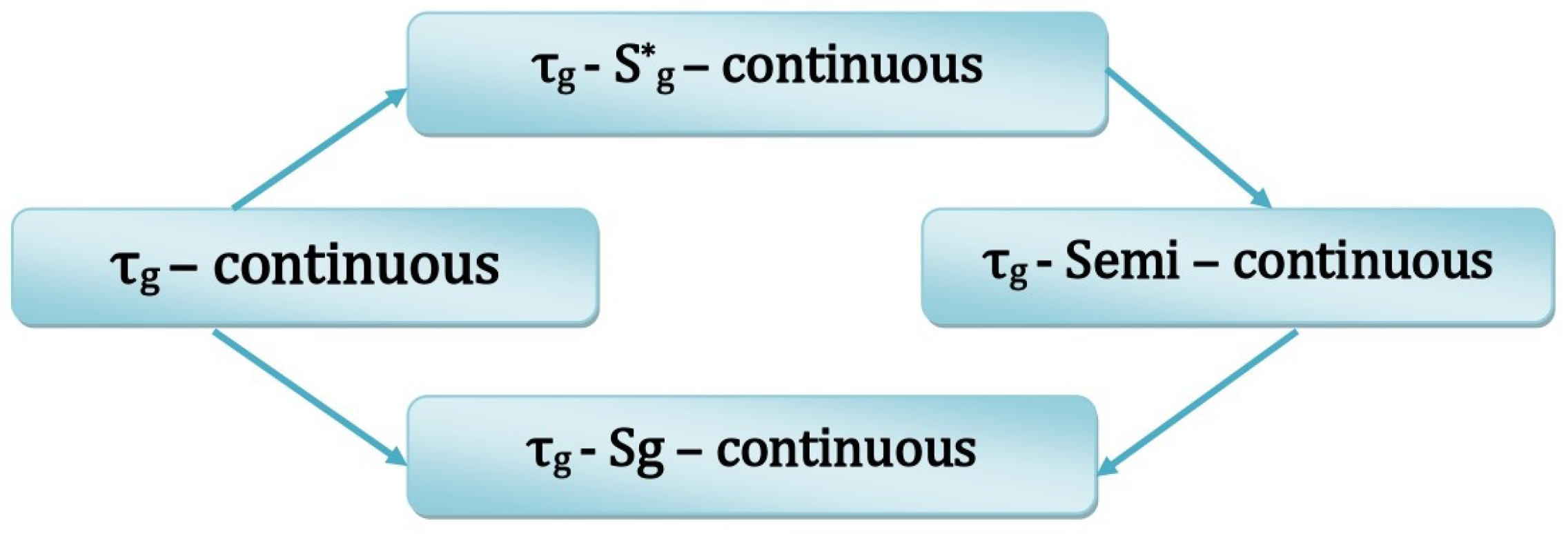
3.1. Functions in
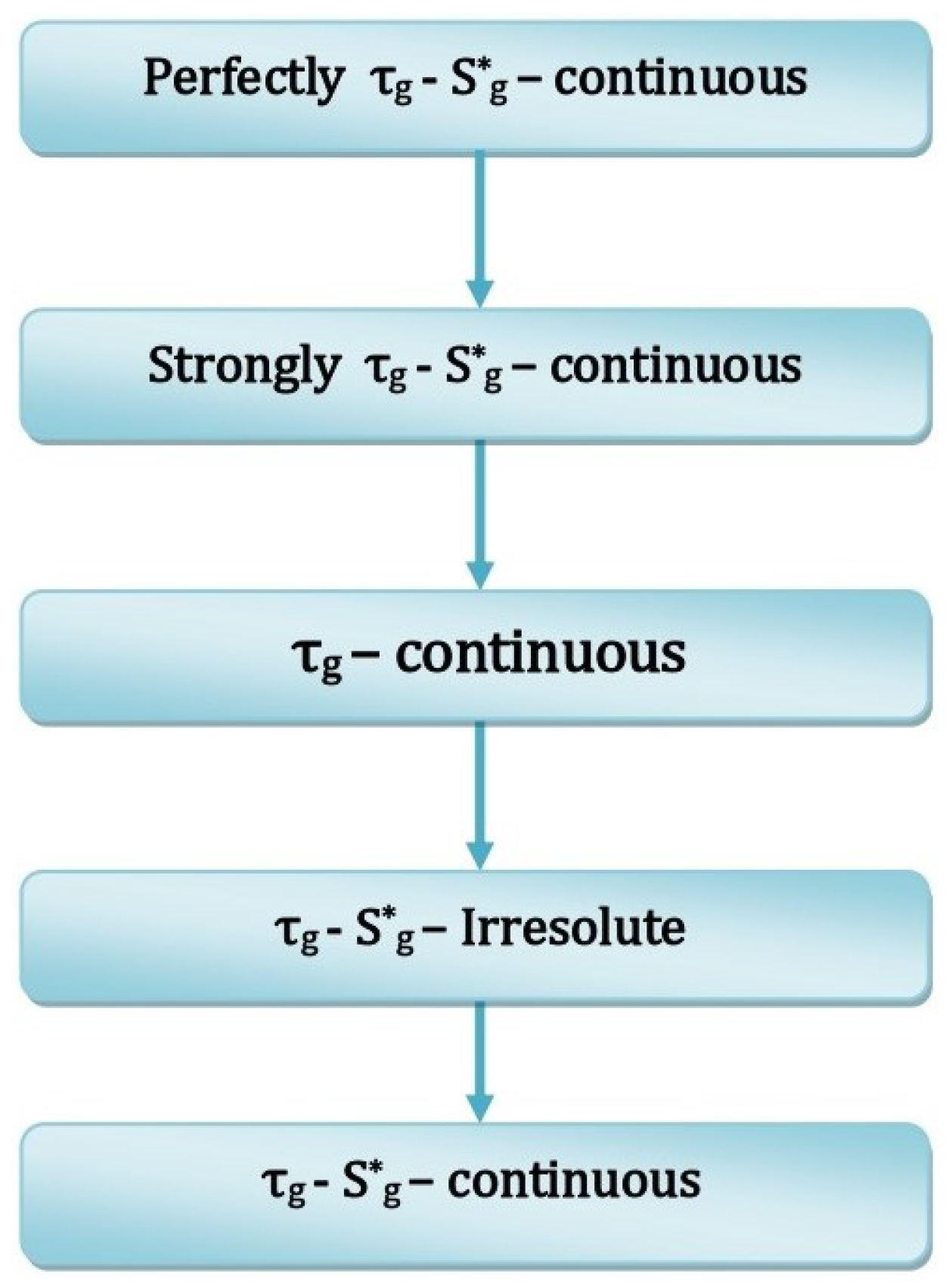
3.1.1. --Continuous Functions
- 1.
- is --continuous.
- 2.
- For every -closed set in , there is an inverse image that is --closed in .
- 3.
- -Cl⊆∀∈.
- 4.
- -Cl⊆∀ in .
- 5.
- ⊆-Int for every in .
3.1.2. --Irresolute Function
3.1.3. Strongly –-Continuous Function
3.1.4. Perfectly –-Continuous Function
3.1.5. –-Open Map
3.1.6. –-Closed Map
3.2. –-Homeomorphism and –-Homeomorphism
3.2.1. –-Homeomorphism
- 1.
- Generalized closed (g-closed), if for any open set of we have Cl whenever .
- 2.
- Generalized semi-closed (gs-closed), if for any open set of we have sCl whenever .
- 3.
- Semi-generalized closed (sg-closed), if for any semi-open set of we have sCl whenever .
- 1.
- Generalized continuous (briefly, -continuous) if for each closed in is g-closed in .
- 2.
- Generalized semi-continuous (briefly, -continuous) if for each closed in is gs-closed in .
- 3.
- Semi-generalized continuous (briefly, -continuous) if for each closed in is sg-closed in .
- 1.
- A -homeomorphism if and are both -continuous.
- 2.
- A -homeomorphism if and are both -continuous.
- 3.
- A -homeomorphism if and are both -continuous.
- 1.
- The inverse function is –-continuous.
- 2.
- is a –-open function.
- 3.
- is a –-closed function
- 1.
- The function is –-open.
- 2.
- is –-homeomorphism.
- 3.
- is a –-closed function
3.2.2. –-Homeomorphism
3.3. Functions in
3.3.1. –-Continuous Functions
- 1.
- is –-continuous.
- 2.
- For every -closed set in , there is an inverse image that is –-closed in .
- 3.
- -Cl⊆∀∈.
- 4.
- -Cl⊆∀ in .
- 5.
- ⊆-Int for every in .
3.3.2. –-Irresolute Function
3.3.3. Strongly –-Continuous Function
3.3.4. Perfectly –-Continuous Function
3.3.5. –-Open Map
3.3.6. –-Closed Map
3.4. –-Homeomorphism and -Homeomorphism
3.4.1. –-Homeomorphism
- 1.
- A generalized primal closed (gp-closed) set if for any open set of , Cl ⊆ whenever ⊆ .
- 2.
- A generalized primal semi-closed (gps-closed) set if for any open set of , sCl ⊆ whenever ⊆ .
- 3.
- A semi-generalized primal closed (sgp-closed) set if for any semi-open set of , sCl ⊆ whenever ⊆ .
- 1.
- Generalized primal continuous (briefly, -continuous) if for each closed in , , , is gp-closed in , , .
- 2.
- Generalized primal semi-continuous (briefly, -continuous) if for each closed in , , , is gps-closed in , , .
- 3.
- Semi-generalized primal continuous (briefly, -continuous) if for each closed in , , , is sgp-closed in , , .
- 1.
- A -homeomorphism if and are both -continuous.
- 2.
- A -homeomorphism if and are both -continuous.
- 3.
- A -homeomorphism if and are both -continuous.
- 1.
- The inverse function is –-continuous.
- 2.
- is a –-open function.
- 3.
- is a –-closed function
- 1.
- The function , , → , , is –-open.
- 2.
- is a –-homeomorphism.
- 3.
- is a –-closed function
3.4.2. –-Homeomorphism
4. Methodology
- Review of Existing Literature: The study starts with a thorough analysis of the existing literature and prior research on generalized topological spaces, generalized primal topological spaces, and – functions. Important basic ideas and earlier research on open maps, continuity, and both irresolute and closed mappings in topological spaces are noted. The definitions and theorems established later are based on this review.
- Definition of – functions: Here, the –-function and all of its associated characteristics are indicated, such as:
- –
- --continuous mapping: A function that maintains –-open sets under continuous mappings.
- –
- –-irresolute: A function such that each –-open set’s inverse image is also –-open.
- –
- Strongly –-continuous mapping: A mapping in which for every –-open set there is an inverse image that is open.
- –
- Perfectly –-continuous mapping: A mapping in which for every –-open set there is an inverse image that is both open and closed.
- –
- –-open and –-closed maps: Functions that respectively map –-open sets to -open sets and –-closed sets to -closed sets.
- Development of Propositions and Theorems: After defining each function type, we proceed to develop associated theorems and propositions. This comprises the following aspects:
- –
- Theorems that specify the circumstances in which a function is either –-irresolute or –-continuous.
- –
- The links between –-open and –-closed maps, along with how they affect the topological structure.
- –
- Theoretical analysis of the behavior of strongly and perfectly –-continuous functions in generalized topological spaces.
- Extension to Generalized Primal Topological Spaces: Subsequently, we broaden the scope of our analysis by including these functions in the context of . Within this framework, we redefine – functions to emphasize the fundamental character of the space. This allows for analysis of these functions under additional conditions and limitations, as the generalized primal topological space provides a more constrained framework.
- Analysis of - and -Homeomorphisms: The fourth stage explores the ways in which these homeomorphisms maintain the -closed and -open sets in various spaces. –-homeomorphisms in generalized topological spaces and --homeomorphisms in generalized primal topological spaces make up this section. Through the use of formal arguments and comparative analysis, the characteristics and behavior of homeomorphisms in both contexts are examined.
- Proofs and Verification: Precise mathematical proofs support every theorem and statement. To confirm the accuracy of our findings, we utilize conventional methods in topology such as continuity rules and arguments from set theory. This stage guarantees that the conclusions are sound both mathematically and logically.
- Comparative Study: We carry out a comparative study of the behaviors of functions, -homeomorphisms, and -homeomorphisms in generalized topological spaces and generalized primal topological spaces to gain a deeper understanding of their relevance. This comparison demonstrates the differences and similarities in their behavior under various topological contexts.
- Conclusions and Upcoming Work: The last phase entails a summary of the main study’s findings and suggestions for future work paths. We explain the consequences of our findings and point out possible directions for future research that might provide fresh insights, especially in more specialized or applied topological situations.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Levine, N. Generalized closed sets in topology. Rend. Circ. Mat. Palermo 1970, 19, 89–96. [Google Scholar] [CrossRef]
- Bhattacharyya, P. Semi-generalized closed sets in topology. Indian J. Math. 1987, 29, 376–382. [Google Scholar]
- Dunham, W.; Levine, N. Further results on generalized closed sets in topology. Kyungpook Math. J. 1980, 20, 169–175. [Google Scholar]
- Dunham, W. T 1/2-SPACES. Kyungpook Math. J. 1977, 17, 161–169. [Google Scholar]
- Kumar, M.V. Between closed sets and g-closed sets. Mem. Fac. Sci. Kochi Univ. (Math.) 2000, 21, 1–19. [Google Scholar]
- Sundaram, P.; Maki, H.; Balachandran, K. Semi-generalized continuous maps and semi-spaces. Bull. Fukuoka Univ. Ed. Part III 1991, 40, 33–40. [Google Scholar]
- Møller, J.M. General Topology; Matematisk Institut: København, Denmark, 2007. [Google Scholar]
- Al-Saadi, H.; Al-Malki, H. Generalized primal topological spaces. AIMS Math. 2023, 8, 24162–24175. [Google Scholar] [CrossRef]
- Császár, Á. Generalized open sets. Acta Math. Hung. 1997, 75, 65–87. [Google Scholar] [CrossRef]
- Császár, A. Generalized open sets in generalized topologies. Acta Math. Hung. 2005, 106, 53–66. [Google Scholar] [CrossRef]
- Császár, A. Intersections of Open Sets in Generalized Topological Spaces. Univ. Sci. Budapestinensis Rolando Eotvos Nomin. 2006, 49, 53–57. [Google Scholar]
- Császár, Á. γ-connected sets. Acta Math. Hung. 2003, 101, 273–279. [Google Scholar] [CrossRef]
- Császár, Á. Product of generalized topologies. Acta Math. Hung. 2009, 123, 127–132. [Google Scholar] [CrossRef]
- Balachandran, K. On generalized continuous maps in topological spaces. Mem. Fac. Sci. Kochi Univ. Ser. A Math. 1991, 12, 5–13. [Google Scholar]
- Iyappan, D.; Nagaveni, N. On Semi Generalized b-Continuous Maps, Semi Generalized b-Closed Maps in Topological Space. Int. J. Math. Anal. 2012, 6, 1251–1264. [Google Scholar]
- Banakh, T.; Bokalo, B. On scatteredly continuous maps between topological spaces. Topol. Its Appl. 2010, 157, 108–122. [Google Scholar] [CrossRef]
- Gierz, G.; Lawson, J. Generalized continuous and hypercontinuous lattices. Rocky Mt. J. Math. 1981, 11, 271–296. [Google Scholar] [CrossRef]
- Cueva, M.C. Semi-generalized continuous maps in topological spaces. Port. Math. 1995, 52, 399–407. [Google Scholar]
- Császár, A. Generalized topology, generized continuity. Acta Math. Hung. 2002, 96, 351–357. [Google Scholar] [CrossRef]
- Khayyeri, R.; Mohamadian, R. On base for generalized topological spaces. Int. J. Contemp. Math. Sci. 2011, 6, 2377–2383. [Google Scholar]
- Sarsak, M.S. On some properties of generalized open sets in generalized topological spaces. Demonstr. Math. 2013, 46, 415–427. [Google Scholar] [CrossRef]
- Maki, H.; Balachandran, K.; Devi, R. Remarks on semi-generalized closed sets and generalized semi-closed sets. Kyungpook Math. J. 1996, 36, 155. [Google Scholar]
- Maki, H.; Rao, K.C.; Gani, A.N. On generalizing semi-open sets and preopen sets. Pure Appl. Math. Sci. 1999, 49, 17–30. [Google Scholar]
- Navalagi, G.; Page, H. ϑ-Generalized semi-open and ϑ-generalized semi-closed functions. Proyecciones-J. Math. 2009, 28, 111–123. [Google Scholar] [CrossRef]
- Acharjee, S.; Özkoç, M.; Issaka, F.Y. Primal topological spaces. arXiv 2022, arXiv:2209.12676. [Google Scholar]
- Özkoç, M.; Köstel, B. On the Topology of Primal Topological Spaces. arXiv 2024, arXiv:2402.08572. [Google Scholar]
- Al-Saadi, H.; Al-Malki, H. Categories of open sets in generalized primal topological spaces. Mathematics 2024, 12, 207. [Google Scholar] [CrossRef]
- Min, W. Generalized continuous functions defined by generalized open sets on generalized topological spaces. Acta Math. Hung. 2010, 128, 299–306. [Google Scholar] [CrossRef]
- Krishnappa, R.; Ittanagi, B. On R#-Closed and R#-Open Maps in Topological Spaces. Int. J. Eng. Technol. 2018, 7, 770. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shahbaz, M.; Kamran, T.; Ishtiaq, U.; Imtiaz, M.; Popa, I.-L.; Maiz, F.M. Some New Notions of Continuity in Generalized Primal Topological Space. Mathematics 2024, 12, 3995. https://doi.org/10.3390/math12243995
Shahbaz M, Kamran T, Ishtiaq U, Imtiaz M, Popa I-L, Maiz FM. Some New Notions of Continuity in Generalized Primal Topological Space. Mathematics. 2024; 12(24):3995. https://doi.org/10.3390/math12243995
Chicago/Turabian StyleShahbaz, Muhammad, Tayyab Kamran, Umar Ishtiaq, Mariam Imtiaz, Ioan-Lucian Popa, and Fethi Mohamed Maiz. 2024. "Some New Notions of Continuity in Generalized Primal Topological Space" Mathematics 12, no. 24: 3995. https://doi.org/10.3390/math12243995
APA StyleShahbaz, M., Kamran, T., Ishtiaq, U., Imtiaz, M., Popa, I.-L., & Maiz, F. M. (2024). Some New Notions of Continuity in Generalized Primal Topological Space. Mathematics, 12(24), 3995. https://doi.org/10.3390/math12243995







