A New Varying-Factor Finite-Time Recurrent Neural Network to Solve the Time-Varying Sylvester Equation Online
Abstract
1. Introduction
- (1)
- In the first step, the error function is defined as . In order to acquire the solution of the Sylvester equation, the error function should converge to zero.
- (2)
- In the next step, for the purpose of acquiring the minimum point of the error function, GNN methods use a negative gradient descent direction. In addition to this, GNN methods employ a constant scalar-type parameter, which accelerates the convergence rate of the error function to solve the Sylvester equation efficiently.
- (1)
- We propose a VFFTRNN algorithm for solving the Sylvester equation.
- (2)
- Compared with VP-CDNN, this network can achieve finite-time convergence.
- (3)
- We theoretically prove the convergence time of the network in the case of three activation functions.
- (4)
- In the situation considering the existence of disturbances, the robustness of VFFTRNN is discussed.
- (5)
- Data simulation results show that the proposed VFFTRNN has better convergence and robustness than the traditional ZNN model under the same initial conditions.
2. Problem Formulation and Knowledge Preparation
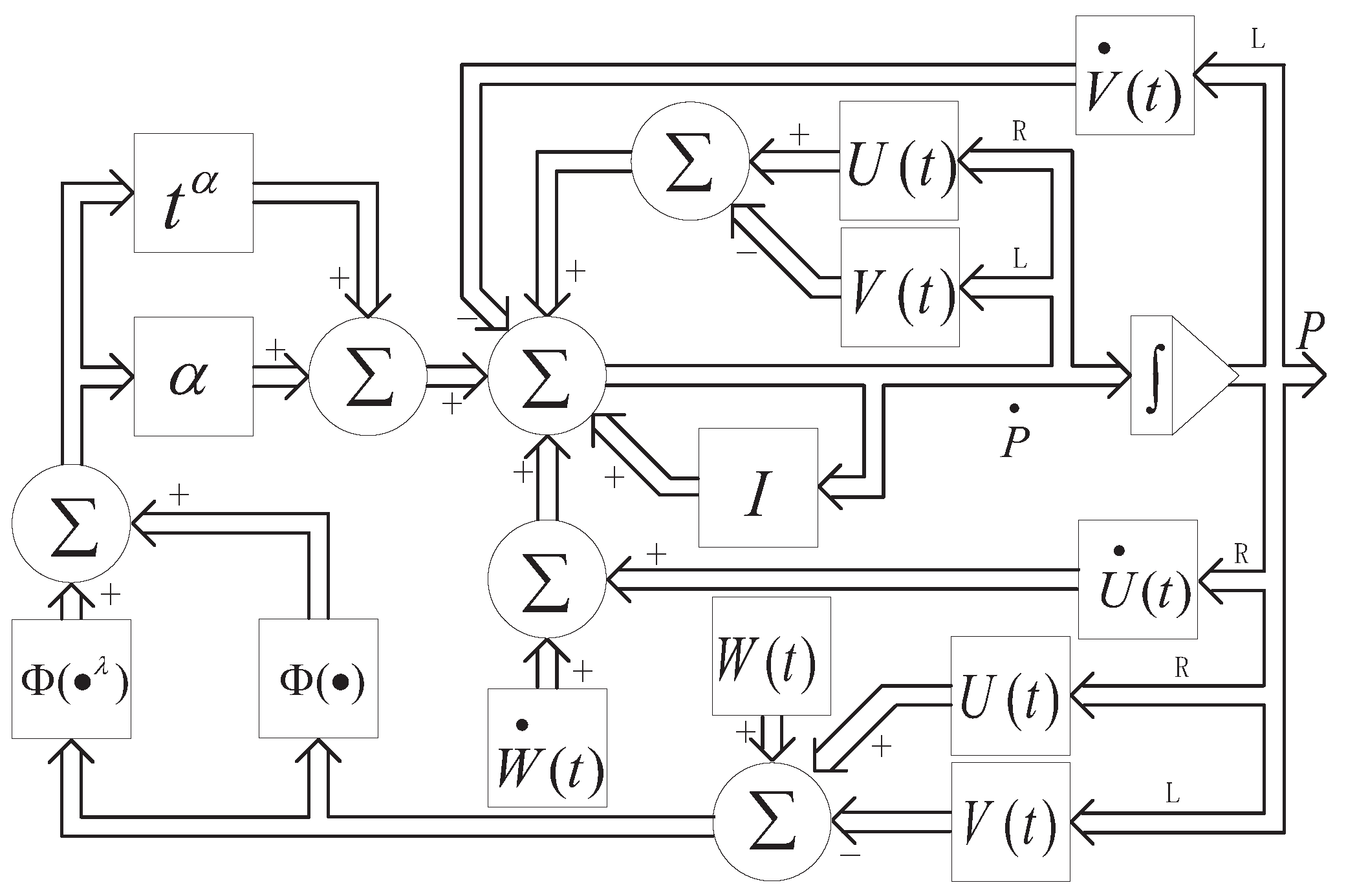
3. Varying-Factor Finite-Time Recurrent Neural Networks
3.1. Convergence Analysis
- (1)
- When we choose the linear activation function (i.e., ), the convergence time of VFFTRNN .
- (2)
- When we choose the bipolar-sigmoid activation function (i.e., , ), the convergence time of VFFTRNN .
- (3)
- When we choose the power activation function (i.e., , and s is an odd number), the convergence time of VFFTRNN .
- (1)
- Linear-type: For the linear-type case, the following equation can be obtained from (10).In light of differential equation theory [34], we can obtain the solution of (12).where . Let in (13) be equal to zero, and we can obtain the following:then we can easily find . In other words, for any i and j in the definitional domain, we have that as , the scalar value . Note that by the definition of above, at this time, the error function in matrix form will also approach zero, which guarantees that the state matrix .To sum up, we can obtain the convergence time when the VFFTRNN system uses the linear-type function as follows:where . This shows that in the case where the activation function is linear, the VFFTRNN method can achieve finite-time convergence in solving the Sylvester equation.
- (2)
- Bipolar-Sigmoid-Type: In this case, we can easily see that the activation function is , where and are scalar factors. The following equation can be obtained from (10).where , . In light of the relevant theory of differential equations, we can rewrite (15) as follows:where . According to the Lyapunov function of this system, we know that either increases or decreases monotonically as t increases. For simplicity, we will next discuss the case where . In this case, we can derive the following:At this point, we consider the following two situations.
- a.
- When , noticing that and are convex, solving (16) giveswhere is a constant, determined by the scalar factor . Similar to linear-type, solving for (17), we obtain
- b.
- Notice that and are monotonically increasing over the interval , so for , and . Therefore, we haveIn light of the results (18) and (21) from the two situations, it can be concluded that when or , the scalar value for any i and j in the defined domain. This means that the convergence of the state matrix is guaranteed. Thus, the convergence time for the bipolar-sigmoid-type activation function can be expressed as
- (3)
- Power-Type: For the power-type case, the activation function is defined as , where s is an odd number and . In this case, the following equation can be derived from (10).
- Similar to (16), we have
- The discussion is divided into the following two situations:
- a.
- When , it can be found that , so . In light of (24), we can obtainThen, the result (25) can be obtained:
- b.
- When , we know that for all , we have . So similarly,Then, the following result (26) can be obtained:
In conclusion, when or , the scalar value for any i and j on the definitional domain. This means that the convergence of state matrix is guaranteed. The convergence time for the power-type activation function can be represented as
- (1)
- Linear-Type:
- a.
- For , in light of (14), can be rewritten aswhere and . Then, let us take the partial derivative with respect to .We know that if is large enough, will become less than zero. Therefore, for , there are two possible situations:In the first situation, decreases as increases. In other words, as increases, decreases simultaneously. Similarly, in the second situation, will first increase and then decrease as increases. This means that when reaches a specific value, determined by the initial error , will attain its maximum.
- b.
- For , in light of (14), it can easily be seen that we only need to analyze . Next, take the partial derivative of this expression:where and . Since the denominator of (30) is always positive, we only need to analyze the numerator:If , then , and . Therefore, the value of (30) is always less than zero. If , let , then . The numerator can be rewritten as follows:Note that the function is monotonically increasing when . Therefore, the value of Equation (32) is always less than zero. In other words, the value of Equation (30) is always less than zero.Based on the above discussion, we can conclude that for any , it is always true that . Considering the relationship between and , we can conclude that when is larger, is smaller.
- (2)
- Bipolar-Sigmoid-Type:
- a.
- For , in light of (22), can be rewritten aswhere . Similar to the analysis of the linear-type above, there are two situations:For the first situation, when increases, decreases. For the second situation, there exists a specific value where is maximized.
- b.
In addition, consider the influence of the factor on the convergence time . We know that , and as increases, also increases. Furthermore, according to Equation (22), the larger is, the smaller becomes. - (3)
- Power-Type:
- a.
- For , let , then we haveSimilar to the analysis of the linear-type case above, there are two possible situations:For the first situation, when increases, decreases. For the second situation, there exists a certain value where is maximized.
- b.
- For , according to (27), we can conclude that the larger is, the larger becomes, especially when . In addition, when , we only need to consider . Let , thenSo in conclusion, it is clear that for , as increases, increases.
- (1)
- For , its relationship to the convergence time can always be divided into two cases. In the first case, as increases, the convergence time decreases. In the second case, the convergence time first increases and then decreases. It is worth noting that even when , the VFFTRNN system will still converge in finite time.
- (2)
- For , the convergence time always increases with the increase in , regardless of the chosen activation function. Clearly, the factor accelerates the convergence process of the proposed VFFTRNN. If , the proposed VFFTRNN becomes VP-CDNN. Furthermore, if the factor , the proposed VFFTRNN reduces to ZNN.
3.2. Robustness Analysis
- (1)
- Coefficient Matrix Perturbation:Theorem 5.If uncharted, smooth coefficient matrix perturbations , and exist in the VFFTRNN model, and if they satisfy the following conditions:where the mass matrices are defined as , . Therefore, the calculation error is bounded.Proof.The following proof uses the linear activation function as an example. First, we define a variable which represents the error in the state matrix . Then, its Frobenius norm can be written aswhere . Furthermore, in light of (1), we can obtain an expression of W:Substitute (36) into (4):In light of Theorem 1, we can acquire its vector form:where and . From Theorem 2 and inequality (3), it is clear that the matrix is invertible. Therefore, we conclude thatSubstituting (13) into (38), we can obtainwhere . The results demonstrate that the VFFTRNN model exhibits super-exponential convergence in solving the Sylvester equation when employing a linear-type activation function.Next, we consider the case where perturbations in the coefficient matrices exist. Based on Equation (8), it is straightforward to derive the implicit dynamic equation of the VFFTRNN system under the influence of these perturbations.where , and . denotes the solution to the VFFTRNN system with perturbation.Furthermore, in light of (36), its vector form can be written aswhere . Then, we can acquireTherefore, we can derive the inequality for the theoretical solution .Let us assume that the theoretical solution of the VFFTRNN system with perturbation is . Similar to (40), we can easily deduce thatIn addition, similar to (39), we can obtainwhere and .Then, based on (41), (42) and (43), we can derive an upper bound for the computation error .In light of the above analysis, we conclude that when using a linear-type activation function, the computation error of the VFFTRNN system with perturbation is bounded. Additionally, it is worth mentioning that the solution process exhibits a super-exponential convergence rate.Similarly, for sigmoid or power activation functions, it is not difficult to prove that the computation error of the VFFTRNN system with perturbation is bounded. Due to the limited space of this paper, the analysis for these two activation functions will not be presented here.Thus, the proof of the robustness of Theorem 5 regarding matrix perturbation is complete. □
- (2)
- Differentiation and Model Implementation Errors:In the process of hardware implementation, dynamics implementation errors and differential errors related to , and are inevitable. These errors are collectively referred to as model implementation errors [35]. In this section, we analyze the robustness of the VFFTRNN system in the presence of these errors. Let us assume that the differential errors for the time derivatives of the matrices and are and , respectively, and the model implementation error is denoted as . Then, based on Equation (8), the implicit dynamic equation for the VFFTRNN system with these errors can be written asTheorem 6.If there exist unknown smooth differentiation errors , and a model implementation error in the VFFTRNN model, which satisfy the following conditions:then its computation error is bounded.Proof.Let us rewrite (45) from matrix form to vector form for easier analysis.where and . In addition, we can easily observe that , and its time derivative is given by . Therefore, Equation (46) can be rewritten asIn light of (37), we can acquireNext, we construct a Lyapunov function candidate in the form , and its time derivative can be computed as follows:By substituting the above two equations into (50), we can obtain the following:where and .We know that for any t, and that increases as t increases. Therefore, there always exists a value , such that for all , . Thus, for Equation (51), we need to consider the following two cases:
- (1)
- For the first situation, it is easy to see that , i.e., . Therefore, the error will decrease monotonically as time t increases, which indicates that will eventually converge to as time increases, i.e., will approach 0.
- (2)
- For the second situation, due to the uncertainty of the sign of , we need to further subdivide it into two cases. If , then the analysis follows the same reasoning as in case 1. Moreover, if , there exists a time such that for all . This indicates that the error will initially increase and then decrease. Based on the results in [36], we can obtain the upper bound of when using a linear activation function:Since and , it is guaranteed that (52) holds true. The design factor should be set greater than in order for the denominator of the fraction to be positive. Therefore, as , the computation error will approach 0.
Summing up the above, as time increases, the computation error tends to zero in both cases. The difference is that in the first situation, the computation error continuously decreases, whereas in the second situation, the computation error first increases and then decreases. Additionally, there exists an upper bound given by . □
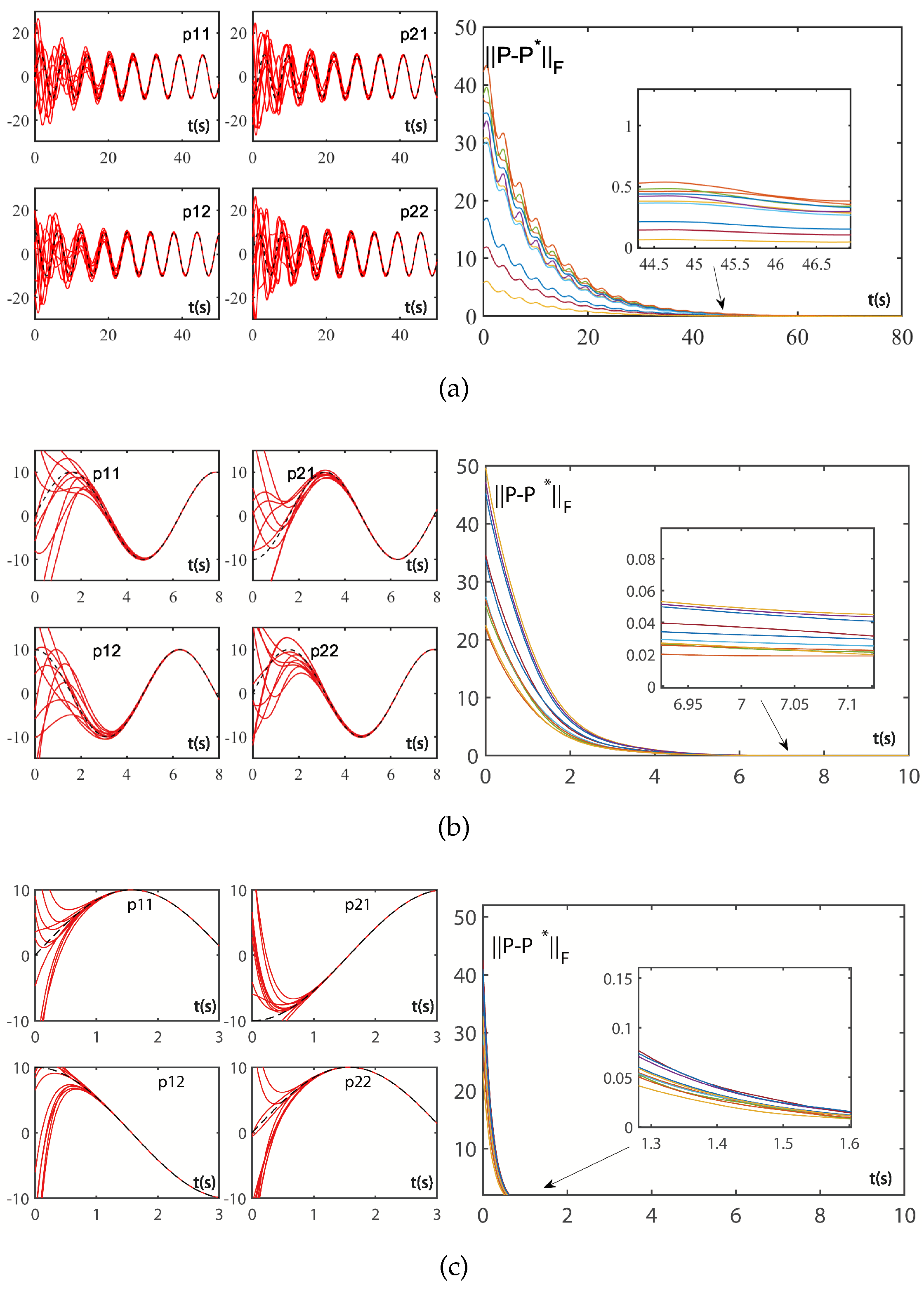
4. Illustrative Example
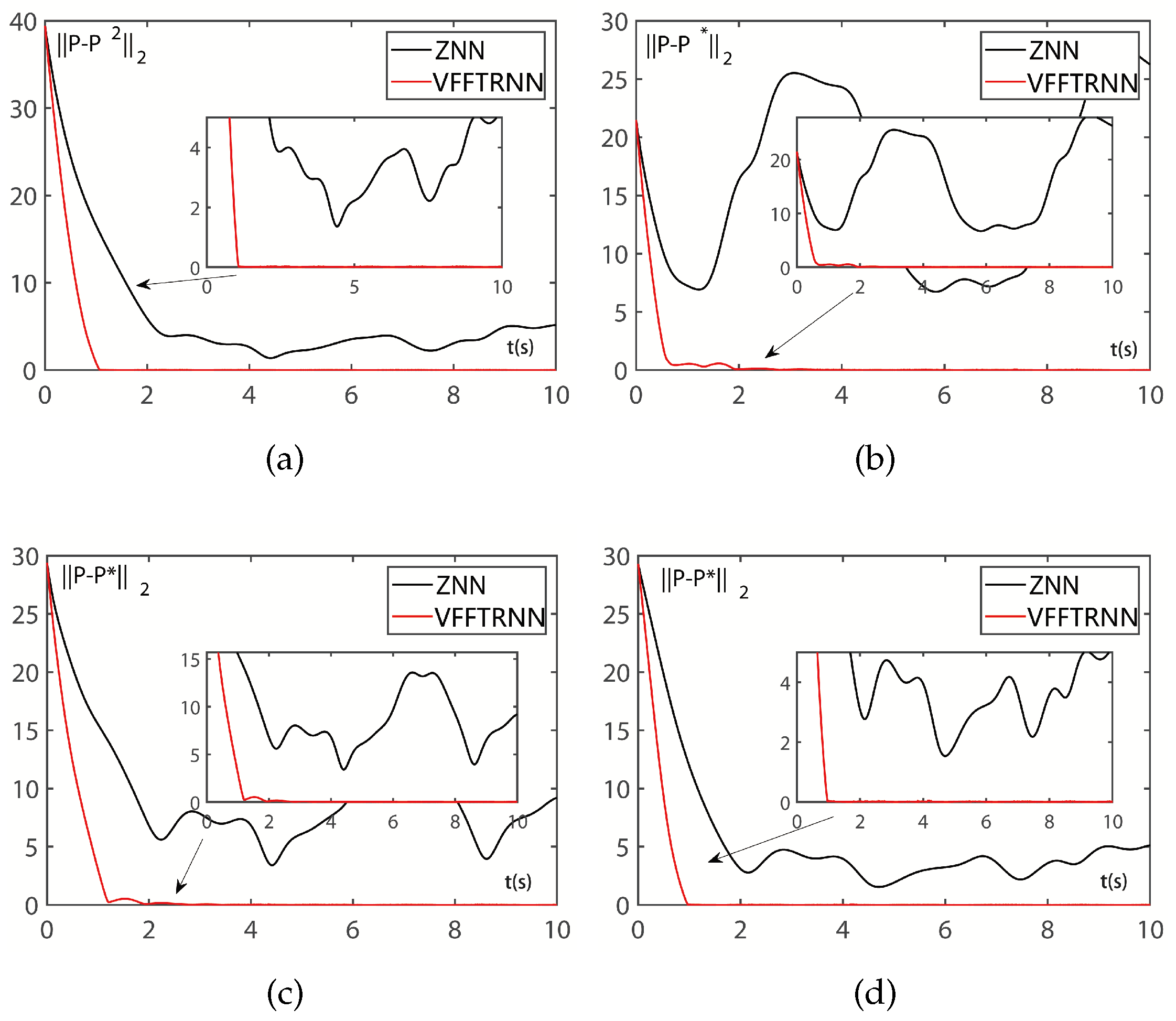
4.1. Convergence Discussion
4.2. Robustness Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wei, Q.; Dobigeon, N.; Tourneret, J.Y.; Bioucas-Dias, J.; Godsill, S. R-FUSE: Robust fast fusion of multiband images based on solving a Sylvester equation. IEEE Signal Process. Lett. 2016, 23, 1632–1636. [Google Scholar] [CrossRef]
- Wang, L.; Li, D.; He, T.; Xue, Z. Manifold regularized multi-view subspace clustering for image representation. In Proceedings of the 2016 23rd International Conference on Pattern Recognition (ICPR), Cancun, Mexico, 4–8 December 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 283–288. [Google Scholar]
- Hu, H.; Lin, Z.; Feng, J.; Zhou, J. Smooth representation clustering. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 3834–3841. [Google Scholar]
- Jang, J.S.; Lee, S.Y.; Shin, S.Y. An optimization network for matrix inversion. In Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 1987. [Google Scholar]
- Fa-Long, L.; Zheng, B. Neural network approach to computing matrix inversion. Appl. Math. Comput. 1992, 47, 109–120. [Google Scholar] [CrossRef]
- Cichocki, A.; Unbehauen, R. Neural networks for solving systems of linear equations and related problems. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 1992, 39, 124–138. [Google Scholar] [CrossRef]
- Xia, Y.; Wang, J. A recurrent neural network for solving linear projection equations. Neural Netw. 2000, 13, 337–350. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, J. Recurrent neural networks for nonlinear output regulation. Automatica 2001, 37, 1161–1173. [Google Scholar] [CrossRef]
- Li, S.; Li, Y. Nonlinearly activated neural network for solving time-varying complex Sylvester equation. IEEE Trans. Cybern. 2013, 44, 1397–1407. [Google Scholar] [CrossRef] [PubMed]
- Xiao, L.; Liao, B.; Luo, J.; Ding, L. A convergence-enhanced gradient neural network for solving Sylvester equation. In Proceedings of the 2017 36th Chinese Control Conference (CCC), Dalian, China, 26–28 July 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 3910–3913. [Google Scholar]
- Zhang, Z.; Zheng, L.; Weng, J.; Mao, Y.; Lu, W.; Xiao, L. A new varying-parameter recurrent neural-network for online solution of time-varying Sylvester equation. IEEE Trans. Cybern. 2018, 48, 3135–3148. [Google Scholar] [CrossRef]
- Zhang, Y.; Jiang, D.; Wang, J. A recurrent neural network for solving Sylvester equation with time-varying coefficients. IEEE Trans. Neural Netw. 2002, 13, 1053–1063. [Google Scholar] [CrossRef]
- Yan, X.; Liu, M.; Jin, L.; Li, S.; Hu, B.; Zhang, X.; Huang, Z. New zeroing neural network models for solving nonstationary Sylvester equation with verifications on mobile manipulators. IEEE Trans. Ind. Inform. 2019, 15, 5011–5022. [Google Scholar] [CrossRef]
- Zhang, Z.; Zheng, L. A complex varying-parameter convergent-differential neural-network for solving online time-varying complex Sylvester equation. IEEE Trans. Cybern. 2018, 49, 3627–3639. [Google Scholar] [CrossRef]
- Deng, J.; Li, C.; Chen, R.; Zheng, B.; Zhang, Z.; Yu, J.; Liu, P.X. A Novel Variable-Parameter Variable-Activation-Function Finite-Time Neural Network for Solving Joint-Angle Drift Issues of Redundant-Robot Manipulators. IEEE/ASME Trans. Mechatron. 2024, 1–12. [Google Scholar] [CrossRef]
- Xu, X.; Sun, J.; Endo, S.; Li, Y.; Benjamin, S.C.; Yuan, X. Variational algorithms for linear algebra. Sci. Bull. 2021, 66, 2181–2188. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Chen, W.; Yang, L. Multistage linear gauss pseudospectral method for piecewise continuous nonlinear optimal control problems. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 2298–2310. [Google Scholar] [CrossRef]
- Wang, X.; Liu, J.; Qiu, T.; Mu, C.; Chen, C.; Zhou, P. A real-time collision prediction mechanism with deep learning for intelligent transportation system. IEEE Trans. Veh. Technol. 2020, 69, 9497–9508. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, S.; Zhang, X. Simulink comparison of varying-parameter convergent-differential neural-network and gradient neural network for solving online linear time-varying equations. In Proceedings of the 2016 12th World Congress on Intelligent Control and Automation (WCICA), Guilin, China, 12–15 June 2016; pp. 887–894. [Google Scholar]
- Zhang, Y.; Chen, D.; Guo, D.; Liao, B.; Wang, Y. On exponential convergence of nonlinear gradient dynamics system with application to square root finding. Nonlinear Dyn. 2015, 79, 983–1003. [Google Scholar] [CrossRef]
- Wang, S.; Dai, S.; Wang, K. Gradient-based neural network for online solution of lyapunov matrix equation with li activation function. In Proceedings of the 4th International Conference on Information Technology and Management Innovation, Shenzhen, China, 12–13 September 2015; Atlantis Press: Amsterdam, The Netherlands, 2015; pp. 955–959. [Google Scholar]
- Ma, W.; Zhang, Y.; Wang, J. Matlab simulink modeling and simulation of zhang neural networks for online time-varying sylvester equation solving. Comput. Math. Math. Phys. 2008, 47, 285–289. [Google Scholar]
- Li, S.; Chen, S.; Liu, B. Accelerating a recurrent neural network to finite-time convergence for solving time-varying sylvester equation by using a sign-bi-power activation function. Neural Process. Lett. 2013, 37, 189–205. [Google Scholar] [CrossRef]
- Shen, Y.; Miao, P.; Huang, Y.; Shen, Y. Finite-time stability and its application for solving time-varying sylvester equation by recurrent neural network. Neural Process. Lett. 2015, 42, 763–784. [Google Scholar] [CrossRef]
- Jin, L.; Zhang, Y.; Li, S.; Zhang, Y. Modified znn for time-varying quadratic programming with inherent tolerance to noises and its application to kinematic redundancy resolution of robot manipulators. IEEE Trans. Ind. Electron. 2016, 63, 6978–6988. [Google Scholar] [CrossRef]
- Mao, M.; Li, J.; Jin, L.; Li, S.; Zhang, Y. Enhanced discrete-time zhang neural network for time-variant matrix inversion in the presence of bias noises. Neurocomputing 2016, 207, 220–230. [Google Scholar] [CrossRef]
- Xiao, L.; Liao, B. A convergence-accelerated zhang neural network and its solution application to lyapunov equation. Neurocomputing 2016, 193, 213–218. [Google Scholar] [CrossRef]
- Liao, B.; Zhang, Y.; Jin, L. Taylor discretization of znn models for dynamic equality-constrained quadratic programming with application to manipulators. Neural Netw. Learn. Syst. IEEE Trans. 2016, 27, 225–237. [Google Scholar] [CrossRef] [PubMed]
- Xiao, L. A finite-time convergent zhang neural network and its application to real-time matrix square root finding. Neural Comput. Appl. 2017, 31, 793–800. [Google Scholar] [CrossRef]
- Zhang, Y.; Mu, B.; Zheng, H. Link between and comparison and combination of zhang neural network and quasi-newton bfgs method for time-varying quadratic minimization. IEEE Trans. Cybern. 2013, 43, 490–503. [Google Scholar] [CrossRef]
- Yan, D.; Li, C.; Wu, J.; Deng, J.; Zhang, Z.; Yu, J.; Liu, P.X. A novel error-based adaptive feedback zeroing neural network for solving time-varying quadratic programming problems. Mathematics 2024, 12, 2090. [Google Scholar] [CrossRef]
- Zhang, Z.; Lu, Y.; Zheng, L.; Li, S.; Yu, Z.; Li, Y. A new varying-parameter convergent-differential neural-network for solvingtime-varying convex QP problem constrained by linear-equality. IEEE Trans. Autom. Control 2018, 63, 4110–4125. [Google Scholar] [CrossRef]
- Horn, R.A.; Johnson, C.R. Topics in Matrix Analysis, 1991; Cambridge University Presss: Cambridge, UK, 1991; Volume 37, p. 39. [Google Scholar]
- Strang, G.; Freund, L. Introduction to applied mathematics. J. Appl. Mech. 1986, 53, 480. [Google Scholar] [CrossRef]
- Mead, C.; Ismail, M. Analog VLSI Implementation of Neural Systems; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 80. [Google Scholar]
- Zhang, Y.; Ruan, G.; Li, K.; Yang, Y. Robustness analysis of the zhang neural network for online time-varying quadratic optimization. J. Phys. A Math. Theor. 2010, 43, 245202. [Google Scholar] [CrossRef]

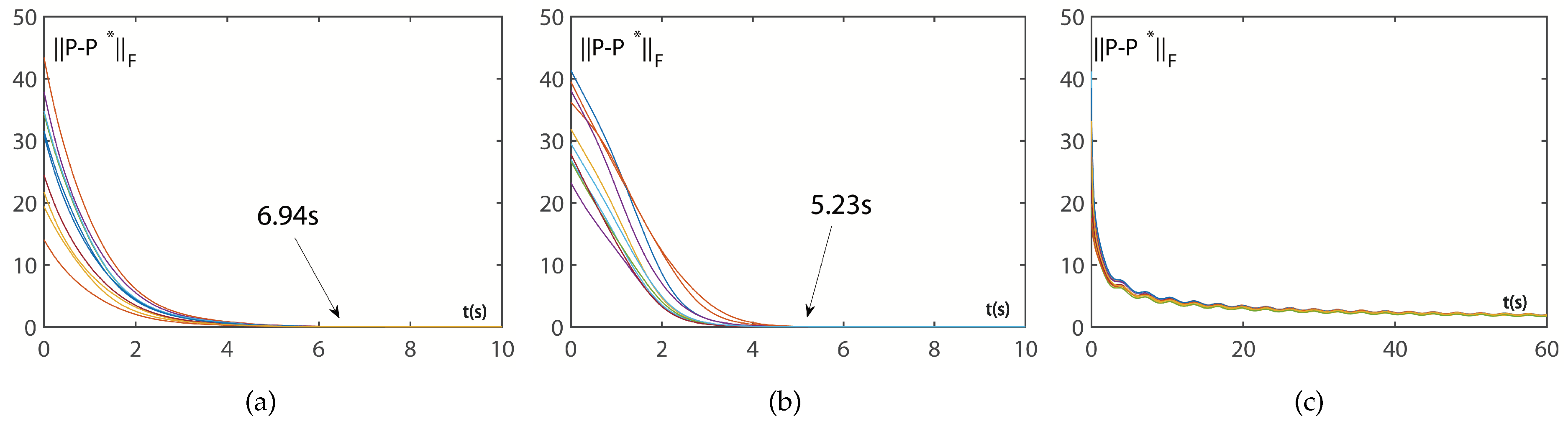
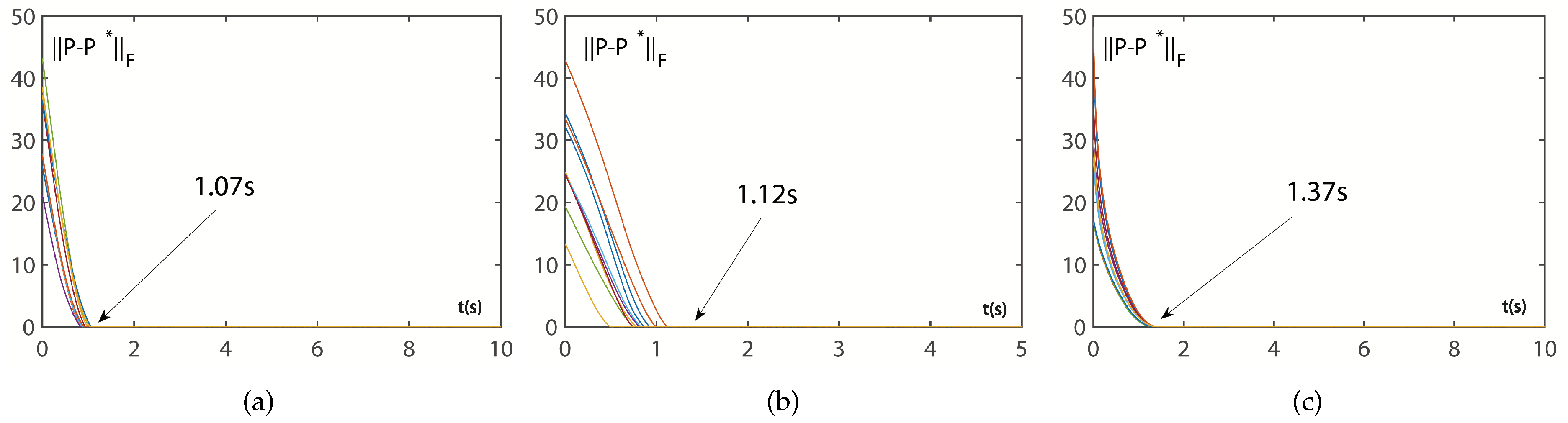
| Parameter | ||
|---|---|---|
| 0.01 | Cannot converge | 2.39 |
| 0.1 | 67.55 | 2.25 |
| 0.2 | 34.20 | 1.99 |
| 0.5 | 13.88 | 1.69 |
| 1 | 6.98 | 1.41 |
| 2 | 3.48 | 1.02 |
| 5 | 1.37 | 0.49 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tan, H.; Wu, J.; Guan, H.; Zhang, Z.; Tao, L.; Zhao, Q.; Li, C. A New Varying-Factor Finite-Time Recurrent Neural Network to Solve the Time-Varying Sylvester Equation Online. Mathematics 2024, 12, 3891. https://doi.org/10.3390/math12243891
Tan H, Wu J, Guan H, Zhang Z, Tao L, Zhao Q, Li C. A New Varying-Factor Finite-Time Recurrent Neural Network to Solve the Time-Varying Sylvester Equation Online. Mathematics. 2024; 12(24):3891. https://doi.org/10.3390/math12243891
Chicago/Turabian StyleTan, Haoming, Junyun Wu, Hongjie Guan, Zhijun Zhang, Ling Tao, Qingmin Zhao, and Chunquan Li. 2024. "A New Varying-Factor Finite-Time Recurrent Neural Network to Solve the Time-Varying Sylvester Equation Online" Mathematics 12, no. 24: 3891. https://doi.org/10.3390/math12243891
APA StyleTan, H., Wu, J., Guan, H., Zhang, Z., Tao, L., Zhao, Q., & Li, C. (2024). A New Varying-Factor Finite-Time Recurrent Neural Network to Solve the Time-Varying Sylvester Equation Online. Mathematics, 12(24), 3891. https://doi.org/10.3390/math12243891





