On Fractal–Fractional Simpson-Type Inequalities: New Insights and Refinements of Classical Results

Abstract

In this paper, we introduce a novel fractal–fractional identity, from which we derive new Simpson-type inequalities for functions whose first-order local fractional derivative exhibits generalized s-convexity in the second sense. This work introduces an approach that uses the first-order local fractional derivative, enabling the treatment of functions with lower regularity requirements compared to earlier studies. Additionally, we present two distinct methodological frameworks, one of which achieves greater precision by refining classical outcomes in the existing literature. The paper concludes with several practical applications that demonstrate the utility of our results.

1. Introduction

Convexity is a fundamental concept in mathematical analysis, essential in fields such as optimization, economics, and functional analysis. A function is generally considered convex if the line segment connecting any two points on its graph lies above or on the graph itself. This seemingly simple geometric property leads to powerful mathematical results, and has extensive applications, including in the development of inequalities and approximation methods. Convexity also provides essential tools in understanding the behavior of complex functions, allowing researchers to draw meaningful conclusions about their properties and the systems they describe.

The renowned Hermite–Hadamard inequality (refer to [1,2]) represents a cornerstone result in the theory of convex functions, and can be expressed as follows.

Theorem 1.

Let $\mathfrak{h}:\left[{𝚤}_1,{𝚤}_2\right]\to \mathbb{R}$ be a convex function. Then, we have

$$\mathfrak{h}\left(\frac{{𝚤}_1+{𝚤}_2}{2}\right)\le \frac{1}{{𝚤}_2-{𝚤}_1}\underset{{𝚤}_1}{\stackrel{{𝚤}_2}{\int }}\mathfrak{h}\left(\varkappa \right)d\varkappa \le \frac{\mathfrak{h}\left({𝚤}_1\right)+\mathfrak{h}\left({𝚤}_2\right)}{2}.$$

Definition 1

([3]). A function $\mathfrak{h}:\left[{𝚤}_1,{𝚤}_2\right]\to \mathbb{R}$ is said to be s-convex in the second sense on $\left[{𝚤}_1,{𝚤}_2\right]$ for some fixed $s\in (0,1]$ if, for all ${\varkappa }_1,{\varkappa }_2\in \mathcal{D}$ and $t\in [0,1]$, the inequality

$$\mathfrak{h}\left(t{\varkappa }_1+\left(1-t\right){\varkappa }_2\right)\le t^s\mathfrak{h}\left({\varkappa }_1\right)+{\left(1-t\right)}^s\mathfrak{h}\left({\varkappa }_2\right)$$

holds.

In [4], Dragomir and Fitzpatrick provided the following Hermite–Hadamard inequality for s-convex functions:

$$2^{s-1}\mathfrak{h}\left(\frac{{𝚤}_1+{𝚤}_2}{2}\right)\le \frac{1}{{𝚤}_2-{𝚤}_1}\underset{{𝚤}_1}{\stackrel{{𝚤}_2}{\int }}\mathfrak{h}\left(\varkappa \right)d\varkappa \le \frac{\mathfrak{h}\left({𝚤}_1\right)+\mathfrak{h}\left({𝚤}_2\right)}{s+1},$$

(1)

where $\mathfrak{h}$ is s-convex in the second sense on $[{𝚤}_1,{𝚤}_2]$.

Within the realm of approximation theory, convexity has been extensively employed to evaluate and enhance numerical techniques for calculating definite integrals. Among these numerical methods, Simpson’s rule is one of the most renowned formulas for approximating definite integrals. It is particularly valued for its simplicity and accuracy when dealing with smooth functions over closed intervals. Simpson’s formula approximates the integral of a function by using quadratic polynomials, offering better accuracy compared to basic methods, such as the midpoint and trapezoidal rules. For a four times continuously differentiable function $\mathfrak{h}$ on the interval $[{𝚤}_1,{𝚤}_2]$, the classical error bounds of Simpson’s formula is given by

$$\left|\frac{1}{6}\left(\mathfrak{h}\left({𝚤}_1\right)+4\mathfrak{h}\left(\frac{{𝚤}_1+{𝚤}_2}{2}\right)+\mathfrak{h}\left({𝚤}_2\right)\right)-\frac{1}{{𝚤}_2-{𝚤}_1}\underset{{𝚤}_2}{\stackrel{{𝚤}_2}{\int }}\mathfrak{h}\left(t\right)dt\right|\le \frac{{\left({𝚤}_2-{𝚤}_1\right)}^4}{2880}{∥{\mathfrak{h}}^{\left(4\right)}∥}_{\infty },$$

where ${∥{\mathfrak{h}}^{\left(4\right)}∥}_{\infty }=\underset{x\in [{𝚤}_1,{𝚤}_2]}{sup}\left|{\mathfrak{h}}^{\left(4\right)}\left(x\right)\right|<\infty$.

Dragomir et al. in [5], pointed out the following Simpson-type inequality expressed in terms of lower derivatives.

Theorem 2

([5]). Let $\mathfrak{h}:\left[{𝚤}_1,{𝚤}_2\right]\to \mathbb{R}$ with ${\mathfrak{f}}^{\prime }\in L\left[{𝚤}_1,{𝚤}_2\right]$. Then, we have

$$\left|\frac{1}{6}\left[\mathfrak{h}\left({𝚤}_1\right)+4\mathfrak{h}\left(\frac{{𝚤}_1+{𝚤}_2}{2}\right)+\mathfrak{h}\left({𝚤}_2\right)\right]-\frac{1}{{𝚤}_2-{𝚤}_1}\underset{{𝚤}_1}{\stackrel{{𝚤}_2}{\int }}\mathfrak{h}\left(t\right)dt\right|\le \frac{{𝚤}_2-{𝚤}_1}{3}{∥{\mathfrak{f}}^{\prime }∥}_1,$$

where ${∥{\mathfrak{f}}^{\prime }∥}_1=\underset{{𝚤}_1}{\stackrel{{𝚤}_2}{\int }}\left|{\mathfrak{f}}^{\prime }\left(\varkappa \right)\right|d\varkappa$.

In [6], Sarikaya et al. established the following inequality for differentiable s-convex functions.

Theorem 3

([6]). Let $\mathfrak{h}:\mathcal{D}\to \mathbb{R}$ be a differentiable function on ${\mathcal{D}}^{\circ }$, ${𝚤}_1,{𝚤}_2\in {\mathcal{D}}^{\circ }$ with ${𝚤}_1<{𝚤}_2$, such that ${\mathfrak{h}}^{\prime }\in L_1\left[{𝚤}_1,{𝚤}_2\right]$. If $\left|{\mathfrak{h}}^{\prime }\right|$ is s-convex in the second sense on $\left[{𝚤}_1,{𝚤}_2\right]$, for some fixed $s\in (0,1]$, then we have

$$\begin{array}{cc}\hfill & \left|\frac{1}{6}\left[\mathfrak{h}\left({𝚤}_1\right)+4\mathfrak{h}\left(\frac{{𝚤}_1+{𝚤}_2}{2}\right)+\mathfrak{h}\left({𝚤}_2\right)\right]-\frac{1}{{𝚤}_2-{𝚤}_1}\underset{{𝚤}_1}{\stackrel{{𝚤}_2}{\int }}\mathfrak{h}\left(t\right)dt\right|\hfill \\ \hfill \le & \left({𝚤}_2-{𝚤}_1\right)\frac{(s-4)6^{s+1}+2\times 5^{s+2}-2\times 3^{s+2}+2}{6^{s+2}(s+1)(s+2)}\left(\left|{\mathfrak{h}}^{\prime }\left({𝚤}_1\right)\right|+\left|{\mathfrak{h}}^{\prime }\left({𝚤}_2\right)\right|\right).\hfill \end{array}$$

Corollary 1

([6]). For $s=1$, Theorem 3 will be reduced to

$$\begin{array}{cc}\hfill & \left|\frac{1}{6}\left[\mathfrak{h}\left({𝚤}_1\right)+4\mathfrak{h}\left(\frac{{𝚤}_1+{𝚤}_2}{2}\right)+\mathfrak{h}\left({𝚤}_2\right)\right]-\frac{1}{{𝚤}_2-{𝚤}_1}\underset{{𝚤}_1}{\stackrel{{𝚤}_2}{\int }}\mathfrak{h}\left(t\right)dt\right|\hfill \\ \hfill \le & \frac{5\left({𝚤}_2-{𝚤}_1\right)}{72}\left(\left|{\mathfrak{h}}^{\prime }\left({𝚤}_1\right)\right|+\left|{\mathfrak{h}}^{\prime }\left({𝚤}_2\right)\right|\right).\hfill \end{array}$$

For further work on Simpson’s inequality using different types of integral operators, we refer the readers to [7,8,9,10,11].

Fractional calculus, which generalizes integrals and derivatives to arbitrary, non-integer orders, has become a potent extension of classical calculus. When modeling processes with memory, when conventional integer-order models are inadequate, this more comprehensive approach works especially well. Fractional calculus is important because it may be used to explain phenomena in a variety of disciplines, including biology, engineering, physics, and economics, where systems show anomalous diffusion, non-local interactions, or viscoelastic behavior. Because of this, fractional calculus has shown itself to be a vital tool for comprehending intricate systems that defy easy explanations. For recent advances in fractional calculus, we refer to [12,13,14,15,16].

In recent years, fractional calculus has seen substantial expansion, attracting considerable interest from scholars in both theoretical and applied domains. This increased interest has led to the development of various fractional operators, each designed for specific applications and mathematical contexts. The introduction of operators such as the Riemann–Liouville, k-Riemann–Liouville, Hadamard, and Conformable fractional integrals, among others, has broadened the reach of fractional calculus, enabling more flexible and precise modeling of complex systems. Using the notion of convexity, several studies have been conducted to establish certain integral inequalities through various types of fractional integrals; see [17,18,19]. To address the diversity of these operators, Sarikaya and Ertuğral, in [20], proposed a generalized fractional operator that unifies many well-known fractional integrals, as follows.

Definition 2

([20]). Let $[{𝚤}_1,{𝚤}_2]$ be a real interval, and $\mathfrak{h}\in L[{𝚤}_1,{𝚤}_2]$. The left- and right-sided generalized fractional integrals are given, respectively, by

$${}_{{𝚤}_1^{+}}J_{\vartheta }\mathfrak{h}\left(\varkappa \right)=\stackrel{\varkappa }{\underset{{𝚤}_1}{\int }}{\displaystyle \frac{\vartheta \left(\varkappa -t\right)}{\varkappa -t}}\mathfrak{h}\left(t\right)dt,{𝚤}_1<\varkappa$$

(2)

and

$${}_{{𝚤}_2^{-}}J_{\vartheta }\mathfrak{h}\left(\varkappa \right)=\stackrel{{𝚤}_2}{\underset{\varkappa }{\int }}{\displaystyle \frac{\vartheta \left(t-\varkappa \right)}{t-\varkappa }}\mathfrak{h}\left(t\right)dt,\varkappa <{𝚤}_2,$$

(3)

where ϑ satisfies

$$\underset{0}{\stackrel{1}{\int }}\frac{\vartheta \left(\varkappa \right)}{\varkappa }d\varkappa <\infty .$$

Remark 1.

The capacity to include several kinds of fractional integrals, such as the Riemann–Liouville, Katugampola, k-Riemann–Liouville, conformable, Hadamard, and others, is the main characteristic of the generalized fractional integrals (2) and (3). The following describes these important special cases:

• For $\vartheta \left(t\right)={\displaystyle \frac{t^{\alpha }}{\Gamma \left(\alpha \right)}}$ with $\alpha >0$, operators (2) and (3) will be reduced to the Riemann–Liouville fractional integrals defined in [21].
• For $\vartheta \left(t\right)={\displaystyle \frac{t^{\frac{\alpha }{k}}}{k{\Gamma }_k\left(\alpha \right)}}$ with $\alpha >0$, we obtain the k-Riemann–Liouville fractional integrals defined in [22].
• For $\vartheta \left(t\right)=t{\displaystyle \frac{{\left(log\left({𝚤}_2\right)-log\left({𝚤}_2-t\right)\right)}^{\alpha -1}}{\Gamma \left(\alpha \right)\left({𝚤}_2-t\right)}}$ with $\alpha >0$ and ${𝚤}_1\ge 1$, the generalized integrals will be reduced to the Hadamard integrals, defined in [21].
• For $\vartheta \left(t\right)=t{\displaystyle \frac{{\left(log\left({𝚤}_2\right)-log\left({𝚤}_2-t\right)\right)}^{\frac{\alpha }{k}-1}}{k{\Gamma }_k\left(\alpha \right)\left({𝚤}_2-t\right)}}$ with $\alpha >0$ and ${𝚤}_1\ge 1$, we obtain the Hadamard k-fractional integrals, defined in [23].
• For $\vartheta \left(t\right)={\displaystyle \frac{{\rho }^{1-\alpha }{\left({𝚤}_2-t\right)}^{\rho }{\left({𝚤}_2^{\rho }-{\left({𝚤}_2-t\right)}^{\rho }\right)}^{\alpha -1}}{\Gamma \left(\alpha \right)}}$ with $\alpha ,\rho >0$, we obtain the Katugampola fractional integrals introduced in [24].
• For $\vartheta \left(t\right)={\displaystyle \frac{t^{\alpha }{e}^{-\lambda t}}{\Gamma \left(\alpha \right)}}$ with $\alpha >0$, we obtain the tempered fractional integrals introduced in [25].
• For $\vartheta \left(t\right)=t{\left({𝚤}_2-t\right)}^{\alpha -1}$ with $\alpha >0$, (2) and (3) will be reduced to the conformable fractional integrals proposed by Khalil et al. in [26].
• For $\vartheta \left(t\right)={\displaystyle \frac{t}{\alpha }}exp\left(-{\displaystyle \frac{1-\alpha }{\alpha }}t\right)$ with $\alpha \in (0,1)$, we obtain the fractional integrals with exponential kernel introduced in [27].

In the realm of fractional calculus, numerous researchers have concentrated on the investigation of Simpson-type inequalities through the use of a various types of fractional integrals [28,29,30,31]. However, the most notable work in this regard is that of Ertuğral and Sarikaya in [32], where the authors established the following generalized Simpson-type inequality.

Theorem 4

([32]). Let $\mathfrak{h}:\mathcal{D}\to \mathbb{R}$ be a differentiable function on ${\mathcal{D}}^{\circ }$, ${𝚤}_1,{𝚤}_2\in {\mathcal{D}}^{\circ }$ with ${𝚤}_1<{𝚤}_2$, such that ${\mathfrak{h}}^{\prime }\in L_1\left[{𝚤}_1,{𝚤}_2\right]$. If $\left|{\mathfrak{h}}^{\prime }\right|$ is convex on $\left[{𝚤}_1,{𝚤}_2\right]$, then we have

$$\begin{array}{cc}\hfill & \left|\frac{1}{6}\left[\mathfrak{h}\left({𝚤}_1\right)+4\mathfrak{h}\left(\frac{{𝚤}_1+{𝚤}_2}{2}\right)+\mathfrak{h}\left({𝚤}_2\right)\right]-\frac{1}{2{\Lambda }_1\left(1\right)}\left({}_{{𝚤}_1^{+}}\mathcal{J}_{\vartheta },\mathfrak{h},\left(\frac{{𝚤}_1+{𝚤}_2}{2}\right),+,{}_{{𝚤}_2^{-}}J_{\vartheta },\mathfrak{h},\left(\frac{{𝚤}_1+{𝚤}_2}{2}\right)\right)\right|\hfill \\ \hfill \le & \frac{{𝚤}_2-{𝚤}_1}{12{\Lambda }_1\left(1\right)}\mathcal{K}\left(\left|{\mathfrak{h}}^{\prime }\left({𝚤}_1\right)\right|+\left|{\mathfrak{h}}^{\prime }\left({𝚤}_2\right)\right|\right),\hfill \end{array}$$

where

$$\mathcal{K}=\underset{0}{\stackrel{1}{\int }}\left|2{\Lambda }_1\left(1\right)-3{\Lambda }_1\left(t\right)\right|dt,$$

with $\Lambda \left(t\right)=\stackrel{t}{\underset{0}{\int }}\frac{\vartheta \left(\frac{\left({𝚤}_2-{𝚤}_1\right)}{2}s\right)}{s^{\varrho }}ds<\infty$, and ${}_{{𝚤}_1^{+}}J_{\vartheta }$, ${}_{{𝚤}_2^{-}}J_{\vartheta }$ are given by (2) and (3), respectively.

Remark 2.

It is worth noting that by choosing $\vartheta \left(t\right)=t$, Theorem 4 simplifies to Corollary 1, provided by Sarikaya et al. in [6].

Fractal sets are geometric structures that frequently possess intricate, irregular shapes and demonstrate self-similarity at various scales. Defined through recursive processes, fractals are fundamental in fields like dynamical systems and signal processing, as they can model natural phenomena with irregular patterns, such as coastlines or turbulent flows. They are also studied for their ability to quantify complexity using concepts like the Hausdorff dimension.

In [33], Yang expanded the notion of convexity to fractal sets as follows.

Definition 3

([33]). Let $\mathfrak{h}:\mathcal{D}\subseteq \mathbb{R}\to {\mathbb{R}}^{\varrho }$, where $0<\varrho \le 1$ is the fractal dimension. For any ${\varkappa }_1,{\varkappa }_2\in \mathcal{D}$ and $t\in [0,1]$, if

$$\mathfrak{h}\left(t{\varkappa }_1+\left(1-t\right){\varkappa }_2\right)\le t^{\varrho }\mathfrak{h}\left({\varkappa }_1\right)+{\left(1-t\right)}^{\varrho }\mathfrak{h}\left({\varkappa }_2\right)$$

holds, then $\mathfrak{h}$ is a generalized convex function on $\mathcal{D}$.

In [34], Mo et al. provided the following definition of generalized s-convexity in the second sense.

Definition 4.

Let $\mathfrak{h}:\mathcal{D}\subseteq \mathbb{R}\to {\mathbb{R}}^{\varrho }$. For any ${\varkappa }_1,{\varkappa }_2\in \mathcal{D}$ and $t\in [0,1]$, if

$$\mathfrak{h}\left(t{\varkappa }_1+\left(1-t\right){\varkappa }_2\right)\le t^{s\varrho }\mathfrak{h}\left({\varkappa }_1\right)+{\left(1-t\right)}^{s\varrho }\mathfrak{h}\left({\varkappa }_2\right)$$

holds for some fixed $s\in (0,1]$, then the function $\mathfrak{h}$ is generalized s-convex in the second sense on $\mathcal{D}$.

Fractal calculus has swiftly evolved as a result of intensive research by different experts and is now widely used in a variety of scientific and technical disciplines. Its growing popularity in recent years can be related to its emphasis on non-differentiable mappings, which provide new insights and methods for modeling complicated and irregular processes.

In the context of integral inequalities on fractal sets, several scholars have developed novel estimations connected to various quadrature formulae and different types of generalized convexity; see [35,36,37,38,39,40,41,42,43,44] and the references therein.

In [45], Yu et al. were the first to introduce generalized fractal integrals. These are called fractal–fractional integrals, and are defined as follows.

Definition 5.

The left and right-sided fractal–fractional integrals are given, respectively, by

$${}_{{𝚤}_1^{+}}{}^{\vartheta }\mathcal{J}^{\left(\varrho \right)}\mathfrak{h}\left(\varkappa \right)=\frac{1}{\Gamma (1+\varrho )}\stackrel{\varkappa }{\underset{{𝚤}_1}{\int }}{\displaystyle \frac{\vartheta \left(\varkappa -t\right)}{{\left(\varkappa -t\right)}^{\varrho }}}\mathfrak{h}\left(t\right){\left(dt\right)}^{\varrho },\varkappa >{𝚤}_1,$$

(4)

and

$${}_{{𝚤}_2^{-}}{}^{\vartheta }\mathcal{J}^{\left(\varrho \right)}\mathfrak{h}\left(\varkappa \right)=\frac{1}{\Gamma (1+\varrho )}\stackrel{{𝚤}_2}{\underset{\varkappa }{\int }}{\displaystyle \frac{\vartheta \left(t-\varkappa \right)}{{\left(t-\varkappa \right)}^{\varrho }}}\mathfrak{h}\left(t\right){\left(dt\right)}^{\varrho },\varkappa <{𝚤}_2,$$

(5)

where $\Gamma (.)$ is the Gamma function, and ϑ satisfies

$$\frac{1}{\Gamma (1+\varrho )}\underset{0}{\stackrel{1}{\int }}\frac{\vartheta \left(\varkappa \right)}{{\varkappa }^{\varrho }}{\left(d\varkappa \right)}^{\varrho }<{\infty }^{\varrho }.$$

In the same paper [45], the authors provided midpoint-type inequalities for twice local fractional differentiable generalized convex functions. Building on this, using fractal–fractional integrals, Butt et al. established Simpson-type inequalities in [46] and parametric inequalities in [47], also for functions whose second-order local fractional derivatives are generalized convex. In [48], Yuan et al. first introduced the class of generalized $(P,m)$-convex functions, and then developed a multi-parameter identity using fractal–fractional integral operators. From this, they were able to establish interesting results related to various formulas for twice local fractional differentiable generalized $(P,m)$-convex functions.

Inspired by the preceding works, we begin this article by presenting a new fractal–fractional identity, from which we derive several new Simpson-type inequalities for functions whose first-order local fractional derivative is generalized s-convex in the second sense. This study is particularly significant because it is the first to prove such inequalities using the first-order local fractional derivative, which does not require high regularity. On the other hand, we examine two ways, one of which produces more refined results, by refining classical results from the literature.

2. Basics of Local Fractional Calculus

In this section, we recall some concepts of fractal theory, as detailed in the monographs [33,49]. It is important to highlight that $\varrho$ does not represent an exponential symbol, but rather a fractal dimension defined on the Cantor set. For $0<\varrho \le 1$, we have the following $\varrho$-type set.

The $\varrho$-type set of integer is defined as the set

$${\mathbb{Z}}^{\varrho }:=\left\{0^{\varrho },\pm 1^{\varrho },\pm 2^{\varrho },...,\pm n^{\varrho },...\right\}.$$

The $\varrho$-type set of the rational numbers is defined as

$${\mathbb{Q}}^{\varrho }:=\left\{m^{\varrho }={\left(\frac{p}{q}\right)}^{\varrho }:p,q\in \mathbb{Z}\mathrm{and}q\ne 0\right\}.$$

The $\varrho$-type set of the irrational numbers is defined as

$${\mathbb{J}}^{\varrho }:=\left\{m^{\varrho }\ne {\left(\frac{p}{q}\right)}^{\varrho }:p,q\in \mathbb{Z}\mathrm{and}q\ne 0\right\}.$$

The $\varrho$-type set of the real line numbers is defined as

$${\mathbb{R}}^{\varrho }:={\mathbb{Q}}^{\varrho }\cup {\mathbb{J}}^{\varrho }.$$

If $u^{\varrho },v^{\varrho }$ and $w^{\varrho }$ belongs the set ${\mathbb{R}}^{\varrho }$ of real line numbers, then we have

1. $u^{\varrho }+v^{\varrho }$ and $u^{\varrho }{v}^{\varrho }$ belongs the set ${\mathbb{R}}^{\varrho }$.

2. $u^{\varrho }+v^{\varrho }=v^{\varrho }+u^{\varrho }={\left(u+v\right)}^{\varrho }={\left(v+u\right)}^{\varrho }$.

3. $u^{\varrho }+\left(v^{\varrho }+w^{\varrho }\right)={\left(u+v\right)}^{\varrho }+w^{\varrho }$.

4. $u^{\varrho }{v}^{\varrho }=v^{\varrho }{u}^{\varrho }={\left(uv\right)}^{\varrho }={\left(vu\right)}^{\varrho }$.

5. $u^{\varrho }\left(v^{\varrho }{w}^{\varrho }\right)=\left(u^{\varrho }{v}^{\varrho }\right)w^{\varrho }$.

6. $u^{\varrho }\left(v^{\varrho }+w^{\varrho }\right)=u^{\varrho }{v}^{\varrho }+u^{\varrho }{w}^{\varrho }$.

7. $u^{\varrho }+0^{\varrho }=0^{\varrho }+u^{\varrho }=u^{\varrho }$ and $u^{\varrho }{1}^{\varrho }=1^{\varrho }{u}^{\varrho }=u^{\varrho }$.

Definition 6

([33]). A non-differentiable function $\mathfrak{h}:\mathbb{R}\to {\mathbb{R}}^{\varrho }$ is local fractional continuous at ${\varkappa }_0$, if

$$\forall ϵ>0,\exists \delta >0:\left|\mathfrak{h}\left(\varkappa \right)-\mathfrak{h}\left({\varkappa }_0\right)\right|<{ϵ}^{\varrho }$$

holds for $|\varkappa -{\varkappa }_0|<\delta$, where $ϵ,\delta \in \mathbb{R}$. We denote the set of all local fractional continuous functions on $({𝚤}_1,{𝚤}_2)$ by $C_{\varrho }({𝚤}_1,{𝚤}_2)$.

Definition 7

([33]). The local fractional derivative of $\mathfrak{h}\left(\varkappa \right)$ of order ϱ at $\varkappa ={\varkappa }_0$ is defined as

$${\mathfrak{h}}^{\left(\varrho \right)}\left({\varkappa }_0\right)={\left.\frac{d^{\varrho }\mathfrak{h}\left(\varkappa \right)}{d{\varkappa }^{\varrho }}\right|}_{\varkappa ={\varkappa }_0}=\underset{\varkappa \to {\varkappa }_0}{lim}\frac{{\Delta }^{\varrho }\left(\mathfrak{h}\left(\varkappa \right)-\mathfrak{h}\left({\varkappa }_0\right)\right)}{{\left(\varkappa -{\varkappa }_0\right)}^{\varrho }},$$

where ${\Delta }^{\varrho }\left(\mathfrak{h}\left(\varkappa \right)-\mathfrak{h}\left({\varkappa }_0\right)\right)\cong \Gamma \left(\varrho +1\right)\left(\mathfrak{h}\left(\varkappa \right)-\mathfrak{h}\left({\varkappa }_0\right)\right)$.

If there exists ${\mathfrak{h}}^{\left(k\varrho \right)}\left(\varkappa \right)=\stackrel{k\mathrm{times}}{\overbrace{D^{\varrho }{D}^{\varrho }...D^{\varrho }}}\mathfrak{h}\left(\varkappa \right)$ for any $\varkappa \in \mathcal{D}\subseteq R$, then we say that $\mathfrak{h}\in D_{k\varrho }\left(I\right)$, where $k=0,1,2,3,...$.

Definition 8

([33]). Let $\mathfrak{h}\left(\varkappa \right)\in C_{\varrho }[{𝚤}_1,{𝚤}_2]$. Then, the local fractional integral is defined by

$${}_{𝚤1}I_{𝚤2}^{\varrho }\mathfrak{h}\left(\varkappa \right)=\frac{1}{\Gamma \left(\varrho +1\right)}\underset{{𝚤}_1}{\stackrel{{𝚤}_2}{\int }}\mathfrak{h}\left(t\right){\left(dt\right)}^{\varrho }=\frac{1}{\Gamma \left(\varrho +1\right)}\underset{\Delta t\to 0}{lim}\stackrel{N-1}{\sum _{j=0}}\mathfrak{h}\left(t_j\right){\left(\Delta t_j\right)}^{\varrho }$$

with $\Delta t_j=t_{j+1}-t_j$ and $\Delta t=max\left\{\Delta t_1,\Delta t_{2,...,\Delta t_{N-1}}\right\}$, where $\left[t_j,t_{j+1}\right],j=0,1,...,N-1$ and $a=t_0<t_1<...<t_N=b$ is partition of interval $\left[{𝚤}_1,{𝚤}_2\right]$.

Here, it follows that ${}_{𝚤1}I_{𝚤2}^{\varrho }\mathfrak{h}\left(\varkappa \right)=0$ if ${𝚤}_1={𝚤}_2$ and ${}_{𝚤1}I_{𝚤2}^{\varrho }\mathfrak{h}\left(\varkappa \right)={-}_{{𝚤}_2}{I}_{{𝚤}_1}^{\varrho }\mathfrak{h}\left(\varkappa \right)$ if ${𝚤}_1<{𝚤}_2$. If for any $\varkappa \in [{𝚤}_1,{𝚤}_2]$, there exists ${}_{𝚤1}I_{𝚤2}^{\varrho }\mathfrak{h}\left(\varkappa \right)$, then we denoted by $\mathfrak{h}\left(\varkappa \right)\in I_{\varkappa }^{\varrho }\left[{𝚤}_1,{𝚤}_2\right]$.

Lemma 1

([33]). Suppose that $\mathfrak{h}\left(\varkappa \right)={\mathfrak{g}}^{\left(\varrho \right)}\left(\varkappa \right)\in C_{\varrho }\left[{𝚤}_1,{𝚤}_2\right]$; then, we have

$${}_{𝚤1}I_{𝚤2}^{\varrho }\mathfrak{h}\left(\varkappa \right)=\mathfrak{g}\left({𝚤}_2\right)-\mathfrak{g}\left({𝚤}_1\right).$$

Lemma 2

([33]). Suppose that $\mathfrak{h},\mathfrak{g}\in D_{\varrho }\left[{𝚤}_1,{𝚤}_2\right]$ and ${\mathfrak{h}}^{\left(\varrho \right)}\left(\varkappa \right),{\mathfrak{g}}^{\left(\varrho \right)}\left(\varkappa \right)\in C_{\varrho }\left[{𝚤}_1,{𝚤}_2\right]$; then, we have

$${}_{𝚤1}I_{𝚤2}^{\varrho }\mathfrak{h}\left(\varkappa \right){\mathfrak{g}}^{\left(\varrho \right)}\left(\varkappa \right)={\left.\mathfrak{h}\left(\varkappa \right)\mathfrak{g}\left(\varkappa \right)\right|}_{{𝚤}_1}^{{𝚤}_2}-{}_{{𝚤}_1}I_{\left({𝚤}_2\right)}^{\varrho }{\mathfrak{h}}^{\left(\varrho \right)}\left(\varkappa \right)\mathfrak{g}\left(\varkappa \right).$$

Lemma 3

([33]). For $\mathfrak{h}\left(\varkappa \right)={\varkappa }^{k\varrho }$, we have the following equations:

$$\begin{array}{cc}\hfill \frac{d^{\varrho }{\varkappa }^{k\varrho }}{d{\varkappa }^{\varrho }}=& \frac{\Gamma \left(1+k\varrho \right)}{\Gamma \left(1+\left(k-1\right)\varrho \right)}{\varkappa }^{\left(k-1\right)\varrho },\hfill \\ \hfill \frac{1}{\Gamma \left(1+\varrho \right)}\underset{{𝚤}_1}{\stackrel{{𝚤}_2}{\int }}{\varkappa }^{k\varrho }{\left(d\varkappa \right)}^{\varrho }=& \frac{\Gamma \left(1+k\varrho \right)}{\Gamma \left(1+\left(k+1\right)\varrho \right)}\left({𝚤}_2^{\left(k+1\right)\varrho }-{𝚤}_1^{\left(k+1\right)\varrho }\right),k\in \mathbb{R}.\hfill \end{array}$$

In [33], Yang presented the generalized Hölder inequality in fractal domain as follows.

Lemma 4

([33]). Let $\mathfrak{h},\mathfrak{g}\in C_{\varrho }[{𝚤}_1,{𝚤}_2]$, and the functions ${\mathfrak{h}}^p$, ${\mathfrak{g}}^q$ are both local fractional integral on $[{𝚤}_1,{𝚤}_2]$ for $p,q>1$ with ${\displaystyle \frac{1}{p}}+{\displaystyle \frac{1}{q}}=1$; then,

$$\frac{1}{\Gamma \left(1+\varrho \right)}\underset{{𝚤}_1}{\stackrel{{𝚤}_2}{\int }}\left|\mathfrak{h}\left(t\right)\mathfrak{g}\left(t\right)\right|{\left(dt\right)}^{\varrho }\le {\left(\frac{1}{\Gamma \left(1+\varrho \right)}\underset{{𝚤}_1}{\stackrel{{𝚤}_2}{\int }}{\left|\mathfrak{h}\left(t\right)\right|}^p{\left(dt\right)}^{\varrho }\right)}^{{\displaystyle \frac{1}{p}}}{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\underset{{𝚤}_1}{\stackrel{{𝚤}_2}{\int }}{\left|\mathfrak{g}\left(t\right)\right|}^q{\left(dt\right)}^{\varrho }\right)}^{{\displaystyle \frac{1}{q}}}.$$

More recently, Luo et al. [50] introduced the following improved version of generalized Hölder integral inequality.

Lemma 5

([50]). Let $\mathfrak{h},\mathfrak{g}\in C_{\varrho }[{𝚤}_1,{𝚤}_2]$, and the functions ${\mathfrak{h}}^p$, ${\mathfrak{g}}^q$ are both local fractional integral on $[{𝚤}_1,{𝚤}_2]$ for $p,q>1$ with ${\displaystyle \frac{1}{p}}+{\displaystyle \frac{1}{q}}=1$; then,

$$\begin{array}{cc}\hfill & \frac{1}{\Gamma \left(1+\varrho \right)}\underset{{𝚤}_1}{\stackrel{{𝚤}_2}{\int }}\left|\mathfrak{h}\left(t\right)\mathfrak{g}\left(t\right)\right|{\left(dt\right)}^{\varrho }\hfill \\ \hfill \le & {\left(\frac{1}{{𝚤}_2-{𝚤}_1}\right)}^{\varrho }\left[{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\underset{{𝚤}_1}{\stackrel{{𝚤}_2}{\int }}{({𝚤}_2-t)}^{\varrho }{\left|\mathfrak{h}\left(t\right)\right|}^p{\left(dt\right)}^{\varrho }\right)}^{{\displaystyle \frac{1}{p}}}{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\underset{{𝚤}_1}{\stackrel{{𝚤}_2}{\int }}{({𝚤}_2-t)}^{\varrho }{\left|\mathfrak{g}\left(t\right)\right|}^q{\left(dt\right)}^{\varrho }\right)}^{{\displaystyle \frac{1}{q}}}\right.\hfill \\ \hfill & +\left.{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\underset{{𝚤}_1}{\stackrel{{𝚤}_2}{\int }}{(t-{𝚤}_1)}^{\varrho }{\left|\mathfrak{h}\left(t\right)\right|}^p{\left(dt\right)}^{\varrho }\right)}^{{\displaystyle \frac{1}{p}}}{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\underset{{𝚤}_1}{\stackrel{{𝚤}_2}{\int }}{(t-{𝚤}_1)}^{\varrho }{\left|\mathfrak{g}\left(t\right)\right|}^q{\left(dt\right)}^{\varrho }\right)}^{{\displaystyle \frac{1}{q}}}\right].\hfill \end{array}$$

In [51], Yu et al. gave the generalized power mean inequality in fractal domain as follows.

Lemma 6

([51]). Let $\mathfrak{h},\mathfrak{g}\in C_{\varrho }[{𝚤}_1,{𝚤}_2]$, and the functions $\mathfrak{h}$, $\mathfrak{h}{\mathfrak{g}}^q$ are both local fractional integral on $[{𝚤}_1,{𝚤}_2]$ for $q\ge 1$; then,

$$\frac{1}{\Gamma \left(1+\varrho \right)}\underset{{𝚤}_1}{\stackrel{{𝚤}_2}{\int }}\left|\mathfrak{h}\left(t\right)\mathfrak{g}\left(t\right)\right|{\left(dt\right)}^{\varrho }\le {\left(\frac{1}{\Gamma \left(1+\varrho \right)}\underset{{𝚤}_1}{\stackrel{{𝚤}_2}{\int }}\left|\mathfrak{h}\left(t\right)\right|{\left(dt\right)}^{\varrho }\right)}^{1-{\displaystyle \frac{1}{q}}}{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\underset{{𝚤}_1}{\stackrel{{𝚤}_2}{\int }}\left|\mathfrak{h}\left(t\right)\right|{\left|\mathfrak{g}\left(t\right)\right|}^q{\left(dt\right)}^{\varrho }\right)}^{{\displaystyle \frac{1}{q}}}.$$

In the same paper, the authors provided the following improved version of generalized power mean inequality.

Lemma 7

([51]). Let $\mathfrak{h},\mathfrak{g}\in C_{\varrho }[{𝚤}_1,{𝚤}_2]$, and the functions $\mathfrak{h}$, $\mathfrak{h}{\mathfrak{g}}^q$ are both local fractional integral on $[{𝚤}_1,{𝚤}_2]$ for $q\ge 1$, then

$$\begin{array}{cc}\hfill & \frac{1}{\Gamma \left(1+\varrho \right)}\underset{{𝚤}_1}{\stackrel{{𝚤}_2}{\int }}\left|\mathfrak{h}\left(t\right)\mathfrak{g}\left(t\right)\right|{\left(dt\right)}^{\varrho }\hfill \\ \hfill \le & {\left(\frac{1}{{𝚤}_2-{𝚤}_1}\right)}^{\varrho }\left[{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\underset{{𝚤}_1}{\stackrel{{𝚤}_2}{\int }}{({𝚤}_2-t)}^{\varrho }\left|\mathfrak{h}\left(t\right)\right|{\left(dt\right)}^{\varrho }\right)}^{1-{\displaystyle \frac{1}{q}}}{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\underset{{𝚤}_1}{\stackrel{{𝚤}_2}{\int }}{({𝚤}_2-t)}^{\varrho }\left|\mathfrak{h}\left(t\right)\right|{\left|\mathfrak{g}\left(t\right)\right|}^q{\left(dt\right)}^{\varrho }\right)}^{{\displaystyle \frac{1}{q}}}\right.\hfill \\ \hfill & +\left.{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\underset{{𝚤}_1}{\stackrel{{𝚤}_2}{\int }}{(t-{𝚤}_1)}^{\varrho }\left|\mathfrak{h}\left(t\right)\right|{\left(dt\right)}^{\varrho }\right)}^{1-{\displaystyle \frac{1}{q}}}{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\underset{{𝚤}_1}{\stackrel{{𝚤}_2}{\int }}{(t-{𝚤}_1)}^{\varrho }\left|\mathfrak{h}\left(t\right)\right|{\left|\mathfrak{g}\left(t\right)\right|}^q{\left(dt\right)}^{\varrho }\right)}^{{\displaystyle \frac{1}{q}}}\right].\hfill \end{array}$$

3. Main Findings

This section commences with the introduction of a novel fractal–fractional integral identity, which will serve as the basis for the establishment of error bounds for the Simpson rule when applied to fractal–fractional integrals. Following this, we will discuss some special cases.

3.1. Fractal–Fractional Identity

In order to prove our results, we need the following lemma. We assume that $\vartheta :\left[0,\infty \right)\to \left[0^{\varrho },{\infty }^{\varrho }\right)$ satisfy the following condition: $\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{0}{\int }}\frac{\left({𝚤}_2-{𝚤}_1\right)\vartheta \left(\varkappa \right)}{{\varkappa }^{\varrho }}{\left(d\varkappa \right)}^{\varrho }<{\infty }^{\varrho }$.

Lemma 8.

Let $\mathfrak{h}:\mathcal{D}\to {\mathbb{R}}^{\varrho }$ be a function such that $\mathfrak{h}\in D_{\varrho }\left({\mathcal{D}}^{\circ }\right)$, ${𝚤}_1,{𝚤}_2\in {\mathcal{D}}^{\circ }$ with ${𝚤}_1<{𝚤}_2$, and ${\mathfrak{h}}^{\left(\varrho \right)}\in C_{\varrho }\left[{𝚤}_1,{𝚤}_2\right]$; then, the following equality holds:

$$\begin{array}{cc}\hfill & \frac{1^{\varrho }}{6^{\varrho }}\left[\mathfrak{h}\left({𝚤}_1\right)+4^{\varrho }\mathfrak{h}\left(\frac{{𝚤}_1+{𝚤}_2}{2}\right)+\mathfrak{h}\left({𝚤}_2\right)\right]-\frac{1^{\varrho }}{2^{\varrho }{\Lambda }_{\varrho }\left(1\right)}\left({}_{{𝚤}_2^{-}}{}^{\vartheta }\mathcal{J}_{\left(\varrho \right)}\mathfrak{h}\left({𝚤}_1\right)+{}_{{𝚤}_1^{+}}{}^{\vartheta }\mathcal{J}_{\varrho }\mathfrak{h}\left({𝚤}_2\right)\right)\hfill \\ \hfill =& \frac{{\left({𝚤}_2-{𝚤}_1\right)}^{\varrho }}{6^{\varrho }{\Lambda }_{\varrho }\left(1\right)}\left(\frac{3^{\varrho }}{\Gamma \left(1+\varrho \right)}\stackrel{{\displaystyle \frac{1}{2}}}{\underset{0}{\int }}{\Lambda }_{\varrho }\left(t\right){\mathfrak{h}}^{\left(\varrho \right)}\left(\left(1-t\right){𝚤}_1+t{𝚤}_2\right){\left(dt\right)}^{\varrho }\right.\hfill \\ \hfill & +\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{{\displaystyle \frac{1}{2}}}{\int }}\left({\Lambda }_{\varrho }\left(t\right)-2^{\varrho }{\Omega }_{\varrho }\left(t\right)\right){\mathfrak{h}}^{\left(\varrho \right)}\left(\left(1-t\right){𝚤}_1+t{𝚤}_2\right){\left(dt\right)}^{\varrho }\hfill \\ \hfill & -\frac{3^{\varrho }}{\Gamma \left(1+\varrho \right)}\stackrel{{\displaystyle \frac{1}{2}}}{\underset{0}{\int }}{\Lambda }_{\varrho }\left(t\right){\mathfrak{h}}^{\left(\varrho \right)}\left(t{𝚤}_1+\left(1-t\right){𝚤}_2\right){\left(dt\right)}^{\varrho }\hfill \\ \hfill & -\left.\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{{\displaystyle \frac{1}{2}}}{\int }}\left({\Lambda }_{\varrho }\left(t\right)-2^{\varrho }{\Omega }_{\varrho }\left(t\right)\right){\mathfrak{h}}^{\left(\varrho \right)}\left(t{𝚤}_1+\left(1-t\right){𝚤}_2\right){\left(dt\right)}^{\varrho }\right),\hfill \end{array}$$

where ${}_{{𝚤}_1^{+}}{}^{\vartheta }\mathcal{J}^{\left(\varrho \right)}$ and ${}_{{𝚤}_2^{-}}{}^{\vartheta }\mathcal{J}^{\left(\varrho \right)}$ are defined as in (4) and (5), respectively, and the functions ${\Lambda }_{\varrho }(.)$ and ${\Omega }_{\varrho }(.)$ are defined as bellow,

$${\Lambda }_{\varrho }\left(t\right)=\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{t}{\underset{0}{\int }}\frac{\vartheta \left(\left({𝚤}_2-{𝚤}_1\right)s\right)}{s^{\varrho }}{\left(ds\right)}^{\varrho }<{\infty }^{\varrho }$$

and

$${\Omega }_{\varrho }\left(t\right)=\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{t}{\int }}\frac{\vartheta \left(\left({𝚤}_2-{𝚤}_1\right)s\right)}{s^{\varrho }}{\left(ds\right)}^{\varrho }<{\infty }^{\varrho }.$$

Proof. 

Let

$$\mathcal{P}=3^{\varrho }({\mathcal{P}}_1-{\mathcal{P}}_3)+{\mathcal{P}}_2-{\mathcal{P}}_4,$$

(6)

where

$$\begin{array}{cc}\hfill {\mathcal{P}}_1=& \frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{{\displaystyle \frac{1}{2}}}{\underset{0}{\int }}{\Lambda }_{\varrho }\left(t\right){\mathfrak{h}}^{\left(\varrho \right)}\left(\left(1-t\right){𝚤}_1+t{𝚤}_2\right){\left(dt\right)}^{\varrho },\hfill \\ \hfill {\mathcal{P}}_2=& \frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{{\displaystyle \frac{1}{2}}}{\int }}\left({\Lambda }_{\varrho }\left(t\right)-2^{\varrho }{\Omega }_{\varrho }\left(t\right)\right){\mathfrak{h}}^{\left(\varrho \right)}\left(\left(1-t\right){𝚤}_1+t{𝚤}_2\right){\left(dt\right)}^{\varrho },\hfill \\ \hfill {\mathcal{P}}_3=& \frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{{\displaystyle \frac{1}{2}}}{\underset{0}{\int }}{\Lambda }_{\varrho }\left(t\right){\mathfrak{h}}^{\left(\varrho \right)}\left(t{𝚤}_1+\left(1-t\right){𝚤}_2\right){\left(dt\right)}^{\varrho },\hfill \\ \hfill {\mathcal{P}}_4=& \frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{{\displaystyle \frac{1}{2}}}{\int }}\left({\Lambda }_{\varrho }\left(t\right)-2^{\varrho }{\Omega }_{\varrho }\left(t\right)\right){\mathfrak{h}}^{\left(\varrho \right)}\left(t{𝚤}_1+\left(1-t\right){𝚤}_2\right){\left(dt\right)}^{\varrho },\hfill \end{array}$$

Using the local fractional integration by parts for ${\mathcal{P}}_1$, we obtain

$$\begin{array}{cc}\hfill {\mathcal{P}}_1=& \frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{{\displaystyle \frac{1}{2}}}{\underset{0}{\int }}{\Lambda }_{\varrho }\left(t\right){\mathfrak{h}}^{\left(\varrho \right)}\left(\left(1-t\right){𝚤}_1+t{𝚤}_2\right){\left(dt\right)}^{\varrho }\hfill \\ \hfill =& {\left.\frac{1^{\varrho }}{{\left({𝚤}_2-{𝚤}_1\right)}^{\varrho }}{\Lambda }_{\varrho }\left(t\right)\mathfrak{h}\left(\left(1-t\right){𝚤}_1+t{𝚤}_2\right)\right|}_0^{{\displaystyle \frac{1}{2}}}\hfill \\ \hfill & -\frac{1^{\varrho }}{{\left({𝚤}_2-{𝚤}_1\right)}^{\varrho }\Gamma \left(1+\varrho \right)}\stackrel{{\displaystyle \frac{1}{2}}}{\underset{0}{\int }}\frac{\vartheta \left(\left({𝚤}_2-{𝚤}_1\right)t\right)}{t^{\varrho }}\mathfrak{h}\left(\left(1-t\right){𝚤}_1+t{𝚤}_2\right){\left(dt\right)}^{\varrho }\hfill \\ \hfill =& \frac{1^{\varrho }}{{\left({𝚤}_2-{𝚤}_1\right)}^{\varrho }}{\Lambda }_{\varrho }\left(\frac{1}{2}\right)\mathfrak{h}\left(\frac{{𝚤}_1+{𝚤}_2}{2}\right)-\frac{1^{\varrho }}{{\left({𝚤}_2-{𝚤}_1\right)}^{\varrho }\Gamma \left(1+\varrho \right)}\stackrel{{\displaystyle \frac{1}{2}}}{\underset{0}{\int }}\frac{\vartheta \left(\left({𝚤}_2-{𝚤}_1\right)t\right)}{t^{\varrho }}\mathfrak{h}\left(\left(1-t\right){𝚤}_1+t{𝚤}_2\right){\left(dt\right)}^{\varrho }.\hfill \end{array}$$

(7)

Similarly, for ${\mathcal{P}}_2$, we obtain

$$\begin{array}{cc}\hfill {\mathcal{P}}_2=& \frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{{\displaystyle \frac{1}{2}}}{\int }}\left({\Lambda }_{\varrho }\left(t\right)-2^{\varrho }{\Omega }_{\varrho }\left(t\right)\right){\mathfrak{h}}^{\left(\varrho \right)}\left(\left(1-t\right){𝚤}_1+t{𝚤}_2\right){\left(dt\right)}^{\varrho }\hfill \\ \hfill =& {\left.\frac{1^{\varrho }}{{\left({𝚤}_2-{𝚤}_1\right)}^{\varrho }}\left({\Lambda }_{\varrho }\left(t\right)-2^{\varrho }{\Omega }_{\varrho }\left(t\right)\right)\mathfrak{h}\left(\left(1-t\right){𝚤}_1+t{𝚤}_2\right)\right|}_{{\displaystyle \frac{1}{2}}}^1\hfill \\ \hfill & -\frac{3^{\varrho }}{{\left({𝚤}_2-{𝚤}_1\right)}^{\varrho }\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{{\displaystyle \frac{1}{2}}}{\int }}\frac{\vartheta \left(\left({𝚤}_2-{𝚤}_1\right)t\right)}{t^{\varrho }}\mathfrak{h}\left(\left(1-t\right){𝚤}_1+t{𝚤}_2\right){\left(dt\right)}^{\varrho }\hfill \\ \hfill =& \frac{1^{\varrho }}{{\left({𝚤}_2-{𝚤}_1\right)}^{\varrho }}{\Lambda }_{\varrho }\left(1\right)\mathfrak{h}\left({𝚤}_2\right)+\frac{1^{\varrho }}{{\left({𝚤}_2-{𝚤}_1\right)}^{\varrho }}\left(2^{\varrho }{\Omega }_{\varrho }\left(\frac{1}{2}\right)-{\Lambda }_{\varrho }\left(\frac{1}{2}\right)\right)\mathfrak{h}\left(\frac{{𝚤}_1+{𝚤}_2}{2}\right)\hfill \\ \hfill & -\frac{3^{\varrho }}{{\left({𝚤}_2-{𝚤}_1\right)}^{\varrho }\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{{\displaystyle \frac{1}{2}}}{\int }}\frac{\vartheta \left(\left({𝚤}_2-{𝚤}_1\right)t\right)}{t^{\varrho }}\mathfrak{h}\left(\left(1-t\right){𝚤}_1+t{𝚤}_2\right){\left(dt\right)}^{\varrho }\hfill \\ \hfill =& \frac{1^{\varrho }}{{\left({𝚤}_2-{𝚤}_1\right)}^{\varrho }}{\Lambda }_{\varrho }\left(1\right)\mathfrak{h}\left({𝚤}_2\right)+\frac{1^{\varrho }}{{\left({𝚤}_2-{𝚤}_1\right)}^{\varrho }}\left(2^{\varrho }{\Lambda }_{\varrho }\left(1\right)-3^{\varrho }{\Lambda }_{\varrho }\left(\frac{1}{2}\right)\right)\mathfrak{h}\left(\frac{{𝚤}_1+{𝚤}_2}{2}\right)\hfill \\ \hfill & -\frac{3^{\varrho }}{{\left({𝚤}_2-{𝚤}_1\right)}^{\varrho }\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{{\displaystyle \frac{1}{2}}}{\int }}\frac{\vartheta \left(\left({𝚤}_2-{𝚤}_1\right)t\right)}{t^{\varrho }}\mathfrak{h}\left(\left(1-t\right){𝚤}_1+t{𝚤}_2\right){\left(dt\right)}^{\varrho },\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill {\mathcal{P}}_3=& \frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{{\displaystyle \frac{1}{2}}}{\underset{0}{\int }}{\Lambda }_{\varrho }\left(t\right){\mathfrak{h}}^{\left(\varrho \right)}\left(t{𝚤}_1+\left(1-t\right){𝚤}_2\right){\left(dt\right)}^{\varrho }\hfill \\ \hfill =& {\left.-\frac{1^{\varrho }}{{\left({𝚤}_2-{𝚤}_1\right)}^{\varrho }}{\Lambda }_{\varrho }\left(t\right)\mathfrak{h}\left(t{𝚤}_1+\left(1-t\right){𝚤}_2\right)\right|}_0^{{\displaystyle \frac{1}{2}}}\hfill \\ \hfill & +\frac{1^{\varrho }}{{\left({𝚤}_2-{𝚤}_1\right)}^{\varrho }\Gamma \left(1+\varrho \right)}\stackrel{{\displaystyle \frac{1}{2}}}{\underset{0}{\int }}\left(\frac{\vartheta \left(\left({𝚤}_2-{𝚤}_1\right)t\right)}{t^{\varrho }}\right)\mathfrak{h}\left(t{𝚤}_1+\left(1-t\right){𝚤}_2\right){\left(dt\right)}^{\varrho }\hfill \\ \hfill =& -\frac{1^{\varrho }}{{\left({𝚤}_2-{𝚤}_1\right)}^{\varrho }}{\Lambda }_{\varrho }\left(\frac{1}{2}\right)\mathfrak{h}\left(\frac{{𝚤}_1+{𝚤}_2}{2}\right)+\frac{1^{\varrho }}{{\left({𝚤}_2-{𝚤}_1\right)}^{\varrho }\Gamma \left(1+\varrho \right)}\stackrel{{\displaystyle \frac{1}{2}}}{\underset{0}{\int }}\left(\frac{\vartheta \left(\left({𝚤}_2-{𝚤}_1\right)t\right)}{t^{\varrho }}\right)\mathfrak{h}\left(t{𝚤}_1+\left(1-t\right){𝚤}_2\right){\left(dt\right)}^{\varrho }\hfill \end{array}$$

(9)

and

$$\begin{array}{cc}\hfill {\mathcal{P}}_4=& \frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{{\displaystyle \frac{1}{2}}}{\int }}\left({\Lambda }_{\varrho }\left(t\right)-2^{\varrho }{\Omega }_{\varrho }\left(t\right)\right){\mathfrak{h}}^{\left(\varrho \right)}\left(t{𝚤}_1+\left(1-t\right){𝚤}_2\right){\left(dt\right)}^{\varrho }\hfill \\ \hfill =& {\left.-\frac{1^{\varrho }}{{\left({𝚤}_2-{𝚤}_1\right)}^{\varrho }}\left({\Lambda }_{\varrho }\left(t\right)-2^{\varrho }{\Omega }_{\varrho }\left(t\right)\right)\mathfrak{h}\left(t{𝚤}_1+\left(1-t\right){𝚤}_2\right)\right|}_{{\displaystyle \frac{1}{2}}}^1\hfill \\ \hfill & +\frac{3^{\varrho }}{{\left({𝚤}_2-{𝚤}_1\right)}^{\varrho }\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{{\displaystyle \frac{1}{2}}}{\int }}\frac{\vartheta \left(\left({𝚤}_2-{𝚤}_1\right)t\right)}{t^{\varrho }}\mathfrak{h}\left(t{𝚤}_1+\left(1-t\right){𝚤}_2\right){\left(dt\right)}^{\varrho }\hfill \\ \hfill =& -\frac{1^{\varrho }}{{\left({𝚤}_2-{𝚤}_1\right)}^{\varrho }}{\Lambda }_{\varrho }\left(1\right)\mathfrak{h}\left({𝚤}_1\right)+\frac{1^{\varrho }}{{\left({𝚤}_2-{𝚤}_1\right)}^{\varrho }}\left({\Lambda }_{\varrho }\left(\frac{1}{2}\right)-2^{\varrho }{\Omega }_{\varrho }\left(\frac{1}{2}\right)\right)\mathfrak{h}\left(\frac{{𝚤}_1+{𝚤}_2}{2}\right)\hfill \\ \hfill & +\frac{3^{\varrho }}{{\left({𝚤}_2-{𝚤}_1\right)}^{\varrho }\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{{\displaystyle \frac{1}{2}}}{\int }}\frac{\vartheta \left(\left({𝚤}_2-{𝚤}_1\right)t\right)}{t^{\varrho }}\mathfrak{h}\left(t{𝚤}_1+\left(1-t\right){𝚤}_2\right){\left(dt\right)}^{\varrho }\hfill \\ \hfill =& -\frac{1^{\varrho }}{{\left({𝚤}_2-{𝚤}_1\right)}^{\varrho }}{\Lambda }_{\varrho }\left(1\right)\mathfrak{h}\left({𝚤}_1\right)-\frac{1^{\varrho }}{{\left({𝚤}_2-{𝚤}_1\right)}^{\varrho }}\left(2^{\varrho }{\Lambda }_{\varrho }\left(1\right)-3^{\varrho }{\Lambda }_{\varrho }\left(\frac{1}{2}\right)\right)\mathfrak{h}\left(\frac{{𝚤}_1+{𝚤}_2}{2}\right)\hfill \\ \hfill & +\frac{3^{\varrho }}{{\left({𝚤}_2-{𝚤}_1\right)}^{\varrho }\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{{\displaystyle \frac{1}{2}}}{\int }}\frac{\vartheta \left(\left({𝚤}_2-{𝚤}_1\right)t\right)}{t^{\varrho }}\mathfrak{h}\left(t{𝚤}_1+\left(1-t\right){𝚤}_2\right){\left(dt\right)}^{\varrho }.\hfill \end{array}$$

(10)

Using (7)–(10) into (6), then multiplying the resulting equality by ${\displaystyle \frac{{\left({𝚤}_2-{𝚤}_1\right)}^{\varrho }}{6^{\varrho }{\Lambda }_{\varrho }\left(1\right)}}$, we obtain the desired result. □

Corollary 2.

In Lemma 8, if we attempt to take $\vartheta \left(s\right)=s^{\varrho }$, we obtain the following Simpson identity via local fractional integral:

$$\begin{array}{cc}\hfill & \frac{1^{\varrho }}{6^{\varrho }}\left[\mathfrak{h}\left({𝚤}_1\right)+4^{\varrho }\mathfrak{h}\left(\frac{{𝚤}_1+{𝚤}_2}{2}\right)+\mathfrak{h}\left({𝚤}_2\right)\right]-\frac{\Gamma \left(1+\varrho \right)}{{\left({𝚤}_2-{𝚤}_1\right)}^{\varrho }}{}_{{𝚤}_1}I_{{𝚤}_2}^{\left(\varkappa \right)}\mathfrak{h}\hfill \\ \hfill =& \frac{{\left({𝚤}_2-{𝚤}_1\right)}^{\varrho }}{6^{\varrho }}\left(\frac{3^{\varrho }}{\Gamma \left(1+\varrho \right)}\stackrel{{\displaystyle \frac{1}{2}}}{\underset{0}{\int }}{t}^{\varrho }\left[{\mathfrak{h}}^{\left(\varrho \right)}\left(\left(1-t\right){𝚤}_1+t{𝚤}_2\right)-{\mathfrak{h}}^{\left(\varrho \right)}\left(t{𝚤}_1+\left(1-t\right){𝚤}_2\right)\right]{\left(dt\right)}^{\varrho }\right.\hfill \\ \hfill & \left.+\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{{\displaystyle \frac{1}{2}}}{\int }}{\left(3t-2\right)}^{\varrho }\left[{\mathfrak{h}}^{\left(\varrho \right)}\left(\left(1-t\right){𝚤}_1+t{𝚤}_2\right)-{\mathfrak{h}}^{\left(\varrho \right)}\left(t{𝚤}_1+\left(1-t\right){𝚤}_2\right)\right]{\left(dt\right)}^{\varrho }\right),\hfill \end{array}$$

which represents a novel contribution to the literature.

Remark 3.

By setting $\varrho =1$ in Corollary 2, we obtain

$$\begin{array}{cc}\hfill & \frac{1}{6}\left[\mathfrak{h}\left({𝚤}_1\right)+4\mathfrak{h}\left(\frac{{𝚤}_1+{𝚤}_2}{2}\right)+\mathfrak{h}\left({𝚤}_2\right)\right]-\frac{1}{{𝚤}_2-{𝚤}_1}\underset{{𝚤}_1}{\stackrel{{𝚤}_2}{\int }}\mathfrak{h}\left(\varkappa \right)d\varkappa \hfill \\ \hfill =& \frac{{𝚤}_2-{𝚤}_1}{6}\left(3\stackrel{{\displaystyle \frac{1}{2}}}{\underset{0}{\int }}t\left[{\mathfrak{h}}^{\prime }\left(\left(1-t\right){𝚤}_1+t{𝚤}_2\right)-{\mathfrak{h}}^{\prime }\left(t{𝚤}_1+\left(1-t\right){𝚤}_2\right)\right]dt\right.\hfill \\ \hfill & \left.+\stackrel{1}{\underset{{\displaystyle \frac{1}{2}}}{\int }}\left(3t-2\right)\left[{\mathfrak{h}}^{\prime }\left(\left(1-t\right){𝚤}_1+t{𝚤}_2\right)-{\mathfrak{h}}^{\prime }\left(t{𝚤}_1+\left(1-t\right){𝚤}_2\right)\right]dt\right),\hfill \end{array}$$

which is proved by Alomari et al. in Lemma 1 from [52].

3.2. Simpson-Type Inequalities via Fractal–Fractional Integrals

Theorem 5.

Let $\mathfrak{h}:\mathcal{D}\to {\mathbb{R}}^{\varrho }$ be a function such that $\mathfrak{h}\in D_{\varrho }\left({\mathcal{D}}^{\circ }\right)$, ${𝚤}_1,{𝚤}_2\in {\mathcal{D}}^{\circ }$ with ${𝚤}_1<{𝚤}_2$, and ${\mathfrak{h}}^{\left(\varrho \right)}\in C_{\varrho }\left[{𝚤}_1,{𝚤}_2\right]$. If $\left|{\mathfrak{h}}^{\left(\varrho \right)}\right|$ is generalized s-convex on $\left[{𝚤}_1,{𝚤}_2\right]$, for some fixed $s\in (0,1]$, then we have

$$\begin{array}{cc}\hfill & \left|\frac{1^{\varrho }}{6^{\varrho }}\left[\mathfrak{h}\left({𝚤}_1\right)+4^{\varrho }\mathfrak{h}\left(\frac{{𝚤}_1+{𝚤}_2}{2}\right)+\mathfrak{h}\left({𝚤}_2\right)\right]-\frac{1^{\varrho }}{2^{\varrho }{\Lambda }_{\varrho }\left(1\right)}\left({}_{{𝚤}_2^{-}}{}^{\vartheta }\mathcal{J}^{\left(\varrho \right)}\mathfrak{h}\left({𝚤}_1\right)+{}_{{𝚤}_2^{-}}{}^{\vartheta }\mathcal{J}^{\left(\varrho \right)}\mathfrak{h}\left({𝚤}_2\right)\right)\right|\hfill \\ \hfill \le & \frac{{\left({𝚤}_2-{𝚤}_1\right)}^{\varrho }}{6^{\varrho }{\Lambda }_{\varrho }\left(1\right)}\left(3^{\varrho }{C}_1\left(\varrho ,s\right)+3^{\varrho }{C}_2\left(\varrho ,s\right)+C_3\left(\varrho ,s\right)+C_4\left(\varrho ,s\right)\right)\left(\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_1\right)\right|+\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_2\right)\right|\right),\hfill \end{array}$$

where

$$C_1\left(\varrho ,s\right)=\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{{\displaystyle \frac{1}{2}}}{\underset{0}{\int }}\left|{\Lambda }_{\varrho }\left(t\right)\right|{\left(1-t\right)}^{s\varrho }{\left(dt\right)}^{\varrho },$$

(11)

$$C_2\left(\varrho ,s\right)=\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{{\displaystyle \frac{1}{2}}}{\underset{0}{\int }}\left|{\Lambda }_{\varrho }\left(t\right)\right|t^{s\varrho }{\left(dt\right)}^{\varrho },$$

(12)

$$C_3\left(\varrho ,s\right)=\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{{\displaystyle \frac{1}{2}}}{\int }}\left|2^{\varrho }{\Lambda }_{\varrho }\left(1\right)-3^{\varrho }{\Lambda }_{\varrho }\left(t\right)\right|{\left(1-t\right)}^{s\varrho }{\left(dt\right)}^{\varrho }$$

(13)

and

$$C_4\left(\varrho ,s\right)=\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{{\displaystyle \frac{1}{2}}}{\int }}\left|2^{\varrho }{\Lambda }_{\varrho }\left(1\right)-3^{\varrho }{\Lambda }_{\varrho }\left(t\right)\right|t^{s\varrho }{\left(dt\right)}^{\varrho }.$$

(14)

Proof. 

From Lemma 8, the properties of the modulus, and the generalized s-convexity of $\left|{\mathfrak{h}}^{\left(\varrho \right)}\right|$, we have

$$\begin{array}{cc}\hfill & \left|\frac{1^{\varrho }}{6^{\varrho }}\left[\mathfrak{h}\left({𝚤}_1\right)+4^{\varrho }\mathfrak{h}\left(\frac{{𝚤}_1+{𝚤}_2}{2}\right)+\mathfrak{h}\left({𝚤}_2\right)\right]-\frac{1^{\varrho }}{2^{\varrho }{\Lambda }_{\varrho }\left(1\right)}\left({}_{{𝚤}_2^{-}}{}^{\vartheta }\mathcal{J}^{\left(\varrho \right)}\mathfrak{h}\left({𝚤}_1\right)+{}_{{𝚤}_1^{+}}{}^{\vartheta }\mathcal{J}^{\varrho }\mathfrak{h}\left({𝚤}_2\right)\right)\right|\hfill \\ \hfill \le & \frac{{\left({𝚤}_2-{𝚤}_1\right)}^{\varrho }}{6^{\varrho }{\Lambda }_{\varrho }\left(1\right)}\left(\frac{3^{\varrho }}{\Gamma \left(1+\varrho \right)}\stackrel{{\displaystyle \frac{1}{2}}}{\underset{0}{\int }}\left|{\Lambda }_{\varrho }\left(t\right)\right|\left|{\mathfrak{h}}^{\left(\varrho \right)}\left(\left(1-t\right){𝚤}_1+t{𝚤}_2\right)\right|{\left(dt\right)}^{\varrho }\right.\hfill \\ \hfill & +\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{{\displaystyle \frac{1}{2}}}{\int }}\left|{\Lambda }_{\varrho }\left(t\right)-2^{\varrho }{\Omega }_{\varrho }\left(t\right)\right|\left|{\mathfrak{h}}^{\left(\varrho \right)}\left(\left(1-t\right){𝚤}_1+t{𝚤}_2\right)\right|{\left(dt\right)}^{\varrho }\hfill \\ \hfill & +\frac{3^{\varrho }}{\Gamma \left(1+\varrho \right)}\stackrel{{\displaystyle \frac{1}{2}}}{\underset{0}{\int }}\left|{\Lambda }_{\varrho }\left(t\right)\right|\left|{\mathfrak{h}}^{\left(\varrho \right)}\left(t{𝚤}_1+\left(1-t\right){𝚤}_2\right)\right|{\left(dt\right)}^{\varrho }\hfill \\ \hfill & +\left.\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{{\displaystyle \frac{1}{2}}}{\int }}\left|{\Lambda }_{\varrho }\left(t\right)-2^{\varrho }{\Omega }_{\varrho }\left(t\right)\right|\left|{\mathfrak{h}}^{\left(\varrho \right)}\left(t{𝚤}_1+\left(1-t\right){𝚤}_2\right)\right|{\left(dt\right)}^{\varrho }\right)\hfill \\ \hfill \le & \frac{{\left({𝚤}_2-{𝚤}_1\right)}^{\varrho }}{6^{\varrho }{\Lambda }_{\varrho }\left(1\right)}\left(\frac{3^{\varrho }}{\Gamma \left(1+\varrho \right)}\stackrel{{\displaystyle \frac{1}{2}}}{\underset{0}{\int }}\left|{\Lambda }_{\varrho }\left(t\right)\right|\left({\left(1-t\right)}^{s\varrho }\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_1\right)\right|+t^{s\varrho }\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_2\right)\right|\right){\left(dt\right)}^{\varrho }\right.\hfill \\ \hfill & +\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{{\displaystyle \frac{1}{2}}}{\int }}\left|{\Lambda }_{\varrho }\left(t\right)-2^{\varrho }{\Omega }_{\varrho }\left(t\right)\right|\left({\left(1-t\right)}^{s\varrho }\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_1\right)\right|+t^{s\varrho }\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_2\right)\right|\right){\left(dt\right)}^{\varrho }\hfill \\ \hfill & +\frac{3^{\varrho }}{\Gamma \left(1+\varrho \right)}\stackrel{{\displaystyle \frac{1}{2}}}{\underset{0}{\int }}\left|{\Lambda }_{\varrho }\left(t\right)\right|\left(t^{s\varrho }\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_1\right)\right|+{\left(1-t\right)}^{s\varrho }\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_2\right)\right|\right){\left(dt\right)}^{\varrho }\hfill \\ \hfill & +\left.\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{{\displaystyle \frac{1}{2}}}{\int }}\left|{\Lambda }_{\varrho }\left(t\right)-2^{\varrho }{\Omega }_{\varrho }\left(t\right)\right|\left(t^{s\varrho }\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_1\right)\right|+{\left(1-t\right)}^{s\varrho }\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_2\right)\right|\right){\left(dt\right)}^{\varrho }\right)\hfill \\ \hfill =& \frac{{\left({𝚤}_2-{𝚤}_1\right)}^{\varrho }}{6^{\varrho }{\Lambda }_{\varrho }\left(1\right)}\left(\frac{3^{\varrho }}{\Gamma \left(1+\varrho \right)}\stackrel{{\displaystyle \frac{1}{2}}}{\underset{0}{\int }}\left|{\Lambda }_{\varrho }\left(t\right)\right|{\left(1-t\right)}^{s\varrho }{\left(dt\right)}^{\varrho }+\frac{3^{\varrho }}{\Gamma \left(1+\varrho \right)}\stackrel{{\displaystyle \frac{1}{2}}}{\underset{0}{\int }}\left|{\Lambda }_{\varrho }\left(t\right)\right|t^{s\varrho }{\left(dt\right)}^{\varrho }\right.\hfill \\ \hfill & +\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{{\displaystyle \frac{1}{2}}}{\int }}\left|2^{\varrho }{\Lambda }_{\varrho }\left(1\right)-3^{\varrho }{\Lambda }_{\varrho }\left(t\right)\right|{\left(1-t\right)}^{s\varrho }{\left(dt\right)}^{\varrho }\hfill \\ \hfill & +\left.\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{{\displaystyle \frac{1}{2}}}{\int }}\left|2^{\varrho }{\Lambda }_{\varrho }\left(1\right)-3^{\varrho }{\Lambda }_{\varrho }\left(t\right)\right|t^{s\varrho }{\left(dt\right)}^{\varrho }\right)\left(\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_1\right)\right|+\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_2\right)\right|\right)\hfill \\ \hfill =& \frac{{\left({𝚤}_2-{𝚤}_1\right)}^{\varrho }}{6^{\varrho }{\Lambda }_{\varrho }\left(1\right)}\left(3^{\varrho }{C}_1\left(\varrho ,s\right)+3^{\varrho }{C}_2\left(\varrho ,s\right)+C_3\left(\varrho ,s\right)+C_4\left(\varrho ,s\right)\right)\left(\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_1\right)\right|+\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_2\right)\right|\right),\hfill \end{array}$$

where we have used (11)–(14), and the fact that ${\Lambda }_{\varrho }\left(t\right)+{\Omega }_{\varrho }\left(t\right)={\Lambda }_{\varrho }\left(1\right)$. The proof is completed. □

3.3. Special Cases

Corollary 3.

In Theorem 5, if we set $\varrho =1$, we obtain the following Simpson-type inequality via generalized fractional integrals:

$$\begin{array}{cc}\hfill & \left|\frac{1}{6}\left[\mathfrak{h}\left({𝚤}_1\right)+4\mathfrak{h}\left(\frac{{𝚤}_1+{𝚤}_2}{2}\right)+\mathfrak{h}\left({𝚤}_2\right)\right]-\frac{1}{2{\Lambda }_1\left(1\right)}\left({}_{{𝚤}_2^{-}}\mathcal{J}^{\vartheta }\mathfrak{h}\left({𝚤}_1\right)+{}_{{𝚤}_1^{+}}J_{\vartheta }\mathfrak{h}\left({𝚤}_2\right)\right)\right|\hfill \\ \hfill \le & \frac{{𝚤}_2-{𝚤}_1}{6{\Lambda }_1\left(1\right)}\left(3C_1\left(1,s\right)+3C_2\left(1,s\right)+C_3\left(1,s\right)+C_4\left(1,s\right)\right)\left(\left|{\mathfrak{h}}^{\prime }\left({𝚤}_1\right)\right|+\left|{\mathfrak{h}}^{\prime }\left({𝚤}_2\right)\right|\right),\hfill \end{array}$$

where $C_i$$(i=1,4)$ are defined as in (11)–(14), respectively, and ${}_{{𝚤}_1^{+}}\mathcal{J}_{\vartheta }$, ${}_{{𝚤}_2^{-}}J_{\vartheta }$ are given by (2) and (3).

Remark 4.

Taking into account the many circumstances covered in Remark 1, the conclusion derived in Corollary 3 represents a multitude of results pertaining to Fractional Simpson’s inequalities.

Corollary 4.

In Corollary 3, if we take $\vartheta \left(t\right)=t$, we obtain

$$\begin{array}{cc}\hfill & \left|\frac{1}{6}\left[\mathfrak{h}\left({𝚤}_1\right)+4\mathfrak{h}\left(\frac{{𝚤}_1+{𝚤}_2}{2}\right)+\mathfrak{h}\left({𝚤}_2\right)\right]-\frac{1}{{𝚤}_2-{𝚤}_1}\underset{{𝚤}_1}{\stackrel{{𝚤}_2}{\int }}\mathfrak{h}\left(t\right)dt\right|\hfill \\ \hfill \le & \left({𝚤}_2-{𝚤}_1\right)\frac{6^{s+2}(s+2)-4\times 3^{s+3}+3\times \left(2^{2s+5}+2^{s+2}\right)}{6^{s+3}\left(s+1\right)\left(s+2\right)}\left(\left|{\mathfrak{h}}^{\prime }\left({𝚤}_1\right)\right|+\left|{\mathfrak{h}}^{\prime }\left({𝚤}_2\right)\right|\right).\hfill \end{array}$$

Remark 5.

We observe that the result obtained in Corollary 4 represents a new estimate similar to the one by Sarikaya in [6], as given by Theorem 3. If we denote by

$$\mathrm{{\rm Y}}\left(s\right)=\frac{(s-4)6^{s+1}+2\times 5^{s+2}-2\times 3^{s+2}+2}{6^{s+2}(s+1)(s+2)},$$

and

$$\Sigma \left(s\right)=\frac{6^{s+2}(s+2)-4\times 3^{s+3}+3\times \left(2^{2s+5}+2^{s+3}\right)}{6^{s+3}\left(s+1\right)\left(s+2\right)},$$

the coefficients of $({𝚤}_2-{𝚤}_1)\left(\left|{\mathfrak{h}}^{\prime }\left({𝚤}_1\right)\right|+\left|{\mathfrak{h}}^{\prime }\left({𝚤}_2\right)\right|\right)$ in Theorem 3 and Corollary 4, respectively.

These are shown in Figure 1, from which we observe that the estimate given in Theorem 3 is finer than that of Corollary 4.

3.4. Refinement of Fractal–Fractional Simpson-Type Inequalities

To improve our result, we will attempt to involve the term $\left|{\mathfrak{h}}^{\left(\varrho \right)}\left(\frac{{𝚤}_1+{𝚤}_2}{2}\right)\right|$ by making the appropriate variable substitutions. This leads to the following theorem.

Theorem 6.

Let $\mathfrak{h}:\mathcal{D}\to {\mathbb{R}}^{\varrho }$ be a function such that $\mathfrak{h}\in D_{\varrho }\left({\mathcal{D}}^{\circ }\right)$, ${𝚤}_1,{𝚤}_2\in {\mathcal{D}}^{\circ }$ with ${𝚤}_1<{𝚤}_2$, and ${\mathfrak{h}}^{\left(\varrho \right)}\in C_{\varrho }\left[{𝚤}_1,{𝚤}_2\right]$. If $\left|{\mathfrak{h}}^{\left(\varrho \right)}\right|$ is generalized s-convex on $\left[{𝚤}_1,{𝚤}_2\right]$, for some fixed $s\in (0,1]$, then we have

$$\begin{array}{cc}\hfill & \left|\frac{1^{\varrho }}{6^{\varrho }}\left[\mathfrak{h}\left({𝚤}_1\right)+4^{\varrho }\mathfrak{h}\left(\frac{{𝚤}_1+{𝚤}_2}{2}\right)+\mathfrak{h}\left({𝚤}_2\right)\right]-\frac{1^{\varrho }}{2^{\varrho }{\Lambda }_{\varrho }\left(1\right)}\left({}_{{𝚤}_2^{-}}{}^{\vartheta }\mathcal{J}^{\left(\varrho \right)}\mathfrak{h}\left({𝚤}_1\right)+{}_{{𝚤}_1^{+}}{}^{\vartheta }\mathcal{J}^{\varrho }\mathfrak{h}\left({𝚤}_2\right)\right)\right|\hfill \\ \hfill \le & \frac{{\left({𝚤}_2-{𝚤}_1\right)}^{\varrho }}{{12}^{\varrho }{\Lambda }_{\varrho }\left(1\right)}\left[D_1\left(\varrho ,s\right)\left(\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_1\right)\right|+\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_2\right)\right|\right)+D_2\left(\varrho ,s\right)\left|{\mathfrak{h}}^{\left(\varrho \right)}\left(\frac{{𝚤}_1+{𝚤}_2}{2}\right)\right|\right],\hfill \end{array}$$

where $D_1$ and $D_2$ are given by

$$D_1\left(\varrho ,s\right)=\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{0}{\int }}\left(\left|2^{\varrho }{\Lambda }_{\varrho }\left(1\right)-3^{\varrho }{\Lambda }_{\varrho }\left(1-\frac{\nu }{2}\right)+3^{\varrho }{\Lambda }_{\varrho }\left(\frac{\nu }{2}\right)\right|\right){\left(1-\nu \right)}^{s\varrho }{\left(d\nu \right)}^{\varrho }$$

(15)

and

$$D_2\left(\varrho ,s\right)=\frac{2^{\varrho }}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{0}{\int }}\left(\left|2^{\varrho }{\Lambda }_{\varrho }\left(1\right)-3^{\varrho }{\Lambda }_{\varrho }\left(1-\frac{\nu }{2}\right)+3^{\varrho }{\Lambda }_{\varrho }\left(\frac{\nu }{2}\right)\right|\right){\nu }^{s\varrho }{\left(d\nu \right)}^{\varrho }.$$

(16)

Proof. 

From Lemma 8, the properties of the modulus, and the generalized s-convexity of $\left|{\mathfrak{h}}^{\left(\varrho \right)}\right|$, we have

$$\begin{array}{cc}\hfill & \left|\frac{1^{\varrho }}{6^{\varrho }}\left[\mathfrak{h}\left({𝚤}_1\right)+4^{\varrho }\mathfrak{h}\left(\frac{{𝚤}_1+{𝚤}_2}{2}\right)+\mathfrak{h}\left({𝚤}_2\right)\right]-\frac{1^{\varrho }}{2^{\varrho }{\Lambda }_{\varrho }\left(1\right)}\left({}_{{𝚤}_2^{-}}{}^{\vartheta }\mathcal{J}^{\left(\varrho \right)}\mathfrak{h}\left({𝚤}_1\right)+{}_{{𝚤}_1^{+}}{}^{\vartheta }\mathcal{J}^{\varrho }\mathfrak{h}\left({𝚤}_2\right)\right)\right|\hfill \\ \hfill =& \left|\frac{{\left({𝚤}_2-{𝚤}_1\right)}^{\varrho }}{6^{\varrho }{\Lambda }_{\varrho }\left(1\right)}\left(\frac{3^{\varrho }}{\Gamma \left(1+\varrho \right)}\stackrel{{\displaystyle \frac{1}{2}}}{\underset{0}{\int }}{\Lambda }_{\varrho }\left(t\right){\mathfrak{h}}^{\left(\varrho \right)}\left(\left(1-t\right){𝚤}_1+t{𝚤}_2\right){\left(dt\right)}^{\varrho }\right.\right.+\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{{\displaystyle \frac{1}{2}}}{\int }}\left({\Lambda }_{\varrho }\left(t\right)-2^{\varrho }{\Omega }_{\varrho }\left(t\right)\right){\mathfrak{h}}^{\left(\varrho \right)}\left(\left(1-t\right){𝚤}_1+t{𝚤}_2\right){\left(dt\right)}^{\varrho }\hfill \\ \hfill & -\frac{3^{\varrho }}{\Gamma \left(1+\varrho \right)}\stackrel{{\displaystyle \frac{1}{2}}}{\underset{0}{\int }}{\Lambda }_{\varrho }\left(t\right){\mathfrak{h}}^{\left(\varrho \right)}\left(t{𝚤}_1+\left(1-t\right){𝚤}_2\right){\left(dt\right)}^{\varrho }-\left.\left.\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{{\displaystyle \frac{1}{2}}}{\int }}\left({\Lambda }_{\varrho }\left(t\right)-2^{\varrho }{\Omega }_{\varrho }\left(t\right)\right){\mathfrak{h}}^{\left(\varrho \right)}\left(t{𝚤}_1+\left(1-t\right){𝚤}_2\right){\left(dt\right)}^{\varrho }\right)\right|\hfill \\ \hfill =& \left|\frac{{\left({𝚤}_2-{𝚤}_1\right)}^{\varrho }}{{12}^{\varrho }{\Lambda }_{\varrho }\left(1\right)}\left(\frac{3^{\varrho }}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{0}{\int }}{\Lambda }_{\varrho }\left(\frac{\nu }{2}\right){\mathfrak{h}}^{\left(\varrho \right)}\left(\left(1-\nu \right){𝚤}_1+\nu \frac{{𝚤}_1+{𝚤}_2}{2}\right){\left(d\nu \right)}^{\varrho }\right.\right.\hfill \\ \hfill & +\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{0}{\int }}\left({\Lambda }_{\varrho }\left(1-\frac{\nu }{2}\right)-2^{\varrho }{\Omega }_{\varrho }\left(1-\frac{\nu }{2}\right)\right){\mathfrak{h}}^{\left(\varrho \right)}\left(\nu \frac{{𝚤}_1+{𝚤}_2}{2}+\left(1-\nu \right){𝚤}_2\right){\left(d\nu \right)}^{\varrho }\hfill \\ \hfill & -\frac{3^{\varrho }}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{0}{\int }}{\Lambda }_{\varrho }\left(\frac{\nu }{2}\right){\mathfrak{h}}^{\left(\varrho \right)}\left(\nu \frac{{𝚤}_1+{𝚤}_2}{2}+\left(1-\nu \right){𝚤}_2\right){\left(d\nu \right)}^{\varrho }\hfill \\ \hfill & -\left.\left.\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{0}{\int }}\left({\Lambda }_{\varrho }\left(1-\frac{\nu }{2}\right)-2^{\varrho }{\Omega }_{\varrho }\left(1-\frac{\nu }{2}\right)\right){\mathfrak{h}}^{\left(\varrho \right)}\left(\left(1-\nu \right){𝚤}_1+\nu \frac{{𝚤}_1+{𝚤}_2}{2}\right){\left(d\nu \right)}^{\varrho }\right)\right|\hfill \\ \hfill =& \left|\frac{{\left({𝚤}_2-{𝚤}_1\right)}^{\varrho }}{{12}^{\varrho }{\Lambda }_{\varrho }\left(1\right)}\left(\frac{1^{\varrho }}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{0}{\int }}\left(3^{\varrho }{\Lambda }_{\varrho }\left(\frac{\nu }{2}\right)-{\Lambda }_{\varrho }\left(1-\frac{\nu }{2}\right)+2^{\varrho }{\Omega }_{\varrho }\left(1-\frac{\nu }{2}\right)\right){\mathfrak{h}}^{\left(\varrho \right)}\left(\left(1-\nu \right){𝚤}_1+\nu \frac{{𝚤}_1+{𝚤}_2}{2}\right){\left(d\nu \right)}^{\varrho }\right.\right.\hfill \\ \hfill & +\left.\left.\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{0}{\int }}\left({\Lambda }_{\varrho }\left(1-\frac{\nu }{2}\right)-2^{\varrho }{\Omega }_{\varrho }\left(1-\frac{\nu }{2}\right)-3^{\varrho }{\Lambda }_{\varrho }\left(\frac{\nu }{2}\right)\right){\mathfrak{h}}^{\left(\varrho \right)}\left(\nu \frac{{𝚤}_1+{𝚤}_2}{2}+\left(1-\nu \right){𝚤}_2\right){\left(d\nu \right)}^{\varrho }\right)\right|\hfill \\ \hfill \le & \frac{{\left({𝚤}_2-{𝚤}_1\right)}^{\varrho }}{{12}^{\varrho }{\Lambda }_{\varrho }\left(1\right)}\left(\frac{1^{\varrho }}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{0}{\int }}\left|3^{\varrho }{\Lambda }_{\varrho }\left(\frac{\nu }{2}\right)-{\Lambda }_{\varrho }\left(1-\frac{\nu }{2}\right)+2^{\varrho }{\Omega }_{\varrho }\left(1-\frac{\nu }{2}\right)\right|\left|{\mathfrak{h}}^{\left(\varrho \right)}\left(\left(1-\nu \right){𝚤}_1+\nu \frac{{𝚤}_1+{𝚤}_2}{2}\right)\right|{\left(d\nu \right)}^{\varrho }\right.\hfill \\ \hfill & +\left.\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{0}{\int }}\left|3^{\varrho }{\Lambda }_{\varrho }\left(\frac{\nu }{2}\right)-{\Lambda }_{\varrho }\left(1-\frac{\nu }{2}\right)+2^{\varrho }{\Omega }_{\varrho }\left(1-\frac{\nu }{2}\right)\right|\left|{\mathfrak{h}}^{\left(\varrho \right)}\left(\nu \frac{{𝚤}_1+{𝚤}_2}{2}+\left(1-\nu \right){𝚤}_2\right)\right|{\left(d\nu \right)}^{\varrho }\right)\hfill \\ \hfill \le & \frac{{\left({𝚤}_2-{𝚤}_1\right)}^{\varrho }}{{12}^{\varrho }{\Lambda }_{\varrho }\left(1\right)}\left(\frac{1^{\varrho }}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{0}{\int }}\left|3^{\varrho }{\Lambda }_{\varrho }\left(\frac{\nu }{2}\right)-{\Lambda }_{\varrho }\left(1-\frac{\nu }{2}\right)+2^{\varrho }{\Omega }_{\varrho }\left(1-\frac{\nu }{2}\right)\right|\left({\left(1-\nu \right)}^{s\varrho }\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_1\right)\right|+{\nu }^{s\varrho }\left|{\mathfrak{h}}^{\left(\varrho \right)}\left(\frac{{𝚤}_1+{𝚤}_2}{2}\right)\right|\right){\left(d\nu \right)}^{\varrho }\right.\hfill \\ \hfill & +\left.\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{0}{\int }}\left|3^{\varrho }{\Lambda }_{\varrho }\left(\frac{\nu }{2}\right)-{\Lambda }_{\varrho }\left(1-\frac{\nu }{2}\right)+2^{\varrho }{\Omega }_{\varrho }\left(1-\frac{\nu }{2}\right)\right|\left({\nu }^{s\varrho }\left|{\mathfrak{h}}^{\left(\varrho \right)}\left(\frac{{𝚤}_1+{𝚤}_2}{2}\right)\right|+{\left(1-\nu \right)}^{s\varrho }\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_2\right)\right|\right){\left(d\nu \right)}^{\varrho }\right)\hfill \\ \hfill =& \frac{{\left({𝚤}_2-{𝚤}_1\right)}^{\varrho }}{{12}^{\varrho }{\Lambda }_{\varrho }\left(1\right)}\left(\left[\frac{1^{\varrho }}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{0}{\int }}\left|3^{\varrho }{\Lambda }_{\varrho }\left(\frac{\nu }{2}\right)-{\Lambda }_{\varrho }\left(1-\frac{\nu }{2}\right)+2^{\varrho }{\Omega }_{\varrho }\left(1-\frac{\nu }{2}\right)\right|{\left(1-\nu \right)}^{s\varrho }{\left(d\nu \right)}^{\varrho }\right]\left(\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_1\right)\right|+\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_1\right)\right|\right)\right.\hfill \\ \hfill & +\left.\left[\frac{2^{\varrho }}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{0}{\int }}\left|3^{\varrho }{\Lambda }_{\varrho }\left(\frac{\nu }{2}\right)-{\Lambda }_{\varrho }\left(1-\frac{\nu }{2}\right)+2^{\varrho }{\Omega }_{\varrho }\left(1-\frac{\nu }{2}\right)\right|{\nu }^{s\varrho }{\left(d\nu \right)}^{\varrho }\right]\left|{\mathfrak{h}}^{\left(\varrho \right)}\left(\frac{{𝚤}_1+{𝚤}_2}{2}\right)\right|\right)\hfill \\ \hfill =& \frac{{\left({𝚤}_2-{𝚤}_1\right)}^{\varrho }}{{12}^{\varrho }{\Lambda }_{\varrho }\left(1\right)}\left[\left(\frac{2^{\varrho }}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{0}{\int }}\left(\left|2^{\varrho }{\Lambda }_{\varrho }\left(1\right)-3^{\varrho }{\Lambda }_{\varrho }\left(1-\frac{\nu }{2}\right)+3^{\varrho }{\Lambda }_{\varrho }\left(\frac{\nu }{2}\right)\right|\right){\nu }^{s\varrho }{\left(d\nu \right)}^{\varrho }\right)\left|{\mathfrak{h}}^{\left(\varrho \right)}\left(\frac{{𝚤}_1+{𝚤}_2}{2}\right)\right|\right.\hfill \\ \hfill & +\left.\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{0}{\int }}\left(\left|2^{\varrho }{\Lambda }_{\varrho }\left(1\right)-3^{\varrho }{\Lambda }_{\varrho }\left(1-\frac{\nu }{2}\right)+3^{\varrho }{\Lambda }_{\varrho }\left(\frac{\nu }{2}\right)\right|\right){\left(1-\nu \right)}^{s\varrho }{\left(d\nu \right)}^{\varrho }\right)\left(\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_1\right)\right|+\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_2\right)\right|\right)\right]\hfill \\ \hfill =& \frac{{\left({𝚤}_2-{𝚤}_1\right)}^{\varrho }}{{12}^{\varrho }{\Lambda }_{\varrho }\left(1\right)}\left[D_1\left(\varrho ,s\right)\left(\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_1\right)\right|+\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_2\right)\right|\right)+D_2\left(\varrho ,s\right)\left|{\mathfrak{h}}^{\left(\varrho \right)}\left(\frac{{𝚤}_1+{𝚤}_2}{2}\right)\right|\right],\hfill \end{array}$$

where $D_1$ and $D_2$ are defined as in (15) and (16), respectively. □

Corollary 5.

By setting $\varrho =1$ and $\vartheta =t$ in Theorem 6, we obtain

$$\begin{array}{cc}\hfill & \left|\frac{1}{6}\left[\mathfrak{h}\left({𝚤}_1\right)+4\mathfrak{h}\left(\frac{{𝚤}_1+{𝚤}_2}{2}\right)+\mathfrak{h}\left({𝚤}_2\right)\right]-\frac{1}{{𝚤}_2-{𝚤}_1}\underset{{𝚤}_1}{\stackrel{{𝚤}_2}{\int }}\mathfrak{h}\left(t\right)dt\right|\hfill \\ \hfill \le & \frac{{𝚤}_2-{𝚤}_1}{12}\left(\frac{2^{s+3}+3^{s+1}\left(s-1\right)}{3^{s+1}\left(s+1\right)\left(s+2\right)}\left(\left|{\mathfrak{h}}^{\prime }\left({𝚤}_1\right)\right|+\left|{\mathfrak{h}}^{\prime }\left({𝚤}_2\right)\right|\right)\right.\hfill \\ \hfill & +\left.2\left(\frac{2+3^{s+1}\left(2s+1\right)}{3^{s+1}\left(s+1\right)\left(s+2\right)}\right)\left|{\mathfrak{h}}^{\prime }\left(\frac{{𝚤}_1+{𝚤}_2}{2}\right)\right|\right).\hfill \end{array}$$

Furthermore, using the convexity of $\left|{\mathfrak{h}}^{\prime }\right|$$\left(\mathrm{i}.\mathrm{e}.,\left|{\mathfrak{h}}^{\prime }\left(\frac{{𝚤}_1+{𝚤}_2}{2}\right)\right|\le \frac{\left|{\mathfrak{h}}^{\prime }\left({𝚤}_1\right)\right|+\left|{\mathfrak{h}}^{\prime }\left({𝚤}_2\right)\right|}{2^{1-s}(s+1)}\right)$, we obtain

$$\begin{array}{cc}\hfill & \left|\frac{1}{6}\left[\mathfrak{h}\left({𝚤}_1\right)+4\mathfrak{h}\left(\frac{{𝚤}_1+{𝚤}_2}{2}\right)+\mathfrak{h}\left({𝚤}_2\right)\right]-\frac{1}{{𝚤}_2-{𝚤}_1}\underset{{𝚤}_1}{\stackrel{{𝚤}_2}{\int }}\mathfrak{h}\left(t\right)dt\right|\hfill \\ \hfill \le & \frac{{𝚤}_2-{𝚤}_1}{12}\left(\frac{\left(2^{s+3}+3^{s+1}(s-1)\right)(s+1)+2^{s+1}+3^{s+1}\left(2^s(2s+1)\right)}{3^{s+1}{\left(s+1\right)}^2\left(s+2\right)}\left(\left|{\mathfrak{h}}^{\prime }\left({𝚤}_1\right)\right|+\left|{\mathfrak{h}}^{\prime }\left({𝚤}_2\right)\right|\right)\right).\hfill \end{array}$$

Moreover, by setting $s=1$, we obtain

$$\begin{array}{cc}\hfill & \left|\frac{1}{6}\left[\mathfrak{h}\left({𝚤}_1\right)+4\mathfrak{h}\left(\frac{{𝚤}_1+{𝚤}_2}{2}\right)+\mathfrak{h}\left({𝚤}_2\right)\right]-\frac{1}{{𝚤}_2-{𝚤}_1}\underset{{𝚤}_1}{\stackrel{{𝚤}_2}{\int }}\mathfrak{h}\left(t\right)dt\right|\hfill \\ \hfill \le & \frac{5\left({𝚤}_2-{𝚤}_1\right)}{72}\left(\left|{\mathfrak{h}}^{\prime }\left({𝚤}_1\right)\right|+\left|{\mathfrak{h}}^{\prime }\left({𝚤}_2\right)\right|\right),\hfill \end{array}$$

which coincides with Corollary 1 obtained by Sarikaya et al. in [6].

Remark 6.

In contrast to Corollary 4, the result in Corollary 5 is a refinement of the one presented in Theorem 3 by Sarikaya et al. in [6], for $s\in (0,1)$.

Indeed, if we denote by

$$\mathrm{\Pi }\left(s\right)=\frac{\left(2^{s+3}+3^{s+1}(s-1)\right)(s+1)+2^{s+1}+3^{s+1}\left(2^s(2s+1)\right)}{4\times 3^{s+2}{\left(s+1\right)}^2\left(s+2\right)},$$

the coefficients of $({𝚤}_2-{𝚤}_1)\left(\left|{\mathfrak{h}}^{\prime }\left({𝚤}_1\right)\right|+\left|{\mathfrak{h}}^{\prime }\left({𝚤}_2\right)\right|\right)$ in the second inequality of Corollary 5. From the representation in Figure 2, it can be seen that the estimate in Corollary 5 is more accurate and finer compared to those in Theorem 3 and Corollary 4.

4. Further Results

Theorem 7.

Let $\mathfrak{h}:\mathcal{D}\to {\mathbb{R}}^{\varrho }$ be a function such that $\mathfrak{h}\in D_{\varrho }\left({\mathcal{D}}^{\circ }\right)$, ${𝚤}_1,{𝚤}_2\in {\mathcal{D}}^{\circ }$ with ${𝚤}_1<{𝚤}_2$, and ${\mathfrak{h}}^{\left(\varrho \right)}\in C_{\varrho }\left[{𝚤}_1,{𝚤}_2\right]$. If ${\left|{\mathfrak{h}}^{\left(\varrho \right)}\right|}^q$ is generalized s-convex on $\left[{𝚤}_1,{𝚤}_2\right]$, where $q>1$ with ${\displaystyle \frac{1}{p}}+{\displaystyle \frac{1}{q}}=1$; then, we have

$$\begin{array}{cc}\hfill & \left|\frac{1^{\varrho }}{6^{\varrho }}\left[\mathfrak{h}\left({𝚤}_1\right)+4^{\varrho }\mathfrak{h}\left(\frac{{𝚤}_1+{𝚤}_2}{2}\right)+\mathfrak{h}\left({𝚤}_2\right)\right]-\frac{1^{\varrho }}{2^{\varrho }{\Lambda }_{\varrho }\left(1\right)}\left({}_{{𝚤}_2^{-}}{}^{\vartheta }\mathcal{J}^{\left(\varrho \right)}\mathfrak{h}\left({𝚤}_1\right)+{}_{{𝚤}_1^{+}}{}^{\vartheta }\mathcal{J}^{\varrho }\mathfrak{h}\left({𝚤}_2\right)\right)\right|\hfill \\ \hfill \le & \frac{{\left({𝚤}_2-{𝚤}_1\right)}^{\varrho }}{{12}^{\varrho }{\Lambda }_{\varrho }\left(1\right)}\left[\left({\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{{\displaystyle \frac{1}{2}}}{\int }}{\left(t-\frac{1}{2}\right)}^{\varrho }{\left|2^{\varrho }{\Lambda }_{\varrho }\left(1\right)-3^{\varrho }{\Lambda }_{\varrho }\left(t\right)\right|}^p{\left(dt\right)}^{\varrho }\right)}^{{\displaystyle \frac{1}{p}}}\right.+3^{\varrho }{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{{\displaystyle \frac{1}{2}}}{\underset{0}{\int }}{\left(\frac{1}{2}-t\right)}^{\varrho }{\left|{\Lambda }_{\varrho }\left(t\right)\right|}^p{\left(dt\right)}^{\varrho }\right)}^{{\displaystyle \frac{1}{p}}}\right)\hfill \\ \hfill & \times \left({\left(L_1\left(\varrho ,s\right){\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_1\right)\right|}^q+L_2\left(\varrho ,s\right){\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_2\right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}+{\left(L_2\left(\varrho ,s\right){\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_1\right)\right|}^q+L_1\left(\varrho ,s\right){\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_2\right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}\right)\hfill \\ \hfill & +\left({\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{{\displaystyle \frac{1}{2}}}{\int }}{\left(1-t\right)}^{\varrho }{\left|2^{\varrho }{\Lambda }_{\varrho }\left(1\right)-3^{\varrho }{\Lambda }_{\varrho }\left(t\right)\right|}^p{\left(dt\right)}^{\varrho }\right)}^{{\displaystyle \frac{1}{p}}}+3^{\varrho }{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{{\displaystyle \frac{1}{2}}}{\underset{0}{\int }}{t}^{\varrho }{\left|{\Lambda }_{\varrho }\left(t\right)\right|}^p{\left(dt\right)}^{\varrho }\right)}^{{\displaystyle \frac{1}{p}}}\right)\hfill \\ \hfill & \times \left.\left({\left(L_3\left(\varrho ,s\right){\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_1\right)\right|}^q+L_4\left(\varrho ,s\right){\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_2\right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}+{\left(L_4\left(\varrho ,s\right){\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_1\right)\right|}^q+L_3\left(\varrho ,s\right){\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_2\right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}\right)\right],\hfill \end{array}$$

where $L_i$$(i=1,2,3,4)$ are defined as in (17)–(20), respectively.

Proof. 

From Lemma 8, the properties of the modulus, the improved generalized Hölder’s inequality, and the generalized s-convexity of ${\left|{\mathfrak{h}}^{\left(\varrho \right)}\right|}^q$, we have

$$\begin{array}{cc}\hfill & \left|\frac{1^{\varrho }}{6^{\varrho }}\left[\mathfrak{h}\left({𝚤}_1\right)+4^{\varrho }\mathfrak{h}\left(\frac{{𝚤}_1+{𝚤}_2}{2}\right)+\mathfrak{h}\left({𝚤}_2\right)\right]-\frac{1^{\varrho }}{2^{\varrho }{\Lambda }_{\varrho }\left(1\right)}\left({}_{{𝚤}_2^{-}}{}^{\vartheta }\mathcal{J}^{\left(\varrho \right)}\mathfrak{h}\left({𝚤}_1\right)+{}_{{𝚤}_1^{+}}{}^{\vartheta }\mathcal{J}^{\varrho }\mathfrak{h}\left({𝚤}_2\right)\right)\right|\hfill \\ \hfill \le & \frac{{\left({𝚤}_2-{𝚤}_1\right)}^{\varrho }}{{12}^{\varrho }{\Lambda }_{\varrho }\left(1\right)}\left[3^{\varrho }{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{{\displaystyle \frac{1}{2}}}{\underset{0}{\int }}{\left(\frac{1}{2}-t\right)}^{\varrho }{\left|{\Lambda }_{\varrho }\left(t\right)\right|}^p{\left(dt\right)}^{\varrho }\right)}^{{\displaystyle \frac{1}{p}}}\right.{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{{\displaystyle \frac{1}{2}}}{\underset{0}{\int }}{\left(\frac{1}{2}-t\right)}^{\varrho }{\left|{\mathfrak{h}}^{\left(\varrho \right)}\left(\left(1-t\right){𝚤}_1+t{𝚤}_2\right)\right|}^q{\left(dt\right)}^{\varrho }\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +3^{\varrho }{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{{\displaystyle \frac{1}{2}}}{\underset{0}{\int }}{t}^{\varrho }{\left|{\Lambda }_{\varrho }\left(t\right)\right|}^p{\left(dt\right)}^{\varrho }\right)}^{{\displaystyle \frac{1}{p}}}{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{{\displaystyle \frac{1}{2}}}{\underset{0}{\int }}{t}^{\varrho }{\left|{\mathfrak{h}}^{\left(\varrho \right)}\left(\left(1-t\right){𝚤}_1+t{𝚤}_2\right)\right|}^q{\left(dt\right)}^{\varrho }\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{{\displaystyle \frac{1}{2}}}{\int }}{\left(1-t\right)}^{\varrho }{\left|{\Lambda }_{\varrho }\left(t\right)-2^{\varrho }{\Omega }_{\varrho }\left(t\right)\right|}^p{\left(dt\right)}^{\varrho }\right)}^{{\displaystyle \frac{1}{p}}}{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{{\displaystyle \frac{1}{2}}}{\int }}{\left(1-t\right)}^{\varrho }{\left|{\mathfrak{h}}^{\left(\varrho \right)}\left(\left(1-t\right){𝚤}_1+t{𝚤}_2\right)\right|}^q{\left(dt\right)}^{\varrho }\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{{\displaystyle \frac{1}{2}}}{\int }}{\left(t-\frac{1}{2}\right)}^{\varrho }{\left|{\Lambda }_{\varrho }\left(t\right)-2^{\varrho }{\Omega }_{\varrho }\left(t\right)\right|}^p{\left(dt\right)}^{\varrho }\right)}^{{\displaystyle \frac{1}{p}}}{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{{\displaystyle \frac{1}{2}}}{\int }}{\left(t-\frac{1}{2}\right)}^{\varrho }{\left|{\mathfrak{h}}^{\left(\varrho \right)}\left(\left(1-t\right){𝚤}_1+t{𝚤}_2\right)\right|}^q{\left(dt\right)}^{\varrho }\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +3^{\varrho }{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{{\displaystyle \frac{1}{2}}}{\underset{0}{\int }}{\left(\frac{1}{2}-t\right)}^{\varrho }{\left|{\Lambda }_{\varrho }\left(t\right)\right|}^p{\left(dt\right)}^{\varrho }\right)}^{{\displaystyle \frac{1}{p}}}{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{{\displaystyle \frac{1}{2}}}{\underset{0}{\int }}{\left(\frac{1}{2}-t\right)}^{\varrho }{\left|{\mathfrak{h}}^{\left(\varrho \right)}\left(t{𝚤}_1+\left(1-t\right){𝚤}_2\right)\right|}^q{\left(dt\right)}^{\varrho }\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +3^{\varrho }{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{{\displaystyle \frac{1}{2}}}{\underset{0}{\int }}{t}^{\varrho }{\left|{\Lambda }_{\varrho }\left(t\right)\right|}^p{\left(dt\right)}^{\varrho }\right)}^{{\displaystyle \frac{1}{p}}}{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{{\displaystyle \frac{1}{2}}}{\underset{0}{\int }}{t}^{\varrho }{\left|{\mathfrak{h}}^{\left(\varrho \right)}\left(t{𝚤}_1+\left(1-t\right){𝚤}_2\right)\right|}^q{\left(dt\right)}^{\varrho }\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{{\displaystyle \frac{1}{2}}}{\int }}{\left(1-t\right)}^{\varrho }{\left|{\Lambda }_{\varrho }\left(t\right)-2^{\varrho }{\Omega }_{\varrho }\left(t\right)\right|}^p{\left(dt\right)}^{\varrho }\right)}^{{\displaystyle \frac{1}{p}}}{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{{\displaystyle \frac{1}{2}}}{\int }}{\left(1-t\right)}^{\varrho }{\left|{\mathfrak{h}}^{\left(\varrho \right)}\left(t{𝚤}_1+\left(1-t\right){𝚤}_2\right)\right|}^q{\left(dt\right)}^{\varrho }\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{{\displaystyle \frac{1}{2}}}{\int }}{\left(t-\frac{1}{2}\right)}^{\varrho }{\left|{\Lambda }_{\varrho }\left(t\right)-2^{\varrho }{\Omega }_{\varrho }\left(t\right)\right|}^p{\left(dt\right)}^{\varrho }\right)}^{{\displaystyle \frac{1}{p}}}\left.{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{{\displaystyle \frac{1}{2}}}{\int }}{\left(t-\frac{1}{2}\right)}^{\varrho }{\left|{\mathfrak{h}}^{\left(\varrho \right)}\left(t{𝚤}_1+\left(1-t\right){𝚤}_2\right)\right|}^q{\left(dt\right)}^{\varrho }\right)}^{{\displaystyle \frac{1}{q}}}\right]\hfill \\ \hfill \le & \frac{{\left({𝚤}_2-{𝚤}_1\right)}^{\varrho }}{{12}^{\varrho }{\Lambda }_{\varrho }\left(1\right)}\left[3^{\varrho }{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{{\displaystyle \frac{1}{2}}}{\underset{0}{\int }}{\left(\frac{1}{2}-t\right)}^{\varrho }{\left|{\Lambda }_{\varrho }\left(t\right)\right|}^p{\left(dt\right)}^{\varrho }\right)}^{{\displaystyle \frac{1}{p}}}\right.{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{{\displaystyle \frac{1}{2}}}{\underset{0}{\int }}{\left(\frac{1}{2}-t\right)}^{\varrho }\left({\left(1-t\right)}^{s\varrho }{\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_1\right)\right|}^q+t^{s\varrho }{\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_2\right)\right|}^q\right){\left(dt\right)}^{\varrho }\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +3^{\varrho }{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{{\displaystyle \frac{1}{2}}}{\underset{0}{\int }}{t}^{\varrho }{\left|{\Lambda }_{\varrho }\left(t\right)\right|}^p{\left(dt\right)}^{\varrho }\right)}^{{\displaystyle \frac{1}{p}}}{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{{\displaystyle \frac{1}{2}}}{\underset{0}{\int }}{t}^{\varrho }\left({\left(1-t\right)}^{s\varrho }{\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_1\right)\right|}^q+t^{s\varrho }{\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_2\right)\right|}^q\right){\left(dt\right)}^{\varrho }\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{{\displaystyle \frac{1}{2}}}{\int }}{\left(1-t\right)}^{\varrho }{\left|{\Lambda }_{\varrho }\left(t\right)-2^{\varrho }{\Omega }_{\varrho }\left(t\right)\right|}^p{\left(dt\right)}^{\varrho }\right)}^{{\displaystyle \frac{1}{p}}}{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{{\displaystyle \frac{1}{2}}}{\int }}{\left(1-t\right)}^{\varrho }\left({\left(1-t\right)}^{s\varrho }{\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_1\right)\right|}^q+t^{s\varrho }{\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_2\right)\right|}^q\right){\left(dt\right)}^{\varrho }\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{{\displaystyle \frac{1}{2}}}{\int }}{\left(t-\frac{1}{2}\right)}^{\varrho }{\left|{\Lambda }_{\varrho }\left(t\right)-2^{\varrho }{\Omega }_{\varrho }\left(t\right)\right|}^p{\left(dt\right)}^{\varrho }\right)}^{{\displaystyle \frac{1}{p}}}{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{{\displaystyle \frac{1}{2}}}{\int }}{\left(t-\frac{1}{2}\right)}^{\varrho }\left({\left(1-t\right)}^{s\varrho }{\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_1\right)\right|}^q+t^{s\varrho }{\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_2\right)\right|}^q\right){\left(dt\right)}^{\varrho }\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +3^{\varrho }{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{{\displaystyle \frac{1}{2}}}{\underset{0}{\int }}{\left(\frac{1}{2}-t\right)}^{\varrho }{\left|{\Lambda }_{\varrho }\left(t\right)\right|}^p{\left(dt\right)}^{\varrho }\right)}^{{\displaystyle \frac{1}{p}}}{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{{\displaystyle \frac{1}{2}}}{\underset{0}{\int }}{\left(\frac{1}{2}-t\right)}^{\varrho }\left(t^{s\varrho }{\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_1\right)\right|}^q+{\left(1-t\right)}^{s\varrho }{\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_2\right)\right|}^q\right){\left(dt\right)}^{\varrho }\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +3^{\varrho }{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{{\displaystyle \frac{1}{2}}}{\underset{0}{\int }}{t}^{\varrho }{\left|{\Lambda }_{\varrho }\left(t\right)\right|}^p{\left(dt\right)}^{\varrho }\right)}^{{\displaystyle \frac{1}{p}}}{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{{\displaystyle \frac{1}{2}}}{\underset{0}{\int }}{t}^{\varrho }\left(t^{s\varrho }{\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_1\right)\right|}^q+{\left(1-t\right)}^{s\varrho }{\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_2\right)\right|}^q\right){\left(dt\right)}^{\varrho }\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{{\displaystyle \frac{1}{2}}}{\int }}{\left(1-t\right)}^{\varrho }{\left|{\Lambda }_{\varrho }\left(t\right)-2^{\varrho }{\Omega }_{\varrho }\left(t\right)\right|}^p{\left(dt\right)}^{\varrho }\right)}^{{\displaystyle \frac{1}{p}}}{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{{\displaystyle \frac{1}{2}}}{\int }}{\left(1-t\right)}^{\varrho }\left(t^{s\varrho }{\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_1\right)\right|}^q+{\left(1-t\right)}^{s\varrho }{\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_2\right)\right|}^q\right){\left(dt\right)}^{\varrho }\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{{\displaystyle \frac{1}{2}}}{\int }}{\left(t-\frac{1}{2}\right)}^{\varrho }{\left|{\Lambda }_{\varrho }\left(t\right)-2^{\varrho }{\Omega }_{\varrho }\left(t\right)\right|}^p{\left(dt\right)}^{\varrho }\right)}^{{\displaystyle \frac{1}{p}}}\left.{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{{\displaystyle \frac{1}{2}}}{\int }}{\left(t-\frac{1}{2}\right)}^{\varrho }\left(t^{s\varrho }{\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_1\right)\right|}^q+{\left(1-t\right)}^{s\varrho }{\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_2\right)\right|}^q\right){\left(dt\right)}^{\varrho }\right)}^{{\displaystyle \frac{1}{q}}}\right]\hfill \\ \hfill \le & \frac{{\left({𝚤}_2-{𝚤}_1\right)}^{\varrho }}{{12}^{\varrho }{\Lambda }_{\varrho }\left(1\right)}\left[3^{\varrho }{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{{\displaystyle \frac{1}{2}}}{\underset{0}{\int }}{\left(\frac{1}{2}-t\right)}^{\varrho }{\left|{\Lambda }_{\varrho }\left(t\right)\right|}^p{\left(dt\right)}^{\varrho }\right)}^{{\displaystyle \frac{1}{p}}}{\left(L_1\left(\varrho ,s\right){\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_1\right)\right|}^q+L_2\left(\varrho ,s\right){\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_2\right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}\right.\hfill \\ \hfill & +3^{\varrho }{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{{\displaystyle \frac{1}{2}}}{\underset{0}{\int }}{t}^{\varrho }{\left|{\Lambda }_{\varrho }\left(t\right)\right|}^p{\left(dt\right)}^{\varrho }\right)}^{{\displaystyle \frac{1}{p}}}{\left(L_3\left(\varrho ,s\right){\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_1\right)\right|}^q+L_4\left(\varrho ,s\right){\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_2\right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{{\displaystyle \frac{1}{2}}}{\int }}{\left(1-t\right)}^{\varrho }{\left|2^{\varrho }{\Lambda }_{\varrho }\left(1\right)-3^{\varrho }{\Lambda }_{\varrho }\left(t\right)\right|}^p{\left(dt\right)}^{\varrho }\right)}^{{\displaystyle \frac{1}{p}}}{\left(L_4\left(\varrho ,s\right){\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_1\right)\right|}^q+L_3\left(\varrho ,s\right){\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_2\right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{{\displaystyle \frac{1}{2}}}{\int }}{\left(t-\frac{1}{2}\right)}^{\varrho }{\left|2^{\varrho }{\Lambda }_{\varrho }\left(1\right)-3^{\varrho }{\Lambda }_{\varrho }\left(t\right)\right|}^p{\left(dt\right)}^{\varrho }\right)}^{{\displaystyle \frac{1}{p}}}{\left(L_2\left(\varrho ,s\right){\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_1\right)\right|}^q+L_1\left(\varrho ,s\right){\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_2\right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +3^{\varrho }{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{{\displaystyle \frac{1}{2}}}{\underset{0}{\int }}{\left(\frac{1}{2}-t\right)}^{\varrho }{\left|{\Lambda }_{\varrho }\left(t\right)\right|}^p{\left(dt\right)}^{\varrho }\right)}^{{\displaystyle \frac{1}{p}}}{\left(L_2\left(\varrho ,s\right){\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_1\right)\right|}^q+L_1\left(\varrho ,s\right){\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_2\right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +3^{\varrho }{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{{\displaystyle \frac{1}{2}}}{\underset{0}{\int }}{t}^{\varrho }{\left|{\Lambda }_{\varrho }\left(t\right)\right|}^p{\left(dt\right)}^{\varrho }\right)}^{{\displaystyle \frac{1}{p}}}{\left(L_4\left(\varrho ,s\right){\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_1\right)\right|}^q+L_3\left(\varrho ,s\right){\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_2\right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{{\displaystyle \frac{1}{2}}}{\int }}{\left(1-t\right)}^{\varrho }{\left|2^{\varrho }{\Lambda }_{\varrho }\left(1\right)3^{\varrho }{\Lambda }_{\varrho }\left(t\right)\right|}^p{\left(dt\right)}^{\varrho }\right)}^{{\displaystyle \frac{1}{p}}}{\left(L_3\left(\varrho ,s\right){\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_1\right)\right|}^q+L_4\left(\varrho ,s\right){\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_2\right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +\left.{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{{\displaystyle \frac{1}{2}}}{\int }}{\left(t-\frac{1}{2}\right)}^{\varrho }{\left|2^{\varrho }{\Lambda }_{\varrho }\left(1\right)-3^{\varrho }{\Lambda }_{\varrho }\left(t\right)\right|}^p{\left(dt\right)}^{\varrho }\right)}^{{\displaystyle \frac{1}{p}}}{\left(L_1\left(\varrho ,s\right){\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_1\right)\right|}^q+L_2\left(\varrho ,s\right){\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_2\right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}\right]\hfill \\ \hfill =& \frac{{\left({𝚤}_2-{𝚤}_1\right)}^{\varrho }}{{12}^{\varrho }{\Lambda }_{\varrho }\left(1\right)}\left[\left({\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{{\displaystyle \frac{1}{2}}}{\int }}{\left(t-\frac{1}{2}\right)}^{\varrho }{\left|2^{\varrho }{\Lambda }_{\varrho }\left(1\right)-3^{\varrho }{\Lambda }_{\varrho }\left(t\right)\right|}^p{\left(dt\right)}^{\varrho }\right)}^{{\displaystyle \frac{1}{p}}}\right.+3^{\varrho }{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{{\displaystyle \frac{1}{2}}}{\underset{0}{\int }}{\left(\frac{1}{2}-t\right)}^{\varrho }{\left|{\Lambda }_{\varrho }\left(t\right)\right|}^p{\left(dt\right)}^{\varrho }\right)}^{{\displaystyle \frac{1}{p}}}\right)\hfill \\ \hfill & \times \left({\left(L_1\left(\varrho ,s\right){\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_1\right)\right|}^q+L_2\left(\varrho ,s\right){\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_2\right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}+{\left(L_2\left(\varrho ,s\right){\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_1\right)\right|}^q+L_1\left(\varrho ,s\right){\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_2\right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}\right)\hfill \\ \hfill & +\left({\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{{\displaystyle \frac{1}{2}}}{\int }}{\left(1-t\right)}^{\varrho }{\left|2^{\varrho }{\Lambda }_{\varrho }\left(1\right)-3^{\varrho }{\Lambda }_{\varrho }\left(t\right)\right|}^p{\left(dt\right)}^{\varrho }\right)}^{{\displaystyle \frac{1}{p}}}+3^{\varrho }{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{{\displaystyle \frac{1}{2}}}{\underset{0}{\int }}{t}^{\varrho }{\left|{\Lambda }_{\varrho }\left(t\right)\right|}^p{\left(dt\right)}^{\varrho }\right)}^{{\displaystyle \frac{1}{p}}}\right)\hfill \\ \hfill & \times \left.\left({\left(L_3\left(\varrho ,s\right){\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_1\right)\right|}^q+L_4\left(\varrho ,s\right){\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_2\right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}+{\left(L_4\left(\varrho ,s\right){\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_1\right)\right|}^q+L_3\left(\varrho ,s\right){\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_2\right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}\right)\right],\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill L_1\left(\varrho ,s\right)=& \frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{{\displaystyle \frac{1}{2}}}{\underset{0}{\int }}{\left(\frac{1}{2}-t\right)}^{\varrho }{\left(1-t\right)}^{s\varrho }{\left(dt\right)}^{\varrho }=\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{{\displaystyle \frac{1}{2}}}{\int }}{\left(t-\frac{1}{2}\right)}^{\varrho }{t}^{s\varrho }{\left(dt\right)}^{\varrho }\hfill \\ \hfill =& \left(1^{\left(s+2\right)\varrho }-{\left(\frac{1}{2}\right)}^{\left(s+2\right)\varrho }\right)\frac{\Gamma \left(1+\left(s+1\right)\varrho \right)}{\Gamma \left(1+\left(s+2\right)\varrho \right)}-\left({\left(\frac{1}{2}\right)}^{\varrho }-{\left(\frac{1}{2}\right)}^{\left(s+2\right)\varrho }\right)\frac{\Gamma \left(1+s\varrho \right)}{\Gamma \left(1+\left(s+1\right)\varrho \right)},\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill L_2\left(\varrho ,s\right)=& \frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{{\displaystyle \frac{1}{2}}}{\underset{0}{\int }}{\left(\frac{1}{2}-t\right)}^{\varrho }{t}^{s\varrho }{\left(dt\right)}^{\varrho }=\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{{\displaystyle \frac{1}{2}}}{\int }}{\left(t-\frac{1}{2}\right)}^{\varrho }{\left(1-t\right)}^{s\varrho }{\left(dt\right)}^{\varrho }\hfill \\ \hfill =& {\left(\frac{1}{2}\right)}^{\left(s+2\right)\varrho }\left(\frac{\Gamma \left(1+s\varrho \right)}{\Gamma \left(1+\left(s+1\right)\varrho \right)}-\frac{\Gamma \left(1+\left(s+1\right)\varrho \right)}{\Gamma \left(1+\left(s+2\right)\varrho \right)}\right),\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill L_3\left(\varrho ,s\right)=& \frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{{\displaystyle \frac{1}{2}}}{\underset{0}{\int }}{t}^{\varrho }{\left(1-t\right)}^{s\varrho }{\left(dt\right)}^{\varrho }=\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{{\displaystyle \frac{1}{2}}}{\int }}{\left(1-t\right)}^{\varrho }{t}^{s\varrho }{\left(dt\right)}^{\varrho }\hfill \\ \hfill =& {\left(\frac{1}{2}\right)}^{2\varrho }\frac{\Gamma \left(1+\varrho \right)}{\Gamma \left(1+2\varrho \right)}-{\left(\frac{1}{2}\right)}^{\left(s+2\right)\varrho }\frac{\Gamma \left(1+\left(s+1\right)\varrho \right)}{\Gamma \left(1+\left(s+2\right)\varrho \right)}\hfill \end{array}$$

(19)

and

$$\begin{array}{cc}\hfill L_4\left(\varrho ,s\right)=& \frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{{\displaystyle \frac{1}{2}}}{\underset{0}{\int }}{t}^{\left(1+s\right)\varrho }{\left(dt\right)}^{\varrho }=\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{{\displaystyle \frac{1}{2}}}{\int }}{\left(1-t\right)}^{\left(1+s\right)\varrho }{\left(dt\right)}^{\varrho }={\left(\frac{1}{2}\right)}^{\left(s+2\right)\varrho }\frac{\Gamma \left(1+\left(s+1\right)\varrho \right)}{\Gamma \left(1+\left(s+2\right)\varrho \right)}.\hfill \end{array}$$

(20)

The proof is completed. □

Theorem 8.

Let $\mathfrak{h}:\mathcal{D}\to {\mathbb{R}}^{\varrho }$ be a function such that $\mathfrak{h}\in D_{\varrho }\left({\mathcal{D}}^{\circ }\right)$, ${𝚤}_1,{𝚤}_2\in {\mathcal{D}}^{\circ }$ with ${𝚤}_1<{𝚤}_2$, and ${\mathfrak{h}}^{\left(\varrho \right)}\in C_{\varrho }\left[{𝚤}_1,{𝚤}_2\right]$. If ${\left|{\mathfrak{h}}^{\left(\varrho \right)}\right|}^q$ is generalized s-convex on $\left[{𝚤}_1,{𝚤}_2\right]$, where $q\ge 1$; then, we have

$$\begin{array}{cc}\hfill & \left|\frac{1^{\varrho }}{6^{\varrho }}\left[\mathfrak{h}\left({𝚤}_1\right)+4^{\varrho }\mathfrak{h}\left(\frac{{𝚤}_1+{𝚤}_2}{2}\right)+\mathfrak{h}\left({𝚤}_2\right)\right]-\frac{1^{\varrho }}{2^{\varrho }{\Lambda }_{\varrho }\left(1\right)}\left({}_{{𝚤}_2^{-}}{}^{\vartheta }\mathcal{J}^{\left(\varrho \right)}\mathfrak{h}\left({𝚤}_1\right)+{}_{{𝚤}_1^{+}}{}^{\vartheta }\mathcal{J}^{\varrho }\mathfrak{h}\left({𝚤}_2\right)\right)\right|\hfill \\ \hfill \le & \frac{{\left({𝚤}_2-{𝚤}_1\right)}^{\varrho }}{{12}^{\varrho }{\Lambda }_{\varrho }\left(1\right)}\left(3^{\varrho }{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{{\displaystyle \frac{1}{2}}}{\underset{0}{\int }}{\left(\frac{1}{2}-t\right)}^{\varrho }\left|{\Lambda }_{\varrho }\left(t\right)\right|{\left(dt\right)}^{\varrho }\right)}^{1-{\displaystyle \frac{1}{q}}}\right.{\left({\eta }_1\left(\varrho ,s\right){\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_1\right)\right|}^q+{\eta }_2\left(\varrho ,s\right){\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_2\right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +3^{\varrho }{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{{\displaystyle \frac{1}{2}}}{\underset{0}{\int }}{t}^{\varrho }\left|{\Lambda }_{\varrho }\left(t\right)\right|{\left(dt\right)}^{\varrho }\right)}^{1-{\displaystyle \frac{1}{q}}}{\left({\eta }_3\left(\varrho ,s\right){\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_1\right)\right|}^q+{\eta }_4\left(\varrho ,s\right){\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_2\right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{{\displaystyle \frac{1}{2}}}{\int }}{\left(1-t\right)}^{\varrho }\left|2^{\varrho }{\Lambda }_{\varrho }\left(1\right)-3^{\varrho }{\Lambda }_{\varrho }\left(t\right)\right|{\left(dt\right)}^{\varrho }\right)}^{1-{\displaystyle \frac{1}{q}}}{\left({\eta }_5\left(\varrho ,s\right){\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_1\right)\right|}^q+{\eta }_6\left(\varrho ,s\right){\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_2\right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{{\displaystyle \frac{1}{2}}}{\int }}{\left(t-\frac{1}{2}\right)}^{\varrho }\left|2^{\varrho }{\Lambda }_{\varrho }\left(1\right)-3^{\varrho }{\Lambda }_{\varrho }\left(t\right)\right|{\left(dt\right)}^{\varrho }\right)}^{1-{\displaystyle \frac{1}{q}}}{\left({\eta }_7\left(\varrho ,s\right){\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_1\right)\right|}^q+{\eta }_8\left(\varrho ,s\right){\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_2\right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +3^{\varrho }{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{{\displaystyle \frac{1}{2}}}{\underset{0}{\int }}{\left(\frac{1}{2}-t\right)}^{\varrho }\left|{\Lambda }_{\varrho }\left(t\right)\right|{\left(dt\right)}^{\varrho }\right)}^{1-{\displaystyle \frac{1}{q}}}{\left({\eta }_2\left(\varrho ,s\right){\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_1\right)\right|}^q+{\eta }_1\left(\varrho ,s\right){\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_2\right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +3^{\varrho }{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{{\displaystyle \frac{1}{2}}}{\underset{0}{\int }}{t}^{\varrho }\left|{\Lambda }_{\varrho }\left(t\right)\right|{\left(dt\right)}^{\varrho }\right)}^{1-{\displaystyle \frac{1}{q}}}{\left({\eta }_4\left(\varrho ,s\right){\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_1\right)\right|}^q+{\eta }_3\left(\varrho ,s\right){\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_2\right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{{\displaystyle \frac{1}{2}}}{\int }}{\left(1-t\right)}^{\varrho }\left|2^{\varrho }{\Lambda }_{\varrho }\left(1\right)-3^{\varrho }{\Lambda }_{\varrho }\left(t\right)\right|{\left(dt\right)}^{\varrho }\right)}^{1-{\displaystyle \frac{1}{q}}}{\left({\eta }_6\left(\varrho ,s\right){\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_1\right)\right|}^q+{\eta }_5\left(\varrho ,s\right){\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_2\right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{{\displaystyle \frac{1}{2}}}{\int }}{\left(t-\frac{1}{2}\right)}^{\varrho }\left|2^{\varrho }{\Lambda }_{\varrho }\left(1\right)-3^{\varrho }{\Lambda }_{\varrho }\left(t\right)\right|{\left(dt\right)}^{\varrho }\right)}^{1-{\displaystyle \frac{1}{q}}}\left.{\left({\eta }_8\left(\varrho ,s\right){\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_1\right)\right|}^q+{\eta }_7\left(\varrho ,s\right){\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_2\right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}\right),\hfill \end{array}$$

where ${\eta }_i$, $(i=1,...,8)$ are given by (21)–(28), respectively.

Proof. 

From Lemma 8, the properties of the modulus, the improved generalized power mean inequality, and the generalized s-convexity of ${\left|{\mathfrak{h}}^{\left(\varrho \right)}\right|}^q$, we have

$$\begin{array}{cc}\hfill & \left|\frac{1^{\varrho }}{6^{\varrho }}\left[\mathfrak{h}\left({𝚤}_1\right)+4^{\varrho }\mathfrak{h}\left(\frac{{𝚤}_1+{𝚤}_2}{2}\right)+\mathfrak{h}\left({𝚤}_2\right)\right]-\frac{1^{\varrho }}{2^{\varrho }{\Lambda }_{\varrho }\left(1\right)}\left({}_{{𝚤}_2^{-}}{}^{\vartheta }\mathcal{J}^{\left(\varrho \right)}\mathfrak{h}\left({𝚤}_1\right)+{}_{{𝚤}_1^{+}}{}^{\vartheta }\mathcal{J}^{\varrho }\mathfrak{h}\left({𝚤}_2\right)\right)\right|\hfill \\ \hfill \le & \frac{{\left({𝚤}_2-{𝚤}_1\right)}^{\varrho }}{{12}^{\varrho }{\Lambda }_{\varrho }\left(1\right)}\left(3^{\varrho }{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{{\displaystyle \frac{1}{2}}}{\underset{0}{\int }}{\left(\frac{1}{2}-t\right)}^{\varrho }\left|{\Lambda }_{\varrho }\left(t\right)\right|{\left(dt\right)}^{\varrho }\right)}^{1-{\displaystyle \frac{1}{q}}}\right.{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{{\displaystyle \frac{1}{2}}}{\underset{0}{\int }}{\left(\frac{1}{2}-t\right)}^{\varrho }\left|{\Lambda }_{\varrho }\left(t\right)\right|{\left|{\mathfrak{h}}^{\left(\varrho \right)}\left(\left(1-t\right){𝚤}_1+t{𝚤}_2\right)\right|}^q{\left(dt\right)}^{\varrho }\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +3^{\varrho }{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{{\displaystyle \frac{1}{2}}}{\underset{0}{\int }}{t}^{\varrho }\left|{\Lambda }_{\varrho }\left(t\right)\right|{\left(dt\right)}^{\varrho }\right)}^{1-{\displaystyle \frac{1}{q}}}{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{{\displaystyle \frac{1}{2}}}{\underset{0}{\int }}{t}^{\varrho }\left|{\Lambda }_{\varrho }\left(t\right)\right|{\left|{\mathfrak{h}}^{\left(\varrho \right)}\left(\left(1-t\right){𝚤}_1+t{𝚤}_2\right)\right|}^q{\left(dt\right)}^{\varrho }\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{{\displaystyle \frac{1}{2}}}{\int }}{\left(1-t\right)}^{\varrho }\left|{\Lambda }_{\varrho }\left(t\right)-2^{\varrho }{\Omega }_{\varrho }\left(t\right)\right|{\left(dt\right)}^{\varrho }\right)}^{1-{\displaystyle \frac{1}{q}}}{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{{\displaystyle \frac{1}{2}}}{\int }}{\left(1-t\right)}^{\varrho }\left|{\Lambda }_{\varrho }\left(t\right)-2^{\varrho }{\Omega }_{\varrho }\left(t\right)\right|{\left|{\mathfrak{h}}^{\left(\varrho \right)}\left(\left(1-t\right){𝚤}_1+t{𝚤}_2\right)\right|}^q{\left(dt\right)}^{\varrho }\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{{\displaystyle \frac{1}{2}}}{\int }}{\left(t-\frac{1}{2}\right)}^{\varrho }\left|{\Lambda }_{\varrho }\left(t\right)-2^{\varrho }{\Omega }_{\varrho }\left(t\right)\right|{\left(dt\right)}^{\varrho }\right)}^{1-{\displaystyle \frac{1}{q}}}{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{{\displaystyle \frac{1}{2}}}{\int }}{\left(t-\frac{1}{2}\right)}^{\varrho }\left|{\Lambda }_{\varrho }\left(t\right)-2^{\varrho }{\Omega }_{\varrho }\left(t\right)\right|{\left|{\mathfrak{h}}^{\left(\varrho \right)}\left(\left(1-t\right){𝚤}_1+t{𝚤}_2\right)\right|}^q{\left(dt\right)}^{\varrho }\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +3^{\varrho }{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{{\displaystyle \frac{1}{2}}}{\underset{0}{\int }}{\left(\frac{1}{2}-t\right)}^{\varrho }\left|{\Lambda }_{\varrho }\left(t\right)\right|{\left(dt\right)}^{\varrho }\right)}^{1-{\displaystyle \frac{1}{q}}}{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{{\displaystyle \frac{1}{2}}}{\underset{0}{\int }}{\left(\frac{1}{2}-t\right)}^{\varrho }\left|{\Lambda }_{\varrho }\left(t\right)\right|{\left|{\mathfrak{h}}^{\left(\varrho \right)}\left(t{𝚤}_1+\left(1-t\right){𝚤}_2\right)\right|}^q{\left(dt\right)}^{\varrho }\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +3^{\varrho }{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{{\displaystyle \frac{1}{2}}}{\underset{0}{\int }}{t}^{\varrho }\left|{\Lambda }_{\varrho }\left(t\right)\right|{\left(dt\right)}^{\varrho }\right)}^{1-{\displaystyle \frac{1}{q}}}{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{{\displaystyle \frac{1}{2}}}{\underset{0}{\int }}{t}^{\varrho }\left|{\Lambda }_{\varrho }\left(t\right)\right|{\left|{\mathfrak{h}}^{\left(\varrho \right)}\left(t{𝚤}_1+\left(1-t\right){𝚤}_2\right)\right|}^q{\left(dt\right)}^{\varrho }\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{{\displaystyle \frac{1}{2}}}{\int }}{\left(1-t\right)}^{\varrho }\left|{\Lambda }_{\varrho }\left(t\right)-2^{\varrho }{\Omega }_{\varrho }\left(t\right)\right|{\left(dt\right)}^{\varrho }\right)}^{1-{\displaystyle \frac{1}{q}}}{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{{\displaystyle \frac{1}{2}}}{\int }}{\left(1-t\right)}^{\varrho }\left|{\Lambda }_{\varrho }\left(t\right)-2^{\varrho }{\Omega }_{\varrho }\left(t\right)\right|{\left|{\mathfrak{h}}^{\left(\varrho \right)}\left(t{𝚤}_1+\left(1-t\right){𝚤}_2\right)\right|}^q{\left(dt\right)}^{\varrho }\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{{\displaystyle \frac{1}{2}}}{\int }}{\left(t-\frac{1}{2}\right)}^{\varrho }\left|{\Lambda }_{\varrho }\left(t\right)-2^{\varrho }{\Omega }_{\varrho }\left(t\right)\right|{\left(dt\right)}^{\varrho }\right)}^{1-{\displaystyle \frac{1}{q}}}\left.{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{{\displaystyle \frac{1}{2}}}{\int }}{\left(t-\frac{1}{2}\right)}^{\varrho }\left|{\Lambda }_{\varrho }\left(t\right)-2^{\varrho }{\Omega }_{\varrho }\left(t\right)\right|{\left|{\mathfrak{h}}^{\left(\varrho \right)}\left(t{𝚤}_1+\left(1-t\right){𝚤}_2\right)\right|}^q{\left(dt\right)}^{\varrho }\right)}^{{\displaystyle \frac{1}{q}}}\right)\hfill \\ \hfill \le & \frac{{\left({𝚤}_2-{𝚤}_1\right)}^{\varrho }}{{12}^{\varrho }{\Lambda }_{\varrho }\left(1\right)}\left(3^{\varrho }{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{{\displaystyle \frac{1}{2}}}{\underset{0}{\int }}{\left(\frac{1}{2}-t\right)}^{\varrho }\left|{\Lambda }_{\varrho }\left(t\right)\right|{\left(dt\right)}^{\varrho }\right)}^{1-{\displaystyle \frac{1}{q}}}\right.{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{{\displaystyle \frac{1}{2}}}{\underset{0}{\int }}{\left(\frac{1}{2}-t\right)}^{\varrho }\left|{\Lambda }_{\varrho }\left(t\right)\right|\left({\left(1-t\right)}^{s\varrho }{\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_1\right)\right|}^q+t^{s\varrho }{\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_2\right)\right|}^q\right){\left(dt\right)}^{\varrho }\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +3^{\varrho }{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{{\displaystyle \frac{1}{2}}}{\underset{0}{\int }}{t}^{\varrho }\left|{\Lambda }_{\varrho }\left(t\right)\right|{\left(dt\right)}^{\varrho }\right)}^{1-{\displaystyle \frac{1}{q}}}{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{{\displaystyle \frac{1}{2}}}{\underset{0}{\int }}{t}^{\varrho }\left|{\Lambda }_{\varrho }\left(t\right)\right|\left({\left(1-t\right)}^{s\varrho }{\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_1\right)\right|}^q+t^{s\varrho }{\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_2\right)\right|}^q\right){\left(dt\right)}^{\varrho }\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{{\displaystyle \frac{1}{2}}}{\int }}{\left(1-t\right)}^{\varrho }\left|2^{\varrho }{\Lambda }_{\varrho }\left(1\right)-3^{\varrho }{\Lambda }_{\varrho }\left(t\right)\right|{\left(dt\right)}^{\varrho }\right)}^{1-{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & \times {\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{{\displaystyle \frac{1}{2}}}{\int }}{\left(1-t\right)}^{\varrho }\left|2^{\varrho }{\Lambda }_{\varrho }\left(1\right)-3^{\varrho }{\Lambda }_{\varrho }\left(t\right)\right|\left({\left(1-t\right)}^{s\varrho }{\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_1\right)\right|}^q+t^{s\varrho }{\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_2\right)\right|}^q\right){\left(dt\right)}^{\varrho }\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{{\displaystyle \frac{1}{2}}}{\int }}{\left(t-\frac{1}{2}\right)}^{\varrho }\left|2^{\varrho }{\Lambda }_{\varrho }\left(1\right)-3^{\varrho }{\Lambda }_{\varrho }\left(t\right)\right|{\left(dt\right)}^{\varrho }\right)}^{1-{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & \times {\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{{\displaystyle \frac{1}{2}}}{\int }}{\left(t-\frac{1}{2}\right)}^{\varrho }\left|2^{\varrho }{\Lambda }_{\varrho }\left(1\right)-3^{\varrho }{\Lambda }_{\varrho }\left(t\right)\right|\left({\left(1-t\right)}^{s\varrho }{\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_1\right)\right|}^q+t^{s\varrho }{\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_2\right)\right|}^q\right){\left(dt\right)}^{\varrho }\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +3^{\varrho }{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{{\displaystyle \frac{1}{2}}}{\underset{0}{\int }}{\left(\frac{1}{2}-t\right)}^{\varrho }\left|{\Lambda }_{\varrho }\left(t\right)\right|{\left(dt\right)}^{\varrho }\right)}^{1-{\displaystyle \frac{1}{q}}}{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{{\displaystyle \frac{1}{2}}}{\underset{0}{\int }}{\left(\frac{1}{2}-t\right)}^{\varrho }\left|{\Lambda }_{\varrho }\left(t\right)\right|\left(t^{s\varrho }{\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_1\right)\right|}^q+{\left(1-t\right)}^{s\varrho }{\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_2\right)\right|}^q\right){\left(dt\right)}^{\varrho }\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +3^{\varrho }{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{{\displaystyle \frac{1}{2}}}{\underset{0}{\int }}{t}^{\varrho }\left|{\Lambda }_{\varrho }\left(t\right)\right|{\left(dt\right)}^{\varrho }\right)}^{1-{\displaystyle \frac{1}{q}}}{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{{\displaystyle \frac{1}{2}}}{\underset{0}{\int }}{t}^{\varrho }\left|{\Lambda }_{\varrho }\left(t\right)\right|\left(t^{s\varrho }{\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_1\right)\right|}^q+{\left(1-t\right)}^{s\varrho }{\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_2\right)\right|}^q\right){\left(dt\right)}^{\varrho }\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{{\displaystyle \frac{1}{2}}}{\int }}{\left(1-t\right)}^{\varrho }\left|2^{\varrho }{\Lambda }_{\varrho }\left(1\right)-3^{\varrho }{\Lambda }_{\varrho }\left(t\right)\right|{\left(dt\right)}^{\varrho }\right)}^{1-{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & \times {\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{{\displaystyle \frac{1}{2}}}{\int }}{\left(1-t\right)}^{\varrho }\left|2^{\varrho }{\Lambda }_{\varrho }\left(1\right)-3^{\varrho }{\Lambda }_{\varrho }\left(t\right)\right|\left(t^{s\varrho }{\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_1\right)\right|}^q+{\left(1-t\right)}^{s\varrho }{\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_2\right)\right|}^q\right){\left(dt\right)}^{\varrho }\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{{\displaystyle \frac{1}{2}}}{\int }}{\left(t-\frac{1}{2}\right)}^{\varrho }\left|2^{\varrho }{\Lambda }_{\varrho }\left(1\right)-3^{\varrho }{\Lambda }_{\varrho }\left(t\right)\right|{\left(dt\right)}^{\varrho }\right)}^{1-{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & \times \left.{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{{\displaystyle \frac{1}{2}}}{\int }}{\left(t-\frac{1}{2}\right)}^{\varrho }\left|2^{\varrho }{\Lambda }_{\varrho }\left(1\right)-3^{\varrho }{\Lambda }_{\varrho }\left(t\right)\right|\left(t^{s\varrho }{\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_1\right)\right|}^q+{\left(1-t\right)}^{s\varrho }{\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_2\right)\right|}^q\right){\left(dt\right)}^{\varrho }\right)}^{{\displaystyle \frac{1}{q}}}\right).\hfill \end{array}$$

So, we have

$$\begin{array}{cc}\hfill & \left|\frac{1^{\varrho }}{6^{\varrho }}\left[\mathfrak{h}\left({𝚤}_1\right)+4^{\varrho }\mathfrak{h}\left(\frac{{𝚤}_1+{𝚤}_2}{2}\right)+\mathfrak{h}\left({𝚤}_2\right)\right]-\frac{1^{\varrho }}{2^{\varrho }{\Lambda }_{\varrho }\left(1\right)}\left({}_{{𝚤}_2^{-}}{}^{\vartheta }\mathcal{J}^{\left(\varrho \right)}\mathfrak{h}\left({𝚤}_1\right)+{}_{{𝚤}_1^{+}}{}^{\vartheta }\mathcal{J}^{\varrho }\mathfrak{h}\left({𝚤}_2\right)\right)\right|\hfill \\ \hfill \le & \frac{{\left({𝚤}_2-{𝚤}_1\right)}^{\varrho }}{{12}^{\varrho }{\Lambda }_{\varrho }\left(1\right)}\left(3^{\varrho }{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{{\displaystyle \frac{1}{2}}}{\underset{0}{\int }}{\left(\frac{1}{2}-t\right)}^{\varrho }\left|{\Lambda }_{\varrho }\left(t\right)\right|{\left(dt\right)}^{\varrho }\right)}^{1-{\displaystyle \frac{1}{q}}}\right.{\left({\eta }_1\left(\varrho ,s\right){\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_1\right)\right|}^q+{\eta }_2\left(\varrho ,s\right){\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_2\right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +3^{\varrho }{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{{\displaystyle \frac{1}{2}}}{\underset{0}{\int }}{t}^{\varrho }\left|{\Lambda }_{\varrho }\left(t\right)\right|{\left(dt\right)}^{\varrho }\right)}^{1-{\displaystyle \frac{1}{q}}}{\left({\eta }_3\left(\varrho ,s\right){\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_1\right)\right|}^q+{\eta }_4\left(\varrho ,s\right){\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_2\right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{{\displaystyle \frac{1}{2}}}{\int }}{\left(1-t\right)}^{\varrho }\left|2^{\varrho }{\Lambda }_{\varrho }\left(1\right)-3^{\varrho }{\Lambda }_{\varrho }\left(t\right)\right|{\left(dt\right)}^{\varrho }\right)}^{1-{\displaystyle \frac{1}{q}}}{\left({\eta }_5\left(\varrho ,s\right){\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_1\right)\right|}^q+{\eta }_6\left(\varrho ,s\right){\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_2\right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{{\displaystyle \frac{1}{2}}}{\int }}{\left(t-\frac{1}{2}\right)}^{\varrho }\left|2^{\varrho }{\Lambda }_{\varrho }\left(1\right)-3^{\varrho }{\Lambda }_{\varrho }\left(t\right)\right|{\left(dt\right)}^{\varrho }\right)}^{1-{\displaystyle \frac{1}{q}}}{\left({\eta }_7\left(\varrho ,s\right){\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_1\right)\right|}^q+{\eta }_8\left(\varrho ,s\right){\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_2\right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +3^{\varrho }{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{{\displaystyle \frac{1}{2}}}{\underset{0}{\int }}{\left(\frac{1}{2}-t\right)}^{\varrho }\left|{\Lambda }_{\varrho }\left(t\right)\right|{\left(dt\right)}^{\varrho }\right)}^{1-{\displaystyle \frac{1}{q}}}{\left({\eta }_2\left(\varrho ,s\right){\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_1\right)\right|}^q+{\eta }_1\left(\varrho ,s\right){\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_2\right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +3^{\varrho }{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{{\displaystyle \frac{1}{2}}}{\underset{0}{\int }}{t}^{\varrho }\left|{\Lambda }_{\varrho }\left(t\right)\right|{\left(dt\right)}^{\varrho }\right)}^{1-{\displaystyle \frac{1}{q}}}{\left({\eta }_4\left(\varrho ,s\right){\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_1\right)\right|}^q+{\eta }_3\left(\varrho ,s\right){\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_2\right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{{\displaystyle \frac{1}{2}}}{\int }}{\left(1-t\right)}^{\varrho }\left|2^{\varrho }{\Lambda }_{\varrho }\left(1\right)-3^{\varrho }{\Lambda }_{\varrho }\left(t\right)\right|{\left(dt\right)}^{\varrho }\right)}^{1-{\displaystyle \frac{1}{q}}}{\left({\eta }_6\left(\varrho ,s\right){\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_1\right)\right|}^q+{\eta }_5\left(\varrho ,s\right){\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_2\right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +{\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{{\displaystyle \frac{1}{2}}}{\int }}{\left(t-\frac{1}{2}\right)}^{\varrho }\left|2^{\varrho }{\Lambda }_{\varrho }\left(1\right)-3^{\varrho }{\Lambda }_{\varrho }\left(t\right)\right|{\left(dt\right)}^{\varrho }\right)}^{1-{\displaystyle \frac{1}{q}}}\left.{\left({\eta }_8\left(\varrho ,s\right){\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_1\right)\right|}^q+{\eta }_7\left(\varrho ,s\right){\left|{\mathfrak{h}}^{\left(\varrho \right)}\left({𝚤}_2\right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}\right),\hfill \end{array}$$

where we have used

$${\eta }_1\left(\varrho ,s\right)=\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{{\displaystyle \frac{1}{2}}}{\underset{0}{\int }}{\left(\frac{1}{2}-t\right)}^{\varrho }\left|{\Lambda }_{\varrho }\left(t\right)\right|{\left(1-t\right)}^{s\varrho }{\left(dt\right)}^{\varrho },$$

(21)

$${\eta }_2\left(\varrho ,s\right)=\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{{\displaystyle \frac{1}{2}}}{\underset{0}{\int }}{\left(\frac{1}{2}-t\right)}^{\varrho }\left|{\Lambda }_{\varrho }\left(t\right)\right|t^{s\varrho }{\left(dt\right)}^{\varrho },$$

(22)

$${\eta }_3\left(\varrho ,s\right)=\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{{\displaystyle \frac{1}{2}}}{\underset{0}{\int }}{t}^{\varrho }\left|{\Lambda }_{\varrho }\left(t\right)\right|{\left(1-t\right)}^{s\varrho }{\left(dt\right)}^{\varrho },$$

(23)

$${\eta }_4\left(\varrho ,s\right)=\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{{\displaystyle \frac{1}{2}}}{\underset{0}{\int }}\left|{\Lambda }_1\left(t\right)\right|t^{\left(1+s\right)\varrho }{\left(dt\right)}^{\varrho },$$

(24)

$${\eta }_5\left(\varrho ,s\right)=\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{{\displaystyle \frac{1}{2}}}{\int }}\left|2^{\varrho }{\Lambda }_{\varrho }\left(1\right)-3^{\varrho }{\Lambda }_{\varrho }\left(t\right)\right|{\left(1-t\right)}^{\left(1+s\right)\varrho }{\left(dt\right)}^{\varrho },$$

(25)

$${\eta }_6\left(\varrho ,s\right)=\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{{\displaystyle \frac{1}{2}}}{\int }}{\left(1-t\right)}^{\varrho }\left|2^{\varrho }{\Lambda }_{\varrho }\left(1\right)-3^{\varrho }{\Lambda }_{\varrho }\left(t\right)\right|t^{s\varrho }{\left(dt\right)}^{\varrho },$$

(26)

$${\eta }_7\left(\varrho ,s\right)=\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{{\displaystyle \frac{1}{2}}}{\int }}{\left(t-\frac{1}{2}\right)}^{\varrho }\left|2^{\varrho }{\Lambda }_{\varrho }\left(1\right)-3^{\varrho }{\Lambda }_{\varrho }\left(t\right)\right|{\left(1-t\right)}^{s\varrho }{\left(dt\right)}^{\varrho }$$

(27)

and

$${\eta }_8\left(\varrho ,s\right)=\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{1}{\underset{{\displaystyle \frac{1}{2}}}{\int }}{\left(t-\frac{1}{2}\right)}^{\varrho }\left|2^{\varrho }{\Lambda }_{\varrho }\left(1\right)-3^{\varrho }{\Lambda }_{\varrho }\left(t\right)\right|t^{s\varrho }{\left(dt\right)}^{\varrho }.$$

(28)

The proof is completed. □

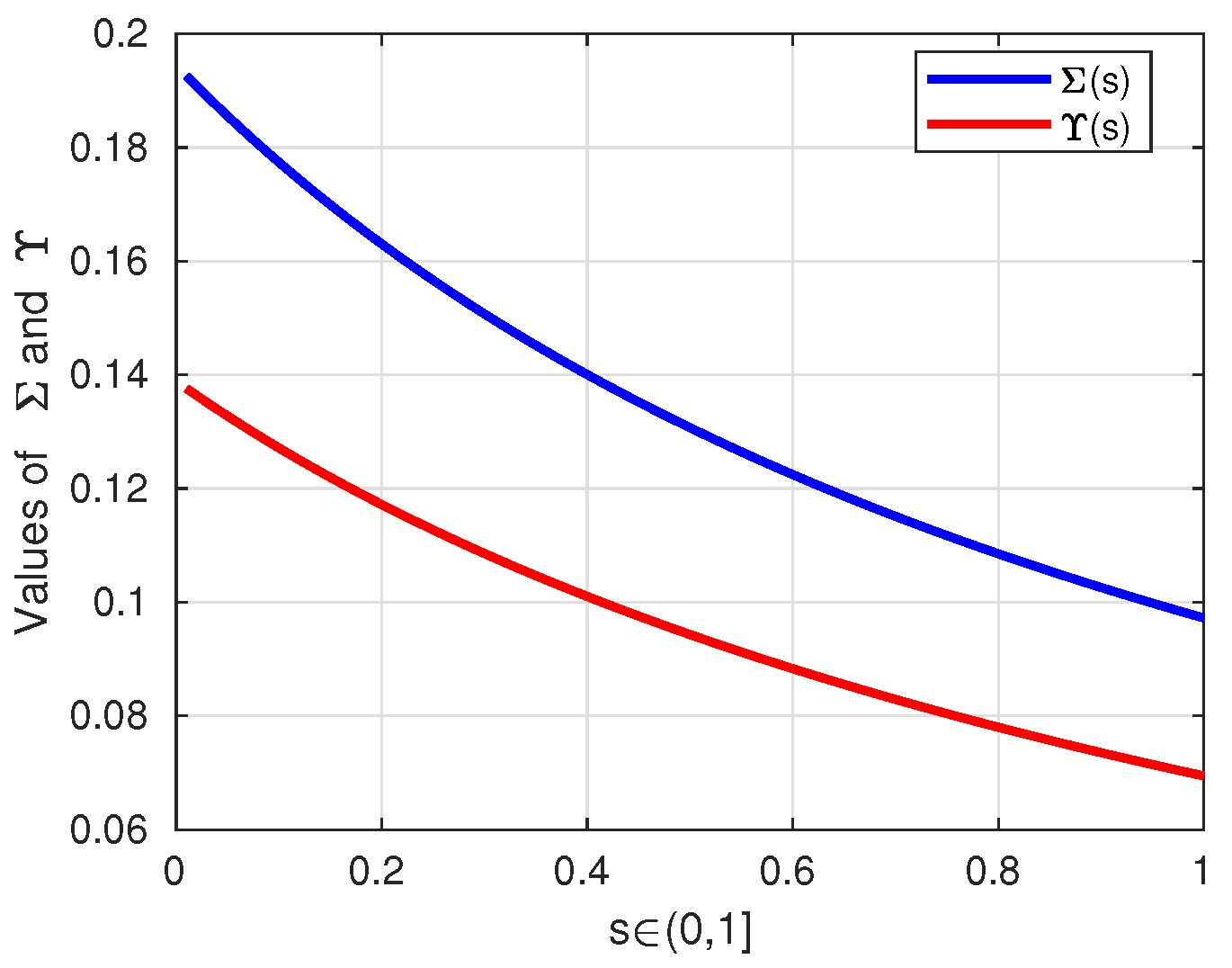
5. Applications

5.1. Quadrature Formula

Let $\Phi$ be the partition of the points ${𝚤}_1=x_0<x_1<...<x_n={𝚤}_2$ of the interval $\left[{𝚤}_1,{𝚤}_2\right]$, and consider the quadrature formula,

$$\frac{1}{\Gamma \left(\varrho +1\right)}\underset{{𝚤}_1}{\stackrel{{𝚤}_2}{\int }}\mathfrak{h}\left(u\right){\left(du\right)}^{\varrho }=\lambda \left(\mathfrak{h},\Phi \right)+R\left(\mathfrak{h},\Phi \right),$$

where

$$\lambda \left(\mathfrak{h},\Phi \right)=\frac{1}{\Gamma \left(\varrho +1\right)}\underset{i=0}{\sum ^{n-1}}\frac{{\left(x_{i+1}-x_i\right)}^{\varrho }}{6^{\varrho }}\left(\mathfrak{h}\left(x_i\right)+4^{\varrho }\mathfrak{h}\left(\frac{x_i+x_{i+1}}{2}\right)+\mathfrak{h}\left(x_{i+1}\right)\right)$$

and $R\left(\mathfrak{h},\Phi \right)$ denotes the associated approximation error.

Proposition 1.

Let $n\in \mathbb{N}$ and $\mathfrak{h}:\left[{𝚤}_1,{𝚤}_2\right]\to {\mathbb{R}}^{\varrho }$ be a differentiable function on $\left[{𝚤}_1,{𝚤}_2\right]$ with $0\le {𝚤}_1<{𝚤}_2$ and ${\mathfrak{h}}^{\left(\varrho \right)}$$\in C_{\varrho }\left[{𝚤}_1,{𝚤}_2\right]$. If $\left|{\mathfrak{h}}^{\left(\varrho \right)}\right|$ is generalized convex function, we have

$$\begin{array}{cc}\hfill & \left|R\left(\mathfrak{h},\Phi \right)\right|\hfill \\ \hfill \le & \frac{1}{\Gamma \left(1+\varrho \right)}\underset{i=0}{\sum ^{n-1}}\frac{{\left(x_{i+1}-x_i\right)}^{2\varrho }}{6^{\varrho }}\left[\frac{3^{2\varrho }-2^{\varrho }}{3^{\varrho }\Gamma \left(1+2\varrho \right)}-\frac{3^{\varrho }-2^{\varrho }}{3^{\varrho }\Gamma \left(1+\varrho \right)}\right]\left(\left|{\mathfrak{h}}^{\left(\varrho \right)}\left(x_i\right)\right|+\left|{\mathfrak{h}}^{\left(\varrho \right)}\left(x_{i+1}\right)\right|\right).\hfill \end{array}$$

Proof. 

Applying Theorem 5 with $\vartheta \left(t\right)=t^{\varrho }$ and $s=1$ on the subintervals $\left[x_i,x_{i+1}\right]$$\left(i=0,1,...,n-1\right)$ of the partition $\Phi$, then using the generalized convexity of $\left|{\mathfrak{h}}^{\varrho }\right|$, we obtain

$$\begin{array}{cc}\hfill & \left|\frac{1^{\varrho }}{4^{\varrho }}\left(\mathfrak{h}\left(x_i\right)+2^{\varrho }\mathfrak{h}\left(\frac{x_i+x_{i+1}}{2}\right)+\mathfrak{h}\left(x_{i+1}\right)\right)-\frac{\Gamma \left(\varrho +1\right)}{{\left(x_{i+1}-x_i\right)}^{\varrho }}{}_{x_i}I_{x_{i+1}}^{\varrho }\mathfrak{h}\left(t\right)\right|\hfill \\ \hfill \le & \frac{\Gamma \left(1+\varrho \right)}{6^{\varrho }}\left(D_1\left(\varrho ,1\right)\left(\left|{\mathfrak{h}}^{\left(\varrho \right)}\left(x_i\right)\right|+\left|{\mathfrak{h}}^{\left(\varrho \right)}\left(x_{i+1}\right)\right|\right)+D_2\left(\varrho ,1\right)\left|{\mathfrak{h}}^{\left(\varrho \right)}\left(\frac{x_i+x_{i+1}}{2}\right)\right|\right),\hfill \end{array}$$

(29)

where $D_1$ and $D_2$ are defined as in (15) and (16), respectively, with

$${\Lambda }_{\varrho }\left(t\right)=\frac{{\left(x_{i+1}-x_i\right)}^{\varrho }}{\Gamma \left(1+\varrho \right)}{t}^{\varrho }.$$

Using the fact that $\left|{\mathfrak{h}}^{\left(\varrho \right)}\left(\frac{x_i+x_{i+1}}{2}\right)\right|\le \frac{\left|{\mathfrak{h}}^{\left(\varrho \right)}\left(x_i\right)\right|+\left|{\mathfrak{h}}^{\left(\varrho \right)}\left(x_{i+1}\right)\right|}{2}$, Inequality (29) gives

$$\begin{array}{cc}\hfill & \left|\frac{1^{\varrho }}{4^{\varrho }}\left(\mathfrak{h}\left(x_i\right)+2^{\varrho }\mathfrak{h}\left(\frac{x_i+x_{i+1}}{2}\right)+\mathfrak{h}\left(x_{i+1}\right)\right)-\frac{\Gamma \left(\varrho +1\right)}{{\left(x_{i+1}-x_i\right)}^{\varrho }}{}_{x_i}I_{x_{i+1}}^{\varrho }\mathfrak{h}\left(t\right)\right|\hfill \\ \hfill \le & \frac{\Gamma \left(1+\varrho \right)}{6^{\varrho }}{D}_3\left(\varrho ,1\right)\left(\left|{\mathfrak{h}}^{\left(\varrho \right)}\left(x_i\right)\right|+\left|{\mathfrak{h}}^{\left(\varrho \right)}\left(x_{i+1}\right)\right|\right),\hfill \end{array}$$

(30)

where $D_3$ is given by

$$D_3\left(\varrho ,1\right)=\frac{{\left(x_{i+1}-x_i\right)}^{\varrho }}{\Gamma \left(1+\varrho \right)}\left(\frac{1}{\Gamma \left(1+\varrho \right)}\stackrel{{\displaystyle \frac{1}{2}}}{\underset{0}{\int }}\left|1^{\varrho }-3t^{\varrho }\right|{\left(dt\right)}^{\varrho }\right)=\frac{{\left(x_{i+1}-x_i\right)}^{\varrho }}{\Gamma \left(1+\varrho \right)}\left[\frac{3^{2\varrho }-2^{\varrho }}{3^{\varrho }\Gamma \left(1+2\varrho \right)}-\frac{3^{\varrho }-2^{\varrho }}{3^{\varrho }\Gamma \left(1+\varrho \right)}\right].$$

Multiplying both sides of Inequality (30) by ${\displaystyle \frac{1}{\Gamma \left(1+\alpha \right)}}{\left(x_{i+1}-x_i\right)}^{\nu }$, and then summing the obtained inequalities for all $i=0$ to $n-1$, and using the triangular inequality, we obtain the desired result. □

5.2. Special Means

For arbitrary real numbers ${𝚤}_1,{𝚤}_2$ we have the following.

The Arithmetic mean: $A_{\varrho }\left({𝚤}_1,{𝚤}_2\right)={\displaystyle \frac{{𝚤}_1^{\varrho }+{𝚤}_2^{\varrho }}{2^{\varrho }}}$.

The n-Logarithmic mean: $L_{n\varrho }\left({𝚤}_1,{𝚤}_2\right)={\left({\displaystyle \frac{\Gamma \left(1+n\varrho \right)}{\Gamma \left(1+\left(n+1\right)\varrho \right)}}{\displaystyle \frac{{𝚤}_2^{\left(n+1\right)\varrho }-{𝚤}_1^{\left(n+1\right)\varrho }}{\left(n+1\right){\left({𝚤}_2-{𝚤}_1\right)}^{\varrho }}}\right)}^{{\displaystyle \frac{1}{n}}}$, ${𝚤}_1,{𝚤}_2>0,{𝚤}_1\ne {𝚤}_2$ and $n\in \mathbb{Z}\setminus \left\{-1,0\right\}$

Proposition 2.

Let ${𝚤}_1,{𝚤}_2\in \mathbb{R}$ with $0<{𝚤}_1<{𝚤}_2$, and $n\in \mathbb{N}$ with $n\ge 2$; then, we have

$$\begin{array}{cc}\hfill & \left|{\Lambda }_{\varrho }\left(1\right)\left[2^{\varrho }{A}_{\varrho }\left({𝚤}_1^n,{𝚤}_2^n\right)+4^{\varrho }{A}_{\varrho }^n\left({𝚤}_1,{𝚤}_2\right)\right]-3^{\varrho }\left({}_{{𝚤}_2^{-}}{}^{\vartheta }\mathcal{J}_{\left(\varrho \right)}\mathfrak{h}\left({𝚤}_1\right)+{}_{{𝚤}_1^{+}}{}^{\vartheta }\mathcal{J}^{\left(\varrho \right)}\mathfrak{h}\left({𝚤}_2\right)\right)\right|\hfill \\ \hfill \le & {\left({𝚤}_2-{𝚤}_1\right)}^{\varrho }\left(C_1\left(\varrho ,1\right)+C_2\left(\varrho ,1\right)+C_3\left(\varrho ,1\right)+C_4\left(\varrho ,1\right)\right){\displaystyle \frac{\Gamma \left(1+n\varrho \right)}{\Gamma \left(1+\left(n-1\right)\varrho \right)}}\left({𝚤}_1^{\left(n-1\right)\varrho }+{𝚤}_2^{\left(n-1\right)\varrho }\right),\hfill \end{array}$$

where $C_i$, $i=1$ to 4 are defined as in (11)–(14), respectively.

Proof. 

The assertion follows from Theorem 5 with $s=1$, applied to the function $\mathfrak{h}\left(x\right)=x^{n\varrho }$. □

Proposition 3.

Let ${𝚤}_1,{𝚤}_2\in \mathbb{R}$ with $0<a<b$, and $n\in \mathbb{N}$ with $n\ge 2$; then, we have

$$\begin{array}{cc}\hfill & \left|{\Lambda }_{\varrho }\left(1\right)\left[2^{\varrho }{A}_{\varrho }\left({𝚤}_1^n,{𝚤}_2^n\right)+4^{\varrho }{A}_{\varrho }^n\left({𝚤}_1,{𝚤}_2\right)\right]-3^{\varrho }\left({}_{{𝚤}_2^{-}}{}^{\vartheta }\mathcal{J}_{\left(\varrho \right)}\mathfrak{h}\left({𝚤}_1\right)+{}_{{𝚤}_1^{+}}{}^{\vartheta }\mathcal{J}^{\left(\varrho \right)}\mathfrak{h}\left({𝚤}_2\right)\right)\right|\hfill \\ \hfill \le & {\displaystyle \frac{{\left({𝚤}_2-{𝚤}_1\right)}^{\varrho }}{2^{n\varrho }}}{\displaystyle \frac{\Gamma \left(1+n\varrho \right)}{\Gamma \left(1+\left(n-1\right)\varrho \right)}}\left(2^{\left(n-1\right)\varrho }{D}_1\left(\varrho ,1\right)+D_2\left(\varrho ,1\right)\right)\left({𝚤}_1^{\left(n-1\right)\varrho }+{𝚤}_2^{\left(n-1\right)\varrho }\right),\hfill \end{array}$$

where $D_1$ and $D_2$ are defined as in (15) and (16), respectively.

Proof. 

The assertion follows from Theorem 7 with $s=1$, applied to the function $\mathfrak{h}\left(x\right)=x^{n\varrho }$. □

6. Conclusions

In conclusion, this work has introduced a new fractal–fractional identity and derived innovative Simpson-type inequalities for functions with generalized s-convexity in the second sense through their first-order local fractional derivatives. By lowering regularity requirements, our approach expands the scope of fractal–fractional calculus applications and provides refined methods that enhance classical results. This research opens new horizons in the study of fractal–fractional integral inequalities, paving the way for further exploration and potential advancements in mathematical analysis and applied sciences.

Additionally, this work lays the groundwork for investigating the error associated with Simpson’s formula under other types of generalized convexity. Future studies could also explore extensions to other quadrature rules, such as Bullen’s and Milne’s formulas, to further enrich the framework of fractal–fractional analysis.