A New Inclusion on Inequalities of the Hermite–Hadamard–Mercer Type for Three-Times Differentiable Functions

Abstract

The goal of this study is to develop numerous Hermite–Hadamard–Mercer (H–H–M)-type inequalities involving various fractional integral operators, including classical, Riemann–Liouville (R.L), k-Riemann–Liouville (k-R.L), and their generalized fractional integral operators. In addition, we establish a number of corresponding fractional integral inequalities for three-times differentiable convex functions that are connected to the right side of the H–H–M-type inequality. For these results, further remarks and observations are provided. Following that, a couple of graphical representations are shown to highlight the key findings of our study. Finally, some applications on special means are shown to demonstrate the effectiveness of our inequalities.

1. Introduction

Mathematicians have been debating the interesting concept of inequalities for a long time. Fractional calculus, quantum calculus, network theory, quantum information theory, operator equations, operator theory, and numerical analysis are among the remarkable applications. As a result of the interactions between several fields, this is currently a very active research topic. Numerical integration and definite integral estimation are necessary in applied science.

Fractional calculus is popular among researchers due to its behavior and applications not only in the field of mathematical sciences but also in different fields of sciences like epidemiology [1], nanotechnology [2], physics [3], bio-engineering [4], and control systems [5]. Researchers have used fractional calculus to construct various fractional integral inequalities because of their significance in approximation theory. Based on their fundamental properties, scholars find novel fractional operators and apply them to numerous real-world problems. There are numerous articles and monographs, where new fractional operators are employed to enhance integral inequalities including the Ostrowski inequality, Simpson inequality, Fejer-type inequality, Hermite–Hadamard (H–H) inequality, Jensen–Mercer (J–M)-type inequality, and so on. The famous H–H inequalitym associated with convex functions, is one such important integral inequality.

A function $f:I\subseteq R\to R$, $I=[{\vartheta }_1,{\vartheta }_2]$ is said to be convex if

$$f\left(\eta {\vartheta }_1+(1-\eta ){\vartheta }_2\right)\le \eta f\left({\vartheta }_1\right)+(1-\eta )f\left({\vartheta }_2\right),$$

holds for all ${\vartheta }_1,{\vartheta }_2\in I$ and $\eta \in [0,1]$. If the above inequality is reversed, then the function f will be concave on $[{\vartheta }_1,{\vartheta }_2]$. Convex functions have been an object of attention in recent decades, and the original notion has been extended and generalized in many directions. Those interested in the aforementioned development can consult [6], where a full exposition of these directions is available.

Let $0<x_1\le x_2\le \dots \le x_n$ and let $\mu =({\mu }_1,{\mu }_2,\dots {\mu }_n)$ be non-negative weights such that ${\Sigma }_{i=1}^n{\mu }_i=1$. The Jensen inequality [7] states that f is a convex function on $[{\vartheta }_1,{\vartheta }_2]$, then

$$f\left({\Sigma }_{i=1}^n{\mu }_i{x}_i\right)\le {\Sigma }_{i=1}^n{\mu }_{i}f\left(x_i\right),$$

where for all $x_i\in [{\vartheta }_1,{\vartheta }_2]$ and ${\mu }_i\in [0,1]$, $(i=\overline{1,n})$. In particular, if $n=2$ and ${\mu }_1={\mu }_2={\displaystyle \frac{1}{2}}$, we have Equation (1) of [8]:

$$f\left({\displaystyle \frac{x_1+x_2}{2}}\right)\le {\displaystyle \frac{f\left(x_1\right)+f\left(x_2\right)}{2}}.$$

The H–H inequality states that if a mapping $f:I\subseteq R\to R$ is a convex function on I with ${\vartheta }_1,{\vartheta }_2\in I$, ${\vartheta }_1<{\vartheta }_2$, then

$$f\left({\displaystyle \frac{{\vartheta }_1+{\vartheta }_2}{2}}\right)\le {\displaystyle \frac{1}{{\vartheta }_2-{\vartheta }_1}}{\int }_{{\vartheta }_1}^{{\vartheta }_2}f\left(x\right)dx\le {\displaystyle \frac{f\left({\vartheta }_1\right)+f\left({\vartheta }_2\right)}{2}}.$$

(1)

This inequality was published by Hermite [9] in 1883 and, independently, by Hadamard in 1893 [10].

In other words, the integral mean value of a convex function interpolates the Jensen Inequality for $n=2$, and we note that this inequality can make a bounded estimation of the integral mean on $[{\vartheta }_1,{\vartheta }_2]$, so it has wide applications in numerical integration. Thus, the H–H inequality is one of the topics that attracts the most attention in mathematical sciences today (see [11,12]).

The double inequality in (1) holds in the reversed direction if f is concave [13].

Theorem 1

(See [14]). If f is a convex function on $I=[{\vartheta }_1,{\vartheta }_2]$, then

$$f\left({\vartheta }_1+{\vartheta }_2-{\Sigma }_{i=1}^n{\mu }_i{x}_i\right)\le f\left({\vartheta }_1\right)+f\left({\vartheta }_2\right)-{\Sigma }_{i=1}^n{\mu }_{i}f\left(x_i\right),$$

for each $x_i\in [{\vartheta }_1,{\vartheta }_2]$ and ${\mu }_i\in [0,1]$, $(i=\overline{1,n})$ with ${\Sigma }_{i=1}^n{\mu }_i=1$.

Remark 1.

For some results related to the J–M inequality, see [14,15,16,17,18].

After these necessary inequalities about convex functions, we will now give the definitions that we will use here. We recall the definitions of R.L and k-R.L fractional integrals.

Definition 1

([19]). “Let $f\in L[{\vartheta }_1,{\vartheta }_2]$. The left sided and right sided R.L fractional integrals $J_{{\vartheta }_1^{+}}^{\alpha }f$ and $J_{{\vartheta }_2^{-}}^{\alpha }f$ of order $\alpha >0$ with ${\vartheta }_1\ge 0$ can be defined respectively by

$$\begin{array}{ccc}\hfill J_{{\vartheta }_1^{+}}^{\alpha }f\left(x\right)& ={\displaystyle \frac{1}{\Gamma \left(\alpha \right)}}{\int }_{{\vartheta }_1}^x{(x-\eta )}^{\alpha -1}f\left(\eta \right)d\eta ,\hfill & \hfill x>{\vartheta }_1,\end{array}$$

and

$$\begin{array}{ccc}\hfill J_{{\vartheta }_2^{-}}^{\alpha }f\left(x\right)& ={\displaystyle \frac{1}{\Gamma \left(\alpha \right)}}{\int }_x^{{\vartheta }_2}{(\eta -x)}^{\alpha -1}f\left(\eta \right)d\eta ,\hfill & \hfill x<{\vartheta }_2,\end{array}$$

here $\Gamma \left(\alpha \right)$ is Euler Gamma function. and $J_{{\vartheta }_1^{+}}^{0}f\left(x\right)=J_{{\vartheta }_2^{-}}^{0}f\left(x\right)=f\left(x\right)$”.

Definition 2

([20,21]). “Let $f\in L[{\vartheta }_1,{\vartheta }_2]$. The left sided and right sided k-R.L fractional integrals _k$J_{{\vartheta }_1^{+}}^{\alpha }f$ and _k$J_{{\vartheta }_2^{-}}^{\alpha }f$ of order ${\displaystyle \frac{\alpha }{k}}>0$ with ${\vartheta }_1\ge 0$ can be defined respectively by

$$\begin{array}{ccc}\hfill {}_{k}J_{{\vartheta }_1^{+}}^{\alpha }f\left(x\right)& ={\displaystyle \frac{1}{k{\Gamma }_k\left(\alpha \right)}}{\int }_{{\vartheta }_1}^x{(x-\eta )}^{{\displaystyle \frac{\alpha }{k}}-1}f\left(\eta \right)d\eta ,\hfill & \hfill x>{\vartheta }_1,\end{array}$$

and

$$\begin{array}{ccc}\hfill {}_{k}J_{{\vartheta }_2^{-}}^{\alpha }f\left(x\right)& ={\displaystyle \frac{1}{k{\Gamma }_k\left(\alpha \right)}}{\int }_x^{{\vartheta }_2}{(\eta -x)}^{{\displaystyle \frac{\alpha }{k}}-1}f\left(\eta \right)d\eta ,\hfill & \hfill x<{\vartheta }_2,\end{array}$$

here ${\Gamma }_k\left(\alpha \right)={\int }_0^{\infty }{\eta }^{\alpha -1}{e}^{{\displaystyle \frac{{\eta }^k}{k}}}d\eta$”.

A new class of functions was introduced by Raina in [22,23] defined by

$${\mathcal{F}}_{\rho ,\lambda }^{\sigma }\left(x\right)=\sum _{k=0}^{\infty }{\displaystyle \frac{\sigma \left(k\right)}{\Gamma (\rho k+\lambda )}}{x}^k$$

with $\rho ,\lambda >0;\left|x\right|<R$, where $\sigma \left(k\right)$ is a bounded sequence of positive real numbers, and R is the set of real numbers.

Definition 3

([23,24]). “The left-sided and right-sided generalized fractional integral operators are respectively defined as follows:

$$\left({\mathcal{J}}_{\rho ,\lambda ,a^{+};w}^{\sigma }f\right)\left(x\right)={\int }_a^x{(x-t)}^{\lambda -1}{\mathcal{F}}_{\rho ,\lambda }^{\sigma }\left[w{(x-t)}^{\rho }\right]f\left(t\right)dt,(x>a>0),$$

$$\left({\mathcal{J}}_{\rho ,\lambda ,b^{-};w}^{\sigma }f\right)\left(x\right)={\int }_x^b{(t-x)}^{\lambda -1}{\mathcal{F}}_{\rho ,\lambda }^{\sigma }\left[w{(t-x)}^{\rho }\right]f\left(t\right)dt,(0<x<b),$$

$\lambda ,\rho >0,w\in R$ and $f\left(t\right)$ is such that the integral exists”. In addition, it is known that $\left({\mathcal{J}}_{\rho ,\lambda ,a^{+};w}^{\sigma }f\right)\left(x\right)$ and $\left({\mathcal{J}}_{\rho ,\lambda ,a^{+};w}^{\sigma }f\right)\left(x\right)$ are bounded integral operators on $L(a,b)$ if

$$\mathcal{M}={\mathcal{F}}_{\rho ,\lambda +1}^{\sigma }\left[w{(b-a)}^{\rho }\right]<\infty .$$

Remark 2.

From Definition 3, one can observe the following:

• If $\lambda =1,$ $\sigma \left(0\right)=1$, and $w=0$, then the generalized fractional integral operators reduce to the classical R.L integrals.
• If $\lambda =\alpha ,$ $\sigma \left(0\right)=1$, and $w=0$, then Definition 3 reduces to Definition 1.

A rising number of publications from recent years have been using new fractional operators to deal with integral inequalities such as the Simpson inequality, Fejer-type inequality, and H–H inequality; see [25,26,27,28]. And for the J–M-type inequality, see, for example, [14,15,16,17,18,29,30,31,32,33]. The authors of [34] recently established H–H–M-type inequalities in the case of twice-differentiable and convex functions with powers of the absolute values of the second derivatives as convex. Several H-H-type inequalities [35] for functions with third derivative, in absolute values, is convex, in the frame of fractional integrals are presented for example in [36].

This study follows an approach different from that in [20], which gives new bounds for H–H–M-type inequalities utilizing the convex functions [34] with powers of the absolute values of the third derivatives. The aim of this paper was to see what happen if the factor from the right member of the key identity, ${\eta }^2(1-\eta )$ will be replaced with $\eta (1-{\eta }^2)$ and how the inequalities will be transformed. Section 1 these recalls the definitions and results that will be used throughout this article. This different approach starts with a new key Lemma 1 in Section 2 and continues with the corresponding Theorems 2–4. In Section 3, these results are generalized for R.L fractional integrals in Lemma 2 and Theorems 5–7 and for k-R.L fractional integrals in Lemma 3 and Theorems 8–10, and Section 4 presents generalized fractional integral operators in Lemma 4 and Theorems 11–13. Then, several remarks and observations—see Remarks 3–18 and Corollaries 1 and 2—are given for these obtained results and the links between them. The key findings of our research are then illustrated using particular examples with graphical representations. Applications of the results in Section 5 for special means of real numbers are additionally addressed. Both papers, this paper and [20], contain four key identities that allow us to develop H–H–M-type inequalities under certain conditions imposed on the function f. However, in this paper, new trapezium-type inequalities are established instead of midpoint H–H–M-type inequalities for convex functions, for fractional integrals, and k-fractional integrals. The factors $\eta -{\eta }^3$, $\eta -{\eta }^{\alpha +2}$, and $\eta -{\eta }^{{\displaystyle \frac{\alpha }{k}}+2}$ and the domain of the new function $\left({\vartheta }_1+{\vartheta }_2-\left({\displaystyle \frac{1-\eta }{2}}{w}_1+{\displaystyle \frac{1+\eta }{2}}{w}_2\right)\right)$ from the right member, instead of ${\eta }^2-{\eta }^3$, ${\eta }^2-{\eta }^{\alpha +2}$, and ${\eta }^2-{\eta }^{{\displaystyle \frac{\alpha }{k}}+2}$ and the domain of the old function $\left({\vartheta }_1+{\vartheta }_2-\left({\displaystyle \frac{\eta }{2}}{w}_1+{\displaystyle \frac{2-\eta }{2}}{w}_2\right)\right)$, respectively, generate a new term $f^{\prime }({\nu }_1+{\nu }_2-{\omega }_2)-f^{\prime }({\nu }_1+{\nu }_2-{\omega }_1)$ in the left member in this paper, and the old term $f({\nu }_1+{\nu }_2-{\displaystyle \frac{{\omega }_1+{\omega }_2}{2}})$ from [20] disappears in these identities. The last identity with corresponding inequalities is presented in this paper for a more general class of operators compared to those presented in [20], for the generalized fractional integral operators. The advantage of this new approach can be seen in Example 1, where the first two inequalities are compared. Finally, a brief conclusion is provided in Section 6.

2. Inequalities of the Hermite–Hadamard–Mercer Type for Convex Functions

In this section, from [20], several inequalities of the H–H–M type will be established for functions whose powers of the absolute values of the third derivatives are convex.

Lemma 1.

Assume that $f:I=[{\vartheta }_1,{\vartheta }_2]\subset R\to R$ is a three-times differentiable mapping on $({\vartheta }_1,{\vartheta }_2)$ such that $f^{‴}\in L[{\vartheta }_1,{\vartheta }_2]$, where ${\vartheta }_1$, ${\vartheta }_2\in I$ with ${\vartheta }_1<{\vartheta }_2$. Then, the following identity holds:

$$\begin{array}{cc}\hfill & {\displaystyle \frac{f({\vartheta }_1+{\vartheta }_2-w_2)+f({\vartheta }_1+{\vartheta }_2-w_1)}{2}}-{\displaystyle \frac{1}{w_2-w_1}}{\int }_{{\vartheta }_1+{\vartheta }_2-w_2}^{{\vartheta }_1+{\vartheta }_2-w_1}f\left(u\right)du+{\displaystyle \frac{w_2-w_1}{12}}[f^{\prime }({\vartheta }_1+{\vartheta }_2-w_2)\hfill \\ & -f^{\prime }({\vartheta }_1+{\vartheta }_2-w_1)]={\displaystyle \frac{{(w_2-w_1)}^3}{96}}{\int }_0^1(\eta -{\eta }^3)[f^{‴}\left({\vartheta }_1+{\vartheta }_2-\left({\displaystyle \frac{1-\eta }{2}}{w}_1+{\displaystyle \frac{1+\eta }{2}}{w}_2\right)\right)\hfill \\ & -f^{‴}\left({\vartheta }_1+{\vartheta }_2-\left({\displaystyle \frac{1+\eta }{2}}{w}_1+{\displaystyle \frac{1-\eta }{2}}{w}_2\right)\right)]d\eta ,\hfill \end{array}$$

for all $w_1,w_2\in [{\vartheta }_1,{\vartheta }_2]$ and $\eta \in [0,1].$

Proof. 

It suffices to note that

$$\begin{array}{cc}\hfill T& ={\int }_0^1(\eta -{\eta }^3)f^{‴}\left({\vartheta }_1+{\vartheta }_2-\left({\displaystyle \frac{1-\eta }{2}}{w}_1+{\displaystyle \frac{1+\eta }{2}}{w}_2\right)\right)d\eta \hfill \\ & -{\int }_0^1(\eta -{\eta }^3)f^{‴}\left({\vartheta }_1+{\vartheta }_2-\left({\displaystyle \frac{1+\eta }{2}}{w}_1+{\displaystyle \frac{1-\eta }{2}}{w}_2\right)\right)d\eta \hfill \\ \hfill & =T_1-T_2.\hfill \end{array}$$

Calculating $T_1$ and $T_2$ by integration by parts three times, we obtain

$$\begin{array}{cc}\hfill T_1& ={\int }_0^1(\eta -{\eta }^3)f^{‴}\left({\vartheta }_1+{\vartheta }_2-\left({\displaystyle \frac{1-\eta }{2}}{w}_1+{\displaystyle \frac{1+\eta }{2}}{w}_2\right)\right)d\eta \hfill \\ \hfill & =-{\displaystyle \frac{2(\eta -{\eta }^3)f^{″}\left({\vartheta }_1+{\vartheta }_2-\left(\frac{1-\eta }{2}{w}_1+\frac{1+\eta }{2}{w}_2\right)\right)}{w_2-w_1}}{|}_0^1\hfill \\ & +{\displaystyle \frac{2}{w_2-w_1}}{\int }_0^1(1-3{\eta }^2)f^{″}\left({\vartheta }_1+{\vartheta }_2-\left({\displaystyle \frac{1-\eta }{2}}{w}_1+{\displaystyle \frac{1+\eta }{2}}{w}_2\right)\right)d\eta \hfill \\ & ={\displaystyle \frac{2}{w_2-w_1}}[-{\displaystyle \frac{2(1-3{\eta }^2)f^{\prime }\left({\vartheta }_1+{\vartheta }_2-\left(\frac{1-\eta }{2}{w}_1+\frac{1+\eta }{2}{w}_2\right)\right)}{w_2-w_1}}{|}_0^1-\hfill \\ & -{\displaystyle \frac{12}{w_2-w_1}}{\int }_0^1\eta f^{\prime }\left({\vartheta }_1+{\vartheta }_2-\left({\displaystyle \frac{1-\eta }{2}}{w}_1+{\displaystyle \frac{1+\eta }{2}}{w}_2\right)\right)d\eta ]\hfill \end{array}$$

$$\begin{array}{cc}\hfill & ={\displaystyle \frac{8f^{\prime }({\vartheta }_1+{\vartheta }_2-w_2)}{{(w_2-w_1)}^2}}{f}^{\prime }+{\displaystyle \frac{4}{{(w_2-w_1)}^2}}{f}^{\prime }\left({\vartheta }_1+{\vartheta }_2-{\displaystyle \frac{w_1+w_2}{2}}\right)\hfill \\ & -{\displaystyle \frac{24}{{(w_2-w_1)}^2}}[-{\displaystyle \frac{2\eta f\left({\vartheta }_1+{\vartheta }_2-\left(\frac{1-\eta }{2}{w}_1+\frac{1+\eta }{2}{w}_2\right)\right)}{w_2-w_1}}{|}_0^1\hfill \\ & +{\displaystyle \frac{2}{w_2-w_1}}{\int }_0^{1}f\left({\vartheta }_1+{\vartheta }_2-\left({\displaystyle \frac{1-\eta }{2}}{w}_1+{\displaystyle \frac{1+\eta }{2}}{w}_2\right)\right)d\eta ]\hfill \\ & ={\displaystyle \frac{8f^{\prime }({\vartheta }_1+{\vartheta }_2-w_2)}{{(w_2-w_1)}^2}}+{\displaystyle \frac{4}{{(w_2-w_1)}^2}}{f}^{\prime }\left({\vartheta }_1+{\vartheta }_2-{\displaystyle \frac{w_1+w_2}{2}}\right)\hfill \\ & +{\displaystyle \frac{48f({\vartheta }_1+{\vartheta }_2-w_2)}{{(w_2-w_1)}^3}}-{\displaystyle \frac{96}{{(w_2-w_1)}^4}}{\int }_{{\vartheta }_1+{\vartheta }_2-w_2}^{{\vartheta }_1+{\vartheta }_2-{\displaystyle \frac{w_1+w_2}{2}}}f\left(u\right)du,\hfill \end{array}$$

and similarly,

$$\begin{array}{cc}\hfill T_2& ={\int }_0^1(\eta -{\eta }^3)f^{‴}\left({\vartheta }_1+{\vartheta }_2-\left({\displaystyle \frac{1+\eta }{2}}{w}_1+{\displaystyle \frac{1-\eta }{2}}{w}_2\right)\right)d\eta \hfill \\ \hfill & ={\displaystyle \frac{8f^{\prime }({\vartheta }_1+{\vartheta }_2-w_1)}{{(w_2-w_1)}^2}}+{\displaystyle \frac{4}{{(w_2-w_1)}^2}}{f}^{\prime }\left({\vartheta }_1+{\vartheta }_2-{\displaystyle \frac{w_1+w_2}{2}}\right)\hfill \\ & -{\displaystyle \frac{48f({\vartheta }_1+{\vartheta }_2-w_1)}{{(w_2-w_1)}^3}}+{\displaystyle \frac{96}{{(w_2-w_1)}^4}}{\int }_{{\vartheta }_1+{\vartheta }_2-{\displaystyle \frac{w_1+w_2}{2}}}^{{\vartheta }_1+{\vartheta }_2-w_1}f\left(u\right)du.\hfill \end{array}$$

By substituting $T_1$ and $T_2$ and then multiplying the result by ${\displaystyle \frac{{(w_2-w_1)}^3}{96}}$, we have the desired identity. □

Theorem 2.

Assume that $f:I=[{\vartheta }_1,{\vartheta }_2]\subset R\to R$ is a three-times differentiable mapping on $({\vartheta }_1,{\vartheta }_2)$ such that $f^{‴}\in L[{\vartheta }_1,{\vartheta }_2]$, where ${\vartheta }_1$, ${\vartheta }_2\in I$ with ${\vartheta }_1<{\vartheta }_2$. If the function $|f^{‴}|$ is convex on $[{\vartheta }_1,{\vartheta }_2]$, then the following inequality holds:

$$\begin{array}{cc}\hfill & |{\displaystyle \frac{f({\vartheta }_1+{\vartheta }_2-w_2)+f({\vartheta }_1+{\vartheta }_2-w_1)}{2}}-{\displaystyle \frac{1}{w_2-w_1}}{\int }_{{\vartheta }_1+{\vartheta }_2-w_2}^{{\vartheta }_1+{\vartheta }_2-w_1}f\left(u\right)du\hfill \\ & +{\displaystyle \frac{w_2-w_1}{12}}\left[f^{\prime }({\vartheta }_1+{\vartheta }_2-w_2)-f^{\prime }({\vartheta }_1+{\vartheta }_2-w_1)\right]|\hfill \\ \hfill & \le {\displaystyle \frac{{(w_2-w_1)}^3}{192}}\left[|f^{‴}\left({\vartheta }_1\right)|+|f^{‴}\left({\vartheta }_2\right)|-{\displaystyle \frac{|f^{‴}\left(w_1\right)|+|f^{‴}\left(w_2\right)|}{2}}\right],\hfill \end{array}$$

for all $w_1,w_2\in [{\vartheta }_1,{\vartheta }_2].$

Proof. 

Using Lemma 1 and the J–M inequality, we find that

$$\begin{array}{cc}\hfill & |{\displaystyle \frac{f({\vartheta }_1+{\vartheta }_2-w_2)+f({\vartheta }_1+{\vartheta }_2-w_1)}{2}}-{\displaystyle \frac{1}{w_2-w_1}}{\int }_{{\vartheta }_1+{\vartheta }_2-w_2}^{{\vartheta }_1+{\vartheta }_2-w_1}f\left(u\right)du\hfill \\ & +{\displaystyle \frac{w_2-w_1}{12}}\left[f^{\prime }({\vartheta }_1+{\vartheta }_2-w_2)-f^{\prime }({\vartheta }_1+{\vartheta }_2-w_1)\right]|\hfill \\ & \le {\displaystyle \frac{{(w_2-w_1)}^3}{96}}\left\{{\int }_0^1\left|(\eta -{\eta }^3)\right|\right|f^{‴}\left({\vartheta }_1+{\vartheta }_2-\left({\displaystyle \frac{1-\eta }{2}}{w}_1+{\displaystyle \frac{1+\eta }{2}}{w}_2\right)\right)|d\eta \hfill \\ \hfill & +{\int }_0^1\left|(\eta -{\eta }^3)\right|\left|f^{‴}\left({\vartheta }_1+{\vartheta }_2-\left({\displaystyle \frac{1+\eta }{2}}{w}_1+{\displaystyle \frac{1-\eta }{2}}{w}_2\right)\right)\right|d\eta \}\hfill \end{array}$$

$$\begin{array}{cc}\hfill & \le {\displaystyle \frac{{(w_2-w_1)}^3}{96}}\{{\int }_0^1\left|(\eta -{\eta }^3)\right|\left(|f^{‴}\left({\vartheta }_1\right)|+|f^{‴}\left({\vartheta }_2\right)|-\left({\displaystyle \frac{1-\eta }{2}}|f^{‴}\left(w_1\right)|+{\displaystyle \frac{1+\eta }{2}}\left|f^{‴}\left(w_2\right)\right|\right)\right)d\eta \hfill \\ \hfill & +{\int }_0^1\left|(\eta -{\eta }^3)\right|\left(|f^{‴}\left({\vartheta }_1\right)|+|f^{‴}\left({\vartheta }_2\right)|-\left({\displaystyle \frac{1+\eta }{2}}|f^{‴}\left(w_1\right)|+{\displaystyle \frac{1-\eta }{2}}\left|f^{‴}\left(w_2\right)\right|\right)\right)d\eta \}\hfill \\ \hfill & ={\displaystyle \frac{{(w_2-w_1)}^3}{384}}\left[2\left(|f^{‴}\left({\vartheta }_1\right)|+|f^{‴}\left({\vartheta }_2\right)|\right)-\left(|f^{‴}\left(w_1\right)|+|f^{‴}\left(w_2\right)|\right)\right],\hfill \end{array}$$

which completes the proof. □

Theorem 3.

Assume that $f:I=[{\vartheta }_1,{\vartheta }_2]\subset R\to R$ is a three-times differentiable mapping on $({\vartheta }_1,{\vartheta }_2)$ with ${\vartheta }_1<{\vartheta }_2.$ If the function $|f^{‴}{|}^q$ is convex on $[{\vartheta }_1,{\vartheta }_2]$, $q\ge 1,$ then the following inequality holds:

$$\begin{array}{cc}\hfill & |{\displaystyle \frac{f({\vartheta }_1+{\vartheta }_2-w_2)+f({\vartheta }_1+{\vartheta }_2-w_1)}{2}}-{\displaystyle \frac{1}{w_2-w_1}}{\int }_{{\vartheta }_1+{\vartheta }_2-w_2}^{{\vartheta }_1+{\vartheta }_2-w_1}f\left(u\right)du\hfill \\ & +{\displaystyle \frac{w_2-w_1}{12}}\left[f^{\prime }({\vartheta }_1+{\vartheta }_2-w_2)-f^{\prime }({\vartheta }_1+{\vartheta }_2-w_1)\right]|\hfill \\ & \le {\displaystyle \frac{{(w_2-w_1)}^3}{384}}[{\left(|f^{‴}\left({\vartheta }_1\right){|}^q+{\left|f^{‴}\left({\vartheta }_2\right)\right|}^q-{\displaystyle \frac{7|f^{‴}\left(w_1\right){|}^q+23{\left|f^{‴}\left(w_2\right)\right|}^q}{30}}\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ & +{\left(|f^{‴}\left({\vartheta }_1\right){|}^q+{\left|f^{‴}\left({\vartheta }_2\right)\right|}^q-{\displaystyle \frac{23|f^{‴}\left(w_1\right){|}^q+7{\left|f^{‴}\left(w_2\right)\right|}^q}{30}}\right)}^{{\displaystyle \frac{1}{q}}}],\hfill \end{array}$$

for all $w_1,w_2\in [{\vartheta }_1,{\vartheta }_2].$

Proof. 

From Lemma 1 and using the power mean inequality for $q\ge 1,$ we have

$$\begin{array}{cc}\hfill & |{\displaystyle \frac{f({\vartheta }_1+{\vartheta }_2-w_2)+f({\vartheta }_1+{\vartheta }_2-w_1)}{2}}-{\displaystyle \frac{1}{w_2-w_1}}{\int }_{{\vartheta }_1+{\vartheta }_2-w_2}^{{\vartheta }_1+{\vartheta }_2-w_1}f\left(u\right)du\hfill \\ & +{\displaystyle \frac{w_2-w_1}{12}}\left[f^{\prime }({\vartheta }_1+{\vartheta }_2-w_2)-f^{\prime }({\vartheta }_1+{\vartheta }_2-w_1)\right]|\hfill \\ & \le {\displaystyle \frac{{(w_2-w_1)}^3}{96}}{\left({\int }_0^1(\eta -{\eta }^3)d\eta \right)}^{1-{\displaystyle \frac{1}{q}}}\{{\left({\int }_0^1(\eta -{\eta }^3)|f^{‴}\left({\vartheta }_1+{\vartheta }_2-\left({\displaystyle \frac{1-\eta }{2}}{w}_1+{\displaystyle \frac{1+\eta }{2}}{w}_2\right)\right){|}^{q}d\eta \right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ & +{\left({\int }_0^1(\eta -{\eta }^3)|f^{‴}\left({\vartheta }_1+{\vartheta }_2-\left({\displaystyle \frac{1+\eta }{2}}{w}_1+{\displaystyle \frac{1-\eta }{2}}{w}_2\right)\right){|}^{q}d\eta \right)}^{{\displaystyle \frac{1}{q}}}\}.\hfill \end{array}$$

Using the J–M inequality because of the convexity of $|f^{‴}{|}^q$, we have

$$\begin{array}{cc}\hfill & |{\displaystyle \frac{f({\vartheta }_1+{\vartheta }_2-w_2)+f({\vartheta }_1+{\vartheta }_2-w_1)}{2}}-{\displaystyle \frac{1}{w_2-w_1}}{\int }_{{\vartheta }_1+{\vartheta }_2-w_2}^{{\vartheta }_1+{\vartheta }_2-w_1}f\left(u\right)du\hfill \\ & +{\displaystyle \frac{w_2-w_1}{12}}\left[f^{\prime }({\vartheta }_1+{\vartheta }_2-w_2)-f^{\prime }({\vartheta }_1+{\vartheta }_2-w_1)\right]|\le {\displaystyle \frac{{(w_2-w_1)}^3}{96}}{\left({\displaystyle \frac{1}{4}}\right)}^{1-{\displaystyle \frac{1}{q}}}\times \hfill \\ & \times \{{\left({\int }_0^1(\eta -{\eta }^3)\left(|f^{‴}\left({\vartheta }_1\right){|}^q+{\left|f^{‴}\left({\vartheta }_2\right)\right|}^q-\left({\displaystyle \frac{1-\eta }{2}}|f^{‴}\left(w_1\right){|}^q+{\displaystyle \frac{1+\eta }{2}}{\left|f^{‴}\left(w_2\right)\right|}^q\right)\right)d\eta \right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +{\left({\int }_0^1(\eta -{\eta }^3)\left(|f^{‴}\left({\vartheta }_1\right){|}^q+{\left|f^{‴}\left({\vartheta }_2\right)\right|}^q-\left({\displaystyle \frac{1+\eta }{2}}|f^{‴}\left(w_1\right){|}^q+{\displaystyle \frac{1-\eta }{2}}{\left|f^{‴}\left(w_2\right)\right|}^q\right)\right)d\eta \right)}^{{\displaystyle \frac{1}{q}}}\}\hfill \end{array}$$

$$\begin{array}{cc}\hfill & ={\displaystyle \frac{{(w_2-w_1)}^3}{384}}[{\left(|f^{‴}\left({\vartheta }_1\right){|}^q+{\left|f^{‴}\left({\vartheta }_2\right)\right|}^q-{\displaystyle \frac{7|f^{″}\left(w_1\right){|}^q+23{\left|f^{″}\left(w_2\right)\right|}^q}{30}}\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +{\left(|f^{‴}\left({\vartheta }_1\right){|}^q+{\left|f^{‴}\left({\vartheta }_2\right)\right|}^q-{\displaystyle \frac{23|f^{″}\left(w_1\right){|}^q+7{\left|f^{″}\left(w_2\right)\right|}^q}{30}}\right)}^{{\displaystyle \frac{1}{q}}}].\hfill \end{array}$$

Therefore, the proof is finished. □

Theorem 4.

Assume that $f:I=[{\vartheta }_1,{\vartheta }_2]\subset R\to R$ is a twice-differentiable mapping on $({\vartheta }_1,{\vartheta }_2)$ such that $f^{‴}\in L[{\vartheta }_1,{\vartheta }_2]$, where ${\vartheta }_1$, ${\vartheta }_2\in I$ with ${\vartheta }_1<{\vartheta }_2$. If the function $|f^{‴}{|}^q$, $q>1$ is convex on $[{\vartheta }_1,{\vartheta }_2]$, then the following inequality holds:

$$\begin{array}{cc}\hfill & |{\displaystyle \frac{f({\vartheta }_1+{\vartheta }_2-w_2)+f({\vartheta }_1+{\vartheta }_2-w_1)}{2}}-{\displaystyle \frac{1}{w_2-w_1}}{\int }_{{\vartheta }_1+{\vartheta }_2-w_2}^{{\vartheta }_1+{\vartheta }_2-w_1}f\left(u\right)du\hfill \\ & +{\displaystyle \frac{w_2-w_1}{12}}\left[f^{\prime }({\vartheta }_1+{\vartheta }_2-w_2)-f^{\prime }({\vartheta }_1+{\vartheta }_2-w_1)\right]|\hfill \\ & \le {\displaystyle \frac{{(w_2-w_1)}^3}{96}}M[{\left(|f^{‴}\left({\vartheta }_1\right){|}^q+{\left|f^{‴}\left({\vartheta }_2\right)\right|}^q-{\displaystyle \frac{|f^{‴}\left(w_1\right){|}^q+3{\left|f^{‴}\left(w_2\right)\right|}^q}{4}}\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ & +{\left(|f^{‴}\left({\vartheta }_1\right){|}^q+{\left|f^{‴}\left({\vartheta }_2\right)\right|}^q-{\displaystyle \frac{3|f^{‴}\left(w_1\right){|}^q+{\left|f^{‴}\left(w_2\right)\right|}^q}{4}}\right)}^{{\displaystyle \frac{1}{q}}}],\hfill \end{array}$$

where $M={\left({\displaystyle \frac{2p}{(p+1)(3p+1)}}\right)}^{{\displaystyle \frac{1}{p}}}$ and ${\displaystyle \frac{1}{p}}+{\displaystyle \frac{1}{q}}=1$ for all $w_1,w_2\in [{\vartheta }_1,{\vartheta }_2].$

Proof. 

From Lemma 1, using Hölder’s inequality, we have

$$\begin{array}{cc}\hfill & |{\displaystyle \frac{f({\vartheta }_1+{\vartheta }_2-w_2)+f({\vartheta }_1+{\vartheta }_2-w_1)}{2}}-{\displaystyle \frac{1}{w_2-w_1}}{\int }_{{\vartheta }_1+{\vartheta }_2-w_2}^{{\vartheta }_1+{\vartheta }_2-w_1}f\left(u\right)du\hfill \\ & +{\displaystyle \frac{w_2-w_1}{12}}\left[f^{\prime }({\vartheta }_1+{\vartheta }_2-w_2)-f^{\prime }({\vartheta }_1+{\vartheta }_2-w_1)\right]|\hfill \\ & \le {\displaystyle \frac{{(w_2-w_1)}^3}{96}}{\left({\int }_0^1{|\eta -{\eta }^3|}^{p}d\eta \right)}^{{\displaystyle \frac{1}{p}}}\{{\left({\int }_0^1|f^{‴}\left({\vartheta }_1+{\vartheta }_2-\left({\displaystyle \frac{1-\eta }{2}}{w}_1+{\displaystyle \frac{1+\eta }{2}}{w}_2\right)\right){|}^{q}d\eta \right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ & +{\left({\int }_0^1|f^{‴}\left({\vartheta }_1+{\vartheta }_2-\left({\displaystyle \frac{1+\eta }{2}}{w}_1+{\displaystyle \frac{1-\eta }{2}}{w}_2\right)\right){|}^{q}d\eta \right)}^{{\displaystyle \frac{1}{q}}}\}.\hfill \end{array}$$

Using the J–M inequality because of the convexity of $|f^{‴}{|}^q$, we have

$$\begin{array}{cc}\hfill & |{\displaystyle \frac{f({\vartheta }_1+{\vartheta }_2-w_2)+f({\vartheta }_1+{\vartheta }_2-w_1)}{2}}-{\displaystyle \frac{1}{w_2-w_1}}{\int }_{{\vartheta }_1+{\vartheta }_2-w_2}^{{\vartheta }_1+{\vartheta }_2-w_1}f\left(u\right)du\hfill \\ & +{\displaystyle \frac{w_2-w_1}{12}}\left[f^{\prime }({\vartheta }_1+{\vartheta }_2-w_2)-f^{\prime }({\vartheta }_1+{\vartheta }_2-w_1)\right]|\hfill \\ & \le {\displaystyle \frac{{(w_2-w_1)}^3}{96}}{\left({\int }_0^1{|\eta -{\eta }^3|}^{p}d\eta \right)}^{{\displaystyle \frac{1}{p}}}\times \hfill \\ & \times \{{\left({\int }_0^1\left(|f^{‴}\left({\vartheta }_1\right){|}^q+{\left|f^{‴}\left({\vartheta }_2\right)\right|}^q-\left({\displaystyle \frac{1-\eta }{2}}|f^{‴}\left(w_1\right){|}^q+{\displaystyle \frac{1+\eta }{2}}{\left|f^{‴}\left(w_2\right)\right|}^q\right)\right)d\eta \right)}^{{\displaystyle \frac{1}{q}}}\hfill \end{array}$$

$$\begin{array}{cc}\hfill & +{\left({\int }_0^1\left(|f^{‴}\left({\vartheta }_1\right){|}^q+{\left|f^{‴}\left({\vartheta }_2\right)\right|}^q-\left({\displaystyle \frac{1+\eta }{2}}|f^{‴}\left(w_1\right){|}^q+{\displaystyle \frac{1-\eta }{2}}{\left|f^{‴}\left(w_2\right)\right|}^q\right)\right)d\eta \right)}^{{\displaystyle \frac{1}{q}}}\}\hfill \\ & ={\displaystyle \frac{{(w_2-w_1)}^3}{96}}{\left({\int }_0^1{|\eta -{\eta }^3|}^{p}d\eta \right)}^{{\displaystyle \frac{1}{p}}}[{\left(|f^{‴}\left({\vartheta }_1\right){|}^q+{\left|f^{‴}\left({\vartheta }_2\right)\right|}^q-{\displaystyle \frac{|f^{‴}\left(w_1\right){|}^q+3{\left|f^{‴}\left(w_2\right)\right|}^q}{4}}\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ & +{\left(|f^{‴}\left({\vartheta }_1\right){|}^q+{\left|f^{‴}\left({\vartheta }_2\right)\right|}^q-{\displaystyle \frac{3|f^{‴}\left(w_1\right){|}^q+{\left|f^{‴}\left(w_2\right)\right|}^q}{4}}\right)}^{{\displaystyle \frac{1}{q}}}].\hfill \end{array}$$

To evaluate the integral ${\int }_0^1{|\eta -{\eta }^3|}^{p}d\eta ,$ we observe that for any $A>B\ge 0$ and $p\ge 1,$ we have ${(A-B)}^p\le A^p-B^p.$ Thus, it follows that

$$|\eta -{\eta }^3{|}^p\le {\eta }^p-{\eta }^{3p},$$

for all $\eta \in [0,1].$ Hence, we have that

$$\begin{array}{cc}\hfill {\int }_0^1{|\eta -{\eta }^3|}^{p}d\eta & \le {\int }_0^1({\eta }^p-{\eta }^{3p})d\eta ={\displaystyle \frac{2p}{(p+1)(3p+1)}}.\hfill \end{array}$$

So, the proof of Theorem 4 is complete. □

3. Inequalities of the Hermite–Hadamard–Mercer Type for Fractional Integrals

In this section, we provide some H–H–M-type inequalities for fractional integrals of functions with a third derivative whose absolute value is convex.

Firstly, we found an integral identity for differentiable functions via R.L fractional integrals, which is useful for the fundamental results.

Lemma 2.

Assume that $f:I=[{\vartheta }_1,{\vartheta }_2]\subset R\to R$ is a three-times differentiable mapping on $({\vartheta }_1,{\vartheta }_2)$ so that $f^{‴}\in L[{\vartheta }_1,{\vartheta }_2]$ with ${\vartheta }_1$, ${\vartheta }_2\in I$, ${\vartheta }_1<{\vartheta }_2$. Then, the following identity for R.L fractional integrals holds:

$$\begin{array}{cc}\hfill & {\displaystyle \frac{f({\vartheta }_1+{\vartheta }_2-w_2)+f({\vartheta }_1+{\vartheta }_2-w_1)}{2}}-{\displaystyle \frac{2^{\alpha -1}\Gamma (\alpha +1)}{{(w_2-w_1)}^{\alpha }}}[J_{{({\vartheta }_1+{\vartheta }_2-w_2)}^{+}}^{\alpha }f\left({\vartheta }_1+{\vartheta }_2-{\displaystyle \frac{w_1+w_2}{2}}\right)\hfill \\ & +J_{{({\vartheta }_1+{\vartheta }_2-w_1)}^{-}}^{\alpha }f\left({\vartheta }_1+{\vartheta }_2-{\displaystyle \frac{w_1+w_2}{2}}\right)]+{\displaystyle \frac{w_2-w_1}{4(\alpha +2)}}\left[f^{\prime }({\vartheta }_1+{\vartheta }_2-w_2)-f^{\prime }({\vartheta }_1+{\vartheta }_2-w_1)\right]\hfill \\ & ={\displaystyle \frac{{(w_2-w_1)}^3}{16(\alpha +2)(\alpha +1)}}{\int }_0^1(\eta -{\eta }^{\alpha +2})[f^{‴}\left({\vartheta }_1+{\vartheta }_2-\left({\displaystyle \frac{1-\eta }{2}}{w}_1+{\displaystyle \frac{1+\eta }{2}}{w}_2\right)\right)\hfill \\ & -f^{‴}\left({\vartheta }_1+{\vartheta }_2-\left({\displaystyle \frac{1+\eta }{2}}{w}_1+{\displaystyle \frac{1-\eta }{2}}{w}_2\right)\right)]d\eta ,\hfill \end{array}$$

for all $w_1,w_2\in [{\vartheta }_1,{\vartheta }_2],$ $\alpha >0$, and $\eta \in [0,1].$

Proof. 

It suffices to note that

$$\begin{array}{cc}\hfill S& ={\int }_0^1(\eta -{\eta }^{\alpha +2})f^{‴}\left({\vartheta }_1+{\vartheta }_2-\left({\displaystyle \frac{1-\eta }{2}}{w}_1+{\displaystyle \frac{1+\eta }{2}}{w}_2\right)\right)d\eta \hfill \\ & -{\int }_0^1(\eta -{\eta }^{\alpha +2})f^{‴}\left({\vartheta }_1+{\vartheta }_2-\left({\displaystyle \frac{1+\eta }{2}}{w}_1+{\displaystyle \frac{1-\eta }{2}}{w}_2\right)\right)d\eta \hfill \\ \hfill & =S_1-S_2.\hfill \end{array}$$

Calculating $S_1$ and $S_2$ by integration by parts three times, we obtain

$$\begin{array}{cc}\hfill S_1& ={\int }_0^1(\eta -{\eta }^{\alpha +2})f^{‴}\left({\vartheta }_1+{\vartheta }_2-\left({\displaystyle \frac{1-\eta }{2}}{w}_1+{\displaystyle \frac{1+\eta }{2}}{w}_2\right)\right)d\eta \hfill \\ \hfill & =-{\displaystyle \frac{2(\eta -{\eta }^{\alpha +2})f^{″}\left({\vartheta }_1+{\vartheta }_2-\left(\frac{1-\eta }{2}{w}_1+\frac{1+\eta }{2}{w}_2\right)\right)}{w_2-w_1}}{|}_0^1\hfill \\ \hfill & +{\displaystyle \frac{2}{w_2-w_1}}{\int }_0^1(1-(\alpha +2){\eta }^{\alpha +1}{f}^{″}\left({\vartheta }_1+{\vartheta }_2-\left({\displaystyle \frac{1-\eta }{2}}{w}_1+{\displaystyle \frac{1+\eta }{2}}{w}_2\right)\right)d\eta \hfill \\ \hfill & ={\displaystyle \frac{2}{w_2-w_1}}[-{\displaystyle \frac{2(1-(\alpha +2){\eta }^{\alpha +1})f^{\prime }\left({\vartheta }_1+{\vartheta }_2-\left(\frac{1-\eta }{2}{w}_1+\frac{1+\eta }{2}{w}_2\right)\right)}{w_2-w_1}}{|}_0^1\hfill \\ \hfill & -{\displaystyle \frac{2(\alpha +2)(\alpha +1)}{w_2-w_1}}{\int }_0^1{\eta }^{\alpha }{f}^{\prime }\left({\vartheta }_1+{\vartheta }_2-\left({\displaystyle \frac{1-\eta }{2}}{w}_1+{\displaystyle \frac{1+\eta }{2}}{w}_2\right)\right)d\eta ]\hfill \\ & ={\displaystyle \frac{2}{w_2-w_1}}\left\{{\displaystyle \frac{2(\alpha +1)}{w_2-w_1}}{f}^{\prime }({\vartheta }_1+{\vartheta }_2-w_2)+{\displaystyle \frac{2}{w_2-w_1}}{f}^{\prime }\left({\vartheta }_1+{\vartheta }_2-{\displaystyle \frac{w_1+w_2}{2}}\right)\right\}\hfill \\ \hfill & -{\displaystyle \frac{4(\alpha +2)(\alpha +1)}{{(w_2-w_1)}^2}}[-{\displaystyle \frac{2{\eta }^{\alpha }f\left({\vartheta }_1+{\vartheta }_2-\left(\frac{1-\eta }{2}{w}_1+\frac{1+\eta }{2}{w}_2\right)\right)}{w_2-w_1}}{|}_0^1\hfill \\ \hfill & +{\displaystyle \frac{2\alpha }{w_2-w_1}}{\int }_0^1{\eta }^{\alpha -1}f\left({\vartheta }_1+{\vartheta }_2-\left({\displaystyle \frac{1-\eta }{2}}{w}_1+{\displaystyle \frac{1+\eta }{2}}{w}_2\right)\right)d\eta ]\hfill \\ & ={\displaystyle \frac{4(\alpha +1)}{{(w_2-w_1)}^2}}{f}^{\prime }({\vartheta }_1+{\vartheta }_2-w_2)+{\displaystyle \frac{4}{{(w_2-w_1)}^2}}{f}^{\prime }\left({\vartheta }_1+{\vartheta }_2-{\displaystyle \frac{w_1+w_2}{2}}\right)\hfill \\ & +{\displaystyle \frac{8(\alpha +2)(\alpha +1)}{{(w_2-w_1)}^3}}f({\vartheta }_1+{\vartheta }_2-w_2)\hfill \\ \hfill & -{\displaystyle \frac{2^{\alpha +3}(\alpha +2)(\alpha +1)\alpha }{{(w_2-w_1)}^{\alpha +3}}}{\int }_{{\vartheta }_1+{\vartheta }_2-w_2}^{{\vartheta }_1+{\vartheta }_2-{\displaystyle \frac{w_1+w_2}{2}}}{\left(\left({\vartheta }_1+{\vartheta }_2-{\displaystyle \frac{w_2-w_1}{2}}\right)-u\right)}^{\alpha -1}f\left(u\right)du\hfill \\ \hfill & ={\displaystyle \frac{4(\alpha +1)}{{(w_2-w_1)}^2}}{f}^{\prime }({\vartheta }_1+{\vartheta }_2-w_2)+{\displaystyle \frac{4}{{(w_2-w_1)}^2}}{f}^{\prime }\left({\vartheta }_1+{\vartheta }_2-{\displaystyle \frac{w_1+w_2}{2}}\right)\hfill \\ & +{\displaystyle \frac{8(\alpha +2)(\alpha +1)}{{(w_2-w_1)}^3}}f({\vartheta }_1+{\vartheta }_2-w_2)\hfill \\ \hfill & -{\displaystyle \frac{2^{\alpha +3}\Gamma (\alpha +3)}{{(w_2-w_1)}^{\alpha +3}}}{J}_{{({\vartheta }_1+{\vartheta }_2-w_2)}^{+}}^{\alpha }f\left({\vartheta }_1+{\vartheta }_2-{\displaystyle \frac{w_1+w_2}{2}}\right),\hfill \end{array}$$

and similarly,

$$\begin{array}{cc}\hfill S_2& ={\int }_0^1(\eta -{\eta }^{\alpha +2})f^{‴}\left({\vartheta }_1+{\vartheta }_2-\left({\displaystyle \frac{1+\eta }{2}}{w}_1+{\displaystyle \frac{1-\eta }{2}}{w}_2\right)\right)d\eta \hfill \\ \hfill & ={\displaystyle \frac{4(\alpha +1)}{{(w_2-w_1)}^2}}{f}^{\prime }({\vartheta }_1+{\vartheta }_2-w_1)+{\displaystyle \frac{4}{{(w_2-w_1)}^2}}{f}^{\prime }\left({\vartheta }_1+{\vartheta }_2-{\displaystyle \frac{w_1+w_2}{2}}\right)\hfill \\ & -{\displaystyle \frac{8(\alpha +2)(\alpha +1)}{{(w_2-w_1)}^3}}f({\vartheta }_1+{\vartheta }_2-w_1)+{\displaystyle \frac{2^{\alpha +3}\Gamma (\alpha +3)}{{(w_2-w_1)}^{\alpha +3}}}{J}_{{({\vartheta }_1+{\vartheta }_2-w_1)}^{-}}^{\alpha }f\left({\vartheta }_1+{\vartheta }_2-{\displaystyle \frac{w_1+w_2}{2}}\right).\hfill \end{array}$$

By substituting $S_1$ and $S_2$ and then multiplying the result by ${\displaystyle \frac{{(w_2-w_1)}^3}{16(\alpha +2)(\alpha +1)}}$, we obtain the desired identity. □

Remark 3.

If we take $\alpha =1$ in Lemma 2, then Lemma 2 gives Lemma 1.

Theorem 5.

Assume that $f:I=[{\vartheta }_1,{\vartheta }_2]\subset R\to R$ is a three-times differentiable mapping on $({\vartheta }_1,{\vartheta }_2)$ such that $f^{‴}\in L[{\vartheta }_1,{\vartheta }_2]$, where ${\vartheta }_1$, ${\vartheta }_2\in I$ with ${\vartheta }_1<{\vartheta }_2$. If the function $|f^{‴}|$ is convex on $[{\vartheta }_1,{\vartheta }_2]$, then we obtain the next inequality for R.L fractional integrals:

$$\begin{array}{cc}\hfill & |{\displaystyle \frac{f({\vartheta }_1+{\vartheta }_2-w_2)+f({\vartheta }_1+{\vartheta }_2-w_1)}{2}}-{\displaystyle \frac{2^{\alpha -1}\Gamma (\alpha +1)}{{(w_2-w_1)}^{\alpha }}}[J_{{({\vartheta }_1+{\vartheta }_2-w_2)}^{+}}^{\alpha }f\left({\vartheta }_1+{\vartheta }_2-{\displaystyle \frac{w_1+w_2}{2}}\right)\hfill \\ & +J_{{({\vartheta }_1+{\vartheta }_2-w_1)}^{-}}^{\alpha }f\left({\vartheta }_1+{\vartheta }_2-{\displaystyle \frac{w_1+w_2}{2}}\right)]+{\displaystyle \frac{w_2-w_1}{4(\alpha +2)}}\left[f^{\prime }({\vartheta }_1+{\vartheta }_2-w_2)-f^{\prime }({\vartheta }_1+{\vartheta }_2-w_1)\right]|\hfill \\ \hfill & \le {\displaystyle \frac{{(w_2-w_1)}^3}{16(\alpha +3)(\alpha +2)}}\left[|f^{‴}\left({\vartheta }_1\right)|+|f^{‴}\left({\vartheta }_2\right)|-{\displaystyle \frac{|f^{‴}\left(w_1\right)|+|f^{‴}\left(w_2\right)|}{2}}\right],\hfill \end{array}$$

for all $w_1,w_2\in [{\vartheta }_1,{\vartheta }_2]$ and $\alpha >0.$

Proof. 

Using Lemma 2 and the J–M inequality, we find that

$$\begin{array}{cc}\hfill & |{\displaystyle \frac{f({\vartheta }_1+{\vartheta }_2-w_2)+f({\vartheta }_1+{\vartheta }_2-w_1)}{2}}-{\displaystyle \frac{2^{\alpha -1}\Gamma (\alpha +1)}{{(w_2-w_1)}^{\alpha }}}[J_{{({\vartheta }_1+{\vartheta }_2-w_2)}^{+}}^{\alpha }f\left({\vartheta }_1+{\vartheta }_2-{\displaystyle \frac{w_1+w_2}{2}}\right)\hfill \\ & +J_{{({\vartheta }_1+{\vartheta }_2-w_1)}^{-}}^{\alpha }f\left({\vartheta }_1+{\vartheta }_2-{\displaystyle \frac{w_1+w_2}{2}}\right)]+{\displaystyle \frac{w_2-w_1}{4(\alpha +2)}}\left[f^{\prime }({\vartheta }_1+{\vartheta }_2-w_2)-f^{\prime }({\vartheta }_1+{\vartheta }_2-w_1)\right]|\hfill \\ & \le {\displaystyle \frac{{(w_2-w_1)}^3}{16(\alpha +2)(\alpha +1)}}\left[{\int }_0^1\left|(\eta -{\eta }^{\alpha +2})\right|\right|f^{‴}\left({\vartheta }_1+{\vartheta }_2-\left({\displaystyle \frac{1-\eta }{2}}{w}_1+{\displaystyle \frac{1+\eta }{2}}{w}_2\right)\right)|d\eta \hfill \\ \hfill & +{\int }_0^1\left|(\eta -{\eta }^{\alpha +2})\right|\left|f^{‴}\left({\vartheta }_1+{\vartheta }_2-\left({\displaystyle \frac{1+\eta }{2}}{w}_1+{\displaystyle \frac{1-\eta }{2}}{w}_2\right)\right)\right|d\eta ]\hfill \\ \hfill & \le {\displaystyle \frac{{(w_2-w_1)}^3}{16(\alpha +2)(\alpha +1)}}[{\int }_0^1|(\eta -{\eta }^{\alpha +2})\left|\right[|f^{‴}\left({\vartheta }_1\right)|+|f^{‴}\left({\vartheta }_2\right)|\hfill \\ & -\left({\displaystyle \frac{1-\eta }{2}}|f^{‴}\left(w_1\right)|+{\displaystyle \frac{1+\eta }{2}}\left|f^{‴}\left(w_2\right)\right|\right)]d\eta \hfill \\ \hfill & +{\int }_0^1\left|(\eta -{\eta }^{\alpha +2})\right|\left[|f^{‴}\left({\vartheta }_1\right)|+|f^{‴}\left({\vartheta }_2\right)|-\left({\displaystyle \frac{1+\eta }{2}}|f^{‴}\left(w_1\right)|+{\displaystyle \frac{1-\eta }{2}}\left|f^{‴}\left(w_2\right)\right|\right)\right]d\eta ]\hfill \\ \hfill & ={\displaystyle \frac{{(w_2-w_1)}^3}{32(\alpha +3)(\alpha +2)}}\left[2\left[\right|f^{‴}\left({\vartheta }_1\right)|+|f^{‴}\left({\vartheta }_2\right)\left|\right]-\left[\right|f^{‴}\left(w_1\right)|+|f^{‴}\left(w_2\right)\left|\right]\right],\hfill \end{array}$$

which finishes the demonstration. □

Remark 4.

If we take $\alpha =1$ in Theorem 5, then Theorem 5 gives Theorem 2.

Theorem 6.

Assume that $f:I=[{\vartheta }_1,{\vartheta }_2]\subset R\to R$ is a three-times differentiable mapping on $({\vartheta }_1,{\vartheta }_2)$ with ${\vartheta }_1<{\vartheta }_2.$ If the function $|f^{‴}{|}^q$ is convex on $[{\vartheta }_1,{\vartheta }_2]$, $q\ge 1,$ then the following inequality for R.L fractional integrals holds:

$$\begin{array}{cc}\hfill & |{\displaystyle \frac{f({\vartheta }_1+{\vartheta }_2-w_2)+f({\vartheta }_1+{\vartheta }_2-w_1)}{2}}-{\displaystyle \frac{2^{\alpha -1}\Gamma (\alpha +1)}{{(w_2-w_1)}^{\alpha }}}[J_{{({\vartheta }_1+{\vartheta }_2-w_2)}^{+}}^{\alpha }f\left({\vartheta }_1+{\vartheta }_2-{\displaystyle \frac{w_1+w_2}{2}}\right)\hfill \\ & +J_{{({\vartheta }_1+{\vartheta }_2-w_1)}^{-}}^{\alpha }f\left({\vartheta }_1+{\vartheta }_2-{\displaystyle \frac{w_1+w_2}{2}}\right)]+{\displaystyle \frac{w_2-w_1}{4(\alpha +2)}}\left[f^{\prime }({\vartheta }_1+{\vartheta }_2-w_2)-f^{\prime }({\vartheta }_1+{\vartheta }_2-w_1)\right]|\hfill \\ & \le {\displaystyle \frac{{(w_2-w_1)}^3}{32(\alpha +3)(\alpha +2)}}[{\left(|f^{‴}\left({\vartheta }_1\right){|}^q+{\left|f^{‴}\left({\vartheta }_2\right)\right|}^q-{\displaystyle \frac{(\alpha +6)|f^{‴}\left(w_1\right){|}^q+(5\alpha +18){\left|f^{‴}\left(w_2\right)\right|}^q}{6(\alpha +4)}}\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +{\left(|f^{‴}\left({\vartheta }_1\right){|}^q+{\left|f^{‴}\left({\vartheta }_2\right)\right|}^q-{\displaystyle \frac{(5\alpha +18)|f^{‴}\left(w_1\right){|}^q+(\alpha +6){\left|f^{‴}\left(w_2\right)\right|}^q}{6(\alpha +4)}}\right)}^{{\displaystyle \frac{1}{q}}}],\hfill \end{array}$$

for all $w_1,w_2\in [{\vartheta }_1,{\vartheta }_2]$ and $\alpha >0.$

Proof. 

Using Lemma 2 and also the power mean inequality when $q\ge 1,$ we have

$$\begin{array}{cc}\hfill & |{\displaystyle \frac{f({\vartheta }_1+{\vartheta }_2-w_2)+f({\vartheta }_1+{\vartheta }_2-w_1)}{2}}-{\displaystyle \frac{2^{\alpha -1}\Gamma (\alpha +1)}{{(w_2-w_1)}^{\alpha }}}[J_{{({\vartheta }_1+{\vartheta }_2-w_2)}^{+}}^{\alpha }f\left({\vartheta }_1+{\vartheta }_2-{\displaystyle \frac{w_1+w_2}{2}}\right)\hfill \\ & +J_{{({\vartheta }_1+{\vartheta }_2-w_1)}^{-}}^{\alpha }f\left({\vartheta }_1+{\vartheta }_2-{\displaystyle \frac{w_1+w_2}{2}}\right)]+{\displaystyle \frac{w_2-w_1}{4(\alpha +2)}}\left[f^{\prime }({\vartheta }_1+{\vartheta }_2-w_2)-f^{\prime }({\vartheta }_1+{\vartheta }_2-w_1)\right]|\hfill \\ & \le {\displaystyle \frac{{(w_2-w_1)}^3}{16(\alpha +2)(\alpha +1)}}{\left({\int }_0^1(\eta -{\eta }^{\alpha +2})d\eta \right)}^{1-{\displaystyle \frac{1}{q}}}\times \hfill \\ & \times \{{\left({\int }_0^1(\eta -{\eta }^{\alpha +2})|f^{‴}\left({\vartheta }_1+{\vartheta }_2-\left({\displaystyle \frac{1-\eta }{2}}{w}_1+{\displaystyle \frac{1+\eta }{2}}{w}_2\right)\right){|}^{q}d\eta \right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ & +{\left({\int }_0^1(\eta -{\eta }^{\alpha +2})|f^{‴}\left({\vartheta }_1+{\vartheta }_2-\left({\displaystyle \frac{1+\eta }{2}}{w}_1+{\displaystyle \frac{1-\eta }{2}}{w}_2\right)\right){|}^{q}d\eta \right)}^{{\displaystyle \frac{1}{q}}}\}.\hfill \end{array}$$

Using the J–M inequality because of the convexity of $|f^{‴}{|}^q$, we have

$$\begin{array}{cc}\hfill & |{\displaystyle \frac{f({\vartheta }_1+{\vartheta }_2-w_2)+f({\vartheta }_1+{\vartheta }_2-w_1)}{2}}-{\displaystyle \frac{2^{\alpha -1}\Gamma (\alpha +1)}{{(w_2-w_1)}^{\alpha }}}[J_{{({\vartheta }_1+{\vartheta }_2-w_2)}^{+}}^{\alpha }f\left({\vartheta }_1+{\vartheta }_2-{\displaystyle \frac{w_1+w_2}{2}}\right)\hfill \\ & +J_{{({\vartheta }_1+{\vartheta }_2-w_1)}^{-}}^{\alpha }f\left({\vartheta }_1+{\vartheta }_2-{\displaystyle \frac{w_1+w_2}{2}}\right)]+{\displaystyle \frac{w_2-w_1}{4(\alpha +2)}}\left[f^{\prime }({\vartheta }_1+{\vartheta }_2-w_2)-f^{\prime }({\vartheta }_1+{\vartheta }_2-w_1)\right]|\hfill \\ & \le {\displaystyle \frac{{(w_2-w_1)}^3}{16(\alpha +2)(\alpha +1)}}{\left({\int }_0^1(\eta -{\eta }^{\alpha +2})d\eta \right)}^{1-{\displaystyle \frac{1}{q}}}\hfill \\ & \times \{{\left({\int }_0^1(\eta -{\eta }^{\alpha +2})\left(|f^{‴}\left({\vartheta }_1\right){|}^q+{\left|f^{‴}\left({\vartheta }_2\right)\right|}^q-\left({\displaystyle \frac{1-\eta }{2}}|f^{‴}\left(w_1\right){|}^q+{\displaystyle \frac{1+\eta }{2}}{\left|f^{‴}\left(w_2\right)\right|}^q\right)\right)d\eta \right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +{\left({\int }_0^1(\eta -{\eta }^{\alpha +2})\left(|f^{‴}\left({\vartheta }_1\right){|}^q+{\left|f^{‴}\left({\vartheta }_2\right)\right|}^q-\left({\displaystyle \frac{1+\eta }{2}}|f^{‴}\left(w_1\right){|}^q+{\displaystyle \frac{1-\eta }{2}}{\left|f^{‴}\left(w_2\right)\right|}^q\right)\right)d\eta \right)}^{{\displaystyle \frac{1}{q}}}\}\hfill \\ & ={\displaystyle \frac{{(w_2-w_1)}^3}{32(\alpha +3)(\alpha +2)}}[{\left(|f^{‴}\left({\vartheta }_1\right){|}^q+{\left|f^{‴}\left({\vartheta }_2\right)\right|}^q-{\displaystyle \frac{(\alpha +6)|f^{‴}\left(w_1\right){|}^q+(5\alpha +18){\left|f^{‴}\left(w_2\right)\right|}^q}{6(\alpha +4)}}\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +{\left(|f^{‴}\left({\vartheta }_1\right){|}^q+{\left|f^{‴}\left({\vartheta }_2\right)\right|}^q-{\displaystyle \frac{(5\alpha +18)|f^{‴}\left(w_1\right){|}^q+(\alpha +6){\left|f^{‴}\left(w_2\right)\right|}^q}{6(\alpha +4)}}\right)}^{{\displaystyle \frac{1}{q}}}].\hfill \end{array}$$

Thus, we find the desired inequality. □

Remark 5.

If we take $\alpha =1$ in Theorem 6, then Theorem 6 gives Theorem 3.

Theorem 7.

Assume that $f:I=[{\vartheta }_1,{\vartheta }_2]\subset R\to R$ is a three-times differentiable mapping on $({\vartheta }_1,{\vartheta }_2)$ such that $f^{‴}\in L[{\vartheta }_1,{\vartheta }_2]$, where ${\vartheta }_1$, ${\vartheta }_2\in I$ with ${\vartheta }_1<{\vartheta }_2$. If the function $|f^{‴}{|}^q$ is convex on $[{\vartheta }_1,{\vartheta }_2]$, when $q>1$, then the following R.L fractional integral inequality holds:

$$\begin{array}{cc}\hfill & |{\displaystyle \frac{f({\vartheta }_1+{\vartheta }_2-w_2)+f({\vartheta }_1+{\vartheta }_2-w_1)}{2}}-{\displaystyle \frac{2^{\alpha -1}\Gamma (\alpha +1)}{{(w_2-w_1)}^{\alpha }}}[J_{{({\vartheta }_1+{\vartheta }_2-w_2)}^{+}}^{\alpha }f\left({\vartheta }_1+{\vartheta }_2-{\displaystyle \frac{w_1+w_2}{2}}\right)\hfill \\ & +J_{{({\vartheta }_1+{\vartheta }_2-w_1)}^{-}}^{\alpha }f\left({\vartheta }_1+{\vartheta }_2-{\displaystyle \frac{w_1+w_2}{2}}\right)]+{\displaystyle \frac{w_2-w_1}{4(\alpha +2)}}\left[f^{\prime }({\vartheta }_1+{\vartheta }_2-w_2)-f^{\prime }({\vartheta }_1+{\vartheta }_2-w_1)\right]|\hfill \\ & \le {\displaystyle \frac{{(w_2-w_1)}^3}{16(\alpha +2)(\alpha +1)}}M[{\left(|f^{‴}\left({\vartheta }_1\right){|}^q+{\left|f^{‴}\left({\vartheta }_2\right)\right|}^q-{\displaystyle \frac{|f^{‴}\left(w_1\right){|}^q+3{\left|f^{‴}\left(w_2\right)\right|}^q}{4}}\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +{\left(|f^{‴}\left({\vartheta }_1\right){|}^q+{\left|f^{‴}\left({\vartheta }_2\right)\right|}^q-{\displaystyle \frac{3|f^{‴}\left(w_1\right){|}^q+{\left|f^{‴}\left(w_2\right)\right|}^q}{4}}\right)}^{{\displaystyle \frac{1}{q}}}],\hfill \end{array}$$

where $M={\left({\displaystyle \frac{p(\alpha +1)}{(p+1)\left(p\right(\alpha +2)+1)}}\right)}^{{\displaystyle \frac{1}{p}}}$ and ${\displaystyle \frac{1}{p}}+{\displaystyle \frac{1}{q}}=1$ for all $w_1,w_2\in [{\vartheta }_1,{\vartheta }_2]$ and $\alpha >0.$

Proof. 

By Lemma 2, and also Hölder’s inequality, we obtain

$$\begin{array}{cc}\hfill & |{\displaystyle \frac{f({\vartheta }_1+{\vartheta }_2-w_2)+f({\vartheta }_1+{\vartheta }_2-w_1)}{2}}-{\displaystyle \frac{2^{\alpha -1}\Gamma (\alpha +1)}{{(w_2-w_1)}^{\alpha }}}[J_{{({\vartheta }_1+{\vartheta }_2-w_2)}^{+}}^{\alpha }f\left({\vartheta }_1+{\vartheta }_2-{\displaystyle \frac{w_1+w_2}{2}}\right)\hfill \\ & +J_{{({\vartheta }_1+{\vartheta }_2-w_1)}^{-}}^{\alpha }f\left({\vartheta }_1+{\vartheta }_2-{\displaystyle \frac{w_1+w_2}{2}}\right)]+{\displaystyle \frac{w_2-w_1}{4(\alpha +2)}}\left[f^{\prime }({\vartheta }_1+{\vartheta }_2-w_2)-f^{\prime }({\vartheta }_1+{\vartheta }_2-w_1)\right]|\hfill \\ & \le {\displaystyle \frac{{(w_2-w_1)}^3}{16(\alpha +2)(\alpha +1)}}({\int }_0^1|\eta -{\eta }^{\alpha +2}{{|}^{p}d\eta )}^{{\displaystyle \frac{1}{p}}}\{{\left({\int }_0^1\right|f^{‴}\left({\vartheta }_1+{\vartheta }_2-\left({\displaystyle \frac{1-\eta }{2}}{w}_1+{\displaystyle \frac{1+\eta }{2}}{w}_2\right)\right){|}^{q}d\eta )}^{{\displaystyle \frac{1}{q}}}\hfill \\ & +{\left({\int }_0^1|f^{‴}\left({\vartheta }_1+{\vartheta }_2-\left({\displaystyle \frac{1+\eta }{2}}{w}_1+{\displaystyle \frac{1-\eta }{2}}{w}_2\right)\right){|}^{q}d\eta \right)}^{{\displaystyle \frac{1}{q}}}\}.\hfill \end{array}$$

Using the J–M inequality because of the convexity of $|f^{‴}{|}^q$, we have

$$\begin{array}{cc}\hfill & |{\displaystyle \frac{f({\vartheta }_1+{\vartheta }_2-w_2)+f({\vartheta }_1+{\vartheta }_2-w_1)}{2}}-{\displaystyle \frac{2^{\alpha -1}\Gamma (\alpha +1)}{{(w_2-w_1)}^{\alpha }}}[J_{{({\vartheta }_1+{\vartheta }_2-w_2)}^{+}}^{\alpha }f\left({\vartheta }_1+{\vartheta }_2-{\displaystyle \frac{w_1+w_2}{2}}\right)\hfill \\ & +J_{{({\vartheta }_1+{\vartheta }_2-w_1)}^{-}}^{\alpha }f\left({\vartheta }_1+{\vartheta }_2-{\displaystyle \frac{w_1+w_2}{2}}\right)]+{\displaystyle \frac{w_2-w_1}{4(\alpha +2)}}\left[f^{\prime }({\vartheta }_1+{\vartheta }_2-w_2)-f^{\prime }({\vartheta }_1+{\vartheta }_2-w_1)\right]|\hfill \\ & \le {\displaystyle \frac{{(w_2-w_1)}^3}{16(\alpha +2)(\alpha +1)}}{\left({\int }_0^1{|\eta -{\eta }^{\alpha +2}|}^{p}d\eta \right)}^{{\displaystyle \frac{1}{p}}}\hfill \\ & \times \{{\left({\int }_0^1\left(|f^{‴}\left({\vartheta }_1\right){|}^q+{\left|f^{‴}\left({\vartheta }_2\right)\right|}^q-\left({\displaystyle \frac{1-\eta }{2}}|f^{‴}\left(w_1\right){|}^q+{\displaystyle \frac{1+\eta }{2}}{\left|f^{‴}\left(w_2\right)\right|}^q\right)\right)d\eta \right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +{\left({\int }_0^1\left(|f^{‴}\left({\vartheta }_1\right){|}^q+{\left|f^{‴}\left({\vartheta }_2\right)\right|}^q-\left({\displaystyle \frac{1+\eta }{2}}|f^{‴}\left(w_1\right){|}^q+{\displaystyle \frac{1-\eta }{2}}{\left|f^{‴}\left(w_2\right)\right|}^q\right)\right)d\eta \right)}^{{\displaystyle \frac{1}{q}}}\}\hfill \\ & ={\displaystyle \frac{{(w_2-w_1)}^3}{16(\alpha +2)(\alpha +1)}}{\left({\int }_0^1{|\eta -{\eta }^{\alpha +2}|}^{p}d\eta \right)}^{{\displaystyle \frac{1}{p}}}[{\left(|f^{‴}\left({\vartheta }_1\right){|}^q+{\left|f^{‴}\left({\vartheta }_2\right)\right|}^q-{\displaystyle \frac{|f^{‴}\left(w_1\right){|}^q+3{\left|f^{‴}\left(w_2\right)\right|}^q}{4}}\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ & +{\left(|f^{‴}\left({\vartheta }_1\right){|}^q+{\left|f^{‴}\left({\vartheta }_2\right)\right|}^q-{\displaystyle \frac{3|f^{‴}\left(w_1\right){|}^q+{\left|f^{‴}\left(w_2\right)\right|}^q}{4}}\right)}^{{\displaystyle \frac{1}{q}}}].\hfill \end{array}$$

To evaluate the integral ${\int }_0^1{|\eta -{\eta }^{\alpha +2}|}^{p}d\eta ,$ we observe that for any $A>B\ge 0$ and $p\ge 1,$ we have ${(A-B)}^p\le A^p-B^p.$ Thus, it follows that

$$|\eta -{\eta }^{\alpha +2}{|}^p\le {\eta }^p-{\eta }^{p(\alpha +2)},$$

for all $\eta \in [0,1].$ Hence, we have that

$$\begin{array}{cc}\hfill {\int }_0^1{|\eta -{\eta }^{\alpha +2}|}^{p}d\eta & \le {\int }_0^1({\eta }^p-{\eta }^{p(\alpha +2)})d\eta \hfill \\ & ={\displaystyle \frac{p(\alpha +1)}{(p+1)\left(p\right(\alpha +2)+1)}}.\hfill \end{array}$$

This completes the demonstration. □

Remark 6.

If we consider $\alpha =1$ in Theorem 7, then Theorem 7 gives Theorem 4.

The following is a comparable integral identity via k-R.L fractional integrals in the case of differentiable functions being necessary to develop the next results.

Lemma 3.

Assume that $f:I=[{\vartheta }_1,{\vartheta }_2]\subset R\to R$ is a three-times differentiable mapping on $({\vartheta }_1,{\vartheta }_2)$ such that $f^{‴}\in L[{\vartheta }_1,{\vartheta }_2]$, where ${\vartheta }_1$, ${\vartheta }_2\in I$ with ${\vartheta }_1<{\vartheta }_2$. Then, the following identity for k-R.L fractional integrals holds:

$$\begin{array}{cc}\hfill & {\displaystyle \frac{f({\vartheta }_1+{\vartheta }_2-w_2)+f({\vartheta }_1+{\vartheta }_2-w_1)}{2}}-{\displaystyle \frac{2^{\frac{\alpha }{k}-1}{\Gamma }_k(\alpha +k)}{{(w_2-w_1)}^{\frac{\alpha }{k}}}}[{}_{k}J_{{({\vartheta }_1+{\vartheta }_2-w_2)}^{+}}^{\alpha }f\left({\vartheta }_1+{\vartheta }_2-{\displaystyle \frac{w_1+w_2}{2}}\right)\hfill \\ & +{}_{k}J_{{({\vartheta }_1+{\vartheta }_2-w_1)}^{-}}^{\alpha }f\left({\vartheta }_1+{\vartheta }_2-{\displaystyle \frac{w_1+w_2}{2}}\right)]+{\displaystyle \frac{k(w_2-w_1)}{4(\alpha +2k)}}\left[f^{\prime }({\vartheta }_1+{\vartheta }_2-w_2)-f^{\prime }({\vartheta }_1+{\vartheta }_2-w_1)\right]\hfill \\ & ={\displaystyle \frac{k^2{(w_2-w_1)}^3}{16(\alpha +2k)(\alpha +k)}}{\int }_0^1(\eta -{\eta }^{{\displaystyle \frac{\alpha }{k}}+2})[f^{‴}\left({\vartheta }_1+{\vartheta }_2-\left({\displaystyle \frac{1-\eta }{2}}{w}_1+{\displaystyle \frac{1+\eta }{2}}{w}_2\right)\right)\hfill \\ & -f^{‴}\left({\vartheta }_1+{\vartheta }_2-\left({\displaystyle \frac{1+\eta }{2}}{w}_1+{\displaystyle \frac{1-\eta }{2}}{w}_2\right)\right)]d\eta ,\hfill \end{array}$$

for all $w_1,w_2\in [{\vartheta }_1,{\vartheta }_2],$ ${\displaystyle \frac{\alpha }{k}}>0$ and $\eta \in [0,1].$

Proof. 

The proof is analogous to that of Lemma 2. □

Remark 7.

In Lemma 3, if we take $\alpha =k=1$, then we obtain Lemma 1.

Remark 8.

In Lemma 3, if we take $k=1,$ then we obtain Lemma 2.

Theorem 8.

Assume that $f:I=[{\vartheta }_1,{\vartheta }_2]\subset R\to R$ is a three-times differentiable mapping on $({\vartheta }_1,{\vartheta }_2)$ such that $f^{‴}\in L[{\vartheta }_1,{\vartheta }_2]$, where ${\vartheta }_1$, ${\vartheta }_2\in I$ with ${\vartheta }_1<{\vartheta }_2$. If the function $|f^{‴}|$ is convex on $[{\vartheta }_1,{\vartheta }_2]$, then we obtain the following inequality for k-R.L fractional integrals:

$$\begin{array}{cc}\hfill & |{\displaystyle \frac{f({\vartheta }_1+{\vartheta }_2-w_2)+f({\vartheta }_1+{\vartheta }_2-w_1)}{2}}-{\displaystyle \frac{2^{\frac{\alpha }{k}-1}{\Gamma }_k(\alpha +k)}{{(w_2-w_1)}^{\frac{\alpha }{k}}}}[{}_{k}J_{{({\vartheta }_1+{\vartheta }_2-w_2)}^{+}}^{\alpha }f\left({\vartheta }_1+{\vartheta }_2-{\displaystyle \frac{w_1+w_2}{2}}\right)\hfill \\ & +{}_{k}J_{{({\vartheta }_1+{\vartheta }_2-w_1)}^{-}}^{\alpha }f\left({\vartheta }_1+{\vartheta }_2-{\displaystyle \frac{w_1+w_2}{2}}\right)]+{\displaystyle \frac{k(w_2-w_1)}{4(\alpha +2k)}}\left[f^{\prime }({\vartheta }_1+{\vartheta }_2-w_2)-f^{\prime }({\vartheta }_1+{\vartheta }_2-w_1)\right]|\hfill \\ \hfill & \le {\displaystyle \frac{k^2{(w_2-w_1)}^3}{16(\alpha +3k)(\alpha +2k)}}\left[|f^{‴}\left({\vartheta }_1\right)|+|f^{‴}\left({\vartheta }_2\right)|-{\displaystyle \frac{|f^{‴}\left(w_1\right)|+|f^{‴}\left(w_2\right)|}{2}}\right],\hfill \end{array}$$

for all $w_1,w_2\in [{\vartheta }_1,{\vartheta }_2]$ and ${\displaystyle \frac{\alpha }{k}}>0.$

Proof. 

The proof is analogous to that of Theorem 5. □

Remark 9.

In Theorem 8, if we take $\alpha =k=1$, then we obtain Theorem 2.

Remark 10.

In Theorem 8, if we take $k=1$, then we obtain Theorem 5.

Theorem 9.

Assume that $f:I=[{\vartheta }_1,{\vartheta }_2]\subset R\to R$ is a three-times differentiable mapping on $({\vartheta }_1,{\vartheta }_2)$ with ${\vartheta }_1<{\vartheta }_2.$ If the function $|f^{‴}{|}^q$ is convex on $[{\vartheta }_1,{\vartheta }_2]$, $q\ge 1,$ then the following inequality for k-R.L fractional integrals is true:

$$\begin{array}{cc}\hfill & |{\displaystyle \frac{f({\vartheta }_1+{\vartheta }_2-w_2)+f({\vartheta }_1+{\vartheta }_2-w_1)}{2}}-{\displaystyle \frac{2^{\frac{\alpha }{k}-1}{\Gamma }_k(\alpha +k)}{{(w_2-w_1)}^{\frac{\alpha }{k}}}}[{}_{k}J_{{({\vartheta }_1+{\vartheta }_2-w_2)}^{+}}^{\alpha }f\left({\vartheta }_1+{\vartheta }_2-{\displaystyle \frac{w_1+w_2}{2}}\right)\hfill \\ & +{}_{k}J_{{({\vartheta }_1+{\vartheta }_2-w_1)}^{-}}^{\alpha }f\left({\vartheta }_1+{\vartheta }_2-{\displaystyle \frac{w_1+w_2}{2}}\right)]+{\displaystyle \frac{k(w_2-w_1)}{4(\alpha +2k)}}\left[f^{\prime }({\vartheta }_1+{\vartheta }_2-w_2)-f^{\prime }({\vartheta }_1+{\vartheta }_2-w_1)\right]|\hfill \\ \hfill & \le {\displaystyle \frac{k^2{(w_2-w_1)}^3}{32(\alpha +3k)(\alpha +2k)}}[{\left(|f^{‴}\left({\vartheta }_1\right){|}^q+{\left|f^{‴}\left({\vartheta }_2\right)\right|}^q-{\displaystyle \frac{(\alpha +6k)|f^{‴}\left(w_1\right){|}^q+(5\alpha +18k){\left|f^{‴}\left(w_2\right)\right|}^q}{6(\alpha +4k)}}\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +{\left(|f^{‴}\left({\vartheta }_1\right){|}^q+{\left|f^{‴}\left({\vartheta }_2\right)\right|}^q-{\displaystyle \frac{(5\alpha +18k)|f^{‴}\left(w_1\right){|}^q+(\alpha +6k){\left|f^{‴}\left(w_2\right)\right|}^q}{6(\alpha +4k)}}\right)}^{{\displaystyle \frac{1}{q}}}],\hfill \end{array}$$

for all $w_1,w_2\in [{\vartheta }_1,{\vartheta }_2]$ and ${\displaystyle \frac{\alpha }{k}}>0.$

Proof. 

The proof is analogous to that of Theorem 6. □

Remark 11.

In Theorem 9, if we take $\alpha =k=1$, then we obtain Theorem 3.

Remark 12.

In Theorem 9, if we take $k=1$, then we obtain Theorem 6.

Theorem 10.

Assume that $f:I=[{\vartheta }_1,{\vartheta }_2]\subset R\to R$ is a three-times differentiable mapping on $({\vartheta }_1,{\vartheta }_2)$ such that $f^{‴}\in L[{\vartheta }_1,{\vartheta }_2]$, where ${\vartheta }_1$, ${\vartheta }_2\in I$ with ${\vartheta }_1<{\vartheta }_2$. If the function $|f^{‴}{|}^q$ is convex on $[{\vartheta }_1,{\vartheta }_2]$, where $q>1$, then we obtain the following inequality for k-R.L fractional integrals:

$$\begin{array}{cc}\hfill & |{\displaystyle \frac{f({\vartheta }_1+{\vartheta }_2-w_2)+f({\vartheta }_1+{\vartheta }_2-w_1)}{2}}-{\displaystyle \frac{2^{\frac{\alpha }{k}-1}{\Gamma }_k(\alpha +k)}{{(w_2-w_1)}^{\frac{\alpha }{k}}}}[{}_{k}J_{{({\vartheta }_1+{\vartheta }_2-w_2)}^{+}}^{\alpha }f\left({\vartheta }_1+{\vartheta }_2-{\displaystyle \frac{w_1+w_2}{2}}\right)\hfill \\ & +{}_{k}J_{{({\vartheta }_1+{\vartheta }_2-w_1)}^{-}}^{\alpha }f\left({\vartheta }_1+{\vartheta }_2-{\displaystyle \frac{w_1+w_2}{2}}\right)]+{\displaystyle \frac{k(w_2-w_1)}{4(\alpha +2k)}}\left[f^{\prime }({\vartheta }_1+{\vartheta }_2-w_2)-f^{\prime }({\vartheta }_1+{\vartheta }_2-w_1)\right]|\hfill \\ \hfill & \le {\displaystyle \frac{k^2{(w_2-w_1)}^3}{16(\alpha +2k)(\alpha +k)}}{M}_k[{\left(|f^{‴}\left({\vartheta }_1\right){|}^q+{\left|f^{‴}\left({\vartheta }_2\right)\right|}^q-{\displaystyle \frac{|f^{‴}\left(w_1\right){|}^q+3{\left|f^{‴}\left(w_2\right)\right|}^q}{4}}\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +{\left(|f^{‴}\left({\vartheta }_1\right){|}^q+{\left|f^{‴}\left({\vartheta }_2\right)\right|}^q-{\displaystyle \frac{3|f^{‴}\left(w_1\right){|}^q+{\left|f^{‴}\left(w_2\right)\right|}^q}{4}}\right)}^{{\displaystyle \frac{1}{q}}}],\hfill \end{array}$$

where $M_k={\left({\displaystyle \frac{p(\alpha +k)}{(p+1)\left(p\right(\alpha +2k)+k)}}\right)}^{{\displaystyle \frac{1}{p}}}$ and ${\displaystyle \frac{1}{p}}+{\displaystyle \frac{1}{q}}=1,$ ${\displaystyle \frac{\alpha }{k}}>0$ for all $w_1,w_2\in [{\vartheta }_1,{\vartheta }_2].$

Proof. 

The proof is analogous to that of Theorem 7. □

Remark 13.

If we take $\alpha =k=1$ in Theorem 10, then Theorem 10 gives Theorem 4.

Remark 14.

If we take $k=1$ in Theorem 10, then Theorem 10 gives Theorem 7.

4. Inequalities of the Hermite–Hadamard–Mercer Type for Generalized Fractional Integral Operators

From [22], this section present several H–H–M-type inequalities for generalized fractional integral operators.

Lemma 4.

Let $f:[{\vartheta }_1,{\vartheta }_2]\to R$ be a three-times differentiable mapping on $({\vartheta }_1,{\vartheta }_2),$ with ${\vartheta }_1<{\vartheta }_2$, $\lambda >0.$ If $f^{‴}\in L[{\vartheta }_1,{\vartheta }_2]$, then the following identity for generalized fractional integral operators is satisfied:

$$\begin{array}{cc}\hfill & {\mathcal{F}}_{\rho ,\lambda +1}^{\sigma }\left[w{\left({\displaystyle \frac{w_2-w_1}{2}}\right)}^{\rho }\right]{\displaystyle \frac{f({\vartheta }_1+{\vartheta }_2-w_2)+f({\vartheta }_1+{\vartheta }_2-w_1)}{2}}-{\displaystyle \frac{w_2-w_1}{4}}\{{\mathcal{F}}_{\rho ,\lambda +3}^{\sigma }\left[w{\left({\displaystyle \frac{w_2-w_1}{2}}\right)}^{\rho }\right]\hfill \\ & -{\mathcal{F}}_{\rho ,\lambda +2}^{\sigma }\left[w{\left({\displaystyle \frac{w_2-w_1}{2}}\right)}^{\rho }\right]\}[f^{\prime }({\vartheta }_1+{\vartheta }_2-w_2)-f^{\prime }({\vartheta }_1+{\vartheta }_2-w_1)]\hfill \\ \hfill & -{\displaystyle \frac{2^{\lambda -1}}{{(w_2-w_1)}^{\lambda }}}[\left({\mathcal{J}}_{\rho ,\lambda ,{({\vartheta }_1+{\vartheta }_2-w_2)}^{+};w}^{\sigma }f\right)({\vartheta }_1+{\vartheta }_2-{\displaystyle \frac{w_1+w_2}{2}})\hfill \\ & +\left({\mathcal{J}}_{\rho ,\lambda ,{({\vartheta }_1+{\vartheta }_2-w_1)}^{-};w}^{\sigma }f\right)({\vartheta }_1+{\vartheta }_2-{\displaystyle \frac{w_1+w_2}{2}})]\hfill \\ \hfill & ={\displaystyle \frac{{(w_2-w_1)}^3}{16}}{\int }_0^1\{\eta {\mathcal{F}}_{\rho ,\lambda +3}^{\sigma }\left[w{\left({\displaystyle \frac{w_2-w_1}{2}}\right)}^{\rho }\right]-{\eta }^{\lambda +2}{\mathcal{F}}_{\rho ,\lambda +3}^{\sigma }\left[w{\left({\displaystyle \frac{w_2-w_1}{2}}\right)}^{\rho }{\eta }^{\rho }\right]\}\times \hfill \\ & \times [f^{‴}({\vartheta }_1+{\vartheta }_2-({\displaystyle \frac{1-\eta }{2}}{w}_1+{\displaystyle \frac{1+\eta }{2}}{w}_2))+f^{‴}({\vartheta }_1+{\vartheta }_2-({\displaystyle \frac{1+\eta }{2}}{w}_1+{\displaystyle \frac{1-\eta }{2}}{w}_2))],\hfill \end{array}$$

for all $w_1,w_2\in [{\vartheta }_1,{\vartheta }_2]$, $\lambda >0$ and $\eta \in [0,1].$

Proof. 

$I_1$ and $I_2$ denote the following integrals:

$$\begin{array}{cc}\hfill I_1& ={\int }_0^1\{\eta {\mathcal{F}}_{\rho ,\lambda +3}^{\sigma }\left[w{\left({\displaystyle \frac{w_2-w_1}{2}}\right)}^{\rho }\right]-{\eta }^{\lambda +2}{\mathcal{F}}_{\rho ,\lambda +3}^{\sigma }\left[w{\left({\displaystyle \frac{w_2-w_1}{2}}\right)}^{\rho }{\eta }^{\rho }\right]\}\times \hfill \\ & \times f^{‴}({\vartheta }_1+{\vartheta }_2-({\displaystyle \frac{1-\eta }{2}}{w}_1+{\displaystyle \frac{1+\eta }{2}}{w}_2))d\eta \hfill \end{array}$$

and

$$\begin{array}{cc}\hfill I_2& ={\int }_0^1\{\eta {\mathcal{F}}_{\rho ,\lambda +3}^{\sigma }\left[w{\left({\displaystyle \frac{w_2-w_1}{2}}\right)}^{\rho }\right]-{\eta }^{\lambda +2}{\mathcal{F}}_{\rho ,\lambda +3}^{\sigma }\left[w{\left({\displaystyle \frac{w_2-w_1}{2}}\right)}^{\rho }{\eta }^{\rho }\right]\}\times \hfill \\ & \times f^{‴}({\vartheta }_1+{\vartheta }_2-({\displaystyle \frac{1+\eta }{2}}{w}_1+{\displaystyle \frac{1-\eta }{2}}{w}_2))d\eta .\hfill \end{array}$$

Integrating by parts three times and then changing the variables, we successively obtain

$$\begin{array}{cc}\hfill & I_1=-{\displaystyle \frac{2}{w_2-w_1}}\{\eta {\mathcal{F}}_{\rho ,\lambda +3}^{\sigma }\left[w{\left({\displaystyle \frac{w_2-w_1}{2}}\right)}^{\rho }\right]-{\eta }^{\lambda +2}{\mathcal{F}}_{\rho ,\lambda +3}^{\sigma }\left[w{\left({\displaystyle \frac{w_2-w_1}{2}}\right)}^{\rho }{\eta }^{\rho }\right]\}\times \hfill \\ & \times f^{″}({\vartheta }_1+{\vartheta }_2-({\displaystyle \frac{1-\eta }{2}}{w}_1+{\displaystyle \frac{1+\eta }{2}}{w}_2)){|}_0^1\hfill \\ \hfill & -{\int }_0^1\{{\mathcal{F}}_{\rho ,\lambda +3}^{\sigma }\left[w{\left({\displaystyle \frac{w_2-w_1}{2}}\right)}^{\rho }\right]-{\eta }^{\lambda +1}{\mathcal{F}}_{\rho ,\lambda +2}^{\sigma }\left[w{\left({\displaystyle \frac{w_2-w_1}{2}}\right)}^{\rho }{\eta }^{\rho }\right]\}\times \hfill \\ & \times f^{″}({\vartheta }_1+{\vartheta }_2-({\displaystyle \frac{1-\eta }{2}}{w}_1+{\displaystyle \frac{1+\eta }{2}}{w}_2))d\eta \hfill \\ \hfill & =-{\displaystyle \frac{2^2}{{(w_2-w_1)}^2}}{\mathcal{F}}_{\rho ,\lambda +3}^{\sigma }\left[w{\left({\displaystyle \frac{w_2-w_1}{2}}\right)}^{\rho }\right]f^{\prime }({\vartheta }_1+{\vartheta }_2-w_2)\hfill \\ \hfill & +{\displaystyle \frac{2^2}{{(w_2-w_1)}^2}}{\left\{{\eta }^{\lambda +1}{\mathcal{F}}_{\rho ,\lambda +2}^{\sigma }\left[w{\left({\displaystyle \frac{w_2-w_1}{2}}\right)}^{\rho }{\eta }^{\rho }\right]f^{\prime }({\vartheta }_1+{\vartheta }_2-({\displaystyle \frac{1-\eta }{2}}{w}_1+{\displaystyle \frac{1+\eta }{2}}{w}_2))\right|}_0^1\hfill \\ \hfill & -{\int }_0^1{\eta }^{\lambda }{\mathcal{F}}_{\rho ,\lambda +1}^{\sigma }\left[w{\left({\displaystyle \frac{w_2-w_1}{2}}\right)}^{\rho }{\eta }^{\rho }\right]f^{\prime }({\vartheta }_1+{\vartheta }_2-({\displaystyle \frac{1-\eta }{2}}{w}_1+{\displaystyle \frac{1+\eta }{2}}{w}_2))d\eta \}\hfill \end{array}$$

$$\begin{array}{cc}\hfill & =-{\displaystyle \frac{2^2}{{(w_2-w_1)}^2}}\{{\mathcal{F}}_{\rho ,\lambda +3}^{\sigma }\left[w{\left({\displaystyle \frac{w_2-w_1}{2}}\right)}^{\rho }\right]-{\mathcal{F}}_{\rho ,\lambda +2}^{\sigma }\left[w{\left({\displaystyle \frac{w_2-w_1}{2}}\right)}^{\rho }\right]\}{f}^{\prime }({\vartheta }_1+{\vartheta }_2-w_2)\hfill \\ \hfill & +{\displaystyle \frac{2^2}{{(w_2-w_1)}^2}}{\mathcal{F}}_{\rho ,\lambda +3}^{\sigma }\left[w{\left({\displaystyle \frac{w_2-w_1}{2}}\right)}^{\rho }\right]f^{\prime }({\vartheta }_1+{\vartheta }_2-{\displaystyle \frac{w_1+w_2}{2}})\hfill \\ \hfill & +{\displaystyle \frac{2^3}{{(w_2-w_1)}^3}}{\left\{{\eta }^{\lambda }{\mathcal{F}}_{\rho ,\lambda +1}^{\sigma }\left[w{\left({\displaystyle \frac{w_2-w_1}{2}}\right)}^{\rho }{\eta }^{\rho }\right]f({\vartheta }_1+{\vartheta }_2-({\displaystyle \frac{1-\eta }{2}}{w}_1+{\displaystyle \frac{1+\eta }{2}}{w}_2))\right|}_0^1\hfill \\ \hfill & -{\int }_0^1{\eta }^{\lambda -1}{\mathcal{F}}_{\rho ,\lambda }^{\sigma }\left[w{\left({\displaystyle \frac{w_2-w_1}{2}}\right)}^{\rho }{\eta }^{\rho }\right]f({\vartheta }_1+{\vartheta }_2-({\displaystyle \frac{1-\eta }{2}}{w}_1+{\displaystyle \frac{1+\eta }{2}}{w}_2))d\eta \}\hfill \end{array}$$

$$\begin{array}{cc}\hfill & =-{\displaystyle \frac{2^2}{{(w_2-w_1)}^2}}\{{\mathcal{F}}_{\rho ,\lambda +3}^{\sigma }\left[w{\left({\displaystyle \frac{w_2-w_1}{2}}\right)}^{\rho }\right]-{\mathcal{F}}_{\rho ,\lambda +2}^{\sigma }\left[w{\left({\displaystyle \frac{w_2-w_1}{2}}\right)}^{\rho }\right]\}{f}^{\prime }({\vartheta }_1+{\vartheta }_2-w_2)\hfill \\ \hfill & +{\displaystyle \frac{2^2}{{(w_2-w_1)}^2}}{\mathcal{F}}_{\rho ,\lambda +3}^{\sigma }\left[w{\left({\displaystyle \frac{w_2-w_1}{2}}\right)}^{\rho }\right]f^{\prime }({\vartheta }_1+{\vartheta }_2-{\displaystyle \frac{w_1+w_2}{2}})\hfill \\ \hfill & +{\displaystyle \frac{2^3}{{(w_2-w_1)}^3}}{\mathcal{F}}_{\rho ,\lambda +1}^{\sigma }\left[w{\left({\displaystyle \frac{w_2-w_1}{2}}\right)}^{\rho }\right]f({\vartheta }_1+{\vartheta }_2-w_2)-{\displaystyle \frac{2^{\lambda +3}}{{(w_2-w_1)}^{\lambda +3}}}\times \hfill \\ & \times {\int }_{{\vartheta }_1+{\vartheta }_2-w_2}^{{\vartheta }_1+{\vartheta }_2-{\displaystyle \frac{w_1+w_2}{2}}}{({\vartheta }_1+{\vartheta }_2-{\displaystyle \frac{w_1+w_2}{2}}-u)}^{\lambda -1}{\mathcal{F}}_{\rho ,\lambda }^{\sigma }\left[w{({\vartheta }_1+{\vartheta }_2-{\displaystyle \frac{w_1+w_2}{2}}-u)}^{\rho }\right]f\left(u\right)du\hfill \end{array}$$

and thus,

$$\begin{array}{cc}\hfill & I_1=-{\displaystyle \frac{2^2}{{(w_2-w_1)}^2}}\{{\mathcal{F}}_{\rho ,\lambda +3}^{\sigma }\left[w{\left({\displaystyle \frac{w_2-w_1}{2}}\right)}^{\rho }\right]-{\mathcal{F}}_{\rho ,\lambda +2}^{\sigma }\left[w{\left({\displaystyle \frac{w_2-w_1}{2}}\right)}^{\rho }\right]\}{f}^{\prime }({\vartheta }_1+{\vartheta }_2-w_2)\hfill \\ \hfill & +{\displaystyle \frac{2^2}{{(w_2-w_1)}^2}}{\mathcal{F}}_{\rho ,\lambda +3}^{\sigma }\left[w{\left({\displaystyle \frac{w_2-w_1}{2}}\right)}^{\rho }\right]f^{\prime }({\vartheta }_1+{\vartheta }_2-{\displaystyle \frac{w_1+w_2}{2}})\hfill \\ \hfill & +{\displaystyle \frac{2^3}{{(w_2-w_1)}^3}}{\mathcal{F}}_{\rho ,\lambda +1}^{\sigma }\left[w{\left({\displaystyle \frac{w_2-w_1}{2}}\right)}^{\rho }\right]f({\vartheta }_1+{\vartheta }_2-w_2)\hfill \\ \hfill & -{\displaystyle \frac{2^{\lambda +3}}{{(w_2-w_1)}^{\lambda +3}}}\left({\mathcal{J}}_{\rho ,\lambda ,{({\vartheta }_1+{\vartheta }_2-w_2)}^{+};w}^{\sigma }f\right)({\vartheta }_1+{\vartheta }_2-{\displaystyle \frac{w_1+w_2}{2}}).\hfill \end{array}$$

Analogously, we have

$$\begin{array}{cc}\hfill & I_2=-{\displaystyle \frac{2^2}{{(w_2-w_1)}^2}}\{{\mathcal{F}}_{\rho ,\lambda +3}^{\sigma }\left[w{\left({\displaystyle \frac{w_2-w_1}{2}}\right)}^{\rho }\right]-{\mathcal{F}}_{\rho ,\lambda +2}^{\sigma }\left[w{\left({\displaystyle \frac{w_2-w_1}{2}}\right)}^{\rho }\right]\}{f}^{\prime }({\vartheta }_1+{\vartheta }_2-w_1)\hfill \\ \hfill & +{\displaystyle \frac{2^2}{{(w_2-w_1)}^2}}{\mathcal{F}}_{\rho ,\lambda +3}^{\sigma }\left[w{\left({\displaystyle \frac{w_2-w_1}{2}}\right)}^{\rho }\right]f^{\prime }({\vartheta }_1+{\vartheta }_2-{\displaystyle \frac{w_1+w_2}{2}})\hfill \\ \hfill & -{\displaystyle \frac{2^3}{{(w_2-w_1)}^3}}{\mathcal{F}}_{\rho ,\lambda +1}^{\sigma }\left[w{\left({\displaystyle \frac{w_2-w_1}{2}}\right)}^{\rho }\right]f({\vartheta }_1+{\vartheta }_2-w_1)\hfill \\ \hfill & +{\displaystyle \frac{2^{\lambda +3}}{{(w_2-w_1)}^{\lambda +3}}}\left({\mathcal{J}}_{\rho ,\lambda ,{({\vartheta }_1+{\vartheta }_2-w_1)}^{-};w}^{\sigma }f\right)({\vartheta }_1+{\vartheta }_2-{\displaystyle \frac{w_1+w_2}{2}}).\hfill \end{array}$$

Then, by subtracting $I_2$ from $I_1$ and then multiplying both sides of the identity with ${\displaystyle \frac{{(w_2-w_1)}^3}{16}}$, we obtain the desired identity. □

Remark 15.

In Lemma 4, if we take $\lambda =1,$ $\sigma \left(0\right)=1$, and $w=0$, then we obtain Lemma 1.

Remark 16.

In Lemma 4, if we take $\lambda =\alpha ,$ $\sigma \left(0\right)=1$, and $w=0$, then we obtain Lemma 2.

Theorem 11.

Let $f:[{\vartheta }_1,{\vartheta }_2]\to R$ be a three-times differentiable mapping on $({\vartheta }_1,{\vartheta }_2),$ with ${\vartheta }_1<{\vartheta }_2$, $\lambda >0.$ If $|f^{‴}|$ is convex on $[{\vartheta }_1,{\vartheta }_2]$, then we have the following inequality for generalized fractional integral operators:

$$\begin{array}{cc}\hfill & |{\mathcal{F}}_{\rho ,\lambda +1}^{\sigma }\left[w{\left({\displaystyle \frac{w_2-w_1}{2}}\right)}^{\rho }\right]{\displaystyle \frac{f({\vartheta }_1+{\vartheta }_2-w_2)+f({\vartheta }_1+{\vartheta }_2-w_1)}{2}}\hfill \\ \hfill & -{\displaystyle \frac{w_2-w_1}{4}}\{{\mathcal{F}}_{\rho ,\lambda +3}^{\sigma }\left[w{\left({\displaystyle \frac{w_2-w_1}{2}}\right)}^{\rho }\right]-{\mathcal{F}}_{\rho ,\lambda +2}^{\sigma }\left[w{\left({\displaystyle \frac{w_2-w_1}{2}}\right)}^{\rho }\right]\}\times \hfill \\ & \times [f^{\prime }({\vartheta }_1+{\vartheta }_2-w_2)-f^{\prime }({\vartheta }_1+{\vartheta }_2-w_1)]\hfill \\ \hfill & -{\displaystyle \frac{2^{\lambda -1}}{{(w_2-w_1)}^{\lambda }}}[\left({\mathcal{J}}_{\rho ,\lambda ,{({\vartheta }_1+{\vartheta }_2-w_2)}^{+};w}^{\sigma }f\right)({\vartheta }_1+{\vartheta }_2-{\displaystyle \frac{w_1+w_2}{2}})\hfill \\ & +\left({\mathcal{J}}_{\rho ,\lambda ,{({\vartheta }_1+{\vartheta }_2-w_1)}^{-};w}^{\sigma }f\right)({\vartheta }_1+{\vartheta }_2-{\displaystyle \frac{w_1+w_2}{2}})\left]\right|\hfill \\ \hfill & \le {\displaystyle \frac{{(w_2-w_1)}^3}{16}}{\mathcal{F}}_{\rho ,\lambda +3}^{{\sigma }_1}\left[w{\left({\displaystyle \frac{w_2-w_1}{2}}\right)}^{\rho }\right]\left\{2\right(|f^{‴}\left({\vartheta }_1\right)|+|f^{‴}\left({\vartheta }_2\right)\left|\right)-\left(\right|f^{‴}\left(w_1\right)|+|f^{‴}\left(w_2\right)\left|\right)\},\hfill \end{array}$$

where

$${\sigma }_1\left(k\right)=\sigma \left(k\right){\displaystyle \frac{\lambda +1+\rho k}{2(\lambda +3+\rho k)}},$$

$\rho ,\lambda >0$, and $w\in R$.

Proof. 

By Lemma 4 and the properties of modulus, we obtain

$$\begin{array}{cc}\hfill & |{\mathcal{F}}_{\rho ,\lambda +1}^{\sigma }\left[w{\left({\displaystyle \frac{w_2-w_1}{2}}\right)}^{\rho }\right]{\displaystyle \frac{f({\vartheta }_1+{\vartheta }_2-w_2)+f({\vartheta }_1+{\vartheta }_2-w_1)}{2}}-{\displaystyle \frac{w_2-w_1}{4}}\{{\mathcal{F}}_{\rho ,\lambda +3}^{\sigma }\left[w{\left({\displaystyle \frac{w_2-w_1}{2}}\right)}^{\rho }\right]\hfill \\ & -{\mathcal{F}}_{\rho ,\lambda +2}^{\sigma }\left[w{\left({\displaystyle \frac{w_2-w_1}{2}}\right)}^{\rho }\right]\}[f^{\prime }({\vartheta }_1+{\vartheta }_2-w_2)-f^{\prime }({\vartheta }_1+{\vartheta }_2-w_1)]\hfill \\ \hfill & -{\displaystyle \frac{2^{\lambda -1}}{{(w_2-w_1)}^{\lambda }}}[\left({\mathcal{J}}_{\rho ,\lambda ,{({\vartheta }_1+{\vartheta }_2-w_2)}^{+};w}^{\sigma }f\right)({\vartheta }_1+{\vartheta }_2-{\displaystyle \frac{w_1+w_2}{2}})\hfill \\ & +\left({\mathcal{J}}_{\rho ,\lambda ,{({\vartheta }_1+{\vartheta }_2-w_1)}^{-};w}^{\sigma }f\right)({\vartheta }_1+{\vartheta }_2-{\displaystyle \frac{w_1+w_2}{2}})\left]\right|\hfill \\ \hfill & \le {\displaystyle \frac{{(w_2-w_1)}^3}{16}}{\int }_0^1|\eta {\mathcal{F}}_{\rho ,\lambda +3}^{\sigma }\left[w{\left({\displaystyle \frac{w_2-w_1}{2}}\right)}^{\rho }\right]-{\eta }^{\lambda +2}{\mathcal{F}}_{\rho ,\lambda +2}^{\sigma }[w{\left({\displaystyle \frac{w_2-w_1}{2}}\right)}^{\rho }{\eta }^{\rho }|\times \hfill \\ \hfill & \times |f^{‴}({\vartheta }_1+{\vartheta }_2-({\displaystyle \frac{1-\eta }{2}}{w}_1+{\displaystyle \frac{1+\eta }{2}}{w}_2))-f^{‴}({\vartheta }_1+{\vartheta }_2-({\displaystyle \frac{1+\eta }{2}}{w}_1+{\displaystyle \frac{1-\eta }{2}}{w}_2))|dt\eta \hfill \\ \hfill & \le {\displaystyle \frac{{(w_2-w_1)}^3}{16}}\times \hfill \\ & \times \left\{\sum _{k=0}^{\infty }{\displaystyle \frac{{\sigma \left(k\right)\left|w\right|}^k}{\Gamma (\rho k+\lambda +3)}}{\left({\displaystyle \frac{w_2-w_1}{2}}\right)}^{\rho k}{\int }_0^1(\eta -{\eta }^{\lambda +2+\rho k})\right|f^{‴}({\vartheta }_1+{\vartheta }_2-({\displaystyle \frac{1-\eta }{2}}{w}_1+{\displaystyle \frac{1+\eta }{2}}{w}_2))|d\eta \hfill \\ \hfill & +\sum _{k=0}^{\infty }{\displaystyle \frac{{\sigma \left(k\right)\left|w\right|}^k}{\Gamma (\rho k+\lambda +3)}}{\left({\displaystyle \frac{w_2-w_1}{2}}\right)}^{\rho k}{\int }_0^1(\eta -{\eta }^{\lambda +2+\rho k})|f^{‴}({\vartheta }_1+{\vartheta }_2-({\displaystyle \frac{1+\eta }{2}}{w}_1+{\displaystyle \frac{1-\eta }{2}}{w}_2))\left|d\eta \right\}.\hfill \end{array}$$

Taking into account that $|f^{‴}|$ is convex on $[{\vartheta }_1,{\vartheta }_2]$ and using the J–M inequality, we have

$$\begin{array}{cc}\hfill & |{\mathcal{F}}_{\rho ,\lambda +1}^{\sigma }\left[w{\left({\displaystyle \frac{w_2-w_1}{2}}\right)}^{\rho }\right]{\displaystyle \frac{f({\vartheta }_1+{\vartheta }_2-w_2)+f({\vartheta }_1+{\vartheta }_2-w_1)}{2}}\hfill \\ \hfill & -{\displaystyle \frac{w_2-w_1}{4}}\{{\mathcal{F}}_{\rho ,\lambda +3}^{\sigma }\left[w{\left({\displaystyle \frac{w_2-w_1}{2}}\right)}^{\rho }\right]-{\mathcal{F}}_{\rho ,\lambda +2}^{\sigma }\left[w{\left({\displaystyle \frac{w_2-w_1}{2}}\right)}^{\rho }\right]\}\times \hfill \\ & \times [f^{\prime }({\vartheta }_1+{\vartheta }_2-w_2)-f^{\prime }({\vartheta }_1+{\vartheta }_2-w_1)]\hfill \\ \hfill & -{\displaystyle \frac{2^{\lambda -1}}{{(w_2-w_1)}^{\lambda }}}[\left({\mathcal{J}}_{\rho ,\lambda ,{({\vartheta }_1+{\vartheta }_2-w_2)}^{+};w}^{\sigma }f\right)({\vartheta }_1+{\vartheta }_2-{\displaystyle \frac{w_1+w_2}{2}})\hfill \\ & +\left({\mathcal{J}}_{\rho ,\lambda ,{({\vartheta }_1+{\vartheta }_2-w_1)}^{-};w}^{\sigma }f\right)({\vartheta }_1+{\vartheta }_2-{\displaystyle \frac{w_1+w_2}{2}})\left]\right|\hfill \\ \hfill & \le {\displaystyle \frac{{(w_2-w_1)}^3}{16}}\sum _{k=0}^{\infty }{\displaystyle \frac{{\sigma \left(k\right)\left|w\right|}^k}{\Gamma (\rho k+\lambda +3)}}{\left({\displaystyle \frac{w_2-w_1}{2}}\right)}^{\rho k}\left\{2\right(|f^{‴}\left({\vartheta }_1\right)|+|f^{‴}\left({\vartheta }_2\right)\left|\right){\int }_0^1(\eta -{\eta }^{\lambda +2+\rho k})d\eta \hfill \\ \hfill & -\left(\right|f^{‴}\left(w_1\right)|+|f^{‴}\left(w_2\right)\left|\right){\int }_0^1(\eta -{\eta }^{\lambda +2+\rho k})d\eta \}\hfill \\ \hfill & \le {\displaystyle \frac{{(w_2-w_1)}^3}{16}}{\mathcal{F}}_{\rho ,\lambda +3}^{\sigma }\left[w{\left({\displaystyle \frac{w_2-w_1}{2}}\right)}^{\rho }\right]\left\{2\right(|f^{‴}\left({\vartheta }_1\right)|+|f^{‴}\left({\vartheta }_2\right)\left|\right)-\left(\right|f^{‴}\left(w_1\right)|+|f^{‴}\left(w_2\right)\left|\right)\}\hfill \end{array}$$

which completes the demonstration. □

Remark 17.

In Theorem 11, if we take $\lambda =1,$ $\sigma \left(0\right)=1$, and $w=0$, then we obtain Theorem 2.

Remark 18.

In Theorem 11, if we take $\lambda =\alpha ,$ $\sigma \left(0\right)=1$, and $w=0$, then we obtain Theorem 5.

Theorem 12.

Let $f:[{\vartheta }_1,{\vartheta }_2]\to R$ be a three-times differentiable mapping on $({\vartheta }_1,{\vartheta }_2),$ with ${\vartheta }_1<{\vartheta }_2$, $\lambda >0.$ If $|f^{‴}{|}^q$ is convex on $[{\vartheta }_1,{\vartheta }_2]$, where $q>1$ and ${\displaystyle \frac{1}{p}}+{\displaystyle \frac{1}{q}}=1$, then the following inequality for generalized fractional integral operators is true:

$$\begin{array}{cc}\hfill & |{\mathcal{F}}_{\rho ,\lambda +1}^{\sigma }\left[w{\left({\displaystyle \frac{w_2-w_1}{2}}\right)}^{\rho }\right]{\displaystyle \frac{f({\vartheta }_1+{\vartheta }_2-w_2)+f({\vartheta }_1+{\vartheta }_2-w_1)}{2}}-{\displaystyle \frac{w_2-w_1}{4}}\{{\mathcal{F}}_{\rho ,\lambda +3}^{\sigma }\left[w{\left({\displaystyle \frac{w_2-w_1}{2}}\right)}^{\rho }\right]\hfill \\ & -{\mathcal{F}}_{\rho ,\lambda +2}^{\sigma }\left[w{\left({\displaystyle \frac{w_2-w_1}{2}}\right)}^{\rho }\right]\}[f^{\prime }({\vartheta }_1+{\vartheta }_2-w_2)-f^{\prime }({\vartheta }_1+{\vartheta }_2-w_1)]\hfill \\ \hfill & -{\displaystyle \frac{2^{\lambda -1}}{{(w_2-w_1)}^{\lambda }}}[\left({\mathcal{J}}_{\rho ,\lambda ,{({\vartheta }_1+{\vartheta }_2-w_2)}^{+};w}^{\sigma }f\right)({\vartheta }_1+{\vartheta }_2-{\displaystyle \frac{w_1+w_2}{2}})\hfill \\ & +\left({\mathcal{J}}_{\rho ,\lambda ,{({\vartheta }_1+{\vartheta }_2-w_1)}^{-};w}^{\sigma }f\right)({\vartheta }_1+{\vartheta }_2-{\displaystyle \frac{w_1+w_2}{2}})\left]\right|\hfill \\ \hfill & \le {\displaystyle \frac{{(w_2-w_1)}^3}{16}}{\mathcal{F}}_{\rho ,\lambda +3}^{{\sigma }_2}\left[w{\left({\displaystyle \frac{w_2-w_1}{2}}\right)}^{\rho }\right][{\left(|f^{‴}\left({\vartheta }_1\right){|}^q+{\left|f^{‴}\left({\vartheta }_2\right)\right|}^q-{\displaystyle \frac{|f^{‴}\left(w_1\right){|}^q+3{\left|f^{‴}\left(w_2\right)\right|}^q}{4}}\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +{\left(|f^{‴}\left({\vartheta }_1\right){|}^q+{\left|f^{‴}\left({\vartheta }_2\right)\right|}^q-{\displaystyle \frac{3|f^{‴}\left(w_1\right){|}^q+{\left|f^{‴}\left(w_2\right)\right|}^q}{4}}\right)}^{{\displaystyle \frac{1}{q}}}],\hfill \end{array}$$

where

$${\sigma }_2\left(k\right)=\sigma \left(k\right){\displaystyle \frac{B^{\frac{1}{p}}\left(\frac{p+1}{\lambda +1+\rho k},p+1\right)}{{(\lambda +1+\rho k)}^{\frac{1}{p}}}},$$

$\rho ,\lambda >0$, and $w\in R$, and B is Euler’s beta function.

Proof. 

Using Lemma 4, we obtain

$$\begin{array}{cc}\hfill & |{\mathcal{F}}_{\rho ,\lambda +1}^{\sigma }\left[w{\left({\displaystyle \frac{w_2-w_1}{2}}\right)}^{\rho }\right]{\displaystyle \frac{f({\vartheta }_1+{\vartheta }_2-w_2)+f({\vartheta }_1+{\vartheta }_2-w_1)}{2}}-{\displaystyle \frac{w_2-w_1}{4}}\{{\mathcal{F}}_{\rho ,\lambda +3}^{\sigma }\left[w{\left({\displaystyle \frac{w_2-w_1}{2}}\right)}^{\rho }\right]\hfill \\ & -{\mathcal{F}}_{\rho ,\lambda +2}^{\sigma }\left[w{\left({\displaystyle \frac{w_2-w_1}{2}}\right)}^{\rho }\right]\}[f^{\prime }({\vartheta }_1+{\vartheta }_2-w_2)-f^{\prime }({\vartheta }_1+{\vartheta }_2-w_1)]\hfill \\ \hfill & -{\displaystyle \frac{2^{\lambda -1}}{{(w_2-w_1)}^{\lambda }}}[\left({\mathcal{J}}_{\rho ,\lambda ,{({\vartheta }_1+{\vartheta }_2-w_2)}^{+};w}^{\sigma }f\right)({\vartheta }_1+{\vartheta }_2-{\displaystyle \frac{w_1+w_2}{2}})\hfill \\ & +\left({\mathcal{J}}_{\rho ,\lambda ,{({\vartheta }_1+{\vartheta }_2-w_1)}^{-};w}^{\sigma }f\right)({\vartheta }_1+{\vartheta }_2-{\displaystyle \frac{w_1+w_2}{2}})\left]\right|\hfill \\ \hfill & \le {\displaystyle \frac{{(w_2-w_1)}^3}{16}}{\int }_0^1|\eta {\mathcal{F}}_{\rho ,\lambda +3}^{\sigma }\left[w{\left({\displaystyle \frac{w_2-w_1}{2}}\right)}^{\rho }\right]-{\eta }^{\lambda +2}{\mathcal{F}}_{\rho ,\lambda +2}^{\sigma }[w{\left({\displaystyle \frac{w_2-w_1}{2}}\right)}^{\rho }{\eta }^{\rho }|\times \hfill \\ \hfill & \times |f^{‴}({\vartheta }_1+{\vartheta }_2-({\displaystyle \frac{1-\eta }{2}}{w}_1+{\displaystyle \frac{1+\eta }{2}}{w}_2))-f^{‴}({\vartheta }_1+{\vartheta }_2-({\displaystyle \frac{1+\eta }{2}}{w}_1+{\displaystyle \frac{1-\eta }{2}}{w}_2))|dt\eta \hfill \\ \hfill & \le {\displaystyle \frac{{(w_2-w_1)}^3}{16}}\times \hfill \\ & \times \left\{\sum _{k=0}^{\infty }{\displaystyle \frac{{\sigma \left(k\right)\left|w\right|}^k}{\Gamma (\rho k+\lambda +3)}}{\left({\displaystyle \frac{w_2-w_1}{2}}\right)}^{\rho k}{\int }_0^1(\eta -{\eta }^{\lambda +2+\rho k})\right|f^{‴}({\vartheta }_1+{\vartheta }_2-({\displaystyle \frac{1-\eta }{2}}{w}_1+{\displaystyle \frac{1+\eta }{2}}{w}_2))|d\eta \hfill \\ \hfill & +\sum _{k=0}^{\infty }{\displaystyle \frac{{\sigma \left(k\right)\left|w\right|}^k}{\Gamma (\rho k+\lambda +3)}}{\left({\displaystyle \frac{w_2-w_1}{2}}\right)}^{\rho k}{\int }_0^1(\eta -{\eta }^{\lambda +2+\rho k})|f^{‴}({\vartheta }_1+{\vartheta }_2-({\displaystyle \frac{1+\eta }{2}}{w}_1+{\displaystyle \frac{1-\eta }{2}}{w}_2))\left|d\eta \right\}.\hfill \end{array}$$

Now, using Hölder’s inequality and the convexity of $|f^{‴}{|}^q$, we obtain the following inequality:

$$\begin{array}{cc}\hfill & {\int }_0^1(\eta -{\eta }^{\lambda +2+\rho k})\left[\right|f^{‴}({\vartheta }_1+{\vartheta }_2-({\displaystyle \frac{1-\eta }{2}}{w}_1+{\displaystyle \frac{1+\eta }{2}}{w}_2))|\hfill \\ & +|f^{‴}({\vartheta }_1+{\vartheta }_2-({\displaystyle \frac{1+\eta }{2}}{w}_1+{\displaystyle \frac{1-\eta }{2}}{w}_2))\left|\right]d\eta \hfill \\ \hfill & \le {\left({\int }_0^1{\eta }^p{(1-{\eta }^{\lambda +1+\rho k})}^{p}d\eta \right)}^{{\displaystyle \frac{1}{p}}}\{{\left({\int }_0^1{\left|f^{‴}({\vartheta }_1+{\vartheta }_2-({\displaystyle \frac{1-\eta }{2}}{w}_1+{\displaystyle \frac{1+\eta }{2}}{w}_2))\right|}^{q}d\eta \right)}^{{\displaystyle \frac{1}{q}}}+\hfill \\ \hfill & +{\left({\int }_0^1{\left|f^{‴}({\vartheta }_1+{\vartheta }_2-({\displaystyle \frac{1+\eta }{2}}{w}_1+{\displaystyle \frac{1-\eta }{2}}{w}_2))\right|}^{q}d\eta \right)}^{{\displaystyle \frac{1}{q}}}\}\hfill \\ \hfill & \le {\displaystyle \frac{B^{\frac{1}{p}}\left(\frac{p+1}{\lambda +1+\rho k},p+1\right)}{{(\lambda +1+\rho k)}^{\frac{1}{p}}}}\{{\left(|f^{‴}\left({\vartheta }_1\right){|}^q+{\left|f^{‴}\left({\vartheta }_2\right)\right|}^q-{\displaystyle \frac{|f^{‴}\left(w_1\right){|}^q+3{\left|f^{‴}\left(w_2\right)\right|}^q}{4}}\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +{\left(|f^{‴}\left({\vartheta }_1\right){|}^q+{\left|f^{‴}\left({\vartheta }_2\right)\right|}^q-{\displaystyle \frac{3|f^{‴}\left(w_1\right){|}^q+{\left|f^{‴}\left(w_2\right)\right|}^q}{4}}\right)}^{{\displaystyle \frac{1}{q}}}\},\hfill \end{array}$$

where we used $x={\eta }^{\lambda +1+\rho k}$ and

$${\int }_0^1{\eta }^p{(1-{\eta }^{\lambda +1+\rho k})}^{p}d\eta ={\displaystyle \frac{B\left(\frac{p+1}{\lambda +1+\rho k},p+1\right)}{(\lambda +1+\rho k)}}.$$

Thus, the proof is completed by combining the last two inequalities. □

Corollary 1.

If we take $\lambda =1,$ $\sigma \left(0\right)=1$, and $w=0$ in Theorem 12, then we have

$$\begin{array}{cc}\hfill & |{\displaystyle \frac{f({\vartheta }_1+{\vartheta }_2-w_2)+f({\vartheta }_1+{\vartheta }_2-w_1)}{2}}-{\displaystyle \frac{1}{w_2-w_1}}{\int }_{{\vartheta }_1+{\vartheta }_2-w_2}^{{\vartheta }_1+{\vartheta }_2-w_1}f\left(u\right)du\hfill \\ & +{\displaystyle \frac{w_2-w_1}{12}}\left[f^{\prime }({\vartheta }_1+{\vartheta }_2-w_2)-f^{\prime }({\vartheta }_1+{\vartheta }_2-w_1)\right]|\hfill \\ & \le {\displaystyle \frac{{(w_2-w_1)}^3}{96\sqrt[p]{2}}}{B}^{{\displaystyle \frac{1}{p}}}\left({\displaystyle \frac{p+1}{2}},p+1\right)[{\left(|f^{‴}\left({\vartheta }_1\right){|}^q+{\left|f^{‴}\left({\vartheta }_2\right)\right|}^q-{\displaystyle \frac{|f^{‴}\left(w_1\right){|}^q+3{\left|f^{‴}\left(w_2\right)\right|}^q}{4}}\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ & +{\left(|f^{‴}\left({\vartheta }_1\right){|}^q+{\left|f^{‴}\left({\vartheta }_2\right)\right|}^q-{\displaystyle \frac{3|f^{‴}\left(w_1\right){|}^q+{\left|f^{‴}\left(w_2\right)\right|}^q}{4}}\right)}^{{\displaystyle \frac{1}{q}}}].\hfill \end{array}$$

Corollary 2.

If we take $\lambda =\alpha ,$ $\sigma \left(0\right)=1$, and $w=0$ in Theorem 12, then we have

$$\begin{array}{cc}\hfill & |{\displaystyle \frac{f({\vartheta }_1+{\vartheta }_2-w_2)+f({\vartheta }_1+{\vartheta }_2-w_1)}{2}}-{\displaystyle \frac{2^{\alpha -1}\Gamma (\alpha +1)}{{(w_2-w_1)}^{\alpha }}}[J_{{({\vartheta }_1+{\vartheta }_2-w_2)}^{+}}^{\alpha }f\left({\vartheta }_1+{\vartheta }_2-{\displaystyle \frac{w_1+w_2}{2}}\right)\hfill \\ & +J_{{({\vartheta }_1+{\vartheta }_2-w_1)}^{-}}^{\alpha }f\left({\vartheta }_1+{\vartheta }_2-{\displaystyle \frac{w_1+w_2}{2}}\right)]+{\displaystyle \frac{w_2-w_1}{4(\alpha +2)}}\left[f^{\prime }({\vartheta }_1+{\vartheta }_2-w_2)-f^{\prime }({\vartheta }_1+{\vartheta }_2-w_1)\right]|\hfill \\ & \le {\displaystyle \frac{{(w_2-w_1)}^3}{16(\alpha +2)(\alpha +1)\sqrt[p]{(\alpha +1)}}}{B}^{{\displaystyle \frac{1}{p}}}\left({\displaystyle \frac{p+1}{\alpha +1}},p+1\right)\times \hfill \\ & \times [{\left(|f^{‴}\left({\vartheta }_1\right){|}^q+{\left|f^{‴}\left({\vartheta }_2\right)\right|}^q-{\displaystyle \frac{|f^{‴}\left(w_1\right){|}^q+3{\left|f^{‴}\left(w_2\right)\right|}^q}{4}}\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +{\left(|f^{‴}\left({\vartheta }_1\right){|}^q+{\left|f^{‴}\left({\vartheta }_2\right)\right|}^q-{\displaystyle \frac{3|f^{‴}\left(w_1\right){|}^q+{\left|f^{‴}\left(w_2\right)\right|}^q}{4}}\right)}^{{\displaystyle \frac{1}{q}}}].\hfill \end{array}$$

Theorem 13.

Let $f:[{\vartheta }_1,{\vartheta }_2]\to R$ be a three-times differentiable mapping on $({\vartheta }_1,{\vartheta }_2),$ with ${\vartheta }_1<{\vartheta }_2$ and $\lambda >0.$ If $|f^{‴}{|}^q$ is convex on $[{\vartheta }_1,{\vartheta }_2]$, $q\ge 1$, then the following inequality for generalized fractional integral operators is obtained:

$$\begin{array}{cc}\hfill & |{\mathcal{F}}_{\rho ,\lambda +1}^{\sigma }\left[w{\left({\displaystyle \frac{w_2-w_1}{2}}\right)}^{\rho }\right]{\displaystyle \frac{f({\vartheta }_1+{\vartheta }_2-w_2)+f({\vartheta }_1+{\vartheta }_2-w_1)}{2}}-{\displaystyle \frac{w_2-w_1}{4}}\{{\mathcal{F}}_{\rho ,\lambda +3}^{\sigma }\left[w{\left({\displaystyle \frac{w_2-w_1}{2}}\right)}^{\rho }\right]\hfill \\ & -{\mathcal{F}}_{\rho ,\lambda +2}^{\sigma }\left[w{\left({\displaystyle \frac{w_2-w_1}{2}}\right)}^{\rho }\right]\}[f^{\prime }({\vartheta }_1+{\vartheta }_2-w_2)-f^{\prime }({\vartheta }_1+{\vartheta }_2-w_1)]\hfill \\ \hfill & -{\displaystyle \frac{2^{\lambda -1}}{{(w_2-w_1)}^{\lambda }}}[\left({\mathcal{J}}_{\rho ,\lambda ,{({\vartheta }_1+{\vartheta }_2-w_2)}^{+};w}^{\sigma }f\right)({\vartheta }_1+{\vartheta }_2-{\displaystyle \frac{w_1+w_2}{2}})\hfill \\ & +\left({\mathcal{J}}_{\rho ,\lambda ,{({\vartheta }_1+{\vartheta }_2-w_1)}^{-};w}^{\sigma }f\right)({\vartheta }_1+{\vartheta }_2-{\displaystyle \frac{w_1+w_2}{2}})\left]\right|\hfill \\ \hfill & \le {\displaystyle \frac{{(w_2-w_1)}^3}{16}}{\mathcal{F}}_{\rho ,\lambda +3}^{{\sigma }_3}\left[w{\left({\displaystyle \frac{w_2-w_1}{2}}\right)}^{\rho }\right],\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill & {\sigma }_3\left(k\right)=\sigma \left(k\right){\left({\displaystyle \frac{\lambda +1+\rho k}{2(\lambda +3+\rho k)}}\right)}^{1-{\displaystyle \frac{1}{q}}}\left\{\right[{\displaystyle \frac{\lambda +1+\rho k}{2(\lambda +3+\rho k)}}\left(\right|f^{‴}\left({\vartheta }_1\right){|}^q+|f^{‴}\left({\vartheta }_2\right){|}^q)\hfill \\ & -({\displaystyle \frac{1}{6}}-{\displaystyle \frac{1}{(\lambda +3+\rho k)(\lambda +4+\rho k)}})·|f^{‴}\left(w_1\right){|}^q-({\displaystyle \frac{5}{6}}-{\displaystyle \frac{2\lambda +7+\rho k}{(\lambda +3+\rho k)(\lambda +4+\rho k)}})|f^{‴}\left(w_2\right){{|}^q]}^{{\displaystyle \frac{1}{q}}}\hfill \\ & +[{\displaystyle \frac{\lambda +1+\rho k}{2(\lambda +3+\rho k)}}\left(\right|f^{‴}\left({\vartheta }_1\right){|}^q+|f^{‴}\left({\vartheta }_2\right){|}^q)-({\displaystyle \frac{5}{6}}-{\displaystyle \frac{2\lambda +7+\rho k}{(\lambda +3+\rho k)(\lambda +4+\rho k)}})·{\left|f^{‴}\left(w_1\right)\right|}^q\hfill \\ & -({\displaystyle \frac{1}{6}}-{\displaystyle \frac{1}{(\lambda +3+\rho k)(\lambda +4+\rho k)}})|f^{‴}\left(w_2\right){|}^q{\left)\right]}^{{\displaystyle \frac{1}{q}}}\},\hfill \end{array}$$

$\rho ,\lambda >0$, and $w\in R$, and B is Euler’s beta function.

Proof. 

We use Lemma 4, the properties of modulus, the power mean inequality, and the convexity of $|f^{‴}{|}^q$ to obtain

$$\begin{array}{cc}\hfill & |{\mathcal{F}}_{\rho ,\lambda +1}^{\sigma }\left[w{\left({\displaystyle \frac{w_2-w_1}{2}}\right)}^{\rho }\right]{\displaystyle \frac{f({\vartheta }_1+{\vartheta }_2-w_2)+f({\vartheta }_1+{\vartheta }_2-w_1)}{2}}-{\displaystyle \frac{w_2-w_1}{4}}\{{\mathcal{F}}_{\rho ,\lambda +3}^{\sigma }\left[w{\left({\displaystyle \frac{w_2-w_1}{2}}\right)}^{\rho }\right]\hfill \\ & -{\mathcal{F}}_{\rho ,\lambda +2}^{\sigma }\left[w{\left({\displaystyle \frac{w_2-w_1}{2}}\right)}^{\rho }\right]\}[f^{\prime }({\vartheta }_1+{\vartheta }_2-w_2)-f^{\prime }({\vartheta }_1+{\vartheta }_2-w_1)]\hfill \\ \hfill & -{\displaystyle \frac{2^{\lambda -1}}{{(w_2-w_1)}^{\lambda }}}[\left({\mathcal{J}}_{\rho ,\lambda ,{({\vartheta }_1+{\vartheta }_2-w_2)}^{+};w}^{\sigma }f\right)({\vartheta }_1+{\vartheta }_2-{\displaystyle \frac{w_1+w_2}{2}})\hfill \\ & +\left({\mathcal{J}}_{\rho ,\lambda ,{({\vartheta }_1+{\vartheta }_2-w_1)}^{-};w}^{\sigma }f\right)({\vartheta }_1+{\vartheta }_2-{\displaystyle \frac{w_1+w_2}{2}})\left]\right|\hfill \\ \hfill & \le {\displaystyle \frac{{(w_2-w_1)}^3}{16}}{\int }_0^1|\eta {\mathcal{F}}_{\rho ,\lambda +3}^{\sigma }\left[w{\left({\displaystyle \frac{w_2-w_1}{2}}\right)}^{\rho }\right]-{\eta }^{\lambda +2}{\mathcal{F}}_{\rho ,\lambda +2}^{\sigma }[w{\left({\displaystyle \frac{w_2-w_1}{2}}\right)}^{\rho }{\eta }^{\rho }|\times \hfill \\ \hfill & \times |f^{‴}({\vartheta }_1+{\vartheta }_2-({\displaystyle \frac{1-\eta }{2}}{w}_1+{\displaystyle \frac{1+\eta }{2}}{w}_2))-f^{‴}({\vartheta }_1+{\vartheta }_2-({\displaystyle \frac{1+\eta }{2}}{w}_1+{\displaystyle \frac{1-\eta }{2}}{w}_2))|dt\eta \hfill \\ \hfill & \le {\displaystyle \frac{{(w_2-w_1)}^3}{16}}{\left\{\sum _{k=0}^{\infty }{\displaystyle \frac{{\sigma \left(k\right)\left|w\right|}^k}{\Gamma (\rho k+\lambda +3)}}{\left({\displaystyle \frac{w_2-w_1}{2}}\right)}^{\rho k}\right({\int }_0^1(\eta -{\eta }^{\lambda +2+\rho k})d\eta )}^{1-{\displaystyle \frac{1}{q}}}\times \hfill \\ \hfill & \times {\left({\int }_0^1(\eta -{\eta }^{\lambda +2+\rho k}){\left|f^{‴}({\vartheta }_1+{\vartheta }_2-({\displaystyle \frac{1-\eta }{2}}{w}_1+{\displaystyle \frac{1+\eta }{2}}{w}_2))\right|}^{q}d\eta \right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +\sum _{k=0}^{\infty }{\displaystyle \frac{{\sigma \left(k\right)\left|w\right|}^k}{\Gamma (\rho k+\lambda +3)}}{\left({\displaystyle \frac{w_2-w_1}{2}}\right)}^{\rho k}({\int }_0^1(\eta -{\eta }^{\lambda +2+\rho k}){d\eta )}^{1-{\displaystyle \frac{1}{q}}}\times \hfill \\ \hfill & \times {\left({\int }_0^1(\eta -{\eta }^{\lambda +2+\rho k}){\left|f^{‴}({\vartheta }_1+{\vartheta }_2-({\displaystyle \frac{1+\eta }{2}}{w}_1+{\displaystyle \frac{1-\eta }{2}}{w}_2))\right|}^{q}d\eta \right)}^{{\displaystyle \frac{1}{q}}}\}\hfill \\ \hfill & \le {\displaystyle \frac{{(w_2-w_1)}^3}{16}}\{\sum _{k=0}^{\infty }{\displaystyle \frac{{\sigma \left(k\right)\left|w\right|}^k}{\Gamma (\rho k+\lambda +3)}}{\left({\displaystyle \frac{w_2-w_1}{2}}\right)}^{\rho k}{\left({\displaystyle \frac{1}{2}}-{\displaystyle \frac{1}{\lambda +3+\rho k}}\right)}^{1-{\displaystyle \frac{1}{q}}}\left\{\right[({\displaystyle \frac{1}{2}}-{\displaystyle \frac{1}{\lambda +3+\rho k}})\hfill \\ & \left(\right|f^{‴}\left({\vartheta }_1\right){|}^q+|f^{‴}\left({\vartheta }_2\right){|}^q)-|f^{‴}\left(w_1\right){|}^q{\int }_0^1(1-\eta )(\eta -{\eta }^{\lambda +2+\rho k})d\eta \hfill \\ & -|f^{‴}\left(w_2\right){{|}^q{\int }_0^1(1+\eta )(\eta -{\eta }^{\lambda +2+\rho k})d\eta ]}^{{\displaystyle \frac{1}{q}}}\hfill \end{array}$$

$$\begin{array}{cc}\hfill & +[({\displaystyle \frac{1}{2}}-{\displaystyle \frac{1}{\lambda +3+\rho k}})\left(\right|f^{‴}\left({\vartheta }_1\right){|}^q+|f^{‴}\left({\vartheta }_2\right){|}^q)-|f^{‴}\left(w_1\right){|}^q{\int }_0^1(1+\eta )(\eta -{\eta }^{\lambda +2+\rho k})d\eta \hfill \\ \hfill & -|f^{‴}\left(w_2\right){|}^q{\int }_0^1(1-\eta )(\eta -{\eta }^{\lambda +2+\rho k})d\eta {]}^{{\displaystyle \frac{1}{q}}}\}.\hfill \end{array}$$

□

Example 1.

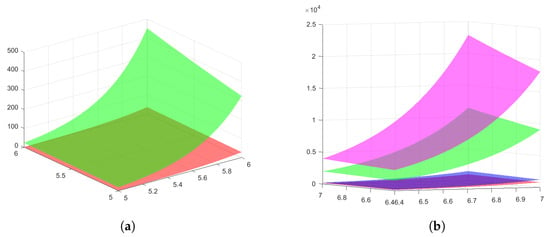
We take into account the function $f:[{\vartheta }_1,{\vartheta }_2]\to R$ defined by $f\left(\theta \right)={(\theta +a_1)}^{\vartheta }$, ${\vartheta }_1=1,{\vartheta }_2=4,{\omega }_1=2,{\omega }_2=3$, and $a_1,\vartheta \in [5,6].$ Then, we have $|f^{‴}\left(\theta \right)|=\vartheta (\vartheta -1)(\vartheta -2){(\theta +a_1)}^{\vartheta -3}$, and it can be seen that the conditions of Theorem 2 are satisfied, which implies that the inequality from Theorem 2 holds. Therefore, we will first compute the left member and then the right member of this inequality, successively obtaining the following:

$$M_s=|{\displaystyle \frac{f\left(2\right)+f\left(3\right)}{2}}-{\int }_2^3{(u+a_1)}^{\vartheta }du+{\displaystyle \frac{1}{12}}[f^{\prime }\left(2\right)-f^{\prime }\left(3\right)]|$$

$$=|{\displaystyle \frac{{(2+a_1)}^{\vartheta }+{(3+a_1)}^{\vartheta }}{2}}-{\displaystyle \frac{{(3+a_1)}^{\vartheta +1}}{\vartheta +1}}+{\displaystyle \frac{{(2+a_1)}^{\vartheta +1}}{\vartheta +1}}+{\displaystyle \frac{\vartheta }{12}}[{(2+a_1)}^{\vartheta -1}-{(3+a_1)}^{\vartheta -1}]|.$$

and

$$M_d={\displaystyle \frac{1}{192}}\left[\right|f^{‴}\left(1\right)|+|f^{‴}\left(4\right)|-{\displaystyle \frac{|f^{‴}\left(2\right)|+|f^{‴}\left(3\right)|}{2}}]$$

$$={\displaystyle \frac{\vartheta (\vartheta -1)(\vartheta -2)}{192}}[{(1+a_1)}^{\vartheta -3}+{(4+a_1)}^{\vartheta -3}-{\displaystyle \frac{{(2+a_1)}^{\vartheta -3}+{(3+a_1)}^{\vartheta -3}}{2}}].$$

In Figure 1a, the graph surfaces of the left member (the graph in red) and the right member (the graph in green) of the inequality from Theorem 2 are given for the particular case where $f\left(\theta \right)={(\theta +a_1)}^{\vartheta }$, ${\vartheta }_1=1,{\vartheta }_2=4,{\omega }_1=2,{\omega }_2=3$, and $a_1,\vartheta \in [5,6].$ The left member and the right member of the inequality from Theorem 6 [20] for the same parameters as before become

$$M{s}_2=|6{\int }_2^{3}f\left(\theta \right)d\theta -4f\left({\displaystyle \frac{5}{2}}\right)-[f\left(3\right)+f\left(2\right)]|,$$

and, respectively,

$$M{d}_2={\displaystyle \frac{1}{96}}\left[\right|f^{‴}\left(1\right)|+|f^{‴}\left(4\right)|-{\displaystyle \frac{1}{2}}\left(\right|f^{‴}\left(2\right)|+|f^{‴}\left(3\right)\left|\right)].$$

Figure 1. (a) The graph surfaces of the left member (graph in red) and the right member (graph in green) of the inequality from Theorem 2 are given for $f\left(\theta \right)={(\theta +a_1)}^{\vartheta }$, ${\vartheta }_1=1,{\vartheta }_2=4,{\omega }_1=2,{\omega }_2=3$, and $a_1,\vartheta \in [5,6]$. (b) Four surfaces that represent the left and the right members of the inequalities from Theorem 2 and from Theorem 6 in [20] are graphically illustrated for $f\left(\theta \right)={(\theta +a_1)}^{\vartheta }$ and the same parameters: ${\vartheta }_1=1,{\vartheta }_2=4,{\omega }_1=2,{\omega }_2=3$, and $a_1,\vartheta \in [6.4,7]$. The left members $M_s$ and $M{s}_2$ are the red and blue surfaces, respectively, and the right members $M_d$ and $M{d}_2$ are the green and magenta surfaces, respectively.

In Figure 1b four surfaces that represent the left and the right members of the inequalities from Theorem 2 and Theorem 6 in [20] are graphically illustrated. The left members $M_s$ and $M{s}_2$ are the red and blue surfaces, respectively, and the right members $M_d$ and $M{d}_2$ are the green and magenta surfaces, respectively.

Example 2.

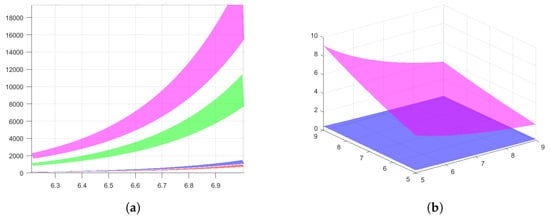
If we consider now the function $f:[{\vartheta }_1,{\vartheta }_2]\to R$ defined by $f\left(\theta \right)={(\theta +a_1)}^5$, ${\vartheta }_1=1,{\vartheta }_2=4,{\omega }_1=2,{\omega }_2=3$, and $a_1,\alpha \in [5,9],$ then we have $|f^{‴}\left(\theta \right)|=60{(\theta +a_1)}^2.$ We can observe that the hypothesis of Theorem 5 is fulfilled; therefore, the inequality from Theorem 5 is satisfied. Analogously, we shall compute the left member and the right member of this inequality, successively obtaining the following:

$$M_s=|{\displaystyle \frac{f\left(2\right)+f\left(3\right)}{2}}-2^{\alpha -1}\Gamma (\alpha +1)[J_{2^{+}}^{\alpha }f\left({\displaystyle \frac{5}{2}}\right)+J_{3^{-}}^{\alpha }f\left({\displaystyle \frac{5}{2}}\right)]+{\displaystyle \frac{1}{4(\alpha +2)}}[f^{\prime }\left(2\right)-f^{\prime }\left(3\right)]\left|\right|$$

$$=|{\displaystyle \frac{{(2+a_1)}^5+{(3+a_1)}^5}{2}}-2^{\alpha -1}\alpha [{\int }_2^{{\displaystyle \frac{5}{2}}}{({\displaystyle \frac{5}{2}}-\eta )}^{\alpha -1}{(\eta +a_1)}^{5}d\eta +{\int }_{{\displaystyle \frac{5}{2}}}^3{(\eta -{\displaystyle \frac{5}{2}})}^{\alpha -1}{(\eta +a_1)}^{5}d\eta ]$$

$$+{\displaystyle \frac{5}{4(\alpha +2)}}[{(2+a_1)}^4-{(3+a_1)}^4]|.$$

$$=|{\displaystyle \frac{{(2+a_1)}^5+{(3+a_1)}^5}{2}}-\alpha (a_1+{\displaystyle \frac{5}{2}})[{\displaystyle \frac{5}{16(\alpha +4)}}+{\displaystyle \frac{5{(a_1+\frac{5}{2})}^2}{2(\alpha +2)}}+{\displaystyle \frac{{(a_1+\frac{5}{2})}^4}{\alpha }}]$$

$$+{\displaystyle \frac{5}{4(\alpha +2)}}[{(2+a_1)}^4-{(3+a_1)}^4]|.$$

and

$$M_d={\displaystyle \frac{1}{16(\alpha +2)(\alpha +3)}}\left[\right|f^{‴}\left(1\right)|+|f^{‴}\left(4\right)|-{\displaystyle \frac{|f^{‴}\left(2\right)|+|f^{‴}\left(3\right)|}{2}}]$$

$$={\displaystyle \frac{15}{4(\alpha +2)(\alpha +3)}}[{(1+a_1)}^2+{(4+a_1)}^2-{\displaystyle \frac{{(2+a_1)}^2+{(3+a_1)}^2}{2}}].$$

In Figure 2a, the same graphics as in Figure 1b, are rotated. Matlab R2023b software was used for all figures. It can be seen from the graphical representation that in this particular case, this new inequality from Theorem 2 is better than the first.But in first inequality doesn’t appear in left member, the terms that contain first derivative of the function.

Figure 2. (a) The same graphics as in Figure 1b are presented, but rotated. (b) The graph surfaces of the left member (graph in blue) and the right member (graph in magenta) of the inequality from Theorem 5 are given for $f\left(\theta \right)={(\theta +a_1)}^5$, ${\vartheta }_1=1,{\vartheta }_2=4,{\omega }_1=2,{\omega }_2=3$, and $a_1,\alpha \in [5,9]$.

In Figure 2b, the graph surfaces of the left member (graph in blue) and the right member (graph in magenta) of the inequality from Theorem 5 are given for the particular case where $f\left(\theta \right)={(\theta +a_1)}^5$, ${\vartheta }_1=1,{\vartheta }_2=4,{\omega }_1=2,{\omega }_2=3$, and $a_1,\alpha \in [5,9].$

5. Applications: Special Means

We present applications of the newly established inequalities to special means of real numbers in this section. For arbitrary positive real numbers ${\vartheta }_1$ and ${\vartheta }_2$ $({\vartheta }_1\ne {\vartheta }_2),$ we consider the following means:

(1)

The arithmetic mean:

$$\mathcal{A}({\vartheta }_1,{\vartheta }_2)={\displaystyle \frac{{\vartheta }_1+{\vartheta }_2}{2,}},{\vartheta }_1,{\vartheta }_2\ge 0.$$

(2)

The generalized logarithmic mean:

$${\mathcal{L}}_{\rho }({\vartheta }_1,{\vartheta }_2)=\{\begin{array}{cc}\hfill {\left[{\displaystyle \frac{{\vartheta }_2^{\rho +1}-{\vartheta }_1^{\rho +1}}{(\rho +1)({\vartheta }_2-{\vartheta }_1)}}\right]}^{{\displaystyle \frac{1}{\rho }}};& {\vartheta }_1\ne {\vartheta }_2,\hfill \\ \hfill {\vartheta }_1;& {\vartheta }_1={\vartheta }_2,\hfill \end{array}{\vartheta }_1,{\vartheta }_2>0;\rho \in Z-\{-1,0\}.$$

Proposition 1.

Let $0<{\vartheta }_1<{\vartheta }_2,$ $\rho \in N,$ and $\rho \ge 1.$ Then, for all $w_1,w_2\in [{\vartheta }_1,{\vartheta }_2],$ we have

$$\begin{array}{cc}\hfill & |12\mathcal{A}\left({({\vartheta }_1+{\vartheta }_2-w_2)}^{\rho +3},{({\vartheta }_1+{\vartheta }_2-w_1)}^{\rho +3}\right)-12{\mathcal{L}}_{\rho +3}^{\rho +3}\left({\vartheta }_1+{\vartheta }_2-w_2,{\vartheta }_1+{\vartheta }_2-w_1\right)\hfill \\ & -{(w_2-w_1)}^2(\rho +2)(\rho +3){\mathcal{L}}_{\rho +1}^{\rho +1}\left({\vartheta }_1+{\vartheta }_2-w_2,{\vartheta }_1+{\vartheta }_2-w_1\right)|\hfill \\ & \le {\displaystyle \frac{(\rho +1)(\rho +2)(\rho +3){(w_2-w_1)}^3}{16}}\left[2\mathcal{A}\left({\vartheta }_1^{\rho },{\vartheta }_2^{\rho }\right)-\mathcal{A}\left(w_1^{\rho },w_2^{\rho }\right)\right].\hfill \end{array}$$

Proof. 

Using Theorem 2 and setting $f\left(\eta \right)={\displaystyle \frac{{\eta }^{\rho +3}}{(\rho +1)(\rho +2)(\rho +3)}}$, we can calculate the intended inequality. □

Proposition 2.

Let $0<{\vartheta }_1<{\vartheta }_2,$ $\rho \in N,$ and $\rho \ge 1.$ Then, for $q\ge 1$ and for all $w_1,w_2\in [{\vartheta }_1,{\vartheta }_2],$ we have

$$\begin{array}{cc}\hfill & |12\mathcal{A}\left({({\vartheta }_1+{\vartheta }_2-w_2)}^{\rho +3},{({\vartheta }_1+{\vartheta }_2-w_1)}^{\rho +3}\right)-12{\mathcal{L}}_{\rho +3}^{\rho +3}\left({\vartheta }_1+{\vartheta }_2-w_2,{\vartheta }_1+{\vartheta }_2-w_1\right)\hfill \\ & -{(w_2-w_1)}^2(\rho +2)(\rho +3){\mathcal{L}}_{\rho +1}^{\rho +1}\left({\vartheta }_1+{\vartheta }_2-w_2,{\vartheta }_1+{\vartheta }_2-w_1\right)|\hfill \\ & \le {\displaystyle \frac{(\rho +1)(\rho +2)(\rho +3){(w_2-w_1)}^3}{32}}[{\left(2\mathcal{A}\left({\vartheta }_1^{\rho q},{\vartheta }_2^{\rho q}\right)-{\displaystyle \frac{1}{15}}\mathcal{A}\left(7w_1^{\rho q},23w_2^{\rho q}\right)\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ & +{\left(2\mathcal{A}\left({\vartheta }_1^{\rho q},{\vartheta }_2^{\rho q}\right)-{\displaystyle \frac{1}{15}}\mathcal{A}\left(23w_1^{\rho q},7w_2^{\rho q}\right)\right)}^{{\displaystyle \frac{1}{q}}}].\hfill \end{array}$$

Proof. 

Using Theorem 3 and setting $f\left(\eta \right)={\displaystyle \frac{{\eta }^{\rho +3}}{(\rho +1)(\rho +2)(\rho +3)}}$, we can calculate the intended inequality. □

Proposition 3.

Let $0<{\vartheta }_1<{\vartheta }_2$ $\rho \in N,$ and $\rho \ge 1.$ Then, we have

$$\begin{array}{cc}\hfill & |12\mathcal{A}\left({\vartheta }_1^{\rho +3},{\vartheta }_2^{\rho +3}\right)-12{\mathcal{L}}_{\rho +3}^{\rho +3}\left({\vartheta }_1,{\vartheta }_2\right)-{({\vartheta }_2-{\vartheta }_1)}^2(\rho +2)(\rho +3){\mathcal{L}}_{\rho +1}^{\rho +1}\left({\vartheta }_1,{\vartheta }_2\right)|\hfill \\ & \le {\displaystyle \frac{(\rho +1)(\rho +2)(\rho +3){({\vartheta }_2-{\vartheta }_1)}^3}{16}}\mathcal{A}\left({\vartheta }_1^{\rho },{\vartheta }_2^{\rho }\right),\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill & |12\mathcal{A}\left({\vartheta }_1^{\rho +3},{\vartheta }_2^{\rho +3}\right)-12{\mathcal{L}}_{\rho +3}^{\rho +3}\left({\vartheta }_1,{\vartheta }_2\right)-{({\vartheta }_2-{\vartheta }_1)}^2(\rho +2)(\rho +3){\mathcal{L}}_{\rho +1}^{\rho +1}\left({\vartheta }_1,{\vartheta }_2\right)|\hfill \\ & \le {\displaystyle \frac{(\rho +1)(\rho +2)(\rho +3){({\vartheta }_2-{\vartheta }_1)}^3}{32\sqrt[q]{15}}}\left[{\mathcal{A}}^{{\displaystyle \frac{1}{q}}}\left(23{\vartheta }_1^{\rho q},7{\vartheta }_2^{\rho q}\right)+{\mathcal{A}}^{{\displaystyle \frac{1}{q}}}\left(7{\vartheta }_1^{\rho q},23{\vartheta }_2^{\rho q}\right)\right].\hfill \end{array}$$

Proof. 

Proposition 3 can be obtained by setting $w_1={\vartheta }_1$ and $w_1={\vartheta }_1$ in the outcomes of Propositions 1 and 2. □

Proposition 4.

Let $0<{\vartheta }_1<{\vartheta }_2,$ $\rho \in N,$ and $\rho \ge 1.$ Then, for $q>1,$ ${\displaystyle \frac{1}{p}}+{\displaystyle \frac{1}{q}}=1$ and for all $w_1,w_2\in [{\vartheta }_1,{\vartheta }_2],$ we have

$$\begin{array}{cc}\hfill & |12\mathcal{A}\left({({\vartheta }_1+{\vartheta }_2-w_2)}^{\rho +3},{({\vartheta }_1+{\vartheta }_2-w_1)}^{\rho +3}\right)-12{\mathcal{L}}_{\rho +3}^{\rho +3}\left({\vartheta }_1+{\vartheta }_2-w_2,{\vartheta }_1+{\vartheta }_2-w_1\right)\hfill \\ & -{(w_2-w_1)}^2(\rho +2)(\rho +3){\mathcal{L}}_{\rho +1}^{\rho +1}\left({\vartheta }_1+{\vartheta }_2-w_2,{\vartheta }_1+{\vartheta }_2-w_1\right)|\hfill \\ & \le {\displaystyle \frac{(\rho +1)(\rho +2)(\rho +3){(w_2-w_1)}^3\sqrt[p]{2p}}{8\sqrt[p]{(p+1)(3p+1)}}}[{\left(2\mathcal{A}\left({\vartheta }_1^{\rho q},{\vartheta }_2^{\rho q}\right)-{\displaystyle \frac{1}{2}}\mathcal{A}\left(w_1^{\rho q},3w_2^{\rho q}\right)\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ & +{\left(2\mathcal{A}\left({\vartheta }_1^{\rho q},{\vartheta }_2^{\rho q}\right)-{\displaystyle \frac{1}{2}}\mathcal{A}\left(3w_1^{\rho q},w_2^{\rho q}\right)\right)}^{{\displaystyle \frac{1}{q}}}].\hfill \end{array}$$

Proof. 

Using Theorem 4 and setting $f\left(\eta \right)={\displaystyle \frac{{\eta }^{\rho +3}}{(\rho +1)(\rho +2)(\rho +3)}}$, we can calculate the intended inequality. □

Proposition 5.

Let $0<{\vartheta }_1<{\vartheta }_2,$ $\rho \in N,$ and $\rho \ge 1.$ Then, for $q>1,$ ${\displaystyle \frac{1}{p}}+{\displaystyle \frac{1}{q}}=1$ and for all $w_1,w_2\in [{\vartheta }_1,{\vartheta }_2],$ we have

$$\begin{array}{cc}\hfill & |12\mathcal{A}\left({({\vartheta }_1+{\vartheta }_2-w_2)}^{\rho +3},{({\vartheta }_1+{\vartheta }_2-w_1)}^{\rho +3}\right)-12{\mathcal{L}}_{\rho +3}^{\rho +3}\left({\vartheta }_1+{\vartheta }_2-w_2,{\vartheta }_1+{\vartheta }_2-w_1\right)\hfill \\ & -{(w_2-w_1)}^2(\rho +2)(\rho +3){\mathcal{L}}_{\rho +1}^{\rho +1}\left({\vartheta }_1+{\vartheta }_2-w_2,{\vartheta }_1+{\vartheta }_2-w_1\right)|\hfill \\ & \le {\displaystyle \frac{(\rho +1)(\rho +2)(\rho +3){(w_2-w_1)}^3}{8\sqrt[p]{2}}}{B}^{{\displaystyle \frac{1}{p}}}\left({\displaystyle \frac{p+1}{2}},p+1\right)[{\left(2\mathcal{A}\left({\vartheta }_1^{\rho q},{\vartheta }_2^{\rho q}\right)-{\displaystyle \frac{1}{2}}\mathcal{A}\left(w_1^{\rho q},3w_2^{\rho q}\right)\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ & +{\left(2\mathcal{A}\left({\vartheta }_1^{\rho q},{\vartheta }_2^{\rho q}\right)-{\displaystyle \frac{1}{2}}\mathcal{A}\left(3w_1^{\rho q},w_2^{\rho q}\right)\right)}^{{\displaystyle \frac{1}{q}}}].\hfill \end{array}$$

Proof. 

Using Corollary 1 and setting $f\left(\eta \right)={\displaystyle \frac{{\eta }^{\rho +3}}{(\rho +1)(\rho +2)(\rho +3)}}$, we can calculate the intended inequality. □

Proposition 6.

Let $0<{\vartheta }_1<{\vartheta }_2,$ $\rho \in N,$ and $\rho \ge 1.$ Then, we have

$$\begin{array}{cc}\hfill & |12\mathcal{A}\left({\vartheta }_1^{\rho +3},{\vartheta }_2^{\rho +3}\right)-12{\mathcal{L}}_{\rho +3}^{\rho +3}\left({\vartheta }_1,{\vartheta }_2\right)-{({\vartheta }_2-{\vartheta }_1)}^2(\rho +2)(\rho +3){\mathcal{L}}_{\rho +1}^{\rho +1}\left({\vartheta }_1,{\vartheta }_2\right)|\hfill \\ & \le {\displaystyle \frac{(\rho +1)(\rho +2)(\rho +3){({\vartheta }_2-{\vartheta }_1)}^3\sqrt[p]{2p}}{8\sqrt[p]{(p+1)(3p+1)}\sqrt[q]{2}}}\left[{\mathcal{A}}^{{\displaystyle \frac{1}{q}}}\left(3{\vartheta }_1^{\rho q},{\vartheta }_2^{\rho q}\right)+{\mathcal{A}}^{{\displaystyle \frac{1}{q}}}\left({\vartheta }_1^{\rho q},3{\vartheta }_2^{\rho q}\right)\right]\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill & |12\mathcal{A}\left({\vartheta }_1^{\rho +3},{\vartheta }_2^{\rho +3}\right)-12{\mathcal{L}}_{\rho +3}^{\rho +3}\left({\vartheta }_1,{\vartheta }_2\right)-{({\vartheta }_2-{\vartheta }_1)}^2(\rho +2)(\rho +3){\mathcal{L}}_{\rho +1}^{\rho +1}\left({\vartheta }_1,{\vartheta }_2\right)|\hfill \\ & \le {\displaystyle \frac{(\rho +1)(\rho +2)(\rho +3){({\vartheta }_2-{\vartheta }_1)}^3}{16}}{B}^{{\displaystyle \frac{1}{p}}}\left({\displaystyle \frac{p+1}{2}},p+1\right)\left[{\mathcal{A}}^{{\displaystyle \frac{1}{q}}}\left(3{\vartheta }_1^{\rho q},{\vartheta }_2^{\rho q}\right)+{\mathcal{A}}^{{\displaystyle \frac{1}{q}}}\left({\vartheta }_1^{\rho q},3{\vartheta }_2^{\rho q}\right)\right]\hfill \end{array}$$

Proof. 

Proposition 6 can be obtained by setting $w_1={\vartheta }_1$ and $w_1={\vartheta }_1$ in the outcomes of Propositions 4 and 5. □

6. Discussion and Conclusions

The most crucial area of fractional calculus and mathematical analysis is integral inequalities. Over the past four decades, the field of mathematical inequalities has expanded significantly, and numerous articles have been published on this topic, introducing novel ideas. Convexity is crucial to establishing the results for this topic, and as a result, numerous generalizations to convexity have been presented. Mathematicians are employing fractional calculus to simulate mathematical inequalities related to various real-life phenomena, as ordinary calculus is not suitable for this topic. This approach has yielded some unforeseen valuable findings.

Since classical derivations cannot adequately model most applied issues, this work analyzes the results of H–H–M-type inequalities using various fractional integral operators, such as classical, R.L, k-R.L, and their generalized fractional integral operators. In addition, we proposed many related fractional integral inequalities linked to the right side of the H–H–M-type inequality for three-times differentiable convex functions. Additional remarks and observations for these results are provided. The validity of the inequalities is then demonstrated with a couple of examples via graphical visualizations. In a special case, note the comparison between Theorems 2 and 6 in [20]. Finally, we examine some applications in the context of special means, which validate the effectiveness of our results. Our investigation concludes that trapezium H–H–M-type inequalities, instead of midpoint H–H–M-type inequalities, exhibit the change in results from changing the factor from the right member of the key identity ${\eta }^2(1-\eta )$ to $\eta (1-{\eta }^2)$ and changing the domain of the function. We hope that these findings will encourage mathematicians studying fractional calculus to prove new results with different generalized forms of convexity and other fractional integral operators.