Optimizing Districting and Seat Allocation for Enhanced Representativeness in Chile’s Chamber of Deputies

Abstract

This paper presents a mathematical programming model to simultaneously create districts and allocate seats in Chile’s Chamber of Deputies, improving representativeness. In addition, it explicitly incorporates constraints that ensure the contiguity of the communes that form the districts while respecting natural and administrative boundaries. Implementing specific strategies and methods has resulted in significant enhancements in particular metrics used to assess the degree of representativeness. These improvements have effectively addressed certain shortcomings and resulted in more accurate and reliable representation measurements in the given context. This study proposes a novel mathematical programming model that simultaneously tackles district creation and seat allocation for Chile’s Chamber of Deputies. This integrated approach aims to achieve a more representative body. The results demonstrate a substantial decrease in malapportionment, from 11.07 in the 2015 reform to 6.55 under the proposed model. Furthermore, the sum of deviations has diminished, and the number of overrepresented districts has decreased from 17 to 13 out of 28 districts. Consequently, the malapportionment has been significantly reduced and falls within the permissible range of deviations, as outlined by the European Commission for Democracy through Law.

1. Introduction

An electoral system is the foundation on which the legal framework of an election process is organized. Depending on the design of the electoral map and its respective allocation of seats, the electoral system will be appropriately representative. If this electoral system is representative, the principle of “one person, one vote”, characteristic of nations with healthy democracies, will be fulfilled.

To ensure representativeness, many countries update their district maps in response to demographic changes. However, this process can be distorted by self-serving actors, which can lead to the misallocation of seats (malapportionment) and gerrymandering of district boundaries to favor certain parties or candidates. Malapportionment occurs when the distribution of seats per district does not proportionally represent the population of the districts. At the same time, gerrymandering involves the manipulation of the geographical shape of electoral areas for political purposes.

The representativeness of an electoral map can be assessed using different indicators. One of them is the Malapportionment Coefficient (Map), which measures the difference between the proportion of seats and the proportion of population in each district. Another indicator is the Advantage Ratio, which calculates the ratio between the proportion of seats and the proportion of the population in each district. The Overrepresented indicator is also used, which takes the value 1 if a district has a higher proportion of seats than its proportion of population and 0 otherwise.

The following text provides a comprehensive overview of the redistricting process and its key components. A fair and representative electoral system design requires careful attention to delimiting electoral boundaries. This process involves dividing a territory into distinct constituencies, each with a predetermined number of seats, to ensure proportional representation and effective democratic governance. The complexity of this task is heightened in the Chilean electoral system by proximity constraints and the need to distribute seats fairly. In the Chilean context, electoral district delimitation aims to establish boundaries that respect geographical contiguity and ensure that each district includes neighboring areas with common social, economic, and cultural characteristics. The aim is to promote effective representation and responsiveness to local needs and to maintain strong communities within each district. The allocation of seats within each constituency is a crucial aspect of the delimitation process. To ensure fair representation for all political parties or interest groups, seats should be distributed proportionately to the population distribution. This distribution must comply with all relevant legal requirements, including minimum and maximum seat limits for each constituency and other criteria in electoral laws and regulations.

Given the complexity of delimiting electoral districts with contiguity restrictions and allocating seats, using precise mathematical and computational models is essential. These models, which combine geographical and demographic data with political considerations, produce optimal district boundaries and seat allocations that satisfy legal requirements and uphold democratic principles of equity and fairness. This study contributes to advancing fair and effective democratic practices by improving understanding of the issues involved and proposing viable solutions. The delimitation of electoral boundaries is a cornerstone of a fair and representative electoral system, involving the division of a territory into distinct electoral districts, each with a fixed number of seats, to ensure proportional representation and effective democratic governance. This process is particularly challenging in the Chilean electoral system, given the proximity constraints and the need for a fair distribution of seats. The goal is to ensure fair representation for all political parties or interest groups by assigning seats based on population distribution.

Seat allocation must comply with all relevant legal requirements, including minimum and maximum seat limits for each constituency and other critical criteria in electoral laws and regulations. Given the complex nature of the delimitation of electoral districts with boundary requirements and seat allocation, applying rigorous mathematical and computational models is essential. These models, which integrate geographic, demographic, and political factors, determine optimal district boundaries and seat allocations that comply with the law and uphold democratic values of equity and fairness.

The issue of contiguity plays a crucial role in the design of districts, presenting challenges such as creating districts with balanced populations while respecting constraints such as contiguity and compactness. The Chilean scenario illustrates the complexity of the contiguity problem, highlighting the need for practical solutions. Contiguity, a requirement for contiguous districts, can influence the shape of districts, potentially resulting in elongated or irregular shapes. Given its impact on population equality, addressing the contiguity issue is crucial. Contiguity constraints can make it challenging to design districts with uniform population densities. In addition, contiguity can hinder the creation of compact districts, as the need for connectivity may force the inclusion of geographically distant areas.

The contiguity issue poses a challenge to fair voter representation and may enable gerrymandering. Addressing these challenges requires a nuanced understanding and strategic solutions. Addressing contiguity is challenging, but it is a worthwhile endeavor. By understanding the hurdles posed by the contiguity problem, we can design fair redistricting systems more representative of voter preferences. Contiguity, which mandates contiguous districts, is valued because it facilitates voter access and communication between representatives and constituents. However, creating districts with uniform population distribution makes it more difficult.

Compactness, which measures the proximity of constituencies, is often seen as fairer, giving each voter an equal voice. However, compactness can also increase susceptibility to gerrymandering. Various approaches, including mathematical models such as compactness optimization and fairness optimization, can deal with contiguity and compactness constraints. The selection of a model depends on the specific goals of the redistricting process, whether the focus is on compactness or fairness.

The application of contiguity and compactness constraints in districting is a multifaceted challenge. There is no one-size-fits-all solution, and the most effective approach will depend on the specific objectives of the districting process. A comprehensive understanding of the intricacies of contiguity and compactness allows for designing fair districting systems that reflect voter preferences. In [1], the proposed constraints can enforce contiguity by introducing edges into the adjacency graph. For example, if two geographic units must be in the same district, an edge can be added between them in the adjacency graph. Moreover, integer-mixed models can be developed for the districting problem to ensure contiguity while meeting additional requirements like equal population and compactness.

The electoral system in Chile until 2015 was the Binominal System. At that time, changes were made to the design of the electoral map, improving representativeness. The Binominal System overrepresented the right-wing coalition, with questionable representativeness in voting strength, understood as equitable districts in the ratio of population or voters per elected seat [2].

This study uses a mathematical programming model to establish district boundaries and comprehensively distribute seats within the Chamber of Deputies. The approach integrates constraints to ensure district contiguity and preserve natural demarcations during district delineation [1]. A key aspect of this research is its resolution of challenges related to district configuration and seat allocation, marking it as a significant advancement in the field.

The rest of the article is organized as follows: Section 2 presents the guiding principles, distortions, and indices for measuring the representativeness of electoral systems and the electoral systems in Chile over the last few decades. Section 3 describes the problem of districting and its application to politics. Section 4 presents the formulation of the mathematical programming model with contiguity constraints and respect for natural boundaries. Section 5 shows the results of the 2015 Electoral System Reform case. Finally, Section 6 presents conclusions and future work.

2. Electoral System

An electoral system is a set of procedures, rules, and mechanisms that guide how the inhabitants of each territory elect those responsible for representing them and carrying out their demands and expectations, i.e., translating votes into public office [3].

An electoral system must verify the following four guiding principles [4,5]. Collectively, these principles underpin the legitimacy and functionality of electoral systems, ultimately contributing to the stability and responsiveness of democratic institutions.

(a)

The principle of representativeness requires that the distribution of seats per district of the country reflects the principle of “one person, one vote” and that the diversity of ideas, approaches, and political parties that coexist in society is reflected proportionally in parliament.

(b)

The principle of governability seeks to facilitate the formation of a limited number of political coalitions in parliament so that the fewer parties there are, the more likely it is that stable alliances will be formed to succeed in turning proposals into law.

(c)

The principle of competitiveness indicates that without competition, there is no democracy. Therefore, it is necessary to ensure that democratic institutions are periodically evaluated to introduce even more competition in areas where it is needed. Uncertainty in election results is one of the most reliable features of an electoral system’s competitiveness, a fact that is evident in healthy democracies.

(d)

The principle of transparency indicates that an electoral system should consist of simple and easily understandable rules and regulations. The more complicated the electoral laws, the higher the barriers to entry for voters to exercise their right to vote.

Many countries tend to renew their district maps in response to demographic changes to guarantee the principle of representativeness. The actors sometimes seek benefits to themselves by distorting the electoral map [6]. Malapportionment arises when the distribution of seats per district does not proportionally represent the population of the districts and may benefit a specific group [7,8,9]; gerrymandering denotes any unfair handling of the geographical shape of electoral areas for political purposes [10].

The representativeness of a country’s electoral map can be calculated from the difference between the proportion of seats and the proportion of population across its constituent districts. The aggregation of district differences yields a coefficient of Malapportionment (Map) of the electoral system. The Map indicator is a variant of the [11] proportionality index, in which, instead of calculating the difference between party votes and seats, it is calculated between the percentages of population and seats in a district [12].

Mathematically, one has the following:

$$Map={\displaystyle \frac{1}{2}}{\displaystyle \sum _{i=1}^D\left|\%E_i-\%P_i\right|}$$

(1)

where $D$ is the number of districts, %$E_i$ is the percentage of seats in the district, $i, i=1,2,\dots ,D,$ and $\%P_i$ is the percentage of the population in the district $i, i=1,2,\dots ,D$.

A second indicator is the Advantage Ratio, which consists of calculating for each district the ratio between the proportion of seats and the proportion of the population, multiplying it by 100, and subtracting 100 from the previous result.

$$AdvRati{o}_i=\left[{\displaystyle \frac{\%E_i}{\%P_i}}\times 100\right]-100 i=1, \dots ,D$$

(2)

In general, the concept of deviation in this context usually refers to the difference between the expected representation (based on population) and the actual representation (based on the number of seats allocated). The sum of deviations is used to aggregate these individual differences across districts in order to provide a comprehensive picture of the electoral system in terms of representativeness. The specific formula for calculating the deviations is not explicitly stated in the summary. The sum of the AdvRatio for each district is used as a measure of deviation. This aggregation allows for a clearer understanding of disparities in representation at the country level.

The third indicator, referred to as Overrepresented, can be represented by a formula. It is described as a binary type indicator that takes the value of 1 when the district is overrepresented (i.e., when the percentage of seats in the district is greater than the percentage of the population) and 0 when the district is underrepresented.

The formula can be expressed as follows:

$$Overrepresente{d}_i=\left\{\begin{array}{l}1; if \%E_i>\%P_i\\ 0; if \%E_i\le \%P_i\end{array}\right.$$

where $\%E_i$ is the percentage of seats in the district $i$, $\%P_i$ is the percentage of the population in the district $i$, and $Overrepresented={\displaystyle \sum _{i=1}^{D}Overrepresente{d}_i}$ [12].

The 1925 Constitution established Chile’s first electoral system for electing senators and deputies. This system was majoritarian, i.e., the candidates with the highest votes were elected, the voter’s choice was limited to one alternative, and individual candidacies were proposed. The political–electoral division was distributed into nine provincial groupings for senators, each responsible for electing five senators. Regarding the territorial distribution of deputies, one deputy was elected for every thirty thousand inhabitants in twenty-five districts. Between two and eighteen deputies were elected per district, depending on the number of inhabitants.

After the 1973 coup d’état and the 1988 referendum, the authorities of the dictatorship elaborated the Binominal Electoral System, moving from a majority system to a proportional system. This system came into force in 1989 and was included in the 1980 Constitution, causing changes regarding the division of the Chilean territory for the elections of senators and deputies to be implemented in the new electoral system with 19 constituencies and 60 districts. In each territorial division, there was a district magnitude equal to two in the cases of both deputies and senators [13].

Since it entered into force in 1989, the Binominal Electoral System has been the subject of much academic discussion and a profound debate among political actors, and numerous legislative initiatives have been presented to reform it, given the controversial situations that have arisen [14]. For example, when the majority list fails to obtain more than double the votes of the second most voted list, a candidate from the competing list is elected with meager votes. Another controversial case is when the candidate with the lowest percentage of votes on the majority list is elected “by trailing”, even though he or she obtained fewer votes than the first candidate on the competing list [13].

The reform projects suggested for the political–electoral division, described by [14], were made under demographic and/or geographic criteria. There have been 19 bills or constitutional reform projects that sought to modify the elements of the Binominal Electoral System. However, none of them became law until 2015, when Law 20.840 reformed the Binominal Electoral System under the government of President Michelle Bachelet [15]. It analyzed the proportionality of the representation of some redistricting proposals, using the 2005 election of deputies, concluding that the proposals did not present significant improvements, and some even increased the distortions of the Binominal System [16].

This new electoral system increases the number of deputies from 120 to 155 to improve representation, decreasing the number of districts from 60 to 28. The number of senators is increased from 38 to 50, and a single senatorial constituency per region is established. The district size varies from three to eight deputies and two to five senators. The election is carried out using the D’Hondt Method, which allows for the number of seats elected in each competing list in proportion to the votes obtained [17].

3. Districting Problem

The Districting Problem is a mathematical programming problem that divides a geographical area into sub-areas to plan some operations. The Districting Problem has a wide range of real applications: in politics with [18,19], in the layout of territories for sales with [20,21], in education with [22], in the delimitation of special economic zones with [23], and emergency systems and health centers with [24].

A classic problem in the territorial planning of a country is Political or Electoral Districting, in which a geographical area is divided into electoral sub-areas according to specific criteria. Once the territorial division has been carried out, the inhabitants of each sub-area must elect their representatives using voting [25].

Districting Problems are mainly modeled through Integer Linear Programming, and for small instances, their solution is found through Branch and Bound algorithms [26,27,28,29,30]. Given its high computational complexity, for larger sizes, it is necessary to use heuristic techniques in the search for solutions, for example, Tabu Search [31,32], Genetic Algorithms [33], and Simulated Annealing [34], among others.

In the Electoral Districting Problem, it is necessary to consider that each minimum geographical or administrative unit is assigned to only one district and that the number of districts to be formed is generally known.

Among the main criteria to be considered in districting are the following:

(a)

Contiguity: a district is contiguous when it is possible to go from any point to another in the district without having to pass through another district;

(b)

Compactness: this is a criterion used to prevent the formation of irregularly shaped districts. Districts should be circular or square rather than elongated or twisted;

(c)

Balance: seeks to create equitable districts in the population ratio or electors per elected seat. Balance can be measured by the indicators described in Section 2;

(d)

Respect for boundaries: natural boundaries (such as rivers, lakes, and mountain ranges) and non-natural boundaries such as administrative divisions and constructions (such as railways and highways) can be considered in the formation of districts;

(e)

Socio-Economic Homogeneity: districts should be sought that are as homogeneous in socio-economic terms as possible to allow for better representation of the population in parliament [10,35].

Balance, Compactness, and Contiguity are the most commonly used districting criteria. In [36], a new criterion was presented for local and global demographic equity, which encourages candidates during campaigning and once elected to achieve better representation. These criteria are added to the criteria of Malapportionment, Balance (minimizing the maximum malapportionment of the districts) and Compactness, in a multi-objective combinatorial optimization problem, applied to the Chilean case of the 2015 Reform.

Ensuring contiguity is particularly difficult because modeling it implies a sharp increase in variables or constraints, even exponentially. Different methods have been proposed to correct this, for example, by setting a maximum radius for the district so that the district can only consist of units within that radius. Another method would be to create a set of “semi-armed” districts so that the model continues the construction of these districts [31,32]. The author of [37] presented an integer linear programming model for the planning of commercial territories that explicitly includes constraints that ensure contiguity; the number of such constraints grows exponentially as the number of units to be allocated increases, so a relaxation scheme of these constraints is used to solve the problem [38,39]. The author of [40] presented a set of restrictions that ensure the contiguity of the districts for allocating geographical units, valid for incorporation in any mixed integer programming model. It summarizes contiguity in terms of a graph, where each geographical unit is a vertex, and each arc represents adjacent edges between each pair of units. Then, to check the contiguity of a set of geographical units S, it must be verified that from one unit in S, another unit in S can be reached by following a sequence of adjacent edges. An alternative set of constraints has been formulated based on the described contiguity condition to guarantee the formation of a contiguous region of a given set of geographical units.

In [41], the authors modeled with mathematical programming the district and seat allocation problem of the Chilean Binominal System Reform, obtaining improvements to the Malapportionment, Deviation, and Overrepresentation indicators concerning the Reform map. The mathematical programming model did not guarantee the contiguity of the districts, but its objective function did promote it. To remedy this situation, constraints forcing the contiguity of districts were incorporated into the optimal solution of the initial model. This process was repeated until all the districts of the electoral map were contiguous. Pioneering integer programming in districting, the authors of [29] achieved compactness even without explicitly enforcing contiguity. However, the authors of [42] reviewed existing contiguity models, proposed two new ones and compared them analytically and through numerical experiments. Contrary to common belief, imposing contiguity does not significantly impact problem difficulty. Following the ideas developed by [43], we propose a flow-based formulation for contiguity adapted from [1].

The research in [44] delves into the application of design and/or territorial distribution problems in various domains, including politics, sales, location/routing, and health. This broadens the scope of the study and highlights its practical relevance. Furthermore, [45] presents a comprehensive review of political districtization, shedding light on its real-world implications.

4. Formulation of the Mathematical Programming Model

Based on the restrictions proposed by [40], which ensure the contiguity of the districts, restrictions are incorporated in this paper, allowing contiguous districts to be obtained using the model of [41]. In addition, natural boundaries are included by modifying the adjacency matrix $F$. The matrix, $F,$ has entries $f_{ij},$ equal to 1 when communes $i$ and $j$ have a common border within the same region, and 0 otherwise; when there is a natural boundary between adjacent communes, the value of $f_{ij}$ is set to 0.

The parameters, sets, and decision variables used in the model are described below.

• Parameters and sets:
• $I$: total number of communes
• $D$: total number of districts
• $R$: a set of pairs of communes belonging to the same region
• $S$: total number of seats to be allocated
• $P$: the total population of the country
• $F$: adjacency matrix between communes
• $p_i$: population of the commune $i, i=1,2,\dots ,I$
• $d_{ij}$: distance between communes $i$ and $j;$ $i=1,2,\dots ,I; j=1,2,\dots ,I; d_{ii}=0; i=1,2,\dots ,I$
• $Ma{p}_{\max }$: the maximum tolerated value of malapportionment
• $M$: a sufficiently large number
• $N_r$: number of communes in the region $r; r=I,II,\dots ,RM$
• $d_{\min }$: minimum number of seats to be allocated to a district center commune
• $d_{\max }$: maximum number of seats to be allocated to a district center commune
• Decision variables:
• $x_{ij}$: takes the value 1 if the commune $i$ is assigned to the district center $j,$ and 0 otherwise; $i=1,2,\dots ,I; j=1,2,\dots ,I; (i,j)\in R; k=1,2,\dots ,I$
• $s_j$: the number of seats assigned to the district center $j,$ represents the number of seats associated with the district with the center in the commune $j; j=1,2,\dots ,I$
• $y_{ijk}$: flow between commune $i$ and $j$ when commune $k$ is a district center. This variable is used to ensure the formation of contiguous districts; $i=1,2,\dots ,I; j=1,2,\dots ,I; (i,j)\in R; k=1,2,\dots ,I$
• $z_{ij}$: takes the value 1 if the seats allocated to the district center $i$ are larger than the district center $j,$ and 0 otherwise; $i=1,2,\dots ,I; j=1,2,\dots ,I; (i,j)\in R$

The objective function (3) minimizes the population-weighted distance of the communes assigned to an active district center, for all districts in the country.

$$Min{\displaystyle \sum _{i=1}^I{\displaystyle \sum _{\begin{array}{c}j=1\\ (i,j)\in R\end{array}}^I{p}_i{d}_{ij}{x}_{ij}}}$$

(3)

The objective function that minimizes the population-weighted distance in the model is intuitive, promotes compactness and contiguity of districts, and is easy to compute. However, it may ignore relevant criteria such as population or voter balance and socio-economic homogeneity.

The first set of constraints (4)–(6) aims at correct districting. In (4), it is required that $D$ districts be formed. In (5), each commune must be assigned to a district center. Constraint (6) allows a commune to be assigned to a possible district center if the latter is chosen as one of the district centers ($x_{ij}=1$).

$${\displaystyle \sum _{j=1}^I{x}_{jj}=D}$$

(4)

$${\displaystyle \sum _{\begin{array}{c}j=1\\ (i,j)\in R\end{array}}^I{x}_{ij}=1} i=1, \dots ,I$$

(5)

$$x_{ij}\le x_{jj} i=1, \dots ,I; j=1, \dots ,I; (i,j)\in R; i\ne j$$

(6)

Constraint (7) demands that more districts be built in the most populated regions.

$${\displaystyle \sum _{j\in XI}{x}_{jj}}\le {\displaystyle \sum _{j\in XII}{x}_{jj}}\le {\displaystyle \sum _{j\in XV}{x}_{jj}}\le \dots \le {\displaystyle \sum _{j\in V}{x}_{jj}}\le {\displaystyle \sum _{j\in VIII}{x}_{jj}}\le {\displaystyle \sum _{j\in RM}{x}_{jj}}$$

(7)

Constraints (8) and (9) enforce the contiguity of districts, creating a path connecting each commune to its district center only through adjacent communes that belong to the district (in the same region).

$${\displaystyle \sum _{\begin{array}{c}j=1\\ (i,j) \in F\end{array}}^I{y}_{ijk}}-{\displaystyle \sum _{\begin{array}{c}j=1\\ (j,i) \in F\end{array}}^I{y}_{jik}}\ge x_{ik} i=1, \dots ,I; k=1, \dots ,I; i\ne k$$

(8)

$${\displaystyle \sum _{\begin{array}{c}j=1\\ (i,j)\in F\end{array}}^I{y}_{ijk}}\le (N_r-1)x_{ik} i=1, \dots ,I; k=1, \dots ,I; i\ne k; r=I, II,\dots ,RM$$

(9)

The following model constraints are aimed at seat allocation. Constraint (10) requires Malapportionment to be less than or equal to a maximum tolerated value.

$${\displaystyle \frac{1}{2}}\left({\displaystyle \sum _{i=1}^D\left|\%E_i-\%P_i\right|}\right)\le Ma{p}_{max}$$

(10)

Constraint (11) seeks to ensure that the maximum difference between the seats allocated to the active district center $j$ ($x_{jj}=1$) and those that should proportionally be allocated to it by population is less than 1. Due to their low population, these restrictions do not apply to communes in regions with a single district. This constraint can be easily linearized.

$$\left|s_j-\left({\displaystyle \frac{S}{P}}{\displaystyle \sum _{\begin{array}{c}i=1\\ (i,j)\in R\end{array}}^I{p}_i{x}_{ij}}\right) -\left((1-x_{ij})M\right)\right|\le 0.99 j=1, \dots ,I$$

(11)

With constraint (12), S seats are allocated in the country’s districts, and (13) forces a minimum $d_{\min }$ and a maximum $d_{\max }$ of seats to be assigned to an active district center commune.

$${\displaystyle \sum _{j=1}^I{s}_j=S}$$

(12)

$$d_{\min } x_{jj}\le s_j\le d_{\max } x_{jj} j=1,\dots , I$$

(13)

Restriction (14) requires more seats to be allocated to more-populated regions.

$${\displaystyle \sum _{j\in XI}{s}_j}\le {\displaystyle \sum _{j\in XII}{s}_j}\le {\displaystyle \sum _{j\in XV}{s}_j}\le \dots \le {\displaystyle \sum _{j\in V}{s}_j}\le {\displaystyle \sum _{j\in VIII}{s}_j}\le {\displaystyle \sum _{j\in RM}{s}_j}$$

(14)

Constraints (15) and (16) require that, in each region, if a district receives more seats, it must have a population greater than or equal to that of districts with equal or fewer seats.

If $z_{ij}$ is equal to 1, through the logical constraint (16), the population of the district center $i,$ is forced to be greater than or equal to the population of the district center $j.$

$$s_i-s_j\le {Mz}_{ij} ; i=1, \dots ,I; j=1, \dots ,I; (i,j)\in R$$

(15)

$$\mathrm{If} z_{ij}=1\to {\displaystyle \sum _{\begin{array}{c}k=1\\ (k,i)\in R\end{array}}^I{p}_k{x}_{ki}\ge }{\displaystyle \sum _{\begin{array}{c}l=1\\ (l,j)\in R\end{array}}^I{p}_l{x}_{lj}}; i=1, \dots ,I; j=1, \dots ,I; (i,j)\in R$$

(16)

The logical constraint (16) for positive, sufficiently large M is written as follows:

$${\displaystyle \sum _{\begin{array}{c}k=1\\ (k,i)\in R\end{array}}^I{p}_k{x}_{ki}-}{\displaystyle \sum _{\begin{array}{c}l=1\\ (l,j)\in R\end{array}}^I{p}_l{x}_{lj}}\ge M(z_{ij}-1)$$

Finally, constraints (17)–(19) show the nature of the variables.

$$x_{ij}, z_{ij}\in \{0,1\}, i=1, \dots ,I; j=1, \dots ,I; (i,j)\in R$$

(17)

$$s_j, \mathrm{integer}, j=1,2,\dots ,I$$

(18)

$$y_{ijk} \ge 0, i=1,2,\dots ,I; j=1,2,\dots ,I; \mathrm{k}=1,2,\dots ,I; \mathrm{i}\ne \mathrm{k}; (i,j)\in R$$

(19)

5. Results

In 2015, Chile was divided into 15 regions, which in turn were subdivided into 346 communes. The model was implemented using the parameters of the 2015 Reform, which allocates 155 deputies to 28 districts. Each district is allocated a minimum of three and a maximum of eight deputies.

Table 1. Main parameters.

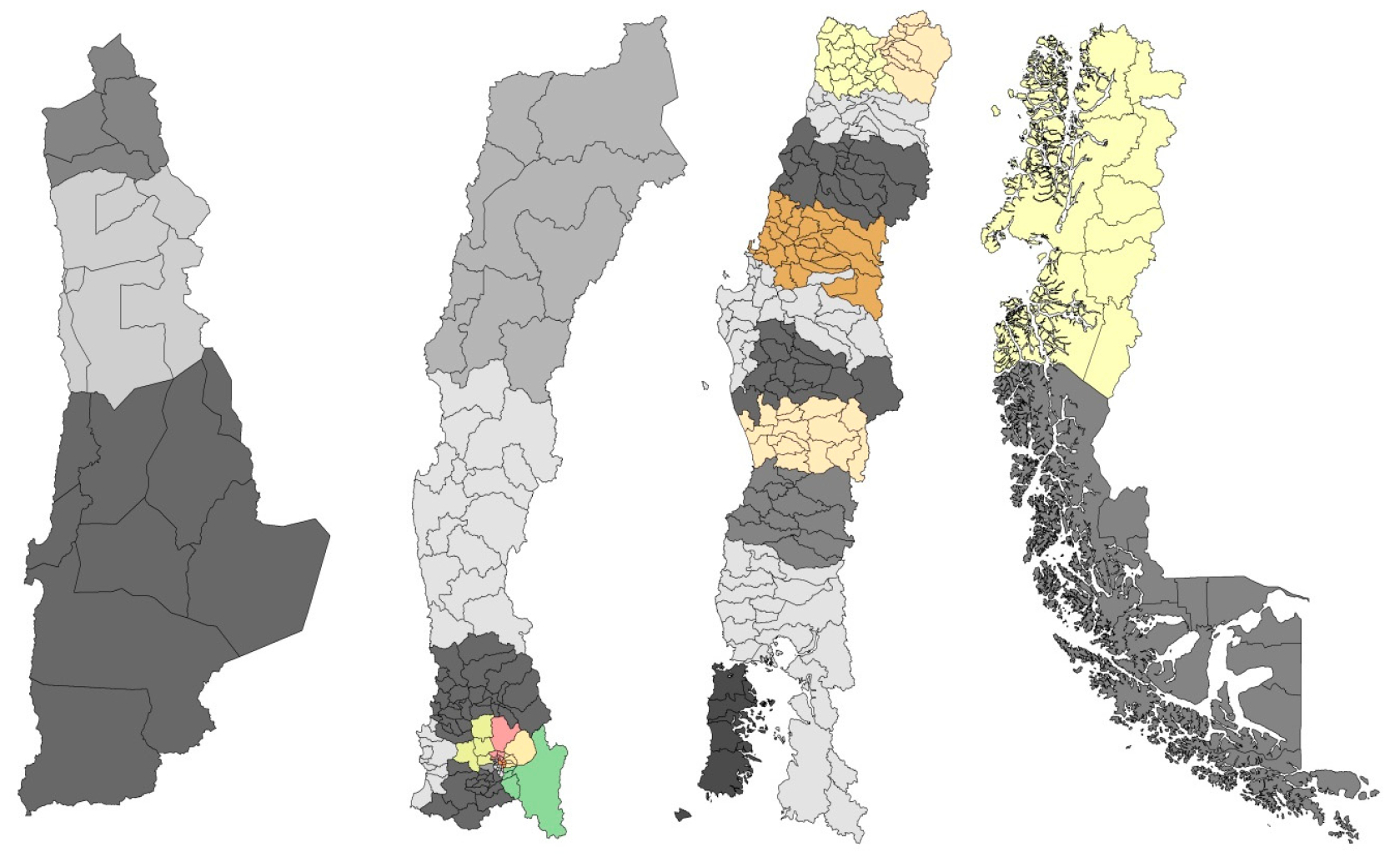
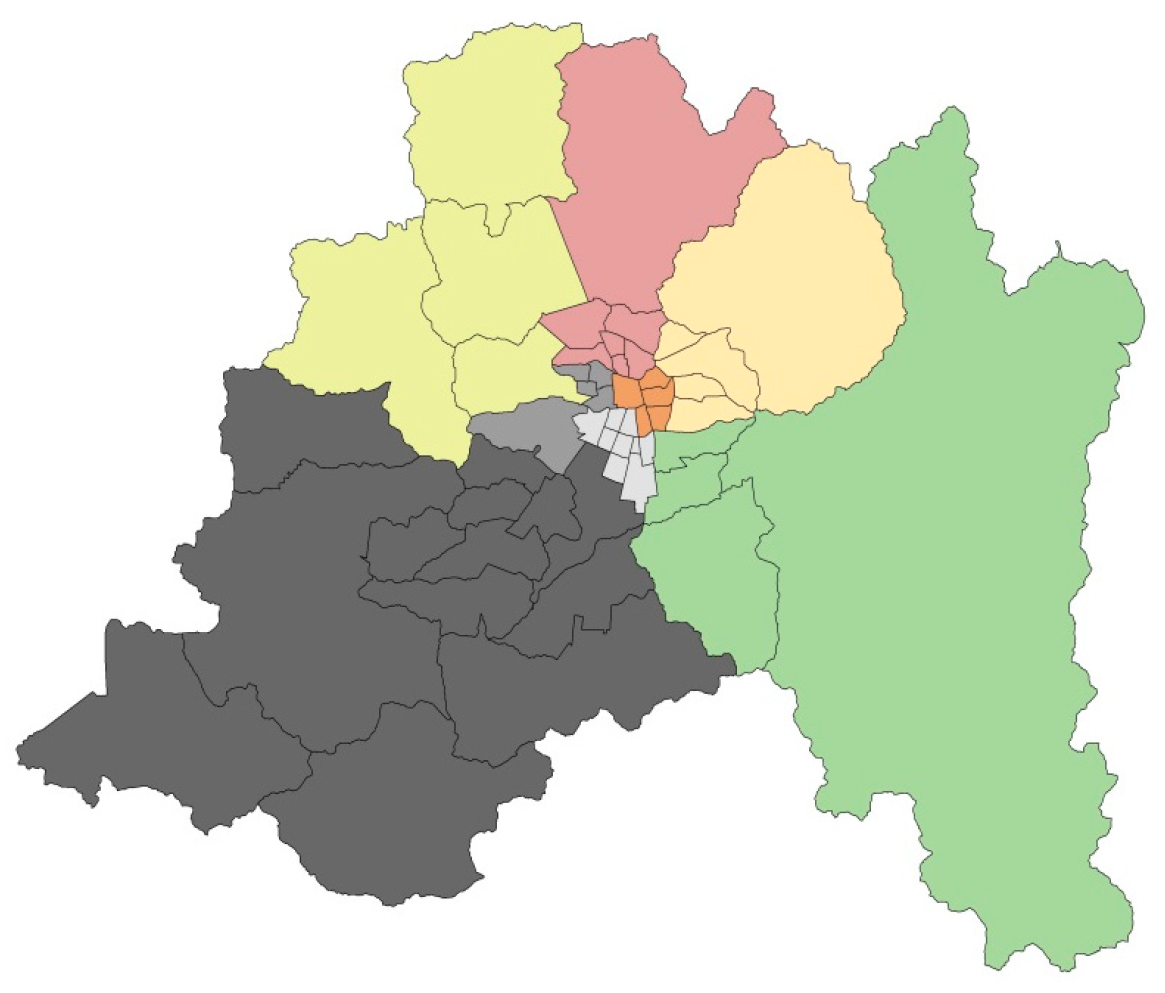
Parameters	Total Number of Communes: (I)	Total Number of Electoral Districts: (D)	Total Number of Deputies to Be Allocated: (S)	Maximum Allowed Malapportionment: (Mapmax)	Minimum Number of Deputies per District (dmin)	Maximum Number of Deputies per District (dmax)
Value	346	28	155	0.07	3	8

Source: Own elaboration based on the parameters of the 2015 Reform.

shows the main parameters used.

The model was implemented in the AMPL 10.0 modeling language [46] and solved with the CPLEX 12.6 solver [47] using population data from the 2017 Census [48]. The model was run with a time limit of 10 h, obtaining a non-optimal solution with a relative GAP of 3.74%, which indicates the quality of the solution concerning the value of a theoretically optimal solution expressed in relative terms.

Figure 1 and Figure 2 show the solution provided by the model for Chile and the Metropolitan region. The proposed map appreciates the districts’ contiguity due to constraints (8) and (9).

Table 2. Distribution of MPs and districts by region.

	Region	XV	I	II	III	IV	V	RM	VI	VII	VIII	IX	XIV	X	XI	XII
Number of Deputies	Reform 2015	3	3	5	5	7	16	47	9	11	18	11	5	9	3	3
	Proposed Map	3	3	6	3	6	16	58	8	10	16	8	4	8	3	3
Number of Districts	Reform 2015	1	1	1	1	1	2	7	2	2	3	2	1	2	1	1
	Proposed Map	1	1	1	1	1	2	8	2	2	2	2	1	2	1	1

Source: Own elaboration based on AMPL/CPLEX results.

shows the number of deputies and districts for each region for the 2015 reform and the proposed map.

The main differences in the number of deputies are in the Metropolitan Region, which increased by eleven deputies, and the XI region, which decreased by three deputies. Regarding the number of districts, changes only occurred in the Metropolitan Region, which increased by one district, and the VIII Region, which decreased by one district.

Table 3. Electoral map representativeness indicators.

	Census 2012			Census 2017
	Malapportionment	AdvRatio	Overrepresented	Malapportionment	AdvRatio	Overrepresented
Binominal System	17.79	21.42	32/60	17.80	21.61	32/60
Reform 2015	10.86	19.43	17/28	11.07	20.26	17/28
Proposed Map	6.69	15.46	15/28	6.55	16.06	13/28

Source: Own elaboration based on AMPL/CPLEX results and the 2012 [49] and 2017 [48] Censuses.

presents the values of the representativeness indicators defined in Section 2. The model’s results, considering the 2017 Census populations, show that the malapportionment of the proposed electoral map decreased to 6.55 from 11.07 in the 2015 Reform. Similarly, the sum of the deviations is reduced, and the number of overrepresented districts decreases from 17 to 13. In addition, Table 3 presents the indicator values for the proposed electoral map with the 2012 Census populations [49].

Table 4. Distribution of seats and population by district ³ center.

District	Region	District Center	Number of Seats	Population by District	Population per Seat
1	XV	Putre	3	226,068	75,356
2	I	Huara	3	330,558	110,186
3	II	Sierra Gorda	6	607,534	101,256
4	III	Copiapó	3	286,168	95,389
5	IV	Monte Patria	6	757,586	126,264
6	V	Calera	8	981,410	122,676
7	V	El Tabo	8	834,492 1	104,312
8	RM	Conchalí	8	987,526	123,441
9	RM	La Cisterna	8	1,018,194	127,274
10	RM	Lo Prado	8	1,007,565	125,946
11	RM	Ñuñoa	8	965,837	120,730
12	RM	Puente Alto	8	979,732	122,467
13	RM	Las Condes	7	820,441	117,206
14	RM	Lampa	3	384,218	128,073
15	RM	Talagante	8	949,295	118,662
16	VI	Peralillo	3	299,882	99,961
17	VI	Olivar	5	614,673	122,935
18	VII	Sagrada Familia	3	338,092	112,697
19	VII	Villa Alegre	7	706,858	100,980
20	VIII	Ránquil	8	1,019,060	127,383
21	VIII	Santa Juana	8	1,018,354	127,294
22	IX	Traiguén	3	298,182	99,394
23	IX	Freire	5	659,042	131,808
24	XIV	Los Lagos	4	384,837	96,209
25	X	Llanquihue	5	660,523	132,105
26	X	Castro	3	168,185	56,062
27	XI	Río Ibáñez	3	103,158	34,386
28	XII	Laguna Blanca	3	166,533 2	55,511

¹ Includes population of the communes of Isla de Pascua and Juan Fernández; ² includes population of the Antarctic commune; ³ single-district regions, where the population does not exceed 1.93% of the country’s population: XV, I, III, XI, and XII. Source: Own elaboration based on AMPL/CPLEX and Census 2017 results [48].

presents the 28 districts with their respective district centers (x_jj = 1) and the number of deputies assigned to each district (s_j), except for regions where the population does not exceed 1.93% (3/155) of the country’s population, which are assigned a single district with three deputies, and Region X, which has a natural boundary separating the mainland from the island of Chiloé, generating two districts with five and three seats. This produces a significant difference in seats per population; the district of the communes of Chiloé Island is 56,062 per seat, and for the rest of the region, it is 132,105. For the rest of the districts, the worst hit is District 23, with 131,808 population per seat, compared to the maximum obtained by the 2015 Reform in District 8, with 182,220 population per seat. In turn, the most favored district is District 24, with 96,209 population per seat compared to District 22’s 74,082 population per seat.

It is worth noting that the balance of population per seat that occurred in the Metropolitan Region, where the minimum and maximum population per seat were 128,691 and 182,220, respectively, with the 2015 Reform district, which for the present proposal takes the values of 117,206 and 128,073, respectively, significantly reducing the difference in voting power between districts in the Metropolitan Region.

6. Conclusions and Future Work

Mathematical programming has established itself as an essential tool for the elaboration of electoral maps that promote the representativeness of the population and the allocation of seats, taking into account several fundamental aspects. The electoral map proposed by the model significantly improves representativeness indicators and successfully incorporates explicit restrictions to guarantee geographical contiguity. These achievements are especially remarkable considering the reasonable computation time achieved for this complex problem.

The results show a substantial decrease in malapportionment from 11.07 in the 2015 reform to 6.55 in the proposed model. In addition, the sum of the deviations has decreased, and the number of over-represented districts has been reduced from 17 to 13 out of 28 districts. Consequently, the malapportionment has been considerably reduced and is within the permissible range, as established by the European Commission for Democracy through Law [12,50].

The achievements of this work are particularly remarkable when considering the computational efficiency achieved in a reasonable time frame for a problem of such complexity. Importantly, the study simultaneously addresses district formation and seat allocation, two challenges that are separately recognized as complex in the scientific literature. Existing research usually treats these problems in isolation, which underlines the unique contribution of this work, which lies in the simultaneous resolution of both problems through an integrative approach.

In future work, we are interested in incorporating socio-economic homogeneity through a measure of dissimilarity between communes based on a cluster analysis that considers variables of economic and social activity, such as schooling, indigenous peoples, poverty, and urban and rural population distribution. This measure can be seamlessly incorporated into the model to take into account the socio-economic dissimilarity of communes in the construction of electoral districts, thus encouraging the formation of districts of communes with similar socio-economic realities. Based on cluster analysis of economic and social variables, this measure will allow for the creation of districts that are not only geographically contiguous and representative in terms of population but also present greater socio-economic homogeneity. By considering this additional dimension, the model can aim for a more holistic and equitable representation. This is intended to deepen the understanding of the challenges of redistricting and contribute to the development of fairer and more representative electoral systems.