Stability and Optimality Criteria for an SVIR Epidemic Model with Numerical Simulation

Abstract

The mathematical modeling of infectious diseases plays a vital role in understanding and predicting disease transmission, as underscored by recent global outbreaks; to delve deep into the dynamic of infectious disease considering latent period presciently is inevitable as it bridges the gap between realistic nature and mathematical modeling. This study extended the classical Susceptible–Infected–Recovered (SIR) model by incorporating vaccination strategies during incubation. We introduced multiple time delays to an account incubation period to capture realistic disease dynamics better. The model is formulated as a system of delay differential equations that describe the transmission dynamics of diseases such as polio or COVID-19, or diseases for which vaccination exists. Critical aspects of the study include proving the positivity of the model’s solutions, calculating the basic reproduction number (${\mathcal{R}}_0$) using next-generation matrix theory, and identifying disease-free and endemic equilibrium points. The local stability of these equilibria is then analyzed using the Routh–Hurwitz criterion. Due to the complexity introduced by the delay components, we examine the stability by studying the roots of a fourth-degree exponential polynomial. The effects of educational campaigns and vaccination efficacy are also investigated as control measures. Furthermore, an optimization problem is formulated, based on Pontryagin’s maximum principle, to minimize the number of infections and associated intervention costs. Numerical simulations of the delay differential equations are conducted, and a modified Runge–Kutta method with delays is used to solve the optimal control problem. Finally, we present a few simulation results to illustrate the analytical findings.

1. Introduction

In ancient times, societies have grappled with numerous infectious diseases, posing significant threats to human health and the environment at large [1,2,3]. According to the World Health Organization (WHO), infectious diseases account for more than 17 million deaths annually [4]. Fortunately, modern health care systems, with the assistance of disease control methods, treatment, and spreading information to communities, continue making these endeavors more effective. Despite these strides, over the past three decades, urban and animal populations have witnessed the emergence of over 30 diseases, some exhibiting alarming characteristics, such as mutations facilitating transmission from animals to humans or between humans [5]. Although modern medical innovation has made it possible to come up with cures and vaccines for some emerging diseases, the process of developing a vaccine that would be immune for all strains is arduous, as was the case with the COVID-19 pandemic that took a long time for an effective vaccine to be developed and rolled out to the world. Socioeconomic inequalities, particularly among impoverished communities unable to effectively isolate, contribute to disease spread. Understanding where diseases concentrate helps inform strategies to control outbreaks, with medical science focusing on vaccine and antibiotic development. Applied mathematicians and epidemiologists are pivotal in developing epidemiological models to analyze disease spread dynamics [6,7,8,9]. Kuniya et al. [10] introduced various SIS epidemic models, while Mouaouine et al. [11] explored diverse SIR epidemic models. Although SIS and SIR models are pivotal in epidemiology [12], they overlook the latent period observed in certain infectious diseases like chickenpox, influenza, and tuberculosis, and vector-borne illnesses such as dengue hemorrhagic fever, west nile virus, and malaria. These diseases are often asymptomatic for a long incubation period, making controlling spread in the initial stages difficult. In other words, they are incubation period bites, during which non-infected individuals are carriers of the pathogen long before they become infectious. Recognizing this, SEIS epidemic models [13,14] and SEIR epidemic models [15,16] have been developed and analyzed.

Still, SEIR models do not represent well in practice because they presume that the individual remains immune to the disease for an infinite time, that is, until the person dies. However, this assumption does not hold for many diseases. For instance, in malaria and rotavirus, even after recovering from the disease, one will only be protected for a short duration, and even the time before this disease manifests is quite long. As a result, such people may be susceptible again with time once their temporary immunity wears off.

It is worth mentioning that some types of epidemic models include other forms of control such as, for instance, quarantine, which consists of confining persons who are suspected of being infected but not yet diagnosed with an infectious disease [17,18], or immunization [19,20,21] as an efficient measure of controlling outbreaks. This approach is beneficial in curbing diseases such as polio and tuberculosis, and vaccination has primarily led to their destruction. The earlier models of epidemics concerning the power of immunization usually assumed total immunity after vaccination [22]. However, this notion does not hold water in every situation. The disease can still be acquired by those vaccinated, although this occurs at a much lower probability than it does for those not vaccinated.

The traditional models have been highlighted as needing more improvement in the recent work conducted on COVID-19. A new “identifiability model” is developed to avoid the additional parameters in the standard Target Cell Limited model, which are rarely helpful in making predictions that “fit” the observations [23]. Likewise, even simple quarantine or treatment compartmental models demonstrate that even minor alterations in the public health policy severely constrain the scope for infection [24]. The discrete SIR models have also been well characterized in the propagation of disease and have aided in controlling the spread of epidemics remarkably [25]. Relatively few such studies account for the combined effect of the two diseases. Co-infection dynamics studies have become predominating, for instance, the dynamics of interplays between dengue, chikungunya, and more complex HIV/HCV infections where a system of fractional derivatives is used to model the system [26,27]. These models help understand the spread strategy and available “best” treatment methods. A better understanding of disease dynamics has been achieved. Hence, some clinicians have advocated using fractional-order derivatives models due to their ability to include history in infectious transmission. Non-local fractional methods are used for a study of the transmission of SARS-CoV-2 [28], and pathologies like multiple sclerosis have recently been modeled this way [29] with an improvement in prediction and detection at an early stage. By integrating factors like co-infections and fractional calculus, these models provide deeper insights into disease spread and control, contributing to more effective public health strategies [30,31].

Delay differential equations (DDEs) can be classified under the dynamical system approach, and their behavior is more complex. The introduction of a suitable time lag in the model can, on the other hand, destabilize an equilibrium that formerly was stable, thereby resulting in population fluctuations. This article emphasizes the utility of time delay in the population models and population dynamics, especially models concerning disease outbreaks. Different infectious diseases have different patterns for their delay in population dissemination. To introduce the relevance of delay differential equations (DDEs) in the context of population dynamics and epidemics, a comprehensive overview delving into delayed logistic-type equations, which are commonly utilized in epidemic modeling, is provided in [32,33].

This study is motivated by recognizing the complexities in infectious disease dynamics, especially in vaccination programs. Traditional models often overlook the impact of time delays in disease modeling from significant factors such as incubation period, vaccination timing, and population response. By incorporating multiple delays, we aim to improve the model’s realistic nature and predictive accuracy, which enhances public health interventions and policy decisions.

Numerous researchers have integrated delays into various scenarios following the initial exploration of time-delayed epidemic models. These include considerations such as the duration of vaccination periods [34], delays in the asymptomatic carriage and infection periods [35], delays in immunity periods, and delays in the incubation or latent periods [35,36]. Several studies have investigated disease transmission models with delays. For example, some studies incorporate delays in specific stages of the disease progression. In [35], a model with delays in incubation and asymptomatic carriage periods is analyzed. Similarly, ref. [37] explores an SEIRS model with constant delays in the latent and immune periods.

Other studies focus on models with general disease transmission dynamics and specific delay structures. In [38], a general model with a latent period and relapse is studied, while [36] investigates a time-delayed SIR model with a nonlinear incidence rate and a Holling type II treatment. Vaccination strategies within time-delayed models have also received attention. In [39], a model with a delay representing the time for susceptible individuals to recognize their infection and seek vaccination is explored while [40] studies different methods of introducing delays. Additionally, refs. [41,42] explore other time-delayed models incorporating vaccination. In [43], the study investigates monkeypox by incorporating a quarantine compartment and optimal control strategies. Inspired by the above approaches, we propose an SVIR epidemic model with multiple delays to analyze the spread of infections in this work.

This paper is organized as follows: In Section 2, we propose a mathematical model with multiple time delay, derive the basic reproduction number, and prove the positivity and boundedness of the solution. Section 3 delves into the proposed models’ stability analysis and examines the sensitivity index of the basic reproduction number (BRN) concerning various parameters. In Section 4, we present the formulation and solution of the associated optimal control system. In Section 5, our theoretical results are affirmed through numerical simulations.

2. Model Formulation and Positivity of the Solution

Modeling the latent period plays a significant role in predicting the spread of infectious diseases. A recently studied model [44,45] has been developed by incorporating numerous improvements to enhance realism and accuracy in depicting the real-life spread of diseases.

This study extends the current framework by incorporating time delays, vaccine effectiveness, and the possibility of waning immunity. The model provides a more realistic representation of disease spread and vaccination efficacy by including these dynamics. The introduction of parameters for delayed transmission, vaccine effectiveness, and immunity loss significantly enhances the model’s applicability to real-world scenarios [46].

This model below introduces an SVIR system for individuals exposed to infection and examines the latent period, which is the interval between an individual becoming infected with a virus and the appearance of disease symptoms. This period can vary significantly, depending on factors such as the specific disease, like polio or COVID-19, and whether individuals have been vaccinated. Vaccination may offer some degree of protection against the virus, potentially affecting the duration or progression of the latent period. However, the extent of this effect can vary based on factors such as the type of vaccine, the individual’s immune response, and the level of virus transmission within the community. Conversely, individuals who have not received any vaccine doses are generally more susceptible to infection and may experience a different latent period. Introducing a delay parameter into the model represents the length of the latent period, which can differ between individuals who have received partial vaccination and those who have not been vaccinated at all. In our analysis, we denote the latent period for susceptible individuals as ${\tau }_1$ and the latent period for vaccinated individuals as ${\tau }_2$. This delay parameter represents the time interval between when an individual is infected and when they become infectious. The above epidemic scenario is modeled as

$$\begin{array}{cc}\hfill & {\displaystyle \frac{dS}{dt}}=\Lambda -\beta SI-\gamma S-\mu S+\rho R,\hfill \\ \hfill & {\displaystyle \frac{dV}{dt}}=\gamma S-(1-\theta )\delta VI-\mu V-\eta V,\hfill \\ \hfill & {\displaystyle \frac{dI}{dt}}=\beta S(t-{\tau }_1)I(t-{\tau }_1)+(1-\theta )\delta V(t-{\tau }_2)I(t-{\tau }_2)-(\mu +\alpha +b)I,\hfill \\ \hfill & {\displaystyle \frac{dR}{dt}}=\eta V+bI-(\mu +\rho )R,\hfill \end{array}$$

(1)

with the initial condition:

$$\begin{array}{c}S(\Theta )={\Psi }_1(\Theta );V(\Theta )={\Psi }_2(\Theta );I(\Theta )={\Psi }_3(\Theta );R(\Theta )={\Psi }_4(\Theta ).\end{array}$$

(2)

Here, ${\Psi }_i\in \mathbb{C}\left([-\tau ,0],{\mathbb{R}}_{+}\right);(i=1,\cdots ,4),$ with $\tau =max\left\{{\tau }_1,{\tau }_2\right\},\Theta \in [-\tau ,0],$ and ${\Psi }_i(\Theta )>0.$

In the traditional infectious disease model, susceptible individuals (S) can contract the infection and transition to the infected (I) state. Infected individuals can then recover and become immune (R). With the rise of COVID-19 and polio vaccinations globally, vaccinated individuals (V) form a significant demographic that must be considered separately. In this context, vaccinated individuals have not received sufficient vaccine doses to confer lifelong immunity. Recent years have seen a resurgence of polio in particular African and Middle Eastern countries, as well as in conflict zones like Syria, as reported by the World Health Organization, see [47]. Polio is a hazardous virus that necessitates multiple doses for lifelong immunity. Those who have only received a single dose remain at risk during periods of virus resurgence. Fully immunized individuals are categorized as recovered (R), indicating a reduced risk of reinfection. Our contribution includes delineating an SVIR epidemic model encompassing four key variables: the susceptible (S) population, the vaccinated (V) population, the infected (I) population, and the recovered (R) population. Additionally, our model accounts for time delays, specifically incorporating disease latent periods denoted by the parameters $\{{\tau }_1,{\tau }_2\}\ge 0$, where ${\tau }_1$ and ${\tau }_2$ represent the respective latent periods. We consider the following assumptions to model the interactions between the four classes:

• $\theta$ is between 0 and 1; when $\theta =0$, the vaccines are invalid and, when $\theta =1$, it shows that the vaccines are completely active.
• Delayed effects: Since individuals who were infected at time $t-{\tau }_1$ (or $t-{\tau }_2$) become infectious at a later time t, we use $\beta S(t-{\tau }_1)I(t-{\tau }_1)$ to represent the contribution of infectious individuals from $t-{\tau }_1$ to the overall infectivity at time t. Similarly, $\delta V(t-{\tau }_2)I(t-{\tau }_2)$ represents the contribution of infectious vaccinated individuals from $t-{\tau }_2$ to the infectivity at time t.
• We assume that vaccinated individuals are susceptible to infection before acquiring immunity, with a disease transmission rate $\delta$ when in contact with infected individuals. It is reasonable to assume $\delta <\beta$ because vaccinated individuals may have partial immunity during the vaccination process or may modify their behavior to reduce contact with infected individuals based on their understanding of disease transmission characteristics. The details of the population flux are shown in Figure 1 and a description of the parameters is given in Table 1.
  

  Figure 1. Illustrative diagram of SVIR model incorporating time delay.
  Table 1. Representation of the parameters used in model (1).

  Parameters	Representation of the Parameters
  $\Lambda$	New recruitment
  $\beta$	Infection rate of susceptible individual
  $\delta$	Infection rate of vaccinated
  $\gamma$	Vaccination coverage rate
  $\mu$	Population natural mortality rate
  $\rho$	The loss of immunity
  $\theta$	Vaccine effectiveness rate
  $\alpha$	Additional death rate due to the infectious disease
  b	Recovery of the infected population

We assume that $b_1=\eta +\mu ,b_2=\alpha +b+\mu ,b_3=\mu +\rho ,g_1=1-\theta ,b_4=\gamma +\mu$. The disease-free equilibrium (DFE) point of model (1) is given as $E_0=(S_0,V_0,I_0,R_0)$, where

$$S_0={\displaystyle \frac{b_1{b}_3\Lambda }{b_1{b}_3{b}_4-\gamma \eta \rho }},V_0={\displaystyle \frac{b_3\gamma \Lambda }{b_1{b}_3{b}_4-\gamma \eta \rho }},I_0=0,R_0={\displaystyle \frac{\gamma \eta \Lambda }{b_1{b}_3{b}_4-\gamma \eta \rho }}.$$

Stability characteristics of the equilibrium points within the system are often influenced by a crucial parameter known as the basic reproduction number (BRN), denoted as ${\mathcal{R}}_0$. This vital parameter represents the number of secondary infections from one infected individual throughout the entire infectious period in an entirely susceptible population. In the context of model (1), the computation of the BRN can be found in references [48,49]:

$${\mathcal{R}}_0={\displaystyle \frac{\beta b_1{b}_3\Lambda +b_3\gamma \delta g_1\Lambda }{b_1{b}_2{b}_3{b}_4-b_2\gamma \eta \rho }}.$$

(3)

This vital parameter helps us to identify the secondary infections resulting from the primary infected individual throughout the entire infectious period. It helps identify which model parameters are crucial in controlling the disease spread. The same will also be discussed in the sensitivity analysis of this paper.

Next, the endemic equilibrium point of model (1) is denoted as $E^{*}=(S^{*},V^{*},I^{*},R^{*})$, where

$$\begin{array}{ccc}\hfill & S^{*}={\displaystyle \frac{I^{*}b\delta g_1\rho +b_3\delta g_1\Lambda +b_2\eta \rho }{b_3\delta g_1(I^{*}\beta +b_4)+\beta \eta \rho }},\hfill & \hfill I^{*}={\displaystyle \frac{-f+\sqrt{f^2-4ac}}{2a}},\\ \hfill & V^{*}={\displaystyle \frac{\gamma (I^{*}b\delta g_1\rho +b_3\delta g_1\Lambda +b_2\eta \rho )}{(I^{*}\delta g_1+b_1)(b_3\delta g_1(I^{*}\beta +b_4)+\beta \eta \rho )}},\hfill & \hfill R^{*}={\displaystyle \frac{I^{*}b+\eta V^{*}}{b_3}},\end{array}$$

(4)

where

$$\begin{array}{cc}\hfill & a=\beta \delta g_1(b_3(\alpha +\mu )+b\mu )>0,\hfill \\ \hfill & f=\beta b_1(b_3(\alpha +\mu )+b\mu )+\delta g_1(-\beta b_3\Lambda -b\gamma \rho +b_2{b}_3{b}_4),\hfill \\ \hfill & c=\beta b_2\delta g_1\mu (1-R_0)((\alpha +\mu )(\mu +\rho )+b\mu )(\gamma (\eta +\mu +\rho )+(\eta +\mu )(\mu +\rho ))/a<0.\hfill \end{array}$$

(5)

Examining $I^{*}$ reveals its positivity, evident from the condition $c<0$ when ${\mathcal{R}}_0>1$. Thus, from the preceding analysis, we observe that the endemic point is positive under the condition ${\mathcal{R}}_0>1$.

Positivity and Boundedness of Solutions

In order to prove the positiveness and eventual boundedness of solutions $S\left(t\right),V\left(t\right),I\left(t\right)$, and $R\left(t\right)$ of Equation (1) we offer the following lemma on the related area.

Lemma 1. 

Let $\left(S\right(t),V(t),I(t),R(t\left)\right)$ be a solution of system (1) with the initial conditions (2). Then,

$$S\left(t\right)>0,V\left(t\right)>0,I\left(t\right)>0andR\left(t\right)>0,forallt\ge 0.$$

(6)

Moreover, for $N_1\left(t\right)=S(t-\tau )+V(t-\tau )+I\left(t\right)+R\left(t\right)$, if $\rho >\eta$ holds, where $\tau =max\{{\tau }_1,{\tau }_2\}$, then

$$\underset{t\to +\infty }{lim\; sup}{N}_1\left(t\right)\le {\displaystyle \frac{\Lambda }{\mu -(\rho -\eta )}}.$$

Proof. 

From initial conditions (2), we obtain $S\left(0\right),I\left(0\right),V\left(0\right),R\left(0\right)>0.$ Continuity of $S\left(t\right),V\left(t\right),$ $I\left(t\right),R\left(t\right)$ ensures through our assumption that $\left(S\right(t),V(t),I(t),R(t\left)\right)$ represents the solution of system (1). Therefore, it is clear that there exists a $t_1-$neighborhood around “0” such that

$$\begin{array}{c}\hfill S\left(0\right),I\left(0\right),V\left(0\right),R\left(0\right)>0\mathrm{for}\mathrm{all}t\in [0,t_1).\end{array}$$

According to the first equation in (1), we obtain $(\mathrm{d}S/\mathrm{d}t)\left(t_1\right)\ge \Lambda >0$, contradicting the assumption that $S\left(t\right)>0$ for $0\le t<t_1$ and $S\left(t_1\right)=0$. Therefore, if there exists a positive $t_1$ where $S_k\left(t\right)>0$, $I_k\left(t\right)>0$, $V_k\left(t\right)>0$, and $R_k\left(t\right)>0$ for any $0\le t<t_1$, then $S\left(t_1\right)>0$.

Moreover, by the second, third, and fourth equations of (1), we have

$$\begin{array}{cc}& V\left(t\right)={\mathrm{e}}^{-(\mu +\eta )t}\left[V\left(0\right)+{\int }_0^t{\mathrm{e}}^{(\mu +\eta )u}(\gamma S\left(u\right)-(1-\theta )\delta V\left(u\right)I\left(u\right))\mathrm{d}u\right],\hfill \\ & I\left(t\right)={\mathrm{e}}^{-(\mu +\alpha +b)t}\left[I\left(0\right)+{\int }_0^t{\mathrm{e}}^{(\mu +\alpha +b)u}(\beta S(u-{\tau }_1)I(u-{\tau }_1)\right.\hfill \\ & +(1-\theta )\delta V(u-{\tau }_2)I(u-{\tau }_2))\mathrm{d}u,\hfill \\ & R\left(t\right)={\mathrm{e}}^{-(\mu +\rho )t}\left[R\left(0\right)+{\int }_0^t{\mathrm{e}}^{(\mu +\rho )u}(\eta V\left(u\right)+bI\left(u\right))\mathrm{d}u\right],\mathrm{for}t>0.\hfill \end{array}$$

Consequently, if a positive $t_1$ exists where $S\left(t\right)>0$, $I\left(t\right)>0$, $V\left(t\right)>0$, and $R\left(t\right)>0$ for all $0\le t<t_1$, then it follows that $I\left(t_1\right)>0$ and $R\left(t_1\right)>0$. Hence, we derive Equation (6). Consider the delayed system in (1) as

$$N_1\left(t\right)=S(t-\tau )+V(t-\tau )+I\left(t\right)+R\left(t\right),\mathrm{where}\tau =max\{{\tau }_1,{\tau }_2\}.$$

From (1) and (2), we have

$$\begin{array}{cc}\hfill {\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}{N}_1\left(t\right)=& {\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}(S(t-\tau )+V(t-\tau )+I\left(t\right)+R\left(t\right))\hfill \\ \hfill =& \Lambda -\mu S(t-\tau )-\mu V(t-\tau )-(\mu +\alpha )I\left(t\right)-\mu R\left(t\right)+\rho \left(R\right(t-\tau )-R(t\left)\right)\hfill \\ & -\eta (V(t-\tau )-V\left(t\right))-\beta S(t-\tau )I(t-\tau )+\beta S(t-{\tau }_1)I(t-{\tau }_1)\hfill \\ & -(1-\theta )\delta V(t-\tau )I(t-\tau )+(1-\theta )\delta V(t-{\tau }_2)I(t-\tau )\hfill \\ \hfill \le & \Lambda -\mu S(t-\tau )-\mu V(t-\tau )-(\mu +\alpha )I\left(t\right)-\mu R\left(t\right)\hfill \\ & +\rho \left(R\right(t-\tau )-R(t\left)\right)-\eta \left(V\right(t-\tau )-V(t\left)\right)\hfill \\ \hfill \le & \Lambda -\mu S(t-\tau )-\mu V(t-\tau )-\mu I\left(t\right)-\mu R\left(t\right)\hfill \\ & +\rho \left(R\right(t-\tau )-R(t\left)\right)-\eta \left(V\right(t-\tau )-V(t\left)\right)\hfill \\ \hfill \le & \Lambda +\mu N_1\left(t\right)+(\rho -\eta )N_1(t-\tau ),\hfill \end{array}$$

with initial conditions

$$\begin{array}{cc}\hfill N_1\left(\theta \right)=& {\Psi }_1\left(\theta \right)+{\Psi }_2\left(\theta \right)+{\Psi }_3\left(\theta \right)+{\Psi }_4\left(\theta \right)\ge 0,\theta \in [-\overline{\tau },0),\hfill \\ \hfill \mathrm{and}{N}_1\left(0\right)=& {\Psi }_1\left(0\right)+{\Psi }_2\left(0\right)+{\Psi }_3\left(0\right)+{\Psi }_4\left(0\right)>0.\hfill \end{array}$$

We proceed by considering the following auxiliary equation (as discussed in [33,50]):

$$\begin{array}{cc}\hfill {\displaystyle \frac{\mathrm{d}v\left(t\right)}{\mathrm{d}t}}& =b-\mu v\left(t\right)+(\rho -\eta )v\left(t-{\tau }_2\right),\hfill \\ \hfill v\left(\theta \right)& ={\Psi }_1\left(\theta \right)+{\Psi }_2\left(\theta \right)+{\Psi }_3\left(\theta \right)+{\Psi }_4\left(\theta \right)\ge 0,\theta \in [-\overline{\tau },0].\hfill \end{array}$$

(7)

The above equation exhibits a unique globally positive equilibrium that is $v^{*}=\Lambda /(\mu -(\rho -\eta ))$. We define the following functional:

$$L_v\left(t\right)={\displaystyle \frac{{\left\{v\left(t\right)-v^{*}\right\}}^2}{2}}+{\displaystyle \frac{(\rho -\eta )}{2}}{\int }_{t-\tau }^t{\left\{v\left(\theta \right)-v^{*}\right\}}^2\mathrm{d}\theta .$$

We proceed by analyzing the time derivative of $L_v$ evaluated along the solution trajectory $v\left(t\right)$ of (7),

$${\displaystyle \frac{\mathrm{d}{L}_v\left(t\right)}{\mathrm{d}t}}=\{v\left(t\right)-v^{*}\}{\displaystyle \frac{\mathrm{d}v\left(t\right)}{\mathrm{d}t}}+{\displaystyle \frac{(\rho -\eta )}{2}}\left[{\{v\left(t\right)-v^{*}\}}^2-{\{v(t-\tau )-v^{*}\}}^2\right].$$

From the equilibrium condition $\Lambda =(\mu -(\rho -\eta ))v^{*}$, we have

$$\begin{array}{cc}\hfill \{v\left(t\right)-v^{*}\}{\displaystyle \frac{\mathrm{d}v\left(t\right)}{\mathrm{d}t}}& =\{v\left(t\right)-v^{*}\}\{\Lambda -\mu v\left(t\right)+(\rho -\eta )v(t-\tau ))\}\hfill \\ & =\{v\left(t\right)-v^{*}\}\left[-\mu \{v\left(t\right)-v^{*})+(\rho -\eta )\{v(t-\tau )-v^{*}\}\right]\hfill \\ & =-\mu {\{v\left(t\right)-v^{*}\}}^2+(\rho -\eta )\{v\left(t\right)-v^{*}\}\left\{v(t-\tau )-v^{*}\right\}\hfill \\ & \le -\mu {\{v\left(t\right)-v^{*}\}}^2+{\displaystyle \frac{(\rho -\eta )}{2}}\left[{\left\{v\left(t\right)-v^{*}\right\}}^2+{\left\{v(t-\tau )-v^{*}\right\}}^2\right].\hfill \end{array}$$

Thus,

$$\begin{array}{cc}\hfill {\displaystyle \frac{\mathrm{d}{L}_v\left(t\right)}{\mathrm{d}t}}\le & \left[-\mu {\{v\left(t\right)-v^{*}\}}^2+{\displaystyle \frac{(\rho -\eta )}{2}}\left[{\{v\left(t\right)-v^{*}\}}^2+{\left\{v(t-\tau )-v^{*}\right\}}^2\right]\right.\hfill \\ \hfill & +{\displaystyle \frac{(\rho -\eta )}{2}}\left[{\left\{v\left(t\right)-v^{*}\right\}}^2-{\{v(t-\tau )-v^{*}\}}^2\right]\hfill \\ \hfill =& -(\mu -(\rho -\eta )){\{v\left(t\right)-v^{*}\}}^2\hfill \\ \hfill \le & 0.\hfill \end{array}$$

(8)

We establish that the functional $L_v$ is non-negative and monotonically decreasing. Furthermore, there exists a non-negative constant ${\widehat{V}}_u$ such that $L_v\left(t\right)$ converges to ${\widehat{V}}_u$ as t approaches positive infinity: $\underset{t\to +\infty }{lim}{L}_v\left(t\right)={\widehat{V}}_u$. Equation (8) is satisfied exclusively when $v\left(t\right)=v^{*}$; we have ${\widehat{L}}_v=0$, which yields $\underset{t\to +\infty }{lim}v\left(t\right)=v^{*}=\Lambda /(\mu -(\rho -\eta ))$. Thus, based on the results of the foregoing discussion and employing the comparison principle, we can conclude that $\underset{t\to +\infty }{lim\; sup}{N}_1\left(t\right)\le \Lambda /(\mu -(\rho -\eta ))$. □

3. Stability Analysis

The present section is dedicated to studying the stability characteristics of the equilibrium points of system (1). Initially, we present the outcomes related to the local asymptotic stability of $E_0$ [51]. As stated in the upcoming theorem, the following is asserted:

Theorem 1. 

The DFE $E^0$ is locally asymptotically stable if ${\mathcal{R}}_0<1$.

Proof. 

At the equilibrium point $E^0$, the Jacobian matrix is

$$J\left(E^0\right)=\left(\begin{array}{cccc}-b_4& 0& -c_{01}& \rho \\ \gamma & -b_1& -c_{02}& 0\\ 0& 0& -b_2+e^{-\lambda {\tau }_1}{c}_{01}+e^{-\lambda {\tau }_2}{c}_{02}& 0\\ 0& \eta & b& -b_3\end{array}\right),$$

where $c_{01}=\beta S_0$ and $c_{02}=\delta g_1{V}_0.$ The characteristic equation adopts the following form for the system

$$(-b_2+c_{01}{e}^{-\lambda {\tau }_1}+c_{02}{e}^{-\lambda {\tau }_2}-\lambda )((-b_1-\lambda )(b_3+\lambda )(b_4+\lambda )+\gamma \eta \rho )=0.$$

(9)

To study the impact of the time delay on the stability of the equilibrium, model (1) is analyzed in four cases:

• If ${\tau }_1={\tau }_2=0$ then (9) becomes

  $$(-b_2+c_{01}+c_{02}-\lambda )({\lambda }^3+A{\lambda }^2+B\lambda +C)=0,$$

  (10)

  where

  $$\begin{array}{ccc}\hfill A& =& b_1+b_3+b_4,\hfill \\ \hfill B& =& b_3{b}_4+b_1{b}_4+b_1{b}_3,\hfill \\ \hfill C& =& \gamma \mu (\eta +\mu +\rho )+\mu (\eta +\mu )(\mu +\rho ).\hfill \end{array}$$
  It is clear that the first eigenvalue of (9) is negative when $R_0<1,$

  $$\begin{array}{cc}\hfill \lambda =& -b_2+c_{01}+c_{02}\hfill \\ \hfill =& b_3\Lambda \left(R_0-1\right)\left(\beta b_1+\gamma \delta g_1\right)/R_0(\gamma \mu (\eta +\mu +\rho )+\mu (\eta +\mu )(\mu +\rho ))<0.\hfill \end{array}$$

  (11)
  Since $A,B,C>0$ and $AB-C=(b_1+b_3)(b_1+b_4)(b_3+b_4)+\gamma \eta \rho >0$, the conditions for stability are satisfied. Hence, according to the Routh–Hurwitz criteria, the real part of all the roots of Equation (10) are negative. Therefore, the DFE $E_0$ of model (1) is locally asymptotically stable for ${\tau }_1={\tau }_2=0$ if $R<1$. We can write (9) as

  $$\begin{array}{cc}\hfill & {\lambda }^4+U_3{\lambda }^3+U_2{\lambda }^2+U_1\lambda +U_0+e^{-\lambda {\tau }_1}(V_3{\lambda }^3+V_2{\lambda }^2+V_1\lambda +V_0)\hfill \\ \hfill & +e^{-\lambda {\tau }_2}(W_3{\lambda }^3+W_2{\lambda }^2+W_1\lambda +W_0)=0,\hfill \end{array}$$

  (12)

  where the expressions for $U_i,W_i,W_i$ for $i\in 1,2,3$ are presented in Appendix A.
• Equation (12) implies that, if ${\tau }_1>0$ and ${\tau }_2=0$, then

  $${\lambda }^4+Z_{13}{\lambda }^3+Z_{12}{\lambda }^2+Z_{11}\lambda +Z_{10}+(I_{13}{\lambda }^3+I_{12}{\lambda }^2+I_{11}\lambda +I_{10})e^{-\lambda {\tau }_1}=0$$

  (13)

  where

  $$\begin{array}{cc}& Z_{10}=U_0+W_0,Z_{11}=U_1+W_1,Z_{12}=U_2+W_2,Z_{13}=U_3+W_3,\hfill \\ & I_{10}=V_0,I_{11}=V_1,I_{12}=V_2,I_{13}=V_3.\hfill \end{array}$$
  Suppose (13) has a root $\lambda =i{\kappa }_1$; then, it results in

  $$\begin{array}{cc}\hfill {\rho }_{11}\left({\kappa }_1\right)cos\left({\tau }_1{\kappa }_1\right)+{\rho }_{12}\left({\kappa }_1\right)sin\left({\tau }_1{\kappa }_1\right)=& {\rho }_{13}\left({\kappa }_1\right),\hfill \\ \hfill {\rho }_{12}\left({\kappa }_1\right)cos\left({\tau }_1{\kappa }_1\right)-{\rho }_{11}\left({\kappa }_1\right)sin\left({\tau }_1{\kappa }_1\right)=& {\rho }_{14}\left({\kappa }_1\right),\hfill \end{array}$$

  (14)

  with

  $$\begin{array}{cc}\hfill & {\rho }_{11}\left({\kappa }_1\right)=-I_{12}{\kappa }_1^2+I_{10},{\rho }_{12}\left({\kappa }_1\right)=-I_{13}{\kappa }_1^3+I_{11}{\kappa }_1,\hfill \\ \hfill & {\rho }_{13}\left({\kappa }_1\right)=-{\kappa }_1^4+Z_{12}{\kappa }_1^2-Z_{10},{\rho }_{14}\left({\kappa }_1\right)=Z_{13}{\kappa }_1^3-Z_{11}{\kappa }_1.\hfill \end{array}$$

  (15)
  Taking the square and adding the two equations of (14) lead to

  $${\kappa }_1^8+{\psi }_{13}{\kappa }_1^6+{\psi }_{12}{\kappa }_1^4+{\psi }_{11}{\kappa }_1^2+{\psi }_{10}=0,$$

  (16)
  Let ${\kappa }_1^2=y_1$; then, (16) becomes

  $$y_1^4+{\psi }_{13}{y}_1^3+{\psi }_{12}{y}_1^2+{\psi }_{11}{y}_1+{\psi }_{10}=0,$$

  (17)

  where

  $$\begin{array}{cc}& {\psi }_{11}=-2Z_{10}{Z}_{12}+Z_{11}^2+2I_{10}{I}_{12}-I_{11}^2,{\psi }_{10}=Z_{10}^2-I_{10}^2,\hfill \\ & {\psi }_{12}=Z_{12}^2+2Z_{10}-2Z_{11}{Z}_{13}-I_{12}^2+2I_{11}{I}_{13},{\psi }_{13}=-2Z_{12}+Z_{13}^2-I_{13}^2.\hfill \end{array}$$
  Now, (17) possessing a positive root $y_1^{*}$ implies that (16) has a positive root ${\kappa }_1=\sqrt{y_1^{*}}$. Now, from (14), we have

  $$\begin{array}{cc}& cos\left({\kappa }_1{\tau }_1^{*}\right)={\displaystyle \frac{{\rho }_{11}\left({\kappa }_1\right){\rho }_{13}\left({\kappa }_1\right)+{\rho }_{12}\left({\kappa }_1\right){\rho }_{14}\left({\kappa }_1\right)}{{{\rho }_{11}\left({\kappa }_1\right)}^2+{{\rho }_{12}\left({\kappa }_1\right)}^2}}\hfill \end{array}$$
  This implies that

  $$\begin{array}{cc}& {\tau }_1^{*}={\displaystyle \frac{1}{{\kappa }_1}}\left\{arccos={\displaystyle \frac{{\rho }_{11}\left({\kappa }_1\right){\rho }_{13}\left({\kappa }_1\right)+{\rho }_{12}\left({\kappa }_1\right){\rho }_{14}\left({\kappa }_1\right)}{{{\rho }_{11}\left({\kappa }_1\right)}^2+{{\rho }_{12}\left({\kappa }_1\right)}^2}}\right\}.\hfill \end{array}$$
• If ${\tau }_2>0$ and ${\tau }_1=0$, then, from (12), we obtain

  $${\lambda }^4+Z_{23}{\lambda }^3+Z_{22}{\lambda }^2+Z_{21}\lambda +Z_{20}+(I_{23}{\lambda }^3+I_{22}{\lambda }^2+I_{21}\lambda +I_{20})e^{-\lambda {\tau }_2}=0,$$

  (18)

  where

  $$\begin{array}{cc}& Z_{20}=U_0+V_0,Z_{21}=U_2+V_2,Z_{22}=U_2+V_2,Z_{23}=U_3+V_3,\hfill \\ & I_{20}=W_0,I_{21}=W_2,I_{22}=W_2,I_{23}=W_3.\hfill \end{array}$$
  Suppose (18) has a root $\lambda =i{\kappa }_2$; then, we deduce that

  $$\begin{array}{cc}\hfill {\rho }_{21}\left({\kappa }_2\right)cos\left({\tau }_2{\kappa }_2\right)+{\rho }_{22}\left({\kappa }_2\right)sin\left({\tau }_2{\kappa }_2\right)=& {\rho }_{23}\left({\kappa }_2\right),\hfill \\ \hfill {\rho }_{22}\left({\kappa }_2\right)cos\left({\tau }_2{\kappa }_2\right)-{\rho }_{21}\left({\kappa }_2\right)sin\left({\tau }_2{\kappa }_2\right)=& {\rho }_{24}\left({\kappa }_2\right),\hfill \end{array}$$

  (19)

  with

  $$\begin{array}{cc}\hfill & {\rho }_{21}\left({\kappa }_2\right)=-I_{22}{\kappa }_2^2+I_{20},{\rho }_{22}\left({\kappa }_2\right)=-I_{23}{\kappa }_2^3+I_{21}{\kappa }_2,\hfill \\ \hfill & {\rho }_{23}\left({\kappa }_2\right)=-{\kappa }_2^4+Z_{22}{\kappa }_2^2-Z_{20},{\rho }_{24}\left({\kappa }_2\right)=Z_{23}{\kappa }_2^3-Z_{21}{\kappa }_2.\hfill \end{array}$$
  Taking the square and adding the two equations of (19) lead to

  $${\kappa }_2^8+{\psi }_{23}{\kappa }_2^6+{\psi }_{22}{\kappa }_2^4+{\psi }_{21}{\kappa }_2^2+{\psi }_{20}=0,$$

  (20)

  let ${\kappa }_2^2=y_2$; then, (20) becomes

  $$y_2^4+{\psi }_{23}{y}_2^3+{\psi }_{22}{y}_2^2+{\psi }_{21}{y}_2+{\psi }_{20}=0,$$

  (21)

  where

  $$\begin{array}{cc}& {\psi }_{21}=-2Z_{20}{Z}_{22}+Z_{21}^2+2I_{20}{I}_{22}-I_{21}^2,{\psi }_{20}=Z_{20}^2-I_{20}^2,\hfill \\ & {\psi }_{22}=Z_{22}^2+2Z_{20}-2Z_{21}{Z}_{23}-I_{22}^2+2I_{21}{I}_{23},{\psi }_{23}=-2Z_{22}+Z_{23}^2-I_{23}^2.\hfill \end{array}$$
  A positive root ${\kappa }_2=\sqrt{y_2^{*}}$ in (20) arises when (21) has a positive root $y_2^{*}$. Now, from (19), we have

  $$\begin{array}{cc}& cos\left({\kappa }_2{\tau }_2^{*}\right)={\displaystyle \frac{{\rho }_{21}\left({\kappa }_2\right){\rho }_{23}\left({\kappa }_2\right)+{\rho }_{22}\left({\kappa }_2\right){\rho }_{24}\left({\kappa }_2\right)}{{{\rho }_{21}\left({\kappa }_2\right)}^2+{{\rho }_{22}\left({\kappa }_2\right)}^2}}\hfill \end{array}$$
  This implies that

  $$\begin{array}{cc}& {\tau }_2^{*}={\displaystyle \frac{1}{{\kappa }_2}}\left\{arccos={\displaystyle \frac{{\rho }_{21}\left({\kappa }_2\right){\rho }_{23}\left({\kappa }_2\right)+{\rho }_{22}\left({\kappa }_2\right){\rho }_{24}\left({\kappa }_2\right)}{{{\rho }_{21}\left({\kappa }_2\right)}^2+{{\rho }_{22}\left({\kappa }_2\right)}^2}}\right\}.\hfill \end{array}$$
• From (12), we obtain that, if ${\tau }_2={\tau }_1=\tau$, then

  $${\lambda }^4+Z_{33}{\lambda }^3+Z_{32}{\lambda }^3+Z_{31}\lambda +Z_{30}+(I_{33}{\lambda }^3+I_{32}{\lambda }^2+I_{31}\lambda +I_{30})e^{-\lambda \tau }=0,$$

  (22)

  where

  $$\begin{array}{cc}& Z_{30}=U_0,Z_{31}=U_1,Z_{32}=U_2,Z_{33}=U_3,I_{30}=V_0+W_0,\hfill \\ & I_{31}=V_1+W_1,I_{32}=V_2+W_2,I_{33}=V_3+W_3.\hfill \end{array}$$
  If $\lambda =i{\kappa }_3$ is a root of (22), then it follows that

  $$\begin{array}{cc}\hfill {\rho }_{32}\left({\kappa }_3\right)sin\left(\tau {\kappa }_3\right)+{\rho }_{31}\left({\kappa }_3\right)cos\left(\tau {\kappa }_3\right)=& {\rho }_{33}\left({\kappa }_3\right),\hfill \\ \hfill -{\rho }_{31}\left({\kappa }_3\right)sin\left(\tau {\kappa }_3\right)+{\rho }_{32}\left({\kappa }_3\right)cos\left(\tau {\kappa }_3\right)=& {\rho }_{34}\left({\kappa }_3\right),\hfill \end{array}$$

  (23)

  with

  $$\begin{array}{cc}\hfill & {\rho }_{31}\left({\kappa }_3\right)=-I_{32}{\kappa }_3^2+I_{30},{\rho }_{32}\left({\kappa }_3\right)=-I_{33}{\kappa }_3^3+I_{31}{\kappa }_3,\hfill \\ \hfill & {\rho }_{33}\left({\kappa }_3\right)=-{\kappa }_3^4+Z_{32}{\kappa }_3^2-Z_{30},{\rho }_{34}\left({\kappa }_3\right)=Z_{33}{\kappa }_3^3-Z_{31}{\kappa }_3,\hfill \end{array}$$
  Taking the square and adding the two equations of (23) lead to

  $${\kappa }_3^8+{\psi }_{33}{\kappa }_3^6+{\psi }_{32}{\kappa }_3^4+{\psi }_{31}{\kappa }_3^2+{\psi }_{30}=0,$$

  (24)

  let ${\kappa }_3^2=y_3$; then, (24) becomes

  $$y_3^4+{\psi }_{33}{y}_3^3+{\psi }_{32}{y}_3^2+{\psi }_{31}{y}_2+{\psi }_{30}=0,$$

  (25)

  where

  $$\begin{array}{cc}& {\psi }_{31}=-2Z_{30}{Z}_{32}+Z_{31}^2+2I_{30}{I}_{32}-I_{31}^2,{\psi }_{30}=Z_{30}^2-I_{30}^2,\hfill \\ & {\psi }_{32}=Z_{32}^2+2Z_{30}-2Z_{31}{Z}_{33}-I_{32}^2+2I_{31}{I}_{33},{\psi }_{33}=-2Z_{32}+Z_{33}^2-I_{33}^2.\hfill \end{array}$$
  Given that (25) has a positive root $y_3^{*}$, (24) has a positive root ${\kappa }_3=\sqrt{y_3^{*}}$. Now, from (23), we have

  $$\begin{array}{cc}& cos\left({\kappa }_3{\tau }^{*}\right)={\displaystyle \frac{{\rho }_{31}\left({\kappa }_3\right){\rho }_{33}\left({\kappa }_3\right)+{\rho }_{32}\left({\kappa }_3\right){\rho }_{34}\left({\kappa }_3\right)}{{{\rho }_{31}\left({\kappa }_3\right)}^2+{{\rho }_{32}\left({\kappa }_3\right)}^2}}\hfill \end{array}$$
  This implies that

  $$\begin{array}{cc}& {\tau }^{*}={\displaystyle \frac{1}{{\kappa }_3}}\left\{arccos={\displaystyle \frac{{\rho }_{31}\left({\kappa }_3\right){\rho }_{33}\left({\kappa }_3\right)+{\rho }_{32}\left({\kappa }_3\right){\rho }_{34}\left({\kappa }_3\right)}{{{\rho }_{31}\left({\kappa }_3\right)}^2+{{\rho }_{32}\left({\kappa }_3\right)}^2}}\right\}.\hfill \end{array}$$
  This completes the proof. □

Theorem 2. 

If ${\mathcal{R}}_0>1$ and the following conditions are satisfied then the endemic equilibrium $E^{*}$ of (1) is locally asymptotically stable:

$$a_i>0(i=0,1,2,3),a_3{a}_2-a_1>0and{a}_1(a_3{a}_2-a_1)-a_0{a}_3^2>0.$$

(26)

Proof. 

The detailed proof of the theorem has been given as Appendix A. □

Next, we study the sensitivity index of the BRN concerning the parameter values defined in model (1). As in [4], first, we define the following:

Definition 1. 

The normalized forward sensitivity index of a function $\mathrm{{\rm Y}}\left({\nu }_1,{\nu }_2,\dots ,{\nu }_n\right)$ for ${\nu }_i(i=1,2,\dots$, $n)$ is denoted by ${𝘍}_{{\nu }_i}^{\mathrm{{\rm Y}}}$, and is defined as

$${𝘍}_{{\nu }_i}^{\mathrm{{\rm Y}}}={\displaystyle \frac{\partial \mathrm{{\rm Y}}}{\partial {\nu }_i}}\times {\displaystyle \frac{{\nu }_i}{\mathrm{{\rm Y}}}}.$$

The following are the results calculated for the model parameters, which determine the BRN:

$${\displaystyle \frac{\mu }{{\mathcal{R}}_0}}{\displaystyle \frac{d{\mathcal{R}}_0}{d\mu }}={\displaystyle \frac{k}{b_2{b}_3(b_1+\gamma )(b_1(b_3+\gamma )+\gamma \rho )(\beta b_1+\gamma \delta g_1)}}<0;$$

$$\begin{array}{ccc}& {\displaystyle \frac{\gamma }{{\mathcal{R}}_0}}{\displaystyle \frac{d{\mathcal{R}}_0}{d\gamma }}={\displaystyle \frac{-b_1\gamma (\beta b_1{b}_3-b_3\delta g_1\mu -\beta \eta \rho )}{(b_1{b}_3\gamma +b_1{b}_3\mu -\gamma \eta \rho )(\beta b_1+\gamma \delta g_1)}}<0;\hfill & \hfill {\displaystyle \frac{\alpha }{{\mathcal{R}}_0}}{\displaystyle \frac{d{\mathcal{R}}_0}{d\alpha }}=-{\displaystyle \frac{\alpha }{\alpha +b+\mu }}<0;\\ & {\displaystyle \frac{\eta }{{\mathcal{R}}_0}}{\displaystyle \frac{d{\mathcal{R}}_0}{d\eta }}={\displaystyle \frac{\gamma \eta (\delta g_1(b_3{b}_4-\gamma \rho )-\beta \mu \rho )}{(\gamma \eta \rho -b_1{b}_3{b}_4)(\beta b_1+\gamma \delta g_1)}}<0;\hfill & \hfill {\displaystyle \frac{\theta }{{\mathcal{R}}_0}}{\displaystyle \frac{d{\mathcal{R}}_0}{d\theta }}={\displaystyle \frac{-\gamma \delta \theta }{\beta b_1+\gamma \delta (1-\theta )}}<0;\\ & {\displaystyle \frac{\rho }{{\mathcal{R}}_0}}{\displaystyle \frac{d{\mathcal{R}}_0}{d\rho }}={\displaystyle \frac{\gamma \eta \mu \rho }{(\mu +\rho )(b_1{b}_4(\mu +\rho )-\gamma \eta \rho )}}>0;\hfill & \hfill {\displaystyle \frac{\beta }{{\mathcal{R}}_0}}{\displaystyle \frac{d{\mathcal{R}}_0}{d\beta }}={\displaystyle \frac{\beta b_1}{\beta b_1+\gamma \delta g_1}}>0;\\ & {\displaystyle \frac{\Lambda }{{\mathcal{R}}_0}}{\displaystyle \frac{d{\mathcal{R}}_0}{d\Lambda }}=1>0;{\displaystyle \frac{b}{{\mathcal{R}}_0}}{\displaystyle \frac{d{\mathcal{R}}_0}{db}}=-{\displaystyle \frac{b}{\alpha +b+\mu }}<0;\hfill & \hfill {\displaystyle \frac{\delta }{{\mathcal{R}}_0}}{\displaystyle \frac{d{\mathcal{R}}_0}{d\delta }}={\displaystyle \frac{\gamma \delta g_1}{\beta b_1+\gamma \delta g_1}}>0;\end{array}$$

where

$$\begin{array}{cc}& k=-\beta b_1^3(-b_2\gamma \mu +b_3\mu (b_3+\gamma )+b_3{b}_2(b_3+\gamma ))-{\gamma }^2(b_2\rho (-\beta b_3\mu +b_3\delta g_1(\gamma +\mu )-\gamma \delta g_1\mu )\hfill \\ & +b_2{b}_3\delta g_1\mu (\gamma +\eta +2\mu )+b_3\gamma \delta g_1\mu \rho )-b_1\gamma \left(b_2\right(b_3(\beta \gamma \rho +\beta \mu (\eta +2\mu )+\gamma \delta g_1(\gamma +\rho ))\hfill \\ & +b_3^2(\delta g_1(\gamma +\mu )-\beta \mu )-\gamma \mu (\beta \rho +\delta g_1(\gamma +\rho )))+b_3\gamma \mu (\delta g_1(b_3+\gamma +\rho )+\beta \rho ))\hfill \\ & -b_1^2\gamma (b_3\mu ((b_3+\gamma )(\beta +\delta g_1)+\beta \rho )+b_2(b_3(\beta (\gamma -\mu +\rho )+\gamma \delta g_1)+b_3^2(\beta +\delta g_1)\hfill \\ & -\mu (\beta (\gamma +\rho )+\gamma \delta g_1)\left)\right).\hfill \end{array}$$

If $\Lambda ,\rho ,\beta$, or $\delta$ values increase/decrease, the BRN also increases/decreases. Suppose $\mu ,\gamma ,\eta ,b,\alpha$, or $\theta$ values increase/decrease; then, the BRN value decreases/increases. By assuming the model parameter values to be as in Table 2, the sensitivity index of the BRN over the model parameter is obtained, and those values are shown in Table 3. Further, the same is depicted in Figure 2.

Table 2. Parameter values of model (1).

$\mathit{\eta }$	$\mathit{\mu }$	b	$\mathit{\alpha }$	$\mathit{\rho }$	$\mathit{\theta }$	$\mathit{\gamma }$	$\mathit{\beta }$	$\mathbf{\Lambda }$	$\mathit{\delta }$
0.22	0.11	0.19	0.12	0.22	0.21	0.33	0.21	0.76	0.11

Table 3. Sensitivity indices of (BRN) ${\mathcal{R}}_0$ corresponding to the parameters.

$\mathit{\eta }$	$\mathit{\mu }$	b	$\mathit{\alpha }$	$\mathit{\rho }$	$\mathit{\theta }$	$\mathit{\gamma }$	$\mathit{\beta }$	$\mathbf{\Lambda }$	$\mathit{\delta }$
−0.0285	−1.0678	−0.4524	−0.2857	0.1667	−0.0778	−0.3323	0.7073	1	0.2927

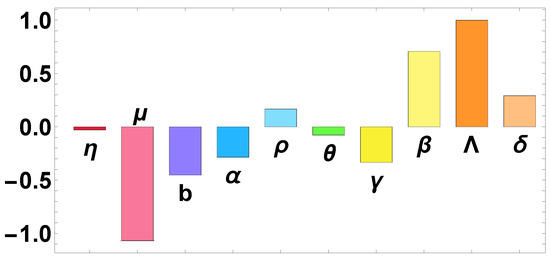
Figure 2. Plot represents the sensitivity of the parameters in the BRN of infection model.

Table 3 shows that parameters $\eta$, $\mu ,b,\alpha ,\theta ,$ and $\gamma$ exhibit negative indices, while $\beta ,\Lambda ,\rho$, and $\delta$ display positive indices, as illustrated in Figure 2. Negative (positive) indices indicate that $R_0$ decreases (increases) with the parameter. For instance, ${𝘍}_{\mu }^{R_0}=-1.0678$ signifies that, if $\mu$ increased by $10\%$, then $\mathcal{R}$ decreased by $10.678\%$. Similarly, ${𝘍}_{\beta }^{R_0}=0.7073$ suggests that a $10\%$ increase in r results in a $7.073\%$ increase in $R_0$. Furthermore, it is notable that $\beta$, the disease transmission rate, and $\Lambda$, the new recruitment, exhibit the highest positive sensitivity indices. Consequently, reducing both the new recruitment $\Lambda$ and the disease transmission rate $\beta$ effectively lowers the value of the basic reproduction number.

The figures (Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7) demonstrate the impact of parameter changes on the basic reproduction number ${\mathcal{R}}_0$.

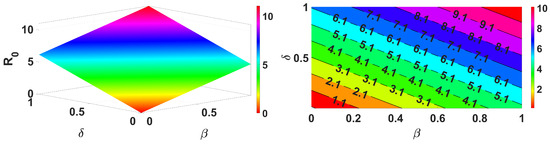
Figure 3. Impact of $\beta$ and $\delta$ on ${\mathcal{R}}_0$.

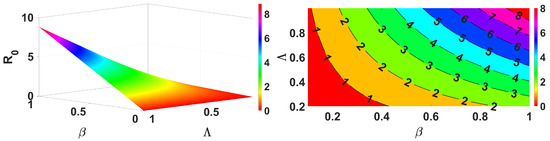
Figure 4. Impact of $\beta$ and $\Lambda$ on ${\mathcal{R}}_0$.

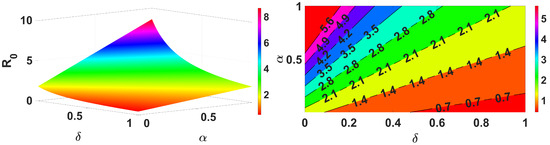
Figure 5. Impact of $\delta$ and $\alpha$ on ${\mathcal{R}}_0$.

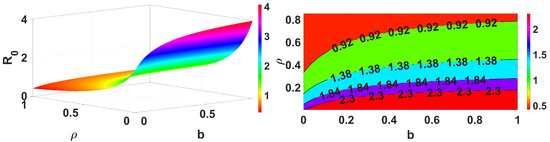
Figure 6. Impact of b and $\rho$ on ${\mathcal{R}}_0$.

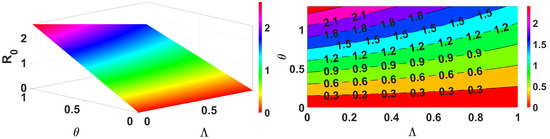
Figure 7. Impact of $\Lambda$ and $\theta$ on ${\mathcal{R}}_0$.

Figure 3 demonstrates that an increase in the spread of infection rate results in an increase in the basic reproduction number. Similarly, Figure 4 shows the impact of the inflow population increasing also making the ${\mathcal{R}}_0$ value greater. These parameters are the key parameters to control the spread of infections. Further, we demonstrate for two different forms, reduction in population (death rate due to infection $\alpha$) and the infection spread rate of the vaccinated $\left(\delta \right)$, and the results are shown in Figure 5. This clearly represents an increase in the infection spread and a decrease in population due to infection death, make the spread of infection greater. Next, we discuss for the impact of recovery rate and loss of immunity in Figure 6; here, it is evident that the lose of immunity plays a vital role in the infection spread, which is easily visible from Figure 6. Finally, the impacts of inflow of the population and vaccine efficiency are considered; this shows that the loss of vaccine efficiency plays a vital role as compared with the inflow of the population to the model. This is clearly shown in Figure 7.

4. Optimal Control for Delay Model

This section focuses on determining the optimal density increasing the rate of individuals moving to the vaccination compartment from the susceptible compartment. Furthermore, it involves calculating the density of the response that maximizes effectiveness. This encompasses raising awareness among the population regarding disease transmission and highlighting the significance of taking appropriate precautions seriously, all while minimizing the associated implementation costs.

4.1. Formulation

First, we establish an optimal control problem utilizing the delay model described as in (1). We consider the control variable aims to increase the vaccination rate of susceptible individuals through education campaigns. This approach reduces the transition of individuals from the vaccinated compartment to the infected compartment.

The proposed model is modified by replacing the parameter $\gamma$ with $v_1\left(t\right)$ as the control variable and by replacing the parameter $\theta$ with $v_2\left(t\right)$ as the control variable. Considering the assumptions above, the control problem with the delay model can be expressed as follows:

$$\left.\begin{array}{cc}\hfill & {\displaystyle \frac{dS}{dt}=\Lambda -\beta SI-v_1\left(t\right)S-\mu S+\rho R,}\hfill \\ \hfill & {\displaystyle \frac{dV}{dt}=v_1\left(t\right)S-(1-v_2\left(t\right))\delta VI-\mu V-\eta V,}\hfill \\ \hfill & {\displaystyle \frac{dI}{dt}=\beta S(t-{\tau }_1)I(t-{\tau }_1)+(1-v_2\left(t\right))\delta V(t-{\tau }_2)I(t-{\tau }_2)-(\mu +\alpha +b)I,}\hfill \\ \hfill & {\displaystyle \frac{dR}{dt}=\eta V+bI-(\mu +\rho )R,}\hfill \end{array}\right\}$$

(27)

with the initial conditions as defined in (2). In this context, the control variables $v_i\left(t\right)$ are implemented as the Lebesgue measurable controls (where $i=1,2$). We introduce the objective functional as

$$\begin{array}{cc}\hfill J(v_1\left(t\right),v_2\left(t\right))=& {\int }_0^T\left[A_{1}S+A_{2}I+{\displaystyle \frac{1}{2}}\left(B_1{v}_1^2+B_2{v}_2^2\right)\right]dt.\hfill \end{array}$$

(28)

In the provided expression, $A_i$ (where $i=1,2$) represents non-negative weight coefficients. Our objective is to determine an optimal variable set denoted as $\left(v_1(·),v_2(·)\right)$ such that

$$J\left(\widehat{v_1}(·),\widehat{v_2}(·)\right)=min\left\{J\left(v_1(·),v_2(·)\right)\mid \left(v_1(·),v_2(·)\right)\in U\right\}.$$

We introduce the optimal control function, denoted by U,

$$U=\left\{\left(v_1(·),v_2(·)\right)\mid ,v_i(·)\in [0,1],v_i(·)\mathrm{is}\mathrm{Lebesgue}\mathrm{measurable}\right\}.$$

(29)

4.2. Existence and Characterization

Now, our investigation centers on the exploration of an optimal control set’s existence over a finite period for the system defined in (27)–(29).

Theorem 3. 

As associated to the optimal solution $\widehat{S},\widehat{V},\widehat{I},\widehat{R}$, there exists $v^{\prime }\left(t\right)=\left(\widehat{v_1},\widehat{v_2}\right)\in U$ as optimal controls, such that

$$J\left(\widehat{v_1},\widehat{v_2}\right)=\underset{\left(v_1,v_2\right)\in U}{min}J\left(v_1,v_2\right),$$

subject to model (27).

Proof. 

To establish the existence of the optimal control problem, we utilize the method proposed in [19,52]. It is noteworthy that the state and strategic control variables are stipulated to be positive. Additionally, the set of controls U, specifically designed to be closed and bounded by definition, guarantees the bounded nature of the optimal system. This boundedness is vital for the compactness required for the existence of an optimal control. Furthermore, the integrand

$${\int }_0^T\left[A_{1}S+A_{2}I+{\displaystyle \frac{1}{2}}\left(B_1{v}_1^2+B_2{v}_2^2\right)\right]dt,$$

demonstrates convexity within the control set U, showcasing both bi-quadratic and quadratic characteristics in the control variables. Additionally, there are positive values ${\varpi }_1$ and ${\varpi }_2$ and constant $v>1$ satisfying the condition

$$\begin{array}{c}\hfill A_{1}S+A_{2}I+{\displaystyle \frac{1}{2}}\left(B_1{v}_1^2+B_2{v}_2^2\right)\ge {\varpi }_1{\left({\left|v_1\right|}^2+{\left|v_2\right|}^2\right)}^{{\displaystyle \frac{v}{2}}}-{\varpi }_2.\end{array}$$

The boundedness of the state variables serves to reinforce the confirmation of the existence of the optimal control. □

By formulating the Hamiltonian function H and application of Pontryagin’s maximum principle considering a delay in the state, the optimal control $v^{\prime }\left(t\right)=\left(\widehat{v_1},\widehat{v_2}\right)$ is characterized, as described in [53,54].

Theorem 4. 

Suppose $\widehat{v_1}$ and $\widehat{v_2}$ are optimal control variables, and the $\widehat{S},\widehat{V},\widehat{I}$, and $\widehat{R}$ are the optimal state variables related to the control system (27); then, there exists an adjoint variable

$$\lambda \left(t\right):=({\lambda }_1\left(t\right),{\lambda }_2\left(t\right),{\lambda }_3\left(t\right),{\lambda }_4\left(t\right))\in {\mathbb{R}}^4,$$

that meets the requirements outlined by the adjoint equations:

$$\begin{array}{cc}\hfill {\displaystyle \frac{d{\lambda }_1}{dt}=}& -[A_1-{\lambda }_1(\beta I-(v_1\left(t\right)+\mu ))+{\lambda }_2{v}_1\left(t\right)+{\chi }_{[0,T-{\tau }_1]}\left(t\right)\left({\lambda }_3(t+{\tau }_1)\beta I(t-{\tau }_1)\right)],\hfill \\ \hfill {\displaystyle \frac{d{\lambda }_2}{dt}=}& -[-{\lambda }_2(1-v_2\left(t\right))\delta I-{\lambda }_2(\mu +\mu )+{\lambda }_4\eta \hfill \\ \hfill & +{\chi }_{[0,T-{\tau }_2]}\left(t\right)\left({\lambda }_3(t+{\tau }_2)(1-v_2\left(t\right))\delta I(t-{\tau }_2)\right],\hfill \\ \hfill {\displaystyle \frac{d{\lambda }_3}{dt}=}& -[A_2-{\lambda }_1\beta S-{\lambda }_2(1-v_2\left(t\right))\delta V-{\lambda }_3(\mu +\alpha +b)+{\lambda }_{4}b\hfill \\ \hfill & +{\chi }_{[0,T-{\tau }_1]}\left(t\right)\left[{\lambda }_3(t+{\tau }_1)\beta S(t-{\tau }_1)\right]+{\chi }_{[0,T-{\tau }_2]}\left(t\right)\left[{\lambda }_3(t-{\tau }_2)(1-v_2\left(t\right))\delta V(t-{\tau }_2)\right],\hfill \\ \hfill {\displaystyle \frac{d{\lambda }_4}{dt}=}& -[+{\lambda }_1\rho -{\lambda }_4(\mu +\rho )].\hfill \end{array}$$

(30)

The transversality conditions

$${\lambda }_i\left(T\right)=0fori=1,\cdots ,4,$$

(31)

are satisfied. Additionally, the corresponding optimal controls are given as

$$\begin{array}{cc}\hfill \widehat{v_1}=& min\left\{max\left\{{\displaystyle \frac{\widehat{S}({\lambda }_1\left(t\right)-{\lambda }_2\left(t\right))}{B_1}},0\right\},1\right\},\hfill \\ \hfill \widehat{v_2}=& min\left\{max\left\{{\displaystyle \frac{{\lambda }_3\left(t\right)\delta \widehat{V}(t-{\tau }_2)\widehat{I}(t-{\tau }_2)-{\lambda }_2\left(t\right)\delta \widehat{V}\widehat{I}}{B_2}},ϵ\right\},1\right\}.\hfill \end{array}$$

(32)

Proof. 

The Hamiltonian is defined as

$$\begin{array}{cc}\hfill H=& A_{1}S+A_{2}I+{\displaystyle \frac{1}{2}}[B_1{v}_1^2+B_2{v}_2^2]+{\lambda }_1[\Lambda -\beta SI-v_1\left(t\right)S-\mu S+\rho R]\hfill \\ \hfill & +{\lambda }_2[v_1\left(t\right)S-(1-v_2\left(t\right))\delta VI-\mu V-\eta V]+{\lambda }_3[\beta S(t-{\tau }_1)I(t-v_2\left(t\right))\hfill \\ \hfill & +(1-\theta )\delta V(t-{\tau }_2)I(t-{\tau }_2)-(\mu +\alpha +b)I]+{\lambda }_4[\eta V+bI-(\mu +\rho )R].\hfill \end{array}$$

(33)

The characteristic function ${\chi }_{[t_i,t_f]}\left(t\right)$ takes the value 1 if $t\in [t_i,t_f]$; for other t, it takes 0. Following Pontryagin’s maximum principle, our analysis establishes the existence of adjoint variables ${\lambda }_i$ (for $i=1,\dots ,4$), satisfying the following canonical equations:

$$\begin{array}{cc}\hfill {\displaystyle \frac{d{\lambda }_1}{dt}}& =-\left[{\displaystyle \frac{\partial H}{\partial S}}\left(t\right)+{\chi }_{\left[0,T-{\tau }_1\right]}\left(t\right){\displaystyle \frac{\partial H}{\partial S\left(t-{\tau }_1\right)}}\left(t\right)\right],\hfill \\ \hfill {\displaystyle \frac{d{\lambda }_2}{dt}}& =-\left[{\displaystyle \frac{\partial H}{\partial V}}\left(t\right)+{\chi }_{\left[0,T-{\tau }_2\right]}\left(t\right){\displaystyle \frac{\partial H}{\partial V\left(t-{\tau }_2\right)}}\left(t\right)\right],\hfill \\ \hfill {\displaystyle \frac{d{\lambda }_3}{dt}}& =-\left[{\displaystyle \frac{\partial H}{\partial I}}\left(t\right)+{\chi }_{\left[0,T-{\tau }_1\right]}\left(t\right){\displaystyle \frac{\partial H}{\partial I\left(t-{\tau }_1\right)}}\left(t\right)+{\chi }_{\left[0,T-{\tau }_2\right]}\left(t\right){\displaystyle \frac{\partial H}{\partial I(t-{\tau }_2)}}\left(t\right)\right],\hfill \\ \hfill {\displaystyle \frac{d{\lambda }_4}{dt}}& =-{\displaystyle \frac{\partial H}{\partial R}}\left(t\right).\hfill \end{array}$$

(34)

The transversality conditions are ${\lambda }_i\left(T\right)=0$, where $(i=1,\cdots ,4)$ are imposed. By including the derivatives associated with the respective variables in the above inequalities and manipulating them, additional insights can be obtained from adjoint Equation (30). Deriving from the optimality conditions, we obtain

$${\displaystyle \frac{\partial H}{\partial v_1}=0,\mathrm{at}{v}_1=\widehat{v_1},\frac{\partial H}{\partial v_2}=0,\mathrm{at}{v}_2=\widehat{v_2}.}$$

Thus, we have

$$\widehat{v_1}={\displaystyle \frac{\widehat{S}({\lambda }_1\left(t\right)-{\lambda }_2\left(t\right))}{B_1}},\widehat{v_2}={\displaystyle \frac{{\lambda }_3\left(t\right)\delta \widehat{V}(t-{\tau }_2)\widehat{I}(t-{\tau }_2)-{\lambda }_2\left(t\right)\delta \widehat{V}\widehat{I}}{B_2}}.$$

(35)

If the values of $v_1,v_2$ are negative, then we treat them as 0. If they exceed 1, we consider them as 1, which is incorporated in the corresponding optimal controls in (32). This completes the proof. □

Substituting $\widehat{v_1}$ and $\widehat{v_2}$ into (27) and (30), we attain the minimized Hamiltonian $H^{\prime }$ with the optimality system as follows:

$$\left.\begin{array}{cc}\hfill & {\displaystyle \frac{d\widehat{S}}{dt}=\Lambda -\beta \widehat{S}\widehat{I}-\widehat{v_1}\left(t\right)\widehat{S}-\mu \widehat{S}+\rho \widehat{R},}\hfill \\ \hfill & {\displaystyle \frac{d\widehat{V}}{dt}=\widehat{v_1}\left(t\right)\widehat{S}-(1-\widehat{v_2}\left(t\right))\delta \widehat{V}\widehat{I}-\mu \widehat{V}-\eta \widehat{V},}\hfill \\ \hfill & {\displaystyle \frac{d\widehat{I}}{dt}=\beta \widehat{S}(t-{\tau }_1)\widehat{I}(t-{\tau }_1)+(1-\widehat{v_2}\left(t\right))\delta \widehat{V}(t-{\tau }_2)\widehat{I}(t-{\tau }_2)-(\mu +\alpha +b)\widehat{I},}\hfill \\ \hfill & {\displaystyle \frac{d\widehat{R}}{dt}=\eta \widehat{V}+b\widehat{I}-(\mu +\rho )\widehat{R},}\hfill \end{array}\right\}$$

(36)

with the initial conditions as defined in (2) for the optimal system variables. The associated adjoint system is given by (30), accompanied by transversality conditions ${\lambda }_i\left(T\right)=0,$ where $(i=1,\cdots ,4)$. The optimal controls $\widehat{v_1},\widehat{v_2}$ remain consistent with (32).

5. Numerical Simulations

The purpose of this section is to substantiate the efficacy of the theoretical insights acquired in the earlier sections.

5.1. Numerical Simulations of Stability of Equilibria

In this subsection, we employ numerical simulations to verify the theoretical findings presented earlier. The model parameter values used in these simulations are outlined in Table 4, with initial values defined as $\left(S\right(\Theta ),V(\Theta ),I(\Theta ),R(\Theta \left)\right)=(0.8,0.8,0.8,0.8)$, where $\Theta \in [-\tau ,0]$ and $\tau =max\{{\tau }_1,{\tau }_2\}$. From Table 5 and the simulations shown in Figure 8, it is evident that lower vaccine efficacy results in a faster spread of the disease, as indicated by a basic reproduction number (${\mathcal{R}}_0$) greater than one. However, as the vaccination rate ($\theta$) increases, there is a noticeable reduction in ${\mathcal{R}}_0$, which significantly slows the transmission of the disease. This is further supported by the model’s results, showing that higher vaccination rates lead to a significant decrease in the number of infected individuals over time. At a lower vaccination rate ($\theta =0.2$), the peak number of infections remains much higher, suggesting greater susceptibility to outbreaks. In contrast, a vaccination rate of ($\theta =0.8$) substantially reduces infection levels, underscoring the importance of improving vaccine efficacy and coverage in controlling outbreaks and enhancing public health. Similarly, Table 6 demonstrates that, as the recovery rate (b) increases, the basic reproduction number (${\mathcal{R}}_0$) decreases. A higher recovery rate reduces the proportion of infectious individuals in the population, which in turn lowers the potential for further transmission. Therefore, increasing recovery rates is an essential factor in mitigating the outbreak and controlling the disease.

Table 4. Numerical values defined for model (1) parameters.

Parameters:	$\mathbf{\Lambda }$	$\mathit{\gamma }$	$\mathit{\beta }$	$\mathit{\mu }$	$\mathit{\rho }$	$\mathit{\delta }$	$\mathit{\eta }$	$\mathit{\alpha }$	$\mathit{\theta }$	b
Values:	0.76	0.33	0.21	0.11	0.22	0.21	0.12	0.12	0.8	0.19

Table 5. Various vaccine efficiency levels and their corresponding values of ${\mathcal{R}}_0$ for model (1).

${\mathcal{R}}_0$	2.5096	2.1743	1.8390	1.5037
$\theta$	0.2	0.4	0.6	0.8

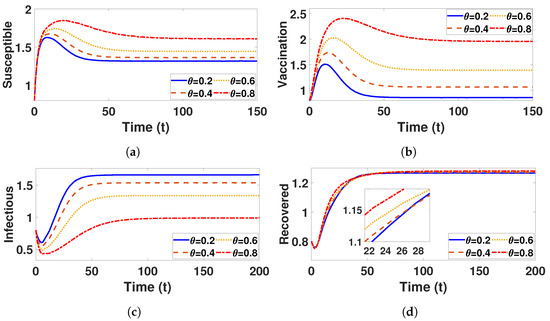
Figure 8. Plots (a–d) represents the populations $S,V,I,R$ as a function of t with ${\tau }_1={\tau }_2=5$ for different vaccine levels, respectively.

Table 6. Various recovery levels and their corresponding values of ${\mathcal{R}}_0$ for model (1).

${\mathcal{R}}_0$	1.5037	1.1278	0.8652	0.7609
b	0.19	0.33	0.5	0.6

In Figure 9a, when ${\tau }_2$ is fixed at 5 and varying values of (${\tau }_1=4,9,14,18$) are considered, it is noticeable that the number of infected humans increases as ${\tau }_1$ increases but, in Figure 10a, when ${\tau }_1$ is fixed at 5 and ${\tau }_2$ takes different values (${\tau }_2=5,10,15,20$), the number of infected individuals slightly increases, indicating that the time delay ${\tau }_1$ has a more significant effect for the behavior status of the infectious than ${\tau }_2$. Nonetheless, despite an increase in ${\tau }_2$, there is a small increase in the number of infected individuals and the stability of the disease-free equilibrium point visible after a certain amount of time.

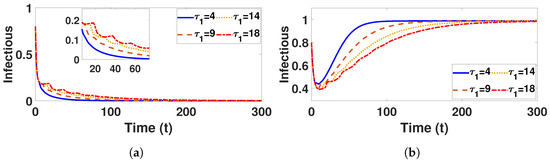
Figure 9. Plot represents infectious population under (a) ${\mathcal{R}}_0=0.7609<1$ with $b=0.6$ and (b) ${\mathcal{R}}_0=1.5037>1$ with $b=0.19$, fixed ${\tau }_2=5$, varied ${\tau }_1$.

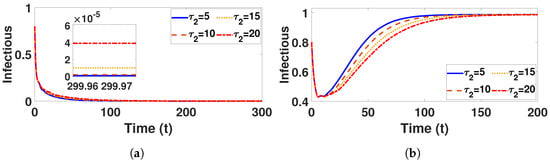
Figure 10. Plot represents infectious population under (a) ${\mathcal{R}}_0=0.7609<1$ with $b=0.6$ and (b) ${\mathcal{R}}_0=1.5037>1$ with $b=0.19$, fixed ${\tau }_1=5$, varied ${\tau }_2$.

Conversely, Figure 9a and Figure 10a confirm that the infectious population diminishes, and $E_0$ is asymptotically stable for all $\{{\tau }_1,{\tau }_2\}\ge 0$ with $b=0.6$. By comparing different ${\tau }_1$ and ${\tau }_2$, it can be observed that the susceptible, vaccinated, and recovered populations exhibit oscillatory convergence, while the infectious population demonstrates the correct qualitative behavior as ${\tau }_1,{\tau }_2$ increase. Figure 11b, Figure 12b and Figure 13b show that, as ${\tau }_1$ increases, the system takes longer to reach a stable endemic point. This behavior can be explained by the fact that larger time delays in infection dynamics cause slower responses in the spread and control of the disease. Biologically, ${\tau }_1$ could represent the incubation period or time it takes for susceptible individuals to become infectious after exposure. Suppose the delay is shorter (${\tau }_1=4$); the disease spreads more rapidly, allowing the system to stabilize sooner as infected individuals quickly move through the compartments. In contrast, with a longer ${\tau }_1$ (e.g., ${\tau }_1=18$), the slower progression of the disease causes a lag in new infections, leading to a slower convergence to the endemic equilibrium. The longer delay signifies that the disease persists in the population for an extended period before stabilizing. In Figure 14b, Figure 15b and Figure 16b, increasing ${\tau }_2$ (the incubation period for vaccinated individuals) results in a faster stabilization and attainment of an endemic equilibrium. This behavior is attributed to several factors: A longer incubation period allows for greater lag in the transition of vaccinated individuals to the infectious class, reducing immediate burdens on the susceptible population and subsequently decreasing infection rates. The feedback mechanisms between compartments lead to fewer interactions between susceptible and infected individuals, enhancing recovery rates and overall immunity. Biologically, these dynamics reflect real-world vaccination campaign patterns, where delays in immune responses can initially increase infection rates but ultimately facilitate a quicker transition to endemicity as immunity builds within the population.

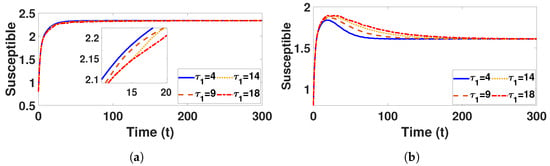
Figure 11. Plot represents susceptible population under (a) ${\mathcal{R}}_0=0.7609<1$ with $b=0.6$ and (b) ${\mathcal{R}}_0=1.5037>1$ with $b=0.19$, fixed ${\tau }_2=5$, varied ${\tau }_1$.

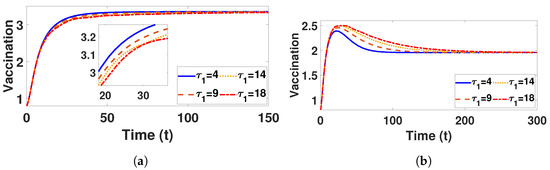
Figure 12. Plot represents vaccination population under (a) ${\mathcal{R}}_0=0.7609<1$ with $b=0.6$ and (b) ${\mathcal{R}}_0=1.5037>1$ with $b=0.19$, fixed ${\tau }_2=5$, varied ${\tau }_1$.

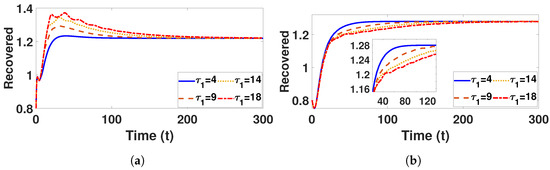
Figure 13. Plot represents recovered population under (a) ${\mathcal{R}}_0=0.7609<1$ with $b=0.6$ and (b) ${\mathcal{R}}_0=1.5037>1$ with $b=0.19$, fixed ${\tau }_2=5$, varied ${\tau }_1$.

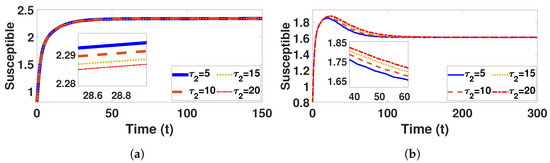
Figure 14. Plot represents susceptible population under (a) ${\mathcal{R}}_0=0.7609<1$ with $b=0.6$ and (b) ${\mathcal{R}}_0=1.5037>1$ with $b=0.19$, fixed ${\tau }_1=5$, varied ${\tau }_2$.

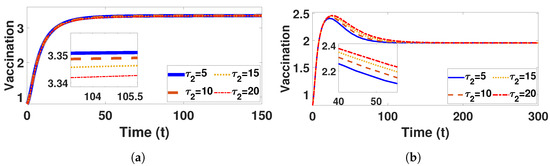
Figure 15. Plot represents vaccination population under (a) ${\mathcal{R}}_0=0.7609<1$ with $b=0.6$ and (b) ${\mathcal{R}}_0=1.5037>1$ with $b=0.19$, fixed ${\tau }_1=5$, varied ${\tau }_2$.

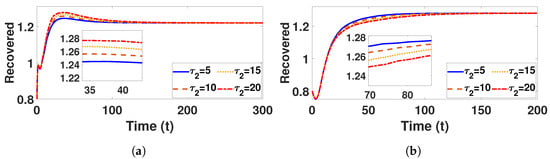
Figure 16. Recovered under (a) ${\mathcal{R}}_0=0.7609<1$ with $b=0.6$ and (b) ${\mathcal{R}}_0=1.5037>1$ with $b=0.19$, fixed ${\tau }_1=5$, varied ${\tau }_2$.

5.2. Numerical Analysis of Optimal Control Strategies

This subsection explores the optimal control strategy for the SVIR model through a numerical example. We begin with an initial population distribution of

$$\left(S\right(\Theta ),V(\Theta ),I(\Theta ),R(\Theta \left)\right)=(0.1,0.1,0.1,0.1).$$

The optimality system is derived from the state and adjoint equations. For numerical simulations, we utilize the time-delayed pandemic model (1), the control system (27), the initial conditions (2), the adjoint Equation (30), and the transversality conditions (31). To reach a higher accuracy in the numerical simulations, we used a method based on a standard Runge–Kutta scheme for the delay system as well as for the optimal control problem. The convergence analysis for this method is discussed in detail in [55].

The infected human population is plotted with and without control interventions. Parameter values are taken from Table 7. In Figure 17, the red lines represent individuals without control, while the blue lines represent those with control. The weights in the objective functional are set as $A_1=100$, $A_2=100$, $B_1=3$, and $B_2=0.000008$. The results demonstrate that the combined application of both control strategies (education campaign and vaccination efficiency) significantly outperforms no control. This combined approach not only dramatically reduces the peak infected and increase vaccinated populations, but also shortens the duration of the disease outbreak for these groups. In essence, control variables $v_1$ and $v_2$ play a crucial role in disease control. The corresponding optimal control functions are shown in Figure 18. The education campaign promotes the highest intensity for a prolonged period at the disease onset. This effectively lowers the peak infected population $\left(I\right(t\left)\right)$ and subsequently increases the peaks of recovery $\left(R\right(t\left)\right)$ and vaccinated $\left(V\right(t\left)\right)$ individuals. Additionally, it works with maximum intensity during the initial stages to reduce the spread of the disease in society as much as possible. This is performed through the optimal use of education campaigns and high-quality vaccination.

Table 7. Numerical values defined for model (1) parameters.

Parameters:	$\Lambda$	$\beta$	$\gamma$	$\mu$	$\rho$	$\theta$	$\delta$	$\eta$	$\alpha$	b
Values:	1	0.7	0.5	0.2	0.02	0.2	0.2	0.6	0.07	0.6

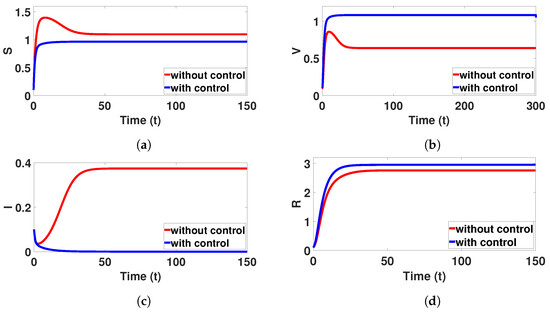
Figure 17. Plots (a–d) represent the impact of control variables $(v_1,v_2)$ in susceptible humans $\left(S\right)$, vaccinated humans $\left(V\right)$, infected $\left(I\right)$, and recovery $\left(R\right)$, respectively, over time $\left(t\right)$; here, ${\tau }_1={\tau }_2=10.$

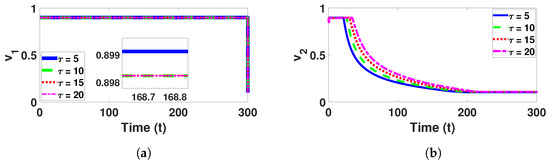
Figure 18. Plots $\left(\mathbf{a}\right)$ and $\left(\mathbf{b}\right)$ represents the values of the control variables $v_1$ and $v_2$ as functions of time t for various delay values respectively.

6. Conclusions

Infectious diseases pose a significant threat to both human health and wildlife, necessitating a comprehensive understanding of their transmission dynamics to inform effective intervention strategies. This study presents a novel $SVIR$ epidemic model that incorporates delays in the incubation period, and demonstrates the following:

• Firstly, model (1) possesses a global positive solution, which is crucial for ensuring realistic population dynamics.
• We employed stability theory to analyze the model, focusing on two key equilibrium points: the disease-free equilibrium and the endemic equilibrium, which arises when ${\mathcal{R}}_0$ exceeds 1. Our findings indicate that the endemic equilibrium is locally asymptotically stable for all $\{{\tau }_1,{\tau }_2\}\ge 0$ when ${\mathcal{R}}_0>1$.
• The model incorporates two essential control measures—education campaigns and vaccination efficiency—as variables. We formulated an optimal control problem, establishing necessary and sufficient conditions for the existence of optimal control functions. Utilizing Pontryagin’s maximum principle, we derived an analytical characterization of the optimal control strategies, providing insights into how best to allocate resources for disease management.
• Numerical simulations confirm the effectiveness of the proposed optimal control strategies and demonstrate the stability of steady states.

Notably, our results suggest that longer incubation periods in human populations may either reduce the number of infected individuals or delay the peak of disease outbreaks, emphasizing the model’s applicability to real-world scenarios. Suppose, if compared to existing models, our findings reveal that incorporating time delays and the dynamics of vaccination leads to improved predictions of disease spread and control. The inclusion of delayed responses reflects more accurately the temporal aspects of intervention measures, providing a greater understanding of the epidemic’s dynamics compared to traditional models that overlook these factors. While this study primarily focuses on time delays in state variables, it is important to recognize the potential for time delays in control variables as well. For instance, there may be significant delays between the initiation of education campaigns and the attainment of widespread public awareness. Future research should aim to formulate an optimal control problem that includes multiple time delays in both state and control variables, as this may significantly influence optimal control solutions and present additional challenges for mathematical analysis.