How Do We Analyze the Accident Causation of Shield Construction of Water Conveyance Tunnels? A Method Based on the N-K Model and Complex Network
Abstract
1. Introduction
- (1)
- Collect and organize the safety accident reports related to shield construction accidents of water transmission projects from major emergency websites in recent years and objectively construct a risk index system;
- (2)
- Define the risk coupling type according to the accident reports and quantify the coupling degree of each coupling form by introducing the N-K model, thus revealing the risk coupling situation and law of the safety system of shield construction of water transmission tunnels;
- (3)
- Construct a causal model of shield tunneling accidents in water conveyance tunnels based on the complex network theory. Then, the network topology parameters are calculated, and the impact and characteristics of nodes are described from different evaluation angles;
- (4)
- The influence of risk coupling on accident occurrence is further considered by integrating the N-K model and the complex network theory, and the centrality of nodes is revised with the coupling value to analyze the key causes comprehensively.
2. Construction of Risk Indicator System
3. Methodology and Model Descriptions
3.1. The Proposed Methods
3.2. Complex Network Model
- Degree of nodes
- 2.
- Closeness centrality of nodes
- 3.
- Betweenness centrality of nodes
- 4.
- Eigenvector centrality of nodes
3.3. N-K Model
- Calculate the frequency of occurrence for different risk coupling forms.
- 2.
- Calculate the probability of occurrence for different forms of risk coupling.
- 3.
- Calculate the coupling values for different risk coupling forms.
4. Implementation
4.1. Accident Causative Model
4.1.1. Construction of Accident Causative Model
4.1.2. Analysis of Characteristic Indicators
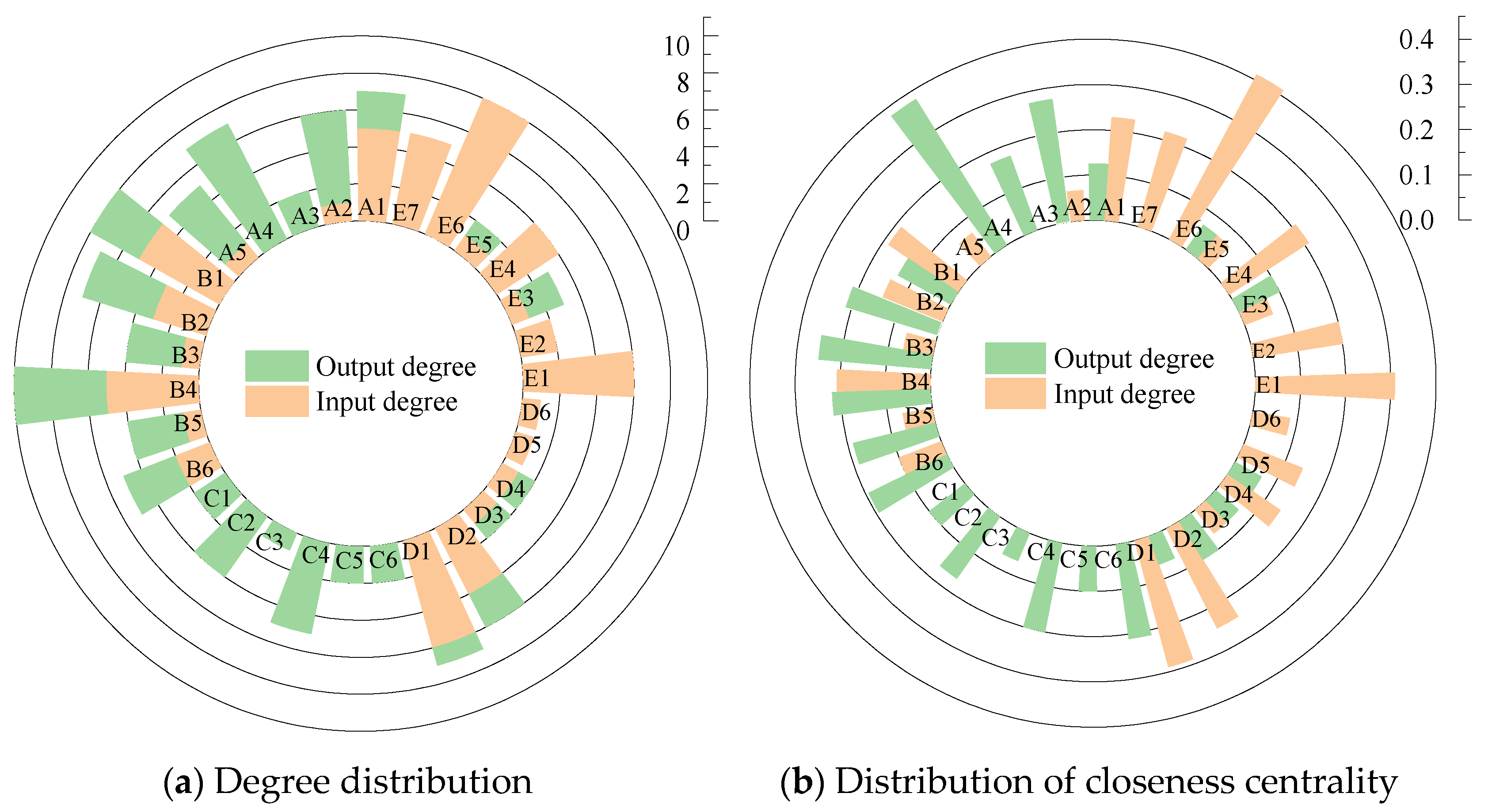
- Degree distribution of nodes
- 2.
- The distribution of closeness centrality
- 3.
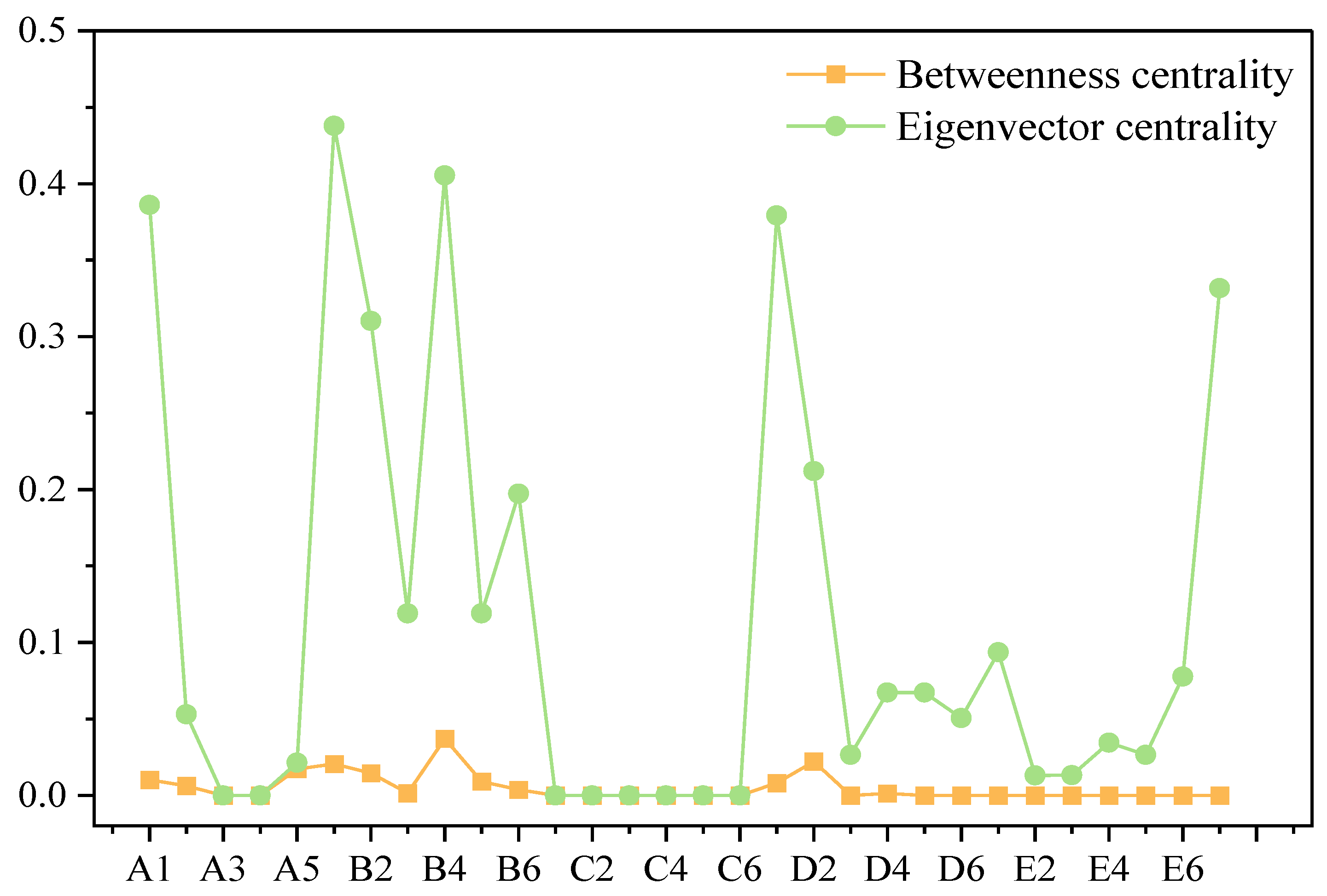
- The distribution of betweenness centrality and eigenvector centrality.
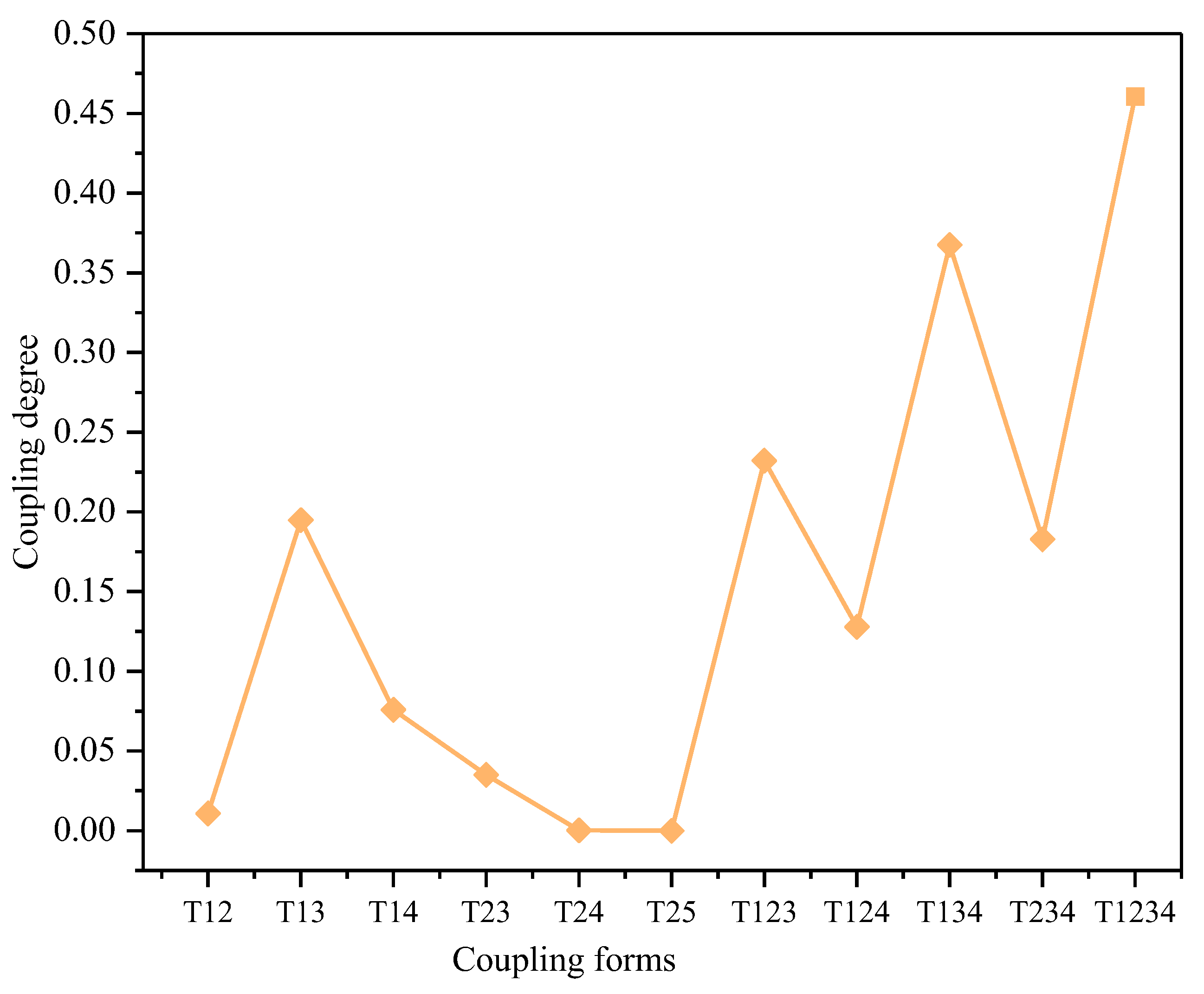
4.2. Risk Coupling Analysis Based on the N-K Model
4.3. Key Factor Analysis
4.3.1. Node Connectivity Analysis
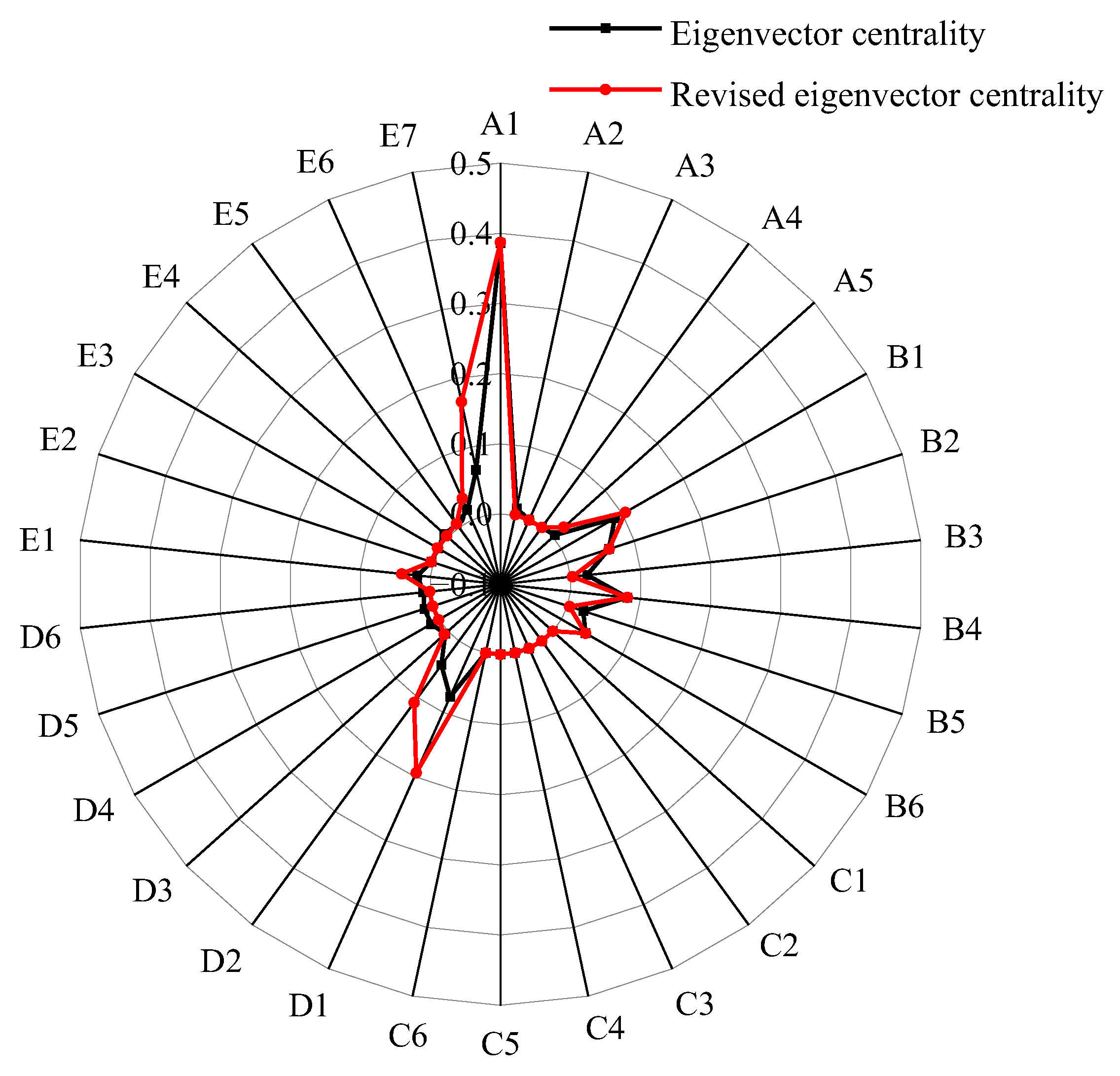
4.3.2. Revision of Eigenvector Centrality
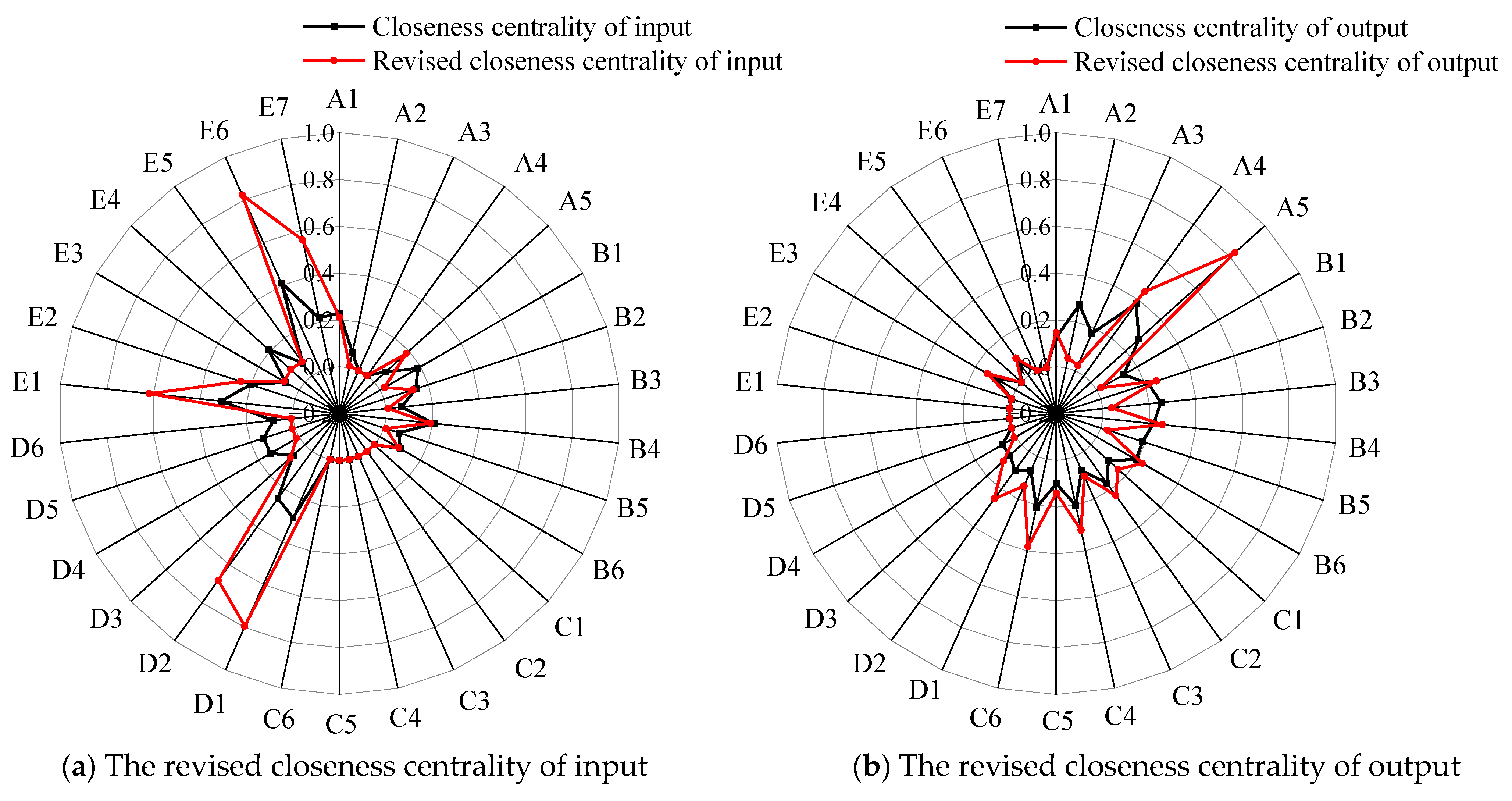
4.3.3. Revision of Closeness Centrality
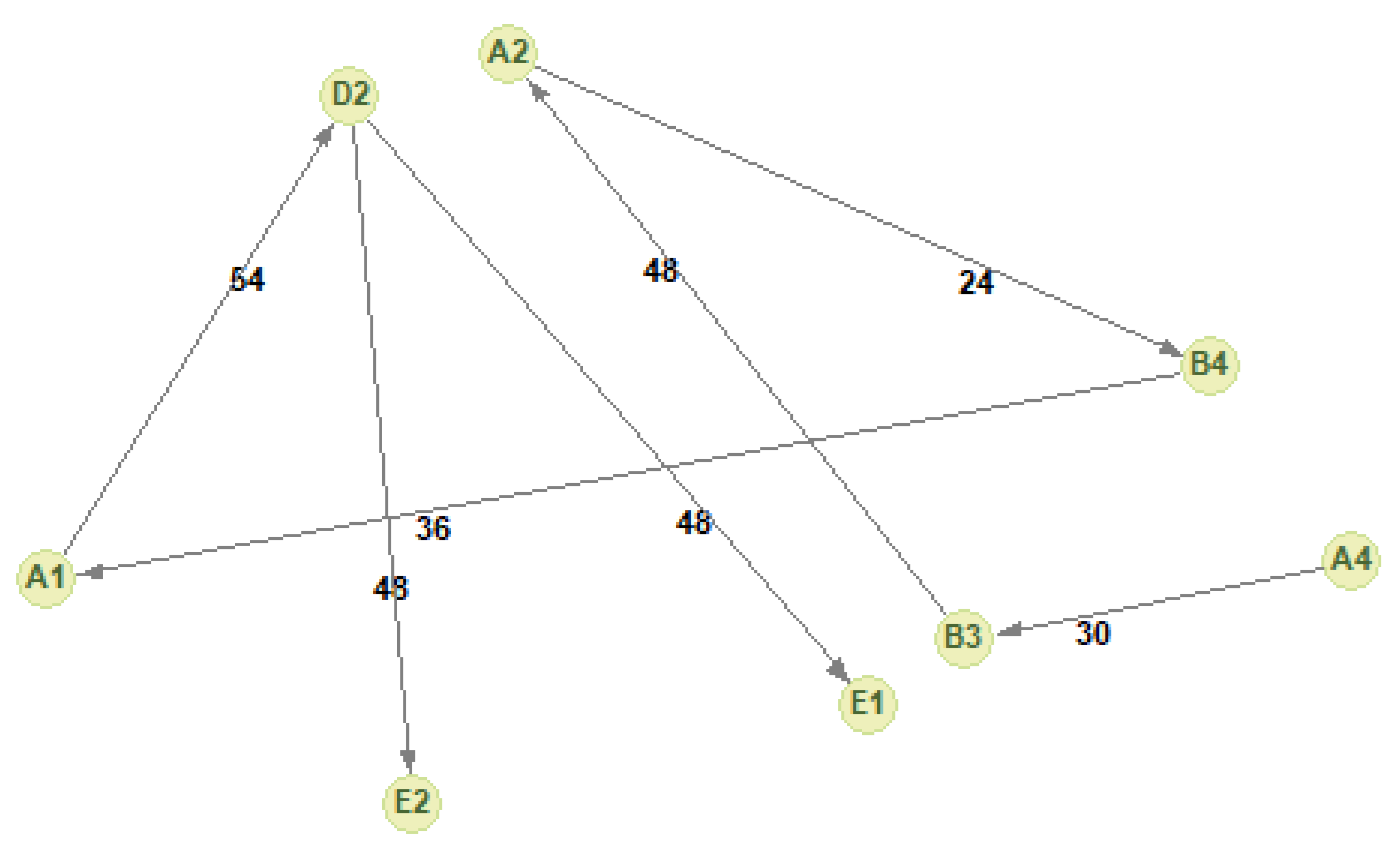
4.4. Key Causative Link Analysis
5. Discussion
- Due to the dynamic nature of time and industry development, there may be new risk factors in this field. Therefore, the causative factors in the safety system of shield construction of water conveyance tunnels need to be perfected. In the following research, we will continue to mine data, expand the scale of the network, and integrate the set of risk factors constantly to achieve a more comprehensive study. Since our research data and conclusions are from China, we will carry out an international investigation of relevant engineering accidents in the future to improve the applicability of this method.
- Due to the limitations of the data, this study fails to consider the effect of time on risk status. Therefore, we plan to predict the risk state and the possibility of risk transmission under different time nodes through statistical methods, such as machine learning, in the future to achieve real-time assessment of the risk situation and system security state. Looking ahead, the causal analysis methods can be further extended to other related construction projects, such as water conservancy engineering and shield construction, which provides a reference for strengthening the risk management of engineering construction.
6. Conclusions and Advice
6.1. Conclusions
- Based on historical accident cases, this paper identifies risk indicators affecting shield construction accidents of water conveyance tunnels from four dimensions, providing theoretical support for risk research in this field. We collect official accident reports, initially screen and sort out the risk indicators, and revise them using expert opinions. Ultimately, the risk indicator system of shield construction of water conveyance tunnels is constructed, addressing human, management, environment, and equipment risks, including 23 secondary factors. The indicator system, based on historical case analysis, is deemed more objective and adaptable to engineering practices and technological development compared to questionnaire surveys and literature analysis. Moreover, analysis based on authoritative accident investigation reports is considered more accurate and convincing. The systematic and structured identification, evaluation, and control of risks based on the risk indicator system provides a management foundation for the actual shield construction project of water conveyance tunnels, enabling managers to make scientific and reasonable decisions to improve safety management practices.
- This paper introduces risk coupling theory into the study of shield construction of water conveyance tunnels and discusses the coupling mechanism of shield construction accidents in water conveyance tunnels. This paper uses the N-K model to analyze risk coupling and defines 15 risk coupling forms, including single-factor coupling, dual-factor coupling, and multi-factor coupling. The quantitative analysis indicates that the number of risks involved in coupling shows a positive correlation with the coupling value overall. However, the coupling value of human-environmental coupling is higher than partial multi-factor coupling, and the multi-factor coupling value including these two types of risks is high. This indicates that human and environmental risks are prone to coupling with other risks in the safety system, greatly impacting construction safety. Due to the objectivity of environmental risks, the relevant department should focus on controlling human risks, reducing the probability of human risks and environmental risks coupling with other factors and ensuring construction safety. The coupling analysis provides a valid basis for early warning and risk control and has important engineering significance for controlling risk diffusion, enabling it to better resist uncertainty and change.
- This paper examines the impact of risk coupling and causality on accidents, focusing on the causes of shield tunnel construction accidents in water conveyance tunnels, which helps to optimize the allocation of risk management resources in practical engineering. Unlike previous causal analyses that only considered the causal relationships of risks, this study also takes into account the impact of risk coupling, using coupling values to modify the characteristic indicators of nodes. From a theoretical perspective, this research reduces the influence of subjective judgment, clarifies the causal and coupling relationships among unsafe behaviors, and further improves the theoretical research framework on accident causes. The identification of key causes through the interaction and causality of risks can help managers deliver more appropriate safety management strategies, thus reducing additional costs, rework, and production defects. This practical assistance can ensure construction safety, improve construction quality, control costs, and enhance efficiency.
6.2. Advice
6.2.1. Key Causal Aspects
6.2.2. Key Causal Chain Aspect
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, Y.Y.; Li, Y.L.; He, J. Strategic countermeasures for China’s water resources security in the new development stage. J. Hydraul. Eng. 2021, 52, 1340–1346. [Google Scholar]
- Chen, X.S.; Fu, Y.B.; Chen, X.; Xiao, H.; Bao, X.; Pang, X.; Wang, X. Progress in underground space construction technology and technical challenges of digital intelligence. China J. Highw. Transp 2022, 35, 1–12. [Google Scholar]
- Einstein, H.H. Risk and risk analysis in rock engineering. Tunn. Undergr. Space Technol. 1996, 11, 141–155. [Google Scholar] [CrossRef]
- Sturk, R.; Olsson, L.; Johansson, J. Risk and decision analysis for large underground projects, as applied to the Stockholm ring road tunnels. Tunn. Undergr. Space Technol. 1996, 11, 157–164. [Google Scholar] [CrossRef]
- Hongbin, G.; Zhanping, S.; Chen, M.; Junbao, W.; Naifei, L.; Desai, G. Shield tunneling risk assessment based on nonlinear fuzzy analytic hierarchy method. Tunn. Constr. 2023, 43, 1862–1871. [Google Scholar]
- Zhang, Y.; Liu, C.; Mou, Y.X. Risk assessment of shield construction of water conveyance tunnels in collapsible loess areas. Yangtze River 2023, 16, 1–10. [Google Scholar]
- Ardeshir, A.; Amiri, M.; Ghasemi, Y.; Errington, M. Risk assessment of construction projects for water conveyance tunnels using fuzzy fault tree analysis. Int. J. Civ. Eng. 2014, 12, 396–412. [Google Scholar]
- Zhang, Z.; Wang, B.; Wang, X.; He, Y.; Wang, H.; Zhao, S. Safety-risk assessment for TBM construction of hydraulic tunnel based on fuzzy evidence reasoning. Processes 2022, 10, 2597. [Google Scholar] [CrossRef]
- Gu, X.B.; Wu, Q.H.; Ma, Y. Risk assessment of the Rockburst intensity in a hydraulic tunnel using an intuitionistic fuzzy sets-TOPSIS model. Adv. Mater. Sci. Eng. 2022, 2022, 4774978. [Google Scholar] [CrossRef]
- Liu, W.L.; Yin, H.; Su, Y. Safety risk evaluation and diagnosis of hydraulic tunnel construction based on G2-AEM-UMT Model. J. Water Resour. Water Eng. 2023, 34, 184–192. [Google Scholar]
- Zhang, Y.L.; Liu, D.H.; Hu, D.J. DS evidence theory-based multi-criteria fuzzy comprehensive evaluation of safety of water conveyance structure. Water Resour. Hydropower Eng. 2019, 50, 104–109. [Google Scholar]
- Zhang, S.; Liu, T.; Wang, C. Multi-source data fusion method for structural safety assessment of water diversion structures. J. Hydroinform. 2021, 23, 249–266. [Google Scholar] [CrossRef]
- Cárdenas, I.C.; Al-jibouri, S.S.; Halman, J.I.; van Tol, F.A. Capturing and integrating knowledge for managing risks in tunnel works. Risk Anal. Int. J. 2013, 33, 92–108. [Google Scholar] [CrossRef] [PubMed]
- Hyun, K.C.; Min, S.; Choi, H.; Park, J.; Lee, I.M. Risk analysis using fault-tree analysis (FTA) and analytic hierarchy process (AHP) applicable to shield TBM tunnels. Tunn. Undergr. Space Technol. 2015, 49, 121–129. [Google Scholar] [CrossRef]
- Huang, Z.; Zhang, W.; Sun, H.; Pan, Q.; Zhang, J.; Li, Y. Risk uncertainty analysis in shield tunnel projects. Tunn. Undergr. Space Technol. 2023, 132, 104899. [Google Scholar] [CrossRef]
- Wang, Y.; Su, J.; Zhang, S.; Guo, S.; Zhang, P.; Du, M. A Dynamic Risk Assessment Method for Deep-Buried Tunnels Based on a Bayesian Network. Geofluids 2020, 1, 8848860. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, Y.; Easa, S.M.; Yan, X. Risk factors influencing tunnel construction safety: Structural equation model approach. Heliyon 2023, 9, e12924. [Google Scholar] [CrossRef]
- Qie, Z.; Yan, H. A causation analysis of Chinese subway construction accidents based on fault tree analysis-Bayesian network. Front. Psychol. 2022, 13, 887073. [Google Scholar] [CrossRef]
- Chung, H.; Park, J.; Kim, B.K.; Kwon, K.; Lee, I.M.; Choi, H. A causal network-based risk matrix model applicable to shield TBM tunneling projects. Sustainability 2021, 13, 4846. [Google Scholar] [CrossRef]
- Wang, F.; Li, H.; Dong, C.; Ding, L. Knowledge representation using non-parametric Bayesian networks for tunneling risk analysis. Reliab. Eng. Syst. Saf. 2019, 191, 106529. [Google Scholar] [CrossRef]
- Perrow, C. Normal Accidents: Living with High Risk Technologies; Princeton University Press: Princeton, NJ, USA, 1999. [Google Scholar]
- Pan, H.; Gou, J.; Wan, Z.; Ren, C.; Chen, M.; Gou, T.; Luo, Z. Research on coupling degree model of safety risk system for tunnel construction in subway shield zone. Math. Probl. Eng. 2019, 1, 5783938. [Google Scholar] [CrossRef]
- Guo, D.; Song, Z.; Xu, T.; Zhang, Y.; Ding, L. Coupling analysis of tunnel construction risk in complex geology and construction factors. J. Constr. Eng. Manag. 2022, 148, 04022097. [Google Scholar] [CrossRef]
- Xue, Y.; Xiang, P.; Jia, F.; Liu, Z. Risk assessment of high-speed rail projects: A risk coupling model based on system dynamics. Int. J. Environ. Res. Public Health 2020, 17, 5307. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Wan, L.; Wang, W.; Yang, G.; Ma, Q.; Zhou, H.; Lu, F. Integrated fuzzy DEMATEL-ISM-NK for metro operation safety risk factor analysis and multi-factor risk coupling study. Sustainability 2023, 15, 5898. [Google Scholar] [CrossRef]
- Chen, D.; Pei, Y.; Xia, Q. Research on human factors cause chain of ship accidents based on multidimensional association rules. Ocean Eng. 2020, 218, 107717. [Google Scholar] [CrossRef]
- Wu, X.G.; Wu, K.B.; Shen, M.F.; Chen, Y.Q.; Zhang, L.M. Research on coupling of safety risks in metro construction based on NK model. China Saf. Sci. J. 2016, 26, 96–101. [Google Scholar]
- Wang, H.X.; Liu, Z.J. Coupling analysis of the risk factors for the maritime transportation safety based on the NK model. J. Saf. Environ. 2021, 21, 56–61. [Google Scholar]
- Huang, W.C.; Shuai, B.; Sun, Y. Study on coupling risk formation mechanism of railway dangerous goods transportation system based on NK model. J. China Railw. Soc. 2019, 41, 1–9. [Google Scholar]
- Dai, S.W.; Liu, X.X.; Wan, F. Coupling analysis on disaster-inducing factors for large deformation accidents in soft rock tunnels. China Saf. Sci. J. 2021, 31, 119–124. [Google Scholar]
- Hai, N.; Gong, D.; Liu, S.; Dai, Z. Dynamic coupling risk assessment model of utility tunnels based on multimethod fusion. Reliab. Eng. Syst. Saf. 2022, 228, 108773. [Google Scholar] [CrossRef]
- Shan, Z.; Qiu, L.; Chen, H.; Zhou, J. Coupled analysis of safety risks in bridge construction based on NK model and SNA. Buildings 2023, 13, 2178. [Google Scholar] [CrossRef]
- Liu, J.; Yang, G.; Wang, W.; Zhou, H.; Hu, X.; Ma, Q. Based on ISM—NK Tunnel Fire Multi-Factor Coupling Evolution Game Research. Sustainability 2022, 14, 7034. [Google Scholar] [CrossRef]
- Wu, B.J.; Jin, L.H.; Zheng, X.Z.; Chen, S. Coupling analysis of crane accident risks based on Bayesian network and the NK model. Sci. Rep. 2024, 14, 1133. [Google Scholar]
- Liu, W.; Zhao, T.; Zhou, W.; Tang, J. Safety risk factors of metro tunnel construction in China: An integrated study with EFA and SEM. Saf. Sci. 2018, 105, 98–113. [Google Scholar] [CrossRef]
- Erdős, P.; Rényi, A. On the evolution of random graphs. Publ. Math. Inst. Hung. Acad. Sci 1960, 5, 17–60. [Google Scholar]
- Wan, C.P.; Liu, Y.F.; Wu, B. Study on risk identification and accident evolution mechanism of maritime traffic accidents based on complex network. J. Saf. Sci. Technol. 2023, 19, 165–171. [Google Scholar]
- Chen, W.; Wang, L.Y.; Yang, J.; Zhou, H.D.; Yang, D.H. Research on the network model of tower crane accidents based on association rules. China Saf. Sci. J. 2023, 23, 1161–1168. [Google Scholar]
- Chen, W.Y.; Li, Y.T.; Song, Z.G. Research on causes of work safety accidents based on complex network theory: A case study of a district in Beijing. China Saf. Sci. J. 2020, 30, 7–12. [Google Scholar]
- Wang, H.Y.; Chu, L.; Xu, J. Construction safety risk analysis of bridge girder-erecting machine based on complex network integrating NK model. China Saf. Sci. J. 2023, 33, 10–17. [Google Scholar]
- Yang, J.F.; Wang, P.C.; Liu, X.Y.; Bian, M.C.; Chen, L.C.; Lv, S.Y.; Tao, J.F.; Suo, G.Y.; Xuan, S.Q.; Li, R.; et al. Analysis on causes of chemical industry accident from 2015 to 2020 in Chinese mainland: A complex network theory approach. J. Loss Prev. Process Ind. 2023, 83, 105061. [Google Scholar] [CrossRef]
- Deng, J.; Liu, S.; Shu, Y.; Hu, Y.; Xie, C.; Zeng, X. Risk evolution and prevention and control strategies of maritime accidents in China’s coastal areas based on complex network models. Ocean Coast. Manag. 2023, 237, 106527. [Google Scholar] [CrossRef]
- Guo, S.; Zhou, X.; Tang, B.; Gong, P. Exploring the behavioral risk chains of accidents using complex network theory in the construction industry. Phys. A Stat. Mech. Appl. 2020, 560, 125012. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, C.; Ding, L.; Sekula, P.; Love, P.E.; Zhou, C. Combining association rules mining with complex networks to monitor coupled risks. Reliab. Eng. Syst. Saf. 2019, 186, 194–208. [Google Scholar] [CrossRef]
- Jiang, J.; Liu, G.; Huang, X.; Ou, X. The Research on Risk Distribution and Evolution of Deep Foundation Pit Construction Adjacent to Existing Tunnels Based on Complex Network. Shock. Vib. 2022, 2022, 1685761. [Google Scholar] [CrossRef]
- Ma, X.; Li, K.P.; Luo, Z.Y.; Zhou, J. Analyzing the causation of a railway accident based on a complex network. Chin. Phys. B 2012, 23, 028904. [Google Scholar] [CrossRef]
- Zhou, J.; Xu, W.; Guo, X.; Ding, J. A method for modeling and analysis of directed weighted accident causation network (DWACN). Phys. A Stat. Mech. Appl. 2015, 437, 263–277. [Google Scholar] [CrossRef]
- Markowitz, H. Portfolio selection. J. Financ. Res. 1952, 7, 77–91. [Google Scholar]
- Brandes, U.; Pich, C. Centrality estimation in large networks. Int. J. Bifurc. Chaos 2007, 17, 2303–2318. [Google Scholar] [CrossRef]
- Kauffman, S.; Levin, S. Towards a general theory of adaptive walks on rugged landscapes. J. Theor. Biol. 1987, 128, 11–45. [Google Scholar] [CrossRef]
- Li, Q.; Li, Z.Y.; Wang, C.S. Prediction of risk event path for shield tunneling of long-distance water conveyance tunnel. South-to-North Water Transf. Water Sci. Technol. 2022, 20, 999–1009. [Google Scholar]
- Zhao, Z.; Yan, H.; Wang, Y.; Guo, D. A Coupled Analysis of Risk Factors of Tower Crane Collapse Accident in Extreme Winds Conditions Based on NK Model. In Proceedings of the International Conference on Construction and Real Estate Management 2023, ICCREM 2023, Xi’an, China, 23–24 September 2023; pp. 973–981. [Google Scholar]

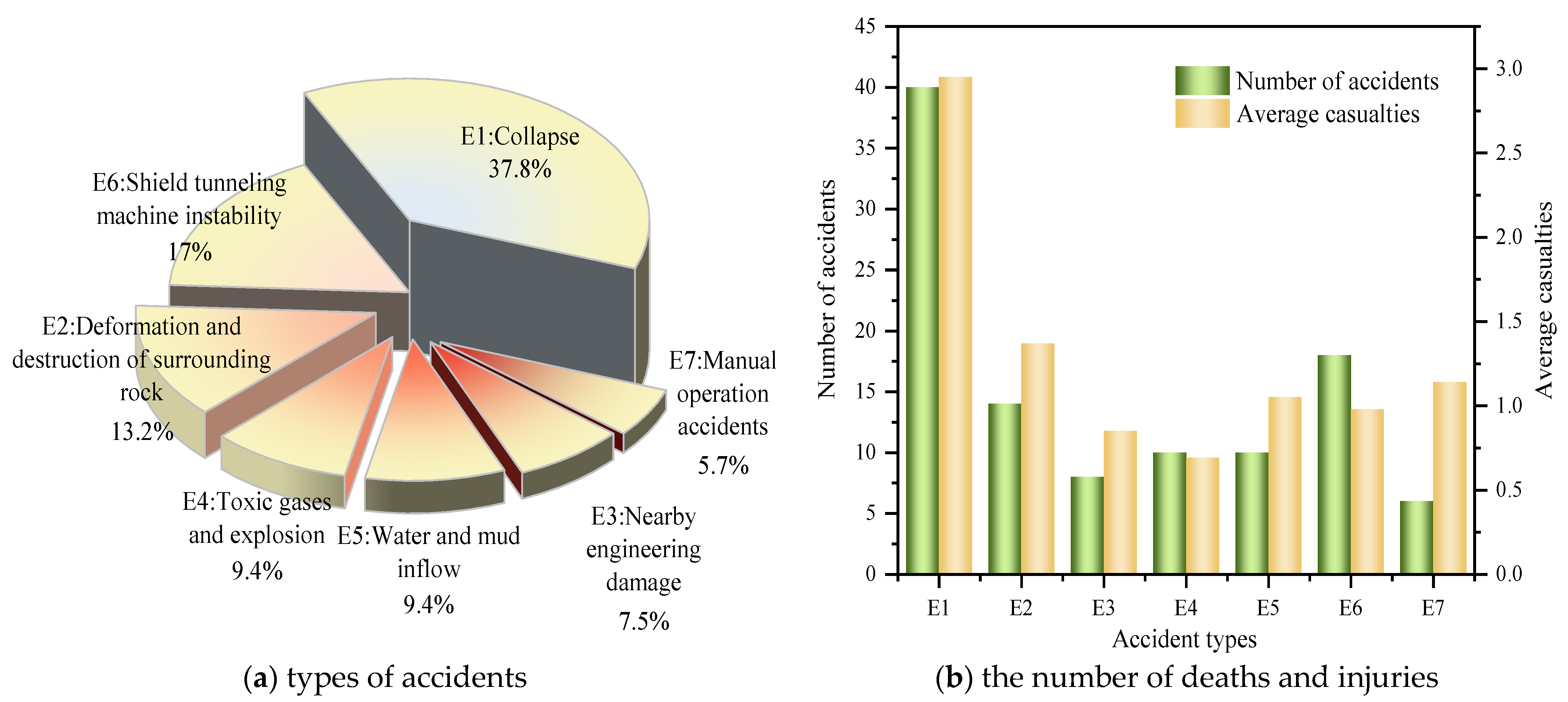
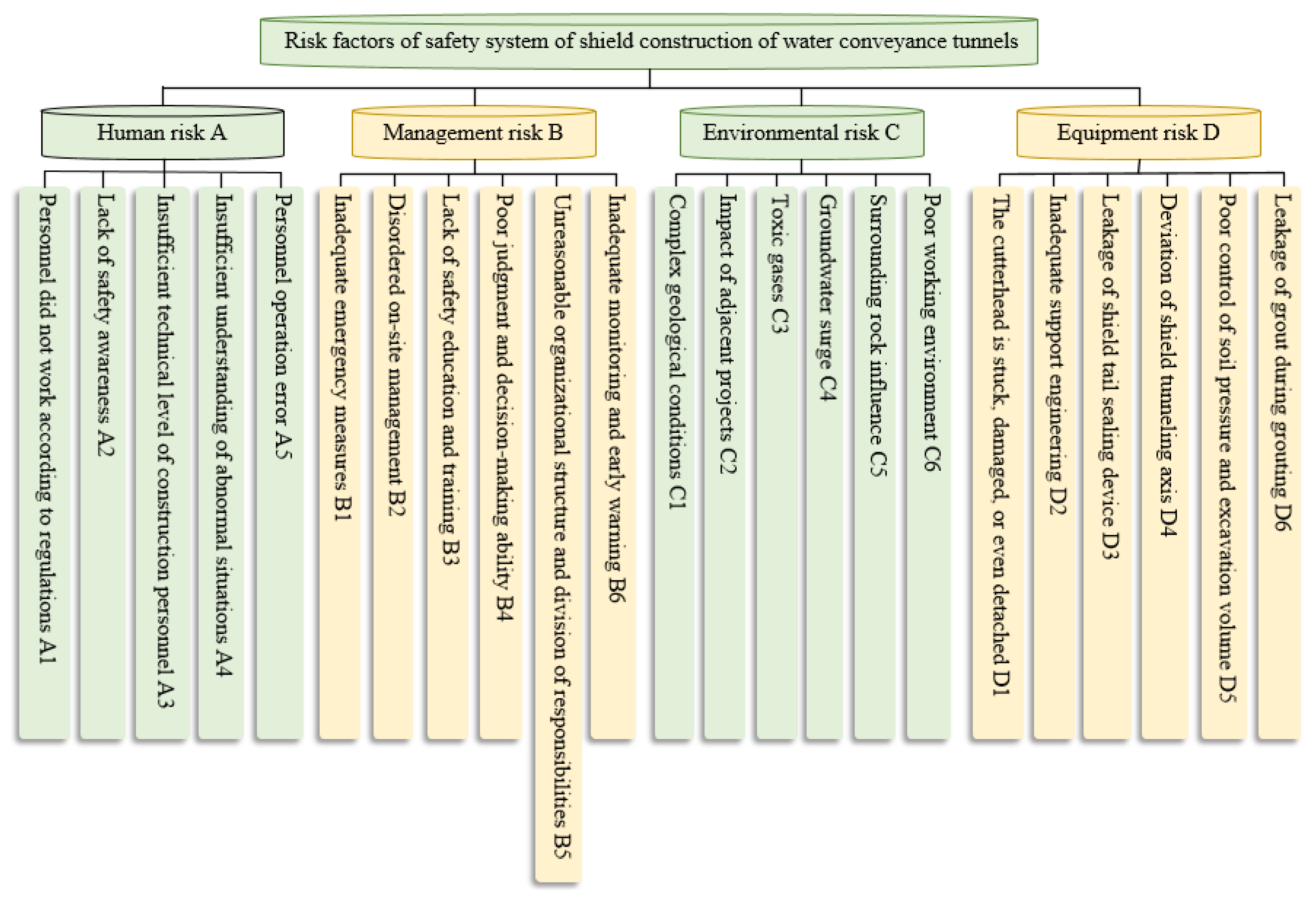
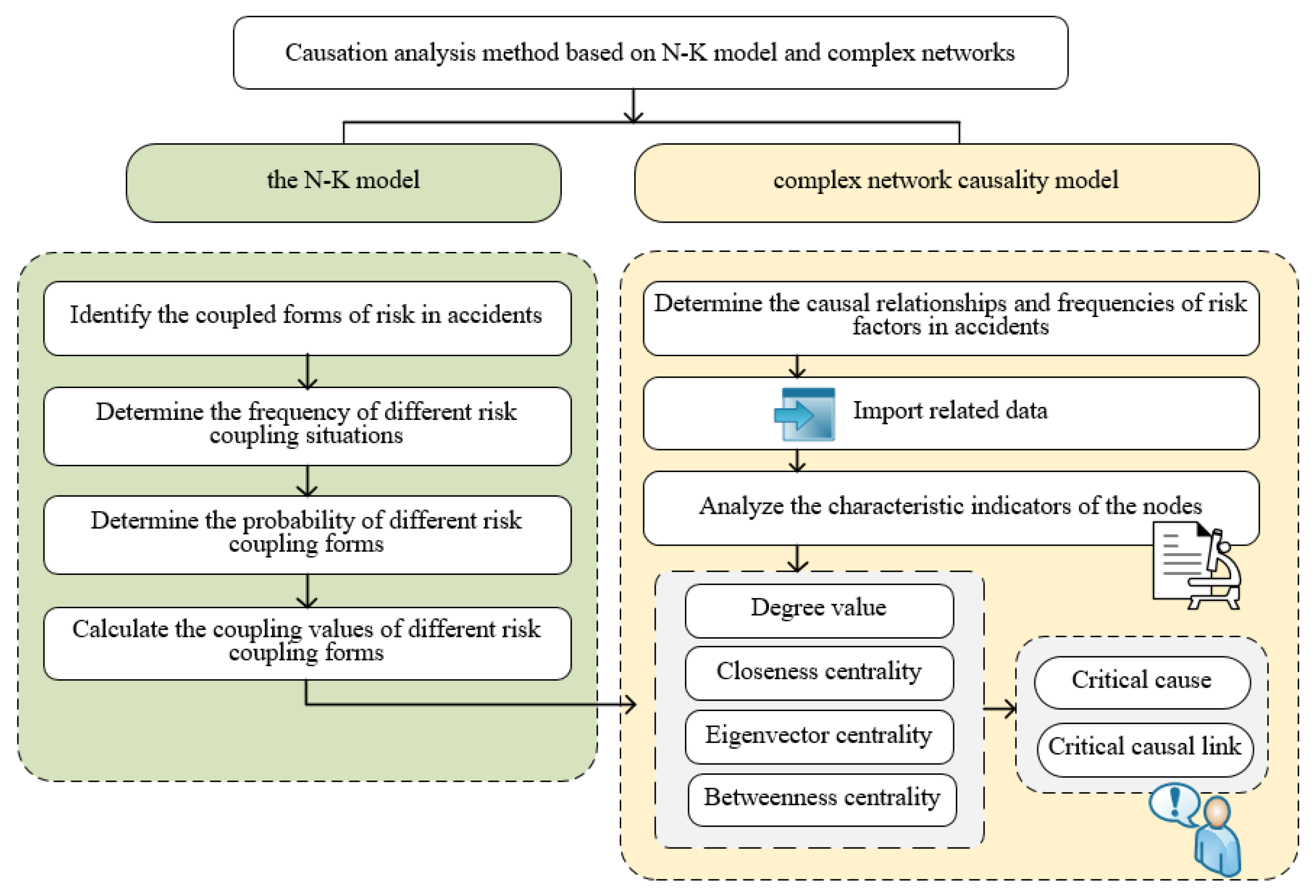
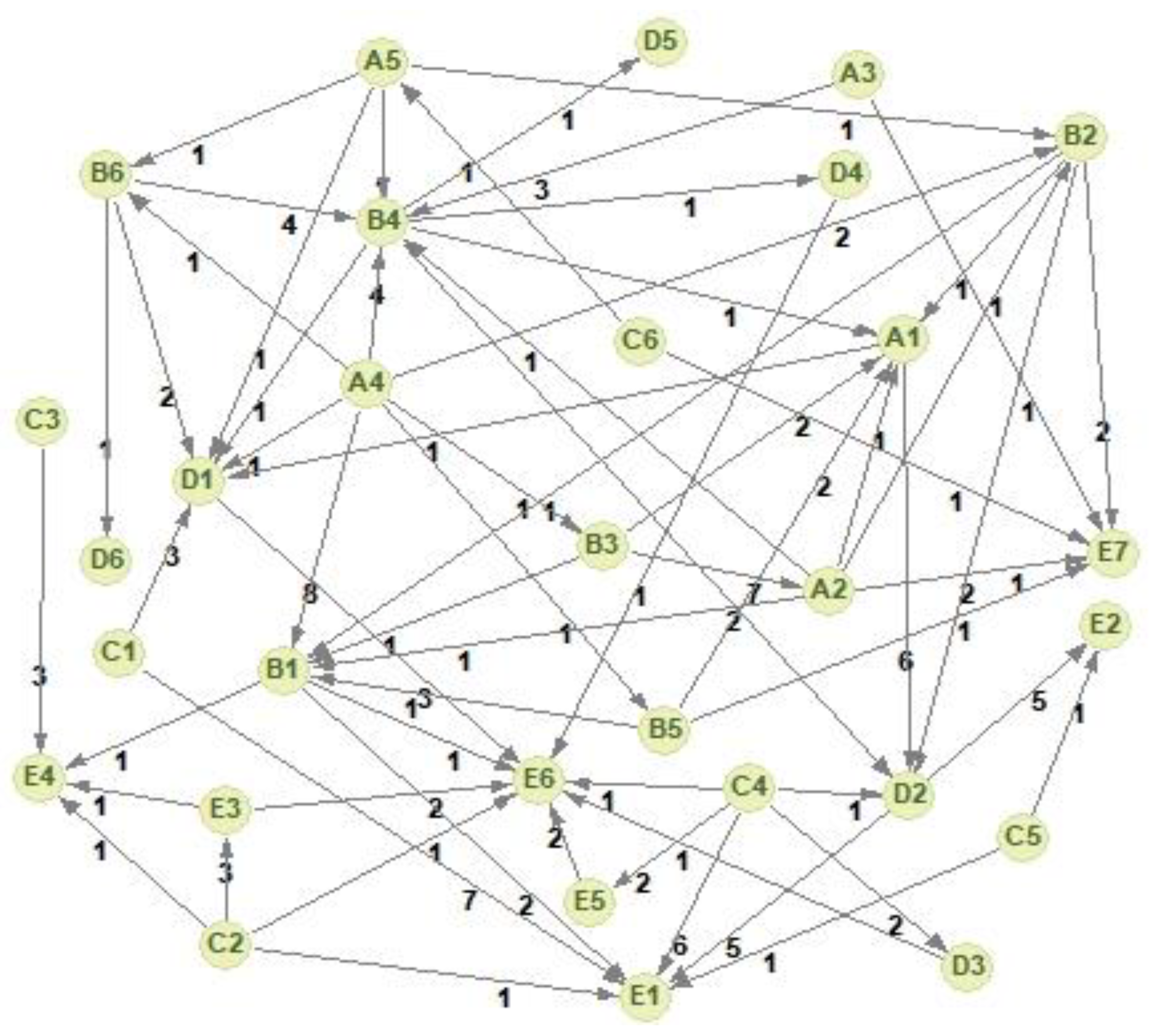
| Time | Accident Location | General Situation of Accident | Accident Consequence |
|---|---|---|---|
| May 2022 | Yunnan Province | In the construction of a water diversion project, the surface water permeates for a long time, and the support strength is insufficient, which leads to sudden mud gushing. | Three died, and the direct property damage was CNY 7.98 million. |
| April 2023 | Hainan Province | In a water supply project, groundwater develops and the weathered rock is saturated with water; the soil strength decreases and the cohesion is lost, resulting in collapse. | One died, and the direct property damage was CNY 1.9 million. |
| August 2021 | Beijing Province | During the construction of the south-to-north water diversion project, the toxic and harmful gases on site exceeded the standard, and the management personnel illegally commanded, resulting in poisoning and suffocation accidents. | Two died, and the economic damage is unknown. |
| July 2018 | Hubei Province | During the construction of a water resource allocation project, the rock fracture caused by water inrush on the tunnel’s palm surface was finally induced by mud inrush. | Six died, and the cost of rescue and disaster disposal was CNY 10.990 and 34.279 million. |
| Coupling Model | Concept | Advantage | Disadvantage |
|---|---|---|---|
| SHEL model | SHEL model analyzes the relationship between personnel and other risks to obtain the factors that affect the whole system. The components of this model include software, hardware, environment, and Liveware. | This method can classify the coupling factors scientifically and focus on exploring the interaction between human factors and other risks. | This method cannot analyze the coupling mechanisms of other factors and cannot quantify coupling degree. |
| Risk conduction coupling model | The risk conduction coupling model holds that the small risks in the system are transferred and diffused through the carrier. Once the coupling degree of the system reaches a threshold, a risk mutation occurs. | This method can systematically summarize and analyze different coupling forms between risks and qualitatively describe the nature and conduction process of coupling. | This method makes it difficult to determine the degree of coupling between risk factors. |
| System dynamics model | The system dynamics model is a method to explore the causal relationship between the elements in a system, which is usually used to deal with dynamic and nonlinear complex problems. | This method can conduct a comprehensive and qualitative analysis of the interaction between risks and provide scientific and reasonable results for further research. | This method cannot quantify the degree of interaction between factors. |
| N-K model | The N-K model is a general method for solving complex network problems. This method relies on a large number of historical data and cases to analyze the risk coupling in the system. | This method can calculate the degree of risk coupling by using the interaction formula through the probability of different risk combinations. | This method requires a large number of sample data and high data accuracy. |
| Coupling degree model | The coupling degree model believes that the coupling degree of each risk factor determines the development of the system from disorder to order, so the coupling degree is used to measure the degree of coordination. | This method does not require a large number of data and samples and can simply and intuitively calculate the degree of risk coupling for analysis. | This method may involve the questionnaire method, so it is subject to slight subjective influence. |
| Accident Report Number | 1 |
|---|---|
| Time | May 2022 |
| Accident location | Yunnan Province |
| Accident consequence | Three people were killed, and the economic loss was CNY 7.98 million. |
| Accident profile | A water diversion project in Yunnan province suddenly had an irresistible geological disaster of mud gushing, which is extremely destructive. |
| Accident cause | Due to the long-term rainfall, the continuous infiltration of surface water causes the surrounding rock to be soaked and softened. In addition to the permeable characteristics of basalt, when surface water enters the water-rich fracture zone or weathering sac, the tunnel surrounding the rock and support engineering is not enough to resist the high-intensity potential energy release. The result is that the groundwater, with sediment, gravel, stone, and other solid materials, bursts instantly in the weak part, forming many sudden tunnel mud-gushing geological disasters. |
| Risk factors | 1. Insufficient risk prediction; 2. Complex geological conditions; 3. Inadequate support engineering; 4. Surrounding rock influence |
| Expert’s Work Organization | Research Institute | Engineering Design Department | Engineering Construction Department | Engineering Management Department |
|---|---|---|---|---|
| Proportion (%) | 25% | 12.5% | 50% | 12.5% |
| Years of working | 0–3 years | 3–6 years | 6–9 years | More than 10 years |
| Proportion (%) | 12.5% | 25% | 25% | 37.5% |
| Age | 20–30 years old | 30–40 years old | 40–50 years old | Age 50 and older |
| Proportion (%) | 12.5% | 25% | 50% | 12.5% |
| Educational status | Doctor’s degree or above | Master’s degree | Bachelor’s degree | College degree or below |
| Proportion (%) | 12.5% | 25% | 37.5% | 25% |
| Professional title | Engineer | Senior engineer | Professor | Professor-level senior engineer |
| Proportion (%) | 25% | 37.5% | 25% | 12.5% |
| Risk Indicators That Need to Be Revised | Reason for Revision | Revised Result |
|---|---|---|
| 1. Underground pipeline damage; 2. Impact of adjacent engineering and buildings | There are intersection and inclusion relations between the two, which can simplify the merger. | Merge: Impact of adjacent projects. |
| 1. Segment transportation problem; 2. The supply of construction materials is not timely; 3. Dust impact on the construction site | These three factors have a low impact on the safety of the construction process of the tunnel, so it is suggested to delete them. | Delete these three risk factors. |
| 1. Combustible gas; 2. Toxic gas | These two risk factors have overlapping and inclusive relationships, and the latter has a large range, so it is recommended to delete the former. | Delete: Combustible gas. |
| 1. The supporting form of the cavern is unreasonable; 2. The support project does not meet the requirements | The meanings of the two are similar, and it is suggested to integrate them into one indicator. | Merge: Inadequate support engineering. |
| Coupling Types | Coupling Forms |
|---|---|
| Dual-factor coupling | human-management risk coupling (T12) |
| human-environmental risk coupling (T13) | |
| human-equipment risk coupling (T14) | |
| management-environmental risk coupling (T23) | |
| management-equipment risk coupling (T24) environmental-equipment risk coupling (T34) | |
| Three-factor coupling | human-management-environmental risk coupling (T123) |
| human-management-equipment risk coupling (T124) | |
| human-environmental-equipment risk coupling (T134) | |
| management-environmental-equipment risk coupling (T234) | |
| Four-factor coupling | human-management-environmental-equipment risk coupling (T1234) |
| Risk Factor | Human Risk | Management Risk | Environmental Risk | Equipment Risks | Potential Coupling Forms |
|---|---|---|---|---|---|
| A1 | 1 | 1 | 0 | 1 | T124 |
| A2 | 1 | 1 | 0 | 0 | T12 |
| A3 | 0 | 1 | 0 | 0 | T12 |
| A4 | 1 | 1 | 0 | 1 | T124 |
| A5 | 0 | 1 | 1 | 1 | T1234 |
| B1 | 1 | 1 | 0 | 0 | T12 |
| B2 | 1 | 1 | 0 | 1 | T124 |
| B3 | 1 | 1 | 0 | 0 | T12 |
| B4 | 1 | 1 | 0 | 1 | T124 |
| B5 | 1 | 0 | 0 | 0 | T12 |
| B6 | 1 | 1 | 0 | 1 | T124 |
| C1 | 0 | 0 | 0 | 1 | T34 |
| C2 | 0 | 0 | 0 | 0 | / |
| C3 | 0 | 0 | 0 | 0 | / |
| C4 | 0 | 0 | 0 | 1 | T34 |
| C5 | 0 | 0 | 0 | 0 | / |
| C6 | 1 | 0 | 0 | 0 | T13 |
| D1 | 1 | 1 | 1 | 0 | T1234 |
| D2 | 1 | 1 | 1 | 0 | T1234 |
| D3 | 0 | 0 | 1 | 0 | T34 |
| D4 | 0 | 1 | 0 | 0 | T24 |
| D5 | 0 | 1 | 0 | 0 | T24 |
| D6 | 0 | 1 | 0 | 0 | T24 |
| E1 | 0 | 1 | 1 | 1 | T234 |
| E2 | 0 | 0 | 1 | 1 | T34 |
| E3 | 0 | 0 | 1 | 0 | / |
| E4 | 0 | 1 | 1 | 0 | T23 |
| E5 | 0 | 0 | 1 | 0 | / |
| E6 | 0 | 1 | 1 | 1 | T234 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Zhang, Q.; Zhang, X.; Li, M.; Qi, G. How Do We Analyze the Accident Causation of Shield Construction of Water Conveyance Tunnels? A Method Based on the N-K Model and Complex Network. Mathematics 2024, 12, 3222. https://doi.org/10.3390/math12203222
Zhang Y, Zhang Q, Zhang X, Li M, Qi G. How Do We Analyze the Accident Causation of Shield Construction of Water Conveyance Tunnels? A Method Based on the N-K Model and Complex Network. Mathematics. 2024; 12(20):3222. https://doi.org/10.3390/math12203222
Chicago/Turabian StyleZhang, Yong, Qi Zhang, Xiang Zhang, Meng Li, and Guoqing Qi. 2024. "How Do We Analyze the Accident Causation of Shield Construction of Water Conveyance Tunnels? A Method Based on the N-K Model and Complex Network" Mathematics 12, no. 20: 3222. https://doi.org/10.3390/math12203222
APA StyleZhang, Y., Zhang, Q., Zhang, X., Li, M., & Qi, G. (2024). How Do We Analyze the Accident Causation of Shield Construction of Water Conveyance Tunnels? A Method Based on the N-K Model and Complex Network. Mathematics, 12(20), 3222. https://doi.org/10.3390/math12203222






