Dynamics of a Price Adjustment Model with Distributed Delay
Abstract
1. Introduction
2. Materials and Methods
2.1. Stability Analysis of Solution
- Case . By substituting into (6), we obtain the quadratic characteristic equationwhereThe local asymptotical stability of the model is guaranteed if both roots of Equation (7) have negative real parts. According to the Routh–Hurwitz criterion, this holds true if and only if and We, therefore, have the following result.
2.2. Stability Switches and Bifurcation
2.3. Existence and Uniqueness of Solution
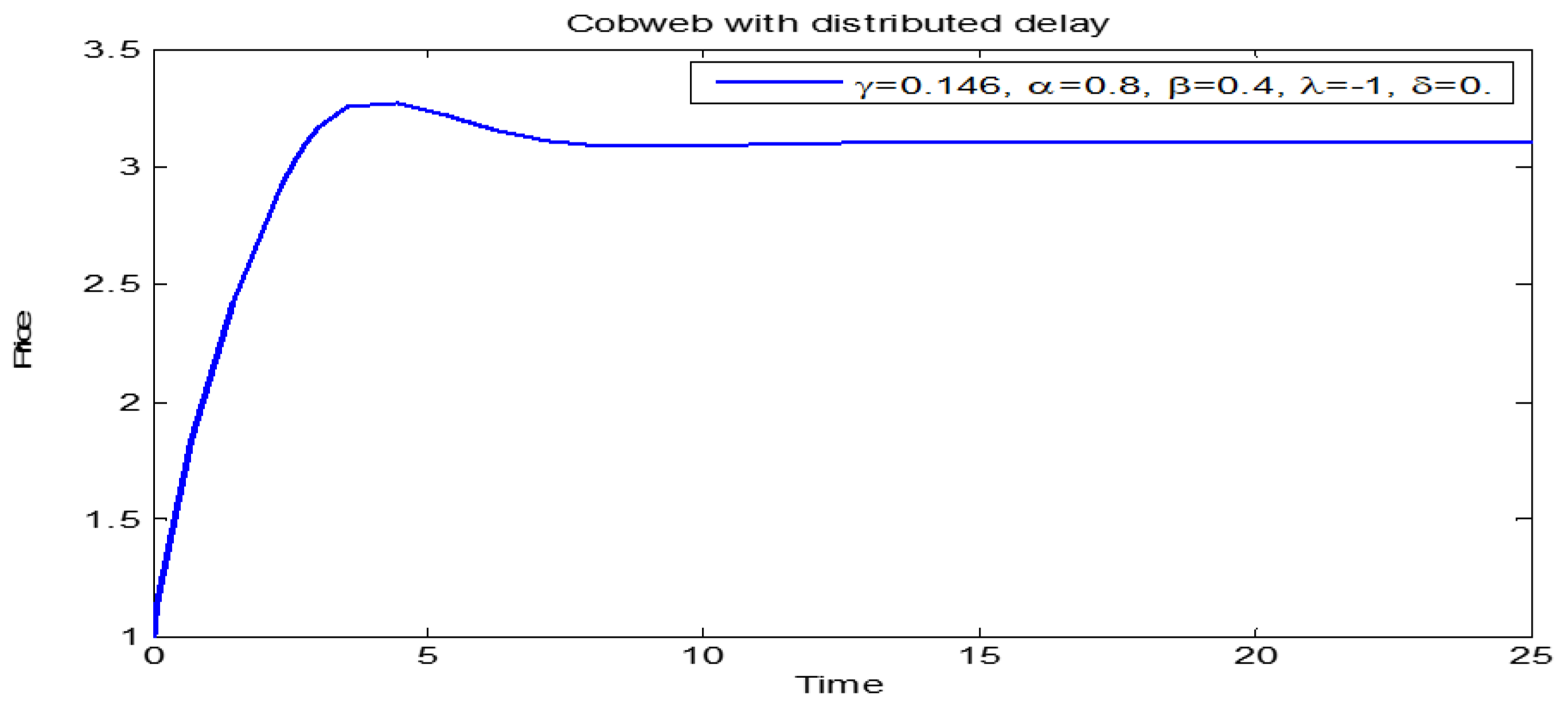
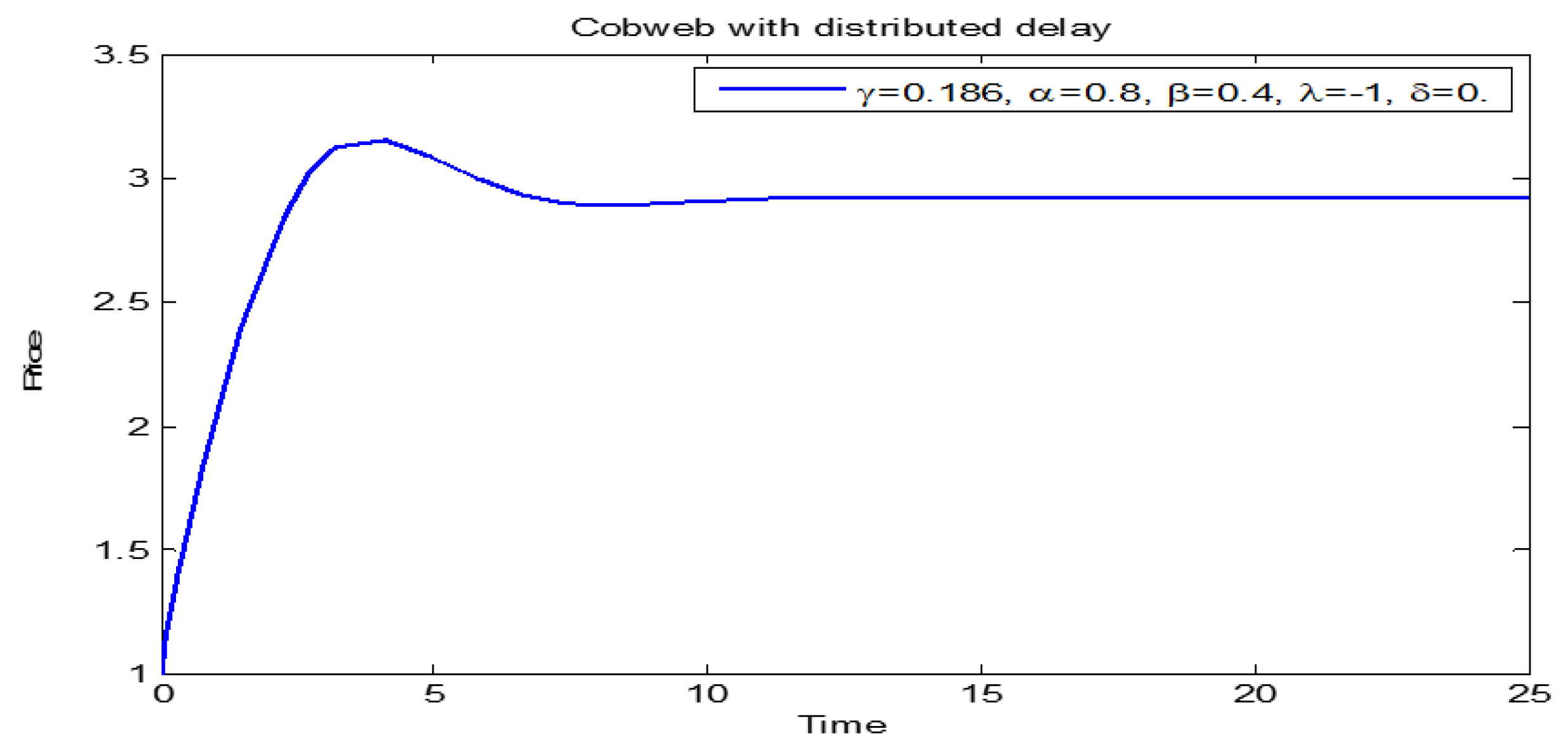
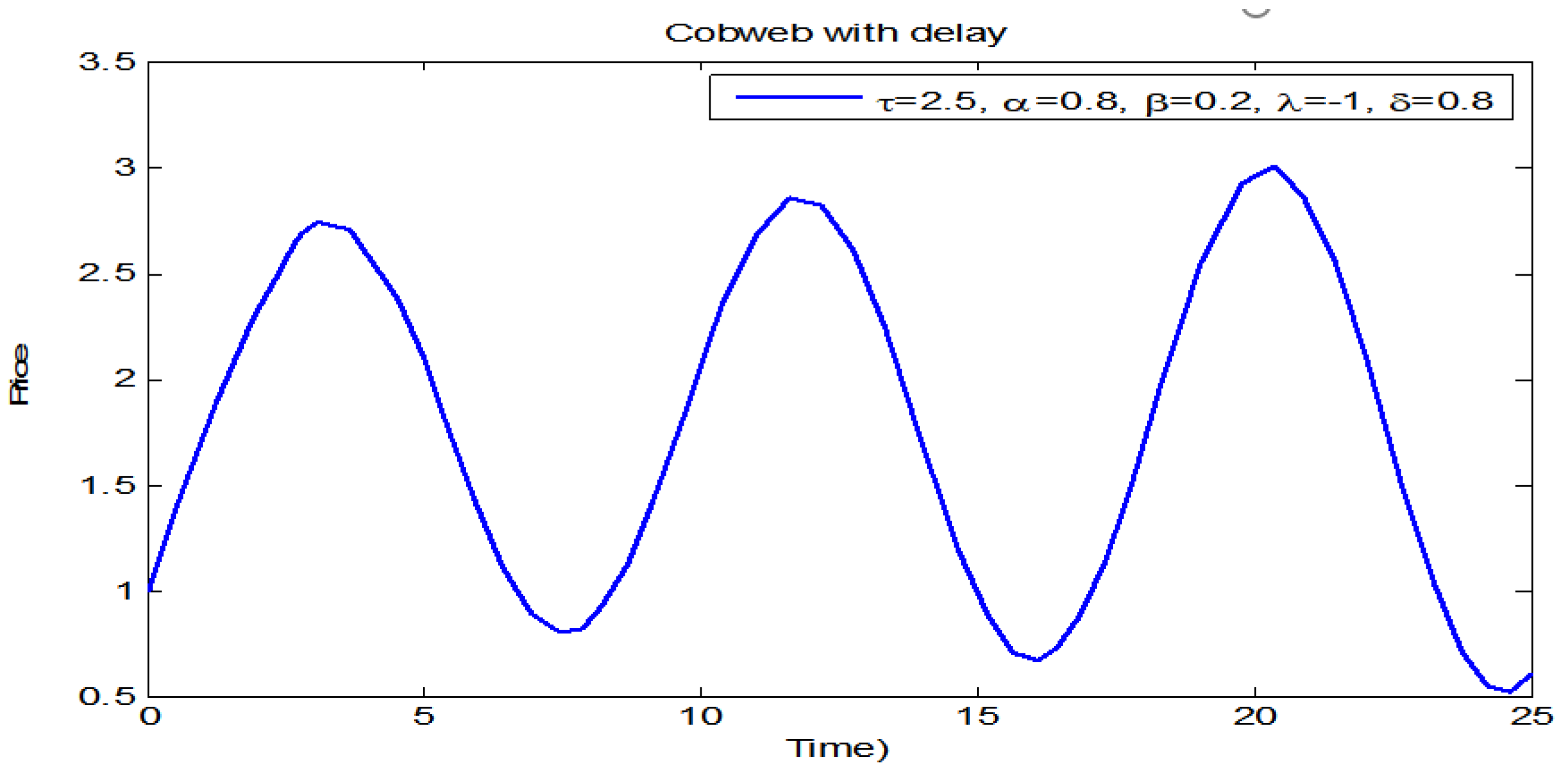
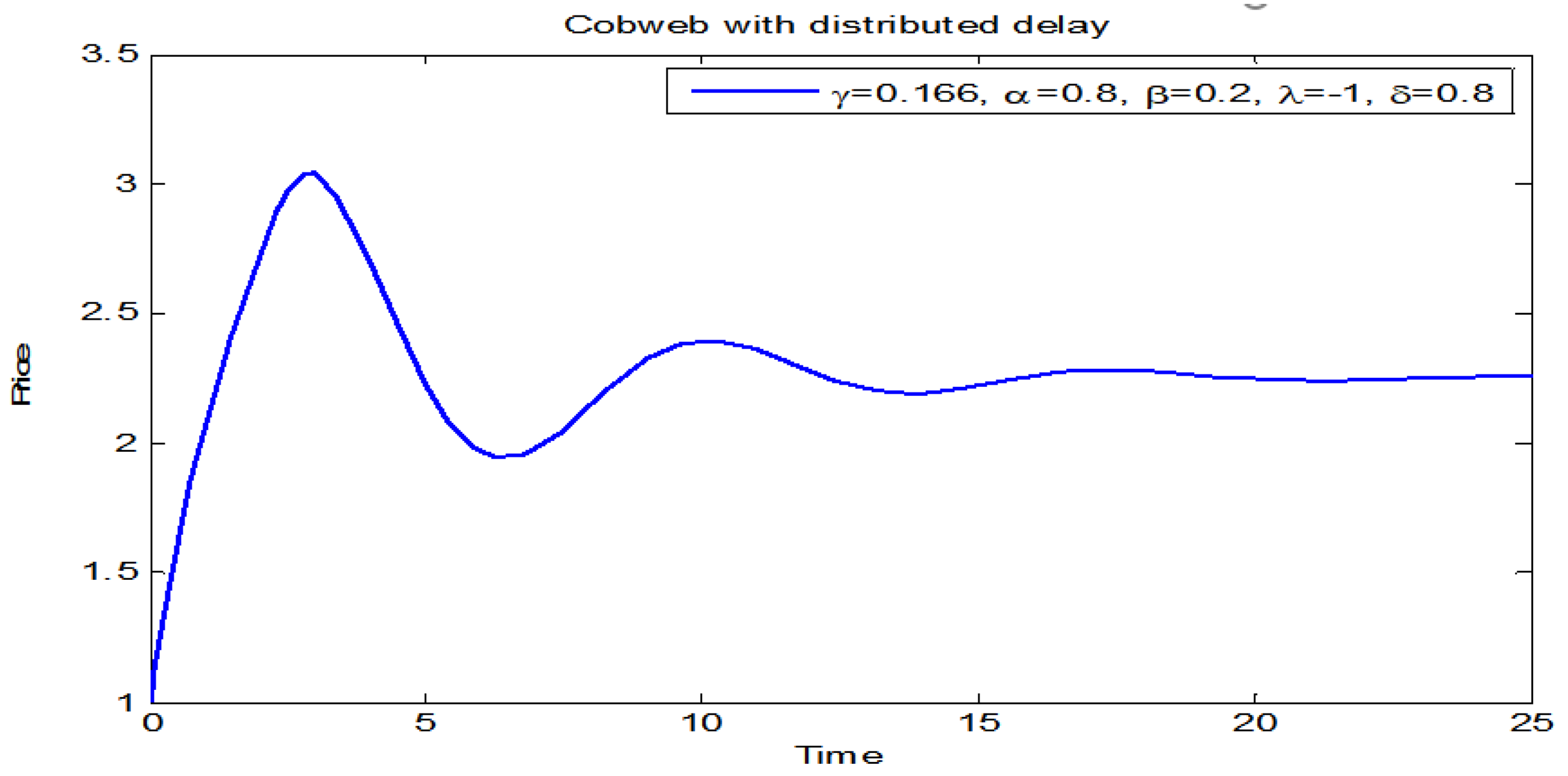
3. Numerical Simulations
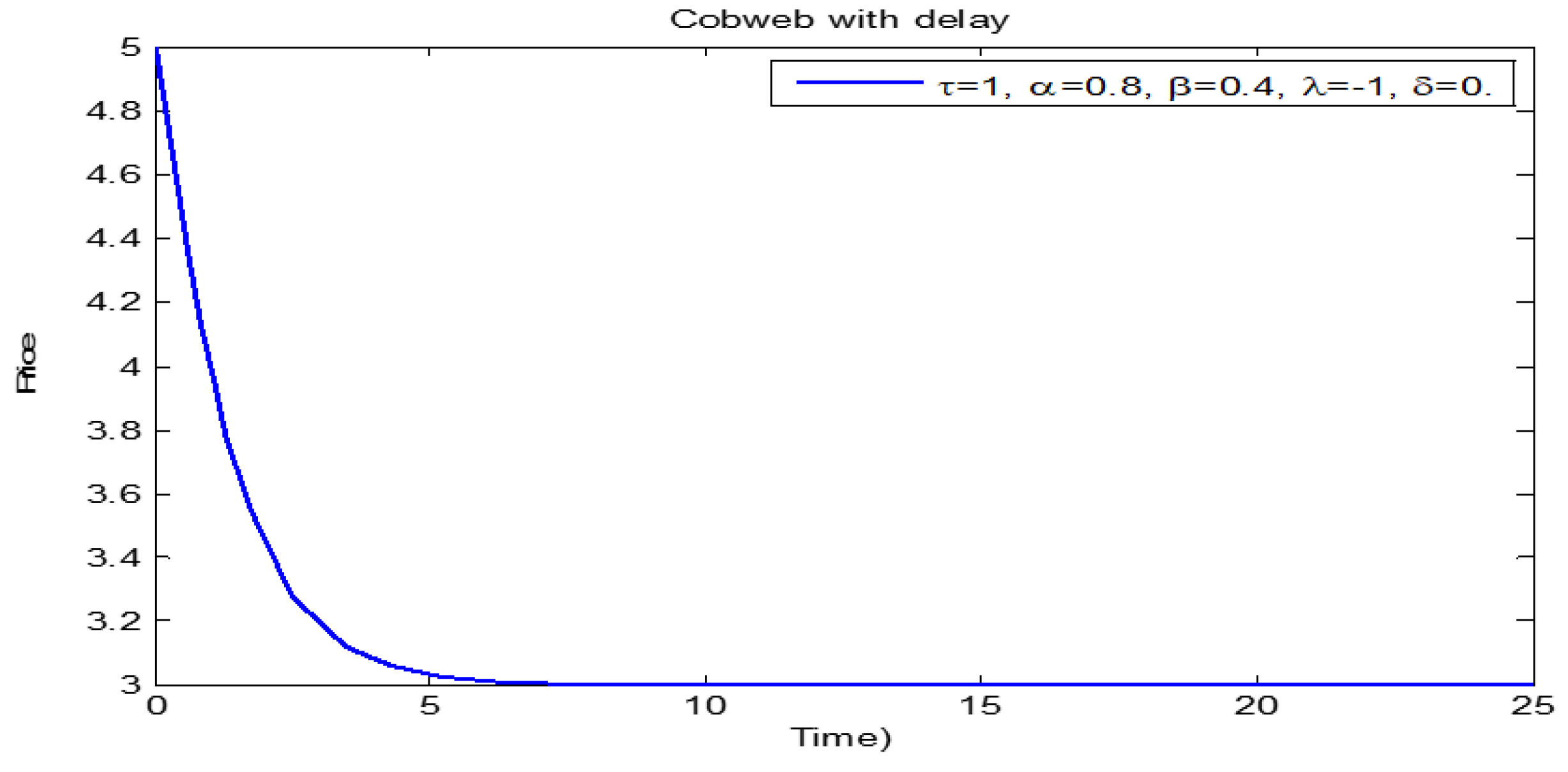
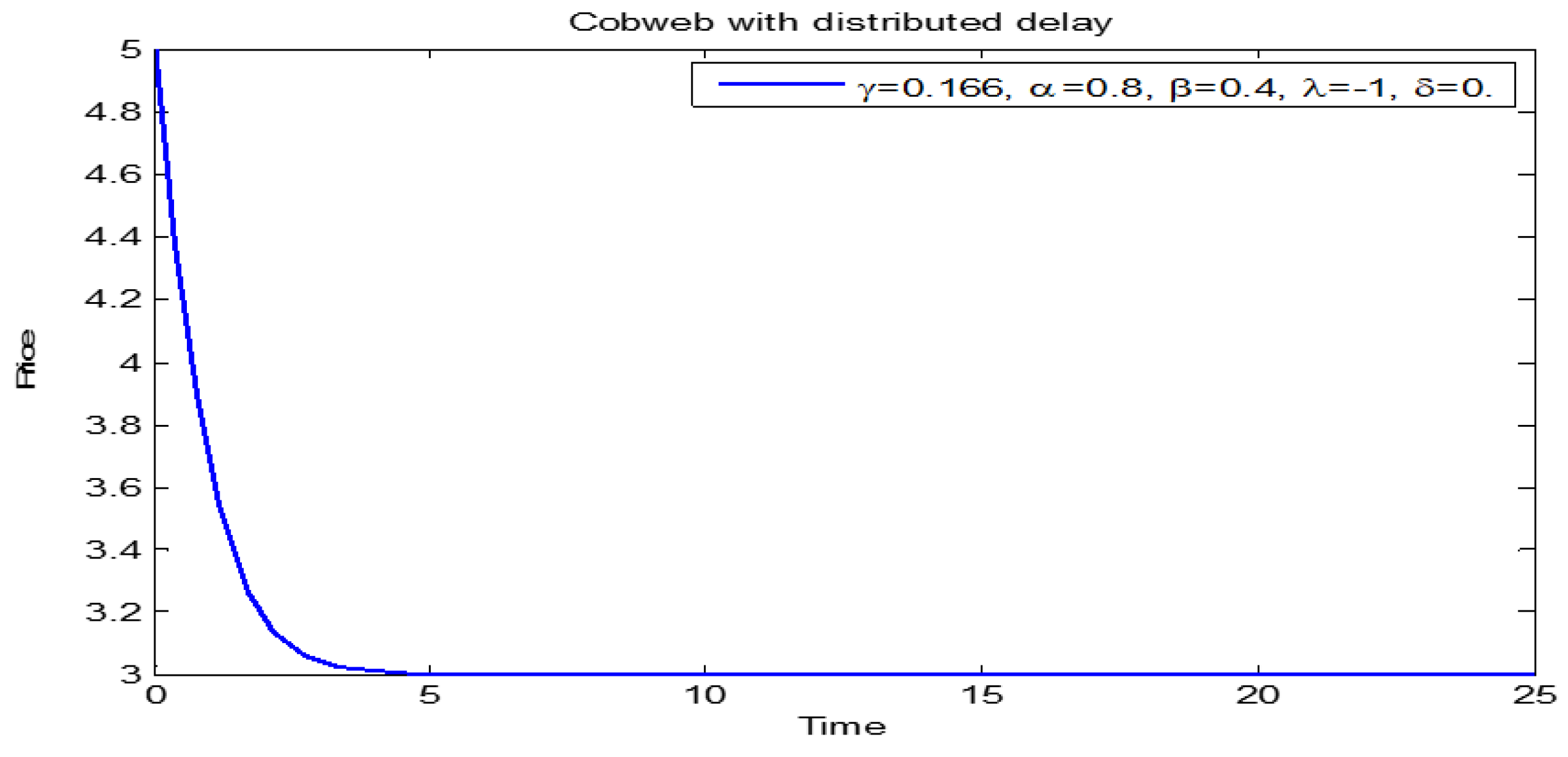
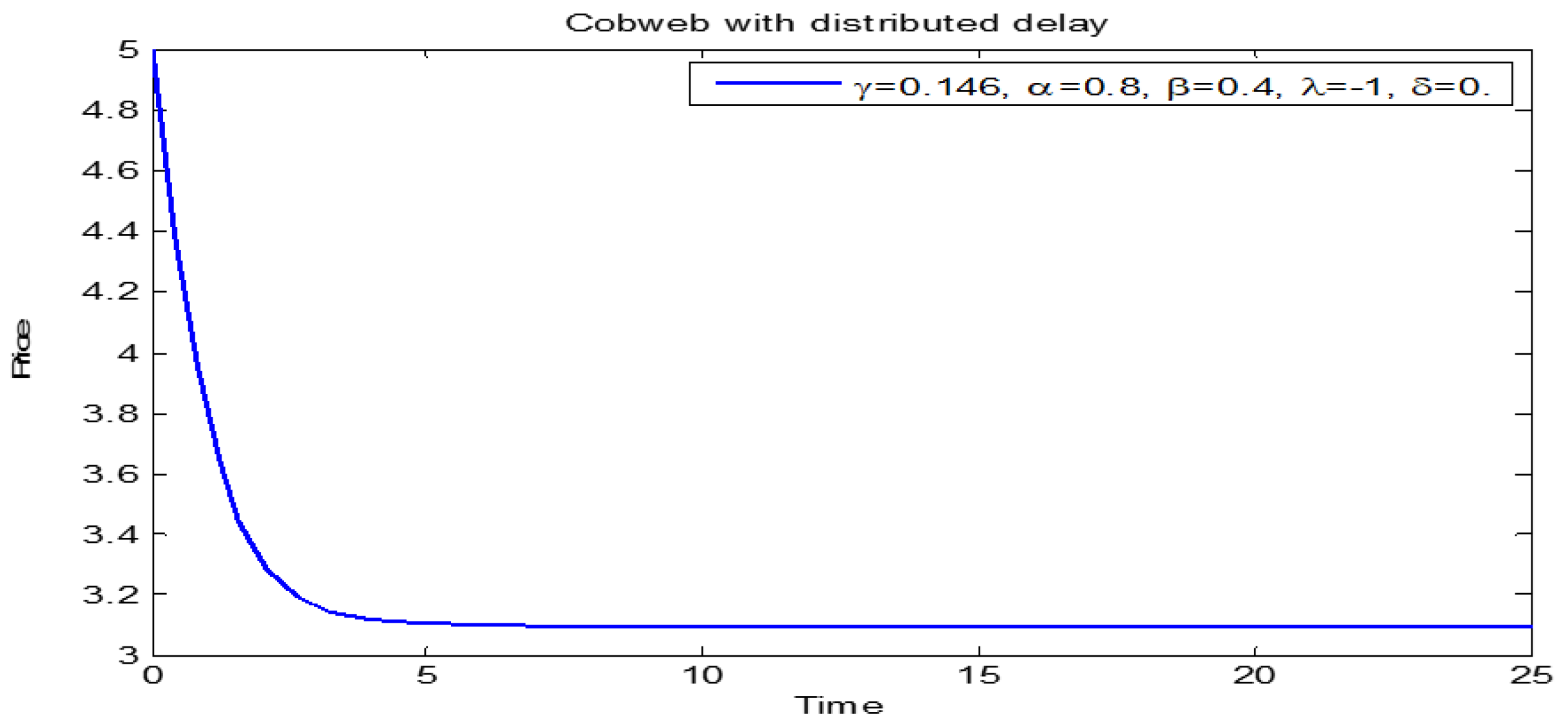
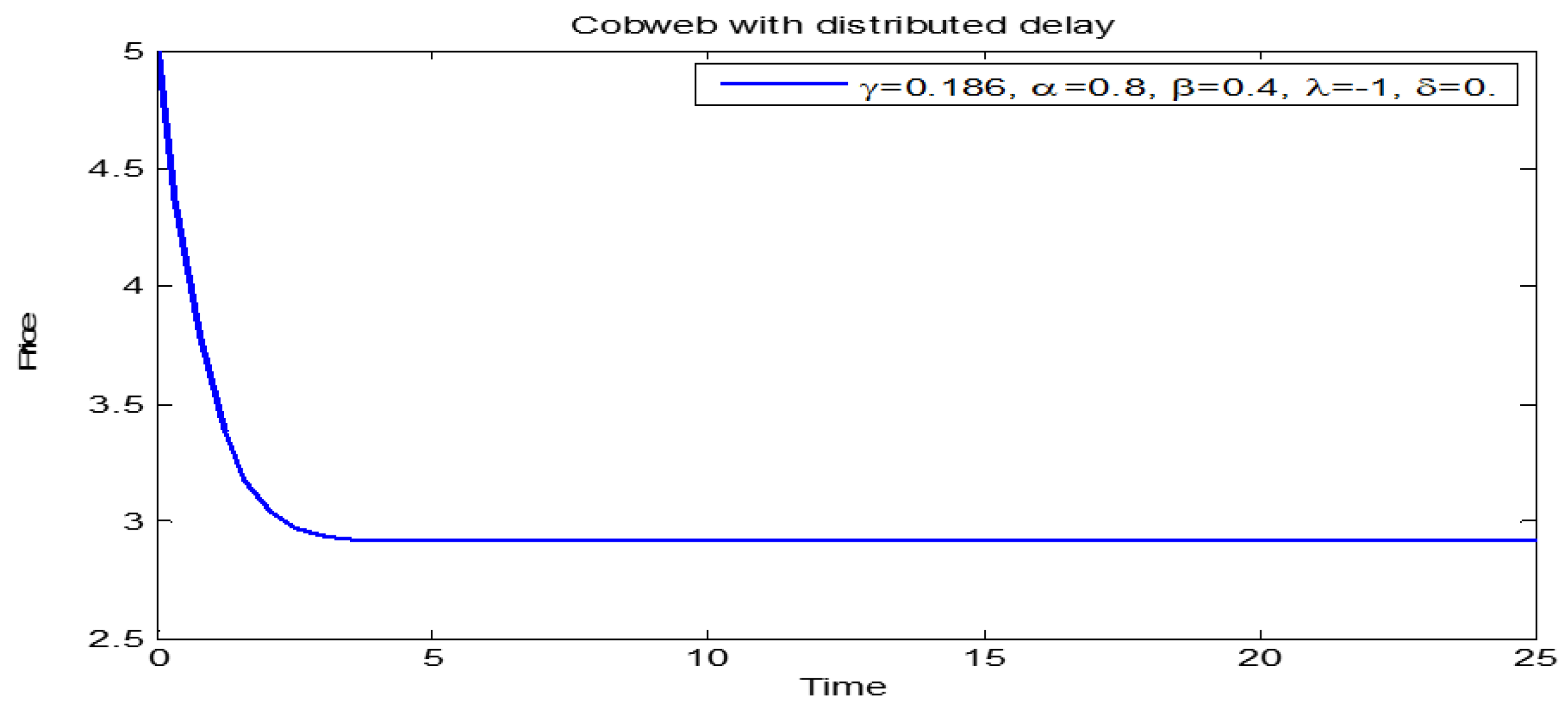
3.1. Price Dynamics of Models (1) and (2)
3.2. Dynamics of Initial Price below the Equilibrium Price
3.3. Dynamics of Initial Price below the Equilibrium Price
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, C.; Bohner, M.; Baoguo, J. Caputo fractional continuous cobweb models. J. Comput. Appl. Math. 2020, 374, 112734. [Google Scholar] [CrossRef]
- Brianzoni, S.; Mammana, C.; Michetti, E.; Zirilli, F. A stochastic cobweb dynamical model. Discrete Dyn. Nat. Soc. 2008, 18, 219653. [Google Scholar] [CrossRef]
- Nerlove, M. Adaptive expectations and cobweb phenomena. Q. J. Econ. 1958, 72, 227–240. [Google Scholar] [CrossRef]
- Muth, J.F. Rational expectations and the theory of price movements. Econometrica 1961, 29, 315–335. [Google Scholar] [CrossRef]
- Hommes, C.H. Adaptive learning and roads to chaos: The case of the cobweb. Econom. Lett. 1991, 36, 127–132. [Google Scholar] [CrossRef]
- Hommes, C.H. Cobwebs, chaos and bifurcations. Ann. Oper. Res. 1992, 37, 97–100. [Google Scholar] [CrossRef]
- Gaffney, J.M.; Pearce, C.E.M. Nonlinear-cobweb dynamics in the approach to equilibrium. ANZIAM J. 2004, 46, 79–83. [Google Scholar] [CrossRef]
- Ezekiel, M. The cobweb Theorem. Q. J. Econ. 1938, 52, 255–280. [Google Scholar] [CrossRef]
- Nagy, A.M.; Assidi, S.; Ben Makhlouf, A. Convergence of solutions for perturbed and unperturbed cobweb models with generalized Caputo derivative. Bound. Value Probl. 2022, 2022, 89. [Google Scholar] [CrossRef]
- Dufresne, D.; Vazquez-Abad, F. Cobweb theorems with production lags and price forecasting. Economics-Kiel 2013, 7, 20130023. [Google Scholar] [CrossRef]
- Eltayeb, H.; Abdeldaim, E. Sumudu decomposition method for solving fractiona delay differential equations. Res. Appl. Math. 2017, 1, 101268. [Google Scholar] [CrossRef]
- Ma, J.; Lingling, M. Complex dynamics in a nonlinear cobweb model for real estate market. Discrete Dyn. Nat. Soc. 2007, 2007, 29207. [Google Scholar] [CrossRef]
- Matsumoto, A.; Szidarovszky, F. The asymptotic behavior in a nonlinear cobweb model with time delays. Discrete Dyn. Nat. Soc. 2015, 2015, 12574. [Google Scholar] [CrossRef]
- Gori, L.; Guerrini, L.; Sodini, M. Hopf bifurcation and stability crossing curves in a cobweb model with heterogeneous producers and time delays. Nonlinear Anal. Hybrid Syst. 2015, 18, 117–133. [Google Scholar] [CrossRef]
- Gori, L.; Guerrini, L.; Sodini, M. Equilibrium and disequilibrium dynamics in cobweb models with time delays. Int. J. Bifurc. Chaos 2015, 25, 1550088. [Google Scholar] [CrossRef]
- Gori, L.; Guerrini, L.; Sodini, M. Hopf bifurcation in a cobweb model with discrete time delays. Discrete Dyn. Nat. Soc. 2014, 37090. [Google Scholar] [CrossRef]
- Matsumoto, A.; Nakayama, K. Nonlinear cobweb model with time delays. Int. Conf. Model. Simul. Appl. Math. 2015, 402–406. [Google Scholar]
- Anokye, M.; Barnes, B.; Boateng, F.O.; Adom-Konadu, A.; Amoah-Mensah, J. Price dynamics of a delay differential Cobweb model. Discrete Dyn. Nat. Soc. 2023, 2023, 296562. [Google Scholar] [CrossRef]
- Miller, R.K. Asymptotic stability properties of linear Volterra integro-differential equations. J. Differ. Equ. 1971, 10, 485–506. [Google Scholar] [CrossRef]
- Kar, M. Pricing strategies in mobile telecommunications markets. Smart J. 2019, 5, 360–371. [Google Scholar] [CrossRef]
- Doldo, P.; Pender, J. A note on the interpretation of distributed delay equations. arXiv 2021, arXiv:2106.11413. [Google Scholar]
- Elaiw, A.M.; Al Agha, A.D. A reaction-diffusion model for oncolytic M1 virotherapy with distributed delays. Eur. Phys. J. Plus 2020, 135, 117. [Google Scholar] [CrossRef]
- Elowitz, M.B.; Levine, A.J.; Siggia, E.D.; Swain, P.S. Stochastic gene expression in a single cell. Science 2002, 297, 1183–1186. [Google Scholar] [CrossRef] [PubMed]
- Arjun, R.; Van Oudenaarden, A. Nature, nurture, or chance: Stochastic gene expression and its consequences. Cell 2008, 135, 216–226. [Google Scholar]
- McAdams, H.H.; Arkin, A. Stochastic mechanisms in gene expression. Proc. Natl. Acad. Sci. USA 1996, 94, 814–819. [Google Scholar] [CrossRef]
- Paulsson, J. Models of stochastic gene expression. Phys. Life Rev. 2005, 2, 157–175. [Google Scholar] [CrossRef]
- Sargood, A.; Gaffney, E.A.; Krause, A.L. Fixed and distributed gene expression time delays in reaction-diffusion systems. Bull. Math. Biol. 2022, 84, 98. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guerrini, L.; Anokye, M.; Sackitey, A.L.; Amoah-Mensah, J. Dynamics of a Price Adjustment Model with Distributed Delay. Mathematics 2024, 12, 3220. https://doi.org/10.3390/math12203220
Guerrini L, Anokye M, Sackitey AL, Amoah-Mensah J. Dynamics of a Price Adjustment Model with Distributed Delay. Mathematics. 2024; 12(20):3220. https://doi.org/10.3390/math12203220
Chicago/Turabian StyleGuerrini, Luca, Martin Anokye, Albert L. Sackitey, and John Amoah-Mensah. 2024. "Dynamics of a Price Adjustment Model with Distributed Delay" Mathematics 12, no. 20: 3220. https://doi.org/10.3390/math12203220
APA StyleGuerrini, L., Anokye, M., Sackitey, A. L., & Amoah-Mensah, J. (2024). Dynamics of a Price Adjustment Model with Distributed Delay. Mathematics, 12(20), 3220. https://doi.org/10.3390/math12203220





