Combining Differential Equations with Stochastic for Economic Growth Models in Indonesia: A Comprehensive Literature Review
Abstract
1. Introduction
- What is the state of research on economic growth models using differential equations combined with stochastics?
- What is the state of research on economic growth models in Indonesia?
- What are the gaps in existing economic growth research?
2. Methods
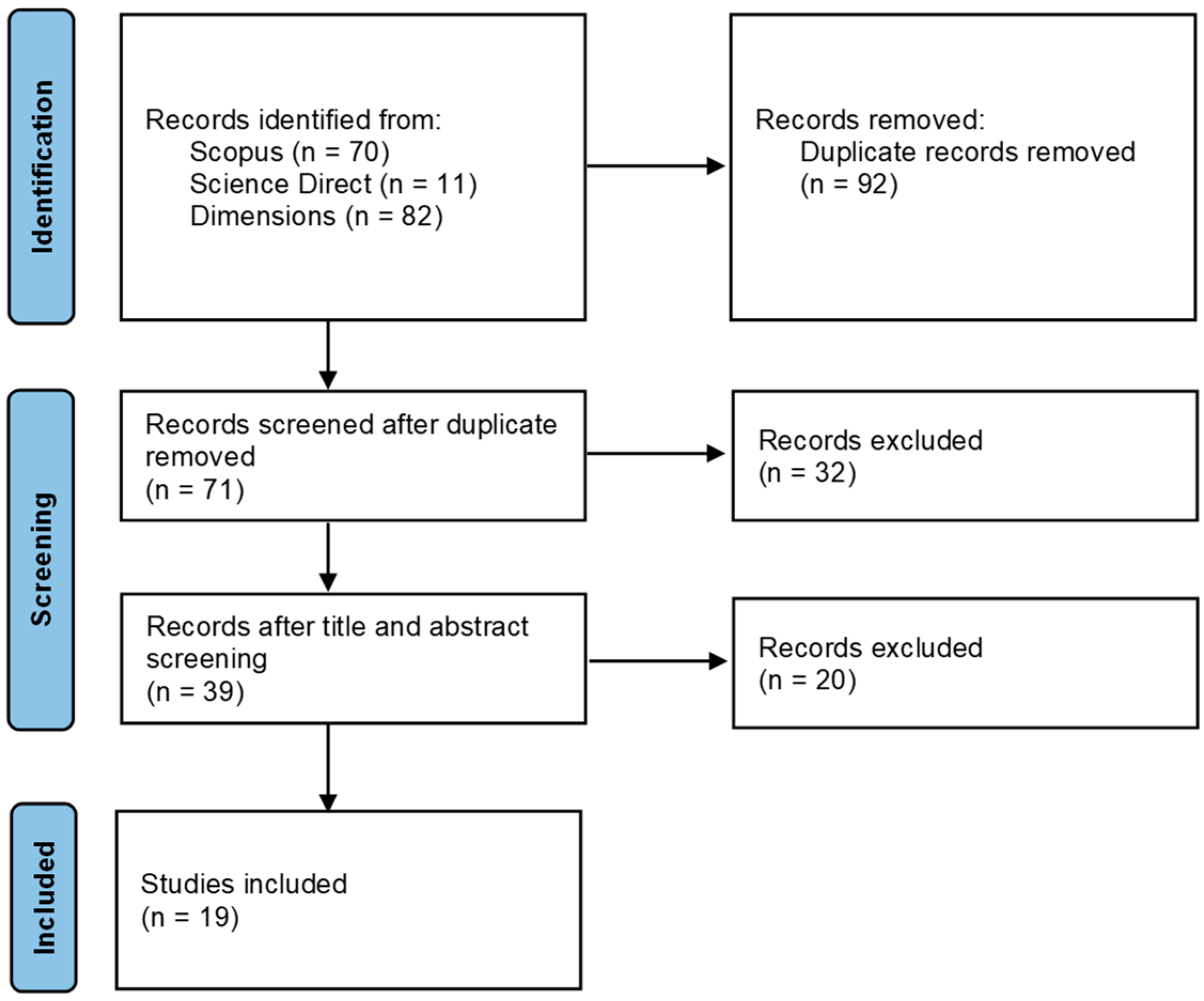
2.1. Article Collection
2.2. Selection Method
2.3. Bibliometric Analysis
3. Results
3.1. Results of Bibliometric Analysis
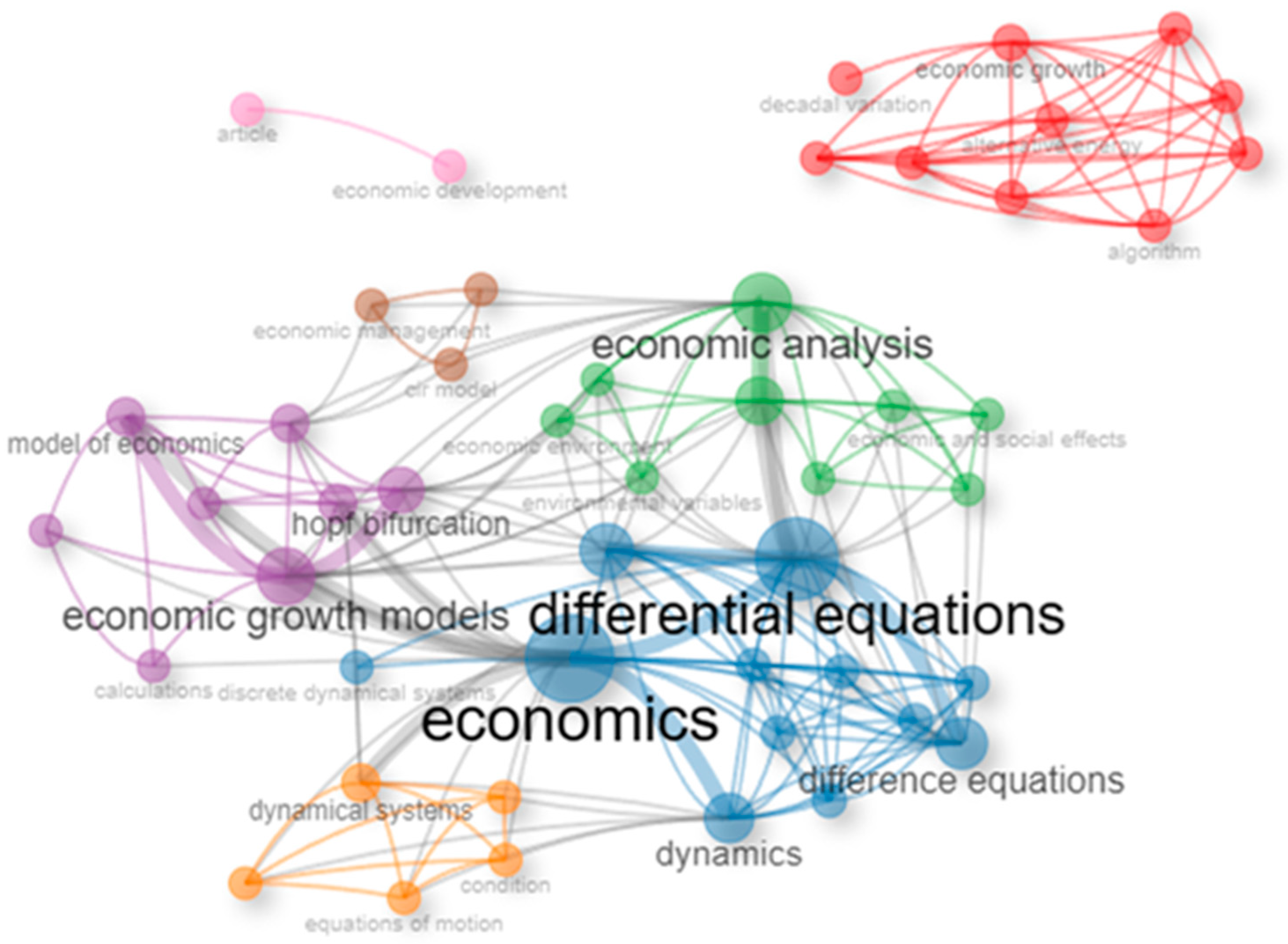
3.1.1. Co-Occurrence Network
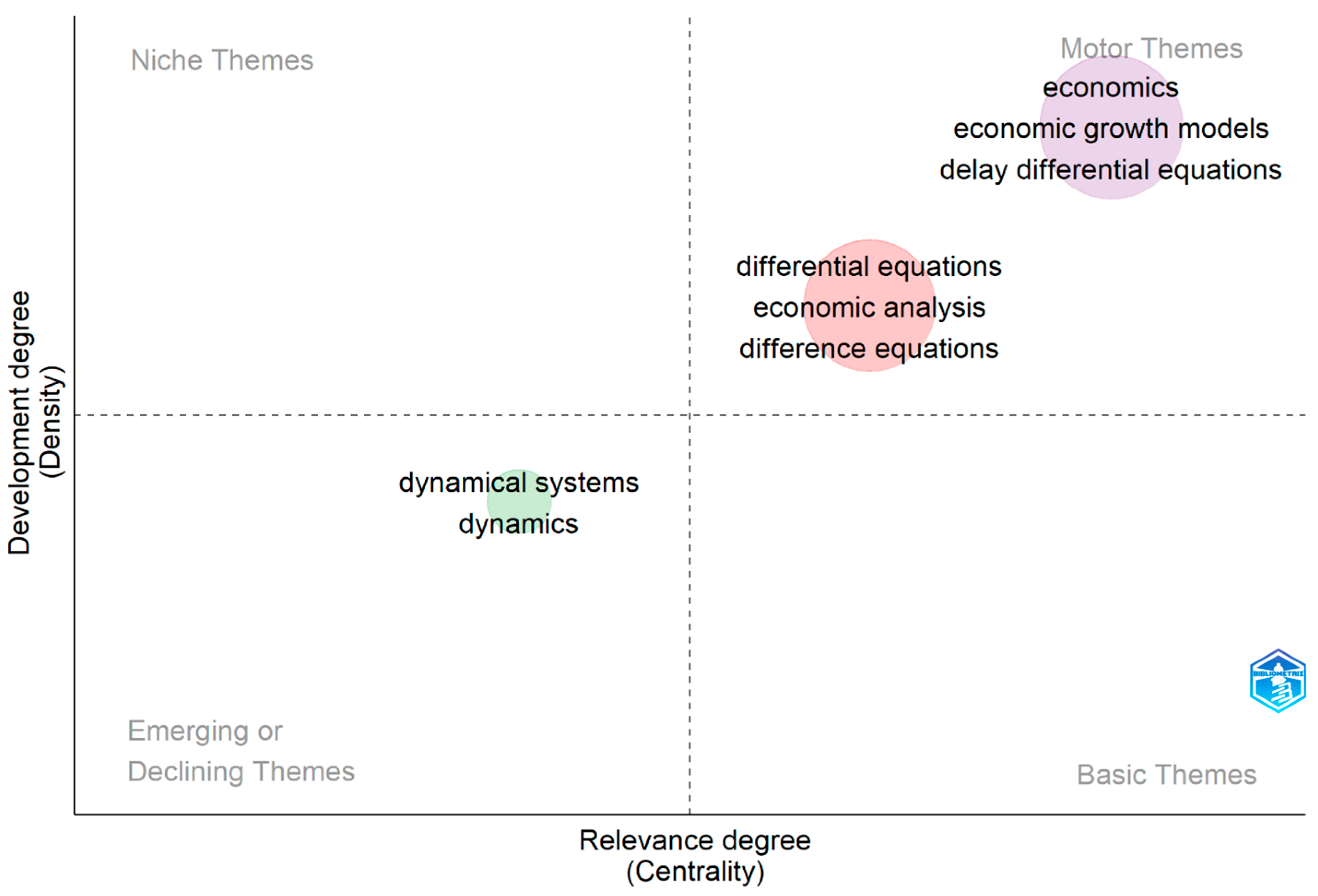
3.1.2. Thematic Mapping
3.2. Results of the Systematic Literature Review
4. Discussion
4.1. Development
- : land area ;
- : cultivation area ;
- : population (millions of people);
- total capital formation (billion);
- : exports of goods and services (billion);
- : general government final consumer spending (billions);
- : GDP (billion).
- GDP in 2010 in USD;
- : weight, constant over time, for each input variable ;
- : land area, measuring available natural resources;
- : population, measuring available human resources;
- : gross capital formation (GCF) in 2010 in USD, which measures the resources produced (this model takes into account the accumulation of resources produced);
- : exports of goods and services in 2010 in USD, which measures the external impact on the economy;
- : general government final consumption expenditure in 2010 in USD, which measures the impact of the budget on the economy.
4.2. Economic Growth Modeling in Indonesia
4.3. Research Gaps and Future Work
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mankiw, N.G. Principles of Microeconomics; Cengage Learning: Boston, MA, USA, 2020. [Google Scholar]
- Todaro, M.P.; Smith, S.C. Economic Development; Pearson: Harlow, UK, 2020. [Google Scholar]
- Barro, R.; Sala-i-Martin, X. Economic Growth, 2nd ed.; The MIT Press: Cambridge, MA, UK, 2024. [Google Scholar]
- Acemoglu, D. Introduction to Modern Economic Growth; Princeton University Press: Princeton, NJ, USA, 2008. [Google Scholar]
- Romer, P.M. Advanced Macroeconomics; Worth Publishers: Belper, UK, 2018. [Google Scholar]
- Solow, R.M. A contribution to the theory of economic growth. Q. J. Econ. 1956, 70, 65–94. [Google Scholar] [CrossRef]
- Wan, X. A literature review on the relationship between foreign direct investment and economic growth. Int. Bus. Res. 2010, 3, 52. [Google Scholar] [CrossRef][Green Version]
- Johnston, L.D. Lectures on Economic Growth. By Robert E. Lucas Jr. Cambridge, MA: Harvard University Press, 2002. pp. xi, 204. $49.95. J. Econ. Hist. 2022, 62, 915–916. [Google Scholar] [CrossRef]
- Yang, X.; Liu, Y.; Park, G.K. Parameter estimation of uncertain differential equation with application to financial market. Chaos Solitons Fractals 2020, 139, 110026. [Google Scholar] [CrossRef]
- Sng, H.Y.; Rahman, S.; Chia, W.M. Economic Growth and Transition: A Stochastic Technological Diffusion Model. J. Econ. Dev. 2009, 34, 1. [Google Scholar] [CrossRef]
- Craigmile, P.; Herbei, R.; Liu, G.; Schneider, G. Statistical inference for stochastic differential equations. Wiley Interdiscip. Rev. Comput. Stat. 2023, 15, e1585. [Google Scholar] [CrossRef]
- Breda, D.; Canci, J.K.; D’Ambrosio, R. An Invitation to Stochastic Differential Equations in Healthcare. In Quantitative Models in Life Science Business: From Value Creation to Business Processes; Springer International Publishing: Cham, Switzerland, 2022; pp. 97–110. [Google Scholar]
- Hagenimana, E.; Uwiliniyimana, C.; Umuraza, C. A study on7 stochastic differential equation using fractional power of operator in the semigroup theory. J. Appl. Math. Phys. 2023, 11, 1634–1655. [Google Scholar] [CrossRef]
- Merton, R.C. Theory of rational option pricing. Bell J. Econ. Manag. Sci. 1973, 4, 141–183. [Google Scholar] [CrossRef]
- Black, F.; Scholes, M. The pricing of options and corporate liabilities. J. Political Econ. 1973, 81, 637–654. [Google Scholar] [CrossRef]
- Kloeden, P.E.; Platen, E. Numerical Solution of Stochastic Differential Equations; Springer: Berlin/Heidelberg, Germany, 1992. [Google Scholar]
- Tranfield, D.; Denyer, D.; Smart, P. Towards a methodology for developing evidence-informed management knowledge by means of systematic review. Br. J. Manag. 2003, 14, 207–222. [Google Scholar] [CrossRef]
- Page, M.J.; Moher, D.; McKenzie, J.E. Introduction to PRISMA 2020 and implications for research synthesis methodologists. Res. Synth. Methods 2022, 13, 156–163. [Google Scholar] [CrossRef] [PubMed]
- Rethlefsen, M.L.; Kirtley, S.; Waffenschmidt, S.; Ayala, A.P.; Moher, D.; Page, M.J.; Koffel, J.B. PRISMA-S: An extension to the PRISMA statement for reporting literature searches in systematic reviews. Syst. Rev. 2021, 10, 39. [Google Scholar] [CrossRef] [PubMed]
- Derviş, H. Bibliometric analysis using bibliometrix an R package. J. Scientometr. Res. 2019, 8, 156–160. [Google Scholar] [CrossRef]
- Rusliana, N.; Komaludin, A.; Firmansyah, M.F. A scientometric analysis of urban economic development: R bibliometrix biblioshiny application. J. Ekon. Pembang. 2022, 11, 80–94. [Google Scholar] [CrossRef]
- Garfield, E.; Sher, I.H. Brief Communication Keywords PlusAlgorithmic Derivative Indexing. J. Am. Soc. Inf. Sci. 1993, 44, 298. [Google Scholar] [CrossRef]
- Zhang, J.; Yu, Q.; Zheng, F.; Long, C.; Lu, Z.; Duan, Z. Comparing keywords plus of WOS and author keywords: A case study of patient adherence research. J. Assoc. Inf. Sci. Technol. 2016, 67, 967–972. [Google Scholar] [CrossRef]
- Mariani, M.C.; Asante, P.K.; Tweneboah, O.K.; Kubin, W. A 3-component superposed Ornstein-Uhlenbeck model applied to financial stock markets. Res. Math. 2022, 9, 2024339. [Google Scholar] [CrossRef]
- Ewald, C.O.; Nolan, C. On the adaptation of the Lagrange formalism to continuous time stochastic optimal control: A Lagrange-Chow redux. J. Econ. Dyn. Control 2024, 162, 104855. [Google Scholar] [CrossRef]
- Hu, H. Asymptotic Behaviors Analysis of the Spatial AK Model with Trade Costs. Theor. Econ. Lett. 2021, 11, 603–614. [Google Scholar] [CrossRef]
- Johansyah, M.D.; Supriatna, A.K.; Rusyaman, E.; Saputra, J. Solving the economic growth acceleration model with memory effects: An application of combined theorem of Adomian decomposition methods and Kashuri–Fundo transformation methods. Symmetry 2022, 14, 192. [Google Scholar] [CrossRef]
- Johansyah, M.D.; Supriatna, A.K.; Rusyaman, E.; Saputra, J. The Existence and Uniqueness of Riccati Fractional Differential Equation Solution and Its Approximation Applied to an Economic Growth Model. Mathematics 2022, 10, 3029. [Google Scholar] [CrossRef]
- Khan, N.A.; Razzaq, O.A.; Riaz, F.; Ahmadian, A.; Senu, N. Dynamics of fractional order nonlinear system: A realistic perception with neutrosophic fuzzy number and Allee effect. J. Adv. Res. 2021, 32, 109–118. [Google Scholar] [CrossRef] [PubMed]
- Polat, G.G.; Özer, T. On group analysis of optimal control problems in economic growth models. Discret. Contin. Dyn. Syst.-Ser. S 2020, 13, 2853–2876. [Google Scholar]
- Polat, G.; Özer, T. On Ramsey Dynamical Model and Closed-Form Solutions. J. Nonlinear Math. Phys. 2021, 28, 209–218. [Google Scholar] [CrossRef]
- Tarasov, V.E.; Tarasova, V.V. Dynamic Keynesian model of economic growth with memory and lag. Mathematics 2019, 7, 178. [Google Scholar] [CrossRef]
- Tarasov, V.E. Non-linear macroeconomic models of growth with memory. Mathematics 2020, 8, 2078. [Google Scholar] [CrossRef]
- Traore, A.; Sene, N. Model of economic growth in the context of fractional derivative. Alex. Eng. J. 2020, 59, 4843–4850. [Google Scholar] [CrossRef]
- Zhang, W.B. Banking and Money in an Extended Solow-Uzawa’s Neoclassical Growth Model. Stud. Bus. Econ. 2021, 16, 221–243. [Google Scholar] [CrossRef]
- Chen, Q.; Kumar, P.; Baskonus, H.M. Modeling and analysis of demand-supply dynamics with a collectability factor using delay differential equations in economic growth via the Caputo operator. AIMS Math. 2024, 9, 7471–7491. [Google Scholar] [CrossRef]
- Akaev, A. Nonlinear differential equation of macroeconomic dynamics for long-term forecasting of economic development. Appl. Math. 2018, 9, 512–535. [Google Scholar] [CrossRef]
- Buedo-Fernández, S.; Liz, E. On the stability properties of a delay differential neoclassical model of economic growth. Electron. J. Qual. Theory Differ. Equ. 2018, 2018, 1–14. [Google Scholar] [CrossRef]
- Burgess, M.G.; Langendorf, R.E.; Moyer, J.D.; Dancer, A.; Hughes, B.B.; Tilman, D. Multidecadal dynamics project slow 21st-century economic growth and income convergence. Commun. Earth Environ. 2023, 4, 220. [Google Scholar] [CrossRef]
- González-Parra, G.; Chen-Charpentier, B.; Arenas, A.J.; Díaz-Rodríguez, M. Mathematical modeling of physical capital diffusion using a spatial solow model: Application to smuggling in Venezuela. Economies 2022, 10, 164. [Google Scholar] [CrossRef]
- Ming, H.; Wang, J.; Fečkan, M. The application of fractional calculus in Chinese economic growth models. Mathematics 2019, 7, 665. [Google Scholar] [CrossRef]
- Tejado, I.; Pérez, E.; Valério, D. Fractional derivatives for economic growth modelling of the group of twenty: Application to prediction. Mathematics 2020, 8, 50. [Google Scholar] [CrossRef]
- Combes, P.P.; Mayer, T.; Thisse, J.F.E.G. The integration of Regions and Nations. Econ. Geogr. 2010, 10, 255–275. [Google Scholar]
- Annannab, H.; Surajo, A.Z.; Ahmad, F. Coal consumption and economic growth in Indonesia: An analysis of restricted structural var. Econ. Bus. Account. Soc. Rev. 2022, 1, 96–103. [Google Scholar]
- Alim, M.B. Impact of Taxes and Technological Improvement for Economic Growth: English. Tamansiswa Account. J. Int. 2022, 4, 72–77. [Google Scholar] [CrossRef]
- Chandra, K.; Sari, W.R.; Sriwulan, D.Y.; Adhimukti, M.R. Effect of Yield Spreads (State Bonds) on Economic Growth Performance in Indonesia. J. Risk Financ. Manag. 2023, 16, 175. [Google Scholar] [CrossRef]
- Harnani, S.; Widarni, E.L.; Bawono, S. The The Role of Human Capital in Natural Sustainability and Economic Growth in Indonesia a Dynamic ARDL Approach: English. Tamansiswa Account. J. Int. 2022, 5, 28–35. [Google Scholar] [CrossRef]
- Abdillah, K. Optimum government size and economic growth in Indonesia: ARDL model approach. Ekuilibrium J. Ilm. Bid. Ilmu Ekon. 2023, 18, 37–47. [Google Scholar] [CrossRef]
- Ajnura, U.; Juliansyah, H. The Effect of Fluctuation World Oil Prices and the Rupiah Exchange Rate on Economic Growth in Indonesia. J. Malikussaleh Public Econ. 2021, 4, 38–44. [Google Scholar] [CrossRef]
- Pertiwi, A.B.; Juwita, A.H.; Suryanto, S. Effects of Poverty, Income Inequality and Economic Growth to Environmental Quality Index (EQI) in 33 Province in Indonesia 2014–2019. Ekuilibrium J. Ilm. Bid. Ilmu Ekon. 2021, 16, 154–163. [Google Scholar] [CrossRef]
- Elfaki, K.E.; Handoyo, R.D.; Ibrahim, K.H. The impact of industrialization, trade openness, financial development, and energy consumption on economic growth in Indonesia. Economies 2021, 9, 174. [Google Scholar] [CrossRef]
- Rhamadhani, R.F.; Fanani, A. Optimizing the Role of Indonesia’s Islamic Financial Industry: Empirical Analysis of Its Impact on Economic Growth. JEKSYAH Islam. Econ. J. 2023, 3, 11–22. [Google Scholar] [CrossRef]
- Elfaki, K.E.; Heriqbaldi, U. Analyzing the Moderating Role of Industrialization on the Environmental Kuznets Curve (EKC) in Indonesia: What Are the Contributions of Financial Development, Energy Consumption, and Economic Growth? Sustainability 2023, 15, 4270. [Google Scholar] [CrossRef]
- Djulius, H. Foreign Direct Investment or External Debt and Domestic Saving: Which has Greater Impacts on Growth. Etikonomi 2018, 17, 37–44. [Google Scholar] [CrossRef]
- Duja, B.; Supriyanto, H. The influence of GDP, interest rate, wage, inflation and exchange rate on residential property price in Indonesia. Plan. Malays. 2019, 17, 389–400. [Google Scholar] [CrossRef]
- Fadli, F.; Hongbing, O.; Liu, Y. Earmarking Tax for Indonesia’s Economic Growth through the Education and Health Sector in the Long and Short Term Period. Bus. Econ. Res. 2020, 10, 1–39. [Google Scholar] [CrossRef]
- Fitriami, R.; Masbar, R.; Miksalmina, M. The Impact of Foreign Trade Policy on Economic Growth of Aceh Province, Indonesia. Int. J. Financ. Econ. Bus. 2020, 1, 109–117. [Google Scholar] [CrossRef]
- Prabowo, B.H.; Drean, B. Green Finance and Green Economic Trade Off Economic and Environtment in Indonesia: English. ASIAN Econ. Bus. Dev. 2022, 4, 7–13. [Google Scholar] [CrossRef]
- Adzimatinur, F.; Gloriman Manalu, V. The Effect of islamic financial inclusion on economic growth: A case study of islamic banking in indonesia. Bp. Int. Res. Crit. Inst.-J. 2021, 4, 976–985. [Google Scholar] [CrossRef]
- Agusalim, L.; Pohan, F.S. Trade openness effect on income inequality: Empirical evidence from Indonesia. Signifikan 2018, 7, 1–14. [Google Scholar] [CrossRef]
- Anggoro, A.C.P. Effect of Exports, Imports of Oil and Gas Products, Inflation, on Economic Growth. Curr. Adv. Res. Sharia Financ. Econ. Worldw. 2022, 2, 148–163. [Google Scholar] [CrossRef]
- Bashir, A.; Thamrin, K.M.; Farhan, M.; Atiyatna, D.P. The causality between human capital, energy consumption, CO2 emissions, and economic growth: Empirical evidence from Indonesia. Int. J. Energy Econ. Policy 2019, 9, 98–104. [Google Scholar]
- Firdaus, E.N.; Septiani, Y. Effect analysis of inflation, exports and imports on economic growth in Indonesia. J. Humanit. Soc. Sci. Bus. 2022, 2, 32–46. [Google Scholar] [CrossRef]
- Rao, T.S.; Rao, S.S.; Rao, C.R. (Eds.) Time Series Analysis: Methods and Applications; Elsevier: Amsterdam, The Netherlands, 2012; Volume 30. [Google Scholar]
- Mills, T.C. Time Series Econometrics: A Concise Introduction; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Afandi, M.A.; Amin, M. Islamic bank financing and its effects on economic growth: A cross province analysis. Signifikan J. Ilmu Ekon. 2019, 8, 243–250. [Google Scholar] [CrossRef]
- Asmarani, T.E.; Ningsih, E.A. Domestic credit and stock market impact on economic growth: A new evidence in Five asean countries. Winners 2022, 23, 95–102. [Google Scholar] [CrossRef]
- Azizurrohman, M.; Hartarto, R.B.; Lin, Y.M.; Nahar, F.H. The Role of Foreign Tourists in Economic Growth: Evidence from Indonesia. J. Ekon. Studi Pembang. 2021, 22, 313–322. [Google Scholar] [CrossRef]
- Gati, S.A. The Effect of Telecommunications Infrastructure on Inclusive Economic Growth in Indonesia 2011−2021. Int. J. Innov. Technol. Soc. Sci. 2023, 2, 1–12. [Google Scholar]
- Asnawi, A.; Irfan, I.; Ramadhani, M.F.C. The Gap in Economic Growth from Foreign Investment and Domestic Investment across Provinces in Indonesia. Electron. J. Educ. Soc. Econ. Technol. 2020, 1, 34–38. [Google Scholar] [CrossRef]
- Bechtel, G.G. Panel regression of arbitrarily distributed responses. J. Data Sci. 2009, 7, 255–266. [Google Scholar] [CrossRef]
- Gonzales, J.T. Implications of AI innovation on economic growth: A panel data study. J. Econ. Struct. 2023, 12, 13. [Google Scholar] [CrossRef]
- Al Shams, T.M.; Ashraf, A. Macroeconomic Indicators of Economic Growth using Panel Data: A Study from South Asian Countries. ABC Res. Alert 2023, 11, 9–20. [Google Scholar] [CrossRef]
- Amaluddin, A. THE The Nexus Between Poverty, Education and Economic Growth in Indonesia. Econ. Dev. Anal. J. 2019, 8, 345–354. [Google Scholar] [CrossRef]
- Erlando, A.; Riyanto, F.D.; Masakazu, S. Financial inclusion, economic growth, and poverty alleviation: Evidence from eastern Indonesia. Heliyon 2020, 6, e05235. [Google Scholar] [CrossRef]
- Gao, J.; Peng, B.; Yan, Y. Time-Varying Vector Error-Correction Models: Estimation and Inference. arXiv 2023, arXiv:2305.17829. [Google Scholar] [CrossRef]

| Code | Keyword Combination |
|---|---|
| A | “differential equation” AND “economic growth” |
| B | “ordinary differential equation” AND “economic growth” |
| C | “partial differential equation” AND “economic growth” |
| D | (“fractional differential” OR “fractional calculus”) AND “economic growth” |
| E | “differential equation” AND “stochastic” AND “economic growth” |
| F | “differential equation” AND “economic growth” AND “Indonesia” |
| Code | Scopus | Science Direct | Dimensions | Total |
|---|---|---|---|---|
| A | 42 | 4 | 52 | 98 |
| B | 6 | 1 | 7 | 14 |
| C | 7 | 1 | 9 | 17 |
| D | 13 | 4 | 13 | 30 |
| E | 2 | 1 | 1 | 4 |
| F | 0 | 0 | 0 | 0 |
| Total | 70 | 11 | 82 | 163 |
| Code | Total | Duplication | Abstract and Title | Full Text | |||
|---|---|---|---|---|---|---|---|
| Excluded | Included | Excluded | Included | Excluded | Included | ||
| A | 98 | 61 | 37 | 17 | 20 | 11 | 9 |
| B | 14 | 11 | 3 | 1 | 2 | 2 | 0 |
| C | 17 | 2 | 15 | 7 | 8 | 4 | 4 |
| D | 30 | 17 | 13 | 7 | 6 | 2 | 4 |
| E | 4 | 1 | 3 | 0 | 3 | 1 | 2 |
| F | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Total | 163 | 92 | 71 | 32 | 39 1 | 20 | 19 2 |
| Author(s) | Research Objectives | Model |
|---|---|---|
| [24] | Developing a complete numerical approach to estimate parameters and level weights for the OU Superposed model | Superposed Ornstein–Uhlenbeck model |
| [25] | Extending the classical Lagrangian approach to solving continuous-time stochastic optimal control problems | Continuous stochastic optimal control model |
| Author(s) | Research Objectives | Model |
|---|---|---|
| [26] | Finding non-negative classical solutions of partial differential equations describing the dynamics of the capital stock. | Spatial AK growth model |
| [27] | Developing quadratic nonlinear cost functions in economic growth models and analyzing appropriate solutions. | Riccati fractional differential equation |
| [28] | Investigating nonlinear RFDE solutions with constant coefficients in economic growth models. | Riccati fractional differential equation |
| [29] | Measuring the dynamics of uncertainty in an economy by restructuring the Cobb–Douglas paradigm of the Solow–Swan model. | Cobb–Douglas paradigm of the Solow–Swan model |
| [30] | Building a Lie group-based approach to analyze optimal control problems in economic growth models. | Nonlinear fractional order single-valued triangular neutrosophic fuzzy differential equations |
| [31] | Analyzing the Ramsey dynamic model with a Hamiltonian optimal control problem in neoclassical growth models by utilizing Lie group theory. | Ramsey dynamical model with Hamiltonian |
| [32] | Building a mathematical model of economic growth influenced by memory and lag. | Fractional differential equation of a Keynesian model with memory and lag |
| [33] | Studying the influence of memory effects on economic growth rates. | Solow model of long-run growth with memory and Solow–Lucas model of a closed economy with memory |
| [34] | Revisiting the Ramsey economic model with fractional order. | Ramsey model represented by the fractional Caputo–Liouville derivative |
| [35] | Studying the relationship between growth and inflation using Taylor’s rule. | Solow–Tobin Model with Taylor rule |
| [36] | Investigating the dynamic interaction between supply and demand, with a focus on aggregation, through the introduction of a new mathematical model using the Caputo operator. | Demand–Supply Dynamic with a collectability factor using delay differential equations |
| Author(s) | Research Objectives | Model | Application |
|---|---|---|---|
| [37] | Construct a general differential equation that describes long-run economic growth in terms of cyclical and trend components. | Continuous RBC (real business cycles) model based on the nonlinear acceleration of induced investment model | Predictions of the dynamics of the United States economy. |
| [38] | Establish sharp global stability conditions to achieve positive equilibrium of the well-known economic growth model when production function delays are considered. | Solow–Swan model with variable delay | Constant saving ratio and no pollution effect; variable saving ratio and no pollution effect; constant saving ratio and pollution effect. |
| [39] | Describe a multidecadal pattern of per capita gross domestic product (GDP) growth that increases and then decreases as a region becomes richer. | Nonlinear differential equation model (DEM) | Calculate the IMF’s projected GDP and population growth rates, and calculate the projected GDP per capita growth rate. |
| [40] | Build an approach model for the diffusion of physical capital across national borders that explains the impact of smuggling on the economic growth of Venezuela or other countries facing similar conditions. | Spatial Solow Model | Economic growth of Venezuela. |
| [41] | Apply Caputo derivatives to simulate China’s gross domestic product (GDP) growth. | Integer Order Model (IOM) and Caputo Fractional Order Model (CFOM) | Forecasting China’s GDP. |
| [42] | Build an economic model for the Group of Twenty (G20) countries in the period of 1970–2018. | Keynesian models of the dynamics of economies | Economic growth model for the Group of Twenty (G20) countries. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Johansyah, M.D.; Rusyaman, E.; Foster, B.; Muslihin, K.R.A.; Supriatna, A.K. Combining Differential Equations with Stochastic for Economic Growth Models in Indonesia: A Comprehensive Literature Review. Mathematics 2024, 12, 3219. https://doi.org/10.3390/math12203219
Johansyah MD, Rusyaman E, Foster B, Muslihin KRA, Supriatna AK. Combining Differential Equations with Stochastic for Economic Growth Models in Indonesia: A Comprehensive Literature Review. Mathematics. 2024; 12(20):3219. https://doi.org/10.3390/math12203219
Chicago/Turabian StyleJohansyah, Muhamad Deni, Endang Rusyaman, Bob Foster, Khoirunnisa Rohadatul Aisy Muslihin, and Asep K. Supriatna. 2024. "Combining Differential Equations with Stochastic for Economic Growth Models in Indonesia: A Comprehensive Literature Review" Mathematics 12, no. 20: 3219. https://doi.org/10.3390/math12203219
APA StyleJohansyah, M. D., Rusyaman, E., Foster, B., Muslihin, K. R. A., & Supriatna, A. K. (2024). Combining Differential Equations with Stochastic for Economic Growth Models in Indonesia: A Comprehensive Literature Review. Mathematics, 12(20), 3219. https://doi.org/10.3390/math12203219







