Abstract
In this paper, we propose utilizing machine learning methods to determine the expected aggregated stock market risk premium based on online investor sentiment and employing the multifold forward-validation method to select the relevant hyperparameters. Our empirical studies provide strong evidence that some machine learning methods, such as extreme gradient boosting or random forest, show significant predictive ability in terms of their out-of-sample performances with high-dimensional investor sentiment proxies. They also outperform the traditional linear models, which shows a possible unobserved nonlinear relationship between online investor sentiment and risk premium. Moreover, this predictability based on online investor sentiment has a better economic value, so it improves portfolio performance for investors who need to decide the optimal asset allocation in terms of the certainty equivalent return gain and the Sharpe ratio.
Keywords:
asset return; machine learning; multifold forward-validation; nonlinearity; portfolio allocations; predictability MSC:
62F12; 62P20; 91B82; 91G15
1. Introduction
The comprehension and prediction of the dynamics of market equity risk premium still remain some of the most challenging and attractive problems for quantitative finance in academies and industries nowadays, although they have gained a lot of attention in recent decades. Since stock return can be predicted by some state variables that are able to capture the economic condition, as addressed in [1], the challenges of stock forecasting focus on two aspects, which are to explore those state variables potentially related to future risk premiums and to seek the functional structure mapping from state variables to future stock return.
Investor sentiment is a neoteric category of the candidates of state variables for forecasting in finance. Since investor sentiment cannot be directly observed, previous applications and analyses are conducted under a framework that abstracts an investor sentiment index constructed from a collection of observable sentiment proxies. Those proxies, such as online investor sentiment proxies, are commonly high-dimensional, due to the rich data used, as it is well known that internet users search for what they are concerned about or interested in, post their thoughts, and also receive other public information. The internet changes the way in which data are generated, spread, and recorded. Therefore, online data possibly reveal a clue about internet users’ actions or decision-making processes. Regarding financial markets, online data can also reveal investor sentiment and imply investors’ market operation. Meanwhile, surges in data, driven by the rapid growth of computation power, such as cloud computation techniques, and the decline in the access cost of computing, machine learning methods have been making notable progress and are widely incorporated for providing state-of-the-art solutions to predictive or descriptive applications in both industries and academies in applied fields. They have attractive features for forecasting market equity risk premiums with online investor sentiment, as machine learning methods are able to conduct the functions of processing high-dimensional sentiment proxies and fitting into unknown complex data generation processes of risk premiums, which traditional regression methods cannot perform well.
In this paper, we explore if there exist any machine learning methods which can process high-dimensional online investor sentiment proxies and capture the unknown relationship between investor sentiment and future aggregated stock return. Indeed, we apply four different architectures of supervised machine learning methods, which are a feedforward neural network (FNN), a recurrent neural network (RNN), a random forest (RF), and an extreme gradient boosting (XGBoost). A comparison is made for the incorporation performance of machine learning methods for stock return prediction based on online investor sentiment. The input variables we use are a collection of internet search query data, which are a set of frequencies of web searches on Google Trends for certain keywords. Such data are used as the proxies of online investor sentiment to indicate the state of the economy and to predict future stock risk premiums. For our empirical study, we have 170 proxies, which are changes in search volume indices (SVIs). The out-of-sample forecasting performance is measured by the out-of-sample , as defined in [2] and denoted by , the root mean squared error (RMSE), and the root mean squared logarithmic error (RMSLE). For comparison, we also apply traditional linear models, like the ordinary least squares (OLS), least absolute shrinkage and selection (LASSO), ridge, and elastic net regressions, as benchmarks of predictive performance. We find that the XGBoost and the RF methods outperform others in terms of . In particular, when out-of-sample horizons are 26 weeks (half a year) and 52 weeks (one year), the XGBoost method has an value of 2.99% and 4.30%, respectively, the RF achieves an value of 0.45% and 1.55%, the RNN has an value of 0.18% and 0.75%, and the FNN expresses an value of −0.77% and 0.03%. Our benchmarks and predictions with OLS, LASSO, ridge, and elastic net also have their s in the negative territory. Moreover, the forecasting results of machine learning methods also outperform those of traditional two-step prediction methods. Finally, the forecasting of the XGBoost method outperforms that of (financial and economic attitudes revealed by search index) and , proposed by [3] in terms of , which are constructed based on the partial least squares (PLS) and LASSO approaches, respectively; see, for example, [3] for details. Such a comparison implies the superiority of a one-step forecasting procedure with machine learning methods. Without a dimension-reduction preprocessing step, machine learning methods can reduce information loss and provide more flexibility in the model structure, capturing the complex nonlinear relationship between sentiment proxies and future risk premium.
To evaluate the economic significance of machine learning forecasting, we build out-of-sample portfolios based on collections of forecasting returns from machine learning methods under the mean-variance framework as in [4], where an investor optimally allocates wealth across a risky asset and a risk-free asset, and test the economic value of predictability, which is measured by the gain of the certainty equivalent return (CER) and the Sharpe ratio. We found that the XGBoost method outperforms other methods in this regard. The XGBoost method achieves the top CER gain and Sharpe ratio across all risk aversion settings in the 52-week out-of-sample horizon. Indeed, the CER gains are 0.95%, 0.32%, and 0.19% for risk aversion, taking 1, 3, and 5, respectively. Meanwhile, RF achieves the second highest CER gain and Sharpe ratio in our test horizon. The RNN and the FNN follow behind in the ranking of CER gains and Sharpe ratios. Our benchmarks and portfolios based on predictions with OLS, LASSO, ridge, and elastic net mostly have underperforming CER gains and Sharpe ratios. For the allocation implication case, the forecasting of the XGBoost method also outperforms and in terms of both CER gains and Sharpe ratios.
Our research is closely related to the literature that uses machine learning methods for stock return predictability and investor sentiment analysis. The empirical finance literature has found that investor sentiment is, indeed, a valid predictor of the stock return; see, for example, [3] and references therein. Since investor sentiment cannot be measured directly, previous studies utilize variable selection or dimension reduction approaches to estimate investor sentiment from proxies developed from market data, media textual content, and surveys, and then forecast equity risk premium with such low-dimensional investor sentiment indices; see, for instance, [5,6,7,8,9,10], and references therein.
Recently, machine learning methods for asset price forecasting and related areas have achieved impressive empirical results in recent years. For example, in the pioneering work by [11], they make a comparison of machine learning methods in both cross-sectional and time series stock return forecasting with economic predictors. Also, Refs. [12,13,14] all predict stock return with neural network methods, while Ref. [15] applies multiple machine learning algorithms to forecast stock return using a set of macroeconomic factors. Furthermore, Ref. [16] utilize a generative adversarial network (GAN), introduced by [17], to estimate stochastic discount factor for asset pricing model and examine its predictive power, while Ref. [18] forecast Chinese stock returns with GAN using firm characteristic factors. When machine learning methods are also applied to analyze online investor sentiment, they are employed mainly to enhance textual analysis with social media, as in [19,20,21,22]; finance forums, as in [23]; and finance news as in [24] Recently, Ref. [25] apply machine learning methods to develop a financial sentiment word dictionary for better sentiment measurement from media texts in Chinese stock market. Finally, machine learning methods have been widely used with no limitation to financial applications. For example, Ref. [26] employ machine learning techniques, specifically extra trees classifier, support vector machine classifier, and multinomial naive Bayes classifier, to predict overall train ratings based on multiple attributes. This multifactor approach aligns with our application of multiple online sentiment proxies to predict stock market returns.
Our motivation comes from three aspects of problems in academic research on online investor sentiment. First, the investor sentiment proxies from search queries are high-dimensional, so traditional prediction methods cannot work well. Since each single sentiment proxy might not have a significant predictive power on stock return and there is much modern theory about sentiment proxies and their selection, we hope to find a data-driven way to process a big collection of sentiment proxies for forecasting. Second, there is ambiguity about the structure form of sentiment proxies linking to market risk premium. Introducing more flexibility or complexity to a predictive model may help in achieving better forecasting performance and understanding the relationship between investor sentiment and risk premium. It is well known that machine learning methods can process high-dimensional data and detect complex nonlinear connections in input datasets, so that they are attractive to our research demands as they allow us to deploy larger collections of sentiment proxies and be able to exploit the unknown prediction structure in a large space. Finally, previous studies mostly follow a two-step framework, which demands estimating or aggregating a sentiment index as a necessary preprocessing step for forecasting. To avoid losing proportion of information, we seek methods to skip the preprocessing and conduct forecasting directly to achieve higher efficiency of information usage and improve prediction performance.
Our main contributions are in twofold. First, we provide a new set of evidence about stock return prediction based on online investor sentiment using machine learning methods, which extends the empirical literature on machine learning in empirical finance. Our research integrates online investor sentiment analysis and machine learning methods in a novel way. Specifically, we show that machine learning can enhance the investor sentiment analysis with search engine inquiries, and exploit invisible unknown interactions in data and improve stock return forecasting. Our results are in line with previous research on forecasting with online investor sentiment. Second, we introduce a novel way to utilize machine learning methods to execute two tasks, extracting investor sentiment from a large collection of noisy and complex proxies and forecasting stock return, in one step. Comparing the forecasting performance with linear models, the improvement of prediction from machine learning models demonstrates the nonlinear relation between sentiment proxies and stock return. As machine learning methods also outperform traditional two-step methods, they have more information and higher efficiency of data processing with using all sentiment proxies directly.
2. Econometric Methodology
2.1. Model Setup
Compared with other categories such as unsupervised machine learning and semisupervised machine leaning, supervised machine learning methods require that the input data should include the target variables and optimize an objective function of target variables and model estimates. We consider four different architectures of supervised machine learning methods. Under the time series forecasting framework, a general form of a predictive model for an asset excess return can be written in the following form
where is the asset return at time and is the conditional expectation of stock return on conditional on available information till time t. Here, is a function of state variables that maximizes the out-of-sample predictive power for return, the state variable is a d-dimensional vector, where d might be very large, say, in our empirical study later, and the function is an unknown function of these state variables.
If is assumed to be a linear function, then we consider a simple linear model in our analysis, which estimates via OLS. This predictive model is used as a benchmark to make a comparison with the features of other machine learning models. Considering that there is a large number of predictors in our case, a simple linear regression is possibly inefficient or inconsistent when the number of observations is not significantly larger than the number of predictors. Thus, we also consider penalized linear regressions, such as LASSO proposed by [27], ridge as in [28], and elastic net as in [29], to reduce the overfitting in model. A penalized linear regression optimizes an objective function that is a sum of squared fitting errors and penalty term, which is absolute sum of estimates ( penalty) in LASSO, squared sum of estimates ( penalty) in ridge, or a linear combination of and penalty in elastic net.
2.2. Machine Learning Methods
First, the feedforward neural network is designed to simulate the working process like a human brain and it consists of an input layer, where predictors enter the models, one or more hidden layers that nonlinearly transform or combine predictors, and an output layer that returns prediction outcomes. Inputs are passed through neurons in hidden layers, where groups of activation functions transform the variables and pass them to the next layer. The flexibility is generated from those embedding hidden layer and nonlinear interactions of inputs and neurons. Theoretically, the FNN is capable of approximating any smooth function, as argued in [16,30,31,32,33]. To provide a rough picture of the FNN method, Figure 1 illustrates the FNN architecture with a simple example. To choose an optimal model for the nonlinear link between investor sentiment and stock market risk premium, we need to select a collection of hyperparameters, including the number of hidden layers, the number of neurons in each layer, and type of activation function in neurons.
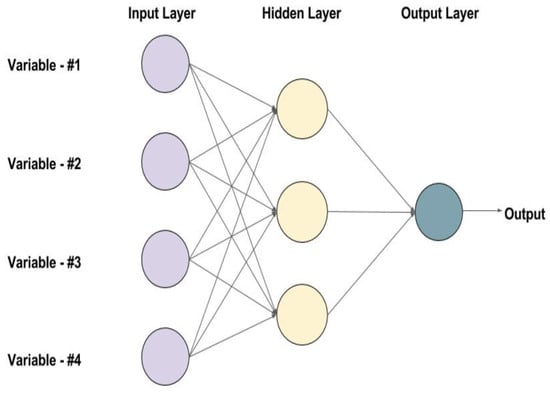
Figure 1.
Feedforward neural network architecture.
Second, the recurrent neural network is a class of neural networks which are derived from the FNN, as in [34,35,36]. The RNNs are featured by their internal state “memory” as they take information from prior inputs and generate latent signals to influence the current outputs. While the FNN only processes inputs independently at time horizon, the RNN estimates current output, taking previous inputs into account. Thus, this feature allows them to explore the time series pattern in data. Figure 2 demonstrates a basic architecture of the RNN. Similar to the FNN, we need to select a collection of hyperparameters, including the number of hidden layers, the number of neurons in each layer, type of activation function in neurons, and, additionally, the sequential lag periods of inputs.
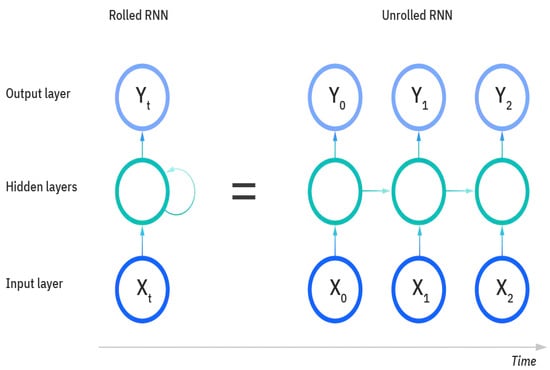
Figure 2.
Recurrent neural network architecture.
Third, the random forest method, proposed by [37], is an ensemble algorithm based on classification and regression trees, and is widely used in purposes of regression and classification, in particular, in econometrics, as in [38], and macroeconomics, as in [39]. Since a single decision tree usually tends to have an overfitting problem without distinguishing the noise, the RF trains multiple decision trees on different subspaces of the whole space. Specifically, each decision tree is trained on a random subset of both all observations and all variables. The final output is decided based on the majority results, which are equally voted by each decision tree. The main idea of this ensemble procedure is the bootstrap aggregation, as in [40], that generates multiple versions of outputs using the bootstrap training sets and obtains an aggregated final output. The RF alleviates the overfitting and the instability problems in the single decision tree method. The RF model is tuned by hyperparameters including depth of the trees, number of variables randomly sampled in each split, and number of trees to grow by bootstrap samples. Figure 3 describes the bootstrap aggregation procedure of RF.
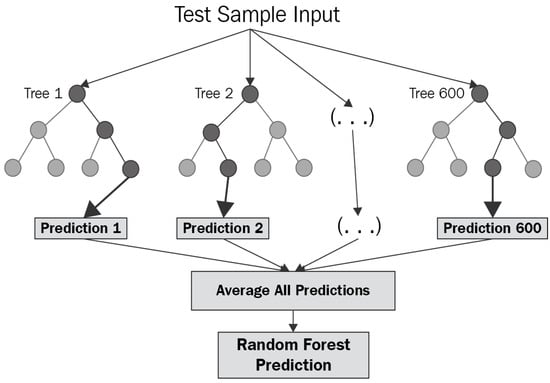
Figure 3.
Random forest architecture.
Finally, the XGBoost method, introduced by [41], is an augmented tree-based ensemble machine learning algorithm. The main idea is a combination of the gradient boosting method with additive components like decision or regression trees to have robust estimation of functions, as in [42]. This method makes a combination of weak learners, which are shallow trees with low accuracy, to produce a strong learner by sequentially training weak learners in a weight-adjusted subspace, where the weights of data are reassigned based on the fitting error of the former learner. The extreme gradient boosting method improves the original gradient boosting method by modifying the algorithms in both procedures of developing each decision or regression tree and tree combination. It features and regularization to control the complexity of estimation and relieve the overfitting problem. The XGBoost model is tuned by hyperparameters including learning rate, depth of the trees, number of training data randomly sampled to growing trees, number of variables randomly sampled, requirement of loss reduction, number of rounds for boosting, and scales of and regularization terms. Figure 4 depicts the boosting procedure of the XGBoost.
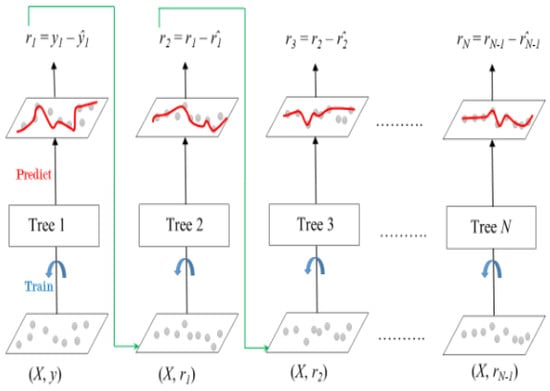
Figure 4.
Extreme gradient boosting architecture.
2.3. Choice of Tuning Parameters
Choosing the hyperparameters is an important step in selecting machine learning models. The hyperparameters control the complexity of a type of machine learning models and balance the model performance between overfitting and underfitting. But, in most cases, there is no theoretical guidance for the selection of hyperparameters. It is common in the literature to use the leave-one-out cross-validation, but it might fail for time series data, as pointed put by [43,44]. Therefore, in this paper, we tune the models based on the multifold forward-validation method; see, for instance, the papers by [43,45] for details, where they argue that it works well for time series data. Specifically, we split the in-sample data set into five chunks of subsets in which data observations keep the original time order. Each time, we use four chunks as the training set and the rest as the validation set. The training set is used to estimate the model with a specific set of hyperparameters. The performance of such a model is evaluated in the validation set in terms of mean square predicting error. We repeat the steps with the other four alternative subsets as the validation sets, reestimate the model, reevaluate the performance, and take an average of five validation performances as the final evaluation of a model with a specific set of hyperparameters. Our purpose is to iteratively search for the set of hyperparameters that minimizes the average mean square predicting error in validation sets. In this procedure, the out-of-sample data subset, the testing set, is neither used in model training nor performance evaluating with validation sets. We avoid the data leakage by excluding the testing set in both models’ training and hyperparameter tuning. Finally, we should mention that an alternative way to choose hyperparameters might be to adopt the recursive time-ordered cross-validation technique, as in [46].
3. Empirical Results
3.1. Data
The search query indices are the sentiment proxies that we use for forecasting the stock return. The aggregated stock market return and risk-free rate are applied in our analysis. In this section, we introduce how to collect data.
Search query data are provided by Google Trends, which is powered by Google. A query data series, search volume index, represents the search volume of an input, which can be a single word or a multiword term. Such an SVI is rescaled by the historical maximum and ranges from 0 to 100. There are options to filter out results by a time period or a chosen region such as United States or worldwide. We use all 150 terms under the economic category including both positive and negative tones from General Inquirer’s Harvard IV-4 Dictionary, a widely used dictionary in the finance and textual analytics research like [3,47,48,49]. Our basic term list includes words such as “rich”, “savings”, “subsidy”, “gold”, “crisis”, “default”, and “jobless”. The query result returns the time series data of SVI at a specific frequency such as hourly, daily, weekly, or monthly. In addition, Google Trends provides a list of related terms, which are popular search queries often associated with the selected term. For example, when we search for the word “contribution” in our term list, the top five related terms are “IRA contribution”, “IRA”, “401k”, “401k contribution”, and “Roth contribution”. Table 1 shows the correlations among the log difference of SVIs of these six related terms in our sample period. We notice that the multiple-word terms usually have high correlations, which can be over 0.8, with the original input. If there are two terms that are highly correlated, these terms probably carry particularly similar information, and the collinearity may cause problems in an estimation. In addition to this high correlation problem, those multiword terms frequently bring in noises, which include phrases or short sentences asking for words’ definitions or synonyms. Since we think it is inappropriate to use those unrelated or duplicated information in our term list, we filter the multiple-word phrases out and only combine single-word related terms to our basic term list as complements. There are 20 related words added to the original term list, such as “IRA”, “401K”, “corruption”, and “anxiety”. Differing from [47], selecting related terms from the results manually, our cleaning procedure does not require personal judgment or manual discrimination for adding the financial terms to the term list. The SVIs of all words in the full term list are collected under the region option of United States and in a weekly frequency. After collecting the SVIs, we filter out those words that do not have at least 80% of observations over our sample period. After the preparation procedure, there are 170 SVIs of corresponding words which are the elements of online investor sentiment information. Our data are sampled weekly from January 2004 through November 2021 with 935 observations. (Of course, one can consider different frequent data, say, daily or monthly data. According to [3], the sentiment index for the daily or monthly data might not have a predicative power for asset returns. Therefore, in this paper, our focus is only on the weekly data). We calculate the natural log differences of SVIs and denote them as SVIs due to their possible nonstationarity, say, unit root (see, for example, [3] for details on this issue).

Table 1.
Correlations among related terms.
To address the issue of outliers, seasonality, and heteroskedasticity, we adjust the search query data in three steps. First, we apply winsorization at the 5% level (2.5% at each tail) for each SVI (change in search volume index). This technique replaces extreme values with less extreme values at the specified percentiles. It is commonly used for handling outliers in financial time series data, as it preserves the information in the extreme values while reducing their impact on the analysis [50]. After winsorization, we regress each SVI on the weekly dummy to remove any seasonal patterns. This step helps to isolate the sentiment signal from regular cyclical patterns that might be present in some search queries. Finally, we standardize each SVI by scaling it by the time series mean and standard deviation, which ensures that all variables are on a comparable scale and helps to further mitigate the impact of any remaining outliers.
We collect weekly returns of the Standard and Poor’s 500 (S&P500) index from Yahoo Finance, downloaded from Yahoo at https://finance.yahoo.com/ (accessed on 1 December 2021), which is the well-known capitalization-weighted stock price index widely used for representing the aggregated stock market return. Weekly level asset returns use the week-over-week log difference of adjusted closing price on Friday. The weekly risk-free rate is obtained from Kenneth French’s data library (the data library address is http://mba.tuck.dartmouth.edu/pages/faculty/ken.french/data_library.html (accessed on 1 December 2021)). Our sample period covers from January 2004 through November 2021. The weekly return of the S&P500 index has the mean of 0.15%, the standard deviation of 2.42%, the skewness of −1.10, and the kurtosis of 13.10. The return ranges from −20.08% to 11.42% with a Sharpe ratio of 0.05.
3.2. Out-of-Sample Forecasting
We evaluate the forecasting performance by the out-of-sample , proposed by [2], which is the proportion of mean squared forecasting error of predictive regression and that of historical average.
where , denoting the historical average benchmark, is the excess asset return at time , is the predicted value of from a predictive regression estimated through period t, and is the size of the rolling window. Clearly, and a positive means that the prediction from specific predictor outperforms the historical average in term of mean squared forecasting error.
In addition to the , we employ the following two metrics to assess the performance of the predictions, commonly used in prediction, as in [51], for machine learning methods. They are the root mean squared error and the root mean squared logarithmic error. The RMSE is defined as follows:
It is well known that the RMSE might be sensitive to large errors, as it penalizes larger deviations more heavily than smaller ones. The RMSLE, on the other hand, captures the ratio between the true and predicted values by measuring the log difference between them, which is useful when errors in predicting smaller values are more significant, given by
Both RMSE and RMSLE provide insights into the performance of predictive models.
Table 2 exhibits the out-of-sample performance evaluated in two different lengths of period, which are half a year (J = 26) and a year (J = 52). Among four machine learning methods, the XGBoost achieves positive of 2.99% and 4.30% when J = 26 and 52, respectively. The RF obtains positive of 0.45% and 1.55% in 26 and 52 out-of-sample periods, respectively. The FNN generates of −0.77% and 0.03%, in such test periods, while the RNN expresses of 0.18% and . Meanwhile, four linear benchmark methods, OLS, LASSO, ridge, and elastic net, have s located in negative territory. The machine learning methods we incorporated outperform these traditional linear models in terms of , which means that those nonlinear models estimated by machine learning methods improve the forecasting performance. To compare with two-step methods, the results of out-of-sample performance of and proposed in [3] are listed. Even though these two investor sentiment indices show strong out-of-sample predictive power indicating by positive , the XGBoost still outperforms such two-step methods in terms of , which suggests the advantage of the one-step method for forecasting. In terms of the RMSE and the RMSLE, the XGBoost consistently shows the lowest values across both time horizons, further confirming its superior predictive performance. The machine learning methods, particularly the XGBoost and the RF, generally exhibit lower RMSE and RMSLE values compared to the traditional linear models and two-step methods, indicating their ability to capture complex patterns in the sentiment data. These results highlight the potential of machine learning methods, such as the XGBoost, in processing high-dimensional online investor sentiment data and capturing nonlinear relationships between sentiment proxies and future stock returns.

Table 2.
Out-of-sample performances via machine learning for different periods.
3.3. Asset Allocation Implications
To examine the economic value of the stock return predictability conducted by machine learning methods based on online investor sentiment, we test the performance of dynamic asset allocation under the Markowitz paradigm. For this case, we consider a mean-variance investor who allocates wealth among one risky asset and one risk-free asset, and rebalances the portfolio at the end of each period based on the out-of-sample forecasting of stock return for next period. Following [2,9], we use the certainty equivalent return (CER) gain and the Sharpe ratio to measure the performance of portfolios and the economic value of predictors.
At the end of period t, the investor optimally allocates in risky asset and in risk-free asset for period , , where is the risk aversion parameter, is the out-of-sample forecast of excess market return, and is the variance forecast of according stock return. Following [8], we evaluate the portfolio performance with the risk aversion parameter of 1, 3, and 5. Following [2], we use a five-year moving window of past weekly returns to forecast the variance of the excess market return. Considering the short-selling and leverage limitation, we constrain asset weights to lie between 0 and 1.5 to exclude short sales and to allow for, at most, leverage. The realized portfolio return in is , where is the portfolio return and is the risk-free return. The CER of a portfolio is
where and are the sample mean and variance, respectively, of the portfolio return over the out-of-sample forecasting evaluation periods. is the CER level of a benchmark portfolio. The CER gain is the difference between the CER for the investor who utilizes the forecasts of market return from method k, where k stands for XGBoost, RF, FNN, RNN, OLS, LASSO, ridge and elastic net, and . For the benchmark portfolio, it is built by using the historical average forecasts in (1). We annualize the weekly CER gain by multiplying by 52 and use it to measure the economic gain from forecasting, explained as a portfolio management fee that an investor is willing to pay to benefit from the predictability of a specific method for higher portfolio return than one based on historical average forecasts.
Table 3 collects the annualized CER gain and the Sharpe ratio for each portfolio with risk aversion , 3, and 5. The out-of-sample period is over 52 weeks from December 2020 through November 2021. When the risk aversion is 1, the CER gain of the XGBoost is 0.95% and ranking the top among all portfolios. The portfolio constructed with the RF has the CER gain of 0.62% and the RNN achieves the CER gain of 0.17%. The FNN has the lowest CER gain of 0.05% among machine learning methods. In this case, the Sharpe ratio of the portfolios built based on the XGBoost is 0.30, which is also higher than those of other portfolios. When the risk aversion is 3, the XGBoost method achieves the best performance with the CER gain of 0.32% and the Sharpe ratio of 0.30. Meanwhile, the RF has the CER gain of 0.21% and the Sharpe ratio of 0.24. The FNN has the CER gain of 0.02% and the Sharpe ratio of 0.31, and the RNN has the CER gain of 0.06% and the Sharpe ratio of 0.33. When risk aversion is 5, the XGBoost also outperforms other machine learning methods with the CER gain of 0.19%. The RF achieves the CER gain of 0.12%. The FNN and the RNN have the CER gains of 0.01% and 0.03%, respectively. Thus, the XGBoost has the best overall performance in terms of CER gains and Sharpe ratios. The RF is ranked at second best, followed by the RNN and the FNN. In every scenario, for risk aversion of 1, 3, and 5, the CER gains of the XGBoost are higher than those of the other three counterparts. The consistently positive CER gains of the XGBoost of 0.95%, 0.32%, and 0.19% can be explained as the maximum annual portfolio management fee that an investor with a risk aversion of 1, 3, and 5, respectively, is willing to pay to enjoy the advantage of predictive power of the XGBoost and have a higher return. The XGBoost is attractive to a mean-variance investor, even with a higher fee, as it consistently generates economic gains more than other portfolios. Likewise, for RF, investors are willing to pay a slightly lower premium for the predictive power generating by the RF with online investor sentiment. The portfolios built on the forecasting of sentiment indices, and , are also displayed. The XGBoost model outperforms these portfolios as well. The Sharpe ratios of the XGBoost and the RF portfolios, which are 0.30 and 0.24, respectively, also exceed the market Sharpe ratio of 0.05, which indicates that the portfolios depending on machine learning forecasting outperform the market index. Compared with linear models and two-step methods, stock return forecasting by machine learning methods, such as the XGBoost or the RF, can create larger economic value robust to common risk aversion levels.

Table 3.
Results for asset allocations.
4. Conclusions
In this paper, we examine the performance of machine learning methods to construct online investor sentiment for stock risk premium prediction, and make a comparison with traditional two-step methods of investor sentiment prediction. The empirical results indicate that machine learning techniques can help in improving the online investor sentiment analysis in finance market. The XGBoost method outperforms benchmark linear models and two-step methods in terms of and the RMSE as well as the RMSLE, which shows the predictive power on aggregated stock market return and the ability of processing online investor sentiment. It is also implied that an estimation of nonlinear functional model brings predictive advantage to machine learning methods, which other linear methods lack. The return predictability of the XGBoost with online investor sentiment also generates economic value for a mean-variance investor in asset allocation. In summary, our findings help us understand the nonlinear relationship between investor sentiment and stock risk premium. The promising performance of machine learning techniques indicates a potential class of powerful tools for economic modeling.
While this study demonstrates the potential of machine learning methods, particularly the XGBoost and the FNN, for processing online investor sentiment and predicting stock returns, there are several limitations to our paper. First, our analysis is limited to a specific set of 170 search terms from Google Trends as proxies for online investor sentiment. While these terms were selected based on the General Inquirer’s Harvard IV-4 Dictionary, they may not capture all aspects of online investor sentiment. Future research could explore different sentiment proxies or alternative data sources, such as social media content or other dictionaries, as described by [52,53,54]. Second, our models are trained and tested on data from 2004 to 2021, which is subject to specific market conditions and events. The performance of these models may vary in different market environments or time periods. To address this limitation, future work should conduct subperiod analyses to examine how different market conditions, such as bull versus bear markets or high- versus low-volatility regimes, affect the models’ predictive power. Third, while we explored several machine learning methods, there are others that could potentially improve predictive performance. For instance, extra trees classifier, support vector machine classifier, or multinomial naive Bayes classifier have shown promising ability in forecasting applications by [26]. Finally, while our out-of-sample tests show promising results, real-world implementation would face challenges such as transaction costs and the need for consistent data updating, which are not fully accounted for in this study.
Author Contributions
Conceptualization, Z.C. and P.C.; methodology, Z.C. and P.C.; validation, Z.C. and P.C.; formal analysis, P.C.; investigation, Z.C. and P.C.; resources, P.C.; data curation, P.C.; writing—original draft preparation, P.C.; writing—review and editing, Z.C. and P.C.; visualization, P.C.; supervision, Z.C.; project administration, Z.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Acknowledgments
We thank anonymous referees for their great comments and suggestions that improved significantly the quality and presentation of the paper. We also thank John Keating and Shahnaz Parsaeian for their comments on earlier versions of this paper. The views, thoughts, and opinions expressed in this article belong solely to the authors, and not necessarily to the authors’ employer, organization, committee or other group or individual.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Rapach, D.; Zhou, G. Forecasting stock returns. In Handbook of Economic Forecasting; Elliott, G., Timmermann, A., Eds.; Elsevier: Amsterdam, The Netherlands, 2013; pp. 328–383. [Google Scholar]
- Campbell, J.Y.; Thompson, S.B. Predicting excess stock returns out of sample: Can anything beat the historical average? Rev. Financ. Stud. 2008, 21, 1509–1531. [Google Scholar] [CrossRef]
- Cai, Z.; Chen, P. Online Investor Sentiment and Asset Returns; Working Paper; Department of Economics, University of Kansas: Lawrence, KS, USA, 2022; Available online: https://ideas.repec.org/p/kan/wpaper/202216.html (accessed on 23 November 2022).
- Markowitz, H. The utility of wealth. J. Political Econ. 1952, 60, 151–158. [Google Scholar] [CrossRef]
- Baker, M.; Wurgler, J. Investor sentiment and the cross-section of stock returns. Rev. Financ. Stud. 2006, 61, 1645–1680. [Google Scholar] [CrossRef]
- Baker, M.; Wurgler, J. Investor sentiment in the stock market. J. Econ. Perspect. 2007, 21, 129–152. [Google Scholar] [CrossRef]
- Brown, G.W.; Cliff, M.T. Investor sentiment and the near-term stock market. J. Empir. Financ. 2004, 11, 1–27. [Google Scholar] [CrossRef]
- Huang, D.; Jiang, F.; Tu, J.; Zhou, G. Investor sentiment aligned: A powerful predictor of stock returns. Rev. Financ. Stud. 2015, 28, 791–837. [Google Scholar] [CrossRef]
- Jiang, F.; Lee, J.; Martin, X.; Zhou, G. Manager sentiment and stock returns. J. Financ. Econ. 2019, 132, 126–149. [Google Scholar] [CrossRef]
- Lemmon, M.; Portniaguina, E. Consumer confidence and asset prices: Some empirical evidence. Rev. Financ. Stud. 2006, 19, 1499–1529. [Google Scholar] [CrossRef]
- Gu, S.; Kelly, B.; Xiu, D. Empirical asset pricing via machine learning. Rev. Financ. Stud. 2020, 33, 2223–2273. [Google Scholar] [CrossRef]
- Feng, G.; He, J.; Polson, N.G. Deep learning for predicting asset returns. arXiv 2018, arXiv:1804.09314. [Google Scholar]
- Feng, G.; Polson, N.G.; Xu, J. Deep learning in characteristics-sorted factor models. J. Financ. Quant. Anal. 2023, 1–36. [Google Scholar] [CrossRef]
- Yi, Y. Machine Learning and Empirical Asset Pricing. Doctor of Business. Administration Dissertation, Olin Business School, Washington University in St. Louis, St. Louis, MI, USA, 2019. [Google Scholar]
- Ndikum, P. Machine learning algorithms for financial asset price forecasting. arXiv 2020, arXiv:2004.01504. [Google Scholar]
- Chen, L.; Pelger, M.; Zhu, J. Deep learning in asset pricing. Manag. Sci. 2024, 70, 714–750. [Google Scholar] [CrossRef]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial networks. Commun. ACM 2020, 63, 139–144. [Google Scholar] [CrossRef]
- Tian, M.; Jiang, F.; Tang, G. Deep learning and factor investing in Chinese stock market. China Econ. Q. 2022, 22, 819–842. [Google Scholar]
- Bartov, E.; Faurel, L.; Mohanram, P.S. Can Twitter help predict firm-level earnings and stock returns? Account. Rev. 2018, 93, 25–57. [Google Scholar] [CrossRef]
- Behrendt, S.; Schmidt, A. The Twitter myth revisited: Intraday investor sentiment, Twitter activity and individual-level stock return volatility. J. Bank. Financ. 2018, 96, 355–367. [Google Scholar] [CrossRef]
- Ranco, G.; Aleksovski, D.; Caldarelli, G.; Grčar, M.; Mozetič, I. The effects of Twitter sentiment on stock price returns. PLoS ONE 2015, 10, e0138441. [Google Scholar] [CrossRef]
- Yang, S.Y.; Mo, S.Y.K.; Liu, A. Twitter financial community sentiment and its predictive relationship to stock market movement. Quant. Financ. 2015, 15, 1637–1656. [Google Scholar] [CrossRef]
- Renault, T. Intraday online investor sentiment and return patterns in the US stock market. J. Bank. Financ. 2017, 84, 25–40. [Google Scholar] [CrossRef]
- Sun, L.; Naj, M.; Shen, J. Stock return predictability and investor sentiment: A high-frequency perspective. J. Bank. Financ. 2016, 73, 147–164. [Google Scholar] [CrossRef]
- Jiang, F.; Meng, L.; Tang, G. Media textual sentiment and Chinese stock return predictability. China Econ. Q. 2021, 12, 1323–1344. [Google Scholar]
- Majumder, S.; Singh, A.; Singh, A.; Karpenko, M.; Sharma, H.K.; Mukhopadhyay, S. On the analytical study of the service quality of Indian Railways under soft-computing paradigm. Transport 2024, 39, 54–63. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression shrinkage and selection via the LASSO. J. R. Stat. Soc. Ser. B 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Hoerl, A.E.; Kennard, R.W. Ridge regression: Biased estimation for nonorthogonal problems. Technometrics 1970, 12, 55–67. [Google Scholar] [CrossRef]
- Zou, H.; Hastie, T. Regularization and variable selection via the elastic net. J. R. Stat. Soc. Ser. B 2005, 67, 301–320. [Google Scholar] [CrossRef]
- Cybenko, G. Approximation by superpositions of a sigmoidal function. Math. Control. Signals Syst. 1989, 2, 303–314. [Google Scholar] [CrossRef]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Networks 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Hornik, K. Approximation capabilities of multilayer feedforward networks. Neural Netw. 1991, 4, 251–257. [Google Scholar] [CrossRef]
- Yarotsky, D. Error bounds for approximations with deep ReLU networks. Neural Netw. 2017, 94, 103–114. [Google Scholar] [CrossRef]
- Elman, J.L. Finding structure in time. Cogn. Sci. 1990, 14, 179–211. [Google Scholar] [CrossRef]
- Elman, J.L. Distributed representations, simple recurrent networks, and grammatical structure. Mach. Learn. 1991, 7, 195–225. [Google Scholar] [CrossRef]
- Lipton, Z.C.; Berkowitz, J.; Elkan, C. A critical review of recurrent neural networks for sequence learning. arXiv 2015, arXiv:1506.00019. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Wager, S.; Athey, S. Estimation and inference of heterogeneous treatment effects using random forests. J. Am. Stat. Assoc. 2018, 113, 1228–1242. [Google Scholar] [CrossRef]
- Coulombe, P.G. The macroeconomy as a random forest. J. Appl. Econom. 2024, 39, 401–421. [Google Scholar] [CrossRef]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; Association for Computing Machinery: New York, NY, USA, 2016; pp. 785–794. [Google Scholar]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Cai, Z.; Fan, F.; Yao, Q. Functional-coefficient regression models for nonlinear time series. J. Am. Stat. Assoc. 2000, 95, 941–956. [Google Scholar] [CrossRef]
- Shao, J. Linear model selection by cross-validation. J. Am. Stat. Assoc. 1993, 88, 486–494. [Google Scholar] [CrossRef]
- Cai, Z.; Gunawan; Sun, Y. A New Nonparametric Combination Forecasting with Structural Breaks; Working Paper; Department of Economics, University of Kansas: Lawrence, KS, USA, 2024; Available online: https://journals.ku.edu/econpapers/article/view/22878 (accessed on 23 September 2024).
- Kelly, B.; Xiu, D. Financial machine learning. Found. Trends Financ. 2023, 13, 205–363. [Google Scholar] [CrossRef]
- Da, Z.; Engelberg, J.; Gao, P. The sum of all FEARS investor sentiment and asset prices. Rev. Financ. Stud. 2015, 28, 1–32. [Google Scholar] [CrossRef]
- Tetlock, P.C. Giving content to investor sentiment: The role of media in the stock market. J. Financ. 2007, 62, 1139–1168. [Google Scholar] [CrossRef]
- Tetlock, P.C.; Saar-Tsechansky, M.; Macskassy, S. More than words: Quantifying language to measure firms’ fundamentals. J. Financ. 2008, 63, 1437–1467. [Google Scholar] [CrossRef]
- Dixon, W.J.; Yuen, K.K. Trimming and winsorization: A review. Stat. Pap. 1974, 15, 157–170. [Google Scholar] [CrossRef]
- Chu, B.; Qureshi, S. Comparing out-of-sample performance of machine learning methods to forecast U.S. GDP growth. Comput. Econ. 2024, 62, 1567–1609. [Google Scholar] [CrossRef]
- Loughran, T.; McDonald, B. When is a liability not a liability? Textual analysis, dictionaries, and 10-Ks. J. Financ. 2011, 66, 35–65. [Google Scholar] [CrossRef]
- Cai, Z.; Yuang, J.; Pan, Y. China economic policy uncertainty and its forecasting based on a new textual mining method. China J. Econom. 2023, 3, 1–21. [Google Scholar]
- Loughran, T.; McDonald, B. Textual analysis in accounting and finance: A survey. J. Account. Res. 2016, 54, 1187–1230. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).