Research on the Route Choice Behavior of Urban Freight Vehicles Based on GPS Data
Abstract
1. Introduction
2. Literature Review
2.1. Current Status of Route Choice Behavior Modeling Research
- (1)
- Research on Route Choice Behavior Based on Theoretical Frameworks
- (2)
- Research on Route Choice Behavior Based on Discrete Choice Models
2.2. Current Status of Vehicle Route Choice Behavior Research
2.3. Current Status of Route Choice Set Research
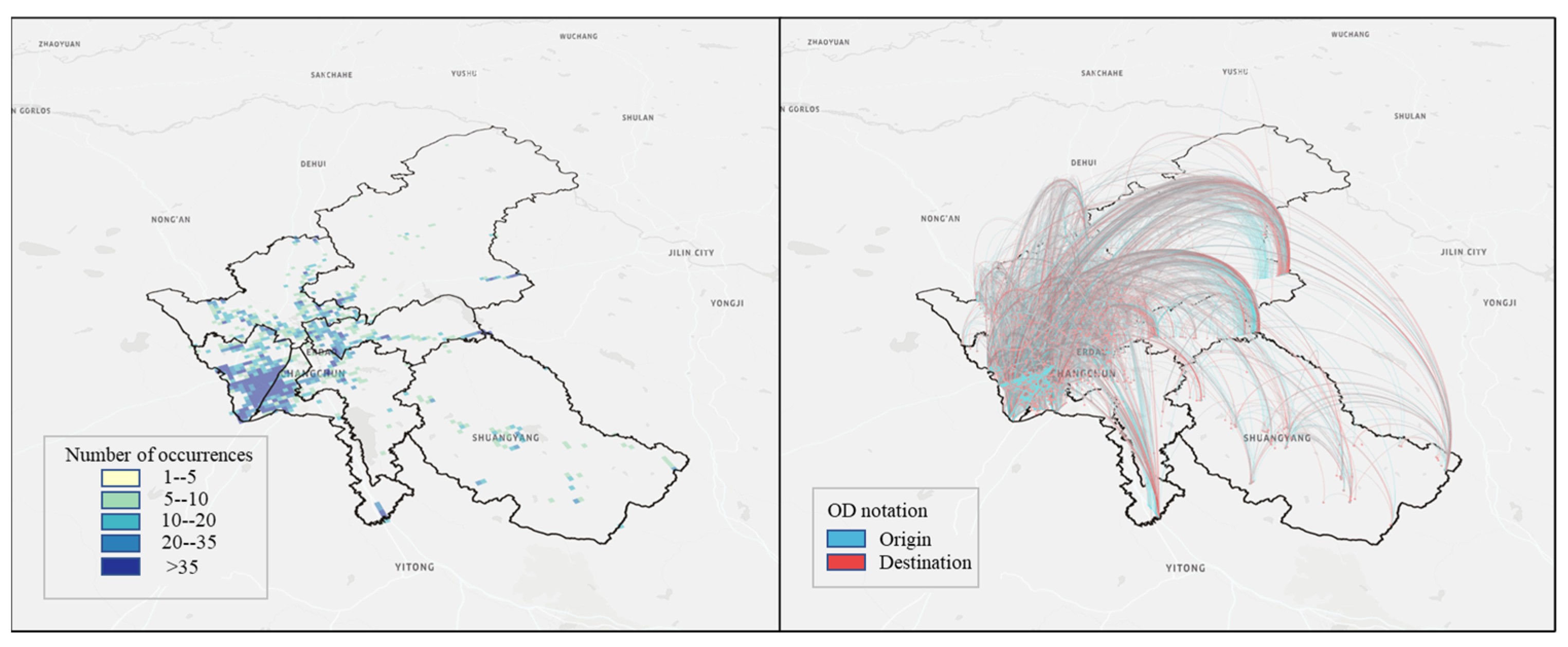
3. Data
3.1. Initial Dataset Processing
- Cleaning of Stationary Vehicle Data: Eliminating GPS data related to stationary vehicles from the dataset.
- Interstate Freight Data Cleaning: Since this study focuses on the route selection behavior within the city, GPS data points that fall outside the administrative boundaries of Changchun City were removed from the dataset.
- Cleaning of Abnormal Time Frequency Data: Cleaning GPS data points that are repeatedly recorded at abnormal time frequencies. For example, in Table 1, three data points within the dashed box exhibit identical time series, latitude, and longitude features, yet they are recorded multiple times. Such data points are considered to have abnormal time frequencies.
- Road Segment Selection: Excluding non-motorized vehicle-specific road segments, such as footways, steps, and pedestrian paths, from the original road network data. These types of roads are not relevant to the route selection behavior of freight vehicles. Road types were consolidated into five categories: highways, expressways, main roads, secondary roads, and local roads.
- Road Segment Division: Dividing road segments at intersections to allow vehicles to make turns at these points, simulating the real-world turning topology at road intersections. Special segments in the road network, such as bridges, expressways, and highways with significant elevation differences from regular ground-level roads, were separately processed.
- Projection Transformation: Transforming the road network from the WGS84 geographic coordinate system into the Xian_1980_3_Degree_GK_CM_120E plane coordinate system and calculating the lengths of the road segments.
- Extracting Road Network Node and Segment Information: Using ArcGIS to construct a network dataset for the road network, extracting nodes for all road segments, and generating node identifiers. The “Connect” tool was employed to associate each road segment with its respective nodes, obtaining information such as the initial node and final node, lengths, and identifiers for each road segment. Table 2 presents the tabular format of the extracted road segment information.
- Building a Road Network Model: Using Python to read the node identifiers, lengths, and segment identifiers for all road segments in the road network, and utilizing the free-flow travel time for each road segment as the weight, the road network model is constructed using the Networkx library.
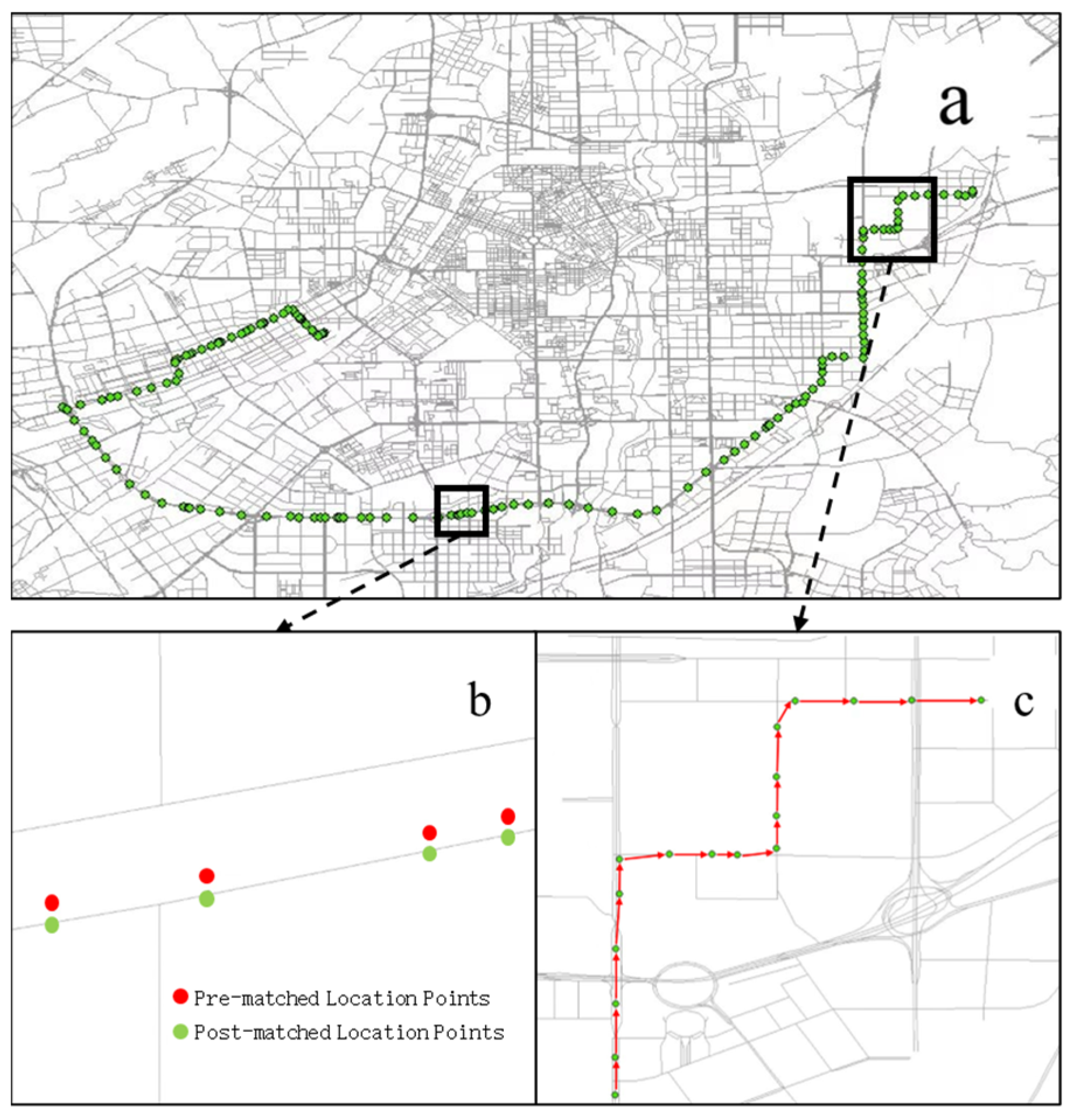
3.2. Map Matching
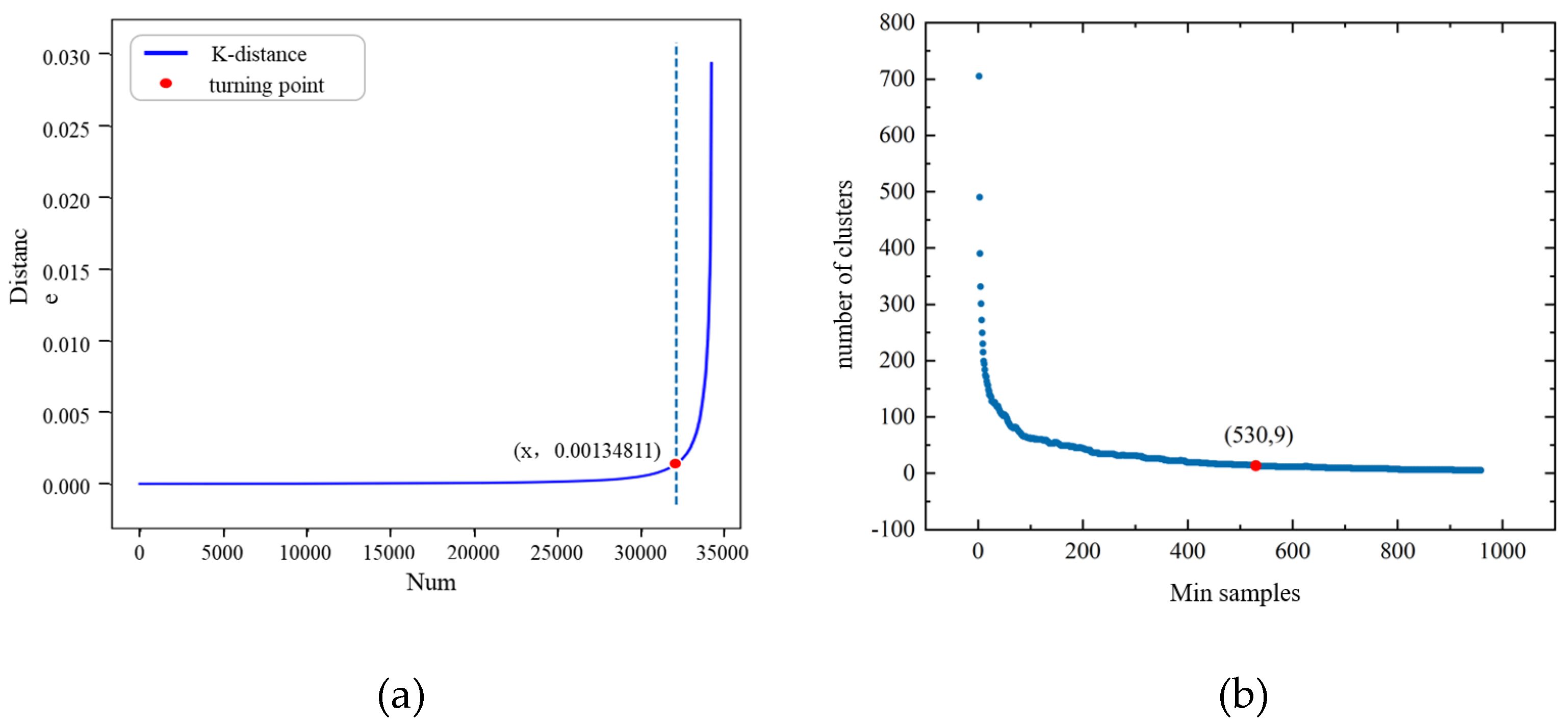
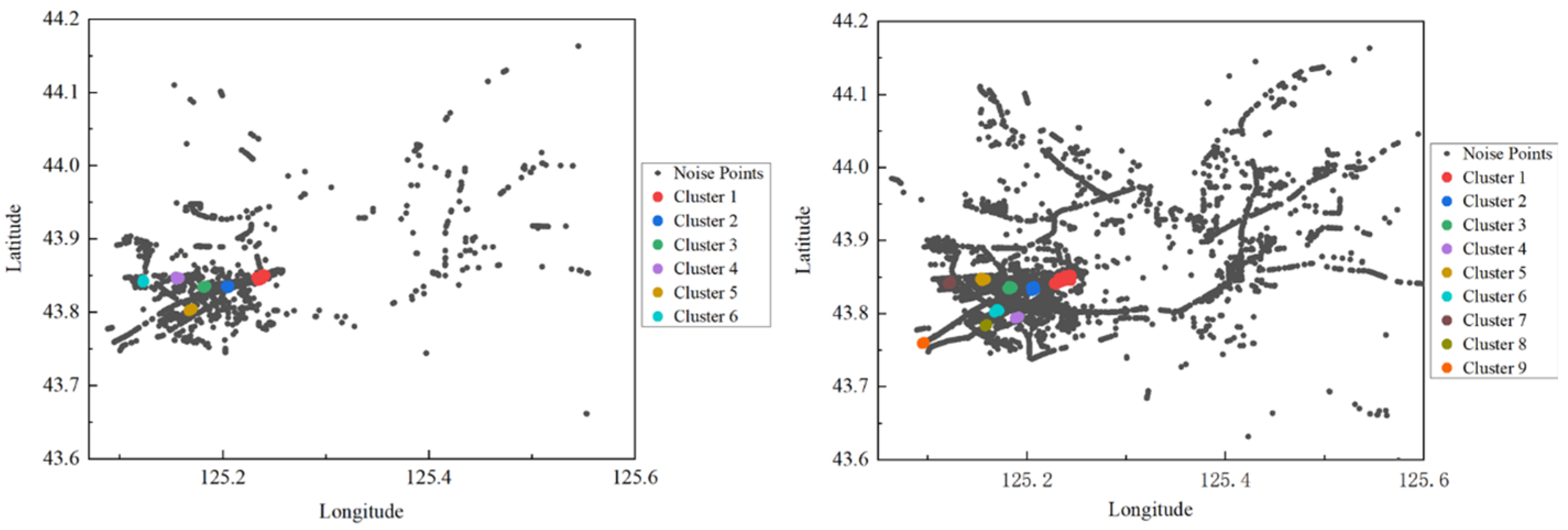
3.3. Clustering Trajectory Data into OD Pairs Using the DBSCAN Algorithm
4. Analysis Methodology
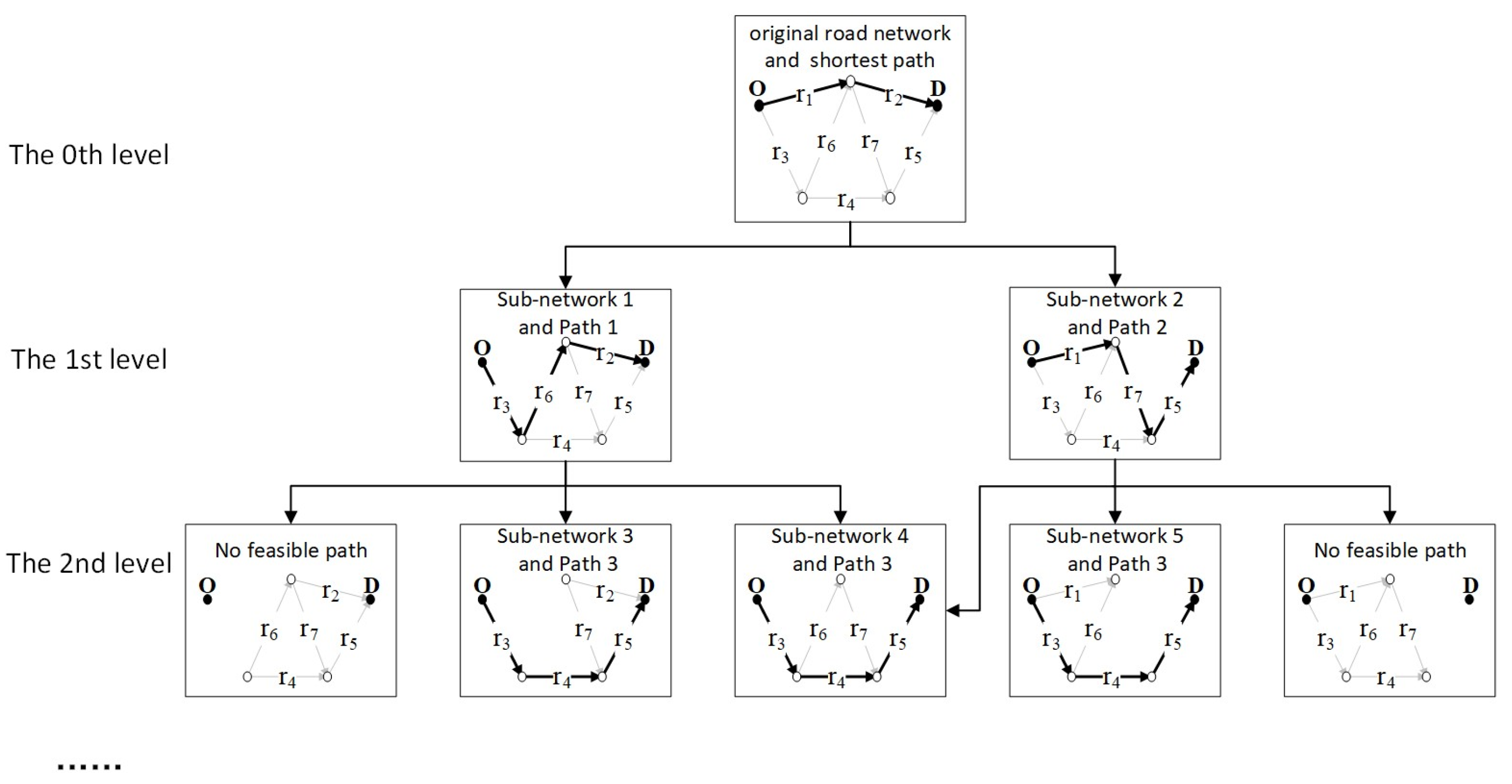
4.1. Constructing the Route Choice Set
- (1)
- To prevent the algorithm from terminating prematurely due to road segment elimination, a new rule is added to the BFS-LE algorithm: the minimum cost search will start from the next node that is connected to at least two road segments in the travel path.
- (2)
- To ensure the uniqueness of each path in the choice set, the study uses a common factor proposed by Cascetta et al. [37] to assess the similarity between paths, setting a critical value of 0.95 for the common factor. Only when the common factor between the newly generated path in the BFS-LE algorithm and the previously generated path is less than or equal to 0.95 will this path be included in the choice set. The formula for calculating the common factor is as follows:In the formula, and represent the lengths of path i and path j, while represents the length of the overlapping section between the two paths.
- (3)
- In a complex urban road network, there may be hundreds of feasible paths between given OD pairs. To prevent an excessively long running times and improve the algorithm efficiency, the algorithm has set termination conditions: it is specified that the algorithm will end when the number of paths generated between OD pairs exceeds 15 or when the algorithm runs for more than 60 min.
4.2. Path Choice Model
4.2.1. Model Feature Variables
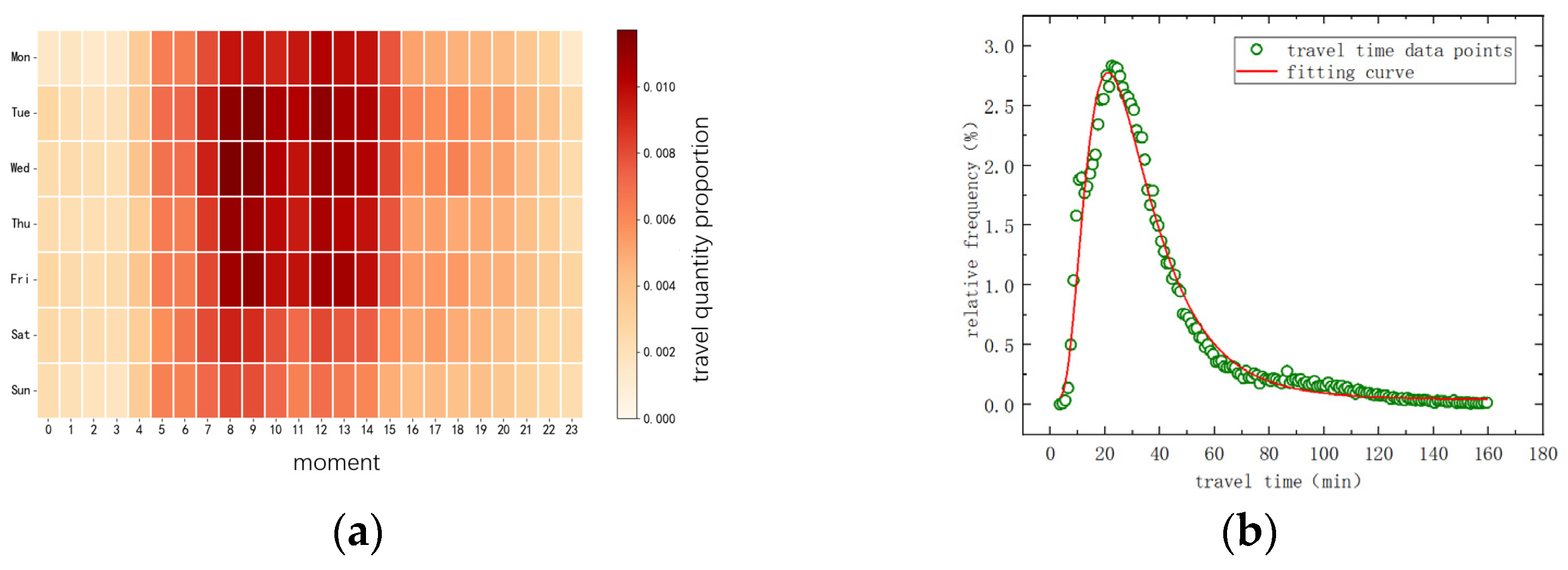
- (1)
- Urban freight truck travel is primarily concentrated on weekdays, with significantly higher travel volumes from Tuesday to Friday compared to the other days of the week. The peak travel periods for freight vehicles in Changchun are from 8:00 to 10:00 and 12:00 to 14:00 daily, with most transport times avoiding the peak commuting hours in the morning and evening within the city.
- (2)
- Urban freight vehicle travel is predominantly short-distance, with the majority of travel times being within 60 min. The relative frequency of travel times for urban freight trucks approximately follows a log-normal distribution, with the highest relative frequency observed at a travel time of 21 min.
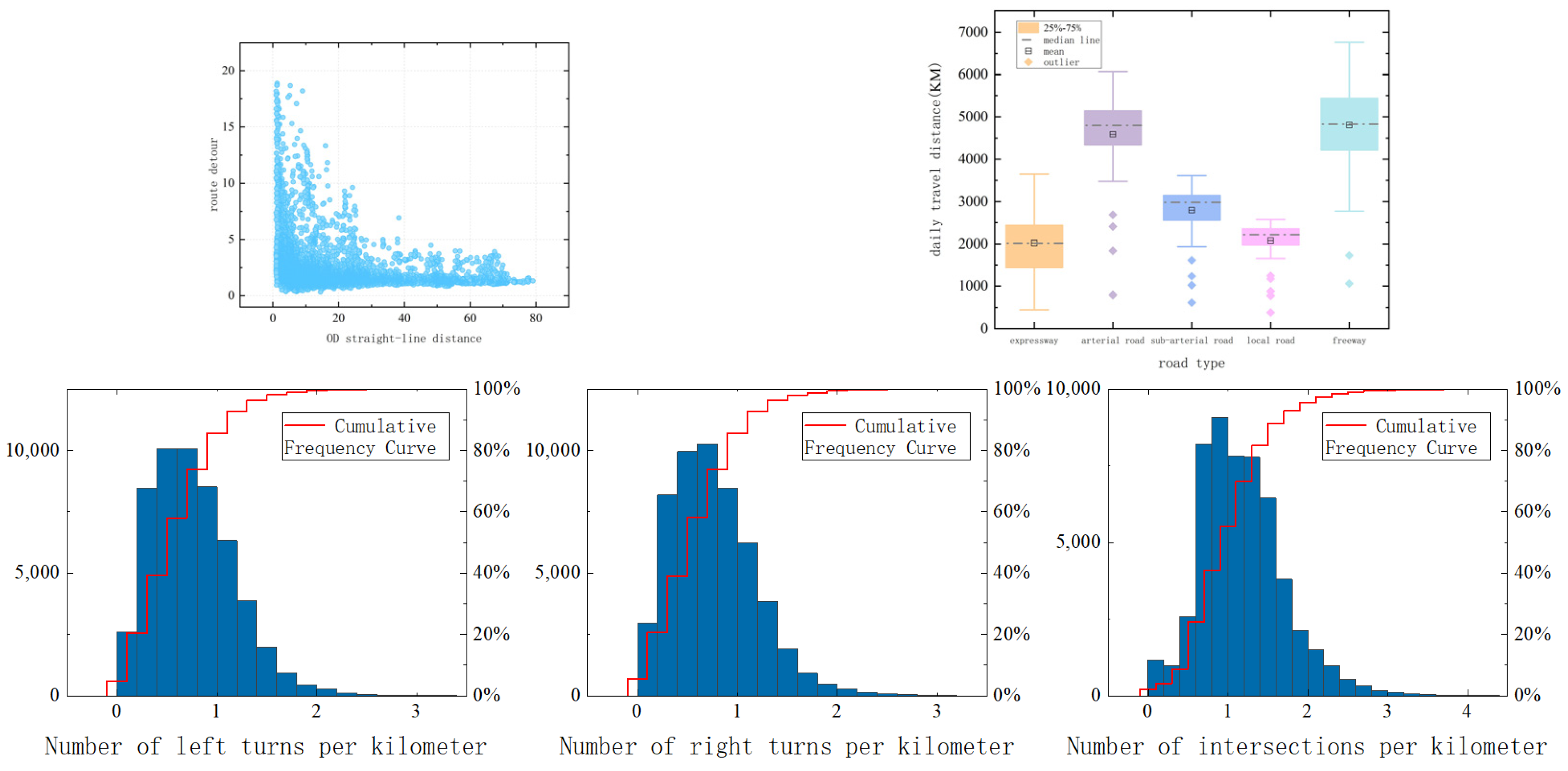
- (1)
- As the OD distance increases, the detour degree of most truck travel paths decreases, and the dispersion of data points gradually decreases. This indicates that as the travel distance increases, truck drivers are less willing to choose detours, and more drivers prefer routes with lower detour degrees.
- (2)
- Urban freight vehicles travel the longest distance on expressways on average each day, but the daily travel distance data on expressways and highways are less concentrated in the 25th percentile than the 75th percentile range, and have relatively high fluctuations in the upper and lower limits. Therefore, arterial roads, sub-arterial roads, and local roads are the main routes for most freight vehicles within the city.
- (3)
- The distribution of the number of left and right turns per kilometer in the travel paths of urban freight vehicles is similar. Most freight vehicles pass an average of 1 intersection per kilometer and make approximately 0.6 left/right turns per kilometer on city roads.
4.2.2. Model Construction
5. Results and Discussion
5.1. Parameter Calibration Results
5.2. Model Evaluation and Predictive Accuracy Test
5.2.1. Model Evaluation
5.2.2. Model Prediction Accuracy Test
5.3. Result Analysis
- (1)
- As anticipated, for all travelers, factors such as travel time, detour length, and the number of left turns/intersections in a path have a negative effect on path selection. In other words, travelers tend to prefer paths with shorter travel times, lower detour lengths, and fewer left turns/intersections. In the PSL model, the positive coefficient for Ln(PS) aligns with the basic principles of path selection models, indicating that the lower the overlap between path i and the other paths in the choice set, the more likely travelers are to select that path.
- (2)
- Unlike commuter and other vehicles’ travel behavior, when truck drivers choose travel paths on urban roads, the percentage of arterial roads and collector roads in the path negatively influences path selection. Meanwhile, the percentage of local roads positively influences path selection. Truck drivers tend to choose paths with lower percentages of arterial and collector roads and relatively higher percentages of local roads. This may be attributed to the fact that arterial roads often have more complex traffic conditions and congestion, leading to increased travel costs like travel time. Additionally, larger truck vehicles are more likely to cause congestion and traffic accidents in complex traffic environments, prompting truck drivers to prefer paths with a higher percentage of local roads.
- (3)
- Combining the urban freight vehicle travel characteristics with the model’s parameter estimation results, we can provide tailored path navigation using electronic mapping software to align with our travel preferences. For different distances of freight vehicles, targeted path induction can be carried out. Furthermore, for the hotspots of truck travel, it is essential to promote the construction of roads suitable for truck travel and establish relevant freight traffic management policies.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Comi, A.; Polimeni, A. Estimating Path Choice Models through Floating Car Data. Forecasting 2022, 4, 525–537. [Google Scholar] [CrossRef]
- Zhou, L.; Burris, M.W.; Baker, R.T.; Geiselbrecht, T. Impact of Incentives on Toll Road Use by Trucks. Transp. Res. Rec. 2009, 2115, 84–93. [Google Scholar] [CrossRef]
- Sun, Y.; Toledo, T.; Rosa, K.; Ben-Akiva, M.E.; Flanagan, K.; Sanchez, R.; Spissu, E. Route Choice Characteristics for Truckers. Transp. Res. Rec. 2013, 2354, 115–121. [Google Scholar] [CrossRef]
- Abdel-Aty, M.A. Using stated preference data for studying the effect of advanced traffic information on drivers’ route choice. Transp. Res. Part C 1997, 5, 39–50. [Google Scholar] [CrossRef]
- Bierlaire, M.; Frejinger, E. Route choice modeling with network-free data. Transp. Res. Part C 2007, 16, 187–198. [Google Scholar] [CrossRef]
- Kahneman, D.A.; Tversky, A.N. Prospect Theory: An Analysis of Decision under Risk. Econometrica 1979, 47, 263–291. [Google Scholar] [CrossRef]
- Katsikopoulos, K.V. Risk Attitude Reversals in Drivers’ Route Choice When Range of Travel Time Information is Provided. Hum. Factors J. Hum. Factors Ergon. Soc. 2002, 44, 466–473. [Google Scholar] [CrossRef]
- Gao, S.; Frejinger, E.; Ben-Akiva, M. Adaptive route choices in risky traffic networks: A prospect theory approach. Transp. Res. Part C 2009, 18, 727–740. [Google Scholar] [CrossRef]
- Teodorovic, D.; Kikuchi, S. Transportation Route Choice Model Using Fuzzy Inference Technique; University of Belgrade: Belgrade, Serbia; University of Delaware: Newark, DE, USA, 1990. [Google Scholar]
- Peeta, S.; Yu, J.W. A Hybrid Model for Driver Route Choice Incorporating En-Route Attributes and Real-Time Information Effects. Netw. Spat. Econ. 2005, 5, 21–40. [Google Scholar] [CrossRef]
- Kerner, B.S. Optimum principle for a vehicular traffic network: Minimum probability of congestion (Article). J. Phys. A Math. Theor. 2011, 44, 092001. [Google Scholar] [CrossRef]
- McFadden, D. Conditional Logit Analysis of Qualitative Choice Behavior. In Frontiers in Econometrics; Academic Press: Cambridge, MA, USA, 1974; pp. 105–142. [Google Scholar]
- Ben-Akiva, M.; Bierlaire, M. Discrete Choice Methods and their Applications to Short Term Travel Decisions. Handb. Transp. Sci. 1999, 23, 5–33. [Google Scholar]
- Chu, C. A paired combinatorial logit model for travel demand analysis. In Proceedings of the Fifth World Conference on Transportation Research, Yokohama, Japan, 10–14 July 1989; pp. 295–309. [Google Scholar]
- Vovsha, P. Application of Cross-Nested Logit Model to Mode Choice in Tel Aviv, Israel, Metropolitan Area. Transp. Res. Rec. 1997, 1607, 6–15. [Google Scholar] [CrossRef]
- Wen, C.H.; Koppelman, F.S. The generalized nested logit model. Transp. Res. Part B Methodol. 2001, 35, 627–641. [Google Scholar] [CrossRef]
- Mcfadden, D.; Train, K. Mixed MNL Models for Discrete Response. J. Appl. Econom. 2000, 15, 447–470. [Google Scholar] [CrossRef]
- Tang, W.; Cheng, L. Analyzing multiday route choice behavior of commuters using GPS data. Adv. Mech. Eng. 2016, 8, 1687814016633030. [Google Scholar] [CrossRef]
- Sun, D.; Zhang, C.; Zhang, L.; Chen, F.; Peng, Z.R. Urban travel behavior analyses and route prediction based on floating car data. Transp. Lett. 2014, 6, 118–125. [Google Scholar] [CrossRef]
- Hood, J.; Sall, E.; Charlton, B. A GPS-based bicycle route choice model for San Francisco, California. Transp. Lett. 2011, 3, 63–75. [Google Scholar] [CrossRef]
- Broach, J.; Dill, J.; Gliebe, J. Where do cyclists ride? A route choice model developed with revealed preference GPS data. Transp. Res. Part A 2012, 46, 1730–1740. [Google Scholar] [CrossRef]
- Luong, T.D.; Tahlyan, D.; Pinjari, A.R. Comprehensive Exploratory Analysis of Truck Route Choice Diversity in Florida. Transp. Res. Record. J. 2017, 2672, 152–163. [Google Scholar] [CrossRef]
- Tian, D.; Shan, X.; Sheng, Z.; Wang, Y.; Tang, W.; Wang, J. Break-taking behaviour pattern of long-distance freight vehicles based on GPS trajectory data. IET Intell. Transp. Syst. 2017, 11, 340–348. [Google Scholar] [CrossRef]
- Arentze, T.; Feng, T.; Timmermans, H.; Robroeks, J. Context-dependent influence of road attributes and pricing policies on route choice behavior of truck drivers: Results of a conjoint choice experiment. Transportation 2012, 39, 1173–1188. [Google Scholar] [CrossRef]
- Hess, S.; Quddus, M.; Rieser-Schüssler, N.; Daly, A. Developing advanced route choice models for heavy goods vehicles using GPS data. Transp. Res. Part E 2015, 77, 29–44. [Google Scholar] [CrossRef]
- Oka, H.; Hagino, Y.; Kenmochi, T.; Tani, R.; Nishi, R.; Endo, K.; Fukuda, D. Predicting travel pattern changes of freight trucks in the Tokyo Metropolitan area based on the latest large-scale urban freight survey and route choice modeling. Transp. Res. Part E Logist. Transp. Rev. 2019, 129, 305–324. [Google Scholar] [CrossRef]
- Fu, Y.; Shi, X. Research on Freight Truck Operation Characteristics Based on GPS Data. Procedia-Soc. Behav. Sci. 2013, 96, 2320–2331. [Google Scholar]
- Huang, J.; Wang, L.; Tian, C. Mining freight truck’s trip patterns from GPS data. In Proceedings of the 17th International IEEE Conference on Intelligent Transportation Systems (ITSC), Qingdao, China, 8–11 October 2014; pp. 1988–1994. [Google Scholar]
- Bliemer, M.C.J.; Bovy, P.H.L. Impact of Route Choice Set on Route Choice Probabilities. Transp. Res. Rec. 2008, 2076, 10–19. [Google Scholar] [CrossRef]
- Shlomo Bekhor, M.B.-A.; Ramming, M. Evaluation of choice set generation algorithms for route choice models. Ann. Oper. Res. 2006, 144, 235–247. [Google Scholar] [CrossRef]
- Ben-Akiva, M.; Bergman, M.J.; Daly, A.J.; Ramaswamy, R. Modeling inter urban route choice behavior. In Proceedings of the 9th International Symposium on Transportation and Traffic Theory, Delft, The Netherlands, 11–13 July 1984. [Google Scholar]
- Prato, C.G.; Bekhor, S. Applying Branch-and-Bound Technique to Route Choice Set Generation. Transp. Res. Rec. 2006, 1985, 19–28. [Google Scholar] [CrossRef]
- Bovy, P.H.L. On Modelling Route Choice Sets in Transportation Networks: A Synthesis. Transp. Rev. 2009, 29, 43–68. [Google Scholar] [CrossRef]
- Frejinger, E.; Bierlaire, M.; Ben-Akiva, M. Sampling of alternatives for route choice modeling. Transp. Res. Part B 2009, 43, 984–994. [Google Scholar] [CrossRef]
- Rieser-Schussler, N.; Balmer, M.; Axhausen, K. Route choice sets for very high-resolution data. Transp. A Transp. Sci. 2013, 9, 825–845. [Google Scholar] [CrossRef][Green Version]
- Tahlyan, D.; Pinjari, A.R. Performance evaluation of choice set generation algorithms for analyzing truck route choice: Insights from spatial aggregation for the breadth first search link elimination (BFS-LE) algorithm. Transp. A Transp. Sci. 2020, 16, 1030–1061. [Google Scholar] [CrossRef]
- Cascetta, E.; Nuzzolo, A.; Russo, F.; Vitetta, A. A modified logit route choice model overcoming path overlapping problems. Specification and some calibration results for interurban networks. In Proceedings of the 13th International Symposium on Transportation and Traffic Theory, Lyon, France, 24–26 July 1996. [Google Scholar]
- Amer, A.; Chow, J.Y.J. A downtown on-street parking model with urban truck delivery behavior. Transp. Res. Part A Policy Pract. 2017, 102, 51–67. [Google Scholar] [CrossRef]
- Vasavada, U. Kmenta, Jan. Elements of Econometrics, 2nd ed. New York: Macmillan Publishing Co., 1986, xii + 786 pp., $26.50. Am. J. Agric. Econ. 1988, 70, 210–211. [Google Scholar] [CrossRef]
- Prato, C.G. Route choice modeling: Past, present and future research directions. J. Choice Model. 2009, 2, 65–100. [Google Scholar] [CrossRef]
- Deng, Y.; Li, M.; Tang, Q.; He, R.; Hu, X. Heterogenous Trip Distance-Based Route Choice Behavior Analysis Using Real-World Large-Scale Taxi Trajectory Data. J. Adv. Transp. 2020, 2020, 8836511. [Google Scholar] [CrossRef]
| user_id | lon | gtm | agl | mlg | spd | hgt | lat |
|---|---|---|---|---|---|---|---|
| 2020-09-10 XXAXX012 | 125.1761 | 2020-09-10 8:21:37 | 252 | 82,001 | 28 | 247 | 43.83352 |
| 2020-09-10 XXAXX012 | 125.1729 | 2020-09-10 8:22:07 | 246 | 82,004 | 10.6 | 246 | 43.83272 |
| 2020-09-10 XXAXX012 | 125.1722 | 2020-09-10 8:22:37 | 243 | 82,004 | 23.5 | 266 | 43.83248 |
| 2020-09-10 XXAXX012 | 125.1678 | 2020-09-10 8:23:07 | 252 | 82,008 | 40.2 | 246 | 43.83145 |
| 2020-09-10 XXAXX012 | 125.1678 | 2020-09-10 8:23:07 | 252 | 82,008 | 40.2 | 246 | 43.83145 |
| 2020-09-10 XXAXX012 | 125.1678 | 2020-09-10 8:23:07 | 252 | 82,008 | 40.2 | 246 | 43.83145 |
| Parameter | Type | Description |
|---|---|---|
| Initial node | Numeric | Node identifier for the starting point of the road segment |
| Final node | Numeric | Node identifier for the ending point of the road segment |
| LINK_ID | Numeric | Identifier for the road segment |
| TT | Numeric | Time required for a vehicle to travel through the road segment under free-flow conditions, measured in seconds |
| Length | Numeric | Length of the road segment, measured in meters |
| Variable Type | Feature Variable | Variable Coefficient | Variable Description |
|---|---|---|---|
| Path Characteristics | Travel Time | Continuous variable, unit: minutes | |
| Deviation Degree | Continuous variable, dimensionless value | ||
| Road Characteristics | Number of Left Turns | Discrete variable, unit: count | |
| Number of Right Turns | Discrete variable, unit: count | ||
| Number of Intersections | Discrete variable, unit: count | ||
| Proportion of Main Roads | Continuous variable, unit: percentage | ||
| Proportion of Secondary Roads | Continuous variable, unit: percentage | ||
| Proportion of Side Roads | Continuous variable, unit: percentage | ||
| Proportion of Side Roads | Path Size Value | Continuous variable, unit: percentage |
| Explanatory Variables | PSL | MNL | ||||
|---|---|---|---|---|---|---|
| Coef | Student’s t-Value | p-Value | Coef | Student’s t-Value | p-Value | |
| Travel Time | −1.140 | −4.813 | 0.000 | −1.420 | −4.515 | 0.000 |
| Route Detour | −2.140 | −4.972 | 0.000 | −0.230 | −2.073 | 0.004 |
| Number of Left Turns | −2.670 | −5.267 | 0.000 | −0.084 | −3.798 | 0.000 |
| Number of Right Turns | 0.079 | 2.890 | 0.032 | 0.825 | 5.143 | 0.000 |
| Number of Intersections Crossed | −0.662 | −3.712 | 0.000 | −0.248 | −4.469 | 0.000 |
| Proportion of Main Roads | −3.180 | −6.474 | 0.000 | −4.690 | −4.363 | 0.000 |
| Proportion of Secondary Roads | −3.700 | −2.928 | 0.004 | −11.700 | −9.398 | 0.000 |
| Proportion of Local Roads | 13.900 | 5.970 | 0.000 | 15.200 | 12.207 | 0.000 |
| 37 | 13.631 | 0.000 | — | — | — | |
| Sample Size | 5405 | 5405 | ||||
| Null log–likelihood | −214.198 | −214.198 | ||||
| Final log–likelihood | −144.155 | −152.937 | ||||
| Rho-square- | 0.327 | 0.286 | ||||
| Adj Rho-square-Adj | 0.285 | 0.244 | ||||
| Model | Number of Path Selections | Number of Correct Model Predictions | Number of Errors | Hit Ratio |
|---|---|---|---|---|
| PSL | 2308 | 1843 | 465 | 79.85% |
| MNL | 2308 | 1618 | 690 | 70.10% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, L.; Gao, T.; Meng, L.; Ding, T.; Chen, W. Research on the Route Choice Behavior of Urban Freight Vehicles Based on GPS Data. Mathematics 2024, 12, 291. https://doi.org/10.3390/math12020291
Zheng L, Gao T, Meng L, Ding T, Chen W. Research on the Route Choice Behavior of Urban Freight Vehicles Based on GPS Data. Mathematics. 2024; 12(2):291. https://doi.org/10.3390/math12020291
Chicago/Turabian StyleZheng, Lili, Tian Gao, Lin Meng, Tongqiang Ding, and Wenhao Chen. 2024. "Research on the Route Choice Behavior of Urban Freight Vehicles Based on GPS Data" Mathematics 12, no. 2: 291. https://doi.org/10.3390/math12020291
APA StyleZheng, L., Gao, T., Meng, L., Ding, T., & Chen, W. (2024). Research on the Route Choice Behavior of Urban Freight Vehicles Based on GPS Data. Mathematics, 12(2), 291. https://doi.org/10.3390/math12020291




