A Validation of the Phenomenon of Linearly Many Faults on Burnt Pancake Graphs with Its Applications
Abstract
1. Introduction
1.1. Background
1.2. Organization
2. Preliminaries
2.1. Definitions and Terminologies
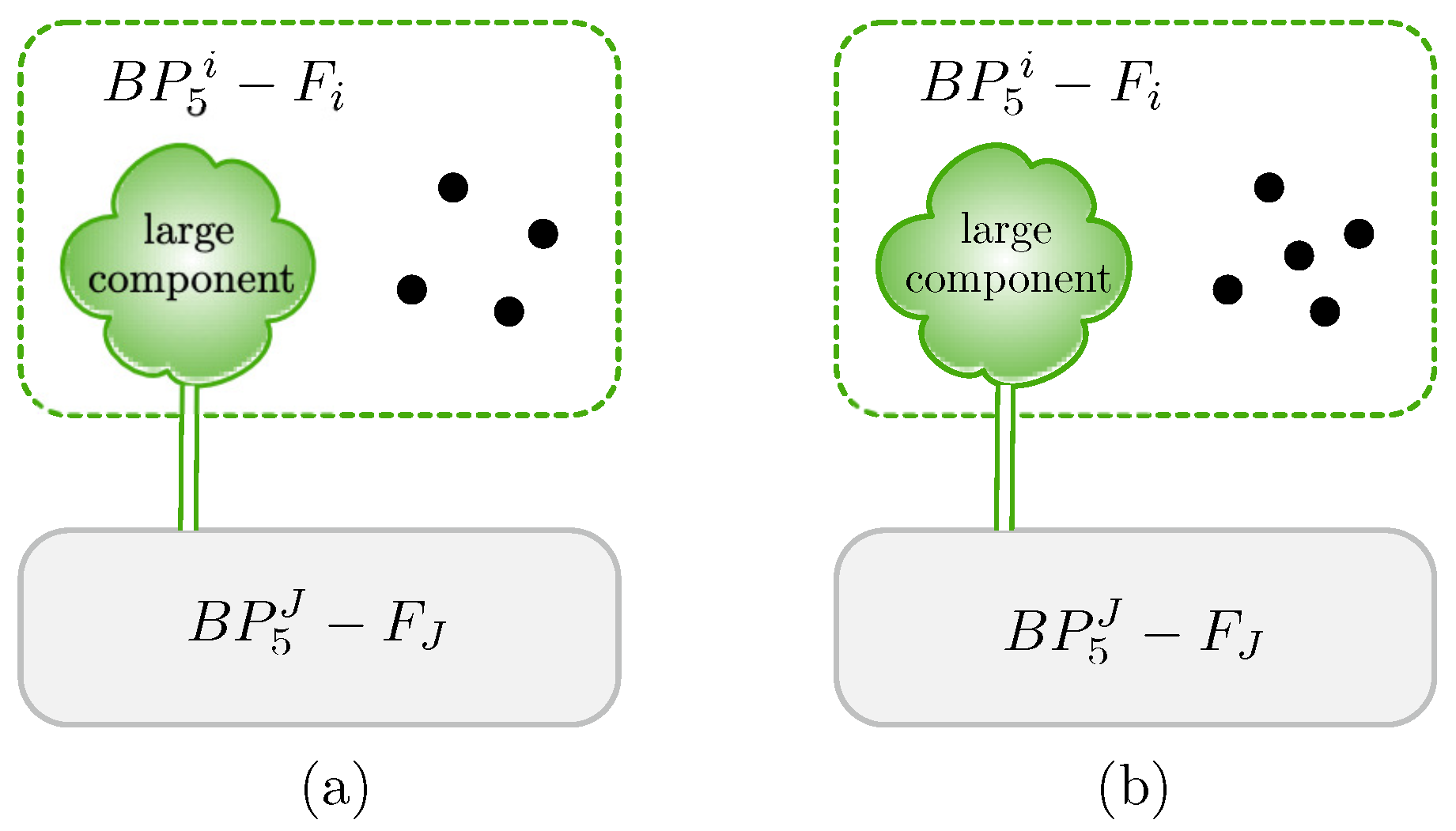
- (i)
- For with , has a large component along with small components containing totally at most vertices;
- (ii)
- For with , has at most k components;
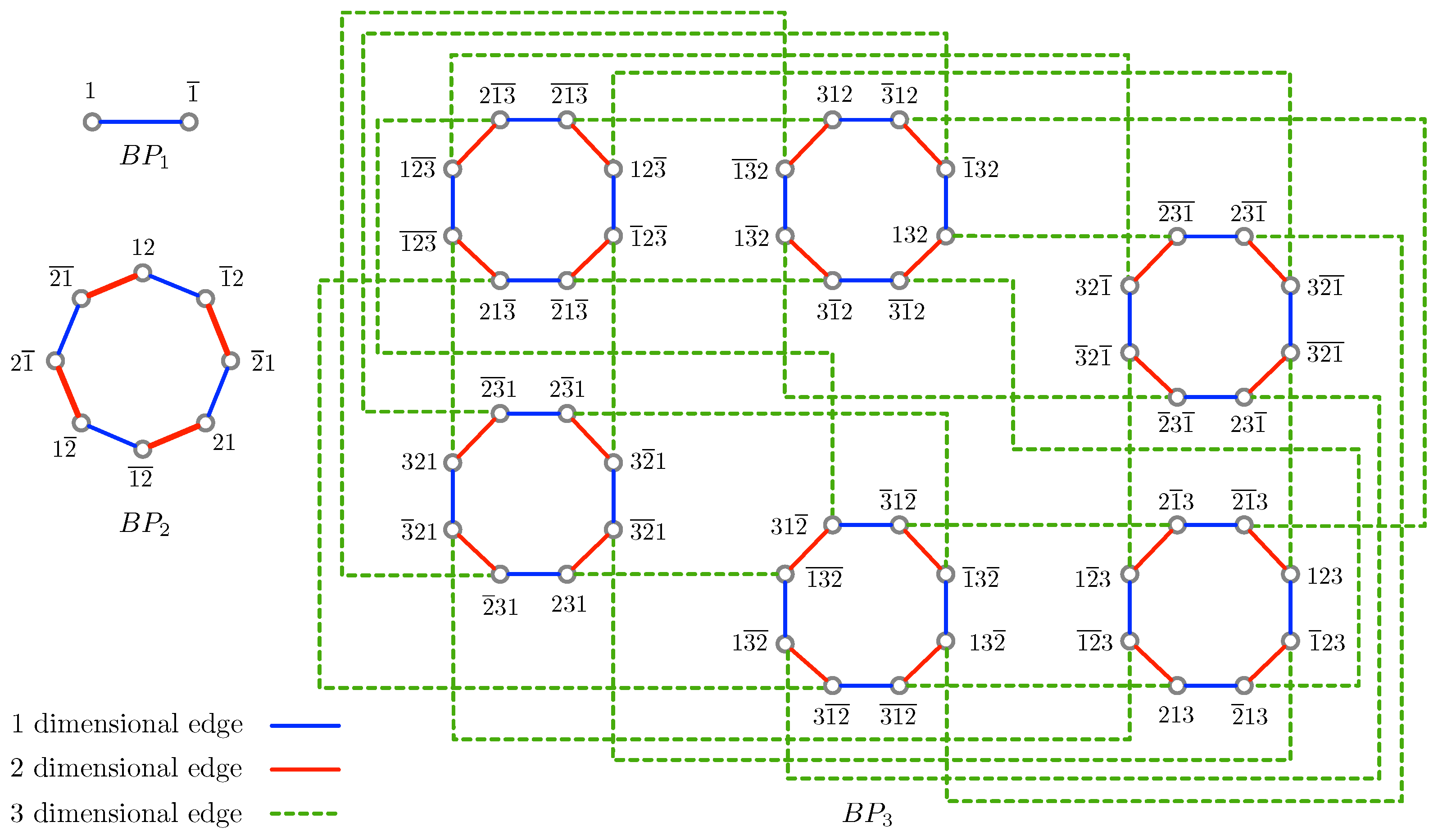
2.2. Burnt Pancake Graphs
- (1)
- is an n-regular graph with edges. if , and .
- (2)
- For , .
- (3)
- For , the girth of is .
- (1)
- If , has two components, one of which is a singleton or an edge. Furthermore, if the small component is an edge, then F is the neighborhood of this edge and .
- (2)
- If , has a large component along with smaller components containing totally at most two vertices.
- (3)
- If , has a large component along with smaller components containing totally at most three vertices.
- (1)
- If , has two components, one of which is a singleton or an edge. Furthermore, if the small component is an edge, then F is the neighborhood of this edge and .
- (2)
- If , has a large component along with smaller components containing totally at most two vertices.
- (3)
- If , has a large component along with smaller components containing totally at most three vertices.
3. Linearly Many Faults in Burnt Pancake Graphs
4. Applications to Extra Edge Connectivity and Component Edge Connectivity
4.1. Relation between and
4.2. Relation between and
4.3. Relation between and
5. Concluding Remarks
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yang, X.; Evans, D.J.; Chen, B.; Megson, G.M.; Lai, H. On the maximal connected component of hypercube with faulty vertices. Int. J. Comput. Math. 2004, 81, 515–525. [Google Scholar] [CrossRef]
- Cheng, E.; Lipták, L. Linearly many faults in Cayley graphs generated by transposition trees. Inf. Sci. 2007, 177, 4877–4882. [Google Scholar] [CrossRef]
- Cheng, E.; Lipták, L.; Sala, F. Linearly many faults in 2-tree-generated networks. Networks 2010, 55, 90–98. [Google Scholar] [CrossRef]
- Li, P.; Meng, X. Linearly many faults in Cayley graphs generated by transposition triangle free unicyclic graphs. Theor. Comput. Sci. 2020, 847, 95–102. [Google Scholar] [CrossRef]
- Yuan, A.; Cheng, E.; Lipták, L. Linearly many faults in (n, k)-star graphs. Int. J. Found. Comput. Sci. 2011, 22, 1729–1745. [Google Scholar] [CrossRef]
- Cheng, E.; Lipták, L.; Yuan, A. Linearly many faults in arrangement graphs. Networks 2013, 61, 281–289. [Google Scholar] [CrossRef]
- Angjeli, A.; Cheng, E.; Lipták, L. Linearly many faults in augmented cubes. Int. J. Parallel Emergent Distrib. Syst. 2013, 28, 475–483. [Google Scholar] [CrossRef]
- Angjeli, A.; Cheng, E.; Lipták, L. Linearly many faults in dual-cube-like networks. Theor. Comput. Sci. 2013, 472, 1–8. [Google Scholar] [CrossRef]
- Cheng, E.; Lipman, M.J.; Lipták, L. Matching preclusion and conditional matching preclusion for regular interconnection networks. Discret. Appl. Math. 2012, 160, 1936–1954. [Google Scholar] [CrossRef]
- Cheng, E.; Qiu, K.; Shen, Z. Connectivity results of complete cubic networks as associated with linearly many faults. J. Interconnect. Netw. 2015, 15, 155007. [Google Scholar] [CrossRef]
- Cheng, E.; Qiu, K.; Shen, Z. A strong connectivity property of the generalized exchanged hypercube. Discret. Appl. Math. 2017, 216, 529–536. [Google Scholar] [CrossRef]
- Gu, M.M.; Hao, R.X.; Cheng, E. Note on applications of linearly many faults. Comput. J. 2020, 63, 1406–1416. [Google Scholar] [CrossRef]
- Harary, F. Conditional connectivity. Networks 1983, 143, 346–357. [Google Scholar] [CrossRef]
- Fábrega, J.; Fiol, M.A. On the extra connectivity graphs. Discret. Math. 1996, 155, 49–57. [Google Scholar] [CrossRef]
- Sampathkumar, E. Connectivity of a graph—A generalization. J. Comb. Inf. Syst. Sci. 1984, 9, 71–78. [Google Scholar]
- Chartrand, G.; Kapoor, S.; Lesniak, L.; Lick, D.R. Generalized connectivity in graphs. Bull. Bombay Math. Colloq. 1984, 2, 1–6. [Google Scholar]
- Hsu, L.-H.; Cheng, E.; Lipták, L.; Tan, J.M.; Lin, C.-K.; Ho, T.-Y. Component connectivity of the hypercubes. Int. J. Comput. Math. 2012, 89, 137–145. [Google Scholar] [CrossRef]
- Zhao, S.; Yang, W.; Zhang, S.; Xu, L. Component edge connectivity of hypercubes. Int. J. Found. Comput. Sci. 2018, 29, 995–1001. [Google Scholar] [CrossRef]
- Yang, W.; Meng, J. Extraconnectivity of hypercubes. Appli. Math. Lett. 2009, 22, 887–891. [Google Scholar] [CrossRef]
- Hsieh, S.-Y.; Chang, Y.-H. Extraconnectivity of k-ary n-cube networks. Theor. Comput. Sci. 2012, 443, 63–69. [Google Scholar] [CrossRef]
- Chang, N.-W.; Hsieh, S.-Y. {2,3}-extraconnectivity of hypercube-like networks. J. Comput. Syst. Sci. 2013, 79, 669–688. [Google Scholar] [CrossRef]
- Li, P.; Xu, M. Fault-tolerant strong Menger (edge) connectivity and 3-extra edge-connectivity of balanced hypercubes. Theoret. Comput. Sci. 2018, 707, 56–68. [Google Scholar] [CrossRef]
- Li, X.; Fan, J.; Lin, C.-K.; Cheng, B.-L.; Jia, X. The extra connectivity, extra conditional diagnosability and t/k-diagnosability of the data center network DCell. Theor. Comput. Sci. 2019, 766, 16–29. [Google Scholar] [CrossRef]
- Chang, J.-M.; Pai, K.-J.; Ro, R.-Y.; Yang, J.-S. The 4-component connectivity of alternating group networks. Theor. Comput. Sci. 2019, 766, 38–45. [Google Scholar] [CrossRef]
- Gu, M.-M.; Hao, R.-X.; Tang, S.-M.; Chang, J.-M. Analysis on component connectivity of bubble-sort star graphs and burnt pancake graphs. Discret. Appl. Math. 2020, 279, 80–91. [Google Scholar] [CrossRef]
- Gu, M.-M.; Chang, J.-M.; Hao, R.-X. On computing component (edge) connectivities of balanced hypercubes. Comput. J. 2020, 63, 1311–1320. [Google Scholar] [CrossRef]
- Gu, M.-M.; Chang, J.-M.; Hao, R.-X. On component connectivity of hierarchical star networks. Int. J. Found. Comput. Sci. 2021, 31, 313–326. [Google Scholar] [CrossRef]
- Liu, J.; Zhou, S.; Zhang, H.; Chen, G. Vulnerability analysis of multiprocessor system based on burnt pancake networks. Discret. Appl. Math. 2022, 314, 304–320. [Google Scholar] [CrossRef]
- Zhao, S.; Yang, W. Conditional connectivity of folded hypercubes. Discret. Appl. Math. 2019, 257, 388–392. [Google Scholar] [CrossRef]
- Hao, R.-X.; Gu, M.-M.; Chang, J.-M. Relationship between extra edge connectivity and component edge connectivity for regular graphs. Theor. Comput. Sci. 2020, 833, 41–55. [Google Scholar] [CrossRef]
- Li, X.; Lin, C.-K.; Fan, J.; Jia, X.; Cheng, B.-L.; Zhou, J. Relationship between extra connectivity and component connectivity in networks. Comput. J. 2021, 64, 38–53. [Google Scholar] [CrossRef]
- Guo, L.; Zhang, M.; Zhai, S.; Xu, L. Relation of extra edge connectivity and component edge connectivity for regular networks. Int. J. Found. Comput. Sci. 2021, 32, 137–149. [Google Scholar] [CrossRef]
- Poulik, S.; Ghorai, G. Determination of journeys order based on graph’s Wiener absolute index with bipolar fuzzy information. Inform. Sci. 2021, 545, 608–619. [Google Scholar] [CrossRef]
- Poulik, S.; Ghorai, G. Connectivity concepts in bipolar fuzzy incidence graphs. Thai J. Math. 2022, 20, 1609–1619. [Google Scholar]
- Poulik, S.; Ghorai, G.; Xin, Q. Explication of crossroads order based on Randic index of graph with fuzzy information. Soft Comput. 2023. [Google Scholar] [CrossRef]
- Poulik, S.; Ghorai, G. First entire Zagreb index of fuzzy graph and its application. Axioms 2023, 12, 415. [Google Scholar]
- Gates, W.H.; Papadimitriou, C.H. Bounds for sorting by prefix reversal. Discret. Math. 1979, 27, 47–49. [Google Scholar] [CrossRef]
- Bulteau, L.; Fertin, G.; Rusu, I. Pancake flipping is hard. J. Comput. Syst. Sci. 2015, 81, 1556–1574. [Google Scholar] [CrossRef]
- Iwasaki, T.; Kaneko, K. Fault-tolerant routing in burnt pancake graphs. Inform. Process. Lett. 2010, 110, 535–538. [Google Scholar] [CrossRef]
- Song, S.; Li, X.; Zhou, S.; Chen, M. Fault tolerance and diagnosability of burnt pancake networks under the comparison model. Theor. Comput. Sci. 2015, 582, 48–59. [Google Scholar] [CrossRef]
- Song, S.; Zhou, S.; Li, X. Conditional diagnosability of burnt pancake networks under the PMC model. Comput. J. 2016, 59, 91–105. [Google Scholar]
- Chin, C.; Weng, T.-H.; Hsu, L.-H.; Chiou, S.-C. The spanning connectivity of the burnt pancake graphs. IEICE Trans. Inform. Syst. 2009, E92-D, 389–400. [Google Scholar] [CrossRef]
- Dilixiati, S.; Sabir, E.; Meng, J. Star structure connectivities of pancake graphs and burnt pancake graphs. Int. J. Parallel Emergent Distrib. Syst. 2021, 36, 440–448. [Google Scholar] [CrossRef]
- Wang, N.; Meng, J.; Tian, Y. Neighbor-connectivity of pancake networks and burnt pancake networks. Theor. Comput. Sci. 2022, 916, 31–39. [Google Scholar] [CrossRef]
- Gu, M.-M.; Chang, J.-M. Neighbor connectivity of pancake graphs and burnt pancake graphs. Discret. Appl. Math. 2023, 324, 46–57. [Google Scholar] [CrossRef]
- Compeau, P.E.C. Girth of pancake graphs. Discret. Appl. Math. 2011, 159, 1641–1645. [Google Scholar] [CrossRef]
| 1 | four singletons | ||
| 2 | an edge and two singletons | ||
| 3 | a 2-path and a singleton | ||
| 4 | two edges | ||
| 5 | a graph isomorphic to | ||
| 6 | a 3-path |
| 1 | five singletons | ||
| 2 | an edge and three singletons | ||
| 3 | two edges and a singleton | ||
| 4 | a 2-path and two singletons | ||
| 5 | a 2-path and an edge | ||
| 6 | a 3-path and a singleton | ||
| 7 | a graph isomorphic to and a singleton | ||
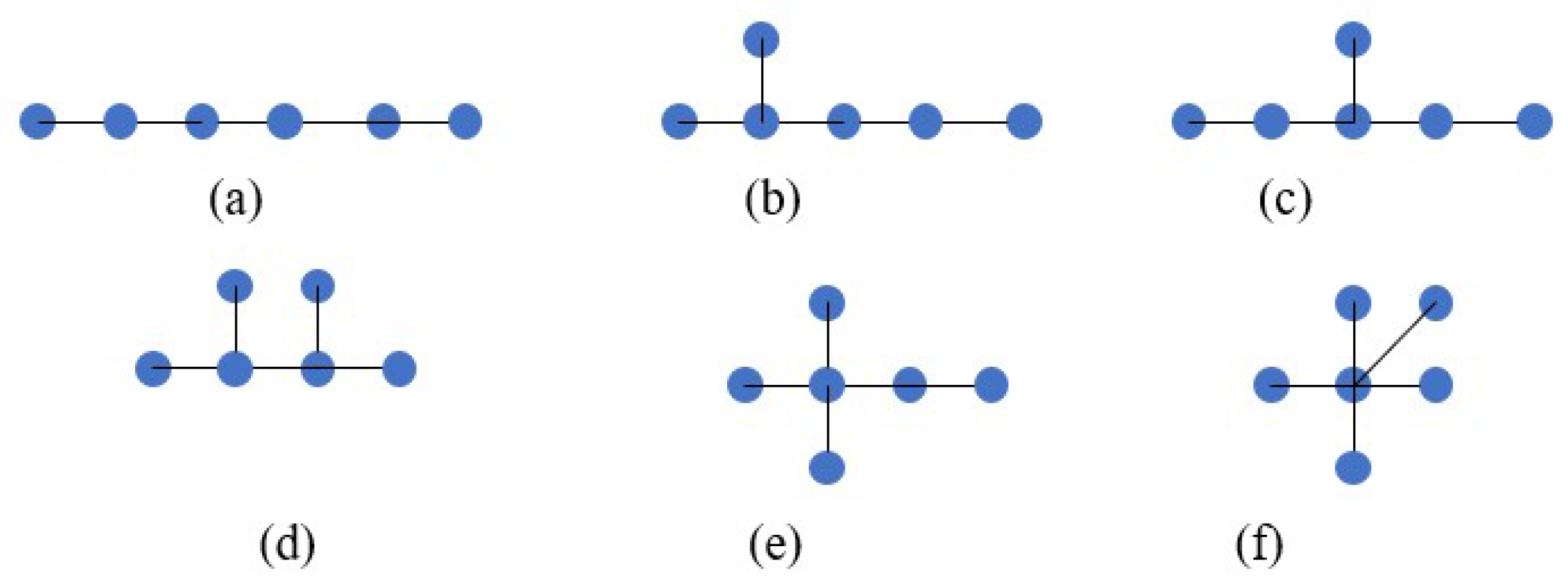
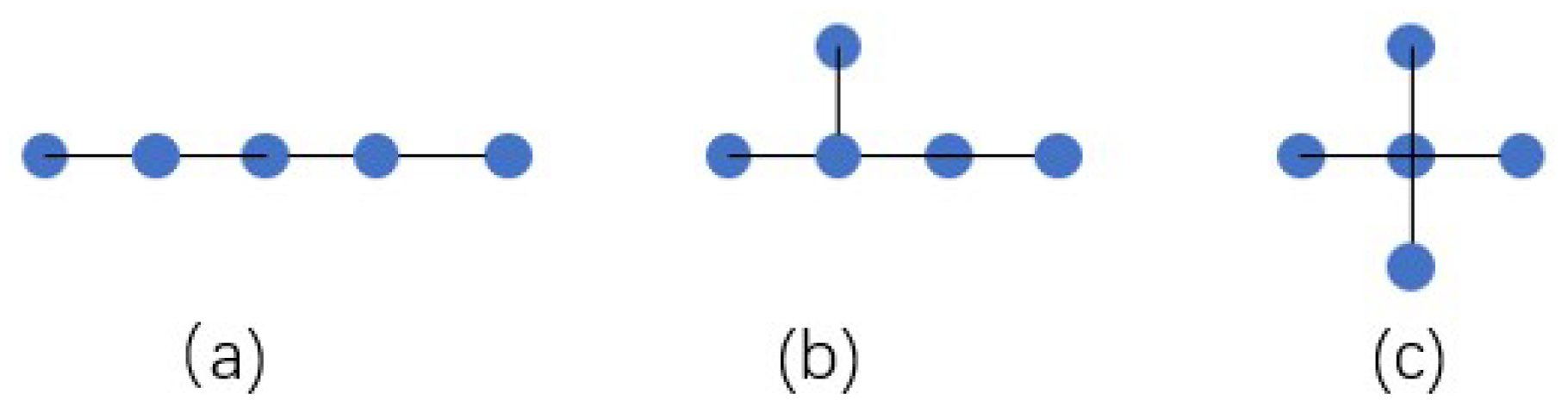
| 8 | a 4-path, Figure 2a | ||
| 9 | a graph isomorphic to , Figure 2c | ||
| 10 | a tree with 5 vertices, Figure 2b |
| 1 | six singletons | ||
| 2 | an edge and four singletons | ||
| 3 | a 2-path and three singletons | ||
| 4 | a 3-path and two singletons | ||
| 5 | two singletons and two edges | ||
| 6 | a 4-path and a singleton | ||
| 7 | a singleton and a graph isomorphic to | ||
| 8 | a singleton and a tree with 5 vertices, Figure 2b | ||
| 9 | three edges | ||
| 10 | an edge and 3-path | ||
| 11 | an edge and a graph isomorphic to | ||
| 12 | an edge, a singleton and 2-path | ||
| 13 | two 2-paths | ||
| 14 | a 5-path, Figure 3a | ||
| 15 | a graph isomorphic to , Figure 3f | ||
| 16 | a tree with 6 vertices, isomorphic to one of Figure 3b–d |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gu, M.-M.; Yan, H.-X.; Chang, J.-M. A Validation of the Phenomenon of Linearly Many Faults on Burnt Pancake Graphs with Its Applications. Mathematics 2024, 12, 268. https://doi.org/10.3390/math12020268
Gu M-M, Yan H-X, Chang J-M. A Validation of the Phenomenon of Linearly Many Faults on Burnt Pancake Graphs with Its Applications. Mathematics. 2024; 12(2):268. https://doi.org/10.3390/math12020268
Chicago/Turabian StyleGu, Mei-Mei, Hong-Xia Yan, and Jou-Ming Chang. 2024. "A Validation of the Phenomenon of Linearly Many Faults on Burnt Pancake Graphs with Its Applications" Mathematics 12, no. 2: 268. https://doi.org/10.3390/math12020268
APA StyleGu, M.-M., Yan, H.-X., & Chang, J.-M. (2024). A Validation of the Phenomenon of Linearly Many Faults on Burnt Pancake Graphs with Its Applications. Mathematics, 12(2), 268. https://doi.org/10.3390/math12020268







