The General Extended Adjacency Eigenvalues of Chain Graphs

Abstract

In this article, we discuss the spectral properties of the general extended adjacency matrix for chain graphs. In particular, we discuss the eigenvalues of the general extended adjacency matrix of the chain graphs and obtain its general extended adjacency inertia. We obtain bounds for the largest and the smallest general extended adjacency eigenvalues and characterize the extremal graphs. We also obtain a lower bound for the spread of the general extended adjacency matrix. We characterize chain graphs with all the general extended adjacency eigenvalues being simple and chain graphs that are non-singular under the general extended adjacency matrix. Further, we determine the explicit formula for the determinant and the trace of the square of the general extended adjacency matrix of chain graphs. Finally, we discuss the energy of the general extended adjacency matrix and obtain some bounds for it. We characterize the extremal chain graphs attaining these bounds.

1. Introduction

Consider a simple graph, G, with vertex set $V\left(G\right)=\{v_1,v_2,\dots ,v_n\}$, edge set $E\left(G\right)$, and degree sequence $\{d_1,d_2,\cdots ,d_n\}$ (or $d_{v_i}$). The number of elements in $V\left(G\right)$ is order n and that of $E\left(G\right)$ is size m of G. If vertices u and v are adjacent, we write $u\sim v$, otherwise $u\nsim v$. If the degree of each vertex is the same, then G is said to be a regular graph. The complete bipartite graph with partite sets $m_1$ and $n_1$ is denoted by $K_{m_1,n_1}$; more graph theoretic notations can be found in [1].

The adjacency matrix $A\left(G\right)=\left(a_{ij}\right)$ of G is a square matrix of order $n,$ where $a_{ij}$ is 1 if $v_i{v}_j\in E\left(G\right)$, and 0 otherwise. The matrix $A\left(G\right)$ is real and symmetric. We list its eigenvalues in non-increasing order as ${\lambda }_1\ge {\lambda }_2\ge \cdots \ge {\lambda }_n$. The largest eigenvalue, ${\lambda }_1$, is known as the spectral radius of G. According to the Perron–Frobenius theorem, ${\lambda }_1$ is unique, and $|{\lambda }_i|\le {\lambda }_1$ and its associated eigenvector state that X has positive entries. In the literature, the trace norm $|{\lambda }_1|+|{\lambda }_2|+\cdots +|{\lambda }_n|$ of $A\left(G\right)$ is studied under the name energy, denoted by $\mathcal{E}\left(A\right(G\left)\right)$, and has its origin in theoretical chemistry, where it helps in approximating the total $\pi$-electron energy of unsaturated hydrocarbons. There is a wealth of literature data regarding energy, as well as the other spectral graph invariants associated with the adjacency matrix $A\left(G\right)$; see [2,3,4,5]. The details of the eigenvalues of the adjacency matrix and Laplacian matrix and bounds on the energy, $\mathcal{E}\left(A\right(G\left)\right)$, are well studied in the literature; see [6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43].

For a graph, $G,$ a general vertex-degree-based topological index, $\varphi$, is defined as

$$\varphi \left(G\right)=\sum _{uv\in E\left(G\right)}{\varphi }_{d_u{d}_v},$$

where ${\varphi }_{d_u{d}_v}$ is a function of vertex degrees satisfying the symmetric property ${\varphi }_{d_u{d}_v}={\varphi }_{d_v{d}_u}$. For particular values of ${\varphi }_{d_u{d}_v}$, we have well known topological indices, such as the arithmetic–geometric index for ${\varphi }_{d_u{d}_v}=\frac{d_u+d_v}{2\sqrt{d_u{d}_v}}$, the general Randić index for ${\varphi }_{d_u{d}_v}={\left(d_u{d}_v\right)}^{\alpha }$ (for $\alpha =-\frac{1}{2}$, we obtain the ordinary Randić index ${\displaystyle R=\sum _{uv\in E\left(G\right)}\frac{1}{\sqrt{d_u{d}_v}}}$), the general Sombor index for ${\varphi }_{d_u{d}_v}={\left(d_u^2+d_v^2\right)}^{\alpha }$ (for $\alpha =\frac{1}{2}$, we obtain the Sombor index ${\displaystyle S=\sum _{uv\in E\left(G\right)}\sqrt{d_u^2+d_v^2}}$), and several other indices, such as the first Zagreb index, the second Zagreb index, the forgotten topological index, the harmonic index, the sum-connectivity index, the geometric–arithmetic index, the atom–bond connectivity index, and all other remaining degree-based indices.

The general adjacency matrix ($A_{\varphi }$-matrix) associated with the topological index $\varphi$ of G is a real symmetric matrix, defined by

$$A_{\varphi }\left(G\right)={\left(a_{\varphi }\right)}_{ij}=\left\{\begin{array}{cc}{\varphi }_{d_u{d}_v}\hfill & \mathrm{if}u\sim v,\hfill \\ 0\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

(1)

The set of all eigenvalues of $A_{\varphi }\left(G\right)$ is known as the general adjacency spectrum ($A_{\varphi }$-spectrum) of G and are denoted by ${\lambda }_1\left(A_{\varphi }\left(G\right)\right)\ge {\lambda }_2\left(A_{\varphi }\left(G\right)\right)\ge \cdots \ge {\lambda }_n\left(A_{\varphi }\left(G\right)\right),$ where ${\lambda }_1\left(A_{\varphi }\left(G\right)\right)$ is the general adjacency spectral radius of $G.$ In addition, for a connected graph, if ${\varphi }_{d_u{d}_v}>0$ whenever $u\sim v$, then by the Perro–Frobenius theorem, ${\lambda }_1\left(A_{\varphi }\left(G\right)\right)$ is unique and its associated eigenvector has positive components. Also in this case, $|{\lambda }_i\left(A_{\varphi }\left(G\right)\right)|\le {\lambda }_1\left(A_{\varphi }\left(G\right)\right),$ for $i=2,\cdots ,n-1,n.$ The energy of general extended adjacency matrix $A_{\varphi }\left(G\right)$, associated with the topological index $\varphi$, was introduced in [16] and is defined as

$${\mathcal{E}}_{\varphi }\left(G\right)=\sum _{i=1}^n\left|{\lambda }_i\left(A_{\varphi }\left(G\right)\right)\right|.$$

If ${\varphi }_{d_u{d}_v}=1,$ when $u\sim v$, then $A_{\varphi }\left(G\right)$ is the much studied adjacency matrix $A\left(G\right)$ and ${\mathcal{E}}_{\varphi }\left(G\right)$ is the usual graph energy, ${\displaystyle \mathcal{E}\left(G\right)=\sum _{i=1}^n\left|{\lambda }_i\right|}$. If ${\varphi }_{d_u{d}_v}=d_u+d_v,$ when $u\sim v$, then $A_{\varphi }\left(G\right)$ represents the first Zagreb matrix and ${\mathcal{E}}_{\varphi }\left(G\right)$ represents the first Zagreb energy of G. If ${\varphi }_{d_u{d}_v}=d_u{d}_v$, when $u\sim v$, then $A_{\varphi }\left(G\right)$ represents the second Zagreb matrix and ${\mathcal{E}}_{\varphi }\left(G\right)$ represents the second Zagreb energy of G. If ${\varphi }_{d_u{d}_v}=\frac{1}{\sqrt{d_u{d}_v}},$ when $u\sim v$, then $A_{\varphi }\left(G\right)$ represents the Randić matrix and ${\mathcal{E}}_{\varphi }\left(G\right)$ represents the Randić energy of G. If ${\varphi }_{d_u{d}_v}=\frac{1}{2}\left(\frac{d_u}{d_v}+\frac{d_v}{d_u}\right),$ when $u\sim v$, then $A_{\varphi }\left(G\right)$ represents the extended adjacency matrix and ${\mathcal{E}}_{\varphi }\left(G\right)$ represents the extended energy of G. If ${\varphi }_{d_u{d}_v}=\frac{1}{\sqrt{d_u+d_v}},$ when $u\sim v$, then $A_{\varphi }\left(G\right)$ represents the sum-connectivity matrix and ${\mathcal{E}}_{\varphi }\left(G\right)$ represents the sum-connectivity energy of G. If ${\varphi }_{d_u{d}_v}=\sqrt{\frac{d_u+d_v-2}{d_u{d}_v}}$, when $u\sim v$, then $A_{\varphi }\left(G\right)$ represents the ABC-matrix and ${\mathcal{E}}_{\varphi }\left(G\right)$ represents the ABC-energy of G. If ${\varphi }_{d_u{d}_v}=\frac{2\sqrt{d_u{d}_v}}{d_u+d_v},$ when $u\sim v$, then $A_{\varphi }\left(G\right)$ represents the geometric–arithmetic matrix and ${\mathcal{E}}_{\varphi }\left(G\right)$ represents the geometric–arithmetic energy of G. If ${\varphi }_{d_u{d}_v}=\frac{d_u+d_v}{2\sqrt{d_u{d}_v}},$ when $u\sim v$, then $A_{\varphi }\left(G\right)$ represents the arithmetic–geometric matrix and ${\mathcal{E}}_{\varphi }\left(G\right)$ represents the arithmetic–geometric energy of G. If ${\varphi }_{d_u{d}_v}=\sqrt{d_u^2+d_v^2},$ when $u\sim v$, then $A_{\varphi }\left(G\right)$ represents the Sombor matrix and ${\mathcal{E}}_{\varphi }\left(G\right)$ represents the Sombor energy of G, and so on.

The spectral properties of matrix $A_{\varphi }\left(G\right)$ have attracted much attention from researchers and as such are one of the hot topics of spectral graph theory. More about the $A_{\varphi }$-matrix, including some recent results, can be found in [16,44,45,46,47,48,49].

Chain graphs are $\{2K_2,C_3,C_5\}$-free graphs. The vertex set of any chain graph, say G, consists of two color classes (or independent sets), each partitioned into h non-empty cells $V_1,V_2,\cdots ,V_h$ and $U_1,U_2,\cdots ,U_h$ of sizes $m_i$ and $n_i$, respectively. All vertices in $V_i$ are joined by (cross) edges to all vertices in ${\bigcup }_{j=1}^{h-(i-1)}{V}_j$ for $i=1,2,\cdots ,h.$ Therefore, if $u_i\in U_{i+1}$ and $u_j\in U_i$ ($v_k\in V_{t+1}$ and $v_l\in V_t$), then $N\left(u_j\right)\subset N\left(u_i\right)$ (respectively, $N\left(v_k\right)\subset N\left(v_l\right)$). From now onwards, we denote a chain graph by $G(m_1,m_2,\cdots ,m_h;n_1,n_2,\cdots ,n_h)$ with order $n={\sum }_{i=1}^h{m}_i+{\sum }_{i=1}^n{n}_i$. 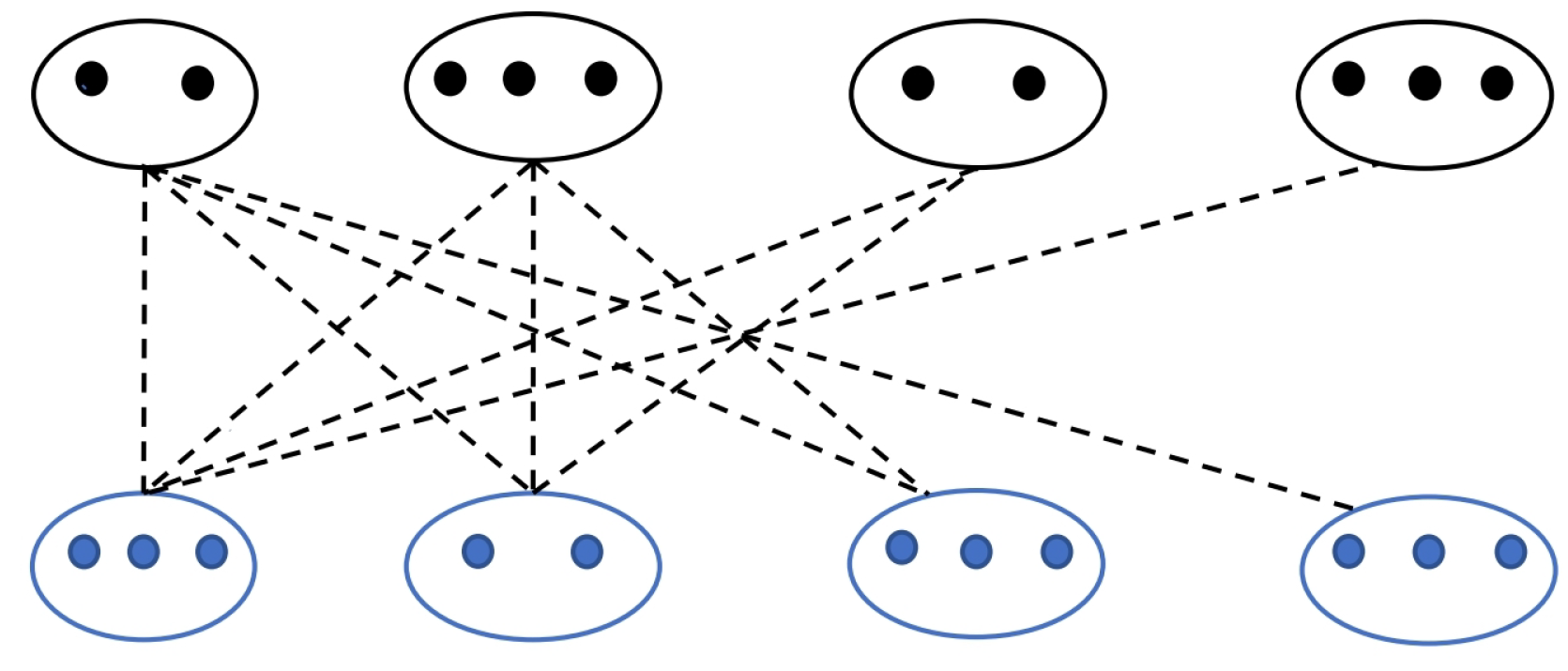For $h=1,$ we obtain the bipartite graph $G(m_1;n_1)\cong K_{m_1,n_1}.$ Figure 1 represents a chain graph, $G(2,3,2,3;3,2,3,3)$, of order $21,$ where black cells represent $V_i$s and blue cells denote $U_i$s. The dashed lines between two cells. $V_i$ and $U_j$, represent that each vertex of $V_i$ is adjacent to every vertex of $U_j$.

Chain graphs are not only important from an application point of view; they are also among the class of graphs that attain the extremal value for various spectral graph invariants. Hence, their spectral study forms a vital part of spectral graph theory. The spectral properties of chain graphs are considered for various graph matrices by different authors. For some recent papers on the spectral properties of chain graphs, we refer to [15,50,51] and the references therein. Here, we aim to extend the spectral study of chain graphs to a general extended adjacency matrix, $A_{\varphi }$.

The rest of the paper is organized as follows. In Section 2, we discuss the general extended adjacency eigenvalues of chain graphs and obtain their general extended adjacency inertia. We also obtain a lower bound for the spread of the general extended adjacency matrix and characterize chain graphs with all the general extended adjacency eigenvalues being simple and chain graphs that are non-singular under the general extended adjacency matrix. In Section 3, we discuss the general extended adjacency energy of chain graphs and obtain some sharp bounds. We characterize the chain graphs that attain these bounds. We end the article with the conclusions.

2. General Extended Adjacency Eigenvalues of Chain Graphs

Any column vector $X={(x_1,x_2,\cdots ,x_n)}^T\in {\mathbb{R}}^n$ can be regarded as a function defined on $V\left(G\right)$ that relates every $v_i$ to $x_i$, that is, $X\left(v_i\right)=x_i$ for all $i=1,2,\cdots ,n.$

A real number, $\lambda$, is the $A_{\varphi }$-eigenvalue with its associated eigenvector X if and only if $X\ne 0$, and for every $v_i\in V\left(G\right)$ we have

$$\lambda X\left(v_i\right)=\sum _{v_j\in N\left(v_i\right)}{\varphi }_{d_{v_i}{d}_{v_j}}X\left(v_j\right).$$

(2)

Equation (2) is the $(\lambda ,X)$-eigenequations for the $A_{\varphi }$-matrix. The following result provides information regarding some of the $A_{\varphi }$-eigenvalues of a graph when the graph has an independent set sharing the same neighborhood outside the independent set.

Theorem 1.

Let G be a connected graph with vertex set $V\left(G\right)=\{v_1,v_2,\cdots ,v_n\}$ and let $S=\{v_1,v_2,\cdots ,v_{\alpha }\}$ be an independent subset of G, such that $N\left(v_i\right)=N\left(v_j\right)$ for all $i,j\in \{1,2,\cdots ,\alpha \}$, then 0 is the eigenvalue of $A_{\varphi }\left(G\right)$ with a multiplicity of at least $\alpha -1$.

Proof. 

Since S is an independent set, where each vertex shares the same neighborhood outside S, by first indexing the vertices in the independent set, the $A_{\varphi }$-matrix of G can be written as

$$A_{\varphi }\left(G\right)=\left(\begin{array}{cc}{\mathbf{0}}_{\alpha }& B_{\alpha \times (n-\alpha )}\\ {\left(B_{\alpha \times (n-\alpha )}\right)}^T& C_{(n-\alpha )}\end{array}\right),$$

where $B_{\alpha \times (n-\alpha )}$ represents the part of matrix $A_{\varphi }\left(G\right)$ that corresponds to edges having one end in S and the other end in $V\left(G\right)\backslash S$ and $C_{(n-\alpha )}$ represents the part of matrix $A_{\varphi }\left(G\right)$ that corresponds to edges having both the ends in $V\left(G\right)\backslash S$. For $i=2,3,\cdots ,\alpha$, consider the vectors given by

$$X_{i-1}={\left(-1,x_{i2},x_{i3},\cdots ,x_{ip},\underset{n-p}{\underbrace{0,0,0,\cdots ,0}}\right)}^T$$

such that $x_{ij}=\left\{\begin{array}{cc}1\hfill & \mathrm{if}i=j,\hfill \\ 0\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$

As the rows of $B_{\alpha \times (n-\alpha )}$ are identical, it is easy to verify that $X_1,X_2,X_3,\cdots ,X_{\alpha -1}$ are the eigenvectors of $A_{\varphi }\left(G\right)$ corresponding to the eigenvalue $0.$ From this, the result follows.  □

The real sequence $b_1^{\prime }\ge b_2^{\prime }\ge \cdots \ge b_m^{\prime }$ is said to interlace the real sequence $b_1\ge b_2\ge \cdots \ge b_n$ ($m<n$) if $b_i\ge b_i^{\prime }\ge b_{n-m+i}$ for $i=1,2,\cdots ,m$, and the interlacing is said to be tight if there exists a positive integer $k\in [0,m]$, such that

$$b_i=b_i^{\prime }\mathrm{for}i=1,2,\cdots ,k\mathrm{and}{b}_{n-m+i}=b_i^{\prime }\mathrm{for}k+1\le i\le m.$$

Consider a square matrix, M, of order n in block form:

$$M=\left(\begin{array}{ccccc}{A}_{1,1}& A_{1,2}& \cdots & A_{1,s-1}& A_{1,s}\\ A_{2,1}& A_{2,2}& \cdots & A_{2,s-1}& A_{2,s}\\ ⋮& ⋮& \ddots & ⋮& ⋮\\ A_{s-1,1}& A_{s-1,2}& \cdots & A_{s-1,s-1}& A_{s-1,s}\\ A_{s,1}& A_{s,2}& \cdots & A_{s,s-1}& A_{s,s}\end{array}\right),$$

whose rows and columns are partitioned according to a partition $\pi =\{P_1,P_2,$$\cdots ,P_s\}$ of the index set $I=\{1,2,\cdots ,n\}.$ The quotient matrix $Q={\left(q_{ij}\right)}_{s\times s}$ (see [1]) is a square matrix of order s, such that the $(i,j)$-th entry of Q is the average row sum of block $A_{ij}$ of M. The partition, P, is said to be equitable (regular) if each block $A_{i,j}$ of M has a constant row sum, and in this case Q is called the equitable quotient matrix.

The following result provides the relation between the eigenvalues of M and the eigenvalues of $Q.$

Theorem 2

([1]). Let M be a real symmetric matrix of order n and Q be its quotient matrix of order $m(n>m)$. Then the following hold:

 (i) 

If the partition π of I of matrix M is not equitable, then the eigenvalues of Q interlace the eigenvalues of M, that is,

${\lambda }_i\left(M\right)\ge {\lambda }_i\left(Q\right)\ge {\lambda }_{i+n-m}\left(M\right),fori=1,2,\cdots ,m.$

 (ii) 

If the partition π of I of matrix M is equitable, then the spectrum of Q is contained in the spectrum of M.

In the next result, we discuss the $A_{\varphi }$-eigenvalues of chain graphs.

Theorem 3.

Let $G\cong G(m_1,\cdots ,m_h;n_1,\cdots ,n_h)$ be the chain graph. Then G has the $A_{\varphi }$-eigenvalue 0 with multiplicity $n-2h$; the remaining $A_{\varphi }$-eigenvalues of G are the eigenvalues of the matrix given in (4).

Proof. 

Labelling the vertices from $V_i$s to $U_i$s, the $A_{\varphi }$ matrix of G is

$$\left(\begin{array}{cc}{\mathbf{0}}_{m_1+m_2+\cdots +m_h}& B\\ B^T& {\mathbf{0}}_{n_1+n_2+\cdots +n_h}\end{array}\right),$$

(3)

where $\mathbf{0}$ is a matrix of zeros and B is a matrix of order $(m_1+m_2+\cdots +m_h)\times$$(n_1+n_2+\cdots +n_h)$, given by

$$B=\left(\begin{array}{ccccc}{\varphi }_{d_1{\mathcal{l}}_1}{J}_{m_1\times n_1}& {\varphi }_{d_1{\mathcal{l}}_2}{J}_{m_1\times n_2}& \cdots & {\varphi }_{d_1{\mathcal{l}}_{h-1}}{J}_{m_1\times n_{h-1}}& {\varphi }_{d_1{\mathcal{l}}_h}{J}_{m_1\times n_h}\\ {\varphi }_{d_2{\mathcal{l}}_1}{J}_{m_2\times n_1}& {\varphi }_{d_2{\mathcal{l}}_2}{J}_{m_2\times n_2}& \cdots & {\varphi }_{d_2{\mathcal{l}}_{h-1}}{J}_{m_2\times n_{h-1}}& {\mathbf{0}}_{m_2\times n_h}\\ {\varphi }_{d_3{\mathcal{l}}_1}{J}_{m_3\times n_1}& {\varphi }_{d_3{\mathcal{l}}_2}{J}_{m_3\times n_2}& \cdots & {\mathbf{0}}_{m_3\times n_{h-1}}& {\mathbf{0}}_{m_3\times n_h}\\ ⋮& ⋮& \ddots & ⋮& ⋮\\ {\varphi }_{d_{h-1}{\mathcal{l}}_1}{J}_{m_{h-1}\times n_1}& {\varphi }_{d_{h-1}{\mathcal{l}}_2}{J}_{m_{h-1}\times n_2}& \cdots & {\mathbf{0}}_{m_{h-1}\times n_{h-1}}& {\mathbf{0}}_{m_{h-1}\times n_h}\\ {\varphi }_{d_h{\mathcal{l}}_1}{J}_{m_h\times n_1}& {\mathbf{0}}_{m_h\times n_2}& \cdots & {\mathbf{0}}_{m_h\times n_{h-1}}& {\mathbf{0}}_{m_h\times n_h}\end{array}\right).$$

Since each $V_i$ (respectively $U_i$) consists of independent vertices and share the common neighborhood, by Theorem 1 it follows that G has the $A_{\varphi }$-eigenvalue of 0 with multiplicity $n-2h.$ For $k=2,3,\cdots ,m_i,\mathcal{l}=2,3,\cdots ,n_i$, the corresponding eigenvectors are

$$\begin{array}{cc}\hfill X_{k-1}^1& ={\left(-1,x_{i2},x_{i3},\cdots ,x_{i{m}_1},\underset{n-m_1}{\underbrace{0,0,0,\cdots ,0}}\right)}^T\hfill \\ \hfill X_{k-1}^2& ={\left(\underset{m_1}{\underbrace{0,0,\cdots ,0}},-1,x_{i2},x_{i3},\cdots ,x_{i{m}_2},\underset{n-m_1-m_2}{\underbrace{0,0,0,\cdots ,0}}\right)}^T\hfill \\ \hfill & ⋮\hfill \\ \hfill X_{k-1}^{h-1}& ={\left(\underset{n-{\sum }_{i=1}^{h-2}{m}_i}{\underbrace{0,0,0,\cdots ,0}},,-1,x_{i2},x_{i3},\cdots ,x_{i{m}_{h-1}},\underset{m_h}{\underbrace{0,0,\cdots ,0}},\underset{{\sum }_{i=1}^h{n}_i}{\underbrace{0,0,\cdots ,0}}\right)}^T\hfill \\ \hfill X_{k-1}^h& ={\left(\underset{n-{\sum }_{i=1}^{h-1}{m}_i}{\underbrace{0,0,0,\cdots ,0}},,-1,x_{i2},x_{i3},\cdots ,x_{i{m}_h},\underset{{\sum }_{i=1}^h{n}_i}{\underbrace{0,0,\cdots ,0}}\right)}^T\hfill \\ \hfill Y_{\mathcal{l}-1}^1& ={\left(\underset{{\sum }_{i=1}^h{m}_i}{\underbrace{0,0,\cdots ,0}},-1,y_{i2},y_{i3},\cdots ,y_{i{n}_1},\underset{{\sum }_{i=2}^h{n}_i}{\underbrace{0,0,\cdots ,0}}\right)}^T\hfill \\ \hfill Y_{\mathcal{l}-1}^2& ={\left(\underset{{\sum }_{i=1}^h{m}_i}{\underbrace{0,0,\cdots ,0}},\underset{n_1}{\underbrace{0,0,0,\cdots ,0}},-1,y_{i2},y_{i3},\cdots ,y_{i{n}_2},\underset{{\sum }_{i=3}^h{n}_i}{\underbrace{0,0,0,\cdots ,0}}\right)}^T\hfill \\ \hfill & ⋮\hfill \\ \hfill Y_{\mathcal{l}-1}^{h-1}& ={\left(\underset{{\sum }_{i=1}^h{m}_i}{\underbrace{0,0,\cdots ,0}},\underset{{\sum }_{i=1}^{h-2}{n}_i}{\underbrace{0,0,0,\cdots ,0}},-1,y_{i2},y_{i3},\cdots ,y_{i{n}_{h-1}},\underset{n_h}{\underbrace{0,0,0,\cdots ,0}}\right)}^T\hfill \\ \hfill Y_{\mathcal{l}-1}^h& ={\left(\underset{{\sum }_{i=1}^h{m}_i}{\underbrace{0,0,\cdots ,0}},\underset{{\sum }_{i=1}^{h-1}{n}_i}{\underbrace{0,0,0,\cdots ,0}},-1,y_{i2},y_{i3},\cdots ,y_{i{n}_h}\right)}^T,\hfill \end{array}$$

where

$$x_{ij}=\left\{\begin{array}{cc}1\hfill & \mathrm{if}i=j\hfill \\ 0\hfill & \mathrm{otherwise}.\hfill \end{array}\right.\mathrm{for}i=2,3,\cdots ,m_i,\mathrm{and}j=2,3,\cdots ,m_i,$$

and

$$y_{ij}=\left\{\begin{array}{cc}1\hfill & \mathrm{if}i=j\hfill \\ 0\hfill & \mathrm{otherwise}.\hfill \end{array}\right.\mathrm{for}i=2,3,\cdots ,n_i,\mathrm{and}j=2,3,\cdots ,n_i.$$

The remaining $2h$ eigenvalues of $A_{\varphi }\left(G\right)$ are the eigenvalues of the following matrix:

$$Q=\left(\begin{array}{cccccccccc}0& 0& \cdots & 0& 0& n_1{\varphi }_{d_1{\mathcal{l}}_1}& n_2{\varphi }_{d_1{\mathcal{l}}_2}& \cdots & n_{h-1}{\varphi }_{d_1{\mathcal{l}}_{h-1}}& n_h{\varphi }_{d_1{\mathcal{l}}_h}\\ 0& 0& \cdots & 0& 0& n_1{\varphi }_{d_2{\mathcal{l}}_1}& n_2{\varphi }_{d_2{\mathcal{l}}_2}& \cdots & n_{h-1}{\varphi }_{d_2{\mathcal{l}}_{h-1}}& 0\\ ⋮& ⋮& \ddots & ⋮& ⋮& ⋮& ⋮& \ddots & ⋮& ⋮\\ 0& 0& \cdots & 0& 0& n_1{\varphi }_{d_{h-1}{\mathcal{l}}_1}& n_2{\varphi }_{d_{h-1}{\mathcal{l}}_2}& \cdots & 0& 0\\ 0& 0& \cdots & 0& 0& n_1{\varphi }_{d_h{\mathcal{l}}_1}& 0& \cdots & 0& 0\\ m_1{\varphi }_{d_1{\mathcal{l}}_1}& m_2{\varphi }_{d_2{\mathcal{l}}_1}& \cdots & m_{h-1}{\varphi }_{d_{h-1}{\mathcal{l}}_1}& m_h{\varphi }_{d_h{\mathcal{l}}_1}& 0& 0& \cdots & 0& 0\\ m_1{\varphi }_{d_1{\mathcal{l}}_2}& m_2{\varphi }_{d_2{\mathcal{l}}_2}& \cdots & m_{h-1}{\varphi }_{d_{h-1}{l}_2}& 0& 0& 0& \cdots & 0& 0\\ ⋮& ⋮& \ddots & ⋮& ⋮& ⋮& ⋮& \ddots & ⋮& ⋮\\ m_1{\varphi }_{d_1{\mathcal{l}}_{h-1}}& m_2{\varphi }_{d_2{\mathcal{l}}_{h-1}}& 0& 0& 0& 0& 0& \cdots & 0& 0\\ m_1{\varphi }_{d_1{\mathcal{l}}_h}& 0& 0& 0& 0& 0& 0& \cdots & 0& 0\end{array}\right).$$

(4)

  □

In general, it is not possible to find the eigenvalues of the matrix given in (2) explicitly, as by definition of the quotient matrix, all the eigenvalues of Q are simple and it is hard to locate them. However, we can still gain some information about them.

In the following results, we find the formula for the determinant of Q and the trace of $Q^2$, where Q is the quotient matrix defined in Theorem 3.

Theorem 4.

The following holds for the quotient matrix given in (4).

 (i) 

The determinant of the quotient matrix Q given in (2) is

$$det\left(Q\right)={(-1)}^h\prod _{i=1}^h{m}_i{n}_i\left({\varphi }_{d_i{\mathcal{l}}_{h-(i-1)}}^2\right)={(-1)}^h\prod _{i=1}^h{m}_i{n}_i\left({\varphi }_{d_{h-(i-1)}{\mathcal{l}}_i}^2\right).$$

 (ii) 

The trace of square of the quotient matrix $Q^2$ is

$$tr\left(Q^2\right)=2\sum _{j=1}^h\sum _{i=1}^{h-(j-1)}{m}_j{n}_i\left({\varphi }_{d_j{\mathcal{l}}_i}^2\right).$$

Proof. 

For the sake of completeness, we denote matrix Q given in (4) by

$$Q(m_1,m_2,\cdots ,m_h,n_1,n_2,\cdots ,n_h).$$

Expanding $det\left(Q\right)$ by the $2h$-th row, there is only one non-zero cofactor,

$$det\left(Q(m_1,m_2,\cdots ,m_h;n_1,n_2,\cdots ,n_{h-1})\right),$$

multiplied by the $(2h,1)$-th entry of Q since the remaining entries of the $2h$-th row are zeros. Similarly, for the $(2h-1)$-th row expansion of $det\left(Q\right(m_1,m_2,\cdots ,m_h;n_1,n_2,$$\cdots ,n_{h-1}\left)\right)$, there is only one non-zero cofactor, $det\left(Q\right(m_1,m_2,\cdots ,m_h;n_1,n_2,$$\cdots ,n_{h-2}\left)\right)$, of order $2h-2$ multiplied by the $(2h-1,2)$-th entry of Q. Thus, we obtain

$$\begin{array}{cc}\hfill det& \left(Q(m_1,m_2,\cdots ,m_h,n_1,n_2,\cdots ,n_h)\right)\hfill \\ \hfill & =(-1)m_1{\varphi }_{d_1{\mathcal{l}}_h}{m}_2{\varphi }_{d_2{\mathcal{l}}_{h-1}}det\left(Q(m_1,m_2,\cdots ,m_h;n_1,n_2,\cdots ,n_{h-2})\right).\hfill \end{array}$$

We continue the above procedure for $det\left(Q(m_1,m_2,\cdots ,m_h;n_1,n_2,\cdots ,n_{h-2})\right)$ from the $(2h-2)$-th row and then the $(2h-3)$-th row of $det\left(Q\right(m_1,m_2,\cdots ,m_h,n_1,n_2,$$\cdots ,n_{h-2}\left)\right),$ and we obtain

$$\begin{array}{cc}\hfill det& \left(Q(m_1,m_2,\cdots ,m_h,n_1,n_2,\cdots ,n_{h-2})\right)\hfill \\ \hfill & =(-1)m_3{\varphi }_{d_3{\mathcal{l}}_{h-2}}{m}_4{\varphi }_{d_4{\mathcal{l}}_{h-3}}det\left(Q(m_1,m_2,\cdots ,m_h;n_1,n_2,\cdots ,n_{h-4})\right).\hfill \end{array}$$

Continuing this process from the $(2h-4)$-th row of $det\left(Q\right(m_1,m_2,\cdots ,m_h;n_1,n_2,$$\cdots ,n_{h-4}\left)\right)$ and combining together, we obtain

$$\begin{array}{cc}\hfill det& \left(Q(m_1,m_2,\cdots ,m_h,n_1,n_2,\cdots ,n_h)\right)\hfill \\ \hfill & =(-1)m_1{\varphi }_{d_1{\mathcal{l}}_h}{m}_2{\varphi }_{d_2{\mathcal{l}}_{h-1}}det\left(Q(m_1,m_2,\cdots ,m_h,n_1,n_2,\cdots ,n_{h-2})\right)\hfill \\ \hfill & ={(-1)}^2\prod _{i=1}^4{m}_i{\varphi }_{d_i{\mathcal{l}}_{h-(i-1)}}det\left(Q(m_1,m_2,\cdots ,m_h;n_1,n_2,\cdots ,n_{h-4})\right)\hfill \\ \hfill & ⋮\hfill \\ \hfill & ={(-1)}^{\frac{h}{2}}\prod _{i=1}^h{m}_i{\varphi }_{d_i{\mathcal{l}}_{h-(i-1)}}det\left(Q(m_1,m_2,\cdots ,m_h)\right)\hfill \\ \hfill & ={(-1)}^{\frac{h}{2}+1}{n}_1{m}_h{n}_2{m}_{h-1}{\varphi }_{d_h{\mathcal{l}}_1}^2{\varphi }_{d_{h-1}{\mathcal{l}}_2}^2·\prod _{i=1}^{h-2}{m}_i{\varphi }_{d_i{\mathcal{l}}_{h-(i-1)}}det\left(Q(m_1,m_2,\cdots ,m_{h-2})\right)\hfill \\ \hfill & ⋮\hfill \\ \hfill & ={(-1)}^{\frac{h}{2}+\frac{h-1}{2}}\prod _{i=1}^{h-2}{m}_{h-(i-1)}{n}_i{\varphi }_{d_{h-(i-1)}{\mathcal{l}}_i}^2·\prod _{i=h-1}^h{m}_{h-(i-1)}{\varphi }_{d_{h-(i-1)}{\mathcal{l}}_i}det(Q(m_1,m_2)\hfill \\ \hfill & ={(-1)}^h\prod _{i=1}^h{m}_i{n}_i{\varphi }_{d_{h-(i-1)}{\mathcal{l}}_i}={(-1)}^h\prod _{i=1}^h{m}_i{n}_i{\varphi }_{d_i{\mathcal{l}}_{h-(i-1)}}.\hfill \end{array}$$

In the second to last step,

$$\begin{array}{cc}\hfill det(Q(m_1,m_2)& =\left|\begin{array}{cc}{n}_{h-1}{\varphi }_{d_1{l}_{h-1}}& n_h{\varphi }_{d_1{l}_h}\\ n_{h-1}{\varphi }_{d_2{l}_{h-1}}& 0\end{array}\right|\hfill \\ \hfill & =-n_h{\varphi }_{d_1{l}_h}{n}_{h-1}{\varphi }_{d_2{l}_{h-1}}.\hfill \end{array}$$

Clearly, the diagonal entries of $Q^2$ are

$$\begin{array}{cc}\hfill & d_{11}=m_1\sum _{i=1}^h{n}_i{\varphi }_{d_1{\mathcal{l}}_i}^2,d_{22}=m_2\sum _{i=1}^{h-1}{n}_i{\varphi }_{d_2{\mathcal{l}}_i}^2,\cdots ,d_{(h-1)(h-1)}=m_{h-1}\sum _{i=1}^2{n}_i{\varphi }_{d_{h-1}{\mathcal{l}}_i}^2,\hfill \\ \hfill & d_{hh}=m_h{n}_1{\varphi }_{d_h{\mathcal{l}}_1}^2,d_{(h+1)(h+1)}=n_1\sum _{i=1}^h{m}_i{\varphi }_{d_i{\mathcal{l}}_1}^2,d_{(h+2)(h+2)}=n_2\sum _{i=1}^{h-1}{m}_i{\varphi }_{d_i{\mathcal{l}}_2}^2,\cdots ,\hfill \\ \hfill & d_{(2h-1)(2h-1)}=n_{h-1}\sum _{i=1}^2{m}_i{\varphi }_{d_i{\mathcal{l}}_{h-1}}^2,d_{\left(2h\right)\left(2h\right)}=n_h{m}_1{\varphi }_{d_1{\mathcal{l}}_h}^2.\hfill \end{array}$$

Therefore, we have

$$\begin{array}{cc}\hfill tr\left(Q^2\right)& =2(\sum _{i=1}^h{m}_1{n}_i{\varphi }_{d_1{\mathcal{l}}_i}^2+\sum _{i=1}^{h-1}{m}_2{n}_i{\varphi }_{d_2{\mathcal{l}}_i}^2+\cdots +2\sum _{i=1}^2{m}_{h-1}{n}_i{\varphi }_{d_{h-1}{\mathcal{l}}_i}^2\hfill \\ \hfill & +m_h{n}_1{\varphi }_{d_h{\mathcal{l}}_i}^2)\hfill \\ \hfill & =2\sum _{j=1}^h\sum _{i=1}^{h-(j-1)}{m}_j{n}_i{\varphi }_{d_j{\mathcal{l}}_i}^2.\hfill \end{array}$$

  □

For a bipartite graph with partite sets of cardinality a and b, the $A_{\varphi }$-matrix can be written as

$$A_{\varphi }\left(G\right)=\left(\begin{array}{cc}\mathbf{0}& B\\ B^T& \mathbf{0}\end{array}\right),$$

where B corresponds to edges between the partite sets. If $\lambda$ is an eigenvalue of $A_{\varphi }\left(G\right)$ with corresponding eigenvector $X={(x_1,x_2)}^T$, then $A_{\varphi }\left(G\right)X=\lambda X$. Using this last equation, it is easy to see that $A_{\varphi }\left(G\right)X^{\prime }=-\eta X^{\prime },$ where $X^{\prime }={(x_1,-x_2)}^T.$ This shows that, for a bipartite graph, if $\lambda$ is an eigenvalue of $A_{\varphi }\left(G\right)$, then $-\lambda$ is also an eigenvalue of $A_{\varphi }\left(G\right)$. Thus, we conclude that the $A_{\varphi }$-eigenvalues of a bipartite graph are symmetric about the origin.

The following corollary gives the number of positive eigenvalues (called positive inertia), the number of eigenvalues equal to zero (called nullity), and the number of negative eigenvalues (called negative inertia) of the $A_{\varphi }$-matrix of chain graphs. Note that the triplet (positive inertia, nullity, negative inertia) is called the inertia of matrix $A_{\varphi }\left(G\right)$ or the general extended adjacency inertia of G.

Corollary 1.

The inertia of $A_{\varphi }\left(G(m_1,\cdots ,m_h;m_1,\cdots ,m_h)\right)$ is $(h,n-2h,h).$

Proof. 

Since chain graphs are bipartite graphs, the result directly follows from Theorem 3 and the fact that the $A_{\varphi }$-eigenvalues of bipartite graphs are symmetric about the origin.  □

It is well known that the eigenvalues of Q are simple, which is the same as saying that the $A_{\varphi }$-eigenvalues of $G(\underset{h}{\underbrace{1,1,\cdots ,1}};\underset{h}{\underbrace{1,1,\cdots ,1}})$ are simple. A natural question that arises here is “What about the multiplicities of the $A_{\varphi }$-eigenvalues when at least one $m_i\ge 2$ or $n_i\ge 2$?” In this regard, we have the following consequence from Theorem 3, which characterizes all the chain graphs with all the general extended adjacency eigenvalues as distinct:

Corollary 2.

Let $G\cong G(m_1,m_2,\cdots ,m_h;n_1,n_2,\cdots ,n_h)$ be the chain graph of order $n.$ Then, the $A_{\varphi }$-eigenvalues of G are simple if and only if exactly one among $m_i$ or one among $n_i$ is at most two, for some $i.$

Proof. 

Since all the eigenvalues of Q in (4) are simple, by Theorem 1, 0 is the $A_{\varphi }$-eigenvalue of G with a multiplicity of one if and only if exactly one $m_i=2$ (or exactly one $n_i=2$) for some i, as 0 cannot be the eigenvalue of $Q,$ since $det\left(Q\right)\ne 0.$  □

Based on Corollary 2, the following is a list of chain graphs with the simple $A_{\varphi }$-eigenvalues for $h=3$:

$$T(1,1,1;1,1,1),T(2,1,1;1,1,1),T(1,2,1;1,1,1),T(1,1,2;1,1,1).$$

In the next result, we identify the non-singular chain graphs with respect to the general extended adjacency matrix.

Corollary 3.

Let $G\cong G(m_1,m_2,\cdots ,m_h;n_1,n_2,\cdots ,n_h)$ be the chain graph of order $n.$ Then the $A_{\varphi }$-matrix of G is non-singular if and only if $G\cong G(\underset{h}{\underbrace{1,1,\cdots ,1}};\underset{h}{\underbrace{1,1,\cdots ,1}}).$

Proof. 

Since the eigenvalues of Q are simple, the result holds for $A_{\varphi }\left(G\right)$ if $m_1=m_2=\cdots =m_h=n_1=\cdots =n_h=1$ and the determinant of Q is non-zero. Conversely, if at least one $m_i$ (or $n_i$) is of multiplicity greater or equal to two, then by Theorem 1, 0 is the eigenvalue of $A_{\varphi }\left(G\right)$. Therefore, the $A_{\varphi }$-matrix of G is not invertible. From this, the result follows.  □

As it is difficult to explicitly find the largest and the smallest eigenvalues of $Q,$ in the next result we establish the sharp bounds for them with the help of the interlacing property of the quotient matrix.

Corollary 4.

Let $G\cong G(m_1,m_2,\cdots ,m_h;n_1,n_2,\cdots ,n_h)$ be the chain graph of order $n.$ Then,

$${\lambda }_1\left(G\right)\ge \frac{\sqrt{\sigma {\sigma }^{\prime }}}{h}and{\lambda }_n\left(G\right)\le -\frac{\sqrt{\sigma {\sigma }^{\prime }}}{h},$$

where $\sigma ={\sum }_{j=1}^h{\sum }_{i=1}^{h-(j-1)}{n}_i{\varphi }_{d_j{\mathcal{l}}_i}$ and ${\sigma }^{\prime }={\sum }_{j=1}^h{\sum }_{i=1}^{h-(j-1)}{m}_i{\varphi }_{d_i{\mathcal{l}}_j}.$ Equalities hold if and only if $h=1$, that is, G is the complete bipartite graph.

Proof. 

The quotient matrix given in (4) with partition $\left\{\right\{1,2,\cdots ,h\},\{1,2,\cdots ,h\left\}\right\}$ can be written in block form as

$$\left(\begin{array}{cccccccccc}0& 0& \cdots & 0& 0& n_1{\varphi }_{d_1{\mathcal{l}}_1}& n_2{\varphi }_{d_1{\mathcal{l}}_2}& \cdots & n_{h-1}{\varphi }_{d_1{\mathcal{l}}_{h-1}}& n_h{\varphi }_{d_1{\mathcal{l}}_h}\\ 0& 0& \cdots & 0& 0& n_1{\varphi }_{d_2{\mathcal{l}}_1}& n_2{\varphi }_{d_2{\mathcal{l}}_2}& \cdots & n_{h-1}{\varphi }_{d_2{\mathcal{l}}_{h-1}}& 0\\ ⋮& ⋮& \ddots & ⋮& ⋮& ⋮& ⋮& \ddots & ⋮& ⋮\\ 0& 0& \cdots & 0& 0& n_1{\varphi }_{d_{h-1}{\mathcal{l}}_1}& n_2{\varphi }_{d_{h-1}{\mathcal{l}}_2}& \cdots & 0& 0\\ 0& 0& \cdots & 0& 0& n_1{\varphi }_{d_h{\mathcal{l}}_1}& 0& \cdots & 0& 0\\ m_1{\varphi }_{d_1{\mathcal{l}}_1}& m_2{\varphi }_{d_2{\mathcal{l}}_1}& \cdots & m_{h-1}{\varphi }_{d_{h-1}{\mathcal{l}}_1}& m_h{\varphi }_{d_h{\mathcal{l}}_1}& 0& 0& \cdots & 0& 0\\ m_1{\varphi }_{d_1{\mathcal{l}}_2}& m_2{\varphi }_{d_2{\mathcal{l}}_2}& \cdots & m_{h-1}{\varphi }_{d_{h-1}{\mathcal{l}}_2}& 0& 0& 0& \cdots & 0& 0\\ ⋮& ⋮& \ddots & ⋮& ⋮& ⋮& ⋮& \ddots & ⋮& ⋮\\ m_1{\varphi }_{d_1{\mathcal{l}}_{h-1}}& m_2{\varphi }_{d_2{\mathcal{l}}_{h-1}}& 0& 0& 0& 0& 0& \cdots & 0& 0\\ m_1{\varphi }_{d_1{\mathcal{l}}_h}& 0& 0& 0& 0& 0& 0& \cdots & 0& 0\end{array}\right)$$

and its quotient matrix is

$$Q^{*}=\left(\begin{array}{cc}0& \frac{\sigma }{h}\\ \frac{{\sigma }^{\prime }}{h}& 0\end{array}\right),$$

(5)

where $\sigma ={\sum }_{j=1}^h{r}_j,$ with $r_1={\sum }_{i=1}^h{n}_i{\varphi }_{d_1{\mathcal{l}}_i},r_2={\sum }_{i=1}^{h-1}{n}_i{\varphi }_{d_2{\mathcal{l}}_i},\cdots ,r_{h-1}={\sum }_{i=1}^2{n}_i{\varphi }_{d_{h-11}{\mathcal{l}}_i}$ and $r_h=n_1{\varphi }_{d_1{\mathcal{l}}_i},$ that is, $\sigma ={\sum }_{j=1}^h{\sum }_{i=1}^{h-(j-1)}{n}_i{\varphi }_{d_j{\mathcal{l}}_i}.$

Likewise, ${\sigma }^{\prime }={\sum }_{j=1}^h{r}_j^{\prime }={\sum }_{j=1}^h{\sum }_{i=1}^{h-(j-1)}{m}_i{\varphi }_{d_i{\mathcal{l}}_j}.$ The eigenvalues of (5) are ${\xi }_1\left(Q^{*}\right)=\frac{\sqrt{\sigma {\sigma }^{\prime }}}{h}$ and ${\xi }_2\left(Q^{*}\right)=-\frac{\sqrt{\sigma {\sigma }^{\prime }}}{h}.$ By (i) of Theorem 2, we have

$${\lambda }_1\left(Q\right)\ge {\xi }_1\left(Q^{*}\right)\ge {\lambda }_2\left(Q\right)\ge {\xi }_2\left(Q^{*}\right)\ge {\lambda }_3\left(Q\right)\ge {\lambda }_4\left(Q\right)\ge \cdots \ge {\lambda }_{2h}\left(Q\right),$$

which in turn implies that

$${\lambda }_1\left(G\right)\ge \frac{\sqrt{\sigma {\sigma }^{\prime }}}{h}\mathrm{and}{\lambda }_n\left(G\right)\le -\frac{\sqrt{\sigma {\sigma }^{\prime }}}{h},$$

with equalities holding if and only if matrix $Q^{*}$ is an equitable quotient matrix, that is, the non-zero block matrices of the above block matrix have constant row sums, that is, $r_1=r_2=\cdots =r_h$ and $r_1^{\prime }=r_2^{\prime }=\cdots =r_h^{\prime }$. In such a situation, the partition $\left\{\right\{1,2,\cdots ,h\},\{1,2,\cdots ,h\left\}\right\}$ is an equitable partition and $Q^{*}$ is an equitable quotient matrix of $Q.$ Hence, each eigenvalue of $Q^{*}$ is an eigenvalue of Q.

We will now discuss the equality case. If $h=1,$ then $G\cong K_{m_1,n_1}$, and by Lemma 1, 0 is the eigenvalue of $A_{\varphi }\left(G\right)$ with multiplicity $m_1+n_1-2$. The other two eigenvalues of $A_{\varphi }\left(G\right)$ are the eigenvalues of the following equitable matrix:

$$\left(\begin{array}{cc}0& n_1{\varphi }_{d_1{l}_1}\\ m_1{\varphi }_{d_1{l}_1}& 0\end{array}\right),$$

and its eigenvalues are $\pm {\varphi }_{d_1{\mathcal{l}}_1}\sqrt{m_1{n}_1}.$ Therefore, we have ${\lambda }_1\left(G\right)={\varphi }_{d_1{\mathcal{l}}_1}\sqrt{m_1{n}_1}$ and ${\lambda }_n\left(G\right)=-{\varphi }_{d_1{\mathcal{l}}_1}\sqrt{m_1{n}_1}.$ Conversely, for $r_1=r_2=\cdots =r_h$ to hold, it is clear from (4) that $m_2=m_3=\cdots =m_h=0$, which in turn implies that $n_2=n_3=\cdots =n_h=0.$ Thus, we are left with $G(m_1;n_1)$, which is the complete bipartite graph and $Q^{*}$ is an equitable quotient matrix with $\sigma =n_1{\varphi }_{d_1{\mathcal{l}}_1}$ and ${\sigma }^{\prime }=m_1{\varphi }_{d_1{\mathcal{l}}_1}.$ Hence, ${\lambda }_1=\sqrt{\sigma {\sigma }^{\prime }}=\sqrt{m_1{n}_1}{\varphi }_{d_1{\mathcal{l}}_1}={\lambda }_1\left(K_{m_1,n_1}\right)$, and likewise ${\lambda }_n\left(K_{m_1,n_1}\right)=-\sqrt{m_1{n}_1}{\varphi }_{d_1{\mathcal{l}}_1}.$  □

The spread of a real symmetric matrix, M, with eigenvalues ${\lambda }_1\left(M\right)\ge {\lambda }_2\left(M\right)\ge \cdots \ge {\lambda }_n\left(M\right)$ is defined as $s\left(M\right)={\lambda }_1\left(M\right)-{\lambda }_n\left(M\right).$ Under this definition, the spread of $A_{\varphi }\left(G\right)$ is defined as $s\left(S\left(G\right)\right)={\lambda }_1-{\lambda }_n,$ called the $A_{\varphi }$-spread or the general extended adjacency spread of G. With notations as in the above corollary, we have the following result for the $A_{\varphi }$-spread of a chain graph:

Corollary 5.

The spread of the $A_{\varphi }$-matrix of $G\cong G(m_1,m_2,\cdots ,m_h;n_1,n_2,\cdots ,n_h)$ is bounded below by $\frac{2}{h}\sqrt{\sigma {\sigma }^{\prime }}$, that is,

$$s\left(S\left(G\right)\right)\ge \frac{2}{h}\sqrt{\sigma {\sigma }^{\prime }},$$

with equality holding if and only if G is the complete bipartite graph.

From Corollary 5, it follows that among all the chain graphs, the complete bipartite graph attains the minimum value for the $A_{\varphi }$-spread.

3. Energy of General Extended Adjacency Matrix

In this section, we discuss the energy of the general extended adjacency matrix of a graph. We obtain some extremal results and characterize the graphs that attain the extremal value.

Let $\{{\gamma }_1,{\gamma }_2,{\gamma }_3,\cdots ,{\gamma }_n\}$ be the set of positive real numbers and let $P_k$ be the average of products of the k-element subset of the set $\{{\gamma }_1,{\gamma }_2,{\gamma }_3,\cdots ,{\gamma }_n\},$ that is,

$$\begin{array}{cc}\hfill P_1& =\frac{{\gamma }_1+{\gamma }_2+{\gamma }_3+\cdots +{\gamma }_n}{n},\hfill \\ \hfill P_2& ={\displaystyle \frac{1}{\frac{n(n-1)}{2}}}\left({\gamma }_1{\gamma }_2+{\gamma }_1{\gamma }_3+\cdots +{\gamma }_1{\gamma }_n+{\gamma }_2{\gamma }_3+\cdots +{\gamma }_{n-1}{\gamma }_n\right),\hfill \\ \hfill & ⋮\hfill \\ \hfill P_n& ={\gamma }_1{\gamma }_2\cdots {\gamma }_n.\hfill \end{array}$$

The following Maclaurin symmetric mean inequality relates $P_i$s among themselves.

Lemma 1

([52]). For positive real numbers ${\gamma }_1,{\gamma }_2,{\gamma }_3,\cdots ,{\gamma }_n,$ we have the following chain of inequalities,

$$P_1\ge P_2^{\frac{1}{2}}\ge P_3^{\frac{1}{3}}\ge \cdots \ge P_n^{\frac{1}{n}},$$

with equalities holding if and only if ${\gamma }_1={\gamma }_2=\cdots ={\gamma }_n.$

The following result provides the estimates for the $A_{\varphi }$-energy of a chain graph. Moreover, the extremal graphs attaining these estimates are characterized.

Theorem 5.

Let$G\cong G(m_1,\cdots ,m_h;n_1,\cdots ,n_h)$be a chain graph. Then the following holds:

 (i) 

$${\mathcal{E}}_{\varphi }\left(G\right)\ge 2\sqrt{\sum _{j=1}^h\sum _{i=1}^{h-(j-1)}{m}_j{n}_i{\varphi }_{d_j{\mathcal{l}}_i}^2+h(h-1){\left(\prod _{i=1}^h{m}_i{n}_i{\varphi }_{d_i{\mathcal{l}}_{h-(i-1)}}^2\right)}^{\frac{1}{h}}},$$

(6)

with equality holding if and only if $G\cong G(m_1;n_1)=K_{m_1,n_1}.$

 (ii) 

$${\mathcal{E}}_{\varphi }\left(G\right)\le 2\sqrt{h\sum _{j=1}^h\sum _{i=1}^{h-(j-1)}{m}_j{n}_i{\varphi }_{d_i{\mathcal{l}}_j}^2},$$

(7)

with equality if and only if$h=1,$that is, if and only if$G\cong K_{m_1,n_2}$.

Proof. 

Let ${\lambda }_1\ge {\lambda }_2\ge \cdots \ge {\lambda }_n$ be the general extended adjacency eigenvalues of G. Since G is bipartite, its $A_{\varphi }$-eigenvalues occur in pairs $\pm {\lambda }_i,$ so we have

$${\mathcal{E}}_{\varphi }\left(G\right)=2\left({\lambda }_1+{\lambda }_2+\cdots +{\lambda }_h\right).$$

(8)

In addition, let ${\eta }_1\ge {\eta }_2\ge \cdots \ge {\eta }_{2h}$ be the eigenvalues of matrix Q given by (4). Then, from Corollary 4, we have

$$\sum _{i=1}^{2h}{\eta }_i^2=tr\left(Q^2\right)=2\sum _{j=1}^h\sum _{i=1}^{h-(j-1)}{m}_j{n}_i{\varphi }_{d_j{\mathcal{l}}_i}^2,$$

that is, the same as

$$\sum _{i=1}^h{\eta }_i^2=\sum _{j=1}^h\sum _{i=1}^{h-(j-1)}{m}_j{n}_i{\varphi }_{d_j{\mathcal{l}}_i}^2.$$

Again, by Corollary 4, we have

$$\prod _{i=1}^{2h}{\eta }_i=det\left(Q\right)={(-1)}^h\prod _{i=1}^h{m}_i{n}_i{\varphi }_{d_i{\mathcal{l}}_{h-(i-1)}}^2,$$

which is equivalent to

$$\prod _{i=1}^h{\eta }_i={\left(\prod _{i=1}^h{m}_i{n}_i{\varphi }_{d_i{\mathcal{l}}_{h-(i-1)}}^2\right)}^{\frac{1}{2}}.$$

(9)

By applying Lemma 1, we have

$$\frac{1}{\frac{h(h-1)}{2}}\sum _{1\le i<j\le h}{\eta }_i{\eta }_j\ge {\left(\prod _{i=1}^h{\eta }_i\right)}^{\frac{2}{h}},$$

(10)

with equality if and only if ${\eta }_1={\eta }_2=\cdots ={\eta }_h.$ By (9), the above expression can be written as

$$2\sum _{1\le i<j\le h}{\eta }_i{\eta }_j\ge h(h-1){\left(\prod _{i=1}^h{m}_i{n}_i{\varphi }_{d_i{\mathcal{l}}_{h-(i-1)}}^2\right)}^{\frac{1}{h}}.$$

As the eigenvalues of Q are the eigenvalues of $A_{\varphi }\left(G\right)$ in some order, by (8) we have

$$\begin{array}{cc}\hfill {\mathcal{E}}_{\varphi }\left(G\right)& =2\sqrt{{\left(\sum _{i=1}^h{\lambda }_i\right)}^2}=2\sqrt{\sum _{i=1}^h{\lambda }_i^2+2\sum _{1\le i<j\le h}{\lambda }_i{\lambda }_j}\hfill \\ \hfill & \ge 2\sqrt{\sum _{j=1}^h\sum _{i=1}^{h-(j-1)}{m}_j{n}_i{\varphi }_{d_j{\mathcal{l}}_i}^2+h(h-1){\left(\prod _{i=1}^h{m}_i{n}_i{\varphi }_{d_i{\mathcal{l}}_{h-(i-1)}}^2\right)}^{\frac{1}{h}}}.\hfill \end{array}$$

This establishes the lower bound for ${\mathcal{E}}_{\varphi }\left(G\right).$

First, if $h=1,$ then $G\cong K_{m_1,n_1}$ and its $A_{\varphi }$-spectrum is

$$\left\{0^{[n-2]},\pm \sqrt{m_1{n}_1}{\varphi }_{d_1{\mathcal{l}}_1}\right\}.$$

Therefore, the $A_{\varphi }$-energy of G is given by

$${\mathcal{E}}_{\varphi }\left(G\right)=2\sqrt{m_1{n}_1}{\varphi }_{d_1{\mathcal{l}}_1},$$

giving that equality occurs in this case.

Conversely, equality holds in inequality (6) if and only if equality holds in (10), which is so if and only if ${\eta }_1={\eta }_2=\cdots ={\eta }_h.$ Since the $A_{\varphi }$-eigenvalues of G are symmetric about the origin, it follows that the rank of G is two, and so G has only three distinct $A_{\varphi }$-eigenvalues: ${\lambda }_1,0$, and $-{\lambda }_1$. By Lemma 2.1 of [53], it follows that G is a complete bipartite graph. This completes the proof of lower bound.

Again by Lemma 1 with ${\gamma }_i={\eta }_i$ and $n=2h$, we have

$${\left(\frac{1}{h}\sum _{i=1}^h{\eta }_i\right)}^2\ge \frac{1}{\frac{h(h-1)}{2}}\sum _{1\le i<j\le h}{\eta }_i{\eta }_j,$$

(11)

that is,

$$h(h-1){\left(\sum _{i=1}^h{\eta }_i\right)}^2\ge 2h^2\sum _{1\le i<j\le h}{\eta }_i{\eta }_j=h^2\left({\left(\sum _{i=1}^h{\eta }_i\right)}^2-\sum _{i=1}^h{\eta }_i^2\right),$$

that is,

$${\left(\sum _{i=1}^h{\eta }_i\right)}^2\le h\sum _{i=1}^h{\eta }_i^2.$$

As ${\eta }_i$s are ${\lambda }_i$s in some order, we have, by the Cauchy–Schwarz inequality:

$${\mathcal{E}}_{\varphi }\left(G\right)\le 2\sqrt{h\sum _{i=1}^h{\lambda }_i^2}=2\sqrt{h\sum _{j=1}^h\sum _{i=1}^{h-(j-1)}{m}_j{n}_i{\varphi }_{d_i{\mathcal{l}}_j}^2}.$$

This proves the upper bound.

If equality holds, then equality holds in (11), and so ${\eta }_1={\eta }_2=\cdots ={\eta }_h$. Therefore, using the fact that the $A_{\varphi }$-spectrum of G is symmetric about the origin, it is implied that $-{\eta }_1=-{\eta }_2=\cdots =-{\eta }_h.$ Thus, we conclude that G has three distinct $A_{\varphi }$-eigenvalues, namely, ${\lambda }_1={\eta }_1,0$, and ${\lambda }_n=-{\eta }_1$. Therefore, by Lemma 2.1 of [53], we conclude that G is the complete bipartite graph. Conversely, it is easy to see that equality holds for $G\cong K_{m_1,n_1}.$  □

The following arithmetic–geometric mean inequality can be found in [54]:

Lemma 2.

If $y_1,y_2,\cdots ,y_n$ are non-negative numbers, then

$$\begin{array}{cc}\hfill n\left[\frac{1}{n}\sum _{j=1}^n{y}_j-{\left(\prod _{j=1}^n{y}_j\right)}^{\frac{1}{n}}\right]& \le n\sum _{j=1}^n{y}_j-{\left(\sum _{j=1}^n\sqrt{y_j}\right)}^2\hfill \\ & \le n(n-1)\left[\frac{1}{n}\sum _{j=1}^n{y}_j-{\left(\prod _{j=1}^n{y}_j\right)}^{\frac{1}{n}}\right].\hfill \end{array}$$

Moreover, equality occurs if and only if $y_1=y_2=\cdots =y_n$.

The next result provides another upper and lower bound for the general extended energy of chain graphs.

Theorem 6.

Let $G\cong G(m_1,\cdots ,m_h;n_1,\cdots ,n_h)$ be a chain graph. Then,

$$\begin{array}{c}\sqrt{2\sum _{j=1}^h\sum _{i=1}^{h-(j-1)}{m}_j{n}_i{\varphi }_{d_j{\mathcal{l}}_i}^2+(2h-1)\Gamma }\le {\mathcal{E}}_{\varphi }\left(G\right)\hfill \\ \le \sqrt{(2h-1)\left(2\sum _{j=1}^h\sum _{i=1}^{h-(j-1)}{m}_j{n}_i{\varphi }_{d_j{\mathcal{l}}_i}^2\right)+\Gamma },\hfill \end{array}$$

where $\Gamma =2h{\left({\prod }_{i=1}^h{m}_i{n}_i{\varphi }_{d_i{\mathcal{l}}_{h-(i-1)}}^2\right)}^{\frac{1}{h}}$. Equality occurs on the left (right) hand side if and only if G is a complete bipartite graph.

Proof. 

Let ${\lambda }_1\ge {\lambda }_2\ge \cdots \ge {\lambda }_n$ be the $A_{\varphi }$-eigenvalues of G. By Theorem 3, among the $A_{\varphi }$-eigenvalues of G only $2h$ eigenvalues are non-zero. Let ${\eta }_1\ge {\eta }_2\ge \cdots \ge {\eta }_{2h}$ be the non-zero $A_{\varphi }$-eigenvalues of G, then it is clear that these $2h$ eigenvalues are the eigenvalues of the matrix Q given by (4). Setting $n=2h$ and $y_j={\left|{\eta }_j\right|}^2={\eta }_j^2,$ for $j=1,2,\cdots ,2h$ in Lemma 2, we have

$$\begin{array}{c}\hfill \beta \le (n-1)\sum _{j=1}^{2h}{\eta }_j^2-{\left(\sum _{j=1}^{2h}{\eta }_j\right)}^2\le (n-2)\beta ,\end{array}$$

that is,

$$\beta \le (n-1)\sum _{j=1}^{2h}{\eta }_j^2-{\left({\mathcal{E}}_{\varphi }\left(G\right)\right)}^2\le (n-2)\beta ,$$

(12)

where

$$\begin{array}{cc}\hfill \beta & =2h\left[\frac{1}{2h}\sum _{j=1}^{2h}{\eta }_j^2-{\left(\prod _{j=1}^{2h}{\eta }_j^2\right)}^{\frac{1}{2h}}\right]\hfill \\ & =\sum _{j=1}^{2h}{\eta }_j^2-2h{\left(det\left(Q\right)\right)}^{\frac{1}{h}}.\hfill \end{array}$$

Using Theorem 4 and the value of $\beta$, from the left inequality of (12) we obtain

$$\begin{array}{c}\hfill {\left({\mathcal{E}}_{\varphi }\left(G\right)\right)}^2\le (2h-1)\sum _{j=1}^{2h}{\eta }_j^2+2h{\left(det\left(Q\right)\right)}^{\frac{1}{h}},\end{array}$$

that is,

$$\begin{array}{c}\hfill {\mathcal{E}}_{\varphi }\left(G\right)\le \sqrt{(2h-1)\left(2\sum _{j=1}^h\sum _{i=1}^{h-(j-1)}{m}_j{n}_i{\varphi }_{d_j{\mathcal{l}}_i}^2\right)+\Gamma },\end{array}$$

where $\Gamma =2h{\left({\prod }_{i=1}^h{m}_i{n}_i{\varphi }_{d_i{\mathcal{l}}_{h-(i-1)}}^2\right)}^{\frac{1}{h}}$. This proves the right-hand inequality.

Again using the value of $\beta$, it follows from the right-hand inequality of (12) that

$$\begin{array}{c}\hfill {\left({\mathcal{E}}_{\varphi }\left(G\right)\right)}^2\ge \sum _{j=1}^{2h}{\eta }_j^2+2h(2h-1){\left(det\left(Q\right)\right)}^{\frac{1}{h}},\end{array}$$

that is,

$$\begin{array}{c}\hfill {\mathcal{E}}_{\varphi }\left(G\right)\ge \sqrt{2\sum _{j=1}^h\sum _{i=1}^{h-(j-1)}{m}_j{n}_i{\varphi }_{d_j{\mathcal{l}}_i}^2+(2h-1)\Gamma },\end{array}$$

which proves the left-hand inequality.

Equality occurs in the left-hand inequality if and only if equality occurs in Lemma 2. Since equality occurs in Lemma 2 if and only if $y_1=y_2=\cdots =y_n$, it follows that equality occurs in the left-hand inequality if and only if ${\eta }_1^2={\eta }_2^2=\cdots ={\eta }_{2h}^2,$ that is, if and only if $|{\eta }_1|=|{\eta }_2|=\cdots =|{\eta }_{2h}|$. Since G being a bipartite graph implies that its $A_{\varphi }$-eigenvalues are symmetric about the origin, it follows that there exists a positive integer, t, such that ${\eta }_1=\cdots ={\eta }_t=k$ and ${\eta }_{t+1}=\cdots ={\eta }_{2h}=-k$. This confirms that equality holds in the left-hand inequality if and only if G has three distinct $A_{\varphi }$-eigenvalues, namely ${\eta }_1,0,$ and $-{\eta }_1$. Therefore, by Lemma 2.1 of [53] we arrive at $G\cong G(m_1;n_1).$ Similarly, we can discuss the equality case for the right-hand inequality.

Conversely, if G is a complete bipartite graph then it is easy to verify that both the inequalities occur as equalities. This completes the proof.  □

4. Concluding Remark

As mentioned in the introduction, for different choices of the function $\varphi$ we have different graph matrices that are well-studied in the literature concerning their spectral properties. Therefore, the results obtained in Section 2 and Section 3 for chain graphs are general results from which we can obtain the corresponding results for the graph matrix, which we arrive at when we fix a value for the function $\varphi$. In particular, if we take ${\varphi }_{d_u{d}_v}=1$ when $u\sim v$, then the results obtained in Section 2 and Section 3 became the corresponding results for the usual graph energy; if ${\varphi }_{d_u{d}_v}=d_u+d_v$ when $u\sim v$, then the results obtained in Section 2 and Section 3 became the corresponding results for the first Zagreb energy; if ${\varphi }_{d_u{d}_v}=d_u{d}_v$ when $u\sim v$, then the results obtained in Section 2 and Section 3 became the corresponding results for the second Zagreb energy; if ${\varphi }_{d_u{d}_v}=\frac{1}{\sqrt{d_u{d}_v}}$ when $u\sim v$, then the results obtained in Section 2 and Section 3 became the corresponding results for the Randić energy; if ${\varphi }_{d_u{d}_v}=\frac{1}{2}\left(\frac{d_u}{d_v}+\frac{d_v}{d_u}\right)$ when $u\sim v$, then the results obtained in Section 2 and Section 3 became the corresponding results for the extended energy; if ${\varphi }_{d_u{d}_v}=\frac{1}{\sqrt{d_u+d_v}}$ when $u\sim v$, then the results obtained in Section 2 and Section 3 became the corresponding results for the sum-connectivity energy; if ${\varphi }_{d_u{d}_v}=\sqrt{\frac{d_u+d_v-2}{d_u{d}_v}}$ when $u\sim v$, then the results obtained in Section 2 and Section 3 became the corresponding results for the ABC-energy; if ${\varphi }_{d_u{d}_v}=\frac{2\sqrt{d_u{d}_v}}{d_u+d_v}$ when $u\sim v$, then the results obtained in Section 2 and Section 3 became the corresponding results for the geometric–arithmetic energy; if ${\varphi }_{d_u{d}_v}=\frac{d_u+d_v}{2\sqrt{d_u{d}_v}}$ when $u\sim v$, then the results obtained in Section 2 and Section 3 became the corresponding results for the arithmetic–geometric energy; if ${\varphi }_{d_u{d}_v}=\sqrt{d_u^2+d_v^2}$ when $u\sim v$, then the results obtained in Section 2 and Section 3 became the corresponding results for the Sombor energy of G, and so on.