Out-of-Distribution Node Detection Based on Graph Heat Kernel Diffusion
Abstract
1. Introduction
2. Preliminary
2.1. Graph Neural Network
2.2. Out-of-Distribution Detection
2.3. Diffusion Equation
3. HOOD
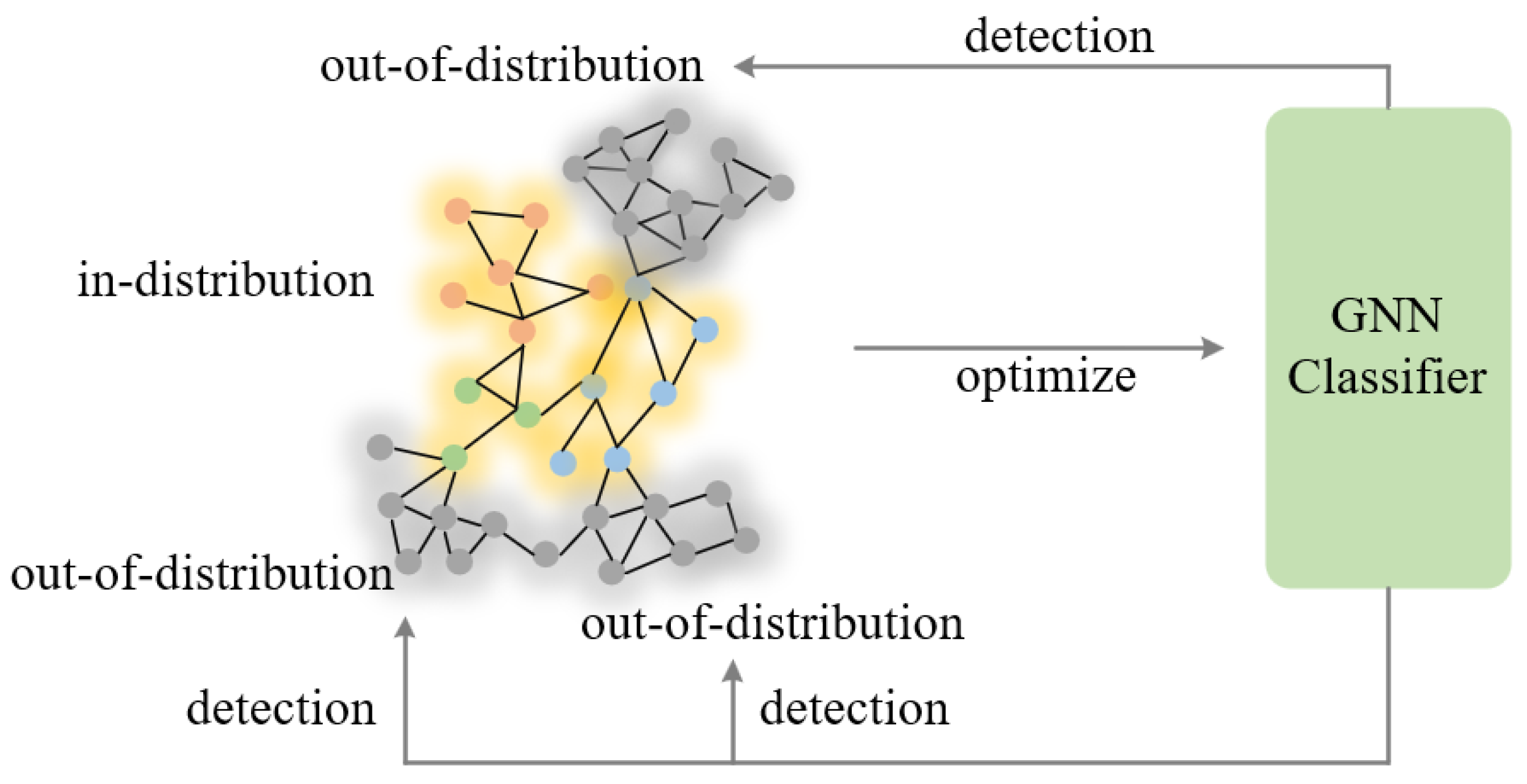
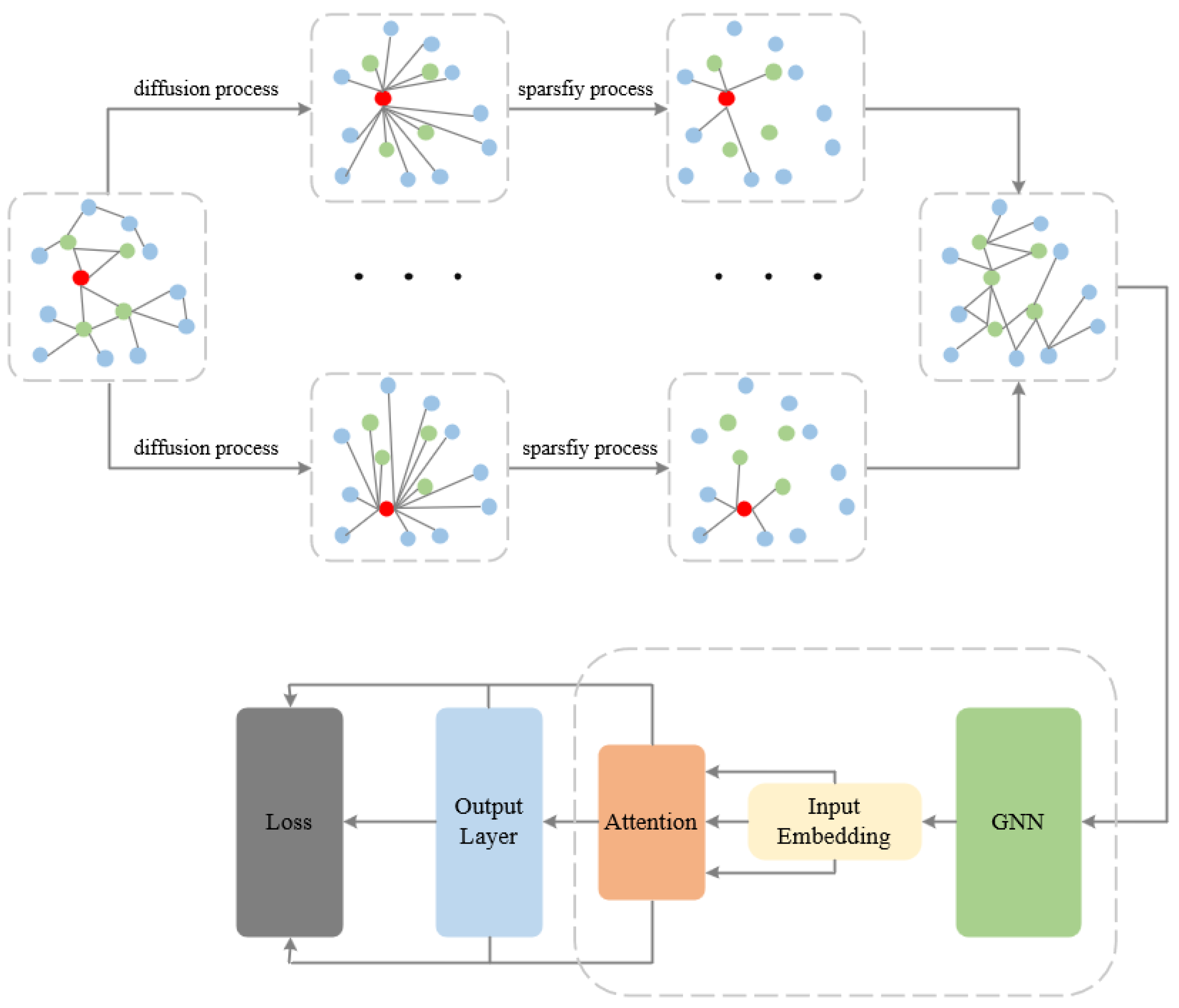
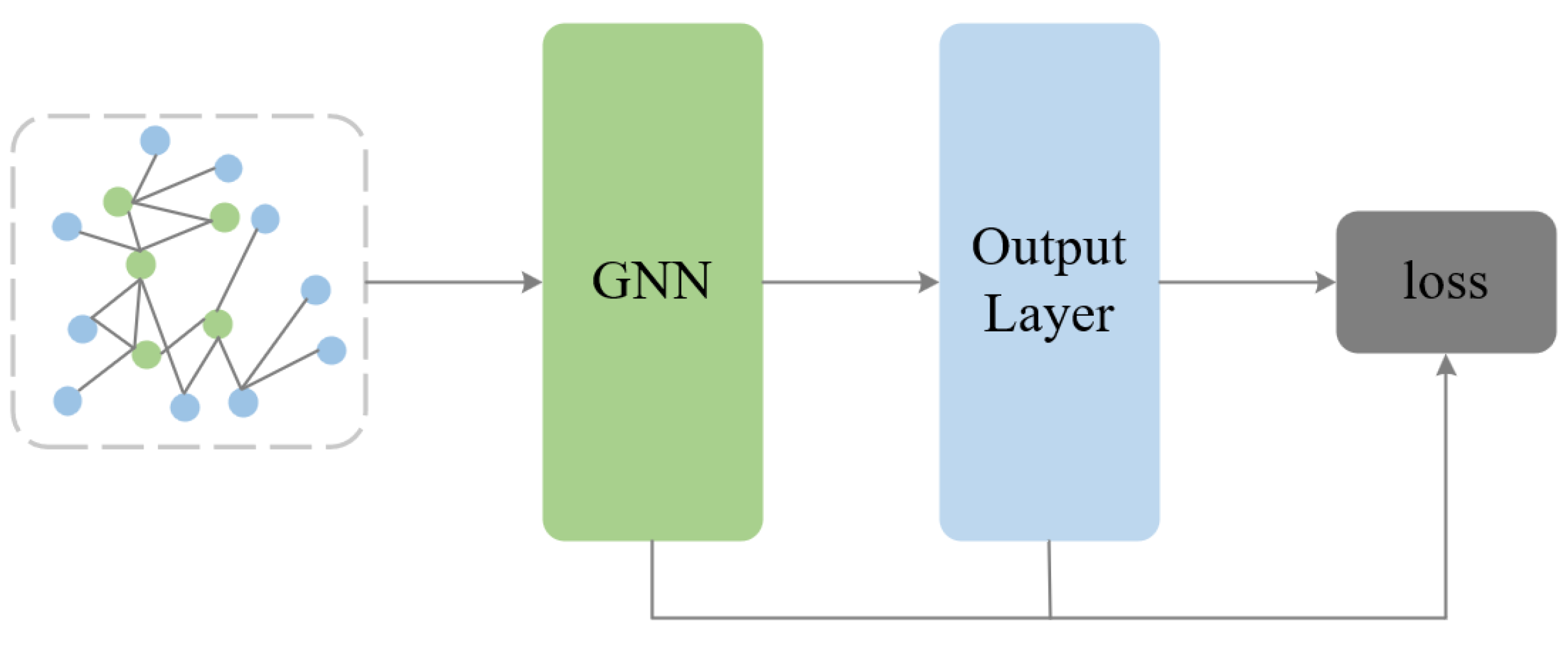
3.1. Overall Framework
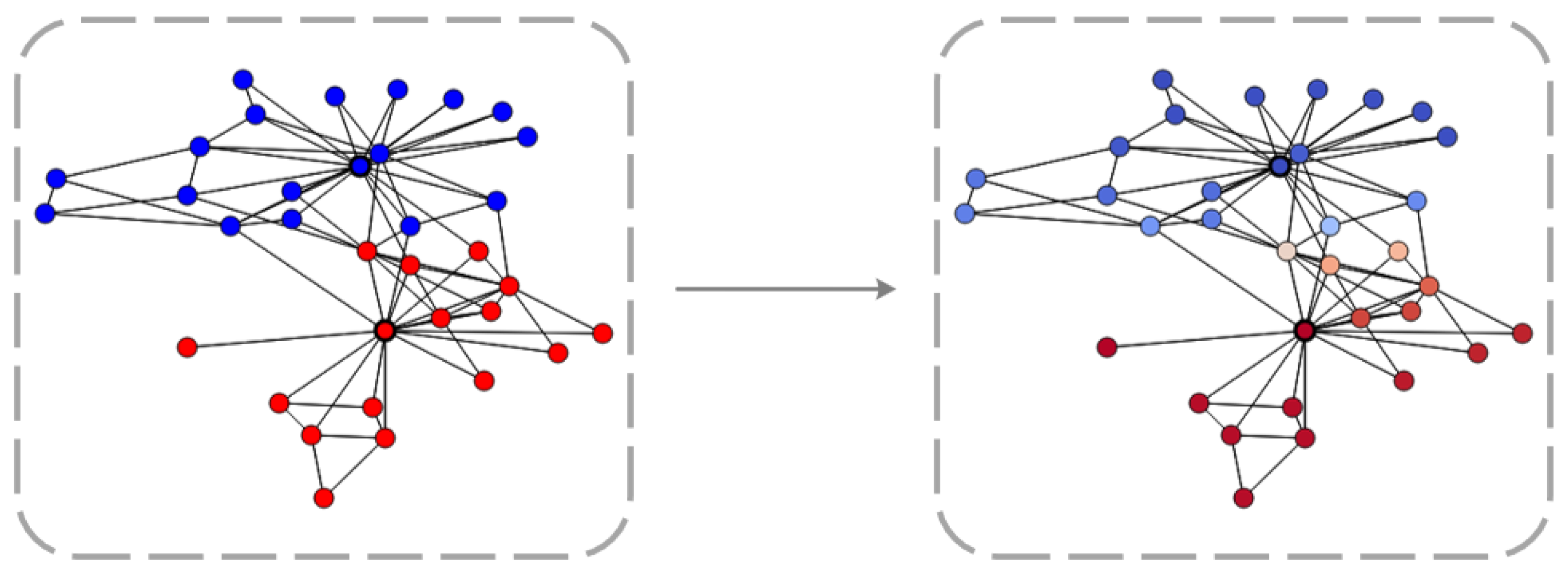
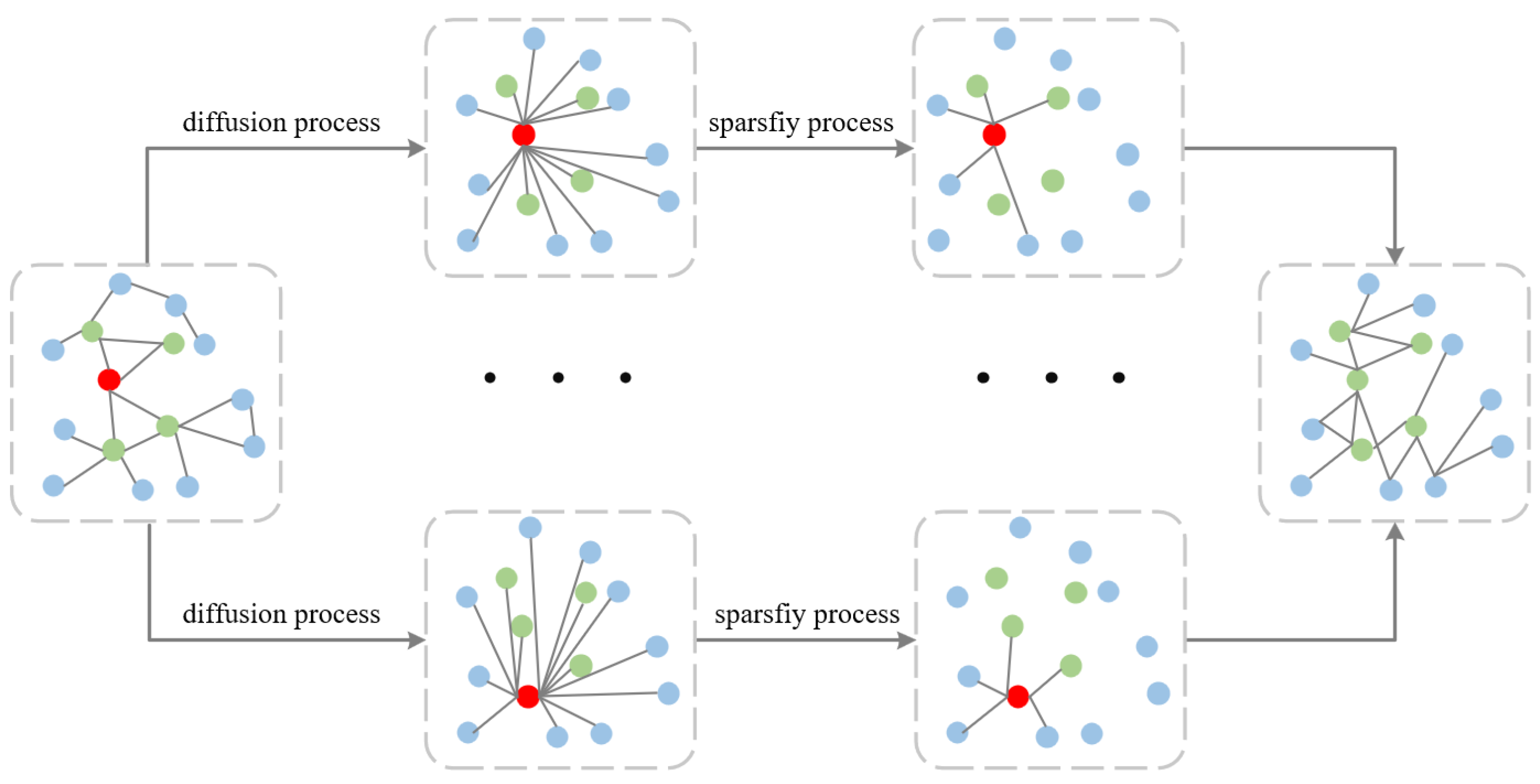
3.2. Out-of-Distribution Node Detection Based on Graph Heat Kernel Diffusion
3.3. Attention Mechanism
3.4. Regularization
4. Experiments
4.1. Datasets
4.2. Baselines
4.3. Evaluation Metrics
4.4. Experimental Settings
4.5. Results
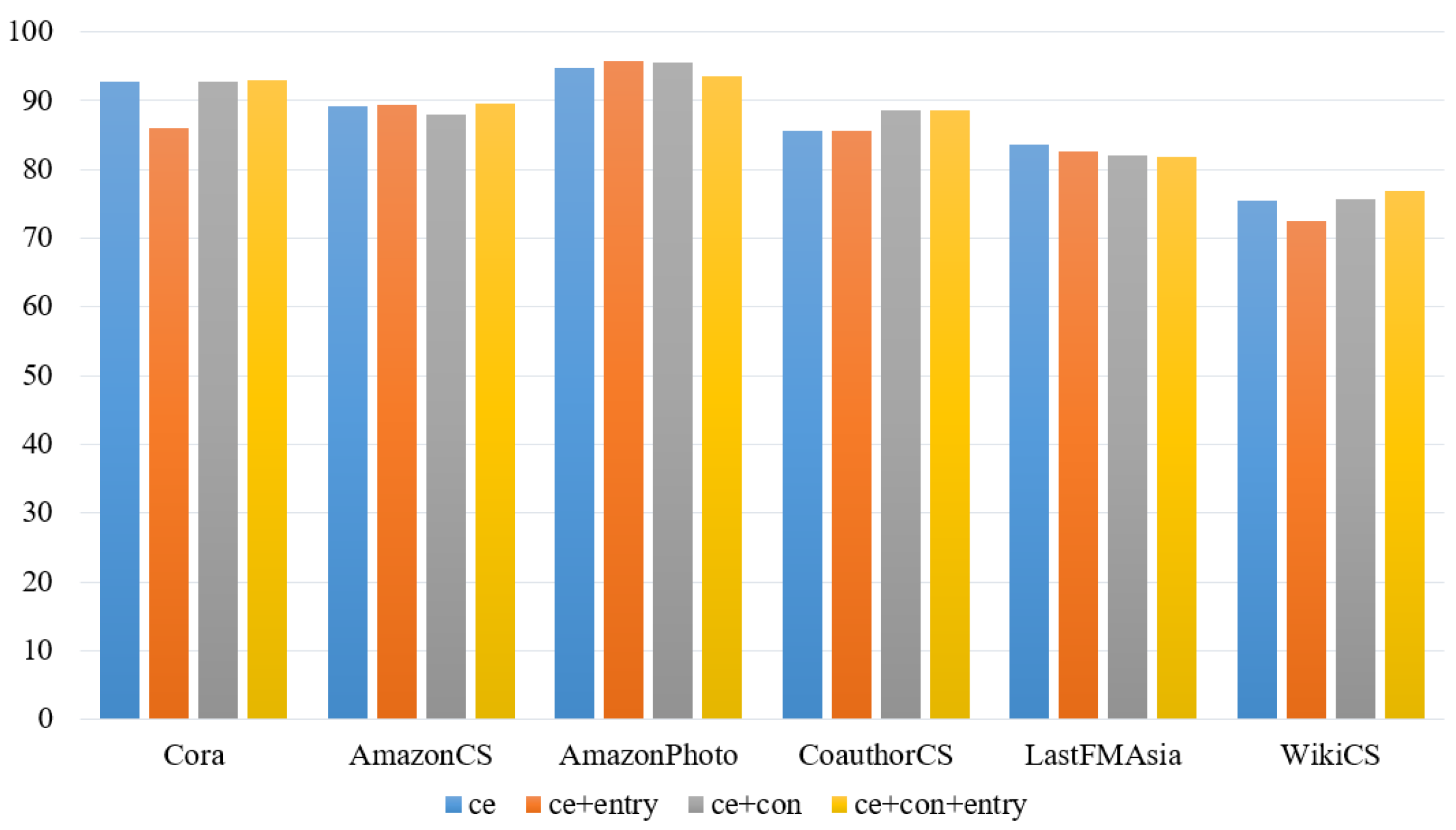
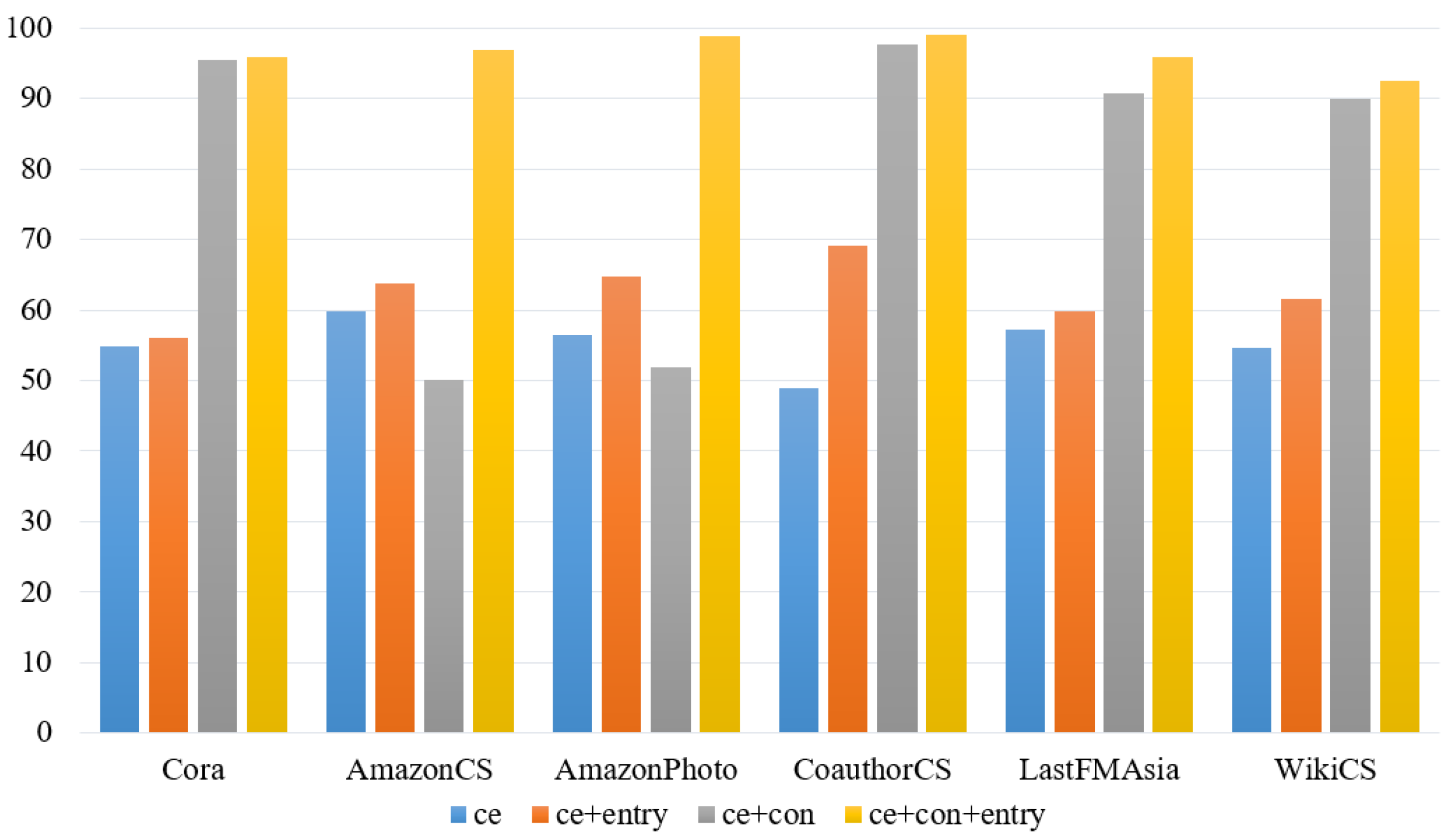
4.6. Ablation Study
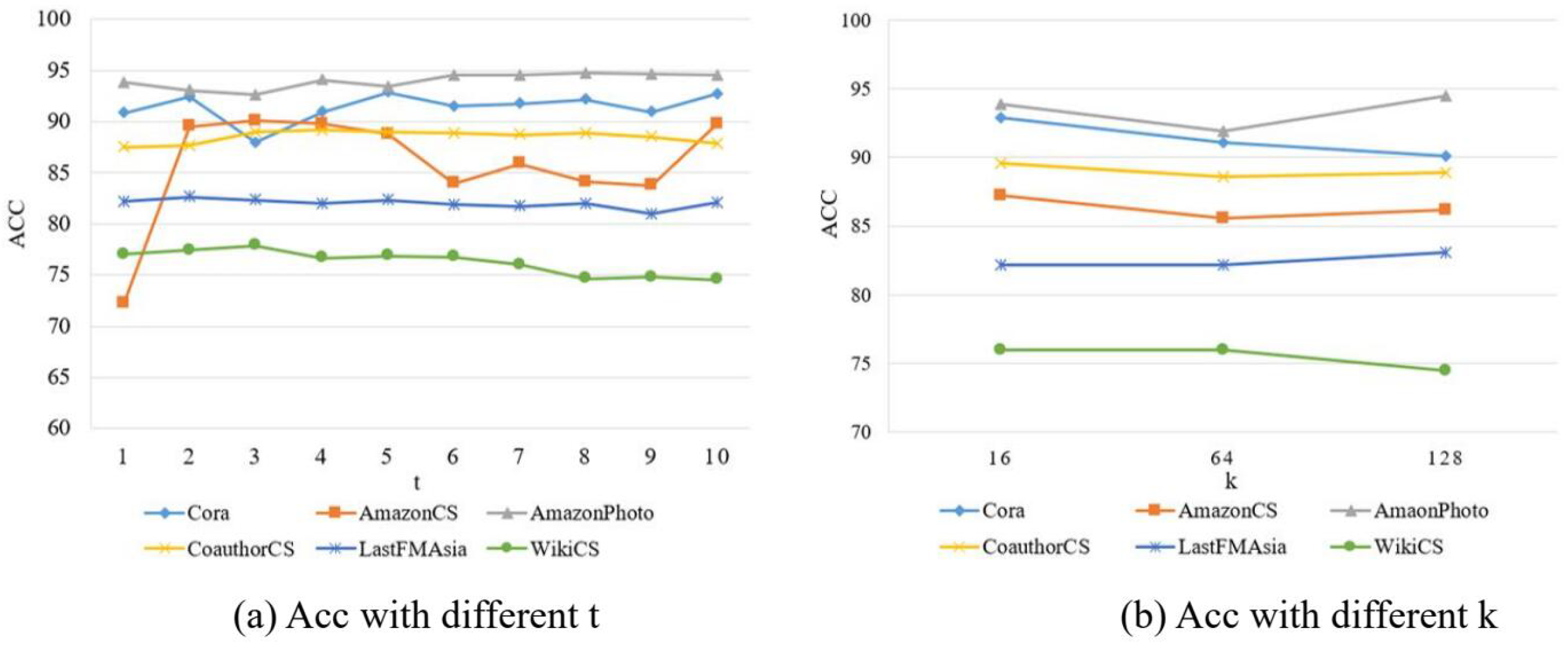
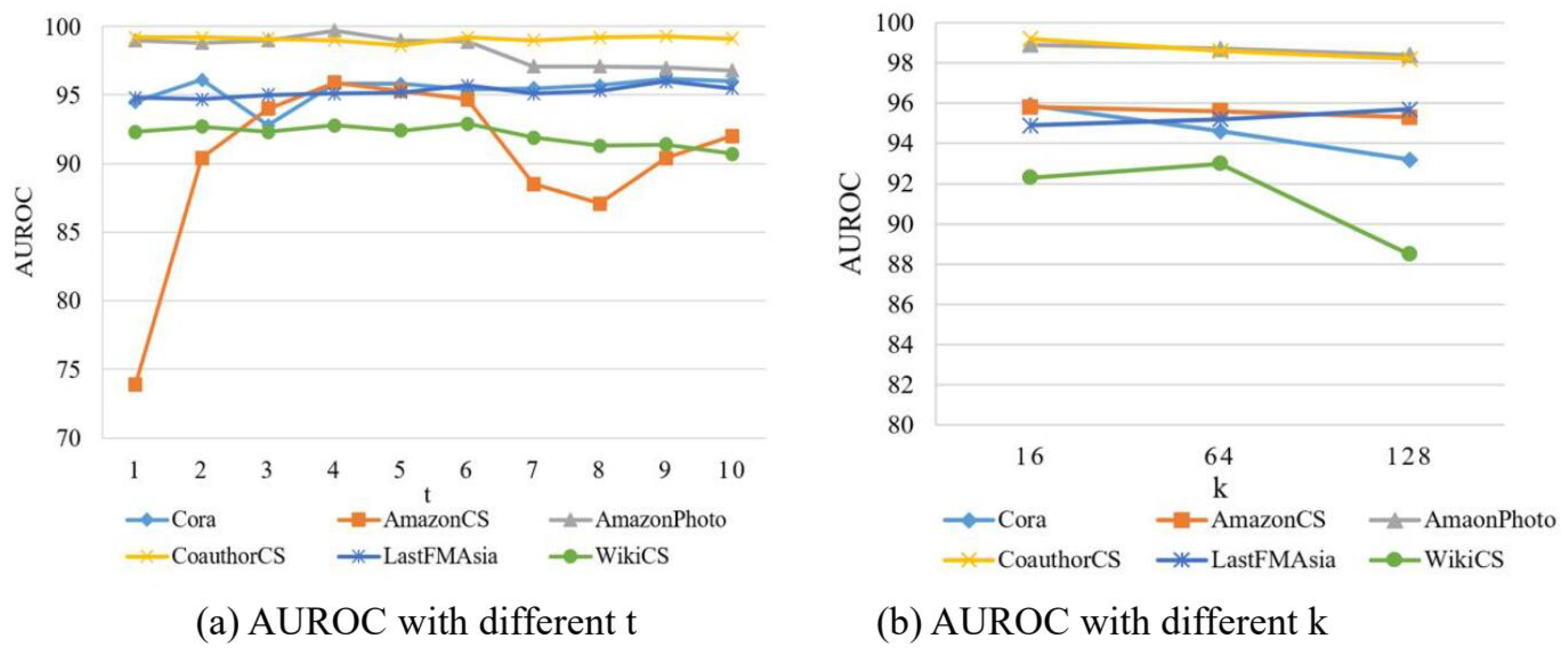
4.7. Impact of Hyper-Parameters on Model Performance
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wu, L.; Cui, P.; Pei, J.; Zhao, L.; Guo, X. Graph neural networks: Foundation, frontiers and applications. In Proceedings of the 28th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, 14–18 August 2022; pp. 4840–4841. [Google Scholar]
- Li, M.M.; Huang, K.; Zitnik, M. Graph representation learning in biomedicine and healthcare. Nat. Biomed. Eng. 2022, 6, 1353–1369. [Google Scholar] [CrossRef] [PubMed]
- Velickovic, P.; Cucurull, G.; Casanova, A.; Romero, A.; Lio, P.; Bengio, Y. Graph attention networks. Stat 2017, 1050, 10–48550. [Google Scholar]
- Zhou, J.; Shen, J.; Shan, Y.; Xuan, Q.; Chen, G. Subgraph augmentation with application to graph mining. Graph Data Min. Algorithm Secur. Appl. 2021, 73–91. [Google Scholar] [CrossRef]
- Xia, F.; Sun, K.; Yu, S.; Aziz, A.; Wan, L.; Pan, S.; Liu, H. Graph learning: A survey. IEEE Trans. Artif. Intell. 2021, 2, 109–127. [Google Scholar] [CrossRef]
- Chen, H.; Yin, H.; Wang, W.; Wang, H.; Nguyen, Q.V.H.; Li, X. PME: Projected metric embedding on heterogeneous networks for link prediction. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, London, UK, 19–23 August 2018; pp. 1177–1186. [Google Scholar]
- Wang, X.; Cui, P.; Wang, J.; Pei, J.; Zhu, W.; Yang, S. Community preserving network embedding. In Proceedings of the AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017; pp. 203–209. [Google Scholar]
- Long, Q.; Wang, Y.; Du, L.; Song, G.; Jin, Y.; Lin, W. Hierarchical community structure-preserving network embedding: A subspace approach. In Proceedings of the 28th ACM International Conference on Information and Knowledge Management (CIKM), Beijing, China, 3–7 November 2019; pp. 409–418. [Google Scholar]
- Shen, X.; Pan, S.; Liu, W.; Ong, Y.S.; Sun, Q.S. Discrete network embedding. In Proceedings of the 27th International Joint Conference on Artificial Intelligence (IJCAI), Stockholm, Sweden, 13–19 July 2018; pp. 3549–3555. [Google Scholar]
- Yang, H.; Pan, S.; Zhang, P.; Chen, L.; Lian, D.; Zhang, C. Binarized attributed network embedding. In Proceedings of the 2018 IEEE International Conference on Data Mining (ICDM), Singapore, 17–20 November 2018; pp. 1476–1481. [Google Scholar]
- Rong, Y.; Huang, W.; Xu, T.; Huang, J. Dropedge: Towards deep graph convolutional networks on node classification. arXiv 2019, arXiv:1907.10903. [Google Scholar]
- Pimentel, M.A.; Clifton, D.A.; Clifton, L.; Tarassenko, L. A review of novelty detection. Signal Process. 2014, 99, 215–249. [Google Scholar] [CrossRef]
- Ma, X.; Wu, J.; Xue, S.; Yang, J.; Zhou, C.; Sheng, Q.Z. A comprehensive survey on graph anomaly detection with deep learning. IEEE Trans. Knowl. Data Eng. 2021, 35, 12012–12038. [Google Scholar] [CrossRef]
- Song, Y.; Wang, D. Learning on graphs with out-of-distribution nodes. In Proceedings of the 28th ACM SIGKDD Conference on Knowledge Discovery and Data Mining (KDD), Washington, DC, USA, 14–18 August 2022; pp. 1635–1645. [Google Scholar]
- Zhang, H.; Wu, B.; Wang, S.; Yang, X.; Xue, M.; Pan, S.; Yuan, X. Demystifying uneven vulnerability of link stealing attacks against graph neural networks. In Proceedings of the International Conference on Machine Learning (PMLR), Honolulu, HI, USA, 23–29 July 2023; pp. 41737–41752. [Google Scholar]
- Dai, E.; Zhao, T.; Zhu, H.; Xu, J.; Guo, Z.; Liu, H.; Tang, J.; Wang, S. A comprehensive survey on trustworthy graph neural networks: Privacy, robustness, fairness, and explainability. arXiv 2022, arXiv:2204.08570. [Google Scholar]
- Wu, W.; Zhang, W.; Hou, W.; Ma, X. Multi-view clustering with graph learning for scRNA-seq data. IEEE/ACM Trans. Comput. Biol. Bioinform. 2023, 20, 3535–3546. [Google Scholar] [CrossRef]
- Jia, J.; Ma, S.; Liu, Y.; Wang, L.; Deng, R.H. A Causality-Aligned Structure Rationalization Scheme Against Adversarial Biased Perturbations for Graph Neural Networks. IEEE Trans. Inf. Forensics Secur. 2023, 19, 59–73. [Google Scholar] [CrossRef]
- Ju, W.; Yi, S.; Wang, Y.; Xiao, Z.; Mao, Z.; Li, H.; Gu, Y.; Qin, Y.; Yin, N.; Wang, S.; et al. A survey of graph neural networks in real world: Imbalance, noise, privacy and ood challenges. arXiv 2024, arXiv:2403.04468. [Google Scholar]
- Zhao, X.; Chen, F.; Hu, S.; Cho, J.H. Uncertainty aware semi-supervised learning on graph data. Adv. Neural Inf. Process. Syst. 2020, 33, 12827–12836. [Google Scholar]
- Stadler, M.; Charpentier, B.; Geisler, S.; Zügner, D.; Günnemann, S. Graph posterior network: Bayesian predictive uncertainty for node classification. Adv. Neural Inf. Process. Syst. 2021, 34, 18033–18048. [Google Scholar]
- Kondor, R.I.; Lafferty, J. Diffusion kernels on graphs and other discrete structures. In Proceedings of the 19th International Conference on Machine Learning, San Francisco, CA, USA, 8–12 July 2002; Volume 2002, pp. 315–322. [Google Scholar]
- Lafon, S.; Lee, A.B. Diffusion maps and coarse-graining: A unified framework for dimensionality reduction, graph partitioning, and data set parameterization. IEEE Trans. Pattern Anal. Mach. Intell. 2006, 28, 1393–1403. [Google Scholar] [CrossRef]
- Xu, B.; Shen, H.; Cao, Q.; Cen, K.; Cheng, X. Graph convolutional networks using heat kernel for semi-supervised learning. arXiv 2020, arXiv:2007.16002. [Google Scholar]
- Ortega, A.; Frossard, P.; Kovačević, J.; Moura, J.M.; Vandergheynst, P. Graph signal processing: Overview, challenges, and applications. Proc. IEEE 2018, 106, 808–828. [Google Scholar] [CrossRef]
- Gasteiger, J.; Weißenberger, S.; Günnemann, S. Diffusion improves graph learning. Adv. Neural Inf. Process. Syst. 2019, 32. [Google Scholar] [CrossRef]
- Hamilton, W.; Ying, R.; Leskovec, J. Inductive representation learning on large graphs. Adv. Neural Inf. Process. Syst. 2017, 30, 1–11. [Google Scholar]
- Liang, S.; Li, Y.; Srikant, R. Enhancing the reliability of out-of-distribution image detection in neural networks. arXiv 2017, arXiv:1706.02690. [Google Scholar]
- Lee, K.; Lee, K.; Lee, H.; Shin, J. A simple unified framework for detecting out-of-distribution samples and adversarial attacks. Adv. Neural Inf. Process. Syst. 2018, 31. [Google Scholar] [CrossRef]
- Wang, X.; Liu, H.; Shi, C.; Yang, C. Be confident! towards trustworthy graph neural networks via confidence calibration. Adv. Neural Inf. Process. Syst. 2021, 34, 23768–23779. [Google Scholar]
| Dataset | # Nodes | # Edges | # Labels |
|---|---|---|---|
| Cora | 2708 | 5429 | 7 |
| Amazon-Computer | 13,752 | 491,722 | 10 |
| Amazon-Photo | 7650 | 238,163 | 8 |
| Coauthor-CS | 18,333 | 163,788 | 15 |
| LastFMAsia | 7624 | 27,806 | 18 |
| Wiki-CS | 11,701 | 216,123 | 10 |
| Cora | AmazonCS | AmazonPhoto | CoauthorCS | LastFMAsia | Wiki-CS | |
|---|---|---|---|---|---|---|
| Acc/AUROC/FPR@95/F1 | ||||||
| MLP | 74.1/72.4/75.5/63.1 | 68.4/65.7/84.6/54.6 | 91.8/80.2/71.9/72.8 | 88.6/95.0/28.9/84.8 | 54.5/57.4/87.0/51.2 | 78.6/71.7/76.4/64.0 |
| GCN | 92.1/88.9/46.0/80.5 | 81.2/83.3/61.9/70.3 | 97.1/88.3/44.6/80.7 | 92.7/94.5/32.2/86.4 | 79.8/72.1/74.7/66.5 | 80.9/71.7/76.6/63.0 |
| SAGE | 90.8/87.7/46.6/79.2 | 83.2/84.6/54.9/71.7 | 97.1/93.5/32.0/87.2 | 92.6/97.0/16.8/89.1 | 79.3/73.7/68.9/67.0 | 78.6/73.0/65.3/66.2 |
| GAT | 91.6/90.1/40.8/81.5 | 82.3/88.5/42.9/76.5 | 96.9/92.5/31.7/86.1 | 92.0/96.6/16.7/89.0 | 82.3/81.1/49.6/75.0 | 79.9/79.8/63.6/70.0 |
| OODGAT | 92.3/93.6/26.1/85.1 | 86.6/93.1/45.2/82.2 | 97.6/98.3/5.8 /93.9 | 92.4/99.6/1.6 /93.5 | 83.3/91.9/27.7/81.0 | 81.4/88.3/51.2/73.7 |
| HOOD | 92.8/95.8/18.6/87.9 | 90.1/94.0/24.2/84.8 | 93.4/99.0/3.3/93.3 | 88.5/99.3/2.8/91.5 | 82.6/94.7/19.2/84.3 | 76.8/92.4/33.1/78.3 |
| GAT | ODIN | Mahalanobis-Distance | CaGCN | OODGAT | HOOD | |
|---|---|---|---|---|---|---|
| AUROC/FPR@95 | ||||||
| Cora | 90.7/36.8 | 90.7/37.2 | 87.3/50.3 | 89.9/45.7 | 94.1/25.0 | 95.8/18.6 |
| AmazonCS | 84.1/51.9 | 84.4/51.2 | 81.8/78.8 | 83.6/56.2 | 92.3/52.0 | 96.3/19.2 |
| AmazonPhoto | 94.3/21.7 | 94.3/26.5 | 77.1/59.6 | 94.4/24.1 | 98.4/4.2 | 99.0/3.3 |
| CoauthorCS | 96.2/19.6 | 96.1/19.8 | 94.0/25.3 | 95.8/22.1 | 99.6/1.4 | 99.3/2.8 |
| LastFMAsia | 78.5/60.7 | 81.1/52.9 | 83.4/51.0 | 89.6/30.4 | 90.5/26.8 | 95.9/15.6 |
| Wiki-CS | 80.4/62.5 | 80.4/62.5 | 74.0/74.4 | 82.7/54.7 | 88.6/49.0 | 92.9/31.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, F.; Wang, Y.; Du, X.; Li, X.; Yu, G. Out-of-Distribution Node Detection Based on Graph Heat Kernel Diffusion. Mathematics 2024, 12, 2942. https://doi.org/10.3390/math12182942
Li F, Wang Y, Du X, Li X, Yu G. Out-of-Distribution Node Detection Based on Graph Heat Kernel Diffusion. Mathematics. 2024; 12(18):2942. https://doi.org/10.3390/math12182942
Chicago/Turabian StyleLi, Fangfang, Yangshuai Wang, Xinyu Du, Xiaohua Li, and Ge Yu. 2024. "Out-of-Distribution Node Detection Based on Graph Heat Kernel Diffusion" Mathematics 12, no. 18: 2942. https://doi.org/10.3390/math12182942
APA StyleLi, F., Wang, Y., Du, X., Li, X., & Yu, G. (2024). Out-of-Distribution Node Detection Based on Graph Heat Kernel Diffusion. Mathematics, 12(18), 2942. https://doi.org/10.3390/math12182942






