Crow Search Algorithm for Modelling an Anaerobic Digestion Process: Algorithm Parameter Influence

Abstract

Corn steep liquor is a waste product from the process of treating corn grain for starch extraction. It is used as a substrate in anaerobic digestion with simultaneous hydrogen and methane production in a cascade of two anaerobic bioreactors. For process research and optimisation, adequate mathematical models are required. So, the authors aim to present a high-quality model of the corn steep liquor process for the sequential production of H₂ and CH₄. This paper proposes a technique for identifying the best mathematical model of the process using the metaheuristics crow search algorithm (CSA). The CSA was applied for the first time to mathematical modelling of the considered two-stage anaerobic digestion process, using real experimental data. Based on the analysis of the numerical data from the model parameter identification procedures, the influence of the main CSA parameters—the flight length, fl, and the awareness probability, AP—was investigated. Applying classical statistical tests and an innovative approach, InterCriteria Analysis, recommendations about the optimal CSA parameter tuning were proposed. The best CSA algorithm performance was achieved for the AP = 0.05, fl = 3.0, followed by AP = 0.10, fl = 2.5, and AP = 0.15, fl = 3.0. The optimal tuning of the CSA parameters resulted in a 29% improvement in solution accuracy. As a result, a mathematical model of the considered two-stage anaerobic digestion process with a high degree of accuracy was developed.

1. Introduction

The use of two-stage anaerobic digestion (TSAD), consisting of a hydrogen process followed by a methanogenic process, is becoming increasingly important, with the aim of good absorption of the substrate and increasing the energy obtained from the process [1]. Modelling is an important step in understanding the anaerobic digestion process as models can be used to optimise and control the process [2,3]. Two-stage models are of particular interest in the modelling of biotechnological processes because they are sufficiently complex to capture the dynamics of the process [4]. TSAD is a highly sensitive and substrate-dependent process whose patterns are highly nonlinear and have multiple parameters that are difficult to determine.

Over the past four decades, fundamental models of varying complexity describing the TSAD process have been developed. Many models describe separately the fermentative H₂ and CH₄ production [5,6,7]. Recently, there have also been works involving models of two-step processes [8,9]. In [10], machine learning models were developed to predict the COD of wastewater. A modified model was proposed in [11] by incorporating experimentally realised online parameter identification and feedback control synthesis. An experimental setup was performed for a two-stage process in an automated bioreactor. Robust feedback control was implemented for each stage. In [12], machine learning models were constructed to predict TSAD efficiency.

It has to be concluded that decision-making with the help of machine learning is an emerging approach. Various machine learning models and algorithms can be applied to predict and optimise the TSAD [13]. With their help, the instability of the process can be reduced. Machine learning has some limitations. As far as the concept of machine learning is concerned with identifying useful data, the result will be incorrect if a reliable large amount of quality data are not provided. So machine learning greatly depends on the data and their quality. Machines require large and expensive resources and high-quality expertise to create the necessary infrastructure. To avoid these drawbacks, structural mathematical models can be applied, and further research and application of novel optimisation algorithms are needed for practical application.

As a scientific endeavour, machine learning grew out of the quest for artificial intelligence (AI). In the field of AI, the concept of metaheuristics plays a key role in process modelling and optimisation. Metaheuristic algorithms have shown a promising performance on such complicated tasks as highly nonlinear dynamics and multiple parameters [14]. The challenging identification procedures for such models are usually handled by metaheuristic techniques as effective alternatives to classical optimisation methods relying on the fact that they lead to a near-optimal solution for a tolerable amount of time [15,16,17].

Several metaheuristic algorithms, such as the genetic algorithm (GA) [18], coyote optimisation algorithm [19], artificial bee colony [20], etc., have been effectively employed to identify parameters in bioprocess models [21,22,23]. These algorithms can handle the considered complex problems. As a result of their application, models with high accuracy are obtained.

Among the existing metaheuristic algorithms, the crow search algorithm (CSA) [24] is a promising algorithm widely adopted in various fields because of its simplicity and ease of use. The CSA is a metaheuristic algorithm based on bird swarm intelligence in searching for and hiding food. In the review [25], it is noted that although the existing works proposed a CSA with enhanced performance from various aspects, there is still room for further improvement. Some of the latest applications of the CSA proposed various modifications and hybridisations of the algorithm. In [26] a variable step crow search algorithm is proposed that uses the cosine function. As a result, both the solution quality of the population and the convergence speed are improved. The searchability of the CSA is balanced and the accuracy is improved by applying the cross-pollination strategy with Cauchy mutation from the flower pollination algorithm [27]. In [28] an adaptive hierarchical learning technique was used in the CSA to improve the diversity of the population. The multi-strategy search for the CSA has been proposed to enrich the search facilities and provide algorithm diversity [29]. Promising results are presented in [30], where the CSA employs a pattern search as a local search algorithm.

The known investigations proposed a modified CSA that led to an overall improvement of the algorithm performance and declared that the algorithms outperformed other representative algorithms in terms of accuracy but did not discuss the resulting algorithm complexity. In many cases, a significant increase in the complexity of the modified algorithm was observed. On the other hand, effective parameter tuning can significantly impact the accuracy, efficiency, and effectiveness of the algorithm. Parameter tuning was the most crucial factor, which was responsible for the efficiency of any metaheuristic algorithm [31,32]. In an extensive review of the CSA, about 135 papers have been collected and summarised [33]. The analysis shows that despite the success and popularity of the CSA, many areas and challenges need to be addressed in the future. One of them is that there is no work in the literature that studies the tuning parameters of the CSA. So, in this paper, proper tuning of CSA parameters is investigated to ensure convergence to the global position more swiftly, further improvements of the algorithm efficiency, and a successful application for modelling of a TSAD process.

The CSA has fewer parameters (flight length, fl, and the awareness probability, AP) that should be empirically determined, which is better since the proper tuning means a large number of experiments, i.e., a complex and time-consuming task.

Different approaches are utilised for parameter adjustment of metaheuristic algorithms: control parameters [34], value calibration method [35], regression analysis [36], full factorial design of experiments [37,38,39], data envelopment analysis method and response surface methodology [40], racing and case-based reasoning [41], etc. Various tuning strategies of metaheuristics are presented in [42], and a comprehensive survey of automatic parameter tuning methods for metaheuristics is performed in [43].

For large systems with many variables (more than 50) and a few interactions between variables, random design is usually used. When it is used properly (in a large system), random design produces an experimental design that is desired. However, random design works poorly for systems with a small number of variables. Among the methods, the Taguchi method is best used when there is an intermediate number of variables (from 4 to 50) [44,45]. Also, since orthogonal arrays do not test all variable combinations, which is essential in this work, the Taguchi method is also inappropriate in the present investigation. The factorial design becomes increasingly complex with an increase in the number of variables, but for scenarios with a small number of parameters and levels (one to three), it can work well [46,47].

The idea in this study was to examine ten levels of factor one (fl) and seven levels of factor two (AP) since the experimental designs discussed above were unsuitable. Therefore, a full combination of the two factors with ten and seven levels was elaborated. To investigate the algorithm performance influence of the fl and AP parameters a total number of 70 combinations (differently tuned CSAs) were designed. All CSAs were applied to the parameter identification of a corn steep liquor TSAD process model.

Corn steep liquor is a waste product from the process of treating corn grain for starch extraction [48]. It is used as a substrate in the process of anaerobic digestion with simultaneous hydrogen and methane production. The process is performed in a cascade of two anaerobic bioreactors, and the process dynamics is represented by a set of five ordinary differential equations and two algebraic equations with nine unknown model parameters.

The main contributions of this study are as follows:

(1)

The CSA was applied for the first time to the mathematical modelling of the TSAD process, based on real experimental data.

(2)

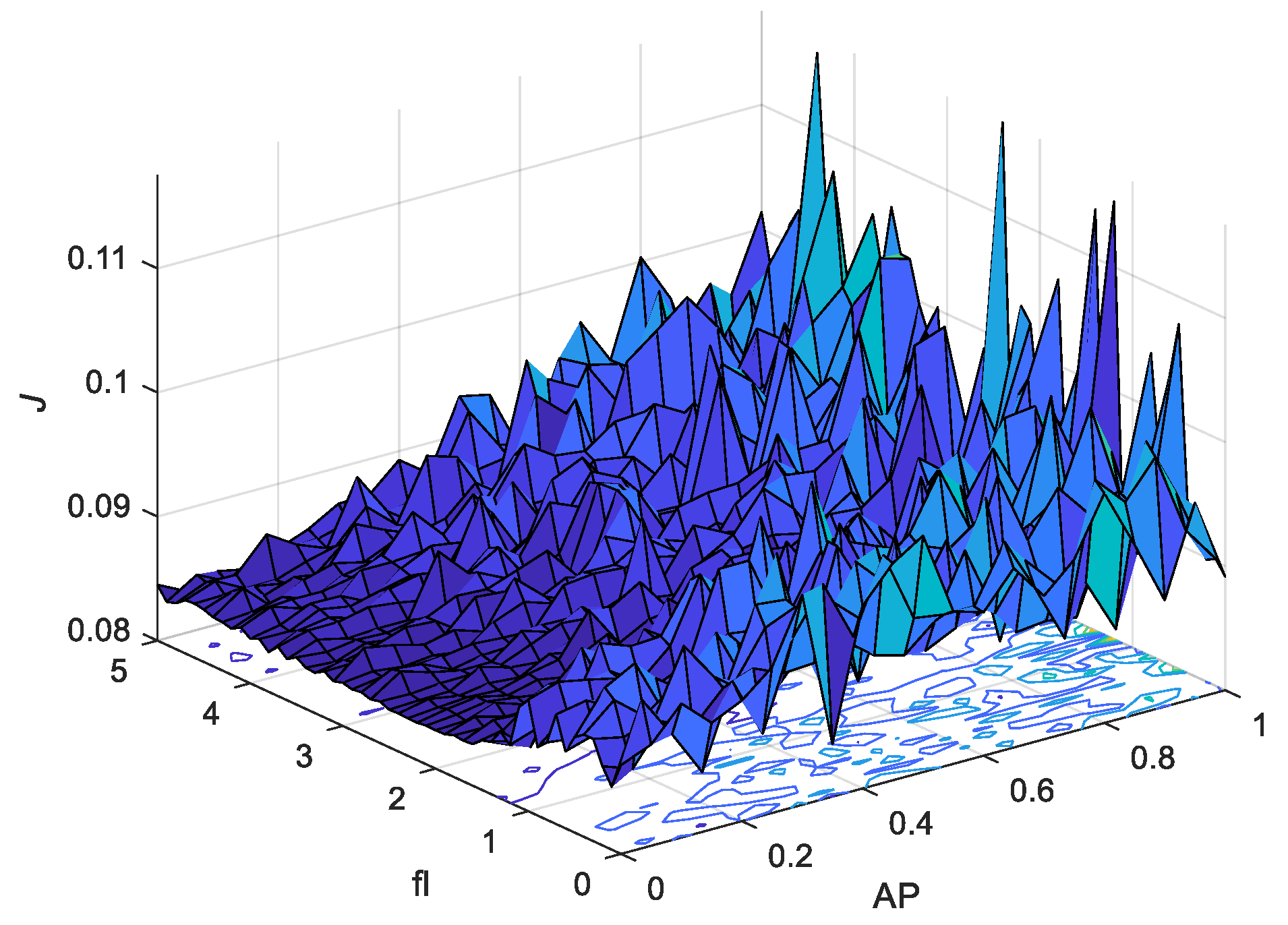
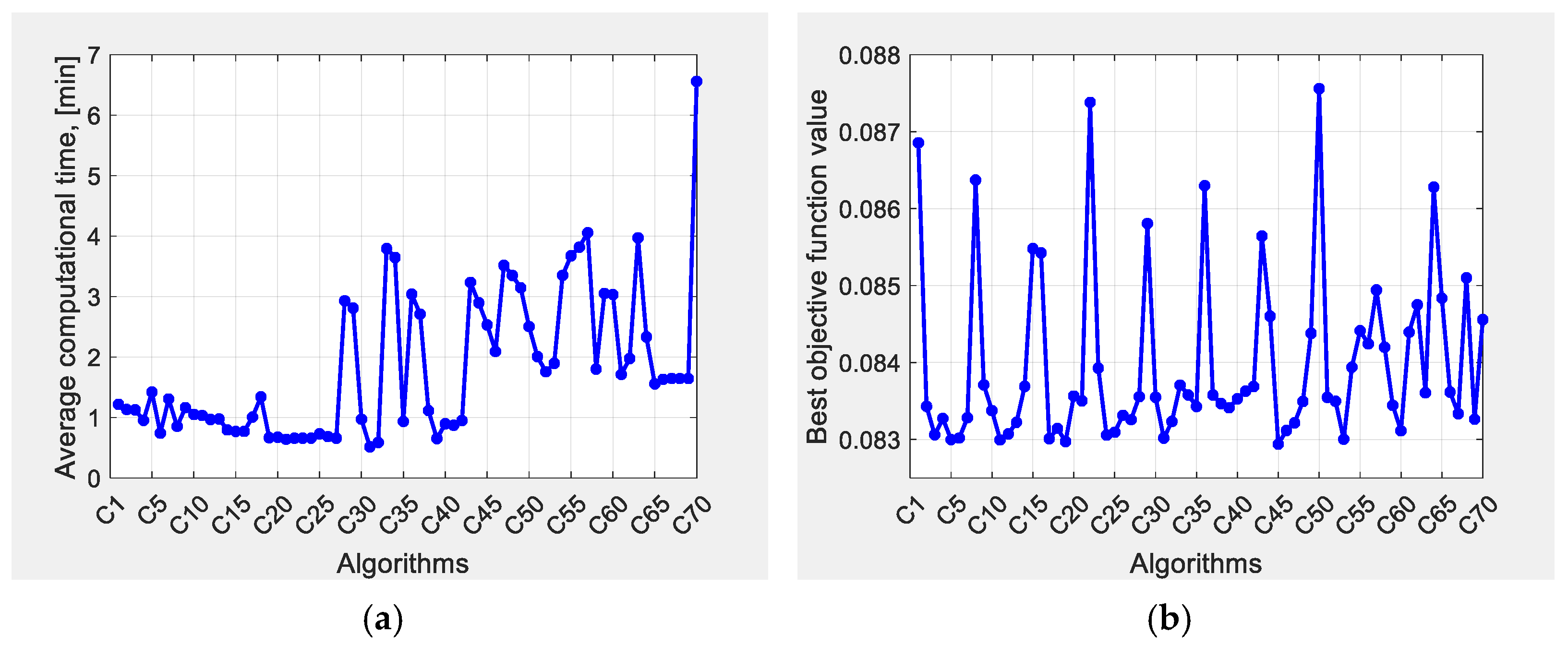
The influence of the main CSA parameters, fl and AP, was investigated based on the analysis of numerical data from the model parameter identification procedures with 70 differently tuned CSA. With the optimal tuning of the CSA parameters, a 29% improvement in solution accuracy was achieved.

(3)

Recommendations about the optimal CSA parameter tuning were provided based on the performed classical statistical tests and an innovative approach, InterCriteria Analysis. Moreover, it was found that the parameter AP was more sensitive than the parameter fl and influenced to a greater extent the CSA performance in terms of the solution accuracy and convergence time.

(4)

The mathematical models of the TSAD process with a high degree of accuracy were developed.

The rest of the paper is organised in the following manner. The mathematical model of the two-stage anaerobic digestion process is described in Section 2. The CSA, algorithm tuning procedure, and applied analysis are presented in Section 3. The obtained numerical results and analysis are presented and discussed in Section 4. A summary of the results and further work directions are given in Section 5.

2. Mathematical Model of the Two-Stage Anaerobic Digestion Process

All the experiments were performed at the Stephan Angeloff Institute of Microbiology, Bulgarian Academy of Sciences, Bulgaria. The TSAD process of corn steep liquor for sequential production of H₂ and CH₄ was carried out in two separate bioreactors [48]. During the first stage, relatively fast-growing acidogenic microorganisms engaged in the production of volatile fatty acids and H₂ were cultivated in the hydrogenic bioreactor (BR₁). Slow-growing acetogenic and methanogenic bacteria were developed during the second stage in the methanogenic bioreactor (BR₂). The volatile fatty acids were later transformed into CH₄ and CO₂ in BR₂. The daily yields of biohydrogen in the first bioreactor of the cascade were in the range of 0.7 to 1.0 L of biogas from a 1 dm³ working volume of the bioreactor. The daily yields of biomethane in the second bioreactor of the cascade varied in the range of 0.4 to 0.85 L of biogas from a 1 dm³ working volume of the bioreactor.

Presented by a set of five ordinary differential equations (ODEs) and two algebraic equations using mass balance, the process dynamics in the cascade BR₁ and BR₂ were as follows:

BR₁:

$${\displaystyle \frac{d{S}_1}{dt}}=-Y_1{\mu }_1{X}_1+D_1\left(S_{1in}-S_1\right),$$

(1)

$${\displaystyle \frac{d{X}_1}{dt}}={\mu }_1{X}_1-D_1{X}_1,$$

(2)

$${\displaystyle \frac{dA{c}_1}{dt}}=Y_2{\mu }_1{X}_1-D_{1}A{c}_1,$$

(3)

$$Q_{H_2}=Y_{H_2}{\mu }_1{X}_1,$$

(4)

$${\mu }_1={\displaystyle \frac{{\mu }_{1max}{S}_1}{K_{S_1}+S_1}}.$$

(5)

BR₂:

$${\displaystyle \frac{d{X}_2}{dt}}={\mu }_2{X}_2-D_2{X}_2,$$

(6)

$${\displaystyle \frac{dA{c}_2}{dt}}=-Y_3{\mu }_2{X}_2+D_2\left(A{c}_1-A{c}_2\right),$$

(7)

$$Q_{C{H}_4}=Y_{C{H}_4}{\mu }_2{X}_2,$$

(8)

$${\mu }_2={\displaystyle \frac{{\mu }_{2max}A{c}_2}{K_{S_2}+A{c}_2}} .$$

(9)

The system (1)–(5) describes the dynamics of the substrate concentration ($S_1$) [g/L], the microbial biomass concentration ($X_1$) [g/L], and the product (acetate) formation ($A{c}_1$) [g/L] in BR₁. The algebraic equation describes the flow rate of the hydrogen ($Q_{H_2}$) [dm³/L·h] in the gas phase of BR₁. $S_{1in}$ [g/L] is the concentration of the input substrate. Monod-type kinetics was applied for the specific growth rate ${\mu }_1$ [day⁻¹] of hydrogen-producing microorganisms. $D_1$ [day⁻¹] is the dilution rate for the first bioreactor BR₁; ${\mu }_{1max}$ [day⁻¹] and $K_{S_1}$ [g/L] are Monod kinetic coefficients; and $Y_1$, $Y_2$, and $Y_{H_2}$ are yield coefficients [g/g].

The system (6)–(8) describes a one-step transformation of the inlet acetate $A{c}_1$ (coming from BR₁) into methane by methanogenic microorganisms. Monod kinetics was also used for the specific growth rate of the methanogenic biomass. In the model, $X_2$ is the microbial biomass concentration in BR₂ [g/L], $A{c}_2$ is the acetate concentration in BR₂ [g/L], $Q_{C{H}_4}$ is the methane flow rate [dm³/L·day], $D_2$ [day⁻¹] is the dilution rate for the second bioreactor BR₂, ${\mu }_2$ is the specific growth rate (Monod type) of methanogens [day⁻¹], $Y_{C{H}_4}$ and $Y_3$ are yield coefficients, and ${\mu }_{2max}$ [day⁻¹] and $K_{S_2}$ [g/L] are kinetic coefficients.

The following vector of nine model parameters should be identified: $p=[{\mu }_{1max}$, ${\mu }_{2max}$, $K_{S_1}$, $K_{S_2}$, $Y_1$, $Y_2$, $Y_3$, $Y_{H_2}$, $Y_{C{H}_4}]$, based on experimental data, to predict the real data in the best possible way.

The mean square deviation between the modelled and experimental data was used as an optimisation criterion (cost function):

$$J=\Vert {N_{\mathrm{mod}\hspace{0.17em}\hspace{0.17em}}-N_{\exp }\Vert }^2\to min$$

(10)

where $\Vert \Vert$ is the ${\mathcal{l}}^2$-vector norm; $N_{\mathrm{mod}}\stackrel{def}{=}\left[Q_{H_2\mathrm{mod}} Q_{C{H}_{4\mathrm{mod}}}\right]$ are modelled data, and $N_{\exp }\stackrel{def}{=}\left[Q_{H_{2\exp }} Q_{C{H}_{4\exp }}\right]$ are experimental data.

The CSA was applied to identify/estimate the mathematical model parameters ${\mu }_{1max}$, ${\mu }_{2max}$, $K_{S_1}$, $K_{S_2}$, $Y_1$, $Y_2$, $Y_3$, $Y_{H_2}$, and $Y_{C{H}_4}$, the parameters for optimisation.

3. Crow Search Algorithm

3.1. CSA Background

The CSA, introduced by Askarzadeh in 2016 [24], depicts the intelligent behaviour of the crows. Below, the basics of the CSA are briefly presented.

The CSA employs N crows in the flock. The current position of each crow is presented as a d-dimensional vector:

$$cro{w}_i=\left\{cro{w}_i^1,\dots , cro{w}_i^d\right\}, i\in \left[1;N\right],$$

(11)

where d is the problem size. In the current research, each crow $cro{w}_i^d$ represents one of the nine model parameters, so the feasible solution of the vector p of the model parameters is represented by each crow position. Initially, all crows in the flock are positioned randomly. The best position of the crow yet is stored in its memory, in the hiding place $me{m}_i$.

At a certain point in time, $cro{w}_i$ may follow $cro{w}_j$. If $cro{w}_j$ is unaware that it is being followed, it will lead $cro{w}_i$ to its hiding place. The current position of $cro{w}_i$ is adjusted accordingly:

$$cro{w}_i=cro{w}_i+r_i\times flight\_length\times \left(me{m}_j-cro{w}_i\right),$$

(12)

where $r_i\in \left[0;1\right]$ is a random number with uniform distribution. However, if $cro{w}_j$ is aware of the presence of $cro{w}_i$, to protect its hiding place, it will try to deceive the pursuer by taking it somewhere random. The position of $cro{w}_i$ is then changed to a randomly generated one. The awareness of a crow is modelled by a random number and compared with an awareness probability parameter.

Mainly, CSA performance depends on a few parameters: the number of crows in the flock N, the maximum number of iterations MaxIter, the flight length fl, and the awareness probability AP. The fl and AP parameters need special attention to evaluate their impacts on the CSA performance in terms of solution accuracy and total computational time.

3.2. CSA Parameter Influence Investigation Methodology

A population size of 40 crows (N) in each flock was chosen with 60 iterations (MaxIter), as recommended in [24]. Larger values of N and MaxIter were investigated. Such values led to an increase in the computational time, and at the same time a significant improvement in the optimisation criterion value was not observed. A series of numerical experiments were conducted using different ranges and steps for the values of the main parameters of the CSA: the flight length fl and the awareness probability AP.

The chosen parameter values that covered the entire space of possible values are summarised in

Table 1. Range and step for the values of the main parameters of the algorithm.

fl Range	fl Step	AP Range	AP Step
1 to 5	1	0 to 1	0.1
0 to 5	0.1	0 to 1	0.05
1 to 4	0.1	0.05 to 0.5	0.05
1.5 to 4	0.1	0.05 to 0.35	0.01
1 to 4	0.5	0.01 to 0.5	0.01
1 to 4	0.5	0.05 to 0.5	0.05

.

In the first step the range of parameter fl was from 1 to 5, and for AP it was from 0 to 1. These results were not sufficient to determine the most appropriate intervals, i.e., where J values were the lowest. For this, the interval for fl was increased to 0 to 5, and the step was also decreased from 1 to 0.1, as well as decreasing the AP step from 0.1 to 0.05. These results are presented as Supplementary Materials (Table S2). A 3D plot of the results is presented here in Figure 1.

Based on these results the decision for the following changes in the parameter ranges and steps were made: fl, from 1 to 4 (step 0.1), and AP, from 0.05 to 0.5 (step 0.05). Next, following Table 1, the ranges were reduced, looking for the area where the smallest J values were obtained.

Finally, after analysing the results from all numerical experiments, it was found that steps 0.5 for fl and 0.05 for AP were more appropriate than 0.1 and 0.01. The algorithm’s performance with a variation of fl and AP based on the smaller steps was very similar in the case of neighbouring parameter pairs. For example, for fl = 1.0, 1.1, or 1.2 and AP = 0.05, 0.06, or 0.07 the CSA performance was almost similar. Therefore, steps of 0.5 and 0.05 were chosen for fl and AP, respectively. Also, applying algorithm parameters in the range of 0 to 1 and 4 to 5 for fl and of 0 to 0.05 and 0.5 to 1 for AP, the CSA performance was not good. The observed value for optimisation criterion J was larger than the J value obtained based on CSA parameters values in the ranges 0.05–0.5 and 1–4.

Finally, based on the results of a preliminary set of tests, the following ranges for the variation of algorithm parameters were chosen:

• fl between 1 and 4 with a step of 0.5;
• AP between 0.05 and 0.5, with a step of 0.05.

Thus, the research surface was formed by seven values for fl, namely 1, 1.5, 2, 2.5, 3, 3.5, and 4, and 10 values for AP, 0.05, 0.1, 0.15, 0.2, 0.25, 0.3, 0.35, 0.4, 0.45, and 0.5. A total set of 70 combinations of the CSA parameters, presented as ordered pairs (fl; AP), resulting in 70 differently tuned algorithms were studied further. For each of these CSA algorithms, 30 runs were performed to show the robustness of the proposed CSA.

The notations used for the 70 algorithms are described in

Table A1. Notations of differently tuned CSA.

Notation	CSA Parameters		Notation	CSA Parameters		Notation	CSA Parameters
	AP	fl		AP	fl		AP	fl
C1	0.05	1.0	C8	0.10	1.0	C15	0.15	1.0
C2		1.5	C9		1.5	C16		1.5
C3		2.0	C10		2.0	C17		2.0
C4		2.5	C11		2.5	C18		2.5
C5		3.0	C12		3.0	C19		3.0
C6		3.5	C13		3.5	C20		3.5
C7		4.0	C14		4.0	C21		4.0
Notation	CSA Parameters		Notation	CSA Parameters		Notation	CSA Parameters
	AP	fl		AP	fl		AP	fl
C22	0.20	1.0	C29	0.25	1.0	C36	0.30	1.0
C23		1.5	C30		1.5	C37		1.5
C24		2.0	C31		2.0	C38		2.0
C25		2.5	C32		2.5	C39		2.5
C26		3.0	C33		3.0	C40		3.0
C27		3.5	C34		3.5	C41		3.5
C28		4.0	C35		4.0	C42		4.0
Notation	CSA Parameters		Notation	CSA Parameters		Notation	CSA Parameters
	AP	fl		AP	fl		AP	fl
C43	0.35	1.0	C50	0.40	1.0	C57	0.45	1.0
C44		1.5	C51		1.5	C58		1.5
C45		2.0	C52		2.0	C59		2.0
C46		2.5	C53		2.5	C60		2.5
C47		3.0	C54		3.0	C61		3.0
C48		3.5	C55		3.5	C62		3.5
C49		4.0	C56		4.0	C63		4.0
Notation	CSA Parameters
	AP	fl
C64	0.50	1.0
C65		1.5
C66		2.0
C67		2.5
C68		3.0
C69		3.5
C70		4.0

, in the Appendix A. For example, the CSA with AP = 0.05 and fl = 1.0 was noted as C1, and the CSA with AP = 0.1 and fl = 2.0 was noted as C10, etc., following Table A1. The selected notations (Ci, i = 1, 2, …, 70) were chosen in a way that helped to present tabular and graphical results more easily and clearly.

3.3. Statistical Approaches and InterCrteria Analysis

To measure the similarity between the performances of the differently tuned CSA, two well-known statistical approaches were performed:

• One-way analysis of variance (ANOVA) [49], a parametric test “analysis of variance” that compares the means of two or more independent groups to determine whether there is statistical evidence that the associated population means are significantly different;
• Wilcoxon test [50], a nonparametric equivalent of the paired t-test, but unlike the t-test, it tests differences in the median rather than the mean.

Further, the InterCriteria Analysis (ICrA) approach [51], based on the apparatus of the index matrices (IM) [52] and the intuitionistic fuzzy sets (IFS) [53,54], was applied. A multi-criteria decision-making approach was proposed, evaluating the relationships in the behaviour of pairs of criteria when evaluating multiple objects. As a result, existing dependencies or independences between a set of indicators (criteria) were identified. ICrA is not a widely known approach, but it has some advantages over known statistical approaches [55,56,57].

As a result of the ICrA application, an index matrix of intuitionistic fuzzy pairs (IFP) [54] is obtained. Each IFP is an estimation of the degrees of “agreement” (consonance) ${\mu }_{C,C^{\prime }}$ and “disagreement” (dissonance) ${\nu }_{C,C^{\prime }}$ between each two criteria, in this work between two considered algorithms. The IFP is an ordered pair of real non-negative numbers $\langle {\mu }_{C,C^{\prime }},{\nu }_{C,C^{\prime }}\rangle$ such that ${\mu }_{C,C^{\prime }}+{\nu }_{C,C^{\prime }}\le 1$. The difference ${\pi }_{C,C^{\prime }}=1-{\mu }_{C,C^{\prime }}+{\mathsf{\nu }}_{C,C^{\prime }}$ is considered as a degree of “uncertainty” [51]. Most simply, the higher value of ${\mu }_{C,C^{\prime }}$ means a stronger connection or similarity is observed between two selected criteria (algorithms).

4. Numerical Results and Discussion

The performance of the CSA was investigated by varying the values of the main algorithm parameters, i.e., the flight length fl and the awareness probability AP. Based on the methodology presented in Section 3.2 of varying the CSA parameters, a total of 70 differently tuned CSAs (C1–C70) were run.

The simulation tests were performed on a machine with the following parameters:

• Core: Intel^® Core™i7-8700 CPU @ 3.20 GHz, 3192 MHz;
• Memory (RAM): 32 GB;
• Operating system: Windows 10 pro (64-bit).

The CSA was implemented in the MATLAB environment (R2019a). Mathematical models (Equations (1) and (9)) were modelled through Simulink implementation. Solver options were variable step and ode4 (Runge–Kutta) with TIMESPAN = [0 12].

Each CSA, with a particular combination of fl and AP parameter values, was run 30 times. The stochastic nature of the algorithm required at least 30 runs to have statistically reliable results. The algorithm searched for the best mathematical model parameters (${\mu }_{1max}$, ${\mu }_{2max}$, $K_{S_1}$, $K_{S_2}$, $Y_1$, $Y_2$, $Y_3$, $Y_{H_2},$ and $Y_{C{H}_4}$ (Equations (1)–(9))) to fit the experimental data in the best way. The model parameters were coded in a specific range (lower bound (Lb) ≤ parameter ≤ upper bound (Ub)) as follows:

$$\begin{gathered} 0.01 \le {\mu }_{1max} \le 0.8; 0.01 \le {\mu }_{2max} \le 0.8; \\ 0.001 \le K_{S_1} \le 1; 0.001 \le K_{S_2} \le 1; \\ 0.01 \le Y_1 \le 10; 0.01 \le Y_2 \le 10; 0.01 \le Y_3 \le 10; \\ 0.01 \le Y_{H_2} \le 10; 0.01 \le Y_{C{H}_4} \le 10. \end{gathered}$$

(13)

The model parameter bounds were chosen based on the authors’ experience with anaerobic digestion processes [23,48] and published results for processes similar to the one considered here [2,9,10,11].

The obtained results are presented as a 3D plot in Figure 2; 3D view 1 and 3D view 2 show the obtained best results, and 3D view 3 and 3D view 4 show the resulting average results of J. Views 2 and 4 show the area of the surface where the lowest values of the objective function J were observed. The CSA provided the best results (lowest J value) for the following fl and AP ordered pairs: (2; 0.35) and (3; 0.15). The best average results were obtained at the combinations (3; 0.05) and (2.5; 0.1).

The results presented in Figure 3a show that the computational time increased significantly for algorithms with AP values in the interval 0.2–0.5. The time was not significantly affected by fl values. Such a result meant that the algorithm convergence speed mainly depended on the AP parameter. For example, algorithms C43, C47, C48, and C57 showed significant increases in the decision time. Their AP and fl values were as follows: (0.35, 1.0), (0.35, 3.0), (0.35, 3.5), and (0.45, 1.0). It can be seen that regardless of whether the fl value was 1.0 or 3.0, if AP was a large value, the computational time increased significantly.

Based on the results presented in Figure 3b it is clear that the algorithm did not achieve solutions with higher accuracy when the value of fl was 1.0. Such a value should be avoided. The best model accuracy was obtained for the AP values from 0.05 to 0.15. There were two cases for which good results were obtained, AP = 0.35 and 0.45 with fl = 2.0 and 2.5, respectively. But in these cases, the observed computational time was significantly bigger because of larger values of AP. Good convergence speed and decision accuracy were achieved for lower values of AP (up to 0.15) and larger values of fl (more than 2.0).

The best five models according to obtained J values (model accuracy) were selected among 70 CSA solutions. The estimated parameters of the best five models and the corresponding computation time and J values are listed in

Table 2. Model parameter values of the best five models.

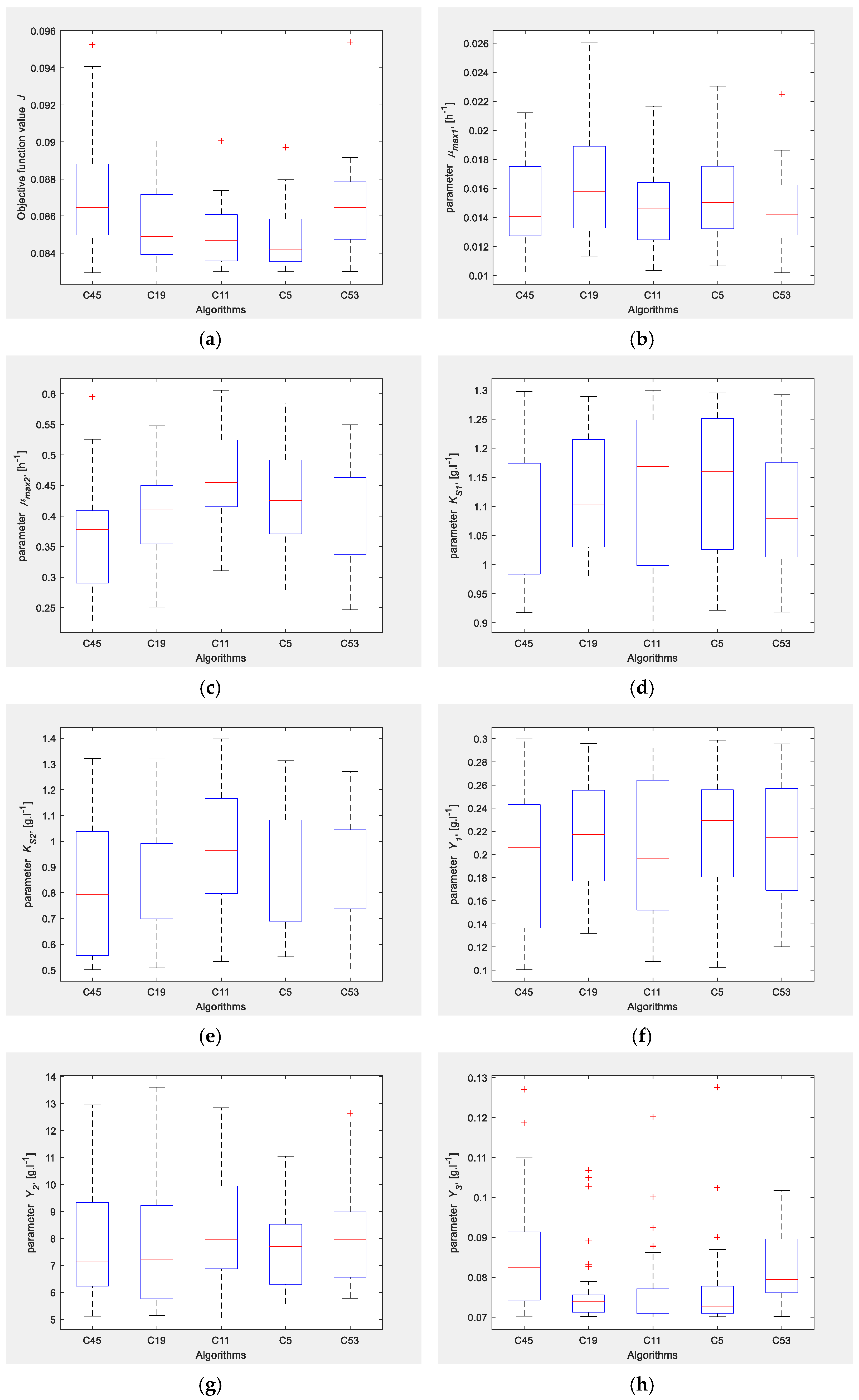
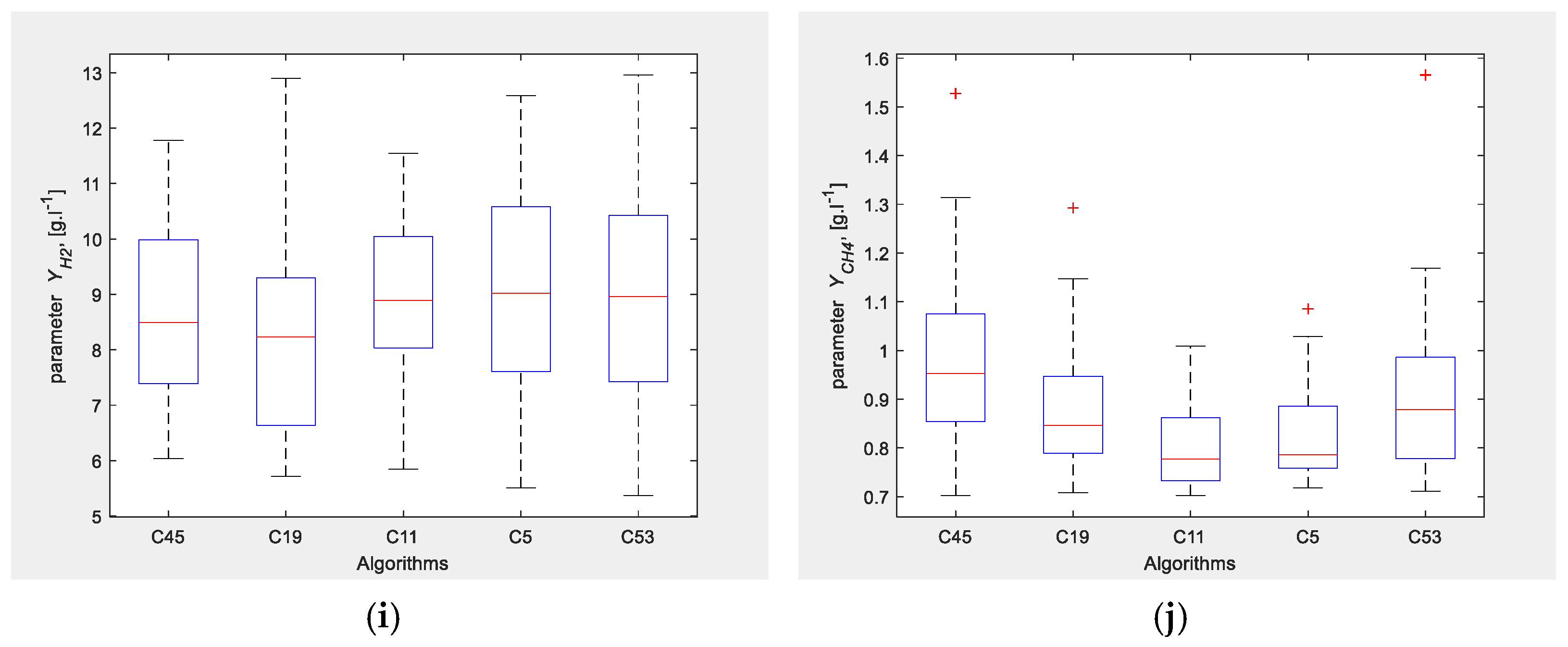
Algorithm/Parameters	C45	C19	C11	C5	C53
fl	2.0	3.0	2.5	3.0	2.5
AP	0.35	0.15	0.10	0.05	0.40
Model parameters
${\mu }_{1max}$	0.014	0.014	0.012	0.017	0.013
${\mu }_{2max}$	0.461	0.508	0.469	0.487	0.456
$K_{S_1}$	1.174	1.249	1.174	1.262	1.012
$K_{S_2}$	0.845	1.000	0.874	1.002	0.883
$Y_1$	0.160	0.260	0.186	0.256	0.145
$Y_2$	9.333	8.678	9.938	7.015	8.801
$Y_3$	0.070	0.070	0.070	0.070	0.070
$Y_{H_2}$	0.013	0.013	11.548	7.607	10.142
$Y_{C{H}_4}$	0.461	0.508	0.701	0.756	0.735
Computation time, min	2.53	0.67	1.03	1.42	1.89
J	0.082939	0.082972	0.082996	0.082998	0.083004

. For better understanding, the corresponding values of the algorithm parameters (fl and AP) are given too. The results showed that the five models described the experimental data with identical accuracy: J = 0.083. The algorithms are listed in the table in increasing order of the value of J, taking into account six decimal places: algorithm C45, followed by the algorithms C19, C11, C5, and C53. Algorithms C11 and C5 were those for which the best average results were obtained. The greatest computation time was observed when AP was 0.35 and 0.40, and the best J values were obtained for fl values between 2.0 and 3.0.

According to the results presented in Figure 1 and in the Supplementary Materials, the worst J value was 0.11754. After performing the optimal tuning of the CSA parameters, an accuracy improvement of 29% was achieved: the best J value obtained was 0.082939.

The estimated values of the model parameters were comparable to those found for similar processes [58]. Some examples of models with similar structures and parameter values are presented in [59,60,61,62]. Since there are no published results for the same process, the obtained parameter values were confirmed by the results in the case of similar processes. Considering Monod kinetics, the following values were estimated for ${\mu }_{max}$: 0.05 and 0.12 in [58], 0.67 in [59], and 0.098 in [61]. These values corresponded to the estimates for ${\mu }_{max}$ obtained here. The published values of the yield coefficient were 0.3-0.67 [58] and 0.48-0.58 [60]. The values estimated here were 0.14-0.26 for $Y_1$ (the yield coefficient in Equation (1)) and also corresponded to the published ones. For other yield coefficients ($Y_2$, $Y_3$, $Y_{H_2}$, and $Y_{C{H}_4}$), there were no published analogous models.

To distinguish the selected models, we can look at the dynamics of the predicted process variables, as well as investigate some statistical characteristics of the numerical data.

The models’ predicted dynamics for hydrogen and methane concentrations compared with the experimental data are presented in Figure 4. The models followed the data as best as possible, given that we had noisy and difficult real measurements, in the cases of both hydrogen and methane dynamics. Data collection could reduce or increase the quality of the results achieved by reducing the possible errors that may occur during sampling. Therefore, a lot of time must be spent on data collection to obtain relevant data. In the present study, obtaining data was a long and difficult process [48].

The performance of the considered five CSA algorithms was statistically evaluated by comparing the observed average value, the standard deviation (SD), and the median of the estimated model parameters and J value. To present summary statistics, box plot diagrams are shown in Figure 5.

According to Figure 5a the algorithm C5 produced the lowest mean value of J, followed by C11 and C19. Statistically (see box plots), the algorithm C5 showed the best performance, followed by C11, C19, C53, and C45. So, the CSA (C5) with AP = 0.05 and fl = 3.0 showed superior performance compared with the other four algorithms. It is known that the AP parameter controls the search capability of crows, and the fl parameter balances the trade-off between exploration and exploitation. The results presented here show that values of fl lower than 2.0 did not ensure a better balance between exploration and exploitation. At the same time, values larger than 0.2 degraded the search capability of the algorithm. The obtained results corresponded to the findings in the latest publications [26,29,63].

The presented box plots show that the algorithms estimated model parameters $Y_3$ and $Y_{C{H}_4}$ most easily. The parameters $K_{S_1}$, $K_{S_2},$ and $Y_3$ were the most difficult to estimate, as commented also in [64].

Next, the parametric test ANOVA and nonparametric Wilcoxon test were performed to estimate the statistical differences between the selected best five CSAs. The tests were run in Matlab R2019a using functions “anova1” and “ranksum” on the numerical results of objective function J and the estimates of the nine model parameters over 30 runs of each algorithm C1–C70. The obtained results are presented in

Table 3. ANOVA results.

Algorithm Pair	“Source”	“SS”	“df”	“MS”	“F”	“Prob > F”
C45 vs.
C19	“Columns”	3.8730 × 105	1	3.8730 × 105	6.2614	0.01518
	“Error”	3.5875 × 104	58	6.1855 × 106	-	-
C11	“Columns”	6.6368 × 105	1	6.6368 × 105	11.8194	0.00109
	“Error”	3.2568 × 104	58	5.6152 × 106	-	-
C5	“Columns”	7.8010 × 105	1	7.8010 × 105	14.0096	4.1957 × 104
	“Error”	3.2296 × 104	58	5.5683 × 106	-	-
C53	“Columns”	4.6988 × 106	1	4.6988 × 106	0.6519	0.42271
	“Error”	4.1803 × 104	58	7.2074 × 106	-	-
C19 vs.
C11	“Columns”	3.6993 × 106	1	3.6993 × 106	1.1048	0.29755
	“Error”	1.9419 × 104	58	3.3481 × 106	-	-
C5	“Columns”	6.8069 × 106	1	6.8069 × 106	2.0619	0.15639
	“Error”	1.9147 × 104	58	3.3012 × 106	-	-
C53	“Columns”	1.6448 × 105	1	1.6448 × 105	3.3293	0.07320
	“Error”	2.8654 × 104	58	4.9403 × 106	-	-
C11 vs.
C5	“Columns”	4.7009 × 107	1	4.7009 × 107	0.1721	0.67975
	“Error”	1.5839 × 104	58	2.7309 × 106	-	-
C53	“Columns”	3.5748 × 105	1	3.5748 × 105	8.1802	0.005877
	“Error”	2.5346 × 104	58	4.3701 × 106	-	-
C5 vs.
C53	“Columns”	4.4417 × 105	1	4.4417 × 105	10.2742	0.002194
	“Error”	2.5074 × 104	58	4.3232 × 106	-	-

and

Table 4. Wilcoxon test results.

Algorithm Pair	p-Value	H	STATS12
			zval	ranksum
C45 vs.
C19	0.012732	1	2.4911	1084
C11	0.001857	1	3.1121	1126
C5	3.9881 × 104	1	3.5408	1155
C53	0.6204	0	0.4952	949
C19 vs.
C11	0.3183	0	0.9979	983
C5	0.1494	0	1.4414	1013
C53	0.0614	0	−1.8702	788
C11 vs.
C5	0.6520	0	0.4509	946
C53	0.005084	1	−2.8016	725
C5 vs.
C53	0.002052	1	−3.08255	706

Statistical differences exist with a significance level of α = 0.05.

.

The observed results from algorithm C45 (AP = 0.35 and fl = 2.0) were statistically different compared with the algorithms C19 (AP = 0.15 and fl = 3.0), C11 (AP = 0.10 and fl = 2.5), and C5 (AP = 0.05 and fl = 3.0). Statistically different were also observed for C11 and C53 (AP = 0.40 and fl = 2.5), and C5 and C53. It can be seen that this difference was due to the larger differences in the parameter values of the algorithms, especially for parameter AP. The results showed that the AP parameter was more sensitive, i.e., changing it affected the performance of the algorithm to a greater extent. The parameter fl was less sensitive compared with AP.

On the other hand, the algorithm C5 was statistically similar to C19 and C11. The same behaviour as C45 was shown by C53, as well as C19. The close values of CSA parameters determined the similarity found.

These results were confirmed by both ANOVA and the Wilcoxon test.

Further, ICrA was carried out using the cross-platform software ICrAData v2.6 [65]. The calculations employed numerical data from 30 runs of 70 CSA for the values of the objective function. The resulting degree of “agreement” ${\mu }_{C,C^{\prime }}$ and degree of “disagreement” ${\nu }_{C,C^{\prime }}$ between the considered algorithms pairs are presented as index matrix in the following form:

	C1	C2	…	C70
C1	--	$\langle {\mu }_{C1,C2},{\nu }_{C1,C2}\rangle$	…	$\langle {\mu }_{C1,C70},{\nu }_{C1,C70}\rangle$
C2	$\langle {\mu }_{C2,C1},{\nu }_{C2,C1}\rangle$	--	…	$\langle {\mu }_{C2,C70},{\nu }_{C2,C70}\rangle$
⋮	⋮	⋮	…	⋮
C70	$\langle {\mu }_{C70,C1},{\nu }_{C70,C1}\rangle$	$\langle {\mu }_{C70,C2},{\nu }_{C70,C2}\rangle$	…	--

The resulting index matrix was too big to be presented in the paper, so it is given as Supplementary Materials (Table S1). Here, in Figure 6, a visualisation of the obtained ${\mu }_{C,C^{\prime }}$ and ${\nu }_{C,C^{\prime }}$ values in the intuitionistic fuzzy interpretation triangle is presented.

The ICrA results are discussed according to the scheme of consonance and dissonance, proposed in [66].

From Figure 6 it is clear that all intuitionistic fuzzy pairs were on the hypotenuse of the triangle, meaning the obtained ${\pi }_{C,C^{\prime }}$ values were zero, i.e., the numerical results were reliable, and there was no uncertainty in the data. Some of the algorithm pairs were in positive consonance (marked in green), and the rest of the pairs were in dissonance (marked in red). There were no pairs in negative consonance.

In

Table 5. Index matrix with the results for the pair algorithms that were in consonance.

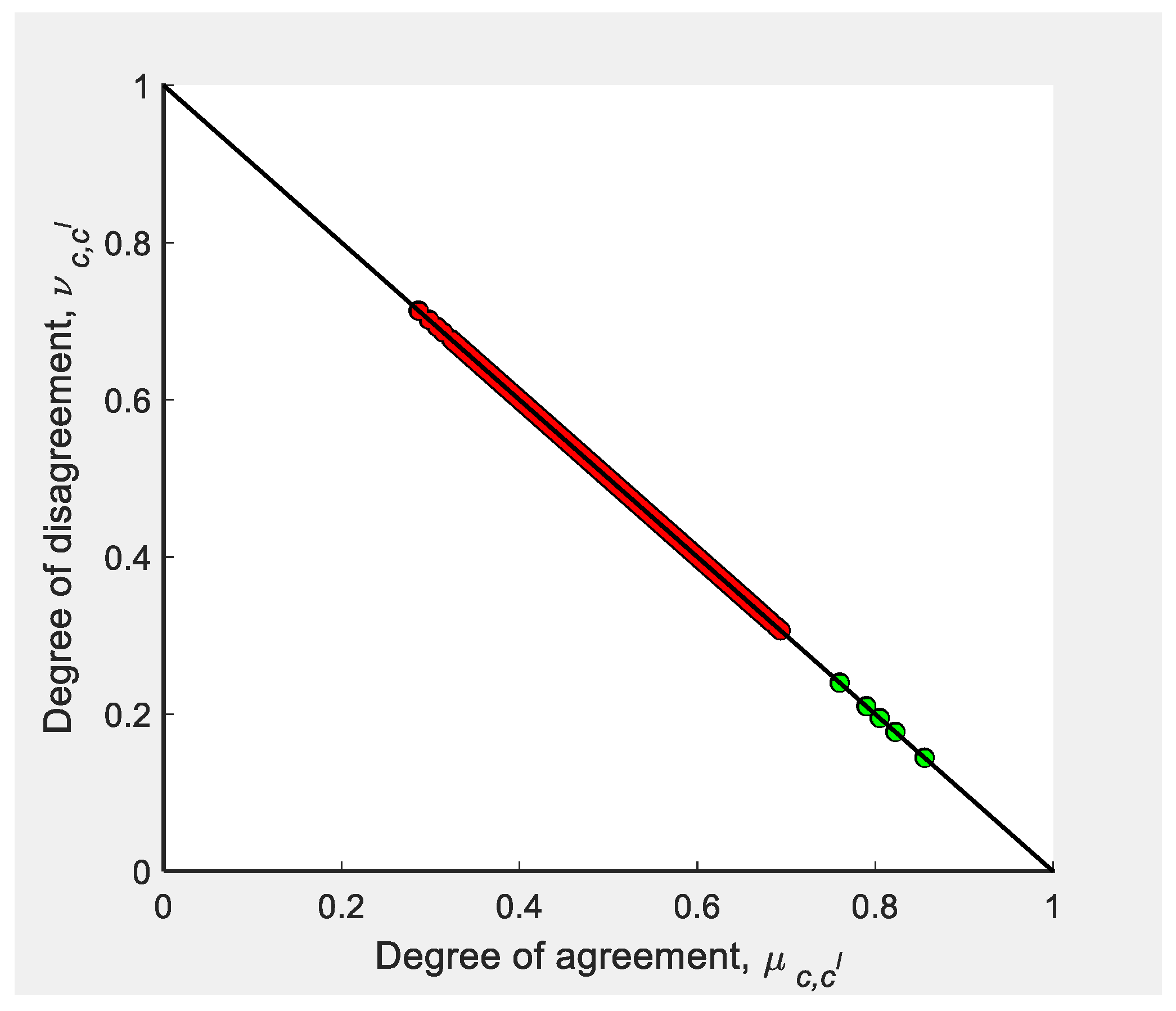
	C5	C11	C19	C45	C53
C5		$\langle 0.8057, 0.1943\rangle$	$\langle 0.7908, 0.2092\rangle$	$\langle 0.5402, 0.4598\rangle$	$\langle 0.4598, 0.5402\rangle$
C11	$\langle 0.8057, 0.1943\rangle$		$\langle 0.8234, 0.1766\rangle$	$\langle 0.4874, 0.5126\rangle$	$\langle 0.4989, 0.5011\rangle$
C19	$\langle 0.7908, 0.2092\rangle$	$\langle 0.8234, 0.1766\rangle$		$\langle 0.4943, 0.5057\rangle$	$\langle 0.7608, 0.2392\rangle$
C45	$\langle 0.5402, 0.4598\rangle$	$\langle 0.4874, 0.5126\rangle$	$\langle 0.4943, 0.5057\rangle$		$\langle 0.8563, 0.1437\rangle$
C53	$\langle 0.4598, 0.5402\rangle$	$\langle 0.4989, 0.5011\rangle$	$\langle 0.7608, 0.2392\rangle$	$\langle 0.8563, 0.1437\rangle$

the index matrix only with the algorithm pairs that were in consonance with the corresponding $\langle {\mu }_{C,C^{\prime }},{\nu }_{C,C^{\prime }}\rangle$ values is presented.

From 70 differently tuned CSAs, only five algorithm pairs were in consonance, i.e., they showed similar performances. The remaining 2410 pairs were in dissonance, i.e., these algorithms showed different behaviour during the 30 performed runs. Such a result indicated that the values for the CSA parameters chosen to be investigated (ten levels of AP and seven levels of fl) were distinctive and specific and led to qualitatively different algorithms being obtained. This fact confirmed the correct choice of algorithm parameters for which to investigate the CSA performance.

A careful analysis of the results presented in Table 5 confirmed the conclusion made based on the statistical analysis. The pair of CSAs that were in positive consonance was C45–C53, where the fl and AP values for both algorithms were closer. Next, the pairs C11–C19, C5–C11, and C5–C19 (with close $\langle {\mu }_{C,C^{\prime }},{\nu }_{C,C^{\prime }}\rangle$ values) were in weak positive consonance: there was a weak similarity between the algorithms’ performances. In this case, the AP values were (0.10–0.15), (0.05–0.10), and (0.05–0.15), whereas the fl values were (2.5–3.0), (3.0–2.5), and (3.0–3.0). As can be seen, the fl values were very close, even the same in one case, which once again showed that the parameter AP was more sensitive. The behaviour of the algorithm largely depended on the AP setting. The behaviour of the algorithms C11–C19, C5–C11, and C5–C19 was slightly similar, due to the differences in the values of the parameter AP, in the case of almost identical values of the parameter fl.

Finally, considering all the results and the above-presented analysis, the best algorithm performance was achieved for the following CSA parameters: AP = 0.05, fl = 3.0, followed by AP = 0.10, fl = 2.5, and AP = 0.15, fl = 3.0. Based on the performed investigation it can be concluded that the best CSA performance can be expected for a lower value of AP in the interval of 0.05-0.15 and larger values of fl in the interval of 2.5–3.0. Thus, a solution with a higher accuracy can be obtained for a reasonable convergence time.

The obtained best mathematical model was compared with the models proposed in [23].

Table 6. Comparison of the mathematical models of the considered TSAD process.

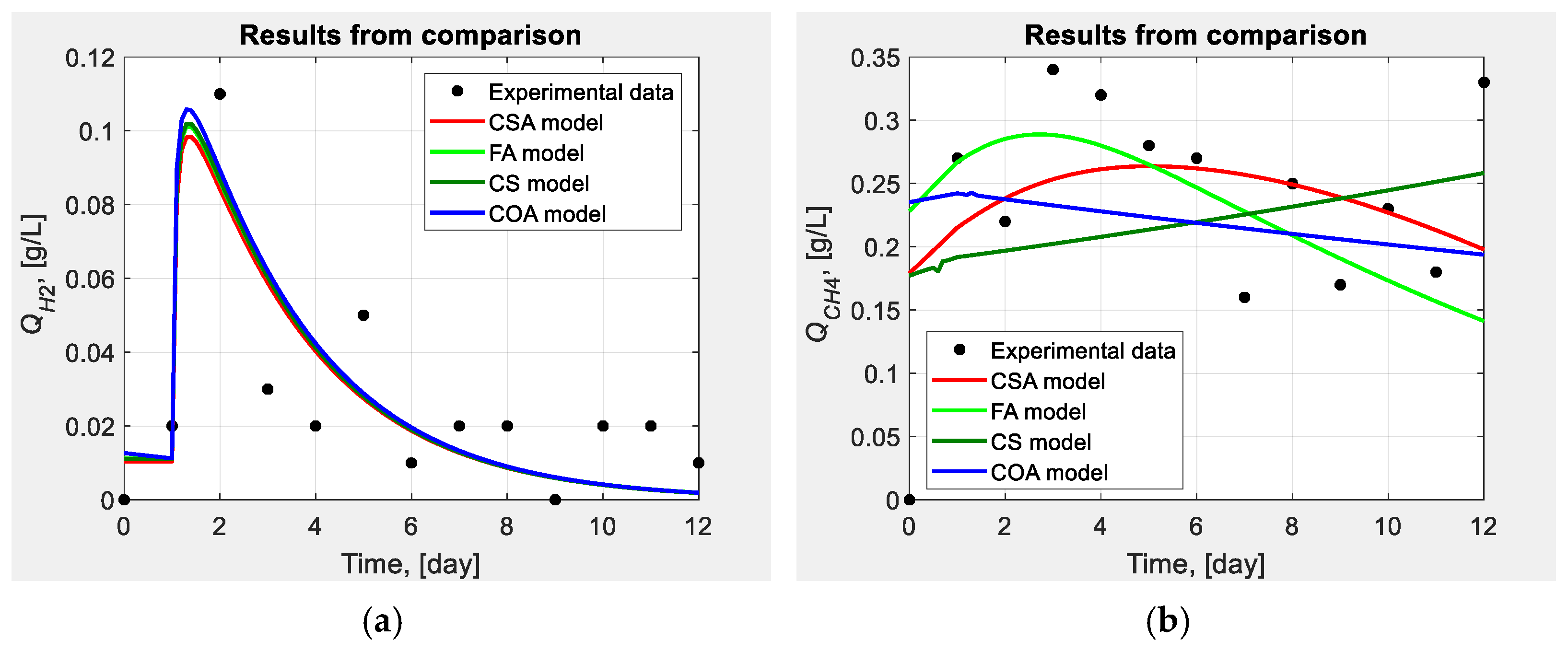
Algorithm	CSA (C45) [This Study]	FA [23]	CS [23]	COA [23]
Parameters	Model parameter estimates
${\mu }_{1max}$	0.014	0.017	0.010	0.012
${\mu }_{2max}$	0.461	0.443	0.077	0.029
$K_{S_1}$	1.174	1.100	1.139	1.004
$K_{S_2}$	0.845	0.919	0.001	0.0001
$Y_1$	0.160	0.222	0.010	12.137
$Y_2$	9.333	10.276	0.122	5.702
$Y_3$	0.070	0.100	19.781	24.272
$Y_{H_2}$	0.013	8.117	13.727	11.598
$Y_{C{H}_4}$	0.461	0.989	2.298	7.993
J	0.0829	0.1075	0.0913	0.0940

presents the resulting model parameter values, estimated with the firefly algorithm (FA) [67], the cuckoo search algorithm (CS) [68], and the coyote optimisation algorithm (COA) [19], all applied to the model (Equations (1)–(9)).

As can be seen, the estimates identified by the four algorithms’ model parameters were different. Each metaheuristic algorithm found a different solution, i.e., local minimum. According to some published mathematical models, the parameter values obtained by the CSA and the FA are the most appropriate [26,29,63]. The questionable estimates obtained from the CS and the COA are those for parameter $K_{S_2}$, due to too-small values.

The behaviour of the models dynamics was also compared. The graphical results are presented in Figure 7.

Graphical results showed that the behaviour of the hydrogen concentration was similar for the four models. The methane concentration dynamics of the CS and COA models was different in comparison with the dynamics of methane of the CSA and FA models. The mathematical model proposed here (CSA/C45) best described the real experimental data compared with the FA, CS, and COA models.

5. Conclusions

In this paper, for the first time, the CSA was applied to estimate the parameters of the proposed mathematical model of the TSAD process. The process dynamics in the cascade BR₁ and BR₂ were described by a set of five ODEs, representing substrate ($S_1$), biomass ($X_1 \mathrm{and} X_2$), and products ($A{c}_1 \mathrm{and} A{c}_2$) in the two bioreactors. The flow rates of the hydrogen ($Q_{H_2}$) and methane ($Q_{C{H}_4})$ were represented by two algebraic equations. The model consisted of nine model parameters that should be identified (${\mu }_{1max}$, ${\mu }_{2max}$, $K_{S_1}$, $K_{S_2}$, $Y_1$, $Y_2$, $Y_3$, $Y_{H_2}$, $\mathrm{and} Y_{C{H}_4}$).

To achieve the best CSA performance the influence of the main algorithm parameters was investigated. Numerous simulation experiments were performed to find the best tuning of the parameters fl and AP. Seventy differently tuned CSA algorithms were studied. Boxplots, the parametric test ANOVA, and the nonparametric Wilcoxon test were used to compare the performance of the best developed CSA. The newly proposed InterCritera Analysis was also performed. The best CSA algorithm performance was achieved for AP = 0.05, fl = 3.0, followed by AP = 0.10, fl = 2.5, and AP = 0.15, fl = 3.0. Moreover, it was found that the awareness probability (AP) was a more sensitive parameter than the flight length (fl) and influenced to a greater extent the CSA solution accuracy and convergence time. As a result, a 29% improvement in the objective function value was achieved.

The developed mathematical models of the TSAD process had a high degree of accuracy and could be used for further process behaviour investigation and process control and optimisation.

Although good results have been obtained so far, some possible future directions for work aimed at further improving the performance of the CSA can be indicated.

Here, the suggested values for the population size (N) and the number of iterations (MaxIter) were chosen to be sufficient to provide the required amount of diversity among generated solutions, and these solutions evolved in a reasonable computation time. The influence of the N and MaxIter can be further investigated more thoroughly to establish their relationship with the fl and AP parameters. This study will lead to the development of a CSA with even better performance.

To achieve better searchability and convergence of CSAs, the process of updating the current positions can be improved by introducing adaptive fl and AP parameters. Some recent results are proposed in [69] where AP is adjusting linearly over the optimisation process and fl is adjusting according to the generalised Pareto probability density function. The authors in [70] present fl as a descending function of time and the AP as the rate of change in fl. All the proposed modified CSAs provided very competitive outcomes over some well-known metaheuristics regarding stability and solution quality.

Knowing very well the influence of the CSA parameters and the dependence and relationships between them, effective functions for dynamically changing fl and AP can be further proposed, which will significantly improve the behaviour of the algorithm.