Block Cipher Nonlinear Component Generation via Hybrid Pseudo-Random Binary Sequence for Image Encryption
Abstract
1. Introduction
- In many cryptographic applications, random numbers are needed for strong cryptosystem designs. In this context, the proposed work is based on a Hybrid Binary Pseudo-Random Number Generator (HPRNG) derived from a feedback shift register known as a Linear Feedback Shift Register (abbreviated as LFSR) and a modified chaotic quadratic map. Since the LFSR-based PRNGs are not resistant to attacks and reveal information about keys to overcome this flaw, the binary stream of random numbers obtained from LFSR is XORed with the random stream of the modified quadratic chaotic map.
- This above-mentioned technique helps in the elimination of the LFSR linearity property and helps in hiding characteristic statistical patterns of binary sequences generated by chaotic maps that are used in estimating their initial conditions. The binary stream generated by exclusive or operation between the LFSR and chaos helps to utilize all the benefits of chaotic maps and LFSRs and avoid all of their drawbacks.
- As cryptographically strong substitution boxes (S-boxes) have important features like nonlinearity, S-box generation using nonlinear sequences is addressed in this work. To design an S-box, a binary stream of numbers generated by HPRNGs is used. After conversion of bits to bytes, an S-box is achieved. Then, the strength of the attained S-box is analyzed via nonlinearity (NL), the Strict-Avalanche Criterion (SAC), bit independence criteria (BIC), and differential and linear approximation probability (DP; LP), which ensures that the S-box is cryptographically strong and has high performance.
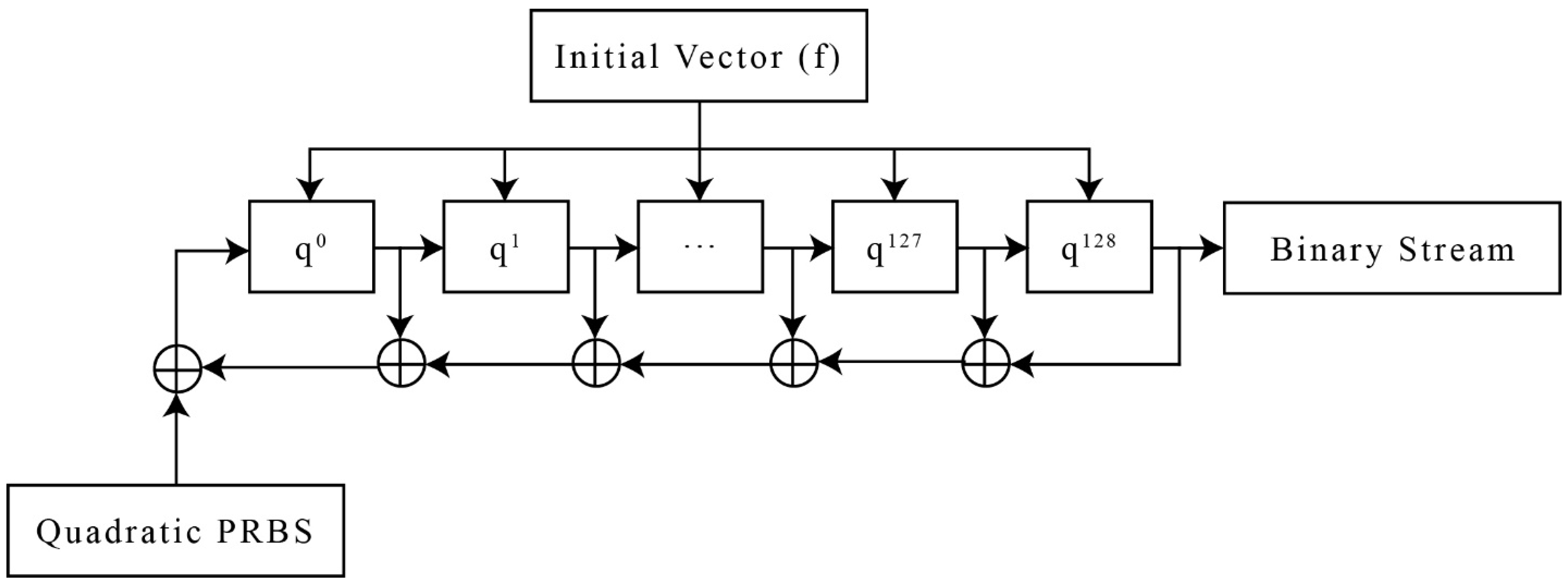
1.1. Linear Feedback Shift Registers (LFSRs)
- (the zero-stage entry) constitutes the output part.
- The entry of -stage is shifted to the stage, for .
- The new entry of the stage is obtained by a subset of -stage entry using Xor.
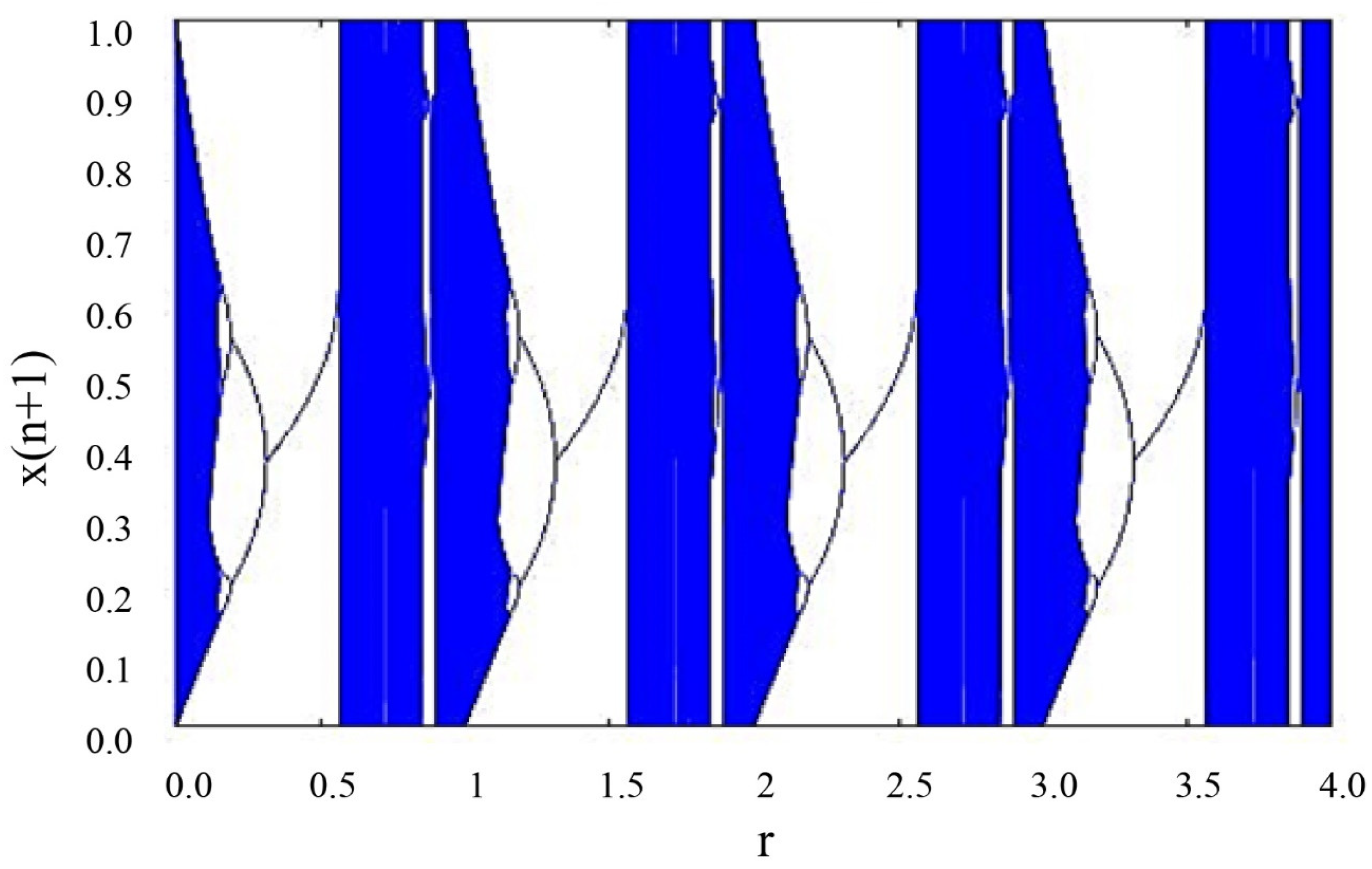
1.2. Modified Quadratic Chaotic Map
2. Binary Sequence Generation Using Modified Quadratic Map
- First, the initial values and parameters are determined from Equation (1), given in Section 1.2.
- The modified quadratic equations are iterated and times, respectively, where and are different constant values.
- By iterating Equation (1), two sequences (decimal) are generated using the following formulas:where the converts the value of to the closest integer equal of less than is used to provide the reminder value after the division, and is used to give the absolute value.
- The following threshold function ( can be applied:After that, a bit stream of pseudo-random numbers is obtained.
- The process is repeated until the desired bit stream of pseudo-random numbers is obtained.
2.1. Hybrid Pseudo-Random Binary Sequence Generation
3. S-Box Construction Using Hybrid Pseudo-Random Binary Sequences
- Step–1: Each block sequence consisting of -bits is generated as follows:
- Step–2: Now, each -bit block, i.e., is converted to integer numbers as .
- Step–3: To obtain distinct values, the repeated numbers are removed.
- Step–4: Create S-boxes.
4. S-Box Algebraic Analysis
4.1. Nonlinearity
4.2. Strict Avalanche Criteria (SAC)
4.3. Bit Independent Criterion (BIC)
4.4. Linear Approximation Probability (LP)
4.5. Differential Approximation Probability (DP)
4.6. S-Box Comparison
5. Image Encryption Scheme
5.1. Permutation Process
- First, take an original color image of length and associate this image with some random security keys taken as whose values lie between 0 and 1, which are then used as initial values and parameters of the modified quadratic chaotic map for Equation (1) given in Section 1.2.
- Apply between the pixel values of matrices as follows:where are the matrices of red, green, and blue channels of the original color image Q.
- Now, the initial and parametric values of the modified quadratic chaotic map are generated by using the following formula:or denotes the decimal fraction value of .
- Iterate the modified quadratic map given in Equation (1) by using the initial values obtained in Step 3. Hence, new sequences are generated. Now, the image pixels are permuted row and column-wise utilizing sequences . Then, the permuted image , is obtained.
5.2. Substitution Process
6. Security Analysis
6.1. Entropy
6.2. Analysis of Key
6.3. Key Sensitivity Analysis
6.4. Analysis for Correlation
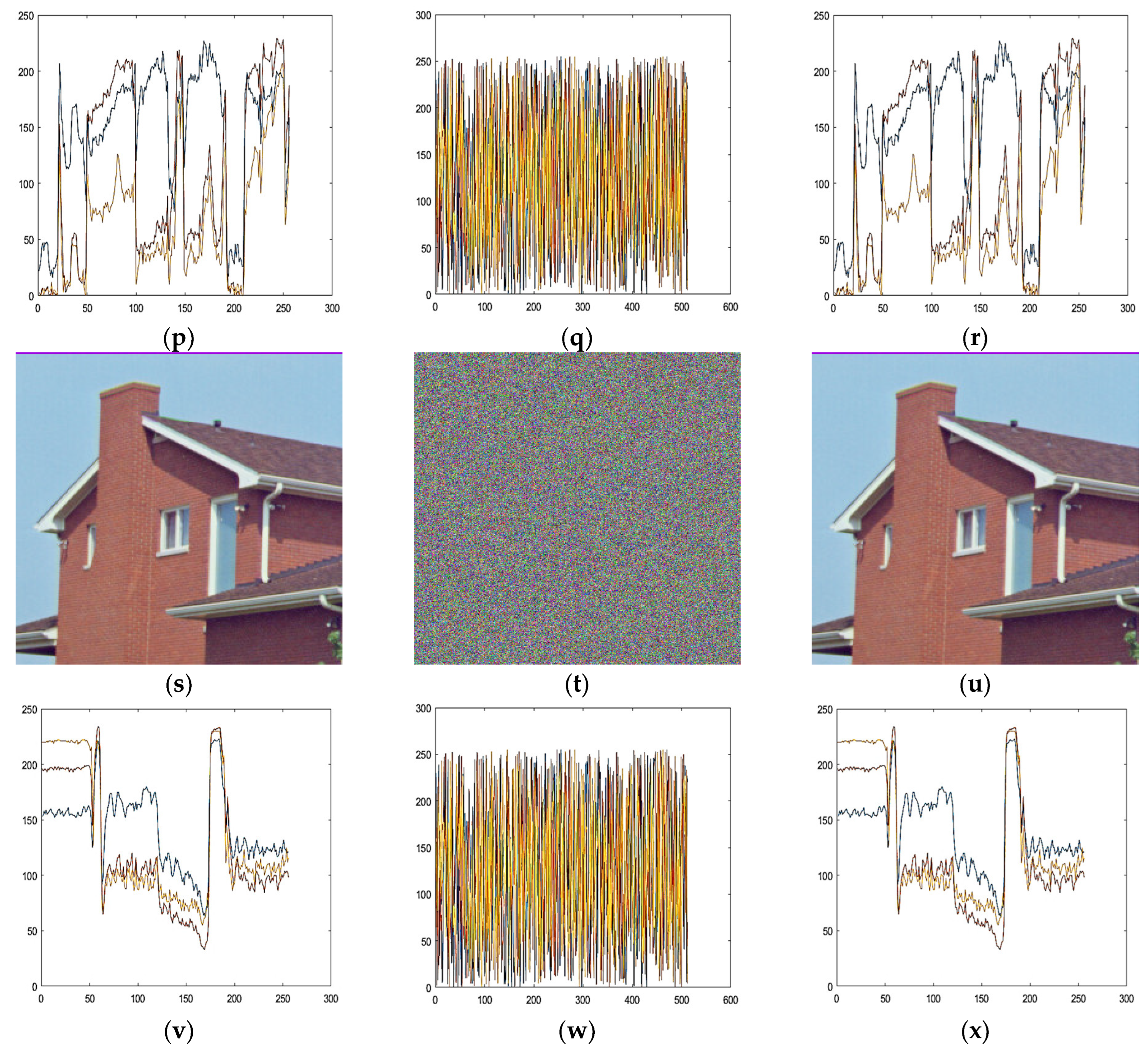
6.5. Histogram Analysis
6.6. Chosen-Plaintext Attack Analysis
6.7. MSE, PSNR and SSIM Analysis
6.8. Differential Attack Analysis
6.9. Occasional Attack Analysis
6.10. Time Complexity
7. NIST Analysis
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cassal-Quiroga, B.B.; Campos-Cantón, E. Generation of Dynamical S-Boxes for Block Ciphers via Extended Logistic Map. Math. Probl. Eng. 2020, 2020, 2702653. [Google Scholar] [CrossRef]
- Carlet, C. S-boxes, boolean functions and codes for the resistance of block ciphers to cryptographic attacks, with or without side channels. In International Conference on Security, Privacy, and Applied Cryptography Engineering; Springer: Cham, Switzerland, 2015. [Google Scholar]
- Detombe, J.; Tavares, S. Constructing large cryptographically strong S-boxes. In International Workshop on the Theory and Application of Cryptographic Techniques; Springer: Berlin/Heidelberg, Germany, 1992. [Google Scholar]
- Shah, T.; Qamar, A.; Hussain, I. Substitution Box on Maximal Cyclic Subgroup of Units of a Galois Ring. Z. Naturforschung Sect. A-A J. Phys. Sci. 2013, 68, 567–572. [Google Scholar] [CrossRef]
- Çavuşoğlu, Ü.; Zengin, A.; Pehlivan, I.; Kaçar, S. A novel approach for strong S-Box generation algorithm design based on chaotic scaled Zhongtang system. Nonlinear Dyn. 2017, 87, 1081–1094. [Google Scholar] [CrossRef]
- Farhan, A.K.; Ali, R.S.; Natiq, H.; Al-Saidi, N.M.G. A New S-Box Generation Algorithm Based on Multistability Behavior of a Plasma Perturbation Model. IEEE Access 2019, 7, 124914–124924. [Google Scholar] [CrossRef]
- Khan, M.; Asghar, Z. A novel construction of substitution box for image encryption applications with Gingerbreadman chaotic map and S8 permutation. Neural Comput. Appl. 2018, 29, 993–999. [Google Scholar] [CrossRef]
- Tian, Y.; Lu, Z. S-box: Six-dimensional compound hyperchaotic map and artificial bee colony algorithm. J. Syst. Eng. Electron. 2016, 27, 232–241. [Google Scholar]
- Zhang, X.-P.; Guo, R.; Chen, H.-W.; Zhao, Z.-M.; Wang, J.-Y. Efficient image encryption scheme with synchronous substitution and diffusion based on double S-boxes. Chin. Phys. B 2018, 27, 080701. [Google Scholar] [CrossRef]
- Wang, X.; Çavuşoğlu, Ü.; Kacar, S.; Akgul, A.; Pham, V.-T.; Jafari, S.; Alsaadi, F.E.; Nguyen, X.Q. S-Box Based Image Encryption Application Using a Chaotic System without Equilibrium. Appl. Sci. 2019, 9, 781. [Google Scholar] [CrossRef]
- Falih, S.M. A Pseudorandom Binary Generator Based on Chaotic Linear Feedback Shift Register. Iraq J. Electr. Electron. Eng. 2016, 12, 155–160. [Google Scholar] [CrossRef]
- Rahimov, H.; Babaei, M.; Farhadi, M. Cryptographic PRNG Based on Combination of LFSR and Chaotic Logistic Map. Appl. Math. 2011, 2, 1531–1534. [Google Scholar] [CrossRef]
- Ramadan, N.; Ahmed, H.E.H.; Elkhamy, S.E.; El-Samie, F.E.A. Chaos-based image encryption using an improved quadratic chaotic map. Am. J. Signal Process. 2016, 6, 1–13. [Google Scholar]
- Williams, H.; Webster, A.; Tavares, S. On the design of s-boxes. In Advances in Cryptology—CRYPTO’85 Proceedings; Springer: Berlin/Heidelberg, Germany, 1986. [Google Scholar]
- Dawson, M.H.; Tavares, S.E. An expanded set of S-box design criteria based on information theory and its relation to differential-like attacks. In Advances in Cryptology—EUROCRYPT’91: Workshop on the Theory and Application of Cryptographic Techniques Brighton, UK, April 8–11, 1991 Proceedings 10; Springer: Berlin/Heidelberg, Germany, 1991. [Google Scholar]
- Biham, E.; Shamir, A. Differential cryptanalysis of DES-like cryptosystems. J. Cryptol. 1991, 4, 3–72. [Google Scholar] [CrossRef]
- Matsui, M. Linear cryptanalysis method for DES cipher. In Workshop on the Theory and Application of of Cryptographic Techniques; Springer: Berlin/Heidelberg, Germany, 1993. [Google Scholar]
- Mahmood, S.; Farwa, S.; Rafiq, M.; Riaz, S.M.J.; Shah, T.; Jamal, S.S. To Study the Effect of the Generating Polynomial on the Quality of Nonlinear Components in Block Ciphers. Secur. Commun. Networks 2018, 2018, 5823230. [Google Scholar] [CrossRef]
- Zhu, S.; Wang, G.; Zhu, C. A Secure and Fast Image Encryption Scheme based on Double Chaotic S-Boxes. Entropy 2019, 21, 790. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Zhang, Y.; Wang, X. A Novel Method for Constructing the S-Box Based on Spatiotemporal Chaotic Dynamics. Appl. Sci. 2018, 8, 2650. [Google Scholar] [CrossRef]
- Belazi, A.; El-Latif, A.A.A. A simple yet efficient S-box method based on chaotic sine map. Optik 2017, 130, 1438–1444. [Google Scholar] [CrossRef]
- Haq, T.U.; Shah, T. 12 × 12 S-box Design and its Application to RGB Image Encryption. Optik 2020, 217, 164922. [Google Scholar] [CrossRef]
- Mahboob, A.; Nadeem, M.; Rasheed, M.W. A study of text-theoretical approach to S-box construction with image encryption applications. Sci. Rep. 2023, 13, 21081. [Google Scholar] [CrossRef]
- Alshammari, B.M.; Guesmi, R.; Guesmi, T.; Alsaif, H.; Alzamil, A. Implementing a Symmetric Lightweight Cryptosystem in Highly Constrained IoT Devices by Using a Chaotic S-Box. Symmetry 2021, 13, 129. [Google Scholar] [CrossRef]
- Haralick, R.M.; Shanmugam, K.; Dinstein, I.H. Textural Features for Image Classification. IEEE Trans. Syst. Man Cybern. 1973, SMC-3, 610–621. [Google Scholar] [CrossRef]
- Chai, X.-L.; Gan, Z.-H.; Lu, Y.; Zhang, M.-H.; Chen, Y.-R. A novel color image encryption algorithm based on genetic recombination and the four-dimensional memristive hyperchaotic system. Chin. Phys. B 2016, 25, 100503. [Google Scholar] [CrossRef]
- Wu, J.; Liao, X.; Yang, B. Color image encryption based on chaotic systems and elliptic curve ElGamal scheme. Signal Process. 2017, 141, 109–124. [Google Scholar] [CrossRef]
- Joshi, A.B.; Kumar, D.; Kumar, S.; Singh, S. A novel method of digital image encryption using graph theory. Multimed. Tools Appl. 2024, 83, 6803–6828. [Google Scholar] [CrossRef]
- Jahangir, S.; Shah, T. Designing S-boxes triplet over a finite chain ring and its application in RGB image encryption. Multimedia Tools Appl. 2020, 79, 26885–26911. [Google Scholar] [CrossRef]
- Biryukov, A.; Wagner, D. Advanced slide attacks. In International Conference on the Theory and Applications of Cryptographic Techniques; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar]
- Pareschi, F.; Rovatti, R.; Setti, G. On Statistical Tests for Randomness Included in the NIST SP800-22 Test Suite and Based on the Binomial Distribution. IEEE Trans. Inf. Forensics Secur. 2012, 7, 491–505. [Google Scholar] [CrossRef]







| 21 | 207 | 120 | 241 | 47 | 146 | 206 | 76 | 169 | 119 | 99 | 128 | 232 | 244 | 36 | 72 |
| 37 | 157 | 237 | 73 | 110 | 126 | 132 | 43 | 153 | 131 | 71 | 181 | 177 | 8 | 101 | 90 |
| 11 | 138 | 186 | 38 | 173 | 16 | 54 | 79 | 56 | 44 | 171 | 7 | 188 | 234 | 143 | 175 |
| 45 | 172 | 20 | 65 | 22 | 155 | 125 | 180 | 198 | 102 | 60 | 142 | 130 | 189 | 95 | 254 |
| 116 | 123 | 229 | 34 | 243 | 176 | 174 | 84 | 227 | 28 | 24 | 178 | 32 | 210 | 27 | 225 |
| 204 | 26 | 255 | 98 | 213 | 164 | 183 | 18 | 58 | 167 | 31 | 88 | 194 | 246 | 92 | 52 |
| 165 | 2 | 74 | 29 | 212 | 149 | 203 | 182 | 159 | 158 | 145 | 35 | 87 | 115 | 89 | 163 |
| 139 | 91 | 216 | 231 | 69 | 12 | 147 | 230 | 40 | 166 | 17 | 190 | 62 | 152 | 113 | 236 |
| 151 | 220 | 1 | 245 | 135 | 148 | 242 | 222 | 109 | 19 | 85 | 122 | 223 | 215 | 195 | 136 |
| 238 | 41 | 168 | 240 | 5 | 209 | 61 | 51 | 193 | 127 | 160 | 75 | 196 | 179 | 39 | 156 |
| 185 | 208 | 48 | 80 | 170 | 224 | 121 | 53 | 141 | 133 | 83 | 9 | 154 | 134 | 59 | 205 |
| 64 | 97 | 46 | 249 | 13 | 100 | 226 | 25 | 250 | 82 | 105 | 78 | 235 | 33 | 117 | 93 |
| 217 | 251 | 111 | 140 | 104 | 6 | 10 | 30 | 191 | 57 | 248 | 144 | 70 | 103 | 106 | 253 |
| 150 | 187 | 112 | 49 | 94 | 4 | 201 | 15 | 68 | 86 | 42 | 161 | 211 | 218 | 66 | 0 |
| 77 | 96 | 108 | 118 | 23 | 247 | 219 | 202 | 192 | 124 | 107 | 63 | 129 | 214 | 233 | 162 |
| 81 | 114 | 55 | 197 | 199 | 67 | 50 | 184 | 252 | 3 | 200 | 14 | 228 | 239 | 137 | 221 |
| 114 | 109 | 119 | 126 | 230 | 122 | 123 | 177 | 68 | 16 | 115 | 90 | 239 | 183 | 218 | 103 |
| 170 | 130 | 184 | 125 | 238 | 60 | 51 | 228 | 217 | 165 | 194 | 219 | 141 | 193 | 102 | 160 |
| 215 | 253 | 150 | 67 | 71 | 95 | 247 | 169 | 69 | 209 | 241 | 244 | 116 | 172 | 84 | 21 |
| 1 | 179 | 82 | 178 | 12 | 135 | 17 | 142 | 19 | 6 | 128 | 226 | 250 | 83 | 198 | 117 |
| 24 | 146 | 73 | 14 | 30 | 107 | 46 | 192 | 38 | 94 | 167 | 214 | 88 | 242 | 91 | 129 |
| 54 | 180 | 0 | 249 | 64 | 237 | 212 | 62 | 106 | 186 | 207 | 92 | 42 | 41 | 44 | 187 |
| 164 | 251 | 202 | 254 | 50 | 57 | 86 | 145 | 49 | 252 | 2 | 127 | 36 | 77 | 159 | 200 |
| 52 | 210 | 32 | 155 | 134 | 157 | 76 | 245 | 205 | 199 | 174 | 80 | 4 | 255 | 246 | 166 |
| 185 | 9 | 22 | 233 | 63 | 151 | 33 | 23 | 161 | 211 | 111 | 93 | 97 | 61 | 28 | 118 |
| 96 | 144 | 59 | 173 | 66 | 74 | 132 | 136 | 35 | 235 | 204 | 5 | 175 | 47 | 26 | 190 |
| 224 | 70 | 78 | 10 | 56 | 3 | 65 | 45 | 162 | 182 | 201 | 98 | 148 | 149 | 225 | 124 |
| 243 | 168 | 87 | 121 | 153 | 181 | 43 | 216 | 105 | 39 | 229 | 234 | 113 | 110 | 203 | 8 |
| 206 | 108 | 81 | 75 | 13 | 195 | 197 | 163 | 232 | 189 | 101 | 31 | 58 | 221 | 154 | 138 |
| 100 | 79 | 213 | 99 | 40 | 18 | 231 | 11 | 112 | 85 | 55 | 220 | 131 | 176 | 29 | 143 |
| 240 | 236 | 140 | 20 | 120 | 188 | 139 | 133 | 158 | 15 | 248 | 23 | 171 | 53 | 72 | 191 |
| 137 | 208 | 152 | 25 | 223 | 227 | 34 | 104 | 48 | 156 | 89 | 27 | 196 | 37 | 222 | 7 |
| 212 | 61 | 245 | 221 | 87 | 220 | 252 | 166 | 17 | 128 | 244 | 216 | 127 | 231 | 218 | 117 |
| 78 | 66 | 142 | 189 | 95 | 141 | 228 | 23 | 186 | 39 | 82 | 250 | 43 | 50 | 85 | 6 |
| 243 | 191 | 195 | 112 | 113 | 249 | 247 | 46 | 49 | 178 | 182 | 151 | 149 | 15 | 145 | 161 |
| 32 | 230 | 208 | 198 | 9 | 99 | 160 | 75 | 224 | 65 | 2 | 86 | 222 | 240 | 83 | 181 |
| 136 | 194 | 56 | 73 | 201 | 124 | 77 | 18 | 69 | 217 | 103 | 211 | 152 | 214 | 248 | 34 |
| 197 | 135 | 0 | 190 | 16 | 63 | 147 | 205 | 92 | 206 | 123 | 153 | 76 | 44 | 13 | 238 |
| 7 | 254 | 90 | 223 | 196 | 172 | 209 | 162 | 164 | 159 | 64 | 253 | 5 | 57 | 235 | 26 |
| 133 | 210 | 4 | 234 | 67 | 171 | 25 | 183 | 59 | 115 | 79 | 144 | 1 | 255 | 215 | 71 |
| 174 | 40 | 193 | 62 | 237 | 227 | 36 | 225 | 38 | 242 | 125 | 185 | 52 | 173 | 137 | 213 |
| 20 | 130 | 236 | 47 | 80 | 88 | 3 | 10 | 100 | 126 | 27 | 33 | 111 | 109 | 200 | 207 |
| 22 | 81 | 89 | 72 | 140 | 96 | 48 | 45 | 70 | 199 | 58 | 84 | 131 | 163 | 54 | 157 |
| 246 | 14 | 241 | 188 | 170 | 167 | 108 | 154 | 60 | 101 | 55 | 94 | 180 | 93 | 122 | 8 |
| 91 | 29 | 176 | 120 | 41 | 114 | 51 | 102 | 30 | 175 | 53 | 233 | 204 | 187 | 202 | 74 |
| 21 | 121 | 179 | 116 | 12 | 192 | 119 | 104 | 148 | 177 | 229 | 155 | 98 | 134 | 169 | 107 |
| 150 | 31 | 11 | 129 | 156 | 143 | 106 | 35 | 203 | 105 | 158 | 225 | 110 | 165 | 24 | 239 |
| 42 | 146 | 138 | 168 | 251 | 118 | 68 | 28 | 132 | 139 | 184 | 232 | 19 | 37 | 219 | 97 |
| - | - | - | ||||
| 106 | 100 | 104 | ||||
| 108 | 103 | 105.5 | ||||
| 110 | 98 | 104 | ||||
| - | - | |||||
| 0.625 | 0.4218 | 0.502 | 0.044 | |||
| 0.625 | 0.421 | 0.502 | 0.015 | |||
| 0.421 | 0.422 | 0.502 | 0.021 | |||
| - | - | - | ||||
| 95 | 105.2 | 0.903 | ||||
| 110 | 103.2 | 3.216 | ||||
| 94 | 104.2 | 2.252 | ||||
| - | - | - | ||||
| 0.474 | 0.502 | 0.0132 | ||||
| 0.480 | 0.503 | 0.0142 | ||||
| 0.472 | 0.500 | 0.0139 | ||||
| - | - | - | - | |||
| 0.0340 | ||||||
| 0.0312 | ||||||
| 0.0457 | ||||||
| - | - | - | - | |||
| 158 | 0.070 | |||||
| 150 | 0.013 | |||||
| 158 | 0.012 |
| 112.0 | 0.5058 | 112.0 | 0.016 | 0.062 | |
| 112.0 | 0.4987 | 112.0 | 0.016 | 0.062 | |
| 112.0 | 0.5058 | 112.0 | 0.016 | 0.062 | |
| 105.7 | 0.4980 | 104.1 | 0.047 | 0.109 | |
| 105.0 | 0.5048 | 103.7 | 0.047 | 0.156 | |
| 99.5 | 0.5012 | 101.7 | 0.281 | 0.132 | |
| [18] | 103.3 | 0.5000 | 104.0 | 0.047 | 0.133 |
| [19] | 105.5 | 0.4990 | 106.0 | 0.125 | 0.133 |
| [20] | 106.5 | 0.4950 | 103.8 | 0.039 | 0.141 |
| [21] | 104.5 | 0.4980 | 104.6 | 0.047 | 0.125 |
| [22] | 105.5 | 0.5000 | 103.8 | 0.047 | 0.125 |
| [23] | 111.75 | 0.4978 | 103.86 | 0.039 | 0.125 |
| [24] | 107 | 0.493 | 102.3 | 0.047 | 0.141 |
| S-box 1 | 104.0 | 0.4940 | 105.2 | 0.032 | 0.016 |
| S-box 2 | 105.5 | 0.5020 | 103.2 | 0.031 | 0.013 |
| S-box 3 | 104.0 | 0.5020 | 104.2 | 0.032 | 0.012 |
| 7.9994 | 7.9995 | 7.9994 | 7.9994 | ||
| 7.9995 | 7.9989 | 7.9995 | 7.9993 | ||
| 7.9988 | 7.9991 | 7.9988 | 7.9989 | ||
| 7.9991 | 7.9990 | 7.9990 | 7.9990 | ||
| 7.9992 | 7.9992 | 7.9988 | 7.9990 | ||
| [26] | Lena | 7.99614 | 7.99408 | 7.99686 | 7.99569 |
| [27] | Lena | 7.99730 | 7.99690 | 7.99710 | 7.99710 |
| [28] | Lena | - | - | - | 7.9975 |
| [29] | Baboon | - | - | - | 7.9994 |
| Difference Rates % | |||||
|---|---|---|---|---|---|
| Secret Keys | |||||
| 0.9988 | 0.99725 | 0.99642 | 0.9988 | 0.99732 | |
| 0.99650 | 0.99762 | 0.99821 | 0.9987 | 0.99832 | |
| 0.99675 | 0.99870 | 0.99745 | 0.99815 | 0.99854 | |
| 0.99790 | 0.99833 | 0.99644 | 0.99647 | 0.99823 | |
| Images | Planes | Horizontal | Vertical | Diagonal | |||
|---|---|---|---|---|---|---|---|
| Original | Encrypted | Original | Encrypted | Original | Encrypted | ||
| 0.9595 | 0.0020 | 0.94499 | 0.00013 | 0.9272 | 0.00076 | ||
| 0.9460 | −0.0005 | 0.9674 | −0.00102 | 0.94136 | 0.00006 | ||
| 0.8956 | −0.00012 | 0.9306 | 0.00050 | 0.9164 | −0.00864 | ||
| 0.9049 | 0.00019 | 0.9612 | −0.00058 | 0.9707 | 0.00062 | ||
| 0.9275 | −0.00002 | 0.9585 | −0.000001 | 0.9491 | −0.0008 | ||
| 0.9260 | 0.00021 | 0.9639 | 0.00006 | 0.9590 | 0.00084 | ||
| 0.8977 | −0.00632 | 0.9432 | 0.000072 | 0.9349 | 0.000032 | ||
| 0.9432 | −0.0052 | 0.9580 | 0.000043 | 0.9671 | 0.00005 | ||
| 0.8821 | 0.00076 | 0.9731 | 0.00801 | 0.9542 | 0.00046 | ||
| 0.8769 | 0.000423 | 0.9565 | 0.000034 | 0.9829 | −0.00005 | ||
| 0.8672 | −0.00002 | 0.9587 | −0.000235 | 0.9764 | −0.00156 | ||
| 0.7949 | 0.000034 | 0.9656 | 0.00003 | 0.9771 | 0.00007 | ||
| 0.9179 | −0.00124 | 0.9810 | 0.000004 | 0.9278 | 0.00058 | ||
| 0.9331 | 0.000047 | 0.9732 | −0.000546 | 0.9652 | 0.00008 | ||
| 0.9650 | −0.000032 | 0.9842 | 0.000065 | 0.9277 | −0.0006 |
| Average | |||||
|---|---|---|---|---|---|
| SSIM | 0.0025 | 0.00210 | 0.00156 | 0.00205 | |
| Proposed | PSNR | 7.85725 | 8.47890 | 7.34291 | 7.67567 |
| MSE | 1.2550012 × 104 | 8.9564245 × 103 | 1.3356792 × 104 | 1.165969 × 104 | |
| SSIM | - | - | - | 0.0078 | |
| [28] | PSNR | - | - | - | 8.5537 |
| MSE | - | - | - | 9.1434 × 103 |
| Images | NPCR | UACI | |||||
|---|---|---|---|---|---|---|---|
| R | G | B | R | G | B | ||
| 0.99657 | 0.99884 | 0.99785 | 0.33012 | 0.33232 | 0.33056 | ||
| 0.99899 | 0.99983 | 0.99889 | 0.33015 | 0.33143 | 0.33543 | ||
| Proposed | 0.99912 | 0.99901 | 0.99943 | 0.33320 | 0.33732 | 0.32271 | |
| 0.99653 | 0.99926 | 0.99748 | 0.31543 | 0.32453 | 0.3301 | ||
| 0.99677 | 0.99596 | 0.99890 | 0.3300 | 0.32893 | 0.33023 | ||
| [26] | Lena | 0.996429 | 0.995956 | 0.995285 | 0.327633 | 0.300491 | 0.275669 |
| [27] | Lena | 0.9960 | 0.9961 | 0.9961 | 0.3356 | 0.3345 | 0.3349 |
| Test | p-Values for Color Encryptions of Ciphered Image | Results | |||
|---|---|---|---|---|---|
| Red | Green | Blue | |||
| 0.45097 | 0.50156 | 0.14563 | |||
| 0.88452 | 0.77680 | 0.50652 | |||
| 0.29191 | 0.29191 | 0.29191 | |||
| 0.90799 | 0.48637 | 0.43652 | |||
| 0.71270 | 0.71270 | 0.71270 | |||
| 0.80798 | 0.85898 | 0.81567 | |||
| 1.00000 | 0.55782 | 0.98932 | |||
| 0.88464 | 0.51806 | 0.11399 | |||
| 0.01672 | 0.24941 | 0.72703 | |||
| 0.99315 | 0.99563 | 0.99143 | |||
| 0.02576 | 0.88574 | 0.04186 | |||
| 0.00041 | 0.80981 | 0.45622 | |||
| 0.23652 | 0.23440 | 0.18932 | |||
| 1.58850 | 0.61835 | 0.09270 | |||
| 0.54297 | 0.02608 | 0.21236 | |||
| 0.45415 | 0.42343 | 0.50684 | |||
| 0.54882 | 0.26033 | 0.64829 | |||
| 0.95535 | 0.44549 | 0.17235 | |||
| 0.67870 | 0.92004 | 0.12441 | |||
| 0.09174 | 0.03408 | 0.38548 | |||
| 3.1754 × 10−8 | 0.03260 | 0.29277 | |||
| 0.11988 | 0.40938 | 0.54159 | |||
| 0.01036 | 0.01305 | 0.78574 | |||
| 0.38132 | 0.85558 | 0.31266 | |||
| 0.04636 | 0.91425 | 0.21878 | |||
| 0.030754 | 0.94459 | 0.2763 | |||
| 0.33466 | 0.95200 | 0.20873 | |||
| 0.59873 | 0.63013 | 0.81366 | |||
| 0.59873 | 0.65143 | 0.75084 | |||
| 1.00000 | 0.46734 | 0.94398 | |||
| 0.83989 | 0.37493 | 0.92901 | |||
| 0.69946 | 0.38827 | 0.79341 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Malik, D.S.; Shah, T.; Tehsin, S.; Nasir, I.M.; Fitriyani, N.L.; Syafrudin, M. Block Cipher Nonlinear Component Generation via Hybrid Pseudo-Random Binary Sequence for Image Encryption. Mathematics 2024, 12, 2302. https://doi.org/10.3390/math12152302
Malik DS, Shah T, Tehsin S, Nasir IM, Fitriyani NL, Syafrudin M. Block Cipher Nonlinear Component Generation via Hybrid Pseudo-Random Binary Sequence for Image Encryption. Mathematics. 2024; 12(15):2302. https://doi.org/10.3390/math12152302
Chicago/Turabian StyleMalik, Dania Saleem, Tariq Shah, Sara Tehsin, Inzamam Mashood Nasir, Norma Latif Fitriyani, and Muhammad Syafrudin. 2024. "Block Cipher Nonlinear Component Generation via Hybrid Pseudo-Random Binary Sequence for Image Encryption" Mathematics 12, no. 15: 2302. https://doi.org/10.3390/math12152302
APA StyleMalik, D. S., Shah, T., Tehsin, S., Nasir, I. M., Fitriyani, N. L., & Syafrudin, M. (2024). Block Cipher Nonlinear Component Generation via Hybrid Pseudo-Random Binary Sequence for Image Encryption. Mathematics, 12(15), 2302. https://doi.org/10.3390/math12152302








