Physical Layer Encryption for CO-OFDM Systems Enabled by Camera Projection Scrambler
Abstract
1. Introduction
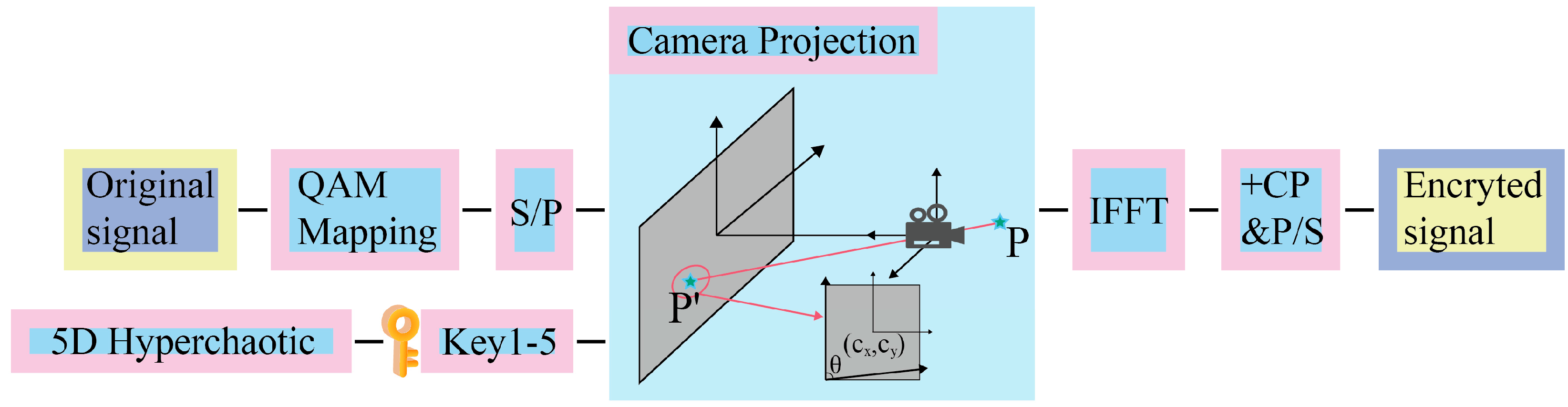
2. Proposed Algorithm
2.1. Camera Skewed Projection
2.2. Key Generation and Processing
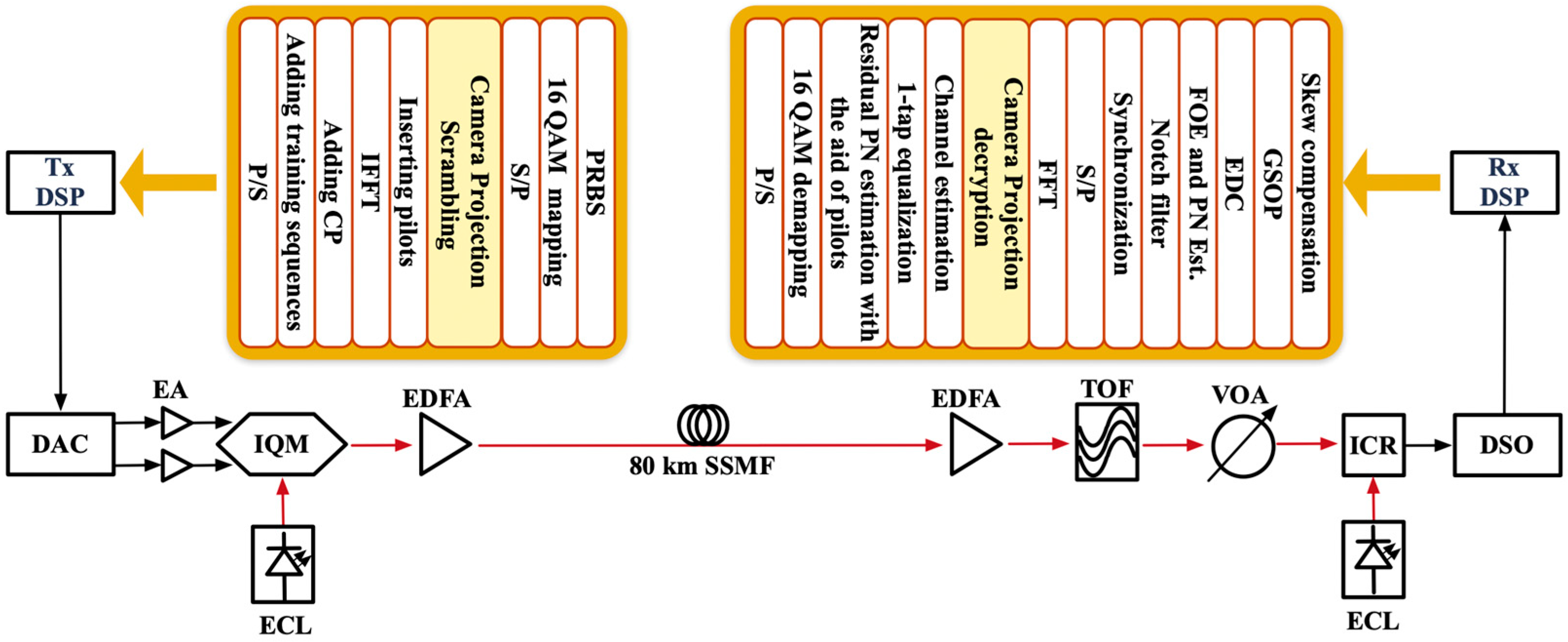
3. Simulation Experiments and Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- William, S.; Djordjevic, I.B. OFDM for Optical Communications; Academic Press: Cambridge, MA, USA, 2009. [Google Scholar]
- Chandrasekhar, S.; Liu, x. Ofdm Based Superchannel Transmission Technology. J. Light. Technol. 2012, 30, 3816–3823. [Google Scholar] [CrossRef]
- Wang, D.; Tang, X.; Xi, L.; Zhang, X.; Zhang, W.; Zhang, H. A scheme to generate 16QAM-OFDM vector mm-wave signal based on a single MZM without optical filter and precoding. Opt. Commun. 2020, 475, 126227. [Google Scholar] [CrossRef]
- Agrawal, G.P. Fiber-Optic Communication Systems; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Agrell, E.; Karlsson, M.; Chraplyvy, A.R.; Richardson, D.J.; Krummrich, P.M.; Winzer, P.; Roberts, K.; Fischer, J.K.; Savory, S.J.; Eggleton, B.J.; et al. Roadmap of optical communications. J. Opt. 2016, 18, 063002. [Google Scholar] [CrossRef]
- Mitev, M.; Pham, T.M.; Chorti, A.; Barreto, A.N.; Fettweis, G. Physical layer security-from theory to practice. IEEE BITS Inf. Theory Mag. 2023, 1–12. [Google Scholar] [CrossRef]
- Zhang, G.; Zhao, Z.; Dai, J.; Yang, S.; Fu, X.; Yang, L. Polarization-Based Quantum Key Distribution Encoder and Decoder on Silicon Photonics. J. Light. Technol. 2022, 40, 2052–2059. [Google Scholar] [CrossRef]
- Su, G.; Pu, T.; Zheng, J.; Tan, Y. Performance Analysis of Multi-User Optical Steganography Transmission System Based on Filtered Amplified Spontaneous Emission Noise. IEEE Access 2019, 7, 170733–170741. [Google Scholar] [CrossRef]
- Ghafouri-Shiraz, H.; Karbassian, M.M. Optical Cdma Networks: Principles, Analysis and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Lu, Y.; Wang, H.; Ji, Y. A Time-Delay Signature Elimination and Broadband Electro-Optic Chaotic System with Enhanced Nonlinearity by Deep Learning. Opt. Express 2022, 30, 17698–17712. [Google Scholar] [CrossRef] [PubMed]
- Lu, Y.; Wang, H.; Ji, Y.; Zhang, Y. Security-enhanced electro-optic chaotic communication system based on the logistic map feedback and dynamic key. J. Opt. Soc. Am. B 2023, 40, 1131–1140. [Google Scholar] [CrossRef]
- Tang, B.; Gao, X.; Su, B.; An, Y.; Wang, A.; Wang, Y.; Qin, Y.; Gao, Z. Time-delay signature concealment in a security-enhanced optical system with dual-loop electro-optic self-feedback phase encryption. IEEE Photon-J. 2023, 15, 7200508. [Google Scholar] [CrossRef]
- Bai, J.; Wang, H.; Ji, Y. Time-delay signature concealing electro-optic chaotic system with multiply feedback nonlinear loops. Opt. Express 2021, 29, 706–718. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, W.; Chen, C.; He, X.; Qiu, K. Physical-Enhanced Secure Strategy for Ofdma-Pon Using Chaos and Deoxyribonucleic Acid Encoding. J. Light. Technol. 2018, 36, 1706–1712. [Google Scholar] [CrossRef]
- Liang, X.; Zhang, C.; Luo, Y.; Wang, X.; Qiu, K. Secure Encryption and Key Management for OFDM-PON Based on Chaotic Hilbert Motion. J. Light. Technol. 2023, 41, 1619–1625. [Google Scholar] [CrossRef]
- Bai, Y.; Liu, B.; Ren, J.; Mao, Y.; Qi, Z.; Chen, S.; Song, X.; Zhu, S.; Yuan, L.; Han, S.; et al. Highly Secure and Reliable 7-Core Fiber Optical OFDM Access System Based on Chaos Encryption Inside Polar Code. IEEE Photon-J. 2022, 14, 7200506. [Google Scholar] [CrossRef]
- Tang, X.; Xu, Z.; Gao, C.; Xiao, Y.; Liu, L.; Zhang, X.; Xi, L.; Xu, H.; Bai, C. Physical layer encryption for coherent PDM system based on polarization perturbations using a digital optical polarization scrambler. Opt. Express 2023, 31, 26791–26806. [Google Scholar] [CrossRef] [PubMed]
- Weng, Z.; Ren, J.; Bo, L.; Mao, Y.; Wu, X.; Song, X.; Chen, S.; Ma, Y.; Zhao, N.; Yu, Y.; et al. A physical layer security scheme for key concealment and distribution based on carrier scrambling. Opt. Express 2024, 32, 15053–15064. [Google Scholar] [CrossRef]
- Zha, Y.; Ren, J.; Liu, B.; Mao, Y.; Wu, X.; Ullah, R.; Song, X.; Chen, S.; Ma, Y.; Wang, F.; et al. Chaos key enhanced physical layer secure transmission method based on the convolutional long short-term memory neural network. Opt. Express 2024, 32, 20515–20527. [Google Scholar] [CrossRef]
- Zhang, Y.; Jiang, N.; Zhao, A.; Liu, S.; Peng, J.; Chen, L.; Lavery, M.P.J.; Abbas, H.T.; Qiu, K. Security enhancement in coherent OFDM optical transmission with chaotic three-dimensional constellation scrambling. J. Light. Technol. 2022, 40, 3749–3760. [Google Scholar] [CrossRef]
- Liu, L.; Tang, X.; Li, F.; Xu, Z.; Zhang, X. Enhanced physical layer security and PAPR performance based on disturbance of data cluster under chaotic sequence color seeking mechanism in CO-OFDM system. J. Light. Technol. 2023, 41, 6507–6513. [Google Scholar] [CrossRef]
- Huang, X.; Zhang, L.; Hu, W.; Turkiewicz, J.P.; Leitgeb, E.; Yang, X. Secure OFDM-PON Using Chaotic Constellation Mapping and Probabilistic Shaping. IEEE Photon-Technol. Lett. 2021, 33, 1139–1142. [Google Scholar] [CrossRef]
- Zeng, W.; Zhang, C.; Liang, X.; Luo, Y.; Wang, X.; Qiu, K. Chaotic phase noise-like encryption based on geometric shaping for coherent data center interconnections. Optics Express 2024, 32, 1595–1608. [Google Scholar] [CrossRef]
- Wu, Y.; Yu, Y.; Hu, Y.; Sun, Y.; Wang, T.; Zhang, Q. Channel-based dynamic key generation for physical layer security in OFDM-PON systems. IEEE Photon-J. 2021, 13, 7900209. [Google Scholar] [CrossRef]
- Yang, Q.; Bai, M. A New 5D Hyperchaotic System Based on Modified Generalized Lorenz System. Nonlinear Dyn. 2016, 88, 189–221. [Google Scholar] [CrossRef]
- Savory, S.J. Digital coherent optical receivers: Algorithms and subsystems. IEEE J. Sel. Top. Quantum Electron. 2010, 16, 1164–1179. [Google Scholar] [CrossRef]
- Chung, H.S.; Chang, S.H.; Kim, K. Effect of IQ mismatch compensation in an optical coherent OFDM receiver. IEEE Photon-Technol. Lett. 2010, 22, 308–310. [Google Scholar] [CrossRef]
- Jansen, S.L.; Morita, I.; Schenk, T.C.W.; Takeda, N.; Tanaka, H. Coherent optical 25.8-Gb/s OFDM transmission over 4160-km SSMF. J. Light. Technol. 2008, 26, 6–15. [Google Scholar] [CrossRef]
- Li, F.; Zou, D.; Ding, L.; Sun, Y.; Li, J.; Sui, Q.; Li, L.; Yi, X.; Li, Z. 100 Gbit/s PAM4 signal transmission and reception for 2-km interconnect with adaptive notch filter for narrowband interference. Opt. Express 2018, 26, 24066–24074. [Google Scholar] [CrossRef]
- Nguyen, T.-H.; Bramerie, L.; Gay, M.; Kazdoghli-Lagha, M.; Peucheret, C.; Gerzaguet, R.; Gorza, S.P.; Louveaux, J.; Horlin, F. Experimental demonstration of the tradeoff between chromatic dispersion and phase noise compensation in optical FBMC/OQAM communication systems. J. Light. Technol. 2019, 37, 4340–4348. [Google Scholar] [CrossRef]




| Schemes | Key Space |
|---|---|
| DNA encoding [14] | 2.25 × 1089 |
| Digital optical polarization scrambling [17] | 1060 |
| Key concealment and distribution based on carrier scrambling [18] | 1082 |
| Chaos key enhanced based on the convolutional long short-term memory neural network [19] | 10241 |
| The proposed scheme | 9 × 1090 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Wang, D.; Ding, H.; Li, Z.; Wang, X. Physical Layer Encryption for CO-OFDM Systems Enabled by Camera Projection Scrambler. Mathematics 2024, 12, 1807. https://doi.org/10.3390/math12121807
Li Y, Wang D, Ding H, Li Z, Wang X. Physical Layer Encryption for CO-OFDM Systems Enabled by Camera Projection Scrambler. Mathematics. 2024; 12(12):1807. https://doi.org/10.3390/math12121807
Chicago/Turabian StyleLi, Yujin, Dongfei Wang, Haiyang Ding, Zhenzhen Li, and Xiangqing Wang. 2024. "Physical Layer Encryption for CO-OFDM Systems Enabled by Camera Projection Scrambler" Mathematics 12, no. 12: 1807. https://doi.org/10.3390/math12121807
APA StyleLi, Y., Wang, D., Ding, H., Li, Z., & Wang, X. (2024). Physical Layer Encryption for CO-OFDM Systems Enabled by Camera Projection Scrambler. Mathematics, 12(12), 1807. https://doi.org/10.3390/math12121807






